Odisha State Board BSE Odisha 10th Class History Important Questions Chapter 17 ଶିକ୍ଷାର ବିକାଶ Important Questions and Answers.
BSE Odisha Class 10 History Important Questions Chapter 17 ଶିକ୍ଷାର ବିକାଶ
Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୬୦ ଗୋଟି ଶବ୍ଦରେ ଲେଖ ।
୧। ମାଧ୍ୟମିକ ଶିକ୍ଷା କାହାକୁ କୁହାଯାଉଥିଲା ? ସ୍ଵାଧୀନତା ବେଳକୁ ଆମ ରାଜ୍ୟରେ ଏହାର ସ୍ଥିତି କିପରି ଥିଲା ?
Answer:
- ଷଷ୍ଠ ଶ୍ରେଣୀଠାରୁ ଏକାଦଶ ଶ୍ରେଣୀ ପର୍ଯ୍ୟନ୍ତ ଶିକ୍ଷାକୁ ମାଧ୍ୟମିକ ଶିକ୍ଷା କୁହାଯାଉଥିଲା ।
- ଷଷ୍ଠ ଓ ସପ୍ତମ ଶ୍ରେଣୀକୁ ମଧ୍ୟ ଇଂରାଜୀ ବିଦ୍ୟାଳୟର ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଉଥିଲା ଓ ଅଷ୍ଟମଠାରୁ ଏକାଦଶ ପର୍ଯ୍ୟନ୍ତ ଚାରିବର୍ଷର ଶିକ୍ଷାକୁ ଉଚ୍ଚ ମାଧ୍ୟମିକ ଶିକ୍ଷା ବା ହାଇସ୍କୁଲ ଶିକ୍ଷା କୁହାଯାଉଥିଲା ।
- ୧୯୫୦ ମସିହାବେଳକୁ ଓଡ଼ିଶାରେ ମଧ୍ୟ ଇଂରାଜୀ ବିଦ୍ୟାଳୟ ସଂଖ୍ୟା ଥିଲା ୪୮୯ ଓ ଏଥିରେ ୪୬, ୨୧୭ ଜଣ ଛାତ୍ରଛାତ୍ରୀ ଅଧ୍ୟୟନ କରୁଥିଲେ ।
- ସେହି ସମୟରେ ହାଇସ୍କୁଲ ସଂଖ୍ୟା ୧୫୩ ଥିଲା ଓ ସେଥିରେ ୪୩,୮୯୩ ଜଣ ଛାତ୍ରଛାତ୍ରୀ ଅଧ୍ୟୟନ କରୁଥିଲେ । ପରେ ବିଦ୍ୟାଳୟ ସଂଖ୍ୟା ବୃଦ୍ଧିପ୍ରାପ୍ତ ହେଲା ।
- ହାଇସ୍କୁଲ ପରୀକ୍ଷା ପରିଚାଳନା ପାଇଁ ୧୯୫୩ ମସିହାରେ ମାଧ୍ୟମିକ ଶିକ୍ଷା ପରିଷଦ ଗଠିତ ହେଲା ।
୨। ଓଡ଼ିଶାରେ ପ୍ରାଥମିକ ଶିକ୍ଷାକୁ ସାର୍ବଜନୀନ କରିବାପାଇଁ କ’ଣ ସବୁ ନୂତନ ବ୍ୟବସ୍ଥାମାନ ଗ୍ରହଣ କରାଯାଇଛି ?
Answer:
- ପ୍ରାଥମିକ ଶିକ୍ଷାକୁ ସାର୍ବଜନୀନ କରିବାକୁ ଅଧ୍ଵରୁ ଅଧିକ ପିଲାଙ୍କ ନାମଲେଖା ଉପରେ ଗୁରୁତ୍ବ ଦିଆଯାଇଛି ।
- ୧୪ ବର୍ଷ ବୟସ ପର୍ଯ୍ୟନ୍ତ ଶିଶୁ ଓ କିଶୋରମାନେ ଯେପରି ବିଦ୍ୟାଳୟ ଛାଡ଼ି ନଯିବେ ସେଥିପାଇଁ ବିହିତ ବ୍ୟବସ୍ଥା ଗ୍ରହଣ କରାଯାଇଛି ।
- ଶିକ୍ଷାର ଗୁଣବତ୍ତା ବୃଦ୍ଧି ପାଇଁ ଉଦ୍ୟମ କରାଯାଇଛି ।
- ଶିଶୁମାନଙ୍କୁ ବିଦ୍ୟାଳୟ ପ୍ରତି ଆକୃଷ୍ଟ କରିବାପାଇଁ ୧୯୯୫ ମସିହାଠାରୁ ସରକାର ବିଦ୍ୟାଳୟରେ ମଧ୍ୟାହ୍ନ ଭୋଜନର ବ୍ୟବସ୍ଥା କରିଛନ୍ତି ।
- କେନ୍ଦ୍ର ସରକାରଙ୍କ ସହାୟତାରେ ‘ଜିଲ୍ଲା ପ୍ରାଥମିକ ଶିକ୍ଷା ଯୋଜନା’ ୧୯୯୬ ମସିହାଠାରୁ ଓଡ଼ିଶାରେ କାର୍ଯ୍ୟକାରୀ ହୋଇଛି ।
୩ । ରାଷ୍ଟ୍ରୀୟ ମାଧ୍ୟମିକ ଶିକ୍ଷା ଅଭିଯାନ (RMSA)ର ଉଦ୍ଦେଶ୍ୟଗୁଡ଼ିକ ଲେଖ ।
Answer:
ରାଷ୍ଟ୍ରୀୟ ମାଧ୍ୟମିକ ଶିକ୍ଷା ଅଭିଯାନର ନିମ୍ନଲିଖିତ ଉଦ୍ଦେଶ୍ୟଗୁଡ଼ିକ ରହିଛି; ଯଥା –
- ଘରଠାରୁ ୫ କି.ମି. ମଧ୍ଯରେ ମାଧ୍ୟମିକ ଶିକ୍ଷା ଓ ୭ରୁ ୧୦ କି.ମି. ମଧ୍ଯରେ ଉଚ୍ଚ ମାଧ୍ୟମିକ ଶିକ୍ଷା ଉପଲବ୍ଧ କରିବାପାଇଁ ସୁଯୋଗ ପ୍ରଦାନ ।
- ଆଗାମୀ ୫ ବର୍ଷ ମଧ୍ୟରେ ମୋଟାମୋଟି ନାମଲେଖା ଅନୁପାତକୁ ୭୫ ପ୍ରତିଶତ ବୃଦ୍ଧି କରିବା ।
- ୨୦୧୭ ମସିହା ସୁଦ୍ଧା ସମସ୍ତଙ୍କୁ ମାଧ୍ୟମିକ ଶିକ୍ଷା ଉପଲବ୍ଧ କରାଇବା ।
- ସବୁ ପିଲାଙ୍କୁ ବିଦ୍ୟାଳୟ ତ୍ୟାଗ କରିବାରୁ ନିବୃତ୍ତ କରିବା ।
- ଅସୁବିଧାରେ ରହୁଥିବା ଗୋଷ୍ଠୀର ପିଲାମାନଙ୍କୁ ମାଧ୍ୟମିକ ଶିକ୍ଷା ଉପଲବ୍ଧ କରାଇବା ଓ ଶିକ୍ଷାର ଗୁଣବତ୍ତା ବୃଦ୍ଧି କରିବା ।

କ୍ଷୁଦ୍ର ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୩୦ ଗୋଟି ଶବ୍ଦରେ ଲେଖ ।
୧। ଓଡ଼ିଶା ପାଇଁ ରେଭେନ୍ସା ମହାବିଦ୍ୟାଳୟର ଗୁରୁତ୍ଵ କ’ଣ ଥିଲା ?
Answer:
- ବିଂଶ ଶତାବ୍ଦୀର ୫ମ ଦଶନ୍ଧି ସୁଦ୍ଧା ଓଡ଼ିଶା ପାଇଁ ରେଭେନ୍ସା ମହାବିଦ୍ୟାଳୟ ଥିଲା ଉଚ୍ଚ ଶିକ୍ଷା କ୍ଷେତ୍ରରେ ଏକମାତ୍ର ଅନୁଷ୍ଠାନ ।
- ୧୯୫୦ ମସିହା ଆଗରୁ ରେଭେନ୍ସା ମହାବିଦ୍ୟାଳୟରେ ଡିଗ୍ରୀ ସ୍ତରରେ ବିଜ୍ଞାନ ଶିକ୍ଷା, ଇଂରାଜୀ, ଓଡ଼ିଆ, ଅର୍ଥନୀତି, ଗଣିତ ଓ ରସାୟନ ବିଜ୍ଞାନରେ ସ୍ନାତକୋତ୍ତର ଶିକ୍ଷାର ବ୍ୟବସ୍ଥା ହୋଇସାରିଥିଲା ।
- ଏବେ କଟକର ରେଭେନ୍ସା ମହାବିଦ୍ୟାଳୟକୁ ଏକକ ବିଶ୍ଵବିଦ୍ୟାଳୟରେ ରୂପାନ୍ତରିତ କରାଯାଇଛି ।
୨। ଏକବିଂଶ ଶତାବ୍ଦୀର ପ୍ରଥମ ଦଶକରେ ଘରୋଇ ଉଦ୍ୟମରେ ଆମ ରାଜ୍ୟର କେଉଁଠାରେ, କେଉଁସବୁ ମେଡ଼ିକାଲ କଲେଜ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ?
Answer:
- ଏକବିଂଶ ଶତାବ୍ଦୀର ପ୍ରଥମ ଦଶକରେ ଘରୋଇ ଉଦ୍ୟମରେ ତିନୋଟି ମେଡ଼ିକାଲ କଲେଜ ଭୁବନେଶ୍ୱରଠାରେ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
- ସେଗୁଡ଼ିକ ହେଲା – ହାଇଟେକ୍ ମେଡ଼ିକାଲ କଲେଜ, କଳିଙ୍ଗ ଇନ୍ଷ୍ଟିଚ୍ୟୁଟ୍ ଅଫ୍ ମେଡ଼ିକାଲ ସାଇନ୍ସ ଓ ହସ୍ପିଟାଲ ଏବଂ ସମହସ୍ପିଟାଲ ଓ ମେଡ଼ିକାଲ କଲେଜ ।
୩। ବାଳିକାମାନଙ୍କୁ ମାଧ୍ୟମିକ ଶିକ୍ଷା ପ୍ରତି ଆକର୍ଷିତ କରିବାପାଇଁ ସରକାରଙ୍କ ତରଫରୁ କେଉଁସବୁ ପଦକ୍ଷେପମାନ ନିଆଯାଇଛି ?
Answer:
- ବାଳିକାମାନଙ୍କୁ ମାଧ୍ୟମିକ ଶିକ୍ଷା ପ୍ରତି ଆକର୍ଷିତ କରିବାପାଇଁ କେନ୍ଦ୍ର ସରକାର ଓ ରାଜ୍ୟ ସରକାର ଅନେକ ପଦକ୍ଷେପ ଗ୍ରହଣ କରିଛନ୍ତି ।
- ଶିକ୍ଷାଦୃଷ୍ଟିରୁ ଅନଗ୍ରସର ଗୋଷ୍ଠୀ ଉନ୍ନୟନ ବ୍ଲକ୍ମାନଙ୍କରେ ଝିଅମାନଙ୍କ ପାଇଁ ଛାତ୍ରୀ ନିବାସ ନିର୍ମିତ ହୋଇଛି ।
- ଛାତ୍ରୀମାନଙ୍କୁ ଜାତୀୟ ପ୍ରୋତ୍ସାହନ ଯୋଜନା ମାଧ୍ୟମରେ ବିଦ୍ୟାଳୟ ଶିକ୍ଷାପ୍ରତି ଆକୃଷ୍ଟ କରାଯାଇଛି । ଶିକ୍ଷା ଦୃଷ୍ଟିରୁ ଅନଗ୍ରସର ବ୍ଲକଗୁଡ଼ିକରେ ସରକାର ମଡ଼େଲ ସ୍କୁଲ ପ୍ରତିଷ୍ଠା କରିଛନ୍ତି ।
୪। ଓଡ଼ିଶାର କେଉଁଠାରେ ଆଞ୍ଚଳିକ ଶିକ୍ଷା ପ୍ରତିଷ୍ଠାନ ଅବସ୍ଥିତ ? ଏହା ଅଧୀନରେ କେଉଁ ସ୍କୁଲ ଆଦର୍ଶ ବିଦ୍ୟାଳୟଭାବେ କାର୍ଯ୍ୟ କରୁଛି ? ଏହି ବିଦ୍ୟାଳୟଟି କାହାଦ୍ଵାରା ପରିଚାଳିତ ?
Answer:
- ଓଡ଼ିଶାର ଭୁବନେଶ୍ୱରଠାରେ ଆଞ୍ଚଳିକ ଶିକ୍ଷା ପ୍ରତିଷ୍ଠାନ ଅବସ୍ଥିତ ।
- ଏହା ଅଧୀନରେ ଡେମଷ୍ଟ୍ରେସନ୍ ମଲ୍ଟିପର୍ପସ୍ (ଡି.ଏମ୍.) ସ୍କୁଲ ଆଦର୍ଶ ବିଦ୍ୟାଳୟଭାବେ କାର୍ଯ୍ୟ କରୁଛି ।
- ଏହି ବିଦ୍ୟାଳୟଟି ଏନ୍.ସି.ଇ.ଆର୍.ଟି. ଦ୍ଵାରା ପରିଚାଳିତ ।
୫। ବ୍ୟାବସାୟିକ ପରିଚାଳନା ଶିକ୍ଷା ପାଇଁ ପ୍ରଥମେ କେଉଁଠାରେ କେଉଁ ଅନୁଷ୍ଠାନ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ? ସେଠାରେ କ’ଣ ଶିକ୍ଷା ପ୍ରଦାନ କରାଯାଉଛି ?
Answer:
- ବ୍ୟାବସାୟିକ ପରିଚାଳନା ଶିକ୍ଷା ପାଇଁ ପ୍ରଥମେ ଭୁବନେଶ୍ଵରରେ ସ୍ଵତନ୍ତ୍ର ଭାବରେ ଜାଭିଅର ଇନ୍ଷ୍ଟିଚ୍ୟୁଟ୍ ଅଫ୍ ମ୍ୟାନେଜମେଣ୍ଟ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।
- ପରବର୍ତୀ ସମୟରେ ଭୁବନେଶ୍ଵର ଓ ଓଡ଼ିଶାର ଅନ୍ୟାନ୍ୟ ସହରରେ ଅନେକ ବ୍ୟାବସାୟିକ ଶିକ୍ଷା ପ୍ରତିଷ୍ଠାନ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
- ସେଠାରେ ଛାତ୍ରଛାତ୍ରୀମାନଙ୍କୁ ଏମ୍.ବି.ଏ. ଶିକ୍ଷା ପ୍ରଦାନ କରାଯାଉଛି ।

ସଂଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୨୦ ଗୋଟି ଶବ୍ଦରେ ଲେଖ ।
୧। କେଉଁ ଶିକ୍ଷା ପଦ୍ଧତି ଗାନ୍ଧିଜୀଙ୍କର ସ୍ୱପ୍ନ ଥିଲା ? ଏଥିରେ କ’ଣ ବ୍ୟବସ୍ଥା ଥିଲା ?
Answer:
- ମୌଳିକ ଶିକ୍ଷା ପଦ୍ଧତି ଥିଲା ଗାନ୍ଧିଜୀଙ୍କର ସ୍ବପ୍ନ ।
- ଏହି ପଦ୍ଧତିରେ ଶିଶୁକୁ କର୍ମାଭିମୁଖୀ ଶିକ୍ଷା ପ୍ରଦାନ କରି ସ୍ଵାବଲମ୍ବୀ କରିବାର ବ୍ୟବସ୍ଥା ଥିଲା ।
୨। ୧୯୫୦ ମସିହାରେ ଓଡ଼ିଶାରେ ପ୍ରାଥମିକ ବିଦ୍ୟାଳୟର ସଂଖ୍ୟା କେତେ ଥିଲା ? ଏଥିରେ ଅଧ୍ୟୟନ କରୁଥିବା ଛାତ୍ରଛାତ୍ରୀଙ୍କ ସଂଖ୍ୟା କେତେ ଥିଲା ?
Answer:
- ୧୯୫୦ ମସିହାରେ ଓଡ଼ିଶାରେ ପ୍ରାଥମିକ ବିଦ୍ୟାଳୟର ସଂଖ୍ୟା ଥିଲା ୧୦, ୧୬୫ ।
- ଏଥରେ ଅଧ୍ୟୟନ କରୁଥିବା ଛାତ୍ରଛାତ୍ରୀମାନଙ୍କ ସଂଖ୍ୟା ଥିଲା ୪,୪୧, ୯୬୭ ।
୩। ଓଡ଼ିଶାର ସରକାରୀ ବିଦ୍ୟାଳୟମାନଙ୍କରେ କେବେ ଓ କାହିଁକି ମଧ୍ୟାହ୍ନ ଭୋଜନ ବ୍ୟବସ୍ଥା କରାଯାଇଛି ?
Answer:
- ୧୯୯୫ ମସିହାଠାରୁ ଓଡ଼ିଶାରେ ସରକାରୀ ବିଦ୍ୟାଳୟମାନଙ୍କରେ ମଧ୍ୟାହ୍ନ ଭୋଜନର ବ୍ୟବସ୍ଥା କରାଯାଇଛି ।
- ଶିଶୁମାନଙ୍କୁ ବିଦ୍ୟାଳୟ ପ୍ରତି ଆକୃଷ୍ଟ କରିବାପାଇଁ ଏହି ଯୋଜନା ପ୍ରବର୍ତ୍ତନ କରାଯାଇଛି ।
୪। ‘ସର୍ବଶିକ୍ଷା ଅଭିଯାନ’ ଯୋଜନା ମାଧ୍ୟମରେ କ’ଣ କରାଯାଇଛି ?
Answer:
- ‘ସର୍ବଶିକ୍ଷା ଅଭିଯାନ’ (SSA) ଯୋଜନା ମାଧ୍ୟମରେ ସମଗ୍ର ଓଡ଼ିଶାରେ ନୂତନ ବିଦ୍ୟାଳୟମାନ ଖୋଲାଯାଇଛି ।
- ପିଲାମାନଙ୍କୁ ମାଗଣାରେ ପାଠ୍ୟପୁସ୍ତକ ଯୋଗାଇଦେବାର ବ୍ୟବସ୍ଥା କରାଯାଇଛି ।
୫। “‘ସମସ୍ତ ଶିଶୁଙ୍କ ପାଖରେ ପ୍ରାଥମିକ ଶିକ୍ଷା ସୁବିଧାକୁ ପହଞ୍ଚାଇବା’’ କେଉଁ ଯୋଜନାର ଉଦ୍ଦେଶ୍ୟ ? ଏହା ଆମ ରାଜ୍ୟରେ କେବେ କାର୍ଯ୍ୟକାରୀ ହୋଇଛି ?
Answer:
- ‘ସମସ୍ତ ଶିଶୁଙ୍କ ପାଖରେ ପ୍ରାଥମିକ ଶିକ୍ଷା ସୁବିଧାକୁ ପହଞ୍ଚାଇବା ଜିଲ୍ଲା ପ୍ରାଥମିକ ଶିକ୍ଷା ଯୋଜନା’’ (DPEP)ର ଉଦ୍ଦେଶ୍ୟ ।
- ଏହା ୧୯୯୬ ମସିହାଠାରୁ ଓଡ଼ିଶାରେ କାର୍ଯ୍ୟକାରୀ ହୋଇଛି ।

୬। ‘‘ରାଷ୍ଟ୍ରୀୟ ମାଧ୍ୟମିକ ଶିକ୍ଷା ଅଭିଯାନ’’ କ’ଣ ?
Answer:
- ୨୦୦୯-୧୦ ଶିକ୍ଷାବର୍ଷଠାରୁ କେନ୍ଦ୍ର ସରକାର ‘ରାଷ୍ଟ୍ରୀୟ ମାଧ୍ୟମିକ ଶିକ୍ଷା ଅଭିଯାନ’ (RMSA) ନାମକ ଏକ ବହୁମୁଖୀ ଶିକ୍ଷା ଯୋଜନାର ଶୁଭାରମ୍ଭ ହୋଇଛି ।
- ଉତ୍ତମ ଗୁଣବତ୍ତାଭିଭିକ ଶିକ୍ଷାଦାନ ଏହି ଅଭିଯାନର ମୂଳ ଲକ୍ଷ୍ୟ ।
୭। ଓଡ଼ିଶାରେ କେଉଁଠାରେ ଆଞ୍ଚଳିକ ଗବେଷଣା ପରୀକ୍ଷାଗାର ପ୍ରତିଷ୍ଠିତ ହୋଇଛି ? କେଉଁ କ୍ଷେତ୍ରରେ କାର୍ଯ୍ୟ କରେ ?
Answer:
- ଓଡ଼ିଶାରେ କେଉଁଠାରେ ଆଞ୍ଚଳିକ ଗବେଷଣା ପରୀକ୍ଷାଗାର ପ୍ରତିଷ୍ଠିତ ହୋଇଛି
- ଏହା ଖଣିଜ ଓ ଧାତବ ପଦାର୍ଥ ଗବେଷଣା କ୍ଷେତ୍ରରେ କାର୍ଯ୍ୟ କରୁଛି ।
୮। ୧୯୫୦ ମସିହାବେଳକୁ ଓଡ଼ିଶାରେ ସର୍ବମୋଟ ମହାବିଦ୍ୟାଳୟ ସଂଖ୍ୟା କେତେ ଥିଲା ? ସେଥିରେ କେତେ ଛାତ୍ରଛାତ୍ରୀ ଅଧ୍ୟୟନ କରୁଥିଲେ ?
Answer:
- ୧୯୫୦ ମସିହାବେଳକୁ ଓଡ଼ିଶାର ସର୍ବମୋଟ ମହାବିଦ୍ୟାଳୟ ସଂଖ୍ୟା ଥିଲା ୧୪।
- ସେଥିରେ ୫୬୮୯ ଛାତ୍ରଛାତ୍ରୀ ଅଧ୍ୟୟନ କରୁଥିଲେ ।
୯। ୧୯୬୭ ଓ ୧୯୮୧ ମସିହାରେ କେଉଁ ସ୍ଥାନମାନଙ୍କରେ ବିଶ୍ଵବିଦ୍ୟାଳୟମାନ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ?
Answer:
- ୧୯୬୭ ମସିହାରେ ସମ୍ବଲପୁର ଓ ବ୍ରହ୍ମପୁରଠାରେ ବିଶ୍ୱବିଦ୍ୟାଳୟମାନ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।
- ୧୯୮୧ ମସିହାରେ ପୁରୀଠାରେ ଶ୍ରୀଜଗନ୍ନାଥ ସଂସ୍କୃତ ବିଶ୍ୱବିଦ୍ୟାଳୟ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।
୧୦। ରାଧାନାଥ ପ୍ରଶିକ୍ଷଣ ମହାବିଦ୍ୟାଳୟ କେଉଁଠାରେ ଅବସ୍ଥିତ ? ବର୍ତ୍ତମାନ ଏହାର ନୂତନ ନାମ କ’ଣ ରଖାଯାଇଛି ?
Answer:
- ରାଧାନାଥ ପ୍ରଶିକ୍ଷଣ ମହାବିଦ୍ୟାଳୟ କଟକରେ ଅବସ୍ଥିତ ।
- ବର୍ତ୍ତମାନ ଏହାର ନୂତନ ନାମ ରଖାଯାଇଛି ‘ଇନ୍ଷ୍ଟିଚ୍ୟୁଟ୍ ଅଫ୍ ଆଡ଼ଭାନ୍ସଡ୍ ଷ୍ଟଡ଼ିଜ୍ ଇନ୍ ଏଡୁକେସନ୍’ (R.N.I.A.S.E.) ।

ପରୀକ୍ଷା ଉପଯୋଗୀ ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତର
Objective Type Questions With Answers
A. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ ।
1. ମୌଳିକ ଶିକ୍ଷାକୁ କାର୍ଯ୍ୟକାରୀ କରିବାପାଇଁ କେଉଁଠାରେ ଦୁଇଟି ପ୍ରଶିକ୍ଷଣ ବିଦ୍ୟାଳୟ ଖୋଲାଯାଇଥିଲା ?
Answer:
୧୯୪୭-୪୮ ଶିକ୍ଷାବର୍ଷରେ ରାଜ୍ୟ ସରକାର ମୌଳିକ ଶିକ୍ଷା ବ୍ୟବସ୍ଥା କାର୍ଯ୍ୟକାରୀ କରିବାପାଇଁ ଅନୁଗୁଳ ଓ ରସୁଲକୋଣ୍ଡାଠାରେ ଦୁଇଟି ଶିକ୍ଷକ ପ୍ରଶିକ୍ଷଣ ବିଦ୍ୟାଳୟ ଖୋଲିଥିଲେ ।
2. ମାଧ୍ୟମିକ ଶିକ୍ଷା କାହାକୁ କୁହାଯାଉଥିଲା ?
Answer:
ଷଷ୍ଠ ଶ୍ରେଣୀଠାରୁ ଏକାଦଶ ଶ୍ରେଣୀ ପର୍ଯ୍ୟନ୍ତ ଶିକ୍ଷାକୁ ମାଧ୍ୟମିକ ଶିକ୍ଷା କୁହାଯାଉଥିଲା ।
3. ଓଡ଼ିଶା ମାଧ୍ୟମିକ ଶିକ୍ଷା ପରିଷଦ କେବେ ଗଠିତ ହୋଇଥିଲା ?
Answer:
ଓଡ଼ିଶା ହାଇସ୍କୁଲ ସାର୍ଟିଫିକେଟ୍ ପରୀକ୍ଷା ପରିଚାଳନା ପାଇଁ ଓଡ଼ିଶା ସେକେଣ୍ଡାରୀ ଏଜୁକେଶନ ଆକ୍ଟ, ୧୯୫୩ ବଳରେ ‘ଓଡ଼ିଶା ମାଧ୍ୟମିକ ଶିକ୍ଷା ପରିଷଦ’ ଗଠିତ ହୋଇଥିଲା ।
4. ମଧ୍ୟାହ୍ନ ଭୋଜନ ବ୍ୟବସ୍ଥା କ’ଣ ?
Answer:
ଶିଶୁମାନଙ୍କୁ ବିଦ୍ୟାଳୟ ପ୍ରତି ଆକୃଷ୍ଟ କରିବାପାଇଁ ୧୯୯୫ ମସିହାଠାରୁ ସରକାରଙ୍କଦ୍ୱାରା ବିଦ୍ୟାଳୟରେ ମଧ୍ୟାହ୍ନ ଭୋଜନର ବ୍ୟବସ୍ଥା କରାଯାଇଛି ।
5. କୋରାପୁଟଠାରେ କେଉଁ ମହାବିଦ୍ୟାଳୟ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ?
Answer:
୧୯୪୭ ମସିହାରେ କୋରାପୁଟଠାରେ ଏକ ଇଷ୍ଟରମିଡ଼ିଏଟ୍ ମହାବିଦ୍ୟାଳୟ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।
6. ୧୯୬୭ ମସିହାରେ କେଉଁ ଦୁଇଟି ବିଶ୍ଵବିଦ୍ୟାଳୟ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ?
Answer:
୧୯୬୭ ମସିହାରେ ସମ୍ବଲପୁର ଓ ବ୍ରହ୍ମପୁରଠାରେ ଦୁଇଟି ବିଶ୍ଵବିଦ୍ୟାଳୟ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।

7. ବାଲେଶ୍ଵର ଓ ବାରିପଦାରେ କେବେ କେଉଁ ବିଶ୍ଵବିଦ୍ୟାଳୟ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ?
Answer:
୧୯୯୯ରେ ଉତ୍ତର ବାଲେଶ୍ଵରଠାରେ ଫକୀରମୋହନ ବିଶ୍ବବିଦ୍ୟାଳୟ ଓ ବାରିପଦାଠାରେ ଉତ୍ତର ଓଡ଼ିଶା ବିଶ୍ୱବିଦ୍ୟାଳୟ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।
8. ରାଧାନାଥ ଟ୍ରେନିଂ ମହାବିଦ୍ୟାଳୟର ବର୍ତ୍ତମାନ ନାମ କ’ଣ ରଖାଯାଇଛି ?
Answer:
ରାଧାନାଥ ଇନ୍ଷ୍ଟିଚ୍ୟୁଟ୍ ଅଫ୍ ଆଡ଼ଭାନ୍ସ ଷ୍ଟଡ଼ିଜ୍ ଇନ୍ ଏଡୁକେସନ୍ (RNIASE) ନାମ ରଖାଯାଇଛି ।
9. କେନ୍ଦ୍ରୀୟ ମଧୁର ଜଳ ମତ୍ସ୍ୟ ଗବେଷଣା କେନ୍ଦ୍ର କେବେ, କେଉଁଠାରେ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ?
Answer:
୧୯୭୭ ମସିହାରେ କୌଶଲ୍ୟାଗଙ୍ଗାଠାରେ କେନ୍ଦ୍ରୀୟ ମଧୁର ଜଳ ମତ୍ସ୍ୟ ଗବେଷଣା ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
10. ଶାରୀରିକ ଶିକ୍ଷା ପାଇଁ କେଉଁ ଅନୁଷ୍ଠାନ କାର୍ଯ୍ୟ କରୁଅଛି ?
Answer:
ଶାରୀରିକ ଶିକ୍ଷାର ବିକାଶ ପାଇଁ ଭୁବନେଶ୍ୱରଠାରେ ଏକ ସରକାରୀ ଶାରୀରିକ ପ୍ରଶିକ୍ଷଣ ମହାବିଦ୍ୟାଳୟ କାର୍ଯ୍ୟ କରୁଅଛି ।

B. ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଲେଖ ।
1. ପ୍ରାଥମିକ ଶିକ୍ଷାକୁ ସାର୍ବଜନୀନ କରିବା ପାଇଁ କାହା ଉପରେ ଗୁରୁତ୍ୱ ଦିଆଯାଇଥିଲା ?
Answer:
ନାମଲେଖା
2. ବ୍ୟାବସାୟିକ ପରିଚାଳନା ଶିକ୍ଷା ପାଇଁ ପ୍ରଥମେ ଭୁବନେଶ୍ବରରେ କେଉଁ ଅନୁଷ୍ଠାନ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ?
Answer:
ଜାଭିଅର ଇନ୍ଷ୍ଟିଚ୍ୟୁଟ୍ ଅଫ୍ ମ୍ୟାନେଜ୍ମେଣ୍ଟ
3. ଜିଲ୍ଲା ପ୍ରାଥମିକ ଶିକ୍ଷା ଯୋଜନା କାହା ସହାୟତାରେ ଓଡ଼ିଶାରେ କାର୍ଯ୍ୟକାରୀ ହୋଇଛି ?
Answer:
କେନ୍ଦ୍ର ସରକାର
4. ଆମ ରାଜ୍ୟରେ ଗଢ଼ି ଉଠିଥିବା ତିନୋଟିଯାକ ଘରୋଇ ମେଡ଼ିକାଲ କଲେଜ କେଉଁଠି ସ୍ଥାପିତ ହୋଇଛି ?
Answer:
ଭୁବନେଶ୍ୱର
5. ଓଡ଼ିଶାର କେଉଁଠାରେ ଜାତୀୟ ଆଇନ ବିଶ୍ବବିଦ୍ୟାଳୟ ସ୍ଥାପନ କରାଯାଇଛି ?
Answer:
କଟକ
6. କେତେ ବର୍ଷ ବୟସର ପିଲାମାନଙ୍କୁ ସୁଲଭ ଶିକ୍ଷା ଯୋଗାଇ ଦେବା ପାଇଁ ‘ରାଷ୍ଟ୍ରୀୟ ମାଧ୍ୟମିକ ଶିକ୍ଷା ଅଭିଯାନ’ର ଲକ୍ଷ୍ୟ ଥିଲା ?
Answer:
୧୪-୧୮ ବର୍ଷ

7. ରାଉରକେଲାସ୍ଥିତ ଯାନ୍ତ୍ରିକ ମହାବିଦ୍ୟାଳୟର ବର୍ତ୍ତମାନ ନାମ କ’ଣ ?
Answer:
ଜାତୀୟ ବୈଷୟିକ ଶିକ୍ଷାନୁଷ୍ଠାନ
8. ଖଣିଜ ଓ ଧାତବ ପଦାର୍ଥ ଗବେଷଣା ପାଇଁ ଓଡ଼ିଶାରେ କେଉଁ ଅନୁଷ୍ଠାନ କାର୍ଯ୍ୟ କରୁଛି ?
Answer:
ଆଞ୍ଚଳିକ ଗବେଷଣା ପରୀକ୍ଷାଗାର
9. ଓଡ଼ିଶାର କେଉଁଠାରେ ଭାରତୀୟ ଗଣ ଯୋଗାଯୋଗ ଶିକ୍ଷାନୁଷ୍ଠାନ ରହିଅଛି ?
Answer:
ଢେଙ୍କାନାଳ
10. କେଉଁ ଯୋଜନା ମାଧ୍ୟମରେ ପିଲାମାନଙ୍କୁ ମାଗଣାରେ ପାଠ୍ୟପୁସ୍ତକ ଯୋଗାଇ ଦେବାର ବ୍ୟବସ୍ଥା କରାଯାଇଛି ?
Answer:
ସର୍ବଶିକ୍ଷା ଅଭିଯାନ
11. କଟକ ପ୍ରଶିକ୍ଷଣ ମହାବିଦ୍ୟାଳୟ ଶିକ୍ଷକଙ୍କ ବ୍ୟତୀତ ଅନ୍ୟ କାହାକୁ ପ୍ରଶିକ୍ଷଣ ପ୍ରଦାନ କରୁଥିଲା ?
Answer:
ଶିକ୍ଷା ପରିଦର୍ଶକ
12. ବୀର ସୁରେନ୍ଦ୍ର ସାଏ ମେଡ଼ିକାଲ କଲେଜ କେଉଁଠାରେ ଅଛି ?
Answer:
ବୁର୍ଲା
13. କେଉଁ ମସିହାଠାରୁ ଓଡ଼ିଶାରେ ‘ଜିଲ୍ଲା ପ୍ରାଥମିକ ଶିକ୍ଷା ଯୋଜନା’ (ଡି.ପି.ଇ.ପି.) କାର୍ଯ୍ୟକାରୀ ହୋଇଛି ?
Answer:
୧୯୯୬
14. ରାଜ୍ୟରେ କେତେ ସଂଖ୍ୟକ ସରକାରୀ ବା ଅନୁଦାନ ପ୍ରାପ୍ତ ମାଧ୍ୟମିକ ବିଦ୍ୟାଳୟ ରହିଛି ?
Answer:
୨୦୦୦ରୁ ଊର୍ଦ୍ଧ୍ୱ
15. ଶିକ୍ଷା ଦୃଷ୍ଟିରୁ ଅନଗ୍ରସର ବ୍ଲକ୍ଗୁଡ଼ିକରେ ସରକାର କେଉଁ ସ୍କୁଲ୍ ପ୍ରତିଷ୍ଠା କରିଛନ୍ତି ?
Answer:
ମଡ଼େଲ ସ୍କୁଲ

C. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
1. ମୌଳିକ ଶିକ୍ଷା ପଦ୍ଧତି ______________ ଙ୍କର ସ୍ଵପ୍ନ ଥିଲା ।
Answer:
ମହାତ୍ମା ଗାନ୍ଧି
2. ________________ ମସିହାଠାରୁ ସରକାର ବିଦ୍ୟାଳୟମାନଙ୍କରେ ମଧ୍ୟାହ୍ନ ଭୋଜନ ବ୍ୟବସ୍ଥା କରିଛନ୍ତି ।
Answer:
୧୯୯୫
3. ‘ରାଷ୍ଟ୍ରୀୟ ମାଧ୍ୟମିକ ଶିକ୍ଷା ଅଭିଯାନ’ ________________ ଶିକ୍ଷାବଷଠାରୁ ଶୁଭାରମ୍ଭ କରାଯାଇଛି ।
Answer:
୨୦୦୯-୧୦
4. _____________ ମସିହା ସୁଦ୍ଧା ସମସ୍ତଙ୍କୁ ମାଧ୍ୟମିକ ଶିକ୍ଷା ଉପଲବ୍ଧ କରିବାପାଇଁ ଲକ୍ଷ୍ୟ ଧାର୍ଯ୍ୟ କରାଯାଇଛି ।
Answer:
୨୦୧୭
5. ସ୍ଵାଧୀନତାବେଳକୁ ଓଡ଼ିଶାରେ _____________ ଟି ବିଶ୍ୱବିଦ୍ୟାଳୟ ଥିଲା ।
Answer:
ଗୋଟିଏ
6. ଉଳଶିକ୍ଷା ଷେତୁରେ _______________ ମହାବିଦ୍ୟାଳୟ ଏକମାତ୍ର ଅନୁଷ୍ଠାନ ଥିଲା ।
Answer:
ରେଭେନ୍ୱା
7. _____________ ମସିହାରେ ପ୍ରତିଷ୍ଠିତ ହେଲା ସମ୍ବଲପୁର ଓ ବ୍ରହ୍ମପୁର ବିଶ୍ୱବିଦ୍ୟାଳୟ ।
Answer:
୧୯୬୭
8. ୧୯୫୬ରେ _____________ ଠାରେ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ଏକ ଯାନ୍ତ୍ରିକ ମହାବିଦ୍ୟାଳୟ ।
Answer:
ବୁର୍ଲା

9. ୨୦୦୨ ମସିହାରେ ______________ ଠାରେ ବିଜୁ ପଟ୍ଟନାୟକ ବୈଷୟିକ ବିଶ୍ୱବିଦ୍ୟାଳୟ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
Answer:
ରାଉରକେଲା
10. ଓଡ଼ିଶା କୃଷି ଓ ବୈଷୟିକ ବିଶ୍ଵବିଦ୍ୟାଳୟ _____________ ମସିହାରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ।
Answer:
୧୯୬୨
11. କେନ୍ଦ୍ର ସରକାର ____________ ଠାରେ ଏକ କେନ୍ଦ୍ରୀୟ ଧାନ ଗବେଷଣା କେନ୍ଦ୍ର ପ୍ରତିଷ୍ଠା କରିଥିଲେ ।
Answer:
କଟକ
12. ମହାରାଜା କୃଷ୍ଣଚନ୍ଦ୍ର ଗଜପତି ମେଡ଼ିକାଲ କଲେଜ _____________ ଠାରେ ପ୍ରତିଷ୍ଠା କରିପାରିଛି ।
Answer:
ବ୍ରହ୍ମପୁର
13. ଭୁବନେଶ୍ୱରଠାରେ ____________ ଟି ଘରୋଇ ମେଡ଼ିକାଲ କଲେଜ ରହିଛି ।
Answer:
୩
14. ସର୍ବଭାରତୀୟ ଆୟୁର୍ବିଜ୍ଞାନ ଅନୁଷ୍ଠାନ ___________ ମସିହାଠାରୁ ଭୁବନେଶ୍ୱର ଶିକ୍ଷାଦାନ କାର୍ଯ୍ୟ ଆରମ୍ଭ କରିଛି ।
Answer:
୨୦୧୨
15. ଉତ୍କଳ ସଂସ୍କୃତି ବିଶ୍ୱବିଦ୍ୟାଳୟ _____________ ଠାରେ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
Answer:
ଭୁବନେଶ୍ୱର

D. ଠିକ୍ ଉକ୍ତି ପାଇଁ (✓) ଚିହ୍ନ ଓ ଭୁଲ୍ ଉକ୍ତି ପାଇଁ (×) ଚିହ୍ନ ଦିଅ ।
1. ୧୯୫୦ ମସିହା ବେଳକୁ ଓଡ଼ିଶାର ହାଇସ୍କୁଲ ସଂଖ୍ୟା ଥିଲା ୧୫୦ ।
Answer:
x
2. ୧୯୫୩ ମସିହାରେ ଓଡ଼ିଶା ମାଧ୍ୟମିକ ଶିକ୍ଷା ପରିଷଦ ଗଠନ କରାଯାଇଥିଲା ।
Answer:
✓
3. ମଧ୍ୟାହ୍ନ ଭୋଜନ ବ୍ୟବସ୍ଥାଦ୍ୱାରା ଶିଶୁମାନଙ୍କୁ ବିଦ୍ୟାଳୟ ପ୍ରତି ଆକୃଷ୍ଣ କରାଯାଇଥାଏ ।
Answer:
✓
4. ରାଜ୍ୟ ସରକାରଙ୍କ ସହାୟତାରେ ‘ଜିଲ୍ଲା ପ୍ରାଥମିକ ଶିକ୍ଷା ଯୋଜନା’ କାର୍ଯ୍ୟକାରୀ ହେଉଛି ।
Answer:
x
5. ରାଜ୍ୟରେ ୫୦୦୦ରୁ ଅଧିକ ଅନୁଦାନପ୍ରାପ୍ତ ମାଧ୍ଯମିକ ସରକାରୀ ବିଦ୍ୟାଳୟ ରହିଛି ।
Answer:
x
6. ‘ସର୍ବଶିକ୍ଷା ଅଭିଯାନ’ ଯୋଜନା ମାଧ୍ୟମରେ ସମଗ୍ର ଓଡ଼ିଶାରେ ନୂତନ ବିଦ୍ୟାଳୟମାନ ଖୋଲାଯାଇଛି ।
Answer:
✓
7. ୧୯୫୦ ମସିହା ବେଳକୁ ଓଡ଼ିଶାରେ ସର୍ବମୋଟ ମହାବିଦ୍ୟାଳୟ ସଂଖ୍ୟା ଥିଲା ୧୫ ।
Answer:
x
8. ଉତ୍ତର ଓଡ଼ିଶା ବିଶ୍ଵବିଦ୍ୟାଳୟ ଭଦ୍ରଖରେ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।
Answer:
x

9. ଫକୀରମୋହନ ବିଶ୍ବବିଦ୍ୟାଳୟ ବାଲେଶ୍ଵରଠାରେ ଅବସ୍ଥିତ ।
Answer:
✓
10. ରାଧାନାଥ ପ୍ରଶିକ୍ଷଣ ମହାବିଦ୍ୟାଳୟ ଭୁବନେଶ୍ଵରରେ ଅବସ୍ଥିତ ।
Answer:
x
11. ସରାଙ୍ଗଠାରେ ଏକ ସରକାରୀ ଯାନ୍ତ୍ରିକ ମହାବିଦ୍ୟାଳୟ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
Answer:
✓
12. ୧୯୫୪ ମସିହାରେ ଭୁବନେଶ୍ଵରରେ ଏକ କୃଷି ମହାବିଦ୍ୟାଳୟ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।
Answer:
✓
13. କୌଶଲ୍ୟାଗଙ୍ଗ ମତ୍ସ୍ୟ ଗବେଷଣା କେନ୍ଦ୍ର ୧୯୭୬ ମସିହାରେ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।
Answer:
x
14. ହୀରାକୁଦର ଅନତିଦୂରରେ ଚିପିଲିମାରେ ଏକ କୃଷି ମହାବିଦ୍ୟାଳୟ ରହିଛି ।
Answer:
✓
15. ବୀର ସୁରେନ୍ଦ୍ର ସାଏ ମେଡ଼ିକାଲ କଲେଜ ୧୯୫୮ ମସିହାରେ ଆରମ୍ଭ ହୋଇଥିଲା ।
Answer:
x
16. ଘରୋଇ ଉଦ୍ୟମରେ ଆମ ଓଡ଼ିଶାରେ ଦୁଇଗୋଟି ମେଡ଼ିକାଲ କଲେଜ ସ୍ଥାପିତ ହୋଇଛି ।
Answer:
x

17. ଓଡ଼ିଶାର ସମସ୍ତ ଘରୋଇ ମେଡ଼ିକାଲ କଲେଜଗୁଡ଼ିକ ଭୁବନେଶ୍ଵର ଅବସ୍ଥିତ ।
Answer:
✓
18. ସର୍ବଭାରତୀୟ ଆୟୁର୍ବିଜ୍ଞାନ ଅନୁଷ୍ଠାନ ୨୦୦୦ ମସିହାରୁ ଭୁବନେଶ୍ଵରରେ ଶିକ୍ଷାଦାନ କାର୍ଯ୍ୟ ଆରମ୍ଭ କରିଛି ।
Answer:
x
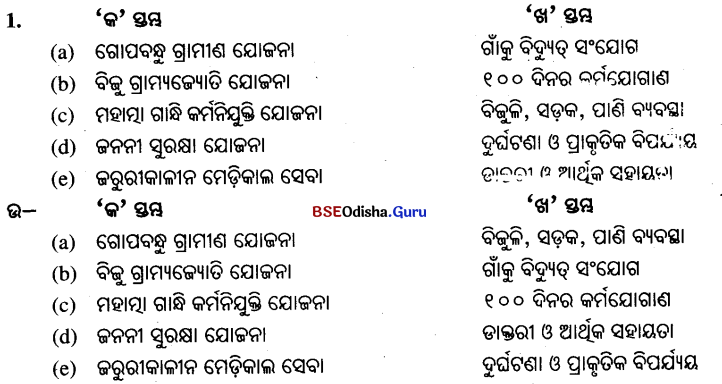
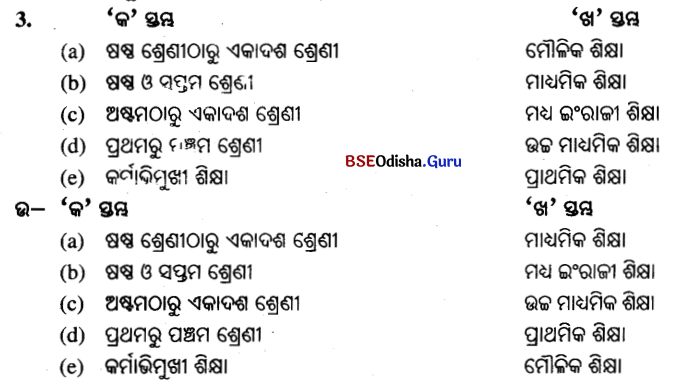
E. ‘କ’ ସ୍ତମ୍ଭ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ମିଳନ କର ।







![]()

![]()

![]()
![]()







 (i) ବେଠି, ବେଗାରୀ, ମାଗଣ, ରସଦ ଓ ଭେଟି ପ୍ରଭୃତି ଅନ୍ୟାୟ ପ୍ରଥାକୁ ବନ୍ଦ କରିବା ।
(i) ବେଠି, ବେଗାରୀ, ମାଗଣ, ରସଦ ଓ ଭେଟି ପ୍ରଭୃତି ଅନ୍ୟାୟ ପ୍ରଥାକୁ ବନ୍ଦ କରିବା ।