Class 12

Odisha State Board CHSE Odisha Class 12 Biology Important Questions Chapter 17 Environmental Issues Important Questions and Answers.

CHSE Odisha 12th Class Biology Important Questions Chapter 17 Environmental Issues

Environmental Issues Class 12 Important Questions CHSE Odisha

Very Short Answer Type Questions

Choose the correct option

Question 1.
The major pollutant from automobile exhaust is known as
(a) NO
(b) CO
(c) SO₂
(d) Soot
Answer:
(b) CO

Question 2.
Which air pollutant could cause rains to be acidic?
(a) Dust particles from cement factories
(b) Insecticides from crop sprays
(c) Smoke from wood fires
(d) Sulphur dioxide from coat-fired power stations
Answer:
(d) Sulphur dioxide from coat-fired power stations

Question 3.
Which process does not result in the return of carbon dioxide to the atmosphere?
(a) Combustion of fossil fuels
(b) Decomposition of humus
(c) Respiration by bacteria
(d) Photosynthesis by green plants
Answer:
(d) Photosynthesis by green plants

Question 4.
Which kind of power station produces sulphur dioxide causing air pollution and acid rain?
(a) Loal-fired
(b) Nuclear
(c) Hydroelectric
(d) Wind-powered
Answer:
(a) Loal-fired

Question 5.
Eutrophication in lakes is the direct result of
(a) a diminished supply of nitrates and phosphates
(b) industrial poisons
(c) nutrient enrichment such as nitrate and phosphate runoffs from the land
(d) an increase in predators
Answer:
(c) nutrient enrichment such as nitrate and phosphate runoffs from the land

Question 6.
Why does the oxygen concentration in the water decrease when sewage is discharged into a river?
(a) Decrease in the number of plants
(b) Increase in the number of fish
(c) Less oxygen absorbed from the air
(d) Rapid growth of bacteria
Answer:
(d) Rapid growth of bacteria

Question 7.
Minamata disease is due to pollution of water by
(a) mercury
(b) lead
(c) tin
(d) methylisocyanate
Answer:
(a) mercury

Question 8.
The effects of radioactive pollutants depend upon
(a) the rate of diffusion
(b) energy releasing capacity
(c) rate of deposition of contaminant
(d) All of the above
Answer:
(d) All of the above

Question 9.
The most harmful types of environment pollutants are
(a) human organic wastes
(b) wastes from faecal
(c) non-biodegradable chemicals
(d) natural nutrients present in excess
Answer:
(c) non-biodegradable chemicals

Question 10.
Taj Mahal is threatened to ……….. the effect of
(a) chlorine
(b) SO₂
(c) oxygen
(d) hydrogen
Answer:
(b) SO₂

Question 11.
CO is a pollutant because it
(a) inactivates nerves
(b) combines with oxygen
(c) combines with Hb
(d) inhibits growth
Answer:
(c) combines with Hb

Question 12.
Flyash is an environmental pollutant produced by
(a) thermal power plant
(b) oil refinery
(c) fertilisation plant
(d) strip mining
Answer:
(d) strip mining

Question 13.
Which type of pollution is caused by scooters?
(a) Air pollution
(b) Soil pollution
(c) Both (a) and (b)
(d) Water pollution
Answer:
(a) Air pollution

Question 14.
Acid rain occurs in areas where
(a) large plantation occurs
(b) small plantation occurs
(c) there are big industries and the atmosphere is polluted with SO₂
(d) there are no industries
Answer:
(c) there are big industries and the atmosphere is polluted with SO₂

Question 15.
Air pollution effects are usually found on the
(a) leaves
(b) flowers
(c) stems
(d) roots
Answer:
(a) leaves

Question 16.
Eutrophic lakes are highly
(a) productive
(b) enriched with phosphates
(c) heavy metal
(d) None of the above
Answer:
(b) enriched with phosphates

Question 17.
Global warming can be controlled by
(a) reducing reforestation, increasing the use of fossil fuel
(b) increasing deforestation, slowing down the growth of human population
(c) increasing deforestation, reducing efficiency of energy usage
(d) reducing deforestation, cutting down use of fossil fuel
Answer:
(d) reducing deforestation, cutting down use of fossil fuel

Question 18.
The common refrigerant that is responsible for the depletion of stratospheric ozone is
(a) CFC
(b) NO
(c) SO₂
(d) Ozone
Answer:
(a) CFC

Question 19.
Slash and burn agriculture is known as
(a) striping farming
(b) intercrop farming
(c) jhum cultivation
(d) intensive farming
Answer:
(c) jhum cultivation

Question 20.
Ozone hole is the
(a) absence of O₃ in stratosphere
(b) presence of O₃ in stratosphere
(c) deficiency of O₃ in stratosphere
(d) deficiency of O₃ in stratosphere
Answer:
(c) deficiency of O₃ in stratosphere

Question 21.
Ozone depletion is occurring due to
(a) PCB
(b) CO
(c) PAN
(d) None of these
Answer:
(d) None of these

Question 22.
The most common and abundant greenhouse gas is
(a) methane
(b) CFC
(c) carbon dioxide
(d) nitrous oxide
Answer:
(c) Carbon dioxide

Question 23.
Women empowerment in Tehri-Garhwal by Sundarlal Bahuguna for the conservation of forests is popularly known as
(a) agro forestry
(b) shifting cultivation
(c) Chipko movement
(d) None of these
Answer:
(c) Chipko movement

Correct the following sentences, if required, by changing the underlined word (s)

Question 1.
Acid rain, a secondary effect of sound pollution.
Answer:
air pollution

Question 2.
The excessive growth of plants in water bodies due to enrichment of nutrients is called bioremediation.
Answer:
Eutrophication

Question 3.
Excessive nourishment that causes algal bloom is known as biomagnification.
Answer:
eutrophication

Question 4.
Photochemical smog consists of O₂ PAN and NO_x.
Answer:
It is Correct

Question 5.
Radioactive pollution is caused by α, ß, γ particles.
Answer:
It is Correct

Question 6.
Ozone hole is present above Antarctica.
Answer:
It is correct.

Question 7.
Greenhouse effect refers to cooling of earth.
Answer:
warming

Question 8.
Nitrogen is a greenhouse gas.
Answer:
Carbon dioxide

Fill in the blanks

Question 1.
Bhopal gas tragedy was due to the release of ……….. gas from Union Carbide’s pesticide plant.
Answer:
methyl isocyanate

Question 2.
The toxic metal that is used as an antiknocking agent in petrol engines of automobiles is ………… .
Answer:
lead (Pb)

Question 3.
The Bharat Emission Norm came into force from ……….. .
Answer:
2000

Question 4.
In a scrubber, the effluent containing sulphur dioxide is passed through spray of ………….. .
Answer:
lime or Water

Question 5.
Most hazardous metal pollutant of automobile exhaust is ……….. .
Answer:
CO

Question 6.
Melting of glaciers is an effect of ………… .
Answer:
global warming

Question 7.
Two greenhouse gases produced by anaerobes are ……….. and ………… .
Answer:
methane, carbon dioxide

Question 8.
In 1980s, the government of India introduced a concept known as ………… .
Answer:
Joint Forest Management

Express in one or two word(s)

Question 1.
The expression that reflects the depleted oxygen content in the extremely polluted water.
Answer:
Biochemical Oxygen Demand (BOD).

Question 2.
Expand DDT.
Answer:
Dichloro Diphenyl Trichloroethane.

Question 3.
Name the gas which was released during Bhopal gas tragedy.
Answer:
Methyl isocyanate

Question 4.
Which metal causes gangrenes?
Answer:
Arsenic

Question 5.
In which year Copenhagen conference was held?
Answer:
2009

Question 6.
In which year was Montreal Protocol signed?
Answer:
1987

Question 7.
Above which region of earth is ozone hole located?
Answer:
Antarctic region

Short Answer Type Questions

Question 1.
State the function of catalytic converter in automobile. Name any two metals used in these converters.
Answer:
Catalytic converters are used in automobiles to reduce the emission of poisonous gases. They convert unburnt hydrocarbons to carbon dioxide and water, carbon monoxide and nitrogen dioxide are converted to carbon dioxide and nitrogen gas respectively.

Question 2.
What are causes of air pollution?
Answer:
The various causes of air pollution are

• Smoke stacks of thermal power plants, forest fires, volcanic eruptions, etc.
• Garbage decomposition releases unwanted gases in the air.
• Excessive use of fossil fuels by automobiles and particulate air pollutants released by industries.

Question 3.
Write a short note on water pollution.
Answer:
Water pollution is any undesirable change in the physical, chemical or biological properties of water that may affect the human beings and aquatic species.
There are various types of water pollutants such as

• Domestic sewage
• Industrial waste
• Agricultural waste

The various effects of water pollution are

• Biomagnification
• Eutrophication
• Increase in Biochemical Oxygen Demand (BOD).

Question 4.
Write short note on algal bloom.
Answer:
Algal bloom is excessive growth of planktonic (free-floating) algae in aquatic bodies due to nutrient enrichment by sewage. It causes fish mortality and deterioration of water quality.

Question 5.
What is BOD?
Answer:
BOD (Biochemical Oxygen Demand) it is the amount of oxygen required by the microorganisms in milligram to breakdown the organic matter in water. Polluted water rises the BOD value of water. Also high BOD causes death of aquatic organisms.

Question 6.
What are the sources of radioactive pollution?
Answer:
Following are the sources of radioactive pollution

• Cosmic rays and radiations
• Nuclear weapons
• Nuclear reactors and fuels
• Radioactive isotopes
• Research and medicines.

Question 7.
Write a note on biomagnification.
Answer:
Biomagnification is defined as the increase in concentration of toxicants at successive trophic levels. Mercury and DDT are well known for biological magnification. Toxic materials cannot be metabolised or excreted. Therefore, they get accumulated in an organism and pass on to higher trophic levels, e.g. DDT accumulates in birds and disturbs calcium metabolism which result in thinning of egg shell. This results in decline of bird population.

Question 8.
Write a note on secondary treatment of sewage.
Answer:
Secondary Treatment of Sewage
1. This treatment is also known as biological treatment because it involves the use of microbes or biota for the treatment of sewage. The effluent from primary treatment is passed into large aeration tanks where it is constantly mechanically agitated and air is pumped into.

2. This air helps in the growth of useful aerobic microbes into floes (masses of bacteria associated with fungal filament to form mesh-likes structures). While growing, these microbes consume major part of the organic matter converting it into mircrobial biomass and releasing lot of minerals. This significantly reduces the BOD (Biochemical Oxygen Demand).

Question 9.
Name an industry which can cause both air and thermal pollution as well as eutrophication.
Answer:
Some of the industries that may cause air and thermal pollution as well as eutrophication are thermal power plants, refineries, smelting and metallurgical processing units, steel mills, fertiliser producing units and the industries using steam or water as coolant. The chemical released from these industries (if rich in nitrogen and phosphorus) may result in eutrophication.

Question 11.
Biological Oxygen Demand or BOD increases with increase in water pollution. In this reference, answer the questions that follows
(i) At a particular segment of the river near a sugar factory, the BOD is much higher than the normal level. What is it indicative of ?
(ii) What will happen to the dissolved oxygen and living organisms in this part of the river?
Answer:
(i) It indicates that the sugar factory releases organic waste in the water body. To degrade the organic matter, microbes utilise the dissolved oxygen in the water, thereby, reducing the levels of dissolved oxygen and increasing the BOD.
(ii) In this part of river, the dissolved oxygen will be depleted making it difficult for aquatic species to survive. It can result in death of fishes in severe cases.

Question 12.
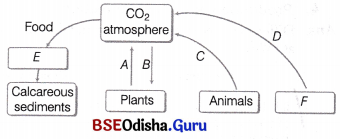
With the help a flow chart exhibit the events of eutrophication.
Answer:
A flow chart showing eutrophication is given below

Stinking eutrophic lake with coloured and turbid water
↑
Loss of species diversity
↑
Death of aquatic animals including fish
↑
Reduced contents of dissolved oxygen
↑
Increase in organic loading of lake
↑
Death of submerged plants due to reduced light
↑
Biological enrichment of water
(algal bloom, planktonic algae and higher plants)
↑
Nutrient enrichment of water
↑
Draining of inorganic nutrients
↑
A young lake

Question 13.
How does algal bloom cause eutrophication of water body?
Answer:
Algal bloom Domestic sewage is rich in nutrients like nitrogen and phosphorus which favours the growth of algae. It causes fish mortality and deterioration of water quality.
Example of a bloom includes red tide.

Question 14.
Why is there a decline in population of fish-eating birds, when the water body is amidst agricultural fields?
Answer:
The reason for decline in fish-eating birds is biomagnification of toxic substances like DDT and other pesticides from the agricultural fields. The pesticides are applied in the fields for protection of crops.

Washed off to water bodies with irrigation water and rain and are indirectly consumed by the fishes entering the food chain. It get(s) accumulated and their concentration increases with each trophic level. Thus, on reaching fish-eating birds, their concentration will be increased many folds.

The high concentration of DDT interferes with calcium metabolism in birds and causes thinning of eggshells and their premature breaking, ultimately causing decline in bird population.

Question 15.
Discuss briefly the following
(i) Radioactive waste
(ii) Defunct ships and e-waste
Answer:
(i) Radioactive waste Radioactive waste is generated from nuclear power plants, nuclear weapon manufacturing facilities, cancer treating hospitals and research laboratories using radioisotopes in investigations. This waste is to be disposed off safely by observing the standard guideline because if it remains for a very long period and continues to emit ionising radiation, it will be extremely hazardous to health of all forms of life.

(ii) Defunct ships Old defunct ships are broken down in developing countries like India, Bangladesh and Pakistan because of cheap labour and demand for scrap metal. These ships however, possess a number of toxic materials like asbestos, lead, mercury and polychlorinated biphenyls. The people involved in ship breaking are exposed to these toxic materials and thus suffer from various diseases. The coastal areas where ship breaking is undertaken also become polluted.

Question 16.
Why does ozone hole form over Antarctica? How will enhanced ultraviolet radiations affect us?
Answer:
In Antarctica, winter months receive no sunlight and thus the temperature is extremely low (-85° C). It facilitates the formation of ice clouds which provide the catalytic surface on which the chlorine atoms react with ozone and degrade it. This happens with the return of sun to Antarctica in springs (September and October). Thus, ozone hole appears over Antarctica mostly during spring.

It is a large area of thinned ozone layer mainly over Antarctic region. At this point, depletion of ozone has occurred more as compared to the rest of the stratosphere.

Question 17.
Write short note on greenhouse effect.
Answer:
It is a naturally occurring phenomenon that is responsible for heating of earth’s surface and atmosphere due to the presence of certain gases in the atmosphere. In the absence of greenhouse gases the average temperature of earth would have been a chill-18° C reather than the present average of 15°C.

These gases radiate heat energy and a major part of which again comes to earth’s surface thus heating it up once again. This cycle is repeated again and again.
High levels of greenhouse gases (CO₂, CFCs, etc.) in the atmosphere allow the heat waves to reach earth but prevent their escape and the earth becomes warm.
This gradual continuous increase in the average temperature of surface of the earth causes global warming.

Question 18.
Write note on ozone depletion.
Answer:
It is the wearing out or reduction of the amount of ozone in the stratosphere. A number of pollutants enter into the stratosphere and deplete the ozone layer. These include CFCs, CH₄ and N₂O. CFCs are widely used as refrigerants. When they are discharged in the lower part of atmosphere, they move upward and reach the stratosphere.

In stratosphere, UV-rays act on them releasing Cl atoms. Cl degrades ozone, releasing molecular oxyen. Cl atoms are not consumed in the reaction. Hence, once CFCs are added to the stratosphere they have permanent and continuous effects on ozone levels.

Question 19.
What is ozone shield?
Answer:
Ozone layer lies in the stratosphere between 10-50 kms above the earth surface. It absorbs 90% of sun’s hazardous UV-radiation and protects plant and animal life. Thus, it is called as ozone shield.
CFC is largely responsible of ozone depletion which causes skin cancer, cataract and weaken immune system.

Question 20.
What is the common household source of CFCs? How these gases affect the ozonalayer?
Answer:
CFCs are widely used as refrigerants. When they are discharged in the lower part of atmosphere, they move upward and reach the stratosphere. In stratosphere, UV-rays act on them releasing Cl atoms. Cl degrades ozone releasing molecular oxygen. Cl atoms are not consumed in this reaction. Hence, once CFCs are added to the stratosphere, they have permanent and continuous effects on ozone levels.

Question 21.
Write, what was the percentage of forest cover of India at the beginning and at the end of 20th century. How different it is from the one recommended by National Forest Policy?
Answer:
In the beginning of the 20th century, the forest cover was about 30% while towards its end it reduced to only 19.4%. The National Forest Policy of India – recommends approximately 67% forest cover for hilly regions including himalayas, while 33% for plains. However, the situation is contrastingly different.

Question 22.
Name any one greenhouse gas and its possible source of production on a large scale. What are the harmful effects of it?
Answer:
Carbon dioxide is a major greenhouse gas. Various human activities such as combustion of fossil fuels, electricity generation, transportation and industries are sources of its large scale production. Excess of CO₂ is harmful and considered as a pollutant. It is because it traps longer wavelength IR radiations reflected by earth’s surface, thus causing global warming.

Question 23.
It has been recorded that the temperature of the earth’s atmosphere has increased by 0.6°C.
(i) What has caused this increase?
(ii) Explain its consequences.
Answer:

• Increase in the level of greenhouse gases (CO₂,CFCS, etc.) in the atmosphere allow the heat waves to reach earth but prevent their escape and thus, the earth becomes warm.
• Effects of increased temperature are
  • Leads to deleterious changes in environment, resulting into odd climatic changes such as El Nino effect.
  • Melting of polar ice caps which will cause the rise in sea level and many coastal areas may also get submerged.

Question 24.
How does Jhum cultivation promote deforestation?
Answer:
Forests are the providers of timber, fuel wood and other products. Forests also provide habitat to different groups of plants and animals. Forests are cut down for various purposes. Some of the reasons are as follows

• Urbanisation
• Overgrazing by animals
• Forest fires
• Demand of wood and other forest products
• Jhum cultivation.

Slash and bum agriculture is known as Jhum Cultivation in the North-Eastern states of India. In this method, the farmers cut down the trees of the forest and burn the plant remains.
The ash is used as a fertiliser and the land is then used for farming or cattle grazing. After cultivation, the area is left for several years so as to allow its recovery.
This same process is repeated at some other area. In initial days, there was ample recovery time, but now-a-days with increasing population and repeated cultivation, this recovery phase is done away with, resulting in deforestation.

Question 25.
How can slash and burn agriculture become environment friendly?
Answer:
Slash and burn agriculture can become environment friendly if

• small widely scattered plots are used for cultivation, so that the forest ecosystem will not suffer damage.
• crop rotation is used so that soil does not loose its entire fertility.
• keeping cropping period small and follow up (unplanted) period longer.

Question 26.
What is the main idea behind ‘Joint Forest Management Concept’ introduced by the Government of India?
Answer:
The main idea behind joint forest management concept introduced by the Government of India was involving the local communities in forest conservation. This concept was adopted considering the extraordinary courage and dedication the local people showed in protecting the wildlife through the movements like Bishnoi’s movement in Jodhpur and Chipko Movement in Garhwal Himalayas.

Question 27.
Write a note on deforestation and enumerate its consequences.
Answer:
It is the conversion of forested areas to non-forested areas. Almost 40% forests have been lost in the tropics, compared to only 1% in the temperate region.
According to a report by the World Commission on Forests and Sustainable Development (WCFSD), from 6 billion hectares, 8000 years ago, there is a decline of 3.6 billion hectares in 1999 of the forest cover. Similar results were also given by the Food and Agriculture Organisation (FAO).
In India, at the beginning of the 20th century, forest covered area was about 30% of land, whereas by the end of the century, it reduced to 19.4%. This shows the alarming condition of our country.

The loss of trees due to their increased cutting is note worthy. Some of the effects due to deforestation are as follows

• Increased levels of CO₂ concentration in atmosphere.
• Loss of biodiversity due to habitat destruction.
• Disturbed hydrologic cycle.

The Andaman and Nicobar islands are the world’s first evergreen forests. The forests also comprise of local comminutes like the Great Andamanese, the Onge, the Jaracuas and the Sentinelese. But, now their population is decreasing 340 km long. Andaman Trunk road was constructed which went through the evergreen forests.
This resulted in clearing of the forest and the tribal communities like Jaracuas original way of life was eroded.

Question 28.
Why has the National Forest Commission of India recommended a relatively larger forest cover for hills than for plains?
Answer:
It is our moral duty to protect, restore and conserve/preserve the forests as they are highly beneficial for mankind.
In India, around 30% of land was covered by forest in early 20th century, which was reduced to 18-19% by the year 2000. National Forest Commission of India (1988) recommended a relatively large forest cover, i.e. 67% for the hills and 33% for the plains. Recommendation of a large forest area for hills is due to its properties like checking soil erosion, percolation and recharging groundwater, checking landslide and other natural calamities and to maintain the original flora and fauna of hills.

Question 29.
How have human activities caused desertification? Explain.
Answer:
The human activities like deforestation, over-cultivation, unrestricted grazing, poor irrigation practices, result in arid patches of land (deforestation).
When these large barren patches extend and remain unattended for long, a desert is created. Because the formation of fertile top layer of soil takes millions of years, desertification easily takes over.

Question 30.
What do you know about Chipko Movement?
Answer:
Chipko Movement happened in 1974, when local women in Garhwal district of India showed enormous bravery in protecting trees from the axe of contractors by hugging them. This movement was world famous and was globally supported.

Question 31.
Discuss the causes and effects of global warming. What measures need to be taken to control global warming?
Answer:
For causes, effects and control measures of global warming.
It has been estimated by computer application studies that there may be a rise of 3°C by the year 2100 on an average.
The major effects of global warming include

1. Climate Earth temperature has increased by 0.6°C during past century, most of it in last three decades. This increased temperature caused changes in precipitation patterns.
2. Glaciers and ice caps Scientists have proposed that this rise in temperature causes deleterious changes in the environment, resulting in odd climatic changes. Thus, leading to melting of the polar ice caps and Himalayan snow caps.
3. Animals and humans The new warmer temperature conditions lead to eruption of diseases in animals and thousands of species will become extinct in a very short period of time. People from coastal areas will start migrating due to climate change.
4. Ocean and coasts The increase in temperature causes melting of polar ice caps and glaciers. This will result in the rise of ocean water level. The increased level of ocean water will cause the submerging of many island nations and coastal cities. The high temperature will cause accelerated vanishing of coral reefs.
5. Water and agriculture The increased temperature will cause decreased productivity in agricultural practice.

Question 32.
Discuss briefly the following
(i) Greenhouse effect
(ii) Ultraviolet-B
Answer:
(i) It is a naturally occurring phenomenon that is responsible for heating of earth’s surface and atmosphere due to the presence of certain gases in the atmosphere. In the absence of greenhouse gases the average temperature of earth would have been a chill-18° C reather than the present average of 15°C.
These gases radiate heat energy and a major part of which again comes to earth’s surface thus heating it up once again. This cycle is repeated again and again.
High levels of greenhouse gases (CO₂, CFCs, etc.) in the atmosphere allow the heat waves to reach earth but prevent their escape and the earth becomes warm.
This gradual continuous increase in the average temperature of surface of the earth causes global warming.

(ii) Ultraviolet-B It is an electromagnetic radiation which has a shorter wavelength than visible light.
It is a harmful radiation that comes from sunlight and penetrates through the ozone hole to the . earth’s surface. It causes many health hazards in humans. UV-B damages DNA and activates the process of skin ageing. It also causes skin darkening and skin cancer. High levels of UV-B cause corneal cataract in human beings.

Question 33.
What depletes ozone in the stratosphere? How does this affect human life?
Answer:
Ozone in the stratosphere is depleted by CFCs, i.e chlorofluorocarbons, released primarily from refrigerators and other industrial emissions.
This affects the human life as it leads to more exposure of UV-radiation, which is considered to be harmful for health. For effects of UV-radiation on human health.
These radations can cause skin cancer, weaker immunity cataract and loss of plant productivity. The thickness of ozone in a column of air from the ground to the top of the atmosphere is measured in terms of Dobson Units (DU).

Differentiate between the following (for complete chapter)

Question 1.
Biomagnification and Eutrophication.
Answer:
Differences between biomagnification and eutrophication are as follows

Biomagnification	Eutrophication
It is the progressive increase in concentration of non-biodegradable substances in the food chain.	It is the enrichment of the water body with plant nutrients like fertilisers from outside.
It is found in all types of ecosystems.	It is found only in aquatic ecosystem and leads to organic loading.
It leads to toxicity in higher order consumers.	It leads to death of most animals and plants in the affected water body.

Question 2.
Deforestation and Reforestation.
Answer:
Differences between deforestation and reforestation are as follows

Deforestation	Reforestation
It is indiscriminate cutting down of trees for human usage.	It involves the planting of new trees in place of the ones cut down.
This reduces the green cover of the particular area.	It is to increase the green cover of a deforested area.
It leads to decline in habitats and biodiversity.	It is done in order to safeguard biodiversity.

Question 3.
Point and Non-point sources of water pollution.
Answer:
Differences between point source of water pollution and non-point source of water pollution are as follows

Point source of water pollution	Non-point source of water pollution
It is pollution caused by discharge of effluents at one point.	It is pollution caused by discharge of pollutants over a wide area.
Due to large scale entry of pollutants at one point the contamination and harmful effect on quality of water is maximum.	There is some dilution of the effect of pollutants due to large size of area.
Treatment plant can be installed in the area of flow of effluents.	Treatment plant is useless for this type of pollution.
Other type of control measures are not required.	Control measures are required on a large scale for non-liberation of pollutants.

Question 4.
Biodegradable pollutants and Non-biodegradable pollutants.
Answer:
Differences between biodegradable pollutants and non-biodegradable pollutauts are as follows

Biodegradable pollutants	Non-biodegradable pollutants
They are those pollutants which are decomposed and degraded by microbes.	The pollutants are not decomposed by microbes.
The pollutants are degraded quite rapidly.	They are degraded very slowly.
Biodegradable pollutants do not pile up.	They often get accumulated.
They can be used to produce energy, manure compost and biogas.	Some of the pollutants of properly separated can be recycled others are not manageable.
They become part of rapid-turnover in biogeochemical cycles.	Many of them do not enter biogeochemical cycles. Others are very slow and often toxic.
Examples garbage, sewage, livestock.	Examples DDT, BHC, plastics, polyethylene, cans, broken glass, etc.

Question 5.
Herbicides and Insecticides
Answer:
Differences between herbicides and insecticides are as follows

Herbicides	Insecticides
These are a type of pesticides used to kill undesirable plants or weeds.	These are type of pesticides that are used to specifically target and kill insects.
Some herbicides kill all the plants they come in contact with, while others are designee to target one species.	The targets are fixed, e.g. snail bait, ant killer and i wasp killer.

Question 6.
Acid rain and Global warming.
Answer:
Difference between acid rain and global warming are as follows

Acid rain	Global warming
Acid rain is the name given to rain, snow or sleet contaminated with acid substance. This occurs when the rain water combines with nitric and sulphuric acids.	Global warming is when the earth’s temperature rises. It happens when carbon dioxide, water vapour, nitrous oxide and methane trap heat and light from the sun in the earth’s atmosphere, which increases the temperature.

Odisha State Board CHSE Odisha Class 12 Biology Important Questions Chapter 16 Biodiversity and its Conservation and Environment Important Questions and Answers.

CHSE Odisha 12th Class Biology Important Questions Chapter 16 Biodiversity and its Conservation

Biodiversity and its Conservation Class 12 Important Questions CHSE Odisha

Very Short Answer Type Questions

Choose the correct option

Question 1.
Indian Giant squirrel in endemic to
(a) Uttar Pradesh
(b) West Bengal
(c) Madhya Pradesh
(d) Manipur
Answer:
(c) Madhya Pradesh

Question 2.
Species richness in any habitat is related to
(a) genetic diversity
(b) species diversity
(c) ecosystem diversity
(d) None of these
Answer:
(b) species diversity

Question 3.
As per IUCN nomenclature, diversity of species across a wide geographical range is called
(a) alpha
(b) beta
(c) gamma
(d) community
Answer:
(c) gamma

Question 4.
Biodiversity is rich in tropics because of
(a) high humidity
(b) stable climate
(c) older community
(d) All of these
Answer:
(d) All of these

Question 5.
The organisation which publishes the Red List of species is
(a) WWF
(b) ICFRE
(c) IUCN
(d) UNEP
Answer:
(c) IUCN

Question 6.
Red Data List was initiated in
(a) 1859
(b) 1963
(c) 1985
(d) 1977
Answer:
(b) 1963

Question 7.
As per the Red List published by the World conservation union, Indian Cheetah is categorised as …………. .
(a) vulnerable
(b) extinct
(c) critically endangered
(d) endangered
Answer:
(b) extinct

Question 8.
Diversity at the level of community and ecosystem is
(a) α – diversity
(b) β – diversity
(c) γ – diversity
(d) All of these
Answer:
(b) β – diversity

Question 9.
Red Data Book is mainted by
(a) CITES
(b) WCU
(c) CBD
(d) IUPAC
Answer:
(b) WCU

Question 10.
Which one is endangered species?
(a) Asiatic lion
(b) Sparrow
(c) Elephant
(d) Dodo
Answer:
(a) Asiatic lion

Question 11.
Which one of the following is not included under in situ conservation?
(a) Wildlife sanctuary
(b) Zoological garden
(c) Biosphere reserve
(d) National park
Answer:
(b) Zoological garden

Question 12.
Conservation and maintenance of wildlife within the natural ecosystem is
(a) in situ conservation
(b) ex situ conservation
(c) botanical gardens
(d) All of the above
Answer:
(a) in situ conservation

Question 13.
In a national park, protection is provided to
(a) entire ecosystem
(b) only fauna
(c) only flora
(d) Both (b) and (c)
Answer:
(a) entire ecosystem

Question 14.
In which zone, limited permitted?
(a) Core zone
(b) Buffer zone
(c) Manipulation zone
(d) Restoration zone
Answer:
(b) Buffer zone

Question 15.
Ramsar convention was held in
(a) India
(b) Iran
(c) Indonesia
(d) Isroel
Answer:
(b) Iran

Question 16.
Bandipur national park is situated in
(a) Kerala
(b) Odisha
(c) Karnataka
(d) Rajasthan
Answer:
(c) Karnataka

Question 17.
The objective of ‘Ramsar convention’ was
(a) forest conservation
(b) wildlife conservation
(c) wetland conservation
(d) biodiversity conservation
Answer:
(c) wetland conservation

Fill in the blanks

Question 1.
Diversity within a community is ……….. .
Answer:
α-diversity.

Question 2.
…………, a struggling shrub from tropical America was introduced as ornamental plant in India has become invasive in the wild.
Answer:
Lantana

Question 3.
A taxon facing high risk of extinction in the wild is ………… .
Answer:
vulnerable

Question 4.
Beaver is a ……….. species
Answer:
keystone

Question 5.
In India hotspots include Western Ghats and ………… .
Answer:
Eastern Himalayas.

Question 6.
The Earth Summit was held in …………. 1992.
Answer:
Brazil

Question 7.
The outer part of biosphere reserve is called ………… .
Answer:
buffer zone.

Question 8.
Wildlife Protection Act was enacted in the year ………. by Government of India.
Answer:
1972

Question 9.
Panna biosphere reserve is located in ……….. .
Answer:
Madhya Pradesh

Question 10.
Private ownership is not permitted in ………… .
Answer:
National Parks

Correct the statement, if required by changing the underlined word

Question 1.
Species diversity decreases as we move away from the equator.
Answer:
Correct statement

Question 2.
Eichhomia called as ‘Terror of Bengal’ is a keystone species.
Answer:
alien species.

Question 3.
The number of species per unit area is ß-diversity.
Answer:
species richness

Question 4.
Zoos, botanical gardens, culture collections are types of ex situ biodiversity conservation.
Answer:
in situ

Question 5.
Exploitation of soil and flora is done in a wildlife sanctuary.
Answer:
Conservation of fauna and flora

Question 6.
The transitional zone of a biosphere reserve is strictly protected to maintain the ecological diversity and integity.
Answer:
core zone

Question 7.
In situ conservation is the conservation of biological diversity outside the boundaries of their natural habitats.
Answer:
ex situ conservation

Express in one or two words

Question 1.
Diversity among individuals of a species.
Answer:
Genetic diversity

Question 2.
The extinction of these species reduces abundance of other species in the community
Answer:
keystone species.

Question 3.
The variety of species within a community.
Answer:
Species diversity

Question 4.
The scientist who developed the concept of hotspots of biodiversity?
Answer:
Norman Myers.

Question 5.
A protected area dedicated to animals life only.
Answer:
Wildlife sanctuaries.

Short Answer Type Questions

Question 1.
Write briefly about the three levels of biological diversity.
Answer:
There are three levels of biological diversity

• Genetic diversity Variations in the genetic composition of individuals within a species or. among species is known as genetic diversity.
• Species diversity It pertains to the variety of species present in a particular area or ecosystem.
• Ecosystem diversity It refers to diversity of habitats, e.g. terrestrial and aquatic ecosystem.

Question 2.
State the importance of species diversity to the ecosystem.
Answer:
The importance of species diversity to the ecosystem are

• Increased biodiversity provides resistance to the ecosystem against natural disasters.
• Ecosystem with more species shows more yields and greater productivity with variation of biomass.
• Community with more species generally tends to be more stable than those with less species.

Question 3.
Species diversity decreases as we move away from the equator towards the poles. What could be the possible reasons?
Answer:
Species diversity decreases as we move towards the poles, because

1. temperature decreases and conditions become harsh.
2. both the amount and intensity of solar radiation decreases.
3. vegetation decreases.
4. less resources available to support species. Speciation is generally a function of time and environmental stability, so if conditions are too harsh, it is difficult for the species to survive and adapt. This results in decrease in biodiversity towards the poles.

Question 4.
Explain giving three reasons why tropic show, greatest levels of species diversity.
Or
Give three hypothesis for explaining, why tropics show greatest level of species richness.
Answer:
It is the variety in the number and richness of a species of a region. Sometimes, a species remains confined to a particular area and is found only in that area. Such species are said to be endemic, e.g., Indian giant squirrel is endemic to Panchmarhi hills in Madhya Pradesh.

The IUCN (International Union for Conservation of Nature and Natural Resources) recognises three types of species diversity, i.e.

1. Alpha (α) diversity It refers to the variety of species within a community. It is also referred to as species richness, i.e., the number of species per unit area.
2. Beta (β) diversity It refers to the diversity of species among communities.
3. Gamma (γ) diversity It refers to the diversity of species across a wide geographical range.

Question 5.
How is biodiversity important for ecosystem functioning?
Answer:
Nature always key a check on these activities to maintain a state of equilibrium (homeostasis), which further helps in the sustainable development of resources. However, overexploitation of biolgical resources by humans leads to destabilisation of ecosystem balance.
For example,

1. Decreased flora of an area leads to CO₂ increase in the atmosphere which causes temperature elevation of that area.
2. Increased carnivore population decreases the . herbivore population by predation which then increase the vegetation.
3. Declined population of microflora prevents the recycling between complex organic matter and simple inorganic matter.

Question 6.
What is a keystone species? Give an example.
Answer:
A keystone species is a species that has a disproportionately large effect on its environment relative to its abundance. Such species are important in maintaining the structure of an ecological community by affecting other organisms in an ecosystem and helping to determine the abundance of other species in the community, e.g. beaver (a mammal) who creates dams, modifies nutrient cycling, influences decomposition dynamics which ultimately influences the plants and animals of that area.

Question 7.
Write an account on loss of biodiversity in the world.
Answer:
The loss of biodiversity is a global crisis. Extinction of species is a natural phenomenon aided by the physical changes in the environment. However, the accelerated rates of species extinctions, that the world is facing now are largely due to human activities.

Till now, five episodes of mass extinction of species have occured in the history of biological evolution. The sixth episode of extinction of species however, is credited to human activities, which otherwise would not have occurred.

Question 8.
How does habitat fragmentation cause depletion of biodiversity?
Answer:
When large habitats are broken up into small fragments due to the various human activities, mammals and birds requiring large territories and certain animals with migratory habits are badly affected, leading to their population decline.

Question 9.
Briefly classify the extinction processes.
Answer:
The extinction of species is a natural process. Many species have disappeared and new ones have evolved to take over their place. There are three types of extinction processes

1. Natural extinction When there is change in environmental conditions, certain species disappear and others, (which are more adapted to changed conditions) take their place. This loss of species that occurred in the geological past at a very slow rate is known as natural extinction.
2. Mass extinction There have been several periods in the earth’s geological history when large number of species become extinct due to catastrophes, e.g. extinction of dinosaurs in end cretaceous period.
3. Anthropogenic extinctions Recently more number of species is disappearing from the face of the earth due to human activities. Man-made mass extinction represents a very severe depletion of biodiversity.

Question 10.
Since the origin of life on earth, there were five episodes of mass extinction of species.
(i) How is the ‘sixth extinction’, presently in progress, different from the previous episodes?
(ii) Who is mainly responsible for the ‘sixth extinction’?
(iii) List any four points that can help to overcome this disaster.
Answer:
(i) The current species extinction rate are estimated to be 100-1000 times faster than in pre-human times.
(ii) Human activities.
(iii) To prevent sixth extinction to take place we should

• prevent habitat loss and fragmentation.
• check over exploitation.
• prevent alien species invasion.
• prevent coextinction.
• conservation and preservation of species

Question 11.
How is diversity at all levels generally conserved?
Ans.
Diversity is recognised by gene pool, species and biotic community. The ecosystem is affected by changes due to the pollution, climatic changes and overexploitation, etc. There is need to prevent further destruction or degradation of habitats in order to conserve the biodiversity. These are on site (in situ) and off site (ex situ) strategies of conservation. Protected areas like national parks, sanctuaries and biosphere reserves also helps to maintain diversity.

Question 12.
State the significances of ex situ conservation.
Answer:
Ex situ conservation is outside conservation strategy, in which zoos help in captive breeding of organisms which are endangered, whereas botanical gardens have seed gene banks, tissue culture labs and other technologies for storing and growing germplasm.

Question 13.
There are many animals that have become extinct in the wild, but continue to be maintained in zoological parks.
(i) Which type of biodiversity conservation is observed in this case?
(ii) Name any other two ways, which help in this type of conservation?
Answer:
(i) It is an example of ex situ (off site) conservation. In this approach, threatened plants and animals are taken out of their natural habitat and placed in suitable settings and given special care.
(ii) Ciyopreservation and tissue culture are two ways that help in ex situ conservation.

Question 14.
Which type of conservation measures, in situ or ex situ will help the larger number species to survive? Explain.
Answer:
Out of the two, the in situ conservation measures will help in the survival of larger number of species.
In situ is onsite conservation, which implies that species are conserved in their natural habitat.
To conserve species in their natural habitat, the entire ecosystem has to be conserved, which include other organisms, biotic and abiotic component of the ecosystem associated with the target species.
Hence, in situ conservation helps in the survival of larger number of species.

Question 15.
What do you mean by national park?
Or
Write a note on national park.
Answer:
A national park is an area dedicated to conserve the environment, natural and historical objects and the wildlife therein. It also aims to provide enjoyment in such a manner and by such a means that will leave them unimpaired for the enjoyment of the future generations, e.g. Jim Corbett National Park, Uttarakhand.

Question 16.
What are hotspots of biodiversity?
Or
Write a note on biodiversity hotspots.
Answer:
Hotspots are areas that are extremely rich in species diversity, have high endemism and are under constant threat of extinction. Out of the total hotspots of the world, three are found in India.
They are Eastern Himalayas which extends from North-Eastern India to Bhutan, Western Ghats which include forests that lie in the states such as Karnataka, Maharashtra and Tamil Nadu and Indo-Burma region.

Question 17.
What is biosphere reserve? Mention its zones.
Or
Briefly discuss the four zones of biosphere reserve.
Answer:
A biosphere reserve is a specified area in which multiple use of the land is permitted. It is divided into four stones
(i) Core zone It is the innermost and legally protected where no human activity is allowed.
(ii) Buffer zone Here, limited human activity is allowed, like sustainable and recreational activities.
(iii) Transitional zone Anthropogenic activities like research and sustainable development is allowed.
(iv) Zone of human encroachment Here, normal anthropogenic activities are allowed.

Differentiate between the following (for complete chapter)

Question 1.
Sanctuary reserve and Biosphere reserve.
Answer:
Differences between sanctuary reserve and biosphere reserve are as follows

Sanctuary reserve	Biosphere reserve
Attention is not given to biotic community, i.e. conservation is species oriented.	Attention is focused on biotic community as a whole, i.e. conservation is ecosystem oriented.
Limits are not circumscribed.	Boundaries are circumscribed by the state legislation.
There occurs limited biotic interference.	There occurs no biotic interference except in buffer zone.
Tourism in a sanctuary is permissible.	Tourism is not permissible inside biosphere reserve
Research and scientific management are lacking.	Research and scientific management are carried out.
Proper attention is not given to gene pool conservation of economic species, particularly in plants.	Due attention is given to the conservation of plants as well as animal species.

Question 2.
Beta (β) diversity and Gamma (γ) diversity.
Answer:
Differences between beta diversity and gamma diversity are as follows

Beta (β) diversity	Gamma (γ) diversity
It is diversity of species among communities.	It refers to the diversity of species across a wide geographical range.
It develops due to change in habitat of community along environment gradients.	It represents the total richness of species in all the habitats found within a region, geographical areas or landscape.
When the difference of species between the habitats is greater, it represents greater Beta-diversity.	When each habitat has a unique biota, gamma diversity is equal to average alpha diversity multiplied by the number of such habitats.

Question 3.
Species diversity and Ecological diversity.
Answer:
Differences between species and ecological diversity are as follows

Species diversity	Ecological diversity
It is related to the number, type and distribution of species found in given area.	It is the variety of ecosystems in a biosphere.
It is the trait of the community.	It is the diversity at the level of communities and ecosystems of region.
It is affected not only by the number of individuals, but also by the heterogeneity of the sample.	It is affected directly by the environment.

Question 4.
Alpha (α) diversity and Beta (β) diversity
Answer:
Differences between alpha and beta diversity are as follows

Alpha (α) diversity	Beta (β) diversity
It is the variety of species within a community.	It is diversity of species between communities.
It was defined by Whittaker as the species richness of a place.	It was defined by Whittaker as the extent of species replacement or biotic change along environmental gradients.
A community will have a high alpha diversity, when there is a high number of species and their abundance are much similar.	Beta diversity measures the turnover of species between two sites in terms of gain or loss of species.

Odisha State Board CHSE Odisha Class 12 Biology Important Questions Chapter 15 Ecosystem and Environment Important Questions and Answers.

CHSE Odisha 12th Class Biology Important Questions Chapter 15 Ecosystem

EcosystemClass 12 Important Questions CHSE Odisha

Very Short Answer Type Questions

Choose the correct option

Question 1.
Biotic components include
(a) producers, consumers and decomposers
(b) producers and consumers
(c) Both (a) and (b)
(d) None of the above
Answer:
(a) producers, consumers and decomposers

Question 2.
The non-green plants are as important as green plants because they
(a) cause human diseases
(b) cause diseases of other plants
(c) are useful in several industries
(d) bring about decomposition of dead animal and plant remains
Answer:
(d) bring about decomposition of dead animal and plant remains

Question 3.
Primary consumers are always
(a) producers
(b) carnivores
(c) herbivores
(d) omnivores
Answer:
(c) herbivores

Question 4.
Man is ………… .
(a) herbivorous
(b) carnivorous
(c) omnivorous
(d) producers
Answer:
(c) omnivorous

Question 5.
Secondary producers are
(a) herbivores
(b) producers
(c) carnivores
(d) None of these
Answer:
(d) None of these

Question 6.
Which of the following is an abiotic component of ecosystem?
(a) Bacteria
(b) Humus
(c) Plants
(d) Fungi
Answer:
(b) Humus

Question 7.
Decomposers are generally
(a) green plants
(b) phytoplanktons
(c) insects
(d) microorganisms
Answer:
(d) microorganisms

Question 8.
Abiotic components of an ecosystem include
(a) producers, consumers and decomposers
(b) producers and consumers
(c) only producers
(d) None of the above
Answer:
(d) None of the above

Question 9.
An ecosystem is not a /an
(a) open system
(b) closed system
(c) variable system
(d) None of the above
Answer:
(b) closed system

Question 10.
Trophic levels in ecosystem are formed by
(a) only bacteria
(b) only plants
(c) only herbivores
(d) organisms linked in food chain
Ans.
(d) organisms linked in food chain.

Question 11.
Detritus food chain begins with
(a) virus
(b) bacteria
(c) protozoan
(d) algae
Answer:
(b) bacteria

Question 12.
Which one of the following has the largest population in food chain?
(a) Producers
(b) Primary consumers
(c) Secondary consumers
(d) Decomposers
Answer:
(d) Decomposers.
As, they include microorganisms, they form largest population in a food chain and decompose dead plants and animals.

Question 13.
The second trophic level in a lake is ………….. .
(a) phytoplanktons
(b) zooplanktons
(c) benthos
(d) fishes
Answer:
(b) Zooplanktons.
They are primary consumers in an aquatic food chain who feed upon phytoplanktons.

Question 14.
A food chain can have trophic levels
(a) one
(b) two
(c) three
(d) multiple
Answer:
(d) multiple

Question 15.
Who proposed the concept of ecological pyramid?
(a) Odum
(b) Elton
(c) Tansley
(d) Clements
Answer:
(b) Elton.

Question 16.
Primary succession is development of communities on
(a) cleared forest area
(b) newly exposed habitat
(c) pond filled after a dry season
(d) freshly harvested crop field
Answer:
(b) newly exposed habitat

Question 17.
Lichen is pioneer in which succession?
(a) Hydrosere
(b) Lithosere
(c) Psammosere
(d) Halosere
Answer:
(b) Lithosere

Question 18.
Plant succession in a saline habitat is called
(a) hydrosere
(b) halosere
(c) psammosere
(d) xerosere
Answer:
(b) halosere

Question 19.
The first species that establishes itself in a barren habitat due to succession is called
(a) climax
(b) migrant
(c) colony
(d) pioneer
Answer:
(d) pioneer

Question 20.
When propagating units like seeds and spores enter a barren area to initiate the process of succession, it is called
(a) nudation
(b) reaction
(c) ecesis
(d) migration
Answer:
(c) ecesis

Question 21.
The rate of release of nutrients into atmosphere is regulated by
(a) temperature
(b) soil nature
(c) pH
(d) All of the above
Answer:
(d) All of the above

Question 22.
Weathering of rocks makes phosphorus available first to
(a) producers
(b) decomposers
(c) consumers
(d) None of the above
Answer:
(a) producers

Fill in the blanks

Question 1.
Plants are called as ……….. because they fix carbon dioxide.
Answer:
autotrophs

Question 2.
In an aquatic ecosystem, the limiting factor for the productivity is …….. .
Answer:
sunlight

Question 3.
Decomposers are generally ……… (green plants, microorganisms, phytoplanktons, insects)
Answer:
microorganisms

Question 4.
A detrivore is animal feeding on …………… .
Answer:
dead matter

Question 5.
Productivity is expressed in terms of …………… .
Answer:
g^-2 yr^-1 (kcal m^-2)yr^-1

Question 6.
Amount of energy transferred from one trophic level to next is ………. .
Answer:
10%.

Question 7.
Tip of an ecological pyramid is occupied by ………. .
Answer:
carnivores.

Question 8.
In an ecosystem dominated by trees, the pyramid of number is ………. type.
Answer:
inverted.

Question 9.
Green plants constitute ………….. trophic level.
Answer:
First

Question 10.
………… represents sedimentary type of nutrient cycle.
Answer:
Phosphorus.

Question 11.
In ……….. succession, dominant organisms are autotrophs.
Answer:
autotrophic

Question 12.
The individual transitional communities are called ………. .
Answer:
serai

Correct the statement if required, by changing the underlined word

Question 1.
The term ecosystem was proposed by Odum.
Answer:
Tansley

Question 2.
The two components of an ecosystem are plants and animals.
Answer:
biotic and abiotic.

Question 3.
Carnivores are always primary consumers.
Answer:
Herbivores

Question 4.
The raw material for decomposition is called vermicompost.
Answer:
detritus

Question 5.
Net primary productivity is GPP + R.
Answer:
GPR-R

Question 6.
Out of the total solar energy, PAR is only 1-5%.
Answer:
50%

Question 7.
Phytoplanktons occupy more than one trophic level in pond ecosystem.
Answer:
Fishes.

Question 8.
Pyramid of energy is always inverted.
Answer:
upright.

Question 9.
Pyramid of energy is always inverted.
Answer:
Always upright

Question 10.
Flow of energy declines as it passes from lower to higher trophic level. This is explained by first law of thermodynamics.
Answer:
It is correct.

Question 11.
Plant succession in a sandy area is lithosere.
Answer:
psammosere

Question 12.
The pioneer community in hydrosere is submerged plants.
Answer:
phytoplanktons

Question 13.
Climate control comes under supporting ecosystem services.
Answer:
Primary productivity

Question 14.
The first species that establishes itself in a barren habitat due to succession is called migrant.
Answer:
pioneer species

Question 15.
Lichens and mosses are the part of halosere.
Answer:
xerosere

Express in one or two words

Question 1.
What is the creating force of an ecosystem?
Answer:
Solar energy.

Question 2.
What type of ecosystem is represented by pond?
Answer:
Freshwater ecosystem.

Question 3.
Name the common detritivores in an ecosystem.
Answer:
Earthworms

Question 4.
Name the two basic categories of an ecosystem.
Answer:
Natural and Artificial ecosystem

Question 5.
Name the largest decomposers of forest floor.
Answer:
Microorganisms

Question 6.
Name the term used for rate of storage of organic matter not used by heterotrophs.
Answer:
Gross primary productivity

Question 7.
Name any two organisms, which can occupy more than one trophic level in an ecosystem.
Answer:
Human beings and birds (e.g. sparrow).

Question 8.
State, what does standing crop of a trophic level represent?
Answer:
Standing crop represents total amount of living matter or organic matter present in an ecosystem in an unit area and at a specific time.

Question 9.
List any two ways of measuring the standing crop of a trophic level.
Answer:
Two ways of measuring the standing crop of a trophic level are

• Biomass of living organisms.
• Number in an unit area.

Question 10.
Expand PAR.
Answer:
Photosynthetically Active Radiation

Question 11.
What is the starting point of a grazing food chain and of a detritus food chain?
Answer:
Producers and dead organic matter, respectively.

Question 12.
Which is the major reservoir of carbon on earth?
Answer:
Ocean.

Question 13.
Under what conditions would a particular stage in the process of succession revert back to an earlier stage?
Answer:
Natural or human induced disturbances like fire, deforestation, etc.

Question 14.
Give one examples of xerarch succession.
Answer:
Sand deserts and rock deserts (as there is no water and the substratum does not absorb rainwater).

Question 15.
How much of carbon is dissolved in the oceans?
Answer:
71%

Question 16.
Name the two forms of reservoir of carbon, that regulate the ecosystem carbon cycle.
Answer:
ocean and fossil fuel

Question 17.
How much carbon is fixed in the biosphere through photosynthesis annually?
Answer:
4 × 10¹³ kg

Question 18.
What do you understand by the term serai stage?
Answer:
The individual transitional communities are termed as serai stage.

Short Answer Type Questions

Question 1.
Write a note on ecosystem.
Answer:
Ecosystem is considered as an interactive system, where biotic and abiotic components interact with each other via energy exchange and flow of nutrients. An ecosystem can be either natural or artificial. Natural ecosystems These are capable of maintaining and operating themselves, without the interference of man. They are further classified as

Artificial ecosystems These are maintained and manipulated by man for different purposes, e.g. cropland, aquarium, etc.

Question 2.
Is an aquarium a complete ecosystem?
Or
Can an aquarium be considered a complete ecosystem?
Answer:
Yes, aquarium is a man-made ecosystem (artificial). If an ecosystem possesses all physical and biological components, then it is said to be complete.
Since, aquarium has biotic components (plants and fishes) and abiotic components (air and water) required for survival of fishes so, it is a complete ecosystem.

Question 3.
Apart from plants and animals, microbes form a permanent biotic component in an ecosystem.
While plants have been referred to as autotrophs and animals as heterotrophs, what are microbes referred to as?
Or
How do these microbes fulfil their energy requirements?
Answer:
Microbes are referred to as heterotrophs and saprotrophs. They fulfil their energy requirement by feeding on dead remains of plants and animals through the process of decomposition.

Question 4.
How are productivity, gross primary productivity, net primary productivity and secondary productivity interrelated?
Answer:
A constant input of solar energy is the basic requirement’ for any ecosystem so that the living organisms can survive, grow (make new cells) and maintain their internal orgnisation. The rate of synthesis of energy containing organic matter or biomass per unit area in unit time is called its productivity. It is expressed in terms of g^-2yr^-1 or (kcal m^-2) yr^-1. Productivity of an ecosystem can be categorised as primary and secondary productivity.

Primary Productivity:
It is the amount of biomass or organic matter produced per unit area over a time period by plants due to photosynthesis. It is expressed in terms of weight (g^-2d^-1) or energy (kcal m^-2).
The primary productivity has two aspects as discussed below

Gross Primary Productivity (GPP):
It is the total amount of produced organic matter during photosynthesis. A considerable amount of GPP is utilised or lost by plants in respiration.

Net Primary Productivity (NPP)
It is the available biomass for the consumption by heterotrophs (herbivores and decomposers). It is actually the amount of energy left in the producers after the utilisation of some energy during respiration. Thus, Gross Primary Productivity (GPP) minus the Respiration Losses (R) gives the Net Primary Productivity.

GPP – R = NPP where, R = Respiration losses.
Net primary productivity differs in different communities of plants, e.g.

• In terrestrial community, GPP is 2.7 times of NPP.
• In ocean community, GPP is 1.5 times of NPP.

Secondary Productivity:
It is the rate of assimilation and formation of new organic matter by consumers. It is small as compared to primary productivity and tends to decrease with an increase in the trophic level.

Question 5.
Primary productivity varies from ecosystem to ecosystem. Explain.
Answer:
Primary productivity varies from ecosystem to ecosystem because it depends on the plant species inhabiting the area and their photosynthetic activity. It also depends on various environmental factors like-light, temperature, rain, etc., and nutrient availability which varies in different ecosystems.

Question 6.
(i) What is primary productivity? Why does it vary in different types of ecosystems?
(ii) State the relation between gross and net primary productivity.
Answer:
(i) RIt is the amount of biomass or organic matter produced per unit area over a time period by plants due to photosynthesis. It is expressed in terms of weight (g^-2d^-1) or energy (kcal m^-2).
Primary productivity varies from ecosystem to ecosystem because it depends on the plant species inhabiting the area and their photosynthetic activity. It also depends on various environmental factors like-light, temperature, rain, etc., and nutrient availability which varies in different ecosystems.

(ii) The relation between the gross and net primary productivity can be shown as P_n = P_g – R
where, P_n = Net Primary Productivity (NPP)
P_g = Gross Primary Productivity (GPP)
R = Respiration

Question 7.
Which of the following ecosystems will be more productive in terms of primary productivity? Justify your answer.
A young forest, a natural old forest, a shallow polluted lake, alpine meadow.
Answer:
Primary productivity can be defined as the rate at which primary producers (e.g. green plants) trap and store solar radiation in the form of biomass. This is measured in terms of weight (g^-2) and in terms of energy (kcal m^-2) per year in a given time. So, primary productivity varies from ecosystem to ecosystem and the ecosystem which possesses more producers will be more productive in terms of primary productivity.

So, young forests grow quicker than older mature forests and are more productive in terms of productivity.
The shallow polluted lake and alpine meadow will be less productive because of less number of producers and high amount of dead organic matter.

Question 8.
Why is the rate of assimilation of energy at the herbivore level called secondary productivity?
Answer:
The rate of assimilation of energy at herbivore (primary consumer) level is called secondary productivity because the biomass available to the organisms of this trophic level is a resultant of the primary productivity, which is formed by autotrophs (plants).

Question 9.
Why are oceans least productive?
Answer:
Oceans are least productive because

• there is insufficient radiation as sunlight decreases with the increasing depth of the ocean.
• oceans are nitrogen deficient which is an important nutrient for plants.
• conditions of high salinity in Ocean are not favourable for all plants.
• there is no substratum to support plants.

Question 10.
Write a note on decomposers.
Answer:
The microorganisms that breakdown the dead remains of plants, animals and organic matter into simpler inorganic substances are called decomposers.
These organisms are mainly aerobic and require oxygen-rich conditions to carry out their functioning. Their mode of nutrition is generally saprophytic as they ingest partially digested food material.

Question 11.
The rate of decomposition of detritus is affected by the abiotic factors like availability of oxygen, pH of the soil substratum, temperature, etc. Discuss.
Answer:
It is the process of breaking down of complex organic matter into inorganic substances like water, carbon dioxide and nutrients by decomposers. Detritus is the raw material for decomposition. It includes dead remains of plants (leaves, bark and flowers) and animals including faecal matter. Different steps involved in the process of decomposition are

1. Fragmentation It is the process of breakdown of detritus into smaller particles by detritivores (e.g. earthworm).
2. Leaching It is the process by which water-soluble inorganic nutrients go down into the soil horizon and get precipitated as unavailable salts.
3. Catabolism It is the process of degradation of detritus into simple organic material by the action of bacterial and fungal enzymes and then they are further converted into simpler inorganic compounds.
4. Humification It is a process that leads to the accumulation of a dark coloured amorphous and colloidal substance called humus. It is highly resistant to microbial action and undergoes decomposition at a very slow rate. Being colloidal in nature, it serves as a reservoir of nutrients.
5. Mineralisation It is the process of degradation of humus by microbial action and release of inorganic nutrients.

Some are eaten by insects and other animals. Nutrients and energy enter food web.

Diagrammatic representation of decomposition cycle in a terrestrial ecosystem

Question 11.
Justify the following statement in terms of ecosystem dynamics.
‘Nature tends to increase the gross primary productivity, while man tends to increase the net primary productivity.’
Answer:
Gross primary productivity of an ecosystem is the rate of production of organic matter during photosynthesis. So, nature tends to increase gross primary productivity through supporting the large number of plants (producers) in an ecosystem.
Net primary productivity is the available biomass for the consumption by heterotrophs (human and animals).
Man tries to increase net primary productivity by cultivating food and other crops to fulfil their needs.

Question 12.
‘The energy flow in an ecosystem is unidirectional’. Justify the statement.
Answer:
Energy in an ecosystem flows from producers to primary consumers, then from primary consumers to secondary consumers and so on. There is never a backflow of energy, i.e. energy cannot come back to a trophic level it has already passed. Therefore, the energy flow is unidirectional in an ecosystem.

Question 13.
The diagram shows the flow of energy through an ecosystem.

Which arrows represent the smallest amount of energy transferred between organisms and the largest amount of energy lost to the ecosystem?
Answer:
The smallest amount of energy transferred is represented by arrow 2 and largest energy loss by arrow 3.

Question 14.
‘The energy flow in the ecosystem follows the second law of thermodynamics’. Explain.
Answer:
According to second law of thermodynamics, every activity involving energy transformation is accompanied by dissipation of energy as heat and increase in disorderliness, except in deep hydrothermal ecosystems.

This is because out of the total PAR only 2-10% is captured by photosynthetic organisms in synthesis of organic matter. Further, this energy is used during various metabolic processes for the formation of food and a very little is stored as biomass. This trapped energy as biomass is transferred to next trophic level according to Lindeman’s law. Only 10% of the stored energy is passed from one trophic level to successive trophic level.

Question 15.
Organisms at a higher trophic level have less energy available. Comment.
Answer:
Energy flow in the ecosystem follows the 10% energy flow law, proposed by Lindeman. According to this law, only 10% of the energy available at each trophic level, gets transferred to the next trophic level, the rest is lost in the environment as heat.

As we move to higher trophic levels, the energy available to organisms keeps on decreasing. Thus, the top . carnivore gains the least energy in a food chain.

Question 16.
The number of trophic levels in an ecosystem are limited. Comment.
Answer:
The number of trophic levels in an ecosystem are limited and are not more than 3-4. Because the amount of energy flow decreases with successive trophic level, as only 10% of energy is transferred from one trophic level . to the next trophic level.
So, rest of the energy is lost in the form of respiration and other vital activities to maintain life. If more trophic levels are present, the residual energy will be limited and will decrease to such an extent that it cannot further support any trophic level. So, the food chain is generally limited to 3-4 trophic levels only.

Question 17.
Write a short note on food chain.
Answer:
The transfer of energy from green plants through a sequence of organisms, in which each eats the one below it in the chain and is eaten by the one above is called a food chain. It is actually a feeding chain of organisms in an ecosystem.

Based on the relationship among the organisms and the source of their nutrition or food, organisms occupy a specific place in the food chain that is known as their trophic level. An assemblage of trophic levels within the ecosystem is known as trophic structure.
A single species may occupy multiple trophic levels in a food.
Example

• Grass → Grasshopper → Frog → Snake → Eagle.
• Grass → Goat → Man

Question 18.
Three food chains are shown below
(i) Grass → Deer → Tiger
(ii) Tree → Beetle → Bacteria
(iii) Flowering plant → Butterfly → Bird
They can be represented by the three pyramids of numbers P, Q and R below

Write the correct combination that correctly matches food chains and pyramids.
Answer:
P → 3, Q → 1, R → 2

Question 19
Define ecological pyramids and describe with examples, pyramids of number and biomass.
Or
Write a short note on ecological pyramids.
Answer:
Ecological pyramids are diagrammatic illustrations of connection between different trophic levels in terms of energy, biomass and number of organisms.
Pyramid of biomass can be both upright and inverted. This can be understood from the examples given below

1. The pyramid of biomass in a pond ecosystem is inverted. Because, the sum total of the weight of phytoplankton (producer) is far less than a few fishes feeding on them, at higher trophic levels.
2. Pyramid of biomass in a forest ecosystem is upright because producers are more in biomass than primary consumers. Primary consumers are more than secondary consumers and secondary consumers are more than tertiary consumers (top).

Pyramid of energy is never inverted (i.e. it is always upright). Because, when energy flows from a particular trophic level to the next trophic level, some energy is always lost as heat at each step.
Each bar in the energy pyramid indicates the amount of energy present at each trophic level in a given time.

Question 20.
Write a note on pyramid of energy.
Answer:
Pyramid of Energy
It represents the total amount of energy utilised by different trophic level organisms in unit area over a period of time.

An ideal pyramid of energy with primary producers storing only 196 of solar energy as NPP

Its unit is kj/ha/yr. Pyramid of energy is always upright, i. e. it can never be inverted, because when energy is transferred from a particular trophic level to the next trophic level, some energy is always lost as heat at each step. It is in accordance with the first law of thermodynamics which states that energy is always conserved, it is neither created nor destroyed.

Question 21.
Fill in the missing stages in the given primary hydrarch succession.
Phytoplankton → A → B → C → Submerged free-floating → D → Forest plant stage
Answer:
A – Reed-swamp stage
B – Submerged plant stage
C – Marsh-meadow stage
D – Shrub stage.

Question 22.
Mention the role of pioneer species in primary succession on rocks.
Answer:
Lichens are pioneer species in primary succession on rocks. They secrete organic acids, which wither the rock and help in soil formation. Lichens by forming soil pave way for the next community, i.e. bryophytes.

Question 23.
Write the notes on the following
(i) Define pioneer species.
(ii) Among bryophytes, lichens and fern, which one is a pioneer species in a xeric succession and why?
Answer:
(i) The species that invade a bare area are called pioneer species.
(ii) In a xeric succession, the pioneer species are usually lichens then bryophytes, which are succeeded by ferns and some other bigger plants.

Lichen produces lichen acid and carbonic acid which corrode rock surface and release minerals required for growth. The corroded rock accumulates soil particle by wind and provides substrate for bryophytes and ferns.

Question 24.
State the function of a reservoir in a nutrient cycle. Explain the simplified model of carbon cycle in nature.
Answer:
The function of reservoir is to meet the deficit which occurs due to imbalance in the rate of influx and efflux.

Question 25.
Why are nutrient cycles in nature called biogeochemical cycles?
Answer:
Nutrient cycles are called biogeochemical cycles because ions/molecules of a nutrient are transferred from the environment (rocks, air and water) to organisms (life) and then brought back to the environment in a cyclic pathway.
The literal meaning of biogeochemical is bio – living organism and geo – rocks, air and water.

Question 26.
Outline the salient features of carbon cycle in an ecosystem.
Answer:
Carbon constitutes 45% of dry weight of organisms and it is next only to water. About 71% carbon is found dissolved in oceans. This oceanic reservoir regulates the amount of carbon dioxide (CO₂) in the atmosphere. The fossil fuels also represent a reservoir of carbon.Therefore, carbon cycling occurs through atmosphere, ocean and through living and dead organisms.

Approximately, 4 × 10¹³ kg of carbon is fixed in the biosphere through photosynthesis annually. Carbon-fixation or carbon assimilation refers to the conversion process of inorganic carbon (carbon dioxide) into organic compound. CO₂ is returned to the atmosphere via respiratory activities of producers and consumers. Decomposers also contribute substantially to CO₂ pool by their processing of waste materials and dead organic matter of land or oceans.

Various activites like burning of wood, forest fire and cqmbustion of organic matter, fossil fuels and volcanic eruption contributes to additional sources of CO₂ release into the atmosphere.
Human activities have significantly influenced the carbon cycle, e.g. rapid deforestation and burning of fossil fuel for energy and transport have significantly increased the rate of release of carbon dioxide into the atmosphere.

Question 27.
Complete the following model of carbon cycle by filling A, B, C, D, E and F.

Answer:
A – Respiration,
B – Photosynthesis,
C – Respiration,
D – Combustion of fossil fuels
E – Aquatic food chain and
E – Coal and oil.

Question 28.
Write important features of a sedimentary cycle in an ecosystem.
Answer:
Phosphorus cycle is an example of sedimentary nutrient cycle, since, it moves from land to the sediments at the bottom of the seas, then back to land again. The natural reservoir of phosphorus is earth’s crust. Rocks contain phosphorus in the form of phosphates.

By weathering and soil erosion, phosphates enter streams, rivers and then to oceans. With great movements of the tectonic plates, sea floor is uplifted and phosphates become exposed to the drained land surfaces. From here, weathering for a long period of time releases phosphates from rocks. Minute amount of these phosphates dissolve in soil and are absorbed by the roots of the plants. Herbivores and other animals obtain this element from the plants.

Question 29.
Describe the advantages for keeping the ecosystems healthy.
Or
Write a short note on ecosystem services.
Answer:
The various benefits that humans obtain from the ecosystem are collectively called ecosystem services.
The advantages of keeping an ecosystem healthy can be grouped into following types

Healthy ecosystems are the base for a wide range of economic, environmental and aesthetic goods and services. Ecosystem services are the products of ecosystem processes, e.g. healthy forest ecosystem purifies air and water, mitigates droughts and floods, cycles nutrients, generates fertile soils, provides wildlife habitat, maintains biodiversity, pollinates crops, provides storage site for carbon and also provides aesthetic, cultural and spiritual values.

Although it is difficult to find out the monitory value of all these services, still it is reasonable to think that biodiversity should carry a hefty price tag.

Robert Constanza and his colleagues recently have tried to put price tag on the nature’s life-support services. Researchers have put a price tag of US $ 33 trillion a year on these fundamental ecosystem services, which we utilise for free. This is almost twice the value of global Gross National Product (GNP), which is of US $ 18 trillion. Out of the total cost of various ecosystem services, soil formation accounts for 50%.

Contribution of other services like recreation and nutrient cycling are less than 10% each. The cost of climate regulation and habitat for wildlife are about 6% each.

Differentiate between the following (for complete chapter)

Question 1.
Standing crop and Standing state.
Answer:
Differences between standing crop and standing state are as follows

Standing crop	Standing state
It is amount of biomass present in an ecosystem.	It is amount of inorganic nutrients found in an ecosystem.
It represents the entire living matter.	It represents a part of non-living matter.
There is no circulation of this matter.	It circulates between living and non-living components of the ecosystem.
Continuous synthesis and consumption of biomass goes on.	It is being regularly depleted and replenished by the living matter.

Question 2.
Primary productivity and Secondary productivity.
Answer:
Differences between primary productivity and secondary productivity are as follows

Primary productivity	Secondary productivity
It is the rate of synthesis of organic matter by producers.	It is the rate of synthesis of organic matter by consumers.
It is comparatively quite high.	It is small and decreases with rise of trophic level.
It is due to synthesis of fresh organic matter from inorganic raw materials.	It is due to synthesis of organic matter from organic matter.

Question 3.
Detritivores and Decomposers.
Answer:
Differences between detritivores and decomposers are as follows

Detritivores	Decomposers
These are animals which feed on detritus.	These are microorganisms which obtain nourishment from organic remains.
These ingest the organic matter.	These decompose the organic matter by secreting digestive enzymes over it.
Ecologically, they cause pulverisation or fragmentation of detritus, e.g. earthworm, carrion beetle.	Ecologically, they cause humification and mineralisation of organic matter, e.g. Pseudomonas, slime moulds.

Question 4.
Production and Decomposition.
Answer:
Differences between production and decomposition are as follows

Production	Decomposition
It is the process of synthesis organic compounds/biomass from inorganic matter using sunlight by producers (e.g. plants).	It is the process of of breaking down of a substance/waste biomass into its constituent parts by decomposers, e.g. bacteria, fungi.
It traps the energy.	It releases the energy.
It builds up biomass from inorganic nutrients.	It releases inorganic nutrients from the biomass.

Odisha State Board CHSE Odisha Class 12 Biology Important Questions Chapter 14 Organisms and Environment Important Questions and Answers.

CHSE Odisha 12th Class Biology Important Questions Chapter 14 Organisms and Environment

Organisms and Environment Class 12 Important Questions CHSE Odisha

Very Short Answer Type Questions

Choose the correct option

Question 1.
Plants and animals living in a particular area constitute
(a) flora and fauna
(b) community
(c) ecosystem
(d) ecology
Ans.
(b) community

Question 2.
Biome is defined as
(a) sum of ecosystem in a geographical area
(b) sum of ecosystem of the whole earth
(c) biotic potential of a population
(d) biotic component of a ecosystem
Ans.
(a) sum of ecosystem in a geographical area

Question 3.
The adaptation of aquatic plants which roots are poorly developed is seen in
(a) Eichhornia
(b) Nymphaea
(c) Dunaliella
(d) Vallisneria
Ans.
(d) Vallisneria

Question 4.
Plenty of aerenchyma are found in
(a) hydrophytes
(b) mesophytes
(c) xerophytes
(d) halophytes
Ans.
(a) hydrophytes

Question 5.
The plant that does not belong to the ecological group, represented by the other plants is
(a) Pistia
(b) Casuarina
(c) Jussiaea
(d) Hydrilla
Ans.
(b) Casuarina

Question 6.
Sunken stomata are seen in
(a) hydrophytes
(b) xerophytes
(c) parasites
(d) symbionts
Ans.
(b) xerophytes

Question 1.
The organisms and their environment in a particular area
(a) bioregion
(b) biosphere
(c) ecosystem
(d) biome
Answer:
(c) ecosystem

Question 2.
Community is a group of independent and interacting population of
(a) different species
(b) same species
(c) same species in a specific area
(d) different species in a specific area
Answer:

Question 3.
Group of two or more than two plant species is called as
(a) plant community
(b) animal ecosystem
(c) plant ecosystem
(d) ecological niche
Answer:
(a) plant community

Question 4.
Which of the following is an animal of benthic zone?
(a) Frog
(b) Chemosynthetic bacteria
(c) Rat
(d) Human being
Answer:
(b) Chemosynthetic bacteria

Question 5.
Example of submerged hydrophyte is
(a) Hydrilla
(b) Lemna
(c) Nelumbium
(d) Eichhornia
Answer:
(a) Hydrilla

Question 6.
An association of two organism living together and benefitting each other is called ……….
(a) mutualism
(b) saprophytism
(c) parasitism
(d) commensalism
Answer:
(a) mutualism

Question 7.
A high density of tiger population is an area can result is
(a) predation
(b) interspecific competition
(c) intraspecific competition
(d) protocooperation
Answer:
(c) intraspecific competition

Question 8.
Which of the following shows detrimental effects on species
(a) mutualism
(b) predation
(c) parasitism
(d) competition
Answer:
(d) competition

Question 9.
Plasmodium is an example of
(a) predator
(b) endoparasite
(c) prey
(d) ectoparasite
Answer:
(b) ectoparasite

Question 10.
Monarch butterfly is not eaten by predators because of
(a) rough skin
(b) bitter taste
(c) foul smell
(d) colouration
Answer:
(b) bitter taste

Question 11.
The association of animals where both partners are benefitted is
(a) commensalism
(b) amensalism
(c) mutualism
(d) parasitism
Answer:
(c) mutualism

Question 12.
There are two optimal ways of exploitation one way is parasitism. Which is the other one?
(a) Antibiosis
(b) Competition
(c) Predation
(d) Commensatism
Answer:
(c) Predation

Question 13.
The most important factor which determined the increase in human population in India during 20th century is
(a) natality
(b) mortality
(c) immigration
(d) emigration
Answer:
(c) immigration

Question 14.
Population density is represented by
(a) N/S
(b) N/t
(c) t/S
(d) DNn/Dt
Answer:
(d) DNn/Dt

Question 15.
Natality increases the
(a) population density
(b) population size
(c) number of organisms in the population
(d) All of the above
Answer:
(d) All of the above

Fill in the blanks

Question 1.
Some xerophytes have multiple epidermis like …………. .
Answer:
Nerium

Question 2.
Leaves are large, broad and thin in …………. plants.
Answer:
mesophytic

Question 3.
Fish, amphibians and reptiles are ……………. .
Answer:
stenothermal animals

Question 4.
Root caps are present in ………….. .
Answer:
mesophytes

Question 5.
………. is the mechanism evolved by competing species for co-existence.
Answer:
Resource partitioning

Question 6.
Fig and wasp show ralationship.
Answer:
mutualistic

Correct the statements, if required by changing the underlined words

Question 1.
Plants which grow in bright light are called sciophytes.
Answer:
heliophytes

Question 2.
The organism which can tolerate a wide range of temperature are called stenothermal organisms.
Answer:
eurythermai

Question 3.
Plants growing in moist habitat are known as xerophytes.
Answer:
mesophytes

Question 4.
Plants growing in dry land are called mesophytes.
Answer:
xerophytes

Question 5.
Lichens represent an intimate mutualistic relationship between fungus and algae.
Answer:
It is correct

Question 6.
Mediterranean orchid ophrys employs sexual compatibility to get pollinated by bee.
Answer:
sexual deceit

Express in one or two words

Question 1.
The type of habitat in which plants are adapted to live in water scarcity.
Answer:
Xeric habitat.

Question 2.
The type of organisms who change their osmotic concentration according to the environment.
Answer:
Osmoconformers.

Question 3.
The factors which are related to soil in a habitat.
Answer:
Edaphic factors.

Question 4.
Plants growing or adapted to live in the shade.
Answer:
Sciophytes

Question 5.
Plants that grow best in direct sunlight.
Answer:
Heliophytes

Question 6.
The mechanism in which one animal kills other and eat it.
Answer:
Predation

Question 7.
The mechanism in which one species depend on the other for food and shelter.
Answer:
Parasitism

Short Answer Type Questions

Question 1.
Write different features of mesophytes.
Answer:
These are plants which grow in moist habitats and need well-aerated soils. These show the following characteristics

1. Root system is well-developed. They are branched, with root caps and root hairs.
2. Stems are aerial and freely branched.
3. Leaves are large, broad and thin.
4. Cuticle in all aerial parts is moderately developed.
5. The stomata are dorsiventral in dicotyledons and isobilateral position in monocot leaves.
6. The photosynthetic are in leaf, i.e., mesophyll tissue in differentiated into palisade, parenchyma and spongy parenchyma.
7. Water and food conductive tissue (vascular tissue) and mechanical tissue (collenchyma and sclerenchyma are well-developed.)

Question 2.
Write a note on hydrophytes.
Answer:
Hydrophytes
The plants growing in abundance of water or wet place are called hydrophytes. These plants may be partially or wholly submerged in water.
The aquatic habit at provides the following to the plant to grow

1. Availabity of nutrients in the water.
2. Plant growth matrix.
3. Approximate constant temperature (with least variation).
4. Availability of light.
5. Movement of water (waves strong or weak).

Based on the relation of plants to water and air.

Question 3.
Write short note on hydrophytic adaptations in roots of plants.
Answer:
Adaptations in hydrophytes can be discussed under three headings, i.e. morphological, anatomical and physiological.
1. Morphological Adaptations
Hydrophytes show various kinds of structural adaptations in their roots, stems and leaves.

• Roots may be entirely absent, e.g. Wolffia, Salvinia or poorly developed, e.g. Hydrilla.
• Roots are well-developed with distinct root caps, e.g. Ranunculus (emergent hydrophytes), aerenchyma present.
• In Eichhornia root caps are replaced by root pockets.
• Some plants, i.e. Jussiaea have two types of roots, one is normal type and other is spongy and negatively geotrophic.

Question 4.
What are free-floating and rooted hydrophytes?
Answer:
Free-floating hydrophytes These plants are absolutely float freely on the water surface and are not linked to the soil or substratum, e.g. Duck weed (Lemna and Wolffia), water hyacinth (Eichhomia crassipes), water ferns (Azolla and Salvinia).

Question 5.
What is habitat? Name some factors which define habitat of an organism.
Answer:
Habitat is a natural abode or a locality where a plant or animal grows or in other words, where a species lives.
The factors which define habitat can be climatic temperature, humidity, edaphic, i.e. related to soil, topographic or physical.

Question 6.
List various adaptations shown by epidermis in xerophytic plants.
Answer:
Physiologically dry habitats have plants of water, but the water is not available to the plant.
Based on their adaptation to water scarcity or drought conditions, xerophytes are of three types

1. Drought resistant plants are such that they can survive in extreme conditions, drought enduring plants can tolerate drought though they may hot have adaptation.
2. Drought enduring plants these do not have distinct adaptation.
3. Drought escaping plants these are short lived plants, complete the life cycle before the arrival of dry condition, e.g. Artemisia, Astragalus.

Question 7.
Does light factor affect the distribution of organisms? Write a brief note giving suitable examples of plants.
Answer:
Plants require sunlight for photosynthesis. Therefore, light is an important factor that affects the distribution of plants, e.g.

1. Many species of small plants (herbs and shrubs) growing in forests are adapted to photosynthesis optimally under very low light conditions so, they are seen distributed in shady areas under tall, canopied trees.
2. Many plants in the shade will grow vertically to gain access to light. These plants will appear to have smaller leafs than others of the same species of the , same age found in conditions with better sunlight.
3. Large sized trees will be present in areas that get abundant sunlight.

Question 8.
List any four characteristics that are employed in human population census.
Answer:
A population has the following characteristics that are employed in human population census

• Natality and mortality
• Sex-ratio
• Population density
• Age distribution

Question 9.
Describe the mutual relationship between the fig tree and wasp and comment on the phenomenon that operates in their relationship.
Answer:
The relationship between fig tree and wasp shows mutualism. The wasp while searching for sites to lay its eggs, pollinates the fig’s inflorescence.
On the other hand, the fig not only provides shelter (fruit) for oviposition, but also allows wasp’s larva to feed on its seeds.

Question 10.
What is mutualism? Mention any two examples where the organisms involved are commercially (2018) exploited in agriculture.
Answer:
It is an interaction that confers benefits to both the interacting species. Some examples of mutualism are

1. Lichens represent an intimate mutualistic relationship between a fungus (mycobiont) and photosynthesising algae (phycobiont) or cyanobacteria. Here, the fungus helps in the absorption of nutrients and provides protection, while algae prepares the food.
2. Mycorrhiza show dose mutual association between fungi and the roots of higher plants. Fungi help the plant in absorption of nutrients, while the plant provides food for the fungus, e.g. many members of genus -Glomus.
3. Plants need help from animals for pollination and dispersal of seeds. In return, plants provide nectar, pollens and fruits to them

Question 11.
Name important defence mechanisms in plants against herbivory.
Answer:
The herbivores are predators of plants and nearly 25% insects are phytophagous (feeding on plants). So, plants show morphological as well as chemical defence against herbivores such as

1. Thorns of rose and Acacia as well as cactus.
2. Certain plants produce chemicals, such as Opium, quinine, caffeine, nicotine, to protect them against being grazed by the animals.
3. Calotropis produces highly poisonous cardiac glycosides. So, the cattle and goats do not eat this plant.

Question 12.
What is predation? Explain with the help of suitable examples why is it required in a community with rich biodiversity.
Answer:
Predation is an interaction where one organisms (predator) kills and eats the other weaker organisms called prey.
Predation is a natural way of transferring the energy fixed by plants, to higher trophic levels.
Examples-snake eating a frog, tiger killing and eating a deer. Predators keep prey population under control which otherwise could achieve very high population densities and cause instability in ecosystem.
They also help in maintaining a species diversity in a community by reducing. The intensity of competition among competing prey species.

Question 13.
Name the interaction in each of the following:
(i) Cuckoo lays her eggs in the crow’s nest.
(ii) Orchid grows on a mango tree.
(iii) Ticks live on the skin of dogs.
Answer:
(i) Brood parasitism.
(ii) Commensalism, orchid is an epiphyte.
(iii) Parasitism, ticks are ectoparasites.

Question 14.
Explain the S-shaped pattern of population growth. How is J-shaped pattern different from it and why?
Answer:
S-shaped pattern of population growth form shows an initial gradual increase, followed by an exponential increase and then a gradual decline to a near constant level. It is different from J-shaped curve because J-shaped pattern shows exponential population growth and its abrupt crash after attaining the peak value. A-When resources are not limiting the growth, plot is exponential. B-When resources are limiting the growth, plot is logistic, K is the carrying capacity.

Question 15.
Explain diagrammatically the age structure of expanding, stable and declining population.
Answer:
The pyramids can be of three difference types as follows
1. Expanding (Triangular) This is a type of a growing population representation is like a triangle.
The population carries a high proportion of pre-reproductive individuals followed by reproductive individuals and post-reproductive individuals. Because of the very large number of pre-reproductive individuals, more and more of them enter reproductive phases and rapidily increases the size of the population.

2. Stable (Bell-shaped) This type of pyramid will represent a stationary or stable population having an equal number of young and middle aged class of individiuals.

3. Declining (Urn-shaped) This group has a small number of pre-reproductive individuals followed by a large number of reproductive individuals. As, there is less number of individuals in pre-reproductive groups.

Differentiate between the following (for complete chapter)

Question 1.
Population and Community.
Answer:
Differences between population and community are as follows

Population	Community
It is a grouping of individuals of a single species found in an area.	It is grouping of individuals of different species found in an area.
All the individuals of a population are morphologically and behaviourly similar.	Different members of a community are morphologically and behaviourly dissimilar.
Individuals of a population interbreed freely.	Interbreeding is absent amongst different members of a community.

Question 2.
Mesophytes and Hydrophytes.
Answer:
Differences between mesophytes and hydrophytes are as follows

Mesophytes	Hydrophytes
The plants grown on terrestrial habitate (land).	These are found in aquatic habitate (water).
The root septum is very cell developed in there plants.	Root system is not very well-developed or absent.
Leaves are broad, large and thin, mucilage covering is absent.	Leaves are, thin ribbon-shaped and covered with mucilage.

Question 3.
Mutualism and Commensalism.
Differences between mutualism and commensalism are as follows

Mutualism	Commensalism
In this two species are involved, both derive benefit from each other.	Two species involved but only one ge{ benefit other remain unharmed.
Example-see-anemone and hermit-crab.	Example-Sucker fish and shark.

Question 4.
Parasitism and Predation.
Answer:
Differences between parasitism and predation are as follows

Parasitism	Predation
It is host specific.	Predators have choice of prey.
Parasites are smaller is size.	Predators are large in size.
These have high reproductive potential.	These have low reproductive potential.

Question 5.
Ectoparasites and Endoparasites.
Answer:
Differences between ectoparasites and endoparasites are as follows

Ectoparasites	Endoparasites
Ectoparasites live on the surface of the host.	Endoparasites live in the body of the host.
They can be temporary, intermittent or permanent.	They are generally permanent parasites.
They can be hemiparasites or holoparasites.	They are usually holoparasites.
Respiration is aerobic.	Respiration is ofter anaerobic.
Specialisation has lead to loss of fewer strutures, e.g. wings in fleas, bedbugs and lice.	Specialisation has led the loss of several structures, e.g, digestive organs in Taenia.

Question 6.
Immigration and Emigration.
Answer:
Differences between immigration and emigration are as follows

Immigration	Emigration
It is permanent inward movement of some individuals into a local population.	It is a permanent outward movement of some individuals from a local population.
Size of gene pool and local population in increases.	Size of gene pool and local population decreases.
It is caused by availability of better living conditions.	It is caused by occurrence of deficiencies and calamities.

Question 7.
Camouflage and Mimicry.
Answer:
Differences between camouflage and mimicry are as follows

Camouflage	Mimicry
It is the ability of animals to blend with the background.	It is resemblance of on species of animals with another species.
Camouflage allows the animals to remain unnoticec from a distance.	Mimicry hides the true 1 identity of the animal species.
It is advantageous to both prey as well as predator.	It is advantageous to mimics against predation.

Question 8.
Intraspecific competition and Interspecific competition.
Answer:
Differences between intraspecific competition and interspecific competition are as follows

Intraspecific competition	Interspecific competition
It is competition among individuals of the same species.	The competition is amongst the members of different species.
The competition is for all the requirements.	The competition is for one or a few requirements.
The competing individuals have similar type of adaptation.	The competing individuals have different types of adaptations.
It is more severe due to similar needs and adaptations.	It is less severe as the similar needs are a few and the adaptations are different.

Odisha State Board CHSE Odisha Class 12 Biology Important Questions Chapter 13 Applications of Biotechnology Important Questions and Answers.

CHSE Odisha 12th Class Biology Important Questions Chapter 13 Applications of Biotechnology

Applications of Biotechnology Class 12 Important Questions CHSE Odisha

Very Short Answer Type Questions

Choose the correct option

Question 1.
A biotech company that released first ever genetically manipulated flower into the market is
(a) Cryobank
(b) Eli Lilly
(c) Florigene
(d) Genentech
Ans.
(c) Florigene

Question 2.
When an abnormal gene is replaced by normal gene, what do you call it? (2023)
(a) Gene mutation
(b) Gene donning
(c) Gene therapy
(d) Gene ligation
Ans.
(c) Gene therapy

Question 3.
Cry II Ab and Cry I Ab produce toxins that control
(a) cotton bollworms and corn borer, respectively
(b) corn borer and cotton bollworms, respectively
(c) tobacco budworms and nematodes, respectively
(d) nematodes and tobacco budworms, respectively
Ans.
(a) cotton bollworms and corn borer, respectively

Question 4.
First genetically modified plant commercially released in India is
(a) golden rice
(b) slow ripening tomatoes
(c) Bt-bringal
(d) Bt-cotton
Ans.
(d) Bt-cotton

Question 5.
Crystals of Bt toxin produced by some bacteria do not kill the bacteria themselves because
(a) bacteria are resistant to the toxin
(b) toxin is immature
(c) toxin is inactive
(d) bacteria enclose toxin in a special sac
Answer:
(c) toxin is inactive

Question 6.
Basic principle of developing transgenic animals is to introduce the gene of interest into the nucleus of
(a) somatic cell
(b) vegetative cell
(c) germ cell
(d) body cell
Answer:
(c) germ cell

Question 7.
Which among the following pharmaceutical products is harvested by using transgenic animals as bioreactors?
(a) Urokinase
(b) Insulin
(c) Lactoferrin
(d) All of these
Answer:
(d) All of these

Question 8.
The superbug can be used in
(a) oil spills
(b) water pollution
(c) eutrophication
(d) air pollution
Answer:
(a) oil spills

Question 9.
Biopatents are usually awarded for the discovery of
(a) new cell lines
(b) new DNA sequences
(c) GM strains
(d) All of these
Answer:
(d) All of these

Question 10.
Exploitation of patent biological resources of a country by another country is known as?
(a) biopatent
(b) biopiracy
(c) biowar
(d) All of these
Answer:
(b) biopiracy

Question 11.
Patents are given for
(a) discoveries
(b) inventions
(c) biopiracy
(d) gene therapy
Answer:
(b) inventions

Questions 12.
Which one of the following known as ‘Superbug’?
(a) Pseudomonas putida
(b) E. coli
(c) Aspergillus niger
(d) Acetobacter aceti
Answer:
(a) Pseudomonas putida

Questions 13.
US Patent on turmeric was challanged by
(a) CSIR
(b) EPO
(c) FSSAI
(d) FDI
Answer:
(a) CSIR

Questions 14.
Biopiracy is
(a) the use of biological patent
(b) thefts of plants and animals
(c) the use of bioresources of a country without proper authorisation
(d) stealing of biological resources
Answer:
(c) the use of bioresources of a country without proper authorisation

Correct the statements, if required, by changing the underlined words

Question 1.
An amorphous mass of parenchyma cells developed by tissue culture is called embryo.
Answer:
Callus

Question 2.
Petunia is ice minus strain which when sprayed on crops prevents frost formation.
Answer:
Pseudomonas

Question 3.
The natural source of vitamin-E is α-tocopherol.
Answer:
γ-tocopherol

Question 4.
The first GMO was created by Watson.
Answer:
Herbert Boyer and Stanley Cohen.

Question 5.
Soil bacterium Nitrosomonas syringae promotes ice nucleation in plants.
Answer:
Pseudomonas

Question 6.
The C-peptide is added during the maturation of pro-insulin to insulin.
Answer:
deleted

Question 7.
ADA treatment uses monocytes.
Answer:
lymphocytes

Question 8.
Antitrypsin is an agent that dissolves blood clot.
Answer:
Tissue Plasminogen Activator (TPA).

Question 9.
The first transgenic cow was Lilly.
Answer:
Rosie

Question 10.
A Pacific transgenic whale was generated by a growth hormone transgene.
Answer:
salmon

Question 11.
Transgenic mouse is smaller than the normal mouse.
Answer:
larger

Question 12.
Human protein α-2-trypin is used to treat emphysema.
Answer:
α-1-antitrypsin

Express in one or two word(s)

Question 1.
Define callus.
Answer:
It is undifferentiated mass of totipotent cells in the culture media.

Question 2.
Name one plant used to create novel transgenic plants.
Answer:
Petunia

Question 3.
Name the drugs isolated from Catharanthus roseus for cancer treatment.
Answer:
Vincristine and vinblastine.

Question 4.
Which microorganism is used as cloning host cell to produce humulin?
Answer:
E. coli

Question 5.
State the number of polypeptides found in mature human insulin.
Answer:
Two

Question 6.
What do you mean by the term transgene?
Answer:
oreign gene that is incorporated in an orgainsm to bring about desirable changes.

Question 7.
Where the LDL receptors are present?
Answer:
On the surface of hepatocytes

Question 8.
What is the name of the scientist who coined a sheep named Dolly?
Answer:
Keith Campbel and Ian Wilmut.

Question 9.
Name the institute that came up with a cloned sheep, named Dolly.
Answer:
Ian Wilmut of Roslin Institute in Scottland.

Question 10.
Which department of the Goverment of India is the nodal centre for Indian biosafety network?
Answer:
Department of biotechnology.

Question 11.
Which bacterium species is involved in Diamond vs Chakraborty case?
Answer:
Pseudomonas

Question 12.
What are transgenic animals?
Answer:
Genetically modified organism

Question 13.
Name the first transgenic cow that produced human protein enriched milk.
Answer:
Rosie

Question 14.
Name a transgenic animal being used in testing the safety of polio vaccine.
Answer:
Mouse

Question 15.
Mention the name of two common diseases that can be treated by medicines that contain biological products of transgenic animals.
Answer:
Cystic fibrosis and rheumatoid arthritis

Question 16.
What is patent?
Answer:
It is an open latter, a set of legal right, privilege and authority granted by a sovereign state to a person or institution for an invention for a limited period of time.

Fill in the blanks

Question 1.
…………… is a mammalian protein that have been successfully expressed in plants.
Answer:
Enkephalin.

Question 2.
Genetically engineered rice rich in vitamin-A is known as ……………… .
Answer:
golden rice

Question 3.
The recombinant human insulin is known as …………. .
Answer:
humulin

Question 4.
The full form of ELISA is ………… .
Answer:
Enzyme Linked Immunosorbant Assay.

Question 5.
Primarily, insulin is synthesised as ……………. .
Answer:
single polypeptide.

Question 6.
SCID is caused due to failure of synthesis of enzyme ………….. .
Answer:
adenosine deaminase.

Question 7.
…………. is the precursor of vitamin-A.
Answer:
ß-carotene

Question 8.
………… infects the roots of tobacco plants.
Answer:
Agrobacterium

Question 9.
The transgenic mouse is called as …………….. .
Answer:
Super mouse

Question 10.
…………. is a transgenic sheep.
Answer
Dolly

Question 11.
…………. is an infant nutrition formula that have been harvested using transgenic animals as bioreactors.
Answer:
Lactoferrin.

Question 12.
In 1990 ……….. the transgenic ewe was born in Scottland.
Answer:
Tracy

Question 13.
Full from of TPA is ……………. .
Answer:
Tissue Plasminogen Activator.

Question 14.
Neem patent case was first awarded in favour of ……………. .
Answer:
USA.

Short Answer Type Questions

Question 1.
Find out from the internet what is golden rice.
Answer:
Golden rice is a genetically modified rice with high levels of ß-carotene and other carotenoids. This rice is modified in order to enhance the quantity of vitamin-A in it. It is called golden due to the gold-like colour it gets from ß-carotene.

Question 2.
Can a disease be detected before its symptoms appear? Explain the principle involved.
Answer:
When the symptoms of the disease are not visible and the pathogen concentration is very low, then detection by conventional diagnostic tests is very difficult. However, detection at the above stated stage is made possible by molecular diagnostic techniques like the amplification of their nucleic acid by Polymerase Chain Reaction (PCR). The principle involved here is that a single DNA molecule can be copied endlessly in a test tube, using primers, DNA polymerase enzyme and free nucleotides and appropriate conditions.

Question 3.
How is DNA recombinant technology helpful in detecting the presence of mutated genes in the cancer patients?
Answer:
Molecular diagnosis in DNA recombinant technology uses a single-stranded DNA or RNA tagged with a radioactive molecules. It is allowed to hybridise to its complementary DNA in a clone of cells followed by detection using autoradiography. The clone having the mutated gene will not appear on the photographic film, because the probe used will not be complementary to the mutated gene. In this way, presence of mutated genes can be detected.

Question 4.
Why is the functional insulin produced, considered better than the ones used earlier by diabetic patients?
Answer:
Insulin prepared by rDNA technology does not produce sensitive allergic reactions and complications to the foreign protein which occurred in the case of earlier extracted insulin from the pancreas of slaughtered cattle or pigs. Thus, it is considered better than the earlier used insulin.

Question 5.
How is a mature, functional insulin hormone different from its pro-hormone form?
Answer:
Mature functional insulin is obtained by the processing of pro-hormone which contains extra peptide called C-peptide. This C-peptide is removed during the maturation of pro-insulin to insulin.

Question 6.
Refer to the diagram given below and answer the questions that follows

(i) The diagram shown above is insulin or proinsulin? Justify.
(ii) How is mature insulin synthesised?
Answer:
(i) The diagram is proinsulin as it contains C-peptide.
(ii) Mature insulin is synthesised by the removal of extra stretch called C-peptide.

Question 7.
How did an American Company, Eli Lilly use the knowledge of rDNA technology to produce human insulin?
Or
How did Eli Lilly synthesise the human insulin? Mention one difference between this insulin and the one produced by the human pancreas.
Or
What is humulin?
Answer:
The production cost was high due to its complex extraction and purification processes. Additionally, the purified insulin was contaminated by many pathogenic viruses. These problems have been overcome by the use of recombinant DNA technology. Insulin that is produced by recombinant DNA technology is known as recombinant human insulin.

Question 8.
Recombinant DNA technology is of great
importance in the field of medicine. With the help of a flow chart, show how this technology has been used in preparing genetically engineered human insulins.
Answer:
Insulin production by using recombinant DNA technology is shown in flow chart below

Question 9.
What is gene therapy? Name the first clinical case in which it was used.
Or
What is gene therapy? Illustrate using the example of Adenosine Deaminase (ADA) deficiency.
Answer:
It is a method of treatment which allows correction of a biochemical (like phenylketonuria) or a genetic defect*that has been diagnosed in a child or embryo. The defective mutant alleles of the gene are replaced by the normal gene insertion to take over the function of and compensate for the non-functional gene. Gene therapy is widely used to treat

• Biochemical disorder, e.g. alkaptonuria, phenylketonuria, albinism, etc.
• Chromosomal and gene disorders, e.g. Down’s syndrome, Turner’s, syndrome, Klinefelter’s syndrome, fragile X-syndrome, cri-du chat, Huntington’s disease, Tay-Sach’s syndrome, etc.

Question 10.
Write a note on genetically modified organism.
Answer:
The plants, bacteria, fungi and animals whose genes have been altered by manipulation are called Genetically Modified Organisms (GMO).
These are also called transgenic organisms, as they contain and express one or more foreign genes called transgenes. Herbert Boyer and Stanley Cohen developed the first GMO in 1973.

They transferred the Kanamycin antibiotic resistance gene of a bacterium into the another Kanamycin sensitive bacterium.
The genes which are being transferred are called transgenes.
The recepient bacterium later acquired Kanamycin resistance. Following many such discoveries, GMOs were developed. Novel plants and animals were created by genetic manipulation for human welfare.

Question 11.
Write a short note on transgenic plants.
Answer:
Herbicide resistant plants Herbicide resistant transgenic plants are generated by transferring bacterial herbicide resistant genes into plant cells grown in culture. Glyphosate is the most widely used broad-spectrum herbicide world over.

A glyphosate resistant gene from Petunia plant is transferred into isolated plant cell§ in culture and glyphosate resistant plants are generated.

Question 12.
Write a short note with 2-3 important points on Bacillus thuringiensis.
Or
Why do the toxic insecticide proteins secreted by Bacillus thuringiensis kill insects?
Answer:
Bacillus thuringiensis (Bt) It is a soil-borne, Gram-positive bacterium. It is used to create transgenic plants having resistance to different pests. The genes having insecticidal properties in the bacterium are isolated and incorporated into plants by using advanced biotechnological methods to create Bt plants. During sporulation, many Bt strains produce crystal proteins (proteinaceous inclusions) called S-endotoxins, that have insecticidal action.

When consumed by insect, these toxins bind to the surface of midgut epithelial cells and create pores that cause cell swelling and lysis, leading to the death of an insect, e.g. 5r-cotton, fir-tomato, soybean, coffee, etc.

Question 13.
Why does Bt toxin cannot kill the bacterium that produces it, but kills the insect that ingests it?
Answer:
Bt toxin is produced by a soil bacterium called Bacillus thuringiensis. This toxin does not kill the bacterium which produces it, because in them, it is present in an inactive and crystalline form. It becomes active and toxic only when it is consumed by insects such as lepidopterans, etc. due to the alkaline pH of the gut.

Question 14.
Bt cotton is resistant to pests, such as lepidopterans, dipterans and coleopterans. Is Bt cotton resistant to other pests as well?
Answer:
Bt cotton is made resistant only to certain specific taxa of pests. It is quite likely that in future some other pests may infest this Bt cotton. It is similar to immunisation against smallpox which does not provide immunity against other pathogens like those that cause cholera, typhoid, etc.

Question 15.
Why certain cotton plants are called Bt cotton?
Answer:
Cotton plants are called Bt cotton because they bear specific Bt toxin genes which were isolated from Bacillus thuringiensis and incorporated into certain cotton plants. This helps the host plants in developing resistance against and various pests like bollworms, etc.

Question 16.
Differentiate the terms ‘Cry’ and ‘cry’.
Answer:
‘Cry’ refers to protein symbol and its first letter is always capital. It is written in Roman letters, ‘cry’ refers to the gene which is usually written in small letters and is invariably in italics.

Question 17.
What are Cry proteins? Name an organism that produces it. How has man exploited this protein to his benefit?
Or
Name the source and type of cry genes used for incorporation into crops by biotechnologists. Explain, how have these genes brought beneficial changes in the genetically modified crops.
Answer:
The proteins encoded by the gene named cry are called Cry proteins. Organism that produces Cry proteins is Bacillus thuringiensis.
The cry genes are incorporated in several crop plants, which then develop resistance to a specific targeted pest, e.g. cry IAc and cry IIAb control the cotton bollworms and cry LAb controls corn borer.

Question 18.
Expand GMO. How is it different from a hybrid?
Answer:
GMO stands for Genetically Modified Organism.
It differs from a hybrid because in a hybrid, cross is done between total genomes of two species or strains, whereas in a GMO, foreign genes from entirely dilferent species are introduced in the organism and are usually maintained as extrachromosomal entity or are integrated into the genome of the organism.

Question 19.
Describe any three potential applications of genetically modified plants.
Answer:
Potential applications of genetically modified plants are

• Nutritional enhancement, e.g vitamin-A enriched rice.
• Stress tolerance crops are more tolerant to abiotic stresses such as cold, drought, etc.
• Creation of tailor made plants by using GM plants to supply alternative resources to industries in the form of starches, biofuels, etc.

Question 20.
What is meant by transgenic animals?
Answer:
Animals that have had their DNA manipulated to possess and express an extra (foreign) gene are known as transgenic animals, e.g. transgenic rats, rabbits, pigs, sheep, cows and fish. Over 95% of all the existing transgenic animals are mice. The gene that is being transferred is called transgene.

Question 21.
Comment on how transgenic animals have proved to be beneficial in
(i) Production of biological products?
(ii) Chemical safety testing?
Answer:
(i) The transgenic animals have been proved to be beneficial in the production of biological products like human protein α-1 antitrypsin (by coding genes from that protein only), in the treatment of emphysema and production of human protein (α-lactalbumin) enriched milk by transgenic cow, i.e. Rosie. This milk was more nutritionally balanced for human beings than natural cow’s milk.
(ii) Transgenic animals are studied for testing toxicity of drugs and other chemicals as they carry genes that make them more sensitive to toxic substances.

Question 22.
What is the utility of transgenic animals?
Or
With respect to understanding diseases, discuss the importance of transgenic animal models.
Answer:
Transgenic animals are important in the following fields
(i) They are being used in basic science research to elucidate the role of genes in the development of diseases like cancer, cystic fibrosis, rheumatoid arthritis and Alzheimer’s disease.
(ii) They are valuable tools in the drug development process itself.
(iii) Milk producing transgenics can produce medicines or human proteins (insulin, growth hormone, etc.) in large quantities.
(iv) Transgenics can be a source of transplant organs as well.

Question 23.
(i) Which animals are being used for testing the safety of vaccines? Name the vaccine for which trials are going on.
(ii) Name the first transgenic cow. Why is it important?
Answer:
(i) Transgenic mice are used for testing the safety of vaccines.
The trials are going on for polio vaccine.
(ii) Rosie was the first transgenic cow. It is important because it produces human protein enriched milk, even better than a natural cow’s milk.

Question 24.
(i) Explain alpha lactalbumin. Where is it produced in human body?
(ii) In what manner biotechnology has helped in production of more nutritionally balanced milk?
Answer:
(i) Alpha lactalbumin is a human milk protein which helps to increase the production of lactose in the body. It is produced in human milk.
(ii) Biotechnology has lead to production of transgenic cow, Rosie that produced around 2.4 g/L human protein enriched milk. This milk contained the human alpha lactalbumin and was nutritionally more balanced than a natural cow’s milk.

Question 25.
While creating genetically modified organisms, genetic barriers are not respected. How can this be dangerous in the long run?
Answer:
Genetic modification of organisms can have unpredictable results when such organisms are introduced into the ecosystem. Because the real effects of gene manipulation are visible only when such organisms interact with other components and organisms of the ecosystem.

Question 26.
Biopiracy should be prevented. State why and how?
Answer:
Biopiracy should he prevented because
(i) The countries and people concerned are not given adequate compensatory payment.
(ii) The countries/people also lose their right to grow and use breeding experiments to improve the other varieties of the same species.
It may be prevented by implementing specific laws that takes into consideration all the biopatents and biopiracy related issues.

Question 27.
State the initiative taken by the Indian Parliament against biopiracy.
Answer:
The Indian Parliament has recently passed the second amendment to the Indian Patents Bill that takes action against biopiracy. In India, the Patent Act was enacted in 1970 to protect their resources and traditional knowledge from being exploited by other countries.
This act has undergone many amendments in 1999, 2002, 2005 and 2006. The Indian biosafety network is headed by the Department of Biotechnology.

Question 28.
Write a self-explanatory note on biopatent.
Or What is patent?
Answer:
When an individual develops a new product or process innovation using his intellect, the innovation becomes his own. Various rules at national and international lands protects the misuse of this innovation, and also safeguards the rights of the innovater.
The new inventions can be safe protected by patents, design trademark, trade secrets and copy rights, etc.

It is a set of exclusive legal rights granted by a government to the inventors or their assignee for a limited period of time to prevent others from commercial use of their invention. When patent is granted for biological entities and for products derived from them, they are called biopatents. Primarily USA, Japan and members of European Union are awarding biopatents.

Question 29.
Name a set of principles that may be used to regulate human activities in relation to the biological world. Why are they important?
Answer:
A set of principles that may be used to regulate human activities in relation to the biological world are called bioethics.
These are important because the genetic modification of an organism can have unpredictable results when such organisms are introduced into the ecosystem.

Question 30.
What is meant by biopiracy?
Answer:
It refers to the use of bioresources by multinational companies and other organisations without proper authorisation from the countries and people concerned without compensatory payment. The majority of industrialised nations are financially rich but poor in biodiversity and traditional knowledge, in comparison to developing and underdeveloped countries.

Another cause of biopiracy is bioprospecting which means a thorough survey of a source material to expand the knowledge and applications in biotechnology. During the course of bioprospecting, scientists may transfer any biological resource which they may consider as novel.

Differentiate between the following (for complete chapter)

Question 1.
Herbicide resistant plants and Frost resistant plants.
Answer:
Differences between herbicide resistant plants and frost resistant plants are as follows

Herbicide resistant plants	Frost resistant plants
Generated by transferring bacterial herbicide resistant gene into plant cells.	Generated by deleting a gene that promotes ice nucleation.
e.g. Petunia contains glyphosate resistant gene which is being isolated to generate glyphosate resistant plants.	e.g. Pseudomonas syringae contains gene promoting ice nucleation. It is deleted by genetic engineering to produce ice minus strain.

Question 2.
Humulin and Wosulin.
Answer:
Differences between humulin and wosulin are as follows

Humulin	Wosulin
Manufactured by Eli Lilly corporation, USA.	Manufactured by wokhardt limited India.
First recombinant drug approved by FDA for human use.	General drug to treat diabetes.

Question 3.
Ex vivo gene therapy and In vivo gene therapy.
Answer:
Differences between Ex vivo gene therapy and In vivo gene therapy are as follows.

Ex vivo gene therapy	In vivo gene therapy
The cells are removed from the patient and genetic material is inserted in them in vitro, prior to transplantation of modified cells.	The genetic material is transferred directly into cells within a patient.
This approach is applicable to tissues that can be removed from the body and returned later and survive for longer period of time, e.g. hematopoietic cells.	It is only possible in tissues where the individual cells cannot be cultured in vitro in sufficient numbers or where cultured cells cannot be efficiently reimplanted, e.g. brain cells.

Odisha State Board CHSE Odisha Class 12 Biology Important Questions Chapter 12 Principles and Processes of Biotechnology Important Questions and Answers.

CHSE Odisha 12th Class Biology Important Questions Chapter 12 Principles and Processes of Biotechnology

Principles and Processes of Biotechnology Class 12 Important Questions CHSE Odisha

Very Short Answer Type Questions

Choose the correct option

Question 1.
GAATTC is the recognition site for which of the following restriction endonucleases?
(a) Hind III
(b) Eco RI
(c) Bam I
(d) Hae III
Answer:
(b) Eco RI

Question 2.
Given below is a sample of a portion of DNA strand giving the base sequence on the opposite strands. What is so special shown in it?
(a) Replication completed
(b) Deletion mutation
(c) Start codon at the 5′ end
(d) Palindromic sequence
Answer:
(d) Palindromic sequence

Question 3.
Agarose extracted from sea weeds is used in
(a) spectrophotometer
(b) tissue culture
(c) PCR
(d) gel electrophoresis
Answer:
(d) gel electrophoresis

Question 4.
The blotting of RNA is called
(a) Northern blot
(b) Southern blot
(c) Western blot
(d) Eastern blot
Answer:
(a) Northern blot

Question 5.
Eco RI cleaves the DNA strands to produce
(a) blunt ends
(b) sticky ends
(c) satellite ends
(d) ori replication end
Answer:
(b) sticky ends

Question 6.
DNA fragments generated by the restriction endonucleases in a chemical reaction can be separated by
(a) electrophoresis
(b) restriction mapping
(c) centrifugation
(d) polymerase chain reaction
Answer:
(a) electrophoresis

Question 7.
Commonly used vectors for human genome sequencing are
(a) T-DNA
(b) BAC and YAC
(c) expression vector
(d) T/A cloning vectors
Answer:
(b) BAC and YAC

Question 8.
Which procedure is followed for amplification of DNA?
(a) Electrophoresis
(b) Autoradiography
(c) Polymerase chain reaction
(d) Southern blotting
Answer:
(c) Polymerase chain reaction

Question 9.
The Polymerase Chain Reaction (PCR) is a technique that is used for
(a) in vivo replication of specific DNA sequence using thermostable DNA polymerase
(b) in vitro synthesis of mRNA
(c) in vitro replication of specific DNA sequence using thermostable DNA polymerase
(d) in-vivo synthesis of mRNA
Answer:
(c) In-vitro replication of specific DNA sequence using thermostable DNA polymerase.

Question 10.
The figure below shows three steps (A, B, C) of Polymerase Chain Reaction (PCR). Select the option giving correct identification together with what it represents?

(a) B – denaturation at a temperature of about 98°C separating the two DNA strands
(b) A – denaturation at a temperature of about 50°C
(c) C – extension in the presence of heat stable DNA polymerase
(d) A – annealing with two sets of primers
Answer:
(a) B – denaturation at a temperature of about 98°C separating the two DNA strands.

Question 11.
In recombinant DNA technique, the term vector refers to
(a) plasmids that can transfer foreign DNA into a living cell
(b) cosmids that can cut DNA at specific base sequence
(c) plasmids that can join different DNA fragments
(d) cosmids that can degrade harmful proteins
Answer:
(a) plasmids that can transfer foreign DNA into a living cell

Question 12.
The rDNA molecule is introduced into the cell of bacterium with the help of.
(a) restriction endonuclease
(b) DNA ligase
(c) electroporation
(d) None of the above
Answer:
(a) restriction endonuclease

Question 13.
The bacterial source of Hpa I is
(a) Haemophilus influenzae
(b) Bacillus amyloliquefaciens
(c) Providentcia stuarth
(d) Haemophilus parainfluenzae
Answer:
(d) Haemophilus parainfluenzae

Question 14.
Klenow fragment does not possess
(a) 5′ → 3′ exonuclease
(b) 3′ → 5′ exonuclease
(c) polymerase
(d) All of the above
Answer:
(a) 5′ → 3′ exonuclease

Correct the statements, if required, by changing the underlined word(s)

Question 1.
Restriction enzymes are used to cut single-stranded DNA.
Answer:
double-stranded DNA.

Question 2.
‘CO’ part in Eco RI stands for coenzyme.
Answer:
coli.

Question 4.
The first isolated restriction endonuclease was Hind III.
Answer:
Eco RI

Question 5.
DNA ligase forms phosphodiester bonds to ligate the DNA fragments.
Answer:
It is correct

Question 6.
Plasmids present in bacterial cells are linear double helical DNA molecules.
Answer:
circular

Question 7.
Taq polymerase is used between annealing and denaturation during PCR.
Answer:
extension.

Question 8.
A hybrid of plasmid and phage is YAC.
Answer:
BAC

Question 9.
Bacteria phage are autonomously replicating circular DNA.
Answer:
Bacteriophage

Fill in the blanks

Question 1.
DNA polymerase can be obtained from ……….. .
Answer:
Thermus aquaticus

Question 2.
The usual source of restriction endonuclease used in gene cloning is ………….. .
Answer:
bacteria .

Question 3.
Other than E. coli ………….. bacteria is used in recombinant DNA technology.
Answer:
Salmonella typhimurium.

Question 4.
First letter of restriction enzymes represents …………. .
Answer:
genus

Question 5.
Alkaline phosphatase is ………. an enzyme.
Answer:
DNA ligase

Question 6.
The vector for T-DNA is ………….. .
Answer:
Agrobacterium tumefaciens.

Question 7.
In biolistic method ………….. particles coated with foreign DNA are bombarded into target cells.
Answer:
gold or tungesten.

Question 8.
……………. is most commonly used process of foreign DNA injection in animal cells.
Answer:
Microinjection

Question 9.
…………. helps in selecting transformants and eliminating non-transformants.
Answer:
Conventional method

Express in one or two word(s)

Question 1.
Molecular scissors used in recombinant technology are known as
Answer:
restriction enzymes.

Question 2.
Which enzyme helps in joining DNA fragments?
Answer:
DNA ligase.

Question 3.
Name the process of transfer of protein molecules onto a membrane.
Answer:
Western blotting

Question 4.
Single-stranded fragments are transferred onto nitrocellulose filter paper by which process?
Answer:
Northern blotting

Question 5.
Name the bacterium that yields thermostable DNA polymerases.
Answer:
Thermus aquaticus

Question 6.
What is particle gun?
Answer:
It is a technique of bombarding microparticles of gold or tungsten with foreign DNA into target cell with high velocity.

Question 7.
Name one chemical that helps foreign DNA to enter host cell.
Answer:
Transformation

Short Answer Type Questions

Question 1.
Write a short note on genetic engineering.
Answer:
Genetic engineering is a modification, of chemical nature of genetic material (DNA/RNA) and their introduction into another organism to change the phenotypic characters of that organism.
This involves recombinant nucleic acid (DNA or RNA) techniques to form new combinations of heritable genetic material followed by the incorporation of material indirecdy through vectors or directly through microinjection and other techniques.

Question 2.
What are restriction enzymes? Mention their functions in recombinant DNA technology.
Answer:
The enzymes used for cutting the DNA during recombinant DNA technology are called restriction enzymes.
Restriction enzymes function as chemical knives or molecular scissors in genetic engineering. It recognises specific nucleotide sequence and makes cuts.

Question 3.
(i) Mention the difference in the mode of action of exonuclease and endonuclease.
(ii) How does restriction endonuclease function?
Answer:
(i) Exonucleases cleave base pairs of DNA at their terminal ends (either 5′ or 3 0 while, the endonucleases cleave DNA at any point within DNA segment at specific position except terminal ends.

(ii) Restriction endonuclease Eco RI cuts the DNA strands a little away from the palindromic sequences, but between the same two bases on the two strands

Question 4.
How are ‘sticky ends’ formed on a DNA strand? Why are they so called?
Or
A recombinant DNA is formed when sticky ends of the vector DNA and the foreign DNA join. Explain how sticky ends are formed and get joined?
Answer:
Restriction enzymes cut the strands of the DNA, a little away from the centre of the palindromic sites, but between the same two bases on opposite strands. This leaves sticky single-stranded position at the ends. These overhanging stretches are called ‘sticky ends’. These are named so, because they form hydrogen bonds with their complementary cut counterparts.

Question 5.
What does Hind and ‘III’ refer to in the enzyme Hind III?
Answer:

1. The first letter ‘H indicates the genus of the organism, from which the enzyme was isolated, i.e. H-genus, Haemophilus.
2. The roman number (III) denotes the sequence in which the restriction endonuclease from that particular genus, species and strain of bacteria have been isolated, i. e., third restriction endonuclease to be isolated from this species.

Question 6.
Collect five examples of palindromic DNA sequences by consulting your teacher. Better try to create a palindromic sequence by following base pair rules.
Answer:

Question 7.
Restriction enzymes should not have more than one site of action in the cloning site of a vector. Comment.
Answer:
Enzymes should not have more than one site of action.
This is because vectors have very few recognition sites for commonly used restriction enzymes.
If it will have more than one restriction sites it will generate various fragments. This will complicate the process of genetic engineering.

Question 8.
Draw agarose gel electrophoresis apparatus. Description is not required.
Answer:

(a) Agarose gel apparatus, (b) Fluorescent bands on the agarose gel slab containing resolved DNA fragments with differing molecular weights.

Question 9.
A mixture of fragmented DNA was electrophoresed in an agarose gel. After staining the gel with ethidium bromide, no DNA bands were observed. What could be the reason?
Answer:
DNA bands may not be observed when a mixture of fragmented DNA was electrophoresed, due to following reasons

1. Concentration of agarose in the gel was not proper, as greater the concentration of agarose gel used, the greater will be separation of small DNA fragments, whereas smaller the concentration of agarose, higher will be the resolution of bands.
2. If the concentration of salt in the buffer was not proper.
3. If DNA sample is contaminated with RNA or any other impurity or if the concentration of DNA is too low.

Question 10.
Name and describe the technique that helps in separating the DNA fragments by the use of restriction endonuclease.
Or
(i) Name the technique used for the separation of DNA fragments.
(ii) Write the type of matrix used in this technique.
(iii) How is the prepared DNA visualised and extracted for use in recombinant technology?
Answer:
(i) DNA fragments can be separated by the technique called gel electrophoresis.
(ii) The most commonly used matrix is agarose gel, which is a natural polymer extracted from sea weeds.
(iii) A compound called Ethidium Bromide (EtBr) stains DNA, which on exposure with ultraviolet radiationals gives orange light. Hence, DNA fragments appear as orange bands.

Question 11.
A plasmid DNA and a linear DNA (both of the same size) have one site for a restriction endonuclease. When cut and separated on agarose gel electrophoresis, plasmid shows one DNA band while, linear DNA shows two fragments. Explain.
Answer:
This is because plasmid is a circular DNA molecule.
When cut with enzyme, it becomes linear, but does not get fragmented. Whereas, a linear DNA molecule gets cut into two fragments. Hence, a single DNA band is observed for plasmid while, two DNA bands are observed for linear DNA in agarose gel.

Question 12.
Write the role of ‘ori’ and ‘restriction site’ in a cloning vector pBR322.
Answer:
Ori is the site where replication starts. This site is responsible for controlling the copy number of a vector. Restriction site is the site of ligation of alien/foreign DNA in the vector, in one of the two antibiotic resistance sites or coding sequence of β- galactosidase.

Question 13.
Write a short note on plasmids.
Answer:
These are small and double-stranded extrachromosomal DNA molecules having an origin of replication. They occur naturally in bacteria. Naturally occurring plasmids are not suitable for the cloning of genes. They are genetically engineered and made suitable for cloning.

Such plasmids are called cloning plasmids. A suitable cloning plasmid should preferably have the following properties

• It should be non-conjugative.
• It should have a relaxed replication and a high copy number.
• It should have an origin of replication.
• It should have unique restriction sites.
• It should have antibiotic marker gene for selection.

The most common cloning plasmid is designated as pBR322, where p stands for the word plasmid and B and R signify the names of its engineers (B. Boliver and R. Rodriguez) 322 is a numerical designation that has a relevance to these workers, who worked out the plasmid.

Question 14.
You have chosen a plasmid as vector for cloning your gene. However, this vector plasmid lacks a selectable marker. How would it affect your experiment?
Answer:
In a gene cloning experiment, first a recombinant DNA molecule is constructed, where the gene of interest is ligated to the vector and introduced inside the host cell (transformation). Since, not all the cells gets transformed with the recombinant/plasmid DNA, in the absence of selectable marker, it will be difficult to distinguish between transformants and non-transformants. Because the role of selectable marker is in the selection of transformants.

Question 15.
Draw a schematic sketch of pBR322 plasmid and label the following in it.
(i) Any two restriction sites
(ii) Ori and rop genes
(iii) An antibiotic resistant gene
Answer:
The labelled diagram of pBR322 plasmid is shown in the figure with
(i) Eco RI and Bam HI as restriction enzymes
(ii) Ori and rop genes
(iii) amp^R (an antibiotic resistant gene)

E. coli cloning vector pBR322

Question 16.
(i) How are recombinant vectors created?
(ii) For creating one recombinant vector only one type of restriction endonuclease is required. Give reason.
Answer:
(i) The vector DNA is cut at a particular restriction site using a restriction enzyme (to cut the desired DNA segment). The alien DNA is then linked with the plasmid DNA using an enzyme called ligase to form the recombinant vector.

(ii) Since, a restriction enzyme recognises and cuts the DNA at a particular sequence is called recognition site, the same restriction enzyme is used for cutting the DNA segment from both the vector and the other source to achieve as ends.

Question 17.
How bacterial cells are made competent to take up DNA?
Or
Describe the role of CaCl₂ in the prepration of competent cell.
Answer:
Since, DNA is a hydrophilic molecule, it cannot pass through the cell membranes. In order to force bacteria to take up the plasmid, the bacterial cells must first be made competent to take up foreign DNA. This is done by treating them with a specific concentration of a divalent cation such as calcium (Ca²⁺), which increases the efficiency with which DNA enters the bacterium through the pores in its cell wall.

Recombinant DNA can then be forced into such cells by incubating the cells with recombinant DNA on ice, followed by placing them briefly at 42°C (heat shock), and then putting them back on ice. This enables the bacteria to take up the recombinant DNA.

Question 18.
PCR is a useful tool for early diagnosis of an infectious disease. Comment.
Answer:
PCR is a very sensitive technique, which enables the specific amplification of desired DNA from a limited amount of DNA containing sample. Hence, it can detect the presence of an infectious organism in the patient at an early stage of infection (even before the infectious organism has multiplied to large number).

Question 19.
(i) Explain how to find whether an E coli bacterium has transformed or not, when a recombinant DNA bearing ampicillin-resistance gene is transferred into it
(ii) What does the ampicillin-resistant gene act as, in the above case?
Answer:
(i) The recombinant/transformant can be selected out from the non-recombinants/ non-transformants by plating the transformants on ampicillin-containing medium. The transformants will grow in it, while the non-transformants will not grow.
(ii) It acts as a selectable marker.

Question 20.
Name the source of the DNA polymerase used in PCR technique. Mention, why it is used ?
Or
Give the name of the organism from where the thermostable DNA polymerase is isolated. State its role in genetic engineering.
Answer:
Bacterium Thermus aquaticus is a source of enzyme Taq polymerase. As, it is a thermostable enzyme and works at high temperature, it is used to amplify DNA in vitro by PCR. The amplified fragment of desired DNA can be used to ligate with the vector for further cloning.

Question 21.
Rearrange the following in the correct sequence to accomplish an important biotechnological reaction
(a) In vitro synthesis of copies of DNA of interest
(b) Chemically synthesised oligonucleotides
(c) Enzyme DNA polymerase
(d) Complementary region of DNA
(e) Genomic DNA template
(f) Nucleotides provided
(g) Primers
(h) Thermostable DNA-polymers (From Thermus aquaticus)
(i) Denaturation of dsDNA
Answer:

(i) Denaturation of dsDNA
↓
(e) Genomic DNA template
↓
(g) Primers
↓
(b) Chemically synthesised oligonucleotides
↓
(d) Complementary region of DNA
↓
(f) Nucleotides provided
↓
(c) Enzyme DNA polymerase
↓
(h) Thermostable DNA polymerase (from Thermus aquaticus )
↓
(a) In vitro synthesis of copies of DNA of interest

Question 22.
While doing a PCR, denaturation step is missed. What will be its effect on the process?
Answer:
If denaturation of double-stranded DNA does not take place, then primers will not be able to anneal to the template. Amplification will not occur and no extension will take place.

Question 23.
A schematic representation of PCR up to the extension stage is given below. Give answers of the following questions.

(i) Name the process A
(ii) Identify B.
(iii) Identify C and mention its importance in PCR.
Answer:
(i) A – Denaturation process
(ii) B – Primers
(iii) C – Taq DNA polymerase.
Taq polymerase is a thermostable enzyme, which remains active during the high temperature and induces denaturation of DNA.

Differentiate between the following (for complete chapter)

Question 1.
Exonucleases and Endonucleases.
Answer:
Differences between exonucleases and endonucleases are as follows

Exonucleases	Endonucleases
Remove nucleotide from the outer ends of the DNA.	Make cuts at specific positions within the DNA.
It makes cut at only one of the two strands of DNA.	It makes cuts at both strands of DNA simultaneously.
e.g., snake venom and spleen phosphodiesterase.	e.g., deoxyribonuclease 1 and II.

Question 2.
Plasmid and Chromosomal DNA.
Answer:
Differences between plasmid and chromosomal DNA are as follows

Plasmid DNA	Chromosomal DNA
Extrachromosomal circular DNA.	Generally linear.
Not associated with histone proteins.	Associated with histone proteins.
Contains very few genes, but may not be necessary for the cell.	It Consists of complete genome vital for the cellular functions.
Replicates independently.	Replicates with genome.

Question 3.
Electroporation and Microinjection.
Answer:
Differences between electroporation and microinjection are as follows

Electroporation	Microinjection
In this method, electric field is applied to cells in order to increase the permeability of the cell membrane, allowing DNA to be introduced into the cell.	This is a vectorless method of direct delivery of recombinant DNA into plant and animal cells.
In this, brief pulses of high voltage electric currents are passed through the medium.	The foreign DNA is delivered into the nucleus with the help of microinjection or micropipette.
This procedure is mostly used for transforming plant protoplasts.	This method is particularly used for mammalian cells.

Question 4.
Type-I endonuclease and Type II endonuclease.
Answer:
Differences between type-I endonuclease and type-II endonuclease are as follows

Type-I endonuclease	Type-II
They consist of 3 different subunits.	They are structurally simple.
Require ATP, Mg2+, S-adenosyl-methionine for restriction.	Required Mg2+; for restriction.
Recognise specific sequences, but do not cut these sites.	Recognise specific sites and cut them.

Odisha State Board CHSE Odisha Class 12 Biology Important Questions Chapter 11 Microbes in Human Welfare Important Questions and Answers.

CHSE Odisha 12th Class Biology Important Questions Chapter 11 Microbes in Human Welfare

Microbes in Human Welfare Class 12 Important Questions CHSE Odisha

Very Short Answer Type Questions

Choose the correct option

Question 1.
The bacterium that converts milk into curd is ………. .
(a) Lactobacillus
(b) Azotobacter
(c) Rkizobium
(d) Clostridium
Answer:
(a) Lactobacillus

Question 2.
Fermentation of milk sugar, ……… is done by Lactobacillus.
(a) glucose
(b) fructose
(c) sucrose
(d) lactose
Answer:
(d) lactose

Question 3.
The antibiotic chloramphenicol can be obtained from the bacterium ……. .
(a) Streptomyces griseus
(b) S. aureofaciens
(c) S. venezuelae
(d) S. noursei
Answer:
(c) Streptomyces venezuelae

Question 4.
Acetobacter is involved in the production of
(a) citric acid
(b) acetic acid
(c) gluconic acid
(d) fumaric acid
Answer:
(b) acetic acid

Question 5.
Yeast and Acetobacter are both involved in the production of ……… from carbohydrates.
(a) penicillin
(b) citrate
(c) methane
(d) vinegar
Answer:(d) vinegar

Question 6.
Lipase enzyme is produced by the activity of
(a) Trichoderma viride
(b) Rhizopus sp.
(c) Aspergillus sp.
(d) None of these
Answer:
(b) Rhizopus sp.

Question 7.
The secondary treatment of sewage includes
(a) biological treatment
(b) chemical treatment
(c) filtration
(d) All of the above
Answer:
(a) biological treatment

Question 8.
In primary treatment of sewage, non-biodegradable particles are removed through a process of …………. .
(a) sedimentation
(b) sterilisation
(c) chemical treatment
(d) biological treatment
Answer:
(a) sedimentation

Question 9.
In secondary treatment of sewage in open bioreactors, the microorganisms grow and multiply to form ………. .
(a) manure
(b) compost
(c) sludge
(d) sediment
Answer:
(c) sludge

Question 10.
Milk enzyme that coagulates during curd formation is
(a) protease
(b) casein
(c) rennin
(d) pectinase
Answer:
(c) rennin

Question 11.
Name the bacterium, which produces Swiss cheese.
(a) Saccharomyces cerevisiae
(b) Propionibacterium shermanii
(c) Penicillium roqueforti
(d) Lactobacillus
Answer:
(b) Propionibacterium shermanii

Question 12.
Nystatin is obtained from
(a) Penicillium sp.
(b) Streptomyces griseus
(c) Streptomyces noursei
(d) Aspergillus sp.
Answer:
(c) Streptomyces noursei

Question 13.
The raw material used for the production of wine is
(a) grapes
(b) barley grain
(c) vinegar
(d) None of these
Answer:
(a) grapes

Question 14.
During commercial production of vinegar, secondary fermentation occurs under
(a) anaerobic conditions
(b) aerobic conditions
(c) Both (a) and (b)
(d) unfavourable conditions
Answer:
(b) aerobic conditions

Question 15.
The bacterium which acts on bio-waste to produce biogas is
(a) Methanobacterium
(b) Trichoderma
(c) Bacillus thuringiensis
(d) Azotobacter
Answer:
(a) Methanobacterium

Question 16.
The principal component of biogas is ……….. .
(a) hydrogen
(b) carbon dioxide
(c) ozone
(d) methane
Answer:
(d) methane

Question 17.
Which one of the following microbes is used as biocontrol agent?
(a) Papilloma virus
(b) Baculovirus
(c) Herpes virus
(d) Pox virus
Answer:(b) Baculovirus

Question 18.
Biopesticides are preferred over chemical pesticides due to their
(a) high pest specificity
(b) biodegradability
(c) non-biodegradability
(d) Both (a) and (b)
Answer:
(d) high pest specificity and biodegrdability

Question 19.
Which one of the following fungi makes symbiotic association with the plants?
(a) Glomus
(b) Nostoc
(c) BGA
(d) Rhizobium
Answer:
(a) Glomus

Question 20.
Which one of the following organisms has been commercialised as blood cholesterol lowering agent?
(a) Trichoderma polysporum
(b) Monascus purpureus
(c) Saccharomyces cerevisiae
(d) Aspergillus niger
Answer:
(b) Monascus purpureus

Question 21.
Which one of the following is mainly produced by the activity of anaerobic bacteria on sewage?
(a) Mustard gas
(b) Biogas
(c) Laughing gas
(d) Propane
Answer:
(b) Biogas

Question 22.
Secondary sewage treatment is mainly a
(a) chemical process
(b) biological process
(c) physical process
(d) mechanical process
Answer:
(b) biological process

Question 23.
Organisms called methanogens are most abundant in a
(a) polluted stream
(b) hot spring
(c) sulphur rock
(d) rumen of these
Answer:
(d) rumen of these

Question 24.
A biofertiliser is
(a) Rhizobium
(b) Azotobacter
(c) Nostoc
(d) All of these
Answer:
(d) All of these

Fill in the blanks

Question 1.
Roquefort cheese is ……….. by growing a specific ………… on it.
Answer:
ripened, fungus

Question 2.
The enzyme ……… is used in detergent formulations to remove oily stains from the laundry.
Answer:
lipase

Question 3.
The ……… from secondary treatment of sewage is generally released into ………. water bodies.
Answer:
effluent, natural

Question 4.
During sewage treatement, aerobic microbes are converted into mesh-like structure called ……………. .
Answer:
floes

Question 5.
Species of ………. is used for production of roquefort cheese.
Answer:
Penicillium

Question 6.
………. is an antibiotic that was used to treat soldiers during World War II.
Answer:
Penicillin

Question 7.
………. enzyme produced by Aspergillus niger is used for clarifying bottled juices.
Answer:
Pectinase

Question 8.
…………. is used as a blood cholesterol lowering agent.
Answer:
Statins

Question 9.
During the secondary treatment of primary effluents, the BOD level ……….. .
Answer:
decreases

Question 10.
During sludge digestion, bacteria produce gases like …………. .
Answer:
CH₄,H₂S, CO₂

Question 11.
The technology of biogas production was developed in India by ……….. .
Answer:
Khadi and Village Industries Commision (KVIC)/Indian Agricultural Research Institute (IARI).

Question 12.
The use of biological methods for controlling plant diseases and pests is called ……….. .
Answer:
biocontrol

Question 13.
…………. are used as biocontrol agents to get rid of moquitoes.
Answer:
Dragonflies

Question 14.
Baculovirus is a rod-shaped ………….. DNA virus.
Answer:
double-stranded

Question 15.
Rhizobium is a ………. bacteria that serves as biofertiliser.
Answer:
symbiotic

Question 16.
The first antibiotic was discovered by ………… .
Answer:
Alexander Fleming

Question 17.
……….. are used in biological control of aphids.
Answer:
Ladybirds

Question 18.
Azospirillum and Azotobacter are ………… bacteria.
Answer:
free-living

Question 19.
Plants with mycorrhizal association show tolerance to …………. and ……….. .
Answer:
salinity, drought

Correct the statement, if required, by changing the underlined word(s)

Question 1.
Antibiotic tetracyclin is obtained from Penicillium notatum.
Answer:
Streptomyces aureofaciens

Question 2.
The first antibiotic to be extracted from bacterial culture was nystatin.
Answer:
streptomycin

Question 3.
In ethyl alcohol production, the unicellular fungus, Penicillium is used.
Answer:
Saccharomyces cerevisiae

Question 4.
Acetic acid is produced by Lactobacillus sp.
Answer:
Acetobacter

Question 5.
In the secondary treatment of sewage, unwanted coarse, non-biodegradable particles are removed.
Answer:
primary treatment

Question 6.
Biogas production technology was developed in India mainly by NBRI and CDRI.
Answer:
KVIC, IARI

Question 7.
Methanogens are present in the liver of cattle.
Answer:
rumen

Question 8.
The major component of biogas is carbon dioxide.
Answer:
methane

Question 9.
Nostoc is present in root nodule of leguminous plants and fixes atmospheric nitrogen.
Answer:
Rhizobium

Question 10.
Biopesticides are non-biodegradable compounds.
Answer:
biodegradable

Question 11.
In paddy fields, blue-green algae fix phosphorus to enrich the soil fertility.
Answer:
nitrogen

Question 12.
Bacillus thuringiensis is a Gram-negative bacteria.
Answer:
positive

Question 13.
Baculoviruses are single-stranded RNA viruses.
Answer:
double-stranded DNA

Question 14.
Mycorrhizae provide cobalt to the roots of plants.
Answer:
phosphorus

Question 15.
Microorganisms belonging to the genus-Penicillium are used as agents of biological control.
Answer:
Nucleopolyhedrovirus

Express in one or two word (s)

Question 1.
The drink produced by fermentation of sap of palm tree.
Answer:
Toddy

Question 2.
The source of antibiotic streptomycin.
Answer:
Streptomyces griseus

Question 3.
Name the molecules which are used as blood cholesterol lowering agents?
Answer:
Statins

Question 4.
An enzyme used for the clarifying bottled fruit juice.
Answer:
Pectinase

Question 5.
Which organic acid gets converted into methane in the final step of biogas production?
Answer:
Acetate

Question 6.
Name a bacterium used as biopesticide.
Answer:
Bacillus thuringiensis.

Question 7.
Give an example of free-living fungi present in root ecosystem.
Answer:
Trichoderma

Question 8.
Name any two major components of biogas.
Answer:
CH₄ and CO₂

Question 9.
Name any one biocontrol agent.
Answer:
Baculovirus

Question 10.
A cheese with large holes produced by Propionibacterium shermanii.
Answer:
Swiss cheese

Question 11.
Name any two cyanobacteria used as biofertilisers
Answer:
Nostoc and Anabaena

Short Answer Type Questions

Question 1.
Write a note on fermentation by microbes and its two applications.
Or
Write a short note on fermentation.
Answer:
Fermentation is the process of conversion of carbohydrates to alcohol and CO₂ by some microorganisms in the absence of O₂. Microbes via fermentation are utilised for the synthesis of a number of products valuable for human beings.

Some of the applications of microbes are

• Production of bread using baker’s yeast.
• Wine, beer and other alcoholic drinks are produced by fermentation.

Question 2.
Mention a product of human welfare obtained with the help of each one of the following microbes.
(i) LAB
(ii) Saccharomyces cerevisiae
(iii) Propionibacterium shermanii
(iv) Aspergillus niger
Answer:

Microbe	Product of human welfare
(i) LAB	Curd
(ii) Saccharomyces cerevisiae	Bread, cakes, wines, beer
(iii) Propionibacterium shermanii	Swiss cheese
(iv) Aspergillus niger	Citric acid

Question 3.
How are fermented beverages prepared?
Or
Write a note on alcoholic beverages.
Answer:
Fermented beverages include wine, beer, whisky, brandy and rum which are obtained by fermenting malted cereals and fruit juices with Saccharomyces cerevisiae or ‘ brewer’s yeast to produce ethanol.

The production of variety of alcoholic drinks depends on the type of raw material used and the’type of processing, e.g. wine and beer are produced without distillation. Whisky, brandy and rum are produced by the distillation of the fermented broth.

Question 4.
How streptomycin is obtained?
Answer:
Streptomycin is an antibiotic that is obtained from Streptomyces griseus. The bacteria are cultured on medium containing glucose, soyameal and mineral salts. The pH of the medium is maintained at 7.4 -7.5. The fermentation is carried out under submerged condition for 5-7 days. It is done at 25-30° C.

Question 5.
Write a short note on alcoholic fermentation.
Answer:
Earlier, people used to produce alcohol by fermentation. Later, another method was used for the same which included catalytic hydration of ethylene. In modern time, again fermentation process is used for the production of ethanol.

It is used for dual purpose, i.e. as chemical and as fuel. Sugar-beet, potatoes, corn, cassava and sugarcane, etc., are used as substrate for the production of ethanol.

Yeasts (like Saccharomyces cerevisiae, S. uvarum, S. carlsbergensis), Candida brassicae, C. utilis and bacteria (Zymomonas mobilis) are used for the production of ethanol at industrial scale. The type’of alcoholic drink depends upon the raw material used for its production.
Beer is obtained by the fermentation of barley grains while wine is produced by grapes. This process of alcohol production is known as brewing. In this process, CO₂ is produced as a byproduct which is further

Question 6.
What are anaerobic sludge digesters?
Answer:
Sludge is the remaining part of organic matter after secondary treatment of sewage. In sludge digesters, other kinds of bacteria, which grow anaerobically, digest the bacteria and the fungi present in the sludge. During this process, bacteria produce a mixture of gases, such as methane, hydrogen sulphide and carbon dioxide which form biogas. It can be used as a source of energy.

Question 7.
Write a short note on secondary treatment of sewage.
Answer:
Secondary treatment of sewage is as follows
(i) This treatment is also known as biological treatment because it involves the use of microbes or biota for the treatment of sewage. The effluent from primary treatment is passed into large aeration tanks, where it is constantly mechanically agitated and air is pumped into it.

(ii) This air helps in the growth of useful aerobic, microbes into floes (masses of bacteria associated with fungal filament to form mesh like structures). The growth of microbes consumes major part of the organic matter, converting it into microbial biomass and releasing lot of minerals. This significantly reduces the BOD (Biochemical Oxyen Demand) of the water.

Question 8.
Write a short note on biogas.
Ans.
It is a complex mixture of gases, like CH₄, CO₂ and H₂, but its major content is methane gas. It is produced by the microbial activity during anaerobic digestion of biomass. Biogas is used as fuel. The type of gas produced by microbes during their growth and metabolism depends upon the microbes and the organic substrates they utilise. Certain bacteria, which grow anaerobically on cellulosic material, produce large amount of methane gas along with CO₂ and H₂ by the process called methanogenesis.

These bacteria are called methanogens and one such common bacterium is Methanobacterium. Methanogens produce large amount of biogas which contains about 50-70% CH₄, 30-40% CO₂, 1-5% H₂ and 0.01% oxygen.

Question 9.
Write a short note on biocontrol agents.
Answer:
Biocontrol agents involve the use of biological methods for controlling plant diseases and pests. Bacteria, fungi and viruses can act as biocontrol agents.
These microbes reduce the target species population through many ecological mechanisms, including pathogenicity, competition, production of chemicals and other interactions.

Question 10.
Write a short note on Bacillus thuringiensis (Bt).
Answer:
Bacillus thuringiensis is a soil-borne, Gram-positive bacterium. It is used to create a transgenic crop plant having resistance to several diseases. The genes encoding for insecticidal properties in the bacterium are isolated and incorporated into crop plants by using advanced biotechnological methods.

The bacterial spores can also be sprayed on the crops. They are ingested by insects and create pores in their gut wall which leads to their death. Thus Br-toxins work as biocontrol agent.

Question 11.
Why is Rhizobium categorised as a symbiotic bacterium? How does it act as a biofertiliser?
Answer:
Rhizobium lives in the root nodules of leguminous plants and fixes the atmospheric nitrogen by converting them into nitrogenous compounds.
These can be utilised by the plants as nutrients. Since, bacteria make the nitrogen available to plants in utilisable form, therefore, it is known as a biofertiliser.

Question 12.
How do plants benefit from having mycorrhizal symbiotic association?
Answer:

• The fungus absorbs phosphorus from the soil and passes it to the plant.
• Plants with mycorrhizal association show resistance to root borne pathogens.
• They show increased tolerance to salinity and drought.

Question 13.
Write short note on biofertiliser.
Answer:
Nutrients in optimum amount are important for the healthy growth, development and maximum productivity of plants.
Many nutrients required for the same include nitrogen and phosphorus which are the constituents of proteins, nucleic acids, coenzymes and some lipids like important biomolecules.
Phosphorus is present as insoluble phosphate in the soil sediments. On the other hand, nitrogen (80%) is present in atmosphere.

However, plants cannot use this atmospheric nitrogen and insoluble phosphates rather they either depend on microbes or chemical fertilisers to meet this basic necessity but, the continuous use of chemical fertilisers causes soil sickness, environmental pollution, etc. Thus, there is a pressure to shift to organic farming. Biofertilisers enrich the nutrient quality of soil by enhancing the availability of nutrients to the crops.

Differentiate between the following (for complete chapter)

Question 1.
Primary and Secondary sewage treatment.
Answer:
Differences between primary and secondary sewage treatment are as follows

Primary sewage treatment	Secondary sewage treatment
It is a physical process.	It is a biological process.
It involves the removal of grit and large pieces of organic matter.	It involves the digestion of organic matter by microbes.
It is carried out by the sedimentation and filtration process.	It is carried out by aerobic and anaerobic biological units.
It is relatively simple and less time consuming process.	It is relatively complex and takes a long time for its completion.

Question 2.
Primary sludge and Activated sludge.
Answer:
Differences between primary sludge and activated sludge are as follows

Primary sludge	Activated sludge
It is sludge formed during primary sewage treatment.	It is sludge formed during secondary sewage treatment.
It does not possess floes of decomposer microbes.	It possesses floes decomposer microbes.
It does not require aeration.	Formation of activated sludge requires aeration.
Little decomposition occurs during the formation of primary sludge.	A lot of decomposition occurs during the formation of activated sludge.

Question 3.
Swiss cheese and Roquefort cheese.
Answer:
Differences between Swiss cheese and Roquefort cheese are as follows

Swiss cheese	Roquefort cheese
They possess large holes.	They have relatively small holes.
These are made by Propionibacterium shermanii	These are ripened by Penicillium roquefort.

Question 4.
Methanogenic bacteria and Symbiotic bacteria.
Answer:
Differences between methanogenic bacteria and symbiotic bacteria are as follows

Methanogenic bacteria	Symbiotic bacteria
There bacteria are involved in energy production.	They are used as biofertilisers.
They live in the rumen of cattle.	They live in the root nodules of leguminous plants.
They produce methane gas by converting cellulose components into simple compounds, e.g. Methanobacterium.	They fix atmospheric nitrogen by converting it into nitrogenous compounds, e.g. Rhizobium.

Question 5.
Biopesticides and Biofertilisers.
Differences between biopesticides and biofertilisers are as follows

Biopesticides	Biofertilisers
They inhibit the growth of pests.	They help in the growth of crop plants.
They increase the yield by killing insects and pests, e.g, Bacillus thuringiensis.	They increase the yield by providing nutrients to the plants, e.g. Nostoc.

Long AnswerType Question

Question 1.
Discuss how waste water treatment can be done.
Answer:
Sewage refers to the municipal waste water generated everyday in cities and towns. Human excreta is the major component of it. It contains large amounts of organic matter and microbes, out of which many are pathogenic. So, it cannot be discharged directly into natural water bodies like rivers, streams, etc.

They need to be treated before their disposal. Conventional methods of waste treatment include cell pits, septic tanks, sewage farms, gravel beds percolating filters and activated sludge process with anaerobic digestion. These methods are less effective and sometimes non-productive.

The domestic sewage contains a large amount of degradable organic compounds. These can be degraded into simpler compounds with the help of microbes. The adequate supply of nutrients, oxygen and other essential compounds helps in the growth of microbes. It consequently enhances the rate of chemical degradation of sewage.

Therefore, modern method includes treatment of sewage before its disposal in local water bodies. Sewage is treated in Sewage Treatment Plants (STPs) in order to make it less polluting. The treatment of waste water is done by the heterotrophic microbes, that are naturally present in the sewage.

This treatment is carried out in the following three stages

Primary Treatment:
It is also known as physical treatment because it basically involves the physical removal of small and large, floating and suspended, non-biodegradable solids from sewage through filtration and sedimentation. Initially, floating debris is removed by sequential filtration. Then, the grit (soil and small pebbles) are removed by sedimentation process in settling tanks. Aluminium or iron sulphate is added in certain places for flocculation.

All solids that settle down during this step form the primary sludge. It traps lots of microbes and debris. The supernatant forms the effluent which is then taken from the primary settling tank for secondary treatment.

Secondary Treatment:
This treatment is also known as biological treatment because it involves the use of microbes or microbiota for the treatment of sewage. The effluent from primary treatment is passed into large aeration tanks, where it Is constantly, mechanically agitated and air is pumped into it.

This air helps in the growth of useful aerobic microbes” into floes (masses of bacteria associated with fungal filament to form mesh-like structures). While growing, these microbes consume major part of the organic matter, converting it into microbial biomass and releasing lot of minerals.
This significantly reduces the Biochemical Oxygen Demand (BOD) of water.

When the BOD of effluent is reduced significantly, it is then passed into a settling tank, where the bacterial ‘floes’ are allowed to sediment. This sediment is called activated sludge. A small part of the activated sludge is then pumped back into the aeration tank to serve as the inoculum. The remaining part of the sludge is pumped back into large tanks called anaerobic sludge digesters, in which other anaerobic bacteria (methanogens) are also present.

They digest the organic mass as well as aerobic microbes (bacteria and fungi of the sludge). During the digestion, mixture of gases like methane (CH₄), hydrogen sulphide (H₂S), carbon dioxide (CO₂), etc., are produced. These gases form biogas that is. used as a source of energy because it is inflammable.
The effluents from secondary treatment plant are released into natural water bodies like rivers and streams.

Tertiary Treatment:
It is an optional process including chemical precipitation. Its effectiveness depends on the number of microbes coming in contact with the pollutant organic molecules. Therefore, the secondary and tertiary treatments are performed in a constantly stirred open bioreactor that are supplied with nutrients.

Other Methods:
Sometimes a percolating or trickling fibre bioreactor is also used. In this method, a stone gravel or plastic sheet is used on which microbes have been immobilised. The sewage is allowed to flow on it. Deep shaft fermentation system is another method of waste water treatment.

This system contains a hole (deep shaft) in the ground. It is divided to allow the cycling and mixing of waste water, air and microbes. In some countries where sunlight hours are high, the algae-bacterial bioreactors are used. The biomass is used in the production of biogas and animal feed.

Odisha State Board CHSE Odisha Class 12 Biology Important Questions Chapter 10 Improvement in Food Production Important Questions and Answers.

CHSE Odisha 12th Class Biology Important Questions Chapter 10 Improvement in Food Production

Improvement in Food Production Class 12 Important Questions CHSE Odisha

Very Short Answer Type Questions

Choose the correct option

Question 1.
Inbreeding increases the frequency of
(a) recessive homozygotes
(b) dominant homozygotes
(c) heterozygotes
(d) Both (a) and (b)
Answer:
(d) Both (a) and (b)

Question 2.
Heterosis is
(a) hybrid inviability
(b) hybrid sterility
(c) hybrid vigour
(d) hybrid incompatibility
Answer:
(c) hybrid vigour

Question 3.
If you want to develop hybrid seeds within a bisexual flower which of the following parts need to be removed from the same flower?
(a) Stigma
(b) Ovary
(c) Anther
(d) Oviduct
Answer:
(c) Anther

Question 4.
Emasculation is one of the major steps during ………… .
(a) hybridisation
(b) pureline selection
(c) micropropagation
(d) crop improvement
Answer:
(a) hybridisation

Question 5.
Nutritional quality of crop plants like rice, maize, etc. is improved through ………… .
(a) biomagnification
(b) bioremediation
(c) biofortification
(d) bioaccumulation
Answer:
(c) biofortification

Question 6.
The capacity of a plant cell to give rise to a new plant is called …………. .
(a) cotipotency
(b) reproduction
(c) budding
(d) regeneration
Answer:
(a) totipotency

Question 7.
Single Cell Protein (SCP) is
(a) protein obtained from a clone of cells
(b) protein obtained from unicellular organisms
(c) biomass obtained from microorganisms
(d) proteins obtained from biomass of microorganisms
Answer:
(c) biomass obtained from microorganisms

Question 8.
Somatic hybridisation can be used for
(a) gene transfer
(b) transfer of cytoplasm
(c) formation of allopolyploids
(d) All of the above
Answer:
(d) All of the above

Question 9.
The emasculation is required for
(a) purelines
(b) cross pollination
(c) natural hybridisation
(d) selective hybridisation
Answer:
(d) selective hybridisation

Question 10.
An example of improved wheat
(a) Jaya
(b) Pusa Swarnim
(c) Sonalika
(d) Pusa Shubra
Answer:
(c) Sonalika

Question 11.
The organic nutrient of a plant tissue culture medium are
(a) sucrose
(b) glucose
(c) fructose
(d) All of these
Answer:
(d) All of these

Question 12.
Embryo like structure produced in vitro culture is called
(a) embryoid
(b) zygote
(c) somatic hybrid
(d) cybrid
Answer:
(a) embryoid

Question 13.
Which one of the following statement regarding pomato is correct ?
(a) It is a product of somatic hybridisation
(b) It is a product of gene manipulation
(c) product of sexual hybridisation
(d) product of cloning
Answer:
(a) It is a product of somatic hybridisation

Question 14.
An indigenous breed of cattle developed through cross breeding is
(a) Red Dane
(b) Karan Swiss
(c) Jersey (d) Rathi
Ans.
(b) Karan Swiss

Question 15.
The cross-breed of cattle is
(a) Ongole
(b) Sunandini
(c) Tharparkar
(d) Kangayam
Ans.
(b) Sunandini

Question 16.
In India, the milk yield of cattle is low due to
(a) inferior breeds
(b) inadequate food
(c) Both (a) and (b)
(d) use of medicines
Answer:
(c) Both (a) and (b)

Question 17.
Which of the following is a disease of cattle?
(a) Ranikhet disease
(b) Coryza
(c) Marek’s disease
(d) All of these
Answer:
(d) All of these

Question 18.
Fowlpox is caused by
(a) ectoparasites
(b) endoparasites
(c) bacteria
(d) virus
Answer:
(d) virus

Question 19.
Which of the following species of bee is commercially cultivated?
(a) Apis dorsata
(b) Apis mellifera
(c) Apis florea
(d) Apis indica
Answer:
(b) Apis mellifera

Question 20.
Which of the following species of honeybee is reared in artificial hives?
(a) Apis indica
(b) Apis dorsata
(c) Apis florea
(d) None of these
Answer:
(a) Apis indica

Question 21.
The term used for birds raised under domesticaton for economic purpose is called
(a) fisheries
(b) poultry
(c) apiculture
(d) aquaculture
Answer:
(b) poultry

Question 22.
Which of the following breed of buffalo has maximum milk fat percentage in its milk?
(a) Nagpuri
(b) Bhadawari
(c) Mehsana
(d) Murrah
Answer:
(d) Murrah

Question 23.
High milk yielding varieties of cows are obtained by
(a) superovulation
(b) artificial insemination
(c) use of surrogate mothers
(d) All of the above
Answer:
(d) All of the above

Question 24.
Artificial insemination is better than natural insemination in cattle because
(a) semen of good bulls can be provided everywhere
(b) there is no likelihood of contagious diseases
(c) it is economical
(d) All of the above
Answer:
(a) semen of good bulls can be provided everywhere

Question 25.
Which of the following about breeding is incorrect?
(a) By inbreeding purelines cannot be evolved
(b) Continued inbreeding, especially closed inbreeding reduces fertility and productivity
(c) Cross breeding allows desirable qualities of different breeds to be confined
(d) Inbreeding exposes harmful recessive genes that are eliminated by selection
Answer:
(a) By inbreeding purelines cannot be evolved

Question 26.
Which one of the following methods of selection is mainly useful for cross pollinated crops?
(a) Mass selection
(b) Pureline selection
(c) Progeny selection
(d) Clonal selection
Answer:
(b) Pureline selection

Question 27.
Which one of the following breeds of buffaloes is in most demand?
(a) Surti
(b) Jaffrabadi
(c) Murrah
(d) Bhadawari
Answer:
(c) Murrah

Question 28.
Heterosis cannot be maintained in sexually reproducing plants as it disappears on
(a) outbreeding
(b) inbreeding
(c) cross-breeding
(d) None of these
Answer:
(c) cross-breeding

Question 29.
Bagging is done to
(a) achieve desired pollination
(b) prevent contamination of unwanted pollen
(c) avoid self-pollination
(d) avoid cross-pollination
Answer:
(b) prevent contamination of unwanted pollen

Question 30.
A nutritional disease, which is found in poultry birds is
(a) rickets
(b) Ranikhet
(c) fowl cholera
(d) aspergillosis
Answer:
(a) rickets

Question 31.
In honeybees, the drones develop from
(a) fertilised egg
(b) unfertilised egg
(c) schizogony
(d) asexual reproduction
Answer:
(a) fertilised egg

Correct the statements, if required, by changing the underlined word(s)

Question 1.
The genetically superior individuals are called clones.
Answer:
hybrids

Question 2.
Selection is mixing out plants with desirable characters in a population.
Answer:
sorting out

Question 3.
Hybridisation is a cross between genetically similar organisms.
Answer:
genetically dissimilar

Question 4.
Hybridisation is one of the best methods adopted for crop improvement.
Answer:
Correct, no change

Question 5.
An amorphous mass of parenchyma cells developed by tissue culture is called embryo.
Or
In tissue culture, amorphous mass of thin-walled parenchymatous cells developing from proliferating cells is called explant.
Answer:
Callus

Question 6.
Naked plant cell without cell wall is called plasmalemma.
Answer:
Protoplast

Question 7.
Tissue culture technique was first attempted by Hanning.
Answer:
Haberlandt

Question 8.
Mutational variations are the ones produced during tissue culture.
Answer:
Somaclonal

Question 9.
NDRI is situated in Lucknow.
Answer:
Karnal

Question 10.
The giant honeybee, yielding maximum honey is Apis mellifera.
Answer:
Apis dorsata

Question 11.
In honeybee, the process of development of male bee without fertilisation is termed as swarming.
Answer:
Parthenogenesis

Question 12.
The branch of agriculture which deals with feeding shelter, health and breeding of domestic animals is called animal husbandry.
Answer:
It is correct

Question 13.
Animal food is generally rich in micronutrients.
Answer:
vitamins and roughage

Question 14.
Removal of stamens before release of pollen grains from the plants is called anthesis.
Answer:
emasculation

Question 15.
Mass selection is the simplest method of plant breeding applied mainly in case of self-pollinated crops.
Answer:
cross-pollinated

Express in one or two word(s)

Question 1.
Name the hormones used in tissue culture.
Answer:
2,4-D(auxin) and cytokinin

Question 2.
What is the use of polyethylene glycol in somatic hybridisation?
Answer:
Promotes protoplast fusion

Question 3.
Name an alga used as single cell protein.
Answer:
Chlorella

Question 4.
Which organs are develop during organogenesis?
Answer:
Root and shoot

Question 5.
The birds reared for meat purpose.
Answer:
Broilers.

Question 6.
Breeding between unrelated individuals.
Answer:
Outbreeding.

Question 7.
The important monosaccharide present in – honey.
Answer:
Levulose.

Question 8.
Name the strategy used to increase the homozygosity in cattles for desired traits.
Answer:
Inbreeding

Question 9.
Name an exotic breed of cow.
Answer:
Jersey

Question 10.
List any two economically important products for human obtained from Apis indica.
Answer:
Honey and beeswax

Question 11.
Name any two poultry diseases.
Answer:
Fowl pox and Ranikhet disease

Fill in the blanks

Question 1.
During hybridisation, emasculated buds need to be ……….. .
Answer:
bagged

Question 2.
Technique for production of disease-free plants is …………… .
Answer:
tissue culture

Question 3.
Crosses between the plants of the same variety are called ………. .
Answer:
inter-varietal

Question 4.
The most convenient way of removal of stamens is ……… .
Answer:
emasculation

Question 5.
Continued close inbreeding reduces fertility and productivity which is called ……….. .
Answer:
inbreeding depression

Question 6.
Milk yielding cattle breeds are known as ………. breeds.
Answer:
milch

Question 7.
Exotic breed of poultry bird is ……….. .
Ans. playmouth rock

Question 8.
The juvenile bees are reared in ……….. chamber of the honeycomb.
Answer:
brood

Question 9.
In bees, dance is meant for ………… .
Answer:
direction and distance

Question 10.
The loss of vigour due to continuous inbreeding is known as …………… .
Answer:
inbreding depression

Question 11.
The characteristic flight of the queen bee during fertilisation is known as ……………… .
Answer:
nuptial flight

Question 12.
Culturing of honeybee on commercial basis is known as …………. .
Answer:
apiculture

Short Answer Type Questions

Question 1.
Write note on hybridisation with 2-3 important points.
Answer:
It is possible by cross hybridising the two parents to produce hybrids that genetically combine the desired characters in a single plant. It is known to be a time consuming and tedious process as it involves collection of pollen grains from the desired plants (male parent) and have to be placed on the stigma of the selected flower (female parent) to incorporate desired traits.

It is also not necessary that the hybrids do combine desired characters. The chances of desirable combination is usually only one in few hundred to a thousand crosses carried out.

Some of the objectives of hybridisation are as follows

• To produce variations in progeny which are useful.
  It is achieved by recombination of characters.
• To make the use of hybrid vigour which is the superiority of progeny over its parents.
• To develop high yielding varieties which are also resistant to diseases.

Question 2.
Write a short note on emasculation.
Answer:
Emasculation It is the process of removal of stamens of a flower, without affecting the female reproductive organs. Emasculation is usually done in bisexual flowers before the anthers mature and stigma has become receptive. It can be done by various methods, such as, hand emasculation, suction method, hot water emasculation, alcohol treatment, cold treatment and genetic emasculation. Among these methods, hand and suction method are mostly used.

For example, in Triticum (wheat) flowers may be exposed to some chemical like 2,4-dichloro phenoxyacetic acid, maleic hydrozide or a panicle of Sorghum is dipped in lukewarm (50°C) water for 10 minutes, etc. These methods are applied on those cases where the methods of physical nature could not be applied.

Question 3.
(i) Mention two ways of inducing artificial mutation in a crop field.
(ii) List two steps that help in introducing the desired mutation into the crop.
Answer:
(i) Artificial mutation can be induced in a crop field by

• Using chemicals (like aniline).
• Radiations (like gamma-radiations).

(ii) Two steps that help in introducing the desired mutation into the crops are

• Screening the plant for resistance.
• Selecting the desirable plants for multiplication and for breeding.

Question 4.
How has mutation breeding helped in improving the production of mung bean crop?
Answer:
Mutation breeding is a phenomenon by which genetic variation is achieved through changes in base sequences within genes.
This creates a new character or trait absent in parental generation. It is the process of breeding by artificially inducing mutations using chemicals or radiations, e.g. in moong bean, resistance to yellow mosaic virus and powdery mildew were introduced by this method.

Question 5.
Discuss the importance of testing of new plant varieties in a geographically vast country like India.
Answer:
Before the new plants are generated through the plant breeding programmes, they need to be evaluated for their yield and other agronomic traits of quality, disease resistance, etc. The testing is done on the farmer’s field for atleast three growing seasons, at different locations in the country representing all the agroclimatic zones, where the crop is usually grown.

The material is evaluated in comparison to the best available local crop cultivar known as a check or reference cultivator.

Question 6.
What is meant by biofortification? Explain.
Answer:
It is a method of breeding crops with higher levels of vitamins, minerals, healthier fats to improve public health. The objective of breeding for improved nutritional quality is to enhance

• Protein, oil content and quality.
• Vitamin content.
• Micronutrients and mineral content.

Question 7.
Why are biofortified maize and wheat considered nutritionally improved?
Answer:
Biofortified maize and wheat are considered nutritionally improved, because of following reasons

• Maize hybrids have twice the amount of amino acid, lysine and tryptophan as compared to existing maize hybrids.
• Atlas-66 has been used as a donor for developing wheat varieties with improved protein content.

Question 8.
Enumerate four objectives for improving the nutritional quality of different crops for the health benefits of the human population by the process of ‘biofortification’.
Answer:
Four objectives for improving nutritional quality of crops

• Protein content and quality.
• Oil content and quality.
• Vitamin content.
• Micronutrient and mineral content.

Question 9.
Write a note on single cell protein.
Answer:
Microbial biomass passess about 45-55% protein, but in certain bacteria, the protein content may be upto almost 80%. The term ‘single cell protein’ refers to microbial biomass which acts as a source of mixed proteins. They are extracted from pure or mixed culture of organisms or cells.

SCP act as a supplement or alternative source of protein that is not supplied by the traditional or conventional agriculture production. Mirobes are being grown commercially as a sources of SCP. They are

• Yeast Saccharomyces cerevisiae
• Filamentous fungi Eusarum graminearum
• Bacteria Methylophilus methybtrophus
• Cyanobacteria Spirulina
• Algae Chlorella

Question 10.
How can healthy potato plants be obtained from a desired potato variety which is viral infected? Explain.
Answer:
Healthy potato plants can be obtained from a desired potato variety which is viral infected with the help of tissue culture.
The apical and axillary meristems of the infected plant remain virus free. Hence, they are removed and grown in vitro to obtain healthy potato plants. This is one of the application of tissue culture.

Question 11.
Write a note on micropropagation with 2-3 important points.
Answer:
Micropropagation or Clonal Propagation:
By the process of plant tissue culture which requires lesser space and lesser time, a large population of plants could be raised. Also since the plants produced are genetically identical, this process is also called as clonal propagation. Examples of plants cutlivated micropropagation include grapes, bamboo, coffee, banana, cardamoms, etc.

Question 12.
(i) Why are the plants raised through micropropagation termed as somaclones?
(ii) Mention two advantages of this technique.
Answer:
(i) The plants produced by micropropagation are genetically identical to the original plant from which they are grown, so they are called somaclones.

(ii) Advantages of this technique are

• More number of plants can be produced in a short time
• Disease free plants can be developed from diseased plants. Also seedless plants can be multiplied.

Question 13.
Why are plants obtained by protoplast culture called somatic hybrids?
Answer:
Plants obtained by protoplast culture are called somatic hybrids because they are formed by the fusion of isolated protoplasts from two different varieties of plants, each having a desirable character, to obtain a hybrid protoplast which can be further grown to form a plant.

Question 14.
Name the steps represented in the following process.

Answer:
A – Collection of germplasm.
B – Cross hybridisation among selected plants.
C – Selection and testing of superior recombinants.

Question 15.
Explain in brief the role of animal husbandry in human welfare.
Answer:
Domesticated animals of any breed or population of animal, which are intentionally kept in an agricultural setting for the benefit of human beings are referred to as ‘lifestock’. The agricultural practice of breeding and raising livestock is called animal husbandry.

It deals with care and breeding of animals like buffaloes, cows, pigs, horses, cattle, sheep, camels, goats, etc. by humans for various products like milk, meat, wool, etc. Poultry farming and fisheries are also considered as the

part of animal husbandry. According to a survey, about 70% of world’s livestock population is in India and China. Despite this huge production, their contribution to the world farm produce is only 25%, i.e the productivity per unit is very low.

Question 16.
What is meant by the term breed? What are the objectives of animal breeding?
Answer:
A breed is a group of animals related by descent and similar in most character like general appearance, features, size configuration, etc. Red Dane, Jersey, Brown Swiss are the examples of foreign breeds of cow.

Objectives of animal breeding are

• To increase the yield of animals.
• To produce disease resistant varieties of animals.
• To improve the desirable qualities of the animal produce such as milk, etc., having high protein content, etc.

Question 17.
What is the difference between breed and species? Give an example for each category.
Answer:
Breed is a specific group of animals or plants having homogeneous appearance, behaviour and other characteristics that distinguishes it from other animals or plants of the same species, e.g. Red Dane, Jersey, Brown Swiss are some common breeds of cow.

Species is one of the basic units of biological classification and a taxonomic rank. It can be defined as the largest group of organisms capable of interbreeding and producing fertile offspring, e.g. lion, cow, dog.

Question 18.
Enumerate any six essentials of good, effective ‘dairy farm management practices?
Answer:
Dairying is the management of animals for milk and its products for human consumption. Dairy farming integrated with agricultural farming has been the base of Indian economy since long time. It mainly deals with the processes and systems to improve quality and quantity of milk. Milk yield mainly depends on the quality of breeds. The dairy farm management includes the following main processes

1. Selection of good breeds with high yielding potential (under the climatic conditions of the area) and resistance to various diseases.
2. Cattle should be housed-well, have sufficient water and should be kept in diseased-free conditions.
3. They should be fed in a scientific manner with an emphasis on quality and quantity of fodder.
4. Regular inspection and keeping proper records of all the activities of dairy is also important.
5. Regular visits of a veterinary doctor is necessary.
6. Stringent cleanliness and hygiene of both the cattle and the handler are very important during milking, storage and transport of milk and its products.

Question 19.
Enlist the steps involved in inbreeding of cattle. Suggest two disadvantages of this practice.
Answer:
The mating of closely related animals within the same breed for 4-6 generations is called inbreeding. The strategies for inbreeding are

1. Superior males and females of the same breed are identified and then mated.
2. The progeny obtained from such type of matings are evaluated and superior males and females among them are identified for further mating.
3. In case of cattle, more milk per lactation is the criteria for superior female for cow and buffalo. Whereas a superior male is the one who give rise to superior progeny.

When the inbreeding is repeated it is called upgrading. Inbreeding is advantageous in the introduction of beneficial genes without changing the original genetic composition. But, inbreeding has disadvantages also. Inbreeding may lead to the expression of harmful effects of the deleterious gene. This results in inbreeding depression as it brings harmful recessive genes together. It cause decrease fertility and hybrid vigour of, in cattle.

Question 20.
State the disadvantage of inbreeding among cattle. How it can be overcome?
Or
How does inbreeding depression set in? Mention the procedure you would suggest to reverse this.
Answer:
Inbreeding depression usually reduces fertility and even productivity. It sets in due to continued inbreeding especially close inbreeding.
When inbreeding depression takes place or happens, selected animals of the breeding population should be mated with the unrelated superior animals of the same breed. This will help to restore the fertility and yield.

Question 21.
Why interspecific crosses are rare in nature and intergeneric crosses almost unknown?
Answer:
In interspecific crosses, male and female animals of two different related species are mated. The resultant progeny may combine desirable features of both the parents are infertile. Thus are rare in nature.
The same applies to intergeneric crosses. It is the crossing of two different animals/plants of different genus. It is almost unknown in nature as the gametes show species specificity.

Question 22.
What is artificial insemination? Mention two ways in which it is useful in breeding of dairy animals.
Answer:
Artificial insemination is a method of improvement in animals by using controlled breeding methods. During this process, the semen collected from the selected superior quality male parent is injected into the reproductive tract of selected female parent by the breeder. Breeding of dairy animals by the artificial insemination methods is useful in following two main ways

1. The bull of superior quality can be made to inseminate with many cows so, as to produce a large number of offsprings with desired trait.
2. The offsprings produced by artificial insemination have higher yield as compared to the normal offspring.

Question 23.
What is meant by transgenic animals?
Answer:
Refer to text on page no. 280.

Question 24.
What is the utility of transgenic animals?
Answer:
Transgenic animals are used to obtain various products like CC-antitrypsin, haemoglobin, iron binding protein, lacteferrin, etc. In Japan, gynogenesis is being used to improve fish size.

Question 25.
What is apiculture? How is it important in our lives?
Answer:
Refer to text on page no. 280.

Question 26.
Briefly describe swarming in honeybees.
Answer:
During early summer, when the beehive becomes loaded with honey and overcrowded by bees, the queen leave the hive with some drones and workers to establish a new colony at some other new place. This process is called as swarming.

Question 27.
Why are beehives kept in a crop field during flowering period ? Name any two crop fields where this is practised.
Answer:
Bees, while collecting nectar from flowers, transfer the pollen grains. Beehives are kept in a crop field during flowering period to enhance the pollination of the crop, which increases the crop yield. Also, bees can easily collect huge amounts of nectar from .the flowers of the crop in a close reach without much foraging.
This in turn increases the production of honey, e.g. this technique is practised in apple and mustard fields.

Question 28.
Social life of honeybees.
Or
Write a note on queen bee.
Answer:
Honeybees are social and polymorphic insects. They are of three main types

1. Queen It is fertile female. It is diploid as it develops from a fertilised egg. It feeds on royal jelly. It has well-developed ovary for laying eggs.
2. Drone It is a fertile male. It is haploid as it develops from unfertilised egg by the process of parthenogenesis. It copulates with queen.
3. Worker It is a sterile female. It is diploid. They are workers of beehives.

Worker bees have some specific structure such as long proboscis to collect nectar pollen basket to collect pollen, wax secreting glands in abdomen to secrete wax and powerful sting for defence.

Question 29.
What is beeswax?
Answer:
Beeswax is a secretory product of hypodermal glands of workers bees abdomen. It is used in the industries for the manufacture of cosmetics, polishes, paints ointments and lubricants.

Differentiate between the following (for complete chapter)

Question 1.
Hybrids and Cybrids.
Answer:
Differences between hybrids and cybrids are as follows

Hybrids	Cybrids
When nuclear and cytoplasmic fusion occur, the product is known as hybrid.	When only cytoplasmic fusion occurs which may be followed by the loss of any one of the nucleus, it is known as cybrid.

Question 2.
Inbreeding and Outbreeding.
Answer:
Differences between inbreeding and outbreeding are as follows

Inbreeding	Outbreeding
Mating of closely related animals of the same breed is called inbreeding.	Mating of unrelated animals belonging to different breeds or different species is called outbreeding.
It Increases homozygosity by which the prepotency of inbreed line increases.	It increases heterozygosity which results in hybrid vigour.
It reduces genetic variance within lines.	It increases genetic variance within lines.

Question 3.
Explant and Callus.
Answer:
Differences between explant and callus are as follows

Explant	Callus
These are small pieces of plant part of tissues that are aseptically cut and used to propagate a plant in vitro.	It is an unorganised and undifferentiated mass of proliferative cells produced when explants are grown on artificial culture medium in vitro.
Explants are readily available from parent plants.	Callus is obtained from culturing of explant within 2-3 weeks.

Question 4.
Callus culture and Suspension culture.
Answer:
Differences between callus culture and suspension culture are as follows

Callus culture	Suspension culture
In this culture, cell division in explant forms a callus. Callus is an irregular unorganised and undifferentiated mass of actively dividing cells.	It consists of single cells and small groups of cells suspended in a liquid medium.
The culture is maintained in agar medium	The culture is maintained in liquid medium
The medium contains growth regulators the auxin such as 2,4-D and cytokinin like BAP.	The medium contains growth regulator auxin such as 2, 4-D only.
Callus is obtained within 2-3 weeks.	Suspension cultrue grow much’faster than callus culture.
It does not need to be agitated.	It must be constantly agitated at 100-250 rpm (revolutions per minute).

Question 5.
Somatic embryogenesis and Somatic hybridisation.
Answer:
Differences between somatic embryogenesis and somatic hybridisation are as follows

Somatic Embryogenesis	Somatic hybridisation
A Somatic Embryo (SE) is an embryo derived from a somatic cell, other than zygote.	Somatic hybrids are formed through the fusion of protoplasts of two plants belonging to different varieties, species and even genera.
Somatic embryos are obtained usually on culture of the somatic cells in vitro, this process is called somatic embryogenesis	The process through which somatic hybrids are formed is known as somatic hybridisation
It is induced by a relatively high concentration of auxin, like 2, 4-D.	The fused protoplasts are either cultured in liquid or semi-liquid agar medium plates.

Question 6.
Broilers and Layers.
Answer:
Differences between broilers and layers are as follows

Broilers	Layers
These are comprised of both male and females.	These are females only.
Broilers are reared for meat production.	Layers are reared for egg production.
These attain a body weight of 2.2-2.4 kg within 6 weeks, this is due to faster growth.	Layers attain a body weight of approximately 1.5-1.8 kg at sexual maturity (20-2 weeks).

Odisha State Board CHSE Odisha Class 12 Biology Important Questions Chapter 9 Health and Diseases Important Questions and Answers.

CHSE Odisha 12th Class Biology Important Questions Chapter 9 Health and Diseases

Health and Diseases Class 12 Important Questions CHSE Odisha

Very Short Answer Type Questions

Choose the correct option

Question 1.
Which of the following diseases are communicable?
(a) Deficiencies
(b) Allergies
(c) Degenerative diseases
(d) Infectious diseases
Answer:
(d) Infectious diseases

Question 2.
The malignant malaria is caused by
(a) Plasmodium vivax
(b) Plasmodium malariae
(c) Plasmodium ovale
(d) Plasmodium falciparum
Answer:
(d) Plasmodium falciparum

Question 3.
Which is the infective stage of Plasmodium falciparum?
(a) Sporozoite
(b) Trophozoite
(c) Cryptozoite
(d) Merozoite
Answer:
(a) Sporozoite

Question 4
………… causes common cold.
(a) Virus
(b) Bacteria
(c) Protozoa
(d) Fungus
Answer:
(a) Virus

Question 5.
The confirmative test for typhoid is ………….. .
(a) Widal
(b) Mantoux
(c) CBC
(d) PCR
Ans.
(a) Widal

Question 6.
Through which vector is Wuchereria bancrofti transmitted?
(a) Anopheles
(b) Aedes
(c) Culex
(d) Tes-tse fly
Answer:
(c) Culex

Question 7.
The disease filariasis is caused by
(a) Treponema pallidum
(b) Neisseria gonorrhoeae
(c) Mycobacterium leprae
(d) Wuchereria bancrofti
Answer:
(d) Wuchereria bancrofti

Question 8.
Which parasitic causes amoebic dysentery?
(a) Escherichia coli
(b) Amoeba proteus
(c) Entamoeba histolytica
(d) Plasmodium vivax
Answer:
(c) Entamoeba histolytica

Question 9.
Which of the following is not a congenital disease?
(a) Haemophilia
(b) Down’s syndrome
(c) Cold
(d) Colour blindness
Answer:
(c) Cold

Question 10.
Common symptoms of typhoid are
(a) high fever and weakness
(b) stomach pain and constipation
(c) headache and loss of appetite
(d) All of the above
Answer:
(d) All of the above

Question 11.
Female Anopheles is a vector of
(a) fllariasis
(b) malaria
(c) typhoid
(d) AIDS
Answer:
(b) malaria

Question 12.
Which of the following is a pair of bacterial diseases?
(a) Typhoid and pneumonia
(b) Malaria and AIDS
(c) Ringworm and AIDS
(d) Cold and malaria
Answer:
(a) Typhoid and pneumonia

Question 13.
During allergic reactions which of the following is secreted?
(a) Allergens
(b) Histamines
(c) Immunoglobulins
(d) Pyrogens
Answer:
(b) Histamines

Question 14.
Cancer is
(a) non-malignant tumour
(b) controlled division of cells
(c) unrestrained division of cells
(d) microbial infection
Answer:
(c) unrestrained division of cells

Question 15.
The spread of cancerous cells to distant sites is termed as
(a) metamorphosis
(b) metagenesis
(c) metastasis
(d) metachrosis
Answer:
(c) metastasis

Question 16.
Blood cancer is called
(a) leukaemia
(b) haemophilia
(c) thrombosis
(d) haemolysis
Answer:
(a) leukaemia

Question 17.
Immunodeficiency syndrome could develop due to
(a) defective thymus
(b) defective liver
(c) weak immune system
(d) AIDS virus
Answer
(d) AIDS virus

Question 18.
Cirrhosis of liver is caused by the chronic intake of
(a) alcohol
(b) tobacco (chewing)
(c) cocaine
(d) opium
Ans.
(a) alcohol

Question 19.
Caffeine is a stimulant present in
(a) coffee
(b) tea
(c) cold drinks
(d) All of these
Ans.
(d) All of these

Question 20.
Cannabis sativa is the source of
(a) opium
(b) LSD
(c) marijuana
(d) cocaine
Ans.
(c) marijuana

Question 21.
The drug which is used for reducing pain is
(a) opium
(b) hashish
(c) bhang
(d) marijuana
Ans.
(a) opium

Question 22.
A tranquilliser is drug which
(a) relieves pain
(b) gives soothing effect to mind
(c) induces sleep
(d) has stimulating effect
Answer:
(a) relieves pain

Question 23.
The drug changes the person’s thought is
(a) cocaine
(b) barbiturate
(c) hallucinogens
(d) insulin
Answer:
(c) hallucinogens

Question 24.
Which one of the following is not correctly matched?
(a) Glossina palpalis – Sleeping sickness
(b) Culex – Filariasis
(c) Aedes – Yellow fever
(d) Anopheles – Leishmaniasis
Answer:
(d) Anopheles – Leishmaniasis

Question 25.
Stomach cleans pathogen by
(a) HCl
(b) gastric hormones
(c) Both (a) and (b)
(d) None of these
Answer:
(b) gastric hormones

Question 26.
Ability of body to fight against disease is called
(a) susceptibility
(b) immunity
(c) vulnerability
(d) irritability
Answer:
(b) immunity

Question 27.
Antigen binding site is present on antibody between
(a) two heavy chains
(b) two light chains
(c) one heavy and one light chain
(d) normal chains
Answer:
(b) two light chains

Question 28.
Which of the following is an opiate narcotic?
(a) Morphine
(b) LSD
(c) Amphetamines
(d) Basbiturates
Answer:
(a) Morphine

Question 29.
Which part of the brain is involved in loss of control when a person drinks alcohol?
(a) Cerebrum
(b) Medulla oblongata
(c) Cerebellum
(d) Pons Varolii
Ans.
(c) Cerebellum

Correct the statements, if required, by changing the underlined word(s)

Question 1.
The diseases which occur due to change in chromosomal structure are called degenerative diseases.
Answer:
congenital diseases

Question 2.
Plasmodicum vivax causes cerebral malaria.
Answer:
Plasmodium falciparum

Question 3.
The toxin released due to rupture of RBCs in malaria is haemoglobin.
Answer:
haemozoin

Question 4.
The other name for filariasis is amoebic dysentery.
Answer:
elephantiasis

Question 5.
Ringworm is a viral disease.
Answer:
fungal disease

Question 6.
Typhoid is diagnosed by Mantoux test.
Answer:
Widal test

Question 7.
Antibody-mediated immunity helps the body to differentiate between self and non-self cells during organ transplantation.
Answer:
Cell-mediated immunity

Question 8.
Cellular changes in body as a result of any wound or injury is called immunisation.
Answer:
inflammation.

Question 9.
Cellular barriers forms first line of defence.
Answer:
Physical barriers.

Question 10.
Viral oncogenes on activation lead to tumour formation.
Answer:
Cellular oncogenes

Question 11.
Which test is conducted to identify HIV ?
Answer:
ELISA

Question 12.
HIV is treated using a combination of madicines called antibacterial therapy.
Answer:
antiretroviral.

Question 13.
The ookinete penetrates through the stomach wall and encysts as an gamete.
Answer:
oocyst

Question 14.
Active immunisation against tetanus and diphtheria is achieved by antibiotics.
Answer:
exotoxins or toxoides

Question 15.
Caffeine is used to make tobacco.
Answer:
Nicotiana tabacum is used to make tobacco.

Question 16.
The mood altering drugs are tranquilisers.
Answer:
The mood altering drugs are psychotropic drugs.

Question 17.
Benzodiazepines is used as a stimulant.
Answer:
Cocaine is used as a stimulant.

Question 18.
Antibody production is assisted by monocytes.
Answer:
B-cells

Question 19.
Cell-mediated immunity is mainly function of paratope.
Answer:
T-cells

Express in one or two word(s)

Question 1.
What is called protein pathogen that does not contain nucleic acid?
Answer:
Prions.

Question 2.
The nature of spread of communicable disease.
Answer:
Epidemiology

Question 3.
Name the test specifically employed to determine the presence of disease causing Salmonella typhi.
Answer:
WIDAL Test

Question 4.
Causative organism of malignant malaria.
Answer:
Plasmodium falciparum

Question 5.
Ringworms belong to the fungal genus.
Answer:
Microsporum

Question 6.
The disease transmitted through contact.
Answer:
Measles

Question 7.
An oral dose of drug given for amoebiasis treatment.
Answer:
Metronidazole

Question 8.
Colostrum is rich in which type of antibody(20l9>
Answer:
IgA

Question 9.
The type of immunisation performed for treating snake bite.
Answer:
Passive immunisation.

Question 10.
The type of immunity responsible for graft rejection.
Answer:
Cell-mediated immunity.

Question 11.
The genetic material of HIV?
(Only DNA, only RNA, Both DNA and RNA, Nucleoproteins)
Answer:
Only single-stranded RNA.

Question 12.
The tissue affected in sarcoma.
Answer:
Bone, muscle and lymphnode

Question 14.
The test conducted to detect HIV infection.
Answer:
ELISA, PCR test

Question 15.
What is the source of LSD?
Answer:
Claviceps purpurea

Question 16.
Give one psychological disorder that occurs due to drug addiction.
Answer:
Epilepsy

Question 17.
Which type of drug is used as tranquliser?
Answer:
Benzodiazepines

Question 18.
Name the drug obtained from coca plant.
Answer:
Cocaine

Fill in the blanks

Question 1.
The asexual cycle of Plasmodium in its primary host …………. .
Answer:
humans

Question 2.
The infective stage of malaria parasite is ………….. .
Answer:
sporozoite

Question 3.
Filariasis is caused by ………… .
Answer:
Wuchereria bancrofii

Question 4.
A parasite …………. causes abdominal pain, constipation, cramps, faeces with excess mucus and blood clots.
Answer:
Entamoeba histolytica

Question 5.
A disease causing agent is called …………. .
Answer:
pathogen

Question 6.
The vaccine used against typhoid fever is …………. .
Answer:
Vi antigen

Question 7.
…………. is acquired through vaccines which generate antibodies when introduced in body.
Answer:
Artificial active immunity

Question 8.
IgE are the antibodies involved in ………….. .
Answer:
allergic reaction

Question 9.
Cancer of muscle is named as …………… .
Answer:
sarcoma

Question 10.
………………. tests are conducted to know number of cell counts during cancer.
Answer:
Blood and bone marrow

Question 11.
HIV virus belongs to a group of …………… .
Answer:
retrovirus

Question 12.
Anti Tetanus Serum (ATS) administration generates ………….. immunity in the body.
Answer:
artificial passive

Question 13.
AIDS virus has ……….. RNA.
Answer:
single-stranded

Question 14.
…………. is the most common skin problem that occur during adolescence.
Answer:
Acne

Question 15.
The strong sense of fear in reference to a particular situation or thing is called …………… .
Answer:
phobia

Question 16.
LSD is a natural drug.
Answer:
psychedlic/hallucinogens

Question 17.
Cocaine is obtained from the plant
Answer:
Erythroxylon coca

Question 18.
…………. are antisleep drugs.
Answer:
Amphetamines

Question 19.
Tobacco is obtained from ……………. .
Answer:
Nicotiana tabacum leaves

Question 20.
Pathogen causing ascariasis is ………….. .
Answer:
Ascaris lumbricoides

Question 21.
Phenomenon of rejection of self cells is called ………….. .
Answer:
Autoimmunity

Short Answer Type Questions

Question 1.
Define health and disease.
Answer:

• Health is defined as a state of complete physical, mental and social well-being.
• Disease is a state when functioning of one or more organs or systems of the body is adversely affected.

Question 3.
What are the two basic groups of diseases? Give one example of each group.
Answer:
Two basic groups of diseases are

• Infectious diseases are those which has the ability of transmitting from one person to another, e.g. AIDS, common cold, etc.
• Non-infectious diseases which does not have the ability of transmitting from one person to another, e.g. cancer, diabetes, etc.

Question 4.
Write a short note on pathogens.
Answer:
Organisms that cause infectious diseases are known as pathogens. These can harm any living individual or organism by living on them or living in them.
These disrupt the normal physiology of organisms either plants or animals and express certain symptoms. These enter in our body through some source like air, water, food, soil, etc.
The major classes of pathogens are viruses, bacteria, fungi, prions and parasitic.

Question 5.
Name two bacterial diseases of human.
Answer:
Two bacterial diseases of human are

• Typhoid It is caused by bacterium (Salmonella typhi) which enters the body through food.
• Pneumonia It is caused by bacterium (Streptococcus pneumoniae) which infect alveoli of the lungs.

Question 6.
State the symptoms of typhoid.
Answer:
The incubation period of parasite is about 1-2 weeks and the duration of illness is about 4-6 weeks. The symptoms of typhoid include fever (39-40°C), lethargy, stomach pain, headache, poor appetite, diarrhoea or constipation and rose spots on abdomen. The intestinal perforation or bleeding may occur in severe cases, which may lead to death. The reccurrence (relapsing) of disease is observed in 10% of patients. Typhoid is diagnosed by WIDAL test.

Question 7.
Answer the following
(i) Name the stage of Plasmodium that gains entry into the human body.
(ii) Explain the cause of periodic recurrence of chill and high fever during malaria attack in human.
Answer:
(i) Sporozoite stage.
(ii) When the Plasmodium enters the RBCs, it causes the rupture of red blood cells. The rupture of RBCs, is associated with the release of chemical haemozoin which causes frequent chills and high fever.

Question 8.
Name the toxin responsible for the appearance of symptoms of malaria in human. Why do these symptoms occur periodically?
Answer:
The toxin responsible for symptoms of malaria is haemozoin. It is released when RBCs get ruptured due to erythrocytic schizogony of Plasmodium that takes place every 48 hours. This is the reason behind periodic occurrence of symptoms.

Question 9.
What is the causative organism of amoebiasis? State the symptoms of the disease.
Answer:

• Amoebiasis is caused by an intestinal endoparasite, Entamoeba histolytica.
• Symptoms of amoebiasis are abdominal pain constipation, cramps, faeces with excess mucous and blood clots.

Question 10.
List the symptoms of ascariasis. How does a healthy person acquire this infection?
Answer:
Symptoms
Most of the patients during light infection do not show any symptoms of Ascaris. However, patients with moderate to heavy infections show some symptoms depending upon the infected organ

1. If intestine is infected Ascaris eggs reach to small intestine through contaminated food or water. They hatch and develop from larva to adult worms in small intestine and remain there till they die. In mild ascariasis, symptoms are mild abdominal pain, nausea and vomitting or diarrhoea with blood stool.
In severe infection, large number of worms are present in a person which may cause severe abdominal pain, fatigue, vomitting and weight loss.

2. If lungs are infected After ingestion of Ascaris eggs, these hatch into larvae in small intestine. These larvae migrate into lungs via blood or lymph. At this stage, symptoms are similar to asthma or pneumonia with cough, breathlessness and wheezing. After 6-10 days in lungs, larvae travel into throat where these are coughed up and swallowed.

Question 11.
(i) What is immunity?
(ii) Give an account of cell-mediated immunity.
Answer:
(i) Immunity is the capactiy of an organism to resist or defend itself from the development of a disease. It has two main types, i.e. innate immunity and acquired immunity.

(ii) Immune response is the specific reactivity induced in a host by an antigentic stimulus. The immune response is of following types
• Humoral Antibody Mediated Immunity (AMI)
• Cell-Mediated Immunity (CMI)

Cell-Mediated Immunity:
It is the responsibility of a sub-group of T-cell, called T-cytotoxic cells. An activated T-cytotoxic cell is specific to a target cell which has been infected and kills the target cell by a variety of mechanisms.

It prevents the completion of life cycle of the pathogen since it depends on an intact host cell. Cell mediated immunity is also invovled in killing of cancer cells. T-cells attack the following
(a) Cells that have become infected by a microorganism most commonly a virus.
(b) Transplanted organs and tissues.
(c) Cancer causing cells.
The whole cell is involved in the attack, so this type of immunityis described as cell-mediated immunity.
T-cells do not relase antibodies.

Question 12.
Write a short note on innate immunity.
Or What is innate immunity?
Answer:
Innate Immunity (Inborn)
It is the type of immunity which is present from birth and is inherited from the parents. That’s why it is also called as natural immunity. It is non-specific in nature as it involves general protective measures against any invasion. Innate immunity provides the early lines of defense against pathogens. The principal components of innate immunity that act as barrier system to prevent the entry of pathogens are given below
1. Mechanical barriers
2. Chemical barriers
3. Phagocytosis
4. Fever
5. Inflammation
6. Acute phase proteins
7. Natural Killer (NK) cells

1. Mechanical or Physical Barriers
They prevent entry of microorganisms in the body, e.g. skin, mucous coating of epithelium lining the respiratory, gastrointestinal and urogenital tracts. These barriers are also called as first line of defence.

• Skin It is outer and tough layer of epidermis that consists of insoluble protein called keratin. It prevents the entry of bacteria and viruses. The periodical sheding off process of skin removes any clinging pathogen.
• Mucous membrane The gastrointestinal tract, urinogenital tract and conjuctiva are lined by mucous membrane.

This membrane secretes mucus which entraps microbes, dust or any foreign particles and finally propelled them out through tears, saliva, coughing and sneezing.

2. Chemical or Physiological Barriers
It includes certain chemicals which dispose off the pathogens.
These are given below

1. Acid of stomach, kills the ingested microorganisms by secreting acid gastric secretion (pH 1.5 – 2.0).
2. Low pH of sebum (i.e. 3.0-5.0) forms a protective film over the skin that inhibits growth of many microbes.
3. Lysozyme is a hydrolytic enzyme present in all mucous secretions like tears, saliva and nasal secretions. It attacks bacteria and dissolves their cell walls.
4. Gastro and duodenal enzymes secrete proteases and lipases. These enzymes digest a variety of structural and chemical constituents of pathogens, e.g. gastric acids easily inactivate rhinoviruses.
5. Mothers milk Lactoferrin and neuraminic acid are antibacterial substances present in human milk to fight against Staphylococci.
6. A group of proteins produced by virus infected cells, i.e. interferons induces a generalised activated state in neighbouring uninfected cells.
7. Humans and some other animals secrete an number of antimicrobial peptides such as defensins. One micrometre thick biofilm of defensins protects the skin from microbial assault.

3. Phagocytosis
When pathogens or microbes penetrate the skin or mucous membrane certain cell types surge towards the site of infection. These can be neutrophils, monocytes and macrophages which engulf the pathogens to form a large intracellular vesicle called phagosome.

The phagosome fuses with lysosome to form phagolysosome. The secretion of lysosomal enzymes digests bacterial cells. The useful products remains in the cell while the waste is egested out of the cell. Therefore, these phagocytes are also known as second line of defence.

4. Fever
It may be brought about by endotoxins or proteins (cytokines) produce by pathogens called endogenous pyrogens.

When enough pyrogens are produced, then there is rise in temperature which strengthens the defence mechanism to inhibit the growth of microbes. Fever is a symptom of an internal diagnoses of the cause of infections.

5. Inflammation
It is a defensive response of the body to tissue damage.
It is characterised by abrasions, chemical irritations, . heat, swelling, redness and pain. Inflammation in a non-specific response of the body to injury. It is an attempt to dispose off microbes, toxins or foreign material at the site of injury by macrophages to prevent their spread to other tissues and to prepare the site for. tissue repair. Thus, it helps to restore tissue homeostasis.

Broken mast cells release histamine, bradykinin, etc., which cause dilation of capillaries and small blood vessels. As a result more blood flows in these areas making them red and warm. Therefore, the accumulation of this results into tissue swelling (oedema).

After few days, due to phagocytosis, a cavity containing necrotic tissue and dead bacteria is formed. This fluid mixture is called pus.

6. Acute Phase Proteins
The chemical messenger of immune cells called cytokines are important low molecular weight proteins. These heterogenous proteins stimulate or inhibit the differentiation, proliferation or function of immune cells and also certain viral infections.

7. Natural Killer Cells
These are non-phagocytic granular lymphocytes which are present in spleen, lymph nodes and bone marrow.

Question 13.
What are interferons?
Ans.
Interferons are antiviral glycoproteins released by the virus infected host cells. They do not inactivate to kill the virus but enter the neighbouring uninfected host cells to prevent viral multiplication in them.
Interferons are host specific as they are produced by one host and will not work in another host.

Q 14.
Mention the origin and importance of T-cells.
Ans.
T-cells or T-lymphocytes are originates in bone marrow in immature forms. In thymus, these cells are transformed into mature T-!ymphocytes.

There are four types of T-cells, i.e. helper T-cells, suppressor T-cells, memory T-cells and cytotoxic T-cells. Helper T-cells stimulate B-cells to produce antibodies and cytotoxic T-killer cells attack foreign cells.
Suppressor T-cells suppress the functions of cytotoxic and helper T-cells and memory cells recognise the original invading antigen to create a more intense immune response.

Question 15.
What are immunoglobins?
Or What is antibody?
Answer:
Humoral response or Antibody-Mediated Immunity (AMI):
It is mediated by antibodies present in blood and lymph. Immunoglobulins or antibodies are glycoproteins produced in the body by B-cells in response to an antigen, e.g. IgA. IgG, IgM, IgE and IgD.
B-cells multiple in large number and transform into larger cells called plasma cells or plasmocytes. The transformation into plasma cells in assisted By T-Helper cells (TH). These antibodies destroy antigens by specific antigen – antibody interaction.

Question 16.
Why is mother’s milk considered the most appropriate food for a newborn infant?
Answer:
Mother’s milk is considered most appropriate for a newborn infant as it provides immunity in the initial period of its life. The yellowish fluid colostrum secreted by mother during the initial days ofdactation has abundant antibodies (IgA) to protect the infant from primary infections like cold, flu, etc.

Question 17.
Write a short note on vaccination.
Answer:
Vaccination refers to the process of injecting a biological or chemical agent that enhances the immunity of a person against the specific disease. It generally involves injection of dead organisms into . host organism.
Vaccination is the best preventive measure against any disease. A number of specific vaccines are given against many disease, e.g. polio vaccine, diphtheria vaccine, etc.

Question 18.
Why are tumour cells dangerous?
Answer:
Tumour cells are dangerous due to the following reasons

• These grow rapidly and also damage normal cells.
• Cells from tumours can get sloughed off and may reach other parts of the body via blood and start a new tumour, i.e. metastasis.
• Tumour cells compete for nutrients and may starve the other cells.

Question 19.
Write a short note on types and causes of cancer.
Or Write short note on cancer.
Answer:
Causes of Cancer
The agents which cause cancer, are called carcinogens.
Cancer can be induced by either physical, chemical or
biological agents.

1. Physical agents These are ionising radiations like X-rays, v-rays and the non-ionising rays like UV-rays which can cause DNA damage leading to neoplastic transformation.
2. Chemical agents These are tobacco smoke, benzene fumes, arsenic, hormones and aflatoxin, etc.
3. Nutritional agents Deficiency of some nutrients like vitamins, minerals and proteins causes cancer.
4. Biological agents Many cancers are caused by viruses. The association of Hepatitis-B and primary liver cancer has been established.
5. Mechanical factors Trauma, irritation and severe friction have been identified to cause malignancy.
6. Host factors These include age, sex, marital status, race, socio-economic status, customs and habits of the host.
7. Environmental factors These include radiation, air pollution, diet, drugs and social environment.
8. Genetic factors All factors have a genetic basis and are caused by genetic transformations of cells.

Question 20.
What is HIV?
Answer:
The HIV name was given in 1986 to AIDS virus. The two more strains of HIV, namely HIV 1 and 2 have been discovered. HIV viruses have originated from non-primates from West-central Africa and transferred to human. HIV 1 is more pathogenic and distributed world-wide, while HIV 2 is less prevalent and less pathogenic. It is distributed in West Africa only.

Question 21.
How is the AIDS provirus formed?
Answer:
HIV first attaches to the host cell surface by adsorption. It then enters CD 4 cells and the HIV RNA changes to DNA (provirus). This HIV provirus gets inserted into DNA of CD \ cell and them begins to replicate using the host’s cellular.

Question 22.
How AIDS can be prevented?
Answer:
There is no effective treatment developed to treat AIDS. Therefore, some preventive measures are recommended to prevent its infection.
The preventive measures are as follows

1. Sterlise all surgical instruments before use.
2. The transfusion of blood should be subjected to HIV test.
3. Infected mother should avoid pregnancy otherwise, it may also transmit to child.
4. Heterosexual activites should be prohibited.
5. Motivate to use condoms during sexual activities.
6. Proper medical dispose off should be established.

Government of Indian launched national AIDS control board, national AIDS committee, national AIDS control organisation, etc., to create awareness among people about HIV transmission and progression of AIDS.

Question 23.
Write short note on drug abuse.
Answer:
Drug Abuse and Addiction:
Drugs are chemicals which are used in the treatment of a disease under the supervision of a physician. But prolonged unnecessary use of a drug makes a person dependent and an addict to that drug.

Question 24.
From which plant cocaine is obtained? Why sports persons are often known to abuse this drug?
Answer:
Cocaine is derived from the leaves and young branches of South American plant Erythroxylum coca or coca plant.
Sports persons abuse this drug because it is a strong stimulant and acts on central nervous system, producing a sense of increased energy. It is highly addictive.

Question 25.
Write the source and effects of following drugs.

1. Morphine
2. Cocaine
3. Marijuana

Answer:

1. Morphine It is obtained from latex of Papaver somniferum.
   It has a sedative effects that slows down the body function.
2. Cocaine is obtained from plant Erythroxylon coca. It affects central nervous system and produces increased sense of happiness.
3. Marijuana It is obtained from Cannabis sativa and affects cardiovascular system of the body.

Differentiate between the following (for complete chapter)

Question 1.
Congenital diseases and Acquired diseases.
Answer:
Differences between congenital diseases and acquired diseases are as follows

Congenital diseases	Acquired diseases
Diseases present from birth	Disease occurs only after birth.
These are occur due to gene or chromosomal mutations.	These are non-heritable but are caused due to some causative agents like bacteria, fungus, virus.
e.g. Down syndrome, haemophilic, etc.	e.g. leprosy, typhoid, malaria, etc.

Question 2.
Amoebiasis and Filariasis.
Answer:
Differences between amoebiasis and filariasis are as follows

Amoebiasis	Filariasis
Entamoeba histolytica is the causative organism of amoebiasis.	Filariasis is caused by filarial nematodes, Wuchereia bancrofti and W. malayi.
Houseflies are mechanical carriers and transmit the parasite from faeces of the infected person to food and contaminate them.	Filarial infectin is caused by different species of mosquitoes, e.g. Culex, Aedes, etc.
Symptoms include constipation, abdominal pain, cramps, etc.	Symptoms include oedema, swelling of lower exteremities and deformation of genital organs.

Question 3.
Primary immune response and Secondary immune response.
Answer:
Differences between primary immune response and secondary immune response are as follows

Primary immune response	Secondary immune response
It occurs as a result of the first contact of the individual with an antigen.	This immune response occurs during second and subsequent contacts with the same antigen.
Its response is feeble to moderate.	Its response is strong.
It takes a longer time to establish immunity.	It is rapid.
It declines rapidly.	It lasts longer, sometimes lifelong.
Receptors for the antigen develops during response.	Receptors are already present.

Question 4.
Active immunity and Passive immunity.
Answer:
Differences between active immunity and passive immunity are as follows

Active immunity	Passive immunity
Develops due to contact with pathogen or its antigen.	Develops when readymade antibodies are injected into the body.
Slow but long lasting.	Fast but lasts for few days.
No or few side effects.	May cause side effects.

Question 5.
Antibody-mediated immune system and Cell- mediated immune system.
Answer:
Differences between antibody mediated immune system and cell-mediated immune system are as follows

Antibody-mediated immune system	Cell-mediated immune system
It is mediated by B-lymphocytes.	It consists of T-lymphocytes.
It operates through formation of antibodies.	It operates directly through T-cells.
It acts on pathogens that invade body fluids.	It operates against those pathogens which invade body cells.
It hardly has any effect against cancers and transplants.	It operates against cancer cells and transplants.

Question 6.
B-lymphocytes and T-lymphocytes.
Answer:
Differences between B-lymphocytes and T-lymphocytes are as follows

B-iymphocytes	T-lymphocytes
B-cells form humoral or Antibody Mediated Immune System (AMIS)	T-cells form Cell-Mediated Immune System (CMIS),
They defend against viruses and bacteria that enter the blood and lymph.	They defend against pathogens including protists and fungi that enter the cells.
They form plasma cells and memory cells by the division.	They form killer, helper and suppressor cells by the division of lymphoblasts.

Question 7.
Antigens and Antibodies.
Answer:
Differences between antigens and antibodies are as follows

Antigens (Immunogens)	Antibodies (Immunoglobins)
They are usually foreign materials such as a protein or polysaccharide molecules.	These are protein molecules.
These trigger the formation of antibodies.	These are synthesised in the body to combat foreign materials.
These may occur on the surface of microbes or as free molecules.	These may occur on the surface of plasma cells and in body fluids.
Antigens bind to macrophages to reach helper T-cells to initiate immune response.	These directly join antigens to destroy them.
They produce diseases or allergic reactions.	These are protective and immobilise or lyse antigenic molecules.

Question 8.
IgG and IgM.
Answer:
Differences between IgG and IgM are as follows

IgG	IgM
It is the most abundant Immunoglobulin in blood.	It is third abundant immunoglobulin in blood.
IgM is replaced by IgG and becomes the principal antibody.	It is first antibody synthesised by the newborn.
It is monomer.	It is pentamer.

Question 9.
Cancer cells and Normal cells.
Answer:
Differences between cancer cells and normal cells are as follows

Cancer cells	Normal cells
The lifespan is not definite.	These cells have a definite lifespan.
These ceils divide in an unregulated and uncontrolled manner.	These cells divide in a regulated manner.
These cells do not have contact inhibition.	The cells show contact inhibition.
These cells do not undergo differentiation.	These cells undergo- differentiation.
These cells do not remain adhered and have lost cell to cell contact.	These cells remain adhered, i.e. have cell to to cell contact.

Question 10.
Stimulants and Hallucinogens.
Answer:
Differences between stimulants and hallucinogens are as follows

Stimulants	Hallucinogens
These increase the activity of CNS.	These damage the CNS performance.
These induce alterness, more wakefulness and excitement	These change thought of a person, feeling and perceptions, cause hallucinations.
e.g. caffeine, cocaine, amphitamines.	e.g. charas, ganja, bhang and marijuana.

Odisha State Board CHSE Odisha Class 12 Biology Important Questions Chapter 7 Molecular Basis of Inheritance Important Questions and Answers.

CHSE Odisha 12th Class Biology Important Questions Chapter 7 Molecular Basis of Inheritance

Molecular Basis of Inheritance Class 12 Important Questions CHSE Odisha

Very Short Answer Type Questions

Choose the correct option

Question 1.
In a DNA strand, the nucleotides are linked together by
(a) glycosidic bonds
(b) phosphodiester bonds
(c) peptide bonds
(d) hydrogen bonds
Answer:
(b) phosphodiester bonds

Question 2.
In DNA double helix, thymine is paired with …………… .
(a) guanine
(b) uracil
(c) cytosine
(d) adenine
Answer:
(d) adenine

Question 3.
Semiconservative mode of replication of DNA was proved by
(a) Hershey and Chase
(b) Griffith
(c) Watson and Crick
(d) Meselson and Stahl
Answer:
(d) Meselson and Stahl

Question 4.
Discontinuous synthesis of DNA occurs in one strand, because
(a) DNA molecule being synthesised is very long
(b) DNA dependent DNA polymerase catalyses polymerisation only in one direction (5′ → 3′)
(c) it is a more efficient process
(d) DNA ligase has to have a role
Answer:
(b) DNA dependent DNA polymerase catalyses polymerisation only in one direction (5′ → 3′)

Question 5.
The enzyme not associated with DNA replication is
(a) polymerase
(b) helicase
(c) topoisomerase
(d) transcriptase
Answer:
(d) transcriptase

Question 6.
Which is the enzyme used for joining the fragments of DNA?
(a) Ligase
(b) Polymerase
(c) Endonuclease
(d) Transferase
Answer:
(a) Ligase

Question 7.
To form a continuous DNA molecule, the enzyme ………… joins Okazaki fragments.
(a) primase
(b) polymerase
(c) helicase
(d) ligase
Answer:
(d) ligase

Question 8.
DNA ligase is commonly known as ……….. .
(a) molecular scissor
(b) molecular marker
(c) molecular probe
(d) milecular glue
Answer:
(d) molecular glue

Question 9.
In eukaryotic cells, the RNA transcribed from DNA is called ………….. .
(a) rRNA
(b) cistron
(c) cDNA
(d) heterogenous mRNA
Answer:
(d) heterogenous mRNA

Question 10.
At 5′ end of a polynucleotide chain
(a) H-bond is present
(b) -OH group is attached
(c) PO^–₄ group is attached
(d) pentose sugar is attached
Answer:
(c) PO^–₄ group is attached

Question 11.
In which one of the following, double-stranded RNA is present?
(a) Bacteria
(b) Chloroplast
(c) Mitochondria
(d) Reovirus
Answer:
(d) Reovirus

Question 12.
DNA replication is
(a) semiconservative, directional and continuous
(b) semiconservative, bidirectional
(c) semiconservative and semidiscontinuous
(d) only semiconservative
Answer:
(c) semiconservative and semidiscontinuous

Question 13.
A double-stranded RNA segment has 120 adenine and 120 cytosine bases. The total number of nucleotides present in the segment is
(a) 120
(b) 240
(c) 60
(d) 480
Answer:
(b) 240

Question 14.
Termination codon which stops, further addition of amino acids to the polypeptide chain is
(a) AAU
(b) GUG
(c) AUG
(d) UAG
Answer:
(d) UAG

Question 15.
Which one is not a non-sense codon?
(a) UAA
(b) UGA
(c) UCA
(d) UAG
Answer:
(c) UCA

Question 16.
A phenomenon where the third base of tRNA at its 5′ end can pair with a non-complementary base ofmRNAis called
(a) universality
(b) colinearity
(c) degenerency
(d) wobbling
Answer:
(d) wobbling

Question 17.
Translation is the synthesis of
(a) DNA from a mRNA template
(b) protein from a mRNA template
(c) RNA from a mRNA template
(d) RNA from a DNA template
Answer:
(b) protein from a OTRNA template

Question 18.
The peptide bonds are present between
(a) nucleic acids
(b) organic acids
(c) fatty acids
(d) amino acids
Answer:
(d) amino acids

Question 19.
Gene which is responsible for the synthesis of a polypeptide chain is called
(a) operator gene
(b) regulatory gene
(c) promoter gene
(d) structural gene
Answer:
(d) structural gene

Question 20.
Repressor protein is produced by
(a) regulator gene
(b) operator gene
(c) structural gene
(d) terminator gene
Answer:
(a) regulator gene

Question 21.
In split genes, the coding sequences are called
(a) cistrons
(b) operons
(c) exons
(d) introns
Answer:
(c) exons

Question 22.
The non-sense codons
(a) have no role in biological systems
(b) act as terminators during protein synthesis
(c) are of little value in transcription
(d) have a poor role in transcription
Answer:
(b) act as terminators during protein synthesis

Question 23.
If a cell is treated with a chemical that blocks nucleic acid synthesis, which of the following processes is the most likely one to be affected first?
(a) DNA replication
(b) tRNA synthesis
(c) mRNA synthesis
(d) Protein synthesis
Answer:
(a) DNA replication

Question 24.
Aminoacyl synthetase takes part in
(a) attachment of mRNA to 30S ribosome
(b) transfer of activated amino acids to tRNA
(c) activation of amino acid
(d) hydrolysis of ATP to AMP
Answer:
(c) activation of amino acid

Correct the statements, if required, by changing the underlined word(s)

Question 1.
Watson and Griffith proposed the double helical structure of DNA.
Answer:
Watson and Crick.

Question 2.
The helical turns are left-handed in Z-DNA.
Answer:
It is correct.

Question 3.
Okazaki fragments are formed on both leading and lagging strand.
Answer:
Okazaki fragments are formed only on lagging strand.

Question 4.
Cytosine is common for both DNA and RNA.
Answer:
It is correct.

Question 5.
RNA does not have guanine as nitrogenous base.
Answer:
Thymine

Question 6.
The complementary base of adenine in RNA molecule is thymine.
Answer:
Uracil

Question 7.
The process of formation of RNA from DNA is translation.
Answer:
Transcription

Question 8.
DNA polymerase-I is mainly responsible for synthesis of new strand during DNA replication.
Answer:
DNA Polymerase

Question 9.
The genetic information from DNA transferred to ribosomes through ribosomal RNA.
Answer:
messenger

Question 10.
The initiation codon AUG normally codes for formylated cystine.
Answer:
methionine

Question 11.
CCC is the initiation codon.
Answer:
AUG

Question 12.
The split genes are needed constantly for cellular activity.
Answer:
housekeeping

Question 13.
The lac operon consists of four regulatory genes only.
Answer:
three

Question 14.
A regulated unit of genetic material for prokaryotic gene expression is called operon.
Answer:
It is correct.

Question 15.
64 codons code for all the 20 essential amino acids.
Answer:
61 codons

Question 16.
Prokaryotic /nRNA is monocistronic.
Answer:
polycistronic

Question 17.
The structural genes are regulated as a unit by a single regulator in operon.
Answer:
promoter

Question 18.
Galactose is an inducer molecule.
Answer:
Lactose

Question 19.
tRNA carries the codes for amino acid sequence.
Answer:
It is correct.

Fill in the blanks

Question 1.
Frederick Griffith discovered the phenomenon called …………… .
Answer:
transformation

Question 2.
The two strands of polynucleotides forming DNA are ……….. and antiparallel.
Answer:
complementary

Question 3.
A ……………. is located towards 3’ end of the coding strand.
Answer:
OH

Question 4.
The correspondence between triplets in DNA (or RNA) and amino acids in protein is known as ……….. .
Answer:
genetic code

Question 5.
……… is a short sequence of DNA where the repressor binds, preventing RNA polymerase from attaching to the ……….. .
Answer:
Operator, promoter

Question 6.
DNA fingerprinting works on the principle of …………. in DNA sequences.
Answer:
polymorphism

Question 7.
RNA can give rise to DNA through the enzyme ……………. .
Answer:
reverse travscriptase

Question 8.
The movement of a ribosome from 5′-3′ end of mRNA to recognise all codons during protein synthesis is called ………… .
Answer:
elongation

Express in one or two word(s)

Question 1.
The enzyme which joins Okazaki fragments to form a continuous DNA molecule.
Answer:
Ligase

Question 2.
The organism on which Meselson and Stahl (1958) provided strong evidence for semiconservative mode of DNA replication?
Answer:
E. coli

Question 3.
The strand which is transcribed into mRNA (RNA transcript).
Answer:
Template strand

Question 4.
The scientist who formulated central dogma of molecular biology in 1958?
Answer:
Crick

Question 5.
The first X-ray diffraction pattern of DNA was given by which scientist?
Answer:
Wilkins

Question 6.
The scientist who suggested that the genetic code should be made of a combination of three nucleotides.
Answer:
George Gamow

Question 7.
The codon which acts as initiation codon and also codes for amino acid methionine.
Answer:
AUG

Question 8.
All terminator codons begin with nucleotide of which base?
Answer:
U

Question 9.
The scientist who proposed the operon concept?
Answer:
Jacob and Monod

Short Answer Type Questions

Question 1.
Write a short note on nitrogenous bases.
Answer:
Nitrogenous bases are heterocyclic compounds in which the rings contain both nitrogen and carbon atoms.
There are two types of nitrogenous bases

• Purines (with double rings) adenine and guanine
• Pyrimidines (with single ring) cytosine, uracil and thymine.

Out of the pyrimidines, cytosine is common for both DNA and RNA while thymine is present only in DNA. Uracil is present in RNA in place of thymine.

Question 2.
If a double-stranded DNA has 20% of cytosine, calculate the percentage of adenine in the DNA.
Answer:
Given, cytosine = 20%
∴ Percentage of guanine = 20%
Now according to Chargaff’s rule,
A + T = 100 – (G + C)
⇒ A + T =100 – 40
∴ Percentage of thymine = Percentage of adenine
= \(\frac{60%}{2}\) = 30%

Question 3.
The base sequence in one of the strands of DNA is TAGCATGAT.
(i) Give the base sequence of the complementary strand.
(ii) How are these base pairs held together in a DNA molecule?
(iii) Explain the base complementarity rule. Give the name of the scientist who framed this rule?
Answer:
(i) ATCGTACTA
(ii) Base pairs are held together by weak hydrogen bonds, adenine pairs with thymine by two H-bonds and guanine pairs with cytosine forming three H-bonds.
(iii) According to base complementarity rule formed by Erwin Chargaff for a double-stranded DNA, the ratios between adenine-thymine and guanine-cytosine are constant and equal to one.

Question 4.
A DNA segment has a total of 1000 nucleotides, out of which 240 of them are adenine containing nucleotides. How many pyrimidine bases this DNA segment possesses?
Answer:
According to ChargafFs rule, ratio of purines to pyrimidines is equal, i.e. A + G = C + T
Since, the number of adenine (A) is equal to the number of thymine (T) and A = 240 (given)
Therefore, T = 240
Also, the number of guanine (G) is equal to cytosine (C)
Thus, G+C = 1000 – (A + T)
G + C = 1000-480 = 520
Hence, G = 260, C = 260
The number of pyrimidine bases, i.e.
C + T = 240 + 260 = 500

Question 5.
It is established that RNA is the first genetic material. Explain giving reasons.
Answer:
RNA is the first genetic material because

• It is capable of both storing genetic information and catalysing chemical reactions.
• Essential life processes such as metabolism, translation, splicing, etc., have evolved around RNA.
• It can directly code for protein synthesis and hence, can easily express the character.

Question 6.
Write short note on RNA.
Answer:
RNA is a genetic material in some viruses.
RNA differs from DNA in having uracil in place of thymine and most RNAs are single-stranded.
It is of three main types, i.e. messenger RNA (mRNA), transfer RNA (tRNA) and ribosomal RNA (rRNA).
mRNA associates with ribosomes for protein synthesis, tRNA is helical and transfers specific amino acids from the cytoplasm to site of protein synthesis while rRNA is part of ribosomes.

Question 7.
Write a short note on tRNA.
Answer:

• tRNA is the smallest form of RNA and functions as in transfering amino acids from cytoplasm to the ribosomes at the time of protein synthesis.
• tRNA has a secondary structure like clover leaf. But its three dimensional structure depicts it as an inverted L-shaped molecule.
• tRNA has five arms or loops, i.e. anticodon loop, amino acid acceptor end, T-loop, D-loop and variable loop.
• tRNAs are specific for specific amino acid.

Question 8.
Explain the two factors responsible for conferring stability to double helix structure of DNA.
Answer:
The factors responsible for stability of double helix structure of DNA are as follows

• Stacking of one base pair over other.
• H-bond between nitrogenous bases.

Question 9.
Which property of DNA double helix led Watson and Crick to hypothesise semiconservative mode of DNA replication? Explain.
Answer:
In the double helical structure of DNA, the two strands of DNA have complementary base pairing and run in opposite direction. This property of DNA double helix led Watson and Crick to hypothesise the semiconservative mode of DNA replication.

Question 10.
Name a few enzymes involved in DNA replication other than DNA polymerase and ligase. Name the key functions for each of them.
Answer:
The enzymes involved in DNA replication other than DNA polymerase and ligase are listed below with their functions

• Helicase – Opens the helix
• Topoisomerases – Removes the tension caused due to unwinding
•  DNA ligase – Joins the cut DNA strands

Question 11.
State the dual role of deoxyribonucleoside triphosphates during DNA replication.
Answer:

• The deoxyribonucleoside triphosphates are the building blocks for the DNA strand (polynucleotide chain) is as substrate.
• These also serve as energy source in the form of ATP and GTP from two terminal phosphates.

Question 12.

Why do you see two different types of replicating strands in the given DNA replication fork? Explain. Name of these strands.
Answer:
Both the parent strands function as template strands.
On the template strand with 3′ → 5′ polarity, the new strand is synthesised as a continuous strand.
The DNA polymerase can carry out polymerisation of the nucleotides only in 5′ → 3′ direction. This is called continuous synthesis and the strand is called leading strand.
On the other template strand with 5′ → 3′ polarity, the new strand is synthesised from the point of replication fork, also in 5′ → 3′ direction. But, in short fragments, they are later joined by DNA ligases to form a strand called lagging strand.

Question 13.
Write a short note on centrol dogma.
Answer:
Central Dogma
It was proposed by Francis Crick (in 1958). According to the central dogma in molecular biology, the flow of genetic information is unidirectional,’ i.e.
DNA → RNA → Protein.

Central dogma

But later in 1970, HM Temin reported that the flow of information can be in reverse direction also, i.e. from RNA to DNA in some viruses (e.g. HIV) which is called as reverse transcription.

Question 14.
Briefly describe transcription in prokaryotes.
Answer:
Prokaryotes
All three RNAs are needed for synthesis of a protein in a cell. DNA dependent RNA polymerase is the single enzyme that catalyses the transcription of all types of bacterial RNA. But for the expression of different genes, different sigma factors may associate with same core enzymes.
In E.coli, σ⁷⁰ is used in normal condition σ³² / σ^H under heat shock, σ⁵⁴ / σ^N under nitrogen starvation and σ²⁸ for chemotaxis.

A typical bacterial transcription unit

Question 15.
Describe the initiation process of transcription in bacteria.
Answer:
Initiation

1. The holoenzyme binds to the promoter region of transcription unit.
2. The sigma polypeptide binds loosely to the promoter sequences so as to form a loose, closed, binary complex.
3. It is followed by the formation of a transcription eye or bubble due to the denaturation of adjacent sequence of DNA, lying next to the complex.
4. The transcription bubble along with the bounded holoenzyme is called open binary complex.
5. In 90% of cases, the start point of transcription is a purine.
6. At the elongation site of enzyme, two nucleotides complementary to the first two nucleotides of template strand binds.
7. A phosphodiester bond is formed between these two ribonucleotides.
8. At this stage, the complex is called ternary complex that consists of partly denatured DNA bounded with holoenzyme having a di-ribonucleotide.
9. The same process continues till a RNA chain of about nine nucleotides is synthesised. The holoenzyme does not move throughout this process.
10. After the completion of initiation process, sigma factor dissociates from RNA polymerase. This facilitates the promoter clearance so that a new holoenzyme can bind to promoter for second round of transcription.

Question 16.
Explain (in one or two lines) the function of the following
(i) Introns
(ii) Exons
Answer:
The primary transcript contains both the exons and introns and these are non-functional.
Such genes are called split genes/interrupted genes. Therefore, they undergo a process called splicing to remove the introns and to join the exons in a proper order to allow translation to take place.

Expression of an interrupted/split gene and RNA splicing

The presence of introns is reminiscent of antiquity and the process of splicing represents the dominance of RNA world. The bnRNA undergoes two additional processes, i. e. post-transcriptional modifications.

Question 17.
State the difference between the structural genes in a transcription unit of prokaryotes and eukaryotes.
Answer:
Prokaryotic structural genes are found in continuity without any non-coding region, while eukaryotic structural genes are divided into exons (coding DNA) and introns (non-coding DNA). Exons appear in mature RNA. Introns are spliced out during splicing.

Question 18.
Depending upon the chemical nature of the template (DNA or RNA) and the nature of nucleic acids synthesised from it (DNA or RNA), list the types of nucleic acid polymerases.
Answer:

• DNA-dependent DNA polymerase uses DNA template to catalyse the polymerisation of deoxynucleotides.
• DNA-dependent RNA polymerase catalyses transcription of all types of RNAs in bacteria.
• In eukaryotes, there are three types of DNA-dependent RNA polymerase
  • RNA polymerase-I transcribes rRNAs.
  • RNA polymerase-II transcribes precursor of mRNA.
  • RNA polymerase-III transcribes tRNA, srRNA and snRNAs.

Question 19.
Why hnRNAis required to undergo splicing?
Answer:
hnKNA is required to undergo splicing because of the presence of introns (the non-coding sequences) in it. These need to be removed and the exons (the coding sequences) have to be joined in a specific sequence for translation to take place.

Question 20.
Write a note on genetic code.
Answer:
Francis Crick conducted an experiment in Viral DNA in 1961 and concluded that genetic code is triplet and with any punctuation it is read continuously. Once the triplet nature of codon was established, different scientists then tried to establish codons for 20 different amino acids found in proteins.

1. Marshall Nirenberg In 1961, he used a synthetic twRNA of uracil only. He found that the translated polypeptide was composed of amino acid-phenylalanine only Thus, he concluded the UUU codon codes for phenylalanine.
2. Nirenberg and Philip Leder In- 1964, they found 47 out of 64 possible codons by employing the technique of triplet binding.
3. Har Gobind Khorana He worked out remaining 17 codons by employing artificial bzRNA.
   Note In 1968, Nirenberg and Khorana shared Nobel Prize with RW Holley (gave details of fRNA structure).

On the basis of above discoveries, the spellings of the genetic code were put together in a checkerboard, as given below

Question 21.
Write short note on peptide bonds.
Answer:
Amino acids are joined together in proteins by peptide bonds. A peptide bond is a covalent bond formed between two molecules when the carboxyl group of one molecule reacts with the amine group of the other molecule. This releases a water molecule. CONH is called a peptide link.

Question 22.
Unambiguous, universal and degenerate are some of the terms used for the genetic code. Explain the salient features of each of them.
Answer:
Unambiguous code means that one codon codes for only one amino acid, i.e. AUG codes only for methionine. Genetic code is universal, as particular codon codes for the same amino acid in all organisms. It is degenerate because some amino acids are coded by more than one codon, e.g. UUU and UUC, both code for phenylalanine.

Question 23.
Write short note on aminoacylation in translation.
Ans.
Amino acids in the cytoplasm are inactive. They cannot take part directly in protein synthesis or translation. The formation of peptide bond requires energy. In the presence of ATP, amino acids become activated by binding with aminoacyl fRNA synthase enzyme, i.e. aminoacylation.

Question 24.
Write short note on operon.
Or
Write a note on operon concept.
Answer:
An operon is a unit of prokaryotic gene expression which includes sequentially regulated structural genes and control elements recognised by the regulatory gene product. F Jacob and J Monod gave the operon concept and were the first ones to describe a transcriptionally regulated system.

Question 25.
What is DNA fingerprinting? Mention its applications.
Or Write a note on DNA fingerprinting.
Answer:
DNA Fingerprinting:
The technique of DNA fingerprinting or DNA typing or DNA profiling was developed and established by British geneticist Dr. Alec Jeffreys based on the fact that like every individual organism is unique in its fingerprints. The DNA pattern also differs in every individual.

Fingerprints can be altered by surgery but there is no known procedure available to alter the DNA design of an individual. For obtaining the DNA fingerprints of an individual, highly polymorphic genes that occur in multiple forms in different individuals are selected.

Applications of DNA Fingerprinting:
This technique can he applied in various fields such as

• Used as a tool in forensic investigations.
• To settle paternity disputes.
• To study evolution by determining the genetic diversities among population.

Question 26.
(i) Explain DNA polymorphism as the basis of genetic mapping of human genome.
(ii) State the role of VNTR in DNA fingerprinting.
Answer:
(i) Polymorphism is inherited from parents to children. So, it is useful for the identification (forensic application) and paternity testing. It arises due to mutations and also plays an important role in evolution and speciation. These mutations in the non-coding sequences have piled up with time and form the basis of DNA polymorphism. It is the basis of genetic mapping of human genome as well as DNA fingerprinting.

(ii) Variable Number of Tandem Repeats (VNTRs) belong to a class of satellite DNA called as minisatellite. VNTR are used as probes in DNA fingerprinting.

Long Answer Type Questions

Question 1.
Describe the structure of DNA with a neat and labelled diagram.
Or Describe the structure of DNA molecule as per the model proposed by Watson and Crick.
Answer:
Primary Structure of DNA
Two nucleotides when linked through a 3′ → 5′ phosphodiester linkage, form a dinucleotide. The phosphodiester linkage is formed when each phosphate group esterifies to the 3′ hydroxy! group of a pentose and to the 5′ hydroxyl group of the next pentose.
In a similar fashion, more nucleotides may join to form a polynucleotide chain (fig. structure of DNA). The polymer chain thus, formed has

• One end with a free phosphate moiety at 5′ end of deoxyribose sugar. This is marked as 5′ end of polynucleotide chain.
• The other end with a free hydroxyl 3′ – OH group marked as 3′ end of the polynucleotide chain.

Thus, the sugar and phosphates form the backbone in a polymer chain and the nitrogenous bases linked to sugar moiety project from this backbone. In RNA, there is an additional – OH group at 2′ position in the ribose of every nucleotide residue.

A Ploynucleotide chain

Secondary Structure of DNA:
Watson and Crick proposed the secondary structure in the form of the famous double helix model in 1953 on the basis of following observations
1. Erwin Chargafif (in 1950) formulated important generalisation on the base and other contents of DNA, called as ChargafFs rule. It states that for a double-stranded DNA, the ratios between adenine (A) and thymine (T) and guanine (G) and cytosine (C) are constant and equal to one.
i.e. \(\frac{A+T}{G+C}\) = 1

2. X-ray diffraction studies by Wilkins in 1952, suggested a helicoidal configuration of DNA.
One of the important features of this model was the complementary base pairing. It means if the sequence of bases in one strand is known, the sequence in other strand can be easily predicted. Also, if each strand from a DNA acts as a template for synthesis of a new strand, the daughter DNA thus produced would be identical to the parental DNA molecule.

Watson and Crick Model of DNA:
Watson and Crick worked out the first correct double helix model of DNA, which explained most of its properties.
The salient features of double helix structure of DNA are as follows
1. DNA is made up of two polynucleotide chains. The backbone is constituted by sugar phosphate, while the nitrogenous bases project inwards.
2. The two chains have anti-parallel polarity, i.e. when one chain has 3′ → 5′ polarity, the other has 5′ → 3′ polarity. Hence, orientation of deoxyribose sugar is opposite in both the strands.
3. The two strands are complementary to each other, i.e. purine base of one strand has pyrimidine counterpart on other strand. The complementary bases in two strands are paired through hydrogen bonds (H-bonds) to form base pairs.
(a) Adenine is bonded with thymine of the opposite strand with the help of two hydrogen bonds.
(b) Guanine is bonded with cytosine of the opposite strand with the help of three hydrogen bonds. So, a purine bonds with a pyrimidine always. Thus, maintaining a uniform distance between the two strands of the helix.
4. The two polypeptide chains are coiled in a right-handed fashion. Pitch of the helix, i.e. length of DNA in one complete turn = 3.4 nm or
3.4 × 10^-9 or 34 Å.
Number of base pairs in each turn = 10. Distance between a base pair in a helix = 0.34 nm. The diameter of DNA molecule is 20 Å (2nm).
5. Percentage calculation of bases is done by A + T = 100 – (G + C).
6. The plane of one base pair stacks over the other in double helix. This provides the stability to the helical structure, in addition to H-bond.
The length of DNA in E. coli is 1.36 mm, while in humans it is 2.2 m.

Structure of DNA : (a) Watson and Crick model of double helix, (b) Double-stranded polynucleotide chain sequence showing hydrogen bonds

Question 2.
Give an account of Griffith’s experiment on transformation.
Answer:
Frederick Griffith in 1928, carried out a series of experiments with Diplococcus pneumoniae (a bacterium that causes pneumonia). He observed that when these bacteria were grown on a culture plate, some of them produced smooth, shiny colonies (S-type), whereas the others produced rough colonies (R-type).

This difference in appearance of colonies (smooth/rough) is due to the presence of mucous (polysaccharide) coat on S-strains (virulent/pathogenic) but not on R-strains (avirulent/non-pathogenic).

Experiment:

1. He first infected two separate groups of mice. The mice that were infected with the S-strain (S-III) died from pneumonia as S-strains are the virulent strains causing pneumonia.
2. The mice that were infected with the R-strain (R-II) did not develop pneumonia and they lived.
3. In the next set of experiments, Griffith killed the bacteria by heating them. The mice that were injected with heat-killed S-strain bacteria did not die and lived.
4. Whereas, on injecting a mixture of heat-killed S-strain and live R-strain bacteria, the mice died. Moreover, living S-bacteria were recovered from the dead mice.

These steps are summarised below

From all these observations Griffith concluded that the live R-strain bacteria, had been transformed by the heat-killed S-strain bacteria, i.e. some ‘transforming principle’ had transferred from the heat-killed S-strain, which helped the R-strain bacteria to synthesise a smooth polysaccharide coat and thus, become virulent.

This must be due to the transfer of the genetic material. However, he was not able to define the biochemical nature of genetic material from his experiments.

Biochemical Characterisation of Transforming Principle:
Oswald Avery, Colin MacLeod and Maclyn McCarty (1933-44) worked in Rockfellar Institute, New Xork, USA to determine the biochemical nature of ‘transforming principle’ in Griffith’s experiment in an in vitro system. Prior to this experiment, the genetic material was thought to be protein.

During this experiment, purified biochemicals (i.e. proteins, DNA, RNA, etc.) from the heat-killed S-III cells were taken, to observe which biochemicals could . transform live R-cells into S-cells.

They discovered that DNA alone from heat-killed S-type bacteria caused the transformation of non-virulent R-type bacteria into S-type virulent bacteria.

They also discovered that protein digesting enzymes (proteases) and RNA digesting enzymes (ribonuclease) did not inhibit this transformation. This proved that the ‘transforming substance’ was neither protein nor RNA.

DNA-digesting enzyme (deoxyribonuclease) caused inhibition of transformation, which suggests that the DNA caused the transformation. This provided the first evidence for DNA as transforming principle or the genetic material.
The steps of this experiment are summarised below

• R-II + DNA extract of S-III + no enzyme = R-II colonies + S-III colonies
• R-II + DNA extract of S-III + Ribonuclease = R-II colonies + S-III colonies
• R-II + DNA extract of S-III + Protease = R-II colonies + S-III colonies
• R-II + DNA extract of S-III + Deoxyribonuclease = Only R-II colonies

Question 3.
State the aim and describe Meselson and Stahl’s experiment.
Answer:
Meselson and Stahl in 1958, aimed to prove that DNA replicates in a semiconservative fashion. The semiconservative DNA replication suggests that, after the completion of replication, each DNA molecule will have one parental and one newly synthesised strand.

Meselson and Stahl’s experiment
Matthew, Meselson and Franklin Stahl in 1958 conducted an experiment in California Institute of technology with Escherichia coli to prove that DNA replicates semiconservatively as follows

1. They grew many generations of E.coli in a medium containing ¹⁵NH₄Cl (¹⁵N is the heavy isotope of nitrogen) as the only source of nitrogen.
The result was that ¹⁵N got incorporated into the newly synthesised DNA after several generations. By centrifugation in a cesium chloride (CsCl) density gradient, this heavy DNA molecule could be distinguished from the normal DNA.

2. The bacterial culture was then washed to make the medium free and the cells were then transferred into a medium containing normal ¹⁴NH₄Cl.

3. The samples were separated independently on CsCl gradient to measure the densities of DNA.

4. At definite time intervals, as the cells multiplied, samples were taken and the DNA which remained as double-stranded helices was extracted.

5. The DNA obtained from the culture, one generation after the transfer from ¹⁵N to ¹⁴N medium (i.e. after 20 minutes because E.coli divides in 20 minutes) had a hybrid or intermediate density.
This hybrid density was the result of replication in which DNA double helix had separated and the old strand (N¹⁵) had synthesised a new strand (N₁₄).

6. The DNA obtained from the culture after another generation (II generation) was composed of equal amounts of hybrid DNA containing (N¹⁵ molecule) and ‘light’ DNA (containing ¹⁴N molecule).

7. With the preeceding growth generations in normal medium, more and more light DNA was present. Hence, the semiconservative mode of DNA replication was confirmed.

Meselson-Stahl experiment to demonstrate semiconservative replication

Similar experiments on a eukaryote, ‘ Vicia faba’ (faba beans) were conducted by Taylor and colleagues in 1958, involving use of radioactive thymidine, i.e. bromodeoxy-uridine. The replicated chromosomes were then, stained with fluorescent dye and Giemsa. The old and new strand were stained differently which confirm that the DNA in chromosomes also replicates semiconservatively.

Question 4.
Describe the process of DNA replication.
Answer:
DNA Replication:
In addition to the double helical structure of DNA, Watson and Crick also proposed a scheme for DNA replication. According to this model, the two strands of double helix separate and act as a template for the synthesis of new complementary strands in which the base sequence of one strand determines the sequence on the other strand.

Watson and Crick model for semiconservative DIMA replication

This is called base complementarity and it ensures the accurate replication of DNA. After the completion of replication, each DNA molecule have one parental and one newly synthesised strand.
This scheme for DNA replication was termed as semiconservative DNA replication.

DNA Replication is Semiconservative:
Meselson and Stahl in 1958, aimed to prove that DNA replicates in a semiconservative fashion. The semiconservative DNA replication suggests that, after the completion of replication, each DNA molecule will have one parental and one newly synthesised strand.

Meselson and Stahl’s experiment
Matthew, Meselson and Franklin Stahl in 1958 conducted an experiment in California Institute of technology with Escherichia coli to prove that DNA replicates semiconservatively as follows

1. They grew many generations of E.coli in a medium containing ¹⁵NH₄Cl (¹⁵N is the heavy isotope of nitrogen) as the only source of nitrogen.
The result was that ¹⁵N got incorporated into the newly synthesised DNA after several generations. By centrifugation in a cesium chloride (CsCl) density gradient, this heavy DNA molecule could be distinguished from the normal DNA.

2. The bacterial culture was then washed to make the medium free and the cells were then transferred into a medium containing normal ¹⁴NH₄Cl.

3. The samples were separated independently on CsCl gradient to measure the densities of DNA.

4. At definite time intervals, as the cells multiplied, samples were taken and the DNA which remained as double-stranded helices was extracted.

5. The DNA obtained from the culture, one generation after the transfer from ¹⁵N to ¹⁴N medium (i.e. after 20 minutes because E.coli divides in 20 minutes) had a hybrid or intermediate density.
This hybrid density was the result of replication in which DNA double helix had separated and the old strand (N¹⁵) had synthesised a new strand (N₁₄).

6. The DNA obtained from the culture after another generation (II generation) was composed of equal amounts of hybrid DNA containing (N¹⁵ molecule) and ‘light’ DNA (containing ¹⁴N molecule).

7. With the preeceding growth generations in normal medium, more and more light DNA was present. Hence, the semiconservative mode of DNA replication was confirmed.

Meselson-Stahl experiment to demonstrate semiconservative replication

Similar experiments on a eukaryote, ‘ Vicia faba’ (faba beans) were conducted by Taylor and colleagues in 1958, involving use of radioactive thymidine, i.e. bromodeoxy-uridine. The replicated chromosomes were then, stained with fluorescent dye and Giemsa. The old and new strand were stained differently which confirm that the DNA in chromosomes also replicates semiconservatively.

Pre-Requisites of DNA Replication:
DNA replication is a complex process that requires many enzymes and protein factors. This process is very fast and accurate. It is seen in both prokaryotes and eukaryotes and involves some basic steps that are listed below
(i) Two parental strands unwind and get separate.
(ii) One of the parental strand acts as a template for the synthesis of new strand. Hence, a new strand is formed by the winding of one old and one new strand.

Major components involved in the process of DNA replication are as follows
I. On (Origin of Replication)

1. It is the specific site on DNA where replication starts and proceeds in one or both directions. This site is known as origin of replication (Ori).
2. Ori specifying DNA segments can be isolated from E. coli, Coli phages, plasmids, yeasts and eukaryotic viruses.
3. Ori in E. coli is called Ori C. It is a DNA sequence of about 245 base pairs that is rich in A-T bases. Hence, the two strands easily get separated at the origin.
4. Ori in Yeast is called Autonomous Replication . Sequence (ARS) which is 150 base pair long. It acts as the binding site for Origin Recognition Complex (ORC).
5. During replication, Ori is recognised by replication initiator complex and the process of replication starts. It proceeds along the replication forks.
6. Each Ori has two termini. A replicon is one Ori (or origin) with its two unique termini. In prokaryotes (E.coli), the entire circular DNA acts as a single replicon. In eukaryotes, DNA is larger and hence, they have several Ori per DNA.
7. In bidirectional replication, the two strands separate at the origin or Ori. It results in the formation of a replication eye and both ends move along the replication, e.g. θ-replication (Theta) in prokaryotes.
   
8. In unidirectional replication, one of the two ends of the replication eye moves along the replication fork while the other end remains stationary, e.g. replication of mitochondrial DNA (mt DNA) in vertebrates.

II. DNA Polymerase

1. It is the main enzyme which uses a DNA template to catalyse the polymerisation of deoxynucleotides. The average rate of polymerisation is 2000 bp (base pairs) per second approximately.
2. DNA polymerase adds deoxyribonucleotides to the 3′-OH end of polynucleotide by the removal of pyrophosphate from nucleoside triphosphate.
3. Polynucleotide (n) + d NTP → Polynucleotide (n + 1) + PPi

Types of DNA Polymerases

1. In prokaryotes, there are three types of DNA polymerases, i.e. DNA polymerase-I, II and III, whereas in eukaryotes, five different DNA polymerases have been indentified, i.e. DNA polymerases α, ß, γ, δ and ε.
2. DNA polymerase was first isolated from Exoli by Arthur Kornberg in Washington University in 1956. It was first called Kornberg enzyme but later its name was changed to DNA polymerase-I due to the discoveries of other polymerases.
3. DNA polymerase-I and II Involved in DNA repair and proofreading in prokaryotes.
4. DNA polymerase-III It has exonuclease activity. It can remove nucleotides from 3′ end of DNA strand, i.e., 3’→5′ exonuclease. It also helps in proofreading so that wrong nucleotide added at 3′ end can be removed.
5. Exonuclease activity of different DNA polymerases is listed below
   

Working of DNA Polymerase
DNA polymerase (Pol) requires a template to synthesise a new strand in 5′-3′ direction. For this, they add a primer to the template strand. The new nucleotides are then added to the 3′-OH end of primer so that the synthesis of DNA proceeds in 5′-3′ direction.
Note A prime is small DNA or RNA strand that is to template strand through hydrogen bonds.

III. Other Enzymes
Besides DNA polymerases, other enzymes involved in the process of DNA replication are as follows

1. Helicase It unwinds the DNA strand, i.e. separates the two strands from one point, for the formation of a
   replication fork.
2. Topoisomerase (DNA gyrase) The unwinding of DNA creates a tension in the DNA strands, which get released by the enzyme topoisomerase.
3. DNA Ligase It facilitates the joining of DNA strands together by catalysing the formation of phosphodiester bond. It plays a role in repairing single-strand breaks in duplex DNA.

Mechanism of DNA Replication:
All the enzymes and protein factors involved in DNA replication constitutes a replicase system or replisome. . The process of replication proceeds in the following steps

1. An initiator protein recognises the Origin of replication (Ori) and binds to it.
2. DNA helicase enzyme breaks the hydrogen bonds between nitrogenous bases and unwinds the ds DNA.
3. To prevent rewinding and attack by single stranded nuclease, Single-Stranded Binding proteins (SSB proteins) bind to the separated strands. SSB also help to keep these ssDNA in extended position.
4. The combined action of helicase and SSB proteins results in the formation of V-shaped replication fork at the origin.
5. As the replication fork moves, DNA unwinds and a positive super coil is formed in the unreplicated portion of DNA, i.e. in front of the fork.
6. The super coil is like a knot that hinders the fork movement. It is removed by the enzyme topoisomerase (gyrase) in E.coli and topoisomerase-I in eukaryotes.

Question 5.
How do mRNA, tRNA and ribosomes help in the process of translation?
Answer:
(i) Binding of mRNA to Ribosome:
Ribosomes occur in the cytoplasm as separate smaller and larger units.
In prokaryotes, IF-3 binds to 30 S subunit to prevent association of subunits. The incoming tRNA containing specific amino acid binds to the A-site. The prokaryotic mRNA has a leader sequence called shine-Delgarno sequence that is present just prior to initiation codon-AUG.

It is homologous to 3′ end of 16S rRNA (ASD region) in 30S subunit. This complementarity ensures correct binding of 30S subunit on mRNA. The peptidyl tRNA containing elongating polypeptide then binds to P-site. The bacterial ribosome contains another site, the E-site or Exit-site to which the discharged tRNA or tRNA whose peptidyl has already been transferred binds before its release from ribosome.

A bacterial ribosome with three sites; E, exit site, P, peptidyl site and A, aminoacyl site

(ii) Aminoacylation
Aminoacylation of tRNA The activation of amino acids takes place through their carboxyl groups. The amino acids are activated in the presence of ATP and linked to their cognate tRNA. In the presence of ATP, amino acids become activated by binding with aminoacyl tRNA synthetase enzyme.

The amino acid AMP-enzyme or AA-AMP enzyme complex is called an activated amino acid.

In the second step, this complex associated with the 3′-OH end of tRNA. AMP gets hydrolysed to form an ester bond between amino acid and tRNA and the enzyme is released.
AA – AMP – enzymes + tRNA → AA – tRNA + AMP + enzyme.

(iii) Transfer of Activated Amino Acids to tRNA
The amino acids are attached to the tRNA by high energy bonds. These bonds are formed between the carboxyl group of amino acid and 3′ hydroxy terminal of ribose of terminal adenosine of CCA and of tRNA.
The complete reaction is carried out by enzyme synthetase which has two active sites, i.e. one for tRNA and another for specific amino acid molecule.

Question 6.
Describe the process of translation in prokaryotes.
Or Describe the initiation step of translation in prokaryotes.
Answer:
Translation requires a machinery which consists of ribosome, wzRNA, rRNAs, aminoacyl rRNA synthetase (enzyme that helps in combining amino acid to particular rRNA) and amino acids.

Initiator tRNA
It is a specific rRNA for the process of initiation and there are no rRNAs for stop codons.

Ribosome
It occurs in cytoplasm and responsible for protein synthesis. It consists of structural RNAs and around 80 different proteins. Ribosome exists as two subunits in its inactive stage
(i) Small subunit When the small subunit encounters an mRNA, translation of mRNA to protein begins.
(ii) Large subunit It consists of two sites where amino acids can bind to and be close to each other for the formation of a peptide bond. Ribosome also acts as a catalyst (23S rRNA in bacteria is the enzyme ribozyme) for peptide bond formation.

Translational Unit:
It is the sequence of RNA flanked by the start codon (AUG) and the stop codon in mRNA. It codes for a polypeptide that has to be produced.

Untranslated Regions (UTR):
These are some additional sequences in an wRNA that are not translated. They are present at both the ends, i.e. at 5′ end (before start codon) and at 3′ end (after stop codon). They improve the efficiency of translation process.

Mechanism of Translation:
The main steps in translation include
(i) Binding of mRNA to ribosome
(ii) Activation of amino acids (aminoacylation of tRNA).
(iii) Transfer of activated amino acids to tRNA.
(iv) Initiation of polypeptide chain synthesis.
(v) Elongation of polypeptide chain.
(vi) Termination of polypeptide chain formation.

(i) Binding of mRNA to Ribosome:
Ribosomes occur in the cytoplasm as separate smaller and larger units.
In prokaryotes, IF-3 binds to 30 S subunit to prevent association of subunits. The incoming tRNA containing specific amino acid binds to the A-site. The prokaryotic mRNA has a leader sequence called shine-Delgarno sequence that is present just prior to initiation codon-AUG.

It is homologous to 3′ end of 16S rRNA (ASD region) in 30S subunit. This complementarity ensures correct binding of 30S subunit on mRNA. The peptidyl tRNA containing elongating polypeptide then binds to P-site. The bacterial ribosome contains another site, the E-site or Exit-site to which the discharged tRNA or tRNA whose peptidyl has already been transferred binds before its release from ribosome.

A bacterial ribosome with three sites; E, exit site, P, peptidyl site and A, aminoacyl site

(ii) Aminoacylation
Aminoacylation of tRNA The activation of amino acids takes place through their carboxyl groups. The amino acids are activated in the presence of ATP and linked to their cognate tRNA. In the presence of ATP, amino acids become activated by binding with aminoacyl tRNA synthetase enzyme.

The amino acid AMP-enzyme or AA-AMP enzyme complex is called an activated amino acid.

In the second step, this complex associated with the 3′-OH end of tRNA. AMP gets hydrolysed to form an ester bond between amino acid and tRNA and the enzyme is released.
AA – AMP – enzymes + tRNA → AA – tRNA + AMP + enzyme.

(iii) Transfer of Activated Amino Acids to tRNA
The amino acids are attached to the tRNA by high energy bonds. These bonds are formed between the carboxyl group of amino acid and 3′ hydroxy terminal of ribose of terminal adenosine of CCA and of tRNA.
The complete reaction is carried out by enzyme synthetase which has two active sites, i.e. one for tRNA and another for specific amino acid molecule.

(iv) Initiation of Polypeptide Chain Synthesis:
The protein synthesis begins from the amino terminal end of the polypeptide, proceeds by the addition of amino acids through peptide bond formation and ends at the carboxyl terminal end. In prokaryotes, the initiation amino acid is formylated methionine while in eukaryotes it is methionine.

Initiation in Prokaryotes
In prokaryotes, two types of tRNA are present for methionine
(a) tRNAf^met for initiation carrying formyl methionine and
(b) tRNA^met for carrying normal methionine to growing polypeptide.

The initiation of polypeptide synthesis requires the following components
mRNA, 30S subunit of ribosome, formylmethionyl-tRNA (f^met-tRNAf^met), initiation factors IF-1, IF-2 and IF-3, GTP, 50S ribosomal subunit and Mg⁺².
The sequence of events occurring during initiation process are
1. The smaller 30S subunit of ribosome binds to the transcription factor IF-3. It prevents the premature association of two ribosomal subunits.

2. Interaction of SD region of mRNA and ASD region of ribosome helps the mRNA to bind to 30S subunit. It also helps AUG to correctly positioned at the P-site of the ribosome.

3. The fMet-tRNAf^met (the specific tRNA aminoacylated to formyl methionine) binds to the AUG codon at the P-site. The tRNAfmct is the only tRNA that binds to its codon present on the P-site. All other fRNA along with their respective amino acids bind to their codon present at the A-site. Therefore, AUG codon present as initiation codon codes for formylmethionine. When it is present at other position it codes for normal methionine.

4. The initiation factor IF-1, binds to the A-site. It prevents the binding of any other aminoacyl tRNA to the codon at the A-site during initiation.

5. The GTP bound IF-2 (GTP-IF-2) and the initiating f Met-tRNAf^met attaches to the complex of 30S subunit-IF3-IF1-mRNA.

6. 50S subunit then attaches the complex formed in the previous step. The GTP bound to IF-2 is hydrolysed to GDP and Pi. After this step, all the three initiation factors leave ribosome. This complex of 70S ribosome, mRNA and f Met-rRNA fmet bound to initiation codon at P site is known as initiation complex.

Stepwise formation of initiation complex in prokaryote

(v) Elongation of Polypeptide Chain
In this step, another charged aminoacyl tRNA complex binds to the A-site of the ribosome, following the hydrolysis of GTP to GDP and Pi. A peptide bond forms between carboxyl group (-COOH) of amino acid at P-site and amino group (-NH₃) of amino acid at A-site by the enzyme peptidyl transferase.

Binding of the second aminoacyl tRNA to the A site of ribosome

Formation of a peptide bond

(vi) Translocation of Polypeptide:
The peptidyl tRNA bounded to A-site comes to the P-site of ribosome.
The empty tRNA comes to E-site and a new codon occupies the A-site for next aminoacyl tRNA.

• This is achieved by the movement or translocation of ribosome by a codon in 5′ to 3′ direction of mRNA in the presence of EF-G (translocase) and GTP.
• tRNA interact with E-site on 50S subunit through it CCA sequence at 3′ end.

The tRNA molecule is then, transferred from A site to P-site and from P-site to E-site by the movement of two subunits of ribosomes.
Finally, the deacylated tRNA is released to cytosol from E-site.

(vii) Termination:
It is accomplished by the presence of any of the three termination codon on mRNA. Which are recognised by the release (termination) factor, RF₁, RF₂ and RF₃.

RF₁ and RF₂ They resemble the structure of tRNA. They compete with tRNA to bind the termination codon at A-site of ribosome. This is called molecular mimicry. RF₁ recognise UAG and RF₂ recognise UGA. UAA is recognised by both of them. RF₃ helps to split the peptidyl tRNA body by using GTP.
Note In eukaryotes, only one release factor is known. It iseRF₁.

Odisha State Board CHSE Odisha Class 12 Biology Important Questions Chapter 6 Sex Determination Important Questions and Answers.

CHSE Odisha 12th Class Biology Important Questions Chapter 6 Sex Determination

Sex Determination Class 12 Important Questions CHSE Odisha

Very Short Answer Type Questions

Choose the correct option

Question 1.
Non-homologous segment of Y-chromosome carries
(a) dominant genes
(b) recessive genes
(c) holandric genes
(d) None of the above
Answer:
(c) holandric genes

Question 2.
Which type of sex determination is found in humans?
(a) XX – XY
(b) Z\V – ZZ
(c) XX – XO
(d) ZZ – ZO
Answer:
(a) XX – XY

Question 3.
In XO-type of sex-determination
(a) females produce two different types of gametes
(b) males produce two different types of gametes
(c) females produce gametes with Y-chromosome
(d) males produce single type of gametes
Answer:
(b) males produce two different types of gametes

Question 4.
Which of the following types of sex-determination is found in grasshopper?
(a) XX female and XY male
(b) ZW female and ZZ male
(c) XX female and XO male
(d) XX male and XO female
Answer:
(c) XX female and XO male

Question 5.
Sex chromosomes of a female bird are represented by
(a) XO
(b) XX
(c) ZW
(d) ZZ
Answer:
(c) ZW

Question 6.
ZZ/ZW type of sex-determination is seen in
(a) snails
(b) peacock
(c) platypus
(d) cockroach
Answer:
(b) peacock

Question 7.
In gynandromorph
(a) all cells have XX genotype
(b) all cells have XY genotype
(c) all cells with XXY genotype
(d) some cells of the body contain XX and some cells with XY genotype
Answer:
(d) some cells of the body contain XX and some cells with XY genotype

Question 8.
In which chromosome is the gene for haemophilia located?
(a) X-chromosome
(b) Y-chromosome
(c) Autosome
(d) Both (a) and (b)
Answer:
(a) X-chromosome

Question 9.
A colourblind person cannot distinguish
(a) all colours
(b) green
(c) red
(d) red and green
Answer:
(d) red and green

Question 10.
Which chromosome-linked genes do cause the genetic metabolic Phenylketonuria (PKU)?
(a) Somatic dominant gene
(b) Somatic recessive gene
(c) Y-linked gene
(d) X-linked gene
Answer:
(b) Somatic recessive gene

Question 11.
Down’s syndrome is an example of
(a) triploidy
(b) polyteny
(c) polyploidy
(d) aneuploidy
Answer:
(d) aneuploidy

Question 12.
What is the diploid chromosome number in a person suffering from Down syndrome?
(a) 45
(b) 46
(c) 47
(d) 48
Answer:
(c) 47

Question 13.
Which is the genotype of Turner’s syndrome?
(a) XO
(b) XXY
(c) XYY
(d) XXX
Answer:
(a) XO

Question 14.
Number of Barr bodies present in Turner’s syndrome is
(a) 0
(b) 1
(c) 2
(d) Both (b) and (c)
Answer:
(a) 0

Question 15.
In which of the following diseases, the man has an extra X-chromosome?
(a) Bleeder’s disease
(b) Turner’s syndrome
(c) Klinefelter’s syndrome
(d) Down’s syndrome
Answer:
(c) Klinefelter’s syndrome

Question 16.
A colour blind person cannot distinguish colour/colours.
(a) all
(b) red
(c) green
(d) red and green
Answer:
(d) red and green

Question 17.
The extra inactive X-chromosome in karyotype of Klinefelter syndrome is called
(a) Barr body
(b) barr chromosome
(c) dosage body
(d) None of these
Answer:
(a) Barr body

Correct the sentences, if required, by changing the underlined word(s)

Question 1.
Heterogametic individual produces similar type of gametes.
Answer:
Homogametic individual produces similar type of gametes.

Question 2.
D. melanogaster with 2A +XX chromosome complement is female.
Answer:
Correct statement.

Question 3.
Gynandromorphs die due to failure of segregation.
Answer:
Correct statement.

Question 4.
Mary F lyon discovered X-chromosome in male bug and described it as X-bodv.
Answer:
Barr body

Question 5.
The genotype of a carrier haemophila is XhXh.
Answer:
XXh

Question 6.
Cystic fibrosis is a sex-linked recessive disease, which is transmitted from an unaffected carrier female to some of the male offsprings.
Answer:
Haemophilia

Question 7.
Down syndrome is an inherited blood disorder, in which the body makes an abnormal form of haemoglobin.
Answer:
Thalassemia

Question 8.
Klinefelter syndrome is an abnormal condition caused by the presence of an extra Y chromosome.
Answer:
X

Fill in the blanks

Question 1.
In humans, males are heterogametic, whereas females are
Answer:
homogametic.

Question 2.
According to genic balance theory, the sex index of 1.0 is a ………….. .
Answer:
Female

Question 3.
The unfertilised egg of honeybee develops into …………….. .
Answer:
drones

Question 4.
In grasshopper, female is ……………. and the male is …………. .
Answer:
XX and XO

Question 5.
…….. is also known as bleeder’s disease.
Answer:
Haemophilia

Question 6.
Down’s syndrome is due to ………….. of chromosome 21.
Answer:
trisomy

Question 7.
Turner’s syndrome is caused due to of one of the X-chromosome.
Answer:
the absence

Question 8.
………….. is an inherited disorder which results in the failure to distinguish red and green colours.
Answer:
Colour Blindness

Express in one or two word(s)

Question 1.
The sex of the child developed from 44A+XX zygote.
Answer:
Female

Question 2.
At high temperature, what sex of turtle is produced?
Answer:
Female

Question 3.
Name the environmental factor that determines the sex in Bonellia.
Answer:
Temperature

Question 4.
Name any one autosomal recessive disease.
Answer:
Thalassemia.

Question 5.
Name the scientist who discovered Down’s syndrome.
Answer:
Langdon Down.

Question 6.
A heritable disorder linked to genes on the non-sex chromosomes.
Answer:
Down’s syndrone

Question 7.
A heritable disease caused by the presence of one defective allele.
Answer:
Thalassemia

Question 8.
Chromosomes fail to sort properly during meiosis.
Answer:
Down’s syndrome

Short Answer Type Questions

Question 1.
What is Barr body?
Answer:
A Barr body is a small darkly stained mass of X-chromosome, which in inactive and are found only in the female cells. Out of the two X-chromosomes in feamales only one is functional and the other remain as Barr body.

Question 2.
How the sex is determined in humans?
Or Write a short note on sex-determination in human.
Answer:
The male and female individuals normally differ in their chromosomal constituents. There are two types of chromosomes, i.e.

1. Sex chromosomes or Allosomes The chromosomes responsible for sex determination, e.g. X and Y-chromosomes.
2. Autosomes The chromosomes which determines the somatic characters.

X-chromosome was first discovered by Henking (1891). He named this structure as X-body. Scientists further explained that X-body was a chromosome and called it as X-chromosome. The concept of autosomes and allosomes was proposed by Wilson and Stevens (1902-1905) in chromosomal theory of sex-determination.

There are various types of chromosomal sex-determination mechanism observed in different animals as follows

Mechanism of sex-determination

Question 3.
What is male heterozygosity?
Answer:
Male heterozygosity is a type of mechanism of sex-determination in organisms. XX and XY type of sex-determination shows the phenomenon of male heterogamety or heterozygosity because in both these cases, males produce two different types of gametes such as • Either with or without X-chromosome.

• Some gametes with X-chromosome and some with Y-chromosome.

Question 4.
Describe sex-determination in grasshoppers.
Answer:
Grasshoppers have XX-XO method of sex-determination. In this, female has XX and produces homogametic eggs, while male has only one chromosome and produces two types of sperms, e.g. gymnosperms (with X) and angiosperms (without X).

Question 5.
(i) why grasshopper and Drosophila show male heterogamety? Explain.
(ii) Explain female heterogamety with the help of examples.
Answer:
(i) Male heterogamety is shown by male grasshopper and Drosophila, as they both produce two types of gametes having 50% X-chromosomes and other with 50% Y-chromosomes.

(ii) In this case, the total number of chromosomes are same in both males and females. But two different types of gametes having different sex chromosomes are produced by females.

1. ZZ-ZW Mechanism
This mechanism of sex-determination is seen in birds, fowls and fishes. Females have one Z and one W-chromosome (i.e. heterogametic) along with autosomes whereas males have a pair of Z-chromosomes (i.e. homogametic). Thus, the sex of an organism is determined by the type of ovum that is fertilised to produce an offspring.

Determination of sex (ZZ-ZW) in fowl and birds

2. ZZ-ZO
In this mechanism of sex-determination, the female is heterogametic (ZO) and male is homogametic (ZZ). It occurs in lepidoptera, e.g. certain butterflies and moths.

Determination of heterogametic and homogametic female and male

Question 6.
Write the types of sex-determination mechanisms of the following crosses. Give an example of each type.
(i) Female XX with male XO
(ii) Female ZW with male ZZ
Answer:
(i) The type of sex-determination mechanism shown in female XX with male XO is male heterogamety, e.g. grasshoppeer.
(ii) The type of sex-determination mechanism shown in female ZW with male ZZ is female heterogamety, e.g. birds.

Question 7.
Write short note on sex-determination in Bonellia viridis.
Answer:
In Bonellia viridis (worm), the environment determines the sex differentiation. In these, when the young ones are reared alone they develop into females, but when the newly hatched eggs are reared in close proximity to an adult female (i.e. attached to female proboscis) they become male.
This is due to the hormones released by female proboscis which induces larvae to differentiate into males.

Question 8.
What is criss-cross inheritance?
Answer:
Criss-cross inheritance is defined as the inheritance of sex-linked characters transmitted from father to daughter, who pass it on to the grandsons. The trait is expressed only in males in alternate generations, e.g. red-green colours blindness, haemophilia, etc.

Question 9.
What is sex-linked inheritance? Discuss the inheritance of haemophilia in man.
Answer:
Inheritance of Haemophilia:
It is a sex-linked recessive disease, which is transmitted from an unaffected carrier female to some of the male offsprings. Due to this, patient continues to bleed even during a minor injury because of defective blood coagulation and hence, it is also called as bleeders disease. The gene for haemophilia is located on X-chromosome and it is recessive to its normal allele. In this disease, a single protein that is part of cascade of proteins involved in blood clotting is affected.

The possibility of a female becoming a haemophilic is extremely rare because mother of such a female has to be atleast carrier and father should be haemophilic, e.g. females suffer from this disease only in homozygous condition, i.e. XCXC. The haemophilic alleles shows criss-cross inheritance and they follow Mendelian pattern of inheritance. The family pedigree of Queen Victoria (who was a carrier of haemophilia) shows a number of haemophilic individual.
The inheritance is explained below


Four crosses explaining the inheritance of haemophilia allele in human ; (a) Normal mother and haemophilic father, (b) Haemophilic mother and normal father, (c) Carrier mother and normal father and (d) Carrier mother and haemophilic father

Question 10.
Haemophilia is a sex-linked inheritance condition in humans where a simple cut causes non-stop bleeding. Study the pedigree chart showing the inheritance of haemophilia in a family. Give reasons, which explain that haemophilia is (i) sex-linked and (ii) caused by X-linked gene.

Answer:
(i) Haemophilia is sex-linked because

• It is transmitted from an unaffected carrier female to some of the male offsprings.
• Female rarely becomes haemophilic as her mother has to be atleast a carrier and father should be haemophilic.

(ii) Gene for haemophilia is present on X-chromosome because the heterozygous female for haemophilia may transmit the disease to sons.

Question 11.
What is sex-linked inheritance? Discuss this taking colour blindness as an example.
Answer:
Sex chromosomes contain genes primarily concerned with the determination the sex of the organism. In addition to sex genes, they also contain the genes to control other body characters, thus are called sex-linked genes. The somatic characters whose genes are located on sex chromosomes are known as sex-linked characters. The inheritance of a trait (phenotype) that is determined by a gene located on one of the sex chromosome is called sex-linked inheritance.

Inheritance of Red-Green Colour Blindness
It is a sex-linked recessive disorder, which results in defect in either red or green cone of eye. It does not mean the incapability to see any colour at all, infact it leads to the failure in discrimination between red and green colour. The gene for colour blindness is present on X-chromosome.
It is present mostly in males (X^CY) because of the presence of only one X-chromosome as compared to two chromosomes in females. A heterozygous female has normal vision, but is a carrier and passes on the disorder to some of her sons. Its inheritance pattern is similar to that of haemophilia.

Question 12.
Write short note on inheritance of colour blindness in man.
Answer:
Sex chromosomes contain genes primarily concerned with the determination the sex of the organism. In addition to sex genes, they also contain the genes to control other body characters, thus are called sex-linked genes. The somatic characters whose genes are located on sex chromosomes are known as sex-linked characters. The inheritance of a trait (phenotype) that is determined by a gene located on one of the sex chromosome is called sex-linked inheritance.

Inheritance of Red-Green Colour Blindness
It is a sex-linked recessive disorder, which results in defect in either red or green cone of eye. It does not mean the incapability to see any colour at all, infact it leads to the failure in discrimination between red and green colour. The gene for colour blindness is present on X-chromosome.

It is present mostly in males (X^CY) because of the presence of only one X-chromosome as compared to two chromosomes in females. A heterozygous female has normal vision, but is a carrier and passes on the disorder to some of her sons. Its inheritance pattern is similar to that of haemophilia.

Question 13.
If a father and son are both defective in red-green colour vision, is it likely that the son inherited the trait from his father. Comment.
Answer:
No, defective gene for red-green colour vision cannot be inherited from father to his son. Gene for colour blindness is X-chromosome linked and sons receive their sole X-chromosome from their mother, not from their father. Male to male inheritance is not possible for X-linked traits in humans.
In the given case, the mother of the son must be a carrier (heterozygous) for colour blindness gene, thus transmitting the gene to her son.

Question 14.
A colourblind child is born to a normal couple. Work out a cross to show how it is possible. Mention the sex of this child.
Answer:
It is a sex-linked recessive disorder, which results in defect in either red or green cone of eye. It does not mean the incapability to see any colour at all, infact it leads to the failure in discrimination between red and green colour. The gene for colour blindness is present on X-chromosome.

It is present mostly in males (X^CY) because of the presence of only one X-chromosome as compared to two chromosomes in females. A heterozygous female has normal vision, but is a carrier and passes on the disorder to some of her sons. Its inheritance pattern is similar to that of haemophilia.

Question 15.
Write the symptoms of Down’s syndrome.
Answer:
The symptoms of Down’s syndrome are

1. Broad forehead
2. Short and broad neck
3. Short and stubby fingers
4. Partially open mouth, furrowed tongue
5. Mental retardation.

Question 16.
How is the child affected, if it has grown from the zygote formed by an XX-egg fertilised by a Y-carrying sperm? What do you call this abnormality?
Answer:

• The zygote will be XXY. It means the zygote is male with feminine characters.
• This abnormality is called Klinefelter’s syndrome.

Question 17.
Name a disorder, give the karyotype and write the symptoms, where a human male suffers as a result of an additional X-chromosome.
Answer:
The disorder is Klinefelter’s syndrome. It is a chromosomal disorder, which occurs in males. The presence of an additional copy of X-chromosome results in karyotype 44 + XXY.

HF Klinefelter first described this condition in 1942.
This genetic disorder occurs due to the presence of an additional copy of the X-chromosome. It is also known as trisomy of X-chromosome. Its estimated birth frequency is 1/500 live male births.

Genetic Basis
The union of an abnormal XX-egg with a normal Y-sperm or a normal X-egg with an abnormal XY-sperms results in the karyotype of 47, XXY in males or 47, XXX in females.

The abnormal eggs and sperms are formed due to the v primary non-disjunction of X and Y chromosomes during the maturation phase of gametogenesis. Although the usual karyotype of this condition is 47 + XXY but sometimes more complex karyotypes also occurs, e.g. XXXY, XXXXY, XXXXXY, XXXXYY, etc.

Long Answer Type Questions

Question 1.
Explain the chromosomal basis of sex-determination in animals.
Or Give an account of chromosomal theory of sex-determination.
Or Explain the chromosomal theory of sex-determination in animals.
Or Discuss the chromosomal theory of sex-determination in animal’s.
Or Describe the chromosomal basis of sex-determination in human, honeybee and birds.
Or Discuss sex-determination in birds and honey bees.
Answer:
Chromosomal Mechanism of Sex-Determination:
The male and female individuals normally differ in their chromosomal constituents. There are two types of chromosomes, i.e.

1. Sex chromosomes or Allosomes The chromosomes responsible for sex determination, e.g. X and Y-chromosomes.
2. Autosomes The chromosomes which determines the somatic characters.

X-chromosome was first discovered by Henking (1891). He named this structure as X-body. Scientists further explained that X-body was a chromosome and called it as X-chromosome. The concept of autosomes and allosomes was proposed by Wilson and Stevens (1902-1905) in chromosomal theory of sex-determination.

There are various types of chromosomal sex-determination mechanism observed in different animals as follows

Mechanism of sex-determination

Sex-Determination involving Heterogametic Males:
It is the mechanism in which male produces two different types of gametes. The two conditions that can occur in males are

• Only one X chromosome containing gamete is present.
• Some gametes with X-chromosome and some with Y-chromosome.

(i) XX-XY Type or Lygaeus Mechanism:
This mechanism was first studied by Wilson and Stevens in the milkweed bug called Lygaeus turcicus.
It is present in certain insects like Drosophila melanogaster and mammals including human.
In males, an X-chromosome is present but its other part is very small called as Y-chromosome, whereas, females have a pair of only X-chromosome, i.e. XX.

Both males and females bear same number of chromosomes. The males have autosomes plus XY-chromosomes and females have autosomes plus XX-chromosomes. The males produce two types of gametes containing X or Y sex chromosome (heterogametic) and females produce only one type of gametes with an X-chromosome (homogametic).

(a) Determination of sex in Drosophila
(b) Pattern of sex chromosomal inheritance in human

Thus, in this type of sex-determination, the presence of Y-chromosomes determines the maleness.

(ii) XX-XO Mechanism
In this pattern, the female has two X-chromosomes (called XX), while male has only one X-chromosome (called XO). The Y-chromosome is completely absent here and it is denoted by the letter O. Thus, the presence of unpaired X-chromosome determines the masculine sex. The female just like the previous method produces, only one type of eggs and male produces two types of sperms, i.e. 50% with one X-chromosome and 50% without any sex chromosome. The sex of offspring depends upon the type of sperm, which fertilises the egg.

Determination of sex in grasshopper (XX-XO type)

Eggs fertilised by sperms having an X-chromosome become females and those fertilised by sperms that do not have X-chromosome become males, e.g. grasshopper and bugs.

Sex-Determination involving Heterogametic Female:
In this case, the total number of chromosomes are same in both males and females. But two different types of gametes having different sex chromosomes are produced by females.

(i) ZZ-ZW Mechanism
This mechanism of sex-determination is seen in birds, fowls and fishes. Females have one Z and one W-chromosome (i.e. heterogametic) along with autosomes whereas males have a pair of Z-chromosomes (i.e. homogametic). Thus, the sex of an organism is determined by the type of ovum that is fertilised to produce an offspring.

Determination of sex (ZZ-ZW) in fowl and birds

(ii) ZZ-ZO
In this mechanism of sex-determination, the female is heterogametic (ZO) and male is homogametic (ZZ). It occurs in lepidoptera, e.g. certain butterflies and moths.

Determination of heterogametic and homogametic female and male

Question 2.
(i) Also describe as to, who determines the sex of an unborn child?
(ii) Mention whether temperature has a role in sex-determination.
Answer:
(i) As a rule, the heterogametic organism determines the sex of the unborn child. In case of humans, since males are heterogametic it is the father and not the mother who decides the sex of the child.
(ii) In some animals like crocodiles, lower temperature favours the hatching of female offsprings and higher temperature leads to hatching of male offsprings.
This pattern is reversed in Bonellia worm where females are produces in high temperature and males are produced in lower temperature.

Question 3.
Describe various environmental factors that help in sex-determination.
Answer:
Environmental Factors in Sex-Determination:
In some lower animals, sex-determination is non-genetic and depends on the factors present in the external environment.
Different environmental factors responsible for sex-determination are given below

Chemotactic Sex-Determination:
It is seen in males of the marine worm Bonellia. These are small, degenerate and live within the reproductive tract of the larger female. All organs of male worm’s body are degenerate except those of the reproductive system.

In Bonellia, the larvae of male and female are genetically and cytolosically similar, i.e. it is hermaphrodite. A newly hatched worm if reared from a single cell kept in isolation, it develops into a female. If the larvae are reared with mature females in water, they adhere to the proboscis.
Later they transform into males who eventually migrate into the female reproductive tract, where they become parasitic.

It has been found that a chemotactic substance secreted by the proboscis of a mature female Bonellia induces the differentiation of larva into males.

Sex-determination in Bonellia

Temperature Dependent Sex-Determination:
In some reptiles, the temperature at which the fertilised eggs are incubated prior to hatching plays a major role in determining the sex of the offspring. Surprisingly high temperature during incubation have opposite effect on sex-determination in different species.

In turtles, high incubation temperature (above 30°C) of eggs results in the production of female progeny whereas in the lizard and crocodiles, high incubation temperature results in the production of male offspring. At the lower temperature range between 22.5-27°C, male turtles are produced. This pattern is reversed in lizards and crocodiles.

Question 4.
What is sex-linked inheritance? Discuss how sex-linked gene inheritance occurs in human, giving two examples.
Or What is sex-linked inheritance? Discuss the mechanism with reference to haemophilia.
Answer:
Inheritance of Haemophilia
It is a sex-linked recessive disease, which is transmitted from an unaffected carrier female to some of the male offsprings. Due to this, patient continues to bleed even during a minor injury because of defective blood coagulation and hence, it is also called as bleeders disease. The gene for haemophilia is located on X-chromosome and it is recessive to its normal allele. In this disease, a single protein that is part of cascade of proteins involved in blood clotting is affected.

The possibility of a female becoming a haemophilic is extremely rare because mother of such a female has to be atleast carrier and father should be haemophilic, e.g. females suffer from this disease only in homozygous condition, i.e. X^CX^C. The haemophilic alleles shows criss-cross inheritance and they follow Mendelian pattern of inheritance. The family pedigree of Queen Victoria (who was a carrier of haemophilia) shows a number of haemophilic individual.
The inheritance is explained below


Four crosses explaining the inheritance of haemophilia allele in human ; (a) Normal mother and haemophilic father, (b) Haemophilic mother and normal father, (c) Carrier mother and normal father and (d) Carrier mother and haemophilic father

Inheritance of Red-Green Colour Blindness:
It is a sex-linked recessive disorder, which results in defect in either red or green cone of eye. It does not mean the incapability to see any colour at all, infact it leads to the failure in discrimination between red and green colour. The gene for colour blindness is present on X-chromosome.

It is present mostly in males (X^CY) because of the presence of only one X-chromosome as compared to two chromosomes in females. A heterozygous female has normal vision, but is a carrier and passes on the disorder to some of her sons. Its inheritance pattern is similar to that of haemophilia

Question 5.
(i) Why are thalassemia and haemophilia categorised as Mendelian disorders? Write the symptoms of these diseases. Explain their pattern of inheritance in humans.
(ii) Write the genotypes of the normal parents producing a haemophilic son.
Answer:
(i) Thalassemia and haemophilia are categorised as
Mendelian disorders because these disorders are due to alteration in a single gene. Also, they are transmitted to offsprings through Mendelian principles of inheritance. Symptoms and pattern of inheritance are given below

(a) Thalassemia It is an autosomal linked recessive blood disorder characterised by defect in a, (3 and 8 chain resulting in abnormal Hb molecule. Symptom Anaemia.
Inheritance Two mutant alleles (one from each parent) must be inherited for an individual to be affected, i.e. homozygous. Heterozygous are carriers and may pass the mutant allele to children.

(b) Haemophilia It is a sex-linked recessive disorder whose gene is located on X-chromosome. Symptom Prolonged clotting time and internal bleeding, even in a minor injury.
Inheritance The gene is present on X-chromosome, so it is inherited by males as they have a single X-chromosome. Affected males are said to be hemizygous. Females have two X-chromosomes, thus possibility of them being affected is rare as the mother of such female has to be atleast carrier and father should be haemophilic.

(ii) Genotypes of the normal parents producing a haemophilic son are X CX (carrier mother) and XY (father).

Carrier Haemophilic Normal Normal daughter son daughter son

Question 6.
Answer the following questions related to Down’s syndrome.

1. When was Down’s syndrome first described?
2. What is its frequency in human and does it also occur in other animals?
3. How does Down’s syndrome arise?
4. Relate it with chromosome dysfunctions.

Answer:

1. It was first described in 1866 by J Langdon Down, so it is called Down’s syndrome.
2. About 1 in every 750 children exhibits Down’s syndrome throughout the world. It is also seen in chimpanzees and other related primates.
3. In humans, it occurs as a result of non-disjunction of chromosome 21 during egg formation. The cause of this primary non-disjunction is not known.
4. The defect is associated with a particular small portion of chromosome 21. When this particular chromosome segment is present in three copies, instead of two, due to translocation Down’s syndrome occurs.