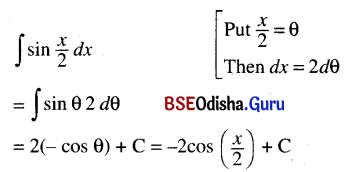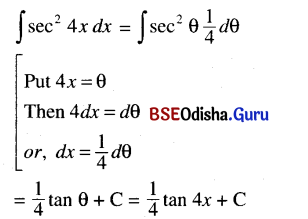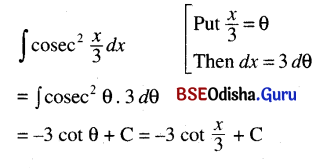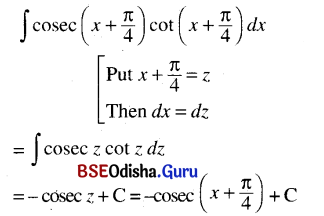Class 12

Odisha State Board CHSE Odisha Class 12 Invitation to English 4 Solutions Grammar Conditionals Textbook Activity Questions and Answers.

CHSE Odisha 12th Class English Grammar Conditionals

Section – 1

The ‘if-sentences’ are generally known as the ‘conditional’ sentences. In this ‘if- sentences’ one can well mark a condition along with a result/effect. A certain action will be fulfilled only if a certain/particular ‘condition’ is performed.

Example
1. I will pardon you if you admit your mistake.
2. If you touch that plate, you’ll bum your fingers.
In the above sentences, we can well see two parts in each sentence, i.e. (i) if-part and (ii) the main part.

The ‘if-part’ is known as the if-clause or conditional clause or the subordinate clause. But the ‘main part’ is usually known as the stem of the long sentence i.e. the principal/main clause, the word ‘if’ is the ‘conjunction’ that joins both the parts of the long sentence. This if part/clause states the condition that must be satisfied before the main part/clause may be true.

In the example in Sentence 1 above, ‘admit’ is the condition and ‘pardon’ is the result. Likewise in Sentence 2, the clause/condition is the ‘touching action ’ and result is the ‘burning action’.

A question comes to mind: “Which action happens first?”
The answer is very simple that the action in if-clause/conditional clause happens first and the action of the main clause happens next/second/later.
In Sentence 1 the main clause is written first and then the if- clause. Sentence 2 is written in reverse order i.e. the if-clause first and the main clause next.
Both the sentences in the examples are grammatical and acceptable. The conditional/if-clause is written/spoken first only when the condition tends to become more emphatic.
Do mark that when the conditional clause is written first, there should be a ‘comma ’ just after the conditional clause. No ‘comma’ is used if the conditional clause is written later or the main clause is written first. A condition can also be signaled without the use of ‘if’.

Example
3. Admit your mistake and I will pardon you.

Types of conditionals
O-Type Conditionals
1. If you heat ice, it melts.
2. If you drop a glass, it breaks.
3. If I make a promise, I keep it.

Let us divide the above sentences into two parts. Look at Sentence 1.
If you heat ice, = X (If-clause)
it melts = Y (Main clause)

X = (Simple present)- heat, heating action- the cause/condition- happens first.
Y = (Simple present)- melts, melting action- the result/- happens later.
The condition as well as the effect (result) remains in a O(zero) state. They are in a balancing state. So the grammarians have rightly named it ‘0- conditionals’.
We may say it a scientific truth/ universal truth. But Sentence 3 above tends the meaning of general happenings or what usually happens. In such cases, ‘Simple Present’ verb is used in both the parts. Here ‘if’ can be substituted by ‘when (ever)’.

(A) Open Condition
If you send the money today, he will get it tomorrow.
In If-part ‘sendign money is the condition and ‘getting it’ is the result in ‘main part’. ‘Your sending money’ is more possible i.e. the condition is open to the speaker and ‘his getting money’ is also more possible in the future. The time reference is futurity.

Notice both the parts of the sentence.
In ‘if-part’ a simple present verb ‘send’ is used and in ‘main part’ ‘will + get’ is used. Will/shall modals are not used in the ‘if-part’ in such conditions. We use this type of conditionals (real condition) sentences to talk about what is probable or possible or more like to happen in the future. This condition is, therefore, called the real condition.
Look at the following sentence.
If you wake up before me, give me a call.
Here ‘if-part, takes a simple present verb and the ‘main part’ is an imperative sentence. This condition is also an open or a real condition for future possibility/probability. Some variations/deviations

Study the following sentences, which are also examples of ‘open’ conditionals, but with a difference.
1. If it’s a holiday tomorrow, we may go for a swim.
2. If I should see him, I will ask him to write.
3. Stop borrowing money or you will be in trouble.
When the imperative is used in place of an ‘if- clause’ the condition changes into a threat, request etc.

Example
If we should miss the 9 o’ clock train, we shouldn’t get there till after lunch. The introduction of ‘should’ (sometimes stressed) in the conditional clause has the effect of making it less likely that the condition will be fulfilled. Here ‘should’ means ‘by any chance’. We may call this a condition of ‘remote possibility’. Note that only ‘should’ (never would) is used in this way.

Now look at the following.
If you will reserve seats, we shall be sure of a comfortable journey. We saw earlier that ‘will’ is not used in a predictive sense in the conditional clause, though the sentence has a future time reference. Here the verb ‘will’ is not an auxiliary indicating future; it is a modal verb which means agreement/cooperation/willingness.
“If you will reserve” = if you are willing/agreeing. The verb ‘will’ when means ‘insistence’, it is used in a conditional clause of this type.
Example
If my brother will mix with the bad boys, what shall I do?
“If my brother will mix” = If my brother is insisting on mixing (not in a predictive sense)

(B) ‘Hypothetical’ or ‘Unreal’ Condition
Example
If I became the Chief Minister, I would put things right at once. Notice that both the parts i.e. the ‘if-part’ as well as ‘the main-part’ contain verbs in the past tense form i.e. became and would. We use this conditional when we talk about unreal or imaginary events/actions.
The use of the past tense has the effect of making the condition seem ‘remote’ or unlikely/distant. That is why the condition is said to be ‘hypothetical’ or unreal. The time reference is futurity.
If I knew his address. I could tell you.
The above sentence represents us with a totally imaginary (or unreal) situation with reference to the time of speaking. It implies that I really don’t know his address and I can’t tell you now. Note that the past tense is used here to indicate present unreality.

The Subjunctive
Compare the two sentences below.
1. If I were you, I would take my work more seriously.
2. If I was you. I would take my work more seriously.
One might think that the first sentence is wrong sicne the verb were being in the plural form does not agree with the singular subject I. This plural verb is called ‘the subjunctive’. It is used to express the unreal or hypothetical condition. In modem English the subjunctive is not used
commonly. Most educated native speakers would prefer now to use “IfI was you” (instead of If I were you …)

Variations
If we were to miss the 9 o’ clock train, we would not get there till after lunch. The use of ‘were to’ in the conditional clause sometimes has the effect of emphasizing the suppositional nature of the condition and some ways analogous to the use of ‘should’ in conditional clause A. ‘were to’ can be substituted ‘by any chance’ without changing the meaning.

(C) Unfulfilled Condition.
Example
If you had asked me for the money, I would have given it to you. Notice that ‘if-part’ contains ‘past perfect form ’ and the main clause ‘would + have with past participle form.
The use of these past- verbs in both the parts tells us that the action (giving of money) was not performed because the condition was not fulfilled. The sentence actually means ‘you really did not ask me for the money and I didn’t give it to you.’ This conditional sentence represents what is contrary to the fact. The past perfect tense is ued to indicate past unreality.
The same meaning is expressed by
Had you asked me for the money, I would have given it to you. (without the use of if) The unfulfilled condition is often used to comment on, or to express regret for, something that did not happen.

Activity – 1
Complete the sentences below, using appropriate words of your own.

1. If we finish early today,________________________.
2. If I lose all my money,___________________.
3. If you go away on a holiday this summer. ________________________.
4. If our friend gets into trouble. _________________________.
5. Will you help me if _____________________________
6. I would be rather disappointed if ________________________.
7. This school will have to be closed if ___________________________
8. We will all be very happy if _____________________________.
9. They will not listen to anybody if _________________________.

Answers
1. If we finish early today, we’ll put some free time to see the match on T. V.
2. If I lose all my money, I’ll be in trouble.
3. If you go away on a holiday this summer. I’ll be very happy.
4. If our friend gets into trouble, we’ll help him.
5. Will you help me if I am in trouble? ‘
6. I would be rather disappointed if von didn’t help me.
7. This school will have to be closed if the lunar eclipse falls on tomorrow.
8. We will all be happy if our team wins the trophy.
9. They will not listen to anybody if von don’t behave them properly

Activity -2
The following are examples of some common superstitions.
1. If you hear an owl hooting at night, a friend will die.
2. If your left hand begins to itch, you will give money away.

Can you think of five other common superstitions? (Use the word if, as shown above.)
Answers
1 . If a cat passes in front of somebody, she/he will face some danger.
2. If three persons start a journey together, they will reap a negative result.
3. If an owl sits on the roof of a person’s house, one of the members of the family will die soon.
4. The man will die if a lizard falls on his shoulders.
5. Man will be crowned if a lizard falls on his forehead.

Activity – 3
Fill in the blank spaces to make meaningful conditions.
If I work hard, I’ll get good marks, If I ____________good marks, I ____________go to a good college and __________a degree. If I _____________ go abroad, I ___________ a highly-paid job. If __________name, fame and money, I _____________ marry a pretty girl. If ______________ only one or two children, I ____________ educate them properly. If _____________ come back to my country, I ______________ some useful work.

Answers
If I work hard, I’ll get good marks, If I get good marks, I will go to a good college and do a degree. If I get go abroad, I will set a highly-paid job. If gel name, fame and money, I will marry a pretty girl. If I only one or two children, I can educate them properly. If1 come back to my country, I will do some useful work.

Activity- 4

How imaginative are you? Complete the following sentences.
(a) If Ibecame a cloud, I would ………………………….
(b) If I could go back to the past,………………………..
(c) If I were a rat,………………………
(d) If I were a tiger, ……………………….
(e) If I ……………………………. I’d write a great novel.
(f) If people ……………………………they would die of boredom.
(g) If the earth …………………… ……, no living creature would survive.
(h) I would stand on my head if …………………………
(i) Would you be well prepared if ……………………..?

Answers
(a) If I became a cloud, I would sail in the sky.
(b) If I could go back to the past, I would not make my hair-dye.
(c) If I were a rat, I would make holes.
(d) If I were a tiger, / would live in the jungle.
(e) If I were a Jane Austin. I’d write a great novel.
(f) If people were dumb and deaf, they would die of boredom.
(g) If the earth was/were a sun, no living creature would survive.
(h) I would stand on my head if I were not a man.
(i) Would you be well prepared if you were a literate?

Activity- 5
How would your life be different if you were :

older      more intelligent     stronger
taller       less intelligent        richer
shorter    more patient         poorer

Answers
1. If I were older, I could beg you for some help.
2. If I were taller, I would join the military service.
3. If I were shorter, I could play the role of a joker.
4. If I were more intelligent, I could/would tackle the world problem.
5. If I were less intelligent, I could/would be in difficulty.
6. If I were more patient, I would tolerate your insulting words.
7. If I were stronger, I could/would fight with a tiger.
8. If I were richer, I would make you my accountant.
9. If I were poorer, I would beg for food.

Activity- 6

Write 5 sentences on the things you would do if you won a lottery. (Use if + past simple in the ‘if – clause” and would in the main clause) If I won a lottery, I would get a lot of money, If I got a lot of money …

Answers
If I won a lottery, I would get a lot of money.
(a) If I got a lot of money, I would buy a car.
(2) If I bought a car, I would take my parents for an outing.
(3) If I went on an outing, I would drive the car.
(4) If I drove the car, I would be very cautious.
(5) If my parents saw my driving, they would be very happy.

Activity – 7

Write a comment on each of the following situations, using the unfulfilled condition. (One example is given)
(a) I didn’t study, so I didn’t do very well in the examination.
Comment: If you had studied, you would have done better.
(b) I didn’t like the food because it was too hot.
Comment: If ______________________________________________________________
(c) They waited at the station for four hours because they did not know that the train was delayed.
Comment: If ______________________________________________________________
(d) The boy met with an accident because he was careless.
Comment: If _______________________________________________________________
(e) She heard the news because she turned on the radio this morning.
Comment: If ______________________________________________________________
(f) They didn’t see us, so they could not laugh at us.
Comment: If ______________________________________________________________
(g) My father earned a lot of money, so life was easy for us.
Comment: If ______________________________________________________________

Answers
(b) I didn’t like the food because it was too hot.
Comment: I would/could have liked the food if it had not been hot.
(c) They waited at the station for four hours because they did not know that the train was delayed.
Comment: If they had known that the train was delayed, they would not have waited at the station.
(d) The boy met with an accident because he was careless.
Comment: The boy could not have met with an accident if he had been careful/if he had not been careless.
(e) She heard the news because she turned on the radio this morning.
Comment: If she had not turned on the radio this morning, she could not have heard the news.
(f) They didn’t see us, so they could not laugh at us.
Comment: If they had seen us, they could have laughed at us.
(g) My father earned a lot of money, so life was easy for us.
Comment: If my father had not earned a lot of money, life would/could not have been easy for us.

Activity – 8
Read the text below and then complete the sentences that follow.
Namita went to Cuttack yesterday. The sun was shining brightly, so she never thought of taking her umbrella. But what a terrible day she had! Everything that could possibly go wrong went wrong. The weather changed, as the weather report had predicted, and Namita got soaked. She slipped on the stairs of a shop and had a bad fall. Someone stole her purse when she was talking to a friend and had her back turned. The bus broke down on the way back and was delayed. Namita’s mother was angry because she returned so late.

(a) If Namita had taken her umbrella, ………………………………
(b) If she had listened to the weather forecast, ………………………
(c) If she had taken the lift in the store ………………………..
(d) If she hadn’t turned her back, …………………….
(e) If the bus hadn’t broken down …………………….
(f) If she’d returned home on time, …………………………
Answers
(a) If Namita had taken her umbrella, she couldn’t have got soaked.
(b) If she had listened to the weather forecast, she could not have drenched.
(c) If she had taken the lift in the store, she could not have fallen.
(d) If she hadn’t turned her back, someone couldn’t have stolen her purse.
(e) If the bus hadn’t broken down, Namita could have returned in time.
(f) If she’d returned home on time, her mother could not have been angry.

Section -2

Other ways of expressing a condition
Look at the following sentences
1. He can’t work unless he eats something.
2. I won’t go to the party unless they invite me.
These sentences with unless could be re-written as
3. He can’t work ifhe doe snot eat something.
4. I won’t go to the party if I am not invited.
Unless has the meaning “if …. not”. It is used to express a negative condition. The same meaning can be expressed by using ‘only if’. So the same sentences could be re-written as
5. He can work only if he eats something.
6. I will go to the party only if he invites me

Activity – 9
Rewrite each of the following sentences using ‘unless’.
(The first sentence has been worked out for you.)
1. We must leave now or we’ll miss the start of the film.
Unless we leave now we’ll miss the start of the film.
2. You should wear your coat or you’ll be cold.
_______________________________________
3. You must give me your address or I can’t write to you.
_______________________________________
4. You have to speak very loudly or we won’t be able to hear you.
_______________________________________
5. You must stop smoking or your cough won’t get better.
_______________________________________
6. You must say you’re sorry or he won’t forgive you
_______________________________________

Answers
1. We must leave now or we’ll miss the start of the film.
Unless we leave now, we’ll miss the start of the film.

2. You should wear your coat or you’ll be cold.
Unless you wear your coat, you’ll be cold.

3. You must give me your address or I can’t write to you.
Unless you give me your address, I can’t write to you.

4. You have to speak very loudly or we won’t be able to hear you.
Unless you speak very loudly, we won’t be able to hear you.

5. You must stop smoking or your cough won’t get better.
Unless you stop smoking, your cough won’t get better.

6. You must say you’re sorry or he won’t forgive you.
Unless you say you’re sorry, he won’t forgive you.

Multiple-Choice Questions (MCQs) with Answers

Question 1.
Unless you ___________the truth, you will suffer.
(A) spoke
(B) speak
(C) do not speak
(D) should
Answer:
(A) spoke

Question 2.
If you were a bird, you ____________ fly.
(A) could
(B) should
(C) would
(D) none of these
Answer:
(C) would

Question 3.
She would come, if she ____________ time.
(A) has
(B) had
(C) would have
(D) should have
Answer:
(B) had

Question 4.
If I had known you, I_ told you.
(A) would have
(B) should have
(C) will have
(D) shall have
Answer:
(A) would have

Question 5.
If I __________ rich, I would help the poor.
(A) was
(B) am
(C) were
(D) shall be
Answer:
(C) were

Question 6.
_________ I find the pen, I will let you have it.
(A) Could
(B) Should
(C) Would
(D) Can
Answer:
(B) Should

Question 7.
If I had had time, I ___________visited the zoo.
(A) would have
(B) should have
(C) could have
(D) shall have
Answer:
(B) should have

Question 8.
If he _____________ a taxi, she would have reached the station in time.
(A) has taken
(B) would take
(C) had taken
(D) should take
Answer:
(C) had taken

Question 9.
If he ___________, he will suffer from indigestion.
(A) ate
(B) had eaten
(C) eats
(D) will eat
Answer:
(C) eats

Question 10.
If they _________ here, I should speak to them.
(A) were
(B) had been
(C) will be
(D) would be
Answer:
(A) were

Question 11.
I’m not tired enough to go to bed yet. I wouldn’t sleep if I ____________ to bed now.
(A) go
(B) went
(C) had gone
(D) would go
Answer:
(B) went

Question 12.
If I were you, I _____________ that coat. It was much too expensive.
(A) won’t buy
(B) don’t buy
(C) am not going to buy
(D) wouldn’t buy
Answer:
(D) wouldn’t buy

Question 13.
I decided to stay at home last night. I would have gone out if I ___________so tired.
(A) wasn’t
(B) weren’t
(C) wouldn’t have been
(D) hadn’t been
Answer:
(D) hadn’t been

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 7 Continuity and Differentiability Ex 7(k) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Exercise 7(k)

Question 1.
State True (T) or False (F).
(i) There is no function whose derivative is log π.
Solution:
False

(ii) There is no function which is its own derivative.
Solution:
False

(iii) A function is not differentiable at x = c ⇒ f is not continuous at x = c.
Solution:
False

(iv) |x²| is differentiable on (- 1, 1).
Solution:
True

(v) |x + 2| is not differentiable at x = 2.
Solution:
False

(vi) Derivative of e^{3 log x} w.r.t. x is 3x².
Solution:
True

(vii) The derivative of a non constant even function is always an odd function.
Solution:
True

(viii) If f and g are not derivable at x₀ then f + g is not derivable at x₀.
Solution:
False

Question 2.
Fill up the gaps by using the correct answer.
(i) If a is a constant and v is a variable then \(\frac{d u^v}{d v}\) = _______. (u^v In v, vu^{v – 1}, u^v In u, uv^{v – 1})
Solution:
u^v In v

(ii) If t = e^a then \(\frac{d}{d x}\)x^t = _______. (tx^{t – 1}, x^t, x^t In a, tx^t)
Solution:
tx^{t – 1}

(iii) If u = t² and v= sin t² then \(\frac{d v}{d u}\) = _______. (cos² t, \(\frac{\sin }{t}\), sec t², cos t²)
Solution:
cos t²

(iv) The tangent to the curve y = (1 + x²)² at x = -1 has slope _______. (4, -4, 8, -8)
Solution:
-8

(v) If v = (gof) (x) then \( \frac{d y}{d x}\) = _______. (\(\frac{d g}{d x} \frac{d x}{d f}\), \(\frac{d g}{d f} \frac{d f}{d x}\), \(\frac{d f}{d x} \frac{d x}{d g}\), \(\frac{d f}{d g} \frac{d g}{d x}\))
Solution:
\(\frac{d g}{d f}\frac{d f}{d x}\)

(vi) If y = sec^-1 \(\frac{\sqrt{x}+1}{\sqrt{x}}\) + \(\frac{\sqrt{x}}{\sqrt{x}+1}\) then \(\frac{d y}{d x}\) = _______. (0, undefined, \(\frac{\pi}{2}\), 1)
Solution:
0

(vii) If (x) = \(\sqrt{x^2-2 x+1}\), x ∈ [0, 2] then at x = 1, f(x) = _______. (1, 0, -1, does not exist)
Solution:
does not exist

(viii) If f(x) = |x²| then f'(\(\frac{3}{2}\)) = _______. (0, 2, 3, does not exist)
Solution:
0

Question 3.
Differentiate from first principles.
(i) e^2x
Solution:
Let y = e^2x

(ii) sin² x
Solution:
Let y = sin² x

(iii) cos x²
Solution:
Let y = cos x²

(iv) \(\boldsymbol{e}^{x^2} \)
Solution:

(v) \(\sqrt{\tan x} \)
Solution:

(vi) x² sin x
Solution:
Let y = x² sin x

(vii) In sin x
Solution:
Let y = In sin x
Then e^y = sin x  … (1)
Let dx be an increment of x and δv be the corresponding increment of y.
Then e^{y + δy} = sin (x + δx)  … (2)
Subtracting (1) from (2) we get,

(viii) sin √x
Solution:
y = sin √x
Put u = √x
Then y = sin u
Let δx be an increment of x and δu, δy be the corresponding increment of u and y respectively.

(ix) cos In x
Solution:
Let y = cos (In x)
Let u = In x
Then y = cos u
Suppose that δx be an increment of x and δu, δy be corresponding increments of u and y respectively.
Then y + δy = cos (u + δu)  ….(3)
and u + δu = In (x + δx)  ….(4)
Subtracting (2) from (3) and (1) from (4) we get
δy = cos (u + δu) – cos u
and δu = In (x + δx) – In x

Question 4.
Test differentiability of the following functions at the indicated points.
(i) f(x) =[x² + 1] at x = –\(\frac{1}{2}\)
Solution:

(ii) f(x) = \(\begin{cases}1-2 x, & x \leq \frac{1}{2} \\ x-\frac{1}{2}, & x>\frac{1}{2}\end{cases}\) at x = \(\frac{1}{2}\)
Solution:

(iii) f(x) = x + |cos x| at x = \(\frac{\pi}{2}\)
Solution:
f(x) = x + |cos x| at c = \(\frac{\pi}{2}\)

Hence onwards domain of a function is to be understood to be its natural domain unless stated otherwise.

Question 5.
Differentiate.
(i) \(\frac{1}{\ln (x \sqrt{x+1})}\)
Solution:

(ii) \(\frac{\ln x}{e^x \sin x}\)
Solution:

(iii) e^x (tan x – cot x)
Solution:
y = e^x (tan x – cot x)
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (e^x) (tan x – cot x) + e^x \(\frac{d}{d x}\) (tan x – cot x)
= e^x (tan x – cot x) + e^x (sec² x + cosec² x)

(iv) \(\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)\)x tan x
Solution:

(v) \(\frac{\cos 3 x-\cos x}{\cos 5 x-\cos 3 x}\)
Solution:

(vi) x² e^x cosec x
Solution:
y = x² e^x cosec x
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (x²) e^x . cosec x + x² \(\frac{d}{d x}\) (e^x) . cosec x + x² e^x \(\frac{d}{d x}\)
= 2x e^x cosec x + x² e^x cosec x – x² e^x . cosec x . cot x

(vii) \(\frac{(x+1) \ln x}{\sqrt{x+2}}\)
Solution:

(viii) (x³ – 1)⁹ sec² x
Solution:

(ix) sin² (cos^-1 x)
Solution:

(x) a^x \(\left(x+\frac{1}{x}\right)^{10}\)
Solution:

(xi) In \(\frac{\sqrt{x+4}-2}{\sqrt{x+4}+2}\)
Solution:

(xii) In \(\frac{4 x^2(2 x-7)^3}{\left(3 x^2-7\right)^5}\)
Solution:

(xiii) 5^{ln sin x}
Solution:

(xiv) \(\sqrt{\sin \sqrt{x}}\)
Solution:

(xv) x^{sin x} + (tan x)^x
Solution:
Let y = x^{sin x} + (tan x)^x
Put u = x^{sin x} , v = (tan x)^x
Then y = u + v

(xvi) \(e^{e^x}\)
Solution:

(xvii) \(x^{\sqrt{x}}\)
Solution:

(xviii) sec^-1(e^x + x)
Solution:

(xix) ln cos e^x
Solution:

(xx) \(a^{\sin ^{-1} x^2}\)
Solution:

(xxi) cos^-1 \(\left(\frac{x^4-1}{x^4+1}\right)\)
Solution:

(xxii) \(\left(\mathbf{x}^{\mathbf{e}}\right)^{\mathbf{e}^{\mathrm{x}}}\) + \(\left(\mathrm{e}^{\mathrm{x}}\right)^{\mathrm{x}^e}\)
Solution:

(xxiii) \(\boldsymbol{x}^{\left(\boldsymbol{x}^x\right)}\)
Solution:

(xxiv) \(\frac{\left(x+1^2\right) \sqrt{x-1}}{\left(x^2+3\right)^3 3^x}\)
Solution:

(xxv) [5 In (x³ + 1) – x⁴]^2/3
Solution:

(xxvi) log₁₀ sin x + log_x 10, 0 < x > π.
Solution:

Question 6.
Differentiate
(i) sec^-1 \(\left(\frac{x^2+1}{x^2-1}\right)\)
Solution:

(ii) \(e^{\tan ^{-1} x^2}\)
Solution:

(iii) \(\frac{x \sin ^{-1} x}{\sqrt{1+x^2}}\)
Solution:

(iv) tan^-1 e^2x
Solution:

(v) tan^-1 \(\frac{\cos x}{1+\sin x}\)
Solution:

(vi) tan^-1 \(\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right) \)
Solution:

(vii) tan^-1 \(\frac{7 a x}{a^2-12 x^2}\)
Solution:

(viii) tan^-1 \(\frac{\sqrt{1+x^2}+\sqrt{1-x^2}}{\sqrt{1+x^2}-\sqrt{1-x^2}}\) (Put x² = cos θ)
Solution:

(ix) x² cos \(\frac{\sqrt{x}-1}{\sqrt{x}+1}\) = x² cosec^-1 \(\frac{\sqrt{x}+1}{\sqrt{x}-1}\)
Solution:

(x) tan^-1 \(\frac{x}{1+\sqrt{1-x^2}}\)
Solution:

(xi) tan^-1 \(\left(\frac{x \sin \alpha}{1-x \cos \alpha}\right)\)
Solution:

Question 7.
Find \(\frac{d y}{d x}\) if
(i) x³ + y³ = 12xy
Solution:

(ii) \(\left(\frac{x}{a}\right)^{2 / 3}\) + \( \left(\frac{y}{b}\right)^{2 / 3}\) = 1
Solution:

(iii) x^y = c
Solution:

(iv) y^x = c
Solution:
y^x = c ⇒ x In y = In c
⇒ in y + \(\frac{x}{y} \frac{d y}{d x}\) = 0
⇒ \(\frac{d y}{d x}\) = –\(\frac{y \ln y}{x}\)

(v) x cot y + cosec x = 0
Solution:

(vi) y² + x² = In (xy) + 1
Solution:

(vii) (cos x)^y = sin y
Solution:

(viii) y² =a^√x
Solution:

(ix) x^m yⁿ = \(\left(\frac{x}{y}\right)^{m+n}\)
Solution:

(x) y = x cot ^-1 \(\left(\frac{x}{y}\right)\)
Solution:

(xi) y = (sin y)^{sin 2x}
Solution:

(xii) y² = x^y
Solution:

(xiii) (x + y)^{cos x} = e ^{x + y}
Solution:

(xiv) x tan y + y tan x = 0
Solution:

(xv) \(\sqrt{x^2+y^2}\) k tan^-1 \(\left(\frac{y}{x}\right)\)
Solution:

Question 8.
Differentiate
(i) tan^-1 \(\frac{2}{1-x^2}\) w.r.t. sin^-1 \(\frac{2}{1+x^2}\)
Solution:

(ii) sec^-1 \(\left(\frac{1}{2 x^2-1}\right)\) w.r.t. \(\sqrt{1-x^2}\)
Solution:

(iii) tan^-1 \(\left(\frac{1+\sin x}{1-\sin x}\right)\) w.r.t. log \(\left(\frac{1+\cos x}{1-\cos x}\right)\)
Solution:

Question 9.
Find the \(\frac{d y}{d x}\) when
(i) x = a [cos t + log tan ( t/2)], y = a sin t
Solution:

(ii) sin x = \(\frac{2 t}{1+t^2}\), tan y = \(\frac{2 t}{1-t^2}\)
Solution:

(iii) cos x= \(\sqrt{\frac{1}{1+t^2}}\), siny = \(\frac{2 t}{1+t^2}\)
Solution:

(iv) cos x = \(\sqrt{\sin 2 u}\), y = \(\sqrt{\cos 2 u}\)
Solution:

(v) x = \(\frac{\cos ^3 t}{\sqrt{\cos 2 t}}\), y = \(\frac{\sin ^3 t}{\sqrt{\cos 2 t}}\)
Solution:

Question 10.
Assuming the validity of the operations on the r.h.s. find \(\frac{d y}{d x}\).
(i) y = [ sin x + { sin x + (sin x +….)}]
Solution:

(ii) y = 1 ÷ [ x + 1 ÷ (x + 1 ÷ (x + 1 ÷ …))]
Solution:

(iii) y = In [x + In (x + In (x + ….))]
Solution:

Question 11.
If cos y = x cos (a + y) then prove that
(i) \(\frac{d y}{d t}\) = \(\frac{\cos ^2(a+y)}{\sin a}\)
Solution:

(ii) If e^θΦ = c + 4 θΦ , show that Φ + θ \(\frac{d \phi}{d \theta}\) = 0.
Solution:

Question 12.
Can you differentiate log log |sin x|? Justify your answer.
Solution:
Clearly for all x ∈ R
sin x ∈ [- 1, 1]
⇒ |sin x| ∈ [ 0,1]
⇒ log |sin x| ∈ (-∞ , 0]
⇒ log log |sin x| is not well defined for all x ∈ R
∴ Log log |sin x| is not a differentiable function.

Question 13.

Solution:

Question 14.
If x = \(\frac{1-\cos ^2 \theta}{\cos \theta}\), y = \(\frac{1-\cos ^{2 n} \theta}{\cos ^n \theta}\) then show that \(\left(\frac{d y}{d x}\right)^2\) = n²\(\left(\frac{y^2+4}{x^2+4}\right)\)
Solution:

Question 15.
Show the \(\frac{d y}{d x}\) is independent of t if.
x = cos^-1\(\frac{1}{\sqrt{t^2+1}}\), y = sin^-1\(\frac{t}{\sqrt{t^2+1}}\)
Solution:

Question 16.
If y \(\sqrt{x^2+1}\) = {\(\sqrt{x^2+1}\) – x} then prove that (x² + 1) \(\frac{d y}{d x}\) + xy + 1 = 0
Solution:

Question 17.
If e^y/x = \(\frac{x}{a+b x}\), then show that x3 \(\frac{d}{d x}\) \(\left(\frac{d y}{d x}\right)\) = \(\left(x \frac{d y}{d x}-y\right)^2\)
Solution:

Question 18.
Find the points where the following functions are not differentiable.
(i) e^|x|
Solution:
e^|x| is not differentiable at x = 0 because |x| is not differentiable at x = 0

(ii) |x² – 4|
Solution:
|x² – 4| is not differentiable at the points where x² – 4 = 0 i.e, x =± 2.

(iii) |x – 1| + |x – 2|
Solution:
|x – 1| + |x – 2| is not differentiable at x = 1 and x = 2.

(iv) sin |x|
Solution:
sin |x| is not differentiable at x = 0.

Odisha State Board CHSE Odisha Class 12 Invitation to English 4 Solutions Grammar Interrogatives Textbook Activity Questions and Answers.

CHSE Odisha 12th Class English Grammar Interrogatives

We usually make questions by changing the word order :

(a) Look at these sentences.

A	B
This is the road to your house.	Is this the road to your house?
He has a car	Has he a car?
There is a canteen in the office	Is there a canteen in the office?

The sentences in ‘A’ are statements and those in ‘B’ are questions. The verb in each sentence in ‘B’ here comes first and the subject is put after it. In other words, there is an inversion of subject and verb. They are all interrogative sentences.
(b) Look at these sentences.

A Statements	B Yes/No Questions
My friend works on a firm	Has he a car?
You sold your car	Is there a canteen in the office?
They go to the cinema every evening.	Do they go to the cinema every evening?

For questions in ‘B’ the auxiliary do or a form of it is provided in questions and it is put before the subject.
(c) 1. (i) Did you see my sister anywhere here?
(ii) Did you see my sister somewhere here?
2. (i) Is anyone absent?
(ii) Is someone absent?

Notice the difference between (1) sentences and (2) sentences. In the latter the speaker tends to believe that the answer is ‘yes’ but not so in the former.

(d) Study those information questions, made with phrases formed by the question word how joined to an adjective or adverb.

A Statements	B Yes/No Questions
There are five colleges in the district	How many colleges are there in the district?
This pen costs twenty rupees.	How much does this pen cost?
The postman comes here two times a day.	How often does the post man come here?

(e) Negative questions (Isn’t it…. ? / didn’t you…. ?) We use negative questions specially to show surprise :
Didn’t you hear the bell? I rang it five times.

Activity -1
Divide the following sentences into two broad categories and state why you have done so.
1. Where’s my pen?
2. Isn’t that my pen?
3. Why haven’t you done your homework?
4. How are you?
5. Would you like something to eat?
6. What’s the time by your watch?
7. Are you listening?
8. You have been to Delhi before, haven’t you?

1. Where	is my pen?
2. Is	not that my pen?
3. Why	(haven’t you done your homework?
4. How	are you?
5. Would	you like something to eat?
6. What	(is) the time by your watch?
7. Are	you listening?
8. You have been to haven’t you? (Yes-No Qn) Delhi before

Activity- 2
Write yes/no questions or wh-questions, using the following expressions :
1 . you / go / to Puri / last year?
2. where / be / Seema / today?
3. you / write / class notes?
4. what / be / the STD code / for Bhubaneswar?
5. where / Samar / live / at the moment?
Answers :
1. Did you go to Puri last year? (Yes – No Qn.)
2. Where is Seema today? (Wh-Qn.)
3. Do you write class notes? (Yes – No Qn.)
4. What is the STD code for Bhubaneswar? (Wh – Qn.)
5. Where does Samar live at the moment? (Wh – Qn.)

Activity -3
Change these statements into wh-questions, using the in the brackets :
1 . Seema put that letter on my desk. (Who)
2. Jatin left his bag on the bus. (Where)
3. That is my friend’s bag. (Whose)
4. He means this one. (Which)
5. All the trains were late yesterday because of heavy rain. (Why)
6. They walked two kilometres before they found the shop. (How far)
7. 54,763 eggs were used in the world’s biggest omelette. (How many)

Answers:
1 . Who put that letter on your desk?
2. Where did Jatin leave his bag?
3. Whose bag is that?
4. Which one does he mean?
5. Why were all the trains late yesterday?
6. How far did they walk before they found the shop?
7. How many eggs were used in the world’s biggest omelette?

Activity- 4
Ask questions to get the following answers.
1. I’m fine, thank you.
2. About 40 kilos.
3. Yesterday evening.
4. The giraffe.
5. Yes, just before my eyes.
Answers :
1. How are you?
2. How much does it weigh?
3. When did you come?
4. Which animal has the longest neck?
5. Did the accident happen before your eyes?

Activity – 5
Work in small groups. One member goes out, and in his / her absence other members choose an object in the classroom. When (s)he comes back, (s)he has to guess the article by asking yes/no questions to the other members, asking them serially, for example :
O: Is it the blackboard?
S1: No, it isn’t.
O: Is it the teacher’s table?
S2: No, it isn’t…

1 . O: Is that the chair?
S1: No, that isn’t
O: Is it the duster in my hand?
S2: No, it isn’t.

2. O: Is it the map of India?
S1: No, it isn’t.
O: Is it a globe?
S2: No, it isn’t

3. O: Is it the blackboard?
S1: Yes, it is.
O: Is it the teacher’s table?
S2: Yes, it is.

4. O: Is that the chair?
S1: Yes, that is.
O: Is it the map of India?
S2: Yes, it is

Activity – 6
One student stands in front of the class. He thinks of a person or a place. Other students ask him yes/no or wh-questions in order to guess the person or the place. The students ask in turn and twenty questions are allowed. If a student guesses correctly, he replaces the first student.

Example :
S, = have you thought of a person.
X = Person.
S2 = Is the person dead?
X = Yes.
S3 = Was the person a man?
X = Yes.
S4 = When did he die?
X = In Twentieth Century. (Here X can refuse to answer, because (s) he may give away
the secret.)
S5 = Was he a filmstar?
X = No.
S6 = Was he famous?
X = Yes.
S7 = In which field was he famous?
X = Politics.
Sg = Was he a freedom fighter?
X = Yes.
S9 = Was he a minister?
X = No.
S10 = Is it Mahatma Gandhi?
X = Yes. [And now S,0 becomes X]

Activity- 7
Look at the questions in the left column and the list of functions in the right column. Decide on a function for each question :

1. What time is it?	a. asking to distinguish
2. Is that poisonous or nonpoisonous?	b. expressing lack of belief.
3. You’re back rather early, aren’t you?	c. offering assistance
4. What do you mean by early?	d. asking for assistance
5. Must you sing at this time of the night?	e. asking for information
6. Shall I do that for you?	f. expressing irritation
7. Would you mind holding this for a moment	g. asking for an opinion
8. Why are you late?	h. expressing mild surprise.
9. What did he look like?	i. asking for an explanation.
10. What do you think of the new bowler?	j. asking for a description

Answers :
1. = e
2. = j
3. = b
4. = h
5. = f
6. = c
7. = d
8. = g
9. = i
10. = a

Activity- 8
In the light of your findings from the previous activity, what is the distinction between the terms question and interrogative?
Questions are used to elicit information or to clear a doubt or problem requiring solution. Interrogative has the force of a question (used formally)

Activity – 9
How many questions can you frame to get the following sentence or a part of it as the answer?
When Amar Nath and his partners took over the place, it was in ruins and was inhabited by bats and mice.
1. What was the place like when Amar Nath and his partners took over it?
2. What was the place inhabited with when Amar Nath and his partners took over it?
3. Who took over the place which was in ruins and was inhabited by bats and mice?
4. Whose partners took over the place?

Multiple-Choice Questions (MCQs)
Transfer the following sentences into interrogative ones

Question 1.
He goes there.
(A) Did he go there?
(B) Does he go there?
(C) Do he go there?
(D) Does he goes there?
Answer:
(B) Does he go there?

Question 2.
My mother cooked well.
(A) Do my mother cook well?
(B) Did my mother cooked well?
(C) Did my mother cook well?
(D) Did my mother cooks well?
Answer:
(C) Did my mother cook well?

Question 3.
You have not seen the Taj Mahal.
(A) Have you not seen the Taj Mahal?
(B) Have you not saw the Taj Mahal?
(C) Have you not see the Taj Mahal?
(D) none of these
Answer:
(A) Have you not seen the Taj Mahal?

Question 4.
My friends go to the cinema.
(A) Does my friends go to the cinema?
(B) Do my friends goes to the cinema?
(C) Do my friends go to the cinema?
(D) Does my friends goes to the cinema?
Answer:
(C) Do my friends go to the cinema?

Question 5.
I like mangoes.
(A) Am I liking mangoes?
(B) Do I liked mangoes?
(C) Does I like mangoes?
(D) Do I like mangoes?
Answer:
(D) Do I like mangoes?

Question 6.
How long you will stay here.
(A) How long will you stay here?
(B) How long you shall stay here?
(C) How long would you stay here?
(D) none of these
Answer:
(A) How long will you stay here?

Question 7.
When you last visited him.
(A) When had you last visited him?
(B) When did you last visit him?
(C) When you had last visited him?
(D) When had you last visit him?
Answer:
(B) When did you last visit him?

Question 8.
This bunch of grapes tastes sour.
(A) Do this bunch of grapes taste sour?
(B) Do this bunch of grapes tastes sour?
(C) Does this bunch of grapes taste sour?
(D) Does this bunch of grapes tastes sour?
Answer:
(C) Does this bunch of grapes taste sour?

Question 9.
I saw you go there.
(A) Do I saw you go there?
(B) Did I saw you go there?
(C) Had I seen you go there?
(D) Did I see you to go there?
Answer:
(D) Did I see you to go there?

Question 10.
We are good friends.
(A) Were we good friends?
(B) Have you been good friends?
(C) Are we good friend?
(D) none of there
Answer:
(C) Are we good friend?

Question 11.
We shall never forget those happy days.
(A) Shall we never forget those happy days?
(B) Should we never forget those happy days?
(C) Shall we ever forget these days?
(D) Can we ever forget those happy days?
Answer:
(C) Shall we ever forget these days?

Question 12.
I have somebody with me.
(A) Have I somebody with me?
(B) Have I anybody with me?
(C) Have I nobody with me?
(D) none of these
Answer:
(B) Have I anybody with me?

Question 13.
I have never been to London.
(A) Have I never been to London?
(B) Have I hardly been to London?
(C) Have I ever been to London?
(D) none of these
Answer:
(C) Have I ever been to London?

Question 14.
A leopard can never change its spot.
(A) Can a leopard change its spot?
(B) Can a leopard never change its spot?
(C) Can a leopard sometimes change its sport?
(D) Can a leopard ever change its spot?
Answer:
(D) Can a leopard ever change its spot?

Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 9 Integration Ex 9(b) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Exercise 9(b)

Integrate the following:
(In some cases suggestions have been given for substitution.)
(i) ∫sin 3x dx
Solution:

(ii) ∫cos ax dx
Solution:

(iii) ∫cos (2 – 7x) dx
Solution:

(iv) ∫sin \(\frac{x}{2}\) dx
Solution:

(v) ∫sec² 4x dx
Solution:

(vi) ∫cosec² \(\frac{x}{3}\) dx
Solution:

(vii) ∫sec (x + 2) tan (x + 2) dx
Solution:
∫sec (x + 2) tan (x + 2) dx
[Put x + 2 = θ
Then dx = dθ]
= ∫sec θ . tan θ dθ
= sec θ + C = sec (x + 2) + C

(viii) ∫cosec (x + \(\frac{\pi}{4}\)) cot (x + \(\frac{\pi}{4}\)) dx (x + \(\frac{\pi}{4}\) = z)
Solution:

(ix) ∫x² cos x³ dx (x³ = z)
Solution:

(x) ∫e^x . sec e^x tan e^x dx (e^x = z)
Solution:
∫e^x . sec e^x . tan e^x dx
[Put e^x = z
Then e^x dx = dz]
= ∫ sec z . tan z dz
= sec z + C = sec e^x + C

(xi) ∫\(\frac{\sec ^2 \sqrt{x}}{\sqrt{x}}\) dx
Solution:

Question 2.
(i) ∫sin x cos x dx (sin x = v)
Solution:
∫sin x cos x dx
[Put sin x = v
Then cos x dx = dv]
= ∫v dv = \(\frac{1}{2}\)v² + C
= \(\frac{1}{2}\)sin² x + C

(ii) ∫tan³ x sec² x dx (tan x = t)
Solution:
∫tan³ x sec² x dx
[Put tan x = t
Then sec² x dx = dt]
= ∫t³ dt = \(\frac{1}{4}\)t⁴ + C
= \(\frac{1}{4}\)tan⁴ x + C

(iii) ∫\(\frac{{cosec}^2 x}{1+\cot x}\) dx
Solution:
∫\(\frac{{cosec}^2 x}{1+\cot x}\) dx
[Put 1 + cot x = t
Then -cosec² x dx = dt
or, cosec² x dx = – dt]
= ∫\(\) = -∫\(\) = -ln |t| + C
= -ln |1 + cot x| + C

(iv) ∫\(\frac{\sin x}{\cos ^3 x}\) dx
Solution:

(v) ∫\(\frac{\cos x}{\sin ^5 x}\) dx
Solution:

(vi) ∫\(\frac{{cosec}^2 x(\ln x)}{x}\) dx (In x = z)
Solution:
∫\(\frac{{cosec}^2 x(\ln x)}{x}\) dx
[Put ln x = z
Then \(\frac{d x}{x}\) = dz]
= ∫cosec² z dz
= -cot z + C = -cot (ln x) + C

(vii) ∫\(\sqrt{1-\sin x}\) cos x dx
Solution:

Question 3.
(i) ∫x\(\sqrt{x^2+3}\) dx (x² + 3 = v)
Solution:

(ii) ∫\(\frac{7 d x}{2-3 x}\) dx
Solution:

(iii) ∫\(\frac{x}{\sqrt{x^2-a^2}}\) dx
Solution:

(iv) ∫\(\frac{x^2+1}{\left(x^3+3 x+7\right)^3}\) dx
Solution:

(v) ∫(x⁴ – 3x² + 1)⁴ (2x³ – 3x) dx
Solution:

Question 4.
(i) ∫e^3x dx
Solution:
∫e^3x dx
[Put 3x = t
Then 3 dx = dt
or, dx = \(\frac{1}{3}\)dt]
= ∫e^t . \(\frac{1}{3}\)dt = \(\frac{1}{3}\)e^t + C
= \(\frac{1}{3}\)e^3x + C

(ii) ∫e^2x+7 dx
Solution:
∫e^2x+7 dx
[Put 2x + 7 = t
Then 2 dx = dt
or, dx = \(\frac{1}{2}\)dt]
= ∫e^t . \(\frac{1}{2}\)dt = \(\frac{1}{2}\)e^t + C
= \(\frac{1}{2}\)e^2x+7 + C

(iii) ∫e^x/3 dx
Solution:
[Put \(\frac{x}{3}\) = t
Then dx = 3 dt
= ∫e^t . 3dt = 3e^t + C = 3e^x/3 + C

(iv) ∫\(e^{x^3}\) x² dx
Solution:

(v) ∫a^2x dx
Solution:

(vi) ∫2\(a^{x^2}\) x dx
Solution:

(vii) ∫e^2tanx sec² x dx
Solution:

(viii) ∫\(\frac{e^x}{\left(e^x-2\right)^2}\) dx
Solution:

(ix) ∫\(e^{\cos ^2 x}\) sin 2x dx
Solution:
∫\(e^{\cos ^2 x}\) sin 2x dx
[Put cos2 x = t
Then 2cos x (-sin x)dx – dt
or, -sin 2x dx = dt
or, sin 2x dx = -dt]
= ∫e^t (-dt) = e^t + C = –\(e^{\cos ^2 x}\) + C

Question 5.
(i)∫\(\frac{\sin ^{-1} x}{\sqrt{1-x^2}}\) dx
Solution:

(ii)∫\(\frac{d x}{\sqrt{1-(x-1)^2}}\)
Solution:

(iii)∫\(\frac{\left(\sec ^{-1} x\right)^2 d x}{x \sqrt{x^2-1}}\)
Solution:

(iv)∫\(\frac{d x}{x\left[1+(\ln x)^2\right]}\)
Solution:

(v)∫\(\frac{d x}{x^2+2 x+2}\) (Integrate \(\frac{d x}{(x+1)^2+1}\))
Solution:

Question 6.
(i) ∫tan 3x dx
Solution:

(ii) ∫cos \(\frac{x}{3}\) dx
Solution:

(iii) ∫sec (2x + 1) dx
Solution:
∫sec (2x + 1) dx
[Put 2x + 1 = t
Then 2 dx = dt
or, dx = \(\frac{1}{2}\)dt]
= ∫sec t . \(\frac{1}{2}\)dt = \(\frac{1}{2}\) ∫sec t dt
= \(\frac{1}{2}\) ln |sec t + tan t| + C
= \(\frac{1}{2}\) ln |sec (2x + 1) + tan (2x + 1)| + C

(iv) ∫cosec 7x dx
Solution:
∫cosec 7x dx
[Put 7x = t
Then 7 dx = dt
or, dx = \(\frac{1}{7}\)dt]
= ∫cosec t . \(\frac{1}{7}\)dt
= \(\frac{1}{7}\) ln |cosec t + cot t| + C
= \(\frac{1}{7}\) ln |cosec 7x + cot x| + C

(v) ∫2x cot (x² + 3) dx    (x² + 3 = z)
Solution:
∫2x cot (x² + 3) dx
[Put x² + 3 = z
Then 2x dx = dz]
= ∫cot dz
= In |sin z| + C
= In |sin (x² + 3)| + C

(vi) ∫e^x tan e^x dx
Solution:
∫e^x tan e^x dx
[Put e^x = t
Then e^x dx = dt]
= ∫tan t dt
= In |sec t| + C
= In |sec e^x| + C

(vii) ∫(sec 2x – 3)² dx
Solution:
∫(sec 2x – 3)² dx
∫sec² 2x dx – 6∫sec 2x dx + 9∫dx
= \(\frac{1}{2}\) tan 2x – 3 ln |sec 2x + tan 2x| + 9x + C

Question 7.
(i) ∫\(\frac{e^x+e^{-x}}{e^x-e^{-x}}\) dx
Solution:
∫\(\frac{e^x+e^{-x}}{e^x-e^{-x}}\) dx
[Put (e^x – e^-x) = t
Then (e^x + e^-x)dx = dt]
= ∫\(\frac{d t}{t}\) = ln |t| + C = ln |(e^x – e^-x| + C

(ii) ∫3^x e^2x dx
Solution:

(iii) ∫\(\frac{(x+1) \ln \left(x^2+2 x+2\right)}{x^2+2 x+2}\) dx
Solution:

Question 8.
(i) ∫\(\frac{\sin x}{\sin (x+\alpha)}\) dx
Solution:

= ∫(cos α – sin α . cot t) dt
= cos α ∫dt – sin α ∫cot dt
= cos α . t – sin α . ln |sin t| + C
= (x + α) cos α – sin α  ln |sin (x + α)| + C
= x cos α – sin α ln |sin (x + α)| + C

(ii) ∫\(\frac{\sin x}{\cos (x-\alpha)}\) dx
Solution:

(iii) ∫\(\frac{\tan x+\tan \alpha}{\tan x-\tan \alpha}\) dx
Solution:

 

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Ex 8(d) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Exercise 8(d)

Question 1.
Find the extreme points of the following functions. Specify if the extremum is a maximum or minimum.
Find the extreme values.
(i) y = x² + 2x + 3
Solution:

(ii) y = 5x² – 2x⁵
Solution:

∴ The function attains minimum at x = 0.
and maximum at x = 1 .
The minimum value = 0
The maximum value = 5 – 2 = 3

(iii) y = \(\frac{3 x}{x^2+1}\)
Solution:

(iv) y = x²\(\sqrt{1-x^2}\)
Solution:

(v) y = 2x³ – 15x² – 36x + 18
Solution:

The function attains maximum at x = -1 and minimum at x = 6.
Maximum value
= -2 – 15 + 36 + 18 = 37
Minimum value
= 2 × 216 – 15 × 36 – 36 × 6 + 13
= 432 – 540 – 216 + 18
= 450 – 756
= -306

(vi) y = 60/(x⁴ – x² + 25)
Solution:

(vii) y = (x – 1)³
Solution:

So the point x = 1 is neither a point of maximum nor a point of minimum. It is an inflexion point.

(viii) y = (x – 2)³ (x + 3)⁴
Solution:

(ix) y = x + \(\frac{1}{x}\)
Solution:

∴ Maximum at x = -1
and minimum at x = 1
Maximum value = -1 – 1 = -2
Minimum value = 2.

(x) y = 4 cos 2x – 3 sin 2x, x ∈ (-\(\frac{\pi}{2}\), \(\frac{\pi}{2}\))
Solution:

(xi) y = sin x cos x, x ∈ (\(\frac{\pi}{8}\), \(\frac{\pi}{2}\))
Solution:

But there is no minimum in the domain.

(xii) y = cos x (1 + sin x), x ∈ [0, 2π]
Solution:

(xiii) y = sin^p x cos^q x; p, q > 0, x ∈ [0, \(\frac{\pi}{2}\))
Solution:

(xiv) y = x e^-x ; x ∈ (-2, 2)
Solution:

Question 2.
Show that the following functions do not possess maximum or minimum.
(i) x³
Solution:
y = x³

Thus the function does not possess a maximum or a minimum. (Proved)

(ii) x⁵
Solution:
Processed as in (i)

(iii) 3x³ – 12x² + 16x – 15
Solution:
Let y = 3x³ – 12x2 + 16x – 5

So the function does not possess a maximum or a minimum. (Proved)

(iv) 4 – 3x + 3x² – x³
Solution:
Processed as in (iii).

(v) ln |x|, x ≠ 0
Solution:
y = ln |x|, x ≠ 0

Which have no solution. Hence the function has neither a maximum nor a minimum.
(Proved)

Question 3.
Use the function f(x) = \(x^{\frac{1}{x}}\), x > 0 to show that e^x > π^c.
Solution:
f(x) = \(x^{\frac{1}{x}}\), x > 0

Question 4.
Prove the inequality x² \(e^{-x^2}\) ≤ e^-1, x ∈ R.
Solution:

Question 5.
If f(x) = a ln x + bx² + x has extreme values at x = -1 and x = 2 then find a and b.
Solution:
f(x) = a ln x + bx² + x
f'(x) = \(\frac{a}{x}\) + 2b x + 1
Given that f(x) attains extreme values at x = -1 and x = 2
Then f(-1) = 0 and f(2) = 0
⇒ -a – 2b + 1 = 0 … (1)
\(\frac{a}{2}\) + 4b + 1 = 0 … (2)
From (1) we get a = -2b + 1
Putting it in (2)
we get \(\frac{1-2 b}{2}\) + 4b + 1 = 0
⇒ 1 – 2b + 8b + 2 = 0
⇒ 3 + 6b = 0
⇒ b = \(-\frac{3}{6}\) = \(-\frac{1}{2}\)
Again a = 1 – 2b = 1 + 1 = 2
∴ a = 2, b = \(-\frac{1}{2}\)

Question 6.
Show that \(\frac{x}{1+x \tan x}\), x ∈ (0, \(\frac{\pi}{2}\)) is maximum when x = cos x.
Solution:

Thus the function attains maximum when x = cos x. (Proved)

Question 7.
Determine the absolute maximum and absolute minimum of the following function on [-1, 1]
f(x) = \(\left\{\begin{array}{l}
(x+1)^2, x \leq 0 \\
(x-1)^2, x>0
\end{array}\right.\)
Solution:
f(x) = \(\left\{\begin{array}{l}
(x+1)^2, x \leq 0 \\
(x-1)^2, x>0
\end{array}\right.\)
f(x) = \(\left\{\begin{array}{l}
2(x+1), x \leq 0 \\
2(x-1), x>0
\end{array}\right.\)
For extremum f'(x) = 0
⇒ x + 1 = 0 if x < 0
or, x – 1 = 0 if x > 0
⇒ x = -1 or x = 1
Now f(-1) = 0, f(1) = 0
Again f is not differentiable at x = 0 and f(0) = 1
The function attains absolute minimum at x = ±1. Absolute minimum value = 0.
The function attains absolute maximum at x = 0. Absolute Maximum value = 1.

Question 8.
Find extreme values of
f(x) = \(\left\{\begin{array}{l}
\frac{x}{1-x^2},-1<x<0 \\
x^3-x, 0 \leq x<2
\end{array}\right.\) on (-1, 2)
Solution:
Given that

Question 9.
Find two numbers x and y whose sum is 15 such that xy² is maximum.
Solution:
Let z = xy²
Given that x + y = 15
Then y = 15 – x
Thus z = x (15 – x)²
\(\frac{d z}{d x}\) = (15 – x)² + x² (15 – x) . (-1)
= (15 – x) (15 – x – 2x)
= (15 – x) (15 – 3x)
= 3(15 – x) (5 – x)
\(\frac{d^2 z}{d x^2}\) = -3(5 – x) – 3(15 – x)
= -3 (20 – 2x)
= -6 (10 – x)
For extreme points
\(\frac{d z}{d x}\) = 0
⇒ 3(15 – x) (5 – x) = 0
⇒ x = 15 or 5.
\(\left.\frac{d^2 z}{d x^2}\right]_{x=15}\) = 30 > 0
\(\left.\frac{d^2 z}{d x^2}\right]_{x=5}\) = 30 < 0
∴ z = xy² is maximum when x = 5.
In this case y = 10
∴The two numbers are 5, 10.

Question 10.
If the sum of two positive numbers in constant then show that their product is maximum when they are equal.
Solution:
Let x and y be two positive numbers such that x + y = c (constant)
Then y = c – x
Let p = xy = x(c – x) = cx – x²

∴ The two numbers are equal. (Proved)

Question 11.
Determine a rectangle of area 25 sq. units which has minimum perimeter.
Solution:
Let x and y be the length and breadth of a rectangle of area 25 sq. units.

∴ The perimeter is minimum when the rectangle is a square of side 5 units.

Question 12.
Find the altitude of a right circular cylinder of maximum volume inscribed in a sphere of radius r.
Solution:
Let ABCD be a right circular cylinder inscribed in a sphere with centre at O and radius ‘r’. Let x be the altitude of the cylinder.

Question 13.
Show that the radius of the right circular cylinder of greatest curved surface that can be inscribed in a given cone is half the radius of the base of the cone.

Solution:
Let ABC be a cone, Let r be the radius of the base and h be the height of the cone. Let PQRS be a cylinder inscribed in the cone whose height is x.
In the diagram OT = x.
Then CT = h – x
Now Δ CTR and Δ RQB are similar.

∴ Radius of the right circular cylinder of greatest curved surface is half the base of the cone. (Proved)

Question 14.
Show that the semi vertical angle of a cone of given slant height is tan^-1√2 when its volume is maximum.
Solution:

Question 15.
A cylindrical open water tank with a circular base is to be made out of 30 sq. metres of metal sheet. Find the dimensions so that it can hold maximum water. (Neglect thickness of sheet)
Solution:

Let ABCD be an open cylindrical tank with circular base.
Let r be the radius of the base and x be the height of the tank.
Given that the tank is made out of 30 square metres of metal sheet.
The surface area of the tank
= 27πrx + πr² [∵ The tank is open.
So 2πrx + πr² = 30
⇒ 2πrx = 30 – πr²

Question 16.
A cylindrical vessel of capacity 500 cubic metres open at the top is to be constructed. Find the dimensions of the vessel if the material used is minimum given that the thickness of the material used is 2 cm.
Solution:

Question 17.
Find the coordinates of the point on the curve x²y – x + y = 0 where the slope of the tangent is maximum.
Solution:
Let (x, y) be the point on the curve
x²y – x + y = 0.

The slope is maximum when x = 0. when x = 0, y = 0
The point is (0, 0) at which the slope of the tangent is maximum.

Question 18.
Find the points on the curve y = x² + 1 which are nearest to the point (0, 2).
Solution:
Let A = (0, 2)
Let P (x, y) be any point on the curve
y = x² + 1. …(1)

Question 19.
Show that the minimum distance of a point on the curve \(\frac{a^2}{x^2}\) + \(\frac{b^2}{y^2}\) = 1
from the origin is a + b.
Solution:
Let P(x, y) be any point on the curve

Question 20.
Show that the vertical angle of a right circular cone of minimum curved surface that circumscribes a given sphere is 2 sin^-1(√2 – 1).
Solution:

Let r is the radius of the given sphere, R is the radius of the base, H is the height and l is the C lant height of the cone ABC. Let θ is the semi vertical angle.

Question 21.
Show that the semi-vertical angle of a right circular cone of minimum volume that circumscribes a given sphere is sin^-1(\(\frac{1}{3}\)).
Solution:

Let ABC be a right circular cone which circumscribes a sphere of radius ‘r’.
Let θ be the semi-vertical angle of the cone.
Let D be the centre of the sphere. By symmetry D must lie on AO, where O is the centre of the base.
In the diagram DO = r.
Again in the Δ ADE

Question 22.
Show that the shortest distance of the point (0, 8a) from the curve ax² = y³ is 2a√11.
Solution:
Given curve is 2x² = y³ … (1)
Let any point on it is P(x, y)
Distance of P from A (0, 8a)

Question 23.
Show that the triangle of greatest area that can be inscribed in a circle is equilateral.
Hints: It BC is any chord then for the Δ ABC to have maximum area, the point A must be on the perpendicular bisector of BC so as to have the largest height AD. Let mDBAD = a. Let BO = OA = r. Then area of Δ ABC = \(\frac{1}{2}\)|BC| |AD| = \(\frac{1}{2}\) . 2r sin 2α (r + r + cos 2α) = r² sin 2a . (1 + cos 2a). Then maximise Δ to obtain 2a = \(\frac{\pi}{3}\)
Solution:

Let ABC be a triangle inscribed in a circle with centre at O and radius ‘r’.
The triangle ABC has maximum area if the point A is on the perpendicular bisector of BC.
Let ∠BAD = α, Let BO = AO = r,
Then ∠BOD = 2α.
In Δ OBD, sin 2α = \(\frac{\mathrm{BD}}{\mathrm{OB}}\)
⇒ BD = OB sin 2α = r sin 2α
Again OD = r cos 2α.
Thus AD = r + r cos 2α
Let Z be the area of the triangle ABC.

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 7 Continuity and Differentiability Ex 7(g) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Exercise 7(g)

Find \(\frac{d y}{d x}\)
Question 1.
xy² + x²y + 1 = 0
Solution:
xy² + x²y + 1 = 0

Question 2.
\(x^{\frac{1}{2}} y^{-\frac{1}{2}}\) + \(x^{\frac{3}{2}} y^{-\frac{3}{2}}\) = 0
Solution:

Question 3.
x² + 3y² = 5
Solution:
x² + 3y² = 5
⇒ \(\frac{d}{d x}\)(x²) + 3 \(\frac{d}{d x}\)(y²) = 0
⇒ 2x + 6y\(\frac{d y}{d x}\) = 0
⇒ \(\frac{d}{d x}\) = –\(\frac{x}{3 y}\)

Question 4.
y² cot x = x² cot y.
Solution:
y² cot x = x² cot y

Question 5.
y = tan xy
Solution:
y = tan xy

Question 6.
x = y In (xy).
Solution:
x = y In (xy).

Question 7.
e^xy + y sin x = 1
Solution:
e^xy + y sin x = 1

Question 8.
In \(\sqrt{x^2+y^2}\) = tan^-1 \(\frac{y}{x}\)
Solution:

Question 9.
y^x = x^{sin y}
Solution:
y^x = x^{sin y}

Question 10.
If sin (x + y) = y cos (x + y) then prove that \(\frac{d y}{d x}\) = –\(\frac{1+y^2}{y^2}\).
Solution:

Question 11.
If \(\sqrt{1-x^4}\) + \(\sqrt{1-y^4}\) = k(x² – y²) then show that \(\frac{d y}{d x}\) = \(\frac{x \sqrt{1-y^4}}{y \sqrt{1-x^4}}\).
Solution:

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Ex 8(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Exercise 8(a)

Question 1.
Find the velocity and acceleration at the end of 2 seconds of the particle moving according to the following rules.
(i) s = 2t² + 3t + 1
Solution:
s = 2t² + 3t + 1

∴ Velocity is 11 units/sec and acceleration is 4 units/sec².

(ii) s = √t +1
Solution:
s = √t +1

(iii) s = \(\frac{3}{2 t+1}\)
Solution:

(iv) s = t³ – 6t² + 15t + 12
Solution:
s = t³ – 6t² + 15t + 12

∴ Velocity is 3 units/sec and acceleration is 0.

Question 2.
The sides of an equilateral triangle are increasing at the rate of √3 cm/sec. Find the rate at which the area of the triangle is increasing when the side is 4 cm long.
Solution:
Let x be the lenght of each side of an equilateral triangle.

∴ Area of the triangle is increasing at the rate of 6 cm²/sec

Question 3.
Find the rate at which the volume of a spherical balloon will increase when its radius is 2 metres if the rate of increase of its radius is 0.3 m/min.
Solution:
Let r be the radius of a spherical balloon.

∴ The volume increase at the rate of 4.8π m³/min.

Question 4.
The surface area of a cube is decreasing at the rate of 15 sq. cm/sec. Find the rate at which its edge is decreasing when the length of the edge is 5 cm.
Solution:
Let s be the surface area of a cube.
Let x be the length of each side of the cube.

∴ The edge is decreasing at the rate of 0.25 cm/sec

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 7 Continuity and Differentiability Ex 7(m) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Exercise 7(m)

Question 1.
Verify Rolle’s theorem for the function
f(x) = x (x – 2)², 0 ≤ x ≤ 2.
Solution:
f(x) = x (x – 2)², 0 ≤ x ≤ 2
Here a = 0, b = 2
f(x) is a polynomial function hence it is continuous and also differentiable.
∴ f is continuous on [0. 2]
f is differentiable on (0, 2)
f(0) = 0 = f(2)
Thus conditions of Rolle’s theorem are satisfied.
f'(x) = (x – 2)² + 2x (x – 2)
= (x – 2) (x – 2 + 2x)
= (x – 2) (3x – 2)
f'(x)= 0 ⇒ x = 2, x = \(\frac{2}{3}\)
But x = 2 ∉ (0, 2). Thus c = \(\frac{2}{3}\) such that f'(c) = 0
Thus Rolle’s theorem is verified.

Question 2.
Examine if Rolle’s theorem is applicable to the following functions:
(i) f(x) = |x| on [-1, 1]
Solution:
f(x) = |x| on [-1, 1]
As f(x) = |x| is not differentiable at x = 0 ∈ (-1, 1)
We have Rolle’s theorem is not applicable.

(ii) f(x) = [x] on [-1, 1]
Solution:
f(x) = [x] on [-1, 1]
f(x) = [x] is not continuous at 0 ∈ [-1, 1]
Rolle’s theorem is not applicable.

(iii) f(x) = sin x on [0, π]
Solution:
f(x) = sin x on [0, π]
f is a trigonometric function hence continuous and differentiable on its domain.
∴ f is continuous on [0, π]
f is differentiable on (0, π]
f(0) = f(π)
Thus Rolle’s theorem is applicable for f(x) = sin x on [0, π]

(iv) f(x) = cot x on [0, π]
Solution:
f(x) = cot x on [0, π]
Clearly cot (0) and cot (π] are not defined hence Rolle’s theorem is not applicable.

Question 3.
Verify Lagrange’s Mean-Value theorem for
F(x) = x³ – 2x² – x + 3 on [1, 2]
Solution:
f(x) = x³ – 2x² – x + 3 on [1, 2]
f is a polynomial function hence continuous as well as differentiable.
∴ f is continuous on [1, 2]
f is differentiable on (1, 2)
Thus Largange’s mean value theorem is applicable.
Now f(1) = 1 – 2 – 1 + 3 = 1
f(2) = 8 – 8 – 2 + 3 = 1
∴ f(x) = 2x² – 4x – 1

Thus Lagrange’s mean value theorem is verified.

Question 4.
Test if Lagrange’s mean value theorem holds for the functions given in question no. 2.
Solution:
(i) f(x) = |x| is not differentiable at x = 0 ∈ (-1, 1)
Thus Lagrange’s mean value theorem, does not hold.

(ii) f(x) = [x] is discontinuous at 0 ∈ [-1, 1]
Thus Lagrange’s mean value theorem is not applicable.

(iii) f(x) = sin x is a trigonometric function, which is continuous as well as differentiable in its domain.
∴ f is continuous on [0, π]
f is differentiable on (0, π)
Thus conditions of Lagrange’s mean value theorem are satisfied.
Hence mean value theorem is applicable.

(iv) f(x) = cot x
Which is undefined x = 0 and x = π
Thus Lagrange’s mean value theorem is not applicable.

Question 5.
(Not for examination) Verify Cauchy’s mean value theorem for the functions x² and x³
in [1, 2].
Solution:
Let f(x) = x², and g(x) = x³ on [1, 2]
Both f and g are polynomial functions, hence continuous and differentiable.
∴ f and g are continuous on [1, 2]
f and g are differentiable on (1, 2)
g'(x) = 3x² ≠ 0 ∀ x ∈ (1, 2)
Thus conditions of Cauchy’s mean value theorem are satisfied.
Now f(1) = 1, f(2) = 4, g(1) = 1, g(2) = 8
f'(x) = 2, and g'(x) = 3x²

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 7 Continuity and Differentiability Ex 7(i) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Exercise 7(i)

Differentiate.
Question 1.
√x w.r.t x².
Solution:

Question 2.
sin x. w.r.t. cot x.
Solution:
Let y = sin x and z = cot x

Question 3.
\(\frac{1-\cos x}{1+\cos x}\) w.r.t \(\frac{1-\sin x}{1+\sin x}\)
Solution:

Question 4.
tan-1 x w.r.t. tan^-1 \( \sqrt{1+x^2} \)
Solution:

Question 5.
sin^-1 \(\left(\frac{2 x}{1+x^2}\right)\) w.r.t cos^-1 \(\left(\frac{1-x^2}{1+x^2}\right)\)
Solution:
Let y = sin^-1 \(\frac{2 x}{1+x^2}\) and z = cos^-1 \(\frac{1-x^2}{1+x^2}\)
Then y = 2 tan^-1 x and z = 2 tan^-1 x
So y = z
∴ \(\frac{d y}{d z}\) = 1.

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 7 Continuity and Differentiability Ex 7(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Exercise 7(a)

Question 1.
Examine the continuity of the following functions at indicated points.
(i) f(x) = \(\left\{\begin{array}{cl}
\frac{x^2-a^2}{x-a} & \text { if } x \neq a \\
a & \text { if } x=a
\end{array}\right.\) at x = a
Solution:

(ii) f(x) = \(\left\{\begin{aligned}
\frac{\sin 2 x}{x} & \text { if } x \neq 0 \\
2 & \text { if } x=0
\end{aligned}\right.\) at x = 0
Solution:

(iii) f(x) = \(\begin{cases}(1+2 x)^{\frac{1}{x}} & \text { if } x \neq 0 \\ e^2 & \text { if } x=0\end{cases}\) at x = 0
Solution:

(iv) f(x) = \(\left\{\begin{array}{l}
x \sin \frac{1}{x} \text { if } x \neq 0 \\
0
\end{array}\right.\) at x = 0
Solution:

(v) f(x) = \(\left\{\begin{array}{l}
\frac{x^2-1}{x-1} \text { if } x \neq 1 \\
2
\end{array}\right.\) at x = 1
Solution:

(vi) f(x) = \(\begin{cases}\sin \frac{1}{x} & \text { if } x \neq a \\ 0 & \text { if } x=0\end{cases}\) at x = 0
Solution:

(vii) f(x) = [3x + 11] at x = –\(\frac{11}{3}\)
Solution:

(viii) f(x) = \(\left\{\begin{array}{l}
\frac{e^{\frac{1}{x}}-1}{e^{\frac{1}{x}}+1} \text { if } x \neq 0 \\
0
\end{array}\right.\) at x= 0
Solution:

(ix) f(x) = \(\left\{\begin{array}{l}
\frac{1}{x+[x]} \text { if } x<0 \\
-1 \quad \text { if } x \geq 0
\end{array}\right.\) at x = 0
Solution:

because [- h]is the greatest integer not exceeding – h
and so [- h ] = – 1
As L.H.L. = R.H.L. = f(0)
f(x) is cntinuous at x = 0.

(x) f(x) = \(\begin{cases}\frac{|x|}{x} & \text { if } x \neq 0 \\ 0 & \text { if } x=0\end{cases}\) at x = 0
Solution:

(xi) f(x) = \(\left\{\begin{array}{l}
2 x+1 \text { if } x \leq 0 \\
x \quad \text { if } 0<x<1 \\
2 x-1 \text { if } x \geq 1
\end{array}\right.\) at x = 0, 1
Solution:

(xii) f(x) = \(\left\{\begin{array}{l}
\frac{1}{e^{\frac{1}{x}}-1} \text { if } x>0 \\
0
\end{array} \text { if } x \leq 0\right.\) at x = 0
Solution:

(xiii) f(x) = sin\(\frac{\pi[x]}{2}\) at x = 0
Solution:

(xiv) f(x) = \(\frac{g(x)-g(1)}{x-1}\) at x = 1
Solution:
g(x) = |x – 1|
Then g(1) = |1 – 11| = 0
Now f(1) = \(\frac{g(1)-f(1)}{1-1}\) = 0/0
which we cannot determine.
Hence f(x) is discontinuous at x = 1.

Question 2.
If a function is continuous at x = a, then find
(i) \(\lim _{h \rightarrow 0}+\frac{1}{2}\{f(a+h)+f(a-h)\}\)
(ii) \(\lim _{h \rightarrow 0}+\frac{1}{2}\{f(a+h)-f(a-h)\}\)
Solution:

Question 3.
Find the value ofa such that the function f defined by \(\begin{cases}\frac{\sin a x}{\sin x} & \text { if } x \neq 0 \\ \frac{1}{a} & \text { if } x=0\end{cases}\)
is continuous at x = 0.
Solution:

Question 4.
If f(x) = \(\left\{\begin{array}{l}
a x^2+b \text { if } x<1 \\
1 \quad \text { if } x=1 \\
2 a x-b \text { if } x>1
\end{array}\right.\)
is continuous at x = 1, then find a and b.
Solution:
Let f(x) be continuous at x = 1
Then L.H.L. = R.H.L. = f(1)

Question 5.
Show that sin x is continuous for every real x.
Solution:
Let f(x) = sin x
Consider the point x = a, where ‘a’ is any real number.
Then f(a) = sin a

Thus L.H.L. = R.H.L. = f(a)
Hence f(x) = sin x is continuous for every real x.
(Proved)

Question 6.
Show that the function f defined by \(\left\{\begin{array}{l}
1 \text { if } x \text { is rational } \\
0 \text { if } x \text { is irrational }
\end{array}\right.\) is discontinuous ∀ ≠ 0 ∈ R.
Solution:
Consider any real point x = a
If a is rational then f(a) = 1.
Again lim_x→a+f(x) = lim_h→0f(a + h)
which does not exist because a + h may be rational or irrational
Similarly lim_x→a-f(x) does not exist.
Thus f(x) is discontinuous at any rational point. Similarly we can show that f(x) is discontinuous at any irrational point.
Hence f(x) is discontinuous for all x ∈ R
(Proved)

Question 7.
Show that the function f defined by f(x) = \(f(x)=\left\{\begin{array}{l}
x \text { if } x \text { is rational } \\
-x \text { if } x \text { is irrational }
\end{array}\right.\)
is continuous at x = 0 and discontinuous ∀ x ≠ 0 ∈ R.
Solution:
f(0) = 0
L.H.L. = lim_x→0f(x) = lim_h→0f(-h)
= \(\lim _{h \rightarrow 0} \begin{cases}-h & \text { if } h \text { is rational } \\ h & \text { if } h \text { is irrational }\end{cases}\) = 0
Similarly R.H.L. = 0
Thus L.H.L. = R.H.L. = f(0)
Hence f(x) is continuous at x = 0.
We can easily show that f(x) is discontinuous at all real points x ≠ 0.

Question 8.
Show that the function f defined by
f(x) = \(\left\{\begin{array}{l}
x \text { if } x \text { is rational } \\
0 \text { if } x \text { is irrational }
\end{array}\right.\)
is discontinuous everywhere except at x = 0.
Solution:
f(0) = 0
L.H.L. = lim_h→0f(-h)
= lim_h→0\(\begin{cases}-h & \text { if }-h \text { is rational } \\ 0 & \text { if }-h \text { is irrational }\end{cases}\)
Similarly R.H.L. = 0
Thus L.H.L. = R.H.L = f(0)
Hence f(x) is continuous at x = 0.
Let a be any real number except 0.
If a is rational then f(a) = a.
L.H.L. = lim_h→0f(a – h) which does not exist because a – h may be rational or may be irrational.
Similarly R.H.L. does not exist.
Thus f(x) is discontinuous at any rational point x – a ≠ 0.
Similarly f(x) is discontinuous at any irrational point.
Hence f(x) is discontinuous everywhere except at x = 0.
(Proved)

Question 9.
Show that f(x) = \(\begin{cases}x \sin \frac{1}{x}, & x \neq 0 \\ 0, & x=0\end{cases}\) is continuous at x = 0.
Solution:
Refer to No. 1(iv) of Exercise – 7(a).

Question 10.
Prove that e^x – 2 = 0 has a solution between 0 and 1. [Hints: Use continuity of e^x– 2 and fact – 2]
Solution:

∴ f(x) is continuous in [0, 1]
f(0). f(1) = (-1) (e – 2) < 0
∴ f(x) has a zero between 0 and 1
i.e. e^x – 2 = 0 has a solution between 0 and 1

Question 11.
So that x⁵ + x +1 = 0 for some value of x between -1 and 0.
Solution:
Let f(x) = x⁵ + x + 1 and any a ∈ (-1, 0)
f(a) = a⁵ + a + 1

= -1 = f(-1)
∴ f is continuous on [-1, 0]
But f(-1) f(0) = 1 × -1 < 0
∴ f has a zero between -1 and 0
⇒ x5 + x + 1 = 0 for some value of x between -1 and 0.

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 6 Probability Ex 6(c) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 6 Probability Exercise 6(c)

Question 1.
There are 3 bags B₁, B₂ and B₃ having respectively 4 white, 5 black; 3 white, 5 black and 5 white, 2 black balls. A bag is chosen at random and a ball is drawn from it. Find the probability that the ball is white.
Solution:
Let
E₁ = The selected bag is B₁,
E₂ = The selected bag is B₂,
E₃ = The selected bag is B₃.
A = The ball drawn is white.

Question 2.
There are 25 girls and 15 boys in class XI and 30 boys and 20 girls in class XII. If a student chosen from a class, selected at random, happens to be a boy, find the probability that he has been chosen from class XII.
Solution:
Let
E₁ = The student is choosen from class XI.
E₂ = The student is choosen from class XII.
A = The student is a boy.

Question 3.
Out of the adult population in a village 50% are farmers, 30% do business and 20% are service holders. It is known that 10% of the farmers, 20% of the business holders and 50% of service holders are above poverty line. What is the probability that a member chosen from any one of the adult population, selected at random, is above poverty line?
Solution:
Let
E₁ = The person is a farmer.
E₂ = The person is a businessman.
E₃ = The person is a service holder.
A = The person is above poverty line.

Question 4.
Take the data of question number 3. If a member from any one of the adult population of the village, chosen at random, happens to be above poverty line, then estimate the probability that he is a farmer.
Solution:
P (a farmer / he is above poverty line)
= P (E₁ | A)

Question 5.
From a survey conducted in a cancer hospital it is found that 10% of the patients were alcoholics, 30% chew gutka and 40% have no specific carcinogenic habits. If cancer strikes 80% of the smokers, 70% of alcoholics, 50% of gutka chewers and 10% of the nonspecific, then estimates the probability that a cancer patient chosen from any one of the above types, selected at random,
(i) is a smoker
(ii) is alcoholic
(iii) chews gutka
(iv) has no specific carcinogenic habits.
Solution:
The question should be modified as from a survey conducted in a cancer hospital, 10% patients are smokers, 20% alcoholics, 30% chew gutka and 40% have no specific carcinogenic habits. If cancer strikes 80% of the smokers, 70% of alcoholic, 50% of gutka chewers and 10% of non specific, then estimate the probability that a cancer patient chosen from any one of the following types selected at random
(i) is a smoker
(ii) is alcoholic
(iii) chews gutka
(iv) has no specific carcinogenic habits.
Let
E₁ = The person is a smoker.
E₂ = The person is alcoholic.
E₃ = The person chew Gutka.
E₄ = The person have no specific habits.
A = The person is a cancer patient.
According to the question