Odisha State Board BSE Odisha 8th Class Hindi Solutions Chapter 4 कुएँ के मेढ़क (ललित निबंध) Textbook Exercise Questions and Answers.
BSE Odisha Class 8 Hindi Solutions Chapter 4 कुएँ के मेढ़क (ललित निबंध)
अनुशीलनी
1. इन प्रश्नों के उत्तर दीजिए
(क) भारी वर्षा हुई तो क्या हुआ ?
उत्तर:
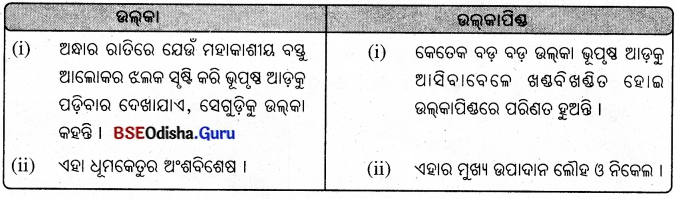
नानी के गाँव में एक बहुत बड़ा कुआँ था । उसमें चार-छह मेंढ़क रहते थे । भारी वर्षा हुई तो कुएँ में पानी भर गया । पानी उस कुएँ से बाहर आने लगा । पानी की उस बाढ़ में कुएँ में रहनेवाले मे ढ़क बाहर निकल आए ।

(ख) बाहर निकले मेंढ़कों की क्या हालत हुई ?
उत्तर:
बाहर निकले मेंढ़कों खुशी से इधर-उधर उछलने लगे । एक शरारती मेंढ़क गर्व से सड़क पर उछलने लगा । एक गाड़ी के पहिए के नीचे वह आ गया, पर बच गया । अपने को बलशाली मानवाला एक मेंढक कूदते सम साँप के मुँह से बच गया । तीसरे मेंढ़क की पिछली टाँग साइकिल से टूट गई ।
(ग) आदमी घर से निकले तो पहले क्या करें ?
उत्तर:
घर से निकले तो पहले अपने को काबू में रखे। अपने को बड़ा न माने । विनयी बने । गुस्सा न करे । दूसरों के साथ अच्छा बर्ताव करे । दूसरों के साथ मिलजुलकर रहना सीखे । उसका व्यवहार दूसरों को बुरा न लगे, किसी को
(घ) कैसा व्यवहार अशिष्ट समझा जाता है ?
उत्तर:
दूसरों से झगड़ना, नाराज होना, गाली-गलौज करना, चिल्लाना, जिद करके अकड़ना, बिना पूछे दूसरों की चीज छूना, दूसरों के काम में दखल देना जैसे व्यवहारों को अशिष्ट समझा जाता है । हमारा व्यवहार दूसरों को बुरा लगना, हमारे कारण को असुबिधा होना या दिल को दुख होना भी अशिष्ट व्यवहार हैं।
(ङ) शिष्टता किन-किन कामों में है ?
उत्तर:
अपनी बुरी आदतों को रोकने, अपने मन और भावों hi काबू में रखने, जोर-जोर से न बोलने, बड़ों और गुरुजनों का सम्मान करने, सहपाठियों से मित्र भाव रखने, छोटों को स्नेह करने, अपनी बारी का इंतज़ार करने, लाईन में आने, स्कूल तथा ट्राफिक के नियम मानने में शिष्टता है ।
(च) आदमी के दोस्त या दुश्मन कैसे बनते हैं ?
उत्तर:
आदमी के व्यवहार से दोस्त या दुश्मन बनते हैं । हम ऐसा व्यवहार करें कि वह दूसरों को बुरा न लगे, उनकी असुविधा न हो, उनके दिल को कोई दुःख न पहुँचे । इससे लोग दोस्त वन जाएँगे । हम झगड़ा करेंगे, गाली देंगे, दूसरों के काम में दखल देंगे तो लोग हमारे दुश्मन बन जाएँगे ।

2. निम्न प्रश्नों के उत्तर एक-दो वाक्यों में दीजिए :
(क) अनुपम कहाँ रहता है ?
उत्तर:
अपुनम भुवनेश्वर में रहता है ।
(ख) एक दिन क्या हुआ ?
उत्तर:
एक दिन भारी वर्षा हुई ।
(ग) कुएँ में कौन थे ?
उत्तर:
कुएँ में चार-छह मेंढ़क रहते थे ।
(घ) बाढ़ आने पर मेंढ़कों की क्या दशा हुई ?
उत्तर:
पानी की उस बाढ़ में मेंढ़क कुएँ से बाहर आ गए।
(ङ) पहले मेंढ़क की क्या हालत हुई ?
उत्तर:
पहला मेंढ़क ऐंठकर सड़क पर उछलते समय एक गाड़ी के पहिए के नीचे आ गया, पर बच गया ।
(च) तीसरे मेंढ़क का स्वभाव कैसा था ?
उत्तर:
तीसरा मेंढ़क बड़ा घमंडी था ।
(छ) मेंढ़की ने अपने बच्चों से क्या कहा ?
उत्तर:
मेंढ़की ने अपने बच्चों से कहा कि खबरदार, बाहर निकलो तो अपने को बचाना सीखो, संभलकर चलो, आफत से बचो !
(ज) विनयी होने का क्या मतलब है ?
उत्तर:
विनयी होने का मतलब है घमंड न करना, अपने को बड़ा न मानना ।
(झ) आदमी के बच्चों को क्या करना चाहिए ?
उत्तर:
आदमी के बच्चों को दूसरों के साथ मिलजुलकर रहना चाहिए ।

3. निम्न प्रश्नों के उत्तर दीजिए :
(क) किसने कहानी सुनाई ?
उत्तर:
नानी ने कहानी सुनाई ।
(ख) मेंढ़क सड़क पर क्या करने लगे ?
उत्तर:
मेंढ़क सड़क पर फुदकने लगे ।
(ग) मेंढ़क की कौन-सी टाँग टूट गई ?
उत्तर:
मेंढ़क की पिछली टाँग टूट गई ।
(घ) अपने अच्छे बर्ताव से लोग क्या बनेंगे ?
उत्तर:
अपने अच्छे बर्ताव से लोग दोस्त बनेंगे।
4. निम्नलिखित विकल्पों में से सही उत्तर चुनिए :
(क) आदमी जानवर से अच्छा है, क्यों कि उसमें ज्यादा:
(i) बल है
(ii) बुद्धि है
(iii) सुंदरता है
(iv) नम्रता है
उत्तर:
(ii) बुद्धि है
(ख) विनय का भाव क्या है ? सही विकल्प चुनिए –
(i) अपने को बड़ा मानना
(ii) अपने को बड़ा न मानना,
(iii) दूसरे को पीटना
(iv) दूसरे के साथ नाचना
उत्तर:
(ii) अपने को बड़ा न मानना

(ग) बड़ों और गुरुजनों का क्या करना चाहिए ?
(i) सम्मान करना
(ii) स्नेह करना
(iii) आदर करना
(iv) इंतजार करना
उत्तर:
(i) सम्मान करना
भाषाकार्य
5. इन शब्दों को देखिए इनके दो रूप होते हैं।

गया, आया, हुआ आदि रूप सही हैं ।
आ, आआ, हुया नहीं होता ।
6. सही वर्तनी लिखिए:
पहिआ, विस्व, सौहाद्र, बजरगं, छाति, एंठ, काबु, नानि, पुछा, भाइ, र्बताव, असिस्ट, भर्द, दुसरा
उत्तर:
- पंहिआ — पहिया
- सौहाद्र — सौहार्द
- छाति — छाती
- विस्व — विश्व
- बजरगं — बजरंग
- एंठ — ऐंठ
- काबउ — काबू
- पुछा — पूछा
- बताव — बर्ताव
- भर्द — भद्र
- नानि — नानी
- भाइ — भाई
- असिस्ट — अशिष्ट
- दुसरा — दूसरा
7. निम्नलिखित वाक्यों को सुधार कर लिखिए:
(i) एक बार भारी वर्षा हुआ ।
(ii) दूसरों के झगड़ना अच्छी बात नहीं ।
(iii) आदमी के आचरण सभ्य होता है ।
(iv) उसका पिछला टाँग टूट गया ।
(v) वह मेरा ओर देखने लगा ।
शुद्ध वाक्य
(i) एक बार भारी वर्षा हुई ।
(ii) दूसरों से झगड़ना अच्छी बात नहीं है ।
(iii) आदमी का आचरण सभ्य हाता है।
(iv) उसकी पिछली टाँग टूट गई ।
(v) वह मेरी ओर देखने लगा ।

जानिए :
निम्नलिखित शब्दों को देखिए इन्हें ‘संज्ञा ” शब्द कहते हैं ।
संज्ञा शब्द कर्त्ता या कर्म हो सकते हैं ।
कुआँ, मेंढक, वर्षा, बाढ़, पानी, रात, कहानी, अनुपम, ‘भुवनेश्वर, मालिक, साँप, बच्चा, खुशी, टोली, आदत, सौहार्द, मित्रता, कक्षा
इन संज्ञा शब्दों को निम्नलिखित वर्गों में सजाइए –
(क) व्यक्तिवाचक
(ख) द्रव्यवाचक
(ग) जातिवाचक
(घ) समूहवाचक
(ङ) भाववाचक
उत्तर:
(क) व्यक्तिवाचक- अनुपम, भुवनेश्वर
(ख) द्रव्यवाचक- पानी
(ग) जातिवाचक – कुआँ, मेंढक, वर्षा, बाढ़, रात, कहानी, मालिक, साँप, बच्चा
(घ) समूहवाचक टोली,कक्षा
(ङ) भाववाचक खुशी, आदत, सौहार्द, मित्रता
8. उचित संज्ञा और विशेषण शब्दों को जोड़िए :
क — ख
अच्छी — दुनिया
भद्र — आदत
भारी — साँप
बड़ा — वर्षा
बुरी — आदत
खुली — दुनिया
उत्तर:
क — ख
अच्छी — कहानी
भद्र — व्यवहार
भारी — वर्षा
बड़ा — साँप
बुरी — आदत
खुली — दुनिया
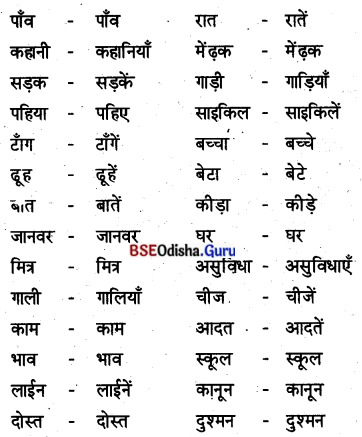
9. उदाहरण के अनुसार वचन बदलिए :
(i) घर – घर
मेंढ़क – मेंढ़क
पाँव — पाँव
साँप — साँप
(ii) रात — टाँगे
सड़क — सड़कें
साइकिल — साइकिलें
टाँग — टाँगो
ढूह — दूहें
आदत — आदतें

(iii) कुआँ — कुऐ
पहिया — पहियाँ
बेटा — बेटे
बच्चा — बच्चे
कीड़ा — कीड़े
लड़का — लड़के
(iv) कहानी — कहानियाँ
गाड़ी — गाड़ियाँ
डाली — डालियाँ
नदी — नदियाँ
लड़की — लड़कियाँ
10. समानार्थी शब्द लिखिए:
- दुश्मन — शत्रु
- सौहार्द — मित्रता
- अशिष्ट — असभ्य
- ढूह — टीला
- ऊधमी — शरारती
11. निम्नलिखित शब्दों के लिंग बदलिए :
- नानी — नाना
- मेंढ़की — मेंढ़क
- बहन — बहनोई
- माँ — बाप
12. विशेषण छाँटिए :
(क) बाहर – ……………..
अचानक – ……………..
दुःखी – ……………..
उत्तर: दु:खी
(ख) मतलब – ……………..
अशिष्ट – ……………..
व्यवहार – ……………..
उत्तर: अशिष्ट
(ग) जरूरी – ……………..
बात – ……………..
उसने – ……………..
उत्तर: जरूरी
(घ) शरारती – ……………..
खुशी – ……………..
के साथ – ……………..
उत्तर: शरारती
(ङ) सम्मान – ……………..
गुरुजन – ……………..
होशियार – ……………..
उत्तर: होशियार

(च) अच्छा – ……………..
जानवर – ……………..
चाहिए – ……………..
उत्तर: अच्छा
(छ) कुआँ – ……………..
बड़ा – ……………..
चिल्लाना – ……………..
उत्तर:
(छ) बड़ा
परीक्षोपयोगी अतिरिक्त प्रश्नोत्तर
एक-एक वाक्य में उत्तर दीजिए :
प्रश्न 1.
अनुपम कहाँ रहता था ?
उत्तर:
अनुपम भुवनेश्वर में रहता था।
प्रश्न 2.
अनुपम के घर कौन आई ?
उत्तर:
अनुपम के घर उसकी नानी आई ।
प्रश्न 3.
नानी ने रात को किसे कहानी सुनाई ?
उत्तर:
नानी ने रात को अनुपम को कहानी सुनाई ।
प्रश्न 4.
नानी ने कब कहानी सुनाई ?
उत्तर:
नानी ने रात को कहनी सुनाई ।
प्रश्न 5.
कुआँ किसके गाँव में था ?
उत्तर:
कुआँ नानी के गाँव में था ।

प्रश्न 6.
कुएँ में कितने मेंढ़क रहते थे ?
उत्तर:
कुएँ में चार-छह मेंढ़क रहते थे ।
प्रश्न 7.
मेंढ़क कुएँ में दिन-रात क्या करते थे ?
उत्तर:
मेंढ़क कुएँ में दिन-रात उछलते-कूदते और टर्र-टर्र करते थे
प्रश्न 8.
मेंढ़क किसके मालिक बने हुए थे ?
उत्तर:
में ढ़क मानो कुएँ के मालिक बने हुए थे ।
प्रश्न 9.
मेंढ़क कुएँ में रहते समय किस स्वभाव के हो गए थे ?
उत्तर:
मेंढक कुएँ में रहते समय उधमी और शरारती हो गए थे ।
प्रश्न 10.
कुएँ में पानी कैसे भर गया ?
उत्तर:
एक बार भारी वर्षा हुई तो कुएँ में पानी भर गया ।
प्रश्न 11.
मेंढ़क कैसे बाहर निकल आए ?
उत्तर:
कुएँ में पानी भरकर बाहर आने लगा तो पानी की उस बहाव में में ढ़क बाहर निकल आए ।
प्रश्न 12.
मेंढ़क क्यों खुशी से फूल उठे ?
उत्तर:
बाहर की खुली दुनिया सामने देखकर में ढ़क खुशी से फूल उठे ।
प्रश्न 13.
कौन-सा मेंढ़क किसीका सुनता न था ?
उत्तर:
मेंढकों में से जो सबसे शरारती था, वह किसीका सुनता न था ।
प्रश्न 14.
शरारती मेंढ़क ने गाड़ी देखकर क्या किया ?
उत्तर:
शरारती मेंढ़क गाड़ी देखकर ऐंठकर उछलने लगा और पहिए के नीचे जा गिरा, पर बच गया ।
प्रश्न 15.
दूसरा मेंढ़क अपने को क्या मानता था ?
उत्तर:
दूसरा मेंढक अपने को बड़ा बजरंगबली मानता था ।
प्रश्न 16.
दूसरा मेंढ़क किससे बच गया ?
उत्तर:
एक साँप मुँह बाये आया तो दूसरा में ढ़क छिपकर बच गया ।

प्रश्न 17.
तीसरे मेंढ़क का स्वभाव कैसा था ?
उत्तर:
तीसरा में ढ़क बड़ा घमंडी था ।
प्रश्न 18.
तीसरा मेंढ़क छाती फुलाकर क्या कहता था ?
उत्तर:
तीसरा में ढ़क छाती फुलाकर कहता था कि मेरी बराबरी करने वाला अभी पैदा नहीं हुआ ।
प्रश्न 19
तीसरे मेंढ़क की क्या दुर्दशा हुई ?
उत्तर:
तीसरे में ढ़क की पिछली टाँग पर एक साइकिल सर्र से निकल गई और उसकी टाँग टूट गई ।
प्रश्न 20.
मेंढ़की पास की ढूह पर क्या कर रही थी ?
उत्तर:
मेंढ़की पास की ढूह पर में ढ़कों की यह दुर्दशा देख रही थी ।
प्रश्न 21.
मेंढ़की ने अपने बच्चों से क्या कहा ?
उत्तर:
मेंढ़की ने अपने बच्चों से कहा “देखो बच्चो ! खबरदार बाहर निकलो तो अपने को बचाना सीखो; संभलकर चलो आफत से बचो ।
प्रश्न 22.
अनुपम ने अपनी नानी से क्या पूछा ?
उत्तर:
अनुपम ने अपनी नानी से पूछा, “नानीजी ! हम घर से बाहर निकलें तो क्या करे ?”
प्रश्न 23.
नानी ने किस प्रकार के व्यवहार को पहली बात कही ?
उत्तर:
नानी ने अपने को काबू में रखने को पहली बात कही।
प्रश्न 24.
अपने को काबू में रखने का मतलब क्या है ?
उत्तर:
अपने को काबू में रखने का मतलब है कि अपने को “बड़ा न मानना ।
प्रश्न 25.
विनय का भाव क्या है ?
उत्तर:
अपने को बड़ा न मानना विनय का भाव है।
प्रश्न 26.
कौन – सा बर्ताव सबको अच्छा लगता है
उत्तर:
गुस्सा न करना, घमंड न करना यह बर्ताव सबको अच्छा लगता है
प्रश्न 27.
अनुपम विनयी होगा तो क्या होगा ?
उत्तर:
अनुपम विनयी होगा तो दूसरे उससे प्यार करेंगे ।
प्रश्न 28.
नानी के अनुसार कौन अपने को बचाते हैं ?
उत्तर:
नानी के अनुसार कीड़े-मकोड़े और जानवर अपने को बचाते हैं ।

प्रश्न 29.
घर में रहते समय बच्चों को क्या सीखना चाहिए ।
उत्तर:
घर में रहते समय बच्चों को माता-पिता की बात मानना, भाई-बहनों के साथ रहना सीखना चाहिए ।
प्रश्न 30.
स्कूल में रहते समय बच्चों को क्या सीखना चाहिए ?
उत्तर:
स्कूल में रहते समय बच्चों को मित्रों के साथ अच्छा बर्ताव करना सीखना चाहिए ।
प्रश्न 31.
घर हो या बाहर, बच्चों को किस ओर सावधान रहना चाहिए ?
उत्तर:
घर हो या बाहर, बच्चों को इस ओर सावधान रहना चाहिए कि उनका व्यवहार दूसरों को बुरा न लगे, किसी को असुविधा न हो, किसी का दिल न दुखे ।
प्रश्न 32.
किस-किस आचरण को अशिष्ट माना जाता है ?
उत्तर:
दूसरों से झगड़ना, नाराज होना, गाली-गलौज करना, चिल्लाना, जिद करके अकड़ना, बिना पूछे दूसरे की चीज छूना, दूसरे के काम में दखल देना आदि आचरणों को अशिष्ट माना जाता है ।
प्रश्न 33.
क्या भद्र व्यवहार कहलाता है ?
उत्तर:
अपनी बुरी आदतों को रोकना, अपने मन और भावों को काबू में रखना भद्र व्यवहार कहलाता है ।
प्रश्न 34.
बड़ों और छोटों को कैसा व्यवहार करने को स्कूल में सिखाया जाता है ?
उत्तर:
बड़ों और गुरुजनों का सम्मान करने और छोटों को स्नेह करने को स्कूल में सिखाया जाता है ?
प्रश्न 35.
सहपाठियों से कैसा व्यवहार करना चाहिए ?
उत्तर:
सहपाठियों से सौहार्द भाव रखना चाहिए ।
प्रश्न 36.
स्कूल में किसका इंतजार करने को सिखाया जाता है?
उत्तर:
स्कूल में अपनी बारी का इंतजार करने को सिखाया जाता है।
प्रश्न 37.
बच्चों को कैसे चलने की सिखाया जाता है ?
उत्तर:
बच्चों को अनुशासन मानकर लाईन बनाकर चलने को सिखाया जाता है ।
प्रश्न 38.
बच्चों को कौन-कौन से नियम और कानून नहीं तोड़ने चाहिए ?
उत्तर:
बच्चों को स्कूल के नियम और ट्रैफिक वे कानून नहीं तोड़ने चाहिए ।
प्रश्न 39.
अच्छे बर्ताव का परिणाम क्या होता है ?
उत्तर:
अच्छे बर्ताव से लोग दोस्त बनते हैं ।
प्रश्न 40.
बुरे आचरण का परिणाम क्या होता है ?
उत्तर:
बुरे आचरण से लोग दुश्मन बन जाते हैं ।
प्रश्न 41.
आदमी जानवर से क्यों अच्छी है ?
उत्तर:
आदमी जानवर से अच्छा है क्योंकि उसका आचरण सभ्य होता है ।

प्रश्न 42.
सारा विश्व कैसे मित्र हो सकता है ?
उत्तर:
जो अच्छा आचरण करेगा, सारा विश्व उसका मित्र हो सकता है।
एक या दो शब्द में उत्तर दीजिए:
1. अनुपम कहाँ रहता है?
उत्तर: भुवनेश्वर में
2. अनुपम के घर कौन आई ?
उत्तर: उसकी नानी
3. रातको नानी ने क्या सुनाई ?
उत्तर: कहानी
4. कुआँ कहाँ था ?
उत्तर: नानी के गाँव में
5. कुएँ में कितने मेंढ़क रहते थे ?
उत्तर: चार-छह
6. मेंढक कुएँ में अपने को क्या मानते थे ?
उत्तर: मालिक
7. मेंढ़क कैसे बाहर निकले ?
उत्तर: पानी की बाढ़ में
8. कौन-सा मेंढ़क सड़क पर कूदक रहा था ?
उत्तर: शरारती मेंढ़क
9.शरारती मेंढ़क कहाँ जा गिरा ?
उत्तर: पहिए के नीचे
10. दूसरा में ढ़क अपने को क्या मानता था ?
उत्तर: बजरंगबली
11. दूसरा में ढ़क किससे छिपकर बच गया ?
उत्तर: साँप से
12. तीसरे में ढ़क का स्वभाव कैसा था ?
उत्तर: घमंडी था
13. किससे मेंढ़क की पिछली टाँग टूट गई ?
उत्तर: साइकिल से

14. अपने बच्चों से संभलकर चलने को किसने कहा ?
उत्तर: मेंढ़की
15. अपने को बड़ा न मानना कैसा भाव है ?
उत्तर: विनय का
16. किसे दूसरे लोग प्यार करते हैं ?
उत्तर: विनयी को
17. हम घर पर किसकी बात मानें ।
उत्तर: माता-पिता की
18. दूसरों से झगड़ना कैसा आचरण हैं ?
उत्तर: अशिष्ट
19. हमें सड़क पर जाते समय किसके कानून नहीं तोड़ने चाहिए ?
उत्तर: ट्रैफिक के
20. हम यदि बुरा आचरण करेंगे लोग क्या बन जाएँगे ?
उत्तर: दुश्मन
मातृभाषा में अनुवाद कीजिए :
प्रश्न 1.
अनुपम भुवनेश्वर में रहता है
उत्तर:
ଅନୁପମ ଭୁବନେଶ୍ଵରରେ ରହେ।
प्रश्न 2.
एक दिन उसकी नानी उनके घर आई ।
उत्तर:
ଦିନେ ତା’ ଆଈ ତାଙ୍କ ଘରକୁ ଆସିଲେ।
प्रश्न 3.
उसने नानी के पाँव छुए ।
उत्तर:
ସେ ଆଈଙ୍କ ପାଦ ଛୁଇଁ ପ୍ରଣାମ କଲା ।
प्रश्न 4.
रात को नानी ने एक अच्छी कहानी सुनाई ।
उत्तर:
ରାତିରେ ଆଈ ଗୋଟିଏ ଭଲ ଗପ ଶୁଣେଇଲେ ।
प्रश्न 5.
मेंढक दिन-रात उछलते-कूदते और टर्र-टर्र करते थे ।
उत्तर:
ବେଙ୍ଗଗୁଡ଼ିକ ଦିନରାତି ଡିଆଁଡ଼େଇଁ କରୁଥିଲେ ଓ କେଁ- କଟର ଶବ୍ଦ କରୁଥିଲେ ।

प्रश्न 6.
वे मानों कुएँ के मालिक बने हुए थे ।
उत्तर:
ସତେଯେପରି ସେମାନେ କୂଅର ମାଲିକ ହୋଇଯାଇଥିଲେ।
प्रश्न 7.
वे उधमी और शरारती हो गए थे ।
उत्तर:
ସେମାନେ ଉପଦ୍ରବୀ ଓ ଦୁଷ୍ଟ ହୋଇଯାଇଥିଲେ।
प्रश्न 8.
एक बार भारी बर्षा हुई।
उत्तर:
‘ଥରେ ଭୀଷଣ ବର୍ଷା ହେଲା।
प्रश्न 9.
उनमें जो सबसे ज्यादा शरारती था, किसी का सुनता
उत्तर:
ସେମାନଙ୍କ ମଧ୍ୟରେ ଯିଏ ସବୁଠାରୁ ଦୁଷ୍ଟ ଥିଲା, ସେ କାହାରି କଥା ଶୁଣୁ ନଥିଲା ।
प्रश्न 10.
वह ऐंठकर उछलने लगा ।
उत्तर:
ସେ ଗର୍ବରେ ଡେଇଁବାକୁ ଲାଗିଲା।
प्रश्न 11.
वह लम्बा कूदता था ।
उत्तर:
ସେ ବହୁତ ଦୂର ପର୍ଯ୍ୟନ୍ତ ଡେଉଁଥିଲା।
प्रश्न 12.
इतने में एक साँप मुँह बायें आ पहुँचा ।
उत्तर:
ଏତିକିବେଳେ ଗୋଟିଏ ସାପ ଆଁ କରି ଆସି ପହଞ୍ଚିଲା ।
प्रश्न 13.
मेंढ़क छिपकर बच गया ।
उत्तर:
ବେଙ୍ଗଟି ଲୁଚିଯାଇ ବଞ୍ଚଗଲା ।
प्रश्न 14.
तीसरा भी बड़ा घमंडी था ।
उत्तर:
ତୃତୀୟଟି ମଧ୍ୟ ବହୁତ ଗର୍ବୀ ଥିଲା ।
प्रश्न 15.
मेरी बराबरी करनेवाला अभी पैदा नहीं हुआ ।
उत्तर:
ମୋ ସାଙ୍ଗରେ ମୁକାବିଲା କରିବାକୁ ବର୍ତ୍ତମାନ ସୁଦ୍ଧା କେହି ଜନ୍ମ ହୋଇ ନାହିଁ ।
प्रश्न 16.
मेंढ़क की पिछली टाँग टूट गई ।
उत्तर:
ବେଙ୍ଗଟିର ପଛଗୋଡ଼ ଭାଙ୍ଗିଗଲା ।
प्रश्न 17.
पास की ढूह पर एक में ढ़की अपने बच्चों के साथ यह सब देख रही थी ।
उत्तर:
ପାଖ ମାଟିକୁଦ ଉପରେ ଗୋଟିଏ ବେଙ୍ଗୁଲୀ ତା’ ପିଲାମାନଙ୍କ ସହିତ ଏସବୁ ଦେଖୁଥିଲା।
प्रश्न 18.
तुम बाहर निकलो तो अपने को बचाना सीखो ।
उत्तर:
ତୁମେମାନେ ବାହାରକୁ ବାହାରିବାବେଳେ ନିଜକୁ ସୁରକ୍ଷିତ ରଖୁବା ଶିଖ ।
प्रश्न 19.
लेकिन अनुपम डरा नहीं ।
उत्तर:
କିନ୍ତୁ ଅନୁପମ ଡରିଗଲା ନାହିଁ।
प्रश्न 20.
पहली बात है कि अपने को काबू में रखना ।
उत्तर:
ପ୍ରଥମ କଥା ହେଉଛି ଯେ ନିଜକୁ ନିୟନ୍ତ୍ରଣରେ ରଖ।

प्रश्न 21.
तुम गुस्सा न करना, घमंड न करना ।
उत्तर:
ତୁମେ କ୍ରୋଧ କରିବ ନାହିଁ, ଗର୍ବ କରିବ ନାହିଁ ।
प्रश्न 22.
ऐसा बर्ताव सबको अच्छा लगता है ।
उत्तर:
ଏଭଳି ବ୍ୟବହାର ସମସ୍ତଙ୍କୁ ଭଲ ଲାଗେ।
प्रश्न 23.
दूसरी बात, कीड़े-मकोड़े और जानवर अपने को बचाते हैं।
उत्तर:
ଦ୍ଵିତୀୟ କଥା, ପୋକ-ଜୋକ ଓ ପଶୁମାନେ ନିଜକୁ, ରକ୍ଷାକରନ୍ତି ।
प्रश्न 24.
लेकिन आदमी के बच्चे दूसरों के साथ मिलजुलकर रहना सीखते हैं ।
उत्तर:
କିନ୍ତୁ ମଣିଷ ପିଲା ଅନ୍ୟମାନଙ୍କ ସହିତ ମିଳିମିଶି ରହିବାକୁ ଶିଖୁଥାଏ ।
प्रश्न 25.
स्कूल में मित्रों के साथ अच्छा बर्ताव करना |
उत्तर:
ତୁମେ ସ୍କୁଲରେ ସାଙ୍ଗମାନଙ୍କ ସହିତ ଭଲ ବ୍ୟବହାର କରିବ ।
प्रश्न 26.
किसी का दिल न दुखे, इस ओर सावधान रहना ।
उत्तर:
କାହାରି ମନରେ ଆଘାତ ନ ଲାଗୁ, ଏଥିପ୍ରତି ସାବଧାନ ରହିବ ।
प्रश्न 27.
दूसरों से झगड़ना, नाराज होना, गाली-गलौज करना, चिल्लाना, जिद करके अकड़ना आदि अशिष्ट आचरण हैं।
उत्तर:
ଅନ୍ୟ ସହିତ କଳିକରିବା, ରାଗିବା, ଗାଳିଗୁଲଜ କରିବା, ପାଟିତୁଣ୍ଡ କରିବା, ଜିଦ କରି ଅଟଳ ରହିବା ଆଦି ଅଶିଷ୍ଟ ଆଚରଣ ।
प्रश्न 28.
इसका मतलब है अपनी बुरी आदतों को रोकना, अपने मन और भावों को काबू में रखना जरूरी है ।
उत्तर:
ଏହାର ଅର୍ଥ ହେଉଛି, ନିଜର ଖରାପ ଅଭ୍ୟାସକୁ ନିୟନ୍ତ୍ରତ କରିବା, ନିଜ ମନ ଓ ଭାବଗୁଡ଼ିକୁ ନିୟନ୍ତ୍ରଣରେ ରଖୁବା ଅତ୍ୟନ୍ତ ଆବଶ୍ୟକ ।

प्रश्न 29.
सहपाठियों से सौहार्द भाव रखना चाहिए।
उत्तर:
ସହପାଠୀମାନଙ୍କ ସହିତ ମିତ୍ରଭାବ ରଖୁବା ଉଚିତ।
प्रश्न 30.
अपनी बारी का इंतजार करना चाहिए ।
उत्तर:
ନିଜ ପାଳି ଆସିବା ପର୍ଯ୍ୟନ୍ତ ଅପେକ୍ଷା କରିବା ଆବଶ୍ୟକ ।
प्रश्न 31.
अपने अच्छे बर्ताव से लोग दोस्त बनेंगे, बुरे आचरण से दुश्मन बन जाएँगे ।
उत्तर:
ନିଜ ଭଲ ବ୍ୟବହାର ଦ୍ବାରା ଲୋକେ ମିତ୍ର ହୋଇଯିବେ, ଖରାପ ଆଚରଣ ଯୋଗୁଁ ଶତ୍ରୁ ପାଲଟିଯିବେ ।
सही उत्तर चूनिए :
प्रश्न 1.
कुएँ और मेंढ़क की बात अनुपम को कैसे मालूम हुई ?
(A) माँ से सुनकर
(B) किताब से पढ़कर
(C) आँखों से देखकर
(D) नानी से सुनकर
उत्तर:
(D) नानी से सुनकर
प्रश्न 2.
कुआँ कहाँ था ?
(A) भुवनेश्वर में
(B) अनुपम के गाँव में
(C) जंगल में
(D) नानी के गाँव में
उत्तर:
(D) नानी के गाँव में

प्रश्न 3.
कुएँ में कितने मेंढ़क थे ?
(A) बहुत-से
(B) दो-चार
(C) पाँच-दस
(D) चार-छह
उत्तर:
(D) चार-छह
प्रश्न 4.
मेंढ़क रात-दिन क्या करते थे ?
(A) उछलते-दौड़ते थे
(B) उछलते-कूदते थे
(C) कूदते-भागते थें
(D) खुशियाँ मनाते थे
उत्तर:
(B) उछलते-कूदते थे
प्रश्न 5.
मेंढ़क कुएँ में अपने को क्या मानते थे ?
(A) शरारती
(B) राजा
(C) अंहकारी
(D) मालिक
उत्तर:
(D) मालिक
प्रश्न 6.
मेंढ़क कुएँ में रहकर क्या हो गए थे ?
(A) शरारती
(B) सहनशील
(C) सद्भावरखने वाले
(D) फुदकने में कुशल
उत्तर:
(A) शरारती
प्रश्न 7.
कुएँ में पानी क्यों भर गया ?
(A) आँधी आने से
(B) पानी डाले जाने से
(C) भारी वर्षा होने से
(D) हल्की वर्षा होने से
उत्तर:
(C) भारी वर्षा होने से
प्रश्न 8.
मेंढ़कों ने कुएँ से निकलकर क्या देखा ?
(A) कुएँ का आकार
(B) नीला आसमान
(C) बाहर की प्रकृति
(D) खुली दुनिया
उत्तर:
(D) खुली दुनिया
प्रश्न 9.
सड़क पर कौन फुदकता था ?
(A) सबसे अधिक शरारती मेंढ़क
(B) वह में ढ़क, जिसकी टाँग टूट गई थी
(C) अपने को बजरंगबली माननेवाला
(D) सबसे बड़ा मेंढ़क
उत्तर:
(A) सबसे अधिक शरारती मेंढ़क
प्रश्न 10.
कौन-सा मेंढ़क पहिए के नीचे जा गिरा ?
(A) चौथा
(B) पहला
(C) तीसरा
(D) दूसरा
उत्तर:
(B) पहला

प्रश्न 11.
कौन-सा मेंढ़क वड़ा घमंड्डी था ?
(A) पहला
(B) दूसरा
(C) तीसरा
(D) सभी
उत्तर:
(C) तीसरा
प्रश्न 12.
कौन-सा मेंढ़क साँप के मुँह से बच गया ?
(A) अपने को बजरंगबली माननेवाला
(B) सबसे शरारती
(C) सबसे बड़ा घमंडी
(D) कुएँ में छिपजानेवाला मेंढ़क
उत्तर:
(A) अपने को बजरंगबली माननेवाला
प्रश्न 13.
तीसरे में ढ़क की पिछली टाँग कैसे टूट गई ?
(A) सड़क पर फुदकते समय
(B) साँप के सामने से भागते समयं
(C) कुएँ में गिरकर
(D) साइकिल की चोट से
उत्तर:
(A) सड़क पर फुदकते समय
प्रश्न 14.
मेरी बराबरी करने वाला अभी पैदा नहीं हुआ – यह किसने कहा ?
(A) घमप्डी मेंढ़क ने
(B) नानी ने
(C) बजरंगी बली मेंढ़क ने
(D) शरारती मेंढ़क ने
उत्तर:
(A) घमप्डी मेंढ़क ने
प्रश्न 15.
बाहर निकलों तो अपने को बचाना सीखो – किसने कहा?
(A) पहले मेंढ़क ने
(B) मेंढ़की ने
(C) नानी ने
(D) अनुपम की माँ ने
उत्तर:
(C) नानी ने
प्रश्न 16.
मेंढ़की ने बच्चों से किससे बचने को कहा ?
(A) शरारती मेंढ़क से
(B) आफत से
(C) ऊधमियों से
(D) साँप से
उत्तर:
(B) आफत से
प्रश्न 17.
नानी ने अपने को काबू में रहने का अर्थ क्या समझाया?
(A) अपनी बात धीरे से कहना
(B) अपना क्रोध दबाना
(C) अपने को बड़ा न मानना
(D) अपने स्वास्थ्य का ख्याल रखना ।
उत्तर:
(B) आफत से
प्रश्न 18.
क्या होने से दूसरों का प्यार मिलता है ?
(A) विनयी
(B) गुसैल
(C) दुखी
(D) सुखी
उत्तर:
(A) विनयी
प्रश्न 19.
बच्चे कैसे रहना सीखते हैं ?
(A) दूसरों को हराकर
(B) दूसरों से मिलजुलकर
(C) खुद बड़ी खुशी से
(D) कीड़े-मकोड़ो से प्यार करके
उत्तर:
(B) दूसरों से मिलजुलकर
प्रश्न 20.
बच्चे को क्या सीखना चाहिए ?
(A) माँ-बाप की बात मानना
(B) गुरु को प्रणाम करना
(C) भाई-बहनों को खिलाना
(D) किताब गंदी न करना
उत्तर:
(A) माँ-बाप की बात मानना
प्रश्न 21.
हमारा व्यवहार कैसा होना चाहिए ?
(A) कोमल और सरल
(B) यह दूसरों को बुरा न लगे
(C) सच पर आधारित
(D) यह दूसरों को सुनाई पड़े
उत्तर:
(B) यह दूसरों को बुरा न लगे

प्रश्न 22.
दूसरों के काम में दखल देना-कैसा आचरण है ?
(A) अशिष्ट
(B) शिष्ट
(C) डरपोक
(D) साहसपूर्ण
उत्तर:
(A) अशिष्ट
प्रश्न 23.
कौन-सा भद्र व्यवहार है ?
(A) झगड़ना
(B) अकड़ना
(C) बुरी आदतों से दूर रहना
(D) नाराज होना
उत्तर:
(C) बुरी आदतों से दूर रहना
प्रश्न 24.
हमें सहपाठियों से कैसा संबंध रखना चाहिए ?
(A) प्रतिद्वन्द्विता का भाव
(B) उनसे मुलाकात करें
(C) दूरी बनाए रखें
(D) सौहार्द भाव रखें
उत्तर:
(D) सौहार्द भाव रखें
प्रश्न 25.
हमें किसका इंतजार करना चाहिए ?
(A) छोटों सेस्नेह का
(B) अपनी लाइन का
(C) अनुशासन का
(D) अपनी बारी का
उत्तर:
(D) अपनी बारी का
प्रश्न 26.
होमें क्या नहीं तोड़ना चाहिए ?
(A) बुरे आचरण
(B) ट्रैफिक के कानून
(C) अपनी होशियारी
(D) ट्रैफिक की लाइन
उत्तर:
(B) ट्रैफिक के कानून
प्रश्न 27.
सारा विश्व हमारा कैसे मित्र बन सकता है ?
(A) अनुशासन में रहने से
(B) माँ-बाप की बात मानने से
(C) सभ्य आचरण से
(D) होशियार बनने से
उत्तर:
(C) सभ्य आचरण से
प्रश्न 28.
हम क्या करने से लोग हमारे दुश्मन बन जाएँगे ?
(A) बुरा आचरण करने से
(B) अच्छा बर्ताव करने से
(C) छोटों को स्नेह न करने से
(D) जानवरों को प्यार करने से
उत्तर:
(A) बुरा आचरण करने से
प्रश्न 29.
कौन-सा काम ठीक नहीं है ?
(A) अच्छा बर्ताव करना
(B) स्कूल के नियम मानना
(C) बुरा आचरण करना
(D) गुरुजनों का सम्मान करना
उत्तर:
(C) बुरा आचरण करना
प्रश्न 30.
शिष्ट आचरण क्या है ?
(A) दूसरों से झगड़ना
(B) दूसरों के दिल को दुखाना
(C) भावों को काबू में रखना
(D) दूसरों को गाली देना
उत्तर:
(C) भावों को काबू में रखना

प्रश्न 31.
अनुपम बहुत खुश हुआ, क्योंकि –
(A) उसकी नानी उनके घर आई
(B) नानी ने उसे कहानी सुनाई
(C) अनुपम होशियार लड़का था
(D) वह भुवंनेश्वर में रहता था
उत्तर:
(A) उसकी नानी उनके घर आई
प्रश्न 32.
मेंढ़क कुएँ से बाहर निकल आए, क्योंकि –
(A) बाहर की खुली दुनिया वे देखना चाहते थे
(B) कुएँ में पानी भर गया और बाहर आने लगा
(C) वे लम्बा कूदते थे और शरारती थे
(D) वे बड़े हो गए थे
उत्तर:
(B) कुएँ में पानी भर गया और बाहर आने लगा
प्रश्न 33.
मेंढ़क साँप के मुँह से बच गया, क्योंकि –
(A) वह कूद गया
(B) वह बड़ा बजरंगबली था
(C) वह छ्छिप गया
(D) साँप उसे पकड़ना चाहता था
उत्तर:
(C) वह छ्छिप गया
प्रश्न 34.
यह विनय का भाव है –
(A) अपने को बड़ा मानना
(B) अपने को बड़ा न मानना
(C) दूसरों के साथ नाचना
(D) दूसरों का गुण-गान करना
उत्तर:
(B) अपने को बड़ा न मानना
प्रश्न 35.
ऐसा बर्ताव सबको अच्छा लगता है –
(A) गुस्सा करना
(B) गुस्सा न करना
(C) दूसरों के काम में दखल देना
(D) दूसरों से कुछ न माँगना
उत्तर:
(B) गुस्सा न करना
प्रश्न 36.
यह एक अशिष्ट आचरण है –
(A) भाई-बहनों के साथ रहना
(B) सहपाठियों से सौहार्द रखना
(C) जिद करके अकड़ना
(D) शाम-सवेरे प्रार्थना करना
उत्तर:
(C) जिद करके अकड़ना
प्रश्न 37.
लोग हमारे दोस्त बन जाएँगे –
(A) हमारे बुरे आचरण से
(B) हमारे अच्छे बर्ताव से
(C) छोटों को स्नेह करने से
(D) किसी से न कुछ लेने से न देने से
उत्तर:
(B) हमारे अच्छे बर्ताव से

प्रश्न 38.
आदमी जानवर से अच्छा है, क्योंकि :
(A) वह अधिक सुंदर है
(B) वह बुद्धिमान है
(C) उसका आचरण सभ्य होता है
(D) उसके पास बोलने के लिए भाषा है
उत्तर:
(B) वह बुद्धिमान है
शून्यस्थानों की पूर्ति कीजिए :
1. अनुपम ………… में रहता है । (पुरी, कटक, भुवनेश्वर)
उत्तर: भुवनेश्वर
2. अनुपम के घर उसकी ………… आई। (दादी, नानी, मौसी
उत्तर: नानी
3. कुएँ में ………… में ढ़क रहते थे । (दो-चार, चार-छह, पाँच-छह)
उत्तर: चार-छह
4. सबसे ज्यादा ………… मेंढक सड़क पर कूद रहा था। (बजरंगबली, शरारती)
उत्तर: शरारती
5. ………… मेंढ़क साँप के मुँह से बच गया । (पहला, दूसरा, तीसरा)
उत्तर: दूसरा
6. ………… में ढ़क की पिछछली टाँग टूट गई । (पहले, दूसरे, तीसरे)
उत्तर: तीसरे
7. एक में ढ़क की पिछली टाँग ………… से धक्का होने से टूट गई । (गाड़ी, साइकिल, पत्थर )
उत्तर: साइकिल
8. अपने को बड़ा न मानना ………… का भाव है । (गुस्से, विनय, हीनता)
उत्तर: विनय

9. दूसरों के काम में दखल देने जैसे आंचरण को ………… माना जाता है । (शिष्ट, अशिष्ट, सहायता)
उत्तर: अशिष्ट
10. अपने मन और ………… को काबूं में रखना जरूरी है । (हृदय, भावों, गुस्से)
उत्तर: भावों
11. छात्रों को सहपाठियों से ………… भाव रखऩा चाहिए । (विनयं, सम्मान, सौहार्द)
उत्तर: सौहार्द
12. छात्रों को अपनी बारी का ………… करना चाहिए । (इंतजार, इंतजाम, आग्रह)
उत्तर: इंतजार
13. स्कूल के नियम, ………… के कानून नहीं तोड़ना चाहिए। (स्कूंल, सड़क, ट्रैफिक)
उत्तर: ट्रैफिक
14. लोग बुरे आचरण से ………… बन जाएँगे । (दोस्त, दुश्मन, शिष्ट)
उत्तर: दुश्मन
उपयुक्त शब्द ले कर खाली जगह भरिए :
1. अनुपम भुवनेश्वर ………… रहता है। (पर, से, में)
उत्तर: में
2. उसने नानी ………… पाँव छुए। (का, के, की)
उत्तर: के
3. रात को नानी ………… कहानी सुनाई। (से,ने, में)
उत्तर: ने
4. कुएँ ………… पानी भंर गया। (पर, में, से)
उत्तर: में
5. वे मानो कुएँ ………… मालिक बने हुएथे। (का, को, के)
उत्तर: के
6. पानी ………… बाढ़ में मेंढ़क बाहर निकल आए। (का, के, की)
उत्तर: के

7. वह सड़क ………… फूदक रहा था। (में, को, पर)
उत्तर: पर
8. में ढ़क ………… पीछली टाँग टूटगई। (का, के, की)
उत्तर: की
9. उसने अपने बच्चों ………… कहा। (को, से, पर)
उत्तर: से
10. तुम आफत ………… बचो। (से, में, पर)
उत्तर: से
11. उसने नानी ………… पूछा। (को, से, में)
उत्तर: से
12. यह विनय ………… भाव है। (का, के, की)
उत्तर: का
13. ऐसा बर्ताव सब ………… अच्छा लगता है। (का, को, ने)
उत्तर: को
14. अपने ………… काबू में रखना। (को, से, पर)
उत्तर: को
15. दूसरों ………… झगड़ना बुरी बात है। (से, में, पर)
उत्तर: से
16. सहपाठियों ………… सौहार्द भाव रखना। (को, से, का)
उत्तर: से

17. अपनी बारी ………… इंतजार करना चाहिए। (का, के, की
उत्तर: का
18. जानवर ………… आदमी अच्छा है। (में, का, से)
उत्तर: से
वर्तनी शुद्ध कीजिए :
1. पहिआ
2. विस्व
3. सोहाद्र
4. बजरगं
5. छाति
6. एंठ
7. काबु
8. नानि
9. पुछा
10. भाइ
11. बताव
12. असिस्ट
13. भर्द
14. दुसरा
15. होसियार
16. जानबर
17. अनुसासन
18. चिलाना
17. स्कुल
17. ब्वबहार
18. शरारति
19. लाइन
उत्तर:
1. पहिया
2. विश्व
3. सौहार्द
4. बजरंगं

5. छाती
6. ऐंठ
7. काबू
8. नानी
9. पूछा
10. भाई
11. बर्ताव
12. अशिष्ट
13. भद्र
14. दूसरा
15. होशियार
16. जानवर
17. अनुशासन
18. चिल्लाना
19. स्कूल
20. व्यवहार
21. शरारती
22. लाईन
वाक्यों को शुद्ध कीजिए :
1. एक बार भारी वर्षा हुआ।
उत्तर:
एक बार भारी वर्षा हुआ।
2. दूसरों के झगड़ना अच्छी बात नहीं ।
उत्तर:
दूसरों के झगड़ना अच्छी बात नहीं ।
3. आदमी के आचरण सभ्य होता है ।
उत्तर:
आदमी के आचरण सभ्य होता है ।
4. उसका पिछला टाँग टूट गया।
उत्तर:
उसका पिछला टाँग टूट गया।
5. वह मेरा ओर देखने लगा।
उत्तर:
वह मेरा ओर देखने लगा।

6. तुमं तो होशियार है ।
उत्तर:
तुमं तो होशियार है ।
7. यह तुम्हारे काम है ।
उत्तर:
ह तुम्हारे काम है ।
8. वह अपने बच्चों से कहा।
उत्तर:
वह अपने बच्चों से कहा।
9. नानी समझाई।
उत्तर:
नानी समझाई।
10. किसका दिल न दुखे, इस ओर सावधान रहना ।
उत्तर:
किसका दिल न दुखे, इस ओर सावधान रहना।
वचन बदलिए :
अव्ययों से रिक्त स्थान भरिए :
1. वे ……………….. कुएँ कें मालिक बने हुए थे ।
उत्तर: माना
2. कुएँ में पानी भर गया ……………….. वे बाहर आने लगा।
उत्तर: और
3. बांहर की खुली दुनिया उन ……………….. थी।
उत्तर: के सामनें
4. वे ……………….. उछलने लगे।
उत्तर: इधर-उधर

5. ……………….. एक गाड़ी आ गई ।
उत्तर: अचानक
6. वह पहिए ……………….. जा गिरा।
उत्तर: के नीचे
7. तीसरा ……………….. बड़ा घमंडी था।
उत्तर: भी
8. ……………….. एक साइकिल सर्र से निकल गई।
उत्तर: तभी उधर से
9. मेंढ़की अपने बच्चों ……………….. यह सब देख रही थी।
उत्तर: के साथ
10. हम घर से ……………….. निकलें तो क्या करें।
उत्तर: बाहर
11. ……………….. हमें स्कूल में कई बातें सिखाई जाती हैं।
उत्तर: इसीलिए

12. तुम ……………….. होशियार हो।
उत्तर: तो
13. ……………….. आचरण आचरण सभ्य होता है ।
उत्तर: क्योंकि
३० शब्दों / दो-तीन वाक्यों में उत्तर दीजिए:
प्रश्न 1.
भारी बर्षा हुई तो क्या हुआ ?
उत्तर:
भारी वर्षा हुई तो कुएँ में पानी भर गया और बाहर आने लगा । पानी की उस बाढ़ में वे सभी मेंढक बाहर निकल आंए। बाहर की खुली दुनिया देखकर मेंढक खुशी से फूल उठे ।
प्रश्न 2.
बाहर निकले मेंठकों की क्या हालत हुई ?
उत्तर:
बाहर निकले मेंढकों में से पहला शरारती मेंढक ऐंठकर सड़क पर उछलते समय पहिए के नीचे आ गया पर बच गया । लम्बा कूदने वाला दूसरा मेंढक छिप कर साँप के मुँह से बच गया । तीसरा घमंडी मेंढक एक साइकिल के नीचे आ गया तो उसकी पिछ्छली टाँग टूट गई ।
प्रश्न 3.
आदमी घर से निकले तो पहले क्या करें ?
उत्तर:
आदमी घर से निकले तो पहली बात है कि हम अपने को काबू में रखे। अपने को बड़ा न मानें; विनयी हों; गुस्सा न करें । घमंड न करें ।
प्रश्न 4.
कैसा व्यवहार अशिष्ट समझा जाता है ?
उत्तर:
हमारा जो व्यवहार दूसरों को बुरा लगे, उनकी असुविधा हो, जिससे उनका दिल दुंखे, वह अशिष्ट व्यवहार समझा जाता है । दूसरों से झगड़ना, नाराज होना, गाली करना, चिल्लाना, जिद करना, बिना पूछ दूसरों की चीज छूना और दूसरों के काम में दखल देना आदि अशिष्ट व्यवहर समझा जाता है ।

प्रश्न 5.
शिष्टता किन-किन कामों में होती है ?
उत्तर:
जोर से न बोलना, गुरुजनों का सम्मान करना,सहपाठियों से मित्रभाव रखना, छोटों को स्नेह करना, अपनी बारी का इंतजार करना, अनुशासन मानना, लाइन में चलना, स्कूल के नियम मानना, ट्रैफिक के कानून न तोड़ना आदि कामों में शिष्टता होती है।
प्रश्न 6.
आदमी के दोस्त या दुश्मन कैसे बनते हैं ?
उत्तर:
एक आदमी अच्छा बर्ताव करता है तो लोग उसका दोस्त बनते है। एक आदमी बुऱा आवर्रण करता है तो लोग उसका दुश्मन बनते हैं । हम अपंने सभ्य आचरण द्वारा सारे विश्व को मित्र बना सकते हैं।
प्रश्न 7.
अनुपम नानी के साथ कैसा व्यवहार करता है ?
उत्तर:
अनुपम के घर पर जब उसकी नानी आती हैं, तब अनुपम बहुत खुश होता है । वह नानी के पाँव छूता है । उसके व्यवहार से नानी बहुत खुश होती हैं।
प्रश्न 8.
मेंढकों का स्वभाव कैसा था ?
उत्तर:
मेंढक कुएँ में दिन-रात उछलते कूदते थे और टर्र-टर्र करते थे । वे अपने को कुएँ के मालिक समझते थे और बहुत शरारती हो गए थे ।
प्रश्न 9.
मेंबकी ने अपने बच्चों से सम्भलकर चलने को क्यों कहा ?
उत्तर:
मेंढकी ने अपने बच्चों को सीख दी कि बाहर निकलते समय अपने को बचाना सीखना चाहिए। संभलकर चलना चाहिए । आफत से बचना चाहिए ।
प्रश्न 10.
आदमी के बच्चे को क्या सीखना चाहिए ?
उत्तर:
आदमी के बच्चे को दूसरे से मिलजुलकर रहना चाहिए । उसे घर में माँ – बाँप की बात मानना, भाई – बहनों के साथ मिलकर रहना, स्कूल में मित्रों के साथ अच्छा बतार्व करना आदि व्यवहार सीखना चाहिए ।
प्रश्न 11.
अनुपम की नानी क्यों खुश हुई?
उत्तर:
अनुपम की नानी उनके घर भुवनेश्वर आई। अनुपम बहुत खुश हुआ और नानी के पाँव छुए। इससे नानी बहुत खुश हुए।
प्रश्न 12.
कौन बहुत शरारती हो गए थे ?
उत्तर:
अनुपम की नानी के गाँव में एक बहुत बड़ा कुआँ था। उसमें चार-छह मेंढ़क उछलते-कुदते थे और अपने को कुएँ के मालिक समझते थे। वे बहुत शरारती हो गए थे।
प्रश्न 13.
अनुपम को स्कूल में क्या सिखाया जाता है ?
उत्तर:
अनुपम को स्कूल में कई बातें सिखाई जाती हैं। बड़ों और गुरुजनों का सम्मान करना, सहपाठियों से सौहार्द भाव रखना, छोटों को स्नेह करना, स्कूल के नियम मानना आदि बातें सि खाई जाती हैं।

प्रश्न 14.
सारा विश्व कैसे मित्र बन सकता है ?
उत्तर:
आदमी का आचरण सभ्य होता है। सभ्य आचरण से सारा विश्व आदमी का मित्र बन सकता है।
विचार-बिन्दु
हम समाज में रहते हैं। घर से बाहर निकलते हैं तो दूसरों के साथ मिलना पड़ता है । उनके पास काम भी रहता है । इसलिए हम मिलजुल कर रहना सीखें । दूसरों से अच्छा वर्ताब करें । भाईचारा बढ़ाएँ । हम कभी गर्व न करें । समाज का नियम मानें । तब हम समाज में शांति से रह सकेंगे ।
शब्दार्थ
नानी- माँ की माँ (ମାଆଙ୍କ ମାଆ, ଆଈ) ।
पाँव छूना -पैर छूना (ପାଦ ଛୁଇଁବା) ।
उछलना-बेग सहित ऊपदु उठना-(ଜୋର୍ରେ ଉପରକୁ ଉଠିବା) ।
उधमी – उत्पाती – (ଉତ୍ପାତିଆ, ଉପଦ୍ରବୀ) ।
शरारती-दुष्ट
फुदकना-उछलकर कूदना (ଉପରକୁ ଡେଇଁବା) ।
खुशी से फूल उठना- बहुत खुश होना- (ବହୁତ ଖୁସି ହେବା)
ऐंठना-गर्व करना (ଆଁ କରିବା) ।
बजरंगबली-हनुमान जैसा दृढ़ शरीर वाला
मुँह बाना-ले – (ହନୁମାନଙ୍କ ଭଳି ଦୃଢ଼ ଶରୀର)
जाने की इच्छा करना – (ନେଇ ନେବାକୁ ଚାହିଁବା)
मुँह फैलाना – (ଆଁ କରିବା) ।
बराबरी – मुकाबला – (ମୁକାବିଲା କରିବା) ।
ढूह-मिट्टी का टीला – (ମାଟି କୁଦ) ।
आफत-विपत्ति (ବିପଦ) ।
काबू-वश (ନିୟନ୍ତ୍ରଣ) ।
बर्ताव-व्यवहार (ବ୍ୟବହାର) ।

घमंड-गर्व (ଗର୍ବ)
नाराज-रुष्ट (ରାଗିବା)
अशिष्ट-अभद्र (ଅଭଦ୍ର)।
आदत-अभ्यास (ଅଭ୍ୟାସ) ।
सौहार्द-मित्रता (ମିତ୍ରତା) ।
इंतजार-प्रतीक्षा (ଅପେକ୍ଷା) ।
अनुशासन-नियम पालन (ନିୟମ ମାନିବା) ।
कानून-नियम (ନିୟମ) ।
होशियार-बुद्धिमान (ବୁଦ୍ଧିମାନ) ।
दोस्त-मित्र (ସାଙ୍ଗ)
दुश्मन-शत्रु (ଶତ୍ରୁ)
जानवंर-पश – (ପଶୁ) ।
सारांश
अनुपम भुवनेश्थर में रहता है । एक बार उसकी नानी उनके घर आई ।अनुपम उनके पाँव हुए। नानी खुश हुई । रात को नानी ने एक कहानी सुनाई । नानी के गाँव के एक बड़े कुएँ में चार-छह मेंढ़क रहते थें। वे अपने को कुएँ के मालिक मानते थे । इसलिए शरारती करते थे ।
एक बार बहुत वर्षा हुई तो कुएँ में पानी भरकर बाहर आने लगा । पानी के साथ मेंढ़क भी कुएँ से बाहर आ गए। बाहरी दुनिया देखकर वे खुश हुए।
उनमें से सबसे शरारती मेंढ़क सड़क पर फुदकते समय एक गाड़ी के पहिए के नीचे आ गया, पर बच गया। अपने को सबसे ताकतवर समझने वाले दूसरे मेंढ़क की ओर एक साँप पुँह खोले आ गया, परछिपकर वह भी बच गया। गर्व करने वाले तीसरे मेंढ़क की साइकिल के धक्के से पिछली टाँगटूट गई ।
पास की एक दूह पर से एक मेंढ़की ने यह सब देखकर अपने बच्चों को चेतावनी दी की बाहर निकलते समय अपने को बचाना चाहिए।
अनुपम ने नानी से पूछ्ठा कि बाहर निकलते समय हम क्या करें ?
नानी नें कहा-पहले अपने को काबू में रखो। गर्व न करो । विनयी बनो । किसी पर गुस्सा न करो ।
समाज में सबसे मिलजुलकर रहो। माँ-बापकी बात मानो । घर में भाई-बहनों के साथ, स्कूल में मित्रों के साथ अच्छा बर्ताव करो । किसी के दिल को दु:ख न पहुँचाओ । झगड़ा करना, गाली देना, जिद करना, बिना पूछ्ठे दूसरों की चीज छूना, दूसरों के काम में दखल देना आदि बुरी आदतों से बचना चाहिए।

अनुपम ने बताया कि हमारे स्कूल में जोर से न बोलना, बडों का आदर करना, सहपाठियों से मित्रता का भाव रखना, छोटों को स्सेह करना, अपनी बारी तक प्रतीक्षा करना, लाईन में जाना, स्कूल के नियम मानना, ट्रैफिक के कानून मानना आदि बातें सिखाई जाती हैं ।
नानी बोली कि अच्छे बर्ताव से लोग मित्र बनते हैं और बुरे बर्ताव से दुश्मन बनते हैं । जिसका आचरण अच्छा होता है, सारा विश्च उसका मित्र बन जाता है ।
ସାରାଂଶ
ଅନୁପମ ଭୁବନେଶ୍ଵରରେ ରହେ । ଥରେ ତା’ ଆଈ ତାଙ୍କ ଘରକୁ ଆସିଲେ । ଅନୁପମ ତାଙ୍କ ପାଦ ଛୁଇଁ ପ୍ରଣାମ କଲା । ଆଈ ଖୁସି ହୋଇଗଲେ । ରାତିରେ ଆଈ ଗପଟିଏ କହିଲେ ।
ଆଈଙ୍କ ଗାଁରେ ଗୋଟିଏ ବଡ଼ କୂଅରେ ଚାରି-ଛଅଟି ବେଙ୍ଗ ରହୁଥିଲେ । ସେମାନେ ନିଜକୁ କୂଅର ମାଲିକ ଭାବୁଥିଲେ । ସେଥିପାଇଁ ବଡ଼ ଦୁଷ୍ଟାମି କରୁଥିଲେ ।
ଥରେ ବହୁତ ବର୍ଷା ହେବାରୁ କୂଅରେ ପାଣି ଭର୍ତ୍ତି ହୋଇ ବାହାରକୁ ବାହାରି ଆସିଲା । ପାଣି ସହିତ ବେଙ୍ଗମାନେ ମଧ୍ୟ କୂଅ ବାହାରକୁ ଚାଲି ଆସିଲେ । ବାହାର ଦୁନିଆ ଦେଖି ସେମାନେ ଖୁସି
ହୋଇଗଲେ । ସେମାନଙ୍କ ମଧ୍ୟରୁ ସବୁଠାରୁ ଅଧିକ ଦୁଷ୍ଟ ବେଙ୍ଗ ସଡ଼କ ଉପରେ ଡେଉଁଥିବା ସମୟରେ ଗୋଟିଏ ଗାଡ଼ିର ଚକ ତଳେ ପଡ଼ିଗଲା । କିନ୍ତୁ ସୌଭାଗ୍ୟବଶତଃ ବଞ୍ଚିଗଲା । ନିଜକୁ ସବୁଠାରୁ ବଳୁଆ ଭାବୁଥୁବା ଆଉ ଗୋଟିଏ ବେଙ୍ଗ ଆଡ଼କୁ ସାପଟିଏ ଆଁ କରି ମାଡ଼ି ଆସିଲା । ସେ କିନ୍ତୁ ଲୁଚି ଯାଇ ବଞ୍ଚିଗଲା । ବହୁତ ଗର୍ବ କରୁଥିବା ତୃତୀୟ ବେଙ୍ଗଟିର ସାଇକେଲ ଧକ୍କାରେ ଗୋଡ଼ ଭାଙ୍ଗିଗଲା ।
ପାଖରେ ମାଟିକୁଦ ଉପରେ ଗୋଟିଏ ବେଙ୍ଗୁଲୀ ଏ ସବୁ ଦେଖି ତା’ ପିଲାମାନଙ୍କୁ ଚେତେଇ ଦେଲା ଯେ ବାହାରକୁ ବାହାରିବା ସମୟରେ ନିଜକୁ ରକ୍ଷା କରିବା ଆବଶ୍ୟକ ।
ଅନୁପମ ଆଈଙ୍କୁ ପଚାରିଲା ଯେ ଆମେ ବାହାରକୁ ବାହାରିବା ସମୟରେ କ’ଣ କରିବୁ ?
ଆଈ ବୁଝାଇଦେଲେ – ଆଗ ନିଜକୁ ନିୟନ୍ତ୍ରଣରେ ରଖିବ, ଗର୍ବ କରିବନି । ବିନୟୀ ହେବ । କାହାରି ଉପରେ ରାଗିବ ନାହିଁ ।
ସମାଜରେ ସମସ୍ତେ ମିଳିମିଶି ଚଳିବ । ବାପା ମାଆଙ୍କ କଥା ମାନିବ । ଘରେ ଭାଇ-ଭଉଣୀଙ୍କ ସହିତ ଓ ସ୍କୁଲରେ ସହପାଠୀମାନଙ୍କ ସହିତ ଭଲ ବ୍ୟବହାର କରିବ । କାହାରି ମନରେ କଷ୍ଟ ଦେବ ନାହିଁ । ଝଗଡ଼ା କରିବା, ଗାଳି ଦେବା, ଜିଦ୍ କରିବା, ନ ପଚାରି କାହା ଜିନିଷରେ ହାତ ଦେବା, ଅନ୍ୟର କାମରେ ଅଯଥାରେ ମୁଣ୍ଡ ପୂରେଇବା ଭଳି ଖରାପ ଅଭ୍ୟାସଠାରୁ ଦୂରେଇ ରହିବ ।
ଅନୁପମ କହିଲା ଯେ ଆମ ସ୍କୁଲରେ ଜୋର୍ରେ ନ କହିବା, ଗୁରୁଜନମାନଙ୍କୁ ସମ୍ମାନ ଦେବା, ସହପାଠୀମାନଙ୍କ ସହ ମିତ୍ରତା ରକ୍ଷା କରିବା, ସାନମାନଙ୍କୁ ସ୍ନେହ କରିବା, ନିଜ ପାଳି ନ ଆସିବା ପର୍ଯ୍ୟନ୍ତ ଅପେକ୍ଷା କରିବା, ଲାଇନରେ ଯିବା, ସ୍କୁଲ୍ର ନିୟମ ମାନିବା, ଟ୍ରାଫିକ୍ ନିୟମ ମାନିବା ଆଦି ଅନେକ କଥା ଶିଖାଯାଉଛି ।
ଆଈ କହିଲେ ଭଲ ବ୍ୟବହାର କଲେ ଲୋକ ମିତ୍ର ହୋଇ ଯାଆନ୍ତି ଓ ଖରାପ ବ୍ୟବହାର କଲେ ଲୋକ ଶତ୍ରୁ ହୋଇଯାଆନ୍ତି । ଯାହାର ବ୍ୟବହାର ଭଲ ହୁଏ, ସାରା ବିଶ୍ୱ ତା’ର ମିତ୍ର ହୋଇଯାଏ ।
![]()

![]()
![]()
![]()