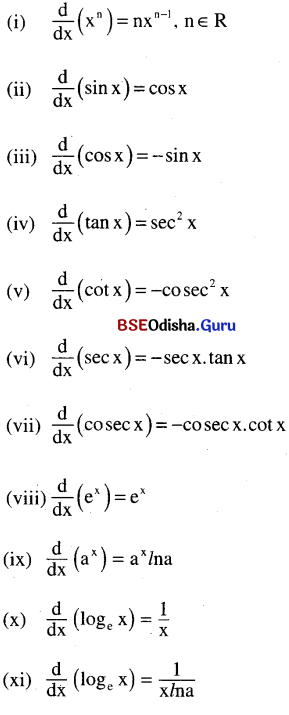Odisha State Board CHSE Odisha Class 11 Math Notes Chapter 14 Limit and Differentiation will enable students to study smartly.
CHSE Odisha 11th Class Math Notes Chapter 14 Limit and Differentiation
Limit Of A Function:
A real number ‘l’ is called the limit of the function f(x) as x tends to ‘a’ if for every ∈ > 0, there exist δ > 0 such that |f(x) – l| < ∈ whenever |x – a| < δ
We write \(\lim _{x \rightarrow a}\) f(x) = l
Left and right hand limit:
Left hand limit of f(x) as x → a is:
\(\lim _{x \rightarrow a-}\) f(x) = \(\lim _{x \rightarrow 0}\) f(a – h)
Right hand limit of f(x) as x → a is:
\(\lim _{x \rightarrow a+}\) f(x) = \(\lim _{h \rightarrow 0}\) f(a + h)
Existance of limit:
\(\lim _{x \rightarrow a}\) f(x) exists if it is unique, irrespective of any type of approach i.e if LHL = RHL. i.e if \(\lim _{x \rightarrow a-}\) f(x) = \(\lim _{x \rightarrow a+}\) f(x)
Indeterminate forms:
The forms : \(\frac{0}{0}, \frac{\infty}{\infty}\), ∞ – ∞, 0 × ∞, 0°, ∞° and 1∞ are called indeterminate forms in mathematics.
![]()
Properties of limit:
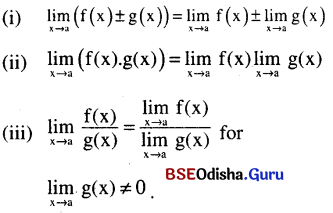
Some standard limits:
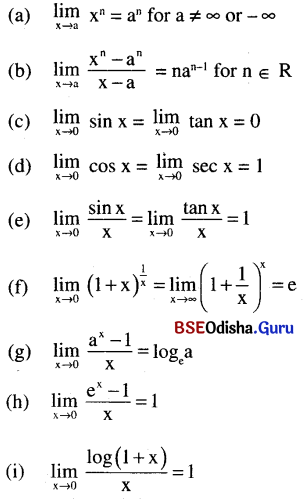
Limit At Infinite And Infinite Limits:
(a) We write \(\lim _{x \rightarrow a}\) f(x) = ∞ if for a given m > 0, there exists δ > 0 such that |x – a| < δ ⇒ f(x) > m for large m.
(b) We write \(\lim _{x \rightarrow a}\) f(x) = -∞ if for a given m < 0, there exists δ > 0 such that |x – a| < δ ⇒ f(x) < m for large |m|.
(c) \(\lim _{x \rightarrow ∞}\) f(x) = l if for given ∈ > 0 there exists k > 0 such that x > k ⇒ |f(x) – l| < ∈ for large x.
(d) \(\lim _{x \rightarrow -∞}\) f(x) = l if for given ∈ > 0, there exists k < 0 such that x < k ⇒ |f(x) – l| < ∈ for large |k|.
(e) We write \(\lim _{x \rightarrow ∞}\) f(x) = ∞ if for m > 0 there exists k > 0 such that x > x ⇒ f(x) > m for large m.
(f) \(\lim _{x \rightarrow ∞}\) xn = \(\left\{\begin{array}{lll}
\infty & \text { if } & n>0 \\
1 & \text { if } & n=0 \\
0 & \text { if } & n<0
\end{array}\right.\)
(g) \(\lim _{n \rightarrow ∞}\) xn = \(\left\{\begin{array}{ccc}
0 & \text { if } & |x|<1 \\
1 & \text { if } & x=1 \\
\infty & \text { for } & x>1
\end{array}\right.\) does not exist for x ≤ -1.
![]()
Some useful expansions:

Techniques to find limit:
If \(\lim _{x \rightarrow a}\) f(x), does not take any indeterminate form then get the limit just by putting x = a(provided that the limit is finite).
If \(\lim _{x \rightarrow a}\) f(x) takes any indeterminate form then either use formula or simplify to remove the indeterminate form before finding limit.
The indeterminate form can be removed by using.
- Factorisation
- Rationalisation
- Expand formula or any other techniques.
Differentiation:
(a) Let y = f(x) is a function.
The derivative (differential coefficient) of y or f(x) with respect to x is \(\frac{d y}{d x}\) = f'(x) = \(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)
(b) The differentiation of y = f(x) at x = a is \(\left.\frac{\mathrm{dy}}{\mathrm{dx}}\right]_{\mathrm{x}=\mathrm{a}}\) = f'(a) = \(\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}\)
(c) Differentiability of y = f(x) at x = a:

(d) Geometrical meaning of differentiation:
Geometrically f'(x) or \(\frac{d y}{d x}\) represents the slope of tangent to y = f(x) at any point P(x, y)
⇒ Slope of tangent to y = f(x) at A(x1, y1) = \(\left.\frac{d y}{d x}\right]_{\left(x_1, y_1\right)}\)
(e) Some rules of differentiation:

![]()
(f) Differentiation of some standard functions: