Odisha State Board Elements of Mathematics Class 11 Solutions CHSE Odisha Chapter 11 Straight Lines Ex 11(a) Textbook Exercise Questions and Answers.
CHSE Odisha Class 11 Math Solutions Chapter 11 Straight Lines Exercise 11(a)
Question 1.
Find the distance between the following pairs of points.
(i) (3, 4), (-2, 1);
Solution:
Distance between points (3, 4) and (-2, 1) is
\(\sqrt{(3+2)^2+(4-1)^2}=\sqrt{25+9}=\sqrt{34}\)
(ii) (-1, 0), (5, 3)
Solution:
The distance between the points (-1, 0) and (5, 3) is
\(\sqrt{(-1-5)^2+(0-3)^2}\)
= \(\sqrt{36+9}=\sqrt{45}=3 \sqrt{5}\)
Question 2.
If the distance between points (3, a) and (6, 1) is 5, find the value of a.
Solution:
Distance between the points. (3, a) and (6, 1) is
\(\sqrt{(3-6)^2+(a-1)^2}=\sqrt{9+(a-1)^2}\)
∴ \(\sqrt{9+(a-1)^2}=5\)
or, 9 + (a – 1)2 = 25
or, (a – 1)2 = 16
or, a – 1 = ± 4
a = 1 ± 4 = 5 or, – 3
Question 3.
Find the coordinate of the points which divides the line segment joining the points A (4, 6), B (-3, 1) in the ratio 2: 3 internally. Find also the coordinates of the point which divides \(\overline{\mathbf{A B}}\) in the same ratio externally.
Solution:


Question 4.
Find the coordinates of the mid-point of the following pairs of points.
(i) (-7, 3), (8, -4);
Solution:
Mid-point of the line segment joining the points (-7, 3) and (8, -4) are \(\left(\frac{-7+8}{2}, \frac{3-4}{2}\right)=\left(\frac{1}{2},-\frac{1}{2}\right)\)
(ii) (\(\frac{3}{4}\), -2), (\(\frac{-5}{2}\), 1)
Solution:
Mid-point of the line segment joining the points. (\(\frac{3}{4}\), -2) and (\(\frac{-5}{2}\), 1) is,
\(\left(\frac{\frac{3}{4}-\frac{5}{2}}{2}, \frac{-2+1}{2}\right)=\left(\frac{-7}{8}, \frac{-1}{2}\right)\)
![]()
Question 5.
Find the area of the triangle whose vertices are (1, 2), (3, 4) (\(\frac{1}{2}\), \(\frac{1}{4}\))
Solution:
Area of the triangle whose vertices are (1, 2), (3, 4) and (\(\frac{1}{2}\), \(\frac{1}{4}\)) is
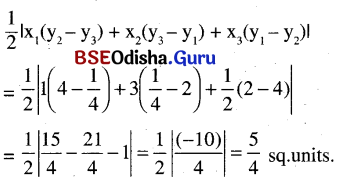
Question 6.
If the area of the triangle with vertices (0, 0), (1, 0), (0, a) is 10 units, find the value of a.
Solution:
Area of the triangle with vertices (0, 0),(1,0), (0, a), is \(\frac{1}{2}\) × 1 × a = \(\frac{a}{2}\)
∴ \(\frac{a}{2}\) = 10 or a = 20
Question 7.
Find the value of a so that the points (1, 4), (2, 7), (3, a) are collinear.
Solution:
As points (1, 4), (2, 7), (3, a) are collinear, we have the area of the triangle with vertices (1, 4), (2, 7), and (3, a) is zero.
∴ \(\frac{1}{2}\) {1(7 – a) + 2(a – 4) + 3 (4 – 7)} = 0
or, 7 – a + 2a – 8 + 12 – 21 =0
⇒ a = 10
Question 8.
Find the slope of the lines whose inclinations are given.
(i) 30°
Solution:
The slope of the line whose inclination is 30°.
tan 30° = \(\frac{1}{\sqrt{3}}\)
(ii) 45°
Solution:
Slope = tan 45° = +1
(iii) 60°
Solution:
Slope = tan 60° = √3
(iv) 135°
Solution:
Slope = tan 135° = – 1
Question 9.
Find the inclination of the lines whose slopes are given below.
(i) \(\frac{1}{\sqrt{3}}\)
Solution:
The slope of the line is \(\frac{1}{\sqrt{3}}\)
∴ tan θ = \(\frac{1}{\sqrt{3}}\) or, θ = 30°
∴ The inclination of the line is 30°
(ii) 1
Solution:
Slope = 1 = tan 45°
∴ The inclination of the line is 45°.
(iii) √3
Solution:
Slope = √3 = tan 60° ∴ θ = 60°
∴ Inclination = 60°
(iv) – 1
Solution:
Slope = – 1 = tan 135°
∴ Inclination = 135°
Question 10.
Find the angle between the pair of lines whose slopes are ;
(i) \(\frac{1}{\sqrt{3}}\), 1
Solution:

(ii) √3, -1
Solution:
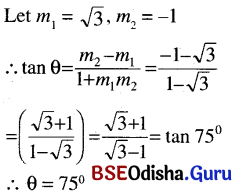
Question 11.
(a) Show that the points (0, -1), (-2, 3), (6, 7), and (8, 3) are vertices of a rectangle.
Solution:
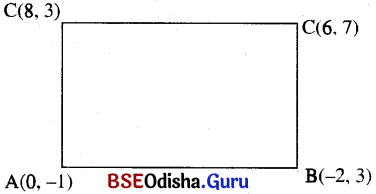
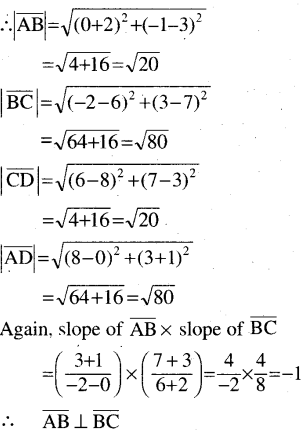
∴ The opposite sides are equal and two consecutive sides are perpendicular. So it is a rectangle.
(b) Show that the points (1, 1), (-1, -1), and (-√3, √3) are the vertices of an equilateral triangle.
Solution:
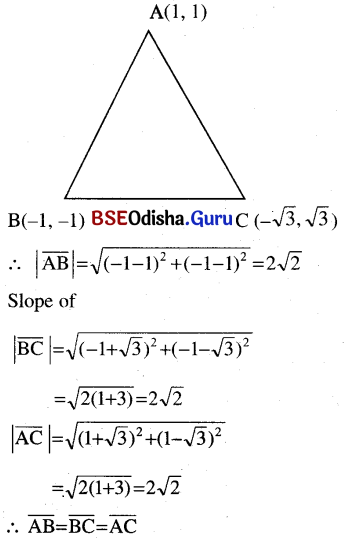
![]()
Question 12.
Find the coordinates of the point P(x, y) which is equidistant from (0, 0), (32, 10), and (42, 0).
Solution:

Question 13.
If the points (x, y) are equidistant from the points (a + b, b – a) and (a – b, a + b), prove that bx = ay.

Question 14.
The coordinate of the vertices of a triangle are (α1, β1), (α2, β2), and (α3, β3). Prove that the coordinates of its centroid is \(\left(\frac{\alpha_1+\alpha_2+\alpha_3}{3}, \frac{\beta_1+\beta_2+\beta_3}{3}\right)\)
Solution:
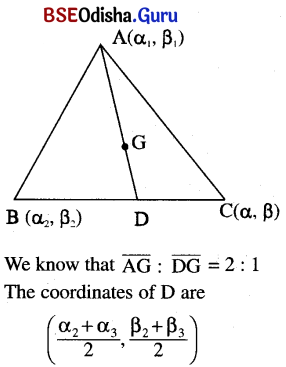

Question 15.
Two vertices of a triangle are (0, -4) and (6, 0). If the medians meet at the point (2, 0), find the coordinates of the third vertex.
Solution:
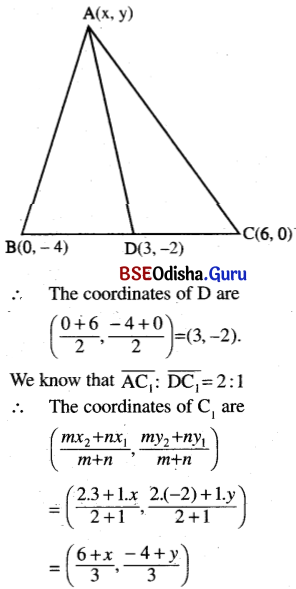
∴ \(\frac{6+x}{3}\) = 2, \(\frac{-4+y}{3}\) = 0
⇒ x = 0, y = 4
∴ The coordinates of the 3rd vertex are (0, 4).
Question 16.
If the point (0, 4) divides the line segment joining(-4, 10) and (2, 1) internally, find the point which divides it externally in these same ratios.
Solution:

Question 17.
Find the ratios in which the line segment joining (-2, -3) arid (5, 4) is divided by the coordinate axes and hence find the coordinates of these points.
Solution:
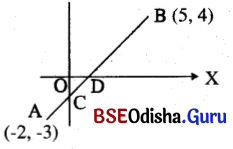

![]()
Question 18.
In a triangle, one of the vertices is at (2, 5) and the centroid of the triangle is at (-1, 1). Find the coordinates of the midpoint of the side opposite to the given angular point.
Solution:
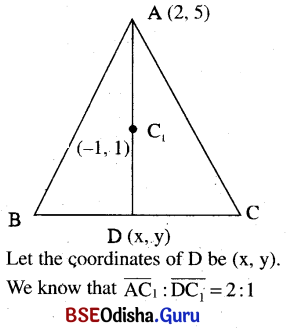
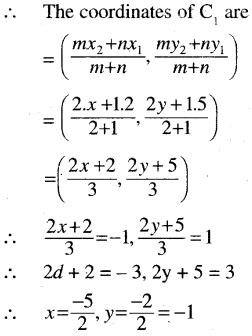
Question 19.
Find the coordinates of the vertices of a triangle whose sides have midpoints at (2, 1), (-1, 3), and (-2, 5).
Solution:

∴ x2 + x3 – 4 or, x2 – 4 – 3 = 1
∴ x1 = – 4 – x2 = -4 – 1 = -5
Similarly y1 + y2 + y3 = 5 + 1 + 3 = 9
As y1 + y2 = 10
we have y3 = 9 – 10 = – 1
Again y1 + y3 = 6
or, y1 = 6 – y3 = 6 + 1 = 7
and y2 = 10 – y1 = 10 – 7 = 3
∴ The coordinates of A, B, and C are (-5, 7), (1, 3), and (3, -1).
Question 20.
If the vertices of a triangle have their coordinates given by rational numbers, prove that the triangle cannot be equilateral.
Solution:
Let us choose the contradiction method. Let the triangle is equilateral if the co¬ ordinate of the vertices is rational numbers.
Let ABC be an equilateral triangle with vertices A (a, 0), B (a, 0), and C (b, c) where a, b, c are rational.
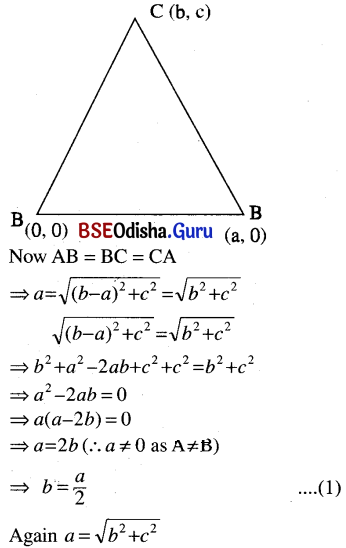
⇒ a2 = b2 + c2 = \(\frac{a^2}{4}\) + c2
⇒ c2 = a2 – \(\frac{a^2}{4}\) = \(\frac{3a^2}{4}\) ⇒ c = \(\frac{\sqrt{3}}{2}\) a ….(2)
Now b = \(\frac{a}{2}\), c = \(\frac{\sqrt{3}}{2}\) a
If a is rational then b is rational but c is irrational, i.e., the coordinates of the vertices are not rational, which contradicts the assumption.
Hence assumption is wrong.
So the triangle cannot be equilateral if the coordinate of the vertices is rational numbers.
Question 21.
Prove that the area of any triangle is equal to four times the area of the triangle formed by joining the midpoints of its sides.
Solution:

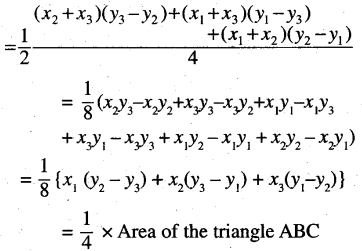
∴ The area of triangle ABC is four times the area of triangle DEF. (Proved)
Question 22.
Find the condition that the point (x, y) may lie on the line joining (1, 2) and (5, -3).
Solution:
![]()
∴ As points A, B, and C are collinear, we have the area of the triangle ABC as 0.
∴ \(\frac{1}{2}\) {1(-3 – y) + 5(y – 2) + x(2 + 3)} = 0
or, – 3 – y + 5y – 10 + 5x = 0
or, 5x + 4y = 13
![]()
Question 23.
Show that the three distinct points (a2, a), (b2, b), and (c2, c) can never be collinear.
Solution:
Area of the triangle with vertices (a2, a), (b2, b) , and (c2, c) is
\(\frac{1}{2}\) {a2(b – c) + b2(c – a) c2(a – b)}
= (a – b)(b – c)(a – c)
which is never equal to zero except when a = b = c, hence the points are not collinear.
Question 24.
If A, B, and C are points (-1, 2), (3, 1), and (-2, -3) respectively, then show that the points which divide BC, CA, and AB in the ratios (1: 3), (4: 3) and (-9: 4) respectively are collinear.
Solution:
Let the points P, Q, and R divides \(\overline{\mathrm{BC}}\), \(\overline{\mathrm{CA}}\), in \(\overline{\mathrm{AB}}\) the ratio 1: 3, 4: 3 and -9: 4
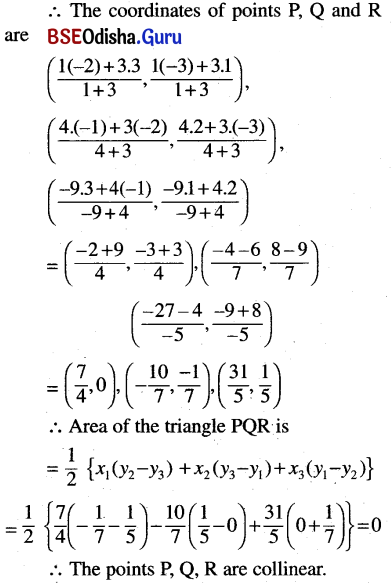
Question 25.
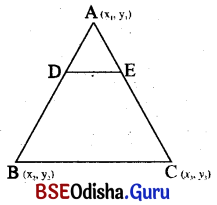
Prove analytically :
(a) The line segment joining the midpoints of two sides of a triangle is parallel to the third and half of its length.
Solution:
Let the coordinates of the triangle ABC be (x1, y1), (x2, y2) and (x3, y3)
The points D and E are the midpoints of the sides \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{AC}}\)

(b) The altitudes of a triangle are concurrent.
Solution:
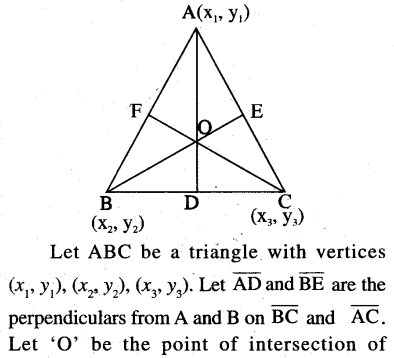


(c) The perpendicular bisectors of the sides of a triangle are concurrent.
Solution:



(d) An angle in a semicircle is a right angle.
Solution:

∴ The angle in a semicircle is a right angle. (Proved)
