CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Ex 7(f)

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 7 Continuity and Differentiability Ex 7(f) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Exercise 7(f)

Find derivatives of the following functions.
Question 1.
x^x
Solution:
Let y = x^x
Then In y = x . In x
⇒ \(\frac{d}{d x}\)(In y) = \(\frac{d}{d x}\)(x . In x)
⇒ \(\frac{1}{y}\)\(\frac{d y}{d x}\) = In x + x . \(\frac{1}{x}\) = In x + 1 = 1 + In x
⇒ \(\frac{d y}{d x}\) = y (1 + In x) = x^x (1 + In x) = x^x In (ex)

Question 2.
\(\left(1+\frac{1}{x}\right)^x\)
Solution:

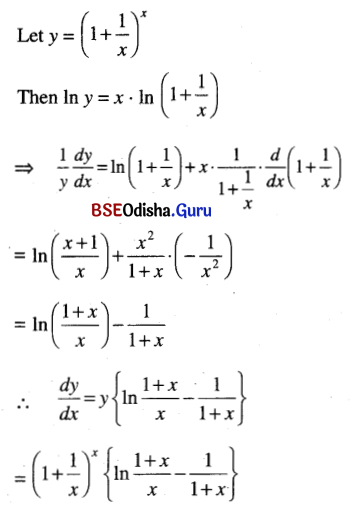
Question 3.
x^{sin x}
Solution:
y = x^{sin x}
⇒ In y = sin x . In x
⇒ \(\frac{1}{y}\)\(\frac{d y}{d x}\) = cos x In x + sin x . \(\frac{1}{x}\)
⇒ \(\frac{d y}{d x}\) = x^{sin x} (cos x . In x + \(\frac{\sin x}{x}\))

Question 4.
(log x)^{tan x}
Solution:
y = (log x)^{tan x}
⇒ log y = tan x . log (log x)
⇒ \(\frac{1}{y}\)\(\frac{d y}{d x}\) = sec² x log (log x) + tan x . \(\frac{1}{\log x}\) . \(\frac{1}{x}\)
⇒ \(\frac{d y}{d x}\) = (log x)^{tan x} {sec² x . log log x + \(\frac{\tan x}{x \log x}\)}

Question 5.
\(2^{\left(2^x\right)}\)
Solution:
y = \(2^{\left(2^x\right)}\)
⇒ In y = 2^x . In 2
⇒ \(\frac{1}{y}\)\(\frac{d y}{d x}\) = 2^x . In 2 . In 2
⇒ \(\frac{d y}{d x}\) = \(2^{\left(2^x\right)}\) . 2^x . (In 2)²

Question 6.
\((1+\sqrt{x})^{x^2}\)
Solution:

Question 7.
\(\left(\sin ^{-1} x\right)^{\sqrt{1-x^2}}\)
Solution:

Question 8.
\((\tan x)^{\log x^3}\)
Solution:

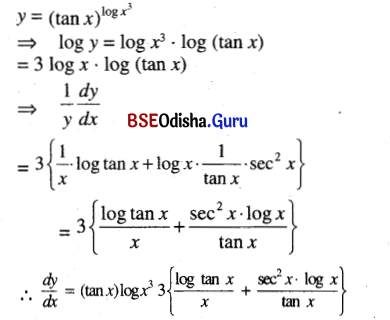
Question 9.
x^1/x + (sin x)^x
Solution:

Question 10.
(cos x)^x + x^{cos x}
Solution:

Question 11.
(x² + 1)^2/3 (3x + 1)^1/4 √x
Solution:

Question 12.
\(\frac{(x+1)(x+2)^2(x+3)^3}{(x-1)(x-2)^2(x-3)^3}\)
Solution:

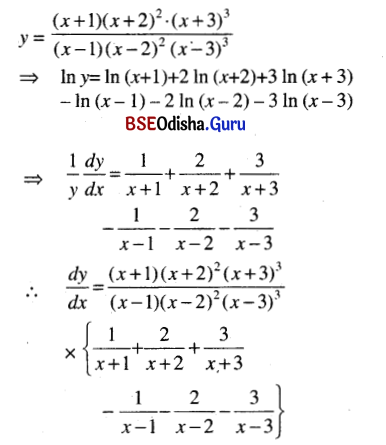
Question 13.
(sin x)^x \(\sqrt{\sin x}\left(1+x^2\right)^{\frac{1}{2}+x}\)
Solution:

Question 14.
(sec x + tan x)^{cot x}
Solution:
y = (sec x + tan x)^{cot x}
⇒ In y = cot x . In (sec x + tan x)
⇒ \(\frac{1}{y}\)\(\frac{d y}{d x}\) = -cosec² x . In (sec x + tan x) + cot x . \(\frac{1}{\sec x+\tan x}\) × (sec x . tan x + sec² x)
= -cosec² x . In (sec x + tan x) + cot x . sec x
∴ \(\frac{d y}{d x}\) = y {-cosec² x . In (sec x + tan x) + cosec x}
= (sec x + tan x)^{cot x} {cosec x – cosec² x . In (sec x + tan x)}

Question 15.
(2^√x)^1+√x
Solution: