CHSE Odisha Class 11 Math Solutions Chapter 14 Limit and Differentiation Ex 14(b)

Odisha State Board Elements of Mathematics Class 11 Solutions CHSE Odisha Chapter 14 Limit and Differentiation Ex 14(b) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 14 Limit and Differentiation Exercise 14(b)

Question 1.

Using the ε – δ definition prove that
(i) \(\lim _{x \rightarrow 0}\) (2x + 3) = 3
Solution:
Let f(x) = 2x + 3
Here a = 0 and ℓ = 3
Let ε be any positive real number however small it may be.
Now |f(x) – ℓ| =| 2x + 3 – 3| =|2x|
Thus |f(x) – ℓ| < ε whenever
|2x| < ε i.e |x| < \(\frac{\varepsilon}{2}\)
Then |f(x) – ℓ| < ε
whenever |x – 0| < δ
under the condition δ = \(\frac{\varepsilon}{2}\)
∴ \(\lim _{x \rightarrow 0}\) (2x + 3) = 3

(ii) \(\lim _{x \rightarrow 1}\) (2x – 1) = 1
Solution:
Here f(x) = 2x – 1, ℓ = l and a = 1
Now |f(x)| = | 2x – 1 – 1|
= |2x – 2| = 2|x – 1|
Thus |f(x) –  ℓ| < ε
whenever 2|x – 1| < ε
i,e. |x – 1| < \(\frac{\varepsilon}{2}\) put δ = \(\frac{\varepsilon}{2}\)
Then |f(x) – ℓ| < ε
whenever|x – 1| < δ
Hence \(\lim _{x \rightarrow 1}\) (2x – 1) = 1

(iii) \(\lim _{x \rightarrow -2}\) (3x + 8) = 2
Solution:
|(3x + 8) – 2|
= |3x + 6| = 3|x + 2|
So |3x + 8 – 2| < ε
whenever 3|x + 2| < ε
i.e. |x + 2| < \(\frac{\varepsilon}{3}\)
Hence |(3x + 8) – 2| < ε
whenever | x + 2 | < δ
∴ \(\lim _{x \rightarrow -2}\) (3x + 8) = 2

(iv) \(\lim _{x \rightarrow 3}\) (x² + 2x – 8) = 7
Solution:
|(x² + 2x – 8) – 7|
= |(x² + 2x – 15|
= |(x + 5) (x – 3)|
=| x + 5| | x – 3|
If |x – 3| < 1 then| x + 5| =| x – 3 + 8| < |x – 3| + 8 < 9
Thus |(x² + 2x – 8) – 7| < 9 |x – 3|
So |(x² + 2x – 8) – 7| < ε
whenever 9|x – 3| < ε
i.e.| x – 3| < \(\frac{\varepsilon}{9}\)
Choose δ = minimum of 1 and \(\frac{\varepsilon}{9}\)
Then |(x² + 2x – 8) – 7| < ε
whenever |x – 3| < δ
∴ \(\lim _{x \rightarrow 3}\) (x² + 2x – 8) = 7   (proved)

(v) \(\lim _{x \rightarrow 9}\) √x = 3
Solution:
|√x – 3| = |\(\frac{(\sqrt{x}-3)(\sqrt{x}+3)}{\sqrt{x}+3}\)|
= \(\frac{|x-9|}{|\sqrt{x}+3|}\)

(v) \(\lim _{x \rightarrow a}\) √x = √a, a > 0
Solution:

(vii) \(\lim _{x \rightarrow 1}\) |3x + 2| = 5
Solution:
When x → 1, 3x + 2 is always positive.
So |3x + 2| = 3x + 2
Thus ||3x + 2| -5| = |3x + 2 – 5|
= 3|x – 1|
∴ ||3x + 2| – 5 | < ε
whenever 3|x – 1| < ε
i.e. |x – 1| < \(\frac{\varepsilon}{3}\)
put δ = \(\frac{\varepsilon}{3}\)
Hence ||3x + 2| – 5| < ε
whenever |x – 1| < δ
∴ \(\lim _{x \rightarrow 1}\) |3x + 2| = 5

(viii) \(\lim _{x \rightarrow 2}\) |5x – 7| = 3
Solution:
Let any arbitrary ε > 0
then |5x – 7 – 3| < ε
If |5(x – 2)| < ε
i.e. if lx – 2| < \(\frac{\varepsilon}{5}\)
Choosing δ = \(\frac{\varepsilon}{5}\) we have
for any arbitrary ε > 0 there exists a δ > 0 depending on ε
Such that
|x – 2| < δ ⇒ |(5x – 7) – 3| < ε
∴ \(\lim _{x \rightarrow 2}\) |5x – 7| = 3

Question 2.
If \(\lim _{x \rightarrow a}\) f(x) = ℓ then prove that \(\lim _{x \rightarrow a}\) |f(x)| = | ℓ | Is the converse true ? Justify your answer with reasons.
Solution:
Let \(\lim _{x \rightarrow a}\) f(x) = ℓ
Then |f(x) – ℓ| < ε whenever |x – a| < δ
Now |f(x)| – ℓ| < |f(x) – ℓ| < ε
whenever |x – a| < δ
So \(\lim _{x \rightarrow a}\) |f(x)| = | ℓ |
The converse is not always true because | ℓ | = | -ℓ |
So \(\lim _{x \rightarrow a}\) f(x) = ℓ or -ℓ

Question 3.
(i) Prove that \(\lim _{x \rightarrow a}\) x = a
Solution:
Let ε is any positive number
Let f(x) = x
Now |f(x) – a| < ε
if |x – a| < ε
Choosing δ = ε we see that for each ε > 0 we find a δ > 0 depending on ε such that
|x – al < d ⇒ |f(x) – a| < ε
⇒ \(\lim _{x \rightarrow a}\) f(x) = a i,e. \(\lim _{x \rightarrow a}\) x = a

(ii) Using (i) and the laws of limits prove that \(\lim _{x \rightarrow a} x^n=a^n\), when n is an integer.
Solution:
Case-1: Let n > 0 and n ε z
Now \(\lim _{x \rightarrow a} x^n=\lim _{x \rightarrow a}\) (x. x. x…….. n factors)
= a. a …… n factors = aⁿ
Case-2: Let n = 0

(iii) Using (ii) and the laws of limits prove that \(\lim _{x \rightarrow a} \frac{x^n-a^n}{x-a}=n a^{n-1}\) where n is an integer.
Solution:

Case-3: n = 0  Hence the case is obvious

(iv) Using (iii), the laws of limits and assuming that \(\lim _{x \rightarrow a} \frac{1}{x^m}=a^{\frac{1}{m}}\) where m is a non-zero integer prove that for any rational number n, \(\lim _{x \rightarrow a} \frac{x^n-a^n}{x-a}=n a^{n-1}\).
Solution:

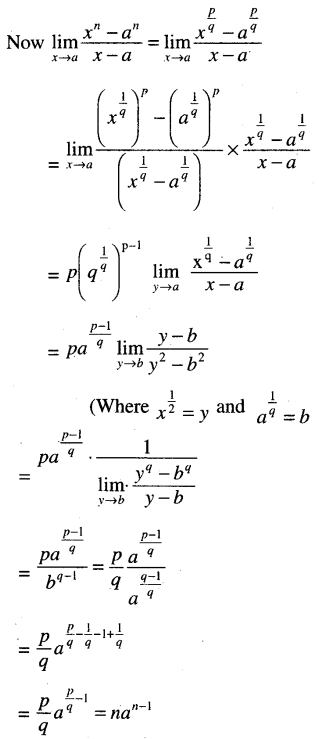
Question 4.
Evaluate the following :
(i) \(\lim _{x \rightarrow 1}\) (1 + 2x – 3x² + 4x³ – 5x⁴)
Solution:
\(\lim _{x \rightarrow 1}\) (1 + 2x – 3x² + 4x³ – 5x⁴)
= 1 + 2 – 3 + 4 – 5 = 7 – 8 = -1

(ii) \(\lim _{x \rightarrow 0}\) (3x² + 4x – 1)(x⁴ + 2x³ – 3x² + 5x + 2)
Solution:
\(\lim _{x \rightarrow 0}\) (3x² + 4x – 1)(x⁴ + 2x³ – 3x² + 5x + 2)
=(-1). 2 = -2

(iii) \(\lim _{x \rightarrow 2}\) \(\frac{x^2+3 x-9}{x+1}\)
Solution:
\(\lim _{x \rightarrow 2}\) \(\frac{x^2+3 x-9}{x+1}\)
\(\frac{2^2+3 \cdot 2-9}{2+1}=\frac{1}{3}\)

(iv) \(\lim _{x \rightarrow 3}\) \(\frac{x^2-9}{x-3}\)
Solution:
\(\lim _{x \rightarrow 3}\) \(\frac{x^2-9}{x-3}\)
= \(\lim _{x \rightarrow 3} \frac{(x-3)(x+3)}{x-3}\)
= \(\lim _{x \rightarrow 3}\) (x + 3) = 3 + 3 = 6

(v) \(\lim _{x \rightarrow 1} \frac{x^3-1}{x-1}\)
Solution:
\(\lim _{x \rightarrow 1} \frac{x^3-1}{x-1}\)
= \(\lim _{x \rightarrow 1} \frac{(x-1)\left(x^2+x+1\right)}{x-1}\)
= \(\lim _{x \rightarrow 3}\) (x² + x + 1)
= 1 + 1 +1 = 3

(vi) \(\lim _{x \rightarrow 2} \frac{x-2}{x^4-16}\)
Solution:

(vii) \(\lim _{x \rightarrow 2} \frac{x^3-8}{x^5-32}\)
Solution:

(viii) \(\lim _{x \rightarrow 3} \frac{x^2+2 x-15}{x^2-x-6}\)
Solution:

(ix) \(\lim _{x \rightarrow 0} \frac{(3+x)^3-27}{x}\)
Solution:

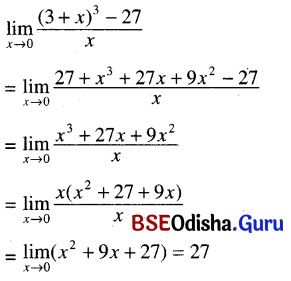
(x) \(\lim _{x \rightarrow 2} \frac{\frac{1}{x^2}-\frac{1}{4}}{x-2}\)
Solution:

(xi) \(\lim _{x \rightarrow 1} \frac{1}{(x-1)}\left\{\frac{1}{x+3}-\frac{2}{3 x+5}\right\}\)
Solution:

(xii) \(\lim _{h \rightarrow 0} \frac{(x+h)^3-x^3}{h}\)
Solution:

(xiii) \(\lim _{h \rightarrow 0} \frac{(x+h)^4-x^4}{h}\)
Solution:

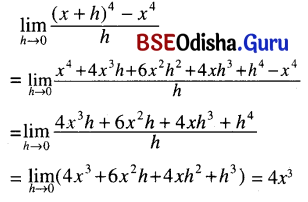
(xiv) \(\lim _{x \rightarrow 1} \frac{x^m-1}{x^n-1}\), where m, n are integers.
Solution:

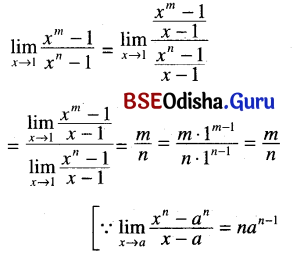
(xv) \(\lim _{x \rightarrow 1} \frac{x^2-2 x+1}{x^2-x}\)
Solution:

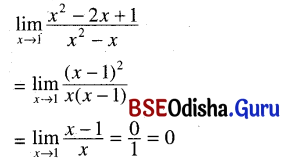
(xvi) \(\lim _{x \rightarrow 1} \frac{x^2+x-2}{x^3-x^2-x+1}\)
Solution:

Question 5.
Evaluate the following :
(i) \(\lim _{x \rightarrow \infty} \frac{2 x+1}{3 x-2}\)
Solution:
\(\lim _{x \rightarrow \infty} \frac{2 x+1}{3 x-2}\)
= \(\lim _{x \rightarrow \infty} \frac{2+\frac{1}{x}}{3-\frac{2}{x}}=\frac{2}{3}\)
[ ∵ As x → ∞, \(\frac{1}{x}\) → 0]

(ii) \(\lim _{x \rightarrow \infty} \frac{3 x^2+x-1}{2 x^2-7 x+5}\)
Solution:
\(\lim _{x \rightarrow \infty} \frac{3 x^2+x-1}{2 x^2-7 x+5}\)
\(=\lim _{x \rightarrow \infty} \frac{3+\frac{1}{x}-\frac{1}{x^2}}{2-\frac{7}{x}+\frac{5}{x^2}}=\frac{3}{2}\)

(iii) \(\lim _{x \rightarrow \infty} \frac{x^3+2 x^2+3}{x^4-3 x^2+1}\)
Solution:
\(\lim _{x \rightarrow \infty} \frac{x^3+2 x^2+3}{x^4-3 x^2+1}\)
\(\lim _{x \rightarrow\infty}\frac{\frac{1}{x}+\frac{2}{x^2}+\frac{3}{x^4}}{1-\frac{3}{x^2}+\frac{1}{x^4}}=\frac{0}{1}\) =0
[ ∵ As x → ∞, \(\frac{1}{x}\) → 0]

(iv) \(\lim _{x \rightarrow \infty} \frac{x^4-5 x+2}{x^3-3 x+1}\)
Solution:
\(\lim _{x \rightarrow \infty} \frac{x^4-5 x+2}{x^3-3 x+1}\)
\(\lim _{x \rightarrow \infty} \frac{x-\frac{5}{x^2}+\frac{2}{x^3}}{1-\frac{3}{x^2}+\frac{1}{x^3}}\) = ∞

(v) \(\lim _{x \rightarrow \infty}\left(\frac{x^3}{2 x^2-1}-\frac{x^2}{2 x+1}\right)\)
Solution:

(vi) \(\lim _{n \rightarrow \infty} \frac{n}{n+1}\)
Solution:
\(\lim _{n \rightarrow \infty} \frac{n}{n+1}\)
= \(\lim _{n \rightarrow \infty} \frac{n}{1+\frac{1}{n}}\) = 1

(vii) \(\lim _{n \rightarrow \infty}\left(\frac{n^2+n+1}{5 n^2+2 n+1}\right)\)
Solution:

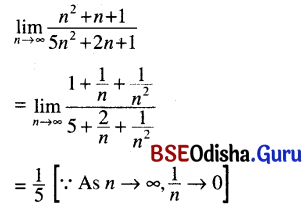
(viii) \(\lim _{n \rightarrow \infty}\left(\frac{\sqrt{n}-1}{\sqrt{n}+1}\right)\)
Solution:
\(\lim _{n \rightarrow \infty}\left(\frac{\sqrt{n}-1}{\sqrt{n}+1}\right)\)
= \(\lim _{n \rightarrow \infty} \frac{1-\frac{1}{\sqrt{n}}}{1+\frac{1}{\sqrt{n}}}\) = 1

(ix) \(\lim _{n \rightarrow \infty}\left(\frac{6 n^5+2 n+1}{n^5+n^4+3 n^3+2 n^2+n+1}\right)\)
Solution:

(x) \(\lim _{n \rightarrow \infty} \frac{1+2+3+\cdots+n}{n^2}\)
Solution:

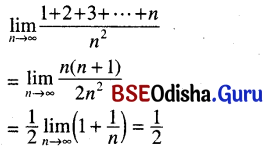
(xi) \(\lim _{n \rightarrow \infty} \frac{1^2+2^2+3^2+\ldots+n^2}{n^3}\)
Solution:

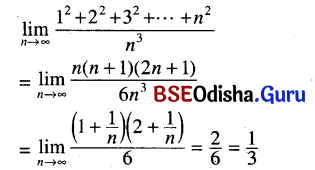
(xii) \(\lim _{n \rightarrow \infty} \frac{1^3+2^3+3^3+\ldots+n^3}{n^4}\)
Solution:

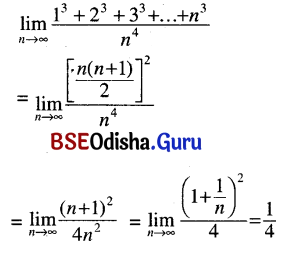
(xiii)  \(\lim _{n \rightarrow \infty} \frac{1+\frac{1}{2}+\frac{1}{2^2}+\ldots+\frac{1}{2^n}}{1+\frac{1}{3}+\frac{1}{3^2}+\ldots \frac{1}{3^n}}\)
Solution:

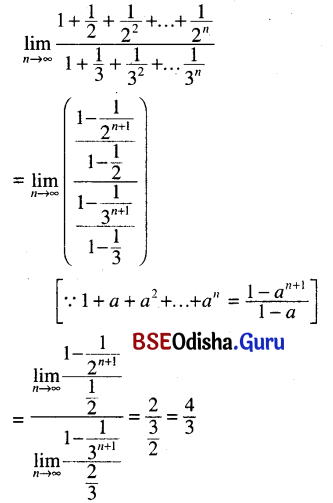
(xiv) \(\lim _{n \rightarrow \infty} \frac{\lfloor n}{\mid n+1-\lfloor n}\)
Solution:

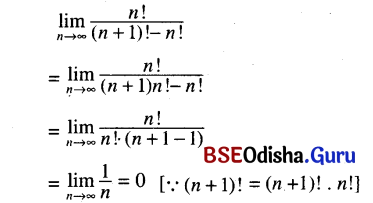
Question 6.
Examine the existence of the following limits :
(i) \(\lim _{x \rightarrow \sqrt{3}}\) [x]
Solution:
L.H.L. = \(\lim _{x \rightarrow \sqrt{3}-}\) [x] = \(\lim _{h \rightarrow 0}\) [√3 – h] = 1
R.H.L. = \(\lim _{x \rightarrow \sqrt{3}+}\) [x] = \(\lim _{h \rightarrow 0}\) [√3 + h] = 1
Thus L.H.L., R.H.L both
exist and L.H.L. = R.H.L.
So the limit exists and its value is 1.

(ii) \(\lim _{x \rightarrow 0}[x]\)
Solution:

(iii) \(\lim _{x \rightarrow-2}[x]\)
Solution:
L.H.L. = \(\lim _{x \rightarrow-2-} \frac{x-2}{|x-2|}\)
= \(\lim _{h \rightarrow 0}\)[-2 – h] = -3
R.H.L. \(\lim _{x \rightarrow-2+}\) [x] = \(\lim _{h \rightarrow 0}\)[-2 + h] = -2
Thus L.H.L. ≠ R.H.L.
So the limit does not exist.

(iv) \(\lim _{x \rightarrow 0} \frac{|x|}{x}\)
Solution:

(v) \(\lim _{x \rightarrow 2} \frac{x-2}{|x-2|}\)
Solution:

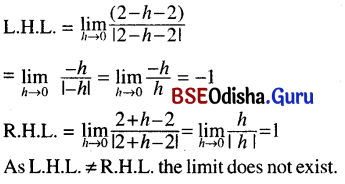
(vi) \(\lim _{x \rightarrow \frac{1}{2}} \frac{|2 x-1|}{2 x-1}\)
Solution:

(vii) \(\lim _{x \rightarrow 1}[2 x+3]\)
Solution:

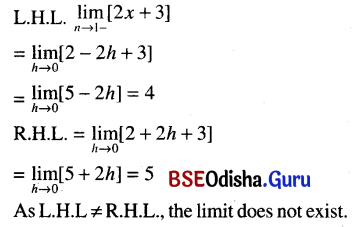
(viii) \(\lim _{x \rightarrow \infty} \frac{x}{[x]}\)
Solution:

(ix) \(\lim _{x \rightarrow \infty} \frac{x^2-x}{\left[x^2-x\right]}\)
Solution:

(x) \(\lim _{x \rightarrow 1} \frac{\left|x^2-3 x+2\right|}{x^2-3 x+2}\)
Solution:

(xi) \(\lim _{x \rightarrow \infty}(-1)^{[x]}\)
Solution:
\(\lim _{x \rightarrow \infty}(-1)^{[x]}\)
[Put n ≤ n + 1,As n→ ∞, x → ∞
= \(\lim _{x \rightarrow \infty}(-1)^n\) [ ∵ [x] = n
= ± 1 [If n is odd, (-1)ⁿ = – 1 and if n is even (-1)ⁿ = 1 ]
We know that whenever the limit exists it must be unique.
So \(\lim _{x \rightarrow \infty}(-1)^{[x]}\) does not exist.

(xii) \(\lim _{x \rightarrow \infty} \sin x\)
Solution:

(xiii) \(\lim _{x \rightarrow \infty} \cos x\)
Solution:

(xiv) \(\lim _{x \rightarrow 0} \cos \frac{1}{x}\)
Solution:

(xv) \(\lim _{x \rightarrow \infty} \sin \frac{1}{x}\)
Solution:

(xvi) \(\lim _{x \rightarrow 1} f(x) \text { if } f(x)= \begin{cases}2 x-1, & x \leq 1 \\ 2 x+1, & x>1\end{cases}\)
Solution:

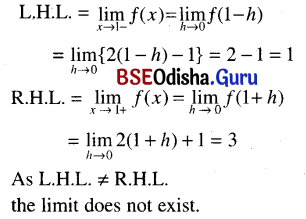
(xvii) \(\lim _{x \rightarrow 0} f(x) \text { and } \lim _{x \rightarrow 1} f(x)\)
if \(f(x)=\left\{\begin{array}{l}
0 . x \leq 0 \\
1-2 x, 0<x \leq 1 \\
3-4 x, x>1
\end{array}\right.\)
Solution:

Question 7.
Let f(x) = {1 if x is rational, 0 if x is irrational then show that \(\lim _{x \rightarrow a}\) f(x) does not exist for any a ∈ R.
Solution:
Let x → a through rational numbers.
Then \(\lim _{x \rightarrow a}\) f(x) = 1
If x → a through rational numbers.
Then \(\lim _{x \rightarrow a}\) f(x) = 0
Thus \(\lim _{x \rightarrow a}\) f(x) does not exist.