Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 9 Integration Ex 9(l) Textbook Exercise questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Exercise 9(l)
Question 1.
\(\int_0^{\frac{\pi}{2}}\)sin10 θ dθ
Solution:
\(\int_0^{\frac{\pi}{2}}\)sin10 θ dθ = \(\frac{9}{10} \cdot \frac{7}{8} \cdot \frac{5}{6} \cdot \frac{3}{4} \cdot \frac{1}{2} \cdot \frac{\pi}{2}\) = \(\frac{405 \pi}{7680}\)
Question 2.
\(\int_0^{\frac{\pi}{2}}\)cos12 θ dθ
Solution:
\(\int_0^{\frac{\pi}{2}}\)cos12 θ dθ = \(\frac{11}{12} \cdot \frac{9}{10} \cdot \frac{7}{8} \cdot \frac{5}{6} \cdot \frac{3}{4} \cdot \frac{1}{2} \cdot \frac{\pi}{2}\) = \(\frac{4455 \pi}{92160}\)
Question 3.
\(\int_0^{\frac{\pi}{2}}\)sin11 θ dθ
Solution:
\(\int_0^{\frac{\pi}{2}}\)sin11 θ dθ = \(\frac{10}{11} \cdot \frac{8}{9} \cdot \frac{6}{7} \cdot \frac{4}{5} \cdot \frac{2}{3}\) = \(\frac{3840}{4455}\)
![]()
Question 4.
\(\int_0^{\frac{\pi}{2}}\)cos9 θ dθ
Solution:
\(\int_0^{\frac{\pi}{2}}\)cos9 θ dθ = \(\frac{8}{9} \cdot \frac{6}{7} \cdot \frac{4}{5} \cdot \frac{2}{3}\) = \(\frac{384}{405}\)
Question 5.
\(\int_0^1 \frac{x^7}{\sqrt{1-x^2}}\) dx
Solution:
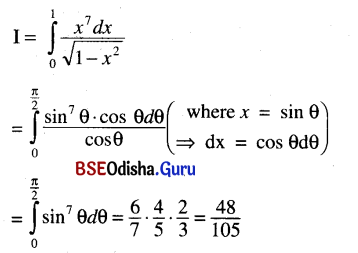
Question 6.
\(\int_0^1 \frac{x^5\left(4-x^2\right)}{\sqrt{1-x^2}}\) dx
Solution:
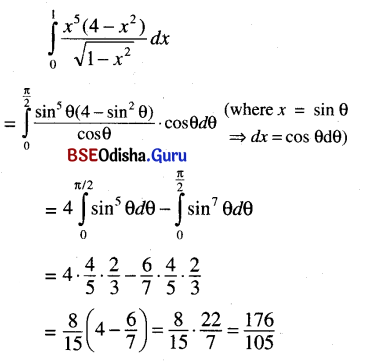
Question 7.
\(\int_0^a x^3\left(a^2-x^2\right)^{\frac{5}{2}}\) dx
Solution:

Question 8.
\(\int_0^1 x^5 \sqrt{\frac{1+x^2}{1-x^2}}\) dx
Solution:

![]()
Question 9.
\(\int_0^{\infty} \frac{x^2}{\left(1+x^6\right)^n}\) dx
Solution:

Question 10.
\(\int_0^\pi\)sin8 θ dθ
Solution:

