Odisha State Board CHSE Odisha Class 11 Math Solutions Chapter 3 Relations And Functions Ex 3(b) Textbook Exercise Questions and Answers.
CHSE Odisha Class 11 Math Solutions Chapter 3 Relations And Functions Exercise 3(b)
Question 1.
Let A = {a, b, c }, |B| = {1, 2}
(a) Determine all the relations from A to B and determine the domain, range, and inverse of each relation.
(b) Determine all the relations from B to A.
(c) Is there any relationship that is both a relation from A to B and B to A? How many?
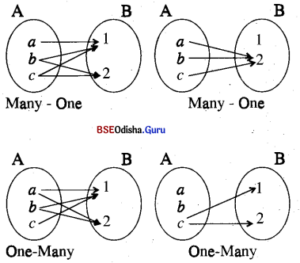
(d) Of all the relations from A to B, identify which relations are many ones, one-many, and one-one and represent this diagrammatically.
Solution:
(a) A = {a, b, c}, B = {1, 2}
∴ A × B = {(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)}
∴ |A × B| = 6
∴ |P(A × B)| = 26 = 64
∴ There are 64 relations from A to B as any subset of A × B. The domain of these relations is any subset of A. The inverse of these relations is any subset of B × A.
(b) There are 64 relations from B to A as any sub-set of B x A is a relation from B to A.
(c) Φ is the only relation that is from A to B and from B to A.
(d) Some many-one relations are {(a, 1), (b, 1), (c, 1), (b, 2) (c, 2)}, {(a, 2), (b, 2), (c, 2)}.
Question 2.
Are the following sets related?
(i) Φ from A to B.
(ii) A × B from A to B.
(iii) A × Φ from A to Φ.
(iv) Φ × B from Φ to B.
(v) Φ × Φ from Φ to Φ.
(vi) Φ × C from A to B.
(vii) Φ × Φ from A to B.
Determine the domain range and inverse of each of the relations mentioned above
Solution :
(i) Φ from A to B is a relation.
(ii) A × B from A to B is a relation.
(iii) A × Φ from A to Φ is a relation.
(iv) Φ × B from Φ to B is a relation.
(v) Φ × Φ from Φ to Φ is a relation.
(vi) Φ × C from A to B is a relation.
(vii) Φ × Φ from A to B is a relation.
∴ Domain of Φ i.e. DΦ = Φ
Range of Φ i.e., RΦ = Φ
Similarly, DA × B = A, RA × B = β
DA × Φ = Φ, RA × Φ = Φ
D Φ × B = Φ = Φ, R Φ × B = Φ
D Φ × Φ = Φ, R Φ × C = Φ
D Φ × C = Φ, R Φ × C = Φ
D Φ × Φ = Φ, R Φ × Φ = Φ
The inverse of the above relations is Φ, B × A, Φ × A, B × Φ, Φ × Φ, C × Φ, and Φ × Φ respectively.
![]()
Question 3.
Express the following relations on A to B in each case in tabular form :
(i) A = {n ∈ N : n ≤ 10}, B = N
f = {(x, y) ∈ A × B : y = x2}
Solution:
A = {n ∈ N : n ≤ 10}
= {1, 2, 3,…..10}, B = N
∴ B = {1, 2, 3}
∴ f ={(x, y) ∈ A × B : y = x2}
= {(1, 1), (2, 4), (3, 9)…..(10, 100)}
(ii) A = B = R
∴ f = {(x, y) : x2 + y2 = 1 and |x – y| = 1}
Solution:
A = B = R
∴ f = {(x, y) : x2 + y2 = 1 and |x – y| = 1}
={(0, 1) (1, 0), (-1, 0), (0, -1)}
(iii) (1, 2, 3, 4), B = {1, 2, 3, 4, 5}
f = {x, y) : 2 divides 3x+y}
Solution:
A = {1, 2, 3, 4}, B = {1, 2, 3, 4, 5}
∴ f = {(x, y) : 2 divides 3x+y}
={(1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (3, 1), (3, 3), (3,5), (4, 2), (4, 4)}
Question 4.
A and B are non-empty sets such that |A| = m, |B| = n. How many relations can be defined from A to B ? (Remember that the number of relations is the number of subsets of (A × B).
Solution:
|A| = m, |B| = n
⇒ |A × B| = mn
A relation is a subset of A to B
∴ Number of relations from A to B
= Number of subsets of A × B
= 2mn (∴ |A × B| = mn)
Question 5.
Give an example of a relation f such that
(i) dom f – rng f (ii) dom f ⊂ rng f
(iii) dom f ⊃ rng f
(iv) f ∪ f-1 = Φ
(v) f = f-1
(vi) f ∪ f-1 ≠ Φ
Solution:
Let A = { 1, 2, 3} = B
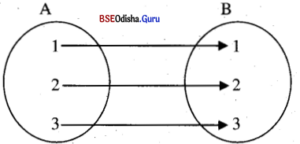
(i) Let f = {(x, y) ∈ A × B : x = y}
∴ Dom f = {1, 2, 3} = Range f
(ii) Let f = {(1, 1), (1, 2), (2, 3)}
on A = (1, 2, 3}
∴ Dom f = {1, 2} ⊂ { 1, 2, 3} = Range f
(iii) Do yourself
(iv) Let f = Φ
∴ f-1 = Φ = f ∪ f-1 = Φ
(v) Let f = {(x, y) ∈ A × B; x2 + y2 = 1}, where A = B = {1, – 1, 0}
= {(1, 0), (0, 1), (-1, 0), (0, -1)}
f-1 = {(0, 1) (1, 0), (0, -1), (-1, 0)}
=f
(vi) Let f = {(1, 3), (3, 1)} on A = { 1, 2, 3}
∴ f-1 = {3, 1), (1, 3)},
so that f ∩ f-1 = Φ.
Question 6.
Let R = {(a, a3) I a is a prime number less than 10}
Fine (i) R, (ii) dom R, (iii) rng R (iv) R-1 (v) dom R-1 (vi) rng R-1
Solution:
R = {(a, a3)} a is a prime number less than 10}
(i) R = {(2, 8), (3, 27), (5, 125), (7, 343)}
(ii) dom R = {2, 3, 5, 7}
(iii) rng R = {8, 27, 125, 343}
(iv) R-1 = {(8, 2), (27, 3), (125, 5), (343, 7)}
(v) Dom R-1 = {8, 27, 125, 343} = rng R
(vi) rng R-1 = {2, 3, 5, 7} = dom R
![]()
Question 7.
Let A = {1, 2, 3, 4, 5, 6} and Let R be a relation on A defined by R = {(a, b)} a divides b
Find (i) R, (ii) dom R, (iii) rng R (iv) R-1, (v) Dom R-1 (vi) rng R-1
Solution:
A = {1, 2, 3, 4, 6}
R on A is defined by
R = {(a, b) | a divides b}
(i) R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6) (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}
(ii) dom R = {1,2, 3, 4, 6} = A
(iii) rng R = {1, 2, 3, 4, 6} = A
(iv) R-1 = {(1, 1), (2, 1), (3, 1), (4, 1), (6, 1), (2, 2) (4, 2), (6, 2), (3, 3), (6, 3), (4, 4), (6, 6)}
(v) dom R-1 = {1, 2, 3, 4, 6} = A
(vi) rng R-1 = {l, 2, 3, 4, 6} = A
