CHSE Odisha Class 11 Math Solutions Chapter 5 Principles Of Mathematical Induction Ex 5

Odisha State Board Elements of Mathematics Class 11 Solutions CHSE Odisha Chapter 5 Principles Of Mathematical Induction Ex 5 Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 5 Principles Of Mathematical Induction Exercise 5

Prove the following by induction.

Question 1.
1 + 2 + 3 + …… + n = \(\frac{n(n+1)}{2}\)
Solution:
Let p_n be the given statement

Question 2.
1² + 2² + …… + n² = \(\frac{n(n+1)(2 n+1)}{6}\)
Solution:
Let p_n be the given statement
when n = 1
1² =1 = \(\frac{1(1+1)(2 \times 1+1)}{6}\)
P₁ is true
Let P_k be true.
i.e. 1² + 2² + … + k² = \(\frac{k(k+1)(2 k+1)}{6}\)
we shall prove P_k + 1 is true i.e., 1² + 2² + … + k² + (k + 1)²
\(=\frac{(k+1)(k+2)(2 k+3)}{6}\)

∴ P_k+1 is true
∴ P_n is true of all values of n∈N.

Question 3.
1 + r + r²+ …. + rⁿ = \(\frac{r^{n+1}-1}{r-1}\)
Solution:
Let P_n be the given statement

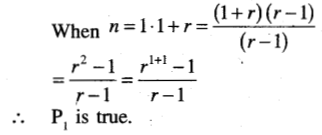
Question 4.
5ⁿ – 1 is divisible by 4.
Solution:
Let P_n = 5ⁿ – 1
When n = 1,
5¹ – 1 = 4 is divisible by 4.
∴ P₁, is true.
Let P_k be true i.e.,
5^k – 1 is divisible by 4.
Let 5^k+1 – 1 = 4m, me Z
Now 5k + 1 – 1 = 5^k. 5 – 5 + 4
= 5 (5^k – 1) + 4
= 5 × 4m + 4 = 4 (5m + 1)
which is divisible by 4.
∴ P_k+1 is true.
∴ P_n is true for all values of n ∈ N

Question 5.
7²ⁿ + 2^3n-3  3^n-1 is divisible by 25 for any natural number n > 1.
Solution:
Let 7²ⁿ + 2^3n-3 . 3^n-1
when n = 1, 7¹ + 2⁰ . 3⁰ ⇒ 49 + 1 = 50
which is divisible by 25.
∴ P₁ is true. Let P_k be true.
i.e., 72^k + 2^3k-3 3^k-1 is divisible by 35
Now \(7^{2 \overline{k+1}}+2^{3 \overline{k+1}-3} 3^{\overline{k+1}-1}\)
=7^2k+2 + 2^3k. 3^k
= 7^2k. 7² + 2^3k-3 2³. 3^k-1. 3¹
= 7^2k. 49 + 2^3k-3. 3^k-1. 24
= 7^2k (25 + 24) + 24. 2^3k-3. 3^k-1
= 7^2k. 25 + 24 (7^2k + 2^3k-3. 3^k-1)
= 7^2k. 25 + 24 × 25m
Which is divisible by 25 (∵ P_k is true)
∴ P_k+1 is true
∴ P_n is true for all values of n > 1.

Question 6.
7. 5^2n-1 + 23ⁿ⁺¹ is divisible by 17 for every natural number n ≥ 1.
Solution:
Let P_n = 7. 5²ⁿ – 1 + 2³ⁿ⁺¹.
When n = 1, 7.5 + 2⁴ = 35 + 16 = 51
Which is divisible by 17.
P₁, is true.
Let P_k be true i.e., 7.5^2k-1 + 2^3k+1  is divisible by 17.
Let 7.5^2k-1 + 2^3k+1 = 17 m, m ∈ Z
Now, \(7.5^{2 \overline{k+1}-1}+2^{3 \overline{k+1}+1}\)
= 7.5^2k-1 + 2^3k+4
= 7.5^2k-1 . 5² + 2^3k+1 . 2³
= 25. 7. 5^2k-1 + 8. 2^3k+1
= (17 + 8) 7.5^2k-1 + 8. 2^3k+1
= 17. 7. 5^2k-1 + 8 (7. 5^2k-1 + 2^3k+1)
= 17 × 7 × 5^2k-1 + 8 × 17m
Which is divisible by 17.
Hence P_k+1. is true.
∴ P_n is true for all values of n ≥ 1.

Question 7.
4ⁿ⁺¹ + 15n + 14 is divisible by 9 for every natural number n ≥ 0.
Solution:
Let P_n = 4ⁿ⁺¹+ 15 n + 14
when n = 1, 4² + 15 + 14 = 45 is divisible by 9.
∴ P₁ is true. Let P_k be true.
i.e., 4^k+1 + 15k + 14 is divisible by 9.
Now, 4^k+1+1 + 15 (k + 1) + 14
= 4^k+2 + 15k + 29
= 4^k+1. 4 + 60k + 56 – 45k – 27
= 4 (4^k+1 + 15k + 14) – 9 (5k + 3)
Which is divisible by 9.
∴ P_k+1, is true.
∴ P_n is true for all values of n ≥ 0.

Question 8.
3^(2n-1) + 7 is divisible by 9 for every natural number n ≥ 2.
Solution:
Let P_n = 3^2(n-1) + 7
When n = 2. 3² + 7 = 16 is divisible by 8.
∴ P₂ is true.
Let P_k be true.
i.e., 5^2(k-1) + 7 is divisible by 8.
Let 3^2k-2 + 7 = 8m. m ∈ Z.
Now \(3^{2(\overline{k+1}-1)}\) + 7 = 3^2k + 7
= 3^2k-2. 3² + 63 – 56
= 9(3^2k-2 + 7) – 56
= 9 × 8m – 56 = 8 (9m – 7)
Which is divisible by 8.
P_k+1 is true.
P_n is true for all values on n ≥ 2.

Question 9.
5^(2n-4)  – 6n + 32 is divisible by 9 for every natural number n ≥ 5.
Solution:
Let P = 5^2(n-4) – 6n + 32
For n = 5, P₅ = 5² – 6. 5 + 32
= 25 – 30 + 32 = 27
Which is divisible by 9.
Hence P₅ is true.
Let P_k is true.
Let P_k is divisible by 9.
Let P_k = 5^2(k-4) – 6k + 32 = 9., m ≥ Z
5^2k+2 = 576 m + 24k  + 25 … (1)
we shall prove that P_k+1 is true.
Now 5^2(K+1)+2 – 24(k+1) – 25
= 5² (5^2k+2) – 24k – 24 – 25
= 5²[576m + 24k + 25] – 24k – 24 – 25
= 25 × 576 m + 25 × 24k + 25 × 25 – 24k – 24 – 25
= 25 × 576 m + 576 k + 576
= 576 [25 m + k + 1]
which is divisible by 576
∴ P_k+1 is true.
So by the method of induction P_n is true for all n.
i.e., 5²ⁿ⁺²  – 24n – 25 is divisible by 576 for all n ∈ N.
Hence P_k+1 is true.
So by methods of induction P_n is true.
i.e., 5²ⁿ⁺² – 24n – 25 is divisible by 576 for all n.

Question 10.
\(\frac{1}{1.2}+\frac{1}{2.3}+\ldots+\frac{1}{n(n+1)}=\frac{n}{n+1}\)
Solution:
when n = 1,

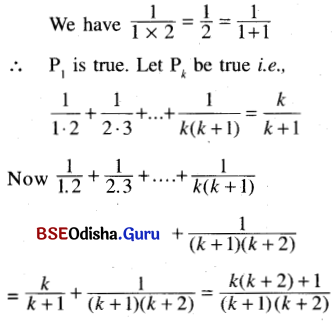
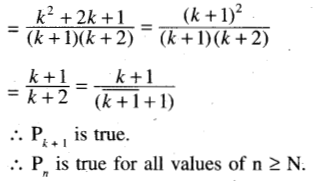
Question 11.
1.3 + 2.4 + 3.5 + …….. + n(n + 2) = \(\frac{n(n+1)(2 n+7)}{6}\)
Solution:
when n = 1,
we have 1.3 = 3 = \(\frac{3 \times 6}{6}\)
\(=\frac{1 \times 2 \times 9}{6}=\frac{1(1+1)(2 \times 1+7)}{6}\)

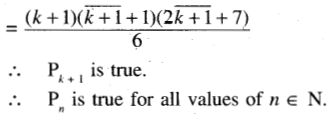
Question 12.
xⁿ – yⁿ = (x – y)(x^n-1 + x^n-2 y + … + xy^n-2 + y^n-1); x, y ∈ R [Hint : Write xⁿ⁺¹ – yⁿ⁺¹ = x(xⁿ – yⁿ) + yⁿ(x – y)]
Solution:
Let p(n) is
xⁿ – yⁿ = (x – y)(x^n-1 + x^n-2 y + … + xy^n-2 + y^n-1); x, y ∈ R
Step – 1:
For n = 2
x² – y² = (x – y) (x + y) (True)
∴ P(1) is true.
Step – 2:
Let P(k) is true.
i.e., x^k – y^k = (x – y)(x^k-1 + x^k-2y + … +xy^k-2 + y^k-1)
Step – 3:
Let us prove P_k+1 is true.
i.e., x^k+1 – y^k+1 = (x – y) (x^k + x^k-1y + … (xy^k-1 + y^k)
L.H.S. = x^k+1 – y^k+1
= x^k+1 – xy^k + xy^k – y^k+1
= x(x^k – y^k) + y^k (x – y)
= x(x – y)(x^k-1 + x^k-2 y + … + xy^k-2 + y^k-1) + y^k(x – y) [by (1)]
= (x – y) [x^k + x^k-1 y + … + xy^k-2 + xy^k-1 + y^k]
= R.H.S.
∴ P_(k+1) is true.
Step – 4:
By Principle Of Mathematical Induction P(n) is true for all n ∈ N.

Question 13.
1 + 3 + 5 + ……. +(2n – 1) = n²
Solution:
Let P(n) is : 1 + 3 + 5 + ……. +(2n – 1) = n².
Step – 1:
For n = 2
L.H.S. = 1 + 3 = 4 = 2² (R.H.S)
∴ P(1) is true.
Step – 2:
Let P(k) is true.
i.e., 1 + 3 + 5 … + (2k – 1) = k² …(1)
Step – 3:
We will prove that P(k + 1) is true
i.e., we want to prove.
1+ 3 + 5 + … + (2k – 1) + (2k + 1) = (k + 1)²
L.H.S. = 1 + 3 + 5 + … + (2k – 1) + (2k + 1)
= k² + 2k + 1          [By – (1)]
= (k + 1)² = R.H.S.
Step – 4:
By the Principle of Mathematical Induction P(n) is true for all n.
i.e., 1 + 3 + 5 ….+ (2n – 1) = n²

Question 14.
n > n; n is a natural number.
Solution:
Let P(n) is 2ⁿ > n
Step – 1:
2¹ > 1 (True)
∴ P(1) is true.
Step – 2:
Let P(k) is true.
⇒ 2^k > k
Step – 3:
We shall prove that P(k + 1) is true
i.e., 2^k+1 > k + 1
Now 2^k+1 = 2.2k > 2k ≥ k + 1 for k ∈ N.
∴ 2^k+1 > k + 1
⇒ P(k + 1) is true.
Step – 4:
By the Principle of Mathematical Induction P(n) is true for all n.
i.e., 2ⁿ > n for n ∈ N

Question 15.
(1, 2, 3 … n)³  > 8 (1³ + 2³ + 3³ + … + n³), for n > 3.
Solution:
Let P(n) is
(1, 2, 3 … n)³  > 8 (1³ + 2³ + 3³ + … + n³), for n > 3.
Step – 1:
For n = 4
(1. 2. 3. 4)³ = 24³ = 13824
8(1³+ 2³ + 3³ + 4³) = 808
∴ (1. 2 . 3 . 4)³ > 8(1³ + 2³ + 3³ + 4³)
∴ P(4) is true.
Step- 2:
Let P(k) is true.
(1. 2. 3…….k)³ > 8(1³ + 2³ + 3³ + …… + k³)
Step – 3:
We shall prove that P_(k+1) is true.
i.e., (1. 2. 3. …….. k(k+1))³ > 8(1³ + 2³ + … + k³ + (k + 1)³)
Now (1. 2. 3. …….. k(k + 1)³)
= (1. 2. 3 … k)³ (k + 1)³
> 8 (1³ + 2³ + … k³) (k + 1)³
> 8 (1³ + 2³ + … k³) + 8(k + 1)³
= 8 (1³ + 2³ + … + k³ + (k + 1)³)
P_(k+1) is true.
Step – 4:
By the Principle of Mathematical Induction P(n) is true for all n ∈ N and n > 3.

Question 16.
\(\frac{1}{n+1}+\frac{1}{n+2}+\ldots+\frac{1}{3 n+1}>\) for every positive integer n.
Solution:
Let P(n) is
\(\frac{1}{n+1}+\frac{1}{n+2}+\ldots+\frac{1}{3 n+1}>\)



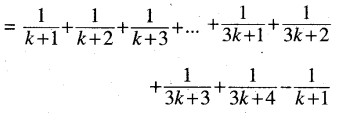
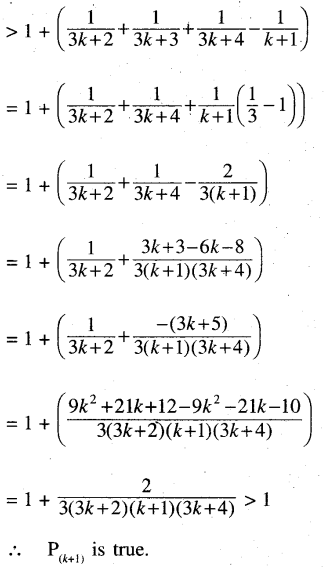
Step-4:
By the Principle of Mathematical Induction P(n) is true for all n ∈ N.