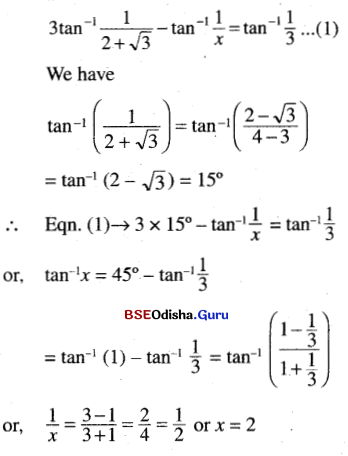Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 2 Inverse Trigonometric Functions Ex 2 Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 2 Inverse Trigonometric Functions Exercise 2
Question 1.
Fill in the blanks choosing correct answer from the brackets:
(i) If A = tan-1 x, then the value of sin 2A = ________. (\(\frac{2 x}{1-x^2}\), \(\frac{2 x}{\sqrt{1-x^2}}\), \(\frac{2 x}{1+x^2}\))
Solution:
\(\frac{2 x}{1+x^2}\)
(ii) If the value of sin-1 x = \(\frac{\pi}{5}\) for some x ∈ (-1, 1) then the value of cos-1 x is ________. (\(\frac{3 \pi}{10}\), \(\frac{5 \pi}{10}\),\(\frac{3 \pi}{10}\))
Solution:
\(\frac{3 \pi}{10}\)
(iii) The value of tan-1 x (2cos\(\frac{\pi}{3}\)) is ________. (1, \(\frac{\pi}{4}\), \(\frac{\pi}{3}\))
Solution:
\(\frac{\pi}{4}\)
(iv) If x + y = 4, xy = 1, then tan-1 x + tan-1 y = ________. (\(\frac{3 \pi}{4}\), \(\frac{\pi}{4}\), \(\frac{\pi}{3}\))
Solution:
\(\frac{\pi}{2}\)
(v) The value of cot-1 2 + tan-1 \(\frac{1}{3}\) = ________. (\(\frac{\pi}{4}\), 1, \(\frac{\pi}{2}\))
Solution:
\(\frac{\pi}{4}\)
(vi) The principal value of sin-1 (sin \(\frac{2 \pi}{3}\)) is ________. (\(\frac{2 \pi}{3}\), \(\frac{\pi}{3}\), \(\frac{4 \pi}{3}\))
Solution:
\(\frac{\pi}{3}\)
![]()
(vii) If sin-1 \(\frac{x}{5}\) + cosec-1 \(\frac{5}{4}\) = \(\frac{\pi}{2}\), then the value of x = ________. (2, 3, 4)
Solution:
x = 3
(viii) The value of sin (tan-1 x + tan-1 \(\frac{1}{x}\)), x > 0 = ________. (0, 1, 1/2)
Solution:
1
(ix) cot-1 \(\left[\frac{\sqrt{1-\sin x}+\sqrt{1+\sin x}}{\sqrt{1-\sin x}-\sqrt{1+\sin x}}\right]\) = ________. (2π – \(\frac{x}{2}\), \(\frac{x}{2}\), π – \(\frac{x}{2}\))
Solution:
π – \(\frac{x}{2}\)
(x) 2sin-1 \(\frac{4}{5}\) + sin-1 \(\frac{24}{25}\) = ________. (π, -π, 0)
Solution:
π
(xi) if Θ = cos-1 x + sin-1 x – tan-1 x, x ≥ 0, then the smallest interval in which Θ lies is ________. [(\(\frac{\pi}{2}\), \(\frac{3 \pi}{2}\)), [0, \(\frac{\pi}{2}\)), (0, \(\frac{\pi}{2}\)])
Solution:
(0, \(\frac{\pi}{2}\)]
(xii) sec2 (tan-1 2) + cosec2 (cot-1 3) = ________. (16, 14, 15)
Solution:
15
Question 2.
Write whether the following statements are true or false.
(i) sin-1 \(\frac{1}{x}\) cosec-1 x = 1
Solution:
False
(ii) cos-1 \(\frac{4}{5}\) + tan-1 \(\frac{2}{3}\) = tan-1 \(\frac{17}{6}\)
Solution:
True
(iii) tan-1 \(\frac{4}{3}\) + cot-1 (\(\frac{-3}{4}\)) = π
Solution:
True
(iv) sec-1 \(\frac{1}{2}\) + cosec-1 \(\frac{1}{2}\) = \(\frac{\pi}{2}\)
Solution:
False
(v) sec-1 (-\(\frac{7}{5}\)) = π – cos-1 \(\frac{5}{7}\)
Solution:
True
(vi) tan-1 (tan 3) = 3
Solution:
False
(vii) The principal value of tan-1 (tan \(\frac{3 \pi}{4}\)) is \(\frac{3 \pi}{4}\)
Solution:
False
(viii) cot-1 (-√3) is in the second quadrant.
Solution:
True
(ix) 3 tan-1 3 = tan-1 \(\frac{9}{13}\)
Solution:
False
(x) tan-1 2 + tan-1 3 = – \(\frac{\pi}{4}\)
Solution:
False
(xi) 2 sin-1 \(\frac{4}{5}\) = sin-1 \(\frac{24}{25}\)
Solution:
False
(xii) The equation tan-1 (cotx) = 2x has exactly two real solutions.
Solution:
True
![]()
Question 3.
Express the value of the foilowing in simplest form.
(i) sin (2 sin-1 0.6)
Solution:
sin (2 sin-1 0.6)
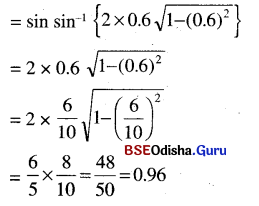
(ii) tan (\(\frac{\pi}{4}\) + 2 cot-1 3)
Solution:

(iii) cos (2 sin-1 x)
Solution:
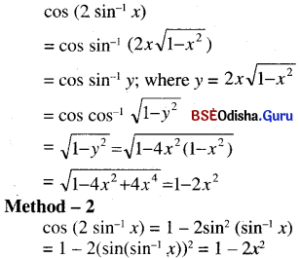
(iv) tan (cos-1 x)
Solution:
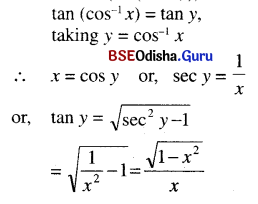

(v) tan-1 (\(\frac{x}{y}\)) – tan-1 \(\frac{x-y}{x+y}\)
Solution:

(vi) cosec (cos-1 \(\frac{3}{5}\) + cos-1 \(\frac{4}{5}\))
Solution:
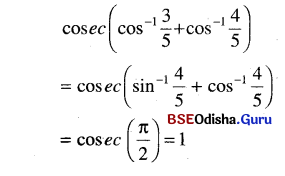
![]()
(vii) sin-1 \(\frac{1}{\sqrt{5}}\) + cos-1 \(\frac{3}{\sqrt{10}}\)
Solution:

(viii) sin cos-1 tan sec √2
Solution:
sin cos-1 tan sec √2
= sin cos-1 tan sec \(\frac{\pi}{4}\)
= sin cos-1 1 = sin 0 = 0
(ix) sin (2 tan-1 \(\sqrt{\frac{1-x}{1+x}}\))
Solution:
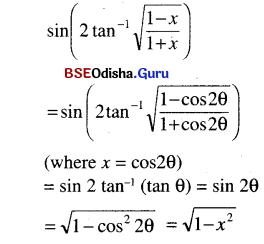
(x) tan \(\left\{\frac{1}{2} \sin ^{-1} \frac{2 x}{1+x^2}+\frac{1}{2} \cos ^{-1} \frac{1-y^2}{1+y^2}\right\}\)
Solution:
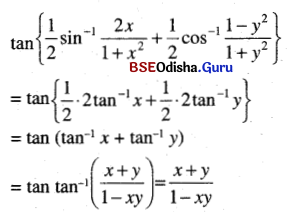
(xi) sin cot-1 cos tan-1 x.
Solution:

(xii) tan-1 \(\left(x+\sqrt{1+x^2}\right)\)
Solution:

Question 4.
Prove the following statements:
(i) sin-1 \(\frac{3}{5}\) + sin-1 \(\frac{8}{17}\) = cos-1 \(\frac{36}{85}\)
Solution:

(ii) sin-1 \(\frac{3}{5}\) + cos-1 \(\frac{12}{13}\) = cos-1 \(\frac{33}{65}\)
Solution:

(iii) tan-1 \(\frac{1}{7}\) + tan-1 \(\frac{1}{13}\) = tan-1 \(\frac{2}{9}\)
Solution:
L.H.S = tan-1 \(\frac{1}{7}\) + tan-1 \(\frac{1}{13}\)
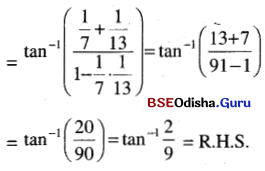
(iv) tan-1 \(\frac{1}{2}\) + tan-1 \(\frac{1}{5}\) + tan-1 \(\frac{1}{8}\) = \(\frac{\pi}{4}\)
Solution:

(v) tan ( 2tan-1 \(\frac{1}{5}\) – \(\frac{\pi}{4}\) ) + \(\frac{7}{17}\) = 0
Solution:
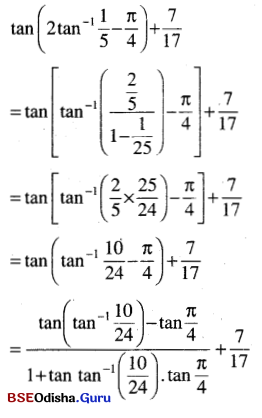
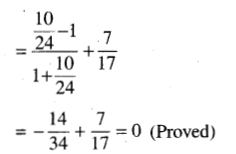
Question 5.
Prove the following statements:
(i) cot-1 9 + cosec-1 \(\frac{\sqrt{41}}{4}\) = \(\frac{\pi}{4}\)
Solution:

(ii) sin-1 \(\frac{4}{5}\) + 2 tan-1 \(\frac{1}{3}\) = \(\frac{\pi}{2}\)
Solution:
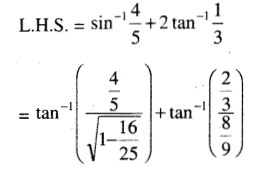

(iii) 4 tan-1 \(\frac{1}{5}\) – tan-1 \(\frac{1}{70}\) + tan-1 \(\frac{1}{99}\) = \(\frac{\pi}{4}\)
Solution:
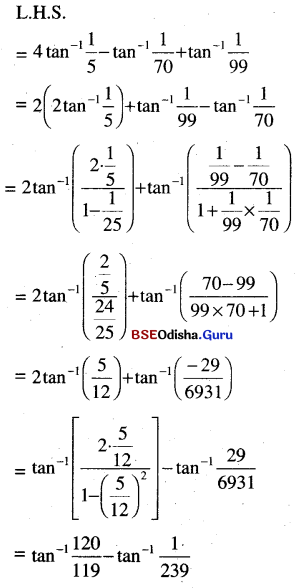
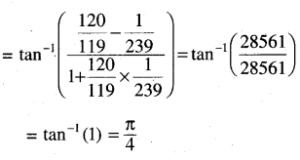
(iv) 2 tan-1 \(\frac{1}{5}\) + sec-1 \(\frac{5 \sqrt{2}}{7}\) + 2 tan-1 \(\frac{1}{8}\) = \(\frac{\pi}{4}\)
Solution:

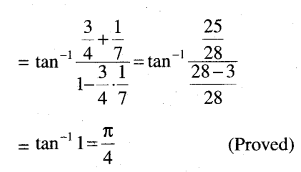
(v) cos-1 \(\frac{12}{13}\) + 2 cos-1 \(\sqrt{\frac{64}{65}}\) + cos-1 \(\sqrt{\frac{49}{50}}\) = cos-1 \(\frac{1}{\sqrt{2}}\)
Solution:


(vi) tan2 cos-1 \(\frac{1}{\sqrt{3}}\) + cot2 sin-1 \(\frac{1}{\sqrt{5}}\) = 6
Solution:
tan2 cos-1 \(\frac{1}{\sqrt{3}}\) + cot2 sin-1 \(\frac{1}{\sqrt{5}}\)
= tan2 tan-1 √2 + cot2 cot-1 (2)
= 2 + 4 = 6
![]()
(vii) cos tan-1 cot sin-1 x = x.
Solution.
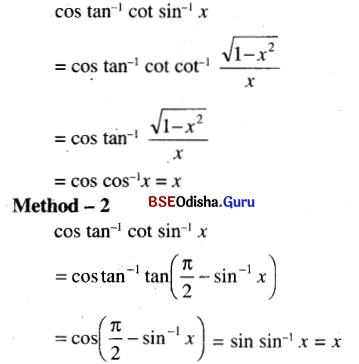
Question 6.
Prove the following statements:
(i) cot-1 (tan 2x) + cot-1 (- tan 2x) = π
Solution:

(ii) tan-1 x + cot-1 (x + 1) = tan-1 (x2 + x + 1)
Solution:

(iii) tan-1 (\(\frac{a-b}{1+a b}\)) + tan-1 (\(\frac{b-c}{1+b c}\)) = tan-1 a – tan-1 c.
Solution:
tan-1 (\(\frac{a-b}{1+a b}\)) + tan-1 (\(\frac{b-c}{1+b c}\))
= tan-1 a – tan-1 b + tan-1 b – tan-1 c
= tan-1 a – tan-1 c.
(iv) cot-1 \(\frac{p q+1}{p-q}\) + cot-1 \(\frac{q r+1}{q-r}\) + cot-1 \(\frac{r p+1}{r-p}\) = 0
Solution:
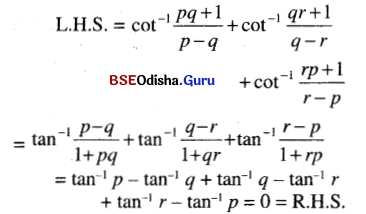
(v)
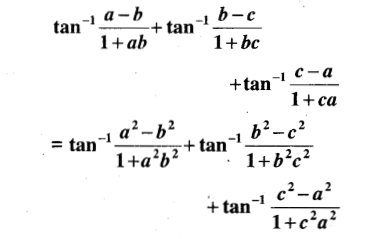
Solution:

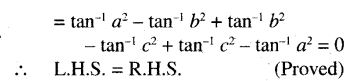
Question 7.
Prove the following statements:
(i) tan-1 \(\frac{2 a-b}{b \sqrt{3}}\) + tan-1 \(\frac{2 b-a}{a \sqrt{3}}\) = \(\frac{\pi}{3}\)
Solution:

(ii) tan-1 \(\frac{1}{x+y}\) + tan-1 \(\frac{y}{x^2+x y+1}\) = tan-1 \(\frac{1}{x}\)
Solution:
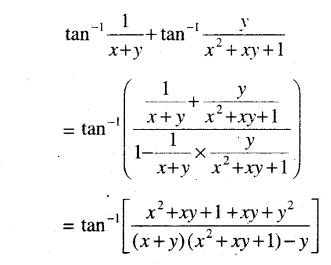

(iii) sin-1 \(\sqrt{\frac{x-q}{p-q}}\) = cos-1 \(\sqrt{\frac{p-x}{p-q}}\) = cot-1 \(\sqrt{\frac{p-x}{x-q}}\)
Solution:

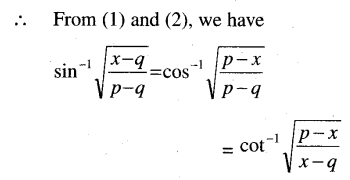
(iv) sin2 (sin-1 x + sin-1 y + sin-1 z) = cos2 (cos-1 x + cos-1 y + cos-1 z)
Solution:
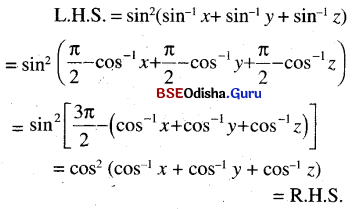
(v) tan (tan-1 x + tan-1 y + tan-1 z) = cot (cot-1 x + cot-1 y + cot-1 z)
Solution:
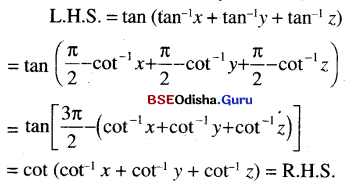
Question 8.
(i) If sin-1 x + sin-1 y + sin-1 z = π, show that x\(\sqrt{1-x^2}\) + x\(\sqrt{1-y^2}\) + x\(\sqrt{1-z^2}\) = 2xyz
Solution:
Let sin-1 x = α, sin-1 y = β, sin-1 z = γ
∴ α + β + γ = π
∴ x = sin α, y = sin β, z = sin γ
or, α + β = π – γ
or, sin(α + β) = sin(π – γ) = sin γ
and cos(α + β) = cos(π – γ) = – cos γ

(ii) tan-1 x + tan-1 y + tan-1 z = π show that x + y + z = xyz.
Solution:
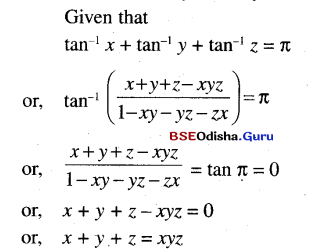
(iii) tan-1 x + tan-1 y + tan-1 z = \(\frac{\pi}{2}\). Show that xy + yz + zx = 1
Solution:
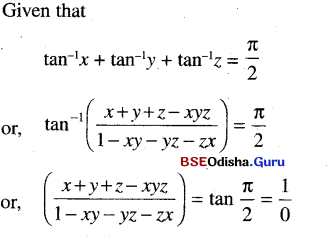
or, 1 – xy – yz – zx = 0
⇒ xy + yz + zx = 1
(iv) If r2 = x2 +y2 + z2, Prove that tan-1 \(\frac{y z}{x r}\) + tan-1 \(\frac{z x}{y r}\) + tan-1 \(\frac{x y}{z r}\) = \(\frac{\pi}{2}\)
Solution:

(v) In a triangle ABC if m∠A = 90°, prove that tan-1 \(\frac{b}{a+c}\) + tan-1 \(\frac{c}{a+b}\) = \(\frac{\pi}{4}\). where a, b, and c are sides of the triangle.
Solution:
L.H.S. tan-1 \(\frac{b}{a+c}\) + tan-1 \(\frac{c}{a+b}\)

Question 9.
Solve
(i) cos (2 sin-1 x) = 1/9
Solution:

(ii) sin-1 x + sin-1 (1 – x) = \(\frac{\pi}{2}\)
Solution:
sin-1 x + sin-1 (1 – x) = \(\frac{\pi}{2}\)
or, sin-1 (1 – x) = \(\frac{\pi}{2}\) – sin-1 x = cos-1 x
or, sin-1 (1 – x) = sin-1 \(\sqrt{1-x^2}\)
or, 1 – x = \(\sqrt{1-x^2}\)
or, 1 + x2 – 2x = 1 – x2
or, 2x2 – 2x = 0
or, 2x (x – 1) = 0
∴ x = 0 or, 1
(iii) sin-1 (1 – x) – 2 sin-1 x = \(\frac{\pi}{2}\)
Solution:
sin-1 (1 – x) – 2 sin-1 x = \(\frac{\pi}{2}\)
⇒ – 2 sin-1 x = \(\frac{\pi}{2}\) – sin-1 (1 – x)
⇒ cos-1 (1 – x)
⇒ cos (– 2 sin-1 x) = 1 – x ….. (1)
Let sin-1 Θ ⇒ sin Θ
Now cos (– 2 sin-1 x) = cos (-2Θ)
= cos 2Θ = 1 – 2 sin2 Θ = 1 – 2x2
Using in (1) we get
1 – 2x2 = 1 – x
⇒ 2x2 – x = 0 ⇒ x (2x – 1) = 0
⇒ x = 0, ½, But x = ½ does not
Satisfy the given equation, Thus x = 0.
![]()
(iv) cos-1 x + sin-1 \(\frac{x}{2}\) = \(\frac{\pi}{6}\)
Solution:

(v) tan-1 \(\frac{x-1}{x-2}\) + tan-1 \(\frac{x+1}{x+2}\) = \(\frac{\pi}{4}\)
Solution:
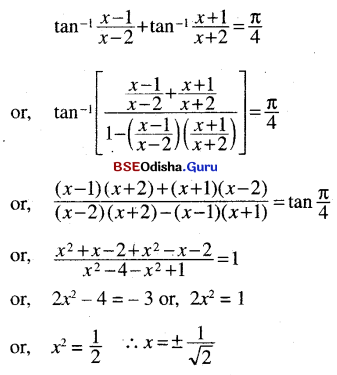
(vi) tan-1 \(\frac{1}{2 x+1}\) + tan-1 \(\frac{1}{4 x+1}\) = tan-1 \(\frac{2}{x^2}\)
Solution:

(vii) 3 sin-1 \(\frac{2 x}{1+x^2}\) – 4 cos-1 \(\frac{1-x^2}{1+x^2}\) + 2 tan-1 \(\frac{2 x}{1-x^2}\) = \(\frac{\pi}{3}\)
Solution:

(viii) cot-1 \(\frac{1}{x-1}\) + cot-1 \(\frac{1}{x}\) + cot-1 \(\frac{1}{x+1}\) = cot-1 \(\frac{1}{3x}\)
Solution:
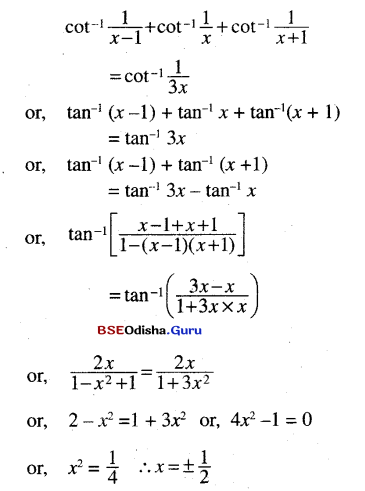
(ix) cot-1 \(\frac{1-x^2}{2 x}\) = cosec-1 \(\frac{1+a^2}{2 a}\) – sec-1 \(\frac{1+b^2}{1-b^2}\)
Solution:

(x) sin-1 \(\left(\frac{2 a}{1+a^2}\right)\) + sin-1 \(\left(\frac{2 b}{1+b^2}\right)\) = 2 tan-1 x
Solution:

(xi) sin-1 y – cos-1 x = cos-1 \(\frac{\sqrt{3}}{2}\)
Solution:

(xii) sin-1 2x + sin-1 x = \(\frac{\pi}{3}\)
Solution:
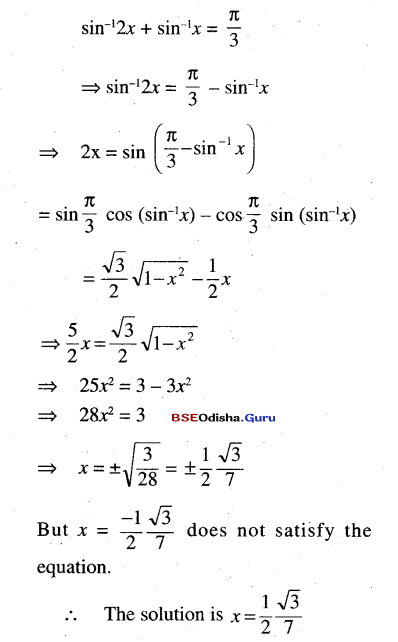
Question 10.
Rectify the error ifany in the following:
sin-1 \(\frac{4}{5}\) + sin-1 \(\frac{12}{13}\) + sin-1 \(\frac{33}{65}\)
Solution:

Question 11.
Prove that:
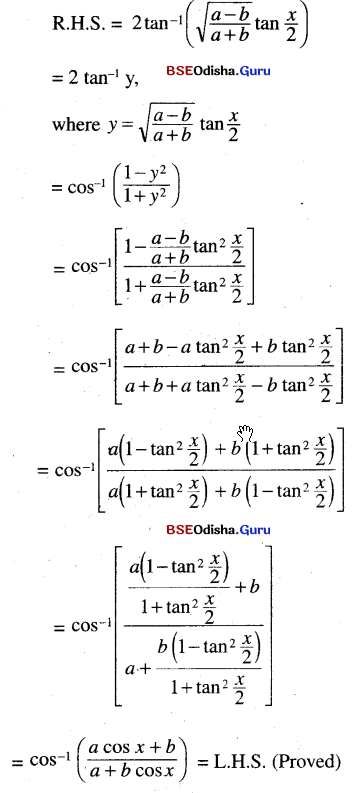
(i) cos-1 \(\left(\frac{b+a \cos x}{a+b \cos x}\right)\) = 2 tan-1 \(\left(\sqrt{\frac{a-b}{a+b}} \tan \frac{x}{2}\right)\)
Solution:
(ii) tan \(\left(\frac{\pi}{4}+\frac{1}{2} \cos ^{-1} \frac{a}{b}\right)\) + tan \(\left(\frac{\pi}{4}-\frac{1}{2} \cos ^{-1} \frac{a}{b}\right)\)
Solution:
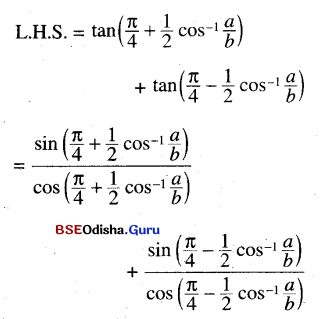
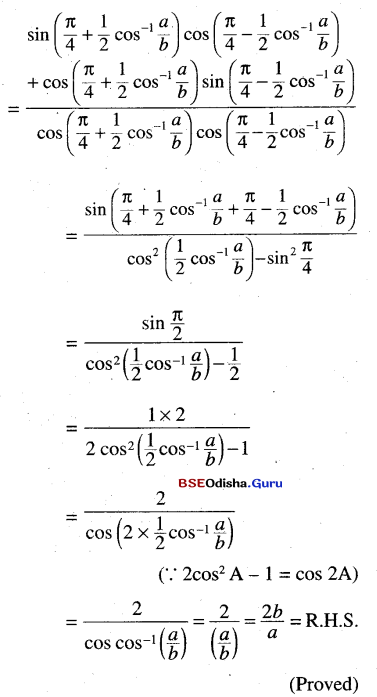
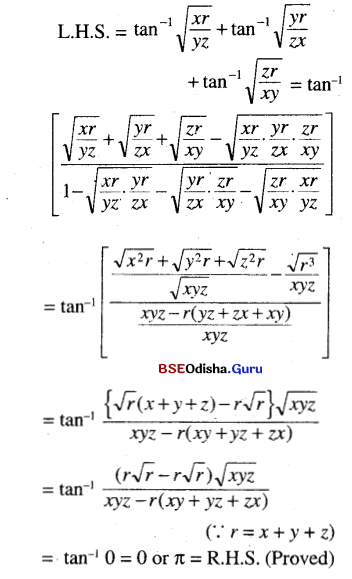
(iii) tan-1 \(\sqrt{\frac{x r}{y z}}\) + tan-1 \(\sqrt{\frac{y r}{y x}}\) + tan-1 \(\sqrt{\frac{z r}{x y}}\) = π where r = x + y +z.
Solution:
Question 12.
(i) If cos-1 (\(\frac{x}{a}\)) + cos-1 (\(\frac{y}{b}\)) = Θ, prove that \(\frac{x^2}{a^2}\) – \(\frac{2 x}{a b}\) cos Θ + \(\frac{y^2}{b^2}\) = sin2 Θ.
Solution:


(ii) If cos-1 (\(\frac{x}{y}\)) + cos-1 (\(\frac{y}{3}\)) = Θ, prove that 9x2 – 12xy cos Θ + 4y2 = 36 sin2 Θ.
Solution:

(iii) If sin-1 (\(\frac{x}{a}\)) + sin-1 (\(\frac{y}{b}\)) = sin-1 (\(\frac{c^2}{a b}\)) prove that b2x2 + 2xy \(\sqrt{a^2 b^2-c^4}\) a2y2 = c2
Solution:
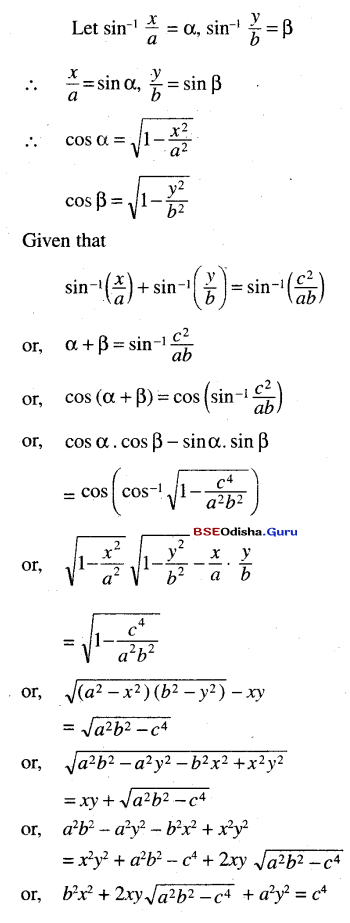
(iv) If sin-1 (\(\frac{x}{a}\)) + sin-1 (\(\frac{y}{b}\)) = α prove that \(\frac{x^2}{a^2}\) + \(\frac{2 x y}{a b}\) cos α + \(\frac{y^2}{b^2}\) = sin2 α
Solution:
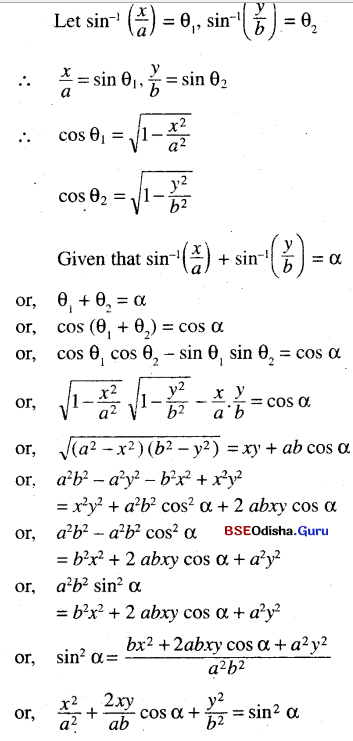
![]()
(v) If sin-1 x + sin-1 y + sin-1 z = π prove that x2 + y2 + z2 + 4x2y2z2 = 2 ( x2y2 + y2z2 + z2x2 )
Solution:
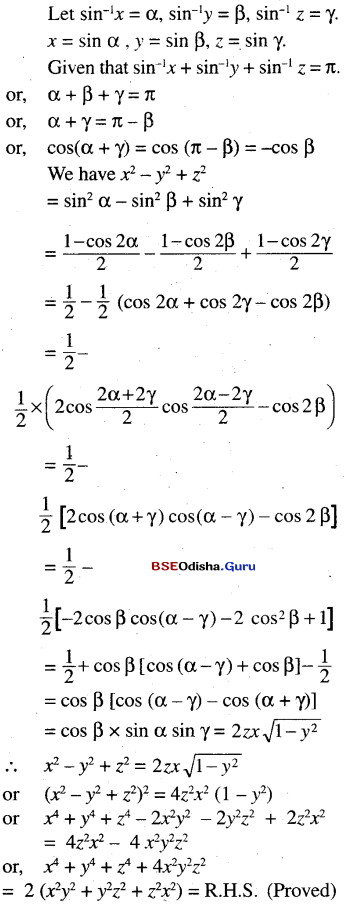
Question 13.
Solve the following equations:
(i) tan-1 \(\frac{x-1}{x+1}\) + tan-1 \(\frac{2 x-1}{2 x+1}\) = tan-1 \(\frac{23}{36}\)
Solution:

(ii) tan-1 \(\frac{1}{3}\) + tan-1 \(\frac{1}{5}\) + tan-1 \(\frac{1}{7}\) + tan-1 x = \(\frac{\pi}{4}\)
Solution:

(iii) cos-1 \(\left(x+\frac{1}{2}\right)\) + cos-1 x+ cos-1 \(\left(x-\frac{1}{2}\right)\) = \(\frac{3 \pi}{2}\)
Solution:


(iv) 3tan-1 \(\frac{1}{2+\sqrt{3}}\) – tan-1 \(\frac{1}{x}\) = tan-1 \(\frac{1}{3}\)
Solution: