Odisha State Board Elements of Mathematics Class 11 CHSE Odisha Solutions Chapter 7 Linear Inequalities Ex 7(b) Textbook Exercise Questions and Answers.
CHSE Odisha Class 11 Math Solutions Chapter 7 Linear Inequalities Exercise 7(b)
Solve graphically
Question 1.
x < y
Solution:
x < y
Step – 1: Let us draw the dotted line x = y
| X | 0 | 1 |
| y | 0 | 1 |
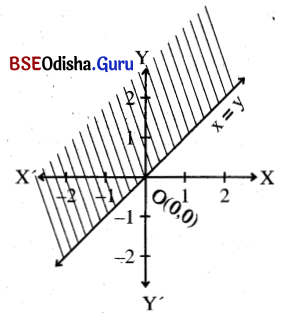
Step – 2: Let us take a point say (1, 0) which is not on the line. Putting x = 1, y = 0 in the equation we get 1 < 0 (false).
⇒ (1, 0) does not satisfy the inequality.
⇒ The solution is the half-plane that does not contain (1, 0)
Step – 3: The shaded region is the solution region.
![]()
Question 2.
3x + 4y ≥ 12
Solution:
3x + 4y ≥ 12
Step – 1: Let us draw the line 3x + 4y = 12
| X | 4 | 0 |
| y | 0 | 3 |
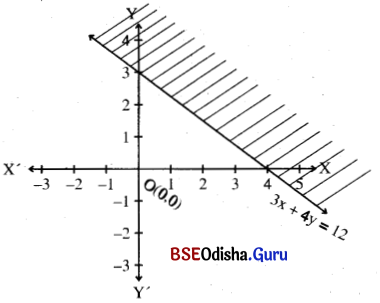
Step – 2: Let us consider the point (0, 0) which is not on the line. Putting x = 0, y = 0 in the inequality we have 0 ≥ 12 (false).
∴ (0, 0) does not satisfy the inequality.
⇒ The half-plane that does not contain (0, 0) is the solution region.
Step – 3: The shaded region is the solution region.
Question 3.
x – y > 0
Solution:
x – y > 0
Step – 1: Let us draw the dotted line x = y.
| X | 0 | 1 |
| y | 0 | 1 |
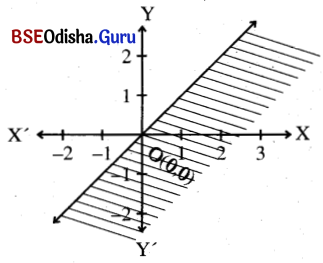
Step – 2: Let us consider (1, 0) which is not on the line.
Putting x = 1, y = 0 in the inequation we get 1 > 0 (True)
⇒ (1, 0) satisfies the inequation.
⇒ The half-plane containing (1, 0) is the solution region.
Question 4.
x + 2y – 5 ≤ 0
Solution:
x + 2y – 5 ≤ 0
Step – 1: Let us draw the line x + 2y – 5 = 0
⇒ y = \(\frac{5-x}{2}\)
| X | 5 | 1 |
| y | 0 | 2 |
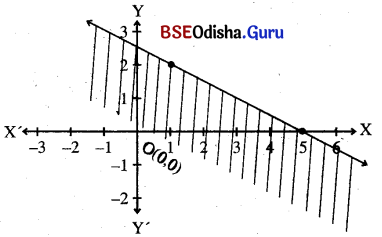
Step – 2: Let us consider the point (0, 0) which does not lie on the line putting x = 0, y = 0 in the inequation we get – 5 < 0 (True).
⇒ The point satisfies the inequation.
⇒ The half-plane containing (0, 0) is the solution region.
Step – 3: The shaded region is the solution region.
![]()
Question 5.
7x – 4y < 14
Solution:
7x – 4y < 14
Step – 1: Let us draw the dotted line 7x – 4y = 14
| X | 2 | 6 |
| y | 0 | 7 |
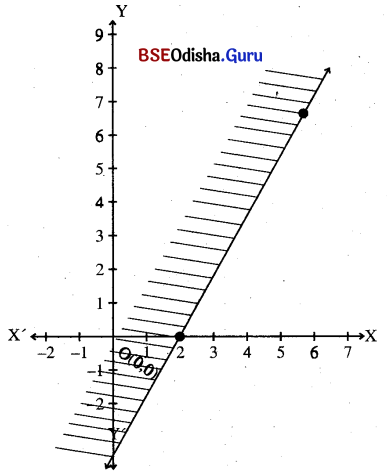
Step – 2: Let us consider the point (0, 0) which does not lie on the line. Putting x = 0, y = 0 in the inequality we get 0 < 14 (True).
⇒ (0, 0) satisfies the inequation.
⇒ The half-plane including (0, 0) is the solution region.
Step – 3: The solution region is the shaded region.
Question 6.
x + 8y + 10 > 0
Solution:
x + 8y + 10 > 0
Step – 1: Let us draw the dotted line x + 8y + 10 = 0
| X | -10 | -2 |
| y | 0 | -1 |
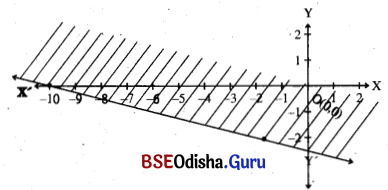
Step – 2: Let us consider the point (0, 0) which does not lie on the line. Putting x = 0, y = 0 in the inequation we get 10 > 0 (True)
⇒ (0, 0) satisfies the inequality.
⇒ The half-plane containing origin is the solution region.
Step – 3: The solution region’ is the shaded region.
Question 7.
5x + 6y < 12
Solution:
5x + 6y < 12
Step – 1: Let us draw the dotted line 5x + 6y = 12
| x | -6 | 0 | 6 |
| y | 7 | 2 | -3 |
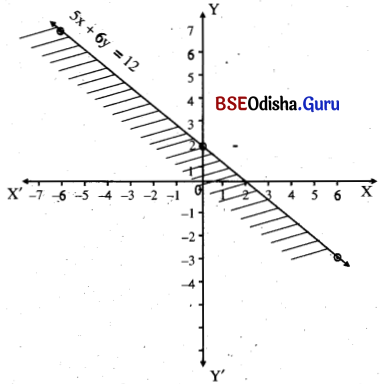
Step – 2: Putting x = 0, y = 0 in the equation we get, 0 < 12 (True)
⇒ The (0, 0) satisfies the equation.
Step – 3: The shaded region is the required solution.
![]()
Question 8.
– 3x + y > 0
Solution:
Step – 1: Let us draw the dotted line – 3x + y = 0
| x | 0 | 1 | -1 |
| y | 0 | 3 | -3 |
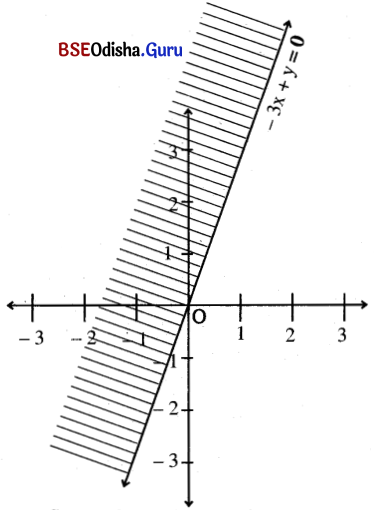
Step – 2: Putting x – 1, y = 0 in the equation we get, – 3 > 0 (false)
∴ Point (1, 0) does not satisfy the in the equation.
Step – 3: The shaded half-plane is the solution.
Question 9.
3x + 8y > 24
Solution:
Step- 1: Let us draw the dotted graph of 3x + 8y = 24
| x | 8 | 0 |
| y | 0 | 3 |
Step- 2: Putting x = 0, y- 0 we get, 0 > 24 (false)
∴ 0, (0, 0) does not satisfy the in equality.
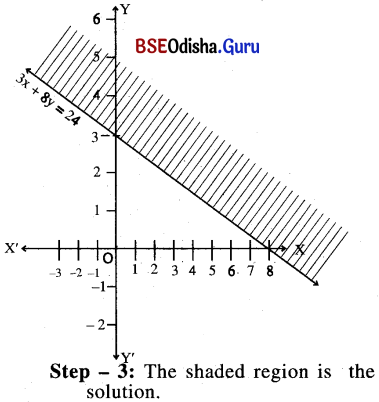
Question 10.
x + y > 1
Solution:
Step – 1: Let us draw the graph x + y = 1
| x | 1 | 0 |
| y | 0 | 1 |
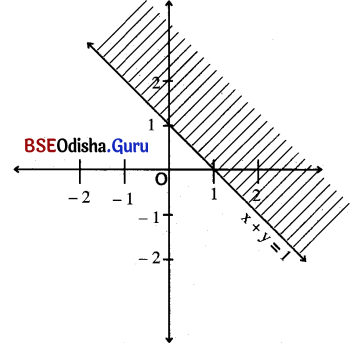
Step – 2: Putting x = 0, y = 0 in the equation we get, 0 > 1 (false)
∴ 0 (0, 0) does not satisfy the in equation
Step – 3: The shaded region is the solution.
Question 11.
x ≤ 0
Solution:
Step – 1: Let us draw the graph x = 0
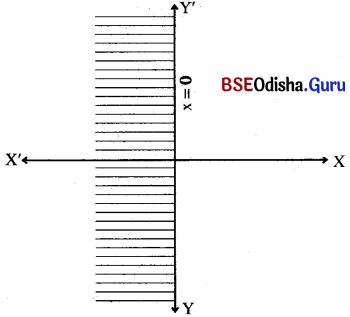
Step – 2: Putting x = – 1 we get, – 1 ≤ 0 (True)
Thus, the shaded region is the solution.
![]()
Question 12.
y > 5
Solution:
Step – 1: Let us draw the dotted graph of y = 5
| x | 0 | 1 | -1 |
| y | 5 | 5 | 5 |
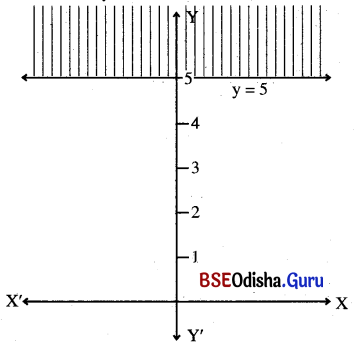
Step- 2: Putting x = 0, y = 0 we have 0 > 5 (false)
we 0(0, 0) does not satisfy. the inequality.
Step – 3: The shaded region is the solution.
