CHSE Odisha Class 11 Math Solutions Chapter 8 Permutations and Combinations Ex 8(c)

Odisha State Board Elements of Mathematics Class 11 Solutions CHSE Odisha Chapter 8 Permutations and Combinations Ex 8(c) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 8 Permutations and Combinations Exercise 8(c)

Question 1.
Compute the following :
(i) ¹²C₃
Solution:
¹²C₃ = \(\frac{(12) !}{3 ! 9 !}=\frac{12 \cdot 11 \cdot 10}{3 \cdot 2}\) = 220

(ii) ¹⁵C₁₂
Solution:
¹⁵C₁₂ = \(\frac{(15) !}{(12) ! 3 !}=\frac{15 \cdot 14 \cdot 13}{3 \cdot 2}\)
= 5.7.13 = 455

(iii) ⁹C₄ + ⁹C₅
Solution:
⁹C₄ + ⁹C₅ = \(\frac{9 !}{4 ! 5 !}+\frac{9 !}{5 ! 4 !}\)
\(=\frac{9 \cdot 8 \cdot 7 \cdot 6}{4 \cdot 3 \cdot 2 \cdot 1}\) × 2 = 252

(iv) ⁷C₃ + ⁶C₄ + ⁶C₃
Solution:
⁷C₃ + ⁶C₄ + ⁶C₃ = ⁷C₃ + ⁶C₄ + ⁶C4-1
= ⁷C₃ + ⁶⁺¹C₄ = ⁷C₃ + ⁷C₄
(∴ ⁿc_r + ⁿC_r-1– = ⁿ⁺¹c_r)
= ⁷C₄ + ⁷C_4-1 = ⁷⁺¹C₄
= ⁸C₄ = \(\frac{8 !}{4 !(8-4) !}=\frac{8 \cdot 7 \cdot 6 \cdot 5}{4 \cdot 3 \cdot 2 \cdot 1}\) = 70

(v) ⁸C₀ + ⁸C₁ + …….. + ⁸c₈
Solution:
⁸C₀ + ⁸C₁ + …….. + ⁸c₈ = 2⁸ = 256

Question 2.
Solve :
(i) ⁿC₄ = ⁿC₁₁ ;
Solution:
ⁿC₄ = ⁿC₁₁ ;  (∴ n = 4 + 11 = 15)

(ii) ²ⁿC₃ : ⁿC₃ = 44: 5
Solution:
²ⁿC₃ : ⁿC₃ = \(\frac{44}{5}\)
⇒ \(\frac{2 n !}{2 n-3 !} / \frac{n !}{n-3 !}=\frac{44}{5}\)

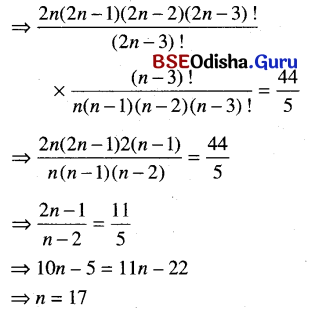
Question 3.
Find n and r if ⁿP_r = 1680, ⁿC_r = 70.
Solution:
ⁿP_r = 1680, ⁿC_r = 70
∴ \(\frac{{ }^n \mathrm{P}_r}{{ }^n \mathrm{C}_r}=\frac{1680}{70}\)
or, r ! = 24 = 4!
∴ r = 4
Again, ⁿC_r = 70 or ⁿC₄ = 70
or, \(\frac{n !}{4 !(n-4) !}=70\)
or, n(n – 1) (n – 2) (n – 3)
= 70 × 4! = 7 × 10 × 4 × 3 × 2
= 8 × 7 × 6 × 5
or, n(n – 1) (n – 2) (n – 3)
or, 8(8 – 1) (8 – 2) (8 – 3)
∴ n = 8

Question 4.
How many diagonals can an n-gon(a polygon with n sides) have?
Solution:
A polygon of n – sides has n vertices.
∴ The number of st. lines joining the n-vertices is ⁿC₂.
∴ The number of diagonals is ⁿC₂ – n

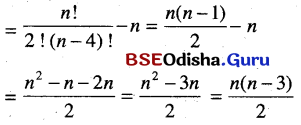
Question 5.
If a set A has n elements and another set B has m elements, what is the number of relations from A to B?
Solution:
If |A| = n, |B| = m
then |A × B| = mn
∴ The number of possible subsets of
A × B = 2^mn
∴ The number of relations from A to B is 2^mn.

Question 6.
From five consonants and four vowels, how many words consist of three consonants and two vowels?
Solution:
Words of consisting of 3 consonants and 2 vowels are to be formed from five consonants and 4 vowels.
∴ The number of ways = ⁵C₃ × ⁴C₂
Again, 5 letters can be arranged among themselves in 5! ways.
∴ The total number of ways
= ⁵C₃ × ⁴C₂ × 5! = 10 × 6 × 120 = 7200.

Question 7.
In how many ways can a committee of four gentlemen and three ladies be formed out of seven gentlemen and six ladies?
Solution:
A committee of 4 gentlemen and 3 ladies is to be formed out of 7 gentlemen and 6 ladies.
∴ The number of ways in which the committee can be formed.
⁷C₄ × ⁶C₃ = \(\frac{7 \cdot 6 \cdot 5}{3.2} \times \frac{6 \cdot 5 \cdot 4}{3 \cdot 2}\) = 700

Question 8.
A bag contains 4 black and 5 white balls out of which 6 balls are drawn arbitrarily. In how many ways can this be done? Find also the number of ways such that at least 3 black balls can be drawn.
Solution:
A bag contains 4 black and 5 white balls out of which 6 balls are drawn arbitrarily.
∴ The number of ways in which balls are drawn \({ }^9 \mathrm{C}_6=\frac{9 \cdot 8 \cdot 7}{3 \cdot 2 \cdot 1}\) = 84 as the total number of balls is 9. If at least 3 black balls are drawn, then the drawing can be made as follows.

Black(4)	White(5)
3	3
4	2

The number of ways in which at least 3 black balls are drawn
= (⁴C₃ × ⁵C₃) + (⁴C₄ × ⁵C₂)
= (4 × 10) + (1 × 10) = 50

Question 9.
How many triangles can be drawn by joining the vertices of a decagon?
Solution:
A decagon has 10 vertices and 3 noncollinear points are required to be a triangle.
∴ The number of triangles formed by the joining of the vertices of a decagon is
¹⁰C₃ = \(\frac{10 !}{3 ! 7 !}=\frac{10 \cdot 9 \cdot 8}{3 \cdot 2 \cdot 1}\) = 120

Question 9.
How many triangles can be drawn by joining the vertices and the center of a regular hexagon?
Solution:
A regular hexagon has six vertices. Triangles are to be formed by joining the vertices and center of the hexagon. So there is a total of 7 points. So the number of triangles formed.
⁷C₃ = \(\frac{7 !}{3 ! 4 !}=\frac{7 \cdot 6 \cdot 5}{3 \cdot 2 \cdot 1}\) = 35
As the hexagon has 3 main diagonals, which pass through the center hence can not form 3 triangles.
∴ The required number of triangles 35 – 3 = 32

Question 11.
Sixty points lie on a plane, out of which no three points are collinear. How many straight lines can be formed by joining pairs of points?
Solution:
Sixty points lie on a plane, out of which no. 3 points are collinear. A straight line required two points. The number of straight lines formed by joining 60 points is
⁶⁰C₂ = \(\frac{60 !}{2 \times 58 !}=\frac{60 \times 59}{2}\) = 1770

Question 12.
In how many ways can 10 boys and 10 girls sit in a row so that no two boys sit together?
Solution:
10 boys and 10 girls sit in a row so that no two boys sit together. So a boy is to be seated between two girls or at the two ends of the row. So the boys are to be sitted in 11 positions in ¹¹C₁₀ ways. Again 10 boys and 10 girls can be arranged among themselves in 10! and 10! ways respectively.
∴ The total number of ways = ¹¹C₁₀ × 10! × 10! = (11)! × (10)!

Question 13.
In how many ways can six men and seven girls sit in a row so that the girls always sit together?
Solution:
Six men and seven girls sit in a row so that the girls always sit together. Considering the 7 girls as one person, there are a total of 7 persons who can sit in 7! ways. Again the 7 girls can be arranged among themselves in 7! ways.
∴ The total number of arrangements
= 7! × 7!
= (7!)²

Question 14.
How many factors does 1155 have that are divisible by 3?
Solution:

∴ In order to be a factor of 1155 divisible by 3, we have to choose one or two of 5, 7, and 11 along with 3 or 3 alone.
∴ The number of ways = ³C₁ + ³C₂ + ³C₀ = 2³ – 1 = 7
∴ The number of factors is 7 excluding 1155 itself.

Question 15.
How many factors does 210 have?
Solution:

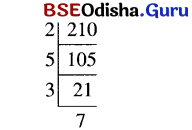
∴ We can choose at least one 2, 3, 5, or 7  to be a factor of 210.
∴ The number of factors.
= ⁴C₁ + ⁴C₂ + ⁴C₃ + ⁴C₄ = 2⁴ – 1 = 15
∴ The number of factors is 210 is 15. (Including 215 itself and excluding 1).

Question 16.
If n is a product of k distinct primes what is the total number of factors of n?
Solution:
n is a product of k distinct primes.
∴ In order to be a factor, of n, we have chosen at least one of k distinct primes.
∴ The number of ways = ^kC₁ + ^kC₂ + ……… ^kC_k-1 = 2^k  – 1 – 1
∴ The number of factors of n is 2^k – 2.
(Excluding 1 as 1 is not prime. It is also not include n.)

Question 17.
If m has the prime factor decomposition P₁^r1, P₂^r2 ….. P_n^rn, what is the total number of factors of m (excluding 1)?
Solution:
m has the prime factor decomposition P₁^r1, P₂^r2 ….. P_n^rn,
∴ m = P₁^r1, P₂^r2 ….. P_n^rn,
P₁ is a factor of m which occurs r₁ times. Each of the factors P₁^r1 will give rise to (r₁ + 1) factors.
Similarly
P₂^r2 gives (r₂ + 1) factors and so on.
∴ The total number of factors (r₁ + 1) (r₂ + 1) ….. (r_n + 1) – 1 (including m).

Question 18.
If 20! were multiplied out, how many consecutive zeros would it have on the right?
Solution:
If 20! were multiplied out, then the number of consecutive zeros on the right is 4. due to the presence of 4 x 5, 10, 14 x 15,20.

Question 19.
How many factors of 10,000 end with a 5 on the right?
Answer:
We have 1000 = 2⁴ × 5⁴ The factors of 10000 ending with 5 are 5, 5 × 5 = 25, 5 × 5 × 5 = 125
5 × 5 × 5 × 5 = 625
∴ There are 4 factors ending With 5.

Question 20.
A man has 6 friends. In how many ways can he invite two or more to a dinner party?
Solution:
A man has 6 friends. He can invite 2 or more of his friends to a dinner party.
∴ He can invite 2, 3, 4, 5, or 6 of his friends in
⁶C₂ + ⁶C₃ + ⁶C₄ + ⁶C₅ + ⁶C₆ = 2⁶ – ⁶C₀ – ⁶C₁
= 64 – 7 = 57 ways.

Question 21.
In how many ways can a student choose 5 courses out of 9 if 2 courses are compulsory?
Solution:
A student is to choose 5 courses out of 9 in which 2 courses are compulsory. as 2 courses are compulsory, he is to choose 3 courses out of 7 courses in ⁷C₃ = 35 ways.

Question 22.
In how many ways can a student choose five courses out of the courses? C₁, C₂, …………. C₉ if C₁, C₂ are compulsory and C₆, C₈ cannot be taken together?
Solution:
A student chooses five courses out of the courses? C₁, C₂, …………. C₉ if C₁, C₂ are compulsory and C₆, C₈ cannot be taken together.
∴ He is to choose 3 courses out of C₃, C₄, ………… ,C₈, C₉.
Without taking any restrictions 3 courses out of C₃, C₄, …… C₉, i.e. from 7 courses in ⁷C₃ ways. If C₆, C₈ are taken together then one course only to be choosen from C₃, C₄, C₅, C₇, C₉ by ⁵C₁ ways. Hence required number of ways.
= ⁷C₃ – ⁵C₁
= \(\frac{7 \times 6 \times 5}{3 \times 2 \times 1}\) – 5
= 35 – 5 = 30 ways.

Question 23.
A cricket team consisting of 11 players is to be chosen from 8 batsmen and 5 bowlers. In how many ways can the team be chosen so as to include at least 3 bowlers?
Solution:
A cricket team consisting of 1 1 player is to be chosen from 8 batsmen and 5 bowlers, as to include at least 3 bowlers.
The selection can be made as follows :

Batsmen(8)	Bowlers(5)
8	3
7	4
6	5

The number of selections is
(⁸C₈ × ⁵C₃) + (⁸C₇ × ⁵C₄) + (⁸C₆ × ⁵C₅)
= (1 × 10) + (8 × 5) + (28 × 1)
= 10 + 40 + 28 = 78

Question 24.
There are n + r points on a plane out of which n points lie on a straight line L and out of the remaining r points that lie outside L, no three points are collinear. What is the number of straight lines that can be formed by joining pairs of their points?
Solution:
There are n + r points on a plane out of which n points are collinear and out of which r points are not collinear.
∴ We can form a straight line by joining any two points.
n-collinear points form one line and r-non-collinear points form ^rC₂ lines.
Again, each of the r non-collinear points when joined to each of the noncollinear points, forms n lines.
∴ The number of such limes is r x n.
∴ The total number of lines

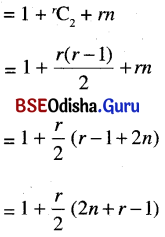
Question 25.
There are 10 books in a shelf with different titles; five of these have red covers and others have green covers. In how many ways can these be arranged so that the red books are placed together?
Solution:
There are 10 books in a shelf with different titles, 5 of these are red covers and others are green covers considering 5 red-covered books as one book, we have a total of 6 books which can be arranged in 6! ways. The five red cover books are arranged among themselves in 5! ways.
∴ The total number of arrangements
= 5! x 6!