Odisha State Board CHSE Odisha Class 12 Logic Solutions Unit 3 ତର୍କଦୋଷ ଓ ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ରି Long Answer Questions.
CHSE Odisha Class 12 Logic Unit 3 Long Answer Questions in Odia Medium
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
1.ନିମ୍ନଲିଖୂତ ତର୍କଦୋଷଗୁଡ଼ିକୁ ବ୍ୟାଖ୍ୟା କର ।
(କ) ଉଚ୍ଚାରତଣଜନିତ ତର୍କଦୋଷ :
Answer:
ବାକ୍ୟଟି ଉଚ୍ଚାରଣ କଲାବେଳେ ବିଭିନ୍ନ ଶବ୍ଦ ଉପରେ ଗୁରୁତ୍ଵ ଦେଲେ ଏହାର ବିଭିନ୍ନ ଅର୍ଥ ପ୍ରକାଶ ପାଇଥାଏ । ଅର୍ଥାତ୍ ଉଦ୍ଦେଶ୍ୟମୂଳକ ଭାବେ କୌଣସି ଶବ୍ଦ ଉପରେ ଗୁରୁତ୍ଵ ଦେଇ ବାକ୍ୟଟିକୁ ଉଚ୍ଚାରଣ କଲେ, ବାକ୍ୟର ଅର୍ଥ ଭିନ୍ନ ପ୍ରକାରର ହୋଇଥାଏ । ଏହାକୁ ଉଚ୍ଚାରଣଜନିତ ତର୍କଦୋଷ କୁହାଯାଏ ।
‘‘ତୁମେ ଏହି ଗାଈଟିକୁ ମୋତେ ବିକ୍ରି କରିଅଛ ।’’
ଏହି ବାକ୍ୟର ବିଭିନ୍ନ ଶବ୍ଦ ଉପରେ ଗୁରୁତ୍ଵ ଦେଲେ ବାକ୍ୟର ଅର୍ଥ ଭିନ୍ନ ଭିନ୍ନ ପ୍ରକାରର ହୋଇଥାଏ; ଯଥା –
‘ତୁମେ’ ଉପରେ ପ୍ରାଧାନ୍ୟ ଦେଲେ, ତୁମେ ବିକ୍ରି କରିଅଛ, ତୁମ ବାପା ବା ଭାଇ ନୁହନ୍ତି ।’
‘ଏହି’ ଉପରେ ପ୍ରାଧାନ୍ୟ ଦେଲେ, ‘ଠିକ୍ ଏହି ଗାଈ, ଅନ୍ୟ ଗାଈ ନୁହେଁ ।’
‘ଗାଈ’ ଉପରେ ପ୍ରାଧାନ୍ୟ ଦେଲେ, ‘ଗାଈ ବିକ୍ରି କରିଅଛ, ଛେଳି ମେଣ୍ଢା କିମ୍ବା ଅନ୍ୟ ପଶୁ ନୁହେଁ ।’
‘ମୋତେ’ ଉପରେ ପ୍ରାଧାନ୍ୟ ଦେଲେ, ‘ଗାଈଟିକୁ ମୋତେ ବିକ୍ରି କରିଅଛ ମୋ ବାପା କିମ୍ବା ଭାଇକୁ ନୁହେଁ ।’
‘ବିକ୍ରି କରିଅଛ’ ଉପରେ ପ୍ରାଧାନ୍ୟ ଦେଲେ, ‘ବିକ୍ରି କରିଅଛ, ମାଗଣା କିମ୍ବା ଉପହାର ଭାବେ ନୁହେଁ ।’
ଏହିପରି ଭାବରେ ବାକ୍ୟଟିର ବିଭିନ୍ନ ଅର୍ଥ ବାହାରିପାରେ । ଏହାକୁ ଦୁର୍ବୋଚ୍ଚାରଣ ଦୋଷ ମଧ୍ୟ କୁହାଯାଏ ।
(ଖ) ଔପାଧ୍ଵତା ଦୋଷ :
Answer:
ଉପାଧ୍ କହିଲେ ସାଧାରଣତଃ ଗୋଟିଏ ଅବସ୍ଥା ବା ସର୍ଭକୁ ବୁଝାଇଥାଏ । ସେହି ଦୃଷ୍ଟିରୁ କୌଣସି ବସ୍ତୁ ବା ବ୍ୟକ୍ତି ବିଷୟରେ ଯାହା ସାଧାରଣ ଭାବରେ କୁହାଯାଇଥାଏ ତାହା ବିଶେଷ କ୍ଷେତ୍ରରେ କହିବା ଠିକ୍ ନୁହେଁ । ଏପରି ଯୁକ୍ତିକୁ ଔପାଧ୍ଵତା ଦୋଷ କୁହାଯାଏ ।
ଏହି ଦୋଷ ତିନି ପ୍ରକାରର ଅଟେ ।
(କ) ପଦମାନଙ୍କର ସାଧାରଣ ପ୍ରୟୋଗରୁ ତା’ର ବିଶେଷ ପ୍ରୟୋଗ
(ଖ) ପଦମାନଙ୍କର ବିଶେଷ ପ୍ରୟୋଗରୁ ସାଧାରଣ ସାଧାରଣ ପ୍ରୟୋଗ
(ଗ) ପଦମାନଙ୍କର ଗୋଟିଏ ବିଶେଷ ପ୍ରୟୋଗରୁ ଅନ୍ୟ ଏକ ବିଶେଷ ପ୍ରୟୋଗ
(କ) ସାଧାରଣ ପ୍ରୟୋଗରୁ ବିଶେଷ ପ୍ରୟୋଗ :
ଜଳ ତରଳ ।
ବରଫ ଜଳ।
___________
∴ ବରଫ ତରଳ ।
ଏଠାରେ ଜଳର ସାଧାରଣ ଅବସ୍ଥା ତରଳ ଅଟେ । ମାତ୍ର ଏହା ବିଶେଷ ଅବସ୍ଥାକୁ ଗତି କରିଅଛି ।
(ଖ) ବିଶେଷ ପ୍ରୟୋଗରୁ ସାଧାରଣ ପ୍ରୟୋଗ :
ନିଜ ବାଡ଼ିର ତୋଳା ପରିବା ୱ୍ଆଯାଏ ।
କଞ୍ଚା କଦଳୀ ବାଡ଼ିତୋଳା ପରିବା ଅଟେ ।
___________________________
∴ କଞ୍ଚା କଦଳୀ ଖୁଯାଏ ।
କନା ତିଆରି ବସ୍ତୁ ପରିଧେୟ । ତକିଆ ଖୋଳ କନା ତିଆରି ବସ୍ତୁ ।
(ଗ) ବିଶେଷ ପ୍ରୟୋଗରୁ ବିଶେଷ ପ୍ରୟୋଗ
କନା ତିଆରି ବସ୍ତୁ ପରିଧେୟ ।
ତକିଆ ଖୋଳ କନା ତିଆରି ବସ୍ତୁ ।
______________________
∴ ତକିଆ ଖୋଳ ପରିଧେୟ ।
ଏଠାରେ ଗୋଟିଏ ବିଶେଷ ଅବସ୍ଥାରୁ ଅନ୍ୟ ଏକ ବିଶେଷ ଅବସ୍ଥାକୁ ଅଗ୍ରସର ହୋଇଅଛି ।
2. କାରଣ ସଂକ୍ରାନ୍ତ ତର୍କଦୋଷଗୁଡ଼ିକୁ ଉଦାହରଣ ସହ ବ୍ୟାଖ୍ୟା କର ।
Answer:
ବୈଜ୍ଞାନିକ କାରଣ ହେଉଛି ‘କାର୍ଯ୍ୟର ସର୍ରାନ୍ତର ଅବ୍ୟବହିତ ନିରପେକ୍ଷ ଅବ୍ୟଭିଚାରୀ ପୂର୍ବବର୍ତ୍ତୀ ଘଟଣା’ । ଯଥାର୍ଥରେ ଯାହା ବୈଜ୍ଞାନିକ କାରଣ ନୁହେଁ ମାତ୍ର ତାହାକୁ ଯଦି କାରଣ ବୋଲି ଧରାଯାଏ ତେବେ ତାହାର କାରଣ ସଂକ୍ରାନ୍ତ ଦୋଷ ଜାତ ହୁଏ ।
(a) ଅତଃ ପରଂ ତସ୍ମାଦତଃ ତର୍କଦୋଷ :
‘ଅତଃ ପରଂ ତସ୍ମାଦତଃ’ର ଅର୍ଥ ହେଲା ‘ଏହା ପରେ ତେଣୁ ଏହି ହେତୁରୁ’ । କାରଣ ହେଉଛି କାର୍ଯ୍ୟର ପୂର୍ବବର୍ତୀ ଘଟଣା; କିନ୍ତୁ ଯେକୌଣସି ପୂର୍ବବର୍ତ୍ତୀ ଘଟଣାକୁ କାରଣ ବୋଲି ଧରାଯାଇ ପାରିବ ନାହିଁ । ମାତ୍ର ଯଦି ଯେକୌଣସି ପୂର୍ବବର୍ତୀ ଘଟଣାକୁ କାରଣ ବୋଲି ଧରାଯାଏ ତେବେ ‘ଅତଃ ପରଂ ତଦ୍ମାବତଃ’ ତର୍କଦୋଷ ଜାତ ହୁଏ ।
ଉଦାହରଣ –
ନବବଧୂର ଗୃହପ୍ରବେଶ ବୃଦ୍ଧଙ୍କର ମୃତ୍ୟୁର କାରଣ ।
ଆକାଶରେ ଧୂମକେତୁର ଆବିର୍ଭାବ ମହାତ୍ମାଙ୍କର ମୃତ୍ୟୁର କାରଣ ।
ଏହାକୁ ମଧ୍ୟ କାକତାଳୀୟ ନ୍ୟାୟ କୁହାଯାଏ । ଯେପରି ତାଳ ଗଛ ଉପରେ କାଉ ବସିବାରୁ ତାଳ ପଡ଼ିଲା । ଏଣୁ ତାଳ ପଡ଼ିବା ହେଉଛି କାଉ ବସିବାର କାରଣ । ଏହି ତର୍କଦୋଷ ସାଧାରଣତଃ ଅନ୍ଧବିଶ୍ବାସ ଉପରେ ପର୍ଯ୍ୟବସିତ ହୋଇଥାଏ ।
(b) ଉପକାରଣକୁ କାରଣ ରୂପେ ଗ୍ରହଣ କରିବା ତର୍କଦୋଷ :
କାରଣ କହିଲେ କେତୋଟି ଉପକାରଣର ସମଷ୍ଟିକୁ ବୁଝାଇଥାଏ । ଅର୍ଥାତ୍ ଉପକାରଣ କାରଣର ଏକ ଅଂଶ ମାତ୍ର ଅଟେ । କିନ୍ତୁ ସେହି ଉପକାରଣକୁ ସମ୍ପୂର୍ଣ୍ଣ ରୂପେ କାରଣ ବୋଲି ଗ୍ରହଣ କଲେ ଏହି ତର୍କଦୋଷ ଜାତ ହୁଏ । ଉଦାହରଣ ସ୍ଵରୂପ- ଜଣେ ବ୍ୟକ୍ତି ଗଛକୁ ଉଠୁଥିବା ସମୟରେ ତଳେ ପଡ଼ି ତାହାର ମୃତ୍ୟୁ ହେଲା । ଲୋକଟିର ମୃତ୍ୟୁ ପାଇଁ ଅନେକ ଉପକାରଣ ଦାୟୀ ହୋଇଥାଏ । ଯଥା- ଲୋକଟିକୁ ଗଛ ଚଢ଼ା ଠିକ୍ ଭାବରେ ଜଣା ନଥୁଲା, ଗଛଟି ବହୁତ ଡେଙ୍ଗା ଥିଲା, ସେଠାରେ କୌଣସି ସ୍ଵାସ୍ଥ୍ୟକେନ୍ଦ୍ର ନଥିଲା ଇତ୍ୟାଦି । ଏଣୁ ଏହିସବୁ ଉପକାରଣ ମଧ୍ୟରୁ ଗୋଟିଏ ଉପକାରଣକୁ କାରଣ ବୋଲି ଗ୍ରହଣ କଲେ ଏହି ତର୍କଦୋଷ ଜାତ ହୁଏ ।
(c) ସହକାର୍ଯ୍ୟ କାରଣତା ଦୋଷ :
ଦୁଇଟି ସହକାର୍ଯ୍ୟ ମଧ୍ୟରୁ ଆମେ ଯଦି ଗୋଟିଏ ସହକାର୍ଯ୍ୟକୁ କାରଣ ଏବଂ ଅନ୍ୟଟିକୁ କାର୍ଯ୍ୟ ବୋଲି ଗ୍ରହଣ କରୁ, ତେବେ ସହକାର୍ଯ୍ୟ କାରଣତା ଦୋଷ ଜାତ ହୁଏ ।
ଉଦାହରଣସ୍ୱରୂପ, ଦିନ ରାତିର କାରଣ । ମାତ୍ର ବାସ୍ତବରେ ପୃଥିବୀ ନିଜ ମେରୁଦଣ୍ଡ ଚାରିପଟେ ଘୂରିବା କାରଣରୁ ଦିନ ଓ ରାତି ହୋଇଥାଏ । ତେଣୁ ଦିନ ଓ ରାତି ପରସ୍ପରର ସହକାର୍ଯ୍ୟ ।
(d) ଦୂରବର୍ତ୍ତୀ କାରଣକୁ କାରଣ ବୋଲି ଗ୍ରହଣ କରିବା ତର୍କଦୋଷ :
କାରଣ ସର୍ବଦା କାର୍ଯ୍ୟର ଅବ୍ୟବହିତ ପୂର୍ବବର୍ତୀ ଘଟଣା । କାରଣ ଓ କାର୍ଯ୍ୟ ମଧ୍ୟରେ କୌଣସି ସମୟର ବ୍ୟବଧାନ ନଥାଏ । ତେଣୁ କାର୍ଯ୍ୟ ସହିତ ସମ୍ପୃକ୍ତ ଗୋଟିଏ ଦୂରବର୍ତ୍ତୀ ଘଟଣାକୁ ତାହାର କାରଣ ବୋଲି ଗ୍ରହଣ କଲେ ଏହି ଦୋଷ ହୋଇଥାଏ । ଉଦାହରଣସ୍ୱରୂପ, ପିତାଙ୍କର ମୃତ୍ୟୁ ହେବା ପୁତ୍ରର ପାଠ ପଢ଼ା ବନ୍ଦ ହେବାର କାରଣ । ସେହିପରି କଂଗ୍ରେସ ଅନୁଷ୍ଠାନ ଗଢ଼ାହେବା ଭାରତର ସ୍ବାଧୀନତା ପାଇବାର କାରଣ ।
(e) ନଞର୍ଥକ ଉପକାରଣ ଉପେକ୍ଷା ଦୋଷ :
ସଦର୍ଥକ ଉପକାରଣର ଉପସ୍ଥିତି ସତ୍ତ୍ବେ ନଞର୍ଥକ ଉପକାରଣ ଅନୁପସ୍ଥିତି ରହିଲେ କାର୍ଯ୍ୟୋତ୍ପାଦନ ହୋଇପାରେ ନାହିଁ । ତେଣୁ ନଞର୍ଥକ ଉପକାରଣମାନଙ୍କୁ ବିଚାରକୁ ନନେଇ ସଦର୍ଥକ ଉପକାରଣଗୁଡ଼ିକର କାର୍ଯ୍ୟୋତ୍ପାଦନରେ କୌଣସି ମୂଲ୍ୟ ନାହିଁ ବୋଲି ମନେକଲେ ଏହି ଦୋଷ ଜାତ ହୋଇଥାଏ । ଉଦାହରଣସ୍ୱରୂପ, ଭଲ ବର୍ଷା ହେବା ସହିତ ଭଲ ଫସଲ ହେବାର କୌଣସି ସମ୍ପର୍କ ନାହିଁ । କାରଣ ପୋକ ଲାଗିବା ଯୋଗୁଁ ଫସଲ ନଷ୍ଟ ହେବା ଅନ୍ୟ ଏକ କାରଣ ବୋଲି ଧରାଯାଇଥାଏ ।
3. ନିମ୍ନଲିଖୂତ ତର୍କଦୋଷଗୁଡ଼ିକୁ ଉଦାହରଣ ସହ ବ୍ୟାଖ୍ୟା କର ।
(a) ଅବୈଧ ସାମାନ୍ୟକରଣ ଦୋଷ :
Answer:
ସାମାନ୍ୟକରଣ ଅର୍ଥାତ୍ ଅଭିଜ୍ଞତାଲବ୍ଧ ଦୃଷ୍ଟାନ୍ତମାନଙ୍କରୁ ଗୋଟିଏ ସାମାନ୍ୟ ତର୍କବାକ୍ୟ ନିର୍ଦ୍ଧାରଣ କରିବା ପ୍ରକ୍ରିୟାକୁ ଅବୈଧ ସାମାନ୍ୟକରଣ ଦୋଷ କହନ୍ତି । ଏଠାରେ ଦୃଷ୍ଟାନ୍ତଗୁଡ଼ିକ ଯେତେ ଅଧିକ ହେବ ସମ୍ଭାବନା ମଧ୍ୟ ଅଧିକ ହେବ । ମାତ୍ର କେତେକ କ୍ଷେତ୍ରରେ ଆମେ ସ୍ଵଳ୍ପ କେତୋଟି ଦୃଷ୍ଟାନ୍ତରୁ ଏକ ସାମାନ୍ୟ ସିଦ୍ଧାନ୍ତ ଗ୍ରହଣ କରିଥାଉ ।
ଉଦାହରଣସ୍ୱରୂପ, ଜଣେ ବିଦେଶାଗତ ବ୍ୟକ୍ତି ଭାରତର କେତୋଟି ସମୃଦ୍ଧିଶାଳୀ ସହରର ଭାରତୀୟ ପରିବାରମାନଙ୍କୁ ପର୍ଯ୍ୟବେକ୍ଷଣ କରି ଏହି ସିଦ୍ଧାନ୍ତରେ ଉପନୀତ ହେଲେ ଯେ ସମସ୍ତ ଭାରତୀୟ ଧନୀ, ଉଚ୍ଚ ଶିକ୍ଷିତ ଓ ବଳବାନ୍ । ବିଦେଶାଗତ ବ୍ୟକ୍ତିଙ୍କର ଏପରି ସିଦ୍ଧାନ୍ତ ଅବୈଧ ସାମାନ୍ୟକରଣ ଦୋଷଯୁକ୍ତ ଅଟେ ।
ସେହିପରି ଅନ୍ୟ ଏକ ଦୃଷ୍ଟାନ୍ତ ନିଆଯାଇ ପାରେ ଯେ, ଗାଁର କେତେକ ଚନ୍ଦାମୁଣ୍ଡିଆ ବ୍ୟକ୍ତି ଧନୀ ଥିବାର ଦେଖ୍ ଜଣେ ଏହି ସିଦ୍ଧାନ୍ତରେ ଉପନୀତ ହେଲେ ଯେ ଗାଁର ସମସ୍ତ ଚନ୍ଦାମୁଣ୍ଡିଆ ବ୍ୟକ୍ତି ଧନୀ ଅଟନ୍ତି ।
(b) ପ୍ରତିପାଦ୍ୟ ସ୍ଵୀକାର ତର୍କଦୋଷ :
Answer:
ଏହାକୁ ସାଧ୍ଯସମ ତର୍କଦୋଷ ମଧ୍ୟ କୁହାଯାଏ । ଯାହାକୁ ପ୍ରମାଣ କରିବା କଥା ତାହାକୁ ହିଁ ହେତୁବାକ୍ୟ ରୂପେ ନେଇ ପ୍ରମାଣ କରିବାକୁ ଚେଷ୍ଟାକଲେ ଏହି ତର୍କଦୋଷ ଜାତ ହୁଏ । ଅର୍ଥାତ୍ ସିଦ୍ଧାନ୍ତରେ ପ୍ରତିପାଦନ କରିବା ପୂର୍ବରୁ ହେତୁବାକ୍ୟରେ ତାହାକୁ ଗ୍ରହଣ କରିନେବାକୁ ପ୍ରତିପାଦ୍ୟ ସ୍ବୀକାର ଦୋଷ କୁହାଯାଏ । ଏହାକୁ ଚକ୍ରକ ଦୋଷ ମଧ୍ଯ କୁହାଯାଏ । କାରଣ ହେତୁବାକ୍ୟ ଓ ସିଦ୍ଧାନ୍ତ ମଧ୍ୟରେ ସମାନ ଅର୍ଥ ପ୍ରକାଶିତ ହେଲେ ଏହି ପ୍ରକାର ଦୋଷ ଜାତ ହୁଏ । ଉଦାହରଣସ୍ୱରୂପ, କାଚ ସ୍ଵଚ୍ଛ ଅଟେ । କାରଣ ଏହା ମଧ୍ୟ ଦେଇ ଦେଖୁହୁଏ । ଏଣୁ ଯାହା ସ୍ଵଚ୍ଛ ଓ ଯାହା ମାଧ୍ୟମରେ ଦେଖିପାରୁ ତାହା କାଚ ଅଟେ ।
ରାମ ଦଶରଥଙ୍କର ପୁତ୍ର ଅଟନ୍ତି । ଦଶରଥ ରାମଙ୍କର ପିତା ଅଟନ୍ତି ।
ପ୍ଲାଟୋ ଆତ୍ମାର ଅମରିତ୍ଵ ସରଳତାରୁ ଓ ସରଳତା ଆତ୍ମାର ଅମରତ୍ଵରୁ ପ୍ରମାଣ କରିଛନ୍ତି ।
(c) ଅସିଦ୍ଧ ହେତୁ ଦୋଷ :
Answer:
ତ୍ରିପଦୀଯୁକ୍ତିରେ ସିଦ୍ଧାନ୍ତ ଦୁଇଟି ହେତୁବାକ୍ୟରୁ ନିଷ୍ପନ୍ନ ହୋଇଥାଏ । ହେତୁବାକ୍ୟ ଯଦି ମିଥ୍ୟା ହୁଏ, ତେବେ ସିଦ୍ଧାନ୍ତ ମଧ୍ୟ ମିଥ୍ୟା ହୁଏ । ତେଣୁ ମିଥ୍ୟା ହେତୁବାକ୍ୟରୁ ନିଃସୃତ ସିଦ୍ଧାନ୍ତ ଗ୍ରହଣ କରିନେଲେ ଏହି ପ୍ରକାର ଦୋଷ ଜାତ ହୁଏ ।
ଉଦାହରଣ –
ଯେଉଁମାନେ ଥାନାକୁ ଯାଆନ୍ତି ସମସ୍ତେ କଏଦୀ ଅଟନ୍ତି ।
ତୁମ ବାପା ଥାନାକୁ ଯାଉଛନ୍ତି ।
___________________
∴ ତୁମ ବାପା ଜଣେ କଏଦୀ ।
(d) ନାନୁମିତିକ ତର୍କଦୋଷ :
Answer:
ଗୋଟିଏ ପ୍ରାକଳ୍ପିକ-ନିରପେକ୍ଷ ମିଶ୍ର ତ୍ରିପଦୀଯୁକ୍ତିରେ ନିୟମ ଅନୁଯାୟୀ –
(୧) ସାଧାବୟବର ପୂର୍ବଗକୁ ପକ୍ଷାବୟବରେ ସ୍ଵୀକାର କଲେ ତାହାର ଅନୁଗକୁ ସିଦ୍ଧାନ୍ତରେ ସ୍ଵୀକାର କରାଯାଏ ।
(୨) ସାଧାବୟବର ଅନୁଗକୁ ପକ୍ଷାବୟବରେ ଅସ୍ବୀକାର କଲେ ତାହାର ପୂର୍ବଗକୁ ସିଦ୍ଧାନ୍ତରେ ଅସ୍ବୀକାର କରାଯାଏ ।
ମାତ୍ର ଏହାର ବିପରୀତ ନିୟମ ପ୍ରଣିଧାନଯୋଗ୍ୟ ନୁହେଁ । ଏହି ନିୟମକୁ ଉଲ୍ଲଙ୍ଘନ କଲେ ନାନୁମିତିକ ତର୍କ ଦୋଷ ଜାତ ହୁଏ ।
ଯଦି ସୂର୍ଯ୍ୟ ଥାଏ ତେବେ ଆଲୋକ ଥାଏ ।
ଆଲୋକ ଅଛି ।
____________
∴ ସୂର୍ଯ୍ୟ ଅଛି ।
ଏହା ଦୋଷଯୁକ୍ତ ଅଟେ ।
(e) ବହୁପ୍ରଶ୍ନ ଦୋଷ :
Answer:
ବେଳେବେଳେ ଏପରି ପ୍ରଶ୍ନ ପଚରାଯାଏ ଯେକୌଣସି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଉତ୍ତର ଦେବା ସମ୍ଭବ ହୁଏ ନାହିଁ । ଅର୍ଥାତ୍ ଉତ୍ତର କେବଳ ‘ହଁ’ କିମ୍ବା ‘ନା’ ରୂପେ ଦେବାକୁ ଦାବି କଲେ ଏହି ତର୍କଦୋଷ ଜାତ ହୁଏ ।
ଉଦାହରଣ :
(୧) ତୁମେ ମଦ ପିଇବା ଛାଡ଼ିଲଣିକି ?
(୨) ତୁମେ ଚୋରି କରିବା ଛାଡ଼ିଲଣିକି ?
(୩) ହର ପାର୍ବତୀ କ’ଣ ନାରୀ ?
ଏହି ଉଦାହରଣଗୁଡ଼ିକର ଉତ୍ତର କେବଳ ହଁ କିମ୍ବା ନା ମଧ୍ଯରେ ଦିଆଯାଇ ପାରେ ନାହିଁ ।
4. ଅବାନ୍ତର ପ୍ରସଙ୍ଗ ଦୋଷଗୁଡ଼ିକ ବ୍ୟାଖ୍ୟା କର ।
Answer:
(a) ପ୍ରତିପକ୍ଷ ଦୁର୍ବଳତା ପ୍ରଦର୍ଶନ ତର୍କଦୋଷ – ପ୍ରତିପକ୍ଷର ମତକୁ ଯୁକ୍ତିଦ୍ୱାରା ଖଣ୍ଡନ କରିବା ପରିବର୍ତ୍ତେ ଯଦି ତାଙ୍କର ଆଚରଣ ବା ବ୍ୟକ୍ତିଗତ ଚରିତ୍ରକୁ କିମ୍ବା ଅଭ୍ୟାସକୁ ଆକ୍ଷେପ କରି ତାଙ୍କ ଯୁକ୍ତିଟି ଭୁଲ୍ ବୋଲି ପ୍ରମାଣିତ କରାଯାଏ, ତେବେ ତାହାକୁ ପ୍ରତିପକ୍ଷ ଦୁର୍ବଳତା ପ୍ରଦର୍ଶନ ତର୍କ ଦୋଷ କହନ୍ତି ।
ଉଦାହରଣ :
(୧) ଜଣେ ବକ୍ତା ପରିବାର ନିୟନ୍ତ୍ରଣ ସପକ୍ଷରେ ବୁଝାଉଛନ୍ତି । ତାଙ୍କ ମତରେ ଆମେ ଦୁଇ ଓ ଆମର ଦୁଇ । ମାତ୍ର ଏହି ସମୟରେ ଜଣେ ଶ୍ରୋତା ଉଠିପଡ଼ି ଜବାବ ଦେଲା ଯେ ବକ୍ତା ନିଜେ ଦଶଗୋଟି ସନ୍ତାନର ଜନକ । ସେ କିପରି ଭାବରେ ଏକଥା କହିପାରୁଛନ୍ତି ?
(୨) ଜଣେ ଶିକ୍ଷକ ଶ୍ରେଣୀଗୃହରେ ଶିକ୍ଷାଦାନ କରୁଥିବା ସମୟରେ କହିଲେ ଯେ ଧୂମପାନ ନିଷେଧ ଅଟେ । ମାତ୍ର ଜଣେ ଛାତ୍ର ଉଠିପଡ଼ି ଉତ୍ତର ଦେଲା – ସାର୍ ଆପଣ ଏପରି କଥା କିପରି ଭାବରେ କହୁଛନ୍ତି ? କାରଣ ଆପଣ ନିଜେ ଧୂମପାନ କରୁଛନ୍ତି ।
(b) ଲୋକ-ଉତ୍ତେଜକ ତର୍କଦୋଷ – ଏହାକୁ ଜନତାଙ୍କୁ ମତେଇବା ଯୁକ୍ତି ମଧ୍ୟ କୁହାଯାଏ । କୌଣସି ମତକୁ ସମର୍ଥନ ବା ଖଣ୍ଡନ କରିବାକୁ କୌଣସି ଯଥାର୍ଥ ଯୁକ୍ତି ନ ବାଢ଼ି ଯଦି ଲୋକଙ୍କୁ ଉତ୍ତେଜକ ଭାଷାର ପ୍ରୟୋଗଦ୍ଵାରା ପ୍ରଭାବିତ କରି ନିଜର ମତ ପ୍ରତିଷ୍ଠା କରିବାର ପ୍ରୟାସ କରାଯାଏ, ତେବେ ତାହାକୁ ଲୋକ-ଉତ୍ତେଜକ ତର୍କ ଦୋଷ କହନ୍ତି ।
ଉଦାହରଣସ୍ୱରୂପ, ଯଦି ଆମେ ଡାରଉଇନ୍ଙ୍କର ଜୈବ ବିବର୍ତ୍ତନବାଦକୁ ସ୍ବୀକାର କରୁ, ତେବେ ଆମକୁ ଗ୍ରହଣ କରିବାକୁ ହେବ ଯେ ଆମର ପୂର୍ବପୁରୁଷମାନେ ଜଣେ ଜଣେ ପାତିମାଙ୍କଡ଼ ଥିଲେ ।
(c) ଆସ୍ତଦ୍ବାହି ତର୍କଦୋଷ – କୌଣସି ମତର ସପକ୍ଷରେ ବା ବିପକ୍ଷରେ ଯଥାଯଥ ଯୁକ୍ତି ଉପସ୍ଥାପନ ନକରି କଥାକଥାକେ ଶାସ୍ତ୍ର, ପୁରାଣ ବା ପ୍ରତିଷ୍ଠାବାନ୍ ବ୍ୟକ୍ତିଙ୍କ ମତକୁ ହେତୁବାକ୍ୟ ରୂପେ ଗ୍ରହଣ କରି ଯୁକ୍ତି କରିବାକୁ ଆପ୍ତଦ୍ବାହି ତର୍କଦୋଷ କୁହାଯାଏ । ଏଠାରେ ଯୁକ୍ତି ସାହାଯ୍ୟରେ କୌଣସି ମତକୁ ଖଣ୍ଡନ ବା ଗ୍ରହଣ କରାଯାଏ ନାହିଁ । ଏଠାରେ ଆଖୁବୁଜି ସେମାନଙ୍କର ମତକୁ ଗ୍ରହଣ କରି ନିଆଯାଏ ।
ଉଦାହରଣ :
(୧) ‘ଅହିଂସା ପରମ ଧର୍ମ’ କାରଣ ଏହା ମହାତ୍ମା ଗାନ୍ଧୀ, ବୁଦ୍ଧଦେବ ଓ ଭଗବଦ୍ ଗୀତା କହିଛନ୍ତି ।
୨) ଭୁବନେଶ୍ଵର ଜଳବାୟୁ ସ୍ଵାସ୍ଥ୍ୟ ପକ୍ଷେ ହିତକାରକ କାରଣ ଏହା ପିତା କହନ୍ତି ।
(୩) ପୁରୀର ଜଳବାୟୁ ସ୍ଵାସ୍ଥ୍ୟ ପକ୍ଷେ ହିତକାରକ କାରଣ ଶିକ୍ଷକ ଏକଥା କହନ୍ତି ।
(d) ପରାଜ୍ଞତା ଦୃଷ୍ଟି। ସ୍ଵମତ ପ୍ରତିଷ୍ଠା ତର୍କଦୋଷ- ପ୍ରତିପକ୍ଷର ଅଜ୍ଞତାର ସୁଯୋଗ ନେଇ ନିଜର ମତ ପ୍ରତିଷ୍ଠା କରିବାକୁ ପରାଜ୍ଞତା ଦୃଷ୍ୟା ସ୍ଵମତ ପ୍ରତିଷ୍ଠା ତର୍କଦୋଷ କହନ୍ତି । ପ୍ରତିପକ୍ଷର ଅଜ୍ଞତାର ସୁଯୋଗ ନେଇ ନିଜର ମତକୁ ଗ୍ରହଣ କରାଇନେବା ହେଉଛି ଏପ୍ରକାର ଯୁକ୍ତିର ଲକ୍ଷ୍ୟ ଅଟେ ।
ଉଦାହରଣସ୍ୱରୂପ, ତୁମେ ପୂର୍ବଜନ୍ମରେ ଗୋଟିଏ ଘୁଷୁରି ଥିଲା । ଏହା ଯଦି ମିଛ, ତେବେ ପ୍ରମାଣ କଲ ଦେଖ୍ – ତୁମେ ଘୁଷୁରୀ ନ ଥୁଲ ବୋଲି । ଯଦି ତୁମେ ଏହା ପ୍ରମାଣ ନ କରିପାର ତେବେ ମୋ କଥା ଠିକ୍ ବୋଲି ଗ୍ରହଣ କରିବାକୁ ତୁମେ ବାଧ୍ୟ ।
(e) ମୁଦ୍ର – ପ୍ରଦର୍ଶନ ତର୍କଦୋଷ – ଯୁକ୍ତିର ସାହଯ୍ୟ ନ ନେଇ ଯଦି ବଳ ପ୍ରୟୋଗ ବା ଧମକଦ୍ୱାରା ଉଦ୍ଦିଷ୍ଟ ମତକୁ ଗ୍ରହଣ କରିବାପାଇଁ ତାହାକୁ ବାଧ୍ୟ କରାଯାଏ, ତେବେ ତାହାକୁ ମୁଦ୍ଗର-ପ୍ରଦର୍ଶନ ତର୍କଦୋଷ କୁହାଯାଏ । କିନ୍ତୁ ଏହାକୁ ଯୁକ୍ତି ବୋଲି କହିବା ମଧ୍ୟ ଅନେକାଂଶରେ ଗ୍ରହଣଯୋଗ୍ୟ ନୁହେଁ ।
ଉଦାହରଣ :
(୧) ମୁଁ ଯାହା ତୁମକୁ କହୁଛି ତାହା ସତ ବୋଲି ତୁମେ ବର୍ତ୍ତମାନ ଲେଖିଦିଅ ନ ହେଲେ ମୁଁ ତୁମକୁ ହତ୍ୟା କରିବି ।
(୨) ସନ୍ତ୍ରାସବାଦୀ ଆନ୍ଦୋଳନର ନେତା ଜଣେ ଧନୀ ବ୍ୟକ୍ତିଙ୍କ ପାଖକୁ ଯାଇ କହିଲା ଯେ ତୁମେ ଆମ ସଂଘକୁ ଏକ ଲକ୍ଷ ଟଙ୍କା ଦିଅ । ପ୍ରଥମେ ଧନୀ ବ୍ୟକ୍ତିଜଣକ ମନାକଲା । ତା’ପରେ ସନ୍ତ୍ରାସବାଦୀ ଜଣକ ବନ୍ଧୁକ ଧନୀ ଲୋକର ମୁଣ୍ଡକୁ ଲଗାଇ କହିଲା ବର୍ତ୍ତମାନ ଦେବୁ କି ନାହିଁ । ତା’ପରେ ଧନୀଲୋକ ଜଣକ ଏକ ଲକ୍ଷ ଟଙ୍କା ଦେଲା । ଏହାକୁ ଜୋର ଯାର ମୂଲକ ତା’ର ମଧ୍ୟ କହନ୍ତି ।
5. ପାରମ୍ପରିକ ତର୍କଶାସ୍ତ୍ର ଓ ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ର ମଧ୍ୟରେ ନିହିତ ସମ୍ପର୍କକୁ ବୁଝାଇଦିଅ । ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ର ଓ ପାରମ୍ପରିକ ତର୍କଶାସ୍ତ୍ରର ଏକ ଉନ୍ନତତର ଅଭିବ୍ୟକ୍ତି କିପରି ? ବୁଝାଅ ।
Answer:
ପାରମ୍ପରିକ ତର୍କଶାସ୍ତ୍ର ଓ ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ର – ଆରିଷ୍ଟଟଲ୍ଙ୍କୁ ପାରମ୍ପରିକ ତର୍କଶାସ୍ତ୍ରର ଜନକ ବୋଲି କୁହାଯାଏ । ପାରମ୍ପରିକ ତର୍କଶାସ୍ତ୍ରର ଭିତ୍ତିଭୂମି ଉପରେ ଆଧୁନିକ ତର୍କଶାସ୍ତ୍ର ଦଣ୍ଡାୟମାନ ହୋଇଅଛି । ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ର ହେଉଛି ପାରମ୍ପରିକ ତର୍କଶାସ୍ତ୍ରର ଏକ ସଂଶୋଧ ଓ ପରିବର୍ଦ୍ଧିତ ସଂସ୍କରଣ । ପାରମ୍ପରିକ ତର୍କଶାସ୍ତ୍ରରେ ଯୁକ୍ତିର ପ୍ରାମାଣିକତା ତଥା ବୈଧତା ପ୍ରମାଣ କରିବା ନିମିତ୍ତ ବହୁ ନିୟମ ପ୍ରଣୟନ କରାଯାଇଅଛି । ତାହାର ଦୃଷ୍ଟାନ୍ତ ତ୍ରିପଦୀଯୁକ୍ତିରେ ଆଲୋଚିତ ହୋଇଅଛି । ଏହି ଦୃଷ୍ଟିରୁ ପାରମ୍ପରିକ ତର୍କଶାସ୍ତ୍ର ଅତ୍ୟନ୍ତ ଉପଯୋଗୀ । କିନ୍ତୁ ସେଥିରେ ଗୋଟିଏ ବଡ଼ ଅଭାବ ପରିଲକ୍ଷିତ ହୁଏ । ଆରିଷ୍ଟଟଲ୍ ଯୁକ୍ତିମାନଙ୍କର ପରୀକ୍ଷା ନିରୀକ୍ଷା କରିବାପାଇଁ ଯେଉଁ ଅବରୋହ ପଦ୍ଧତି ଦେଇଥିଲେ ତାହା କେବଳ ଭାଷାରେ ଲିଖ ଯୁକ୍ତମାନଙ୍କପାଇଁ ଉଦ୍ଦିଷ୍ଟ । ମାତ୍ର ବିଭିନ୍ନ ପ୍ରକାରର ଯୁକ୍ତିର ବୈଧତା ଏହି ପଦ୍ଧତି ମାଧ୍ୟମରେ ପରୀକ୍ଷା କରିବା ସମ୍ଭବ ନୁହେଁ ।
ଏହି ଅସୁବିଧାକୁ ଲକ୍ଷ୍ୟକରି ଆରିଷ୍ଟଟଲ୍ ଯୁକ୍ତିମାନଙ୍କୁ ବିଭିନ୍ନ ସଂସ୍ଥାନ ଏବଂ ନ୍ୟାୟରୂପରେ ବର୍ଗୀକରଣ କରି ବିଭିନ୍ନ ନିୟମମାନଙ୍କଦ୍ୱାରା ସେଗୁଡ଼ିକର ପ୍ରାମାଣିକତା ନିର୍ଣ୍ଣୟ କରିବାର ଉପାୟ ଦେଇଥିଲେ । କେବଳ ସେତିକି ନୁହେଁ, ସେ ମଧ୍ଯ କେତେକ ବର୍ଣ୍ଣ; ଯଥା – ଅ, ପ, ମ ଦ୍ବାରା ଯୁକ୍ତିଗୁଡ଼ିକୁ ପ୍ରତୀକାତ୍ମକ ରୂପ (ଆକାର) ଦେଇଥିଲେ; ଯଥା – ସମସ୍ତ ମନୁଷ୍ୟ ମରଣଶୀଳ, ରାମ ଜଣେ ଛାତ୍ର, .. ରାମ ମରଣଶୀଳ ଅଟେ । ଏହାକୁ ଆରିଷ୍ଟଟଲ୍ ନିନିମ୍ନଲିଖଭାବେ ପ୍ରତୀକାତ୍ମକ ରୂପ ଦେଇଥିଲେ ଯଥା –
ସମସ୍ତ ମ ପ ଅଟେ ।
ସମସ୍ତ ଅ ମ ଅଟେ ।
___________________
∴ ସମସ୍ତ ଅ ପ ଅଟେ ।
ଏହି ବର୍ଷମାନଙ୍କୁ ‘ଚଳ’ କୁହାଯାଏ । କାରଣ ଏହି ବର୍ଷଗୁଡ଼ିକ ଅଥବା ଏହିପରି ଆଉ କେତେକ ବର୍ଣ୍ଣ; ଯଥା – କ, ଖ, ଗ ଇତ୍ୟାଦି ଯେକୌଣସି ଯୁକ୍ତିରେ ବ୍ୟବହୃତ ପଦ (ରାମ, ଯଦୁ, ପର୍ବତ, ମରଣଶୀଳ) ଇତ୍ୟାଦି ପରିବର୍ତ୍ତେ ବ୍ୟବହାର କରାଯାଏ । ଆରିଷ୍ଟଟଲ୍ ଏହି ଚଳକୁ ବ୍ୟବହାର କରିବାର ଉଦ୍ଦେଶ୍ୟ ଥିଲା, ଭାଷାରେ ଲିଖ ଯୁକ୍ତିମାନଙ୍କୁ ଗୋଟିଏ ଆକାରରେ ପକାଇବା, ଯାହା ଯୁକ୍ତିର ପ୍ରାମାଣିକତା ପରୀକ୍ଷା କରିବାରେ ସାହାଯ୍ୟ କରୁଥିଲା । ଆଧୁନିକ ତର୍କଶାସ୍ତ୍ରବିଦ୍ମାନେ ଏପ୍ରକାର ପ୍ରଣାଳୀ ଉପରେ କେତେକ ନୂତନ ପରିବର୍ତ୍ତନ ତଥା ଅଭିବୃଦ୍ଧି ନିମିତ୍ତ ପ୍ରୟାସ କରିଛନ୍ତି । ସେମାନେ କେତେକ ଅବାଚନିକ ପ୍ରତୀକ ବ୍ୟବହାର କରିଛନ୍ତି । ଏ.ଏନ୍. ହ୍ଵାଇଟ୍ହେଡ୍, ବର୍ଟାଣ୍ଡ ରସେଲ୍, ସି.ଏସ୍. ପାଏର୍ସ ଆଦି ଗଣିତଶାସ୍ତ୍ର ବିଶାରଦମାନେ ପାରମ୍ପରିକ ତର୍କଶାସ୍ତ୍ରକୁ ଆଧୁନିକୀକରଣ କରି ଗଣିତାଭିମୁଖୀ କରିଛନ୍ତି । ଗଣିତଶାସ୍ତ୍ରର ବିକାଶ ଓ ଉତ୍କର୍ଷ ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ରର ଉତ୍କର୍ଷ ପାଇଁ ବହୁପରିମାଣରେ ଦାୟୀ ।
ଗାଣିତିକ ତର୍କଶାସ୍ତ୍ରକୁ ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ର କୁହାଯାଏ । ଏହା ଗାଣିତିକ ପଦ୍ଧତି ଅନୁସରଣ କରେ ଓ ଗଣିତର ସ୍ୱରୂପକୁ ମଧ୍ୟ ଅନୁଧ୍ୟାନ କରେ । ଏହା ମଧ୍ଯ ଯୁକ୍ତିର ବିଷୟଗତ ସତ୍ୟତା ଉପରେ ଗୁରୁତ୍ୱ ନ ଦେଇ ଆକାରଗତ ସତ୍ୟତା ଉପରେ ଗୁରୁତ୍ଵ ଦିଏ । ଗଣିତ ଶାସ୍ତ୍ରରେ x, y, z ପରି ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ରରେ ଅ, ପ, ମ ଆଦି ବର୍ଣ୍ଣଗୁଡ଼ିକୁ ‘ଚଳ’ ଭାବରେ ବ୍ୟବହାର କରାଯାଏ । ଏହା ବ୍ୟତୀତ ତର୍କବାକ୍ୟଗୁଡ଼ିକୁ ମଧ୍ୟ କ, ଖ, ଗ ଆଦି ବିଭିନ୍ନ ପ୍ରତୀକ ମାଧ୍ୟମରେ ବ୍ୟବହାର କରାଯାଇଥାଏ । ଗଣିତଶାସ୍ତ୍ରରେ =, +, -, ×, ÷ ଆଦି ସ୍ଥିରାଙ୍କ (Constant) ଭଳି ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ରରେ ଦୁଇଟି ତର୍କବାକ୍ୟ ମଧ୍ୟରେ •, ∼, ⊃, ∨, ∧, ≡ ଆଦି ସ୍ଥିରାଙ୍କଦ୍ୱାରା ସୂଚାଇ ଦିଆଯାଇଥାଏ ।
ଏହି ଗଣିତଶାସ୍ତ୍ରର ବିକାଶ ଓ ଉତ୍କର୍ଷ ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ରର ଉତ୍କର୍ଷ ପାଇଁ ବହୁପରିମାଣରେ ସହାୟକ । ଜର୍ଜ ବୁଲେଙ୍କର ଉଲ୍ଲେଖଯୋଗ୍ୟ ଅବଦାନ ଶ୍ରେଣୀ-ସମ୍ପର୍କିତ ବୀଜଗଣିତ, ରସେଲ୍ ଏବଂ ଦ୍ଵାଇଟ୍ହେଡ୍ଙ୍କର ‘Principia Mathematica’ ଇତ୍ୟାଦି ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ରର ଉତ୍କର୍ଷ ସାଧନ ପାଇଁ ବହୁ ପରିମାଣରେ ଦାୟୀ । ବୁଲେଙ୍କର ଶ୍ରେଣୀ-ସମ୍ବନ୍ଧୀୟ ବୀଜଗଣିତ ଓ ଦ୍ଵାଇଟ୍ ହେଡ୍ଙ୍କର Principia Mathematica ରେ ବର୍ଣ୍ଣିତ ଗଣିତଶାସ୍ତ୍ରର ତାର୍କିକ ଭିତ୍ତିଭୂମି ଇତ୍ୟାଦିକୁ ଗଭୀର ଭାବରେ ଚର୍ଚ୍ଚା କରି ଯୁକ୍ତିଗୁଡ଼ିକର ବୈଧତା ପରୀକ୍ଷା କରିବାପାଇଁ କେତେକ ‘ତାର୍କିକ ଆକାର’ ସ୍ଥିର କରାଯାଇଛି ।
ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ରର ସ୍ଵରୂପ :
ସି.ଆଇ. ଲିଉଇସ ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ରର ତିନୋଟି ମୁଖ୍ୟ ବୈଶିଷ୍ଟ୍ୟ ଉଲ୍ଲେଖ କରିଛନ୍ତି । ସେଗୁଡ଼ିକ ହେଉଛି –
(୧) ଚିନ୍ତାତ୍ମକ ଚିହ୍ନର ବ୍ୟବହାର
(୨) ଅବରୋହ ପଦ୍ଧତିର ପ୍ରୟୋଗ
(୩) ଚଳ ଓ ସ୍ଥିରାଙ୍କର ବ୍ୟବହାର ।
(୧) ଚିନ୍ତାତ୍ମକ ବା ପ୍ରତ୍ୟୟାତ୍ମକ ଚିହ୍ନର ବ୍ୟବହାର – ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ରର ବିଶେଷ ବୈଶିଷ୍ଟ୍ୟ ହେଉଛି ଯେ ଏହା ଧ୍ଵନ୍ୟାତ୍ମକ ଚିହ୍ନ (Phonogram) ପରିବର୍ଭେ ପ୍ରତ୍ୟୟାତ୍ମକ ଚିହ୍ନ (Ideogram) ର ବ୍ୟବହାର କରିଥାଏ । ଗୋଟିଏ ଯୁକ୍ତିରେ ବ୍ୟବହୃତ କଥ୍ତ ଭାଷା; ଯଥା – ରାମ, ମନୁଷ୍ୟ, ମରଣଶୀଳ ଇତ୍ୟାଦି ଧ୍ଵନ୍ୟାତ୍ମକ ଚିହ୍ନ ଅଟେ । ମାତ୍ର ତ, ଥ, ଦ, ତ ∨ ଥ, ତ ⊃ ଥ, ତ ≡ ଥ ଇତ୍ୟାଦି ପ୍ରତ୍ୟୟାତ୍ମକ ଚିହ୍ନ ଅଟେ ।
ବର୍ଣ୍ଣମାଳାର ପ୍ରତ୍ୟେକ ଅକ୍ଷର ଧ୍ଵନିସୂଚକ । ତେଣୁ ଅକ୍ଷରଗୁଡ଼ିକ ସାହାଯ୍ୟରେ ଲିପିବଦ୍ଧ ‘ପ୍ରଶ୍ନସୂଚକ ଚିହ୍ନ’ ଓ ଉଚ୍ଚାରିତ ‘ପ୍ରଶ୍ନସୂଚକ’ ଚିହ୍ନ ମଧ୍ଯରେ ଏକ ସାକ୍ଷାତ୍ ସମ୍ବନ୍ଧ ବିଦ୍ୟମାନ । ଉଦାହରଣସ୍ୱରୂପ- ପରଶ୍ନବାଚକ ଚିହ୍ନ ଓ ‘ ? ’ । ପ୍ରଥମରେ ଅକ୍ଷରଗୁଡ଼ିକରେ ଲିପିବଦ୍ଧ ‘ପ୍ରଶ୍ନବାଚକ ଚିହ୍ନ’ ଯାହାକି କଥୁତ ଭାଷାରେ ବ୍ୟବହୃତ ହୁଏ, ତାହା ଧ୍ଵନ୍ୟାତ୍ମକ ଚିହ୍ନ ଅଟେ ଏବଂ ‘?’ ପ୍ରତୀକଟି ଯାହା ଅବାଚନିକ ଏବଂ ଚିନ୍ତାକୁ ସାକ୍ଷାତ୍ ଭାବରେ ଉପସ୍ଥାପନ କରିଥାଏ, ତାହାକୁ ପ୍ରତ୍ୟୟାତ୍ମକ ଚିହ୍ନ କୁହାଯାଏ । ପ୍ରତ୍ୟୟାତ୍ମକ ଚିହ୍ନର ବ୍ୟବହାରଦ୍ୱାରା ଏକ ଦୀର୍ଘ ଉକ୍ତିକୁ ସହଜରେ ବୁଝିହୁଏ; ଯଥା – ‘ଅଣତିରିଶ ଗୁଣନ ଏଗାର’ କହିବା ପରିବର୍ତ୍ତେ ‘୨୯ × ୧୧’ କହିବା ଅଧ୍ଵ ସୁବିଧାଜନକ ହୋଇଥାଏ ।
(୨) ଅବରୋହ ପ୍ରଣାଳୀ – ଅବରୋହ ପ୍ରଣାଳୀଦ୍ଵାରା ଭକ୍ତିର ଅନ୍ତର୍ନିହିତ ତଥ୍ୟ ପରିସ୍ଫୁଟ ଓ ପରିପୁଷ୍ଟ ହୁଏ । ଏହାର ଉଦାହରଣ ଜ୍ୟାମିତିରେ ରହିଛି । ଅଳ୍ପସଂଖ୍ୟକ କେତେଗୁଡ଼ିଏ ଉକ୍ତିରୁ ସୀମିତ ସଂଖ୍ୟକ କେତେକ ନୀତିର ପ୍ରୟୋଗଦ୍ଵାରା ବହୁ ଅଧ୍ଵସଂଖ୍ୟକ ଭକ୍ତିର ନିଃସରଣ ଏହି ପଦ୍ଧତିର ବୈଶିଷ୍ଟ୍ୟ । ଏହି ନିଃସୃତ ଉକ୍ତିଗୁଡ଼ିକ ଅନେକତ୍ର ମୂଳ ଉକ୍ତିମାନଙ୍କଠାରୁ ପର୍ଯ୍ୟାପ୍ତ ପରିମାଣରେ ଭିନ୍ନ । ଏହି ପଦ୍ଧତିରେ ପ୍ରୟୋଗଦ୍ଵାରା ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ର ଏକ ଶୁଦ୍ଧ ଅବରୋହ ତନ୍ତ୍ର ଗଠନ କରିବାରେ ସମର୍ଥ ହୁଏ ।
(୩) ଚଳ ଓ ସ୍ଥିରାଙ୍କର ବ୍ୟବହାର – ପାରମ୍ପରିକ ତର୍କଶାସ୍ତ୍ରରେ କିଛି ମାତ୍ରାରେ ଚଳ ଓ ସ୍ଥିରାଙ୍କର ବ୍ୟବହାର ହୋଇଥିଲେ ମଧ୍ୟ ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ରରେ ଏହାର ବହୁଳ ବ୍ୟବହାର ଦେଖାଯାଏ । ଏହି ଚଳ ଓ ସ୍ଥିରାଙ୍କର ବ୍ୟବହାରଦ୍ୱାରା ଯୁକ୍ତିର ବୈଧତା ପରୀକ୍ଷା କରିବା ସହଜ ହୋଇଥାଏ । ଏକ ପ୍ରକାରର ଅନେକ ଯୁକ୍ତିକୁ ଚଳ ଓ ସ୍ଥିରାଙ୍କଦ୍ୱାରା ସୁବ୍ୟବସ୍ଥିତ କରାଯାଇଥାଏ । +, -, ×, ÷, =, ≡, ∨, ∧, ⊃, • ଆଦି ଚିହ୍ନଗୁଡ଼ିକ ସ୍ଥିରାଙ୍କ ଓ କ, ଖ, ଗ (x, y, z) ଆଦି ବର୍ଣ୍ଣଗୁଡ଼ିକୁ ଚଳ ବୋଲି କୁହାଯାଏ ।
6. ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ର କହିଲେ କ’ଣ ବୁଝାଯାଏ ? ତର୍କଶାସ୍ତ୍ରୀୟ ଚଳ ଓ ତର୍କଶାସ୍ତ୍ରୀୟ ସ୍ଥିରାଙ୍କ କହିଲେ କ’ଣ ବୁଝ ଆଲୋଚନା କର ।
Answer:
ଯେଉଁ ତର୍କଶାସ୍ତ୍ର ବିଶେଷଧରଣର ପ୍ରତୀକ ବ୍ୟବହାର କରି ଯୁକ୍ତିକୁ ପ୍ରକାଶ କରେ ଓ ତାହାର ମୂଲ୍ୟାୟନ କରେ ତାହାକୁ ସାଧାରଣ ଭାବରେ ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ର କୁହାଯାଏ । ଆଧୁନିକ ତର୍କଶାସ୍ତ୍ରକୁ ପ୍ରତୀକାତ୍ମକ ତର୍କଶାସ୍ତ୍ର କୁହାଯାଏ ।
ତର୍କଶାସ୍ତ୍ରୀୟ ଚଳ – ଚଳ କହିଲେ ତାହାକୁ ହିଁ ବୁଝାଯାଏ ଯାହା ପରିବର୍ତ୍ତନଶୀଳ । ଭିନ୍ନ ଭିନ୍ନ କ୍ଷେତ୍ରରେ ଏହାର ମୂଲ୍ୟ ଭିନ୍ନ ଭିନ୍ନ ହୋଇପାରେ । ତେଣୁ ଏହାର ମୂଲ୍ୟ ପରିବର୍ତ୍ତନଶୀଳ ହୋଇଥିବାରୁ ଏହାକୁ ‘ଚଳ’ କୁହାଯାଏ । କ, ଖ, ଗ (x, y, z) ଇତ୍ୟାଦିକୁ ‘ଚଳ’ କୁହାଯାଏ । କ, ଖ, ଗ ଆଦି ‘ଚଳ’ ଗୁଡ଼ିକୁ ବିଭିନ୍ନ ତର୍କବାକ୍ୟ କ୍ଷେତ୍ରରେ ବ୍ୟବହାର କରାଯାଇ ସେଗୁଡ଼ିକୁ ପ୍ରତୀକାତ୍ମକ କରାଯାଇଥାଏ । ଉଦାହରଣସ୍ୱରୂପ –
(୧) ରାମ ସୀତାକୁ ଭଲ ପାଏ ।
(୨) କ ଖ କୁ ଭଲ ପାଏ ।
ଯଦି ଭଲ ପାଏ ସମ୍ପର୍କକୁ ପ୍ରତୀକାତ୍ମକ କରାଯାଏ, ତେବେ ଏହା କ ସମ୍ପର୍କ ଖ କୁ ବୁଝାଏ । ‘କ’ ଓ ‘ଖ’ ହେଲେ ‘ଚଳ’ । ଏମାନଙ୍କଦ୍ୱାରା ତର୍କବାକ୍ୟର ଆକାର ନିର୍ଦ୍ଧାରିତ ହୋଇଥାଏ ।
ଗଣିତ ଶାସ୍ତ୍ରରେ x2 = 9 ର ଅର୍ଥ ହେଉଛି x = ±3, x = 3 / x = -3 (x କୁ ‘କ’ ରୂପେ ନିଆଯାଇପାରେ) କ ଓ ଖ ‘ଚଳ’ର ସଙ୍କେତ ହୋଇଥିଲେ ବି ସେଗୁଡ଼ିକ ସ୍ଥାନରେ ସ୍ଥିରାଙ୍କ ସଂକେତ ବ୍ୟବହାର କରାଯାଇଥାଏ । ଚଳ ଗୋଟିଏ ଗୋଟିଏ ତର୍କବାକ୍ୟପାଇଁ ମଧ୍ୟ କରାଯାଇପାରେ; ଯଥା –
(୧) ସମସ୍ତ ମନୁଷ୍ୟ ମରଣଶୀଳ । – ତ
(୨) କ୍ଷୀର ଶ୍ବେତ ଅଟେ । – ଥ
ଏଠାରେ ‘ତ’ ଓ ‘ଥ’ ଦୁଇଟି ତର୍କବାକ୍ୟକୁ ବୁଝାଉଅଛି । ତର୍କବାକ୍ୟର ପ୍ରତୀକରୂପେ ବର୍ଣ୍ଣମାଳାର ଯେକୌଣସି ବର୍ଣ୍ଣ ବା ଅକ୍ଷରକୁ ବ୍ୟବହାର କରାଯାଇପାରେ । ବୀଜଗଣିତରେ ସଂଖ୍ୟାମୂଳକ ଚଳରୂପେ ବ୍ୟବହାର କରାଯାଉଥିବା କ, ଖ, ଗ (x, y, z) ଇତ୍ୟାଦି ଯେପରି ଯେକୌଣସି ସଂଖ୍ୟାକୁ ବୁଝାଇଥାଏ; ସେହିପରି ତ, ଥ, ଦ, ଧ ଇତ୍ୟାଦି ଯେକୌଣସି ତର୍କବାକ୍ୟକୁ ପ୍ରତୀକାନ୍ବିତ କରେ ।
ତର୍କଶାସ୍ତ୍ରୀୟ ସ୍ଥିରାଙ୍କ – ସ୍ଥିରାଙ୍କର ଆକ୍ଷରିକ ଅର୍ଥ ହେଲା ଯାହା ସ୍ଥିର ରହେ, ଅର୍ଥାତ୍ ଯାହା ପରିବର୍ତ୍ତନଶୀଳ ନୁହେଁ । ତର୍କଶାସ୍ତ୍ର ତଥା ଗଣିତଶାସ୍ତ୍ରରେ ବ୍ୟବହୃତ ହେଉଥିବା ସ୍ଥିରାଙ୍କଗୁଡ଼ିକର ଅର୍ଥ ସର୍ବଦା ଅପରିବର୍ତିତ ରହେ । ତର୍କଶାସ୍ତ୍ରରେ ତର୍କଶାସ୍ତ୍ରୀୟ ସ୍ଥିରାଙ୍କଗୁଡ଼ିକ ଅପରିବର୍ତ୍ତିତ ଥିବାସ୍ଥଳେ ସେମାନଙ୍କଦ୍ୱାରା ସମ୍ପର୍କିତ ହୋଇଥିବା ଚଳଗୁଡ଼ିକର ପରିବର୍ତ୍ତନ ହୋଇପାରେ । ଏଣୁ ଏହା ତର୍କବାକ୍ୟର ସମର୍ଥନରେ ସିଦ୍ଧାନ୍ତ ନିଷ୍ପନ୍ନ ହୋଇଥାଏ ।
ଏଠାରେ ‘ତ’ ଓ ‘ଥ’ ଦୁଇଟି ତର୍କବାକ୍ୟକୁ ବୁଝାଉଅଛି । ତର୍କବାକ୍ୟର ପ୍ରତୀକରୂପେ ବର୍ଣ୍ଣମାଳାର ଯେକୌଣସି ବର୍ଣ୍ଣ ବା ଅକ୍ଷରକୁ ବ୍ୟବହାର କରାଯାଇପାରେ । ବୀଜଗଣିତରେ ସଂଖ୍ୟାମୂଳକ ଚଳରୂପେ ବ୍ୟବହାର କରାଯାଉଥିବା କ, ଖ, ଗ (x, y, z) ଇତ୍ୟାଦି ଯେପରି ଯେକୌଣସି ସଂଖ୍ୟାକୁ ବୁଝାଇଥାଏ; ସେହିପରି ତ, ଥ, ଦ, ଧ ଇତ୍ୟାଦି ଯେକୌଣସି ତର୍କବାକ୍ୟକୁ ପ୍ରତୀକାନ୍ବିତ କରେ ।
ତର୍କଶାସ୍ତ୍ରୀୟ ସ୍ଥିରାଙ୍କ – ସ୍ଥିରାଙ୍କର ଆକ୍ଷରିକ ଅର୍ଥ ହେଲା ଯାହା ସ୍ଥିର ରହେ, ଅର୍ଥାତ୍ ଯାହା ପରିବର୍ତ୍ତନଶୀଳ ନୁହେଁ । ତର୍କଶାସ୍ତ୍ର ତଥା ଗଣିତଶାସ୍ତ୍ରରେ ବ୍ୟବହୃତ ହେଉଥିବା ସ୍ଥିରାଙ୍କଗୁଡ଼ିକର ଅର୍ଥ ସର୍ବଦା ଅପରିବର୍ତିତ ରହେ । ତର୍କଶାସ୍ତ୍ରରେ ତର୍କଶାସ୍ତ୍ରୀୟ ସ୍ଥିରାଙ୍କଗୁଡ଼ିକ ଅପରିବର୍ତ୍ତିତ ଥିବାସ୍ଥଳେ ସେମାନଙ୍କଦ୍ୱାରା ସମ୍ପର୍କିତ ହୋଇଥିବା ଚଳଗୁଡ଼ିକର ପରିବର୍ତ୍ତନ ହୋଇପାରେ । ଏଣୁ ଏହା ତର୍କବାକ୍ୟର ସମର୍ଥନରେ ସିଦ୍ଧାନ୍ତ ନିଷ୍ପନ୍ନ ହୋଇଥାଏ ।
‘~’ଏହି ଚିହ୍ନକୁ ‘ନୁହେଁ’ର ପ୍ରତୀକରୂପେ ଅର୍ଥାତ୍ ନେତି ବା ବିରୁଦ୍ଧତାର ସୂଚକରୂପେ ବ୍ୟବହାର କରାଯାଏ । ସେହିପରି ‘•’ ହେଉଛି ଏବଂ ଅର୍ଥାତ୍ ସଂଯୋଜକର ସୂଚକ, ‘∨’ ହେଉଛି ‘କିମ୍ବା’ ଅର୍ଥାତ୍ ବିଯୋଜକର ସୂଚକ, ‘⊃’ ହେଉଛି ଆତ୍ପାଦନ (ଯଦି …………. ତେବେ)ର ସୂଚକ (କେତେକ ତାର୍କିକ ଏ କ୍ଷେତ୍ରରେ ‘→’ ଚିହ୍ନର ବ୍ୟବହାର କରନ୍ତି), ଏବଂ ‘≡’ ହେଉଛି ସମତୁଲ୍ୟତାର ସୂଚକ । ଏହି ପ୍ରତୀକଗୁଡ଼ିକୁ ତର୍କଶାସ୍ତ୍ରୀୟ ସ୍ଥିରାଙ୍କ ବୋଲି କୁହାଯାଏ । କାରଣ ଏହି ଚିହ୍ନଗୁଡ଼ିକର ଅର୍ଥ ଯେକୌଣସି ତାର୍କିକ ଅଭିବ୍ୟକ୍ତିରେ ଅପରିବର୍ତ୍ତିତ ରହେ । ଏଗୁଡ଼ିକ ଗାଣିତିକ ଚିହ୍ନ +, x, + ଇତ୍ୟାଦିର ଅନୁରୂପ । ଏଗୁଡ଼ିକ ବ୍ୟତୀତ ଏହି ସ୍ଥିରାଙ୍କଗୁଡ଼ିକର ପରିସର ସୂଚିତ କରିବା ନିମନ୍ତେ ‘( )’ ଏହି ଚିହ୍ନ ଅର୍ଥାତ୍ ବନ୍ଧନୀର ବ୍ୟବହାର କରିବାକୁ ପଡ଼େ । ଉଦାହରଣସ୍ୱରୂପ, ~ତ, (ତ ∨ ଥ), (ତ ⊃ ଥ), (ତ ∧ ଥ), (ତ • ଥ), (ତ ≡ ଥ) ସଂଯୋଜିତ ହୋଇଥିବା ବିଷୟ ସୂଚିତ ।
ବର୍ତ୍ତମାନ ଏହି ସ୍ଥିରାଙ୍କ ଓ ଚଳର ପ୍ରୟୋଗ କରି କେତେକ ତର୍କବାକ୍ୟର ପ୍ରତୀକାତ୍ମକ ରୂପ ନିର୍ଣ୍ଣୟ କରାଯାଉ ।
(କ) ସୂର୍ଯ୍ୟ ରହିଛି । – ତ
(ଖ) ସୂର୍ଯ୍ୟ ନାହିଁ । – ~ତ
(ଗ) ଆଲୋକ ରହିଛି । – ଥ
(ଘ) ଆଲୋକ ନାହିଁ । – ~ଥ
(ଙ) ସୂର୍ଯ୍ୟ ରହିଛି ଏବଂ ଆଲୋକ ମଧ୍ୟ ରହିଛି । – (ତ • ଥ)
(8) ଯଦି ସୂର୍ଯ୍ୟ ଥାଏ, ତେବେ ଆଲୋକ ଥାଏ । – (ତ ⊃ ଥ)
(ଛ) ଯେତେବେଳେ ଆଲୋକ ନ ଥାଏ, ସେତେବେଳେ ସୂର୍ଯ୍ୟ ମଧ୍ୟ ନଥାଏ । – ~ଥ ⊃ ~ତ
(ଜି) ସୂର୍ଯ୍ୟ ଥିଲେ ଆଲୋକ ଥାଏ ବୋଲି କହିବା ଯାହା ହୁଏତ ସୂର୍ଯ୍ୟ ନାହିଁ କିମ୍ବା ଆଲୋକ ଅଛି ବୋଲି କହିବା ମଧ୍ୟ ତାହା । – (ତ ⊃ ଥ) ≡ ( ~ ତ ∨ ଥ)
7. ସତ୍ୟଫଳନ କାହାକୁ କୁହାଯାଏ ? ବିଭିନ୍ନ ପ୍ରକାରର ସତ୍ୟଫଳନ ସମ୍ପର୍କରେ ସୂଚନା ଦିଅ ।
Answer:
ଫଳନ (Function) ଶବ୍ଦଟି ଗଣିତ ଶାସ୍ତ୍ରରେ ପ୍ରୟୋଗ ହୋଇଥାଏ । ଗଣିତରେ ଗୋଟିଏ ଅଭିବ୍ୟକ୍ତିକୁ ଅନ୍ୟର ଫଳନ ବୋଲି କୁହାଯାଏ । ଯେତେବେଳେ ସେହି ଅଭିବ୍ୟକ୍ତିଟିର ମୂଲ୍ୟ ଅନ୍ୟ ଅଭିବ୍ୟକ୍ତି ଉପରେ ନିର୍ଭରଶୀଳ ହୁଏ, ଅର୍ଥାତ୍ x = y + 1 । ଏଠାରେ xର ମୂଲ୍ୟ ଦୂର ମୂଲ୍ୟ ଉପରେ ନିର୍ଭରଶୀଳ । y ଯଦି 5 ହୁଏ, ତେବେ xର ମୂଲ୍ୟ ହେବ 6 ।
ତର୍କଶାସ୍ତ୍ରରେ ଯେକୌଣସି ତର୍କବାକ୍ୟ ସତ୍ୟ ଅଥବା ମିଥ୍ୟା ହେବ । ତେଣୁ ପ୍ରତ୍ୟେକ ତର୍କବାକ୍ୟର ସତ୍ୟ-ମିଥ୍ୟା ମୂଲ୍ୟ ଅବଶ୍ୟ ରହିବ । ମାତ୍ର ଗୋଟିଏ ତର୍କବାକ୍ୟର ମୂଲ୍ୟ ଯେତେବେଳେ ଅନ୍ୟ ଗୋଟିଏ ତର୍କବଚନର ମୂଲ୍ୟ ଉପରେ ନିର୍ଭର କରେ, ସେତେବେଳେ ପ୍ରଥମ ଅଭିବ୍ୟକ୍ତିଟିକୁ ଦ୍ବିତୀୟର ସତ୍ୟଫଳନ ବୋଲି କୁହାଯାଏ । ସେହିପରି ଗୋଟିଏ ଯୌଗିକ ତର୍କବଚନରେ ସତ୍ୟଫଳନ ନିର୍ଦ୍ଧାରଣ କଲାବେଳେ ତଦନ୍ତର୍ଗତ ତର୍କବଚନମାନଙ୍କର ସତ୍ୟ-ମିଥ୍ୟା ମୂଲ୍ୟ ଏବଂ ସେହି ବାକ୍ୟମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କ ଉପରେ ନିର୍ଭରଶୀଳ । ତର୍କବଚନଗୁଡ଼ିକ ‘ଚଳ’ ଏବଂ ସେମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କ ସ୍ଥିରାଙ୍କ ହୋଇଥବାରୁ ଏପରି ଗୋଟିଏ ତାର୍କିକ ଅଭିବ୍ୟକ୍ତିର ସତ୍ୟଫଳନ ତଦନ୍ତର୍ଗତ ‘ଚଳ’ ଓ ସ୍ଥିରାଙ୍କ ଉପରେ ନିର୍ଭରଶୀଳ ।
(୧) ବିରୁଦ୍ଧ ଫଳନ – ଗୋଟିଏ ତର୍କବଚନ ସତ୍ୟ ହେଲେ ତା’ର ବିରୁଦ୍ଧ ତର୍କବଚନଟି ମିଥ୍ୟା ହୁଏ । ସେହିପରି ଗୋଟିଏ ମିଥ୍ୟା ହେଲେ ତା’ର ବିରୁଦ୍ଧଟି ସତ୍ୟ ହୁଏ । ଉଦାହରଣସ୍ୱରୂପ – ପୁଷ୍ପଟି ଶ୍ଵେତ ଅଟେ – (ତ), ପୁଷ୍ପଟି ଶ୍ଵେତ ନୁହେଁ — (~ ତ) । ଏହି ସତ୍ୟଫଳନର ସତ୍ୟ ସାରଣୀ ନିମ୍ନୋକ୍ତ ଭାବେ ଗଠନ କରାଯାଏ ।
| ତ | ~ତ | ତ • ~ତ |
| ୧ | ୦ | ୦ |
| ୦ | ୧ | ୦ |
ମେଟ୍ରିକ୍ ସଂଖ୍ୟା (Matrix number) ୦୦ ।
(୨) ସଂଯୋଜକ ଫଳନ – ସଂଯୋଜକ ତର୍କବାକ୍ୟଟି ଏକ ଯୌଗିକ ତର୍କବାକ୍ୟ । ଏଥିରେ ଦୁଇ ବା ତତୋଽଧ୍ୱକ ତର୍କବାକ୍ୟ ‘ଏବଂ’ ଦ୍ବାରା ସଂଯୁକ୍ତ ହୋଇଥାଆନ୍ତି । ଯଥା — କମଳା ଜଣେ ନର୍ତ୍ତକୀ ଏବଂ ଅପରାଜିତା ଜଣେ ‘ଗାୟିକା’ । ଏହି ସଂଯୋଜକ ତର୍କବାକ୍ୟରେ ଦୁଇଟି ତର୍କବାକ୍ୟ ସେତିକିବେଳେ ସତ୍ୟ ହୁଏ, ଯେତେବେଳେ ଏହି ଦୁଇଟି ତର୍କବାକ୍ୟ ସତ୍ୟ ହୋଇଥାଏ । କିନ୍ତୁ ଯେକୌଣସି ଗୋଟିଏ ତର୍କବାକ୍ୟ କିମ୍ବା ଉଭୟ ତର୍କବାକ୍ୟ ମିଥ୍ୟା ହେଲେ ସଂଯୋଜକ ତର୍କବାକ୍ୟଟି ମିଥ୍ୟା ବୋଲି ପରିଗଣିତ ହେବ ।
ଉଦାହରଣସ୍ୱରୂପ – କମଳା ଜଣେ ନର୍ତ୍ତକୀ – ତ
ଅପରାଜିତା ଜଣେ ଗାୟିକା — ଥ ନିଆଯାଉ ।
ଏହାର ପ୍ରତୀକାତ୍ମକରୂପ ହେଉଛି (ତ • ଥ) ।
| ତ | ଥ | ତ • ଥ |
| ୧ | ୧ | ୧ |
| ୧ | ୦ | ୦ |
| ୦ | ୧ | ୦ |
| ୦ | ୦ | ୦ |
ମେଟ୍ରିକ୍ ସଂଖ୍ୟା (Matrix number) ୧୦୦୦ ।
(୩) ବିଯୋଜକ ଫଳନ – ଏକ ବିଯୋଜକ ତର୍କବାକ୍ୟ; ଯଥା — ରାମ ବିଚକ୍ଷଣ ଅଟେ (ତ) କିମ୍ବା ସେ ପରିଶ୍ରମୀ ଅଟେ (ଥ), ସତ୍ୟ ବୋଲି ବିବେଚିତ ହେବାପାଇଁ କଳ୍ପ ଦୁଇଟିରୁ ଯେକୌଣସି ଗୋଟିଏ ସତ୍ୟ ହେବା ଆବଶ୍ୟକ । ଉଭୟ କଳ୍ପ ସତ୍ୟ ହୋଇଥିବା ସ୍ଥଳେ ମଧ୍ଯ ବିଯୋଜକ ତର୍କବାକ୍ୟଟି ସତ୍ୟ, କିନ୍ତୁ ଉଭୟ କଳ୍ପ ମିଥ୍ୟା ହୋଇଥିଲେ ତାହା ମିଥ୍ୟା । ସୁତରାଂ ବିଯୋଜକ ଫଳନର ସତ୍ୟସାରଣୀ ନିମ୍ନରୂପ ହୋଇଥାଏ ।
| ତ | ଥ | ତ ∨ ଥ |
| ୧ | ୧ | ୧ |
| ୧ | ୦ | ୧ |
| ୦ | ୧ | ୧ |
| ୦ | ୦ | ୦ |
ମେଟ୍ରିକ୍ ସଂଖ୍ୟା (Matrix number) ୧୧୧୦ ।
(୪) ବୈକଳ୍ପିକ ଫଳନ – ବୈକଳ୍ପିକ ତର୍କବାକ୍ୟଟି ମଧ୍ୟ ଏକ ଯୌଗିକ ତର୍କବାକ୍ୟ । ଏଥିରେ ଦୁଇଟି ତର୍କବାକ୍ୟ ‘ଉଭୟ ନୁହେଁ’ ଦ୍ବାରା ସମ୍ପର୍କିତ ହୋଇଥାନ୍ତି । ‘ରାମ ଉଭୟ ବୁଦ୍ଧିଆ ଏବଂ ନିର୍ବୁଦ୍ଧିଆ ନୁହେଁ’– ଏଥରେ ମଧ୍ଯ ଦୁଇଟି ବିକଳ୍ପ ରହିଥାଏ । ସାଧାରଣତଃ ଗୋଟିଏ ବିକଳ୍ପ ସତ୍ୟ ହେଲେ ବୈକଳ୍ପିକ ତର୍କବାକ୍ୟଟି ସତ୍ୟ ହୋଇଥାଏ । ଦୁଇଟିଯାକ ବିକଳ୍ପ ମିଥ୍ୟା ହୋଇପାରେ କିନ୍ତୁ ଦୁଇଟିଯାକ ସତ୍ୟ ହୋଇପାରିବ ନାହିଁ । ଏଥିରେ ଗୋଟିଏ ‘ତ’ ହେଲେ ଅନ୍ୟଟି ‘ଥ’ ହୋଇଥାଏ । ତ ଓ ଥ ଦୁଇଟି ତର୍କବାକ୍ୟ ହେଲେ ବୈକଳ୍ପିକ ଫଳନର ସତ୍ୟସାରଣୀ ନିମ୍ନଭାବରେ ଗଠନ ହୋଇପାରେ ।
| ତ | ଥ | ତ ∧ ଥ |
| ୧ | ୧ | ୦ |
| ୧ | ୦ | ୧ |
| ୦ | ୧ | ୧ |
| ୦ | ୦ | ୧ |
ମେଟ୍ରିକ୍ ସଂଖ୍ୟା (Matrix number) ୦୧୧୧ ।
(୫) ଆପାଦନ ଫଳନ– ଏକ ପ୍ରାକଚ୍ଛିକ ବା ଆପାଦନମୂଳକ ତର୍କବାକ୍ୟର ଆକାର ହେଉଛି ଯଦି ତ, ତେବେ ଥ । ତର୍କଶାସ୍ତ୍ରରେ ଏହାକୁ ‘ହୁଏତ ‘ତ’ ମିଥ୍ୟା କିମ୍ବା ‘ଥ’ ସତ୍ୟ ବୋଲି ଅର୍ଥ କରାଯାଏ । କାରଣ ଏହାହିଁ ହେଉଛି ସର୍ବନିମ୍ନ ସର୍ଭ, ଯାହାର ପୂରଣ ବିନା ଏ ପ୍ରକାର କୌଣସି ତର୍କବାକ୍ୟକୁ ସ୍ଵୀକାର କରାଯାଇ ନପାରେ । ଯଦି ବର୍ଷା ହୁଏ, ତେବେ ବନ୍ୟା ହୁଏ ।
ବର୍ଷା ହୁଏ । – ତ
ବନ୍ୟା ହୁଏ । – ଥ
ଏହାର ପ୍ରତୀକାତ୍ମକ ରୂପ (ତ ⊃ ଥ ) ଅଟେ ।
ବର୍ତ୍ତମାନ ଆପାଦନ ଫଳନର ସତ୍ୟସାରଣୀ ଗଠନ କରାଯାଉ ।
| ତ | ଥ | ତ ⊃ ଥ |
| ୧ | ୧ | ୧ |
| ୧ | ୦ | ୦ |
| ୦ | ୧ | ୧ |
| ୦ | ୦ | ୧ |
ମେଟ୍ରିକ୍ ସଂଖ୍ୟା (Matrix number) ୧୦୧୧ ।
(୬) ସମତୁଲ୍ୟତା ଫଳନ — ଦୁଇଟି ତର୍କବାକ୍ୟର ସମତୁଲ୍ୟତା ଥାଏ, ଅର୍ଥାତ୍ ସେମାନେ ସମତୁଲ୍ୟ ହୁଅନ୍ତି ଯଦି ଗୋଟିକର ସତ୍ୟତା ଅନ୍ୟର ସତ୍ୟତା ଏବଂ ଗୋଟିକର ମିଥ୍ୟାତ୍ମ ଅନ୍ୟର ମିଥ୍ୟାତ୍ବ ଉପରେ ନିର୍ଭରଶୀଳ ହୁଏ । ଏହି ସମତୁଲ୍ୟତାକୁ ନିର୍ଦ୍ଧାରଣ କରିବାପାଇଁ ତର୍କଶାସ୍ତ୍ରବିଦ୍ମାନେ ‘କେବଳ ଏବଂ କେବଳ ଯଦି’ (Only and only if) ଦ୍ୱାରା ସୂଚିତ କରିଥାଆନ୍ତି । ଏହାର ପ୍ରତୀକାତ୍ମକ ରୂପ ହେଲା ତ = ଥ । ରାମ ରାବଣକୁ ମାରିଥିବେ ଯଦି ଏବଂ କେବଳ ଯଦି ରାବଣ ରାମଙ୍କଦ୍ଵାରା ହତ ହୋଇଥବ । ସମତୁଲ୍ୟତାର ସତ୍ୟସାରଣୀ ହେଲା –
| ତ | ଥ | ତ ≡ ଥ |
| ୧ | ୧ | ୧ |
| ୧ | ୦ | ୦ |
| ୦ | ୧ | ୦ |
| ୦ | ୦ | ୧ |
ମେଟ୍ରିକ୍ ସଂଖ୍ୟା (Matrix number) ୧୦୦୧ ଅଟେ ।
8. ପୁନରୁକ୍ତିକ, ବିରୁଦ୍ଧ ଓ ଆପାତିକ ତର୍କବାକ୍ୟମୂଳକ ସୂତ୍ରଗୁଡ଼ିକୁ ସତ୍ୟ ସାରଣୀ ପଦ୍ଧତିଦ୍ଵାରା ବୁଝାଅ ।
Answer:
ପୁନରୁକ୍ତିକ ତର୍କବାକ୍ୟମୂଳକ ସୂତ୍ର — ଗୋଟିଏ ତର୍କବାକ୍ୟର ସତ୍ୟ କିମ୍ବା ମିଥ୍ୟା ଏପରି ଦୁଇଟି ମୂଲ୍ୟ ଥାଏ । ଦୁଇଟି ତର୍କବାକ୍ୟର ସତ୍ୟ-ମିଥ୍ୟା ମୂଲ୍ୟକୁ ନେଇ ଏକ ସତ୍ୟଫଳନ ଗଠନ କରାଯାଏ । ଏହି ସତ୍ୟଫଳନର ମୂଲ୍ୟ ଯଦି ସର୍ବଦା ସତ୍ୟ ହୁଏ ଅର୍ଥାତ୍ ଯଦି ସତ୍ୟସାରଣୀର ମୁଖ୍ୟ ସଂଯୋଜକରେ ମେଟ୍ରିକ୍ ସଂଖ୍ୟା ବା ସୂଚକ ସଂଖ୍ୟା କେବଳ ‘୧’କୁ ନେଇ ଗଠିତ ହୁଏ, ତେବେ ସେହି ସୂତ୍ରଟିକୁ ପୁନରୁକ୍ମିକ ସୂତ୍ର ବୋଲି କୁହାଯାଏ । ଏହା ତର୍କବାକ୍ୟ ଦୃଷ୍ଟିରୁ ସର୍ବଦା ସତ୍ୟ ହୋଇଥାଏ । ଉଦାହରଣ ସ୍ଵରୂପ ତ ∨ ~ ତ ହେଉଛି ଏକ ପୁନରୁକ୍ତିକ ସୂତ୍ର ।
ସତ୍ୟସାରଣୀ :
| ତ | ~ତ | ତ ∨ ~ତ |
| ୧ | ୦ | ୧ |
| ୦ | ୧ | ୧ |
ଏହିପରି ଅନେକ ଉଦାହରଣମାନ ରହିଛି; ଯଥା – (ତ • ଥ) ⊃ ତ ଇତ୍ୟାଦି ।
ବିରୁଦ୍ଧ ତର୍କବାକ୍ୟମୂଳକ ସୂତ୍ର — ଯେଉଁ କ୍ଷେତ୍ରରେ ଦୁଇଟି ତର୍କବାକ୍ୟର ସତ୍ୟ-ମିଥ୍ୟା ମୂଲ୍ୟକୁ ନେଇ ଗଠିତ ସତ୍ୟ ଫଳନର ମୂଲ୍ୟ ସର୍ବଦା ମିଥ୍ୟା ହୁଏ ଅର୍ଥାତ୍ ସତ୍ୟ ସାରଣୀର ମୁଖ୍ୟ ସଂଯୋଜକରେ ମେଟ୍ରିକ୍ ସଂଖ୍ୟା କେବଳ ‘୦’ କୁ ନେଇ ଗଠିତ ହୁଏ, ସେହି ସୂତ୍ରକୁ ବିରୁଦ୍ଧ ସୂତ୍ର ବୋଲି କୁହାଯାଏ । ଏହା ତର୍କବାକ୍ୟ ଦୃଷ୍ଟିରୁ ସର୍ବଦା ମିଥ୍ୟା ହୋଇଥାଏ । ଉଦାହରଣ ସ୍ୱରୂପ, (ତ • ~ତ) ଏକ ବିରୁଦ୍ଧ ସୂତ୍ର । ଏହି ଦୃଷ୍ଟିରୁ ଏକ ସତ୍ୟ ସାରଣୀ ଗଠନ କରାଯାଇପାରେ ।
ସତ୍ୟସାରଣୀ :
| ତ | ~ତ | ତ • ~ତ |
| ୧ | ୦ | ୦ |
| ୦ | ୧ | ୦ |
ଏହି ସତ୍ୟସାରଣୀର ମୁଖ୍ୟ ସଂଯୋଜକ ହେଲା ‘•’ ଏବଂ ମେଟ୍ରିକ୍ ସଂଖ୍ୟା ୦୦ ।
ଆପାତିକ ତର୍କବାକ୍ୟମୂଳକ ସୂତ୍ର — ଯେଉଁ କ୍ଷେତ୍ରରେ ଦୁଇଟି ତର୍କବାକ୍ୟର ସତ୍ୟ-ମିଥ୍ୟା ମୂଲ୍ୟକୁ ନେଇ ଗଠିତ ସତ୍ୟ ଫଳନର ମୂଲ୍ୟ ଅନିଶ୍ଚିତ ହୁଏ ଅର୍ଥାତ୍ କେତେକ କ୍ଷେତ୍ରରେ ସତ୍ୟ ଏବଂ କେତେକ କ୍ଷେତ୍ରରେ ମିଥ୍ୟା ହୁଏ ଅର୍ଥାତ୍ ସତ୍ୟସାରଣୀର ମୁଖ୍ୟ ସଂଯୋଜକରେ ମେଟ୍ରିକ୍ ସଂଖ୍ୟା ‘୧’ ଏବଂ ‘୦’କୁ ନେଇ ଗଠିତ ହୋଇଥାଏ, ସେହି ସୂତ୍ରକୁ ଆପାତିକ ସୂତ୍ର ବୋଲି କୁହାଯାଏ । ଏହା ତର୍କଦୃଷ୍ଟିରୁ ବେଳେବେଳେ ସତ୍ୟ ଏବଂ ବେଳେବେଳେ ମିଥ୍ୟା ହୋଇଥାଏ । ଉଦାହରଣସ୍ୱରୂପ (ତ ∨ ଥ) ହେଉଛି ଏକ ଆପାତିକ ସୂତ୍ର ।
ସତ୍ୟସାରଣୀ :
| ତ | ଥ | ତ ∨ ଥ |
| ୧ | ୧ | ୧ |
| ୧ | ୦ | ୧ |
| ୦ | ୧ | ୦ |
| ୦ | ୦ | ୦ |
ଏହାର ମେଟ୍ରିକ୍ ସଂଖ୍ୟା ୧୧୧୦ ଅଟେ ।
9. ସତ୍ୟସାରଣୀ ପଦ୍ଧତିଟି କ’ଣ ? ଏହା ଯୁକ୍ତିମାନଙ୍କର ବୈଧତା ନିର୍ଦ୍ଧାରଣ କରିବାରେ କିପରି ସହାୟକ ଉଦାହାରଣ ସହ ବୁଝାଇ ଲେଖ ।
Answer:
ଗୋଟିଏ ତାର୍କିକ ଅଭିବ୍ୟକ୍ତି ଉଦାହରଣସ୍ୱରୂପ (ତ – ଥ)ର ସତ୍ୟଫଳନ ନିର୍ଦ୍ଧାରଣ କରିବାପାଇଁ ତର୍କଶାସ୍ତ୍ରବିଦ୍ଗଣ କେତେକ ପଦ୍ଧତି ଅବଲମ୍ବନ କରିଛନ୍ତି । ସେମାନଙ୍କ ମଧ୍ୟରୁ ଗୋଟିଏ ସରଳ ଉପାୟ ହେଲା ସତ୍ୟସାରଣୀ ଗଠନ । ଆଗରୁ କୁହାଯାଇଛି ଯେ ଗୋଟିଏ ତର୍କବାକ୍ୟ ହୁଏତ ସତ୍ୟ ଅଥବା ମିଥ୍ୟା ହେବ । ଏହାକୁ ତର୍କବାକ୍ୟର ‘ସତ୍ୟଫଳନ ମୂଲ୍ୟ’ ବୋଲି କୁହାଯାଏ । ଦୁଇଟି ତର୍କବାକ୍ୟ ଯେକୌଣସି ସ୍ଥିରାଙ୍କଦ୍ୱାରା ସମ୍ବନ୍ଧିତ ହେଲେ ସେହି ସମ୍ବନ୍ଧର ସତ୍ୟଫଳନ ଅନ୍ତର୍ଗତ ଚଳମାନଙ୍କର ସତ୍ୟ-ମିଥ୍ୟା ମୂଲ୍ୟ ଉପରେ ନିର୍ଭର କରେ । ଅର୍ଥାତ୍ (ତ ୬ ଥ)ର ସତ୍ୟ ଫଳନ ତ ଓ ଥ ର ସତ୍ୟ-ମିଥ୍ୟା ମୂଲ୍ୟ ଉପରେ ନିର୍ଭରଶୀଳ । ଏହି ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ ପାଇଁ ସତ୍ୟସାରଣୀ ଗଠନ ଆବଶ୍ୟକ ।
ସତ୍ୟସାରଣୀ ଗଠନ ପ୍ରଣାଳୀ – ପ୍ରତ୍ୟେକ ତର୍କବାକ୍ୟର ମୂଲ୍ୟ ସତ୍ୟ କିମ୍ବା ମିଥ୍ୟା ହୋଇପାରେ । ସତ୍ୟକୁ (୧) ଏବଂ ମିଥ୍ୟାକୁ (୦) ବୋଲି ନିଆଯାଏ । ଗୋଟିଏ ତାର୍କିକ ଅଭିବ୍ୟକ୍ତିରେ ଏକାଧ୍ଵ ଚଳର ସ୍ଥିତି ଦୃଷ୍ଟିରୁ ଏହାର ସତ୍ୟ ଫଳନର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ ପାଇଁ ନିର୍ଦ୍ଦିଷ୍ଟ ପ୍ରଣାଳୀ ଅବଲମ୍ବନ କରିବାକୁ ହୁଏ । ଯଦି ଦୁଇଟି ଚଳ ଥାଏ (ତ ଏବଂ ଥ) ତେବେ ପ୍ରତ୍ୟେକଟି ସତ୍ୟ କିମ୍ବା ମିଥ୍ୟା ହୋଇଥବା ଦୃଷ୍ଟିରୁ ଦୁଇଟି ଚଳର ମୂଲ୍ୟ ଚାରିଥର ଅର୍ଥାତ୍ ୨ର ବର୍ଗ ହେବ । ସେହିପରି ତିନିଗୋଟି ଚଳ ହେଲେ ୨ × ୨ × ୨ = ୮ଟି ସତ୍ୟ-ମିଥ୍ୟା ମୂଲ୍ୟ ହେବ । ବର୍ତ୍ତମାନ ଦୁଇଟି ଚଳ ତ ଓ ଥ କୁ ନେଇ ସେମାନଙ୍କର ସତ୍ୟ-ମିଥ୍ୟା ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କରାଯାଉ ।
| ‘ତ’ ‘ଥ’ | ତ | ଥ | |
| (୧) | ‘ତ’ ସତ୍ୟ ହେଲେ ‘ଥ’ ସତ୍ୟ ହୁଏ | ୧ | ୧ |
| (୨) | ‘ତ’ ସତ୍ୟ ହେଲେ ‘ଥ’ ମିଥ୍ୟା ହୁଏ | ୧ | ୦ |
| (୩) | ‘ତ’ ମିଥ୍ୟା ହେଲେ ‘ଥ’ ସତ୍ୟ ହୁଏ | ୦ | ୧ |
| (୪) | ‘ତ’ ମିଥ୍ୟା ହେଲେ ‘ଥ’ ମିଥ୍ୟା ହୁଏ | ୦ | ୦ |
ସତ୍ୟସାରଣୀ ପଦ୍ଧତି ପ୍ରୟୋଗରେ ଯୁକ୍ତିମାନଙ୍କର ବୈଧତା ବିଚାର :
ଏହି ପଦ୍ଧତିର ପ୍ରୟୋଗରେ ଯୁକ୍ତିମାନଙ୍କର ବୈଧତା ମଧ୍ୟ ବିଚାର କରାଯାଏ । ବୈଧତା ବିଚାର କରିବାକୁ ଗଲାବେଳେ ଦେଖୁବାକୁ ହେବ ଯେ ଯୁକ୍ତିଗୁଡ଼ିକ ପୁନରୁକ୍ତିକ (Tautology) କିମ୍ବା ବିରୁଦ୍ଧ (Contradictory) ଅଥବା ଆପାତିକ (Contingent)
ଅଟନ୍ତି ।
ଦୁଇଟି ତର୍କବାକ୍ୟ ମଧ୍ୟରେ ଥିବା ସମ୍ବନ୍ଧର ସତ୍ୟ ସାରଣୀ ଯଦି ଏପରି ହୁଏ ଯେ ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ତାହାର ମୂଲ୍ୟ ୧ ହୁଏ ତେବେ ସେହି ସୂତ୍ରଟିକୁ ପୁନରୁକ୍ତିକ ସୂତ୍ର କୁହାଯାଏ ।
| ତ | ~ତ | ତ ∨ ~ତ |
| ୧ | ୦ | ୧ |
| ୦ | ୧ | ୧ |
ଯେଉଁ କ୍ଷେତ୍ରରେ ତର୍କବାକ୍ୟ ଦ୍ଵୟର ସମ୍ବନ୍ଧ ନିର୍ଦ୍ଧାରଣ କଲାବେଳେ ସତ୍ୟସାରଣୀ କେବଳ ୦ ଅଥବା ମିଥ୍ୟା ହୁଏ ସେହି ସମ୍ବନ୍ଧକୁ ବିରୁଦ୍ଧ ସୂତ୍ର କୁହାଯାଏ ।
| ତ | ~ତ | • ~ତ |
| ୧ | ୦ | ୦ |
| ୦ | ୧ | ୦ |
ତର୍କବାକ୍ୟ ଦ୍ଵୟର ସମ୍ବନ୍ଧ ସ୍ଥିର କରିବାପାଇଁ ସତ୍ୟସାରଣୀର ମୂଲ୍ୟ ଯଦି କେତେକ କ୍ଷେତ୍ରରେ ସତ୍ୟ ଏବଂ କେତେକ କ୍ଷେତ୍ରରେ ମିଥ୍ୟା ହୁଏ ତେବେ ତାହାକୁ ଏକ ଆପାତିକ ସୂତ୍ର କୁହାଯାଏ ।
| ତ | ଥ | ତ ∨ ଥ |
| ୧ | ୧ | ୧ |
| ୧ | ୦ | ୧ |
| ୦ | ୧ | ୧ |
| ୦ | ୦ | ୦ |
ସତ୍ୟସାରଣୀ ମାଧ୍ୟମରେ ଯୁକ୍ତିର ପ୍ରମାଣସିଦ୍ଧତା ପରୀକ୍ଷା :
ଉଦାହରଣ – ୧
ଯଦି ସୂର୍ଯ୍ୟ ଥାଏ, ତେବେ ଆଲୋକ ଥାଏ, ଏବଂ ଏବେ ସୂର୍ଯ୍ୟ ରହିଛି ∴ ଆଲେକ ଅଛି ।
ଏହାର ପ୍ରତୀକାତ୍ମକ ଆକାର ହେଉଛି – ଯଦି ତ, ତେବେ ଥ, ଏବଂ ତ, ∴ ଥ ।
((ତ ⊃ ଥ) • ତ) ⊃ ଥ
ସତ୍ୟସାରଣୀ
| ୧ ତ |
୨ ଥ |
୩ ତ ⊃ ଥ |
୪ (ତ ⊃ ଥ) • ତ |
୫ ((ତ ⊃ ଥ) • ତ) ⊃ ଥ |
| ୧ | ୧ | ୧ | ୧ | ୧ |
| ୧ | ୦ | ୦ | ୦ | ୧ |
| ୦ | ୧ | ୧ | ୦ | ୧ |
| ୦ | ୦ | ୧ | ୦ | ୧ |
ବ୍ୟାଖ୍ୟା — ତ ଏବଂ ଥର ସତ୍ୟ-ମିଥ୍ୟା ମୂଲ୍ୟ ବିଷୟକ ସମସ୍ତ ସମ୍ଭବପର ସମନ୍ବୟ ୧ମ ଓ ୨ୟ ସ୍ତମ୍ଭରେ ଦିଆଯାଇଛି । ଆପାଦନ ଫଳନର ସତ୍ୟ ସାରଣୀ ଅନୁଯାୟୀ (ତ ୬ ଥ)ର ସତ୍ୟତା ମୂଲ୍ୟ ୩ୟ ସ୍ତମ୍ଭରେ ନିର୍ଦ୍ଧାରିତ ହୋଇଛି । ୩ୟ ଓ ୧ମ ସ୍ତମ୍ଭର ସମ୍ପର୍କ ପ୍ରତିଷ୍ଠା କରି ସଂଯୋଜକ ଫଳନର ସତ୍ୟ ସାରଣୀ ଅନୁଯାୟୀ (ତ୬ ଥ) •ତର ସତ୍ୟତା ମୂଲ୍ୟ ୪ର୍ଥ ସ୍ତମ୍ଭରେ ସ୍ଥିରୀକୃତ ହୋଇଛି । ପରିଶେଷରେ ୪ର୍ଥ ଓ ୨ୟ ସ୍ତମ୍ଭର ସମ୍ପର୍କ ପ୍ରତିଷ୍ଠା କରି ଆପାଦନ ଫଳନର ସତ୍ୟ ସାରଣୀ ଅନୁଯାୟୀ ((ତ ୬ ଥ) • ତ) ୬ ଥର ସତ୍ୟତା ମୂଲ୍ୟ ୫ମ ସ୍ତମ୍ଭରେ ପ୍ରଦର୍ଶିତ ହୋଇଛି ।
ମୁଖ୍ୟ ଅର୍ଥାତ୍ ସର୍ବଶେଷ ସ୍ତମ୍ଭର ମେଟ୍ରିକ୍ ସଂଖ୍ୟା ୧ ଗୁଡ଼ିକଦ୍ଵାରା ଗଠିତ । ତେଣୁ ଏହା ଏକ ପୁନରୁକ୍ତିକ ସୂତ୍ର । ଏଣୁ ଏହି ଯୁକ୍ତିଟି ସିଦ୍ଧ ବା ବୈଧ ଅଟେ ।
ଉଦାହରଣ – ୨
ଯଦି ସୂର୍ଯ୍ୟ ଥାଏ, ତେବେ ଆଲୋକ ଥାଏ ଏବଂ ଏବେ ଆଲୋକ ରହିଛି ।
∴ ସୂର୍ଯ୍ୟ ଅଛି ।
ସୂର୍ଯ୍ୟ ଥାଏ । – ତ
ଆଲୋକ ଥାଏ । – ଥ
ପ୍ରତୀକାତ୍ମକ ଆକାର – ((ତ ⊃ ଥ) • ଥ ) ⊃ ତ
ସତ୍ୟସାରଣୀ
| ୧ ତ |
୨ ଥ |
୩ ତ ⊃ ଥ |
୪ (ତ ⊃ ଥ) • ତ |
୫ ((ତ ⊃ ଥ) • ତ) ⊃ ଥ |
| ୧ | ୧ | ୧ | ୧ | ୧ |
| ୧ | ୦ | ୦ | ୦ | ୧ |
| ୦ | ୧ | ୧ | ୧ | ୦ |
| ୦ | ୦ | ୧ | ୦ | ୧ |
ବ୍ୟାଖ୍ୟା – ୧ମ, ୨ୟ ଓ ୩ୟ ସ୍ତମ୍ଭର ବିଷୟବସ୍ତୁ ସୁପ୍ରତ୍ୟକ୍ଷ ୪ର୍ଥ ସ୍ତମ୍ଭଦ୍ଵାରା ୩ୟ ଓ ୨ୟ ସ୍ତମ୍ଭର ସତ୍ୟତା ମୂଲ୍ୟର ସଂଯୋଗ ବିଧାନ କରାଯାଇଛି ଏବଂ ୫ମ ସ୍ତମ୍ଭଦ୍ୱାରା ୪ର୍ଥ ଓ ୧ମ ସ୍ତମ୍ଭର ସତ୍ୟତା ମୂଲ୍ୟର ସମ୍ପର୍କ ସଂସ୍ଥାପିତ ହୋଇଛି । ଏହାର ମୁଖ୍ୟ ଅର୍ଥାତ୍ ସବିଶେଷ ସ୍ତମ୍ଭର ମେଟ୍ରିକ୍ସ୍ ସଂଖ୍ୟା ଉଭୟ ୧ ଓ ୦ ଗୁଡ଼ିକୁ ନେଇ ଗଠିତ । ତେଣୁ ଏହା ଏକ ଆପାତିକ ସୂତ୍ର ।
ଉଦାହରଣ – ୩
ରାମ ହୁଏତ ବୁଦ୍ଧିମାନ୍ ଅଥବା ନିର୍ବୁଦ୍ଧିଆ ଅଟେ ।
ସେ ବୁଦ୍ଧିମାନ୍ ନୁହେଁ ।
∴ ସେ ନିର୍ବୁଦ୍ଧିଆ ଅଟେ ।
ରାମ ବୁଦ୍ଧିମାନ୍ ଅଟେ । – ତ
ସେ ନିର୍ବୁଦ୍ଧିଆ ଅଟେ । – ଥ
((ତ ∨ ଥ) • ~ ତ) ⊃ ଥ
ସତ୍ୟସାରଣୀ
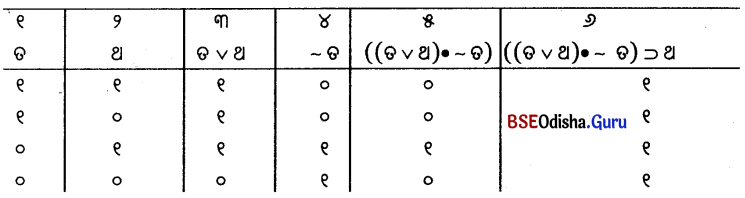
ବ୍ୟାଖ୍ୟା —୧ମ, ୨ୟ ଓ ୩ୟ ସ୍ତମ୍ଭର ବିଷୟବସ୍ତୁ ସୁପ୍ରତ୍ୟକ୍ଷ ବିରୁଦ୍ଧ ଫଳନର ସତ୍ୟ ସାରଣୀ ଅନୁଯାୟୀ ~ ତ ର ସତ୍ୟତା ମୂଲ୍ୟ ୪ର୍ଥ ସ୍ତମ୍ଭରେ ନିର୍ଦ୍ଧାରିତ । ୫ମ ସ୍ତମ୍ଭଦ୍ଵାରା ୩ୟ ଓ ୪ର୍ଥ ସ୍ତମ୍ଭର ସତ୍ୟତା ମୂଲ୍ୟର ସଂଯୋଗ ସ୍ଥାପନ କରାଯାଇଛି ଏବଂ ୬ଷ୍ଠ ସ୍ତମ୍ଭଦ୍ଵାରା ୫ମ ଓ ୨ୟ ସ୍ତମ୍ଭର ସତ୍ୟତା ମୂଲ୍ୟର ସମ୍ପର୍କ ସଂସ୍ଥାପିତ ହୋଇଛି । ଏହାର ମୁଖ୍ୟ ସ୍ତମ୍ଭର ମେଟ୍ରିକ୍ ସଂଖ୍ୟା କେବଳ ୧ ଗୁଡ଼ିକୁ ନେଇ ଗଠିତ । ଏଣୁ ଏହା ଏକ ପୁନରୁକ୍ତିକ ସୂତ୍ର ।
10. ବିଭିନ୍ନ ସତ୍ୟଫଳନମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କକୁ ବୁଝାଇଦିଅ ।
Answer:
ସତ୍ୟଫଳନମାନଙ୍କ ମଧ୍ୟରେ ପାରସ୍ପରିକ ସମ୍ପର୍କ ରହିଅଛି । ତ ⊃ ଥ କୁ ମଧ୍ୟ ~ତ ∨ ଥ ରୂପେ କିମ୍ବା ~ (ତ • ~ଥ ) ରୂପେ ପ୍ରକାଶ କରାଯାଇପାରେ ।
ଉଦାହରଣ – ୧
ସେ ଯଦି ଆସେ, ତେବେ ମୁଁ ଯିବି ।
ସେ ଆସେ । – ତ
ମୁଁ ଯିବି । – ଥ
ଏହାକୁ ନିମ୍ନୋକ୍ତ ମଧେ ବ୍ୟକ୍ତ କରାଯାଇପାରେ ।
(ତ ⊃ ଥ) ଯଥା – ସେ ଆସିବ ନାହିଁ ଅଥଚ ମୁଁ ଯିବି । – ~ ତ ∨ ଥ
କିମ୍ବା ସେ ଆସିବ ଅଥଚ ମୁଁ ଯିବି ନାହିଁ, ଏହା ସମ୍ଭବ ନୁହେଁ ।
ଏହାର ପ୍ରତୀକାତ୍ମକ ଅଭିବ୍ୟକ୍ତି ହେଲା – • ~ (ତ • ~ ଥ )
ସତ୍ୟସାରଣୀ
| ୧ମ | ୨ୟ | ୩ୟ | ୪ର୍ଥ |
| ତ ଥ | ତ ⊃ ଥ | ~ ତ ∨ ଥ | • ~ (ତ • ~ ଥ ) |
| ୧ ୧ | ୧ | ୦ ୧ ୧ | ୧ ୧ ୦ ୦ ୧ |
| df | |||
| ୧ ୦ | ୦ | ୦ ୦ ୦ | ୦ ୧ ୧ ୧ ୦ |
| df | |||
| ୦ ୧ | ୧ | ୧ ୧ ୧ | ୧ ୦ ୦ ୦ ୧ |
| ୦ ୦ | ୧ | ୧ ୧ ୦ | ୧ ୦ ୦ ୧ ୦ |
ଏହି ସତ୍ୟସାରଣୀରୁ ଜଣାପଡୁଛି ଯେ ୨ୟ, ୩ୟ ଓ ୪ର୍ଥ ସତ୍ୟ ଫଳନଗୁଡ଼ିକର ସତ୍ୟତା ମୂଲ୍ୟ ସମାନ ଅଛି । ଏହାର ପ୍ରତ୍ୟେକ ସ୍ତମ୍ଭରେ ୧୦୧୧ ହୋଇଥିବାରୁ ଗୋଟିଏ ସତ୍ୟଫଳନକୁ ଅନ୍ୟର ସଂଜ୍ଞାତୁଲ୍ୟ ବୋଲି କୁହାଯାଇଛି ।
ଉଦାହରଣ – ୨
ଗୋପାଳ ଜଣେ ସଟ ଓ ସରଳ ଲୋକ ଅଟେ ।
ଏହା ଗୋଟିଏ ସଂଯୋଜକ ଫଳନ ଅଟେ ।
ଗୋପାଳ ଜଣେ ସଛୋଟ ଲୋକ ଅଟେ । – ତ
ସେ ଜଣେ ସରଳ ଲୋକ ଅଟେ । – ଥ
ପ୍ରତୀକାତ୍ମକରୂପ = (ତ • ଥ)
ଗୋପାଳ ସଟ ନୁହେଁ ଅଥବା ସରଳ ନୁହେଁ, ଏକଥା ସତ ନୁହେଁ । ଏହାର ପ୍ରତୀକାତ୍ମକରୂପ ହେଲା – ~(~ତ ∨ ~ ଥ )
~(~ତ ∨ ~ ଥ ) ର ଅର୍ଥ ହେବ ~ (ତ ⊃ ~ ଥ) ।
ଏଥୁରୁ ପ୍ରମାଣିତ ହେଲା ଯେ – ତ • ଥ = df ~ (~ତ ∨ ~ ଥ ) df ~ (ତ ⊃ ~ ଥ)
ସତ୍ୟସାରଣୀ
| ୧ମ | ୨ୟ | ୩ୟ | ୪ର୍ଥ |
| ତ ଥ | ତ • ଥ | ~ (~ତ ∨ ~ ଥ ) | ~ (ତ ⊃ ~ ଥ) |
| ୧ ୧ | ୧ | ୧ ୦ ୦ ୦ | ୧ ୧ ୦ ୦ |
| ୧ ୦ | ୦ | ୦ ୦ ୧ ୧ | ୦ ୧ ୧ ୧ |
| ୦ ୧ | ୦ | ୦ ୧ ୧ ୦ | ୦ ୦ ୧ ୦ |
| ୦ ୦ | ୦ | ୦ ୧ ୧ ୧ | ୦ ୦ ୧ ୧ |
ଏହି ସତ୍ୟସାରଣୀରୁ ଜଣାପଡୁଛି ଯେ ୨ୟ, ୩ୟ ଓ ୪ର୍ଥର ସତ୍ୟଫଳନଗୁଡ଼ିକର ସତ୍ୟତା ମୂଲ୍ୟ ସମାନ ଅଛି । ଅର୍ଥାତ୍ ଏହା ପ୍ରତ୍ୟେକ ୧୦୦୦ ହୋଇଥିବାରୁ ଗୋଟିଏ ସତ୍ୟଫଳନକୁ ଅନ୍ୟଟିର ସଂଜ୍ଞାତୁଲ୍ୟ ବୋଲି କୁହାଯାଇଛି ।
ଉଦାହରଣ – ୩
ଆମ୍ବଟି ଖଟା କିମ୍ବା ମିଠା । – (ତ ∨ ଥ)
ଏହା ଏକ ବିଯୋଜକ ଫଳନ ଅଟେ । ଏଠାରେ ମଧ୍ୟ ପ୍ରକାଶ କରାଯାଇପାରେ ଯେ ଆମ୍ବଟି ଖଟା ନୁହେଁ ଏବଂ ମିଠା ନୁହେଁ, ଏକଥା ସତ୍ୟ ନୁହେଁ । ଏହାର ପ୍ରତୀକାତ୍ମକ ଅଭିବ୍ୟକ୍ତି ହେଲା –
~ (~ ତ • ~ ଥ ) । ତେଣୁ ଏହାର ପ୍ରତୀକାତ୍ମକ ଅଭିବ୍ୟକ୍ତି ହେଲା –
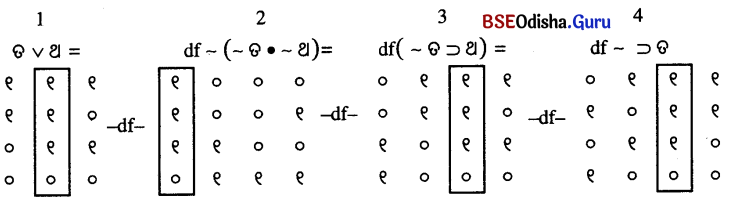
ଏହି ସତ୍ୟସାରଣୀରୁ ଅନୁମେୟ ଯେ ପ୍ରତ୍ୟେକ ସତ୍ୟସାରଣୀର ସତ୍ୟଫଳନ ସମାନ ଅଟେ । ଏହା ୧୧୧୦ ଅଟେ । ଶେଷରେ ଆମେ ଜାଣିଲେ ଯେ –
(୧) ତ ⊃ ଥ = df ~ ତ ∨ ଥ = df ~ (ତ • ~ ଥ)
(୨) ତ • ଥ = df ~ (~ ତ ∨ ~ ଥ) = df ~ (ତ ⊃ ~ ଥ)
(୩) ତ ∨ ଥ = df ~ (ତ • ~ ଥ) = df ~ (ତ ⊃ ~ ଥ) = df ~ ଥ ⊃ ତ
ସେହିପରି ତ ⊃ ଥ ମଧ୍ୟ ~ ଥ ⊃ ~ ତ ସହିତ ସମତୁଲ୍ୟ ହୋଇଥାଏ । ଏହାକୁ ସତ୍ୟସାରଣୀଦ୍ଵାରା ପ୍ରମାଣ କରାଯାଇପାରେ ।
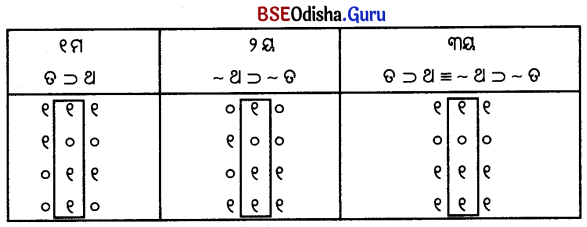
୧ମ ଓ ୨ୟ ସ୍ତମ୍ଭରୁ ଏହା ସ୍ପଷ୍ଟ ହେଉଅଛି ଯେ ତ ⊃ ଥ ଏବଂ ~ ଥ ⊃ ~ତ ର ସତ୍ୟତା ମୂଲ୍ୟ ୧୦୧୧ ଅଟେ । ୩ୟ ସ୍ତମ୍ଭରେ ତ ⊃ ଥ ≡ ~ଥ ⊃ ~ତ ର ସତ୍ୟତା ମୂଲ୍ୟ ୧୦୧୧ ହୋଇଥିବାରୁ ଏହା ପ୍ରମାଣିତ ହେଲା ଯେ ତ ⊃ ଥ ≡ ~ଥ ⊃ ~ତ ଅଟେ ।
11. ନିମ୍ନଲିଖୂତ ଯୁକ୍ତିଗୁଡ଼ିକର ସତ୍ୟ ସାରଣୀ ରଚନା କରି ସେମାନଙ୍କର ବୈଧତା ବିଚାର କର ।
(କ)
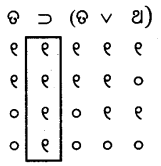ପୁନରୁକ୍ମିକ
(ଖ)
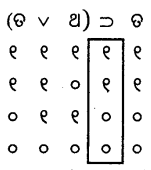ଆପାତିକ
(ଗ)
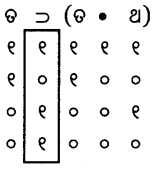ଆପାତିକ
(ଘ)
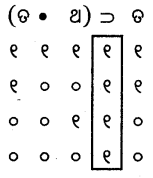ପୁନରୁକ୍ମିକ
(ଙ)
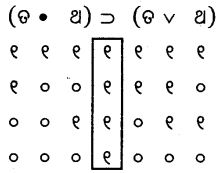ପୁନରୁକ୍ମିକ
(ଚ)
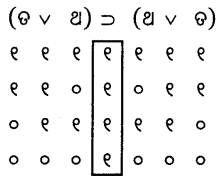ପୁନରୁକ୍ମିକ
(ଛ)
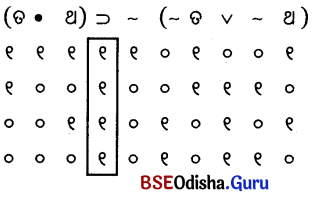ପୁନରୁକ୍ମିକ
(ଜ)
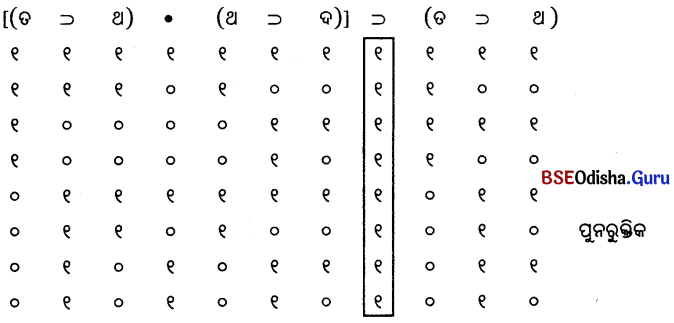
12. ନିମ୍ନଲିଖତ ଯୁକ୍ତିଗୁଡ଼ିକର ସମତୁଲ୍ୟତା ସତ୍ୟସାରଣୀ ମାଧ୍ୟମରେ ଦର୍ଶାଅ ।
(କ)
୧ମର ମୂଲ୍ୟ ୨ୟ ସହିତ ସମାନ
(ଖ)
୧ମର ମୂଲ୍ୟ ୨ୟ ସହିତ ସମାନ
(ଗ)
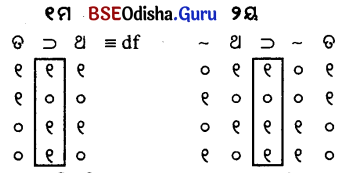୧ମ ଓ ୨ୟର ମୂଲ୍ୟ ସମାନ
13. ନିମ୍ନଲିଖ ଯୁକ୍ତିଗୁଡ଼ିକର ସତ୍ୟସାରଣୀଦ୍ଵାରା ବୈଧତା ପରୀକ୍ଷା କର ।
(କ)
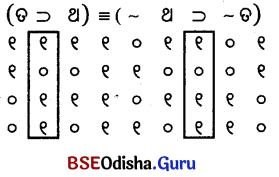ପୁନରୁକ୍ମିକ
(ଖ)
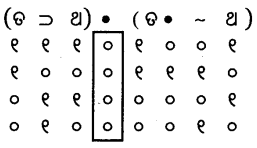ବିରୁଦ୍ଧ
(ଗ)
ଆପାତିକ