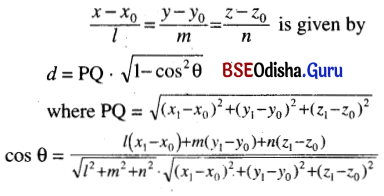Odisha State Board CHSE Odisha Class 12 Math Notes Chapter 13 Three Dimensional Geometry will enable students to study smartly.
CHSE Odisha 12th Class Math Notes Chapter 13 Three Dimensional Geometry
Important Formulae:
Distance Formula:
The distance between two points (x1, y1, z1) and (x2, y2, z2)
= \(\sqrt{\left(x_1-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}\)
Division Formula:
(i) Internal division:
If P (x, y, z) divides the line segment joining, A (x1, y1, z1) and B (x2, y2, z2) into the ratio m : n internally then

![]()
Remark:
(i) If P (x, y, z) divides the line segment joining the points A (x1, y1, z1) and B (x2, y2, z2) into the ratio λ : 1 then
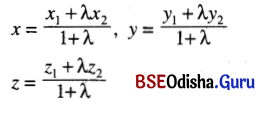
(ii) Co-ordinates of the mid-point of the line segment joining the points (x1, y1, z1) and (x2, y2, z2) are
\(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2}\right)\)
Direction Cosines:
Suppose that a straight line makes angles α, β, γ with the positive directions of x-axis, y-axis and z-axis respectively.
Then direction cosines of the line are < cos α, cos β, cos γ >
We denote l = cos α, m = cos β and n = cos γ
Then l2 + m2 + n2 = 1
Direction Ratios:
The direction ratios of a straight line are proportional to direction cosines.
If < a, b, c > are d. rs. and < l, m, n > are d.cs then

Direction ratios of a line segment joining the points (x1, y1, z1) and (x2, y2, z2) are
< x2 – x1, y2 – y1, z2 – z1 >
The projection of a line segment joining the points A (x1, y1, z1) and B (x2, y2, z2) onto the line ‘L’ with d.cs. < l, m, n >
= l (x2 – x1) + m (y2 – y1) + n (z2 – z1)
Angle between two lines:
Angle between two lines with d.cs.
< l1, m1, n1 > and < l2, m2, n2 > is given by cos θ = l1l2 + m1m2 + n1n2
(i) Two lines are parallel if their d.cs. are equal or d.r.s. are proportional.
(ii) Two lines are perpendicular if l1l2 + m1m2 + n1n2 = 0
![]()
Plane
Important formulae:
1. The general equation of the plane is ax + by + cz + d = 0
2. Equation of the plane passing through a poing (x1, y1, z1) and having l, m, n direction cosines of the normal to the plane is l (x – x1) + m (y – y1) + n (z – z1) = 0
3. Equation of the plane in intercept form is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1
where a, b, c are the intercepts from the axes.
4. Equation of the plane in normal form is lx + my + nz = p
where < l, m, n > are d.cs of the normal and p is the length of the normal.
5. Equation of the plane passing through three points.
(x1, y1, z1), (x2, y2, z2) and (x3, y3, z3) is
\(\left|\begin{array}{rrr}
x-x_1 & y-y_1 & z-z_1 \\
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
x_3-x_1 & y_3-y_1 & z_3-z_1
\end{array}\right|\) = 0
6. (i) Angle between two planes is the angle between their normals.
(ii) If two planes are
a1x + b1y + c1z + d1 = 0 and
a2x + b2y + c2z + d2 = 0
then the direction ratios of their normal are < a1, b1, c1 > and < a2, b2, c2 >
(iii) If θ is the angle between two planes then
cos θ = \(\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\sqrt{a_1^2+b_1^2+c_1^2} \cdot \sqrt{a_2^2+b_2^2+c_2^2}}\)
(iv) Two planes a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0 are parallel if \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\).
(v) The above two planes are perpendicular if a1a2 + b1b2 + c1c2 = 0.
7. The distance of a point (x1, y1, z1) from a plane ax + by + cz + d = 0 is
\(\left|\frac{a x_1+b y_1+c z_1+d}{\sqrt{a^2+b^2+c^2}}\right|\)
8. Equations of the planes bisecting the angle between two planes
a1x + b1y + c1z + d1 = 0 and
a2x + b2y + c2z + d2 = 0 are
\(\frac{a_1 x+b_1 y+c_1 z+d_1}{\sqrt{a_1^2+b_1^2+c_1^2}}=\pm \frac{a_2 x+b_2 y+c_2 z+d_2}{\sqrt{a_2^2+b_2^2+c_2^2}}\)
The Straight Line
Important formulae:
1. Unsymmetrical From:
The joint equation of two planes represent a stright line. Thus the equation of a straight line in unsymmetrical form a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0
2. Symmetrical Form:
Equation of a straight line through a point (x0, y0, z0) and having d.c. < l, m, n > is
\(\frac{x-x_0}{l}=\frac{y-y_0}{m}=\frac{z-z_0}{n}\)
3. Two-point Form:
The equation of a straight line passing through two points (x1, y1, z1) and (x2, y2, z2) is
\(\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}\)
![]()
4. Condition that a line will lie on a Plane:
The straight line
\(\frac{x-x_0}{l}=\frac{y-y_0}{m}=\frac{z-z_0}{n}\) lie in a plane ax + by + cz + d = 0
if (i) al + bm + cn = 0
and (ii) ax0 + by0 + cz0 + d = 0
5. Condition for Two Lines to be Coplanar:

6. Angle between a line and a plane:
The angle between the line
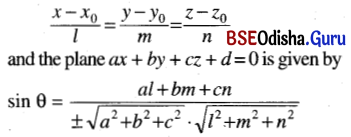
7. Distance of a Point from a Line:
The distance of a point (x1, y1, z1) from a line