Odisha State Board CHSE Odisha Class 12 Math Notes Chapter 7 Continuity and Differentiability will enable students to study smartly.
CHSE Odisha 12th Class Math Notes Chapter 7 Continuity and Differentiability
Definition:
A function f is said to be continuous at a point a Df if
(i) f(x) has definite value f(a) at x = a,
(ii) limx->a f(x) exists,
(iii) limx->a f(x) = f(a).
If one or more of the above conditions fail, the function f is said to be discontinuous at x = a. The above definition of continuity of a function at a point can also be formulated as follows:
A function f is said to be continuous at x = a if
(i) holds and for a given ∈ > 0, there exists a δ > 0 depending on ∈ such that
|x – a| < 8 ⇒ |f(x) – f(a)| < ∈.
A function f is continuous on an interval if it is continuous at every point of the interval.
If the interval is a closed interval [a, b] the function f is continuous on [a, b] if it is continuous on (a, b),
limx->a+ f(x) = f(a) and limx->b- f(x) = f(b).
![]()
Differentiation of a function:
(a) Differential coefficient (or derivative) of a function y = f(x) with respect to x is
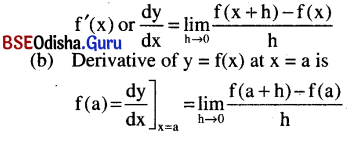
Fundamental theorems:
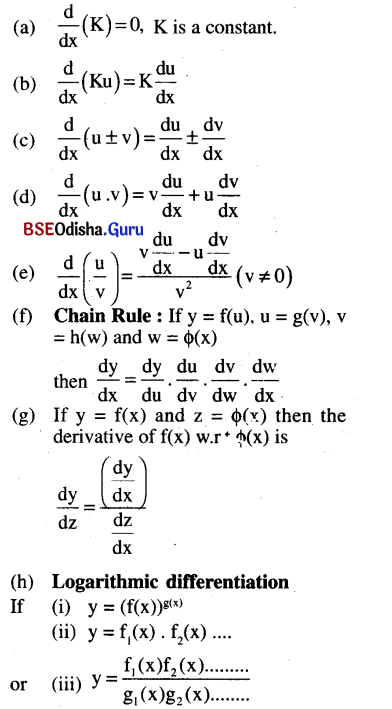
Then to get \(\frac{d y}{d x}\) it is convenient to take log of both sides before differentiation.
Derivative of some functions:

Higher order derivative:
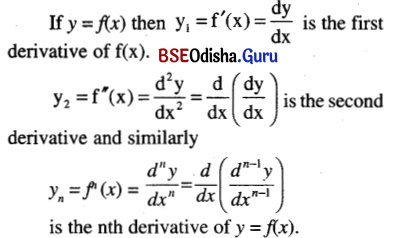
![]()
Leibnitz Theorem:
If ‘u’ and ‘v’ are differentiable functions having ‘n’th derivative then
\(\frac{d^n}{d x^n}\)(u.v) = C0unv + C1un-1v1 + C2un-2v2 + ….. + Cnuvn
Partial derivatives and Homogeneous functions:
(a) If z = f(x, y) is any function of two variables then the partial derivative of z w.r.t. x and y are given below.

(b) Homogeneous function:
z = f(x > y) is a homogeneous function of degree ‘n’ if f(tx, ty) = tn f(x, y).
Euler’s Theorem:
If z = f(x, y) is a homogeneous function of degree ‘n’ then \(x \frac{\partial f}{\partial x}+y \frac{\partial f}{\partial y}\) = nf(x, y).
