Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 12 Vectors Additional Exercise Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 12 Vectors Additional Exercise
Question 1.
Prove that the sum of the vectors directed from the vertices to the midpoints of opposite sides of a triangle is zero.
Solution:
Let D, E, F are midpoints of side BC, CA and AB of ΔABC

Question 2.
Prove by vector method that the diagonals of a quadrilateral bisect each other iff it is a parallelogram.
Solution:

![]()
Question 3.
If G is the centroid of a triangle ABC, prove that \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\).
Solution:

Question 4.
If M is the midpoint of the side B͞C of a triangle ABC, prove that \(\overrightarrow{AB}+\overrightarrow{AC}=2 \overrightarrow{AM}\).
Solution:

Question 5.
If \(\vec{a} \text { and } \vec{b}\) are the vectors represented by the adjacent sides of a regular hexagon, taken in order, what are the vectors represented by the other sides taken in order?
Solution:

Question 6.
If the points with position vectors 10î +3ĵ, 12î – 5ĵ and aî +11ĵ are collinear, find the value of a.
Solution:
Let the points are A, B and C.
As A, B and C are co-llinear.
We have \(\overrightarrow{AB}=\overrightarrow{AC}\)
\(\overrightarrow{AB}=\lambda \overrightarrow{AC}\)
⇒ (12i – 5j) – (10i + 3j)
⇒ λ [(ai + 11j) – (10i + 3j)
⇒ 2i – 8j = (a – 10)λ i + 8λ j
Comparing the components we have
8λ = -8
⇒ λ = -1
(a – 10) (-1) = 2
⇒ -a + 10 = 2
⇒ a = 8
![]()
Question 7.
Prove that the four points with position vectors \(2 \vec{a}+3 \vec{b}-\vec{c}, \vec{a}-2 \vec{b}+3 \vec{c}, 3 \vec{a}+4 \vec{b}-2 \vec{c}\) and \(\vec{a}-6 \vec{b}+6 \vec{c}\) are coplanar.
Solution:
Let the points are A, B, C

Question 8.
For any vector \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\) prove that \(\vec{r}=(\vec{r} \cdot \hat{i}) \hat{i}+(\vec{r} \cdot \hat{j}) \hat{j}+(\vec{r} \cdot \hat{k}) \hat{k}\).
Solution:
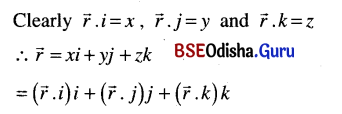
Question 9.
If two vectors \(\vec{a} \text { and } \vec{b}\) are such \(|\vec{a}|={3},|\vec{b}|=2 \text { and } \vec{a} \cdot \vec{b}={6}\text { find }|\vec{a}+\vec{b}| \text { and }|\vec{a}-\vec{b}|\).
Solution:
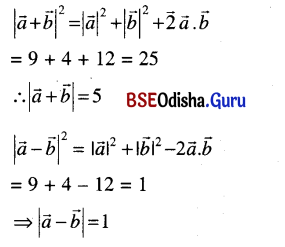
Question 10.
If \(\vec{a}\) makes equal angles with î, ĵ and k̂ and has magnitude 3, prove that the angle between \(\vec{a}\) and each of î ,ĵ and k̂ is \(\cos ^{-1}\left(\frac{1}{\sqrt{3}}\right)\).
Solution:
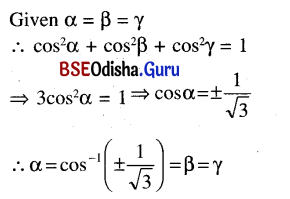
Question 11.
If \(\vec{a}, \vec{b}, \vec{c}\) are such that \(\vec{a} \cdot \vec{b}=\vec{a} \cdot \vec{c}\) then show that \(\vec{a}=\overrightarrow{0} \text { or } \vec{b}=\vec{c} \text { or } \vec{a}\) is perpendicular to \(\vec{b}-\vec{c}\)
Solution:

Question 12.
If \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0},|\vec{a}|={3},|\vec{b}|={5}\text { and }|\vec{c}|=7\), find the angle between \(\vec{a} \text { and } \vec{b}\).
Solution:

Question 13.
If \(\vec{a}, \vec{b}, \vec{c}\) are unit vectors such that \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\), find the value of \(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}\).
Solution:

![]()
Question 14.
Find the angles which the vector \(\vec{a}=\hat{i}-\hat{j}+\sqrt{2} \hat{k}\) makes with the coordinate axes.
Solution:

Question 15.
Find the angle between \(\vec{a} \text { and } \vec{b}\) if \(|\vec{a} \times \vec{b}|=\vec{a} \cdot \vec{b}\).
Solution:

