CHSE Odisha Class 12 Math Solutions Chapter 12 Vectors Ex 12(a)

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 12 Vectors Ex 12(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 12 Vectors Exercise 12(a)

Question 1.
Each question given below has four possible answers out of which only one is correct. Choose the correct one.
(i) \(\vec{a}\) = î + 2ĵ + k̂, \(\vec{b}\) = 2î – 2ĵ + 2k̂ and \(\vec{c}\) = -î + 2 ĵ + k̂ then
(a) \(\vec{a}\) and \(\vec{b}\) have the same direction
(b) \(\vec{a}\) and \(\vec{c}\) have opposite directions.
(c) \(\vec{b}\) and \(\vec{c}\) have opposite directions
(d) no pair of vectors have same direction
Solution:
(d) no pair of vectors have same direction

(ii) If the vectors \(\vec{a}\) = 2î + 3ĵ – 6k̂ and \(\vec{b}\) = -α î – ĵ + 2k̂ are parallel, then α = ______.
(a) 2
(b) \(\frac{2}{3}\)
(c) –\(\frac{2}{3}\)
(d) \(\frac{1}{3}\)
Solution:
(c) –\(\frac{2}{3}\)

(iii) If the position vectors of two points A and B are 3î + k̂, and 2î + ĵ – k̂, then the vector \(\overrightarrow{BA}\) is
(a) -î + ĵ – 2k̂
(b) î + ĵ
(c) î – ĵ + 2k̂
(d) î – ĵ – 2k̂
Solution:
(c) î – ĵ + 2k̂

(iv) If \(|k \vec{a}|\) = 1, then
(a) \(\vec{a}=\frac{1}{k}\)
(b) \(\vec{a}=\frac{1}{|k|}\)
(c) \(k=\frac{1}{|\vec{a}|}\)
(d) \(k=\frac{+1}{|\vec{a}|}\)
Solution:
(d) \(k=\frac{+1}{|\vec{a}|}\)

(v) The direction cosines of the vectors \(\overrightarrow{PQ}\) where \(\overrightarrow{OP}\) = (1, 0, -2) and \(\overrightarrow{OQ}\) = (3, -2, 0) are
(a) 2, -2, 2
(b) 4, -2, -2
(c) \(\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\)
(d) \(\frac{2}{\sqrt{6}},-\frac{1}{\sqrt{6}},-\frac{1}{\sqrt{6}}\)
Solution:
(c) \(\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\)

Question 2.
Rectify the mistakes, if any
(i) \(\vec{a}-\vec{a}\) = 0
Solution:
\(\overrightarrow{0}\)

(ii) The vector \(\overrightarrow{0}\) has unique direction.
Solution:
indefinite direction

(iii) All unit vectors are equal.
Solution:
equal magnitude

(iv) \(|\vec{a}|=|\vec{b}| \Rightarrow \vec{a}=\vec{b}\)
Solution:
\(\vec{a}=\vec{b} \Rightarrow|\vec{a}|=|\vec{b}|\)

(v) Subtraction of vectors is not commutative.
Solution:
true

Question 3.
(i) If \(\vec{a}\) = (2, 1), \(\vec{b}\) = (-1, 0), find \(3 \vec{a}+2 \vec{b}\).
Solution:
\(3 \vec{a}+2 \vec{b}\) = 3 (2, 1) + 2 (-1, 0)
= (6 – 2, 3 + 0)
= (4, 3 )

(ii) If \(\vec{a}\) = (1, 1, 1) , \(\vec{b}\) = (-1, 3, 0) and \(\vec{c}\) =(2, 0, 2), find \(\vec{a}+2 \vec{b}-\frac{1}{2} \vec{c}\).
Solution:
\(\vec{a}+2 \vec{b}-\frac{1}{2} \vec{c}\)
= (1, 1, 1) + 2 (-1, 3, 0) – \(\frac{1}{2}\)(2, 0, 2)
= (1 – 2 – 1, 1 + 6 – 0, 1 + 0 – 1)
= (-2, 7, 0)

Question 4.
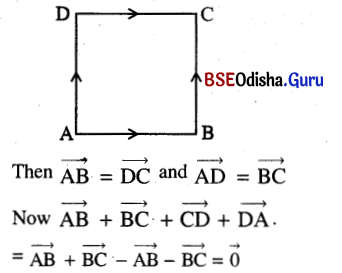
If A, B, C and D are the vertices of a square, find \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}\).
Solution:
Let ABCD be a square.

Question 5.
The given points A, B, C are the vertices of a triangle. Determine the vectors \(\overrightarrow{A B}, \overrightarrow{B C} \text { and } \overrightarrow{C A}\) and the lengths of these vectors in the following cases.
(i) A (4, 5, 5), B (3, 3, 3), C (1, 2, 5)
Solution:

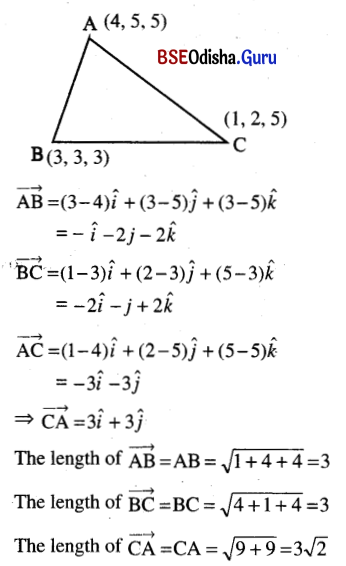
(ii) A (8, 6, 1), B (2, 0, 1), C (-4, 0, -5)
Solution:

Question 6.
Find the vector from origin to the midpoint of the vector \(\overrightarrow{{P}_1 {P}_2}\) joining the points P₁(4, 3) and P₂(8, -5).
Solution:
P₁ = (4, 3) and P₂ = (8, -5)
If P is the mid-point of P₁P₂ then P = (6, -1).
Position vector of P = \(\overrightarrow{{OP}}\) = 6î – ĵ

Question 7.
Find the vectors from the origin to the points of trisection the vector \(\overrightarrow{{P}_1 {P}_2}\) joining P₁ (-4, 3) and P₂ (5, -12).
Solution:

Question 8.
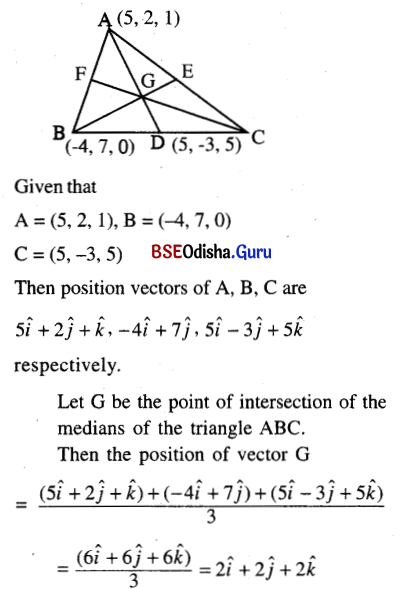
Find the vector from the origin to the intersection of the medians of the triangle whose vertices are A (5, 2, 1), B(-4, 7, 0) and C (5, -3, 5).
Solution:

Question 9.
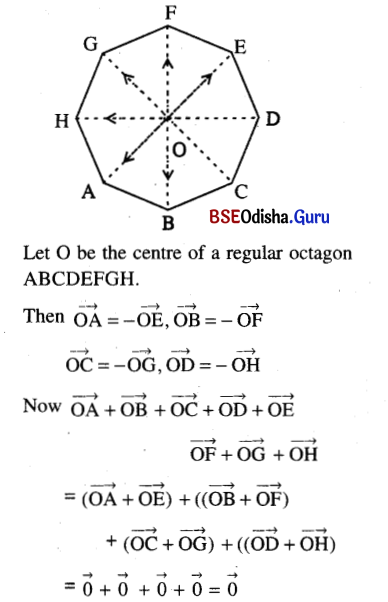
Prove that the sum of all the vectors drawn from the centre of a regular octagon to its vertices is the null vector.
Solution:

Question 10.
Prove that the sum of the vectors represented by the sides of a closed polygon taken in order is a zero vector.
Solution:
Consider a closed polygon ABCDEFA.

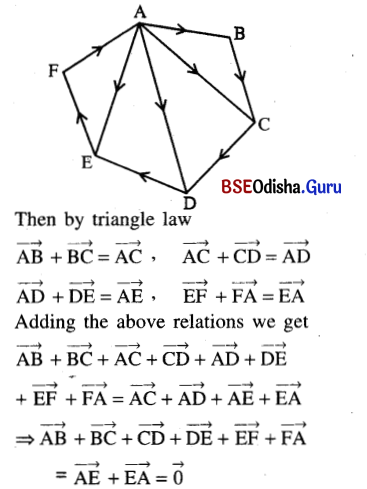
Question 11.
(a) Prove that:
(i) \(|\overrightarrow{a}+\overrightarrow{{b}}| \leq|\overrightarrow{a}|+|\overrightarrow{b}|\)
State when the equality will hold;
Solution:

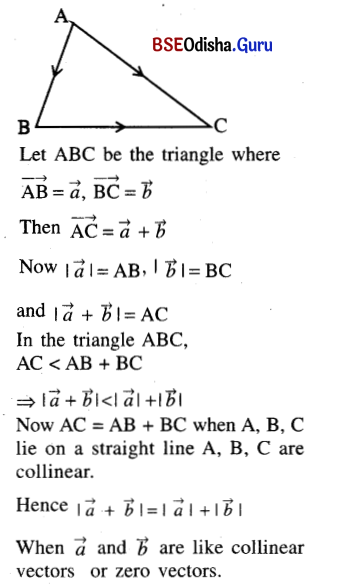
(ii) \(|\overrightarrow{a}-\overrightarrow{b}| \geq|\overrightarrow{a}|-|\overrightarrow{b}|\)
Solution:

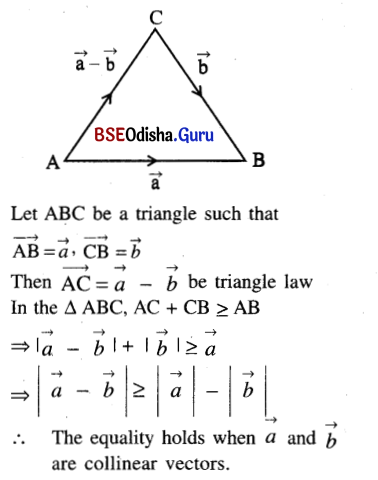
(b) What is the geometrical significance of the relation \(|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}-\overrightarrow{b}|\)?
Solution:

Question 12.
Find the magnitude of the vector \(\overrightarrow{PQ}\), its scalar components and the component vectors along the coordinate axes, if P and Q have the coordinates.
(i) P (-1, 3), Q (1, 2)
Solution:

(ii) P (-1, -2), Q (-5, -6)
Solution:

(iii) P (1, 4, -3), Q (2, -2, -1).
Solution:

Question 13.
In each of the following find the vector \(\overrightarrow{PQ}\), its magnitude and direction cosines, if P and Q have co-ordinates.
(i) P (2, -1, -1), Q (-1, -3, 2);
Solution:

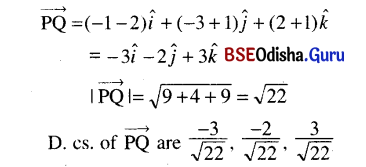
(ii) P (3, -1, 7), Q (4, -3, -1).
Solution:

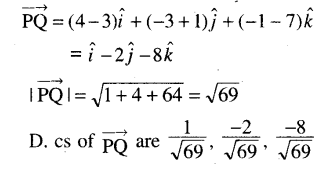
Question 14.
If \(\vec{a}\) = (2, -2, 1), \(\vec{b}\) = (2, 3, 6) and \(\vec{c}\) = (-1, 0, 2), find the magnitude and direction of
\(\vec{a}-\vec{b}+2 \vec{c}\).
Solution:

Question 15.
Determine the unit vector having the direction of the given vector in each of the following problems:
(i) 5î – 12ĵ
Solution:

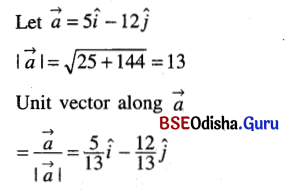
(ii) 2î + ĵ
Solution:

(iii) 3î + 6ĵ – k̂
Solution:

(iv) 3î + ĵ – 2k̂
Solution:

Question 16.
Find the unit vector in the direction of the vector \(\overrightarrow{r_1}-\overrightarrow{r_2}\), where \(\vec{r}_1\) = î + 2ĵ + k̂ and \(\vec{r}_2\) = 3î + ĵ – 5k̂.
Solution:

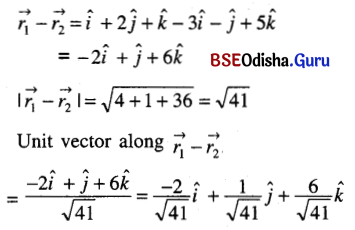
Question 17.
Find the unit vector parallel to the sum of the vectors \(\vec{a}\) = 2î + 4ĵ – 5k̂ and \(\vec{b}\) = î + 2ĵ + 3k̂. Also find its direction cosines.
Solution:

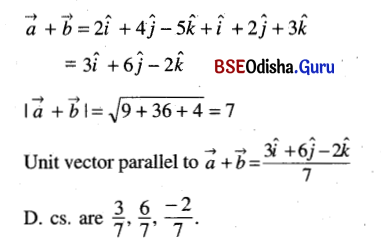
Question 18.
If the sum of two unit vectors is a unit vector, show that the magnitude of their difference is √3.
Solution:

Question 19.
The position vectors of the points A, B, C and D are 4î + 3ĵ – k̂, 5î + 2ĵ + 2k̂, 2î – 2ĵ – 3k̂ and 4î – 4ĵ + 3k̂ respectively. Show that AB and CD are parallel.
Solution:
Given that the
position vector of A = 4î + 3ĵ – k̂
position vector of B = 5î + 2ĵ + 2k̂
position vector of C = 2î – 2ĵ – 3k̂
position vector of D = 4î – 4ĵ + 3k̂

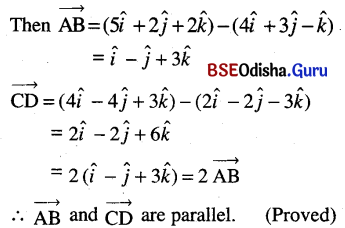
Question 20.
In each of the following problems, show by vector method that the given points are collinear.
(i) A (2, 6, 3), B (1, 2, 7) and C (3, 10, -1)
Solution:
Given that A = (2, 6, 3), B = (1, 2, 7) and C = (3, 10, -1)
Then

(ii) P (2, -1, 3), Q (3, -5, 1) and R (-1, 11, 9).
Solution:
Given that P = (2, -1, 3) Q = (3, -5, 1) and R = (-1, 11, 9)

Hence the points P, Q, R are collinear. (Proved)

Question 21.
Prove that the vectors 2î – ĵ + k̂, î – 3ĵ – 5k̂, 3î – 4ĵ – 4k̂ are the sides of a right angled triangle.
Solution:
Let A, B and C be the points whose position vectors are 2î – ĵ – k̂, î – 3ĵ – 5k̂ and 3î – 4ĵ – 4k̂ respectively.

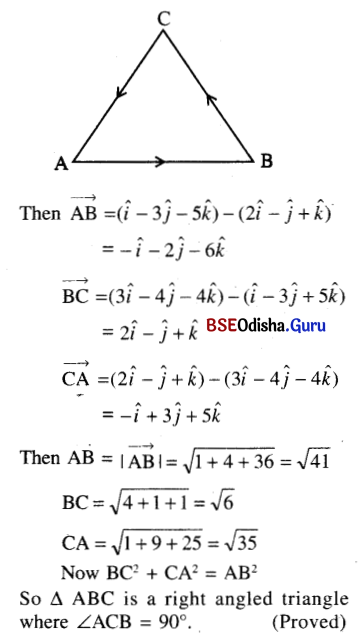
Question 22.
Prove by vector method that:
(a) the medians of a triangle are concurrent;
Solution:

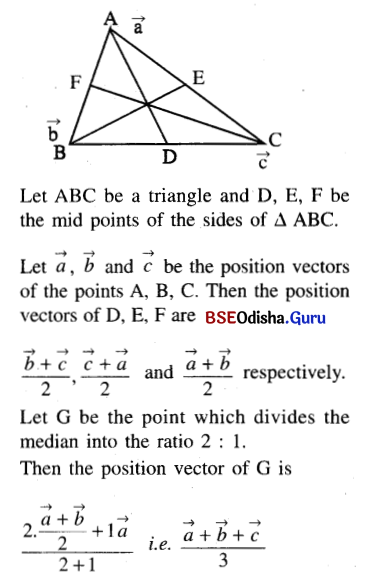
The symmetry of the result shows that the point G also lies on the other two medians.
Hence the medians are concurrent. (Proved)

(b) the diagonals of a parallelogram bisect each other;
Solution:

(c) the line segment joining the midpoints of two sides of a triangle is parallel to the third and half of it;
Solution:

(d) the lines joining the midpoints of consecutive sides of a quadrilateral is a parallelogram;
Solution:

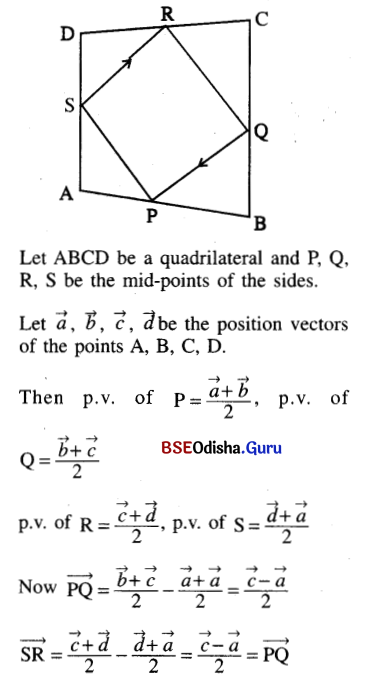
⇒ SR = PQ and SR || PQ
Hence PQRS is a parallelogram.
(Proved)

(e) in any triangle ABC, the point P being on the side \(\overrightarrow{B C} \text {; if } \overrightarrow{P Q}\) is the resultant of the vectors \(\overrightarrow{A P}, \overrightarrow{P B}\) and \(\overrightarrow{P C}\) then ABQC is a parallelogram;
Solution:

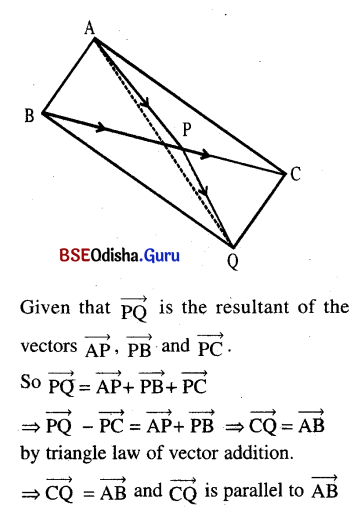
Hence ABQC is parallelogram. (Proved)

(f) In a parallelogram, the line joining a vertex to the midpoint of an opposite side trisects the other diagonal.
Solution:

⇒ P divides BD into the ratio 1 : 2.
Similarly we can show that Q divides BD into the ratio 2 : 1.
Hence P, Q are the points of trisection of the diagonal BD. (Proved)