CHSE Odisha Class 12 Math Solutions Chapter 13 Three Dimensional Geometry Ex 13(b)

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 13 Three Dimensional Geometry Ex 13(b) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 13 Three Dimensional Geometry Exercise 13(b)

Question 1.
State, which of the following statements are true (T) or false (F).
(a) Through any four points one and only one plane can pass.
Solution:
False

(b) The equation of xy-plane is x + y = 0.
Solution:
False

(c) The plane ax + by + c = 0 is perpendicular to z-axis.
Solution:
False

(d) The equation of the plane parallel to xz-plane and passing through (2, -4, 0) is y + 4 = 0.
Solution:
True

(e) The planes 2x – y + z – 1 = 0 and 6x – 3y + 3z = 1 are coincident.
Solution:
False

(f) The planes 2x + 4y – z + 1 = 0 and x – 2y – 6z + 3 = 0 are perpendicular to each other.
Solution:
True

(g) The distance of a point from a plane is same as the distance of the point from any line lying in that plane.
Solution:
False

Question 2.
Fill in the blanks by choosing the appropriate answer from the given ones:
(a) The equation of a plane passing through (1, 1, 2) and parallel to x + y + z – 1 = 0 is ______. [x + y + z = 0, x + y + 2z – 1 = 0, x + y + z = 0, x + y + z = 4]
Solution:
x + y + z = 4

(b) The equation of plane perpendicular to z-axis and passing through (1, -2, 4) is ______. [x = 1, y + 2 = 0, z – 4 = 0, x + y + z – 3 = 0]
Solution:
z – 4 = 0

(c) The distance between the parallel planes 2x – 3y + 6z + 1 = 0 and 4x – 6y + 12z – 5 = 0 is ______. \(\left[\frac{1}{2}, \frac{1}{7}, \frac{4}{7}, \frac{6}{7}\right]\)
Solution:
\(\frac{1}{2}\)

(d) The plane y – z + 1 = 0 is ______. [parallel to x-axis, perpendicular to x-axis, parallel xy-plane, perpendicular to yz-plane].
Solution:
parallel to x-axis

(e) A plane whose normal has direction ratios < 3, -2, k > is parallel to the line joining (-1, 1, -4) and (5, 6, -2). Then the value of k = ______. [6, -4, -1, 0]
Solution:
k = -4

Question 3.
Find the equation of planes passing through the points.
(a) (6, -1, 1), (5, 1, 2) and (1, -5, -4)
Solution:
Equation of the plane through the points (6, -1, 1), (5, 1, 2) and (1, -5, -4) is

⇒ (x – 6) (-10 + 4) – (y + 1) (5 + 5) + (z – 1) (4 + 10) = 0
⇒ -6 (x – 6) – 10 (y + 1) + 14 (z – 1) = 0
⇒ -6x + 36 – 10y – 10 + 14z – 14 = 0
⇒ -6x – 10y + 14z + 12 = 0
⇒ 3x + 5y – 7z – 6 = 0

(b) (2, 1, 3), (3, 2, 1) and (1, 0, -1)
Solution:
Equation of the plane though the given points is

⇒ (x – 2) (-4 – 2) – (y – 1) (-4 – 2) + (z – 3) (-1 + 1) = 0
⇒ (x – 2) (-6) – (y – 1) (-6) = 0
⇒ x – y – 1 = 0

(c) (-1, 0, 1), (-1, 4, 2) and (2, 4, 1)
Solution:
Equation of the plane through the given points is

⇒ (x + 1) (0 – 4) – y ( 0 – 3) + (z – 1) (0 – 12) = 0
⇒ -4x – 4 + 3y – 12z + 12 = 0
⇒ -4x + 3y – 12z + 8 = 0
⇒ 4x – 3y + 1 2z – 8 = 0

(d) (-1, 5, 4), (2, 3, 4) and (2, 3, -1)
Solution:
Equation of the plane through the given points is

⇒ (x + 1) (10 – 0) – (y – 5) (-15 – 0) + (z – 4) (-6 + 6) = 0
⇒ 10x + 10 + 15y – 75 = 0
⇒ 2x + 3y – 13 = 0

(e) (1, 2, 3), (1, -4, 3) and (-1, 3, 2)
Solution:
Equation of the plane through the given points is

⇒ (x – 1) (6 – 0) – (y – 2) (0 – 0) + ( z – 3) ( 0 – 12) = 0
⇒ (x – 1) 6 + (z – 3) (-12) = 0
x – 1 – 2z + 6 = 0
⇒ x – 2z + 5 = 0

Question 4.
Find the equation of plane in each of the following cases:
(a) Passing through the point (2, 3, -1) and parallel to the plane 3x – 4y + 7z = 0.
Solution:
Given plane is 3x – 4y + 7z = 0 … (1)
Any plane parallel to the plane (1) is given by 3x – 4y + 7z + d = 0.
If it passes through the point (2, 3, -1) then 6 – 12 – 7 + d = 0 or, d = 13
Equation of the plane is 3x – 4y + 7z + 13 = 0

(b) Passing through the point (2, -3, 1) and (-1, 1, -7) and perpendicular to the plane x – 2y + 5z + 1 = 0.
Solution:
Equation of the plane passing through the point (2, -3, 1) is
a (x – 2)+ b (y + 3) + c (z – 1) = 0 … (1)
If it passes through the point (-1, 1, -7)
then a (-1 – 2) + b (1 + 3) + c (-7 – 1) = 0
or 3a – 4b + 8c = 0 … (2)
Again given that plane (1) is perpendicular to the plane
x – 2y + 5z + 1 = 0
so a – 2b + 5c = 0 … (3)
Solving (2) and (3) we get
\(\frac{a}{-20+16}=\frac{b}{8-15}=\frac{c}{-6+4}\)
or, \(\frac{a}{-4}=\frac{b}{-7}=\frac{c}{-2} \text { or, } \frac{a}{4}=\frac{b}{7}=\frac{c}{2}\)
Equation of the required plane is
4 (x – 2) + 7 (y + 3) + 2 (z – 1) = 0
or, 4x + 7y + 2z + 11 = 0

(c) Passing through the foot of the perpendiculars drawn from P (a, b, c) on the coordinate planes.
Solution:
Let A, B, C be the feet of the perpendiculars drawn from point P(a, b, c) on to the coordinate axes. Then
A = (a, 0, 0), B = (0, b, 0), C = (0, 0, c)
Equation of the plane through A, B, C is
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1

(d) Passing through the point (-1, 3, 2) perpendicular to the planes x + 2y + 2z = 5 and 3x + 3y + 2z = 8.
Solution:
Equation of the plane through the point (-1, 3, 2) is
a (x + 1) + b (y – 3) + c (z – 2) = 0
If this plane is perpendicular to the plane
x + 2y + 2z = 5 and 3x + 3y + 2z = 8
then a + 2b +2c = 0
3a + 3b + 2c = 0
Solving we get \(\frac{a}{4-6}=\frac{b}{6-2}=\frac{c}{3-6}\)
or \(\frac{a}{-2}=\frac{b}{4}=\frac{c}{-3} \text { or, } \frac{a}{2}=\frac{b}{-4}=\frac{c}{3}\)
Equation of the required plane is
2 (x + 1) – 4 (y – 3) + 3 (z – 2) = 0
or, 2x – b – 3z – 8 = 0

(e) Bisecting the line segment joining (-1, 4, 3) and (5, -2, -1) at right angles.
Solution:

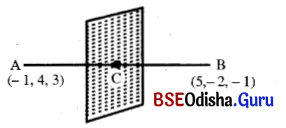
Let A = (-1, 4, 3) and B (5, -2, -1).
Suppose that a plane bisects AB at right angle. Let C be the mid-point of AB. Then the plane passes through C and the line AB is perpendicular to the plane
C = \(\left(\frac{-1+5}{2}, \frac{4-2}{2}, \frac{3-1}{2}\right)\) = (2, 1, 1)
D.rs. of AB are < 6, -6, -4 >
Equation of the plane is
6 (x – 2) – 6 (y – 1) – 4 (z – 1) = 0
or, 3x – 6 – 3y + 3 – 2z + 2 = 0
or, 3x – 3y – 2z – 1 = 0

(f) Parallel to the plane 2x – y + 3z + 1 = 0 and at a distance 3 units away from it.
Solution:
Given plane is 2x – y + 3z + 1 = 0 … (1)
Equation of the plane parallel to the plane (1) is 2x – y + 3z +k = 0 … (2)
Given that the distance between two planes (1) and (2) is 3 units.
We see that (0, 1, 0) is a point on (1).
The length of the perpendicular from (0, 1, 0) onto the plane (2).

Question 5.
(a) Write the equation of the plane 3x – 4y + 6z – 12 = 0 in intercept form and hence obtain the coordinates of the point where it meets the co-ordinate axes.
Solution:
Given plane is 3x – 4y + 6z – 12 = 0
⇒ 3x – 4y + 6z = 12
⇒ \(\frac{x}{4}+\frac{y}{-3}+\frac{z}{2}\) = 1
This is in intercept form. The coordinates of the points where the plane meets the coordinate axes are (4, 0, 0), (0, -3, 0), (0, 0, 2).

(b) Write the equation of the plane 2x – 3y + 5z + 1 = 0 in normal form and find its distance from the origin. Find also the distance from the point (3, 1, 2).
Solution:
Given plane is 2x – 3y + 5z + 1 = 0
2x – 3y + 5z = -1
-2x + 3y – 5z = 1
Its normal form is

(c) Find the distance between the parallel planes 2x – 2y + z + 1 = 0 and 4x – 4y + 2z + 3 = 0.
Solution:
The parallel planes are
2x – 2y + z + 1 = 0 … (1)
and 4x – 4y + 2z + 3 = 0 … (2)
We see that (0, 0, -1) lies on the plane (1).
Distance between two planes = Length of the perpendicular from (0, 0, -1) onto the plane (2)
\(=\left|\frac{-2+3}{\sqrt{16+16+4}}\right|=\frac{1}{6}\)

Question 6.
In each of the following cases, verify whether the four given points are coplanar or not.
(a) (1, 2, 3), (-1, 1, 0), (2, 1, 3), (1, 1, 2)
Solution:
As

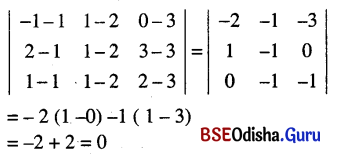
The given points are coplanar.

(b) (1, 1, 1), (3, 1, 2), (1, 4, 0), (-1, 1, 0)
Solution:
As

The given points are coplanar.

(c) (0, -1, -1), (4, 5, 1), (3, 9, 4), (-4, 4, 4)
Solution:
As

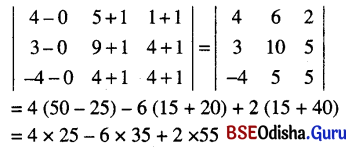
= 100 – 210 + 110
= 0
The given points are coplanar.

(d) (-6, 3, 2), (3, -2, 4), (5, 7, 3) and (-13, 17, -1)
Solution:
As

= 14 × (-26) + 2 × 182 = 0
The given points are coplanar.

Question 7.
Find the equation of plane in each of the following cases:
(a) Passing through the intersection of planes 2x + 3y – 4z + 1 = 0, 2x – y + z + 2 = 0 and passing through the point (3, 2, 1).
Solution:
Given planes are
2x + 3y – 4z + 1 = 0 … (1)
and 3x – y + z + 2 = 0 … (2)
Any plane through the line of intersection of the planes (1) and (2) is
(2x + 3y – 4z + 1) + k (3x – y + z + 2) = 0
or (2 + 3k) x + (3 – k) y + (k – 4) z + (2k + 1) = 0 … (3)
If the plane (3) passes through the point (3, 2, 1)
then (2 + 3k) 3 + (3 – k) 2 + (k – 4) + 2k + 1 = 0
⇒ 6 + 9k + 6 – 2k + k – 4 + 2k + 1 = 0

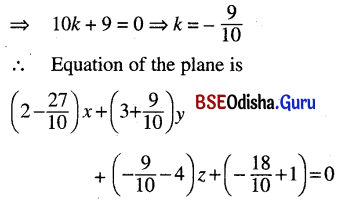
or, -7x + 39y – 49z – 8 = 0
or, 7x – 39y + 49z + 8 = 0

(b) Which contains the line of intersection of the planes x + 2y + 3z – 4 = 0 and 2x + y – z + 5 = 0 and perpendicular to the plane 5x + 3y + 6z + 8 = 0.
Solution:
Given planes are
x + 2y + 3z – 4 = 0 … (1)
and 2x + y – z + 5 = 0 … (2)
Any plane containing the line of intersection of the planes (1) and (2) is
x + 2y + 3z – 4 + k (2x + y – z + 5) = 0
⇒ (2k + 1) x + (k + 2) y + (3 – k) z + (5k – 4) = 0 … (3)
Given that the plane (3) is perpendicular to the plane
5x + 3y + 6z + 8 = 0 … (4)
Two planes are perpendicular if their normals are perpendicular.
D.rs. of the normal of the plane (3) are < 2k + 1, k + 2, 3 – k >.
D.rs. of the normal of the plane (4) are < 5, 3, 6 >.
If the normal are perpendicular then
5 (2k + 1) + 3 (k + 2) + 6 (3 – k) = 0
⇒ 10k + 3k – 6k + 5 + 6 + 18 = 0
⇒ 7k = -29

or, -51x – 15y + 50z – 173 = 0
or, 51x + 15y – 50z + 173 = 0

(c) Passing through the intersection of ax + by + cz + d = 0 and a₁x + b₁y + c₁z + d₁ = 0 and perpendicular to xy-plane.
Solution:
Given planes are
ax + by + cz + d = 0 … (1)
and a₁x + b₁y + c₁z + d₁ = 0 … (2)
Any plane passing through the line of intersection of the planes (1) and (2) is given by:
ax + by + cz + d + k (a₁x + b₁y + c₁z + d₁) = 0
or, (a + ka₁) x + (b + kb₁) y + (c + kc₁) z + (d + kd₁) = 0 … (3)
D.rs. of the normal of the plane (3) are < a + ka₁, b + kb₁, c + kc₁).
D.rs. of the normal of the xy-plane i.e., z = 0 are < 0, 0, 1 >
If the plane (3) is perpendicular to the xy-plane then
(a + ka₁) × 0 + (b + kb₁) × 0 + (c + kc₁) × 1 = 0

(d) Passing through the intersection of the planes x + 3y – z + 1 = 0 and 3x – y+ 5z + 3 = 0 and is at a distance 2/3 units from origin.
Solution:
Given planes are
x + 3y – z + 1 = 0 … (1)
and 3x – y + 5z + 3 = 0 … (2)
Any plane through the line of intersection of the planes (1 ) and (2) is
(x + 3y – z + 1)+ k (3x – y + 5z + 3) = 0
⇒ (3k + 1) x + (3 – k) y + (5k – 1) z + (3k + 1) = 0
The length of the perpendicular from origin onto the plane (3)
\(\frac{3 k+1}{\sqrt{(3 k+1)^2(3-k)^2+(5 k-1)^2}}=\frac{2}{3}\) (Given)
⇒ 9 (3k + 1)²
⇒ 4 {(3k + 1)² + (3 – k)² + (5k – 1)²}
⇒ 81k² + 54k + 9
= 4 {9k² + 6k + 1 + 9 + k² – 6k + 25k² + 1 – 10k}
= 4 {35k² – 10k + 11}
= 140k² – 40k + 44
⇒ 59k² – 94k + 35 = 0
⇒ 59k² – 59k – 35k + 35 = 0
⇒ 59k (k – 1) – 35 (k – 1) = 0
⇒ (k – 1) (59k – 35) = 0
⇒ k – 1 = 0 or 59k – 35 = 0
⇒ k = 1 or, k = \(\frac{35}{59}\)
∴ The planes are 4x + 2y + 4z + 4 = 0 and 82x + 71y + 58z + 82 = 0

Question 8.
Find the angle between the following pairs of planes.
(a) x + 3y – 5z + 1 = 0 and 2x + y – z+ 3 = 0
Solution:
Given planes are
x + 3y – 5z + 1 = 0 … (1)
and 2x + y – z + 3 = 0 … (2)
Angle between two planes is equal to the angle between their normals.
D.rs. of the normal to the plane (1) are < 1, 3, -5 >
D.rs. of the normal to the plane (2) are < 2, 1, -1 >.
If θ is the angle between the planes then

(b) x + 2y + 2z – 3 = 0 and 3x + 4y + 5z + 1 = 0
Solution:
Given planes are
x + 2y + 2z – 3 = 0 and 3x + 4y + 5z + 1 = 0
D.rs. of normals of two planes are < 1, 2, 2 > and < 3, 4, 5 >.
If θ is the angle between the planes then

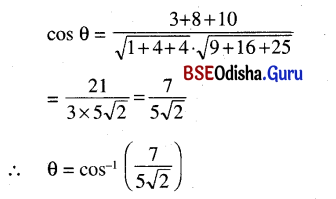
(c) x + 2y + 2z – 7 = 0 and 2x – y +z = 6
Solution:
Two planes are
x + 2y + 2z – 7 = 0 and 2x – y + z = 6
The d.rs. of the normals are < 1, 2, 2 > and <2, -1, 1 >.
If θ is the angle between two planes then

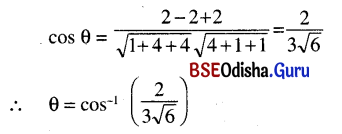
Question 9.
(a) Find the equation of the bisector of the angles between the following pairs of planes and specify the ones which bisects the acute angles;
(i) 3x – 6y + 2z + 5 = 0 and 4x – 12y + 3z – 3 = 0
Solution:
Given planes are
3x – 6y + 2z + 5 = 0 … (1)
and 4x – 12y + 3z – 3 = 0 … (2)
The equations of the bisectors are given by

So the plane (3) is a bisector for obtuse angle and the plane (4) is the bisector for acute angle.

(ii) 2x + y – 2z – 1 = 0 and 4x – 12y + 3z + 3 = 0
Solution:
Given planes are
2x + y – 2z – 1 = 0 … (1)
and 4x – 12y + 3z + 3 = 0 … (2)
The equation of bisector planes are

∴ θ > 45°
∴ Equation (3) is the bisector of the use angle and equation (4) is the bisector of acute angle.

(b) Show that the origin lies in the interior of the acute angle between planes.
x + 2y + 2z + 9 and 4x – 3y + 12z + 13 = 0;
Find the equation of bisector of the acute angle.
Solution:
Given planes are x + 2y + 2z – 9 = 0
and 4x – 3y + 12z + 13 = 0
These equations can be written as
-x – 2y – 2z+ 9 = 0 … (1)
4x – 3y+ 12z + 13 = 0 … (2)
Here a₁a₂ + b₁b₂ + c₁c₂
= (-1) 4 + (-2) (-3) + (-2) . 12
= -4 + 6 – 24 = -22 < 0
So the origin lies in the acute angle between the given planes.
The equations of the planes bisecting the angle between the given planes are

⇒ tan θ < 1 ⇒ θ < 45°
Hence the plane (3) bisects the acute angle between the given planes.

Question 10.
(a) Prove that the line joining (1, 2, 3), (2, 1, -1) intersects the line joining (-1, 3, 1) and (3, 1, 5)
Solution:
Let A = (1, 2, 3), B = (2, 1, -1), C = (-1, 3, 1), D = (3, 1, 5)
The line AB intersects CD if A, B, C, D are coplanar.
Equation of the plane

or, (x – 1) (2 + 4) – (y – 2) (-2 – 8) + (z – 3) (1 – 2) = 0
or, 6 (x – 1) + 10 (y – 2) – (z – 3) = 0
or, 6x+ 10y – z – 23 = 0
The point (3, 1, 5) lies on the plane (1) because
6x + 10y – z – 23 = 18 + 10 – 5 – 23 = 0 … (1)
As (1) is satisfied for the point (3, 1, 5), the point lies on the plane (1).
Hence the four points are coplanar. So the line AB is either parallel to the line CD.
or, AB is intersecting to CD.
D.rs. of AB are < 1, -1, -4 >.
D.rs. of CD are < 4, -2, 4 >.
So d.rs. of AB are not proportional to d.rs. of CD. So they are not parallel. Hence they are intersecting.

(b) Show that the point (-\(\frac{1}{2}\), 2, 0) is the circumcentre of the triangle formed by the points (1, 1, 0), (1, 2, 1) and (-2, 2, -1).
Solution:

Thus PA = PB = PC
Hence P is the circumcentre of the ΔABC.

Question 11.
Show that plane ax + by + cz + d = 0 divides the line segment joining
(x₁, y₁, z₁) and (x₂, y₂, z₂) in a ratio – \(\frac{a x_1+b y_1+c z_1+d}{a x_2+b y_2+c z_2+d}\).
Solution:
Let A = (x₁, y₁, z₁) , B = (x₂, y₂, z₂)
Suppose that the line AB intersects the plane
ax + by + cz + d = 0 at P. … (1)
Suppose the P divides AB into the ratio m:n.
Then the coordinates of P are

Question 12.
A variable plane is at a constant distance p from the origin and meets the axes at A, B, C. Through A, B, C planes are drawn parallel to the co-ordinate planes. Show that the locus of their points of intersection is \(\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}=\frac{1}{p^2}\).
Solution:

The planes through the points A, B, C parallel to the coordinate planes are
x = a, y = b and z = c respectively.
Let P be the point of intersection of these planes.
Then p = (a, b, c)
Hence the locus of P is obtained by putting a = x, b = y, c = z in (2).
Hence the required locus is
\(\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}=\frac{1}{p^2}\). (Proved)

Question 13.
A variable plane passes through a fixed point (a, b, c) and meets the co-ordinate axes at A, B, C. Show that the locus of the point common to the planes drawn through A, B and C parallel to the coordinate planes is \(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\) = 1.
Solution:
Let the variable plane be
\(\frac{a}{\alpha}+\frac{b}{\beta}+\frac{c}{\gamma}\) = 1 … (1)
It meets the axes at A (α, 0, 0), B (0, β, 0) and C (0, 0, γ).
If P is the point of intersection of the planes drawn through A, B and C parallel to the coordinate planes then P = (α, β, γ).
Again the plane (1) passes through a fixed point (a, b, c).
So \(\frac{a}{\alpha}+\frac{b}{\beta}+\frac{c}{\gamma}\) = 1
∴ The locus of P is \(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\) = 1. (Proved)

Question 14.
The plane 4x + 7y + 4z + 81 = 0 is rotated through a right angle about its line of intersection with the plane 5x + 3y + 10z – 25 = 0. Find the equation of the plane in new position.
Solution:
Given that the plane
4x + 7y + 4z + 81 = 0 … (1)
is rotated through a right angle about the line of intersection with the plane
5x + 3y + 10z – 25 = 0 … (2)
Let the equation of the plane in new position be
4x + 7y + 4z + 81 + λ (5x + 3y -10z – 25) = 0
or, (4 + 5λ) x + (7 + 3λ) y + (4 + 10λ) z + (81 – 25λ) = 0
Then the angle between the planes (1 ) and (3) is 90° i.e., they are perpendicular.
So 4 (4 + 5λ) + 7 (7 + 3λ) + 4 (4 + 10λ) = 0
16 + 20λ + 49 + 21λ + 16 + 40λ = 0
81λ = -81
⇒ λ = -1
∴ The equation of plane in new position is
-x + 4y – 6z + 106 = 0
or, x – 4y + 6z – 106 = 0

Question 15.
The plane lx + my = 0 is rotated about its line of intersection with the plane z = 0 through angle measure α. Prove that the equation of the plane in new position is lx + my ± z \(\sqrt{l^2+m^2}\) tan α = 0.
Solution:
Given plane is lx + my = 0 … (1)
The plane (1) is rotated through an angle α about line of intersection of the plane (1) and the plane z = 0 … (2)
Let the equation of the plane in it’s new position be lx + my + kz = 0. … (3)
D.rs. of the normal to the plane (1) are < l, m, 0 >.
D.rs. of the normal to the plane (3) are < l, m, k >.
If α is the angle between the planes (1) and (3) then