CHSE Odisha Class 12 Math Solutions Chapter 13 Three Dimensional Geometry Ex 13(c)

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 13 Three Dimensional Geometry Ex 13(c) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 13 Three Dimensional Geometry Exercise 13(c)

Question 1.
State which of the following statements are true (T) or false (F):
(a) The line \(\frac{x-1}{2}=\frac{y-1}{2}=\frac{z-1}{2}\) pass through the origin.
Solution:
True

(b) The lines \(\frac{x+2}{-k}=\frac{y-3}{k}=\frac{z+4}{k}\) and \(\frac{x-4}{-4}=\frac{y-3}{k}=\frac{z+1}{2}\) are perpendicular every value of k.
Solution:
True

(c) The line \(\frac{x+5}{-2}=\frac{y-3}{1}=\frac{z-2}{3}\) lies on the plane x – y + z + 1 = 0
Solution:
False

(d) The line \(\frac{x-2}{3}=\frac{1-y}{4}=\frac{5-z}{1}\) is parallel to the plane 2x – y – 2z = 0
Solution:
False

(e) The line \(\frac{x+3}{-1}=\frac{y-2}{3}=\frac{z-1}{4}\) is perpendicular to the plane 3x – 3y + 3z – 1 = 0
Solution:
False

Question 2.
Fill in the blanks by choosing the correct alternative from the given ones:
(a)

[parallel, perpendicular, coincident]
Solution:
perpendicular.

(b) The line passing through (-1, 0, 1) and perpendicular to the plane x + 2y + 1 = 0 is _____.

Solution:
\(\frac{x+1}{1}=\frac{y}{2}=\frac{z-1}{0}\)

(c) The line \(\frac{x+1}{2}=\frac{y-6}{1}=\frac{z-4}{0}\) is _____. [parallel to x-axis, perpendicular to y-axis, perpendicular to z-axis]
Solution:
perpendicular to. z-axis

(d) If the line \(\frac{x-3}{2}=\frac{y+k}{-1}=\frac{z+1}{-5}\) lies on the plane 2x – y + z – 7 = 0; then k = -(2, -1, -2)
Solution:
2

(e) If l, m, n be d.cs. of a line, then the line is perpendicular to the plane x – 3y + 2z + 1 = 0 if _____. [(i) l = 1, m = -3, n = 2, (ii) \(\frac{l}{1}=\frac{m}{-3}=\frac{n}{2}\) , (iii) l – 3m + 2n = 0]
Solution:
\(\frac{l}{1}=\frac{m}{-3}=\frac{n}{2}\)

Question 3.
Find the equation of lines joining the points.
(i) (4, -6, 1) and (0, 3, -1)
Solution:
Equation of the line joining the points (4, -6, 1) and (0, 3, -1) is

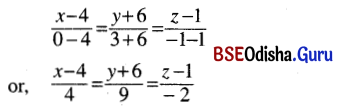
(ii) (a, a, a) and (a, 0, a)
Solution:
Equation of the line joining the points (a, a, a) and (a, 0, a) is

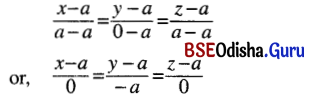
(iii) (2, 1, 3) and (4, -2, 5).
Solution:
Equation of the line joining the points (2, 1, 3) and (4, -2, 5) is

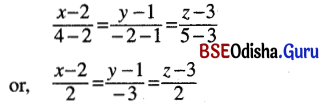
Question 4.
Write the symmetric form of equation of the following lines:
(i) x-axis
Solution:
D.cs. of x-axis are < 1, 0, 0 >.
x-axis passes through the origin.
So the equation of x-axis in symmetrical form is
\(\frac{x-0}{1}=\frac{y-0}{0}=\frac{z-0}{0}\)

(ii) y = b, z = c
Solution:
Given line in unsymmetrical from is y = b, z = c
⇒ y – b = 0 and z – c = 0.
The straight line is parallel to x-axis.
D.rs. of the straight line are < 0, 0, k >.
So the equation of the line is
\(\frac{y-b}{0}=\frac{z-c}{0}=\frac{x}{k}\)

(iii) ax + by + d = 0, 5z = 0
Solution:
Given lines ax + by + d = 0, 5z = 0

(iv) x – 2y = 3, 2x + y – 5z = 0;
Solution:
Given straight line is x – 2y – 3 = 0 … (1)
and 2x + y – 5z = 0 … (2)
Putting z = 0 in (1) and (2) we get x – 2y – 3 = 0 and 2x + y = 0.
Solving we get y = -2x and x + 4x – 3 = 0

(v) 4x + 4y – 5z – 12 = 0, 8x + 12y – 13z = 32;
Solution:
Given straight line in unsymmetrical form is
4x + 4y – 5z – 12 = 0 … (1)
8x + 12y – 13z – 32 = 0 … (2)
Putting z = 0 in (1) and (2) we get
4x + 4y – 12 = 0 ⇒ x + y – 3 =0
8x + 12y – 32 = 0 ⇒ 2x + 3y – 8 = 0
Solving we get

(vi) 3x – 2y + z = 1, 5x + 4y – 6z = 2
Solution:
Given straight line is
3x – 2y + z – 1 = 0 … (1)
and 5x – 4y + 6z – 2 = 0 … (2)
Putting x = 0 in (1) and (2) we get

Question 5.
(a) Obtain the equation of the line through the point (1, 2, 3) and parallel to the line x – y + 2z – 5 = 0, 3x + y + z = -6
Solution:
Equation of the straight line through

(b) Find the equation of the line through the point (3, -1, 2) and parallel to the planes x + y + 2z – 4 = 0 and 2x – 3y + z + 3 = 0
Solution:
Equation of the straight line through the point (3, -1, 2) is

Question 7.
(a) Show that the line passing through the points (a₁, b₁, c₁) and (a₂, b₂, c₂) passes through the origin, if a₁a₂ + b₁b₂ + c₁c₂ = p₁p₂, where p₁ and p₂ are distances of the points from origin.
Solution:
The equation of the line passing through the points (a₁, b₁, c₁) and (a₂, b₂, c₂) is

(b) Prove that the lines x = az + b, y = cz + d and x = a₁z + b₁, y = c₁z + d₁ are perpendicular if aa₁ + cc₁ + 1 = 0.
Solution:
Given lines are
x – az – b = 0 = y – cz – d … (1)
and x – a₁z – b₁ = 0 and < l₂, m₂, n₂ > … (2)
Let < l₁, m₁, n₁ > and < l₂, m₂, n₂ > be the d.cs. of the lines (1) and(2)

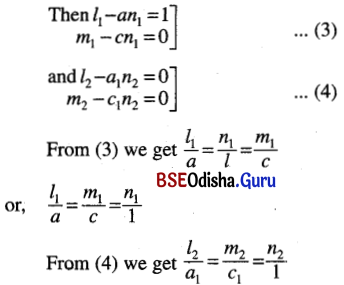
D.rs. of the two lines are < a, c, 1 > and < a₁, c₁, 1 >.
If the lines are perpendicular then the sum of product of d.rs. is zero.
So aa₁ + cc₁ + 1 = 0 (Proved)

Question 8.
Find the points of intersection of the line \(\frac{x-1}{1}=\frac{y+2}{3}=\frac{z-1}{-1}\) and the plane 2x + y + a = 9.
Solution:
Given line is \(\frac{x-1}{1}=\frac{y+2}{3}=\frac{z-1}{-1}\) = r (say)
∴ Any point on (1) is (r + 1, 3r – 2, -r + 1)
If it lies on the plane 2x + y + z – 9 = 0 then
2 (r + 1) + 3r – 2 + (-r + 1) – 9 = 0
or, 2r + 3r – r + 2 – 2 + 1 – 9 = 0
or, 4r = 8, or, r = 2
∴ The point of intersection is (3, 4, -1).

Question 9.
Find the coordinates of the point where the line joining (3, 4, -5) and (2, -3, 1), meets the plane 2x + y + z – 7 = 0.
Solution:
The straight line joining the points (3, 4, -5) and (2, -3, 1) is
\(\frac{x-3}{2-3}=\frac{y-4}{-3-4}=\frac{z+5}{1+5}\)
or, \(\frac{x-3}{-1}=\frac{y-4}{-7}=\frac{z+5}{6}\) = r (say)
Any point on the line is
(-r + 3, -7r + 4, 6r – 5)
If this point is the point of intersection of the line with the plane 2x + y + z – 7 = 0 then
2 (-r + 3) + (-7r + 4) + 6r – 5 – 7 = 0
or, -2r + 6 – 7r + 4 + 6r – 12 = 0
or, -3r = 2 or, r = \(\frac{-2}{3}\)
∴ The point of intersection is
\(\left(\frac{11}{3}, \frac{26}{3}, \frac{-27}{3}\right) \text { i.e., }\left(\frac{11}{3}, \frac{26}{3},-9\right)\).

Question 10.
(a) Find the distance of the point (-1, -5, -10) from the point of intersection of the line \(\frac{x-2}{2}=\frac{y+1}{4}=\frac{z-2}{12}\) and the plane x – y + z = 5.
Solution:
Given line is
\(\frac{x-2}{2}=\frac{y+1}{4}=\frac{z-2}{12}\) = z
Any point on (1) is (2r + 2, 4r – 1, 12r + 2).
If this point is the point of intersection of the line with the plane
x – y + z = 5
then 2r + 2 – 4r + 1 + 12r + 2 = 5
or, 10r = 0, or, r = 0
The point of intersection is (2, -1, 2).
Distance between the points (-1, -5, -10) and the point of intersection of the given line and plane.
= \(\sqrt{9+16+144}=\sqrt{169}\) = 13

(b) Find the image of the point (2, -1, 3) in the plane 3x – 2y + z – 9 = 0
Solution:

Let A = (2, -1, 3)
Let B be the image point of A with respect to the plane
3x – 2y + z – 9 = 0 … (1)
Then AB is normal to the plane.
Again let C be the point of intersection of the line with the plane (1).
Again as B is the image point of A then C must be the mid-point of AB.
Now d.rs. of AB are < 3, -2, 1 > because AB is perpendicular to the plane.
Eqn. of the line AB is

Question 11.
Prove that the lines, \(\frac{x+3}{2}=\frac{y+5}{3}=\frac{z-7}{-3}\) and \(\frac{x+1}{4}=\frac{y+1}{5}=\frac{z+1}{-1}\) are coplanar.
Find the equation of the plane containing them.
Solution:
Given lines are

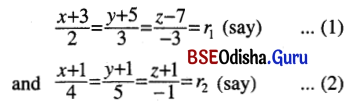
Two lines are co-planar if either they are parallel or intersecting. Now the line (1) and (2) are not parallel because their d.rs. are not proportional. So we shall show that they are intersecting.
Any point on (1) is (2r₁ – 3, 3r₁ – 5, -3r₁ + 7)
Any point on (2) is (4r₂ – 1, 5r₂ – 1, -r₂ – 1)
If the lines are intersecting then for some values of r₁ and r₂.
2r₁ – 3 = 4r₂ – 1 … (3)
3r₁ – 5 = 5r₂ – 1 … (4)
-3r₁ + 7 = -r₂ – 1 … (5)
From (3) we get r₁ = \(\) = 2r₂ + 1
Putting it in (4) we get 6r₂ + 3 – 5 = 5r₂ – 1
or, r₂ = 1. Again r₁ = 3
With these values r₁ = 3, r₂ = 1
We see that eqn. (5) is satisfied. So the straight lines are intersecting. Hence they are coplanar.
The equation of the plane containing the line (1) is:
a (x + 3) + b (y + 5) + c (z – 7) = 0 … (6)
where 2a + 3b – 3c = 0 … (6)
If the plane (6) contains the line (2) then
4a + 5b – c = 0 … (8)
Solving (7) and (8) we get

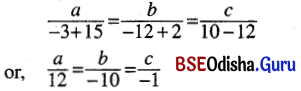
Equation of the plane is
6 (x + 3) – 5 (y + 5) – 1 (z – 7) = 0
or, 6x – 5y – z = 0

Question 12.
Prove that the lines \(\frac{x+4}{3}=\frac{y+6}{5}=\frac{z-1}{-2}\) and 3x – 2y + z + 5 = 0 = 2x + 3y + 4z – 4 are co-planar.
Solution:
Given lines are
\(\frac{x+4}{3}=\frac{y+6}{5}=\frac{z-1}{-2}\) = r (say) … (1)
and 3x – 2y + z + 5 = 0
= 2x + 3y + 4z – 4 … (2)
Any point on (1) and (2) are coplanar if they are either parallel or intersecting. If the line are intersecting then
3 (3r – 4) – 2 (5r – 6) + (-2r + 1) + 5 = 0 … (3)
and 2 (3r – 4) + 3 (5r – 6) + 4 (-2r + 1) – 4 = 0 … (4) are consistent.
Solving (3) we get
9r – 12 – 10r + 12 – 2r + 1 + 5 = 0
or, -3r + 6 = 0 or, r = 2
For r = 2, eqn (4) is satisfied. Thus the lines are intersecting and hence they are co-planar. (Proved)

Question 13.
Show that the lines 7x – 4y + 7z + 16 = 0 = 4x + 3y – 2z + 3 and x – 3y + 4z + 6 = z – y + z + 1 intersect. Find the coordinates of their point of intersection and equation of the plane containing them.
Solution:
Let < l₁, m₁, n₁ > and < l₂, m₂, n₂ > be the d.cs. of the lines.
7x – 4y + 7z + 16 = 0 = 4x + 3y – 2z + 3 … (1)
and x – 3y + 4z + 6 = 0 = x – y + z + 1 … (2)
Then 7l₁ – 4m₁ + 7n₁ = 0
4l₁ + 3m₁ – 2n₁ = 0

Question 14.
Show that the line joining the points (0, 2, -4) and (-1 , 1, -2) and the lines joining the points (-2, 3, 3) and (-3, -2, 1) are co-planar. Find their point of intersection.
Solution:
The eqn. of the line joining the points (0, 2, -4) and (-1, 1, -2) is

The lines (1) and (2) are coplanar if either they are parallel or intersecting. These lines are not parallel. So we have to prove that they are intersecting.
Any point on (1) is (-r₁, -r₁ + 2, 2r₁ – 4)
Any point on (2) is (-r₂ – 2, -5r₂ + 3, -2r₂ + 3)
If two lines are intersecting then for some r₁ and r₂
-r₁ = -r₂ – 2 … (1)
-r₁ + 2 = -5r₂ + 3 … (2)
2r₁ – 4 = -2r₁ + 3 … (3)
From (3), r₁ = r₂ + 2

Question 15.
Show that the lines x – mz – a = 0 = y – nz – b and x – m’z’ – a’ = 0 = y – n’z’ – b’ intersect, if (a – a’) (n – n’) = (b – b’) (m – m’).
Solution:
Given lines are
x – mz – a = 0 = y – nz – b … (1)
and x – m’z’ – a’ = 0 = y – n’z’ – b … (2)
Putting z = 0 in (1) we get x = a and y = b.
So (a, b, 0) is a point on (1).
Again putting z = 0 in (2) we get x = a’, y = b’.
So (a’, b’, 0) is a point on (2).
Let < L₁, M₁, N₁ > and < L₂, M₂, N₂ > be the d.cs. of the lines (1) and (2).
Then L₁ – mN₁ = 0, M₁ – nN₁ = 0

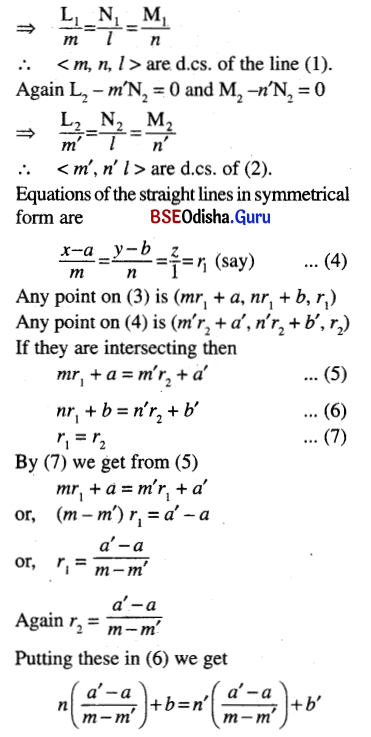
or, n (a’ – a) + b (m – m’)
= n’ (a’ – a) + b (m – m’)
⇒ (a – a’) (n – n’) = (b – b’) (m – m’) (Proved)

Question 16.
Proved that the line \(\frac{x-1}{2}=\frac{y+2}{-3}=\frac{z-3}{1}\) lies on the plane 7x + 5y + z = 0
Solution:
Given line is
\(\frac{x-1}{2}=\frac{y+2}{-3}=\frac{z-3}{1}\) = r (say) … (1)
Any point on (1) is (2r + 1, -3r – 2, r + 3)
The straight line lies on the plane 7x + 5y + z = 0 … (2)
if every point of the line lies on (2).
Now 7 × (2r + 1) + 5 (-3r -2) + (r + 3)
= 14r + 7 – 15r – 10 + r + 3 = 0
Thus the point (2r + 1, -3r – 2, r + 3) lies on (2).
Hence the straight line lies on the plane. (Proved)

Question 17.
(a) Find the angle between the plane x + y + 4 = 0 and the line \(\frac{x+3}{2}=\frac{y-1}{1}=\frac{z+4}{-2}\).
Solution:

(b) Find the angle between the plane 4x + 3y + 5z – 1 = 0 and the line \(\frac{x+3}{2}=\frac{y-1}{3}=\frac{z+4}{6}\).
Solution:
Given plane and the line have equations
4x + 3y + 5z – 1 = 0 … (1)

Question 18.
(a) Find the equation of the line passing through the point (1, 0, -1) and intersecting the lines x = 2y = 2z; 3x + 4y – 1 = 0 = 4x + 5z – 2.
Solution:
Given lines are x = 2y = 2z … (1)
and 3x + 4y – 1 = 0 = 4x + 5z – 2 … (2)
Any plane containing the line (1)
i.e., x – 2y = 0 and y – z = 0 is
x – 2y + k₁ (y – z)= 0 = 0
or, x + (k₁ – 2) y – k₁z = 0
If it passes through the point (1, 0, -1) then 1 + k₁ = 0 or, k₁ = -1
The plane containing the line (1) and passing through the point (1, 0, -1) is x – 3y + z = 0
Again any plane containing the line (2) is
3x + 4y – 1 + k₂ (4x + 5z – 2) = 0
or, (3 + 4k₂) x + 4y + 5k₂z – (2k₂ + 1) = 0
If it passes through the point (1, 0, -1) then
3 + 4k₂ – 5k₂ – 2k₂ – 1 = 0
or, 3k₂ = 2 or, k₂ = \(\frac{2}{3}\)
The equation of the plane through the line (2) and passing through (1, 0, -1) is

(b) A line with direction ratios < 2, 1, 2 > meets each of the lines x = y + a = z and x + a = 2y = 2z. Find the coordinates of the points of intersection.
Solution:
Given lines are
x = y + a = z and x + a = 2y = 2z
These can be written in symmetrical form as
\(\frac{x}{1}=\frac{y+a}{1}=\frac{z}{1}\) = r₁ (say)
and \(\frac{x+a}{2}=\frac{y}{1}=\frac{z}{1}\) = r₂ (say)
Any point on (1) is (r₁, r₁ – a, r₁)
Any point on (2) is (2r₂ – a, r₂, r₂)
Suppose that the line meets the lines (1) and (2) at P and Q respectively.
Let P = (r₁, r₁ – a, r₁), Q = (2r₂ – a, r₂, r₂)
D.rs. of PQ are
< r₁ – 2r₂ + a, r₁ – r₂ – a, r₁ – r₂ >
But given that d.rs. are < 2, 1, 2 >.
So \(\frac{r_1-2 r_2+a}{2}=\frac{r_1-r_2-a}{1}=\frac{r_1-r_2}{2}\)
From the 1st two ratios we get
r₁ – 2r₂ + a = 2r₁ – 2r₂ – 2a ⇒ r₁ = 3a
From the last two ratios we get
2r₁ – 2r₂ – 2a = r₁ – r₂
⇒ r₁ = r₂ + 2a ⇒ 3a = r₂ + 2a ⇒ r₂ = a
∴ P (3a, 2a, 3a), Q = (a, a, a)
∴ The co-prdinates of the points of intersection and (3a, 2a, 3a) and (a, a, a).

Question 19.
Obtain the co-ordinates of the foot of the perpendicular drawn from the point (3, -1, 11) to the line \(\frac{x}{2}=\frac{y-2}{3}=\frac{z-3}{4}\). Obtain the equation of the perpendicular also.
Solution:

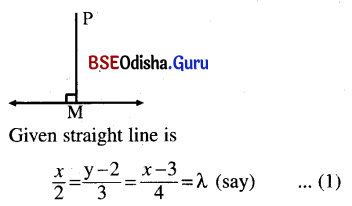
Let P be the given point (3, -1, 11).
Draw PM perpendicular from P onto the straight line.
Any point on (1) is (2λ, 3λ + 2, 4λ + 3)
Let M = (2λ, 3λ + 2, 4λ + 3)
D.rs. of PM are 2λ – 2, 3λ + 3, 4λ – 8
As PM is perpendicular to the line then
(2λ – 3) . 2 +3 (3λ + 3) + (4λ – 8) . 4 = 0
or, 4λ – 6 + 9λ + 9 + 16λ – 32 = 0
or, 29λ – 29 = 0 or, λ = 1
∴ The foot of the perpendicular is (2, 5, 7)
Equation of the perpendicular line is
\(\frac{x-3}{2-3}=\frac{y+1}{5+1}=\frac{z-11}{7-11}\)
or, \(\frac{x-3}{1}=\frac{y+1}{-6}=\frac{z-11}{4}\)

Question 20.
Find the perpendicular distance of the point (-1, 3, 9) from the line \(\frac{x-13}{5}=\frac{y+8}{-8}=\frac{z-31}{1}\).
Solution:
Let P be the point (-1, 3, 9).
Suppose that M is the foot of the perpendicular drawn from P onto the straight line.
\(\frac{x-13}{5}=\frac{y+8}{-8}=\frac{z-31}{1}\) = λ (say)
Let M = (5λ + 13, -8λ – 8, λ + 31)
D.rs. of PM are
< 5λ + 14, -8λ – 11, λ + 22 >
As PM is perpendicular to the line (1) then
5 (5λ + 14) – 8 (-8λ – 11) + λ + 22 = 0
or, 25λ + 64λ + λ + 70 + 88 + 22 = 0
or, 90λ = -180 or, λ = -2
Thus M = (3, 8, 29)
Distance PM = \(\sqrt{(3+1)^2+(8-3)^2+(29-9)^2}\)
= \(\sqrt{16+25+400}\) = \(\sqrt{441}\) = 21

Question 21.
Find the distance of the point (1, -2, 3) from the plane x – y + z = 5, measured parallel to the line \(\frac{x}{2}=\frac{y}{3}=\frac{z}{-6}\).
Solution:
Let P be the point (1, 2, 3). Draw the straight line PM parallel to the line

Question 22.
Find the distance of the point (1, -1, -10) from the line \(\frac{x-4}{1}=\frac{y+3}{-4}=\frac{z+1}{7}\) measured parallel to the line \(\frac{x+2}{2}=\frac{y-3}{-3}=\frac{z-4}{8}\).
Ans.
Let P be the point (1, -1, -10). Equation of the line through P parallel to the line

∴ Distance of the point (1, -1, -10) from the given line is √308.

Question 23.
Find the equation of plane through the point (2, 0, -3) and containing the line 3x + y + z – 5 = 0 = x – 2y + 4z + 4
Solution:
Any plane containing the line
3x + y + z – 5 = 0 = x – 2y + 4z + 4
3x + y + z – 5 + k (x – 2y + 4z + 4) = 0
or, (3 + k) x + (1 – 2k) y + (1 + 4k) z + (4k – 5) = 0 … (1)
If this plane contains the point (2, 0, -3) then
2 (3 + k)² + (1 – 2k) . 0 + (1 + 4k) . (-3) + 4k – 5 = 0
⇒ 6 + 2k – 3 – 12k + 4k – 5 = 0
⇒ -6k – 2 = 0 ⇒ k = –\(\frac{1}{3}\)
Required plane is
\(\left(3-\frac{1}{3}\right) x+\left(1+\frac{2}{3}\right) y+\left(1-\frac{4}{3}\right) z+\left(-\frac{4}{3}-5\right)\) = 0
⇒ 8x + 5y – z – 19 = 0

Question 24.
Find the equation of the plane containing the line x + 2 = 2y – 1 = 3z and parallel to the line x = 1 – 5y = 2z – 7. Also find the shortest distance between the two lines.
Solution:
Given line is x + 2 = 2y – 1 = 3z
[x – 2y + 3 = 0
2y – 3z – 1 = 0] … (1)
Any plane containing the line (1) is
(x – 2y + 3) + k (2y – 3z – 1) = 0
or, x + (2k – 2) y – 3kz + (3 – k) = 0… (2)
Again given that the plane (2) is parallel to the line
x = 1 – 5y = 2z – 7
⇒ \(\frac{x}{10}=\frac{y-\frac{1}{5}}{-2}=\frac{z-\frac{7}{2}}{5}\) … (3)
D.rs. of the line (3) are < 10, -2, 5 >
If the plane (2) is parallel to the line (3) then the normal plane (2) is perpendicular to the line (3). D.rs. of the normal of the plane(2) are
< 1, 2k – 2, -3k >.
Thus 10 – 2 (2k – 2) – 15 k = 0
⇒ 10 – 4k + 4 – 15k = 0

We have to find the shortest distance between the lines (3) and (4). The shortest distance is the line segment perpendicular to both the lines. Let < l, m, n > be the d.cs. of the shortest distance.
Then 6l + 3m + 2n = 0
10l – 2m+ 5n = 0
Solving we get

Question 25.
Find the equation of the two planes through the origin and parallel to the line \(\frac{x-1}{2}=\frac{y+3}{-1}=\frac{z+1}{-2}\) and at a distance \(\frac{5}{3}\) from it.
Solution:
Equation of the plane through the origin is ax + by + cz = 0 … (1)
If the plane (1) is parallel to the line

⇒ 9b² = 4a² + 4b² + 4c²
⇒ 4a² – 5b² + 4c² = 0 … (4)
From (3) we get b = 2a – 3c.
Putting it in (4) we get
4a² – 5 × 4 (a – c)² + 4c² = 0
⇒ a² – 5a² – 5c² + 10ac + c² = 0
⇒ -4a² – 4c² + 10ac = 0
⇒ 2a² + 2c² – 5ac = 0
⇒ 2a² + 2c² – 4ac – ac = 0
⇒ 2a (a – 2c) – c (a – 2c) = 0
⇒ (a – 2c) (2a – c) = 0

∴ The plane is x – 2y + 2z = 0
Hence the planes are
2x + 2y + z = 0 and x – 2y + 2z = 0.

Question 26.
Find the equation of the straight line perpendicular to the line \(\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-6}{7}\) and lying in the plane x – 2y + 4z – 51 = 0.
Solution:
Let < l, m, n > be the d.cs. of the straight line perpendicular to the line.

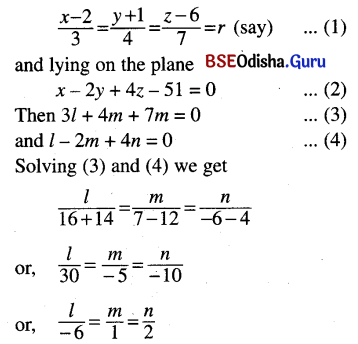
D.rs. of the line is < -6, 1, 2 >.
Again let A be the point of intersection of the line with the line (1).
Let A = (3r + 2, 4r – 1, 7r + 6)
Then this point a lies also on the plane (2).
So 3r + 2 – 8r + 2 + 28r + 24 – 51 =0
or, 23r – 23 = 0 or, r = 1
∴ A = (5, 3, 13)
Hence the equation of the required line is
\(\frac{x-5}{-6}=\frac{y-3}{1}=\frac{z-13}{2}\)

Question 27.
Find the shortest distance between the lines \(\frac{x-3}{3}=\frac{y-8}{-1}=\frac{z-3}{1}\) and \(\frac{x+3}{-3}=\frac{y+7}{2}=\frac{z-6}{4}\). Find also the equation of the line of shortest distance.
Solution:
Given lines are

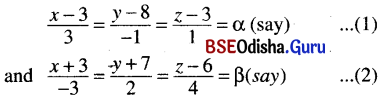
Any point on the line (1) and (2) are P (3 + 3α, 8 – α, 3 + α) and Q (-3 – 3β, -7 + 2β, 6 + 4β) respectively.
D.r.s. of PQ are < 6 + 3α + 3β, 15 – α – 4β >
D.r.s. of the lines are < 3, -1, 1 > and < -3, 2, 4 > respectively.
PQ is perpendicular to the given lines.
∴ 3 (6 + 3α + 3β) – (15 – α – 2β) + 1 (-3 + α – 4β) = 0
and -3 (6 + 3α + 3β) + 2 (15 – α – 2β) + 1 (-3 + α – 4β)
⇒ 18 + 9α + 9β – 15 + α + 2β – 3 + α – 4β = 0
and -18 – 9α – 9β + 30 – 2α – 4β – 12 + 4α – 16β = 0
⇒ 11a + 7b = 0
and -7a – 29b = 0
⇒ a = b = 0
co-ordinates P and Q are (3, 8, 3) and (-3, -7, 6) respectively.
The shortest distance

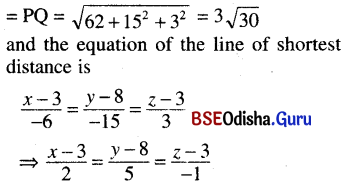
Question 28.
Show that the shortest distance between the lines x + a = 2y = -12z and x = y + 2a = 6z – 6a is 2a.
Solution:
Given lines are
x + a = 2y = -12z
and x = y + 2a – 6z – 6a

Question 29.
Find the length and equation of the line of shortest distance between the lines 3x – 9y + 5z = 0 = x + y – z and 6x + 8y + 3z – 13 = 0 = x + 2y + z – 3
Solution:
Given lines are
3x – 9y + 5z = 0
x + y – z = 0 … (1)
and 6x + 8y + 3z – 13 = 0
x + 2y + z – 3 = 0 … (2)
Let us consider the line (1)
Now z = x + y
∴ 3x – 9y + 5 ( x + y) = 0
⇒ 8x – 4y = 0 ⇒ 2x = y
Again y = z – x
∴ 3x – 9 (z – x) + 5z = 0
⇒ 12x – 4z = 0
⇒ 3x = z
∴ 6x = 3y = 2z