CHSE Odisha Class 12 Math Solutions Chapter 5 Determinants Ex 5(a)

Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 5 Determinants Ex 5(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 5 Determinants Exercise 5(a)

Question 1.
Evaluate the following determinants.
(i) \(\left|\begin{array}{ll}
1 & 1 \\
2 & 3
\end{array}\right|\)
Solution:
\(\left|\begin{array}{ll}
1 & 1 \\
2 & 3
\end{array}\right|\) = 3 – 2 = 1

(ii) \(\left|\begin{array}{ll}
2 & -3 \\
1 & -4
\end{array}\right|\)
Solution:
\(\left|\begin{array}{ll}
2 & -3 \\
1 & -4
\end{array}\right|\) = -8 + 3 = -5

(iii) \(\left|\begin{array}{ll}
\sec \theta & \tan \theta \\
\tan \theta & \sec \theta
\end{array}\right|\)
Solution:
\(\left|\begin{array}{ll}
\sec \theta & \tan \theta \\
\tan \theta & \sec \theta
\end{array}\right|\) = sec² θ – tan² θ = 1

(iv) \(\left|\begin{array}{ll}
0 & x \\
2 & 0
\end{array}\right|\)
Solution:
\(\left|\begin{array}{ll}
0 & x \\
2 & 0
\end{array}\right|\) = 0 – 2x = -2x

(v) \(\left|\begin{array}{cc}
1 & \omega \\
-\omega & \omega
\end{array}\right|\)
Solution:
\(\left|\begin{array}{cc}
1 & \omega \\
-\omega & \omega
\end{array}\right|\) = ω + ω² = -1

(vi) \(\left|\begin{array}{cc}
4 & -1 \\
3 & 2
\end{array}\right|\)
Solution:
\(\left|\begin{array}{cc}
4 & -1 \\
3 & 2
\end{array}\right|\) = 8 + 3 = 11

(vii) \(\left|\begin{array}{ll}
\cos \theta & \sin \theta \\
\sin \theta & \cos \theta
\end{array}\right|\)
Solution:
\(\left|\begin{array}{ll}
\cos \theta & \sin \theta \\
\sin \theta & \cos \theta
\end{array}\right|\) = cos² θ – sin² θ = cos 2θ

(viii) \(\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right|\)
Solution:
\(\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right|\) = 0
as the rows are identical.

(ix) \(\left|\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right|\)
Solution:
\(\left|\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right|\) = 1\(\left|\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right|\) = 1 – 0 = 1

(x) \(\left|\begin{array}{ccc}
2 & 3 & 1 \\
0 & 0 & 0 \\
-1 & 2 & 0
\end{array}\right|\)
Solution:
\(\left|\begin{array}{ccc}
2 & 3 & 1 \\
0 & 0 & 0 \\
-1 & 2 & 0
\end{array}\right|\) = 0
as all the entries in the 2nd row are zero.

(xi) \(\left|\begin{array}{ccc}
1 & x & y \\
0 & \sin x & \sin y \\
0 & \cos x & \cos y
\end{array}\right|\)
Solution:
\(\left|\begin{array}{ccc}
1 & x & y \\
0 & \sin x & \sin y \\
0 & \cos x & \cos y
\end{array}\right|\) = 1\(\left|\begin{array}{cc}
\sin x & \sin y \\
\cos x & \cos y
\end{array}\right|\)
= sin x cos y – cos x sin y = sin (x – y)

(xii) \(\left|\begin{array}{lll}
1 & 2 & 3 \\
1 & 2 & 3 \\
3 & 4 & 5
\end{array}\right|\)
Solution:
\(\left|\begin{array}{lll}
1 & 2 & 3 \\
1 & 2 & 3 \\
3 & 4 & 5
\end{array}\right|\) = 0 (∵ R₁ = R₂)

(xiii) \(\left|\begin{array}{lll}
0.2 & 0.1 & 3 \\
0.4 & 0.2 & 7 \\
0.6 & 0.3 & 2
\end{array}\right|\)
Solution:
\(\left|\begin{array}{lll}
0.2 & 0.1 & 3 \\
0.4 & 0.2 & 7 \\
0.6 & 0.3 & 2
\end{array}\right|\)
= 2\(\left|\begin{array}{lll}
0.2 & 0.1 & 3 \\
0.4 & 0.2 & 7 \\
0.6 & 0.3 & 2
\end{array}\right|\) = 0 (∵ C₁ = C₂)

(xiv) \(\left|\begin{array}{ccc}
1 & \omega & \omega^2 \\
\omega & \omega^2 & 1 \\
\omega^2 & 1 & \omega
\end{array}\right|\)
Solution:
\(\left|\begin{array}{ccc}
1 & \omega & \omega^2 \\
\omega & \omega^2 & 1 \\
\omega^2 & 1 & \omega
\end{array}\right|\)

(xv) \(\left|\begin{array}{lll}
1 & 1 & 1 \\
2 & 2 & 2 \\
3 & 3 & 3
\end{array}\right|\)
Solution:
\(\left|\begin{array}{lll}
1 & 1 & 1 \\
2 & 2 & 2 \\
3 & 3 & 3
\end{array}\right|\) = 0 (∵ C₁ = C₂)

(xvi) \(\left|\begin{array}{ccc}
-6 & 0 & 0 \\
3 & -5 & 7 \\
2 & 8 & 11
\end{array}\right|\)
Solution:
\(\left|\begin{array}{ccc}
-6 & 0 & 0 \\
3 & -5 & 7 \\
2 & 8 & 11
\end{array}\right|\)
= (-6) \(\left|\begin{array}{cc}
-5 & 7 \\
8 & 11
\end{array}\right|\) = = (-6) (- 55 – 56)
= (-6) (-111) = 666

(xvii) \(\left|\begin{array}{lll}
1 & 0 & 0 \\
2 & 3 & 5 \\
4 & 1 & 3
\end{array}\right|\)
Solution:
\(\left|\begin{array}{lll}
1 & 0 & 0 \\
2 & 3 & 5 \\
4 & 1 & 3
\end{array}\right|\)
= 1 \(\left|\begin{array}{ll}
3 & 5 \\
1 & 3
\end{array}\right|\) = 9 – 5 = 4

(xviii) \(\left|\begin{array}{ccc}
-18 & 17 & 19 \\
3 & 0 & 0 \\
-14 & 5 & 2
\end{array}\right|\)
Solution:
\(\left|\begin{array}{ccc}
-18 & 17 & 19 \\
3 & 0 & 0 \\
-14 & 5 & 2
\end{array}\right|\)
= -3 \(\left|\begin{array}{cc}
17 & 19 \\
5 & 2
\end{array}\right|\)
(Expanding along 2nd row)
= – 3 (34 – 95)
= (-3) (-61) = 183

Question 2.
State true or false.
(i) If the first and second rows of a determinant be interchanged then the sign of the determinant is changed.
Solution:
True

(ii) If first and third rows of a determinant be interchanged then the sign of the determinent does not change.
Solution:
False

(iii) If in a third order determinant first row be changed to second column. Second row to 1st column and third row to third column, then the value of the determinant does not change.
Solution:
False

(iv) A row and a column of a determinant can have two or more common elements.
Solution:
False

(v) The minor and the co-factor of the element a₃₂ of a determinant of third order are equal.
Solution:
False

(vi) \(\left|\begin{array}{lll}
3 & 1 & 3 \\
0 & 4 & 0 \\
1 & 3 & 1
\end{array}\right|\) = 0
Solution:
True

(vii) \(\left|\begin{array}{lll}
6 & 4 & 2 \\
4 & 0 & 7 \\
5 & 3 & 4
\end{array}\right|\) = \(\left|\begin{array}{lll}
6 & 4 & 5 \\
4 & 0 & 3 \\
2 & 7 & 3
\end{array}\right|\)
Solution:
True

(viii) \(\left|\begin{array}{lll}
2 & 3 & 4 \\
5 & 6 & 7 \\
1 & 2 & 3
\end{array}\right|\) = \(\left|\begin{array}{lll}
4 & 2 & 3 \\
7 & 5 & 6 \\
3 & 1 & 2
\end{array}\right|\)
Solution:
True

Question 3.
Fill in the blanks with appropriate answer from the brackes.
(i) The value of \(\left|\begin{array}{ccc}
0 & 8 & 0 \\
25 & 520 & 25 \\
1 & 410 & 0
\end{array}\right|\) = _______. (0, 25, 200, -250)
Solution:
200

(ii) If ω is the cube root of unity, then \(\left|\begin{array}{ccc}
1 & \omega & \omega^2 \\
\omega & \omega^2 & 1 \\
\omega^2 & 1 & \omega
\end{array}\right|\) = _______. (1, 0, ω, ω²)
Solution:
0

(iii) The value of the determinant \(\left|\begin{array}{lll}
1 & a & b+c \\
1 & b & c+a \\
1 & c & a+b
\end{array}\right|\) = _______. (a + b – c, (a + b + c)², 0, 1 + a + b + c)
Solution:
0

(iv) If \(\left|\begin{array}{lll}
a & b & c \\
b & a & b \\
x & b & c
\end{array}\right|\) = 0, then x = _______. (a, b, c, a + b + c)
Solution:
a

(v) \(\left|\begin{array}{lll}
a_1+a_2 & a_3+a_4 & a_5 \\
b_1+b_2 & b_3+b_4 & b_5 \\
c_1+c_2 & c_3+c_4 & c_5
\end{array}\right|\) can be expressed at the most as _______, different 3rd order determinants. (1, 2, 3, 4)
Solution:
4

(vi) Minimum value of \(\left|\begin{array}{cc}
\sin x & \cos x \\
-\cos x & 1+\sin x
\end{array}\right|\) is _______. (-1, 0, 1, 2)
Solution:
0

(vii) The determinant \(\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 2 & 3 \\
1 & 3 & 6
\end{array}\right|\) is not equal to _______. \(\left(\left|\begin{array}{lll}
2 & 1 & 1 \\
2 & 2 & 3 \\
2 & 3 & 6
\end{array}\right|,\left|\begin{array}{lll}
2 & 1 & 1 \\
3 & 2 & 3 \\
4 & 3 & 6
\end{array}\right|,\left|\begin{array}{lll}
1 & 2 & 1 \\
1 & 5 & 3 \\
1 & 9 & 6
\end{array}\right|,\left|\begin{array}{ccc}
3 & 1 & 1 \\
6 & 2 & 3 \\
10 & 3 & 6
\end{array}\right|\right)\)
Solution:
\(\left|\begin{array}{lll}
2 & 1 & 1 \\
2 & 2 & 3 \\
2 & 3 & 6
\end{array}\right|\)

(viii) With 4 different elements we can construct _______ number of different determinants of order 2. (1, 6, 8, 24)
Solution:
6

Question 4.
Solve the following:
(i) \(\left|\begin{array}{cc}
4 & x+1 \\
3 & x
\end{array}\right|\)
Solution:
\(\left|\begin{array}{cc}
4 & x+1 \\
3 & x
\end{array}\right|\) = 5
or, 4x – 3x – 3 = 5 or, x = 8

(ii) \(\left|\begin{array}{ccc}
\boldsymbol{x} & a & a \\
m & m & m \\
b & x & b
\end{array}\right|\) = 0
Solution:

(Replacing C₁ and C₂ by C₁ – C₃ and C₂ – C₃ respectively)
⇒ m |(x – a) (-x + b)| = 0
⇒ m (x – a) (b – x) – 0 ⇒ x = a, b

(iii) \(\left|\begin{array}{lll}
7 & 6 & x \\
2 & x & 2 \\
x & 3 & 7
\end{array}\right|\) = 0
Solution:

or, (x – 7) (7x + x² – 1 8) = 0
or, (x – 7) (x² + 7x – 18) = 0
or, (x – 7) (x + 9) (x – 2) = 0
∴ x = -9, 2, 7

(iv) \(\left|\begin{array}{ccc}
0 & x-a & x-b \\
x+a & 0 & x-c \\
x+b & x+c & 0
\end{array}\right|\) = 0
Solution:

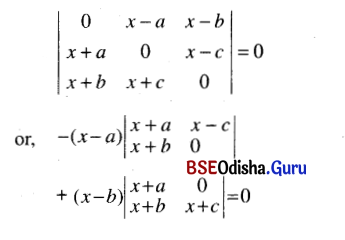
or, – (x – a) {0 – (x + b) (x – c)} + (x – b) (x + a) (x + c) = 0
or, (x – a) (x + b) (x – c) + (x – b) (x + a) (x + c) = 0
or, (x² + bx – ax – ab) (x – c) + (x² + ax – bx – ab) (x + c) = 0
or, x³ – cx² + bx² – bcx – ax² + acx – abx + abc + x³ + cx² + ax² + acx- bx² – bcx – abx – abc = 0
or, 2x³ – 2abx – 2bcx + 2acx = 0
or, 2x (x² – ab – bc + ac) = 0
x = 0, x² = ab + bc – ca
∴ x = 0, x = \(\sqrt{a b+b c-c a}\)

(v) \(\left|\begin{array}{ccc}
\boldsymbol{x}+\boldsymbol{a} & \boldsymbol{b} & \boldsymbol{c} \\
\boldsymbol{b} & \boldsymbol{x}+\boldsymbol{c} & \boldsymbol{a} \\
\boldsymbol{c} & \boldsymbol{a} & \boldsymbol{x}+\boldsymbol{b}
\end{array}\right|\) = 0
Solution:

⇒ (x + a + b + c) {x² + bx + cx + bc – a² – bx – b² + ca + ab – cx – c² = 0}
⇒ (x + a + b + c) {x² – a² – b² – c² + ab + bc + ca} = 0
⇒ x + a + b + c = 0
or, x² – a² – b² – c² + ab + bc + ca = 0
⇒ x = – (a + b + c)
∴ or x = \(\sqrt{a^2+b^2+c^2-a b-b c-c a}\)

(vi) \(\left|\begin{array}{ccc}
1+x & 1 & 1 \\
1 & 1+x & 1 \\
1 & 1 & 1+x
\end{array}\right|\) = 0
Solution:

(vii) \(\left|\begin{array}{ccc}
1 & 4 & 20 \\
1 & -2 & 5 \\
1 & 2 x & 5 x^2
\end{array}\right|\) = 0
Solution:

⇒ -30x² + 30 + 30x + 30 = 0
⇒ -30x² + 30x + 60 = 0
⇒ x² – x – 2 = 0
⇒ x² – 2x + x + 2 = 0
⇒ (x – 2) (x + 1) = 0
⇒ x = 2, -1

(viii) \(\left|\begin{array}{ccc}
x+1 & \omega & \omega^2 \\
\omega & x+\omega^2 & 1 \\
\omega^2 & 1 & x+\omega
\end{array}\right|\) = 0
Solution:

⇒ x(x² + xω – xω² + xω² + ω³ – ω⁴ – xω – ω² + ω³ – 1 + ω² + ω – ω³) = 0
⇒ x(x² + ω³ – ω⁴ – ω² + ω³ – 1 + ω² + ω – ω³) = 0
⇒ x(x² + ω³ – ω + ω – 1) = 0
⇒ x(x² + 1 – ω + ω – 1) = 0 (∵ ω³ = 1)
⇒ x³ = 0
⇒ x = 0

(ix) \(\left|\begin{array}{ccc}
2 & 2 & x \\
-1 & x & 4 \\
1 & 1 & 1
\end{array}\right|\) = 0
Solution:

or, 10 + 10x – x² – 8x – x – 8 = 0
or, x² – 2x + x – 2 = 0
or, (x – 2) (x + 1) = 0
x = 2, x = -1

(x) \(\left|\begin{array}{lll}
x & 1 & 3 \\
1 & x & 1 \\
3 & 6 & 3
\end{array}\right|\) = 0
Solution:

or, x(3x – 6) – 0 + 3(6 – 3x) = 0
or, 3x² – 6x + 18 – 9x = 0
or, 3x² – 15x + 18 = 0
or, x² – 5x + 6 = 0
or, (x – 3) (x – 2) = 0
x = 3 or, x = 2

Question 5.
Evaluate the following
(i) \(\left|\begin{array}{ccc}
2 & 3 & 4 \\
1 & -1 & 3 \\
4 & 1 & 10
\end{array}\right|\)
Solution:

(ii) \(\left|\begin{array}{lll}
\boldsymbol{x} & \mathbf{1} & 2 \\
\boldsymbol{y} & \mathbf{3} & 1 \\
z & 2 & 2
\end{array}\right|\)
Solution:

(iii) \(\left|\begin{array}{ccc}
x & 1 & -1 \\
2 & y & 1 \\
3 & -1 & z
\end{array}\right|\)
Solution:

= x (yz + z – z + 1) – (2z – 2 – 3y – 3)
= xyz + x – 2z + 3y + 5
= xyz + x + 3y – 2z + 5

(iv) \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|\)
Solution:

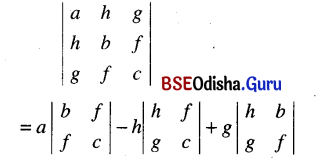
= a(bc – f²) – h (ch – fg) + g (hf – bg)
= abc – af² – ch² + fgh + fgh – bg²
= abc + 2fgh – af² – bg² – ch²

(v) \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|\)
Solution:

(vi) \(\left|\begin{array}{ccc}
\sin ^2 \theta & \cos ^2 \theta & 1 \\
\cos ^2 \theta & \sin ^2 \theta & 1 \\
-10 & 12 & 2
\end{array}\right|\)
Solution:

(vii) \(\left|\begin{array}{ccc}
-1 & 3 & 2 \\
1 & 3 & 2 \\
1 & -3 & -1
\end{array}\right|\)
Solution:

(viii) \(\left|\begin{array}{ccc}
11 & 23 & 31 \\
12 & 19 & 14 \\
6 & 9 & 7
\end{array}\right|\)
Solution:

(ix) \(\left|\begin{array}{ccc}
37 & -3 & 11 \\
16 & 2 & 3 \\
5 & 3 & -2
\end{array}\right|\)
Solution:

(x) \(\left|\begin{array}{ccc}
2 & -3 & 4 \\
-4 & 2 & -3 \\
11 & -15 & 20
\end{array}\right|\)
Solution:

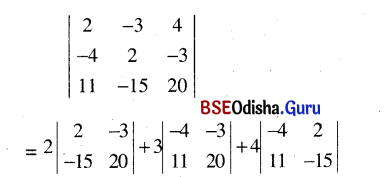
= 2(40 – 45) + 3(-80 + 33) + 4(60 – 22)
= -10 – 141 + 152 = -151 + 152 = 1

Question 6.
Show that x = 1 is a solution of \(\left|\begin{array}{ccc}
x+1 & 3 & 5 \\
2 & x+2 & 5 \\
2 & 3 & x+4
\end{array}\right|\) = 0
Solution:

or, (x + 9) {(x – 1)²} – 0
or, x = -9, 1
∴ x = 1 is a solution of the given equation.

Question 7.
Show that (a + 1) is a factor of \(\left|\begin{array}{ccc}
a+1 & 2 & 3 \\
1 & a+1 & 3 \\
3 & -6 & a+1
\end{array}\right|\) = 0
Solution:

= (a+ 1) {(a + 1)² + 18} – 2(a + 1 – 9) + 3(- 6 – 3a – 3)
= (a + 1) (a² + 2a + 1 + 18) – 2(a – 8) + 3(- 9 – 3a)
= (a + 1) (a² + 2a + 19) – 2a + 16 – 27 – 9a
= (a + 1) (a² + 2a + 19) – 11a – 11
= (a + 1) (a² + 2a + 19) – 11(a + 1)
= (a + 1) (a² + 2a + 19 – 11)
= (a + 1) (a² + 2a + 8)
∴ (a + 1) is a factor of the above determinant.

Question 8.
Show that \(\left|\begin{array}{ccc}
a_1 & b_1 & -c_1 \\
-a_2 & b_2 & c_2 \\
a_3 & b_3 & -c_3
\end{array}\right|=\left|\begin{array}{lll}
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2 \\
a_3 & b_3 & c_3
\end{array}\right|\)
Solution:

Question 9.
Prove the following
(i) \(\left|\begin{array}{lll}
a & b & c \\
\boldsymbol{x} & y & z \\
\boldsymbol{p} & q & r
\end{array}\right|=\left|\begin{array}{lll}
\boldsymbol{y} & \boldsymbol{b} & \boldsymbol{q} \\
\boldsymbol{x} & \boldsymbol{a} & p \\
z & c & r
\end{array}\right|=\left|\begin{array}{lll}
\boldsymbol{x} & \boldsymbol{y} & z \\
\boldsymbol{p} & \boldsymbol{q} & r \\
a & b & c
\end{array}\right|\)
Solution:

(ii) \(\left|\begin{array}{ccc}
1+a & 1 & 1 \\
1 & 1+b & 1 \\
1 & 1 & 1+c
\end{array}\right|\) = abc \(\left(1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
Solution:

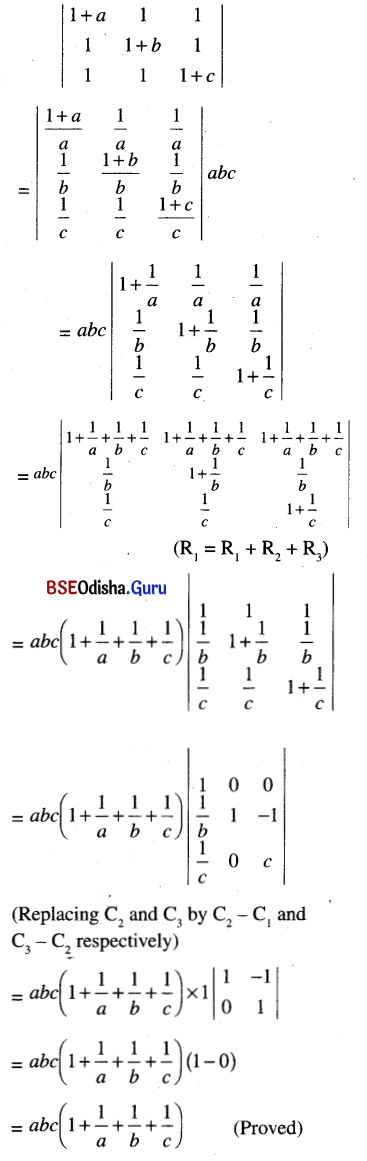
(iii) \(\left|\begin{array}{lll}
b+c & c+a & a+b \\
q+r & r+p & p+q \\
y+z & z+x & x+y
\end{array}\right|=2\left|\begin{array}{lll}
a & b & c \\
p & q & r \\
x & y & z
\end{array}\right|\)
Solution:

(iv) \(\left|\begin{array}{lll}
(a+1)(a+2) & a+2 & 1 \\
(a+2)(a+3) & a+3 & 1 \\
(a+3)(a+4) & a+4 & 1
\end{array}\right|\) = -2
Solution:

(v) \(\left|\begin{array}{ccc}
a+d & a+d+k & a+d+c \\
c & c+b & c \\
d & d+k & d+c
\end{array}\right|\) = abc
Solution:

(vi) \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
b+c & c+a & c+a \\
b^2+c^2 & c^2+a^2 & a^2+b^2
\end{array}\right|\) = (b – c) (c – a) (a – b)
Solution:

(vii) \(\left|\begin{array}{lll}
a & a^2 & a^3 \\
b & b^2 & b^3 \\
c & c^2 & c^3
\end{array}\right|\) = abc (a – b) (b – c) (c – a)
Solution:

(viii) \(\left|\begin{array}{ccc}
\boldsymbol{b}+\boldsymbol{c} & \boldsymbol{a} & \boldsymbol{a} \\
\boldsymbol{b} & \boldsymbol{c}+\boldsymbol{a} & \boldsymbol{b} \\
\boldsymbol{c} & \boldsymbol{c} & \boldsymbol{a}+\boldsymbol{b}
\end{array}\right|\) = 4abc
Solution:

= (b + c – a) {(a + b) (c + a – b) – b (c – a – b)} + a (b – c – a) (c – a – b)
= (b + c – a)(ca + a² – ab + bc + ab – b² – bc + ab + b²) + a(bc – ab – b² – c² + ca + bc – ac + a² + ab)
= (b + c – a) (a² + ab + ca) + a (a² – b² – c² + 2bc)
= a²b + ab² + abc + ca² + abc + c²a – a³ – a²b – ca² + a³ – b²a – c²a + 2abc = 4abc

(ix) \(\left|\begin{array}{ccc}
b^2+c^2 & a b & a c \\
a b & c^2+a^2 & b c \\
c a & c b & a^2+b^2
\end{array}\right|\) = 4a²b²c²
Solution:

(x) \(\left|\begin{array}{ccc}
a & b & c \\
a^2 & b^2 & c^2 \\
b c & c a & a b
\end{array}\right|\) = (b – c) (c – a) (a – b) (bc + ca + ab)
Solution:

= (a – b) (b – c) (c – a) – (- ab + c²) + c (a + b + c)
= (a – b) (b – c) (c – a) (ab – c² + ca + bc + c²)
= (a – b) (b – c) (c – a) (ab + bc + ca)

(xi) \(\left|\begin{array}{ccc}
a-b-c & 2 a & 2 a \\
2 b & b-c-a & 2 b \\
2 c & 2 c & c-a-b
\end{array}\right|\) = (a + b+ c)³
Solution:

(xii) \(\left|\begin{array}{ccc}
(v+w)^2 & u^2 & u^2 \\
v^2 & (w+u)^2 & v^2 \\
w^2 & w^2 & (u+v)^2
\end{array}\right|\) = 2uvw (u + v + w)³
Solution:

Question 10.
Factorize the following
(i) \(\left|\begin{array}{ccc}
x+a & b & c \\
b & x+c & a \\
c & a & x+b
\end{array}\right|\)
Solution:

= (x + a + b + c) [(x + c – b) (x + b – a) – (a – c) (a – x – c)]
= (x + a + b + c) (x² + xb – ax + cx +bc – ca – bx – b² + ab – a² + ax + ac + ac – cx – c²)
= (x + a + b + c) (x² – a² – b² – c² + ab + bc + ca)

(ii) \(\left|\begin{array}{ccc}
a & b & c \\
b+c & c+a & a+b \\
a^2 & b^2 & c^2
\end{array}\right|\)
Solution:

(iii) \(\left|\begin{array}{ccc}
x & 2 & 3 \\
1 & x+1 & 3 \\
1 & 4 & x
\end{array}\right|\)
Solution:

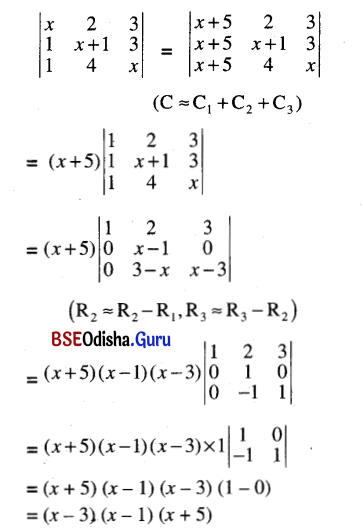
Question 11.
Show that by eliminating α and from the equations.
a_i α + b_i β + c_i = 0, i = 1, 2, 3 we get \(\left|\begin{array}{lll}
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2 \\
a_2 & b_3 & c_3
\end{array}\right|\) = 0
Solution:
We have
a₁ α + b₁ β + c₁ = 0    …..(1)
a₂ α + b₂ β + c₂ = 0    …..(2)
a₃ α + b₃ β + c₃ = 0    …..(3)
Solving (2) and (3) by cross-multiplication method we have

Question 12.
Prove the following:
(i) \(\left|\begin{array}{lll}
1 & b c & a(b+c) \\
1 & c a & b(c+a) \\
1 & a b & c(a+b)
\end{array}\right|\) = 0
Solution:

(ii) \(\left|\begin{array}{ccc}
x+4 & 2 x & 2 x \\
2 x & x+4 & 2 x \\
2 x & 2 x & x+4
\end{array}\right|\) = (5x + 4) (4- x)²
Solution:

(iii) \(\left|\begin{array}{l}
\sin \alpha \cos \alpha \cos (\alpha+\delta) \\
\sin \beta \cos \beta \cos (\beta+\delta) \\
\sin \alpha \cos \gamma \cos (\gamma+\delta)
\end{array}\right|\) = 0
Solution:

(iv) \(\left|\begin{array}{ccc}
1 & x & x^2 \\
x^2 & 1 & x \\
x & x^2 & 1
\end{array}\right|\) = (1 -x³)²
Solution:

Question 13.
Prove that the points (x₁, y₁), (x₂, y₂), (x₃, y₃) are collinear if \(\left|\begin{array}{lll}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1
\end{array}\right|\) = 0
Solution:
From geometry, we know that, if the points A, B, C, are collinear, then the area of the triangle ABC with vertices (x₁, y₁), (x₂, y₂) and (x₃, y₃) is zero.
\(\left|\begin{array}{lll}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1
\end{array}\right|\) = 0

Question 14.
If A + B + C = π, prove that \(\left|\begin{array}{lll}
\sin ^2 A & \cot A & 1 \\
\sin ^2 B & \cot B & 1 \\
\sin ^2 C & \cot C & 1
\end{array}\right|\) = 0
Solution:

Question 15.
Eliminate x, y, z from a = \(\frac{x}{y-z}\), b = \(\frac{y}{z-x}\), c = \(\frac{z}{x-y}\)
Solution:
We have
a = \(\frac{x}{y-z}\), b = \(\frac{y}{z-x}\), c = \(\frac{z}{x-y}\)
ay – az – x = 0, bz – bx – y = 0, cx – cy – z = 0
x – ay + az = 0
bx + y – bz = 0
cx – cy – z = 0
Now eliminating x, y, z from the above equations we have,

or, – 1 – bc + a(-b + bc) + a(-bc – c) = 0
or, – 1 – bc – ab + abc – abc – ac = 0
or, ab + bc + ca + 1 = 0

Question 16.
Given the equations
x = cy + bz, y = az + ex and z = bx + ay where x, y and z are not all zero, prove that a² + b² + c² + 2abc = 1 by determinant method.
Solution:
x = cy + bz, y = az + cx and z = bx + ay

or, 1 – a² + c(-c – ab) – b(ca + b) = 0
or, 1 – a² – c² – abc – abc – b² = 0
or, a² + b² + c² + 2abc = 1

Question 17.
If ax + hy + g = 0, hx + by +f = 0 and gx + fy + c = λ, find the value of λ, in the form of a determinant.
Solution: