Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 6 Probability Ex 6(b) Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 6 Probability Exercise 6(b)
Question 1.
A bag contains 5 white and 3 black marbles and a second bag contains 3 white and 4 black marbles. A bag is selected at random and a marble is drawn from it. Find the probability that it is white. Assume that either bag can be chosen with the same probability.
Solution:
A bag contains 5 white and 3 black marbles and a second bag contains 3 white and 4 black marbles. A bag is selected at random and a marble is drawn from it.
Let W1 be the event that 1st bag is choosen and a white marble is drawn and let W2 be the event that 2nd bag is choosen and a white marble is drawn and these two events are mutually exclusive.

Question 2.
A bag contains 5 white and 3 black balls; a second bag contains 4 white and 5 black balls; a third bag contains 3 white and 6 black balls. A bag is selected at random and a ball is drawn. Find the probability that the ball is black.
(i) Do the problem assuming that the probability of choosing each bag is same.
(ii) Do the problem assuming that the probability of choosing the first bag is twice as much as choosing the second bag, which is twice as much as choosing the third bag.
Solution:
A bag contains 5 white and 3 black balls, a 2nd bag contains 4 white and 5 black balls, a 3rd bag contains 3 white and 6 black balls. A bag is selected at random and a ball is drawn.
(i) Let B1, B2, B3 be the events that 1st bag is choosen and a black ball is draw. 2nd bag is choosen and a black ball is drawn, 3rd bag is drawn and a black ball is drawn. These events are mutually exclusive.
Probability of drawing a black ball
= P(B1) + P(B2) + P(B3)
= \(\frac{1}{3}\) × \(\frac{3}{8}\) + \(\frac{1}{3}\) × \(\frac{5}{9}\) + \(\frac{1}{3}\) × \(\frac{6}{9}\) = \(\frac{115}{216}\)
(ii) Let the probability of choosing 1st bag be 4x. The probability of choosing the 2nd bag is 2x and that of 3rd bag is x.
It is obvious that probability of choosing 3 bags = 1
4x + 2x + x = 1 or, 7x = 1.
x = \(\frac{1}{7}\)
Probability of drawing a black ball
= \(\frac{4}{7}\) × \(\frac{3}{8}\) + \(\frac{2}{7}\) × \(\frac{5}{9}\) + \(\frac{1}{7}\) × \(\frac{6}{9}\)
= \(\frac{108+80+48}{8 \times 9 \times 7}\) = \(\frac{236}{8 \times 9 \times 7}\) = \(\frac{59}{126}\)
![]()
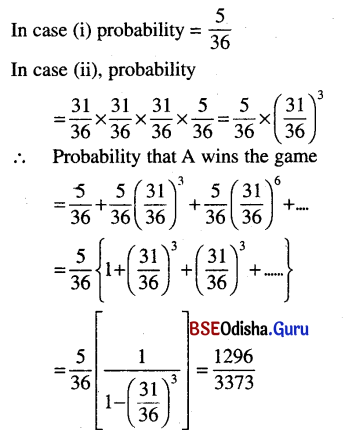
Question 3.
A and B play a game by alternately throwing a pair of dice. One who throws 8 wins the game. If A starts the game, find their chances of winning.
Solution:
A and B play a game by alternately throwing a pair of dice. One who throws 8 wins the game. A starts the game.
We can obtain 8 as follows:
{(6, 2), (5, 3), (4, 4) (3, 5), (6, 2)}.
∴ |S| = 62 = 36
∴ P(B) = \(\frac{5}{36}\)
⇒ P(not 8) = 1 – \(\frac{5}{36}\) = \(\frac{31}{36}\)
Since A starts the game, A can win the following situations.
(i) A throws 8
(ii) A does not throws, B does not throw 8, A throws 8,
(iii) A does not throw 8, B does not throw 8, A does not throw 8, B does not throw 8, A throws 8, etc.

Question 4.
A, B, C play a game by throwing a pair of dice in that order. One who gets 8 wins the game. If A starts the game, find their chances of winning.
Solution:
A, B, C play a game by throwing a pair of dice in that order. One who gets 8 wins the game and A starts the game.
P(B) = \(\frac{5}{36}\), P(not 8) = \(\frac{31}{36}\)
If A starts the game, then
(i) A throws 8.
(ii) A does not throw 8, B does not throw 8, C does not throw 8, A throws 8.
(iii) A does not throw 8, B does not throw 8, C does not throw 8, A does not throw 8, B does not throw 8, C does not throw 8, A throws 8, etc.
Similarly, If B wins the game, then
(i) A does not throw 8, B throw 8.
(ii) A does not throw 8, B does not throw 8, C does not throw 8, A does not throw 8, B throws 8.
(iii) A does not throw 8, B does not throw 8, C does not throw 8, A does not throw 8, B does not throw 8, C does not throw 8, A does not throw 8, B throws 8, etc.

Question 5.
There are 6 white and 4 black balls in a bag. If four are drawn successively (and not replaced), find the probability that they are alternately of different colour.
Solution:
There are 6 white and 4 black balls in a bag. Four balls are drawn without replacement. Let W and B denotes the white and black ball. There are two mutually exclusive cases WBWB and BWBW.

Question 6.
Five boys and four girls randomly stand in a line. Find the probability that no two girls come together.
Solution:
Five boys and 4 girls randomly stand in a line such that no two girls come together.
|S| = 9!

The 4 girls can stand in 6 positions in 6P4 ways. Further 5 boys can stand in 5! ways.
Probability that they will stand in a line such that no two girls come together.
= \(\frac{5 ! \times{ }^6 P_4}{9 !}\) = \(\frac{5}{42}\)
Question 7.
If you throw a pair of dice n times, find the probability of getting at least one doublet. [When you get identical members you call it a doublet. You can get a double in six ways: (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) and (6, 6); thus the probability of getting a doublet is \(\frac{6}{36}\) = \(\frac{1}{6}\), so that the probability of not getting a doublet in one throw is \(\frac{5}{6}\)].
Solution:
A pair of dice is thrown n times. We get
the doublet as (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6).
Probability of getting a doublet in one throw
= \(\frac{6}{36}\) = \(\frac{1}{6}\)
Probability of not getting a doublet
= 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
If a pair of dice is thrown n-times, the probability of not getting a doublet
= \(\left(\frac{5}{6}\right)^n\)
Probability of getting atleast one doublet
= 1 – \(\left(\frac{5}{6}\right)^n\)
![]()
Question 8.
Suppose that the probability that your alarm goes off in the morning is 0.9. If the alarm goes off, the probability is 0.8 that you attend your 8 a.m. class. If the alarm does not go off, the probability that you make your 8 a.m. class is 0.5. Find the probability that you make your 8 a.m. class.
Solution:
Let A be the event that my alarm goes off and let B be the event that I make my 8 a. m. class.
Since S = a ∪ A’, B = (B ∩ A) ∪ (B ∩ A’)
Where B ∩ A and B ∩ A’ are mutually
exclusive events.
P(B) = P (B ∩ A) + P (B ∩ A’)
= P(A). P(\(\frac{B}{A}\)) + P(A’). P(\(\frac{\mathrm{B}}{\mathrm{A}^{\prime}}\))
= 0.9 × 0.8 + 0.1 × 0.5 = 0.77
Question 9.
If a fair coin is tossed 6 times, find the probability that you get just one head.
Solution:
A fair coin is tossed 6 times.
∴ |S| = 26
The six mutually exclusive events are
HTTTTT, THTTTT, TTHTTT, TTTHTT, TTTTHT, TTTTTH.
Probability of getting just one head = \(\frac{6}{2^6}\)
Question 10.
Can you generalize this situation? If a fair coin is tossed six times, find the probability of getting exactly 2 heads.
Solution:
A fair coin is tossed 6 times. Let A be the event of getting exactly 2 heads.
∴ |A| = 6C2 = 15
∴ P(A) = \(\frac{15}{2^6}\)
Yes we can generalize the situation, i.e., if a fair coin is tossed n-times, then probability of getting exactly 2 heads
= \(\frac{{ }^n \mathrm{C}_2}{2^n}\) = \(\frac{{ }^6 C_2}{2^6}\)
