CHSE Odisha Class 11 Math Solutions Chapter 8 Permutations and Combinations Ex 8(b)

Odisha State Board Elements of Mathematics Class 11 Solutions CHSE Odisha Chapter 8 Permutations and Combinations Ex 8(b) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 8 Permutations and Combinations Exercise 8(b)

Question 1.
Find the number of ways in which 5 different books can be arranged on a shelf.
Solution:
The number of ways in which 5 different books can be arranged on a shelf is 5! = 5. 4. 3. 2. 1 = 120

Question 2.
Compute ⁿP_r for
(i) n = 8, r = 4
Solution:
∴ ⁿP_r = \(\frac{n !}{(n-r) !}=\frac{8 !}{(8-4) !}\)
\(=\frac{8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 . !}{4 !}\) = 8.7.6.5 = 1680

(ii) n = 10, r = 3
Solution:
n = 10, r = 3
∴ ⁿP_r = \(\frac{n !}{(n-r) !}=\frac{10 !}{7 !}\)

(iii) n = 11, r = 0
Solution:
n = 11, r = 0
∴ ⁿP_r = ¹¹P₀ = 1

Question 3.
Compute the following :
(i) \(\frac{10 !}{5 !}\)
Solution:
\(\frac{10 !}{5 !}\) = 10. 9. 8. 7. 6 = 30240

(ii) 5! + 6!
Solution:
5 ! + 6! = 5 ! + 6.5 !
= 5 ! (1 + 6) = 120. 7 = 840

(iii) 3! × 4!
Solution:
3 ! × 4 ! = 6 × 24 = 144

(iv) \(\frac{1}{8 !}+\frac{1}{9 !}+\frac{1}{10 !}\)
Solution:

(v) 2!^3! = 2⁶ = 64
(vi) 2³! = 8! =40320

Question 4.
Show that 2.6.10 ……. to n factors = \(\frac{(2 n) !}{n !}\)
Solution:
2.6.10 ……. to n factors = \(\frac{(2 n) !}{n !}\)

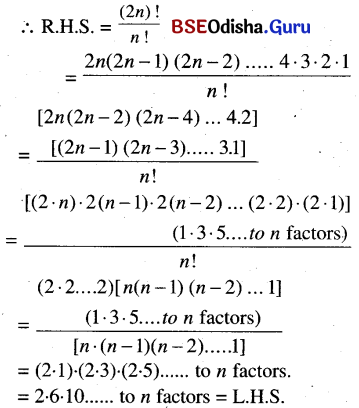
Question 5.
Find r if P(20, r) = 13. P (20, r – 1).
Solution:

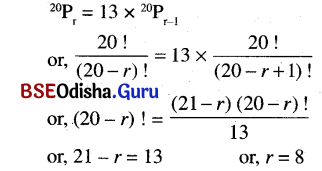
Question 6.
Find n if P(n, 4) = 12. P(n, 2).
Solution:
ⁿP₄ = 12 × ⁿP₂
or, \(\frac{n !}{(n-4) !}=12 \times \frac{n !}{(n-2) !}\)
or, (n – 2)! = 12 (n – 4)!
or, (n – 2) (n – 3) (n – 4)! = 12 (n – 4)!
or, (n – 2) (n – 3) = 12
or, n² – 5n – 6 = 60
or, (n – 6) (n + 1) = 0
or, n = 6 – 1
Hence n = 6 as n is a natural number.

Question 7.
If P (n – 1, 3) : P (n + 1, 3) = 5: 12, Find n.
Solution:

Question 8.
Find m and n  if P(m + n, 2) = 56, P(m – n, 2) = 12
Solution:
^m+nP₂ = 56, ^m-nP₂ = 12
or, \(\frac{(m+n) !}{(m+n-2) !}=56, \frac{(m-n) !}{(m-n-2) !}=12\)
or, (m + n) (m + n – 1) = 8 × 7
(m – n) (m – n – 1) = 4 × 3
∴ (m + n) = 8, m – n = 4
∴ m = 6, n = 2

Question 9.
Show that
(i) P(n, n) = P(n, n – 1) for all positive integers.
Solution:

(ii) P(m, 1) + P(n, 1) = P(m + n, 1) for all positive integers m, n.
Solution:
^mp₁ + ⁿp₁ = ^m+np₁ ∀ m, n ∈ Z
∴ L.H.S.
= ^mp₁ + ⁿp₁ = m + n = ^m+np₁ = R.H.S.
(∴ ⁿp₁ = n)

Question 10.
How many two-digit even numbers of distinct digits can be formed with the digits 1, 2, 3, 4, and 5?
Solution:
Two-digit even numbers of distinct digits are to be formed with the digits 1, 2, 3, 4, and 5. Here the even numbers must end with 2 or 4. When 2 is placed in the unit place, the tenth place can be filled up by the other 4 digits in 4 different ways. Similarly, when 4 is placed in the unit place, the tenth place can be filled up in 4 different ways.
∴ The total number of two-digit even numbers = 4 + 4 = 8.

Question 11.
How many 5-digit odd numbers with distinct digits can be formed with the digits 0, 1, 2, 3, and 4?
Solution:
5-digit odd numbers are to be formed with distinct digits from the digits 0, 1, 2, 3, and 4. The numbers are to end with 1 or 3 and must not begin with 0.
The 5th place can be filled up by any one of 1 or 3 by 2 ways.

1st

2nd

3rd

4th

5th

Places
The 1st place can be filled by the rest 3 digits except 0 and the digit in 5th place.
The 2nd, 3rd, and 4th places can be filled up by the rest 3 digits in 3! ways.
So total no. of ways = 2 × 3 × 3 ! = 2 × 3 × 2 = 36 ways.

Question 12.
How many numbers, each less than 400 can be formed with the digits 1, 2, 3, 4, 5, and 6 if repetition of digits is allowed?
Solution:
Different numbers each less than 400 are to be formed with the digits 1, 2, 3, 4, 5, and 6 with repetition. Here the numbers are 1-digit, 2-digit, and 3-digit.
∴ The number of 1-digit numbers = 6.
The number of 2-digit numbers = 6² = 36.
The 3-digit number each less than 400 must begin with 1, 2, or 3. So the hundred’s place can be filled by 3 digits and ten’s and unit place can be filled by 6 digits each. So the number of 3 digit numbers = 3 × 6 × 6 = 108.
∴ The total number of numbers = 6 + 36 + 108 = 150.

Question 13.
How many four-digit even numbers with distinct digits can be formed out of digits 0, 1, 2, 3, 4, and 5, 6?
Solution:
Four-digit even numbers mean, they must end with 0, 4, 2, 6. When 0 is placed in last, the 1st place is filled by 1, 2, 3, 4, 5, 6, and the remaining 2 places can be filled by ⁵P₂ ways.
The number of numbers ending with 0 = ⁵P₂ × 6 = 120
Similarly, the number of numbers ending. with 2, 4 and 6 = ⁵P₂  × 5 × 3 = 300
∴ The total number of numbers = 420.

Question 14.
How many integers between 100 and 1000 (both inclusive) consist of distinct odd digits?
Solution:
Integers are to be formed with distinct odd digits between 100 and 1000.
The numbers between 100 and 1000 are 3-digited.
The odd digits are 1, 3, 5, 1, and 9.
The number of distinct 3-digit odd numbers = ⁵P₃ = 5.4.3 = 60.

Question 15.
An unbiased die of six faces, marked with the integers 1, 2, 3, 4, 5, 6, one on each face, thrown thrice in succession. What is the total number of outcomes?
Solution:
An unbiased die of six faces, marked with the integers 1, 2, 3, 4, 5, 6, one on each face is thrown thrice in succession.
∴ The total number of outcomes = 6³ = 216.

Question 16.
What is the total number of integers with distinct digits that exceed 5500 and do not contain 0, 7, and 9?
Solution:
The integer exceeding 55000 must be 4-digited, 5-digited, 6-digited, and 7-digited, as there are seven digits i.e. 1, 2, 3, 4, 5, 6, and 8 to be used for the purpose.
In the 4-digit integers, when 1st place is filled by 5 and 2nd place by .6, the rest two places can be filled by the remaining 5 digits in ⁵P₂ ways. Similarly, when 5 is in 1st place and 8 in 2nd place, the remaining 5 digits be used in ⁵P₂ ways. So the number of 4-digit integers beginning with 5 is 2 × 5P = 40.
When 6 is placed in 1st place, the remaining 3 placed be filled by the remaining 6 digits in 6P3 ways. Similarly, when 8 is placed in 1 st place, the remaining 3 places be filled by the remaining 6 digits in ⁶P₃ ways.
So the number of 4-digit integers starting with 6 and 8 is 2 × ⁶P₃  = 240.
∴ The total number of 4-digit numbers is 40 + 240 = 280.
The number of 5-digit integers is ⁷P₅ = 2520.
The number of 6-digit numbers is ⁷P₆ = 5040 and the number of 7 -digit numbers is ⁷P₆  = 5040.
∴ The total number of integers exceeding 5500 and not containing 0, 7, and 9 is 280 + 2520 + 5040 + 5040 = 12880.

Question 17.
Find the total number of ways in which the letters of the word PRESENTATION can be arranged.
Solution:
The number of letters in the word “PRESENTATION” is 12, out of which there are 2N’s, 2E’s, and 2T’s. So the total number of arrangements.
\(=\frac{12 !}{2 ! 2 ! 2 !}=\frac{1}{8}(12) !\)

Question 18.
Find the numbers of all 4-lettered words (not necessarily having meaning) that can be formed using the letters of the word BOOKLET.
Solution:
We have to form 4-lettered words using the letters of the word BOOKLET. The word contains 7 letters out of which there are 20’s. So there are 6 letters.
∴ The number of 4-lettered words = ⁷P₄ – ⁶P₄ = 7.6.5.4 – 6.5.4.3 = 480

Question 19.
In how many ways can 2 boys and3 girls sit in a row so that no two girls sit side by side?
Solution:
Two boys and 3 girls sit in a row so that no two girls sit side by side.
So the only possibility is boys should be situated in between the two girls. In between 3 girls there are 2 gaps where 2 boys will be site.
The girls will be arranged in 3! and boys in 2! ways.
∴ The total number of ways = 2! × 3!=2 × 6= 12

Question 20.
Five red marbles, four white marbles, and three blue marbles the same shape and size are placed in a row. Find the total number of possible arrangements.
Solution:
5 red, 4 white, and 3 blue marbles of the same size and shape are placed in a row.
∴ The total number of marbles is 12 out of which 5 are of one kind, 4 are of 2nd kind and 3 are of 3rd kind
∴ The total number of possible arrangements
\(=\frac{12 !}{5 ! 4 ! 3 !}=\frac{12 \cdot 11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6}{4 \cdot 3 \cdot 2 \cdot 3 \cdot 2}\)
= 12.11.10.3.7 = 27720.

Question 21.
Solve example 2.
Solution:
We have |A| = n, |B| = m
∴ The number of one-one functions from A to B is ^mP_n = \(\frac{m !}{(m-n) !}\) when m> n.
If m = n, the number of one-one functions is \(\frac{m !}{(m-m) !}=\frac{m !}{0 !}\) = m! = n!
If m < n, then there is no possibility of one-one functions.

Question 22.
In how many ways can three men and three women sit at a round table so that no two men can occupy adjacent positions?
Solution:
Since no 2 men are to sit together, there are 4 places available for them corresponding to any one way of sitting of 2 men i.e., two places between the women and 2 places at two ends.

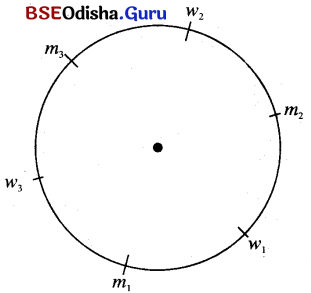
Let m₁ be fixed m₂ can sit in 2 places, w₁ can sit in 3 places, m₃ can sit in 1 place, w₂ can sit in 2 places w₃ can sit in 1 place.
∴ The total number of ways = 2 × 3 × 1 × 2 × 1 = 12