Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 7 Continuity and Differentiability Ex 7(d) Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Exercise 7(d)
Question 1.
Prove the formulae (4) to (7).
Solution:
(4) \(\frac{d}{d x}\)(cos-1 x) = \(\frac{-1}{\sqrt{1-x^2}}\)
Let y = cos-1 x
⇒ x = cos y
⇒ \(\frac{d}{d x}\) = \(\frac{1}{\left(\frac{d x}{d y}\right)}\) = \(\frac{1}{-\sin y}\)
But sin y ≥ 0 when
y ∈ [0, π] ( ∵ [0, π] is the principal value branch for cos-1 x)
∴ \(\frac{d y}{d x}\) = \(\frac{-1}{\sqrt{1-\cos ^2 y}}\) = \(\frac{-1}{\sqrt{1-x^2}}\)
(5) Let y = tan-1 x
⇒ x = tan y
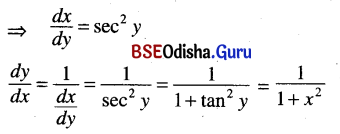
![]()
(6) Let y = cot-1 x
⇒ x = cot y
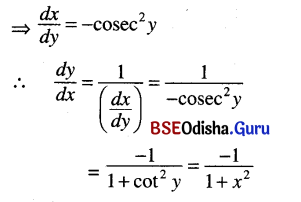
(7) Let y = cosec-1 x
⇒ x = cosec y

Question 2.
Find derivatives of the following functions.
sin-1 2x
Solution:
y = sin-1 2x

Question 3.
cot-1 √x
Solution:
cot-1 √x
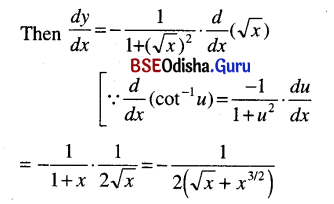
Question 4.
sec-1 (2x + 1)
Solution:
y = sec-1 (2x + 1)

Question 5.
cos-1 \(\sqrt{\frac{1+x}{2}}\)
Solution:

Question 6.
cos-1 \(\left(\frac{x-\frac{1}{x}}{x+\frac{1}{x}}\right)\)
Solution:

![]()
Question 7.
tan-1 (cos √x)
Solution:
y = tan-1 (cos √x)
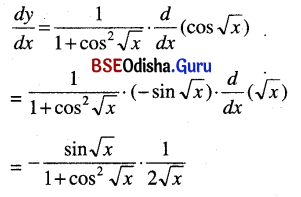
Question 8.
x2 cosec-1 \(\left(\frac{1}{\ln x}\right)\)
Solution:
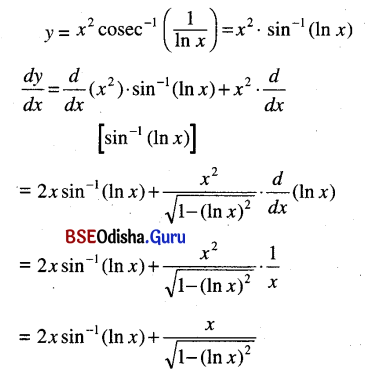
Question 9.
cot-1 \( \frac{\sqrt{1-x^2}}{x} \)
Solution:
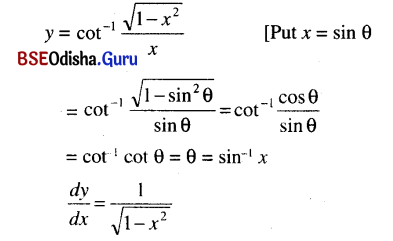
Question 10.
(x sin-1 x)15
Solution:
y = (x sin-1 x)15
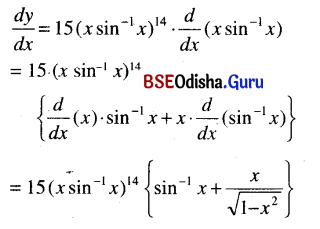
Question 11.
sin-1 \( \sqrt{\frac{1-x}{1+x}} \)
Solution:

