CHSE Odisha Class 11 Math Solutions Chapter 10 Sequences and Series Ex 10(a)

Odisha State Board Elements of Mathematics Class 11 CHSE Odisha Solutions Chapter 10 Sequences and Series Ex 10(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 10 Sequences and Series Exercise 10(a)

Question 1.
Which of the following in a sequence?
(i) f(x) = [x], x ∈ R
(ii) f(x) = |x|, x ∈ R
(iii) f(x) = \(\sqrt[n]{\pi}\) ,n∈ N
Solution:
(iii) f(x) = \(\sqrt[n]{\pi}\) ,n∈ N is a sequence f(n) : N → X, X ⊂ R.

Question 2.
Determine if (t_n) is an arithmetic sequence if :
(i) t_n = an² + bn
Solution:
t_n = an² + bn
⇒ t_n+1 = a(n + 1)² + b(n – 1)
⇒ t_n+1 – t_n = a{(n + 1)² – n²} + b{n + 1 – n}
= a(2n + 1) + b
Which is not independent of n.
∴ (t_n) is not an A.P.

(ii) t_n = an + b
Solution:
t_n = an + b
⇒ t_n+1 = a(n + 1) + b
Now t_n+1 – t_n
= {a(n + 1) + b} – {an + b}
= a (constant)
∴ (t_n) is an arithmetic sequence.

(iii) t_n = an² + b
Solution:
t_n = an² + b
⇒ t_n+1 = a(n + 1)² + b
∴ t_n+1 – t_n = a[(n + 1)² – n²] + b – b
= a(2n + 1)
(does not independent of n)
∴ (t_n) is not an arithmetic sequence.

Question 3.
If a geometric series converges which of the following is true about its common ratio r?
(i) r > 1
(ii) -1 < r < 1
(iii) r > 0
Solution:
(ii) -1 < r < 1

Question 4.
If an arithmetic series ∑tn converges, which of the following is true about t_n?
(i) t_n < 1
(ii) |t_n| < 1
(iii) t_n = 0
(iv) t_n → 0
Solution:
(iii) t_n = 0

Question 5.
Which of the following is an arithmetic-geometric series?
(i) 1 + 3x + 7x² + 15x³+ ….
(ii) x + \(\frac{1}{2}\)x + \(\frac{1}{3}\)x² + ….
(iii) x + (1 + 2)x² + (1 + 2 + 3)x³ +…
(iv) x + 3x² + 5x³ + 7x⁴ + …
Solution:
(iv) x + 3x² + 5x³ + 7x⁴ + … is an arithmetic geometric series with a = 1, d = 2, r = x.

Question 6.
For an arithmetic sequence (t_n) t_p = q, t_q = p, (p ≠ q), find t_n.
Solution:
t_p = q ⇒ a + (p – 1)d = q    ……(1)
t_q = p ⇒ a + (q – 1)d = p    ……(2)
From (1) and (2) we have (p – q)d = q – p
⇒ d = (-1)
Putting d = (-1) in (1)
we have a = p + q – 1
∴ t_n = a + (n – 1)d
= (P + q – 1) + (n – 1) (-1)
= p + q – n

Question 7.
For an arithmetic series, ∑a_n S_p = q and S_q = p (p ≠ q) find S_p+q
Solution:
S_p = q and S_q = p

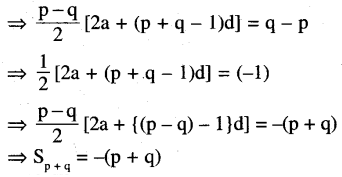
Question 8.
The sum of a geometric series is 3. The series of squares of its terms have a sum of 18. Find the series.
Solution:

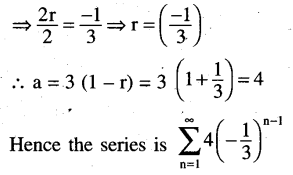
Question 9.
The sum of a geometric series is 14, and the series of cubes of its terms have a sum of 392 find the series.
Solution:


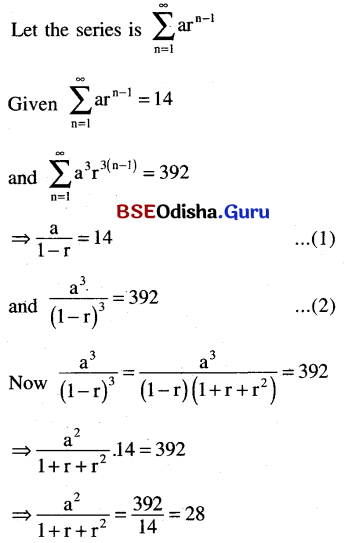
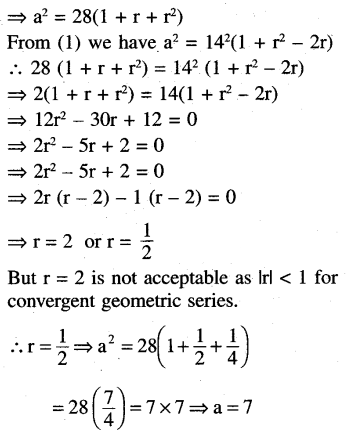
∴ The series is \(\sum_{n=1}^{\infty} \frac{7}{2^{n-1}}\)

Question 10.
Find the sum as directed
(i) 1 + 2a + 3a² + 4a³ + …..(first n terms(a ≠ 1))
Solution:

(ii) 1 + (1 + x)y + (1 + x + x²)y² + …..(to infinity)
Solution:
Let S_∞ = 1 + (1 + x)y + (1x + x²)y² + …
⇒ S_n = 1 + (1 + 1 + x)y + (1 + x + x²)y² + ……+(1 + x + …. x^n-1)y^n-1

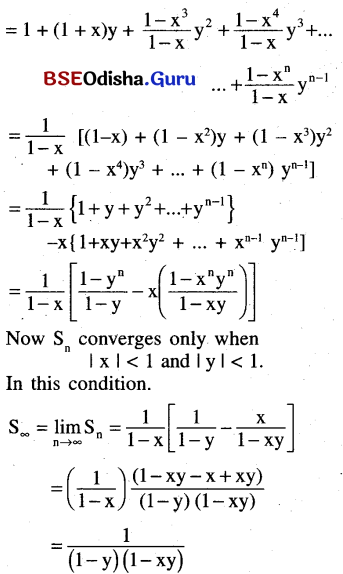
(iii) 1 + \(\frac{3}{5}\) + \(\frac{7}{25}\) + \(\frac{15}{125}\) + \(\frac{31}{625}\) + …..(to infinity)
Solution:

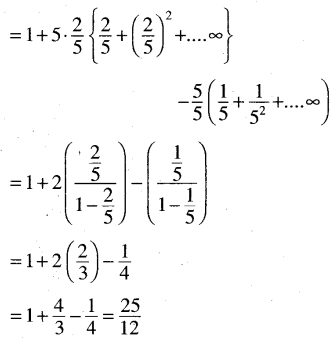
(iv) 1 + 4x + 8x² + 13x³ + 19x⁴ + …..(to infinity). Assuming that the series has a sum for |x| < 1.
Solution:

(v) 3.2 + 5.2² + 7.2³ + …..(first n terms)
Solution:
Sn = 3.2 + 5.22 + 7.3 + ….n terms = 2[3 + 5.2 + 7.22 + ….n terms]

Question 11.
Find the sum of the infinite series.
(i) \(\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\frac{1}{3 \cdot 4}+\ldots\)
Solution:

= 1 – \(\frac{1}{n+1}\)
∴ \(S_{\infty}=\lim _{n \rightarrow \infty} S_n=1\)

(ii) \(\frac{1}{1 \cdot 2 \cdot 3}+\frac{1}{2 \cdot 3 \cdot 4}+\frac{1}{3 \cdot 4 \cdot 5}+\ldots\)
Solution:
\(\frac{1}{1 \cdot 2 \cdot 3}+\frac{1}{2 \cdot 3 \cdot 4}+\frac{1}{3 \cdot 4 \cdot 5}+\ldots\)

(iii) \(\frac{1}{2 \cdot 5 \cdot 8}+\frac{1}{5 \cdot 8 \cdot 11}+\frac{1}{8 \cdot 11 \cdot 14}+\ldots\)
Solution:
Here t_n = \(\frac{1}{(3 n-1)(3 n+2)(3 n+5)}\)
The denominator of t_n is the product of 3 consecutive terms of A.P. Now multiplying and dividing by (3n + 5) – (3n – 1) we have
\(t_n=\frac{(3 n+5)-(3 n-1)}{6(3 n-1)(3 n+2)(3 n+5)}\)

(iv) \(\frac{3}{1^2 \cdot 2^2}+\frac{5}{2^2 \cdot 3^2}+\frac{7}{3^2 \cdot 4^2}+\ldots\) [Hint : take t_n = \(\frac{2 n+1}{n^2(n+1)^2}=\frac{(n+1)^2-n^2}{n^2(n+1)^2}\)]
Solution:

(v) \(\frac{1}{1 \cdot 5}+\frac{1}{3 \cdot 7}+\frac{1}{5 \cdot 9}+\ldots .\)
Solution:

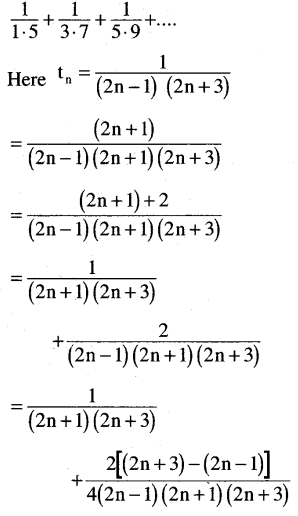
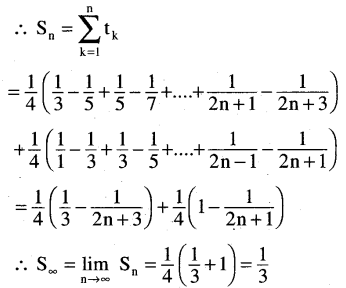
Question 12.
Find S_n for the series.
(i) 1.2 + 2.3 + 3.4 + ….
Solution:

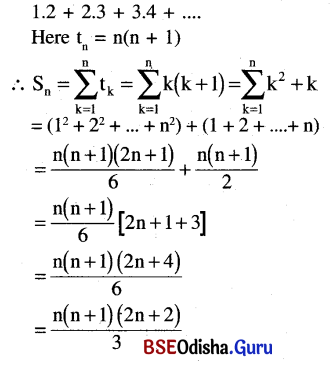
(ii) 1.2.3 + 2.3.4 + 3.4.5 + …
Solution:

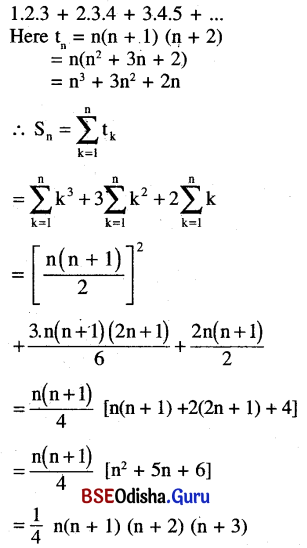
(iii) 2.5.8 + 5.8.11 + 8.11.14 +…
Solution:

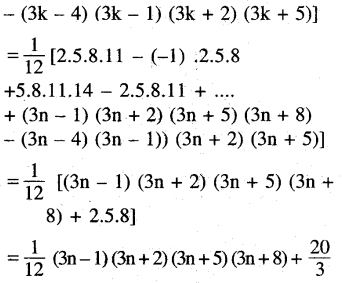
(iv) 1.2.3.4 + 2.3.4.5 + 3.4.5.6 + …
[Hint : t_n = (3n – 1) (3n + 2)(3n + 5)]
Solution:

(v) 1.5 + 2.6 + 3.7 + …
[Hint: t_n = n(n + 4) is not a product of two successive terms of an A.P. for the term following n should be n+1, not n+4. So the method of previous exercises is not applicable. Instead, write t_n = n² + 4n and find S_n = \(\sum_{k=1}^n k^2+4 \sum_{k=1}^n k\) applying formulae]
Solution:

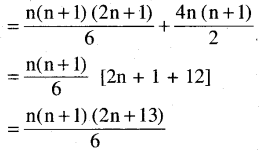
(vi) 2.3 + 3.6 + 4.11 + …
[Hint : Take t_n = (n + 1) (n² + 2)]
Solution:

(vii) 1.3² + 2.5² + 3.7² + ….
Solution:

Question 13.
Find the sum of the first n terms of the series:
(i) 5 + 6 + 8 + 12 + 20 + …
Solution:

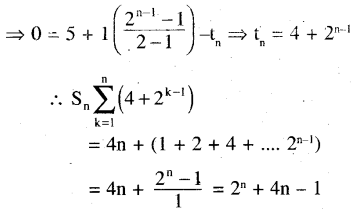
(ii) 4 + 5 + 8 + 13 + 20 + …
Solution:

Question 14.
(i) Find the sum of the product of 1,2,3….20 taken two at a time. [Hint: Required sum = \(\frac{1}{2}\left\{\left(\sum_{k=1}^{20} k\right)^2-\sum_{k=1}^{20} k^2\right\}\)]
Solution:
We know that
(x₁ + x₂ + x₃ + …. + x_n)²
= (x²₁ + xⁿ₂ + … + x²_n) + 2 (Sum of all possible Products taken two at a time)
∴ 2 (Sum of products of 1. 2, 3,…… 20 taken two at a time)
= (1 + 2 + 3 + … 20)² – (1² + 2² + … + 20²)
\(=\left(\frac{20 \times 21}{2}\right)^2-\frac{20(20+1)(40+1)}{6}\)
= (210)² – 70 × 41
= 44100 – 2870 = 41230
∴ The required sum = \(\frac{41230}{2}\) = 20615

(ii) Do the same for 1, 3, 5, 7,….19.
Solution:
Here the required sum

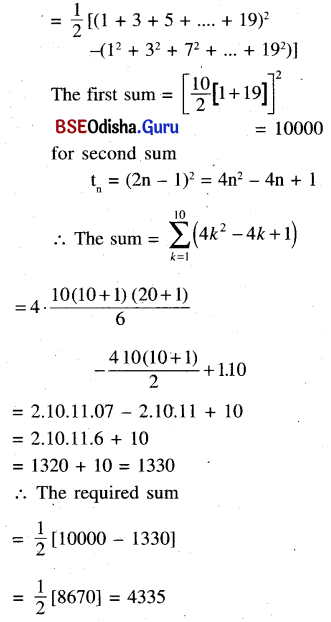
Question 15.
If a = 1 + x + x² + ….. and b = 1 + y + y² + ….|x| <  1 and |y| <  1, then prove that 1 – xy + x²y² + x³y³ + ….. =  \(\frac{a b}{a+b-1}\)
Solution:

Question 16.
If a, b, c are respectively the pth, qth, rth terms of an A.P., then prove that a(q – r) + b(r – p) + c(p – q) = 0
Solution:
Let the first term of an A.P. = A and the common difference = D.
According to the question
t_P = a, t_q = b, t_r = c
⇒ A + (p – q)D = a      …..(1)
A + (q – 1)D = b           …..(2)
A + (r – 1)D = c            …..(3)
L.H.S = a(q – r) + b (r – p) + c (p – q)
= (A + (p – 1)D) (q – r) + (A + (q – 1)D)
(r- p) + (A + (r – 1)D) (p – q)
= A (q – r + r – p + p – q) + D [(p – 1)
(q – r) + (q – 1) (r – p) + (r – 1) (p – q)]
= D (pq – pr + qr – pq + pr – qr) – D (q – r + r – p + p – q) = 0

Question 17.
If \(\frac{1}{a}, \frac{1}{b}, \frac{1}{c}\) are in A.P. and a + b + c ≠ 0, prove that \(\frac{\mathbf{b}+\mathbf{c}}{\mathbf{a}}, \frac{\mathbf{c}+\mathbf{a}}{\mathbf{b}}, \frac{\mathbf{a}+\mathbf{b}}{\mathbf{c}}\) are in A.P.
Solution:

Question 18.
If a², b², c² are in A.P. Prove that \(\frac{1}{b+c}, \frac{1}{c+a}, \frac{1}{a+b}\) are in A.P.
Solution:

Question 19.
If \(\frac{b+c}{a}, \frac{c+a}{b}, \frac{\mathbf{a}+\mathbf{b}}{c}\) are in A.P.,prove that \(\frac{\mathbf{1}}{\mathbf{a}}, \frac{\mathbf{1}}{\mathbf{b}}, \frac{\mathbf{1}}{\mathbf{c}}\) are inA.P.given a + b + c ≠ 0
Solution:

Question 20.
If (b – c)², (c – a)², (a – b)² are in A.P., prove that \(\frac{1}{b-c}, \frac{1}{c-a}, \frac{1}{a-b}\) are in A.P.
Solution:

Question 21.
If a, b, c are respectively the sum of p, q, r terms of an A.P., prove that \(\frac{a}{p}(q-r)+\frac{b}{q}(r-p)+\frac{c}{r}(p-q)\) = 0
Solution:

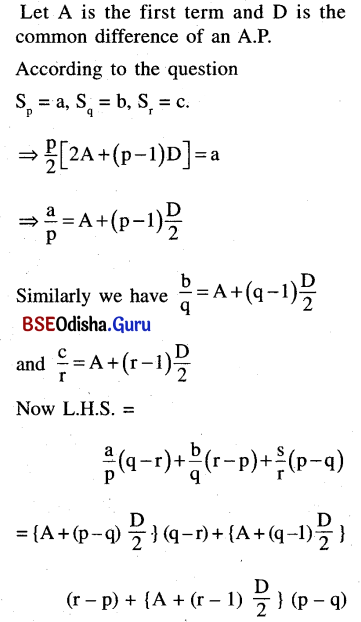
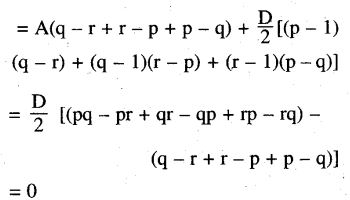
Question 22.
If a, b, c,d are in G.P., prove that (a² + b² + c²)(b² + c² + d²) = (ab + bc + cd)².
Solution:
Let a, b, c, and d are in G.P.
Let the common ratio = r
⇒ b = ar, c = ar², d = ar³
LHS = (a² + b² + c²) (b² + c² + d²)
= (a² + a²r² + a²r⁴) (a²r² + a²r⁴ + a²r⁶)
= a⁴r² (1 + r² + r⁴)²
= (a²r + a²r³ + a²r⁵)²
= (a.ar + ar.ar² + ar².ar³)²
= (ab + bc + cd)² = R.H.S. (proved)