CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Ex 7(g)

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 7 Continuity and Differentiability Ex 7(g) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Exercise 7(g)

Find \(\frac{d y}{d x}\)
Question 1.
xy² + x²y + 1 = 0
Solution:
xy² + x²y + 1 = 0

Question 2.
\(x^{\frac{1}{2}} y^{-\frac{1}{2}}\) + \(x^{\frac{3}{2}} y^{-\frac{3}{2}}\) = 0
Solution:

Question 3.
x² + 3y² = 5
Solution:
x² + 3y² = 5
⇒ \(\frac{d}{d x}\)(x²) + 3 \(\frac{d}{d x}\)(y²) = 0
⇒ 2x + 6y\(\frac{d y}{d x}\) = 0
⇒ \(\frac{d}{d x}\) = –\(\frac{x}{3 y}\)

Question 4.
y² cot x = x² cot y.
Solution:
y² cot x = x² cot y

Question 5.
y = tan xy
Solution:
y = tan xy

Question 6.
x = y In (xy).
Solution:
x = y In (xy).

Question 7.
e^xy + y sin x = 1
Solution:
e^xy + y sin x = 1

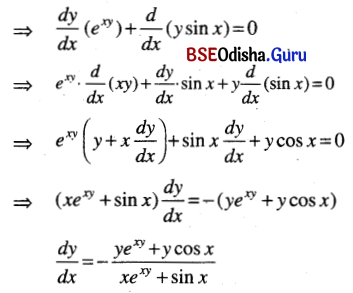
Question 8.
In \(\sqrt{x^2+y^2}\) = tan^-1 \(\frac{y}{x}\)
Solution:

Question 9.
y^x = x^{sin y}
Solution:
y^x = x^{sin y}

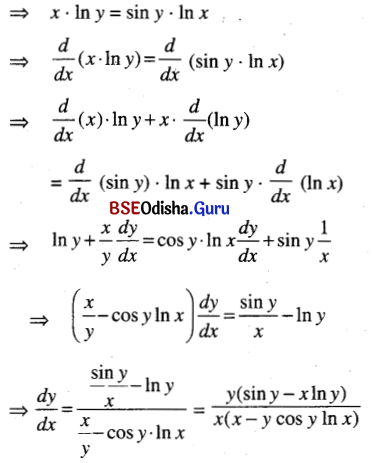
Question 10.
If sin (x + y) = y cos (x + y) then prove that \(\frac{d y}{d x}\) = –\(\frac{1+y^2}{y^2}\).
Solution:

Question 11.
If \(\sqrt{1-x^4}\) + \(\sqrt{1-y^4}\) = k(x² – y²) then show that \(\frac{d y}{d x}\) = \(\frac{x \sqrt{1-y^4}}{y \sqrt{1-x^4}}\).
Solution: