CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Ex 8(a)

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Ex 8(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Exercise 8(a)

Question 1.
Find the velocity and acceleration at the end of 2 seconds of the particle moving according to the following rules.
(i) s = 2t² + 3t + 1
Solution:
s = 2t² + 3t + 1

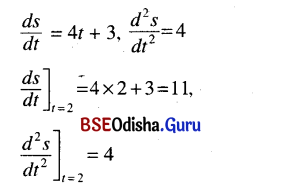
∴ Velocity is 11 units/sec and acceleration is 4 units/sec².

(ii) s = √t +1
Solution:
s = √t +1

(iii) s = \(\frac{3}{2 t+1}\)
Solution:

(iv) s = t³ – 6t² + 15t + 12
Solution:
s = t³ – 6t² + 15t + 12

∴ Velocity is 3 units/sec and acceleration is 0.

Question 2.
The sides of an equilateral triangle are increasing at the rate of √3 cm/sec. Find the rate at which the area of the triangle is increasing when the side is 4 cm long.
Solution:
Let x be the lenght of each side of an equilateral triangle.

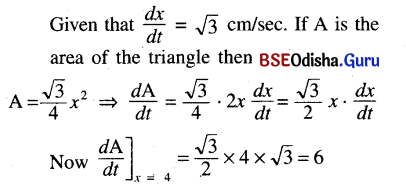
∴ Area of the triangle is increasing at the rate of 6 cm²/sec

Question 3.
Find the rate at which the volume of a spherical balloon will increase when its radius is 2 metres if the rate of increase of its radius is 0.3 m/min.
Solution:
Let r be the radius of a spherical balloon.

∴ The volume increase at the rate of 4.8π m³/min.

Question 4.
The surface area of a cube is decreasing at the rate of 15 sq. cm/sec. Find the rate at which its edge is decreasing when the length of the edge is 5 cm.
Solution:
Let s be the surface area of a cube.
Let x be the length of each side of the cube.

∴ The edge is decreasing at the rate of 0.25 cm/sec