Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Ex 8(e) Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Exercise 8(e)
Question 1.
Determine the differentials in each of the following cases.
(i) y = x3 – 1
Solution:
y= x3 – 1
Then dy = 3x2 dx
(ii) y = sin2 x
Solution:
y = sin2 x
Then dy = 2 sin x cos x dx = sin 2x dx
(iii) y = \(\frac{1+\sqrt{x}}{1-\sqrt{x}}\)
Solution:

(iv) z = cos 2t – 2 cot t
Solution:
z = cos 2t – 2 cot t
dz = (-2 sin 2t + 2 cosec2 t) dt
(v) r = \(\frac{4}{1+\sin \theta}\)
Solution:
r = \(\frac{4}{1+\sin \theta}\)
dz = \(\frac{-4 \cos \theta}{(1+\sin \theta)^2}\) . dθ
= \(-\frac{4 \cos \theta}{(1+\sin \theta)^2}\) dθ
(vi) x2y = 2
Solution:
⇒ y = \(\frac{2}{x^2}\)
dy = \(\frac{4}{x^3}\)
(vii) xy2 + yx2 = 1
Solution:
⇒ dx . y2 + x . 2y dy + dy . x2 + y . 2x dx = 0
⇒ (2 xy + x2) dy = – (y2 + 2xy) dx
⇒ dy = –\(\frac{y^2+2 x y}{x^2+2 x y}\)dx
![]()
Question 2.
Find δf and df when
(i) f(x) = 2x2 – 1, x = 1, δx = 0.02
Solution:
f(x) = 2x2 – 1, x = 1, δx = 0.02
Then δf = f(x + δx) – f(x)
= f(1.02) – f(1)
= 2 (1.02)2 – 1 – (2 – 1)
= 2.0808 – 2 = 0.0808
Again df = 4x dx
= 4 × 1 × 0.02 = 0.08
(ii) f(x) = √x, x = 16, δx = 0.3
Solution:
f(x) = √x, x = 16, δx = 0.3
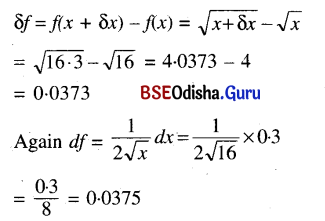
(iii) f(x) = (x + 1)3, x = 8, δx = 0.04
Solution:
f(x) = (x + 1)3, x = 8, δx = 0.04
δf = f(x + δx) – f(x)
= (9.04)3 – (8 +1)3
= (9.04)3 – 93 = 9.7632
Again df = 3(x + 1)2 dx = 3 × 92 × 0.04
= 243 × 0.04 = 9.72
(iv) f(x) = In (1 + x), x = 1, δx = 0.04
Solution:
f(x) = In (1 + x), x = 1, δx = 0.04
δf = f(x + 8x) – f(x)
= In (1 + x + 5x) – ln (1 + x)
= In (2.04) – In (2) = 0.0198
Again df = \(\frac{1}{1+x}\)dx = \(\frac{1}{2}\) × 0.04 = 0.02
Question 3.
Find approximate values of the following:
(i) \(\sqrt[3]{28}\)
Solution:
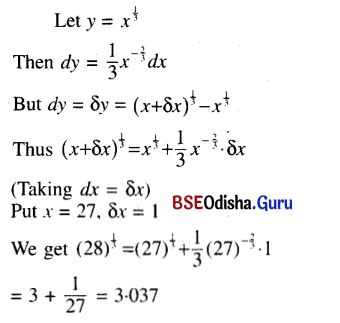
(ii) \(\sqrt[6]{63}\)
Solution:

(iii) \(\sqrt{48 \cdot 96}\)
Solution:
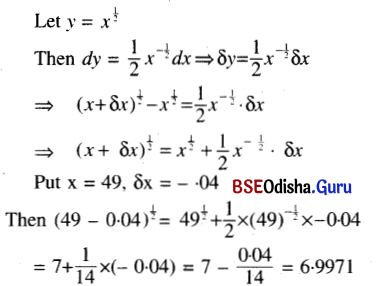
(iv) (1.99)7
Solution:
Let y = x7
Then dy = 7x6 dx
⇒ δy = 7x6 δx
⇒ (x + δx)7 – x7 = 7x6 δx
(x + δx)7 = x7 + 7x6 δx
Put x = 2 and δx = -0.01
Then (1.99)7 = 27 – 7 × 26 × 0.01
= 128 – 7 × 64 × 0.01
= 128 – 4.48 = 123.52
(v) 23.02
Solution:
Let y = 2x
Then dy = 2x In 2 dx
⇒ δy = 2x In 2 . δx
⇒ 2x + δx – 2x = 2x In 2 . δx
⇒ 2x + δx = 2x + 2x In 2 δx
Then 23.02 = 23 + 23 In 2 × 0.02
= 8 + 8 In 2 × 0.02 = 8.1109
(vi) sin 59°
Solution:
Let y = sin x
Then dy = cos x dx ⇒ δy = cos x . δx
⇒ sin (x + δx) – sin x = cos x × δx
⇒ sin (x + δx) = sin x + cos x × δx
Put x = 60°, δx = -1°
Then sin 59° = sin 60° + cos 60° x – \( \frac{\pi}{180} \)
\(\frac{\sqrt{3}}{2}\) – \(\frac{1}{2}\) × \(\frac{\pi}{180}\)
[ ∵ 1° = \(\frac{\pi}{180}\) radian = 0.85729
![]()
Question 4.
find the percentage of error in calculation of the surface area of a spherical balloon of diameter 14.02 m. if the true diameter is 14m.
Solution:
Let S be the surface area of a spherical balloon of radius V.
Then S = 4πr2
Then dS = 8πr dr

Question 5.
Find approximately the difference between the volumes of two cubes of sides 3 cm and 3.04 cm.
Solution:
Let V be the volume of a cube of side x cm.
Then V = x3 ⇒ dV = 3x2 dx
Here x = 3 cm and dx = (3.04 – 3) cm = 0.04 cm
Thus dV = 3 × 9 × 0.04 = 1.08 cm3
∴ Difference of two volumes is 1.08 cm3.
Question 6.
The height of a regular cone is 3 times the radius of its base. The radius of the base was wrongly measured to be 5 cm. whereas its true radius is 4.88 cm. Find the relative error in measuring the curved surface area of the cone.
Ans.
Consider a regular cone of height h and radius of its base x.
Then h = 3x.
If S is the area of the curved surface of the cone
then S = πxl
Where l is the slant height of the cone.

= 0.049
Must Refer:
