CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Ex 9(j)

Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 9 Integration Ex 9(j) Textbook Exercise questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Exercise 9(j)

Evaluate the following Integrals.
Question 1.
(i) $\int_{-2}^3$x⁴ dx
Solution:

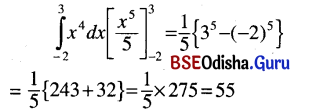
(ii) $\int_0^1 x^{\frac{1}{3}}$ dx
Solution:
$\int_0^1 x^{\frac{1}{3}}$ dx = $\left[\frac{x^{\frac{4}{3}}}{\frac{4}{3}}\right]_0^1$ = \frac{3}{4}

(iii) $\int_1^4 \frac{d x}{\sqrt{x}}$ dx
Solution:

(iv) $\int_1^3 \frac{d x}{x^3}$ dx
Solution:

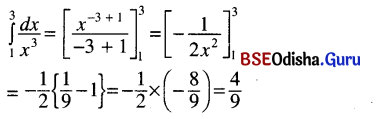
(v) $\int_1^2\left(4 x+\sqrt{x}+\frac{1}{x^{\frac{1}{3}}}+\frac{1}{x^2}\right)$ dx
Solution:

(vi) $\int_{-1}^2$(2x + 1)(x – 2) dx
Solution:

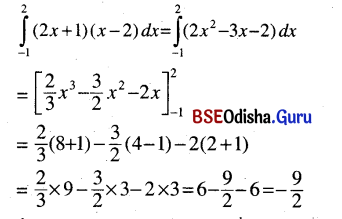
(vii) $\int_0^1$(x + 1)⁴ dx
Solution:

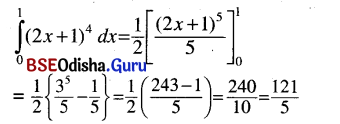
(viii) $\int_0^1 x^7\left(1+x^8\right)^{\frac{1}{3}}$ dx
Solution:

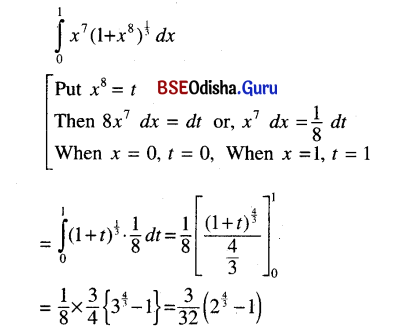
(ix) $\int_1^4 \frac{x^2-3 x+5}{\sqrt{x}}$ dx
Solution:

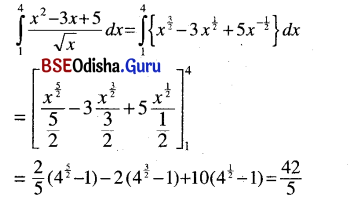
(x) $\int_1^4 \frac{(x+2)\left(x^2+3\right)}{\sqrt{x}}$ dx
Solution:

Question 2.
(i) $\int_0^{\frac{\pi}{2}}$(cos x – sin x) dx
Solution:

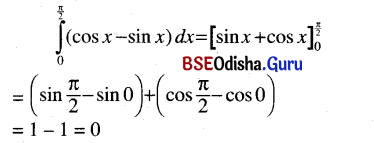
(ii) $\int_0^{\frac{\pi}{2}}$cos 2x dx
Solution:

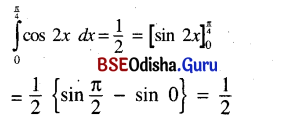
(iii) $\int_0^{\frac{\pi}{4}}$tan² x dx
Solution:

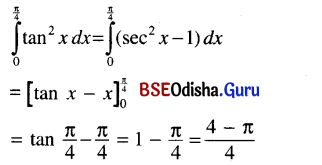
(iv) $\int_0^\pi 3 \sin \frac{x}{2} \cos \frac{x}{2}$ dx
Solution:

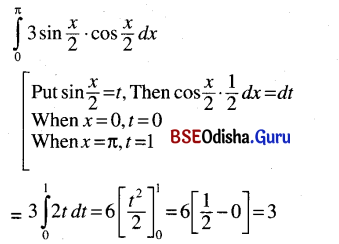
(v) $\int_0^{\frac{\pi}{4}}$sin 2x cos x dx
Solution:

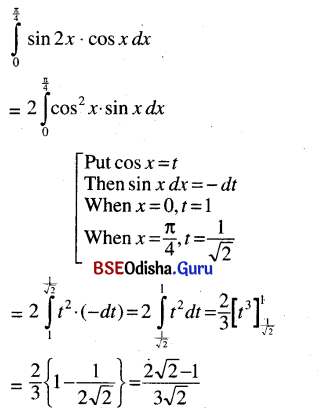
(vi) $\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{1+\cos 2 x}{1-\cos 2 x}$ dx
Solution:

(vii) $\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}$cos x dx
Solution:

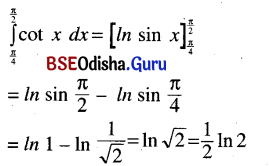
(viii) $\int_0^{\frac{\pi}{4}}$ cos² 2x sin³ 4x dx
Solution:

Question 3.
(i) $\int_1^2$e^4x+1 dx
Solution:
$\int_1^2$e^4x+1 dx = $\left[\frac{e^{4 x+1}}{4}\right]_1^2$ = $\frac{1}{4}${e⁹ – e⁵}

(ii) $\int_0^2$3^x+2 dx
Solution:
$\int_0^2$3^x+2 dx = $\left[\frac{3^{x+2}}{\ln 3}\right]_0^2$ = $\frac{1}{\ln 3}${3⁴ – 3²} = $\frac{72}{\ln 3}$

(iii) $\int_0^1$cos h 2x dx
Solution:

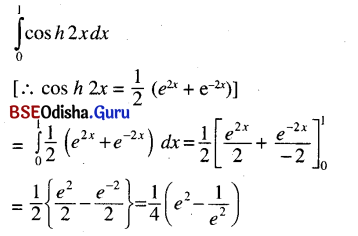
(iv) $\int_0^1 \frac{e^x-e^{-x}}{e^x+e^{-x}}$ dx
Solution:

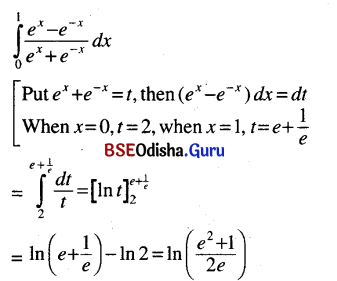
(v) $\int_0^2 x^2 e^{x^3}$ dx
Solution:

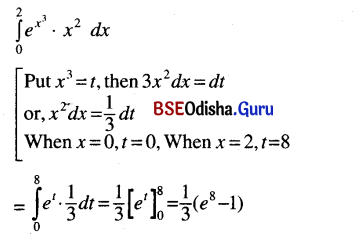
Question 4.
(i) $\int_0^1 \frac{d x}{\sqrt{1-x^2}}$
Solution:

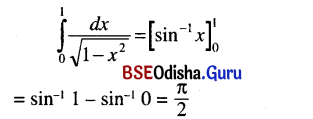
(ii) $\int_{\frac{2}{\sqrt{3}}}^2 \frac{d x}{x \sqrt{x^2-1}}$
Solution:

(iii) $\int_0^{\sqrt{3}} \frac{d x}{1+x^2}$
Solution:

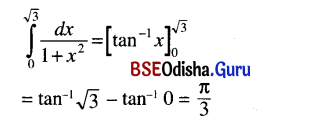
(iv) $\int_0^{\ln 2} \frac{d x}{\sqrt{e^{2 x}-1}}$ dx
Solution:

Question 5.
(i) $\int_0^1 \frac{d x}{3 x+2}$
Solution:

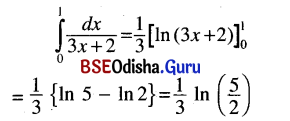
(ii) $\int_0^4 \frac{d x}{\sqrt{x^2+9}}$
Solution:

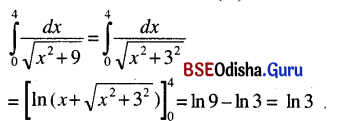
(iii) $\int_2^3 \frac{d x}{\sqrt{x^2-2}}$
Solution:

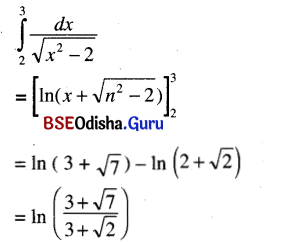
(iv) $\int_0^4 \sqrt{x^2+9}$ dx
Solution:

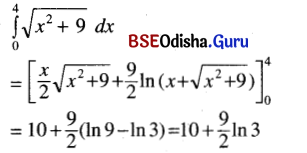
Question 6.
(i) $\int_{-2}^1$(|x| + x) dx
Solution:

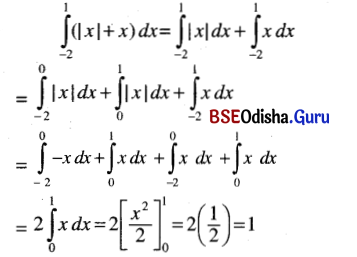
(ii) $\int_2^5$[x] dx
Solution:

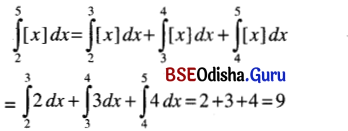
(iii) $\int_0^{\frac{3}{2}}$[2x] dx
Solution:

(iv) $\int_0^2$[x²] dx
Solution:

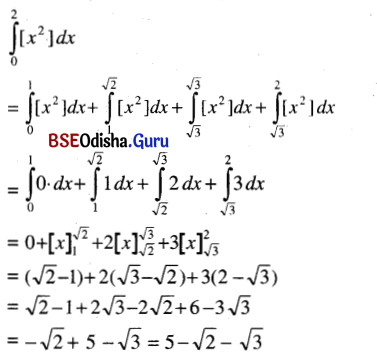
Question 7.
(i) $\int_1^2$e^x . (x + 1) dx
Solution:

(ii) $\int_0^{\frac{\pi}{4}}$x sin x dx
Solution:

(iii) $\int_1^2$x log x dx
Solution:

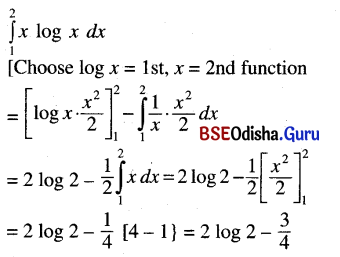
(iv) $\int_0^1$x tan^-1 x dx
Solution:

(v) $\int_0^1 \frac{x d x}{(2x+1)(x+1)}$
Solution:

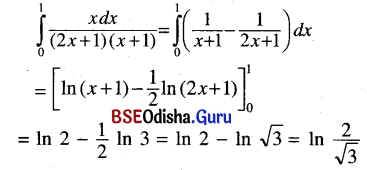
(vi) $\int_0^{\frac{\pi}{2}} \frac{\cos x d x}{(\sin x+1)(\sin x+2)}$
Solution:

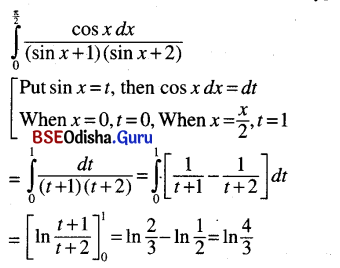
(vii) $\int_\theta^{\frac{\pi}{2}}$e^x cos x dx
Solution: