Odisha State Board CHSE Odisha Class 12 Biology Solutions Chapter 3 Human Reproduction Textbook Questions and Answers.
CHSE Odisha 12th Class Biology Chapter 3 Question Answer Human Reproduction
Human Reproduction Class 12 Questions and Answers CHSE Odisha
Very Short Answer Type Questions
Choose the correct option
Question 1.
Which of the following is not a gonadotropin?
(a) FSH
(b) hCG
(c) LH
(d) Testosterone
Answer:
(d) Testosterone
Question 2.
Which of the following hormones is not a steroid?
(a) Relaxin
(b) Estradiol
(c) Progesterone
(d) Testosterone
Answer:
(a) Relaxin
Question 3.
Which of the following is not secreted by the acrosome?
(a) Hyaluronidase
(b) Corona penetrating enzyme
(c) Zonalysin
(d) Fertilizin
Answer:
(d) Fertilizin
Question 4.
Blastocyst formation follows
(a) fertilisation
(b) spermatogenesis
(c) gametogenesis
(d) cleavage
Answer:
(d) cleavage
Question 5.
Placenta secretes the hormone
(a) testosterone
(b) human chorionic gonadotropin
(c) oxytocin
(d) growth hormone
Answer:
(b) human chorionic gonadotropin
Question 6.
Fallopian tube is part of
(a) ureter
(b) oviduct
(c) uterus
(d) vas deferens
Answer:
(b) oviduct
![]()
Question 7.
In human, fertilisation usually occurs in the
(a) vagina
(b) cervix
(c) uterine cavity
(d) uterine tube
Answer:
(d) uterine tube
Question 8.
Which of the following is not a male secondary sexual character?
(a) Beard
(b) Enlarged penis
(c) Coarse voice
(d) Increased fat in the buttocks
Answer:
(d) Increased fat in the buttocks
Question 9.
The chief source of circulating oestrogen is
(a) theca interna
(b) granulosa
(c) theca externa
(d) stroma
Answer:
(a) theca interna
Question 10.
Which of the following is not an accessory sex organ?
(a) Testis
(b) Epididymis
(c) Bulbourethral gland
(d) Seminal vesicles
Answer:
(a) Testis
Question 11.
Delivery of a human baby following pregnancy is known as
(a) ovulation
(b) parturition
(c) abortion
(d) conception
Answer:
(b) parturition
Question 12.
Sertoli cells are regulated by
(a) GH
(b) LH
(c) FSH
(d) TSH
Answer:
(c) FSH
Question 13.
Which of the following is a source of progesterone?
(a) Corpus luteum
(b) Corpus spongiosum
(c) Corpus albicans
(d) Corpus haemorrhagicum
Answer:
(a) Corpus luteum
Question 14.
Milk ejection from the breasts of a woman following the birth of a baby is stimulated by
(a) LH
(b) FSH
(c) GH
(d) oxytocin
Answer:
(d) oxytocin
Question 15.
Find the mismatch
(a) Acrosome – Dissolution
(b) Tail – Nutrition
(c) Mitochondria – Energy production
(d) Centriole – Cleavage
Answer:
(b) Tail provides motility not nutrition.
![]()
Fill in the blanks
1. All but one X-chromosomes in human female cells are condensed and inactive. Such X-chromosomes are known as ___
Answer:
Barr body
2. The Testis Determining Factor (TDF) is a polypeptide, expressed by ___ gene present on the Y-chromosome.
Answer:
sry
3. The factor responsible for the regression of the mullerian duct in the human male foetus is known as ___ secreted by ___ cell of the testis.
Answer:
AMH, Sertoli
4. Gonadotropins (FSH and LH) are secreted from ___ .
Answer:
anterior pituitary gland
5. FSH stimulates the Sertoli cells to synthesise three polypeptides, namely inhibin ___ and ___ .
Answer:
activins, transferrin
6. The early development of the ovarian follicles is stimulated by ___ and oestrogen.
Answer:
FSH
7. Luteinizing hormone stimulates ___ cells of the testis.
Answer:
Leydig
8. The final maturation of the ovarian follicles and ovulation are stimulated by ___ .
Answer:
LH
9. The prostatic fluid contains an acid called ___ .
Answer:
citric acid
10. Prostate Specific Antigens (PSA) help in the diagnosis of ___ .
Answer:
prostate cancer
11. The swollen tip of the penis is known as ___ .
Answer:
glans penis
12. The erectile tissue of the penis is constituted by ___ and ___ .
Answer:
corpus cavernosa, corpus spongiosum
13. The seminal vesicles discharge into vas deferens through ___ .
Answer:
ejaculatory duct
![]()
14. The peritoneal fold by which the ovary is attached to the broad ligament is called ___ .
Answer:
mesovarium
15. The primary oocytes are arrested at ___ stage of first meiosis until the onset of puberty.
Answer:
diplotene
16. The layers of cuboidal follicular cells surrounding the primary oocyte constitutes ___ .
Answer:
granulosa cells
17. Stromal cells, surrounding the granulosa cells are known as ___ cells.
Answer:
thecal
18. The egg is ovulated at ___ stage.
Answer:
ovulatory/secretory
19. The non-cellular layer surrounding the primary oocyte is known as ___ .
Answer:
corona radiata
20. The inner epithelial lining of the uterus is known a s ___ .
Answer:
endometrium
21. The menstrual cycle spans ___ days and the ovulation occurs on the day ___ .
Answer:
28, 14
22. The secondary oocyte is arrested at ___ before fertilisation.
Answer:
metaphase-II
23. Penetration of spermatozoan into the egg at fertilisation triggers metaphase-II in the secondary oocyte. This phenomenon is known as ___ .
Answer:
egg activation
24. Following the failure of fertilisation, the corpus luteum regresses into a structure called ___
Answer:corpus albicans
25. Corpus luteum is the main source of oestrogen and ___ .
Answer:progesterone
Answer each of the following in one word or more words, whenever necessary
1. Retention of testis in the abdominal cavity.
Answer:
Cryptorchidism
2. The canal through which the testis descends into the scrotum.
Answer:
Inguinal canal
3. The plexus of blood capillaries that helps maintain the temperature of the testis for normal functioning.
Answer:
Pampiniform plexus
4. The connective tissue capsule of the testis.
Answer:
Tunica albuginea
![]()
5. The seminal fluid contains a monosaccharide as the energy source.
Answer:
Fructose
6. The passage through which both the urine and semen are discharged.
Answer:
Urethra
7. The glans penis is covered by a fold of loose skin.
Answer:
Prepuce
8. The forcible expulsion of semen through the urethra.
Answer:
Ejaculation
9. The low count of sperms in human semen.
Answer:
Oligospermia
10. The mucopolysaccharide layer surrounding a primary ovarian follicle.
Answer:
Layer of granulosa cells
11.The hillock of granulosa cells connecting the granulosa cells surrounding the oocyte with the peripheral granulosa cells layer in a Graafian follicle.
Answer:
Cumulus oophorus
12.The loose mass of connective tissue, in which are present different stages of ovarian follicles.
Answer:
Medulla of ovary
13. The regressing follicles and the act of regression.
Answer:
Atretic follicles and follicular atresia
14. The uterine layer that is sloughed off during menstrual cycle.
Answer:
Endometrium
15. The arteries of the uterine wall that undergo disintegration during the menstrual cycle.
Answer:
Basal and spiral arteries
16. The height of LH secretion, 16-26 hours before ovulation.
Answer:
LH surge
17. The tissue formed by the apposition of both the maternal and foetal tissues during pregnancy.
Answer:
Placenta
18. The modified sweat glands in the female that serve as the source of food for neonatal babies.
Answer:
Alveoli
19. The fertilizin-antifertilizin reaction that stops the march of a large number of sperms towards the egg.
Answer:
Agglutination reaction
20. The penetration of the spermatozoan into the egg sets in a reaction in the cortical cytoplasm, which results in the formation of fertilisation membrane.
Answer:
Cortical reaction (slow block)
![]()
Short Answer Type Questions
Question 1.
What are the disadvantages of asexual reproduction?
Answer:
Disadvantages of asexual reproduction
- There is no mixing of genetic material, therefore, no variation takes place.
- Since, variations do not occur, asexual reproduction has no role in evolution.
- Due to rapid multiplication, it causes overcrowding.
- The organisms produced through asexual reproduction have low adaptability to the changed environment.
Question 2.
Explain sexual dimorphism.
Answer:
Sexual dimorphism means presence of male and female reproductive organs in different individuals. Such individuals are called dioecious or unisexual. Male and female exhibits different body type structurally and functionally. .
Question 3.
How do gametes acquire haploid number of chromosomes?
Answer:
The haploid number of chromosomes in gametes is contributed by the process called gametogenesis from the undifferentiated diploid germ cells in the gonads.
It is called spermatogenesis in males and oogenesis in females.
Question 4.
Is a Y-chromosome essential for the development of testis in human? Explain.
Answer:
Yes, Y-chromosome is necessary for the development of testes in humans. It contains sry gene which encodes for Testis Determining Factor (TDF) in foetus. In the presence of TDF, foetus develops into male, else female sex is developed.
Question 5.
What is the role of antimullerian hormone? Where is it secreted from?
Answer:
Antimullerian Hormone (AMH) helps in the testicular descent to the inguinal region. This dimeric glycoprotein is produced by Sertoli cells throughout the childhood in males and declines after puberty.
Question 6.
Explain, what is puberty?
Answer:
Puberty is a period when reproductive organs start functioning. It is attained between 13-16 years and gonadotropins play an important role in it. This period is marked by the development of sexual secondary structures in both the sexes and menarche in females only.
Question 7.
Name two gonadotropins. Where are these secreted from?
Answer:
Luteinizing hormone and follicle stimulating hormone are the gonadotropins secreted by anterior lobe of pituitary under the influence of Gonadotropin Releasing Hormone (GnRH) secreted by hypothalamus. In females, oestrogen is also secreted along with LH and FSH.
![]()
Question 8.
Describe the major role of LH in both male and female.
Answer:
In males, LH may be called Interstitial Cells Stimulating Hormone (ICSH) because it stimulates the interstitial or Leydig’s’ cells of the seminiferous tubules of the testes to secrete androgens. In females, LH stimulates the corpus luteum to secrete progesterone.
High level of LH on the day 14 of menstrual cycle results in the release of secondary oocyte from the mature Graafian follicle. This process is called ovulation which is the result of LH surge on day 14.
Question 9.
What is a cremasteric reflex?
Answer:
In cold wheather, the testes are elevated by the contraction of a band of muscle, known as cremasteric muscle to get the warmth of the trunk. This effect is called cremasteric reflex. The same effect occurs when the thigh of a man is stroked.
Question 10.
Explain the counter-current heat exchange mechanism in human testis.
Answer:
Testicular arteries that descend into the scrotum are surrounded by a plexus of veins, which ascend the testis and form a pampiniform plexus. Blood that returns from the testes through these plexus is cooler than the blood in testicular arteries.
The arterial blood is cooled by venous blood by a counter-current heat exchange mechanism.
Question 11.
Describe the functions of the Sertoli cells.
Answer:
Sertoli cells or subtentacular cells are present in between the germinal epithelial cells of seminiferous tubules.
They provide nourishment to the developing spermatozoa. These cells secrete Androgen Binding Protein (ABP) that concentrates testosterone in the seminiferous tubules. It also secretes inhibin protein which suppresses FSH synthesis.
Question 12.
What is blood testis barrier? How does it help the testis?
Answer:
The basal lamina of the germinal epithelium, muscle-like myoid cells at the base of basal lamina and tight junction between adjacent Sertoli cells constitute a blood testis barrier. This barrier prevents many macromolecules from moving into the tubular lumen.
Question 13.
What are the functions of epididymis?
Answer:
Epididymis is a mass of long narrow closely coiled tubule, which lies along the inner side of each testis. It stores the sperms and secretes a fluid which nourish the sperms.
Question 14.
Name five secondary sexual characters in human male.
Answer:
Secondary sexual characters in males include muscular build up, beard, moustaches, underdeveloped mammary glands, high BMR, predominantly abdominal breathing, etc.
Question 15.
What do you mean by accessory sex organs? Give five examples in human male.
Answer:
Accessory sex organs are those that do not produce gametes but they are essential for reproduction. In males scrotum, epididymis, vasa deferentia, ejaculatory ducts, urethra and penis are the example of accessory sex organs.
Question 16.
What is the function of the prostate glands
Answer:
The prostate gland is a single large gland that surround the urethra. It produces a milky secretion with pH 6.5 which forms 25% of the volume of semen. This secretion contains citric acid, enzymes and prostaglandins secretions of prostate gland nourishes and activates the spermatozoa to swim.
Question 17.
What is the role of corpus luteum following fertilisation and implantation?
Answer:
Corpus luteum acts as a temporary endocrine gland. It secretes large amount of progesterone which is essential for the maintenance of endometrium, necessary for implantation of the fertilised egg and other events of pregnancy. It degenerates in the absence of fertilisation.
![]()
Question 18.
Explain LH surge.
Answer:
When the blood level of oestrogen rises to a peak near the middle of the cycle, it gives positive feedback and stimulates more LH secretion. It is called LH surge and it stimulates ovulation.
Question 19.
What is spermiogenesis?
Answer:
Formation of spermatozoa (Spermiogenesis) Each haploid spermatid is a typical immotile cell containing a haploid nucleus, cytoplasm and cytoplasmic organelles. The metamorphosis of spermatids into motile sperms occurs because a sperm possesses many structures which are not typical to a spermatid.
All the structures confer motility to the sperm. After spermiogenesis, sperm heads are embedded in the Sertoli cell and finally released from the seminiferous tubule by the process of spermiation.
Question 20.
What is the role of acrosome in fertilisation?
Answer:
The sperm head contains an oval haploid nucleus, the anterior part of which is capped by structure called acrosome.
The acrosome secretes enzymes that help dissolve the egg barriers during fertilisation. The sperm lysins present in acrosome include hyaluronidase, corona penetrating enzyme and acrosis. They digest zona pellucida and corona radiata and help the sperm to enter the egg.
Question 21.
Placenta is an endocrine tissue. Explain.
Answer:
The placenta acts as an endocrine tissue and produces several hormones like human Chorionic Gonadotropin (hCG), human Placental Lactogen (hPL), oestrogen, progesterone, etc. In the later phase of pregnancy, a hormone called relaxin is also secreted by the placenta. Hormones such as hCG, hPL and relaxin are produced in women only during pregnancy. In addition, during pregnancy the levels of other hormones like oestrogens, progesterone, cortisol, prolactin, thyroxine, etc., are increased several fold in the maternal blood. Increased production of these hormones is essential for supporting foetal growth, metabolic changes in the mother and maintenance of pregnancy.
Question 22.
Enlist the hormones regulating menstrual cycle and mention the role of each.
Answer:
The hormones that regulate menstrual cycle along with their functions are
1.Pituitary gonadotropins (LH, FSH and Oestrogen) These help in the proliferation of Graafian follicle and endometrium of uterus.
- FSH Stimulates the growth of ovarian follicle and secretion of oestrogen.
- Oestrogen Increased level of oestrogen gives positive feedback and stimulates more LH production.
- LH Stimulates ovulation.
2. Progesterone Essential for the maintenance of endometrium.
Question 23.
What do you understand by follicular atresia? Where does it occur?
Answer:
At birth around 2.5 millions of primary follicles are found in each ovary but at puberty only 60,000-80,000 primary follicles are left. The rest degenerate, in a process called follicular atresia. It occurs in the ovaries of females.
Question 24.
Where do the granulosa and thecal cells originate from and what are their functions?
Answer:
Granulosa cells and thecal cells surround the primary follicles to form secondary follicles in the ovaries. The innermost layer of granulosa cells that surround the oocyte is known as the corona radiata. A glycoprotein protective layer, known as the zona pellucida appears between the oocyte and corona radiata. Cells from the stroma surround the granulosa cells and differentiate as the thecal cells.
During ovulation, granulosa and thecal cells proliferate and become glandular.
They collectively form luteal cells which is the source of oestrogon and progesterone.
Question 25.
How is the mammary gland hormonally regulated?
Answer:
Mammary glands are modified sweat glands that lie over the pectoral muscles. In the female, breasts are undeveloped until puberty. At puberty they begin to develop under the influence of oestrogen and progesterone.
The glands proliferate during pregnancy and start producing milk towards the end of pregnancy by the process called lactation.
It is induced by hormones like Prolactin (PRL) and oxytocin secreted from the mother’s pituitary gland. Lactation helps the mother in feeding the newborn.
Milk production is stimulated by prolactin and ejection of milk is induced by oxytocin.
![]()
Write brief notes on the following
Question 1.
Secondary sexual characters
Answer:
Secondary sexual characters are those which help distinguish the two sexes morphologically. The appearance of these characteristics is influenced by the secretion of hormones at the onset of puberty. Testosterone and oestrogen are responsible for the production of secondary sexual characters in males and females, respectively.
Testosterone is involved in greater bone density, high muscle mass, larger voice box, beard and moustaches development, etc.
Oestrogen is involved in breast development, increased* fat tissue around hips, wider pelvic bone, etc. ’ .
Question 2.
Accessory sex organs
Answer:
Reproductive organs other than testes and ovaries are called accessory sex organs. These organs help in the maturation of sex cells. In males, they include seminal vesicles, prostate gland and Cowper’s/ Bulbourethral glands. In female reproductive system, accessory sex organ includes Bartholin’s gland.
Question 3.
Seminiferous tubule
Answer:
The seminiferous tubules are the site of germination, maturation and transportation of sperm cells within the male testes. They are made up of columnar Sertoli cells surrounded by spermatogenic cells on the epithelial interior. They are located within the testes and are formed from the testis cords that develop from the primitive gonadal cords formed gonadal ridge.
Question 4.
Graafian follicle
Answer:
Graafian follicle is a mature fluid-filled cavity in a mammalian ovary that ruptures during ovulation to release an egg on the day of ovulation. Graafian follicle represents the follicular stage after the first meiotic division but before ovulation.
It is characterised by a large antrum that makes up most of the follicle. The secondary oocyte is surrounded by zona pellucida and a layer of corona radiata.
Question 5.
Corpus luteum
Answer:
The corpus luteum is a temporary endocrine structure in female that is involved in ovulation and early pregnancy. This yellow body is formed in ovary Graafian follicle that has matured and released its ovum. The corpus luteum is made up of lutein cells which develop immediately following ovulation, when yellow pigment and lipids accumulate within the granulosa cells lining the follicle.
The corpus luteum secretes oestrogen and progesterone which helps in setting the suitable environment for pregnancy. In the absence of pregnancy, this structure regresses and gets converted into white body called corpus albicans.
Question 6.
Prostate gland
Answer:
The prostate gland is located between the bladder and the penis just in front of rectum in males. It secretes fluid that nourish and protect sperms. Its secretions are alkaline and milky in appearance and it constitutes about 30% of the volume of semen. The alkalinity of semen helps to neutralise the acidity of vaginal tract. Inflammation of prostate gland causes prostatitis which may be benign or cancerous.
Question 7.
Seminal vesicles
Answer:
The seminal vesicles are a pair of tube-like glands in males. They are found behind the bladder and their secretion makes about 70% of the content of semen.
The secretion of seminal vesicle is rich in sugars (especially fructose) which feeds the sperms. The fluid also has clotting properties that makes the semen sticky. Prostaglandins in seminal fluid are believed to aid fertilisation by causing the mucous lining of the cervix to be more receptive to sperm as well as by aiding the movement of sperm towards the ovum with peristalic contractions of uterus and Fallopian tubes.
![]()
Question 8.
Bulbourethral gland
Answer:
The bulbourethral gland, also called Cowper’s gland are exocrine glands in males,. They are homologous to Bartholin’s glands in females. They are compound tubulo-alveolar glands located posterior and lateral to the membranous portion of the urethra at the base of penis. Their secretion contribute about 0.1-0.2 mL of the ejaculate. It is a clear fluid that is rich in mucoproteins. The secretion helps to lubricate the distal urethra and neutralise the acidic urine which remains in the urethra.
Question 9.
Blood testis barrier
Answer:
The Blood Testis Barrier (BTB) is one of the tightest blood tissue barriers in mammalian body. It divides the seminiferous epithelium into the basal and apical compartments. Meiosis-I and II, spermiogenesis and spermiation all occur in a specialised microenvironment behind BTB in the apical compartment but spermatogonial renewal and differentiation and cell cycle progression up to preleptotene spermatocyte stage takes place outside of the BTB in the basal compartment.
BTB is different from most other tissue barriers in that it is not only comprised of tight junctions. Desmosomes, gap junctions and ectoplasmic specialisations also occur in it.
Question 10.
Luteal phase
Answer:
The luteal phase is one stage of menstrual cycle. It occurs after ovulation. It begins with the formation of corpus luteum and ends in either pregnancy or luteolysis, i.e regression of corpus luteum. The main hormone associated with this stage is progesterone which is secreted by corpus luteum. This phase lasts between 10-16 days. Luteal phase of less than 12 days may make it difficult to achieve pregnancy.
Question 11.
Menopause
Answer:
Menopause (Gr. Men = month, pausis = cessation)
It is a phase in woman’s life when ovulation and menstruation stop. It occurs between 45-55 years of age. Some women have irregular cycles for, months or years prior to menopause. Others simply stop menstruating abruptly.
Cause One theory is that menopause is a result of changes in pituitary gland and the nearby hypothalamus. Another theory suggests that menopause may begin when no follicles are left in the ovaries. In fact decline in oestrogen and progesterone level leads to menopause. Symptoms The uterus and the vagina gradually become atrophic (decreased work). Women may suffer temporarily depression, hot flashes, and other physiological and psychological problems in menopause. Most of these symptoms can be relieved by taking hormones prescribed by a physician. But this replacement of hormones is not encouraged due to some side effects.
Question 12.
Gonadotropins
Answer:
Gonadotropins are glycoprotein polypeptide hormones secreted by gonadotroph cells of the anterior pituitary gland. These are stimulated by Gonadotropin Releasing Hormones (GnRH) secreted by hypothalamus. The major gonadotropins are Follicle Stimulating Hormone (FSH) and Luteinizing Hormone (LH). They stimulate the gonads, i.e. testes and ovaries in males and females, respectively.
Question 13.
Placenta
Answer:
Placenta is the intimate connection between the foetus and uterine wall of the mother to exchange the materials. In humans, chorion takes part in the formation of placenta hence called chorionic placenta. It consists of foetal part, the chorion and a maternal part, the decidua basalis.
The degree of intimacy is so strong that the blood vessels of the chorionic villi are bathed in the mother’s blood. This type of placenta which is based on the intimacy between foetal and maternal parts of the placenta is referred to as haemochorial placenta. It provides nutrition, aids in respiration and excretion of the foetus.
Question 14.
Parturition Or What is parturition?
Answer:
Parturition is the act of expelling the full term young one from the mother’s uterus at the end of gestation period.
It is induced by both nervous system and hormones secreted by the endocrine glands of the mother. The signals for childbirth (parturition) originates from the fully matured foetus and placenta which induce mild uterine contractions called foetal-ejection reflex.
This causes quick release of oxytocin from maternal posterior lobe of pituitary. The amount of oxytocin is increased just before and during labour pains which promote contractions of the uterine muscles. Relaxin increases the flexibility of the pubis symphysis and helps to dilate the uterine cervix.
![]()
Question 15.
Spermiogenesis
Answer:
Spermiogenesis is the process of transformation of spermatids into spermatozoa (sperms). Four sperms are formed from one spermatogonium by the differentiation process. After spermiogenesis, sperm head becomes embedded in the Sertoli cells and are finally released from the seminiferous tubules by the process called spermiation. Spermiogenesis is also called spermateliosis.
Question 16.
Lactation
Answer:
Lactation is the process of production of milk in the mammary glands of females towards the end of pregnancy and after the birth of the young one. Secretion and storage of milk generally begins after birth of young one, usually within 24 hours under the influence of prolactin (PRL) hormone secreted by anterior lobe of pituitary gland.
However, the ejection of milk is stimulated by the Hormone Oxytocin (OT) released from the posterior lobe of pituitary gland.
The first milk which comes from the mammary glands of mother just after childbirth, for 2-3 days is called colostrum.
Differentiate between two words in the following pairs of words
Question 1.
Leydig cell and Sertoli cell
Answer:
Differences between Leydig cells and Sertoli cells are as follows
| Leydig’s cells (Interstitial cells) | Sertoli cells (Sustentacular cells) |
| They are present in between the seminiferous tubules. | They are present in between the germinal epithelial cells of the seminiferous tubules. |
| Leydig’s cells are found in small groups and are rounded in shape. | Sertoli cells are found singly and are elongated. |
| They secrete androgens (e.g. testosterone) male sex hormones. | They provide nourishment to the developing spermatozoa (sperms), Sertoli cells secrete ABP(Androgen Binding Protein) that concentrates testosterone in the seminiferous tubules. It also secretes another protein inhibin which suppresses FSH synthesis. |
Question 2.
Corpus haemorrhagicum and Corpus luteum
Answer:
Differences between corpus haemorrhagicum and corpus luteum are as follows
| Corpus haemorrhagicum | Corpus luteum |
| It is a temporary structure formed immediately after ovulation from the ovarian follicle as it collapses and is filled with blood that clots quickly | It is formed from corpus haemorrhagicum formed after the release of secondary oocyte after ovulation. |
| Non- endocrine. | Thmporary endocrine. |
Question 3.
Follicular phase and Luteal phase
Answer:
Differences between follicular phase and luteal phase are as follows
| Follicular phase | Luteal phase |
| It extends for about 10-12 days usually from day 6-13 in a 25 days cycle. | It extends for about 13-14 days after ovulation usually from day 15-28 in a 28 days cycle. |
| Primary follicle changes into Graafian follicle. | Empty Graafian follicle changes into corpus luteum. |
| Oestrogens are secreted. | Progesterone is secreted. |
| Endometrium is about 2-3 mm thick. The uterine glands do not secrete watery secretion. | Endometrium is about 5 mm thick. The uterine glands secrete watery secretion. |
Question 4.
Antral follicle and Graafian follicle
Answer:
Differences between antral follicle and Graafian follicle are as follows
| Antral follicle | Graafian follicle |
| Formed from secondary follicle. | Formed from tertiary follicle. |
| Cellular differentiation are at peak. | Cellular differentiation is completed. |
| Occur in follicular phase. | Occur in ovulatory phase. |
| Under the influence of FSH, it gets converted in Graafian follicle. | Under the influence of LH, it ruptures to release secondary oocyte and gets converted into corpus luteum. |
![]()
Question 5.
Granulosa and Thecal cells.
Answer:
Differences between granulosa cells and thecal cells are as follows
| Granulosa | Thecal cells |
| Inner,ost cells that surrounds the oocyte. | Cells of that stroma surround granulosa cells. |
| After ovulation, they become the source of progesterone. | After ovulation, they become the source of oestrogen. |
Question 6.
First maturation division and Second maturation division.
Answer:
Differences between first maturation division and second maturation division are as follows
| First maturation division | Second maturation division |
| The primary oocyte divides into two unequal haploid daughter cells a large secondary oocyte and a very small first polar body. | The first polar body may divide to form second polar bodies. The secondary oocyte again divide into unequal daughter cells a large ootid and a very small second polar body. |
Question 7.
Spermatogenesis and Oogenesis.
Answer:
Differences between spermatogenesis and oogenesis are as follows
| Spermatogenesis | Oogenesis |
| It occurs in the testes. | It occurs in the ovaries. |
| Spermatogonia change to primary spermatocytes. | Oogonia change to primary oocytes. |
| A primary spermatocyte divides to form two secondary spermatocytes. | A primary oocyte divides to form one secondary oocyte and one polar body. |
| A secondary spermatocyte divides to form two spermatids. | A secondary oocyte divides to form one ootid and one polar body. |
| No polar body is formed. | Polar bodies are formed. |
| A spermatogonium forms four spermatozoa. | An oogonium forms one ovum. |
| Sperms are minute, yolkless and motile. | Ova are much larger often with yolk and non-motile. |
| It is generally completed in the tests and thus mature, sperms are released from the tests. | It is often completed in the female reproductive tract or in many animals in water because oocytes are released from the ovaries. |
Long Answer Type Questions
Question 1.
Discuss about different methods of asexual reproduction in animal, as studied by you.
Answer:
In asexual reproduction, a single parent gives rise to two or more young ones that have hereditary – traits similar to that of parent. It occurs by various processes like fission, budding, etc. It is mostly found in lower groups of organisms like some plants, protozoans, sponges, coelenterates, etc.
![]()
Question 2.
Describe the male reproductive system in human.
Answer:
Male Reproductive System:
The male reproductive system is located in the pelvis region. It consists of scrotum a pair of testes, excurrent ducts and accessory glands.
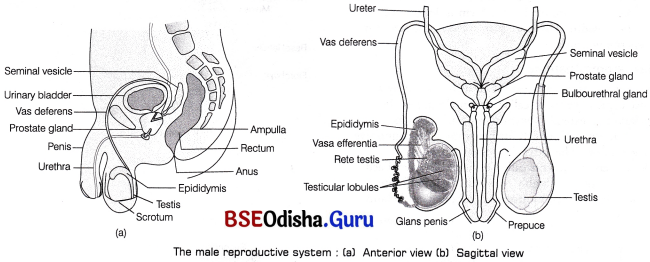
Scrotum:
It is a pouch-like structure of pigmented skin arising from the lower abdominal wall and hanging between the leg. It is divided internally into right and left scrotal sacs by a muscular partition called septum scrota. The testis originates in the abdominal cavity, but later during the seventh month of development, it descend into the respective scrotal sacs through the passages called inguinal canals.
Testicular descent to inguinal region during gestation period is affected by Antimullerin Hormone (AMH) secreted by Sertoli cells. 90% of babies have completely descended testes, when they are born. In 10% of new-borns, testes fail to descend and retained in the abdominal cavity. This condition is called cryptochidism. It can be treated by gonadotropins or surgery.
In cold weather, the testes are elevated by the contraction of a band of muscle, known as cremasteric muscle to get the warmth of the trunk. This effect is known as cremasteric reflex.
The same effect occurs when the thigh of a man is stroked. In the baby, this stimulus causes the testes to ascend up into the abdominal cavity through the inguinal canal.
Functions of Scrotum:
Scrotum keeps the temperature of testes about 2-2.5°C lower than the internal body temperature, which is essential for the production of sperms, i.e. spermatogenesis. This temperature is maintained by perspiration and evaporation from the scrotal surface. These processes occur due to the presence of pampiniform plexus that surround testiculae arteries which ascend from the testis. Venous blood returning from testis through pampiniform plexus is cooler than the blood in testicular arteries. The countercurrent heat exchange mechanism between the arterial and venous blood cools down the arterial blood.
Testes: Microscopic Anatomy:
Testes are the primary sex organs in men. These are the male gonads, i.e. the site where the male gametes or sperms are made. A pair of testis is situated outside the abdominal cavity within the scrotum. Each testis is oval in shape and measures about 4-5 cm in length and 2-3 cm in width. These are suspended in the scrotum by spermatic cords.
Microscopic Anatomy:
The outermost covering of the testis is formed by a dense connective tissue called tunica albuginea. It thickens and extends inwardly into each testis as mediastinum testis which further forms thin connective tissue septum. The latter divides each testis into 200-300 compartments called testicular lobules. Each lobule contains 1-3 highly convoluted seminiferous tubules that is lined by stratified cuboidal epithelium.
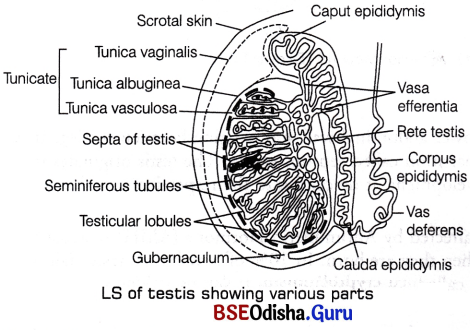
Seminiferous Tubule:
It is the structural and functional unit of testis in which sperms are produced. Each seminiferous tubule is present in the mass of loose connective tissue that contain fibroblast, epithelial cells, nerves, blood and lymphatic vessels, etc. Inside these tubules, two types of highly specialised cells are present namely Sertoli cells (nurse cells) and spermatogenic cells.
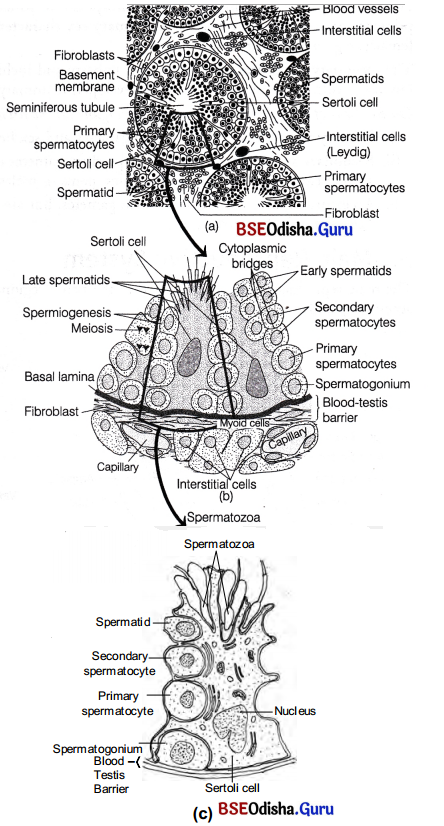
Transverse section through human testis : (a) A single seminiferous tubule with cells of Leydig in the interstitial tissue, (b) A magnified part of the seminiferous tubule showing the blood-testis barrier, Sertoli cells and its relationship to the differentiating spermatogenic cells and (c) A Sertoli cell with spermatogenic cells in different stages of development
1. Spermatogenic cells These are majority of dividing cells or male germ cells (cuboidal cells) which produce spermatogonia by mitotic division. The spermatogonia further grows into primary spermatocytes and undergo meiosis producing haploid cells, first secondary spermatocytes and then spermatids.
2. Sertoli or Sustentacular cells They are tall, pyramidal, non-dividing somatic cells. They serve the supporting and nourishing function for the spermatogenic cells in different stages of their differentiation. The basal lamina of the germinal epithelium, muscle-like myoid cells at the base of the basal lamina and tight junctions between adjacent Sertoli cells constitute a blood testis barrier which performs the following functions
- Prevents many macromolecules from moving into the tubular lumen.
- Prevents the blood borne noxious chemical agents from entering into the tubule.
- Prevents the passage of antigenic agents from the tubule into the blood, which are likely to generate an autoimmune response.
The region outside the seminiferous tubules called interstitial spaces contain small blood vessels and masses of cells called interstitial cells or Leydig cells. These cells synthesise and secrete the testicular hormones called androgens. Leydig cells are endocrine in function and thus, regulate and maintain male sex characteristics. Other immunologically competent cells are also present in this region.
Accessory or Excurrent Duct System:
These ducts store and transport the sperms along with other glandular secretions from the testis to the outside through urethra. The male’s sex accessory ducts include-tubuli recti, rete testis, vasa efferentia (intratesticular ducts), epididymis, vas deferens and urethra (extratesticular ducts). The ends of seminiferous tubules converge and join to form short straight tubules called tubuli recti.
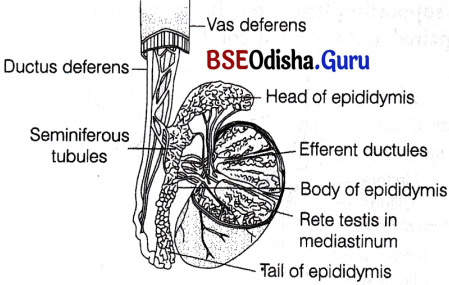
Duct system in human testis
The tubuli recti open into a network of wider, irregular tubules called rete testis, that further open into 12 short efferent ductules or ductuli efferentes.
The latter open into the epididymis and carry sperms outside the testis. Epididymis is a long tube, which is greatly coiled and tightly packed to form an elongated flattened body. It is located along the posterior surface of each testis.
Sperms undergo physiological maturation, acquiring increased motility and fertilising capacity (i.e. capacitation) in epididymis. After that, they pass down to the tail of epididymis, where they stay for a very short period before entering the two vas deferens or ductus deferens.
The vas deferens ascends to the abdomen and lopps over urinary bladder. It receives a duct from seminal vesicle to form ejaculatory duct. The ejaculatory duct enters the prostate gland and opens into the prostatic urethra.
The prostatic urethra extends through the penis to its external opening called urethral meatus or penile urethra. The urethra carries urine from bladder as well . as spermatozoa and secretions from the Cowper’s and prostate glands.
Accessory Glands:
The accessory glands or the secondary glands in males are described below
1. Prostate gland It is a single gland that lies » inferior to the bladder. It receives two ejaculatory ducts that joins to form prostatic urethra. The latter receives ductules from prostate. It secretes a milky, slightly alkaline fluid, that contains lipids, enzymes, citric acid, etc.
It is released during ejaculation and helps to neutralise the acidic medium of vagina, making sperms more active to swim. Prostatic fluid accounts for nearly 20-30% of semen volume.
2. Seminal vesicles This paired gland is present posterior to the bladder above prostate. Its ducts empties in the ampulla of ductus deferens.
They secrete mucus and a watery alkaline fluid that contains fructose (acts as an energy source for the sperms). Prostaglandins (stimulate uterine contractions for sperm movement) and a clotting protein form a temporary clot after ejaculation. Later, fibrolysins dissolves the coagulate or clot so that it assume a liquid form. Calcium and certain other enzymes are also a part of seminal plasma.
Fructose, produced by seminal vesicles, is not present elsewhere in the body. Therefore, during forensic test for rape, its presence in females genital tract confirms sexual intercourse. The seminal vesicles and prostrate degenerates or atrophy after the removal of testes because they are androgen dependent glands.
3. Bulbourethral or Cowper’s gland These are situated beneath the bladder and behind the urethra. There ductules discharge into the prostatic urethra. They secrete mucus and an alkaline fluid into the urethra. The mucus helps in the lubrication of penis and neutralises any urinary acids in urethra
![]()
Questions 3.
Describe the female reproductive system in human.
Answer:
Female Reproductive System:
It consists of a pair of ovaries, glands, a duct system and many supporting structures. Its components are found in both paired and unpaired condition.
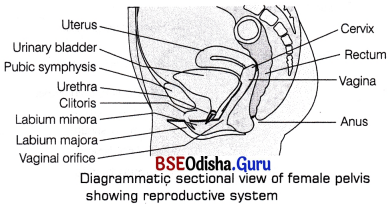
The female reproductive system consists of the following organs
Ovaries:
Ovaries are the primary sex organs of female that is situated in the pelvic cavity.
They produce female gametes (ovum) and several steroid hormones (ovarian hormones). The ovaries are almond-shaped, lying in the lower part of the abdomen and held to the broad ligament by double folds of peritoneum called mesovarium. Each ovary is about 2-4 cm in length and is connected by an ovarian ligament to the uterus and by a suspensory ligament to the lateral pelvic wall. Each ovary is covered by a thin epithelium layer called germinal epithelium.
Next to this layer, dense irregular connective tissue mass called tunica albuginea is present. Inner to this, cortex is present which is followed by highly vascularised connective tissue called cortex or stroma ovarian stroma, which contains connective tissues, blood vessels and mature follicles. The stroma is divided into two parts, i.e. a peripheral cortex and an inner medulla or stroma. There is no distinct boundary between the cortex and medulla.
Microscopic Anatomy of Ovary:
The production of eggs in females begins before birth, i.e. during the embryonic development stage, but is completed only after fertilisation. It takes place in ovaries. Cells of germinal epithelium undergo mitotic or equational division during multiplication phase, producing undifferentiated germ cells called oogonia or egg mother cells within each foetal ovary. These cells enter into the phase of maturation and start two meiotic divisions to enter prophase-I of meiotic division as primary oocytes. They get temporarily arrested at diplotene state and remains as such until the onset of puberty.
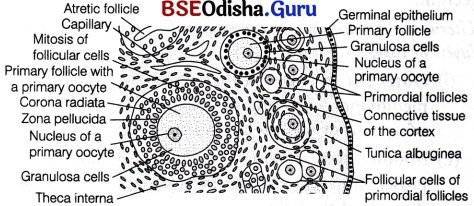
Primordial and primary follicles in the cortex of the ovary
Each primary oocyte then gets surrounded by a single layer of squamous follicle cells and is called the primordial follicle. About 2 million of these follicles exist in ovarian cortex of females before birth. A large number of these follicles degenerate during the phase from birth to puberty. Therefore, at puberty only 60000-80000 primary follicles are left in each ovary.
The primordial follicles get surrounded by more layers of cuboidal granulosa cells and a new theca. This process is stimulated by the pituitary gonadotropins-FSH and LH. Later the squamous follicular cells of primordial follicle changes to cuboidal or low columnar cells. This follicle is called primary follicle.
The follicular cells of primary follicle divide by mitosis and forms the new cuboidal-shaped granulosa cells. At this stage follicle is called secondary follicle.
The innermost layer of granulosa cells is corona radiata that surrounds the oocyte. Between the oocyte and eorona radiata, a glycoprotein layer called zona pellucida appears. The stromal cells that surround granulosa cells differentiate to form thecal cells. These cells differentiate as an outer theca externa and inner theca interna.
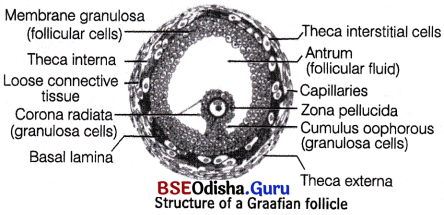
A thin basement membrane separates granulosa cells from the theca interna. This follicular stage is known as mature or Graafian follicle stage.
Structure of a Graafian (mature) follicle : A part(inset) is magnified to show the elaborate structure of the egg with the associated follicle cells
Development of Ovarian Follicle:
- The primary follicle grow in size and a fluid called liquor folliculi or follicular fluid accumulates in a cavity called antrum of granulosa cells. These follicles with an antrum are called antral or secondary follicles.
- The synthesis of liquor folliculi continues, antrum grows in volume and further segregation of granulosa cells occur. Due to this, few cells surround the oocytes and some other are displaced to periphery.
- Theca externa cells form multiple layers around theca interna cells which leads to the formation of mature or Graafian follicle. At this stage, the first meiosis of primary oocyte gets completed to form a secondary oocyte.
- The Graafian follicle, ruptures to release the secondary oocyte from the ovary.
- The secondary ooctye is captured by the fimbriae of Fallopian tube which transport it to the uterus.
- The remaining portion of Graafian follicle gets filled with blood to form corpus haemorrhagicum.
- The theca and granulosa cells proliferate and become glandular to form theca lutein and granulosa lutein cell, respectively. These lutein cells are the source of oestrogen and progesterone. This post ovulatory follicle is called corpus luteum (endocrine structure) which secrete estradiol, progesterone and relaxin (peptide hormone).
Fate of Corpus Luteum:
- If fertilisation occurs Corpus luteum persist and no mensuration occurs, zygote undergoes embryonic development and implants in the endometrium of uterus.
- If fertilisation does not occur Corpus luteum degenerates to form corpus albicans and menstruation occurs.
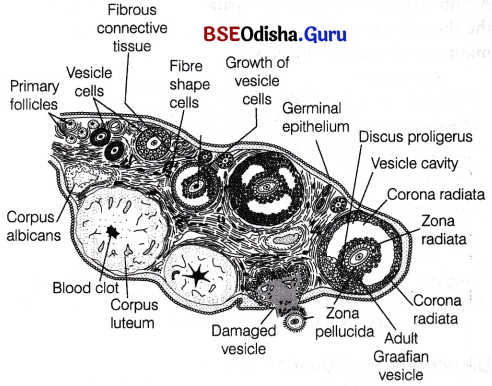
Not all ovarian follicles reach maturity. Only one dominant follicle gets matured and ovulated. Rest of them degenerates by the process called follicular atresia and the resultant follicles are known as atretic follicles which are replaced by connective tissue.
Fallopian Tube (Uterine Ducts):
These are two small accessory tubes of 10-12 cm length, lying on either sides of uterus near the kidney. These tubes carry the egg from the ovary to the uterus and also provides the appropriate environment for its fertilisation.
The Fallopian tubes or oviducts show four regions, i.e. infundibulum, ampulla, isthmus and interstitial region,
(i) Infundibulum is broad and funnel-shaped with its edges bearing motile, finger-like projections called fimbriae. It helps in the collection of ovum after ovulation.
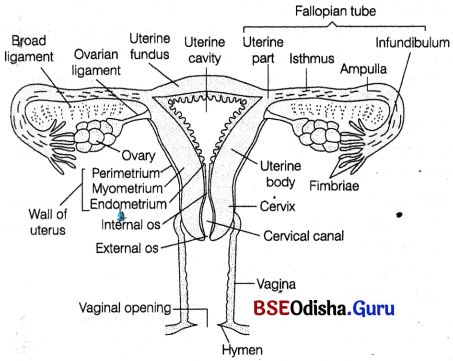
Female reproductive system
(ii) Ampulla is the long, wide, thin-walled part of the Fallopian tube next to the infundibulum where fertilisation takes place.
(iii) Isthmus is a short narrow lumen that follows ‘ ampulla and joins the uterus.
(iv) Interstitial region passes through the uterine wall and communicates with the uterine cavity.
Uterus (Womb):
It is about 7.5 cm long, 5 cm wide, like an inverted pear in shape. It is supported by ligaments attached to the pelvic wall. It lies between the urinary bladder and rectum.
Uterus has a thick, highly vascular wall, composed of three layers of tissues
- Outer perimetrium A thin single-layered membranous covering of uterus wall that is composed of squamous epithelial cells.
- Middle myometrium A thick layer of smooth muscle fibres, which contracts strongly during the delivery of the baby.
- Inner endometrium A glandular layer with many blood vessels. It consists of simple cuboidal or columnar epithelium. It undergoes cyclic changes during the menstrual cycle.
Blood Supply to Uterus:
The arteries that supply blood to uterus gets divided into arcuate arteries and spreads in the myometrium. The arcuate arteries further gets divided into parts so as to supply blood to endometrium.
These include
- Straight arteries These are short, supply blood to basalis layer.
- Spiral arteries These are long and coiled, supply blood to functionalis layer. Decreased supply to this layer during menstruation causes it to degenerate and cast off.
The endometrium descends into the lamina propria and form numerous uterine glands. Functionally, the layer is divided into two layers
- Luminal stratum functionalis During menstruation, this layer cast off along with blood vessels and uterine glands.
- Stratum basalis It helps to form a new functionalis layer.
Functions of Utreus:
Uterus receives the ovum from the Fallopian tube, forms placenta for the development of foetus and also expels the young one at the time of birth.
Cervix:
It is the narrow entrance of the uterus into the vagina. It has strongest sphincter in its wall and is normally blocked by a plug of mucus. The cavity of cervix is called cervical canal which along with vagina forms the birth canal.
Vagina:
It is about 10 cm long and acts as a receptacle for the penis during copulation, for allowing menstrual flow and for serving as a birth canal during parturition. It opens to the exterior by an aperture called vaginal orifice situated posterior to the opening of urethra.
Accessory Glands:
1. A pair of greater vestibular or Bartholin’s gland occurs on each side of the vaginal orifice. They are small rounded bodies.
These glands correspond-to the Cowper’s gland of the male and secrete a clear, viscid fluid under sexual excitement. This fluid serves as a lubricant during copulation.
2. Numerous glands of skene are present on either sides of urethral orifice. They are homologous to male’s prostate and secrete mucus. These are also called lesser vestibular or paraurethral glands.
External Genitalia (Vulva):
The external genitalia of females consists of the following parts
1. Mons pubis It is the anteriormost structure of vulva and is covered with skin and pubic hairs.
2. Two longitudinal folds of tissue called labia majora form the boundary of the vulva. It also covers two additional folds of tissue called the labia minora.
Both labia majora and labia minora protect the vaginal and urethral openings.
3. Clitoris It is the small erectile organ, which lies at the upper junction of the labia minora above the urethral opening. It is a homologous structure to glans penis of males.
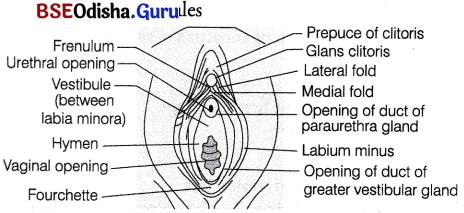
Frontal view of vagina with its associated structures
4. Hymen The vaginal orifice is normally covered by a membrane, called hymen. It is a thin mucous membrane, which covers the vaginal opening either partly or completely. It is often torn during the first coitus (intercourse), but may be present in some women even after coitus. Hymen may also get stretched or torn by normal activities such as horseback riding and therefore, the presence or absence is not an accurate indicator of a woman’s virginity or sexual experience.
Disorders of the Female Reproductive System
| Disorder | Description |
| Breast cancer | Incidence increases after menopause. Signs include lump in breast, change in breast shape, fluid from nipple, etc. |
| Cervical | Slow growing cancer. Unnoticed until invades other tissues. |
| cancer | Fluid filled tumours of the ovary. |
| Ovarian cysts | Growth of endometrial tissue outside the uterus. |
| Endometriosis | Implantation of embryo at a place other than uterus. |
| Ectopic | Description |
| pregnancy | Incidence increases after menopause. Signs include lump in breast, change in breast shape, fluid from nipple, etc. |
![]()
Question 4.
What is menstrual cycle? Describe the cycle in human with a reference to cyclic changes in the ovary and uterine endometrium.
Answer:
Menstrual Cycle:
It is the reproductive cycle in female primates, e.g. monkeys, apes and human beings.
The first menstruation begins at puberty and is called menarche. In human females, menstruation is repeated at an average interval of about 28/29 days. The menstrual cycle stops at around 50 years of age in human females and this stage is termed as menopause.
The cyclic menstruation is an indication of normal reproductive phase and extends between menarche and menopause. The cycle of events starting from one menstruation till the next one is called menstrual cycle. One ovum is released during the middle of each menstrual cycle.
The menstrual cycle consists of following four phases
Menstrual (Bleeding) Phase:
The cycle starts with menstrual phase. It lasts for about 3-5 days and involves the following events
- If fertilisation does not occur, the unfertilised egg undergoes autolysis.
- Reduction of LH level causes regression of corpus luteum by autolysis and thus, a consequent fall in the progesterone level occurs in the blood.
- The endometrial lining of the uterus breaks down due to the deficiency of progesterone and is sloughed off. Blood vessels rupture, causing bleeding through vagina. The process is called menstruation or menstrual flow. It occurs only when ovum is not fertilised.
Follicular (Proliferative) Phase:
It lasts for about 14 days and involves the following events
- The primary follicles in the ovary grow to become a fully mature Graafian follicle.
- The endometrium of uterus regenerates through proliferation.
- The changes in the ovary and the uterus are induced by changes in the levels of pituitary and ovarian hormones, i.e. FSH and oestrogen.
- The secretion of gonadotropins (LH and FSH) increases gradually during the follicular phase and stimulates follicular development as well as secretion of oestrogens by the growing follicles.
Ovulatory Phase:
Both LH and FSH attain a peak level in the middle of cycle (about 14th day).
- Rapid secretion of LH leading to its maximum level during the midcycle is called LH surge. It induces rupture of Graafian follicle and thereby, the release of ovum, i.e. ovulation.
- The ovulation (ovulatory phase) is followed by the luteal phase.
Secretory (Luteal) Phase:
This phase lasts for about 10 days and involves the following events
- The remaining parts of Graafian follicle transform into the corpus luteum.
- The corpus luteum secretes large amounts of progesterone which is essential to maintain endometrium.
- The endometrium is necessary for implantation of the fertilised ovum and other events of pregnancy. During pregnancy, all events of the menstrual cycle stop and there is no menstruation. In the absence of fertilisation, the corpus luteum degenerates.
- This causes disintegration of endometrium, leading to menstruation.
Only the basal part of endometrium persists, which forms the source of new lining and a new cycle starts.
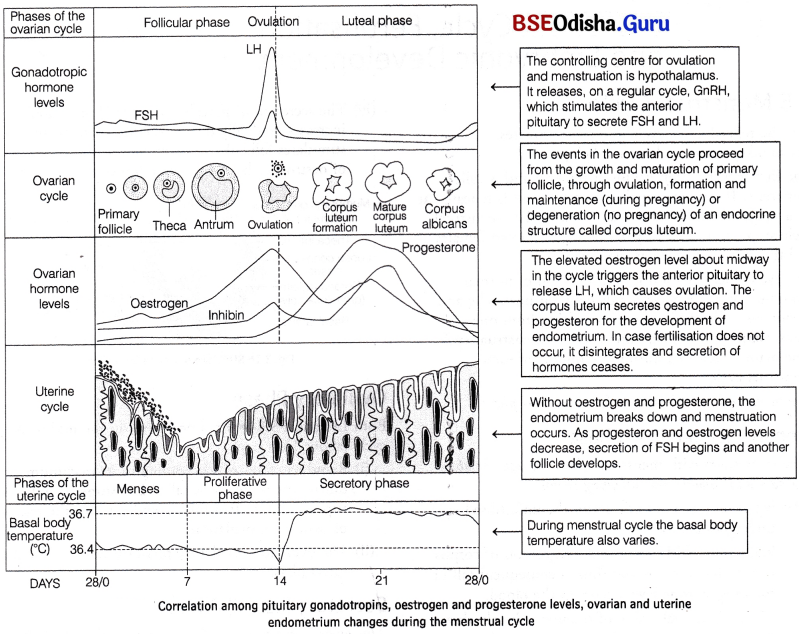
Menstrual cycle is absent temporarily during pregnancy and lactation periods and permanently after menopause. However, it can be absent due to stress, poor health, etc. Menstruation is also called ‘weeping of uterus for the lost ovum’ or ‘funeral of unfertilised egg’. Cyclic menstruation is an indicator of normal fertility period in women. It extends from menarche to menopause.
Question 5.
Draw a neat labelled diagram of the male reproductive system in human (Description is not required).
Answer:

Question 6.
Draw a neat labelled diagram of the female reproductive system in human (Description is . not required).
Answer:

Question 7.
Draw a neat labelled diagram of the cross-section through the human ovary (Description is not required).
Answer:

![]()
Question 8.
Draw a neat labelled diagram of seminiferous tubule (Description is not required).
Answer:

Question 9.
Draw a neat labelled diagram of a Graafian follicle (Description is not required).
Answer: