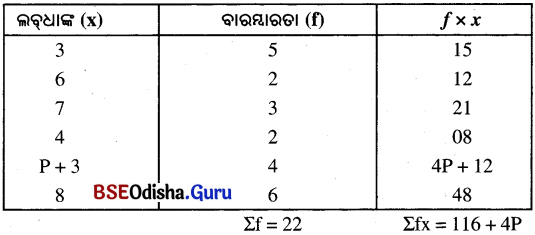
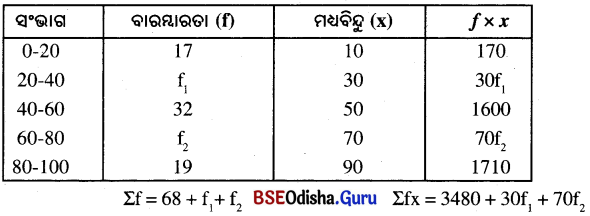
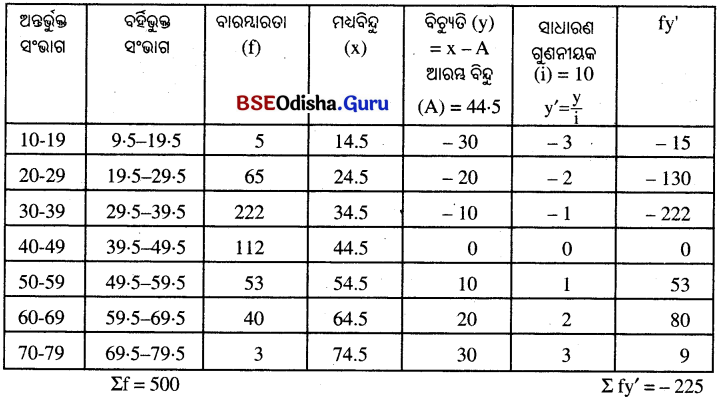
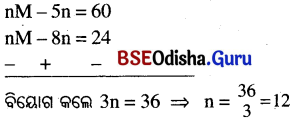Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter 1 ସେଟ୍ ପ୍ରକ୍ରିୟା ଏବଂ ସେଟ୍ର ପ୍ରୟୋଗ Ex 1(a) Textbook Exercise Questions and Answers.
BSE Odisha Class 9 Maths Solutions Algebra Chapter 1 ସେଟ୍ ପ୍ରକ୍ରିୟା ଏବଂ ସେଟ୍ର ପ୍ରୟୋଗ Ex 1(a)
Question 1.
ବନ୍ଧନୀରୁ ଠିକ୍ ଚିହ୍ନ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) a ___ {a, b, c} [∈, ∉, ⊂, =]
ସମାଧାନ:
a ∈ {a, b, c} [ ଏଠାରେ a, {a, b, c} ସେଟ୍ର ଏକ ଉପାଦାନ ଅଟେ ।
(ii) d ___ {a, b, c} [∈, ∉, ⊂, =]
ସମାଧାନ:
d ∉ {a, b, c} [କାରଣ d, {a, b, c} ସେଟ୍ର ଉପାଦାନ ନୁହେଁ ।
(iii) {a, c, d} ___ {a, b, c} [∈, ∉, =, ≠]
ସମାଧାନ:
{a, c, b} = {a, b, c} [କାରଣ ଉପାଦାନମାନଙ୍କ କ୍ରମ ବଦଳିଲେ ସେଟ୍ ଅପରିବର୍ତ୍ତିତ ରହେ ।]
(iv) {a, a, b, c} ___ {a, b, c} [∈, ∉, =, ≠]
ସମାଧାନ:
{a, a, b, c} = {a, b, c} [କାରଣ ସେଟ୍ର କୌଣସି ଉପାଦାନକୁ ଏକାଧ୍ଵକ ବାର ଲେଖୁଲେ ସେଟ୍ ଅପରିବର୍ତିତ ରହେ ।]
(v) {a} ___ {a, b, c} [=, ⊂, ∈, ⊃]
ସମାଧାନ:
{a} ⊂ {a, b, c} [ଏଠାର {a} ଏକ ସେଟ୍ ଏବଂ ଏହି ଉପାଦାନଟି {a, b, c} ସେଟ୍ରେ ରହିଥିବାରୁ ଉତ୍ତର {a} ⊂ {a, b, c} ହେବ ।]
(vi) {a, b, c} ___ {a} [=, ⊂, ∈, ≠]
ସମାଧାନ:
{a, b, c} # {a} [∵ {a, b, c} ସେଟ୍ ଓ {a} ସେଟ୍ ଉଭୟ ସମାନ ଉପାଦାନମାନଙ୍କୁ ନେଇ ଗଠିତ ସେଟ୍ ନୁହେଁ ।]

Question 2.
A = {1, 2, 3}, B = {3, 4, 5} ଓ C = {5, 6} ହେଲେ ନିମ୍ନଲିଖତ ସେଗୁଡ଼ିକୁ ନିରୂପଣ କର ।
(i) B ∪ C
ସମାଧାନ:
B ∪ C = {3, 4, 5} ∪ {5, 6} = {3, 4, 5, 6}
(ii) A ∪ B
ସମାଧାନ:
A ∪ B = {1, 2, 3} ∪ {3, 4, 5} = {1, 2, 3, 4, 5}
(iii) A ∪ C
ସମାଧାନ:
A ∪ C = {1, 2, 3} ∪ {5, 6} = {1, 2, 3, 5, 6}
(iv) B ∩ C
ସମାଧାନ:
B ∩ C = {3, 4, 5} ∩ {5, 6} = {5}
(v) A ∩ B
ସମାଧାନ:
A ∩ B = {1, 2, 3} ∩ {3, 4, 5} = {3}
(vi) A ∩ C
ସମାଧାନ:
A ∩ C = {1, 2, 3} ∩ {5, 6} = Φ ବା { }
(vii) B – C
ସମାଧାନ:
B – C = {3, 4, 5} – {5, 6} = {3, 4}
(viii) A – B
ସମାଧାନ:
A – B = {1, 2, 3} – {3, 4, 5} = {1, 2}
(ix) A – C
ସମାଧାନ:
A – C = {1, 2, 3} – {5, 6} = {1, 2, 3}
(x) C – B
ସମାଧାନ:
C – B = {5, 6} – {3, 4, 5} = {6}
(xi) B – A
ସମାଧାନ:
B – A = {3, 4, 5} – {1, 2, 3} = {4, 5}
(xii) C – A
ସମାଧାନ:
C – A= {5, 6} – {1, 2, 3} = {5, 6}
Question 3.
ଆମ ଆଲୋଚନା ଅନ୍ତର୍ଗତ ସେଗୁଡ଼ିକ ନିମ୍ନରେ ଦିଆଯାଇଛି ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ବ୍ୟାପକ ସେଟ୍ E ସ୍ଥିର କର ।
(i) A = {2, 3, 5}, B = {1, 2, 3, 4, 5, 8}, C = {10, 11}, D = {6, 7, 9}
ସମାଧାନ:
E = A ∪ B ∪ C ∪ D
= {2, 3, 5} ∪ {1, 2, 3, 4, 5, 8} ∪ {10, 11} ∪ {6, 7, 9}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
ଏହାକୁ ସୂତ୍ର ପଦ୍ଧତିରେ ଲେଖିଲେ E = {x | x ∈ N ଓ x ≤ 11}
ଅଥବା E = {x | x ∈ N} ଓ x < 12
କାରଣ A, B, C, D ପ୍ରତ୍ୟେକ N ସେଟ୍ର ଉପସେଟ୍ ଅଟେ ।
(ii) A = {1, 6, 12}, B = {1, 3, 5, 7, 9, 11}, C = {2, 4, 6, 8, 10}
ସମାଧାନ:
E = A ∪ B ∪ C
= {1, 6, 12} ∪ {1, 3, 5, 7, 9, 11} ∪ {2, 4, 6, 8, 10}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
‘E’ ସେଟ୍କୁ ସୂତ୍ର ପଦ୍ଧତିରେ ଲେଖୁଲେ = {x | x ∈ N ଏବଂ x ≤ 12}
ଅଥବା E = {x | x ∈ N}
କାରଣ A, B, C, D ସେଟ୍ ପ୍ରତ୍ୟେକ N ସେଟ୍ର ଉପସେଟ୍ ଅଟନ୍ତି ।
Question 4.
A = {1, 2, 3, 4}, B = {4, 5, 6, 7}, C = {6, 7, 8, 9} ହେଲେ ନିମ୍ନଲିଖୂତ ଭକ୍ତିମାନଙ୍କର ସତ୍ୟତା ପରୀକ୍ଷା କର ।
(i) A ∪ B = B ∪ A
ସମାଧାନ:
A ∪ B = B ∪ A
L.H.S. = A ∪ B = {1, 2, 3, 4} ∪ {4, 5, 6, 7} = {1, 2, 3, 4, 5, 6, 7}
R.H.S. = B ∪ A = {4, 5, 6, 7} ∪ { 1, 2, 3, 4}
= {1, 2, 3, 4, 5, 6, 7}
L.H.S. = R.H.S. (ପ୍ରମାଣିତ)
(ii) B ∩ C = C ∩ B
ସମାଧାନ:
B ∩ C = C ∩ B
L.H.S. = B ∩ C = {4, 5, 6, 7} ∩ {6, 7, 8, 9} = {6, 7}
R.H.S. = C ∩ B = {6, 7, 8, 9} ∩ {4, 5, 6, 7} = {6, 7}
L.H.S. = R.H.S. (ପ୍ରମାଣିତ)
(iii) A ∪ (B ∪ C) = (A ∪ B) ∪ C
ସମାଧାନ:
A ∪ (B ∪ C) = (A ∪ B) ∪ C
L.H.S. = A ∪ (B ∪ C) = A ∪ ({4, 5, 6, 7} ∪ {6, 7, 8, 9})
= {1,2, 3, 4} ∪ {4, 5, 6, 7, 8, 9} = {1, 2, 3, 4, 5, 6, 7, 8, 9}
R.H.S. = (A ∪ B) ∪ C = ({ 1, 2, 3, 4} ∪ {4, 5, 6, 7} ∪ C
= {1, 2, 3, 4, 5, 6, 7} ∪ {6, 7, 8, 9} = {1, 2, 3, 4, 5, 6, 7, 8, 9}
L.H.S. = R.H.S. (ପ୍ରମାଣିତ)
(iv) A ∩ (B ∩ C) = (A ∩ B) ∩ C
ସମାଧାନ:
A ∩ (B ∩ C) = (A ∩ B) ∪ C
L.H.S. = A ∩ (B∩ C) = A ∩ ({4, 5, 6, 7} ∩ {6, 7, 8, 9},
= {1, 2, 3, 4} ∩ {6, 7} = Φ
R.H.S. = (A ∩ B) ∩ C = {1, 2, 3, 4} ∪ {4, 5, 6, 7} ∩ C
= {4} ∩ {6, 7, 8, 9} = Φ
L.H.S = R.H.S. (ପ୍ରମାଣିତ)
(v) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
ସମାଧାନ:
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
L.H.S. = A ∪ (B ∩ C) = A ∪ {4, 5, 6, 7} ∩ {6, 7, 8, 9}
= {1, 2, 3, 4} ∪ {6, 7} = {1, 2, 3, 4, 6, 7}
R.H.S. = (A ∪ B) ∩ (A ∪ C)
= [{1, 2, 3, 4} ∪ {4, 5, 6, 7}] ∩ [{1, 2, 3, 4} ∪ {6, 7, 8, 9}]
= {1, 2, 3, 4, 5, 6, 7 } ∩ {1, 2, 3, 4, 6, 7, 8, 9 } = {1, 2, 3, 4, 6, 7 }
L.H.S = R.H.S. (ପ୍ରମାଣିତ)
(vi) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ B)
ସମାଧାନ:
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
L.H.S. = A ∩ (B ∪ C) = A ∩ {4, 5, 6, 7} ∪ {6, 7, 8, 9}
= {1, 2, 3, 4} ∩ {4, 5, 6,7, 8, 9} = {4}
R.H.S. = (A ∩ B)∪ (A ∩ C)
= {1, 2, 3, 4} ∩ {4, 5, 6, 7} ∪ {1, 2, 3, 4} ∩ {6, 7, 8, 9}
= {4} ∩ Φ = {4}
L.H.S. = R.H.S. (ପ୍ରମାଣିତ)
(vii) A – B ≠ B – A
ସମାଧାନ:
A -B ≠ B – A
L.H.S. = A – B = {1, 2, 3, 4} – {4, 5, 6, 7} = {1, 2, 3}
R.H.S. = B – A = {4, 5, 6, 7} – {1, 2, 3, 4} = {5, 6, 7}
L.H.S. ≠ R.H.S. (ପ୍ରମାଣିତ)
(viii) (A – B) – C ≠ A – (B – C)
ସମାଧାନ:
(A – B) – C ≠ A – (B – C)
L.H.S. = (A – B) – C = {1, 2, 3, 4} – {4, 5, 6, 7} – C
= {1, 2, 3} – {6, 7, 8, 9} = {1, 2, 3}
R.H.S. = A – (B – C)
= A – [{4, 5, 6, 7} – {6, 7, 8, 9}] = {1, 2, 3, 4} – {4, 5} = { 1, 2, 3}
ଏଠାରେ (A – B) – C = A – (B – C) ଉକ୍ତିଟି ସତ୍ୟ ହେଲେ ଉଦ୍ଭଟି ସର୍ବଦା ସତ୍ୟ ନୁହେଁ ।
 A = {1, 2, 3, 4, 8}, B = {4, 5, 6, 7}, C = {6, 7, 8, 9}
A = {1, 2, 3, 4, 8}, B = {4, 5, 6, 7}, C = {6, 7, 8, 9}
L.H.S. = (A – B) – C = ({1, 2, 3, 4, 8} – {4, 5, 6, 7}) – C
= {1,2, 3, 8} – {6, 7, 8, 9} = {1, 2, 3}
R.H.S. = A – (B – C) = A – ({4, 5, 6, 7} – {6, 7, 8, 9})
= {1, 2, 3, 4, 8} – {4, 5} = {1, 2, 3,8}
ଏଠାରେ L.H.S. ≠ R.H.S.
∴ (A – B) – C ≠ A – (B – C) (ପ୍ରମାଣିତ)

Question 5.
ନିମ୍ନରେ ସୂଚିତ ପ୍ରତ୍ୟେକ ସେଟ୍, ବନ୍ଧନୀ ମଧ୍ଯରେ ଦିଆଯାଇଥିବା କେଉଁ ସେଟ୍ ସହ ସମାନ ?
(i) {x | x2 – 1 = 0} [Φ, {1}, {-1}, {1, -1}, {0, 1}]
ସମାଧାନ:
{1, -1}
[କାରଣ x2 – 1 = 0 ⇒ (x + 1) (x – 1) = 0
⇒ x = -1 ବା x = 1
(ii) {x | x ସଂଖ୍ୟାଟି 6 ଅପେକ୍ଷା କ୍ଷୁଦ୍ରତର ଯୁଗ୍ମ ଗଣନ ସଂଖ୍ୟା} [Φ, {1, 2, 3, 4, 5}, {2, 4}, {1, 3, 5}]
ସମାଧାନ:
{2, 4}; କାରଣ 6 ଠାରୁ ସାନ ଯୁଗ୍ମ ସଂଖ୍ୟା 2, 4 ଅଟେ ।
(iii) {x | x ଏକ ଯୁଗ୍ମ ଗଣନ ସଂଖ୍ୟା ଓ 2 < x < 4} [Φ, (2), (4), (2, 4)]
ସମାଧାନ:
Φ ; କାରଣ 2 ଓ 4 ମଧ୍ୟରେ କୌଣସି ଯୁଗ୍ମ ଗଣନ ସଂଖ୍ୟା ନାହିଁ ।
(iv) {x| x = N*, x ≤ 3} [{0, 1, 2}, {0, 3}, {1, 2}, {0, 1, 2, 3}]
ସମାଧାନ:
{0, 1, 2, 3}; [କାରଣ 3 ଏବଂ 3 ଠାରୁ ସାନ ସଂପ୍ରସାରିତ ସ୍ଵାଭାବିକ୍ ସଂଖ୍ୟା 0, 1, 2, 3]
Question 6.
A = {a, b, d, e, p}, ଓ B = (b, p, a, n, m, x, y}, C = {n, x, z, s, t} 
(i) (A – B) ∪ (A ∩ B)
ସମାଧାନ:
(A – B) ∪ (A ∩ B)
A – B = {a, b, d, e, p} – {b, p, a, n, m, x, y} = {d, e}
A ∩ B = {a, b, d, e, p} ∩ {b, p, a, n, m, x, y} = {a, b, p}
(A – B) ∪ (A n B) = {d, e} ∪ {a, b, p} = {a, b, d, e, p}
(ii) (A ∪ B) ∩ (B ∪ C)
ସମାଧାନ:
(A ∪ B) n (B ∪ C)
A ∪ B = {a, b, d, e, p} ∪ {b, p, a, n, m, x, y}
= {a, b, d, e, m, n, p, x, y}
B ∪ C = {b, p, a, n, m, x, y} ∪ {n, x, z, s, t}
= {a, b, m, n, p, s, t, x, y, z}
(A ∪ B) n (B ∪ C) = {a, b, d, e, m, n, p, x, y} ∩ {a, b, m, n, p, s, t, x, y, z}
= {a, b, m, n,p, x, y}
(iii) (A ∩ B) ∪ (B – C) 
ସମାଧାନ:
(A ∩ B) ∪ (B – C)
(A ∩ B) = {a, b, d, e, p} ∩ {b, p, a, n, m, x, y} = {a, b, p}
(B – C) = {b, p, a, n, m, x, y} – {n, x, z, s, t}
= {a, b, m, p, y}
(A ∩ B) ∪ (B – C) = {a, b, p} ∪ {a, b, m, p, y}
= {a, b, m, p, y}
Question 7.
A = {a, b, c, d, e}, B = {a, e, i, o, u} 
(i) (A – B) ∩ (A ∩ B) = Φ,
ସମାଧାନ:
A – B = {a, b, c, d, e} – {a, e, i, o, u} = {b, c, d}
A ∩ B = {a, b, c, d, e} ∩ {a, e, i, o, u} = {a, e}
L.H.S. = (A – B) ∩ (A ∩ B) = {b, c, d} ∩ {a, e} = Φ = R.H.S. (ପ୍ରମାଣିତ)
(ii) (B – A) ∩ (A ∩ B)
ସମାଧାନ:
B – A = {a, e, i, o, u} – {a, b, c, d, e} = {i, o, u}
(A ∩ B) = {a, b, c, d, e} ∩ {a, e, i, o, u} = {a, e}
L.H.S. = (B – A) ∩ (A ∩ B) = {i, o, u} ∩ {a, e} = Φ = R.H.S (ପ୍ରମାଣିତ)
(iii) (A – B) ∩ (B – A) = Φ
ସମାଧାନ:
A – B = {a, b, c, d, e} – {a, e, i, o, u} = {b, c, d}
B – A = {a, e, i, o, u} – {a, b, c, d, e} = {i, o, u}
L.H.S. = (A – B) ∩ (B – A) = {b, c, d} ∩ {i, o, u} = Φ = R.H.S. (ପ୍ରମାଣିତ)
Question 8.
(i) (A ∩ B) ∪ (A – B)
ସମାଧାନ:

(ii) (A ∩ B) ∪ (B – A)
ସମାଧାନ:

(iii) (A ∪ B) – (A ∩ B)
ସମାଧାନ:

Question 9.
ଏକ ଉଦାହରଣ ନେଇ ଦର୍ଶାଅ ଯେ—
(A – B) ∪ (B – A) = (A ∪ B) – (A ∩ B) (ଯେଉଁଠାରେ A ଓ B ପ୍ରତ୍ୟେକ ସସୀମ ସେଟ୍)
ସମାଧାନ:
ଦାନେକର A = {1, 2, 3, 4, 5, 6), B = {3, 5, 6, 8, 9}
L.H.S. = (A – B) ∪ (B – A)
= ({1, 2, 3, 4, 5, 6} – {3, 5, 6, 8, 9}) ∪ ({3, 5, 6, 8, 9} – { 1, 2, 3, 4, 5, 6})
= {1, 2, 4} ∪ {8, 9} = {1, 2, 4, 8, 9}
R.H.S. = (A ∪ B) – (A∩ B)
= ({1, 2, 3, 4, 5, 6} ∪ {3, 5, 6, 8, 9}) – ({1, 2, 3, 4, 5, 6} ∩ {3, 5, 6, 8, 9})
= {1, 2, 3, 4, -5, 6, 8, 9} – {3, 5, 6} = {1, 2, 4, 8, 9}
L.H.S. = R.H.S. (ପ୍ରମାଣିତ)

Question 10.
ଯଦି In = {1,2,3, 4 ….. n} ହୁଏ ତେବେ I20 – I16 ଏବଂ I16 – I20 ସେଟ୍ ଦ୍ଵୟକୁ ତାଲିକା ପ୍ରଣାଳୀରେ ଲେଖ ।
ସମାଧାନ:
In = {1, 2, 3, 4, ….. n}
I20 – I16 = {1, 2, 3,…..16, 17, 18, 19, 20} – {1, 2, 3,….., 16} = { 17, 18, 19, 20}
I16 – I20 = { 1, 2, 3,…..16} – { 1, 2, 3……16, 17, 18, 19, 20} = Φ
![]()