Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 11 ପରିମିତି Ex 11.2 Textbook Exercise Questions and Answers.
BSE Odisha Class 6 Maths Solutions Chapter 11 ପରିମିତି Ex 11.2
Question 1.
ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ରର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ 7 ସେ.ମି. । ଏହାର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ବର୍ଗକ୍ଷେତ୍ରର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ = 7 ସେ.ମି.
ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (7 × 7) ବ.ସେ.ମି. = 49 ବ.ସେ.ମି.
Question 2.
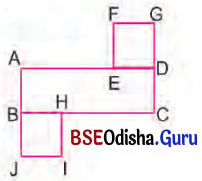
ପାର୍ଶ୍ଵ ଚିତ୍ରରେ ABCD ଏକ ଆୟତଚିତ୍ର ଏବଂ EDGF ଓ BJIH ପ୍ରତ୍ୟେକ ଗୋଟିଏ ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ର ।
AD = 20 ସେ.ମି., AB = 9 ସେ.ମି., ED = 7 ସେ.ମି. ଓ BJ = 8 ସେ.ମି. ହେଲେ, ସମଗ୍ର କ୍ଷେତ୍ରର ପରିସୀମା ଓ କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
AD = 20 ସେ.ମି., AB = 9 ସେ.ମି., ED = 7 ସେ.ମି. ଓ BJ = 8 ସେ.ମି.
ABCD କ୍ଷେତ୍ରର ପରିସୀମା = 2 × (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ )
= 2 × (20 + 9) ସେ.ମି. = 58 ସେ.ମି.
EF + FG + GD = (7 + 7 + 7) ସେ.ମି. = 21 ସେ.ମି.
BJ + JI + IH = (8 + 8 + 8) ସେ.ମି. = 24 ସେ.ମି.
∴ ସମଗ୍ର କ୍ଷେତ୍ରର ପରିସୀମା = (58 + 21 + 24) ସେ.ମି. = 103 ସେ.ମି.
ମୋଟ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ABCD ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ + EDGF ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ + BJIH ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ
= (20 × 9) ବର୍ଗ ସେ.ମି. + (7 × 7) ବର୍ଗ ସେ.ମି. + (8 × 8) ବର୍ଗ ସେ.ମି.
= (180 + 49 + 64 ) ବର୍ଗ ସେ.ମି.
= 293 ବର୍ଗ ସେ.ମି.
![]()
Question 3.
ଗୋଟିଏ ବର୍ଗାକୃତି ବିଶିଷ୍ଟ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ 64 ବର୍ଗ.ମି. । ଏହାର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ କେତେ ?
(ସୂଚନା : ଏଠାରେ 64 କୁ ମୌଳିକ ଗୁଣନୀୟକ ମାନଙ୍କର ଗୁଣଫଳ ରୂପେ ପ୍ରକାଶ କରି 64 କୁ ଦୁଇଟି ସମାନ ସଂଖ୍ୟାର ଗୁଣଫଳରେ ପ୍ରକାଶ କରାଯାଇ ପାରିବ । ସେହି ସଂଖ୍ୟା ଦୁଇଟି ମଧ୍ୟରେ ଗୋଟିଏ ହେବ 64 ର ବର୍ଗମୂଳ ।)
ସମାଧାନ:
ବର୍ଗାକୃତିବିଶିଷ୍ଟ କ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = କ୍ଷେତ୍ରଫଳର ବର୍ଗମୂଳ
= \(\sqrt{64}\) ବ.ମି.
= \(\sqrt{4 \times 4 \times 2 \times 2}\)
= 4 × 2 = 8 ମି.
Question 4.
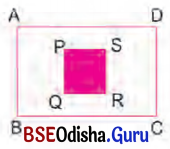
ABCD ଗୋଟିଏ ଆୟତାକୃତି ବିଶିଷ୍ଟ ବଗିଋକୁ ସୂରଉଛି। ଏହି ଜମିରେ ଖୋଳାଯାଇଥବା ଏକ ବର୍ଗାକୃତି ବିଶିଷ୍ଟ ପୋଖରୀର ଚିତ୍ର ହେଉଛି PQRS । AB = 40 ମି., AD = 50 ମି. ଓ PQ = 22 ମି. ହେଲେ, ବଗିର ଭିତରେ ଥିବା ବଳକା ଜମିର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ABCD ଆୟତାକୃତି ବଗିଚାର ଦୈର୍ଘ୍ୟ = 50 ମି. ଓ ପ୍ରସ୍ଥ = 40 ମି.
∴ ABCD ଆୟତାକାର ବଗିଚାର କ୍ଷେତ୍ରଫଳ = ଦୈର୍ଘ୍ୟ × ପ୍ରସ୍ଥ = (50 × 40) ବ.ମି. = 2000 ବ.ମି.
PQRS ବର୍ଗୀକୃତି ପୋଖରୀର ବାହୁ = 22 ମି.
PQRS ବର୍ଗାକାର ପୋଖରୀର କ୍ଷେତ୍ରଫଳ = ଦୈର୍ଘ୍ୟ × ଦୈର୍ଘ୍ୟ = (22 × 22) ବ.ମି. = 484 ବ.ମି.
∴ ବଗିଚା ଭିତରେ ଥିବା ବଳକା ଜମିର କ୍ଷେତ୍ରଫଳ = 2000 ବ.ମି. – 484 ବ.ମି. = 1516 ବ.ମି.
Question 5.
ଗୋଟିଏ ଆୟତାକୃତି ବିଶିଷ୍ଟ ଜମିର ଦୈର୍ଘ୍ୟ 30 ମିଟର ଓ ପ୍ରସ୍ଥ 28 ମିଟର। ଏକ ବର୍ଗମିଟର ଜମିର ଦାମ୍ 275 ଟଙ୍କା ହେଲେ, ସେହି ଜମିକୁ ବିକ୍ରି କରି ଜମି ମାଲିକ କେତେ ଟଙ୍କା ପାଇବେ ?
ସମାଧାନ:
ଆୟତାକୃତି ଜମିର ଦୈର୍ଘ୍ୟ = 30 ମି. ଓ ପ୍ରସ୍ଥ = 28 ମି. ।
ଆୟତାକୃତି ଜମିର କ୍ଷେତ୍ରଫଳ = (30 × 28) ବ.ମି. = 840 ବ.ମି.
1 ବ.ମି. ଜମିର ଦାମ୍ = 275 ଟଙ୍କା ।
∴ 840 ବ.ମି. ଜମିର ଦାମ୍ = 275 × 840 = 2,31,000 ଟଙ୍କା ।
∴ ସେହି ଜମିକୁ ବିକ୍ରିକରି ଜମିମାଲିକ 2,31,000 ଟଙ୍କା ପାଇବ ।
Question 6.
ଗୋଟିଏ ଟେବୁଲର ଉପରିଭାଗ ବର୍ଗାକୃତି ବିଶିଷ୍ଟ । ଏହାର ପ୍ରତ୍ୟେକ ଧାରର ଦୈର୍ଘ୍ୟ 1 ମିଟର 20ସେ.ମି., ଏହାର ଉପରିଭାଗର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ବର୍ଗୀକୃତି ଟେବୁଲର ପ୍ରତ୍ୟେକ ଧାରର ଦୈର୍ଘ୍ୟ 1 ମି. 20 ସେ.ମି. = 120 ସେ.ମି.
∴ ଉପରିଭାଗର କ୍ଷେତ୍ରଫଳ = (ଦୈର୍ଘ୍ୟ)2 = (120 × 120) ବର୍ଗ ସେ.ମି. = 14400 ବର୍ଗ ସେ.ମି.
Question 7.
ତଳେ ତିନୋଟି ଆୟତ କ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ଦିଆଯାଇଛି ।
(କ) 9 ମି. ଓ 6 ମି. (ଖ) 17 ମି. ଓ 3 ମି. (ଗ) 15 ମି. ଓ 4 ମି.
କେଉଁ ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ସର୍ବାଧିକ ?
କେଉଁ ଆୟତକ୍ଷେତ୍ରର ପରିସୀମା ସର୍ବାଧିକ ?
ସମାଧାନ:
(କ) ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (9 × 6) ବ.ମି. = 54 ବ.ମି.
ଆୟତକ୍ଷେତ୍ରର ପରିସୀମା = 2 (9 + 6) ମି. = 300 ମି.
(ଖ) ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (17 × 3) ବ.ମି. = 51 ବ.ମି.
ପରିସୀମା = 2 (17 + 3) ମି. = 40 ମି.
(ଗ) ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (15 × 4) ବ.ମି. = 60 ବ.ମି.
ପରିସୀମା = 2 (15 + 4) ମି. = 38 ମି.
ତୃତୀୟ ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ସର୍ବାଧ୍କ ।
ଦ୍ୱିତୀୟ ଆୟତକ୍ଷେତ୍ରର ପରିସୀମା ସର୍ବାଧ୍କ ।
![]()
Question 8.
ଗୋଟିଏ ଆୟତାକୃତି ବିଶିଷ୍ଟ କାର୍ଡ଼ବୋର୍ଡ଼ର କ୍ଷେତ୍ରଫଳ 36 ବର୍ଗ ସେ.ମି. । ଏହାର ଦୈର୍ଘ୍ୟ ଓ ସେ.ମି. ହେଲେ ଏହାର ପ୍ରଭୁ କେତେ ?
ଉପରେ ଦିଆଯାଇଥିବା ପ୍ରଶ୍ନକୁ ଭଲଭାବେ ପଢ଼ ଓ ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ –

(i) ଆୟତାକୃତି ବିଶିଷ୍ଟ କାର୍ଡ଼ ବୋର୍ଡ଼ର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
36 ବ.ସେ.ମି.
(ii) ଏହାର ଦୈର୍ଘ୍ୟ କେତେ ?
ସମାଧାନ:
9 ସେ.ମି.
(iii) କୌଣସି ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ଓ ଦୈର୍ଘ୍ୟ ଜଣାଥିଲେ ତା’ର ପ୍ରସୁ କିପରି ବାହାରେ ?
ସମାଧାନ:
ପ୍ରସ୍ଥ = କ୍ଷେତ୍ରଫଳ ÷ ଦୈର୍ଘ୍ୟ
(iv) ଏଠାରେ ଆୟତାକୃତି ବିଶିଷ୍ଟ କାର୍ଡ଼ବୋର୍ଡ଼ର ପ୍ରସୁ କେତେ ହେବ ?
ସମାଧାନ:
ପ୍ରସ୍ଥ = 36 ÷ 9 = 4 ସେ.ମି.
Question 9.
16 ମିଟର ଦୈର୍ଘ୍ୟ ଓ 12 ମିଟର ପ୍ରସ୍ଥ ବିଶିଷ୍ଟ ଗୋଟିଏ କୋଠରିର ଚଟାଣରେ ଟାଇଲ ବିଛାଗଲା । ଏହି କାର୍ଯ୍ୟ ଲାଗି କେତୋଟି 2 ମି. ଦୀର୍ଘ ବାହୁବିଶିଷ୍ଟ ବର୍ଗାକୃତି ବିଶିଷ୍ଟ ଟାଇଲ ଦରକାର ହେବ ?
ସମାଧାନ:
ଚଟାଣର ଦୈର୍ଘ୍ୟ = 16 ମି. ଓ ପ୍ରସ୍ଥ = 12 ମି.
ଚଟାଣର କ୍ଷେତ୍ରଫଳ = (16 × 12) ବ.ମି. = 192 ବ.ମି.
ବର୍ଗାକୃତି ଟାଇଲର ଦୈର୍ଘ୍ୟ 2 ମି. ହେଲେ ଟାଇଲର କ୍ଷେତ୍ରଫଳ = (2 × 2) ବ.ମି. = 4 ବ.ମି.
∴ ଚଟାଣ ପାଇଁ ଟାଇଲ ଦରକାର = 192 ÷ 4 = 48 ଟି
Question 10.
ଗୋଟିଏ ବର୍ଗାକୃତି ବିଶିଷ୍ଟ ଜମିର ପରିସୀମା ହେଉଛି 124 ମିଟର। ଏହି ଜମିକୁ ଋଷ କରିବା ପାଇଁ ପ୍ରତି ବର୍ଗମିଟରକୁ 4 ଟଙ୍କା ହିସାବରେ ମୋଟ କେତେ ଟଙ୍କା ଦରକାର ?
ସମାଧାନ:
ଗୋଟିଏ ବଗାକୃତି ବିଶିଷ୍ଟ ଜମିର ପରିସୀମା ହେଉଛି 124 ମିଟର ।
ବର୍ଗୀକୃତି ଜମିର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ = 124 ÷ 4 = 31 ମିଟର
ବର୍ଗୀକୃତି ଜମିର କ୍ଷେତ୍ରଫଳ = (31 × 31) ବ.ମି. = 961 ବ.ମି.
1 ବ.ମି.କୁ ଚାଷ କରିବାପାଇଁ ଲାଗେ 4 ଟଙ୍କା ।
∴ 961 ବ.ମି.କୁ ଚାଷ କରିବାପାଇଁ ଲାଗେ 4 × 961 = 3844 ଟଙ୍କା ।
Question 11.
12 ମିଟର ଦୀର୍ଘ ଗୋଟିଏ ଆୟତାକୃତି ବିଶିଷ୍ଟ ଜମିର କ୍ଷେତ୍ରଫଳ 120 ବର୍ଗମିଟର। ଏହାର ଊରିପାଖରେ ବାଡ଼ଦେବାପାଇଁ 1 ମିଟରକୁ ଯଦି 10 ଟଙ୍କା ଆବଶ୍ୟକ ପଡ଼େ, ତେବେ ଜମିଟିର ଋରିପାଖକୁ ବାଡ଼ଦେବା ପାଇଁ ମୋଟ କେତେ ଟଙ୍କା ଦରକାର ହେବ ?
ସମାଧାନ:
12 ମି. ଦୈର୍ଘ୍ୟ ଗୋଟିଏ ଆୟତାକୃତି ବିଶିଷ୍ଟ ଜମିର କ୍ଷେତ୍ରଫଳ = 120 ବ.ମି.
∴ ସେହି ଜମିର ପ୍ରସ୍ଥ = କ୍ଷେତ୍ରଫଳ ÷ ଦୈର୍ଘ୍ୟ = 120 ବ.ମି. – 12 ମି. = 10 ମି.
∴ ସେହି ଜମିର ପରିସୀମା = 2 (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ) = 2 (12 + 10) ମି. = 2 × 22 ମି. = 44 ମି.
1 ମିଟରକୁ ବାଡ଼ଦେବା ପାଇଁ ଖର୍ଚ୍ଚ ହୁଏ = 10 ଟଙ୍କା
44 ମିଟରକୁ ବାଡ଼ଦେବା ପାଇଁ ଖର୍ଚ୍ଚ ହେବ = 10 × 44 = 440 ଟଙ୍କା
∴ ଜମିର ଚାରିପାଖକୁ ବାଡ଼ଦେବା ପାଇଁ ମୋଟ 440 ଟଙ୍କା ଦରକାର ହେବ ।
![]()
Question 12.
20 ସେ.ମି. ଦୀର୍ଘ ତାରଟିଏ ନେଇ ତାକୁ ବଙ୍କାଇ ବିଭିନ୍ନ ମାପ ବିଶିଷ୍ଟ ଆୟତକ୍ଷେତ୍ରରେ ପରିଣତ କରାଯିବ (ଯେପରି ପ୍ରତ୍ୟେକର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥର ମାପ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟକ ସେ.ମି. ହେବ)। ତାରଟିକୁ କେତୋଟି ଭିନ୍ନ ଆୟତକ୍ଷେତ୍ରରେ ପରିଣତ କରିବା ସମ୍ଭବ ? ସେମାନଙ୍କ ମଧ୍ୟରୁ କେତୋଟି ବର୍ଗାକୃତି ବିଶିଷ୍ଟ ହେବ ? ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ପରିସୀମା ଓ କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ଆୟତକ୍ଷେତ୍ରର ପରିସୀମା = 20 ସେ.ମି. ଅର୍ଥାତ୍, 2 × (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ) = 20 ସେ.ମି.
ଅର୍ଥାତ୍, ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ = 20 ÷ 2 = 10 ସେ.ମି.
କ୍ଷେତ୍ରଟିକୁ ଭିନ୍ନ ଭିନ୍ନ କ୍ଷେତ୍ରରେ ପରିଣତ କଲେ ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ଯଥାକ୍ରମେ
9 ଓ 1, 8 ଓ 2, 7 ଓ 3,6 ଓ 4, 5 ଓ 5 ।
ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ଯଥାକ୍ରମେ 9 ସେ.ମି. ଓ 1 ସେ.ମି. ହେଲେ ପରିସୀମା
= 2 (9 + 1) = 20 ସେ.ମି. ଏବଂ କ୍ଷେତ୍ରଫଳ = 9 × 1 = 9 ବର୍ଗ ସେ.ମି.
ଆୟତ କ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ଯଥାକ୍ରମେ 8 ସେ.ମି. ଓ 2 ସେ.ମି.ହେଲେ
ପରିସୀମା = 2 (8 + 2) = 20 ସେ.ମି. ଓ କ୍ଷେତ୍ରଫଳ = 8 × 2 = 16 ବର୍ଗ ସେ.ମି.
ଆୟତ କ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ଯଥାକ୍ରମେ 7 ସେ.ମି. ଓ 3 ସେ.ମି. ହେଲେ
ପରିସୀମା = 2 (7 + 3) = 20 ସେ.ମି. ଓ କ୍ଷେତ୍ରଫଳ = 7 × 3 = 21 ବର୍ଗ ସେ.ମି.
ଆୟତ କ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ଯଥାକ୍ରମେ 6 ସେ.ମି. ଓ 4 ସେ.ମି. ହେଲେ
ପରିସୀମା = 2 (6 + 4) = 20 ସେ.ମି. ଓ କ୍ଷେତ୍ରଫଳ = 6 × 4 = 24 ବର୍ଗ ସେ.ମି.
ବର୍ଗକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ଉଭୟ 5 ସେ.ମି. ହେଲେ ପରିସୀମା = 4 × 5 = 20 ସେ.ମି. ଓ
କ୍ଷେତ୍ରଫଳ = 5 × 5 = 25 ବର୍ଗ ସେ.ମି.
∴ 4 ଟି ଭିନ୍ନ ଆୟତକ୍ଷେତ୍ର ଓ ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ର ହେବ ।
