Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 10 ପରିମିତି Ex 10.3 Textbook Exercise Questions and Answers.
BSE Odisha Class 7 Maths Solutions Chapter 10 ପରିମିତି Ex 10.3
Question 1.
ନିମ୍ନଲିଖ୍ ଚିତ୍ରଗୁଡ଼ିକର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
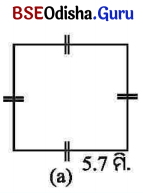
ସମାଧାନ:
ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = 5.7 ମି.
ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (5.7)2 ବର୍ଗ ମିଟର = 32.49 ବର୍ଗ ମିଟର
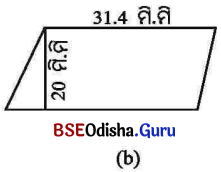
ସମାଧାନ:
ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଭୂମି = 31.4 ମି.ମି. ଓ ଉଚ୍ଚତା = 20 ମି.ମି.
ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 20 ମି.ମି. × 31.4 ମି.ମି. = 628 ବର୍ଗ ମି.ମି. ।
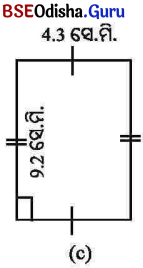
ସମାଧାନ:
ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ = 9.2 ସେ.ମି. ଓ ପ୍ରସ୍ଥ = 4.3 ସେ.ମି.
ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 9.2 ସେ.ମି. × 4.3 ସେ.ମି. = 39.56 ବର୍ଗ ସେ.ମି. ।
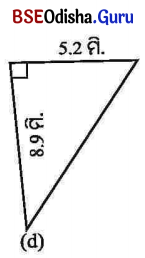
ସମାଧାନ:
ସମକୋଣୀ ତ୍ରିଭୁଜର ଭୂମି ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 8.9 ମି. ଓ 5.2 ମି. ।
ସମକୋଣୀ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × 8.9 ମି. × 5.2 ମି. = 23.14 ବର୍ଗ ସେ.ମି. ।
![]()
Question 2.
ଶୂନ୍ୟ କୋଠରିଗୁଡ଼ିକ ପୂରଣ କର ।
| କ୍ଷେତ୍ରର ନାମ | କ୍ଷେତ୍ରଫଳ | ଭୂମି | ଉକତା |
| ସାମାନ୍ତରିକ କ୍ଷେତ୍ର | 17 ବର୍ଗ. ମି. | 15 ମି. | ? |
| ତ୍ରିଭୁଜ | 1 ବର୍ଗ. ମି. | ? | 25 ବର୍ଗ. ମି. |
| ସାମାନ୍ତରିକ କ୍ଷେତ୍ର | 1 ବର୍ଗ. କି.ମି. | ? | 2000 ମି. |
| ଆୟତକ୍ଷେର | 15.36 ବର୍ଗ. ମି.ମି. | 48 ମି.ମି. | ? |
| ତ୍ରିଭୁଜ | 64.95 ବର୍ଗ. ମି. | ? | 15 ମି. |
ସମାଧାନ:
| କ୍ଷେତ୍ରର ନାମ | କ୍ଷେତ୍ରଫଳ | ଭୂମି | ଉକତା |
| ସାମାନ୍ତରିକ କ୍ଷେତ୍ର | 17 ବର୍ଗ. ମି. | 15 ମି. | 11.6 ମି. |
| ତ୍ରିଭୁଜ | 1 ବର୍ଗ. ମି. | 80 ମି. | 25 ବର୍ଗ. ମି. |
| ସାମାନ୍ତରିକ କ୍ଷେତ୍ର | 1 ବର୍ଗ. କି.ମି. | 500 ମି. | 2000 ମି. |
| ଆୟତକ୍ଷେର | 15.36 ବର୍ଗ. ମି.ମି. | 48 ମି.ମି. | 3.2 ମି.ମି. |
| ତ୍ରିଭୁଜ | 64.95 ବର୍ଗ. ମି. | 8.66 ମି. | 15 ମି. |
Question 3.
ଗୋଟିଏ ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ 500 ବର୍ଗ ମି. । ଏହାର ଦୈର୍ଘ୍ୟ 25 ମି. । ଏହାର ପ୍ରସ୍ଥ କେତେ ? ଏହି କ୍ଷେତ୍ରର ଚାରିପାଖରେ ବାଡ଼ ଦେବା ଲାଗି ମିଟର ପ୍ରତି ଟ. 9.50 ହିସାବରେ କେତେ ଖର୍ଚ୍ଚ ହେବ ?
ସମାଧାନ:
ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 500 ବର୍ଗ ମି. ଏବଂ ଦୈର୍ଘ୍ୟ = 25 ମି.
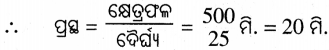
∴ ଆୟତ କ୍ଷେତ୍ରର ପରିସୀମା = 2 (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ) = 2(25 ମି. + 20 ମି.) = 2 × 45 ମି. = 90 ମି.
1 ମିଟରକୁ ବାଡ଼ ଦେବାରେ ଖର୍ଚ୍ଚ ଟ. 9.50 ।
90 ମିଟରକୁ ବାଡ଼ ଦେବାରେ ଖର୍ଚ୍ଚ = 90 × ଟ. 9.50 = 855 ଟଙ୍କା ।
∴ ଆୟତକ୍ଷେତ୍ରର ଚାରିପାଖରେ ବାଡ଼ ଦେବା ଲାଗି 855 ଟଙ୍କା ଖର୍ଚ୍ଚ ହେବ ।
Question 4.
15 ସେ.ମି. ଦୀର୍ଘ ବାହୁ ବିଶିଷ୍ଟ ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ, ଗୋଟିଏ 15 ସେ.ମି. ଭୂମି ବିଶିଷ୍ଟ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ ସହ ସମାନ ହେଲେ ତ୍ରିଭୁଜର ଉଚ୍ଚତା କେତେ ?
ସମାଧାନ:
ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = 15 ସେ.ମି. ।
∴ ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (15 ସେ.ମି.)2 = 225 ବର୍ଗ ସେ.ମି.
ତ୍ରିଭୁଜର ଭୂମିର ଦୈର୍ଘ୍ୟ = 15 ସେ.ମି. । ମନେକର ତ୍ରିଭୁଜର ଉଚ୍ଚତା × ସେ.ମି. ।
∴ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × 15 × x = 225
⇒ x = \(\frac{225×2}{15}\) = 15 × 2 = 30 ସେ.ମି.
∴ ତ୍ରିଭୁଜର ଉକତା 30 ସେ.ମି. ।
![]()
Question 5.
ତ୍ରିଭୁଜ ଆକୃତି ବିଶିଷ୍ଟ ଖଣ୍ଡେ ଜମିର ଭୂମି 60 ମି. ଓ ଉଚ୍ଚତା 20 ମି. । ବର୍ଗମିଟର ପ୍ରତି ଜମିର ଦାମ୍ 1500 ଟଙ୍କା ହେଲେ, ସେହି ତ୍ରିଭୁଜାକୃତି ବିଶିଷ୍ଟ ଜମିର ଦାମ୍ କେତେ ହେବ ସ୍ଥିର କର ।
ସମାଧାନ:
ତ୍ରିଭୁଜାକୃତି ଜମିର ଭୂମି = 60 ମି. ଓ ଉଚ୍ଚତା = 20 ମି. ।
ତ୍ରିଭୁଜାକୃତି ଜମିର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ଭୂମି × ଉଚ୍ଚତା = \(\frac{1}{2}\) × 60 ମି. × 20 ମି. = 600 ବର୍ଗମିଟର
1 ବର୍ଗମିଟର ଜମିର ଦାମ୍ 1500 ଟଙ୍କା ।
∴ 600 ବର୍ଗମିଟର ଜମିର ଦାମ୍ = 1500 ଟଙ୍କା × 600 = 9,00,000 ଟଙ୍କା ।
∴ ତ୍ରିଭୁଜାକୃତି ବିଶିଷ୍ଟ ଜମିର ଦାମ୍ 9,00,000 ଟଙ୍କା ।
Question 6.
50 ସେ.ମି. ଉଚ୍ଚତା ବିଶିଷ୍ଟ ଦୁଇଟି ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳର ସମଷ୍ଟି 1 ବର୍ଗ ମିଟର ଅଟେ । ଗୋଟିଏ ତ୍ରିଭୁଜର ଭୂମିର ଦୈର୍ଘ୍ୟ 160 ସେ.ମି. ହେଲେ, ଅନ୍ୟ ତ୍ରିଭୁଜର ଭୂମିର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ପ୍ରଥମ ତ୍ରିଭୁଜର ଭୂମିର ଦୈର୍ଘ୍ୟ 160 ସେ.ମି. ଓ ଉଚ୍ଚତା 50 ସେ.ମି. ।
∴ ପ୍ରଥମ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ଭୂମି × ଉଚ୍ଚତା
= \(\frac{1}{2}\) × 160 × 50 ବର୍ଗ ସେ.ମି. = 4000 ବର୍ଗ ସେ.ମି.
ଦୁଇଟି ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳର ସମଷ୍ଟି = 1 ବର୍ଗ ମିଟର = 10000 ବର୍ଗ ସେ.ମି.
∴ ଦ୍ବିତୀୟ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = (10000 – 4000) ବର୍ଗ ସେ.ମି. = 6000 ବର୍ଗ ସେ.ମି.
ଦ୍ବିତୀୟ ତ୍ରିଭୁଜର ଉଚ୍ଚତା = 50 ସେ.ମି.
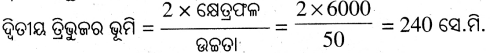
∴ ଅନ୍ୟ ତ୍ରିଭୁଜର ଭୂମିର ଦୈର୍ଘ୍ୟ 240 ସେ.ମି. ।
