Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 12 ଜ୍ୟାମିତିକ ଅଙ୍କନ Ex 12.6 Textbook Exercise Questions and Answers.
BSE Odisha Class 7 Maths Solutions Chapter 12 ଜ୍ୟାମିତିକ ଅଙ୍କନ Ex 12.6
Question 1.
EF = 7:2 ସେ.ମି., m∠E = 90°, m∠F = 90° କୁ ନେଇ Δ EFG ଅଙ୍କନ ସମ୍ଭବ କି? ତୁମର ଉତ୍ତର ସପକ୍ଷରେ କାରଣ ଲେଖ ।
ସମାଧାନ:
ଏଠାରେ m∠E + m∠F = 90° 90° = 180°
ତେଣୁ ତ୍ରିଭୁଜ ଅଙ୍କନ ସମ୍ଭବ ନୁହେଁ କାରଣ ∠G ର ମାନ ନାହିଁ ।
Question 2.
Δ XYZ ଅଙ୍କନ କର, ଯାହାର m∠X = 60°, m∠Y = 30° ଏବଂ XY = 62 ସେ.ମି.
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ:
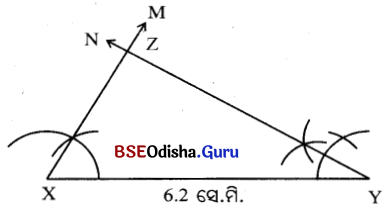
(i) \(\overline{\mathrm{XY}}\) ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ 6.2 ସେ.ମି.
(ii) XY ର X ବିନ୍ଦୁଠାରେ 60° ପରିମିତ କୋଣ ଅଙ୍କନ କର । ଫଳରେ \(\overrightarrow{\mathrm{XM}}\) ମିଳିବ ।
(iii) Y ବିନ୍ଦୁରେ XY ଉପରେ 30° ପରିମିତ କୋଣ ଅଙ୍କନ କର । ଫଳରେ \(\overrightarrow{\mathrm{YN}}\) ମିଳିବ । \(\overrightarrow{\mathrm{XM}}\) ଓ \(\overrightarrow{\mathrm{YN}}\) ଯେଉଁ ବିନ୍ଦୁରେ ଫରସ୍ପରକୁ ଛେଦ କରିବେ, ତା’ର ନାମ Z ହେଉ ।
∴ XYZ ଆବଶ୍ୟକୀୟ ତ୍ରିଭୁଜ ।
Question 3.
Δ KLM ଅଙ୍କନ କର, ଯାହାର LM = 5.4 ସେ.ମି., m∠L = 45°, m∠M = 90°
ସମାଧାନ:
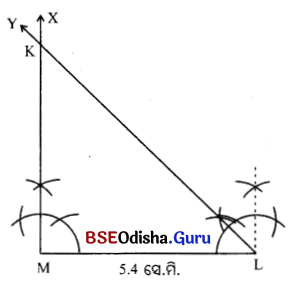2 ନମ୍ବର ‘ଅଙ୍କନ ପ୍ରଣାଳୀ’ ଅନୁସରଣ କରି Δ KLM ଅଙ୍କନ କର ।
(କ) ଏହି ତ୍ରିଭୁଜର ଅନ୍ୟ ଦୁଇ ବାହୁର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
MK = 5.4 ସେ.ମି., LK = 7.6 ସେ.ମି.
(ଖ) ଏହାର ∠N ର ପରିମାଣ କେତେ?
ସମାଧାନ:
∠K ର ପରିମାଣ ∠45° ।
(ଗ) ବାହୁ ମାନଙ୍କର ଦୈର୍ଘ୍ୟ ଅନୁଯାୟୀ ଏହା କି ପ୍ରକାରର ତ୍ରିଭୁଜ?
ସମାଧାନ:
(ଘ) କୋଣମାନଙ୍କର ମାପ ଅନୁଯାୟୀ ଏହା କି ପ୍ରକାରର ତ୍ରିଭୁଜ?
ସମାଧାନ:
ସମକୋଣୀ ତ୍ରିଭୁଜ
ଏବେ ଗୋଟିଏ ଟ୍ରେସିଂ-କାଗଜରେ ΔPQR ଅଙ୍କନ କର, ଯାହାର PR = 5.4 ସେ.ମି. m∠P=45°, m∠R=45°
PQR ତ୍ରିଭୁଜକୁ ଆଣି ΔLMN ଉପରେ ରଖ, ଯେପରି ΔPQR ର P ବିନ୍ଦୁ ଓ Q ବିନ୍ଦୁ ଯଥାକ୍ରମେ ΔLMN ର L ଓ M ବିନ୍ଦୁ ଉପରେ ରହିବ ।
ΔPQR ଓ ΔLMN ମଧ୍ଯରେ କ’ଣ ସମ୍ବନ୍ଧ ଅଛି ? କାରଣ କ’ଣ?
ସମାଧାନ:
ଟ୍ରେନିଂ କାଗଜରେ Δ PQR ଅଙ୍କନ କରିବା PR = 5.4 ସେ.ମି., ∠P = 45°, m∠R = 45° । ଦତ୍ତ ଅଛି ବର୍ତ୍ତମାନ Δ PQR କୁ Δ KLM ଉପରେ ଏପରି ପକାଇବ ଯେପରି M, Q ବିନ୍ଦୁ ସହ ମିଳିବ, K ଓ P ବିନ୍ଦୁ ପରସ୍ପର ମିଳିତ ହେବେ ଏବଂ L ଓ R ବିନ୍ଦୁ ମିଳିତ ହେବ ।
ଅର୍ଥାତ୍ Δ KML ≅ Δ PQR ହେବ, କାରଣ କୋ-ବା-କୋ ସର୍ବସମତା ରହିଛି ।
Question 4.
ABC Δ ଅଙ୍କନ କର, ଯାହାର BC = 5.3 ସେ.ମି., m∠B = 45° ଓ m∠A = 75° ଏହି ତ୍ରିଭୁଜ ଅଙ୍କନର ସୋପାନଗୁଡ଼ିକୁ ଲେଖ
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ:
m∠C = 180° – (m∠A + m∠B) = 180° – (75° + 45°) = 60°
(i) BC ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ 5.3 ସେ.ମି. ।
(ii) BC ର B ବିନ୍ଦୁଠାରେ 45° ପରିମାଣର କୋଣ ଅଙ୍କନ କରାଯିବା ଫଳରେ \(\overrightarrow{\mathrm{BZ}}\) ମିଳିବ।
(iii) C ବିନ୍ଦୁରେ \(\overline{\mathrm{CB}}\) ଉପରେ 60° ପରିମିତ କୋଣ ଅଙ୍କନ କର । ଫଳରେ \(\overrightarrow{\mathrm{CY}}\) ମିଳିବ। \(\overrightarrow{\mathrm{BZ}}\) ଓ \(\overrightarrow{\mathrm{CY}}\) ଯେଉଁ ବିନ୍ଦୁରେ ପରସ୍ପରକୁ ଛେଦ କରିବେ, ତା’ର ନାମ A ହେଉ ।
∴ Δ ABC ଆବଶ୍ୟକୀୟ ତ୍ରିଭୁଜ ।