Odisha State Board BSE Odisha 9th Class Maths Notes Algebra Chapter 2 ବାସ୍ତବ ସଂଖ୍ୟା will enable students to study smartly.
BSE Odisha Class 9 Maths Notes Algebra Chapter 2 ବାସ୍ତବ ସଂଖ୍ୟା
ବିଷୟବସ୍ତୁ ସମ୍ବନ୍ଧୀୟ ସୂଚନା ଓ ବିଶ୍ଳେଷଣ
ଗଣନ ସଂଖ୍ୟା ବା ସ୍ଵାଭାବିକ ସଂଖ୍ୟା (Natural Number) :
(i) ସମସ୍ତ ଗଣନ ସଂଖ୍ୟା (Counting Numbers) କିମୃ। ସ୍ଵାଭାବିକ ସଂଖ୍ୟା (Natural Numbers) ସେଟ୍ (N) = {1, 2, 3, …….} ।
(ii) ସମସ୍ତ ପୂର୍ଣସଂଖ୍ୟା (Integers) ମାନଙ୍କର ସେଟ୍ (Z) = {….. – 3, − 2, – 1, 0, 1, 2, 3,….} ଅର୍ଥାତ୍ ଗଣନ ସଂଖ୍ୟା, 0 (ଶୂନ) ଏବଂ ସମସ୍ତ ଋଣାତ୍ମକ ପୂର୍ବସଂଖ୍ୟାର ସେଟ୍ ।
(iii) N ସେଟ୍ରେ 0 (ଶୂନ) ଉପାଦାନଟିକୁ ନେଇ ବିଚାର କଲେ ସଂପ୍ରସାରିତ ସ୍ବଭାବିକ ସଂଖ୍ୟା ସେଟ୍ (N*) ମିଳିଥାଏ ।
N* = {0, 1, 2, 3,…….}
- ଶୂନ (0) ଏବଂ ଋଣାତ୍ମକ ପୂର୍ଣ୍ଣସଂଖ୍ୟା (…… – 3, – 2, – 1) ପ୍ରାଚୀନ ଭାରତୀୟଙ୍କ ଅବଦାନ ।
- ବ୍ରହ୍ମଗୁପ୍ତଙ୍କ ଦ୍ବାରା ରଚିତ ବ୍ରହ୍ମସିଦ୍ଧାନ୍ତ ପୁସ୍ତକରେ ଋଣାତ୍ମକ ସଂଖ୍ୟା ଉଲ୍ଲେଖ କରାଯାଇଛି ।
(iv) ସମସ୍ତ ପରିମେୟ ସଂଖ୍ୟା (Rational Numbers) ମାନଙ୍କ ସେଟ୍ Q = {\(\frac{p}{q}\) : p ଓ ରୁ ପୂର୍ବସଂଖ୍ୟା ଓ q ≠ 0}
ମନେରଖ : ଯେକୌଣସି ପୂର୍ବସଂଖ୍ୟା ମଧ୍ୟ ଗୋଟିଏ ପରିମେୟ ସଂଖ୍ୟା ।
(v) N, N*, Z ଓ Q ମଧ୍ୟରେ ସମ୍ବନ୍ଧ : N ⊂ N* ⊂ Z ⊂ Q
N ସେଟ୍ରେ ଯୋଗ ଓ ଗୁଣନ ପ୍ରକ୍ରିୟାର ବୀଜଗାଣିତିକ ଧର୍ମ :
ଏଠାରେ ବ୍ୟବହୃତ ସଙ୍କେତ m, n ଓ p ପ୍ରତ୍ୟେକ ଗୋଟିଏ ଗୋଟିଏ ଗଣନ ସଂଖ୍ୟା । ଅର୍ଥାତ୍ m, n, p ∈ N
ଯୋଗ ପ୍ରକ୍ରିୟାର ଧର୍ମ :
(i) ସଂବୃତ୍ତି ନିୟମ (Closure property) : m + n ∈ N ଅର୍ଥାତ୍ ଦୁଇଟି ଗଣନ ସଂଖ୍ୟାର ଯୋଗଫଳ ଏକ ଗଣନ ସଂଖ୍ୟା ।
(ii) କ୍ରମ ବିନିମୟୀ ଧର୍ମ (Commutative property) : m + n = n + m
(iii) ସହଯୋଗୀ ଧର୍ମ (Associative property) : m + (n + p) = (m + n) + p
ଗୁଣନ ପ୍ରକ୍ରିୟାର ଧର୍ମ :
(iv) ସଂବୃତ୍ତି ଧର୍ମ : mn ∈ N ଅର୍ଥାତ୍ ଦୁଇଟି ଗଣନ ସଂଖ୍ୟାର ଗୁଣଫଳ ଏକ ଗଣନ ସଂଖ୍ୟା ।
(v) କ୍ରମବିନିମୟୀ ଧର୍ମ ; mn = nm
(vi) ସହଯୋଗୀ ଧର୍ମ : m (np) = (mn) p
(vii) ଅଭେଦ ଧର୍ମ (Identity property) : ଗୁଣନ ପ୍ରକ୍ରିୟାରେ ସଂଖ୍ୟା 1 (ଏକ) ଅଭେଦ ଓ m · 1 = 1 · m = m
{1କୁ ଗୁଣନାତ୍ମକ ଅଭେଦ (Multiplicative Identity) କୁହାଯାଏ ।}
(viii) ବଣ୍ଟନ ଧର୍ମ (Distributive property) : m(n + p) = mn + mp ଅର୍ଥାତ୍ ଗୁଣନ ପ୍ରକ୍ରିୟା ଯୋଗ ପ୍ରକ୍ରିୟାକୁ ବଣ୍ଟନ କରିଥାଏ ।
![]()
ଗଣନ ସଂଖ୍ୟାର କ୍ରମ (Order) :
N ସେଟ୍ରେ ଉପାଦାନଗୁଡ଼ିକ କ୍ରମିତ (Ordered) I N ସେଟ୍ରେ 1 < 2 < 3 < 4 …….
ଯୋଗର ଅଭେଦ ଧର୍ମ (Additive Identity) :
ଯେକୌଣସି ଉପାଦାନ m – N* ହେଲେ 0 + m = m |
{0 କୁ ଯୋଗାତ୍ମକ ଅଭେଦ (Additive Identity) କୁହାଯାଏ ।}
N* ସେଟ୍ର ସିଦ୍ଧ ହେଉଥିବା ଯୋଗ ଓ ଗୁଣନ ପ୍ରକ୍ରିୟାର ସମସ୍ତ ଧର୍ମ ପୂର୍ବସଂଖ୍ୟା ସେଟ୍ Zରେ ସତ୍ୟ ଅଟନ୍ତି ।
ଯୋଗ ପ୍ରକ୍ରିୟାପାଇଁ ବିଲୋମୀ ଧର୍ମ (Inverse Property) :
ଯେକୌଣସି ସେଟ୍ରେ ପୂର୍ଣ୍ଣସଂଖ୍ୟା m ପାଇଁ ଏହାର ବିଲୋମୀ (Inverse) ଟି – m ଓ – m ∈ Z
ଏବଂ m+ (-m) = 0 = (-m) + m ଏଠାରେ m ଓ – m ପରସ୍ପର ବିଲୋପୀ ଅଟନ୍ତି ।
ଶୂନର ଯୋଗାତ୍ମକ ବିଲୋମୀ 0
ପୂର୍ବସଂଖ୍ୟା ସେଟ୍ରେ ବୀଜଗାଣିତିକ ଧର୍ମ :
Z ସେଟ୍ଟି ମଧ୍ୟକ୍ରମିକ ଅର୍ଥାତ୍ … < – 4 < – 3 < – 2 < – 1 < 0 < 1 < 2 < 3 < ……. ।
ଦୁଇଗୋଟି ପୂର୍ବ ସଂଖ୍ୟାର ବିୟୋଗଫଳ ଏକ ପୂର୍ବସଂଖ୍ୟା । ତେଣୁ ବିୟୋଗ ପ୍ରକ୍ରିୟାଟି Z ସେଟ୍ରେ ସଂବୃତ୍ତି ନିୟମ ପାଳନ କରେ । ମାତ୍ର ବିୟୋଗ ପ୍ରକ୍ରିୟା ସହଯୋଗୀ କିମ୍ବା କ୍ରମବିନିମୟୀ ନିୟମ ପାଳନ କରେ ନାହିଁ ।
ପୂର୍ବସଂଖ୍ୟାମାନଙ୍କ ପାଇଁ ନିମ୍ନଲିଖ ଉକ୍ତିଗୁଡ଼ିକ ସତ୍ୟ –
(i) -(-m) m (ii) (-m) (-n) = mn (iii) 0 × m = m × 0 = 0
କେତେକ ଗୁରୁତ୍ଵପୂର୍ତ୍ତି ଧାରଣା :
(a) ଇଉକ୍ଲିଡାୟ ପଦ୍ଧାତି (Euclidean algorithm):
P > 1 ଏକ ସ୍ବାଭାବିକ ସଂଖ୍ୟା ଓ n ଏକ ପୂର୍ଣ୍ଣସଂଖ୍ୟା ହେଲେ, n = mp + r
ଯେଉଁଠାରେ m r ପୂର୍ଣ୍ଣସଂଖ୍ୟା ଓ 0 < 1 < p n = mp + r ପରିପ୍ରକାଶଟି ଅନନ୍ୟ ।
ଏଠାରେ n = ଭାଜ୍ୟ (devidend), p = ଭାଜକ (divisor), m = ଭାଗଫଳ (quotient) ଓ r = ଭାଗଶେଷ (remainder ବା residue) |
ଅର୍ଥାତ୍ ଭାଜ୍ୟ = ଭାଜକ x ଭାଗଫଳ + ଭାଗଶେଷ
ଯଦି ଭାଗପ୍ରକ୍ରିୟାର r = 0, ତେବେ ଆମେ କହିଥାଉ n ସଂଖ୍ୟାଟି p ଦ୍ୱାରା ବିଭାଜ୍ୟ ।
(b) ଯୁଗ୍ମ ଓ ଅଯୁଗ୍ମ ସଂଖ୍ୟା (Even and Odd Numbers) :
- ଯେଉଁ ପୂର୍ଣ୍ଣସଂଖ୍ୟା 2 ଦ୍ବାରା ବିଭାଜ୍ୟ ତାହାକୁ ଯୁଗ୍ମ ସଂଖ୍ୟା (Even numbers) କୁହାଯାଏ । ଏହାର ସାଧାରଣ ରୂପ 2m (m ∈ Z) ।
- ଯେଉଁ ସଂଖ୍ୟାଗୁଡ଼ିକ 2 ଦ୍ୱାରା ବିଭାଜ୍ୟ ନୁହଁନ୍ତି ସେମାନଙ୍କୁ ଅଯୁଗ୍ମ ସଂଖ୍ୟା କୁହାଯାଏ ।
ଏହାର ସାଧାରଣ ରୂପ 2m + 1 (m ∈ Z) । - ଦୁଇଟି ସଂଖ୍ୟା ପରସ୍ପର ମୌଳିକ (relatively prime) ଯଦି ହୁଏ ସେମାନଙ୍କ ଗ.ସା.ଗୁ. 1 ହେବ । m ଓ
n ପରସ୍ପର ମୌଳିକ ଯଦି (m, n) = 1 ।
(c) ମୌଳିକ ସଂଖ୍ୟା ଓ ଯୌଗିକ ସଂଖ୍ୟା (Prime and Composite Numbers) :
(i) ଯେଉଁ ସଂଖ୍ୟାଟି 1 ଓ ସେହି ସଂଖ୍ୟାଦ୍ଵାରା ବିଭାଜ୍ୟ ତାହାକୁ ମୌଳିକ ସଂଖ୍ୟା କୁହାଯାଏ ।
(ii) ଯେଉଁ ସଂଖ୍ୟା l ଓ ସେହି ସଂଖ୍ୟା ବ୍ୟତୀତ ଅନ୍ୟ ସଂଖ୍ୟାଦ୍ୱାରା ବିଭାଜ୍ୟ ତାହାକୁ ଯୌଗିକ ସଂଖ୍ୟା କୁହାଯାଏ ।
(iii) ପ୍ରତ୍ୟେକ ଗଣନ ସଂଖ୍ୟାର ସେ ନିଜେ ଓ 1 ଉତ୍ପାଦକଦ୍ବୟ ରହିଲେ ଏହି ଦୁଇଗୋଟି ଉତ୍ପାଦକକୁ ନଗଣ୍ୟ ଉତ୍ପାଦକ (Trivial factors) କୁହାଯାଏ । ମାତ୍ର ଯୌଗିକ ସଂଖ୍ୟାମାନଙ୍କର ନଗଣ୍ୟ ଉତ୍ପାଦକ ବ୍ୟତୀତ ଗଣ୍ୟ ଉତ୍ପାଦକ (Not-trivial factors) ଥାଏ ।
{1 ଓ 11000 ମଧ୍ୟରେ 168ବି, 1000 ଓ 2000 ମଧ୍ୟରେ 135ବି, 2000ରୁ 3000 ମଧ୍ୟରେ 127ବି, 3000ରୁ 4000 ମଧ୍ଯରେ 120ଟି, 4000ରୁ 5000 ମଧ୍ୟରେ 119ଟି ମୌଳିକ ସଂଖ୍ୟା ଅଛି ।}
(iv) ସ୍ଵାଭାବିକ ସଂଖ୍ୟାର ଉତ୍ପାଦକୀକରଣ ଅନନ୍ୟ (Unique), ଅର୍ଥାତ୍ କୌଣସି ସ୍ଵାଭାବିକ ସଂଖ୍ୟାକୁ ଦୁଇ ପ୍ରକାର ମୌଳିକ ସଂଖ୍ୟାର ଉତ୍ପାଦକର ଗୁଣଫଳରେ ପ୍ରକାଶ କରାଯାଇନପାରେ ।
- 1 ଭିନ୍ନ ପ୍ରତ୍ୟେକ ସ୍ଵାଭାବିକ ସଂଖ୍ୟା ଅନନ୍ୟ ଭାବରେ ମୌଳିକ ସଂଖ୍ୟାର ଗୁଣଫଳରୂପେ ପ୍ରକାଶ କରାଯାଇପାରେ ।
- ଏହି ତଥ୍ୟ Fundamental Theorem of Arithmetic ବା Unique Factorisation Theorem ନାମରେ ଅଭିହିତ ।
- 1 ଏକ ମୌଳିକ ସଂଖ୍ୟା ନୁହେଁ ।
(v) ଯୌଗିକ ସଂଖ୍ୟାର ମୌଳିକ ରାଶିମାନଙ୍କର ଉତ୍ପାଦକୀକୃତ ରୂପକୁ (Standard) ବା (Canonical) ରୂପ କୁହାଯାଏ । ଏ ପରିମେୟ ସଂଖ୍ୟା
ପରିମେୟ ସଂଖ୍ୟା (Rational Numbers) :
ପରିମେୟ ସଂଖ୍ୟା ସେଟ୍ ଠୁକୁ ବିଚାର କଲେ ଚାରିଟିଯାକ ପ୍ରକ୍ରିୟା (ଯୋଗ, ବିୟୋଗ, ଗୁଣନ ଓ ହରଣ) ସଂବୃତ୍ତି ନିୟମ ପାଳନ କରନ୍ତି । କେବଳ ହରଣ କ୍ଷେତ୍ରରେ ଭାଜକଭାବେ ରହିଥିବା ପରିମେୟ ସଂଖ୍ୟାଟି ଅଣଶୂନ୍ୟ ହେବା ଆବଶ୍ୟକ । ଯୋଗ ଓ ଗୁଣନ ପ୍ରକ୍ରିୟା ଦ୍ଵୟ ପାଇଁ ନିମ୍ନଲିଖ ବୀଜଗାଣିତିକ ନିୟମଗୁଡ଼ିକ ସତ୍ୟ । ଏଠାରେ x, y, z ∈ Q
ଯୋଗ ପ୍ରକ୍ରିୟାର ନିୟମ :
(i) ସଂବୃତ୍ତି ନିୟମ : x + y = Q
(ii) କ୍ରମବିନିମୟୀ ନିୟମ : x + y = y + x
(iii) ସହଯୋଗୀ ନିୟମ : x + (y + z) = (x + y) + z
(iv) ଅଭେଦ ନିୟମ : x + 0 = x (‘0’ କୁ ଯୋଗାତ୍ମକ ଅଭେଦ କୁହାଯାଏ)
(v) ବିଲୋମୀ ନିୟମ : x + (− x) = 0 (x ଓ – x ପରସ୍ପର ଯୋଗାତ୍ମକ ବିଲୋମୀ)
ଗୁଣନା ପ୍ରକ୍ରିୟାର ନିୟମ :
(i)ସଂବୃତ୍ତି ନିୟମ : xy ∈ Q
(ii) କ୍ରମବିନିମୟୀ ନିୟମ : xy = yx
(iii) ସହଯୋଗୀ ନିୟମ : x (yz) = (xy) z
(iv) ଅଭେଦ ନିୟମ : x · 1 = x (1କୁ ଗୁଣନାତ୍ମକ ଅଭେଦ କୁହାଯାଏ ।)
(v) ବିଲୋମୀ ନିୟମ : x(x ≠ 0)ର ବିଲୋମୀ \(\frac{1}{x}\) (କିମ୍ବା x-1) ଓ x . \(\frac{1}{x}\) = 1 (x ଓ \(\frac{1}{x}\) ପ୍ରତ୍ୟେକ ପରସ୍ପରର ଗୁଣନାତ୍ମକ ବିଲୋମୀ ।)
![]()
ଯୋଗ ଓ ଗୁଣନ ପ୍ରକ୍ରିୟାଦ୍ୱୟର ନିୟମ :
(i) ବଣ୍ଟନ ନିୟମ : x(y + z) = xy + xz |
(ii) ଯେଉଁ ସେଟ୍ର ଉପାଦାନଗୁଡ଼ିକ ଉପରୋକ୍ତ ଯୋଗାତ୍ମକ, ଗୁଣନାତ୍ମକ ତଥା ବଣ୍ଟନ ନିୟମ ପାଳନ କରୁଥୁବେ, ସେହି ସେଟ୍କୁ ଗୋଟିଏ ଫିଲ୍ଡ (Field) କୁହାଯାଏ । ପରିମେୟ ସଂଖ୍ୟା ସେଟ୍ Q ଏକ ଫିଲ୍ଡ
- Q ସେଟ୍ରେ ଗୁଣନର ବିଲୋମୀ ନିୟମ ସତ୍ୟ; ମାତ୍ର ଏହା Z ସେଟ୍ରେ ସତ୍ୟ ହେଉନଥିଲା ।
- a + a + a + ….. (n ଥର) = na ଓ a × a × a × ….. (n ଥର) = an ⇒ an ସଂକେତକୁ ପ୍ରଥମେ ଫରାସୀ ଗଣିତଜ୍ଞ (Rene Descartes) ବ୍ୟବହାର କରିଥିଲେ ।
ପରିମେୟ ସଂଖ୍ୟା କ୍ଷେତ୍ରରେ ନିମ୍ନଲିଖ୍ ଅସମୀକରଣଗୁଡ଼ିକ ସତ୍ୟ ଅଟନ୍ତି ।
(i) ତ୍ରିମୁଖୀ ନିୟମ : ଦୁଇଗୋଟି ପରିମେୟ ସଂଖ୍ୟା x ଓ y ଦିଆଯାଇଥିଲେ ତୁଳନା କରି କହିହେବ
(a) x > y, (b) x < y କିମ୍ବା (c) x = y ଏହାକୁ ତ୍ରିମୁଖୀ ନିୟମ (Trichotomy law) କୁହାଯାଏ ।
ମନେକର x = \(\frac{p}{q}\) ଓ y = \(\frac{r}{s}\); p, q, r, s ∈ Z ଓ q ≠ 0 ଓ s ≠ 0
x < y ବା \(\frac{p}{q}\) < \(\frac{r}{s}\) ଯଦି ଓ କେବଳ ଯଦି ps < qr ବା ps – qr < 0
x > y ବା \(\frac{p}{q}\) > \(\frac{r}{s}\) ଯଦି ଓ କେବଳ ଯଦି ps > qr ବା ps – qr > 0
(ii) ନିମ୍ନଲିଖ୍ ଅସମୀକରଣଗୁଡ଼ିକ ସତ୍ୟ ଅଟନ୍ତି ଯେଉଁଠାରେ x, y, z ∈ Q।
(a) x < y ଓ y < z ହେଲେ x < z ଏହା ସଂକ୍ରମୀ ନିୟମ (Law of transitivity) ଅଟେ ।
(b) x < y ହେଲେ x + z < y + z
(c) x < y ଓ z > 0 ହେଲେ xz < yz
(d) x < y ଓ z < 0 ହେଲେ xy > yz
(e) 0 < x < y ହେଲେ \(\frac{1}{x}\) > \(\frac{1}{y}\) ଓ y < x < 0 ହେଲେ \(\frac{1}{y}\) > \(\frac{1}{x}\)
ପରିମେୟ ସଂଖ୍ୟାରି ଘନତୃ (Density of Rational Numbers) :
ଯେକୌଣସି ଦୁଇଟି ପରିମେୟ ସଂଖ୍ୟା ମଧ୍ୟବର୍ତ୍ତୀ ଅସଂଖ୍ ପରିମେୟ ସଂଖ୍ୟା ଥାଏ ।
a ଓ b ଦୁଇଟି ପରିମେୟ ସଂଖ୍ୟା ଏବଂ a < b ହେଲେ a < \(\frac{a+b}{2}\) < b
ପରିମେୟ ସଂଖ୍ୟାର ଦଶମିକ ରୂପ :
- \(\frac{p}{q}\) (q ≠ 0) ପରିମେୟ ସଂଖ୍ୟାରେ pକୁ ପୃଦ୍ୱାରା ଭାଗକଲେ କେତେକ କ୍ଷେତ୍ରରେ ଭାଗ ପ୍ରକ୍ରିୟାଟିର ପରିସମାପ୍ତି ଘଟେ ଓ ଆଉ କେତେକ କ୍ଷେତ୍ରରେ ଭାଗ ପ୍ରକ୍ରିୟାର ପରିସମାପ୍ତି କେବେହେଲେବି ଘଟେ ନାହିଁ
- ଯେଉଁ ଭଗ୍ନସଂଖ୍ୟାରେ ଭାଗପ୍ରକ୍ରିୟାର ପରିସମାପ୍ତି ଘଟିଥାଏ, ତାହାକୁ ସସୀମ ବା ସରନ୍ତି (terminating) ଦଶମିକ ଭଗ୍ନସଂଖ୍ୟା କୁହାଯାଏ ।
\(\frac{1}{2}\) = 0.5, \(\frac{1}{4}\) = 0.25, \(\frac{1}{5}\) = 0.2 ଇତ୍ୟାଦି ସସୀମ ଦଶମିକ ଭଗ୍ନସଂଖ୍ୟା । - ଯେଉଁ ଭଗ୍ନସଂଖ୍ୟାରେ ଭାଗପ୍ରକ୍ରିୟାର ପରିସମାପ୍ତି ଘଟେ ନାହିଁ ତାହାକୁ ଅସୀମ ବା ଅସରନ୍ତି (non-terminating) ଦଶମିକ ଭଗ୍ନସଂଖ୍ୟା କୁହାଯାଏ ।
\(\frac{1}{3}\) = 0.3333 ….., \(\frac{1}{7}\) = 0.14285714285714 ….., \(\frac{5}{6}\) = 0.83333 …., ଇତ୍ୟାଦି ଅସୀମ ଦଶମିକ ଭଗ୍ନସଂଖ୍ୟା - ଯେଉଁ ଦଶମିକ ଭଗ୍ନସଂଖ୍ୟାରେ ଦଶମିକ ବିନ୍ଦୁ ପରବର୍ତ୍ତୀ ଗୋଟିଏ ଅଙ୍କ ବା ଏକାଧିକ ଅଙ୍କମାନ ବାରମ୍ବାର କ୍ରମାନ୍ୱୟରେ ଆବିର୍ଭାବ ହୁଏ, ତାହାକୁ ପୌନଃପୁନିକ ଦଶମିକ ଭଗ୍ନସଂଖ୍ୟା (Recurring Decimals) କୁହାଯାଏ ।
0.3333 ….. = \(0 . \overline{3}\) = 0.14285714285714 = \(0 \cdot \overline{142857}\), 0.8333 ….. = \(0 . \overline{83}\) ଇତ୍ୟାଦି ପୌନଃପୁନିକ ଦଶମିକ ଭଗ୍ନସଂଖ୍ୟା
ପ୍ରତ୍ୟେକ ପରିମେୟ ସଂଖ୍ୟା ଦୁଇଟି ରୂପରେ ପ୍ରକାଶିତ ହୋଇପାରେ; ଯଥା :
(a) ସସୀମ ଦଶମିକ (terminating decimals) ରୂପ ଏବଂ
(b) ଅସୀମ ପୌନଃପୁନିକ ଦଶମିକ (non-terminating and recurring decimals) ରୂପ ।
- ପ୍ରତ୍ୟେକ ସସୀମ ଦଶମିକ ଭଗ୍ନସଂଖ୍ୟା ଏବଂ ପ୍ରତ୍ୟେକ ଅସୀମ ଅଥଚ ପୌନଃପୁନିକ ଦଶମିକ ଭଗ୍ନସଂଖ୍ୟା ଗୋଟିଏ ଗୋଟିଏ ପରିମେୟ ସଂଖ୍ୟା ଅଟନ୍ତି ।
- ଯେଉଁ ଦଶମିକ ଭଗ୍ନସଂଖ୍ୟାରୁଡ଼ିକ ଅସୀମ (non-terminating) କିନ୍ତୁ ପୌନଃପୁନିକ ନୁହଁନ୍ତି, ସେଗୁଡ଼ିକ ପରିମେୟ ସଂଖ୍ୟା ନୁହଁନ୍ତି ।
ପରିମେୟ ସଂଖ୍ୟା ସେଟ୍ ଠୁର ଅଭାବତ୍ଵ (Inadequacy of Rationals) ଓ ଅପରିମେୟ ସଂଖ୍ୟା (Irrational numbers) :
(i) ଯେଉଁ ସଂଖ୍ୟାଗୁଡ଼ିକ ପୂର୍ଣବର୍ଗ ନୁହେଁ ସେହି ସଂଖ୍ୟାମାନଙ୍କର ବର୍ଗମୂଳ ଅପରିମେୟ ସଂଖ୍ୟା ଅଟେ ।
(ii) √2, √3, √5, √17, √11 ଆଦି ସଂଖ୍ୟାଗୁଡ଼ିକ ଅପରିମେୟ ସଂଖ୍ୟା ।
[p ମୌଳିକ ହେଲେ √p ଅପରିମେୟ ହେବ]
ଅସୀମ ଓ ଅଣପୌନଃପୁନିକ ଦଶମିକ ରାଶି (Non-terminating and non-recurring Decimals):
(i) ପ୍ରତ୍ୟେକ ପରିମେୟ ସଂଖ୍ୟାକୁ ଏକ ଅସୀମ ଦଶମିକ ଭଗ୍ନସଂଖ୍ୟାରେ ବା ଅସୀମ ଓ ପୌନଃପୁନିକ ଦଶମିକ ଭଗ୍ନସଂଖ୍ୟାରେ ପ୍ରକାଶ କରିହେବ । କିନ୍ତୁ ପରିମେୟ ସଂଖ୍ୟାଗୁଡ଼ିକର ଦଶମିକ ରୂପ ଅସୀମ ହେବ ଏବଂ ଅଣ ପୌନଃପୁନିକ ହେବ ।
(ii)କେବଳ ବର୍ଗମୂଳ ଜରିଆରେ (ଯଥା: √2, √3, √5 ଇତ୍ୟାଦି) ଯେ ଅପରିମେୟ ସଂଖ୍ୟା ଉତ୍ପନ୍ନ ହୁଏ ତାହା ନୁହେଁ । ସମୀକରଣ x3 = 2, x4 = 2….. ଇତ୍ୟାଦି ସମୀକରଣକୁ ସମାଧାନ କରି \(\sqrt[3]{2}, \sqrt[4]{2}\) ….. ଇତ୍ୟାଦି ଅପରିମେୟ ସଂଖ୍ୟା ପାଇହେବ ।
ମନେରଖ :
ବାସ୍ତବିକ ଯେତେ ପରିମେୟ ସଂଖ୍ୟା ଅଛି ତାଠାରୁ ଯଥେଷ୍ଟ ଅଧିକ ସଂଖ୍ୟାର ଅପରିମେୟ ସଂଖ୍ୟା ଅଛି ।
![]()
ଅପରିମେୟ ରାଣି (Irrational number π) :
(i) ପ୍ରତ୍ୟେକ ସସୀମ ଦଶମିକ ସଂଖ୍ୟା ଯିଏ ପୌନଃପୁନ୍ୟ ହୋଇନଥ୍ବ, ତାହା ଏକ ଅପରିମେୟ ସଂଖ୍ୟା । ଉଦାହରଣ -√2, √3, √5 ଇତ୍ୟାଦି ଅପରିମେୟ ସଂଖ୍ୟା ।
(ii) ଯେକୌଣସି ବୃତ୍ତରେ ପରିଧୂ ଓ ବ୍ୟାସର ଦୈର୍ଘ୍ୟର ଅନୁପାତ ଏକ ଧ୍ରୁବକ ସଂଖ୍ୟା (Constant); ଯାହାକୁ r ଦ୍ଵାରା ସୂଚିତ କରାଯାଇଥାଏ ।
\(\frac{ବୃତ୍ତର ପରିଧୂ}{ବ୍ୟାସର ଦୈର୍ଘ୍ୟ}\) = π
{1761 ମସିହାରେ ଗଣିତଜ୍ଞ Lambert ଯୁକ୍ତିମୂଳକ ପ୍ରମାଣ କରି ଦର୍ଶାଇଥିଲେ ଯେ, “π ଏକ ଅପରିମେୟ ସଂଖ୍ୟା”}
(iii) ଗ୍ରୀକ୍ ଦାର୍ଶନିକ ଆର୍କିମେଡ଼ିସ୍ fର ଆସନ୍ନମାନ \(\frac{22}{7}\) ବୋଲି ନିର୍ଣ୍ଣୟ କରିଥିଲେ । ବିଭିନ୍ନ କ୍ଷେତ୍ରରେ ନରେ ଆସନ୍ନମାନ \(\frac{22}{7}\) ବ୍ୟବହୃତ ହୋଇ ଗାଣିତିକ ହିସାବ କରାଯାଏ ।
(iv) ଅପରିମେୟ ସଂଖ୍ୟା π ଓ e ର ମୂଲ୍ୟ 2 ଓ 3 ମଧ୍ୟରେ ଥାଏ ।
(v) ପରିମେୟ ସଂଖ୍ୟାର ଯୋଗ ଓ ଗୁଣନ ସଂବୃତ୍ତି ନିୟମ ପାଳନ କର ।
ବାସ୍ତବ ସଂଖ୍ୟା (Real Numbers) :
(i) ସମସ୍ତ ଅପରିମେୟ ସଂଖ୍ୟାମାନଙ୍କ ସେଟ୍କୁ Q’ ସଂକେତ ଦ୍ୱାରା ଲେଖାଯାଏ ।
(ii) ସମସ୍ତ ପରିମେୟ ସଂଖ୍ୟା ସେଟ୍ ଠୁ ଓ ଅପରିମେୟ ସଂଖ୍ୟା ସେଟ୍ ଠୁ’ ର ସଂଯୋଗରୁ ଯେଉଁ ନୂତନ ସେଟ୍ ମିଳେ ତାହାକୁ ବାସ୍ତବ ସଂଖ୍ୟା (Real Number) ସେଟ୍ କୁହାଯାଏ । ଏହି ସେଟ୍ର ସଂକେତ R
Q ∪ Q’ = R, Q ∩ Q’ = Φ, N ⊂ Z ⊂ Q ⊂ R
ବାସ୍ତବ ସଂଖ୍ୟାମାନଙ୍କ ବୀଜଗାଣିତିକ ଧର୍ମ (Algebraic Properties in Reals) :
ଯୋଗପ୍ରକ୍ରିୟାର ଧର୍ମ :
x, y, Z E R ହେଲେ
(i) ସଂବୃତ୍ତି ଧର୍ମ x ∈ R ଓ y ∈ R ହେଲେ x + y ∈ R
(ii) କ୍ରମବିନିମୟୀ ଧର୍ମ x ∈ R ଓ y ∈ R ହେଲେ x + y = y + x
(iii) ସହଯୋଗୀ ଧର୍ମ x, y, z ∈ R ହେଲେ x + (y + z) = (x + y) + z
(iv) ଅଭେଦ ଧର୍ମ ; X € R = x + 0 = x; 0 (0, R ସେଟ୍ରେ ଯୋଗାତ୍ମକ ଅଭେଦ ଅଟେ ।)
(v) ବିଲୋମୀ ଧର୍ମ : ପ୍ରତ୍ୟେକ ବାସ୍ତବ ସଂଖ୍ୟା xର ଯୋଗାତ୍ମକ୍ ବିଲୋମୀ (-x) ଓ x + (-x) = 0
(x ମଧ୍ଯ (-x)ର ଯୋଗାତ୍ମକ ବିଲୋମୀ)
ଗୁଣନ ପ୍ରକ୍ରିୟାର ଧର୍ମ :
x, y, Z ∈ R ହେଲେ
(i) ସଂବୃତ୍ତି ଧର୍ମ : xy ∈ R
(ii) କ୍ରମବିନିମୟୀ ଧର୍ମ ; xy = yx
(iii) ସହଯୋଗୀ ଧର୍ମ ; x (yz) = (xy) z
(iv) ଅଭେଦ ଧର୍ମ : x × 1 = x (1 (ଏକ) ସଂଖ୍ୟାଟି ଗୁଣନାତ୍ମକ ଅଭେଦ ।)
(v) ବିଲୋମୀ ଧର୍ମ : ପ୍ରତ୍ୟେକ x + 0 ପାଇଁ ଏକ ଅନନ୍ୟ ବାସ୍ତବ ସଂଖ୍ୟା \(\frac{1}{x}\) ବା x-1 ରହିଛି, ଯେପରିକି x . x-1 = 1 \(\frac{1}{x}\) ବା x-1 କୁ xର ଏବଂ xକୁ x-1 ର ଗୁଣନାତ୍ମକ ବିଲୋମୀ ଅଟେ ।
ଯୋଗ ଓ ଗୁଣନ ପ୍ରକ୍ରିୟାଦ୍ୱୟର ଧର୍ମ :
(i) ବଣ୍ଟନ ନିୟମ : x (y + z) = xy + xz (ଗୁଣନ ପ୍ରକ୍ରିୟାଟି ଯୋଗ ପ୍ରକ୍ରିୟା ଉପରେ ବାଛି ହେବ ।)
(ii) ଦୁଇଟି ପରିମେୟ ସଂଖ୍ୟା x ଓ yର ଯୋଗଫଳ ତଥା ଗୁଣନଫଳ ପରିମେୟ (Q ସେଟ୍ରେ ସଂବୃତ୍ତି ନିୟମ) x, y ∈ Q ହେଲେ, x + y ∈ Q ଏବଂ xy ∈ Q
(iii) ଦୁଇଟି ବାସ୍ତବ ସଂଖ୍ୟା x ଓ y ମଧ୍ୟରୁ ଗୋଟିଏ ପରିମେୟ ଓ ଅନ୍ୟଟି ଅପରିମେୟ ହେଲେ ଯୋଗଫଳ x + y ଅପରିମେୟ ଓ ପରିମେୟ ସଂଖ୍ୟାଟି ଅଣଶୂନ୍ୟ ହେଲେ ଗୁଣଫଳ ମଧ୍ୟ ଅପରିମେୟ । ମାତ୍ର ଗୁଣଫଳ = 0 ହେବ ଯଦି ପରିମେୟ ସଂଖ୍ୟା 0 ହେବ
(iv) ଯେକୌଣସି ବାସ୍ତବ ସଂଖ୍ୟାକୁ x ସହ (କୁ ଗୁଣନକଲେ ଗୁଣଫଳ ଶୂନ ହେବ । [Zero Law : x × 0 = 0]
(v) x ଓ y ବାସ୍ତବ ସଂଖ୍ୟା ଏବଂ x = Q’ ଓ y ∈ Q’ ହେଲେ x + y କିମ୍ବା xy ପରିମେୟ କିମ୍ବା ଅପରିମେୟ ହୋଇପାରନ୍ତି ।
(vi) Q’ ସେଟ୍ରେ ଯୋଗ ଓ ଗୁଣନ ପ୍ରକ୍ରିୟା ସଂବୃତ୍ତି ନିୟମ ପାଳନ କରନ୍ତି ନାହିଁ ।
(vii) an ରେ aକୁ ଆଧାର (base) ଓ nକୁ ଘାତ (index) କୁହାଯାଏ ।
R ସେଟ୍ର ଯୋଗ ଓ ଗୁଣନ ସମ୍ବନ୍ଧୀୟ କିଛି ଅଧ୍ବକ ତଥ୍ୟ :
x, y, z ∈ R ହେଲେ
ଅନୁସିଦ୍ଧାନ୍ତ – 1: x + y = x + z ହେଲେ, y = z ଓ y + x = z + x ହେଲେ y = z |
ଏ ଦୁଇଟିକୁ ଯୋଗର ବିଲୋପନ ନିୟମ (Cancellation law of addition) କୁହାଯାଏ ।
ଅନୁସିଦ୍ଧାନ୍ତ – 2: x + 0 ଏବଂ xy = xz ହେଲେ y = z ଓ yx = zx ହେଲେ y = z I
ଏ ଦୁଇଟିକୁ ଗୁଣନର ବିଲୋପନ ନିୟମ (Cancellation law of multiplication) କୁହାଯାଏ ।
ଅନୁସିଦ୍ଧାନ୍ତ – 3: (i) x × 0 = 0, (ii) (-x) = x, (iii) x ≠ 0 ହେଲେ (x-1)-1 = x
ଅନୁସିଦ୍ଧାନ୍ତ – 4 (i) x (-y) = (-x) y = -(xy) (ii) (-x) (-y) = xy
![]()
ସଂଖ୍ୟାରେଖା (Number Line) :
(1) ବୀଜଗାଣିତିକ ରାଶି ଓ ଜ୍ୟାମିତି ସହ ସଂପର୍କକୁ ନେଇ ବିଶ୍ଳେଷଣାତ୍ମକ ଜ୍ୟାମିତି (Analytical Geometry)ର ସୃଷ୍ଟି ହୋଇଛି ।
(2) ଯେକୌଣସି ବାସ୍ତବ ସଂଖ୍ୟାକୁ ଏକ ସରଳରେଖାର ଏକ ବିନ୍ଦୁଦ୍ଵାରା ସୂଚିତ କରାଯାଇପାରିବ । ପ୍ରତ୍ୟେକ ବାସ୍ତବ ସଂଖ୍ୟାକୁ ଗୋଟିଏ ଗୋଟିଏ ବିନ୍ଦୁଦ୍ୱାରା ସୂଚିତ କରି ସେଗୁଡ଼ିକୁ ଯୋଡ଼ିଦେଲେ ଗୋଟିଏ ନିରବଚ୍ଛିନ୍ନ ସରଳରେଖା ସୃଷ୍ଟି ହେବ । ଏହା ବିଖ୍ୟାତ ଗାଣିତିକ ଜେଜେକିଣ୍ଡ (Dedekind) ଓ କାଣ୍ଟର (Cantor)ରଙ୍କ ଅବଦାନ ।
(3) ଯେକୌଣସି ଜ୍ୟାମିତିକ ବିଷୟବସ୍ତୁକୁ ଆମେ ବୀଜଗଣିତ ସାହାଯ୍ୟରେ ସମାଧାନ କରିପାରିବ ।
ସଂଖ୍ୟାରେଖାରେ ବାସ୍ତବ ସଂଖ୍ୟାମାନଙ୍କର ସ୍ଥାପନ (Representation of real numbers on the number line) :
(i) ବାସ୍ତବ ସଂଖ୍ୟାଗୁଡ଼ିକର ଜ୍ୟାମିତିକ ପରିପ୍ରକାଶ କରିବାପାଇଁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବିନ୍ଦୁ ୦ ନିଆଯାଉ । ଏହି ବିନ୍ଦୁଦେଇ \(\overleftrightarrow{X^{\prime} \mathrm{OX}}\) ସରଳରେଖା ଅଙ୍କନ କରାଯାଉ ।
(ii) O ବିନ୍ଦୁକୁ ମୂଳବିନ୍ଦୁ (Origin) ଓ \(\overleftrightarrow{\mathrm{XX’}}\) ରେଖାକୁ ସଂଖ୍ୟାରେଖା (Number Line) ବା ବାସ୍ତବ ଅକ୍ଷ (Real axis) କୁହାଯାଏ ।
(iii) ଠ ର ଏକ ପାର୍ଶ୍ବ \(\overrightarrow{\mathrm{OX}}\) କୁ ଧନାତ୍ମକ ଦିଗ (Positive side) ଓ ଏହାର ବିପରୀତ ପାର୍ଶ୍ବ \(\left(\overrightarrow{\mathrm{OX}^{\prime}}\right)\) କୁ ଋଣାତ୍ମକ ଦିଗ (Negative side) କୁହାଯାଏ ।
(a) ପୂର୍ବସଂଖ୍ୟାମାନଙ୍କର ସ୍ଥାପନ :
- କୌଣସି ଏକ ରେଖାଖଣ୍ଡ ନେଇ ତାହାର ଦୈର୍ଘ୍ୟକୁ ଏକ ଏକକ ବୋଳି ନିଆଯାଉ । ଠ ବିନ୍ଦୁର ସୂଚକ ସଂଖ୍ୟା (0) ଶୂନ ହେଉ
- ତତ୍ତ୍ଵ ଏକକ ସହ ସମାନ କରି ଠ ବିନ୍ଦୁରୁ \(\overrightarrow{\mathrm{OX}}\) ଦିଗରେ OA ଛେଦ କରାଯାଉ । ଅର୍ଥାତ୍ OA ଏକ ଏକକ ପ୍ରାପ୍ତ A ବିନ୍ଦୁର ସୂଚକ ସଂଖ୍ୟା 1 ହେଲା ।
- ବିପରୀତ ଦିଗ \(\overrightarrow{\mathrm{OX’}}\) ରୁ ଏକ ଏକକ ସହ ସମାନ କରି OA’ ଛେଦକଲେ, A’ ବିନ୍ଦୁର ସୂଚକ ସଂଖ୍ୟା –1 ହେବ । \(\stackrel{\leftrightarrow}{\mathrm{xx}^{\prime}}\) ରେଖା ଉପରେ ଯଥାକ୍ରମେ O, A, A’ B, B’ ଇତ୍ୟାଦି ବିନ୍ଦୁମାନଙ୍କ ସ୍ଥାନାଙ୍କ (Co-ordinate) ଦର୍ଶାଯାଇଛି ।
(b) ପରିମେୟ ସଂଖ୍ୟାର ସ୍ଥାପନ :
- ମନେକର b > 1 ଏକ ଧନାତ୍ମକ ପୂର୍ଣ୍ଣସଂଖ୍ୟା । ତେଣୁ \(\frac{1}{b}\) ଏକ ପ୍ରକୃତ ଭଗ୍ନାଂଶ (Proper fraction) ହୋଇଥିବାରୁ, ଏହି ସଂଖ୍ୟାଟି ଠ ଓ A ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ୟରେ କୌଣସି ଏକ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ହେବ ।
- OA (ଅର୍ଥାତ୍ ଏକ ଏକକ) ରେଖାଖଣ୍ଡକୁ b ସମାନ ଭାଗରେ ବିଭକ୍ତ କଲେ, ପ୍ରତି ସମାନ ଭାଗର ଦୈର୍ଘ୍ୟ \(\frac{1}{b}\) ହେବ । ଛେଦବିନ୍ଦୁଗୁଡ଼ିକ ଯଥାକ୍ରମେ Q1, Q2, Q3 …. ହେଲେ, ଏହି ଛେଦବିନ୍ଦୁମାନଙ୍କର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ \(\frac{1}{b}, \frac{2}{b}, \frac{3}{b}\) …. ହେବ । ସେହିପରି ଋଣାତ୍ମକ ପରିମେୟ ରାଶି \(-\frac{1}{\mathrm{~b}},-\frac{2}{\mathrm{~b}},-\frac{3}{\mathrm{~b}}\) ….. ରଣଦିଗ \(\overrightarrow{\mathrm{OX’}}\) ଉପରେ ଅବସ୍ଥିତ ହେବ ।

(c) ଅପରିମେୟ ସଂଖ୍ୟାମାନଙ୍କର ସ୍ଥାପନ :
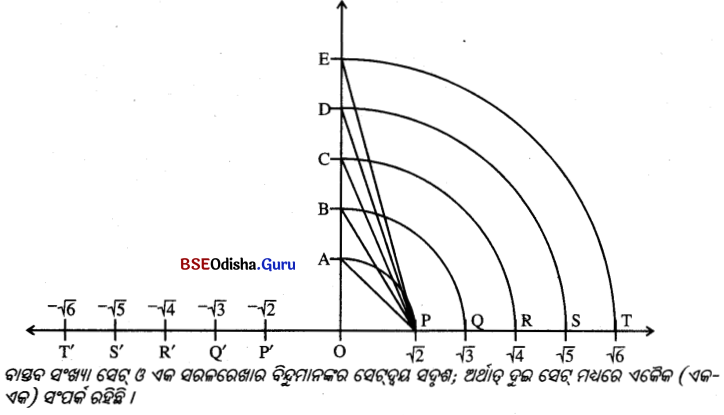
ବାସ୍ତବ ସଂଖ୍ୟାମାନଙ୍କର କ୍ରମ (Order in R) :
(i) a ଓ b ଦୁଇଟି ବାସ୍ତବ ସଂଖ୍ୟା ହେଲେ, ହୁଏତ a > b ବା a < b, a = b ହୋଇପାରେ । ଏହାକୁ ତ୍ରିମୁଖୀ ନିୟମ (Law of Trichotomy) କୁହାଯାଏ ।
(ii) a, b, c ତିନୋଟି ବାସ୍ତବ ସଂଖ୍ୟା ମଧ୍ୟରେ, a < b ଏବଂ b < c ହେଲେ a < c ହେବ । ଏହାକୁ ସଂକ୍ରମୀ ନିୟମ (Law of Transitivity) କୁହାଯାଏ ।
(iii) a < b ଏବଂ c > 0 ହେଲେ, ac < bc ହେବ ।
(iv) ଯଦି a < b ହୁଏ, ତେବେ ସମସ୍ତ ବାସ୍ତବ ସଂଖ୍ୟା c ପାଇଁ a + c < b + c ହେବ ।
(iv) a > 0 ଓ b > 0 ହେଲେ, ab > 0 1
(v) a ଏକ ବାସ୍ତବ ଧନାତ୍ମକ ସଂଖ୍ୟା ଅର୍ଥାତ୍ a > 0 ହୁଏ, ତେବେ ସଂଖ୍ୟାରେଖାରେ 0 (ଶୂନ)ର ଡାହାଣକୁ ରହେ । ଯଦି a ଏକ ଋଣାତ୍ମକ ବାସ୍ତବ ସଂଖ୍ୟା ଅର୍ଥାତ୍ a < 0 ହୁଏ ତେବେ a, 0 (ଶୂନ)ର ବାମ ପାର୍ଶ୍ଵରେ ରହେ ।
{ଶୂନ ଏକମାତ୍ର ବାସ୍ତବ ସଂଖ୍ୟା ଯାହା ଧନାତ୍ମକ ନୁହେଁ ବା ଋଣାତ୍ମକ ନୁହେଁ ।}
ବାସ୍ତବ ସଂଖ୍ୟା ‘x’ର ପରମମାନ :
- ଏକ ଧନାତ୍ମକ ହେଉ ବା ଋଣାତ୍ମକ ହେଉ, ଯେକୌଣସି ବାସ୍ତବ ସଂଖ୍ୟା xର ସାଂଖ୍ୟକ ମାନକୁ |x| ଭାବରେ ପ୍ରକାଶ କରାଯାଏ । ଏହି ।x ସର୍ବଦା ଏକ ଧନାତ୍ମକ ବାସ୍ତବ ରାଶି ଓ ଏହାକୁ xର ପରମମାନ (Absolute value) କୁହାଯାଏ ।
x ଧନାତ୍ମକ, ଶୂନ ବା ଋଣାତ୍ମକ ବାସ୍ତବ ସଂଖ୍ୟାହେଲେ,
|x| ={ x, ଯେତେବେଳେ x > 0, -x, ଯେତେବେଳେ x < 0} - x ଯେକୌଣସି ଏକ ବାସ୍ତବ ସଂଖ୍ୟା ହେଲେ,
(a) |x| = |-x| ≥ 0 (b) |x| ≥ x (c) |x| ≥ -x (d) |x| ≤ a ହେଲେ, -a ≤ x ≤ a ହେବ
ସଂଖ୍ୟାରେଖାରେ ଦୁଇ ବିନ୍ଦୁ ମଧ୍ୟରେ ଦୂରତା :
ସଂଖ୍ୟାରେଖାସ୍ଥିତ P ଓ Q ବିଦୁଦ୍ଵୟର ସାଂଖ୍ୟକ ମାନ ବା ସ୍ଥାନଙ୍କ ଯଥାକ୍ରମେ a ଓ b ହେଲେ
PQ = |a – b| ଅର୍ଥାତ୍ P ଓ Q ମଧ୍ୟରେ ଦୂରତା = |a – b|
ଘାତାଙ୍କ ରାଣି (Exponential Numbers):
(i) a ଏକ ବାସ୍ତବ ସଂଖ୍ୟା ଓ n ଏକ ଗଣନ ସଂଖ୍ୟା ହେଲେ, aର ଅର୍ଥ a × a × a × a × a × ….. n (ଥର) ଅଟେ
(ii) an ଏକ ବାସ୍ତବ ସଂଖ୍ୟା ଓ ଏହାର କାରଣ ହେଲା ବାସ୍ତବ ସଂଖ୍ୟା ସେଟ୍ରେ ଗୁଣନ ପ୍ରକ୍ରିୟାଟି ସଂବୃତ୍ତି ନିୟମ ପାଳନ କରେ ।
(iii) a ରୂପକୁ ଘାତାଙ୍କ ରୂପ (exponential from) କୁହାଯାଏ । ଯେଉଁଠାରେ a ଆଧାର (base) ଓ n ଘାତାଙ୍କ ।
(iv) n = 0 ହେଲେ a0 = 1 ଓ ଏଠାରେ a ≠ 0, ଏହା ଏକ ସଂଜ୍ଞା ।
(v) a ≠ 0 ହେଲେ a-1 = \(\frac{1}{a}\) ଏବଂ a-m = \(\frac{1}{a^m}\) (a ≠ 0, m ∈ N)
(vi) a ଅଣଶୂନ୍ୟ ବାସ୍ତବ ସଂଖ୍ୟା ଓ ଘାତାଙ୍କ n ଏକ ପୂର୍ଣସଂଖ୍ୟା (n ∈ Z) ହେଲେ ଅର୍ଥାତ୍ a, b ∈ R ଓ a ≠ 0, b ≠ 0; m, n ∈ Z
⇒ (a) am × an = am + n (b) am ÷ an = am-n
⇒ (c) (ab)m = am × bm (d) (am)n = amn
(vii) √a ଓ \(\sqrt[3]{a}\) କୁ ଯଥାକ୍ରମେ \(a^{\frac{1}{2}}\) ଏବଂ \(a^{\frac{1}{2}}\) ରୂପେ ଲେଖାଯାଇ ପାରିବ । ବ୍ୟାପକଭାବେ q ଏକ ଗଣନ ସଂଖ୍ୟା ହେଲେ \(a^{\frac{1}{q}}\) ଏକ ଧନାତ୍ମକ ବାସ୍ତବ ସଂଖ୍ୟା ଓ ଏହାକୁ q ତମ ମୂଳ (qth root) କୁହାଯାଏ ।
(viii) \(a^{\frac{1}{q}}\) ରାଶିକୁ p ଥର ଗୁଣନ କଲେ ପାଇବା \(a^{\frac{1}{9}} \times a^{\frac{1}{q}} \times a^{\frac{1}{q}} \times\) ….. (P ଥର) \(a^{\frac{p}{q}}=\left(a^p\right)^{\frac{1}{q}}=\sqrt[q]{a^p}=(\sqrt[q]{a})^p\)
