Odisha State Board CHSE Odisha Class 12 Economics Solutions Chapter 12 ଜାତୀୟ ଆୟ Long Answer Questions.
CHSE Odisha 12th Class Economics Chapter 12 Long Answer Questions in Odia Medium
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
1. ମୋଟ ଦେଶୀୟ (ଘରୋଇ) ଉତ୍ପାଦ ଓ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ ବ୍ୟାଖ୍ୟା କର । ଉପାଦାନ ପରିବ୍ୟୟ ଆକାରରେ ଓ ବଜାର ଦାମ୍ରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ ଏବଂ ଉପାଦାନ ପରିବ୍ୟୟ ଓ ବଜାର ଦାମ୍ ଆକାରରେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ ମଧ୍ଯରେ ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।
Answer:
ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷରେ ଦେଶରେ ଚୂଡ଼ାନ୍ତଭାବେ ଉତ୍ପାଦିତ ହୋଇଥିବା ଦ୍ରବ୍ୟ ଓ ସେବାର ବଜାର ଦାମ୍ଭିକୁ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ କୁହାଯାଏ । ହସ୍ତାନ୍ତରଣ ଦେୟ, ପୁଞ୍ଜିଲାଭ ଏବଂ ପୁରୁଣା ଦ୍ରବ୍ୟର ଦାମ୍ ପ୍ରଭୃତି ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦରୁ ବାଦ୍ ଦିଆଯାଏ ।
ବଜାର ଦରରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ (GDP at MP) – ମୋଟ ଦେଶୀୟ ପ୍ରଚଳିତ ବଜାର ଦାମ୍ରେ ଓ ଉପାଦାନ ପରିବ୍ୟୟରେ ବ୍ୟାଖ୍ୟା କାରଯାଇପାରେ । ପ୍ରଚଳିତ ବଜାର ଦାମ୍ରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ (Gross Domestic Product at Market Price) କହିଲେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷରେ କୌଣସି ଅର୍ଥବ୍ୟବସ୍ଥାରେ ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟ ଓ ସେବାକୁ ସାମଗ୍ରୀକଭାବେ ବଜାର ଦରରେ ମୂଲ୍ୟାୟନକୁ ହିଁ ଦର୍ଶାଇଥାଏ । ଏହାକୁ ଆକଳନ କରିବାକୁ ଉତ୍ପାଦିଦ ଦ୍ରବ୍ୟ ଓ ସେବାର ପରିମାଣକୁ ବଜାର ଦରରେ ଗୁଣନ କରାଯାଇଥାଏ ।
ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ (ବଜାର ଦରରେ) ତିନିପ୍ରକାର ଅନ୍ତିମ ଦ୍ରବ୍ୟକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରିଥାଏ; ଯଥା – ଉପଭୋଗ୍ୟ ଦ୍ରବ୍ୟ ଯାହା ଉପଭୋକ୍ତାଙ୍କୁ ପ୍ରତ୍ୟକ୍ଷ ପରିତୃପ୍ତି ପ୍ରଦାନ କରେ, ପୁଞ୍ଜି ଦ୍ରବ୍ୟ ଏବଂ ସରକାରଙ୍କଦ୍ବାରା ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟ ଓ ସେବା ।
ବୈଶିଷ୍ଟ୍ୟ :
(i) ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦକୁ ମୁଦ୍ରା ଆକାରରେ ପ୍ରକାଶ କରାଯାଏ । ଦେଶରେ ଉତ୍ପାଦିତ ସମସ୍ତ ଦ୍ରବ୍ୟ ଓ ସେବାର ମୌଦ୍ରିକ ମୂଲ୍ୟକୁ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ କୁହାଯାଏ ।
(ii) କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷରେ ଉତ୍ପାଦିତ ସମସ୍ତ ଚୂଡ଼ାନ୍ତ ବା ଅନ୍ତିମ ଦ୍ରବ୍ୟ ଓ ସେବାକୁ ଏଥିରେ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇଥାଏ ।
(iii) ଏହାକୁ ପ୍ରଚଳିତ ବଜାର ଦାମ୍ରେ ପରିପ୍ରକାଶ କରାଯାଏ ।
(iv) ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ କେବଳ ବଜାରକୁ ବିକ୍ରି ଉଦ୍ଦେଶ୍ୟରେ ପ୍ରେରିତ ଦ୍ରବ୍ୟ ଓ ସେବାକୁ ହିଁ ବିଚାରକୁ ନେଇଥାଏ ।
(v) ପୁଞ୍ଜି ଦ୍ରବ୍ୟର ଅବକ୍ଷୟଜନିତ ମୂଲ୍ୟକୁ ଏହା ବିଚାରକୁ ନେଇ ନ ଥାଏ ।
(vi) ହସ୍ତାନ୍ତରୀଣ ଆୟ, ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦର ଅଂଶବିଶେଷ ନୁହେଁ ।
(vii) ପୁଞ୍ଜିଲାଭ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦର ଅନ୍ତର୍ଭୁକ୍ତ ହୁଏ ନାହିଁ । ତେଣୁ ବଜାର ଦରରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ = ଦେଶର ମୋଟ ଉତ୍ପାଦିତ ହେଉଥିବା ଦ୍ରବ୍ୟ ଓ ସେବାର ମୌଦ୍ରିକ ମୂଲ୍ୟ – ଅନ୍ତର୍ବର୍ତ୍ତୀ ଦ୍ରବ୍ୟ ଓ ସେବାର ମୌଦ୍ରିକ ମୂଲ୍ୟ ।
ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦରୁ ଅବକ୍ଷୟଜନିତ ବ୍ୟୟକୁ ବିୟୋଗ କରାଗଲେ ନିଟ୍ ଦେଶୀୟ ଉତ୍ପାଦ (ବଜାର ଦରରେ) ମିଳିଥାଏ ।
ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦକୁ ପ୍ରଚଳିତ ଦାମ୍ରେ ଏବଂ ସ୍ଥିର ଦାମ୍ରେ ଆକଳନ କରାଯାଇଥାଏ । ପ୍ରଚଳିତ ଦାମ୍ରେ ଦ୍ରବ୍ୟ ଓ ସେବାର ମୂଲ୍ୟାୟନ କରିବାଦ୍ୱାରା ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦର ମୂଲ୍ୟ ସୂଚିତ ହୁଏ । ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ ବୃଦ୍ଧି ହେବା ଅର୍ଥବ୍ୟବସ୍ଥାର ସୁସ୍ଥତା ସୂଚିତ କରେ । ପୂର୍ବ ବର୍ଷ ସହ ତୁଳନା କରି ଦେଶର ହୋଇଥିବା ଅର୍ଥନୈତିକ ବିକାଶ ସଂପର୍କରେ ଧାରଣା କରିହୁଏ । ଦରଦାମ୍ ସ୍ତରଜନିତ ହେଉଥିବା ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦର ମୂଲ୍ୟ ବୃଦ୍ଧି ଭ୍ରାନ୍ତିଯୁକ୍ତ ହୋଇଥାଏ । ଏଥିପାଇଁ ଅର୍ଥବ୍ୟବସ୍ଥାର ପ୍ରକୃତ ଚିତ୍ର ମିଳି ନ ଥାଏ । ସ୍ଥିର ଦାମ୍ରେ ହିସାବ କଲେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ ବୃଦ୍ଧିର ପ୍ରକୃତ ଚିତ୍ର ପ୍ରଦର୍ଶିତ ହୋଇଥାଏ ।
ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ (ବଜାର ଦରରେ) – ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ କହିଲେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷରେ ଦେଶବାସୀଙ୍କ ଦ୍ଵାରା ଦେଶ ଭିତରେ ଏବଂ ବିଦେଶରେ ଉତ୍ପାଦନ କରାଯାଉଥିବା ଦ୍ରବ୍ୟ ଓ ସେବାର ମୂଲ୍ୟକୁ ବୁଝାଏ । ଅନ୍ୟ ଅର୍ଥରେ, ବର୍ଷକ ମଧ୍ୟରେ ଦେଶରେ ଚୂଡ଼ାନ୍ତଭାବରେ ଉତ୍ପାଦନ କରାଯାଉଥିବା ଦ୍ରବ୍ୟ ଓ ସେବାର ମୌଦ୍ରିକ ମୂଲ୍ୟ ଓ ବିଦେଶରୁ ଅର୍ଜିତ ଆୟର ସମାହାର ହିଁ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ । ଦ୍ରବ୍ୟ ଓ ସେବାର ପରିମାଣକୁ ଏହାର ଦାମ୍ ସହ ଗୁଣନ କରି ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ କଳନା କରିହୁଏ । ଏହି କଳନାରୁ ଅବକ୍ଷୟ ପରିବ୍ୟୟ, ହସ୍ତାନ୍ତରଣ ଦେୟ, ପୁଞ୍ଜିଲାଭ ମଧ୍ୟବର୍ତ୍ତୀ ଦ୍ରବ୍ୟର ଦାମକୁ ବାଦ୍ ଦିଆଯାଏ ।
ମୋଟ ଜାତୀୟ ଉତ୍ପାଦକୁ ତିନିଗୋଟି ଦିଗରୁ ବିଚାର କରାଯାଏ; ଯଥା ଉତ୍ପାଦ ଦିଗ, ଆୟ ଦିଗ ଓ ଖର୍ଚ୍ଚ ଦିଗ । ଉତ୍ପାଦ ଦିଗରୁ ବିଶ୍ଳେଷଣ କଲେ ଓ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ କହିଲେ ଦେଶର ସବୁ ଉତ୍ପାଦନକାରୀ ଉଦ୍ୟୋଗଦ୍ଵାରା ହେଉଥିବା ସଂଯୁକ୍ତ ମୂଲ୍ୟର ମୋଟ ସମିଶ୍ରଣକୁ ବୁଝାଇଥାଏ । ଆୟ ଦିଗରୁ ବିଚାର କଲେ, କର୍ମଚାରୀଙ୍କ ପ୍ରତିଦାନ, କାର୍ଯ୍ୟକାରୀ ଉଦ୍ବୃରାଂଶ, ଆତ୍ମନିଯୁକ୍ତିଙ୍କ ମିଶ୍ରିତ ଆୟ, ନିଟ୍ ପରୋକ୍ଷ କର ଏବଂ ସ୍ଥିର ପୁଞ୍ଜି ଉପଭୋଗର ସମଷ୍ଟିକୁ ହିଁ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ କୁହାଯାଏ । ବ୍ୟୟ (ଖର୍ଚ୍ଚ) ଦୃଷ୍ଟିରୁ ବିଚାର କଲେ, ଘରୋଇ ଉପଭୋଗ ଖର୍ଚ୍ଚ, ସରକାରଙ୍କ ଉପଭୋଗ ଖର୍ଚ୍ଚ, ମୋଟ ଦେଶୀୟ ପୁଞ୍ଜିଗଠନ ଏବଂ ନିଟ୍ ରପ୍ତାନିକୁ ନେଇ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ ସ୍ଥିର କରାଯାଏ ।
ବୈଶିଷ୍ଟ୍ୟ :
(i) ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ଦ୍ରବ୍ୟ ଓ ସେବାର ଅବକ୍ଷୟଜନିତ ମୂଲ୍ୟକୁ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦର ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଏ ନାହିଁ ।
(ii) ହସ୍ତାନ୍ତରୀଣ ଦେୟ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦରୁ ବାଦ୍ ଦିଆଯାଇଥାଏ ।
(iii) ବଜାରକୁ ପ୍ରେରିତ ହେଉଥିବା ଦ୍ରବ୍ୟ ଓ ସେବାକୁ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦରେ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇଥାଏ ।
(iv) ପୁଞ୍ଜିଲାଭକୁ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦରୁ ବାଦ୍ ଦିଆଯାଏ ।
(v) ଏହା ମଧ୍ୟବର୍ତୀ ଦ୍ରବ୍ୟର ମୂଲ୍ୟକୁ ଗ୍ରହଣ କରି ନ ଥାଏ । କେବଳ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷରେ ଉତ୍ପାଦିତ ଅନ୍ତିମ ଦ୍ରବ୍ୟ ଓ ସେବାର ମୂଲ୍ୟ ମୋଟ ଜାତୀୟ ଆୟରେ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଏ ।
ମୋଟ ଜାତୀୟ ଉତ୍ପାଦରୁ ଅବକ୍ଷୟ ପରିବ୍ୟୟକୁ ବାଦ୍ ଦେଇ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ ସ୍ଥିର କରାଯାଇଥାଏ । ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦରୁ ଚଳନ୍ତି ଉପଭୋଗ ଏବଂ ନବୀକରଣ ପରିବ୍ୟୟ ଉପରେ ହେଉଥିବା ମୋଟ ଉତ୍ପାଦନର ନିଟ୍ ବୃଦ୍ଧି ସୂଚିତ ହୁଏ !
ଉପାଦାନ ପରିବ୍ୟୟ ଏବଂ ବଜାର ଦାମ୍ରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ – ହିସାବ ଅନ୍ତର୍ଭୁକ୍ତ ବର୍ଷରେ ଦେଶୀୟ ଅଞ୍ଚଳରେ ଚୂଡ଼ାନ୍ତଭାବେ ଉତ୍ପାଦନ କରାଯାଉଥିବା ଦ୍ରବ୍ୟ ଓ ସେବାର ମୂଲ୍ୟକୁ ଉପାଦାନ ପରିବ୍ୟୟ ଆକାରରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ କୁହାଯାଏ । ଦେଶ ଭିତରେ ଉତ୍ପାଦନ କରାଯାଉଥିବା ମୋଟ ଉତ୍ପାଦ ମୂଲ୍ୟରୁ ମଧ୍ୟବର୍ତ୍ତୀ ଉପଭୋଗର ମୂଲ୍ୟକୁ ବାଦେଇ ବଢ଼ାର ଦାମ୍ରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ ସ୍ଥିର କରାଯାଇଥାଏ ।
ଉପାଦାନ ପରିବ୍ୟୟ ଏବଂ ବଜାର ଦାମ୍ରେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ – ବର୍ଷକ ମଧ୍ୟରେ ଦେଶରେ ଉତ୍ପାଦନ କରାଯାଉଥିବା ସମସ୍ତ ଅନ୍ତିମ ଦ୍ରବ୍ୟ ଓ ସେବାର ଉପାଦାନ ପରିବ୍ୟୟ ସମ୍ମିଶ୍ରଣ କରି ଉପାଦାନ ପରିବ୍ୟୟ ଆକାରରେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ ସ୍ଥିର କରାଯାଏ । ପ୍ରକାରାନ୍ତରେ କହିବାକୁ ଗଲେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦରେ କର୍ମଚାରୀଙ୍କ ପ୍ରତିଦାନ, ଆତ୍ମନିଯୁକ୍ତଙ୍କ ମିଶ୍ରିତ ଆୟ, କାର୍ଯ୍ୟକାରୀ ଉଦ୍ବୃତ୍ତାଶ ଏବଂ ସ୍ଥିର ପୁଞ୍ଜି ଉପଭୋଗ ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇଥାଏ ।
ବଜାର ଦାମ୍ରେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ କହିଲେ ବଜାର ଦାମ୍ରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ ଏବଂ ବିଦେଶରୁ ମିଳୁଥିବା ଉପାଦାନ ଆୟକୁ ବୁଝାଏ । ଦେଶର ନାଗରିକ ବିଦେଶରେ ଉତ୍ପାଦନ କରୁଥିବା ଦ୍ରବ୍ୟର ମୂଲ୍ୟରୁ ଦେଶ ମଧ୍ୟରେ ନାଗରିକମାନଙ୍କଦ୍ୱାରା ଉତ୍ପାଦନ କରାଯାଉଥିବା ଦ୍ରବ୍ୟର ମୂଲ୍ୟକୁ ବାଦ୍ ଦେଇ ବିଦେଶରୁ ମିଳୁଥିବା ନିଟ୍ ଆୟ ସ୍ଥିର କରାଯାଏ ।
ତୁଳନାତ୍ମକ ଉପସ୍ଥାପନା :
ବଜାର ଦରରେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ
= ବଜାର ଦରରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ + ବିଦେଶରୁ ମିଳୁଥିବା ନିଟ୍ ଉପାଦାନ ଆୟ
= କର୍ମଚାରୀଙ୍କ ପ୍ରତିଦାନ + କାର୍ଯ୍ୟକାରୀ ଉଦ୍ବୃରାଂଶ + ଆତ୍ମନିଯୁକ୍ତଙ୍କ ମିଶ୍ରିତ ଆୟ + ସ୍ଥିର ପୁଞ୍ଜି ଉପଭୋଗ + ନିଟ୍ ପରୋକ୍ଷ କର । (ଆୟ ପଦ୍ଧତିରେ ପରିମାପ କରାଯାଇଛି)
= ଘରୋଇ ଅନ୍ତିମ ଉପଭୋଗ + ସରକାରୀ ଉପଭୋଗ + ଘରୋଇ ବିନିଯୋଗ + ରପ୍ତାନି – ଆମଦାନି (ବ୍ୟୟ ପଦ୍ଧତିରେ ପରିମାପ କରାଯାଇଛି)
ବଜାର ଦରରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ
= ଦେଶରେ ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟ ଓ ସେବାର ମୂଲ୍ୟ – ଉପଭୋଗ ହେଉଥିବା ମଧ୍ୟବର୍ତ୍ତୀ ଦ୍ରବ୍ୟର ମୂଲ୍ୟ ତେଣୁ ବଜାର ଦରରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ
= ବଜାର ଦରରେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ – ବିଦେଶରୁ ମିଳୁଥିବା ନିଟ୍ ଆୟ ।

2. ଘରୋଇ ଆୟ ଏବଂ ବ୍ୟକ୍ତିଗତ ଆୟ ଅଭିଧାରଣା ବ୍ୟାଖ୍ୟା କର । ବ୍ୟକ୍ତିଗତ ଆୟ ଏବଂ ବ୍ୟବହାରଯୋଗ୍ୟ ଆୟ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।
Answer:
ଘରୋଇ ଆୟ – ଘରୋଇ ଆୟ କହିଲେ ଉପାଦାନ ଆୟ ଓ ହସ୍ତାନ୍ତରୀଣ ପ୍ରାପ୍ୟକୁ କୁହାଯାଏ । ଉପାଦାନ ପରିବ୍ୟୟରେ ମୋଟ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ, ହସ୍ତାନ୍ତରୀଣ ପ୍ରାପ୍ୟ, ସରକାରୀ ଋଣ ଉପରେ ସୁଧ, ସାମାଜିକ ସୁରକ୍ଷା ଉପରେ ପ୍ରାପ୍ୟ, ରାଷ୍ଟ୍ରାୟତ୍ତ ସଂସ୍ଥାରୁ ମିଳୁଥିବା ଲାଭ ଏବଂ ଉଦ୍ବୃତ୍ତାଶକୁ ନେଇ ଘରୋଇ ଆୟ କଳନା କରାଯାଏ । ଘରୋଇ ଆୟକୁ ଜାତୀୟ ଆୟଠାରୁ ଭିନ୍ନ ବୋଲି ବିଚାର କରାଯାଏ । କାରଣ ଜାତୀୟ ଆୟରେ ଉଭୟ ଘରୋଇ କ୍ଷେତ୍ରରୁ ଓ ରାଷ୍ଟ୍ରାୟତ୍ତ କ୍ଷେତ୍ରରୁ ମିଳୁଥିବା ଆୟ ଅନ୍ତର୍ଭୁକ୍ତ, ମାତ୍ର ଘରୋଇ ଆୟରେ ରାଷ୍ଟ୍ରୀୟର କ୍ଷେତ୍ରରୁ ମିଳୁଥିବା ଆୟ ଅନ୍ତର୍ଭୁକ୍ତ ହୁଏ ନାହିଁ । ପୁନଶ୍ଚ ଜାତୀୟ ଋଣ ଉପରେ ମିଳୁଥିବା ସୁଧ ଜାତୀୟ ଆୟର ଅଂଶବିଶେଷ ନ ହୋଇଥିବା ସ୍ଥଳେ ତାହା ଘରୋଇ ଆୟରେ ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇଥାଏ ।
ବ୍ୟକ୍ତିଗତ ଆୟ – ବ୍ୟକ୍ତିଗତ ଆୟ କହିଲେ ଦେଶରେ ବର୍ଷକ ମଧ୍ୟରେ ବ୍ୟକ୍ତିବିଶେଷ କିମ୍ବା ପରିବାରବର୍ଗଙ୍କୁ ମଜୁରି, ବେତନ, ଅଶେଷ, ସୁଧ ଏବଂ ଲାଭାଂଶ ଆକାରରେ ମିଳୁଥିବା ଆୟକୁ ବୁଝାଏ । ବ୍ୟକ୍ତିଗତ ଆୟରେ ଆତ୍ମନିଯୁକ୍ତଙ୍କ ମିଶ୍ରିତ ଆୟ ମଧ୍ଯ ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇଥାଏ । ସୁତରାଂ ବ୍ୟକ୍ତିଗତ ଆୟର ସଂଜ୍ଞାପ୍ରକରଣ କ୍ରମରେ କୁହାଯାଇପାରେ ଯେ, ସରକାର ଏବଂ ବ୍ୟବସାୟ କ୍ଷେତ୍ରରୁ ହସ୍ତାନ୍ତରୀଣ ଆୟ ସମେତ ଅନ୍ୟାନ୍ୟ ସମସ୍ତ ସୂତ୍ରରୁ ଲୋକମାନଙ୍କୁ ମିଳୁଥିବା ଚଳନ୍ତି ଆୟକୁ ବ୍ୟକ୍ତିଗତ ଆୟ କୁହାଯାଏ । ବ୍ୟକ୍ତିଗତ ଆୟ ଜାତୀୟ ଆୟଠାରୁ ଭିନ୍ନ ହୋଇଥାଏ ।
ବ୍ୟକ୍ତିଗତ ଆୟକୁ ମିଶ୍ରଣ କରି ଜାତୀୟ ଆୟ ନିର୍ଦ୍ଧାରଣ କରାଯାଇପାରେ ନାହିଁ । କାରଣ ପ୍ରତିଷ୍ଠାନବର୍ଗ ଅର୍ଜନ କରୁଥିବା ଆୟ ସାମଗ୍ରିକଭାବେ ଉତ୍ପାଦନ ଉପାଦାନଙ୍କ ମଧ୍ୟରେ ବଣ୍ଟନ ହୋଇନଥାଏ । ପ୍ରତିଷ୍ଠାନର ଆୟରୁ କିଛି ଅଂଶ ଭବିଷ୍ୟତ ସଂପ୍ରସାରଣ ଏବଂ ନିଗମ କର ଦେୟ ଉଦ୍ଦେଶ୍ୟରେ ରଖାଯାଇ ଥାଏ । ସୁତରାଂ କେବଳ ଉପାଦାନ ଆୟକୁ ଜାତୀୟ ଆୟ କୁହାଯାଏ । ବ୍ୟକ୍ତିଗତ ଆୟକୁ ମଧ୍ୟ ଘରୋଇ ଆୟଠାରୁ ଭିନ୍ନଭାବେ ବିଚାର କରାଯାଏ । କାରଣ ଘରୋଇ ଆୟରେ ସଞ୍ଚୟ ଓ ନିଗମ କର ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇଥିଲାବେଳେ ବ୍ୟକ୍ତିଗତ ଆୟରୁ ଏହି ଦୁଇ ପ୍ରକାର ଦେୟକୁ ବାଦ୍ ଦିଆଯାଇଥାଏ ।
ବ୍ୟବହାରଯୋଗ୍ୟ ଆୟ : ସରକାରଙ୍କଦ୍ଵାରା ଆରୋପିତ ଆୟକର ଏବଂ ସମ୍ପତ୍ତି କର ପଇଠ କଲା ପରେ ବ୍ୟକ୍ତିବିଶେଷଙ୍କର ଯେଉଁ ଆୟ ରହେ ତାହାକୁ ବ୍ୟବହାରଯୋଗ୍ୟ ଆୟ ରୂପେ ବିଚାର କରାଯାଏ । ଏହି ବ୍ୟବହାରଯୋଗ୍ୟ ଆୟକୁ ଲୋକମାନେ ଉପଭୋଗ ଏବଂ ସଞ୍ଚୟ ଉଦ୍ଦେଶ୍ୟରେ ଉପଯୋଗ କରିଥା’ନ୍ତି । ପ୍ରତ୍ୟେକ ବ୍ୟକ୍ତି ବା ପରିବାର ସଚେତନ ଥା’ନ୍ତି ଯେ, ସେମାନଙ୍କୁ କର ଓ ଫିସ୍ ଆକାରରେ କିଛି ଦେବାକୁ ହେବ । ତେଣୁ ସେମାନେ ସମସ୍ତ ଆୟକୁ ଖର୍ଚ୍ଚ କରିନଥା’ନ୍ତି ।
ବ୍ୟକ୍ତିଗତ ଆୟ ଓ ବ୍ୟବହାରଯୋଗ୍ୟ ଆୟ : ଯେଉଁ ଆୟ ଦେଶବାସୀ ମଜୁରି, ବେତନ, ଅଧ୍ଵଶେଷ, ସୁଧ, ଲାଭାଂଶ ଏବଂ ଆତ୍ମନିଯୁକ୍ତିରୁ ମିଳୁଥିବା ମିଶ୍ରିତ ଆୟ ଆକାରରେ ପାଇଥା’ନ୍ତି, ତାହାକୁ ବ୍ୟକ୍ତିଗତ ଆୟ କୁହାଯାଏ । ବ୍ୟବହାରଯୋଗ୍ୟ ଆୟ ହେଉଛି ବ୍ୟକ୍ତିଗତ ଆୟର ଏକ ଅଂଶ ଯାହାକି ବ୍ୟକ୍ତିଗତ ଆୟରୁ ସମସ୍ତ ପ୍ରକାର କର ପଇଠ ହେଲା ପରେ ସ୍ଥିର ହୋଇଥାଏ ।
3. ଜାତୀୟ ଆୟ ସଂପର୍କିତ ବିଭିନ୍ନ ଅଭିଧାରଣା ସଂପର୍କରେ ବ୍ୟାଖ୍ୟା କର ଓ ଏମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ଆନ୍ତଃସଂପର୍କ ଦର୍ଶାଅ ।
Answer:
କୌଣସି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ହିସାବ ବର୍ଷରେ ଉପାଦାନମାନଙ୍କଦ୍ଵାରା ଦେଶ ଭିତରେ ଉତ୍ପାଦିତ ହେଉଥିବା ସାମଗ୍ରିକ ମୌଦ୍ରିକ ମୂଲ୍ୟକୁ ଜାତୀୟ ଆୟ କୁହାଯାଏ । ତେଣୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷରେ ଉତ୍ପାଦିତ ସମସ୍ତ ଅନ୍ତିମ ଦ୍ରବ୍ୟର ମୌଦ୍ରିକ ମୂଲ୍ୟାୟନ ହିଁ ମୋଟ ଜାତୀୟ ଆୟ । ଏହି ଜାତୀୟ ଆୟ ସଂପର୍କିତ ବିଭିନ୍ନ ଅଭିଧାରଣା ରହିଛି ଯାହା ନିମ୍ନରେ ବର୍ଣ୍ଣନା କରାଗଲା ।
(1) ବଜାର ଦାମ୍ରେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ (Gross National Product at Market Price) – କୌଣସି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷରେ ଉତ୍ପାଦିତ ହୋଇଥିବା ସମସ୍ତ ଅନ୍ତିମ ଦ୍ରବ୍ୟର ବଜାର ମୂଲ୍ୟାୟନରୁ ହିଁ ବଜାର ଦାମ୍ରେ ଜାତୀୟ ଉତ୍ପାଦ କଳନା କରାଯାଏ । ଏହାକୁ ଆକଳନ କରିବାପାଇଁ ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟ ଓ ସେବାର ପରିମାଣକୁ ବଜାର ଦାମ୍ରେ ଗୁଣନ କରାଯାଏ ।
ମୋଟ ଜାତୀୟ ଉତ୍ପାଦର କଳନା ସମୟରେ ଅବକ୍ଷୟଜନିତ ପରିବ୍ୟୟ, ପୁଞ୍ଜିଲାଭ, ହସ୍ତାନ୍ତରୀଣ ବ୍ୟୟ, ମଧ୍ୟବର୍ତ୍ତୀ ଦ୍ରବ୍ୟର ମୂଲ୍ୟକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଏ ନାହିଁ । କେବଳ ବଜାରକୁ ପ୍ରେରିତ ଦ୍ରବ୍ୟ ଓ ସେବାର ମୌଦ୍ରିକ ମୂଲ୍ୟକୁ ଏହାର ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଏ । ତେଣୁ ବଜାର ଦାମ୍ରେ ମୋଟ୍ ଜାତୀୟ ଉତ୍ପାଦ = ପାରିବାରିକ ଉପଭୋଗଜନିତ ବ୍ୟୟ + ମୋଟ ପୁଞ୍ଜି ଗଠନ + ରପ୍ତାନି – ଆମଦାନି + ବିଦେଶରୁ ମିଳୁଥିବା ନିଟ୍ ଉପାଦାନ ଆୟ ।
ସେହିପରି ମୋଟ ଜାତୀୟ ଉତ୍ପାଦକୁ ତିନୋଟି ଦୃଷ୍ଟିକୋଣରୁ ବିଚାର କରାଯାଇଥାଏ । ଉତ୍ପାଦ ଦିଗରୁ ବିଚାର କରାଗଲେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ = ଉପଭୋଗ ହେଉଥିବା ଦ୍ରବ୍ୟ ଓ ସେବାର ବଜାର ମୂଲ୍ୟ + ସରକାରଙ୍କଦ୍ବାରା ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟ ଓ ସେବାର ବଜାର ମୂଲ୍ୟ + ମୋଟ ଘରୋଇ ବିନିଯୋଗ + (ରପ୍ତାନି – ଆମଦାନି)
ଆୟ ଦିଗରୁ ବିଶ୍ଳେଷଣ କରାଗଲେ :
ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ = କର୍ମଚାରୀଙ୍କ ପ୍ରତିଦାନ + କାର୍ଯ୍ୟକାରୀ ଉଦ୍ବୃତ୍ତାଶ+ ଆତ୍ମନିଯୁକ୍ତିଙ୍କ ମିଶ୍ରିତ ଆୟ + ନିଟ୍ ପରୋକ୍ଷ କର + ସ୍ଥିର ପୁଞ୍ଜିର ଉପଭୋଗ
ବ୍ୟୟ ଦିଗରୁ ଆଲୋଚନା କରାଗଲେ :
ବଜାର ଦାମ୍ରେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ = ବେସରକାରୀ (ଘରୋଇ)ଉପଭୋଗ + ସରକାରୀ ଉପଭୋଗ + ମୋଟ ଘରୋଇ ବିନିଯୋଗ + ରପ୍ତାନି – ଆମଦାନି ।
(2) ବଜାର ଦାମ୍ରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ (Gross Domestic Product at Market Price) – କୌଣସି ବର୍ଷରେ ଦେଶର ଭୌଗୋଳିକ ସୀମା ମଧ୍ୟରେ ଉତ୍ପାଦିତ ହୋଇଥିବା ଦ୍ରବ୍ୟ ଓ ସେବାର ମୌଦ୍ରିକ ମୂଲ୍ୟକୁ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ କୁହାଯାଏ । ଏହି ଅଭିଧାରଣାରେ କେବଳ ବଜାରକୁ ପ୍ରେରିତ ଅନ୍ତିମ ଦ୍ରବ୍ୟ ଓ ସେବାକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇଥାଏ । ହସ୍ତାନ୍ତରୀଣ ଆୟ, ପୁଞ୍ଜିଲାଭ ଆଦିକୁ ଏହି ହିସାବରୁ ବହିର୍ଭୁକ୍ତ କରାଯାଇଥାଏ । ତେଣୁ ଏ ଅର୍ଥରେ – ବଜାର ଦରରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ = ଦେଶରେ ଉତ୍ପାଦିତ ହୋଇଥିବା ମୋଟ ଉତ୍ପାଦର ମୂଲ୍ୟ – ଦ୍ରବ୍ୟର ମୂଲ୍ୟ ।
(3) ବଜାର ଦାମ୍ରେ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ (Net National Product at Market Price) – ମୋଟ ଜାତୀୟ ଉତ୍ପାଦରୁ ଅବକ୍ଷୟଜନିତ ପରିବ୍ୟୟ ବିୟୋଗ କରାଗଲେ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ ମିଳିଥାଏ; ଯଥା – ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ = ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ – ଅବକ୍ଷୟ ପରିବ୍ୟୟ ।
ସେହି ଅର୍ଥରେ ବଜାର ଦାମ୍ରେ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ କହିଲେ କୌଣସି ଅର୍ଥବ୍ୟବସ୍ଥାରେ ଏକ ବର୍ଷରେ ଉତ୍ପାଦିତ ହେଉଥିବା ଅନ୍ତିମ ଦ୍ରବ୍ୟସମୂହର ନିଟ୍ ବଜାର ମୂଲ୍ୟକୁ ବୁଝାଇଥାଏ ।
ତେଣୁ ବଜାର ଦାମ୍ରେ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ = ବଜାର ଦାମ୍ରେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ – ପୁଞ୍ଜି ଉପଭୋଗଜନିତ ଦେୟ
= ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ (ବଜାର ଦାମ୍ ) – ଅବକ୍ଷୟଜନିତ ପରିବ୍ୟୟ
= ପ୍ରାଥମିକ କ୍ଷେତ୍ରରେ ଉପାଦାନ ପରିବ୍ୟୟରେ ସଂଯୁକ୍ତ ମୂଲ୍ୟ + ମାଧ୍ୟମିକ କ୍ଷେତ୍ରରେ ଉପାଦାନ ପରିବ୍ୟୟରେ ସଂଯୁକ୍ତ ମୂଲ୍ୟ + ସେବା କ୍ଷେତ୍ରରେ ଉପାଦାନ ପରବ୍ୟୟରେ ସଂଯୁକ୍ତ ମୂଲ୍ୟ + ନିଟ୍ ପରୋକ୍ଷ କର – ବିଦେଶରୁ ମିଳୁଥିବା ନିଟ୍ ଆୟ + ଅବକ୍ଷୟଜନିତ ମୂଲ୍ୟ ।
(4) ବଜାର ଦାମ୍ରେ ନିଟ୍ ଦେଶୀୟ ଉତ୍ପାଦ (Net Domestic Product at Market Price) – ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷରେ ଦେଶରେ ଓ ବିଦେଶରେ ଉତ୍ପାଦିତ ହେଉଥିବା ଅନ୍ତିମ ଦ୍ରବ୍ୟର ମୂଲ୍ୟକୁ ବଜାର ଦାମ୍ରେ ନିଟ୍ ଦେଶୀୟ ଉତ୍ପାଦ କୁହାଯାଏ ।
ନିଟ୍ ଦେଶୀୟ ଉତ୍ପାଦ (ବଜାର ଦାମ୍ ) = ବଜାର ଦାମ୍ରେ ନି ଟ୍ ଜାତୀୟ ଉତ୍ପାଦ – ବିଦେଶରୁ ମିଳୁଥିବା ନିଟ୍ ଉପାଦାନ ଆୟ
⇒ ନିଟ୍ ଦେଶୀୟ ଉତ୍ପାଦ (ବଜାର ଦାମ୍) = ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ (ବଜାର ଦାମ୍) – ଅବକ୍ଷୟଜନିତ ପରିବ୍ୟୟ ।
(5) ଉପାଦାନ ପରିବ୍ୟୟରେ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ (Net National Product at Factor Cost) – ଉପାଦାନ ପରିବ୍ୟୟରେ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ କହିଲେ କୌଣସି ବର୍ଷରେ ଦେଶରେ ଓ ବିଦେଶରେ ଅର୍ଜନ କରାଯାଉଥିବା ବିଭିନ୍ନ ଉପାଦାନମାନଙ୍କର ସାମଗ୍ରିକ ଆୟକୁ ବୁଝାଇଥାଏ ।
ତେଣୁ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ (ଉପାଦାନ ପରିବ୍ୟୟରେ) = ଉପାଦାନ ପରିବ୍ୟୟରେ ନିଟ୍ ଦେଶୀୟ ଉତ୍ପାଦ + ବିଦେଶରୁ ମିଳୁଥିବା ଉପାଦାନର ନିଟ୍ ଆୟ
= କର୍ମଚାରୀଙ୍କ ପ୍ରତିଦାନ + କାର୍ଯ୍ୟକାରୀ ଉଦ୍ବୃତ୍ତ + ମିଶ୍ରିତ ଆୟ + ବିଦେଶରୁ ମିଳୁଥିବା ନିଟ୍ ଜାତୀୟ ଉପାଦାନ ଆୟ
ଏହି ଅର୍ଥରେ ବିଚାର କରାଗଲେ ଉପାଦାନ ପରିବ୍ୟୟରେ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ = ବଜାର ଦାମ୍ରେ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ – ପରୋକ୍ଷ କର ।
ଉପାଦାନ ପରିବ୍ୟୟରେ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ = ବଜାର ଦାମ୍ରେ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ + ସବ୍ସଡ଼ି – ପରୋକ୍ଷ କର
ତେଣୁ ଉପାଦାନ ପରିବ୍ୟୟରେ ନିଟ୍ ଉପାଦାନ ଉତ୍ପାଦ = ଉପାଦାନ ପରିବ୍ୟୟରେ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ – ବିଦେଶରୁ ମିଳୁଥିବା ଉପାଦାନମାନଙ୍କର ଆୟ ।
(6) ଉପାଦାନ ପରିବ୍ୟୟରେ ନିଟ୍ ଦେଶୀୟ ଉତ୍ପାଦ (Net Domestic Product at Factor Cost) – କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷରେ ବିଭିନ୍ନ ଉପାଦାନମାନଙ୍କଦ୍ଵାରା ଅର୍ଜନ କରୁଥିବା ଆୟର ସମଷ୍ଟିକୁ ଉପାଦାନ ପରିବ୍ୟୟରେ ନିଟ୍ ଦେଶୀୟ ଉତ୍ପାଦ କୁହାଯାଏ ।
ଉପାଦାନ ପରିବ୍ୟୟରେ ନିଟ୍ ଦେଶୀୟ ଉତ୍ପାଦ = ଉପାଦାନ ପରିବ୍ୟୟରେ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ – ବିଦେଶରୁ ମିଳୁଥିବା ଉପାଦାନମାନଙ୍କ ଆୟ
= ବଜାର ମୂଲ୍ୟରେ ନିଟ୍ ଦେଶୀୟ ଉତ୍ପାଦ – ପରୋକ୍ଷ କର + ସବ୍ସିଡ଼ି
(7) ଉପାଦାନ ପରିବ୍ୟୟରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ (Gross Domestic Product at Factor Cost) – କୌଣସି ଦେଶରେ ଉତ୍ପାଦନକାରୀଙ୍କଦ୍ବାରା ନିଟ୍ ସଂଯୁକ୍ତ ମୂଲ୍ୟର ସମଷ୍ଟିକୁ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ (ଉପାଦାନ ପରିବ୍ୟୟ) କୁହାଯାଏ ।
ତେଣୁ, ଉପାଦାନ ପରିବ୍ୟୟରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ = ଉପାଦାନ ପରିବ୍ୟୟରେ ନିଟ୍ ଦେଶୀୟ ଉତ୍ପାଦ + ଅବକ୍ଷୟର ମୂଲ୍ୟ
= ବଜାର ଦରରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ – ପରୋକ୍ଷ କର + ସବ୍ସିଡ଼ି
(8) ଉପାଦାନ ପରିବ୍ୟୟରେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ (Gross National Product at Factor Cost) – ବଜାର ଦରରେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦରୁ ନିଟ୍ ପରୋକ୍ଷ କର ବିୟୋଗ କରାଗଲେ ଉପାଦାନ ପରିବ୍ୟୟରେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ ମିଳିଥାଏ ।
ତେଣୁ, ଉପାଦାନ ପରିବ୍ୟୟରେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ = ଉପାଦାନ ପରିବ୍ୟୟରେ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ + ଅବକ୍ଷୟ ପରିବ୍ୟୟ
(9) ଘରୋଇ ଆୟ (Private Income) – ବିଭିନ୍ନ ଉତ୍ସରୁ ବିଭିନ୍ନ ବ୍ୟକ୍ତିବିଶେଷଙ୍କଦ୍ଵାରା ଅର୍ଜିତ ଆୟସମୂହର ସମଷ୍ଟିକୁ ଘରୋଇ ଆୟ କୁହାଯାଏ ।
ତେଣୁ ଘରୋଇ ଆୟ = ଉପାଦାନ ପରିବ୍ୟୟରେ ଜାତୀୟ ଆୟ + ହସ୍ତାନ୍ତରଣ ଦେୟ + ସରକାରୀ ଋଣର ସୁଧ – ସାମାଜିକ ନିରାପତ୍ତା ବ୍ୟୟ – ସରକାରୀ ଉଦ୍ୟୋଗର ଲାଭାଂଶ ।
(10) ବ୍ୟକ୍ତିଗତ ଆୟ (Personal Income) – ଦେଶର ବ୍ୟକ୍ତିବିଶେଷଙ୍କଦ୍ଵାରା ସଂଗୃହୀତ ଆୟର ସମାହାର ହିଁ ବ୍ୟକ୍ତିଗତ ଆୟ ।
ବ୍ୟକ୍ତିଗତ ଆୟ = ଘରୋଇ ଆୟ – ବେସରକାରୀ ଉଦ୍ୟୋଗର ସଞ୍ଚୟ ।
(11) ବ୍ୟବହାରଯୋଗ୍ୟ ଆୟ (Disposable Income) – ପରିବାର ଓ ବ୍ୟକ୍ତିବିଶେଷଙ୍କଦ୍ୱାରା ଉପଭୋଗ ଉଦ୍ଦେଶ୍ୟରେ ବ୍ୟୟଯୋଗ୍ୟ ଆୟକୁ ବ୍ୟବହାରଯୋଗ୍ୟ ଆୟ କୁହାଯାଏ । ଏହି ଅର୍ଥରେ,
ବ୍ୟବହାର ଯୋଗ୍ୟ ଆୟ = ବ୍ୟକ୍ତିଗତ ଆୟ – ପ୍ରତ୍ୟକ୍ଷ କର ।

4. ଜାତୀୟ ଆୟର ପରିମାପ ସଂପର୍କରେ ଅନୁସୃତ ତିନୋଟି ପଦ୍ଧତି ବର୍ଣ୍ଣନା କର । ଏସବୁର ସୁବିଧା ଓ ଅସୁବିଧା ସଂପର୍କରେ ସୂଚନା ଦିଅ ।
Answer:
ଦେଶର ଜାତୀୟ ଆୟ ପରିମାପ କରିବାର ତିନୋଟି ପଦ୍ଧତି ମଧ୍ୟରୁ ଯେକୌଣସି ଗୋଟିଏ ପଦ୍ଧତି ଅବଲମ୍ବନ କରାଯାଇଥାଏ । ସେହି ପଦ୍ଧତିଗୁଡ଼ିକ ହେଲା ଉତ୍ପାଦ ପଦ୍ଧତି, ଆୟ ପଦ୍ଧତି ଓ ବ୍ୟୟ ପଦ୍ଧତି । ଉତ୍ପାଦ ପଦ୍ଧତିକୁ ଅନ୍ୟ ଅର୍ଥରେ ମୂଲ୍ୟ ସଂଯୁକ୍ତ ପଦ୍ଧତି କୁହାଯାଏ ।
ଉତ୍ପାଦ ପଦ୍ଧତି – ଉତ୍ପାଦ ପଦ୍ଧତି ଅନୁସାରେ ବଜାର ଦାମ୍ରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ କଳନା କରିବାପାଇଁ ବର୍ଷକ ମଧ୍ୟରେ ଉତ୍ପାଦନ କରାଯାଉଥିବା ସମସ୍ତ ଅନ୍ତିମ ଦ୍ରବ୍ୟ ଓ ସେବାର ମୂଲ୍ୟକୁ ଯୋଗ କରାଯାଏ । ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦରୁ ମଧ୍ୟବର୍ତ୍ତୀ ଦ୍ରବ୍ୟର ମୂଲ୍ୟ ଏବଂ ଅବକ୍ଷୟ ପରିବ୍ୟୟକୁ ବାଦ୍ ଦେଇ ନିଟ୍ ଦେଶୀୟ ଉତ୍ପାଦ ସ୍ଥିର କରାଯାଇଥାଏ । ଅର୍ଥବ୍ୟବସ୍ଥାରେ ନିୟୋଜିତ ସମସ୍ତ ଉଦ୍ୟୋଗରେ ଉତ୍ପାଦନ କରାଯାଉଥିବା ଦ୍ରବ୍ୟ ପରିମାଣକୁ ଦାମ୍ ସହ ଗୁଣନ କରି ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦର ମୂଲ୍ୟ ପରିମାପ କରାଯାଇଥାଏ ।
ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦର କଳନା କଲାବେଳେ ଜାତୀୟ ଉତ୍ପାଦର ଯେପରି ଦ୍ବୈତ ଗଣନା କରାନଯାଏ, ସେଥ୍ୟପ୍ରତି ଧ୍ୟାନ ଦିଆଯିବା ଉଚିତ । ମୂଲ୍ୟ ସଂଯୁକ୍ତ ପଦ୍ଧତି ଅବଲମ୍ବନଦ୍ୱାରା ଏହି ଅସୁବିଧା ଦୂର କରାଯାଇପାରେ । ନିଟ୍ ସଂଯୁକ୍ତ ମୂଲ୍ୟରୁ ପରୋକ୍ଷ କରକୁ ବାଦ୍ ଦେଇ ଉପାଦାନ ପରିବ୍ୟୟରେ ନିଟ୍ ସଂଯୁକ୍ତ ମୂଲ୍ୟ ସ୍ଥିର କରାଯାଇଥାଏ ।
ଅସୁବିଧା – ଉତ୍ପାଦ ପଦ୍ଧତି ଅବଲମ୍ବନଦ୍ୱାରା ଜାତୀୟ ଆୟ ପରିମାପରେ କେତେକ ଅସୁବିଧା ପରିଲକ୍ଷିତ ହୋଇଥାଏ । ପ୍ରଥମତଃ ଉପାଦାନ ପରିବ୍ୟୟରେ ଏବଂ ବଜାର ଦାମ୍ରେ ଜାତୀୟ ଆୟ ପରିମାପ ଏକ ଭ୍ରାନ୍ତ ଧାରଣା ସୃଷ୍ଟି କରେ । ସୁତରାଂ ଦ୍ବିତୀୟତଃ, ଅନ୍ତିମ ଦ୍ରବ୍ୟ ଓ ମଧ୍ୟବର୍ତ୍ତୀ ଦ୍ରବ୍ୟ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ସ୍ପଷ୍ଟ ନ ହୋଇଥିବାରୁ ମଧ୍ୟବର୍ତ୍ତୀ ଦ୍ରବ୍ୟର ମୂଲ୍ୟକୁ ବାଦ୍ ଦେଲାବେଳେ ଫଳାଫଳ ତ୍ରୁଟିପୂର୍ଣ୍ଣ ହୋଇଥାଏ । ତୃତୀୟତଃ, ସ୍ଵଉପଭୋଗ କ୍ଷେତ୍ରରେ ଦ୍ରବ୍ୟ ବଜାରକୁ ଆସୁ ନ ଥିଲାବେଳେ ସେସବୁର ମୂଲ୍ୟାୟନ ସମ୍ଭବ ହୋଇ ନ ଥାଏ । ଚତୁର୍ଥତଃ, ଅବକ୍ଷୟଜନିତ ପରିମାପରେ ମଧ୍ୟ ସମସ୍ୟା ଦେଖାଦିଏ । ପଞ୍ଚମତଃ, ନିର୍ଭରଯୋଗ୍ୟ ଏବଂ ଯଥେଷ୍ଟ ତଥ୍ୟର ଅଭାବ ଓ ଦ୍ଵୈତ ଗଣନାର ସମ୍ଭାବନା ରହିଥାଏ ।
ଆୟ ପଦ୍ଧତି – ଆୟ ପଦ୍ଧତି ଅବଲମ୍ବନ କରି ଉପାଦାନ ଅଧିକାରୀଗଣ ଲାଭ କରୁଥିବା ଆୟର ସମଷ୍ଟି ନିର୍ଦ୍ଧାରଣଦ୍ୱାରା ଜାତୀୟ ଆୟ ପରିମାପ କରାଯାଇଥାଏ । ଏହାକୁ ଉପାଦାନ ପରିବ୍ୟୟ ଆକାରରେ ଜାତୀୟ ଆୟ କୁହାଯ. ଏ ଯାହାକି ଜାତୀୟ ଉତ୍ପାଦର ମୂଲ୍ୟ ସହ ସମାନ ହୋଇଥାଏ । ଅବଶ୍ୟ ହସ୍ତାନ୍ତରଣ ପ୍ରାପ୍ୟ, ପୁଞ୍ଜିଲାଭ ଏବଂ ପରୋକ୍ଷ କରକୁ ଜାତୀୟ ଆୟ ପରିମାପରୁ ବାଦ୍ ଦିଆଯାଇଥାଏ । ମୋଟ ଜାତୀୟ ଆୟରେ ମଜୁରି, କର୍ମଚାରୀଙ୍କ ପ୍ରତିଦାନ, ସାମାଜିକ ନିରାପତ୍ତା ପରିଯୋଜନାକୁ ଅବଦାନ, ଆତ୍ମନିଯୁକ୍ତଙ୍କ ମିଶ୍ରିତ ଆୟ, ଅଶେଷ, ସୁଧ, ଲାଭାଂଶ, ରାଷ୍ଟ୍ରାୟତ୍ତ ଉଦ୍ୟୋଗରୁ ମିଳୁଥିବା ଆୟ ଏବଂ ବିଦେଶରୁ ମିଳୁଥିବା ନିଟ୍ ଉପାଦାନ ଆୟ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇଥାଏ । ଅବକ୍ଷୟ ପରିବ୍ୟୟକୁ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦରୁ ବାଦ୍ ଦେଇ ନିଟ୍ ଜାତୀୟ ଆୟ ସ୍ଥିର କରାଯାଇଥାଏ ।
ଅସୁବିଧା – ଏହି ପଦ୍ଧତିରେ କେତେକ ଅସୁବିଧା ପରିଲକ୍ଷିତ ହୋଇଥାଏ । ଏହି ପଦ୍ଧତିର ଜାତୀୟ ଆୟ କଳନା କରିବାକୁ ହେଲେ ଆୟର ଶ୍ରେଣୀ ପ୍ରକରଣ କରିବା ଆବଶ୍ୟକ ହୋଇଥାଏ । ମାତ୍ର, ମଜୁରି ଆୟ ଏବଂ ଅଣମଜୁରି ଆୟ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଚିହ୍ନଟ କରିବା ଅସୁବିଧାଜନକ ହୋଇଥାଏ । ବିଶେଷତଃ ମିଶ୍ରିତ ଆୟ କ୍ଷେତ୍ରରେ ମିଳୁଥିବା ଆୟ ଏବଂ ସମ୍ପତ୍ତି ଆୟ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଅନୁଧ୍ୟାନ କରିବା ସମ୍ଭବପର ହୋଇ ନ ଥାଏ । ଅର୍ଥବ୍ୟବସ୍ଥାରେ ଅଣସଂଗଠିତ କ୍ଷେତ୍ରରେ ଆୟର ସଠିକ୍ ପରିମାପ ସମ୍ଭବ ନୁହେଁ । ଏହିସବୁ ଅସୁବିଧା ଦୂର କରାଗଲେ ଆୟ ପଦ୍ଧତି ଜାତୀୟ ଆୟ ପରିମାପର ଏକ ଉତ୍ତମ ପଦ୍ଧତି ବୋଲି ବିବେଚିତ ହୋଇପାରିବ ।
ବ୍ୟୟ ପଦ୍ଧତି – ବ୍ୟୟ ପଦ୍ଧତିରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ ପାଇଁ କରାଯାଉଥିବା ଚୂଡ଼ାନ୍ତ ବ୍ୟୟକୁ ବିଚାରକୁ ନିଆଯାଇଥାଏ । ଘରୋଇ ଉପଭୋଗ ଖର୍ଚ୍ଚ, ସରକାରୀ ଖର୍ଚ୍ଚ, ମୋଟ ପୁଞ୍ଜି ଗଠନ ଏବଂ ନିଟ୍ ରପ୍ତାନି ଚୂଡ଼ାନ୍ତ ବ୍ୟୟରେ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇଥାଏ । ଘରୋଇ ଏବଂ ସରକାରୀ ସ୍ତରରେ ଚୂଡ଼ାନ୍ତ ଉପଭୋଗ ଏବଂ କ୍ଷୟପ୍ରାପ୍ତ ଯନ୍ତ୍ରପାତିର ନବୀକରଣ ପାଇଁ ଖର୍ଚ୍ଚ କରିବା ଆବଶ୍ୟକ ମନେକରାଯାଏ । ନିଟ୍ ରପ୍ତାନି ମଧ୍ଯ ଖର୍ଚ୍ଚର ଏକ ଅଂଶରୂପେ ବିବେଚିତ ହୁଏ । ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ ଉପରେ ଏବଂ ଚୂଡ଼ାନ୍ତ ଉପଭୋଗ ପାଇଁ କରାଯାଉଥିବା ଖର୍ଚ୍ଚ ଜାଣିବାପାଇଁ ଚୂଡ଼ାନ୍ତ ବିକ୍ରୟ ପରିମାଣ ସହିତ ଦାମକୁ ଗୁଣନ କରିବାକୁ ହୋଇଥାଏ । ଘରୋଇ ଚୂଡ଼ାନ୍ତ ଉପଭୋଗ ଖର୍ଚ୍ଚ ସହ ସ୍ଥାୟୀ ଅଧିବାସୀଙ୍କଦ୍ଵାରା ବିଦେଶରୁ ପ୍ରତ୍ୟକ୍ଷଭାବରେ କରାଯାଉଥିବା କ୍ରୟକୁ ଯୋଗ କରିବାକୁ ହୁଏ ଏବଂ ଅସ୍ଥାୟୀ ଅଧ୍ବବାସୀଙ୍କ କ୍ରୟକୁ ବାଦ୍ ଦେବାକୁ ହୋଇଥାଏ ।
କର୍ମଚାରୀଙ୍କୁ ପ୍ରଦତ୍ତ ପ୍ରତିଦାନ ଏବଂ ବିଦେଶରୁ କରାଯାଉଥିବା ନିଟ୍ କ୍ରୟକୁ ସରକାରଙ୍କ ଚୂଡ଼ାନ୍ତ ଉପଭୋଗ ଖର୍ଚ୍ଚ କୁହାଯାଏ । ଏତଦ୍ବ୍ୟତୀତ ଏଥ୍ ସହିତ ପୁଞ୍ଜିଗଠନ ମୂଲ୍ୟ ଯୋଗ କରାଯାଏ । ନିଟ୍ ରପ୍ତାନି ଦେଶୀୟ ଉତ୍ପାଦ ଉପରେ କରାଯାଉଥିବା ଖର୍ଚ୍ଚକୁ ମଧ୍ଯ ଅନ୍ତର୍ଭୁକ୍ତ କରିଥାଏ । ମାତ୍ର ପୁରୁଣା ଦ୍ରବ୍ୟ କ୍ରୟ ବାବଦ ଖର୍ଚ୍ଚ, ଅଂଶଧନ ଆଦି କ୍ରୟରେ ହେଉଥିବା ଖର୍ଚ୍ଚ, ହସ୍ତାନ୍ତରଣ ପ୍ରାପ୍ୟ ପରିଶୋଧ, ସାମାଜିକ ନିରାପତ୍ତା ଯୋଜନାକୁ ଅବଦାନ ଏବଂ ମଧ୍ୟବର୍ତ୍ତୀ ଦ୍ରବ୍ୟର ଦାମ୍ ଇତ୍ୟାଦିକୁ ଏଥୁରୁ ବାଦ୍ ଦିଆଯାଏ ।
ବଜାର ଦାମ୍ରେ ମୋଟ ଜାତୀୟ ଆୟ ଜାଣିବାପାଇଁ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ ସହ ବିଦେଶରୁ ମିଳୁଥିବା ନିଟ୍ ଉତ୍ପାଦନ ଆୟକୁ ଯୋଗ କରିବାକୁ ହୋଇଥାଏ । ମୋଟ ଜାତୀୟ ଉତ୍ପାଦରୁ ନିଟ୍ ପରୋକ୍ଷ କର ଏବଂ ଅବକ୍ଷୟ ପରିବ୍ୟୟକୁ ବିୟୋଗ କରି ଉପାଦାନ ପରିବ୍ୟୟରେ ନିଟ୍ ଜାତୀୟ ଉତ୍ପାଦ ସ୍ଥିର କରାଯାଇଥାଏ ।
ଅସୁବିଧା – ବ୍ୟୟ ପଦ୍ଧତିର ସଫଳତା ତଥ୍ୟର ସଠିକତା ଉପରେ ନିର୍ଭର କରେ । ସଠିକ୍ ତଥ୍ୟ ନ ମିଳିଲେ ବ୍ୟୟ ପଦ୍ଧତିରେ ପରିମାପ ହୋଇଥିବା ଜାତୀୟ ଆୟ ଅତିରଞ୍ଜିତ ହୋଇଥାଏ ।
ଦ୍ଵିତୀୟତଃ, ସ୍ଥାୟୀ ଦ୍ରବ୍ୟରୁ ମାଲିକଙ୍କୁ ଦୀର୍ଘକାଳ ଧରି ସେବା ମିଳିଥାଏ । ସେ ପ୍ରକାର ଦ୍ରବ୍ୟ ସାଧାରଣତଃ ଉଚ୍ଚମୂଲ୍ୟବିଶିଷ୍ଟ ହୋଇଥାଏ । ପ୍ରତ୍ୟେକ ବର୍ଷ ଉପଭୋଗ ହେଉଥିବା ପରିମାଣର ମୂଲ୍ୟ ପରିମାପ କରିବା ସହଜ ଏବଂ ସମ୍ଭବ ହୁଏ ନାହିଁ । ସୁତରାଂ ବ୍ୟୟ ପଦ୍ଧତିରେ ଜାତୀୟ ଆୟ କଳନା ଭ୍ରମାତ୍ମକ ହୋଇପାରେ ।
ତୃତୀୟତଃ, ସମୟ ସମୟରେ ଉପଭୋଗ ଖର୍ଚ୍ଚ ଓ ବିନିଯୋଗ ଖର୍ଚ୍ଚ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ରେଖା ଟାଣିବା ସହଜ ହୋଇନଥାଏ । ଉପରୋକ୍ତ ଆଲୋଚନାରୁ ପ୍ରତୀୟମାନ ହୁଏ ଯେ ଉପରୋକ୍ତ କୌଣସି ପଦ୍ଧତି ଜାତୀୟ ଆୟ କଳନା କ୍ଷେତ୍ରରେ ସଠିକ୍ ଚିତ୍ର ପ୍ରଦାନ କରି ନ ପାରେ । ତେଣୁ ଜାତୀୟ ଆୟ କଳନାରେ ଉପରୋକ୍ତ ତିନୋଟି ପଦ୍ଧତିର ସମକାଳୀନ ପ୍ରୟୋଗ ସଠିକ୍ ଚିତ୍ର ପ୍ରଦାନ କରିପାରେ ।
5. ଜାତୀୟ ଆୟ ପରିମାପରେ ଆୟ ପଦ୍ଧତି ବର୍ଣ୍ଣନା କର । ଏହି ପଦ୍ଧତିର ସଫଳତା ପାଇଁ କି ପ୍ରକାର ସତର୍କତା ଅବଲମ୍ବନ କରାଯିବା ଉଚିତ ଓ ଏହାର ଅସୁବିଧାଗୁଡ଼ିକ କ’ଣ ?
Answer:
ଜାତୀୟ ଆୟ ପରିମାପ କ୍ଷେତ୍ରରେ ଆୟ ପଦ୍ଧତି ଏକ ବିଶେଷଭାବରେ ପ୍ରଚଳିତ ପଦ୍ଧତି । ଏହି ପଦ୍ଧତିରେ ବିଭିନ୍ନ ଉପାଦାନମାନଙ୍କରୁ ମିଳୁଥିବା ଆୟକୁ ଯୋଗ କରାଯାଇ ଜାତୀୟ ଆୟର ପରିମାପ କରାଯାଏ । ଉତ୍ପାଦନ ସଂସ୍ଥାମାନେ କରୁଥିବା ପ୍ରାପ୍ୟ ପରିଶୋଧକୁ ଯୋଗକରି ଅଥବା ଉପାଦାନମାନେ ପାଉଥିବା ଆୟକୁ ଯୋଗକରି ଜାତୀୟ ଆୟ କଳନା କରାଯାଏ । ସରଳ ଭାଷାରେ କହିବାକୁ ଗଲେ, ଆୟ ପଦ୍ଧତି ଅନୁସାରେ ଦେଶର ନାଗରିକଗଣ ବର୍ଷକ ମଧ୍ୟରେ ପାଉଥିବା ଆୟକୁ ଯୋଗକରି ଜାତୀୟ ଆୟ କଳନା କରାଯାଏ ।
ଏହି ପଦ୍ଧତିରେ ଜାତୀୟ ଆୟ କଳନା କଲାବେଳେ ମଜୁରି, କର୍ମଚାରୀଙ୍କ ପ୍ରତିଦାନ, ସାମାଜିକ ନିରାପତ୍ତା ପରିଯୋଜନାକୁ ନିଯୁକ୍ତିଦାତାଙ୍କ ଅବଦାନ, ଆତ୍ମନିଯୁକ୍ତଙ୍କ ମିଶ୍ରିତ ଆୟ, ଅଶେଷ, ସୁଧ, ଲାଭାଂଶ, ରାଷ୍ଟ୍ରାୟତ୍ତ ଉଦ୍ୟୋଗରୁ ମିଳୁଥିବା ଉଦ୍ବୃତ୍ତ ଆୟ ଏବଂ ବିଦେଶରୁ ମିଳୁଥିବା ନିଟ୍ ଉପାଦାନକୁ ଯୋଗ କରିବାକୁ ପଡ଼ିଥାଏ । ଏହି ପଦ୍ଧତିରେ କଳନା ହୋଇଥିବା ଆୟକୁ ମୋଟ ଜାତୀୟ ଆୟ କୁହାଯାଏ ! ନିଟ୍ ଜାତୀୟ ଆୟ ହେଉଛି ମୋଟ ଜାତୀୟ ଆୟର ଏକ ଅଂଶ । ମୋଟ ଜାତୀୟ ଆୟରୁ ଅବକ୍ଷୟ ପରିବ୍ୟୟକୁ ବିୟୋଗ କରି ନିଟ୍ ଜାତୀୟ ଆୟ ସ୍ଥିର କରାଯାଇଥାଏ ।
ଅସୁବିଧା – ଆୟ ପଦ୍ଧତିରେ ଜାତୀୟ ଆୟ କଳନା କଲାବେଳେ ନିମ୍ନଲିଖିତ ଅସୁବିଧା ସୃଷ୍ଟି ହୋଇଥାଏ । ପ୍ରଥମତଃ, ଆୟର ଶ୍ରେଣୀ ପ୍ରକରଣରେ ମତପାର୍ଥକ୍ୟ ଦେଖାଦେଇଥାଏ । ଉଦାହରଣସ୍ୱରୂପ ମଜୁରି ଓ ଅଣମଜୁରି ଆୟ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଦର୍ଶାଇବା କଷ୍ଟକର ହୋଇଥାଏ । ସେହିପରି ମିଶ୍ରିତ ଆୟ କ୍ଷେତ୍ରରେ କାର୍ଯ୍ୟରୁ ମିଳୁଥିବା ଆୟ ଏବଂ ସଂପରିରୁ ମିଳୁଥିବା ଆୟକୁ ପୃଥକ୍ କରିବା କଷ୍ଟକର ହୋଇଥାଏ ।
ଦ୍ଵିତୀୟତଃ, ଲାଭାଂଶ ବଣ୍ଟନ କରିବାରେ ବିଭ୍ରାନ୍ତି ସୃଷ୍ଟି ହୁଏ । ପରିବାର, ସରକାର ଏବଂ ଲାଭ ଆଶାରହିତ ଅନୁଷ୍ଠାନମାନଙ୍କୁ ଦିଆଯାଉଥିବା ଲାଭାଂଶକୁ ଉପାଦାନ ଆୟରୂପେ ବିଚାର କରାଯାଉଥିବାବେଳେ ନିଗମମାନଙ୍କ ମଧ୍ୟରେ ଲାଭାଂଶ ବଣ୍ଟନ ଜାତୀୟ ଆୟରୁ ବାଦ୍ ପଡ଼ିଥାଏ ।
ତୃତୀୟତଃ, ଦ୍ରବ୍ୟର ଦାମ୍ ପରିବର୍ତ୍ତନ ଏକ କ୍ରମାଗତ ପ୍ରକ୍ରିୟା ହୋଇଥିବାରୁ ଦାମ୍ ବୃଦ୍ଧିଜନିତ ପରିସ୍ଥିତିରେ ଜାତୀୟ ଆୟ ଏବଂ ଦାମ୍ ହ୍ରାସଜନିତ ପରିସ୍ଥିତିରେ ଜାତୀୟ ଆୟ ଭିନ୍ନ ହୋଇଥାଏ ।
ଚତୁର୍ଥତଃ, ଅର୍ଥବ୍ୟବସ୍ଥାରେ ଅସଂଗଠିତ କ୍ଷେତ୍ରରେ ଆତ୍ମନିଯୁକ୍ତ ବ୍ୟକ୍ତିଗଣ ଆୟ ସଂପର୍କୀୟ ସଠିକ୍ ତଥ୍ୟ ରଖ୍ ନ ଥା’ନ୍ତି, ଯାହାଫଳରେ ଜାତୀୟ ଆୟ ପରିମାପରେ ଅସୁବିଧା ସୃଷ୍ଟି ହୁଏ ।
ସତର୍କତାମୂଳକ ପଦକ୍ଷେପ – ଆୟ ପଦ୍ଧତିଦ୍ୱାରା ଜାତୀୟ ଆୟ ପରିମାପରେ ନିମ୍ନଲିଖିତ ସତର୍କତା ଅବଲମ୍ବନ କରାଯିବା ଉଚିତ । ପ୍ରଥମତଃ, ପରିବାରବର୍ଗ ଓ ପ୍ରତିଷ୍ଠାନମାନଙ୍କଠାରୁ ସରକାରଙ୍କୁ ଏବଂ ସରକାରଙ୍କଠାରୁ ପରିବାର ଏବଂ ପ୍ରତିଷ୍ଠାନମାନଙ୍କୁ କରାଯାଉଥିବା ହସ୍ତାନ୍ତରଣ ପ୍ରାପ୍ୟ ପରିଶୋଧକୁ ଜାତୀୟ ଆୟ ପରିମାପରୁ ବାଦ୍ ଦିଆଯିବା ଉଚିତ । ଦ୍ବିତୀୟତଃ, ପୁରୁଣା ଦ୍ରବ୍ୟ ବିକ୍ରୟରୁ ମିଳୁଥିବା ଆୟକୁ ବାଦ୍ ଦିଆଯିବା ଉଚିତ ।
ତୃତୀୟତଃ, ଲଟେରୀ ପ୍ରଭୃତିରୁ ମିଳୁଥିବା ଅପ୍ରତ୍ୟାଶିତ ଆୟ କୌଣସି ଉତ୍ପାଦନଶୀଳ କାର୍ଯ୍ୟାବଳୀରୁ ସୃଷ୍ଟି ନ ହେଉଥିବାରୁ ତାହାକୁ ଜାତୀୟ ଆୟ ପରିମାପରୁ ବାଦ୍ ଦିଆଯିବା ଉଚିତ । ଚତୁର୍ଥତଃ, ସ୍ଵଉପଭୋଗରେ ଲାଗୁଥିବା ଦ୍ରବ୍ୟର ମୂଲ୍ୟ ଓ ଆରୋପିତ ଅଶେଷ ଜାତୀୟ ଆୟରେ ଅନ୍ତର୍ଭୁକ୍ତ ହେବା ଉଚିତ ।
ପଞ୍ଚମତଃ, ଜାତୀୟ ଆୟ ପରିମାପ କଲାବେଳେ ନିଗମ କର ସମେତ ଲାଭକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରିବାକୁ ହୋଇଥାଏ । ସଂକ୍ଷେପରେ କହିଲେ କର୍ମଚାରୀଙ୍କ ପ୍ରତିଦାନ, ଅଧୂଶେଷ, ସୁଧ, ଲାଭ ଏବଂ ବିଦେଶରୁ ମିଳୁଥିବା ନିଟ୍ ଉପାଦାନ ଆୟକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇ ଆୟ ପଦ୍ଧତି ସାହାଯ୍ୟରେ ଜାତୀୟ ଆୟ ପରିମାପ କରାଯାଇଥାଏ ।

6. ଜାତୀୟ ଆୟ ପରିମାପର ବ୍ୟୟ ପଦ୍ଧତି ବ୍ୟାଖ୍ୟା କର ଏବଂ ଏହାର ସତର୍କତାମୂଳକ ପଦକ୍ଷେପ ସଂକ୍ଷେପରେ ବର୍ଣ୍ଣନା କର ।
Answer:
ବ୍ୟୟ ପଦ୍ଧତି ସାହାଯ୍ୟରେ ଜାତୀୟ ଆୟ ପରିମାପ କଲାବେଳେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ ପାଇଁ କରାଯାଉଥିବା ଚୂଡ଼ାନ୍ତ ଖର୍ଚ୍ଚ ବିଚାରକୁ ନିଆଯାଇଥାଏ । ଦ୍ରବ୍ୟ ଓ ସେବାର ଅନ୍ତିମ ଉପଭୋଗରେ କରାଯାଉଥିବା ଖର୍ଚ୍ଚକୁ ଚୂଡ଼ାନ୍ତ ଖର୍ଚ୍ଚ କୁହାଯାଏ । ଏହି ଖର୍ଚ୍ଚରେ ଘରୋଇ ଚୂଡ଼ାନ୍ତ ଉପଭୋଗ ଖର୍ଚ୍ଚ, ସରକାରୀ ଚୂଡ଼ାନ୍ତ ଉପଭୋଗ ଖର୍ଚ୍ଚ, ମୋଟ ପୁଂଜିଗଠନ ଏବଂ ନିଟ୍ ରପ୍ତାନି ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇଥାଏ । ପରିବାରବର୍ଗ ଏବଂ ସରକାର ଚୂଡ଼ାନ୍ତ ଉପଭୋଗ ଉଦ୍ଦେଶ୍ୟରେ ବଜାରରୁ ଦ୍ରବ୍ୟ ଓ ସେବା କ୍ରୟ କରନ୍ତି ।
ସେମାନେ ମଧ୍ୟ ଅଚଳ ହୋଇଥବା ଯନ୍ତ୍ରପାତି ବଦଳାଇବା ଉଦ୍ଦେଶ୍ୟରେ ପୁଞ୍ଜି ଦ୍ରବ୍ୟ କ୍ରୟ କରିବା ସହିତ ବିଦେଶରୁ ଦ୍ରବ୍ୟ ଆମଦାନି କରିଥା’ନ୍ତି । ସେହିପରି ଦେଶୀୟ ଦ୍ରବ୍ୟ ଓ ସେବା ରପ୍ତାନି ଆକାରରେ ବିଦେଶକୁ ବିକ୍ରି କରାଯାଏ । ରପ୍ତାନି ମୂଲ୍ୟ ଏବଂ ଆମଦାନି ମୂଲ୍ୟ ମଧ୍ଯରେ ପାର୍ଥକ୍ୟକୁ ନିଟ୍ ରପ୍ତାନି କୁହାଯାଏ ଯାହାକି ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ ଉପରେ କରାଯାଉଥିବା ଖର୍ଚ୍ଚରେ ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇଥାଏ ।
ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ ଉପରେ କରାଯାଉଥିବା ଚୂଡ଼ାନ୍ତ ଖର୍ଚ୍ଚ ପରିମାପ କରିବାପାଇଁ ଦ୍ରବ୍ୟ ଓ ସେବାର ଖୁଚୁରା ମୂଲ୍ୟ ଏବଂ ପରିମାଣ ଜାଣିବା ଆବଶ୍ୟକ ହୁଏ । ଦାମ୍ ସହିତ ପରିବାରବର୍ଗ ଏବଂ ଅଣଲାଭକାରୀ ଅନୁଷ୍ଠାନମାନଙ୍କୁ ଚୂଡ଼ାନ୍ତ ବିକ୍ରୟ ପରିମାଣକୁ ଗୁଣନ କରି ଚୂଡ଼ାନ୍ତ ଉପଭୋଗ ଖର୍ଚ୍ଚ ସ୍ଥିର କରାଯାଇଥାଏ । ସ୍ଥାୟୀ ଅଧ୍ବବାସୀଙ୍କ ପରିବାରବର୍ଗ ମଧ୍ୟ ବିଦେଶରୁ କିଛି ସିଧାସଳଖ କ୍ରୟ କରିଥା’ନ୍ତି । ଏହି ବାବଦରେ କରାଯାଉଥିବା ଖର୍ଚ୍ଚକୁ ଚୂଡ଼ାନ୍ତ ଉପଭୋଗ ଖର୍ଚ୍ଚରେ ଯୋଗ କରାଯାଇଥାଏ । ଅସ୍ଥାୟୀ ପରିବାରଗଣ ଦେଶୀୟ ବଜାରରେ ଦ୍ରବ୍ୟ ଓ ସେବା ପ୍ରତ୍ୟକ୍ଷଭାବରେ କ୍ରୟ କରନ୍ତି ଯାହାକୁ ଚୂଡ଼ାନ୍ତ ଘରୋଇ ଉପଭୋଗ ଖର୍ଚ୍ଚରୁ ବାଦ୍ ଦେବାକୁ ପଡ଼ିଥାଏ ।
ସରକାରୀ ସ୍ତରରେ ଚୂଡ଼ାନ୍ତ ଉପଭୋଗ ଖର୍ଚ୍ଚ ଜାଣିବାକୁ ହେଲେ ସରକାରଙ୍କଦ୍ୱାରା କ୍ରୟ କରାଯାଉଥିବା ଦ୍ରବ୍ୟ ଓ ସେବା ସହିତ କର୍ମଚାରୀଙ୍କୁ ଦିଆଯାଉଥିବା ପ୍ରତିଦାନକୁ ଯୋଗ କରିବାକୁ ହୁଏ । ଦେଶୀୟ ବଜାରରେ ସରକାରଙ୍କ ଖର୍ଚ୍ଚ ଜାଣିବାକୁ ହେଲେ ବିକ୍ରୟ ପରିମାଣକୁ ଖୁଚୁରା ବିକ୍ରୟ ମୂଲ୍ୟ ସହିତ ଗୁଣନ କରି ବାକୁ ହୁଏ । ସରକାର ମଧ୍ୟ ବିଦେଶରୁ ଦ୍ରବ୍ୟ ଓ ସେବା କ୍ରୟ କରନ୍ତି । ସୁତରାଂ ଦେଶୀୟ ବଜାରରେ କ୍ରୟ ପାଇଁ କରାଯାଉଥିବା ସରକାରୀ ଖର୍ଚ୍ଚ, ବିଦେଶରୁ କ୍ରୟ ବାବଦ ଖର୍ଜ ଏବଂ କର୍ମଚାରୀଙ୍କ ପ୍ରତିଦାନକୁ ଯୋଗକରି ସରକାରଙ୍କ ଚୂଡ଼ାନ୍ତ ଉପଭୋଗ ଖର୍ଚ୍ଚ ସ୍ଥିର କରାଯାଇଥାଏ ।
ଜାତୀୟ ଆୟ ପରିମାପରେ ପୁଞ୍ଜିଗଠନ ଅନ୍ୟତମ ଉପାଦାନ । ପୁଞ୍ଜିଗଠନ କହିଲେ ବର୍ଷକ ମଧ୍ୟରେ ଦେଶରେ କରାଯାଉଥିବା ଉପଭୋଗଠାରୁ ଉତ୍ପାଦନ ଅଧିକ ହେବା ବୁଝିବାକୁ ହୁଏ । ପୁଞ୍ଜିଗଠନ, ମୋଟ ସ୍ଥିର ପୁଞ୍ଜିଗଠନ ଏବଂ ଭଣ୍ଡାର ପରିବର୍ତ୍ତନ ଆକାରରେ କରାଯାଇଥାଏ । ଉପରୋକ୍ତ ଦୁଇଗୋଟି ବାବଦରେ ଖର୍ଚ୍ଚ ମୋଟ ପୁଞ୍ଜିଗଠନରେ ହେଉଥିବା ମୋଟ ଖର୍ଚ୍ଚର ସୂଚନା ଦେଇଥାଏ । ନିର୍ମାଣକାର୍ଯ୍ୟ ଏବଂ ଯନ୍ତ୍ରପାତି ସଂଗ୍ରହରେ ହେଉଥିବା ବ୍ୟୟ ମୋଟ ସ୍ଥିର ପୁଞ୍ଜି ଗଠନରେ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଏ । ନିର୍ମାଣ କାର୍ଯ୍ୟରେ ହେଉଥିବା ଖର୍ଚ୍ଚ ଜାଣିବାକୁ ହେଲେ ନିବେଶ ଦାମ୍ ସହିତ ବ୍ୟବହୃତ ହେଉଥିବା ନିବେଶ ପରିମାଣକୁ ଗୁଣନ କରି ତା’ ସହିତ କର୍ମଚାରୀଙ୍କ ପ୍ରତିଦାନ, ଅଧୂଶେଷ, ସୁଧ, ଲାଭକୁ ଯୋଗ କରାଯାଇଥାଏ ।
ନିଜ ଉଦ୍ଦେଶ୍ୟରେ ଉତ୍ପାଦନ କରାଯାଉଥିବା ସ୍ଥିର ପରି ସମ୍ପତ୍ତି, ପରିବାରବର୍ଗଙ୍କ ପାଇଁ କ୍ରୟ କରାଯାଉଥିବା ନୂତନ ଗୃହ, ଚାଲୁ ରହିଥିବା କାମ ଏବଂ ପୁରାତନ ଗୃହର ନବୀକରଣ ଚୂଡ଼ାନ୍ତ ଖର୍ଚ୍ଚରେ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯିବା ଉଚିତ । ସେହିପରି ଯନ୍ତ୍ରପାତି, କଳକବ୍ଜା ବାବଦରେ କରାଯାଉଥିବା ଚୂଡ଼ାନ୍ତ ଖର୍ଚ୍ଚ କଳନା କରିବାକୁ ହେଲେ ବର୍ଷକ ମଧ୍ୟରେ ଉତ୍ପାଦନ କରାଯାଉଥିବା ଯନ୍ତ୍ରପାତିର ପରିମାଣ ସହ ବଜାର ଦାମ୍ଭିକୁ ଗୁଣନ କରାଯାଇଥାଏ । ଏହି ଖର୍ଚ ସହ ନିଜ ଉଦ୍ଦେଶ୍ୟରେ ଉତ୍ପାଦନର ମୂଲ୍ୟକୁ ଯୋଗ କରାଯାଏ ।
ଭଣ୍ଡାର ପରିବର୍ତ୍ତନରେ ହେଉଥିବା ଖର୍ଚ୍ଚ ଜାଣିବାକୁ ହେଲେ ଦ୍ରବ୍ୟ ଭଣ୍ଡାରରେ ଶାରୀରିକ ପରିବର୍ତ୍ତନ ସହିତ ବଜାର ଦାମ୍କୁ ଗୁଣନ କରିବାକୁ ହୁଏ । ସୁତରାଂ ମୋଟ ପୁଞ୍ଜି ଗଠନରେ ହେଉଥିବା ମୋଟ ଖର୍ଚ୍ଚ ଜାଣିବାକୁ ହେଲେ ଦେଶୀୟ ଉତ୍ପାଦ ଏବଂ ସେବାର ଭଣ୍ଡାରରେ ପରିବର୍ତ୍ତନକୁ ଯୋଗ କରିବାକୁ ହୁଏ ।
ପରବର୍ତ୍ତୀ ବିଚାର୍ଯ୍ୟ ବିଷୟ ହେଉଛି ନିଟ୍ ରପ୍ତାନି । ବର୍ଷକ ମଧ୍ୟରେ ହେଉଥିବା ରପ୍ତାନି ଏବଂ ଆମଦାନି ମଧ୍ୟରେ ପାର୍ଥକ୍ୟକୁ ନିଟ୍ ରପ୍ତାନି କୁହାଯାଏ । ନିଟ୍ ରପ୍ତାନି ବାବଦରେ କରାଯାଉଥିବା ଖର୍ଚ୍ଚ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦ ବାବଦରେ ହେଉଥିବା ଖର୍ଚ୍ଚର ଅଂଶବିଶେଷ ହୋଇଥାଏ ।
ସତର୍କତାମୂଳକ ପଦକ୍ଷେପ – ବ୍ୟୟ ପଦ୍ଧତିରେ ଜାତୀୟ ଆୟ କଳନା କଲାବେଳେ ପୁରୁଣା ଦ୍ରବ୍ୟ କ୍ରୟରେ ହେଉଥିବା ଖର୍ଚ୍ଚ, ଅଂଶଧନ ଏବଂ ତମସୁକପତ୍ର କ୍ରୟରେ ହେଉଥିବା ଖର୍ଚ୍ଚ, ଅବସରକାଳୀନ ଭତ୍ତା ଆକାରରେ ହସ୍ତାନ୍ତରଣ ପ୍ରାପ୍ୟ, ବେକାରୀ ଭତ୍ତା ଏବଂ ସାମାଜିକ ନିରାପତ୍ତା ପରିଯୋଜନାକୁ ଅବଦାନ ଯେପରି ଜାତୀୟ ଆୟ ପରିମାପରେ ସ୍ଥାନ ନପାଏ ସେଥିପାଇଁ ଧ୍ୟାନ ଦିଆଯିବା ଉଚିତ । ଅବଶ୍ୟ ସ୍ବ-ଉପଭୋଗ ଉଦ୍ଦେଶ୍ୟରେ ଉତ୍ପାଦନ କରାଯାଉଥିବା ଦ୍ରବ୍ୟର ମୂଲ୍ୟ ଚୂଡ଼ାନ୍ତ ଉପଭୋଗ ଖର୍ଚ୍ଚରେ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯିବା ଆବଶ୍ୟକ । ସେହିପରି ଆରୋପିତ ଅଶେଷ ବାବଦରେ ଖର୍ଚ୍ଚ ଚୂଡ଼ାନ୍ତ ଉପଭୋଗ ଖର୍ଚ୍ଚରେ ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇଥାଏ ।
ବ୍ୟୟ ପଦ୍ଧତିରୁ ବଜାର ଦାମ୍ରେ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦର ସୂଚନା ମିଳିଥାଏ । ବିଦେଶରୁ ମିଳୁଥିବା ନିଟ୍ ଉପାଦାନ ଆୟ ସହ ମୋଟ ଦେଶୀୟ ଉତ୍ପାଦକୁ ଯୋଗକରି ବଜାର ଦାମ୍ରେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ ସ୍ଥିର କରାଯାଏ । ଉପାଦାନ ପରିବ୍ୟୟରେ ଜାତୀୟ ଉତ୍ପାଦ ସ୍ଥିର କରିବାକୁ ହେଲେ ମୋଟ ଜାତୀୟ ଉତ୍ପାଦରୁ ପରୋକ୍ଷ କର ଏବଂ ଅବକ୍ଷୟ ପରିବ୍ୟୟ ବାଦ୍ ଦେବାକୁ ହୁଏ ।
ଅସୁବିଧା – ବ୍ୟୟ ପଦ୍ଧତିରେ ଜାତୀୟ ଆୟ କଳନା କଲାବେଳେ ନିମ୍ନଲିଖିତ ଅସୁବିଧା ପରିଲକ୍ଷିତ ହୋଇଥାଏ । ପ୍ରଥମତଃ, ସଠିକ୍ ତଥ୍ୟ ନ ମିଳିଲେ ଏହି ପଦ୍ଧତି ତ୍ରୁଟିଯୁକ୍ତ ହୋଇଥାଏ । ବିଭିନ୍ନ ପର୍ଯ୍ୟାୟରେ ସଂଗୃହୀତ ସଠିକ୍ ଖର୍ଚ୍ଚ ଏକ କଷ୍ଟକର ବ୍ୟାପାର ହୋଇଥିବାରୁ ଜାତୀୟ ଆୟର ପରିମାପର ସଠିକତା ଉପରେ ଆଶଙ୍କା ପ୍ରକାଶ ପାଇଥାଏ । ଯଦି ଖର୍ଚ୍ଚର ଦ୍ବୈତ ଗଣନା ସମ୍ଭାବନା ଥାଏ ଏବଂ ତାହାକୁ ଏଡ଼ାଇ ଦିଆଯାଇ ନ ପାରେ, ତେବେ ଜାତୀୟ ଆୟର ପରିମାପ ତ୍ରୁଟିପୂର୍ଣ୍ଣ ହୋଇପାରେ ।
ଦ୍ଵିତୀୟତଃ, ସ୍ଥାୟୀ ଉପଭୋଗ ଦ୍ରବ୍ୟ କ୍ଷେତ୍ରରେ ଉପଭୋଗ ଖର୍ଚ୍ଚ ଏବଂ ବିନିଯୋଗ ଖର୍ଚ୍ଚ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଦର୍ଶାଇବା ଅସମ୍ଭବ ମନେହୁଏ । ଏହି କ୍ଷେତ୍ରରୁ ପ୍ରତିବର୍ଷ ମିଳୁଥିବା ସେବାର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କରି ତାହାକୁ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷର ଖର୍ଚ୍ଚରେ ଅନ୍ତର୍ଭୁକ୍ତ କରିବା କଷ୍ଟସାଧ୍ୟ ହୁଏ । ତୃତୀୟତଃ, ବେଳେବେଳେ ସରକାରଙ୍କଦ୍ବାରା କରାଯାଉଥିବା ଉପଭୋଗ ଖର୍ଚ୍ଚ ଏବଂ ବିନିଯୋଗ ଖର୍ଚ୍ଚକୁ ପୃଥକ୍ କରିବା ସମ୍ଭବ ନୁହେଁ ।
7. ବିଦେଶରୁ ମିଳୁଥିବା ନିଟ୍ ଉପାଦାନ ଆୟ କହିଲେ କ’ଣ ବୁଝାଯାଏ ? ଏହାର ଉପାଦାନଗୁଡ଼ିକ କ’ଣ ?
Answer:
ବିଦେଶରୁ ମିଳୁଥିବା ଉପାଦାନ ଆୟ କହିଲେ ବିଦେଶରେ କାର୍ଯ୍ୟରତ ସ୍ଵଦେଶୀୟ ମଜୁରି, ଅଶେଷ, ସୁଧ ଏବଂ ଲାଭ ଆକାରରେ ଅର୍ଜନ କରୁଥିବା ଆୟକୁ ବୁଝାଇଥାଏ । ବିଦେଶରେ ଦେଶୀୟ ଅଞ୍ଚଳରେ କାର୍ଯ୍ୟ କରୁଥିବା ଅଣଅଧିବାସୀ ଶ୍ରମିକମାନେ ମଧ୍ୟ ମଜୁରି ଆକାରରେ ଆୟ ଅର୍ଜନ କରିଥା’ନ୍ତି । ସେମାନଙ୍କର ମଧ୍ୟ ବିଦେଶରେ କିଛି ସଂପରି ଥାଇପାରେ । କୋଠାବାଡ଼ି, କଳକାରଖାନା, ଦୋକାନ ଏବଂ ଅଂଶଧନ ରୂପକ ଆର୍ଥିକ ପରିସଂପରି ଏହି ପ୍ରକାର ସଂପତ୍ତିର ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇଥାଏ ।
ସେମାନେ ଅଶେଷ ଓ ସୁଧ ଆକାରରେ ଏଥୁରୁ ଆୟ ଅଜର୍ନ କରିଥା’ନ୍ତି । ସେମାନେ ମଧ୍ୟ ବିଦେଶରେ ଦ୍ରବ୍ୟ ଓ ସେବା ଉତ୍ପାଦନ କରି ଲାଭ ଅର୍ଜନ କରିଥା’ନ୍ତି । ସେହପରି ଅଣଅସ୍ଵାସୀଗଣ ଉପାଦାନ ସେବା ଯୋଗାଇ ଆୟ ଅର୍ଜନ କରିଥା’ନ୍ତି । ବିଦେଶରୁ ମିଳୁଥିବା ଆୟ ଏବଂ ଅସ୍ଥାୟୀ ଅଧିବାସୀମାନଙ୍କ ଉପାଦାନ ସେବା ବିନିମୟରେ ଦିଆଯାଉଥିବା ଦେୟ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟରୁ ବିଦେଶରୁ ମିଳୁଥିବା ନିଟ୍ ଉପାଦାନ ଆୟର ପରିମାପ କରାଯାଇଥାଏ ।
ବିଦେଶରୁ ମିଳୁଥିବା ନିଟ୍ ଉପାଦାନ ଆୟର ତିନିଗୋଟି ଉତ୍ସ ପରିଲକ୍ଷିତ ହୁଏ; ଯଥା – କର୍ମଚାରୀଙ୍କ ପ୍ରତିଦାନ, ଉଦ୍ୟୋଗରୁ ମିଳୁଥିବା ନିଟ୍ ଆୟ ଏବଂ ବିଦେଶରେ କାର୍ଯ୍ୟରତ ସ୍ଵଦେଶୀୟଙ୍କ ସଞ୍ଚ ଆୟ । ଏହା ବିଶଦଭାବେ ନିମ୍ନରେ ବର୍ଣ୍ଣନା କରାଯାଇଛି ।
(i) କର୍ମଚାରୀଙ୍କ ନିଟ୍ ପ୍ରତିଦାନ – ସ୍ବଦେଶୀ ଶ୍ରମିକ ବିଦେଶରେ ଅସ୍ଥାୟୀ ନିଯୁକ୍ତିରୁ ପ୍ରତିଦାନ ଲାଭ କରିଥା’ନ୍ତି । ସେହିପରି ଅସ୍ଥାୟୀ ଅଧ୍ବବାସୀ ଶ୍ରମିକଗଣ ଦେଶୀୟ ଅଞ୍ଚଳରେ କାର୍ଯ୍ୟକରି ପ୍ରତିଦାନ ପାଇଥା’ନ୍ତି । ପ୍ରାପ୍ତ ପ୍ରତିଦାନ ଏବଂ ପ୍ରଦତ୍ତ ପ୍ରତିଦାନ ମଧ୍ୟରେ ଥିବା ପାର୍ଥକ୍ୟକୁ ନିଟ୍ ପ୍ରତିଦାନରୂପେ ଅଭିହିତ କରାଯାଏ । ବିଦେଶାଗତ କର୍ମଚାରୀଙ୍କୁ ମିଳୁଥିବା ପ୍ରତିଦାନରେ ଦୂତାବାସ ଏବଂ ଆନ୍ତର୍ଜାତିକ ସଂଗଠନମାନଙ୍କରେ କାର୍ଯ୍ୟରତ ସ୍ଥାନୀୟ କର୍ମଚାରୀ ଅନ୍ତ ର୍ଭୁକ୍ତ ହୋଇଥା’ନ୍ତି ।
(ii) ଉଦ୍ୟୋଗରୁ ମିଳୁଥିବା ନିଟ୍ ଆୟ – ଦେଶର ସ୍ଥାୟୀ ଅଧ୍ବବାସୀ ବିଦେଶରେ ଅଧ୍ୟାତ ସଂପରିରୁ ସୁଧ, ଅଶେଷ ଏବଂ ଲାଭାଂଶ ଆକାରରେ ଆୟ ପ୍ରାପ୍ତ ହୋଇଥା’ନ୍ତି । ସେହିପରି ପୃଥିବୀର ଅନ୍ୟାନ୍ୟ ଦେଶର ଅଧିବାସୀମାନଙ୍କୁ ଅନୁରୂପ ପ୍ରାପ୍ୟ ମିଳିଥାଏ । ଏହି ଦୁଇ ମଧ୍ଯରେ ପାର୍ଥକ୍ୟକୁ ସଂପରିରୁ ମିଳୁଥିବା ନିଟ୍ ଆୟ କୁହାଯାଏ ।
(iii) ବିଦେଶରୁ ମିଳୁଥିବା ନିଟ୍ ସତ୍ତ୍ୱେ ଆୟ କମ୍ପାନୀମାନେ ବଣ୍ଟନ ନ କରୁଥିବା ଲାଭାଂଶକୁ ସତ୍ତ୍ୱେ ଆୟ କୁହାଯାଏ । ସେମାନେ ସମଗ୍ର ଲାଭକୁ ଅଂଶୀଦାରମାନଙ୍କ ମଧ୍ୟରେ ଲାଭାଂଶ ଆକାରରେ ବଣ୍ଟନ ନ କରି ଲାଭର କିଛି ଅଂଶ ଭବିଷ୍ୟତରେ ଉତ୍ପାଦନ ସଂପ୍ରସାରଣ ଉଦ୍ଦେଶ୍ୟରେ ରଖିଥା’ନ୍ତି । ବିଦେଶରେ କାର୍ଯ୍ୟରତ ଦେଶୀୟ କମ୍ପାନୀମାନେ ମଧ୍ୟ ବିଦେଶରେ ବିନିଯୋଗ ଉଦ୍ଦେଶ୍ୟରେ ଲାଭର କିଛି ଅଂଶ ରଖୁ’ନ୍ତି । ସେହିପରି ବିଦେଶୀ କମ୍ପାନୀମାନେ କାର୍ଯ୍ୟ କରୁଥିବା ଦେଶରେ ବ୍ୟବସାୟରେ ରତ ଥା’ନ୍ତି । ଦେଶୀୟ କମ୍ପାନୀର ସଞ୍ଚିତ ଆୟ ଏବଂ ବିଦେଶୀ କମ୍ପାନୀର ସଞ୍ଚ ଆୟ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ, ବିଦେଶରେ ଦେଶୀୟ କମ୍ପାନୀର ନିଟ୍ ସଞ୍ଚ ଆୟ ସୂଚିତ କରେ ।
8. ଆୟର ଚକ୍ରୀୟ ପ୍ରବାହ ପରିପ୍ରେକ୍ଷୀରେ ଆୟ ସର୍ଜନା ପ୍ରକ୍ରିୟାର ବ୍ୟାଖ୍ୟା କର ।
Answer:
ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ଆୟ ସର୍ଜନା ହୋଇଥାଏ ଏବଂ ଅର୍ଥବ୍ୟବସ୍ଥାରେ ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟା ଏକ ନିରନ୍ତର ପ୍ରକ୍ରିୟା । ଉତ୍ପାଦନ, ଆୟ ଓ ବ୍ୟୟ – ଏହି ତିନୋଟି ପରସ୍ପର ଆନ୍ତଃ ନିର୍ଭରଶୀଳ କ୍ରିୟା । ଏହି ତିନୋଟି କ୍ରିୟା ଝରଣାର ଜଳସ୍ରୋତ ଭଳି ଅବିଶ୍ରାନ୍ତ ଚାଲିଥାଏ । ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ଦ୍ରବ୍ୟ ଓ ସେବା ଉତ୍ପନ୍ନ ହେବା ସଙ୍ଗେ ସଙ୍ଗେ ଆୟର ସୃଷ୍ଟି ହୋଇଥାଏ । ଆୟ ହିଁ ଦ୍ରବ୍ୟ ଓ ସେବା ପାଇଁ ଚାହିଦା ସୃଷ୍ଟି କରିଥାଏ । ଚାହିଦା ବା ଦ୍ରବ୍ୟ ପାଇଁ ବ୍ୟୟ ପୁନଶ୍ଚ ଉତ୍ପାଦନ ପାଇଁ ପଥ ପରିଷ୍କାର କରିଥାଏ ଏବଂ ପୁଣି ଉତ୍ପାଦନ ଯୋଗୁଁ ଆୟ ସର୍ଜନ ଓ ତା’ପରେ ବ୍ୟୟ ହୋଇଥାଏ ।
ଏହିପରି ଉତ୍ପାଦନ, ଆୟ ଓ ବ୍ୟୟର ପ୍ରବାହକୁ ଚକ୍ରୀୟ ପ୍ରବାହ (Circular flow) କୁହାଯାଏ । ଉତ୍ପାଦନ, ଆୟ ଓ ବ୍ୟୟର ଚକ୍ରୀୟ ପ୍ରବାହ ତିନୋଟି ସମ୍ବନ୍ଧିତ ପର୍ଯ୍ୟାୟକୁ ସୂଚାଇଥାଏ; ଯଥା – ଉତ୍ପାଦନ, ଆୟ ସୃଜନ ଓ ବ୍ୟୟ ।
ଆୟର ଚକ୍ରୀୟ ପ୍ରବାହରୁ ଜାଣିପାରିବା ଯେ, ଜାତୀୟ ଆୟକୁ ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟ ଓ ସେବାର ପ୍ରବାହ ଆକାରରେ ଦେଖୁରିବା କିମ୍ବା ଆୟର ପ୍ରବାହ ଆକାରରେ ଦେଖୁପାରିବା କିମ୍ବା ଦ୍ରବ୍ୟ ଓ ସେବା ବାବଦରେ ବ୍ୟୟ ଆକାରରେ ଦେଖୁପାରିବା ।
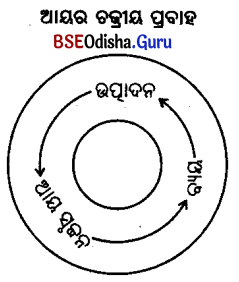
ଚିତ୍ର ସୂଚାଇ ଦେଉଛି ଯେ, ଉତ୍ପାଦନ ଯୋଗୁଁ ଆୟ ସୃଷ୍ଟି ହେଉଛି । ଆୟର ସୃଷ୍ଟି ଯୋଗୁଁ ଦ୍ରବ୍ୟ ଓ ସେବାର ଚାହିଦା ସୃଷ୍ଟି ହେଉଛି, ଚାହିଦା ଯୋଗୁଁ ଉତ୍ପାଦନରେ ବୃଦ୍ଧି ଘଟିଥାଏ ଇତ୍ୟାଦି । ତେଣୁ ଉତ୍ପାଦନ, ଆୟର ବଣ୍ଟନ ଓ ବ୍ୟୟର ପ୍ରବାହ ଚକ୍ରୀୟ ଆକାରରେ ଅନବରତ ଚାଲିଥାଏ । ଏହାକୁ ଆୟର ଚକ୍ରୀୟ ପ୍ରବାହ କୁହାଯାଏ ।
ଉତ୍ପାଦନକାରୀ ଭୂମି, ଶ୍ରମ, ପୁଞ୍ଜି ପ୍ରଭୃତି ଉପାଦାନକୁ ଉପଯୋଗ କରି ଉତ୍ପାଦନ କରିଥା’ନ୍ତି । ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାକୁ ସେମାନଙ୍କ ଅବଦାନ ପାଇଁ ପ୍ରତିଦାନସ୍ବରୂପ ଉପାଦାନ ଅଧିକାରୀଗଣ ଯାହା ପାରିତୋଷିକ ଲାଭ କରିଥା’ଛି ତାହା ସେମାନଙ୍କର ଆୟରୂପେ ବିବେଚିତ ହୁଏ । ଉତ୍ପାଦନକାରୀଙ୍କ ଦୃଷ୍ଟିରୁ ଏହି ପ୍ରକାର ଦେୟ ଉପାଦାନ ଦେୟ ରୂପେ ବିବେଚିତ ହୁଏ ଏବଂ ଉପାଦାନମାନଙ୍କ ଦୃଷ୍ଟିରୁ ଏହି ପ୍ରକାର ପ୍ରାପ୍ୟ ଆୟରୂପେ ପରିଗଣିତ ହୁଏ ।
ଏହିପରି ପାରସ୍ପରିକ ବିନିମୟ ପ୍ରକ୍ରିୟାରେ ପରିବାର ଏବଂ ପ୍ରତିଷ୍ଠାନମାନଙ୍କର ଆୟ ସର୍ଜନା ହୁଏ । ବେଳେବେଳେ ପରିବାର ଓ ପ୍ରତିଷ୍ଠାନବର୍ଗକୁ ହସ୍ତାନ୍ତରଣ ପ୍ରାପ୍ୟ ଆକାରରେ ଆୟ ମିଳିଥାଏ । ହସ୍ତାନ୍ତରଣ ପ୍ରାପ୍ୟ କହିଲେ ସେହି ପ୍ରକାର ଆୟକୁ ବୁଝାଏ ଯେଉଁଥପାଇଁ କୌଣସି ଉତ୍ପାଦନଶୀଳ ସେବା ଯୋଗାଇବାକୁ ହୋଇନଥାଏ । ସେହି କାରଣରୁ ହସ୍ତାନ୍ତରଣ ପ୍ରାପ୍ୟକୁ ଏକପାକ୍ଷୀୟ ପ୍ରାପ୍ୟ କୁହାଯାଏ । ଅବସରକାଳୀନ ଭତ୍ତା, ବୃତ୍ତି, ଉପହାର, ଦାନ ପ୍ରଭୃତି ହସ୍ତାନ୍ତରଣ ପ୍ରାପ୍ୟର ଉଦାହରଣ । ହସ୍ତାନ୍ତରଣ ପ୍ରାପ୍ୟ ଜାତୀୟ ଆୟ ଆକଳନରେ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇ ନଥାଏ ।
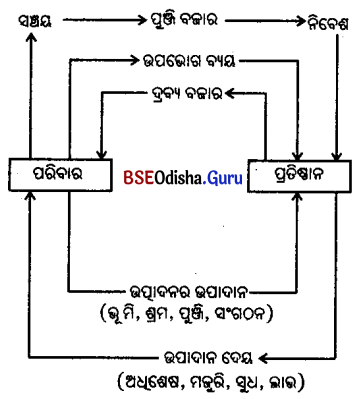
ଚିତ୍ରରୁ ପ୍ରତୀୟମାନ ଯେ, ପରିବାର ପ୍ରତିଷ୍ଠାନକୁ ଉତ୍ପାଦନର ଉପାଦାନ ବିକ୍ରୟ କରି ତା’ବଦଳରେ ଆୟ ପାଇଥାଏ । ଅଶେଷ, ମଜୁରି, ସୁଧ ଓ ଲାଭ ଆକାରରେ ପରିବାର ପାଇଥିବା ସମସ୍ତ ଆୟ ହିଁ ଜାତୀୟ ଆୟ । ପରିବାର ଅର୍ଜନ କରୁଥିବା ଆୟର ଏକ ଅଂଶ ଉପଭୋଗରେ ବ୍ୟୟ ହୋଇଥାଏ ଏବଂ ଅନ୍ୟ ଅଂଶଟି ସଞ୍ଚୟ କରାଯାଇଥାଏ । ଆୟର ଯେଉଁ ଅଂଶ ସଞ୍ଚୟ କରା ଯାଇଥାଏ ତାହା ପୁଞ୍ଜି ବଜାରରେ ପ୍ରବେଶ କରେ ଏବଂ ଏହାକୁ ପ୍ରତିଷ୍ଠାନରେ ନିବେଶ କରାଯାଏ ।
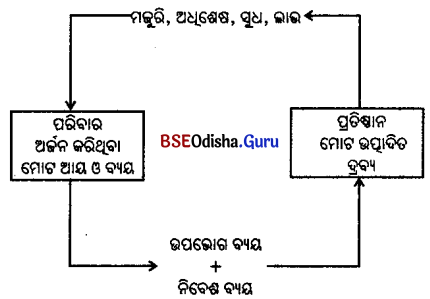
ତେଣୁ ପରିବାରର ଆୟ ଉଭୟ ଉପଭୋଗ ବ୍ୟୟ ଓ ନିବେଶ ବ୍ୟୟ ଆକାରରେ ପ୍ରତିଷ୍ଠାନ ମଧ୍ୟକୁ ପ୍ରବେଶ କରିଥାଏ । ପ୍ରତିଷ୍ଠାନଦ୍ୱାରା ଅର୍ଜିତ ଆୟ ପୁନର୍ବାର ଉତ୍ପାଦନର ଉପାଦାନ କ୍ରୟ କରିବାପାଇଁ ବ୍ୟବହୃତ ହୋଇଥାଏ । ଏହା ପରିବାରର ଆୟରେ ପରିଣତ ହୁଏ । ଏହି ପ୍ରକ୍ରିୟା ସର୍ବଦା ଚାଲୁ ରହିଥାଏ । ନିମ୍ନ ଚିତ୍ରରେ ଏକ ସଂକ୍ଷିପ୍ତ ଧାରଣା ବ୍ୟକ୍ତ କରାଯାଇଛି ।

9. ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ ବୃଦ୍ଧିରେ ଅର୍ଥନୈତିକ କଲ୍ୟାଣ ବୃଦ୍ଧି ହୋଇପାରିବ କି ? ଆଲୋଚନା କର ।
Answer:
ଗୋଟିଏ ଜାତି ବା ବ୍ୟକ୍ତି ପ୍ରତ୍ୟେକଙ୍କର ପ୍ରଗତିର ମାପକାଠି ହେଉଛି ତାଙ୍କର ଆୟ । ଜାତୀୟ ଆୟ ଦେଶର ଅଧିବାସୀମାନଙ୍କର ଜୀବନଧାରଣର ମାନ ନିର୍ଣ୍ଣୟ କରେ । ଜୀବନଧାରଣର ମାନ କହିଲେ ଜଣେ ବ୍ୟକ୍ତି ବା ଜାତି । ଏହାର ଅଭାବ ଅଭାବର କେତେ ଶତାଂଶ ପୂରଣ କରିବାକୁ ସମର୍ଥ ବୋଲି ବୁଝିବାକୁ ହେବ । ଜାତୀୟ ଆୟ ଅର୍ଥନୀତିକ ଅଭିବୃଦ୍ଧିର ଓ ଜୀବନଧାରଣମାନର ଏକ ପ୍ରଧାନ ପରିମାପକ । ତେଣୁ ଆଜିକାଲି ପୃଥୁବୀର ସମସ୍ତ ଦେଶଗୁଡ଼ିକ ସେମାନଙ୍କର ଜାତୀୟ ଆୟ ସଂକ୍ରାନ୍ତୀୟ ପରିସଂଖ୍ୟାନ ଉପରେ ଗୁରୁତ୍ବ ଆରୋପ କରୁଛନ୍ତି ।
ଏହି ଜାତୀୟ ଆୟର ଅଭିବୃଦ୍ଧିକୁ ସମସ୍ତ ଅର୍ଥନୈତିକ କାର୍ଯ୍ୟକଳାପର ପ୍ରଧାନ ଲକ୍ଷ୍ୟ ବୋଲି ମଧ୍ୟ ବିବେଚନା କରାଯାଉଅଛି । ଜାତୀୟ ଆୟ ପରିମାଣରେ ଘଟୁଥ୍ । ପରିବର୍ତ୍ତନକୁ ଇକ୍ଷ୍ୟକରି ଅର୍ଥନୀତିକ ବିକାଶ ସମ୍ବନ୍ଧରେ ସ୍ପଷ୍ଟ ଚିତ୍ର ଗୋଟିଏ ଦେଶ ଜାଣିପାରେ । ଯୁକ୍ତିଯୁକ୍ତ ସରକାରୀ ନୀତି ନିର୍ଣ୍ଣୟ କ୍ଷେତ୍ରରେ ବିଧାନପାଇଁ ସେମାନଙ୍କର ନୀତି ଓ ଉଦ୍ୟମ କେତେଦୂର ସଫଳ ହୋଇଛି ତାହା ଜାତୀୟ ଆୟ ଅଧ୍ୟୟନରୁ ହିଁ ଜାଣିପାରୁଛନ୍ତି । ତେଣୁ, କୌଣସି ଦେଶର ବାସ୍ତବ ଜୀବନର ଚିତ୍ର ପାଇବାକୁ ହେଲେ ଏହାର ଜାତୀୟ ଆୟର ବିଶଦ ଅଧ୍ୟୟନ କରିବା ଉଚିତ ।
ପାରମ୍ପରିକ ଭାବରେ ଜାତୀୟ ଆୟକୁ ଅର୍ଥନୈତିକ ଉନ୍ନୟନର ଏକ ପରିମାପକ ବା ସୂଚକାଙ୍କ ଭାବରେ ଗ୍ରହଣ କରାଯାଏ । କୌଣସି ଏକ ରାଷ୍ଟ୍ରରେ ଉତ୍ପାଦିତ ହୋଇଥିବା ସମସ୍ତ ଚୂଡ଼ାନ୍ତ ଦ୍ରବ୍ୟ ଓ ସେବା ସମୂହର ବଜାର ମୂଲ୍ୟକୁ ମୋଟ ଘରୋଇ ଉତ୍ପାଦ କୁହାଯାଏ । ଏହା ରାଷ୍ଟ୍ରର ଭୌଗୋଳିକ ପରିସୀମା ମଧ୍ୟରେ ଉତ୍ପାଦିତ ଏବଂ ବଜାର ଦରକୁ ଭିଭିକରି ଆକଳନ ହୋଇଥିବା ମୋଟ ଉତ୍ପାଦର ମୁଦ୍ରାଗତ ମୂଲ୍ୟ । ତେଣୁ, ଏହାକୁ ବଜାର ଦର ଭିତ୍ତିକ ଘରୋଇ ଉତ୍ପାଦ (GDP at market price) କୁହାଯାଏ । ମୋଟ ଘରୋଇ ଉତ୍ପାଦ ମୁଣ୍ଡପିଛା ଆୟକୁ ଅର୍ଥନୈତିକ ପ୍ରଗତିର ମାନକ ରୂପେ ଗ୍ରହଣ କରାଯାଏ ।
ଅର୍ଥନୈତିକ ଉନ୍ନୟନ ଏକ ବ୍ୟାପକ ଅର୍ଥବୋଧକ ଅବଧାରଣା । ଏହା ବହୁବିଧ ଉପାଦାନଦ୍ୱାରା ପ୍ରଭାବିତ ତଥା ନିର୍ଦ୍ଧାରିତ । କୌଣସି ରାଷ୍ଟ୍ରର ଜନସାଧାରଣଙ୍କ ଜୀବନଧାରଣମାନର ଉନ୍ନତିସହ ଦାରିଦ୍ର୍ୟ ପ୍ରପୀଡ଼ିତ ବ୍ୟକ୍ତିବିଶେଷଙ୍କର ଶିକ୍ଷା, ସ୍ୱାସ୍ଥ୍ୟ ଓ ସାକ୍ଷରତା ହାରରେ ଉନ୍ନତି ତଥା ରାଷ୍ଟ୍ରରେ ଉତ୍ପାଦନଶୀଳତା ଓ ଆୟ ବୃଦ୍ଧି ସହ ସଂଶ୍ଳିଷ୍ଟ ।
ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ ବୃଦ୍ଧି ଉପରେ ପ୍ରତ୍ୟେକ ଦେଶ ଗୁରୁତ୍ଵ ଆରୋପ କରୁଥିଲେ ମଧ୍ୟ ଅନେକ ପ୍ରଶ୍ନର ଉତ୍ତର ବର୍ତ୍ତମାନ ସୁଧା ସମାଧାନ ହୋଇପାରିନାହିଁ । ମୋଟ ଜାତୀୟ ଉତ୍ପାଦ ବୃଦ୍ଧିରେ କଲ୍ୟାଣ ବୃଦ୍ଧି ହୋଇପାରିବ କି ? ଦେଶର ଉତ୍ପାଦ ବୃଦ୍ଧି ପାଇଲେ ମନୁଷ୍ୟର ସୁଖସ୍ୱାଚ୍ଛନ୍ଦ୍ୟ ଯେ ନିଶ୍ଚୟ ବୃଦ୍ଧିପାଇବ, ଏହାର କୌଣସି ନିଶ୍ଚିତତା ନାହିଁ । ମୋଟ ଉତ୍ପାଦ ଅନ୍ତିମ ଦ୍ରବ୍ୟ ଓ ସେବାକୁ ବିଚାରକୁ ନେଇଥାଏ; ଯାହା ବଜାରକୁ ପ୍ରବେଶ କରେ । ଯେଉଁ କାର୍ଯ୍ୟ ବା ସେବା ବିକ୍ରି-କଣା ହୋଇପାରେ ନାହିଁ; ଯଥା- ମା’ର ସେବା, ଅବକାଶ ସମୟର କାର୍ଯ୍ୟ ଇତ୍ୟାଦି ଜାତୀୟ ଉତ୍ପାଦରେ ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇନଥାଏ । କେତେକ ଉପାଦାନ ଯଥା ସ୍ଥିର ସରକାର ।
ଆୟର ବଣ୍ଟନ ଇତ୍ୟାଦି ଜାତୀୟ ଉତ୍ପାଦରେ ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇନଥାଏ ଯାହାକି ପ୍ରତ୍ୟକ୍ଷ ବା ପରୋକ୍ଷ ଭାବରେ କଲ୍ୟାଣ କରିଥାଏ । ଜାତୀୟ ଉତ୍ପାଦ ବୃଦ୍ଧି ହେବା ଅର୍ଥ ଦେଶରେ ଉତ୍ପାଦ ପରିମାଣ ବୃଦ୍ଧି ହୋଇଛି । କିନ୍ତୁ ଏହି ଉତ୍ପାଦର ବୃଦ୍ଧି ସହିତ ସମାଜର ଅନେକ କ୍ଷତି ହୋଇଥାଏ । ଶିଳ୍ପବିପ୍ଳବ ପରେ ପରେ ଇଂଲଣ୍ଡ ଏକ ଧନଶାଳୀ ରାଷ୍ଟ୍ର ହୋଇଉଠିଲା । ଅନ୍ୟପକ୍ଷରେ ଅଗଣିତ ଶ୍ରମିକ ଓ କୃଷକଙ୍କ ଦୁଃଖର ସୀମା ରହିଲା ନାହିଁ । ଦୈନିକ 16 ଓ 17 ଘଣ୍ଟା ପରିଶ୍ରମ କରି ମଧ୍ୟ ଶ୍ରମିକ ଦୁଇବେଳା ଖାଇବାକୁ ପାଇଲା ନାହିଁ । ସୁତରାଂ, ଦେଶର ସମ୍ପଦ ବୃଦ୍ଧି ପାଇଥିଲେ ମଧ୍ୟ ସାଧାରଣ ଲୋକଙ୍କର ସୁଖସ୍ବାଚ୍ଛନ୍ଦ୍ୟ ବୃଦ୍ଧି ପାଇପାରିଲା ନାହିଁ ।
ସଭ୍ୟତାର କ୍ରମ ବିକାଶ ଯୋଗୁଁ ଭୌତିକ କଲ୍ୟାଣ ପ୍ରତି ମନୁଷ୍ୟ ଅଧିକ ଆଗ୍ରହୀ । ତେଣୁ ଅର୍ଥନୈତିକ ଅଭିବୃଦ୍ଧି ନିମନ୍ତେ କଳକାରଖାନା, ବାସଗୃହ ପ୍ରକରଣ, ଗମନାଗମନ ଆଦି କ୍ଷେତ୍ରରେ ବିଭିନ୍ନ ଯୋଜନା କାର୍ଯ୍ୟକାରୀ କରାଯାଏ । ଫଳରେ ପ୍ରକୃତି ଦତ୍ତ ପରିବେଶ ଅବହେଳିତ ହୋଇ ସମଗ୍ରମାନବ ଜାତି ପ୍ରତି ବହୁମୁଖୀ ସମସ୍ୟା ସୃଷ୍ଟି କରିଛି । ପରିବେଶ ଅବକ୍ଷୟ କେବଳ ଅର୍ଥନୈତିକ ଓ ସାମାଜିକ ସ୍ଥିତି ପ୍ରତି ବିପଦ ସୃଷ୍ଟିକରିନାହିଁ । ବରଂ ଏହା ସମଗ୍ର ମାନବଜାତିର ଜୀବନ ପ୍ରତି ବିପଦ ସୃଷ୍ଟି କରିଚାଲିଛି ।
ଅଶୀଦଶକର ପ୍ରାରମ୍ଭରୁ ହିଁ ପରିବେଶର ଅବକ୍ଷୟ ଆରମ୍ଭ ହୋଇଛି । ସଭ୍ୟତାର ଦ୍ବାହି ଦେଇ ଅର୍ଥନୈତିକ ଉନ୍ନୟନ ନିମନ୍ତେ ଭୌତିକ କଲ୍ୟାଣର ପରିସର ବୃଦ୍ଧି କରାଇବା ଦିଗରେ ସମଗ୍ର ପୃଥିବୀର ଅଧିବାସୀମାନେ ତତ୍ପରତା ପ୍ରକାଶ କରିବା ଫଳରେ ଆମର ପ୍ରାକୃତିକ ପରିବେଶ କଳୁଷିତ ଓ ପ୍ରଦୂଷିତ ହୋଇଛି । ତେଣୁ ଆଜିର ଅର୍ଥନୈତିକ ଅଭିବୃଦ୍ଧି ପରିବେଶ ପ୍ରଦୂଷଣ ବଦଳରେ ସମ୍ଭବ ହୋଇପାରିଛି । ଅର୍ଥାତ୍ ଅତୀତର ସମସ୍ତ ଅର୍ଥନୈତିକ ଅଭିବୃଦ୍ଧି ଯାହାକିଛି ମାନବର ଭୌତିକ କଲ୍ୟାଣରେ ଉନ୍ନତି ଆଣିପାରିଛି । ତାହାପଛରେ ପର୍ଯ୍ୟାବରଣର ବହୁ ଅଧୋଗତି ସଂଶ୍ଳିଷ୍ଟ ।
ତେଣୁ କେବଳ ଜାତୀୟ ଉତ୍ପାଦ ବୃଦ୍ଧି ବା ମୁଣ୍ଡପିଛା ଆୟ ବୃଦ୍ଧି ଅର୍ଥନୀତିକ ପ୍ରଗତିର ସ୍ପଷ୍ଟ ଚିତ୍ର ପ୍ରଦାନ କରିନଥାଏ, ଯଦି ଏହା ଅର୍ଥନୈତିକ କଲ୍ୟାଣ ସାଧନ କରିପାରେନାହିଁ ।
ଅର୍ଥନୈତିକ କଲ୍ୟାଣ ସାଧନ ନିମନ୍ତେ ଜାତୀୟ ଉତ୍ପାଦ ବୃଦ୍ଧି ଓ ମୁଣ୍ଡପିଛା ଆୟ ବୃଦ୍ଧିର ଆବଶ୍ୟକତା ରହିଛି । ମାତ୍ର ଏଥ୍ ସହିତ ସୁଷମ ବଣ୍ଟନ, ଜନସାଧାରଣଙ୍କର ଉପଭୋଗର ମାତ୍ରା ବୃଦ୍ଧିର ଆବଶ୍ୟକତା ରହିଛି । ତେଣୁ ଉପରୋକ୍ତ ସମସ୍ତ ଉପାଦାନର ସମନ୍ଵୟ ଘଟିଲେ ଅର୍ଥନୈତିକ କଲ୍ୟାଣ ସାଧ୍ୟ ହୋଇପାରିଥାଏ । ଜାତୀୟ ଉତ୍ପାଦ ସହିତ ସୁଷମ ବଣ୍ଟନ ଏବଂ ଦରଦାମ୍ ହାରରେ ସ୍ଥିରତା ରକ୍ଷା ମଧ୍ୟ ଅର୍ଥନୈତିକ କଲ୍ୟାଣ ନିମନ୍ତେ ଅତ୍ୟନ୍ତ ଆବଶ୍ୟକ ।
![]()
![]()
![]()
![]()
![]()
![]()
![]()



