Class 7

Odisha State Board BSE Odisha 7th Class English Solutions Follow-Up Lesson 3 Mum Textbook Exercise Questions and Answers.

BSE Odisha Class 7 English Solutions Follow-Up Lesson 3 Mum

BSE Odisha 7th Class English Follow-Up Lesson 3 Mum Text Book Questions and Answers

Mum, you’re like an angel,
Sent from up above;
With all your kindness, tenderness,
And everlasting love.

You have always looked after me,
And taught me right from wrong;
And when I am down and worried,
It’s always you that come along.

You are not just mum but a friend of mine,
A friend I cannot replace;
And every time I think of you,
All I see is your smilling face.

I thank you mum, for bearing me,
And allowing me to see these times;
Because if it wasn’t- for you, dear mother,
I could never write down these lines.

ଓଡ଼ିଆ ଅନୁବାଦ:

ତୁମେ ତ ମା’ ଏକ ସ୍ଵର୍ଗଦୂତ
ତୁମର ସମସ୍ତ ଦୟା, କୋମଳତା ସହିତ,
ପ୍ରେରିତ ହୋଇଛ ଉପର ଧାମରୁ
ଚିରନ୍ତନ ପ୍ରେମମୟ ପଥକୁ ଆବୋରି ।

ସବୁବେଳେ ଯନ୍ତ୍ର ନିଅ ମୋର
ମୋତେ ଶିଖାଇଦିଅ କିଏ ଠିକ୍ କିଏ ଅବା ଭୁଲ୍
ଏବଂ ଯେତେବେଳେ ମୁଁ ତଳକୁ ଓ ଚିନ୍ତିତ,
ସେହି ତୁମେ ପାଖେ ପାଖେ ସଦାବେଳେ ସାଥ୍‌ରେ ସାଥ୍‌ରେ ।

ନୁହଁ ତୁମେ କେବଳ ଯେ ମାମା
କିନ୍ତୁ ଏକ ସାଥୀ ଜୀବନର ସାଥୀ ଏକ ଯାହାକୁ ମୁଁ ବଦଳି ପାରେନି
ସର୍ବଦା ଓ ସବୁବେଳେ ଭାବେ ତୁମ କଥା
ଦେଖେ ଯାହା କେବଳ ସେ ତୁମ ହାସ୍ୟ ମୁଖ ।

ଧନ୍ୟବାଦ ମାମା, ତୁମେ ମୋତେ ଜନ୍ମ ଯେ ଦେଇଛ
ଏହି ସମୟ ସବୁକୁ ଦେଖିବାକୁ ଦେଇଛ ସୁଯୋଗ
କିନ୍ତୁ ଯଦି ତୁମେ ତ ନଥା’ନ୍ତ
ହେ ସ୍ନେହମୟୀ ମାମା
ଏପରି ଧାଡ଼ିଏ ମୁଁ ଲେଖୁ ଯେ ନଥା’ନ୍ତି ।

Notes And Glossary: (ଶବ୍ଦାର୍ଥ) :
Angel (ଆଞ୍ଜେଲ୍) – ସ୍ବର୍ଗଦୂତ
above ( ଏବଭ୍) – ଉପର
kindness (କାଇଗ୍‌ନେସ୍) – ଦୟା
tenderness (ଟେଣ୍ଡରନେସ୍) – କୋମଳତା
everlasting ( ଏଭରଲାଷ୍ଟିଙ୍ଗ୍) – ଚିରନ୍ତନ
look after (ଲୁକ୍ ଆପ୍‌ର) – ଯନ୍ତ୍ର ନେବା
right from wrong (ରାଇଟ୍ ଫ୍ରମ୍ ରଙ୍ଗ୍) –ଭୁଲ
worried (ଓରିଡ୍) – ବ୍ୟସ୍ତ, ବିବ୍ରତ
replace (ରିପ୍ଲେସ୍) – ବଦଳେଇବା
bearing (ବିୟରିଙ୍ଗ୍) – ପାଳିବା

Write answers to the following questions : (ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।)
Question 1.
Mother is like an angel. What angel like qualities does she have?
(ମାଆ ଜଣେ ସ୍ଵର୍ଗଦୂତ ପରି । ସ୍ବର୍ଗଦୂତ ଭଳି ତାଙ୍କର କି କି ଗୁଣ ଅଛି ?)
Answer:
Mother like an angel has kindness, tenderness and everlasting love.

Question 2.
Which of the following sentences is not true of the mother?
(ମା’ ସମ୍ବନ୍ଧରେ ନିମ୍ନଲିଖ୍ ବାକ୍ୟଗୁଡ଼ିକ ମଧ୍ୟରୁ କେଉଁଟି ସତ୍ୟ ନୁହେଁ ?
(i) She looks after me. (ସେ ମୋତେ ଯନ୍ ନିଅନ୍ତି ।)
(ii) She always quarrels with me. (ସେ ମୋ ସହିତ ସର୍ବଦା କଳହ କରନ୍ତି ।)
(iii) She teaches me right from wrong. (ସେ ମୋତେ ଭୁଲଠାରୁ ଠିକ୍ କ’ଣ ଶିଖାନ୍ତି ।)
(iv) She stands by me in my troubles. (ସେ ମୋ ଅସୁବିଧାବେଳେ ପାଖେ ପାଖେ
Answer:
(ii) She always quarrels with me.

Question 3.
What does the child see when it thinks of the mother?
(ପିଲାଟି ଯେତେବେଳେ ମା’ଙ୍କ କଥା ଭାବେ ସେ କ’ଣ ଦେଖେ ?)
Answer:
When the child thinks of the mother it always sees her smiling face.

Question 4.
Which line in the stanza-4 says that mother has given birth to the child?
(୪ର୍ଥ ପଦରେ ଥ‌ିବା କେଉଁ ଶବ୍ଦ ମା’ ପିଲାଟିକୁ ଜନ୍ମ ଦେଇଥୁବାର ସୂଚାଏ ?)
Answer:
“I thank you mum, for bearing me”. This line of stanza-4 shows that mother has given birth to the child.

Question 5.
What is the child now? Who has helped it to be so great?
(ପିଲାଟି ବର୍ତ୍ତମାନ କ’ଣ ? କିଏ ତାକୁ ଏତେ ବଡ଼ ହେବାରେ ସାହାଯ୍ୟ କରନ୍ତି ?)
Answer:
The child is now a renowned poet. Mother has helped the child to be so great.

Word Note: (The words /phrases have been defined mostly on their contextual meanings)

angel (ଆଞ୍ଜେଲ୍) – messenger of god (ଦେବଦୂତ, ମହାନ୍ ବ୍ୟକ୍ତି)
bearing me (ବିୟରିଙ୍ଗ ମି) – giving birth to me (ମୋତେ ଜନ୍ମ ଦେଇଥ‌ିବାରୁ)
brave (ବ୍ରେକ୍) -courageous, fearless
down and worried (ଡାଉନ୍ ଆଣ୍ଡ୍ ଓରିଡ୍) – when I am in trouble / in problems (ସମସ୍ୟାରେ ବ୍ୟସ୍ତ ବିବ୍ରତ ହେଉଥିଲାବେଳେ)
everlasting (ଏଭର୍‌ଲାଷ୍ଟିଙ୍ଗ୍) – something that lasts for ever
looked after (ଲୁକ୍‌ ଆପ୍‌ର) – (you have) taken care (ଲାଳନ ପାଳନ କରିଛ, ଯତ୍ନ ନେଇଛ)
magic (ମ୍ୟାଜିକ୍) – special power, (here) magic of mother’s love (ଯାଦୁ, କୁହୁକ, ମା’ ମମତାର ଯାଦୁକରୀ ଶକ୍ତି)
replace – fill up the place (ଅନ୍ୟଦ୍ୱାରା ସ୍ଥାନ ପୂରଣ କରିବା)
tenderness (ଟେଣ୍ଡର୍‌ନେସ୍) – affectionate behaviour (ସ୍ନେହପୂର୍ଣ ବ୍ୟବହାର)

BSE Odisha 7th Class English Solutions Follow-Up Lesson 3 Mum Important Questions and Answers

(A) Choose the right answer from the options.
Question 1.
Mum, you’re like ___________.
(i) an angel
(ii) a human being
(iii) an actress
(iv) a goddess
Answer:
(i) an angel

Question 2.
Mother is sent to you by God from _____________.
(i) Earth
(ii) other countries
(iii) Mars
(iv) up above
Answer:
(iv) up above

Question 3.
Mother’s love is _____________.
(i) shortlived
(ii) immortal
(iii) longlasting
(iv) everlasting
Answer:
(iv) everlasting

Question 4.
Mother is a _____________ that can’t be replaced.
(i) teacher
(ii) goddess
(iii) philosopher
(iv) guide
Answer:
(iv) guide

(B) Answer the following questions.
Question 1.
Why does a child love its mother?
Answer:
A child loves her mother for her kindness, tenderness and deep love towards him/her. Her advice makes him/her good, brave and true.

Question 2.
What is the mother for a child?
Answer:
For a child the mother is a friend, philosopher and guide. She loves her child dearly and solve all problems of the child.

Odisha State Board BSE Odisha 7th Class Hindi Solutions Chapter 5 आज इतवार है Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Hindi Solutions Chapter 5 आज इतवार है

1. निम्नलिखित प्रश्नों के उत्तर दीजिए :

(i) स्कूल और दफ्तर किस दिन बंद रहते हैं ?
उत्तर:
स्कूल और दफ्तर इतवार के दिन बंद रहते हैं ।

(ii) इतवार के दिन लोग कहाँ और क्यों जाते हैं ?
उत्तर:
इतवार के दिन लोग बाज़ार जाते हैं । वहाँ जाकर वे ज़रूरत की चीजें खरीदते हैं ।

(iii) माँ ने कौन-कौन सी सब्जियाँ खरीदीं ?
उत्तर:
माँ ने आलू, प्याज, बैंगन, पपीता, गाजर, मूली, परवल, पालक, कच्चा केला, करैला, मिर्च, नींबू, फूलगोभी आदि कई सब्जियाँ खरीदीं ।

(iv) मदन ने मिठाइयाँ कहाँ से और क्यों खरीदीं थीं।
उत्तर:
मदन ने मिठाइयाँ हलवाई की दुकान से खरीदीं। उसने मिठाइयाँ स्कूल में टिफिन के साथ ले जाने के लिए खरीदी थीं ।

(v) क्लास टीचर सोमवार को बच्चों से क्या पूछती हैं ?
उत्तर:
क्लास टीचर सोमवार को बच्चों से पूछती हैं कि कल तुमने क्या-क्या चीजें खरीदीं ।

2. रिक्त स्थानों में उपयुक्त शब्द भरिए :

(i) माँ ………… की दुकान में पहुँचीं ।
(ii) रानी को कई ………… के नाम मालूम नहीं थे ।
(iii) मुझे तो भाई ………… बहुत अच्छी लगती है ।
(iv) पिताजी को फल बहुत ………… हैं।
(v) ………… का माहौल बहुत अच्छा लगा।
उत्तर:
(i) सब्जी’
(ii) सब्जियों
(iii) जलेबी
(iv) पसंद
(v) बाजार

3. निम्नलिखित प्रश्नों के सही विकल्प उत्तर पर (✓) का निशान लगाइए :

(i) रानी को कहाँ घूमना अच्छा लगता था ?
(क) बाज़ार में
(ख) पहाड़ी पर
(ग) शहर में
(घ) गाँव में
उत्तर:
(क) बाजार

(ii) मदन को बाजार में कौन मिल गया ?
(क) रमेश
(ख) पंकज
(ग) शाश्वत
(घ) अनुराग
उत्तर:
(ग) शाश्वत

(iii) पिताजी ने बाजार में क्या खरीदे ?
(क) सब्जियाँ
(ख) मिठाइयाँ
(ग) कपड़े
(घ) फल
उत्तर:
(क) सब्जियाँ

(iv) बाजार का माहौल कैसा था ?
क) अच्छा
(ख) बुरा
(ग) उमस भरा
(घ) सर्द
उत्तर:
(क) अच्छा

भाषा-कार्य :

4. दिए गए शब्दों के विलोम शब्द लिखिए :

दिन, अच्छा, ताजा, पसंद, ज्यादा, अपना
उत्तर:
शब्द — विलोम
दिन — रात
अच्छा — बुरा
ताजा — बासी
पसंद — नापसंद
ज्यादा — कम
अपना — पराया

5. निम्नलिखित शब्दों का वाक्यों में प्रयोग कीजिए :

छुट्टी, बाजार, सब्जी, दुकान, हलवाई
उत्तर:

• छुट्टी – रमन गर्मी की छुट्टियों में अपने गाँव गया था ।
• बाजार – बाजार से हमलोग अपनी जरूरत की चीजें खरीदते हैं ।
• सब्जी – हरी सब्जियाँ खाने से सेहत अच्छी रहती है ।
• दुकान – दुकान में बहुत भीड़ थी ।
• हलवाई – हलवाई मिठाइयाँ बनाता है ।

अन्य परीक्षोपयोगी प्रश्नोत्तर

1. निम्नलिखित प्रश्नों के उत्तर दीजिए :

(i) स्कूल और दफ्तर कब बंद रहते हैं ?
उत्तर:
स्कूल और दफ्तर इतवार को बंद रहते हैं ।

(ii) मदन माँ के साथ कभी-कभी बाजार क्यों जाता है ?
उत्तर:
मदन माँ के साथ कभी-कभी उनकी मदद करने को बाजार जाता है।

(iii) रानी को क्या अच्छा लगता है ?
उत्तर:
रानी को बाजार में घूमना अच्छा लगता है ।

(iv) शाश्वत ने हलवाई की दुकान पर क्या देखीं?
उत्तर:
शाश्वत ने हलवाई की दुकान पर अपनी पसंद की मिठाई और नमकीन चीजें देखीं ।

(v) किसको रसगुल्ले अच्छे लगते हैं ?
उत्तर:
मदन को रसगुल्ले अच्छे लगते हैं।

2. सही कथनों के सामने (✓) का और गलत कथनों के सामने (✗) का निशान लगाइए :

(i) शनिवार छुट्टी का दिन है । (✗)
(ii) रानी को फल बहुत पसंद हैं । (✗)
(iii) मदन हलवाई की दुकान में पहुँचा । (✓)
(iv) क्लास टीचर का नाम रश्मि वर्मा है । (✗)
(v) कल तुमने क्या－क्या चीजें खरीदीं ？－यह प्रश्न पिताजी ने पूछा । (✗)

3. निम्नलिखित प्रश्नों के सही विकल्प उत्तर पर (✓) का निशान लगाइए ：

(i) माँ ने कौन－सी सब्जी नहीं खरीदी ？
(क) बैंगन
(ख) टिंडा
(ग) परवल
(घ) करैला
उत्तर:
(ख) टिंडा

(ii) मदन को क्या ज्यादा पसंद है ？
(क) रसगुल्ले
(ख) गुलाबजामुन
(ग) नमकीन
(घ) जलेबी
उत्तर:
(घ) जलेबी

(iii) पिताजी को बहुत पसंद है ：
(क) सब्जी
(ख) शाश्वत
(ग) मदन
(घ) फल
उत्तर:
(घ) फल

(iv) बाज़ार में क्या ज्यादा थी ？
(क) फल
(ख) सब्जी
(ग) भीड़
(घ) मिठाइयाँ
उत्तर:
(ग) भीड़

भाषा-कार्य

4. दिए गए वाक्यों के रिक्त स्थानों में सही कारकचिह्न भरिए :
( में, ने, की, को, से )

(i) उनकी मदद करने ——- मदन कभी-कभी चला जाता है।
(ii) रानी को बाजार ——- घूमना अच्छा लगता है।
(iii) माँ ——- सब्जियाँ खरीदीं ।
(iv) वे जलेबी ——- ज्यादा अच्छे नहीं ।
(v) उसने अपनी पसंद ——- मिठाई देखी ।
उत्तर:
(i) को
(ii) में
(iii) ने
(iv) से
(v) की

5. दिए गए शब्दों के एक-एक पर्यायवाची शब्द लिखिए:
फौरन, मदद, काफी, ज्यादा, जरूरत, रोज
उत्तर:
फौरन – शीघ्र ज्यादा – अधिक
मदद – सहायता जरूरत – आवश्यकता
काफी – पर्याप्त रोज – हर दिन

6. ‘क’ स्तम्भ के साथ ‘ख’ स्तम्भ के उपयुक्त शब्दों का मिलान कीजिए :
‘क’ स्तम्भ — ‘ख’ स्तम्भ
रविवार — क्लास टीचर
सब्जी की दुकान — मूली
हलवाई की दुकान — सब्जी
माँ — फल
पिताजी — रसगुल्ले
रश्मि शर्मा — छुट्टी का दिन
उत्तर:
‘क’ स्तम्भ — ‘ख’ स्तम्भ
रविवार — छुट्टी का दिन
सब्जी की दुकान — मूली
हलवाई की दुकान — रसगुल्ले
माँ — सब्जी
पिताजी — फल
रशिम शर्मा — क्लास टीचर

7. इन शब्दों से वाक्य बनाइए :
मदद, घूमना, केला, दुकान, बताना, अपना}
उत्तर:

• मदद – तुम मेरी मदद करो।
• घूमना – सुबह खुली हवा में घूमना अच्छा है ।
• केला – मैं केला खरीदूँगा।
• बताना – मुझे रास्ता बता दो ।
• अपना – तुम अपना काम करो ।

पाठ का सारांशः

आज इतवार है । छुट्टी का दिन होने के कारण स्कूल और दफ्तर बंद हैं । माँ बाजार जाती है तो मदन भी उनकी मदद करने साथ जाता है । रानी पिताजी के साथ बाजार घूमने और जरूरत की चीजें खरीदने जाती है ।

माँ ने सब्जी की दुकान से ताजी सब्जियाँ खरीदीं । रानी को कई सब्जियों के नाम पहली बार मालूम हुए । मदन ने हलवाई की दुकान से मिठाइयाँ खरीदीं ।

वहाँ मदन की भेंट शाश्वत से हुई । मदन ने बताया कि उसे रसगुल्लों से भी अधिक जलेबियाँ अच्छी लगती हैं । मदन के पिताजी को फल पसंद हैं । उन्होंने रानी के साथ फल खरीदे।

बाजार में चहल-पहल थी । मौसम अच्छा था, सब अपनाअपना काम कर रहे थे । बच्चे जब सोमवार को स्कूल जाते हैं तो उसकी क्लास टीचर रश्मि शर्मा बच्चों से इतवार को खरीदी गई चीज़ों के बारे में पूछती हैं । सब बच्चे उनका उत्तर देते हैं ।

ସାରାଂଶ

ଆଜି ରବିବାର । ଛୁଟିଦିନ ଯୋଗୁଁ ସ୍କୁଲ, ଅଫିସ୍ ସବୁ ବନ୍ଦ। ମା’ ବଜାର ବାହାରିଲେ। ତେଣୁ ତାଙ୍କୁ ସାହାଯ୍ୟ କରିବା ପାଇଁ ମଦନ ତାଙ୍କ ସହିତ ଗଲା । ରାଣୀ ମଧ୍ୟ ବାପାଙ୍କ ସହିତ ବଜାର ବୁଲିବାକୁ ଓ କିଛି ଜରୁରୀ ଜିନିଷ ପାଇଁ ଗଲା। ମା’ ପରିବା ଦୋକାନରୁ କିଛି ତଟକା ପରିବା କିଣିଲେ। ରାଣୀ ପ୍ରଥମଥର ପାଇଁ କେତେକ ପରିବାର ନାଁ ଜାଣିଲା। ମଦନ ଗୁଡ଼ିଆ ଦୋକାନରୁ କିଛି ମିଠା କିଣିଲା।

ସେଠାରେ ମଦନର ଶାଶ୍ଵତ ସହିତ ଭେଟ ହେଲା। ମଦନ କହିଲା ଯେ ତାକୁ ରସଗୋଲା ଅପେକ୍ଷା ଜିଲାପି ଅଧ୍ବକ ଭଲ ଲାଗେ । ମଦନର ବାପାଙ୍କୁ ଫଳ ଭଲ ଲାଗେ। ସେ ରାଣୀ ସାଥୀରେ ଫଳ କିଣିଲେ। ବଜାରରେ ଗହଳି ଥିଲା। ପାଗ ଭଲ ଥିଲା। ସମସ୍ତେ ନିଜ ନିଜ କାମରେ ଲାଗିଥିଲେ। ପିଲାମାନେ ସୋମବାର ଦିନ ସ୍କୁଲକୁ ଗଲାପରେ ସେମାନଙ୍କ ଶ୍ରେଣୀ ଶିକ୍ଷୟିତ୍ରୀ ରଶ୍ମି ଶର୍ମା । ପିଲାମାନଙ୍କୁ ରବିବାର ଦିନ କିଣାଯାଇଥିବା ଜିନିଷଗୁଡ଼ିକ ବିଷୟରେ ପରରିଲେ। ସମସ୍ତେ ଉ ର ଦେଲେ।

शब्दार्थ :

Odisha State Board BSE Odisha 7th Class Geography Important Questions Chapter 3 ବାରିମଣ୍ଡଳ Important Questions and Answers.

BE Odisha Class 7 Geography Important Questions Chapter 3 ବାରିମଣ୍ଡଳ

Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ଆଟଲାଣ୍ଟିକ ମହାସାଗରର ଅବସ୍ଥିତି ଓ ବିଶେଷତ୍ଵଗୁଡ଼ିକ ଲେଖ ।
Answer:

1. ଆଟଲାଣ୍ଟିକ୍ ମହାସାଗର ପୃଥିବୀର ଦ୍ଵିତୀୟ ବୃହତ୍ତମ ମହାସାଗର । ଏହା ସମଗ୍ର ପୃଥ‌ିବୀପୃଷ୍ଠର ଏକ-ଷଷ୍ଠୀଶ ସ୍ଥାନ ଅଧିକାର କରିଅଛି ।
2. ଏହାର ପୂର୍ବ ଦିଗରେ ଇଉରୋପ ଓ ଆଫ୍ରିକା, ପଶ୍ଚିମରେ ଉତ୍ତର ଆମେରିକା ଓ ଦକ୍ଷିଣ ଆମେରିକା, ଉତ୍ତର ଦିଗରେ ସୁମେରୁ ମହାସାଗର ଓ ଦକ୍ଷିଣ ଦିଗରେ ଆଣ୍ଟାର୍କଟିକା ମହାଦେଶ ଅବସ୍ଥିତ ।
3. ଏହି ମହାସାଗର ରେ ବ୍ରିଟିଶ ଦ୍ଵୀପପୁଞ୍ଜ, ପଶ୍ଚିମ ଭାରତୀୟ ଦ୍ଵୀପପୁଞ୍ଜ, ଗ୍ରୀଲ୍ୟାଣ୍ଡ ଓ ଆଇସ୍‌ଲ୍ୟାଣ୍ଡ ପ୍ରଭୃତି ଦ୍ଵୀପ ରହିଛି ।
   ବିଶେଷତ୍ଵ :
4. ଏହି ମହାସାଗର ଉପକୂଳ ଅଧିକ ଦନ୍ତୁରିତ ଥ‌ିବାରୁ ଏଠାରେ ଅନେକ ପ୍ରାକୃତିକ ପୋତାଶ୍ରୟ ଓ ବନ୍ଦରମାନ ଗଢ଼ିଉଠିଛି ।
5. ଏହାର ଦୁଇ ପାଖରେ ଇଉରୋପ ଓ ଉତ୍ତର ଆମେରିକା ଭଳି ଦୁଇ ସମୃଦ୍ଧିଶାଳୀ ମହାଦେଶର ଅବସ୍ଥିତି ଯୋଗୁ ଏହି ମହାସାଗର ବାଣିଜ୍ୟ କାରବାର ପାଇଁ ପ୍ରସିଦ୍ଧ ।

Question 2.
ନିରକ୍ଷୀୟ ସ୍ରୋତର ଉତ୍ପଷ୍ଟି ଓ ଗତିପଥ ଉଲ୍ଲେଖ କର ।
Answer:

1. ବିଷୁବ ଅଞ୍ଚଳ ତଥା କ୍ରାନ୍ତି ଅଞ୍ଚଳରେ ଅଧ୍ବକ ସୌରଶକ୍ତି ସଂଗୃହୀତ ହୋଇଥାଏ । ତେଣୁ ବିଷୁବ ଅଞ୍ଚଳର ସମୁଦ୍ର ଜଳରାଶି ଅଧ୍ବକ ଉଷ୍ମ ହୋଇ ପ୍ରସାରିତ ହୁଏ । ଫଳରେ ଏହାର ଆୟତନ ବୃଦ୍ଧି ପାଏ ।
2. ସେହିପରି ମେରୁ ଅଞ୍ଚଳରେ ଶୀତଳ ଜଳରାଶି ସଙ୍କୁଚିତ ହେବାରୁ ଜଳସ୍ତର ସାମାନ୍ୟ ହ୍ରାସ ପାଏ । ଜଳସ୍ତରରେ ସମତା ରକ୍ଷାପାଇ ବିଷୁବ ତଥା କ୍ରାନ୍ତି ଅଞ୍ଚଳରୁ ଉଷ୍ମ ଜଳରାଶି ସମୁଦ୍ର ପୃଷ୍ଠରେ ମେରୁ ଆଡ଼କୁ ପ୍ରବାହିତ ହୁଏ । ଏହାକୁ ଉଷ୍ମ ନିରକ୍ଷୀୟ ସ୍ରୋତ କୁହାଯାଏ ।
3. ପୃଥ‌ିବୀର ଆବର୍ତ୍ତନ, ବାୟୁପ୍ରବାହ ଆଦି କାରଣରୁ ଏହି ସ୍ରୋତ ସିଧାସଳଖ ମେରୁ ଆଡ଼କୁ ଯାଇପାରେ ନାହିଁ । ପୂର୍ବାବାୟୁ (ନିୟତ ବାୟୁପ୍ରବାହ) ପ୍ରଭାବରେ ଏହି ସ୍ରୋତ ବିଷୁବରେଖାର ଉଭୟ ପାର୍ଶ୍ଵରେ ପଶ୍ଚିମ ଦିଗକୁ ଗତି କରେ ।
4. ଉତ୍ତର ଗୋଲାର୍ଦ୍ଧରେ ଏହା ଉତ୍ତର ନିରକ୍ଷୀୟ ସ୍ରୋତ ଓ ଦକ୍ଷିଣ ଗୋଲାର୍ଦ୍ଧରେ ଦକ୍ଷିଣ ନିରକ୍ଷୀୟ ସ୍ରୋତ ନାମ ଧାରଣ କରି ପ୍ରାୟ ୪୦° ସମାକ୍ଷରେଖା ପର୍ଯ୍ୟନ୍ତ ପ୍ରବାହିତ ହୋଇଥାଏ ।
5. ଏଠାରୁ ପଶ୍ଚିମାବାୟୁ ପ୍ରଭାବରେ ପୂର୍ବ ଉପକୂଳକୁ ପ୍ରବାହିତ ହୋଇଥାଏ ଏବଂ କ୍ରମେ ମେରୁ ଅଞ୍ଚଳରେ ପ୍ରବେଶ କରେ ।

Question 3.
ସାମୁଦ୍ରିକ ସ୍ରୋତ କିପରି ଜଳବାୟୁକୁ ପ୍ରଭାବିତ କରେ ବୁଝାଇ ଲେଖ ।
Answer:

1. ସାମୁଦ୍ରିକ ସ୍ରୋତ ଉପକୂଳ ଅଞ୍ଚଳର ଜଳବାୟୁକୁ ପ୍ରଭାବିତ କରେ । ଉଷ୍ଣସ୍ରୋତ ପ୍ରବାହିତ ହେଉଥ‌ିବା ଅଞ୍ଚଳରେ ଜଳବାୟୁ ଉଷ୍ଣ ରହେ ଓ ଶୀତଳ ସ୍ରୋତ ପ୍ରବାହିତ ହେଉଥ‌ିବା ଅଞ୍ଚଳରେ ଜଳବାୟୁ ଶୀତଳ ରହେ ।
2. ଉଷ୍ଣ ସ୍ରୋତ ଉପରେ ପ୍ରବାହିତ ବାୟୁ ଉଷ୍ଣ ଓ ଜଳୀୟବାଷ୍ପପୂର୍ଣ୍ଣ ହୋଇଥ‌ିବାରୁ ଏହା ପ୍ରବାହିତ ହେଉଥ‌ିବା ଉପକୂଳବର୍ତ୍ତୀ ଅଞ୍ଚଳରେ ପ୍ରଚୁର ବୃଷ୍ଟି କରାଏ ।
3. ଶୀତଳ ସ୍ରୋତ ଉପରିସ୍ଥ ବାୟୁ ଶୀତଳ ଓ ଶୁଷ୍କ ହୋଇଥୁବାରୁ ଏହା ପ୍ରବାହିତ ହେଉଥ‌ିବା ଉପକୂଳ ଅଞ୍ଚଳରେ ପ୍ରାୟ ବର୍ଷା ହୁଏ ନାହିଁ, ତେଣୁ ମରୁଭୂମି ସୃଷ୍ଟି ହୁଏ ।
4. ଉଷ୍ଣ ଓ ଶୀତଳ ସ୍ରୋତର ମିଳନସ୍ଥଳରେ ଘନ କୁହୁଡ଼ି ଦେଖାଯାଏ । ଏହି ମିଳନସ୍ଥଳରେ ଶିଉଳିଜାତୀୟ ବିଭିନ୍ନ ମତ୍ସ୍ୟ ଖାଦ୍ୟ ପ୍ରଚୁର ମିଳୁଥ‌ିବାରୁ ଏହା ମାଛଧରା କେନ୍ଦ୍ରରୂପେ ପ୍ରସିଦ୍ଧ; ଯଥା- ନିଉଫାଉଣ୍ଡଲ୍ୟାଣ୍ଡ ଉପକୂଳ ।
5. ସାମୁଦ୍ରିକ ସ୍ରୋତର ଅନୁକୂଳରେ ଜାହାଜ ଚଳାଇବା ସୁବିଧାଜନକ । ଏହା ଜାହାଜର ଗତି ବଢ଼ାଇଥିବା ସହିତ ସମୟ ଓ ଅର୍ଥ ବ୍ୟୟ କମାଇଥାଏ ।

Question 4.
ଆଙ୍ଗ୍‌ଲାଷ୍ଟିକ ମହାସାଗରର ଅବସ୍ଥିତି ଓ ଗୁରୁତ୍ଵ ଲେଖ ।
Answer:

1. ଆଟଲାଣ୍ଟିକ୍ ମହାସାଗର ପୃଥ‌ିବୀର ଦ୍ଵିତୀୟ ବୃହତ୍ତମ ମହାସାଗର । ଏହା ସମଗ୍ର ପୃଥ‌ିବୀପୃଷ୍ଠର ଏକ-ଷତାଂଶ ସ୍ଥାନ ଅଧିକାର କରିଅଛି ।
2. ଏହାର ପୂର୍ବ ଦିଗରେ ଇଉରୋପ ଓ ଆଫ୍ରିକା, ପଶ୍ଚିମରେ ଉତ୍ତର ଆମେରିକା ଓ ଦକ୍ଷିଣ ଆମେରିକା, ଉତ୍ତର ଦିଗରେ ସୁମେରୁ ମହାସାଗର ଓ ଦକ୍ଷିଣ ଦିଗରେ ଆଣ୍ଟାର୍କଟିକା ମହାଦେଶ ଅବସ୍ଥିତ ।
3. ଏହି ମହାସାଗରରେ ବ୍ରିଟିଶ ଦ୍ଵୀପପୁଞ୍ଜ, ପଶ୍ଚିମ ଭାରତୀୟ ଦ୍ଵୀପପୁଞ୍ଜ, ଗ୍ରୀଲ୍ୟାଣ୍ଡ ଓ ଆଇସ୍‌ଲ୍ୟାଣ୍ଡ ପ୍ରଭୃତି ଦ୍ବୀପ ରହିଛି ।
   ବିଶେଷତ୍ଵ :
4. ଏହି ମହାସାଗର ଉପକୂଳ ଅଧିକ ଦନ୍ତୁରିତ ଥିବାରୁ ଏଠାରେ ଅନେକ ପ୍ରାକୃତିକ ପୋତାଶ୍ରୟ ଓ ବନ୍ଦରମାନ ଗଢ଼ିଉଠିଛି ।
5. ଏହାର ଦୁଇ ପାଖରେ ଇଉରୋପ ଓ ଉତ୍ତର ଆମେରିକା ଭଳି ଦୁଇ ସମୃଦ୍ଧିଶାଳୀ ମହାଦେଶର ଅବସ୍ଥିତି ଯୋଗୁ ଏହି | ମହାସାଗର ବାଣିଜ୍ୟ କାରବାର ପାଇଁ ପ୍ରସିଦ୍ଧ ।

ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ପୃଥ‌ିବୀର ଜଳଭାଗ ଓ ସ୍ଥଳଭାଗର କ୍ଷେତ୍ରଫଳ ଶତକଡ଼ାରେ ପ୍ରକାଶ କଲେ କେତେ ହେବ ?
Answer:
ପୃଥ‌ିବୀର ଜଳଭାଗର କ୍ଷେତ୍ରଫଳ ଶତକଡ଼ା ୭୧ ଭାଗ ଓ ସ୍ଥଳଭାଗର କ୍ଷେତ୍ରଫଳ ଶତକଡ଼ା ୨୯ ଭାଗ ।

Question 2.
ପୃଥ‌ିବୀର ମଧୁର ଜଳର ମୁଖ୍ୟ ଉତ୍ସଗୁଡ଼ିକର ନାମ କ’ଣ ?
Answer:
ପୃଥିବୀର ମଧୁର ଜଳର ମୁଖ୍ୟ ଉତ୍ସଗୁଡ଼ିକର ନାମ, ଯଥା-

1. ହିମୋଟୋପର
2. ଭୂତଳ ଜଳ
3. ମଧୁର ଜଳ ହ୍ରଦ
4. ବାୟୁମଣ୍ଡଳ ଏବଂ
5. ନଦୀ, କୂଅ, ପୋଖରୀ ।

Question 3.
ଜଳଚକ୍ର କାହାକୁ କୁହାଯାଏ ?
Answer:

1. ବାଷ୍ପୀଭବନ ପ୍ରକ୍ରିୟାରେ ପୃଥିବୀପୃଷ୍ଠର ଜଳ ଜଳୀୟବାଷ୍ପ ରୂପେ ବାୟୁମଣ୍ଡଳରେ ପ୍ରବେଶ କରେ ।
2. ଏହି ଜଳୀୟବାଷ୍ପ ଘନୀଭବନ ପ୍ରକ୍ରିୟାରେ ମେଘରେ ପରିଣତ ହୁଏ ।,
3. ପୁନର୍ବାର ତାହା ବର୍ଷଣ ପ୍ରକ୍ରିୟା ଦ୍ବାରା ଭୂପୃଷ୍ଠକୁ ଫେରିଆସେ । ଜଳର ଏପ୍ରକାର ଚକ୍ରାକାର ଗତିକୁ ଜଳଚକ୍ର କୁହାଯାଏ ।

Question 4.
ବାରିମଣ୍ଡଳ କାହାକୁ କୁହାଯାଏ ?
Answer:

1. ଭୂପୃଷ୍ଠରେ ଥିବା ମହାସାଗର, ସାଗର, ହ୍ରଦ, ନଦୀ, ହିମବାହ, ଭୂତଳ ଜଳ ଏବଂ ବାୟୁମଣ୍ଡଳର ଜଳୀୟବାଷ୍ପକୁ ନେଇ ବାରିମଣ୍ଡଳ ଗଠିତ ।
2. ଏହି ବାରିମଣ୍ଡଳ ସମଗ୍ର ପୃଥ‌ିବୀ କ୍ଷେତ୍ରଫଳର ପ୍ରାୟ ୭୧% ଅଧିକାର କରିଛି ।

Question 5.
ପୃଥ‌ିବୀର ମହାସାଗରଗୁଡ଼ିକର ନାମ କ’ଣ ?
Answer:

1. ପୃଥ‌ିବୀରେ ମୁଖ୍ୟ ୪ ଗୋଟି ମହାସାଗର ରହିଛି, ଯଥା-
   ପ୍ରଶାନ୍ତ ମହାସାଗର, ଆଟ୍‌ଲାଣ୍ଟିକ୍ ମହାସାଗର, ଭାରତ ମହାସାଗର ଓ ଉତ୍ତର ବା ସୁମେରୁ ମହାସାଗର ।
2. ଏହାବ୍ୟତୀତ ଦକ୍ଷିଣ ମହାସାଗର ବା କୁମେରୁ ମହାସାଗରକୁ ମହାସାଗର ଭାବେ ଉଲ୍ଲେଖ କରାଯାଇଛି ।

Question 6.
ମହାସାଗର ତଳ କ’ଣ ?
Answer:

1. ମହୀଢାଲୁର ନିମ୍ନ ଅଂଶରୁ ସମୁଦ୍ର ତଳର ବିସ୍ତୃତ ଶଯ୍ୟାକୁ ମହାସାଗର ସମତଳ କୁହାଯାଏ ।
2. ଏଠାରେ ଭୂମିର ଢାଲୁ ଅତି ନଗଣ୍ୟ, ମାତ୍ର ସଂପୂର୍ଣ୍ଣ ସମତଳ ନୁହେଁ ।
3. ଏଠାରେ ମହାସାଗର ଖାତ, ନିମଜ୍ଜିତ ପର୍ବତଶ୍ରେଣୀ ଆଦି ଦେଖାଯାଏ ।
4. ମହାସାଗର ତଳରେ ସାମୁଦ୍ରିକ ଉଦ୍ଭଦ ଓ ଜୀବଜନ୍ତୁଙ୍କ ଧ୍ଵଂସାବଶେଷ ଜମାହୋଇ କୋମଳ ପଙ୍କ ବିଶିଷ୍ଟ ସିନ୍ଧୁମଳ ସୃଷ୍ଟି ହୋଇଥାଏ ।

Question 7.
ସମୁଦ୍ର ତରଙ୍ଗ କାହାକୁ କୁହାଯାଏ ?
Answer:

1. ପ୍ରବାହିତ ବାୟୁର ଘର୍ଷଣ ଫଳରେ ସାଗର ପୃଷ୍ଠରେ ଜଳର ଭାଙ୍ଗ ପଡ଼ିଯାଏ । ଏହାକୁ ତରଙ୍ଗ କୁହାଯାଏ ।
2. ସମୁଦ୍ର କୂଳରେ ତରଙ୍ଗର ଗତି ଆଗକୁ ଓ ପଛକୁ ହୋଇଥିବାବେଳେ ସମୁଦ୍ର ବକ୍ଷରେ ଏହାର ଗତି ଉର୍ଷକୁ ଓ ନିମ୍ନକୁ ହୋଇଥାଏ ।

Question 8.
କୁଆର କ’ଣ ?
Answer:

• ସୂର୍ଯ୍ୟ ଓ ଚନ୍ଦ୍ରଙ୍କ ଆକର୍ଷଣ ଯୋଗୁଁ ପୃଥ‌ିବୀର ଜଳଭାଗ ଅଧିକ ଆକର୍ଷିତ ହୋଇଥାଏ । ଫଳରେ ମହାସାଗର ଜଳସ୍ତର ସାମୟିକ ଭାବେ ଫୁଲିଉଠେ । ଏହାକୁ ଜୁଆର କୁହାଯାଏ ।
• ଅର୍ଥାତ୍ ସମୁଦ୍ର ଜଳର ନିୟମିତ ଉତ୍‌ଥାନକୁ ଜୁଆର କୁହାଯାଏ ।
• ପୃଥ‌ିବୀ, ଚନ୍ଦ୍ର ଓ ସୂର୍ଯ୍ୟର ଅବସ୍ଥାନକୁ ନେଇ ଜୁଆରକୁ ଗୁରୁ ଜୁଆର, ଲଘୁ ଜୁଆର, ପ୍ରତ୍ୟକ୍ଷ ଜୁଆର ଓ ପରୋକ୍ଷ ଜୁଆର ନାମରେ ନାମିତ କରାଯାଇଛି ।

Question 8.
ସାମୁଦ୍ରିକ ସ୍ରୋତ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଭୂପୃଷ୍ଠରେ ବାୟୁ ପ୍ରବାହ ଭଳି ବିଭିନ୍ନ କାରଣରୁ ସମୁଦ୍ର ଜଳ ଗତିଶୀଳ ହୋଇଥାଏ । ସମୁଦ୍ରର ଏକ ଅଞ୍ଚଳରୁ ଅନ୍ୟ ଅଞ୍ଚଳକୁ ହେଉଥ‌ିବା ଏହି ଜଳପ୍ରବାହକୁ ସାମୁଦ୍ରିକ ସ୍ରୋତ କୁହାଯାଏ ।

Question 9.
ଲବଣତା କହିଲେ କ’ଣ ବୁଝ ? ସମୁଦ୍ର ଜଳର ହାରାହାରି ଲବଣତା କେତେ ?
Answer:

1. କିଲୋଗ୍ରାମ୍ ଜଳରେ ଯେତେ ଗ୍ରାମର ଲବଣ ଦ୍ରବୀଭୂତ ଥାଏ, ତାହା ଜଳର ଲବଣତାକୁ ସୂଚାଏ ।
2. ସମୁଦ୍ର ଜଳର ହାରାହାରି ଲବଣତା ହେଉଛି ଏକ କିଲୋଗ୍ରାମ୍ ପ୍ରତି ୩୫ ଗ୍ରାମ୍ ।

Question 10.
ପୃଥିବୀର ଗଭୀରତମ ଖାତର ନାମ କ’ଣ ? ଏହାର ଗଭୀରତା କେତେ ?
Answer:

1. ମେରିଆନା ଖାତ ପୃଥ‌ିବୀର ଗଭୀରତମ ଖାତ ।
2. ପ୍ରଶାନ୍ତ ମହାସାଗରରେ ଅବସ୍ଥିତ ଏହି ଖାତର ଗଭୀରତା ପ୍ରାୟ ୧୧.୦୨୨ କିଲୋମିଟର ବା ୧୧ କି.ମି.ରୁ ଅଧିକ ।

Question 11.
ମହୀସୋପାନ କ’ଣ ? ଏହାର ଗୁରୁତ୍ଵ ଲେଖ ।
Answer:

1. ସମୁଦ୍ରକୂଳଠାରୁ କିଛି ଦୂର ପର୍ଯ୍ୟନ୍ତ ମହାଦେଶର ଅଳ୍ପ ଗଡ଼ାଣିଆ ଭୂଭାଗ ଜଳ ଭିତରେ ବୁଡ଼ି ରହିଛି । ଏହାକୁ ମହୀସୋପାନ କୁହାଯାଏ ।
2. ଏଠାରେ ବିଭିନ୍ନ ପ୍ରକାର ସାମୁଦ୍ରିକ ଜୀବଜନ୍ତୁ ଓ ଉଭିଦ ଦେଖାଯାନ୍ତି । ଏହି ଅଞ୍ଚଳରୁ ଖଣିଜତୈଳ, ପୋହଳା ଓ ମୁକ୍ତା ସଂଗ୍ରହ କରାଯାଏ । ଏଠାରେ ମାଛଧରା କେନ୍ଦ୍ରମାନ ରହିଛି ।

Question 12.
କ୍ରାନ୍ତୀୟ ମଣ୍ଡଳରେ ସମୁଦ୍ର ଜଳର ଲବଣତା ଅଧିକ ହେବାର କାରଣ କ’ଣ ?
Answer:

1. କ୍ରାନ୍ତୀୟ ତଥା ବିଷୁବ ଅଞ୍ଚଳରେ ଅଧ‌ିକ ପରିମାଣରେ ସମୁଦ୍ରଜଳର ବାଷ୍ପୀଭବନ ହୋଇଥାଏ ।
2. ତେଣୁ ଏଠାରେ ଜଳର ଲବଣତା ହାର ଅଧିକ ।

Question 13.
ଅଷ୍ଟମୀ ତିଥିରେ ଲଘୁ ଜୁଆର କାହିଁକି ହୋଇଥାଏ ?
Answer:

1. ପ୍ରତ୍ୟେକ ମାସର ଶୁକ୍ଳପକ୍ଷ ଅଷ୍ଟମୀ ତିଥ୍ ଓ କୃଷ୍ଣପକ୍ଷ ଅଷ୍ଟମୀ ତିଥ୍ୟରେ ଚନ୍ଦ୍ର ଓ ସୂର୍ଯ୍ୟ ପୃଥ‌ିବୀକୁ କେନ୍ଦ୍ରକରି ପ୍ରାୟ ସମକୋଣରେ ଅବସ୍ଥାନ କରନ୍ତି ।
2. ଉଭୟଙ୍କର ଆକର୍ଷଣ ପରସ୍ପର ବିରୋଧୀ ହୋଇଥାଏ । ତେଣୁ ଜୁଆରର ମାତ୍ରା ଅଧିକ ନହୋଇ କମ୍ ହୋଇଥାଏ ।

Question 14.
ପ୍ରଶାନ୍ତ ମହାସାଗରରେ ଅବସ୍ଥିତ ଚାରିଗୋଟି ଦ୍ଵୀପପୁଞ୍ଜର ନାମ ଲେଖ ।
Answer:

• ଫିଲିପାଇନ୍‌ସ
• ନ୍ୟୁଜିଲ୍ୟାଣ୍ଡ
• ଜାପାନ ଓ
• ହାୱାଇ ଦ୍ଵୀପପୁଞ୍ଜ ।

Question 15.
ଆଟ୍‌ଲାଣ୍ଟିକ୍ ମହାସାଗର ଥବା ଦୁଇଟି ଦ୍ଵୀପପୁଞ୍ଜର ନାମ ଲେଖ ।
Answer:

1. ବ୍ରିଟିଶ୍ ଦ୍ଵୀପପୁଞ୍ଜ ଓ
2. ପଶ୍ଚିମ ଭାରତୀୟ ଦ୍ଵୀପପୁଞ୍ଜ ।

Question 16.
ଭାରତ ମହାସାଗର ଚତୁଃପାର୍ଶ୍ୱସ୍ଥ ମହାଦେଶର ନାମ ଲେଖ ।
Answer:

• ଏସିଆ
• ଆଫ୍ରିକା ଓ
• ଅଷ୍ଟ୍ରେଲିଆ ।

ସଂକ୍ଷିପ୍ତ ଟିପ୍ପଣୀ ଲେଖ ।

1. ସିନ୍ଧୁମଳ :
Answer:

• ମହାସାଗର ସମତଳରେ ଭୂପୃଷ୍ଠରୁ କ୍ଷୟପ୍ରାପ୍ତ ଅତି ସୂକ୍ଷ୍ମ ଶିଳାରେଣୁ, ଆଗ୍ନେୟ ଭସ୍ମ ପ୍ରଭୃତି ପଦାର୍ଥ ଭାସିଯାଇ ଜମାହୁଏ ।
• ଏହାବ୍ୟତୀତ ବିଭିନ୍ନ ସାମୁଦ୍ରିକ ଉଦ୍ଭଦ ଓ ଜୀବଜନ୍ତୁଙ୍କ ଧ୍ବଂସାବଶେଷ ମହାସାଗର ତଳ ଅଂଶରେ ଜମାହୋଇ ଏକପ୍ରକାର କୋମଳ ପଙ୍କ ସୃଷ୍ଟି କରେ । ଏହାକୁ ସିନ୍ଧୁମଳ କୁହାଯାଏ ।

2. ମହୀକାଲୁ :
Answer:

• ମହୀସୋପାନର ଶେଷଭାଗରୁ ଭୂମି ଅଧିକ ଢାଲୁ ହୋଇଯାଇ ଗଭୀର ସମୁଦ୍ର ଆଡ଼କୁ ଲମ୍ବିଯାଇଥାଏ ।
• ସମୁଦ୍ର ତଳର ଏହି ଅଧୂକ ଗଡ଼ାଣିଆ ଅଞ୍ଚଳକୁ ମହୀଜାଲୁ କୁହାଯାଏ ।

3. ସୁନାମି :
Answer:

• ବେଳେବେଳେ ମହାସାଗର ନିମ୍ନସ୍ଥ ଭୂଭାଗ ଅଭ୍ୟନ୍ତରରେ ଭୂମିକମ୍ପ ସୃଷ୍ଟି ହେଲେ ସମୁଦ୍ର ଜଳରାଶିରେ କମ୍ପନ ସୃଷ୍ଟି ହୁଏ । ଫଳରେ ବିରାଟ ବିରାଟ ତରଙ୍ଗମାନ ସୃଷ୍ଟି ହୁଏ ।
• ଏପରିଭାବେ ସୃଷ୍ଟି ହେଉଥିବା ବିରାଟ ସାମୁଦ୍ରିକ ତରଙ୍ଗକୁ ଜାପାନୀ ଭାଷାରେ ସୁନାମି (Tsunami) କୁହାଯାଏ ।
• ସୁନାମି ତରଙ୍ଗର ଉଚ୍ଚତା ପ୍ରାୟ ୧୫ ମିଟର । ଭୂମିକମ୍ପର ତୀବ୍ରତା ଅଧିକ ହେଲେ ଏହାର ଉଚ୍ଚତା ୧୫୦ ମିଟର ପର୍ଯ୍ୟନ୍ତ ହୋଇଥାଏ ଓ ଘଣ୍ଟାକୁ ୭୦୦ କି.ମି. ବେଗରେ ଉପକୂଳ ଅଞ୍ଚଳ ଆଡ଼କୁ ମାଡ଼ିଆସେ ।

4. ପରୋକ୍ଷ ଜୁଆର :
Answer:

• ଆବର୍ତ୍ତନ ସମୟରେ ଚନ୍ଦ୍ରର ସମ୍ମୁଖୀନ ହେଉଥିବା ପୃଥ‌ିବୀର ମହାସାଗର ଜଳରାଶିରେ ଚନ୍ଦ୍ରର ଆକର୍ଷଣ ଯୋଗୁ ପ୍ରତ୍ୟକ୍ଷ ଜୁଆର ହୋଇଥାଏ ।
• ଏହି ସମୟରେ ପ୍ରତ୍ୟକ୍ଷ ଜୁଆର ହେଉଥିବା ମହାସାଗର ଅଂଶର ବିପରୀତ ପାର୍ଶ୍ବରେ ଚନ୍ଦ୍ରର ଆକର୍ଷଣ ନ ଥାଏ । ମାତ୍ର ଭୂପୃଷ୍ଠର କଠିନ ଅଂଶ କିଛି ମାତ୍ର ଚନ୍ଦ୍ର ଆଡ଼କୁ ଆକର୍ଷିତ ହୁଏ । ଫଳରେ ଜଳଭାଗ ଓ କଠିନ ଭୂଭାଗ ମଧ୍ୟରେ ସୃଷ୍ଟ ଶୂନ୍ୟସ୍ଥାନକୁ ପୂରଣ ପାଇଁ ଭୂପୃଷ୍ଠର ଅନ୍ୟ ଅଞ୍ଚଳର ଜଳରାଶି ସେ ସ୍ଥାନକୁ ପ୍ରବାହ ହୋଇଥାଏ । ସେଠାରେ ସମୁଦ୍ର ଜଳ ସ୍ତ୍ରୀତ ହୋଇ ପରୋକ୍ଷ ଜୁଆର ସୃଷ୍ଟି ହୁଏ ।

5. ଇଉରୋପର ଉଷ୍ମ କମ୍ବଳ :
Answer:

• ଇଉରୋପର ପଶ୍ଚିମ ଉପକୂଳରେ ଉଷ୍ମ ଆଙ୍ଗ୍‌ଲାଷ୍ଟିକ୍ ଉପସାଗରୀୟ ଧୀର ସ୍ରୋତ ପ୍ରବାହିତ ।
• ଏହି ସ୍ରୋତର ଉଷ୍ମତା ପ୍ରଭାବରେ ଇଉରୋପର ପଶ୍ଚିମ ଉପକୂଳର ବନ୍ଦରଗୁଡ଼ିକ ବରଫମୁକ୍ତ ରହେ । ତେଣୁ ଏହି ଉଷ୍ମ ସାମୁଦ୍ରିକ ସ୍ରୋତକୁ ‘ଇଉରୋପର ଉଷ୍ମ କମ୍ବଳ’ କୁହାଯାଏ ।

6. ପ୍ରବାଳ ବନ୍ଧ :
Answer:

• କ୍ରାନ୍ତୀମଣ୍ଡଳୀୟ ସମୁଦ୍ରରେ ପ୍ରାୟ ୨୧° ସେଲ୍‌ସିୟସ୍‌ ଅଧିକ ତାପମାତ୍ରା ଥ‌ିବା ଜଳରେ ଅଧ‌ିକ ସଂଖ୍ୟକ ପ୍ରବାଳ ବାସ କରନ୍ତି ।
• ସେହି ପ୍ରବାଳମାନଙ୍କ ମୃତ ଶରୀର ଜମିଯାଇ ପ୍ରବାଳ ସ୍ତୂପ ସୃଷ୍ଟି ହୁଏ ।
• ପାଖାପାଖୁ ପ୍ରବାଳ ସ୍ତୂପ ପରସ୍ପର ସଂଲଗ୍ନ ହେଲେ ପ୍ରବାଳ ବନ୍ଧ ସୃଷ୍ଟି ହୁଏ ।
• ଅଷ୍ଟ୍ରେଲିଆ ମହାଦେଶର ପୂର୍ବ ଉପକୂଳର ଅନତିଦୂରରେ ‘ଗ୍ରେଟ୍ ବ୍ୟାରିଅର୍ ରିଫ୍’ ନାମକ ଏକ ବୃହତ୍ ପ୍ରବାଳ ବନ୍ଧ ରହିଛି ।

7. ଆଟୋଲ :
Answer:

• ସମୁଦ୍ରର କେତେକ ସ୍ଥାନରେ ବୃତ୍ତାକାର ଖଣ୍ଡିତ ପ୍ରବାଳ ଘେରିବନ୍ଧ ସୃଷ୍ଟି ହୋଇଥାଏ ।
• ଏହାକୁ ଆଟୋଲ୍ କୁହାଯାଏ ।

8. ପ୍ଲାଙ୍କ୍‌ଟନ୍‌ :
Answer:

• ପ୍ଲାନ୍ଟଟନ୍ ଏକ ସାମୁଦ୍ରିକ ଶୈବାଳ ଜାତୀୟ ଉଦ୍ଭବ । – ଏହା ମାଛମାନଙ୍କର ଏକ ପ୍ରକୃଷ୍ଟ ଖାଦ୍ୟ ।
• ଶୀତଳ ସାମୁଦ୍ରିକ ସ୍ରୋତ ଓ ଉଷ୍ଣ ସ୍ରୋତର ମିଳନସ୍ଥଳୀରେ ପ୍ରଚୁର ପରିମାଣରେ ପ୍ଲାନ୍‌ ଜାତୀୟ ଉଦ୍ଭିଦ ଜନ୍ମେ । ତେଣୁ ସେଠାରେ ପସିଦ୍ଧ ମାଛଧରା କେନ୍ଦ୍ର ଗଢିଉଠିଛି ।

ଭୌଗୋଳିକ କାରଣ ଦର୍ଶାଅ।

Question 1.
ପୂର୍ଣ୍ଣିମା ତିଥିରେ ଗୁରୁ ଜୁଆର ହୋଇଥାଏ ।
Answer:

1. ପୂର୍ଣିମା ତିଥିରେ ସୂର୍ଯ୍ୟ, ପୃଥ‌ିବୀ ଓ ଚନ୍ଦ୍ର ପ୍ରାୟ ଏକ ସରଳରେଖାରେ ଅବସ୍ଥାନ କରିଥାନ୍ତି ।
2. ସେହିଦିନ ସୂର୍ଯ୍ୟ ଓ ଚନ୍ଦ୍ର ମଝିରେ ପୃଥ‌ିବୀର ଅବସ୍ଥାନ ହୋଇଥାଏ ।
3. ତେଣୁ ପୃଥ‌ିବୀର ଉଭୟ ପାର୍ଶ୍ଵରେ ଚନ୍ଦ୍ର ଓ ସୂର୍ଯ୍ୟର ଆକର୍ଷଣ ଯୋଗୁ ଉଚ୍ଚ ଜୁଆର ହୋଇଥାଏ ।

Question 2.
ଡଗରବ୍ୟାଙ୍ଗ୍ ଏକ ପ୍ରସିଦ୍ଧ ମାଛଧରା କେନ୍ଦ୍ର ।
Answer:

• ଡଗରବ୍ୟାକ୍ ନିକଟରେ ଉଷ୍ଣ ସାମୁଦ୍ରିକ ସ୍ରୋତ ଓ ଶୀତଳ ସାମୁଦ୍ରିକ ସ୍ରୋତର ମିଳନ ଘଟିଥିବାରୁ ସେଠାରେ ପ୍ଲାକ୍ଟିନ ଜାତୀୟ ଉଦ୍ଭବ ପ୍ରଚୁର ପରିମାଣରେ ଜମାହୁଏ ।
• ଏହା ମାଛମାନଙ୍କର ପ୍ରକୃଷ୍ଟ ଖାଦ୍ୟ ହୋଇଥିବାରୁ ଏହା ପ୍ରସିଦ୍ଧ ମାଛଧରା କେନ୍ଦ୍ର ହୋଇପାରିଛି ।

Question 3.
ପୃଥ‌ିବୀର ସାମୁଦ୍ରିକ ବାଣିଜ୍ୟର ଅଧିକାଂଶ ଭାଗ ଆଟ୍‌ଲାଣ୍ଟିକ୍ ମହାସାଗର ଦେଇ ହୋଇଥାଏ ।
Answer:

1. ଆଟ୍‌ଲାଣ୍ଟିକ ମହାସାଗରର ଉଭୟ ପାର୍ଶ୍ଵରେ ଇଉରୋପ ଓ ଉତ୍ତର ଆମେରିକା ଭଳି ସମୃଦ୍ଧିଶାଳୀ ମହାଦେଶ ଅବସ୍ଥିତ ।
2. ଏହି ମହାସାଗରର ଉପକୂଳ ଦନ୍ତୁରିତ ଥିବାରୁ ଏଠାରେ ଅନେକ ପ୍ରାକୃତିକ ପୋତାଶ୍ରୟ ଓ ବନ୍ଦରମାନ ଗଢ଼ିଉଠିଛି । ତେଣୁ ଏହି ମହାସାଗର ଦେଇ ଅନେକ ବାଣିଜ୍ୟ କାରବାର ହୋଇଥାଏ ।

Question 4.
ନିଜଫାଉଣ୍ଡଲ୍ୟାଣ୍ଡ ଉପକୂଳ ଏକ ପ୍ରସିଦ୍ଧ ମାଛଧରା କେନ୍ଦ୍ର ହୋଇପାରିଛି ।
Answer:

1. ନିଉଫାଉଣ୍ଡଲ୍ୟାଣ୍ଡ ଉପକୂଳରେ ଶୀତଳ ସ୍ରୋତ ଓ ଉଷ୍ଣ ସ୍ରୋତର ମିଳନ ଘଟିଛି । ଫଳରେ ଏଠାରେ ପ୍ଲାନ୍ ଜାତୀୟ ବିଭିନ୍ନ ମତ୍ସ୍ୟଖାଦ୍ୟ ପ୍ରଚୁର ମିଳେ ।
2. ତେଣୁ ନିଉଫାଉଣ୍ଡଲ୍ୟାଣ୍ଡ ଉପକୂଳ ଏକ ପ୍ରସିଦ୍ଧ ମାଛଧରା କେନ୍ଦ୍ର ହୋଇପାରିଛି ।

Question 5.
ଶୀତଳ ସ୍ରୋତ ଅନ୍ତଃସ୍ରୋତ ଭାବେ ପ୍ରବାହିତ ।
Answer:

1. ମେରୁ ଅଞ୍ଚଳରୁ ଶୀତଳ ସ୍ରୋତ ସୃଷ୍ଟି ହେଉଥିବାରୁ ଏହା ସଙ୍କୁଚିତ ହୋଇଥାଏ ।
2. ତେଣୁ ଅନ୍ତଃସ୍ରୋତ ଭାବେ ଏହା ପ୍ରବାହିତ ହୁଏ ।

Question 6.
ଉଭୟ ମେରୁ ଅଞ୍ଚଳରେ ସମୁଦ୍ର ଜଳର ଲବଣତା କମ୍ ।
Answer:

1. ଉଭୟ ମେରୁ ଅଞ୍ଚଳରେ ସୂର୍ଯ୍ୟଙ୍କ ଅତି ତୀର୍ଯ୍ୟକ୍ କିରଣ ଥିବାରୁ ଏହା ହିମମଣ୍ଡଳ ।
2. ଏଠାରେ ବାଷ୍ପୀଭବନ କମ୍ ହୋଇଥାଏ, ତେଣୁ ଏଠାରେ ସମୁଦ୍ର ଜଳର ଲବଣତା କମ୍ ।

ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ

1. ଉପଦୀପ ଓ ଉପସାଗର
Answer:

2. ମହୀସୋପାନ ଓ ମହୀକାଳୁ
Answer:

3. ଜୁଆର ଓ ଭଟ୍ଟା
Answer:

4. ଜଷ ସ୍ରୋତ ଓ ଶୀତଳ ସ୍ରୋତ
Answer:

5. ପ୍ରବଳ ଜୁଆର ଓ ଲଘୁ ଜୁଆର
Answer:

ଅତିସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ।

Question 1.
କାହାକୁ ନେଇ ବାରିମଣ୍ଡଳ ଗଠିତ ?
Answer:
ଭୂପୃଷ୍ଠରେ ଥିବା ମହାସାଗର, ସାଗର, ହ୍ରଦ, ନଦୀ, ହିମବାହ, ଭୂତଳ ଜଳ ଏବଂ ବାୟୁମଣ୍ଡଳର ଜଳୀୟବାଷ୍ପକୁ ନେଇ ପୃଥିବୀର ବାରିମଣ୍ଡଳ ଗଠିତ।

Question 2.
ସମଗ୍ର ପୃଥିବୀ କ୍ଷେତ୍ରଫଳର ଜଳ ଓ ସ୍ଥଳ କେତେ ଭାଗ ରହିଛି ?
Answer:
ସମଗ୍ର ପୃଥ‌ିବୀ କ୍ଷେତ୍ରଫଳର ପ୍ରାୟ ୭୧% ଜଳଭାଗ ଏବଂ ୨୯% ସ୍ଥଳଭାଗ ରହିଛି ।

Question 3.
ଜଳର ଲବଣତା କହିଲେ କ’ଣ ବୁଝ ?
Answer:
କିଲୋଗ୍ରାମ୍ ଜଳରେ ଯେତେ ଗ୍ରାମର ଲବଣ ଦ୍ରବୀଭୂତ ଥାଏ ତାହାକୁ ଜଳର ଲବଣତା କୁହାଯାଏ।

Question 4.
ବିଶ୍ବ ଜଳ ଦିବସ କେବେ ପାଳିତ ହୁଏ ?
Answer:
ପ୍ରତି ବର୍ଷ ମାର୍ଚ୍ଚ ୨୨ ତାରିଖକୁ ‘ବିଶ୍ବ ଜଳ ଦିବସ’ ରୂପେ ପାଳନ କରାଯାଏ।

Question 5.
ହିମଟୋପର କାହାକୁ ନେଇ ଗଠିତ ?
Answer:
ଉଚ୍ଚ ପର୍ବତ ଶିଖରରେ ଓ ମେରୁ ଅଞ୍ଚଳରେ ଜମି ରହିଥିବା ବରଫ ରାଶିକୁ ନେଇ ପୃଥୁବୀର ହିମଟୋପର ଗଠିତ।

Question 6.
ବାରିମଣ୍ଡଳରେ ଥିବା ଜଳରାଶିର କେତେ ଭାଗ ମୁଖ୍ୟତଃ ପୃଥ‌ିବୀର ମହାସାଗରର ଲୁଣି ଜଳଦ୍ଵାରା ଗଠିତ ?
Answer:
ବାରିମଣ୍ଡଳରେ ଥିବା ଜଳରାଶିର ଶତକଡ଼ା ପ୍ରାୟ ୯୭ ଭାଗ ମୁଖ୍ୟତଃ ପୃଥ‌ିବୀର ମହାସାଗରର ଲୁଣି ଜଳଦ୍ଵାରା ଗଠିତ ।

Question 7.
ମେରିଆନା ଖାତ କେଉଁ ମହାସାଗରରେ ରହିଛି ?
Answer:
ମେରିଆନା ଖାତ ପ୍ରଶାନ୍ତ ମହାସାଗରରେ ରହିଛି।

Question 8.
କେଉଁ ମହାସାଗର ବେଜିଂ ପ୍ରଣାଳୀଦ୍ଵାରା ପ୍ରଶାନ୍ତ ମହାସାଗର ସହିତ ସଂଯୁକ୍ତ ହୋଇଛି ?
Answer:
ଆଟ୍‌ଲାଣ୍ଟିକ୍ ମହାସାଗର ବେନିଂ ପ୍ରଣାଳୀଦ୍ଵାରା ପ୍ରଶାନ୍ତ ମହାସାଗର ସହିତ ସଂଯୁକ୍ତ ହୌଛି ।

Question 9.
କେଉଁ ସାଗରଟି ପୃଥିବୀର ସାଗରଗୁଡ଼ିକ ମଧ୍ୟରେ ସବୁଠାରୁ ବଡ଼ ?
Answer:
ପୃଥ‌ିବୀର ସାଗରଗୁଡ଼ିକ ମଧ୍ୟରେ ଦକ୍ଷିଣ ଚୀନ ସାଗର ସବୁଠାରୁ ବଡ଼ ।

Question 10.
ଦକ୍ଷିଣ ଚୀନ୍ ସାଗର କେଉଁ ମହାସାଗରର ଅଂଶବିଶେଷ ?
Answer:
ଦକ୍ଷିଣ ଚୀନ ସାଗର ପ୍ରଶାନ୍ତ ମହାସାଗରର ଅଂଶବିଶେଷ ।

Question 11.
କାହାକୁ ଏକ ଅନ୍ତର୍ଦେଶୀୟ ହ୍ରଦ କୁହାଯାଏ ?
Answer:
କାପ୍ସିୟାନ ସାଗର ଏକ ଅନ୍ତର୍ଦେଶୀୟ ହ୍ରଦ।

Question 12.
କାହାକୁ ମହୀସୋପାନ କୁହାଯାଏ ?
Answer:
ସମୁଦ୍ର କୂଳଠାରୁ କିଛି ଦୂର ପର୍ଯ୍ୟନ୍ତ ଜଳ ଭିତରେ ବୁଡ଼ିରହିଥ‌ିବା ମହାଦେଶର ଅଳ୍ପ ଗଢ଼ାଣିଆ ଭୂଭାଗକୁ ମହୀସୋପାନ କୁହାଯାଏ ।

Question 13.
ମହାଜାଳୁ କାହାକୁ କୁହାଯାଏ ?
Answer:
ମହୀସୋପାନର ଶେଷଭାଗରୁ ଭୂମି ଅଧ‌ିକ ଢାଲୁ ହୋଇଯାଇ ଗଭୀର ସମୁଦ୍ର ଆଡ଼କୁ ଲମ୍ବିଯିବା ଫଳରେ ସୃଷ୍ଟି ହେଉଥିବା ସମୁଦ୍ରଜଳର ଗଡ଼ାଣିଆ ଅଞ୍ଚଳକୁ ମହୀଢାଲୁ କୁହାଯାଏ ।

Question 14.
ମହାସାଗର ସମତଳ କାହାକୁ କୁହାଯାଏ ?
Answer:
ମହୀଢାଲୁର ନିମ୍ନଅଂଶରୁ ସମୁଦ୍ର ତଳର ବିସ୍ତୃତ ଶଯ୍ୟାକୁ ମହାସାଗର ସମତଳ କୁହାଯାଏ।

Question 15.
ସିନ୍ଧୁମଳ କହିଲେ କ’ଣ ବୁଝ ?
Answer:
ବିଭିନ୍ନ ସାମୁଦ୍ରିକ ଉଭିଦ ଓ ଜୀବଜନ୍ତୁଙ୍କ ଧ୍ବଂସାବଶେଷ ମହାସାଗର ତଳ ଅଂଶରେ ଜମାହୋଇ ସୃଷ୍ଟି ହେଉଥ‌ିବା କୋମଳ ପଙ୍କକୁ ସିନ୍ଧୁମଳ କୁହାଯାଏ।

Question 16.
କେଉଁ ଅଞ୍ଚଳ ଅନ୍ତର୍ଗତ ସାଗର, ମହାସାଗର ଜଳର ଲବଣତା ଅଧିକ ?
Answer:
କ୍ରାନ୍ତୀୟ ଉଷ୍ମମଣ୍ଡଳ ଅନ୍ତର୍ଗତ ସାଗର, ମହାସାଗର ଜଳର ଲବଣତା ଅଧିକ ।

Question 17.
କେଉଁ ଅଞ୍ଚଳରେ ଥିବା ସମୁଦ୍ର ଜଳର ଲବଣତା କମ୍ ?
Answer:
ଉଭୟ ମେରୁ ଅଞ୍ଚଳରେ ଥିବା ସମୁଦ୍ର ଜଳର ଲବଣତା କମ୍ ।

Question 18.
ସାଧାରଣତଃ ସୁନାମି ତରଙ୍ଗର ଉଚ୍ଚତା କେତେ ?
Answer:
ସାଧାରଣତଃ ସୁନାମି ଜ୍ଵରଙ୍ଗର ଉଚ୍ଚତା ପ୍ରାୟ ୧୫ ମିଟର।

Question 19.
ଭୂକମ୍ପର ତୀବ୍ରତା ଅଧ‌ିକ ହୋଇଥିଲେ ଜେଜର ଉଚ୍ଚତା କେତେ ପର୍ଯ୍ୟନ୍ତ ହୋଇଥାଏ ?
Answer:
ଭୂକମ୍ପର ତୀବ୍ରତା ଅଧ‌ିକ ହୋଇଥିଲେ ଢେଉର ଉଚ୍ଚତା ୧୫୦ ମିଟର ପର୍ଯ୍ୟନ୍ତ ହୋଇଥାଏ।

Question 20.
ସାଗର ଓ ମହାସାଗର ବକ୍ଷରେ ପ୍ରତିଦିନ ନିୟମିତ କେତେଥର ଲେଖାଏଁ ଜୁଆର ଓ ଭଟ୍ଟା ହୋଇଥାଏ ?
Answer:
ସାଗର ଓ ମହାସାଗର ବକ୍ଷରେ ପ୍ରତିଦିନ ନିୟମିତ ଦୁଇଥର ଲେଖାଏଁ ଜୁଆର ଓ ଭଟ୍ଟା ହୋଇଥାଏ।

Question 21.
ସୂର୍ଯ୍ୟ ଓ ଚନ୍ଦ୍ରଙ୍କ ଆକର୍ଷଣ ଯୋଗୁଁ ପୃଥ‌ିବୀର କେଉଁ ଭାଗ ଅଧୂକ ଆକର୍ଷିତ ହୋଇଥାଏ ?
Answer:
ସୂର୍ଯ୍ୟ ଓ ଚନ୍ଦ୍ରଙ୍କ ଆକର୍ଷଣ ଯୋଗୁଁ ପୃଥ‌ିବୀର ଜଳଭାଗ ଅଧିକ ଆକର୍ଷିତ ହୋଇଥାଏ।

Question 22.
ଗୁରୁଜୁଆର କାହାକୁ କୁହାଯାଏ ?
Answer:
ଉଭୟ ପୂର୍ଣ୍ଣିମା ଓ ଅମାବାସ୍ୟା ତିଥ୍ୟରେ ହେଉଥ‌ିବା ଉଚ୍ଚ ଜୁଆରକୁ ଗୁରୁଜୁଆର କୁହାଯାଏ ।

Question 23.
ସାମୁଦ୍ରିକ ସ୍ରୋତ କହିଲେ କ’ଣ ?
Answer:
ସମୁଦ୍ରର ଏକ ଅଞ୍ଚଳରୁ ଅନ୍ୟ ଅଞ୍ଚଳକୁ ହେଉଥ‌ିବା ଜଳପ୍ରବାହକୁ ସାମୁଦ୍ରିକ ସ୍ରୋତ କୁହାଯାଏ।

Question 24.
ପ୍ରବାଳ ବନ୍ଧ କିପରି ସୃଷ୍ଟି ହୁଏ ?
Answer:
ପାଖାପାଖୂ ହୋଇ ଜମା ହେଉଥିବା କେତେକ ପ୍ରବାଳସ୍ତୂପ ପ୍ରାୟ ପରସ୍ପର ସଂଲଗ୍ନ ହୋଇ ‘ପ୍ରବାଳ ବନ୍ଧ’ ସୃଷ୍ଟି ହୋଇଥାଏ।

ପ୍ରତ୍ୟେକର ସଂଜ୍ଞା ଗୋଟିଏ ବାକ୍ୟରେ ପ୍ରକାଶ କର।

i. ଲବଣତା
Answer:
କିଲୋଗ୍ରାମ୍ ଜଳରେ ଯେତେ ଗ୍ରାମର ଲବଣ ଦ୍ରବୀଭୂତ ଥାଏ, ତାହାକୁ ଜଳର ଲବଣତା କୁହାଯାଏ ।

ii. ଉପଦ୍ୱୀପ
Answer:
ଯେଉଁ ସ୍ଥଳଭାଗର ତିନି ପାର୍ଶ୍ୱ ବିସ୍ତୀର୍ଣ୍ଣ ଜଳଭାଗ ଦ୍ୱାରା ବେଷ୍ଟିତ ତାହାକୁ ଉପଦ୍ଵୀପ କୁହାଯାଏ ।

iii. ଉପସାଗର
Answer:
ଯେଉଁ ଜଳଭାଗର ତିନି ପାର୍ଶ୍ଵ ବିସ୍ତୀର୍ଣ୍ଣ ସ୍ଥଳଭାଗ ଦ୍ଵାରା ପରିବେଷ୍ଟିତ, ତାହାକୁ ଉପସାଗର କୁହାଯାଏ ।

iv. ମହୀସୋପାନ
Answer:
ସମୁଦ୍ର ଜଳ ଭିତରେ ବୁଡ଼ି ରହିଥିବା ସମୁଦ୍ରକୂଳଠାରୁ କିଛି ଦୂର ପର୍ଯ୍ୟନ୍ତ ମହାଦେଶର ଅଳ୍ପ ଗଡ଼ାଣିଆ ଭୂଭାଗ ।

v. ମହୀଢାଲୁ
Answer:
ମହୀସୋପାନର ଶେଷଭାଗରୁ ଭୂମି ଅଧିକ ଢାଲୁ ହୋଇ ଗଭୀର ସମୁଦ୍ର ଆଡ଼କୁ ଲମ୍ବିଥୁବା ଅଞ୍ଚଳ ।

vi. ମହାସାଗର ସମତଳ
Answer:
ମହୀଢାଲୁର ନିଗ୍ନାଂଶରୁ ସମୁଦ୍ର ତଳର ବିସ୍ତୃତ ଶଯ୍ୟା ।

vii. ସିନ୍ଧୁମଳ
Answer:
ମହାସାଗର ତଳ ଅଂଶରେ ଜମା ହେଉଥ‌ିବା ସାମୁଦ୍ରିକ ଉଦ୍ଭଦ ଓ ଜୀବଜନ୍ତୁଙ୍କ ଧ୍ବଂସାବଶେଷରୁ ସୃଷ୍ଟ କୋମଳ ପଙ୍କ ।

viii. ତରଙ୍ଗ
Answer:
ପ୍ରବାହିତ ବାୟୁର ଘର୍ଷଣ ଫଳରେ ସାଗର ପୃଷ୍ଠ ଜଳରେ ପଡ଼ୁଥିବା ଭାଙ୍ଗ ।

ix. ତରଙ୍ଗ ଶୀର୍ଷ
Answer:
ତରଙ୍ଗର ଉଚ୍ଚତମ ଅଂଶ ।

x. ତରଙ୍ଗ ପାଦ
Answer:
ତରଙ୍ଗର ନିମ୍ନତମ ଅଂଶ ।

xi. ତରଙ୍ଗ ଦୈର୍ଘ୍ୟ
Answer:
ପାଖାପାଖୁ ଅବସ୍ଥିତ ଦୁଇଟି ତରଙ୍ଗ ଶୀର୍ଷ କିମ୍ବା ତରଙ୍ଗ ପାଦର ମଧ୍ୟବର୍ତ୍ତୀ ବ୍ୟବଧାନ ।

xii. ତରଙ୍ଗ ଉଚ୍ଚତା
Answer:
ତରଙ୍ଗ ପାଦଠାରୁ ତରଙ୍ଗର ଶୀର୍ଷ ପର୍ଯ୍ୟନ୍ତ ଉଚ୍ଚତା ।

xiii. ସୁନାମି
Answer:
ମହାସାଗର ନିମ୍ନସ୍ଥ ଭୂଭାଗ ଅଭ୍ୟନ୍ତରରେ ଭୂମିକମ୍ପ ଦ୍ଵାରା ସୃଷ୍ଟି ବିରାଟ ସାମୁଦ୍ରିକ ତରଙ୍ଗ ।

xiv. ଜୁଆର
Answer:
ସାମୁଦ୍ରିକ ଜଳର ଉତ୍‌ଥାନକୁ ଜୁଆର କୁହାଯାଏ ।

xv. ଭଟ୍ଟା
Answer:
ସାମୁଦ୍ରିକ ଜଳର ପତନକୁ ଭଙ୍ଗା କୁହାଯାଏ ।

xvi. ଗୁରୁ କୁଆର
Answer:
ପୂର୍ଣ୍ଣିମା ଓ ଅମାବାସ୍ୟା ତିଥିରେ ହେଉଥ‌ିବା ଉଚ୍ଚ ଜୁଆର ।

xvil. ଲଘୁ ଜୁଆର
Answer:
କୃଷ୍ଣପକ୍ଷ ଅଷ୍ଟମୀ ଓ ଶୁକ୍ଳପକ୍ଷ ଅଷ୍ଟମୀ ତିଥିରେ ହେଉଥ‌ିବା କମ୍ ଉଚ୍ଚତା ବିଶିଷ୍ଟ ଜୁଆର ।

xvii. ସାମୁଦ୍ରିକ ସ୍ରୋତ
Answer:
ସମୁଦ୍ରର ଏକ ଅଞ୍ଚଳରୁ ଅନ୍ୟ ଅଞ୍ଚଳକୁ ହେଉଥ‌ିବା ଜଳପ୍ରବାହ ।

xix. ପ୍ଲାଙ୍କ୍‌କ୍
Answer:
ଶୀତଳ ସ୍ରୋତ ଓ ଉଷ୍ଣ ସ୍ରୋତର ମିଳନ ସ୍ଥଳରେ ଜମା ହେଉଥ‌ିବା ମାଛ ଖାଦ୍ୟ ଜାତୀୟ ଉଦ୍ଭଦ ।

xx. ପ୍ରବାଳ ସ୍ତୂପ
Answer:
ପ୍ରବାଳମାନଙ୍କ ମୃତାବଶେଷରୁ ସୃଷ୍ଟ ହୁଙ୍କା ଆକାର ଭୂମିରୂପ ।

xxi. ପ୍ରବାଳ ବନ୍ଧ
Answer:
ପାଖାପାଖୁ କେତେକ ପ୍ରବାଳ ସ୍ତୂପ ପରସ୍ପର ସଂଲଗ୍ନ ହୋଇ ସୃଷ୍ଟି ହେଉଥ‌ିବା ପ୍ରାକୃତିକ ବନ୍ଧ ।

xxii. ଆଗୋଳ
Answer:
ବୃତ୍ତାକାର ଖଣ୍ଡିତ ପ୍ରବାଳ ଘେରିବନ୍ଧକୁ ଆଟୋଲ୍ କୁହାଯାଏ ।

ପ୍ରତ୍ୟେକ ବାକ୍ୟାଶକୁ ଗୋଟିଏ/ଦୁଇଟି ଭୌଗୋଳିକ ପଦରେ ପ୍ରକାଶ କର ।

i. ପୃଥ‌ିବୀର ସର୍ବବୃହତ୍ ତଥା ଗଭୀରତମ ମହାସାଗର ।
Answer:
ପ୍ରଶାନ୍ତ ମହାସାଗର

ii. ସମଗ୍ର ପୃଥ‌ିବୀପୃଷ୍ଠର ପ୍ରାୟ ଏକ-ଷକ୍ଷାଂଶ ସ୍ଥାନ ଅଧିକାର କରିଥିବା ମହାସାଗର ।
Answer:
ଆଟଲାଣ୍ଟିକ୍ ମହାସାଗର

iii. ପୃଥିବୀର ତୃତୀୟ ବୃହତ୍ତମ ମହାସାଗର ।
Answer:
ଭାରତ ମହାସାଗର

iv. ପ୍ରଶାନ୍ତ ମହାସାଗର ସହ ସୁମେରୁ ମହାସାଗରକୁ ସଂଯୋଗ କରୁଥିବା ପ୍ରଣାଳୀ ।
Answer:
ବେରିଂ ପ୍ରଣାଳୀ

v. ପୃଥ‌ିବୀର ସବୁଠାରୁ ବଡ଼ ସାଗର ।
Answer:
ଦକ୍ଷିଣ ଚୀନ୍ ସାଗର

vi. ଭାରତ ମହାସାଗରରେ ଅବସ୍ଥିତ ଏକ ସାଗର ।
Answer:
ଆରବ ସାଗର

vii. ମାଛଧରା କେନ୍ଦ୍ର ଥିବା ମହାସାଗରୀୟ ଅଂଶ ।
Answer:
ମହୀସୋପାନ

viii. ଚନ୍ଦ୍ରର ସମ୍ମୁଖୀନ ହେଉଥିବା ପୃଥିବୀର ଜଳଭାଗ ଅଂଶର ବିପରୀତ ପାର୍ଶ୍ଵରେ ସୃଷ୍ଟ ଜୁଆର ।
Answer:
ପରୋକ୍ଷ ଜୁଆର

ix. ଇଉରୋପ ମହାଦେଶର ପଶ୍ଚିମ ଉପକୂଳରେ ପ୍ରବାହିତ ହେଉଥ‌ିବା ଉଷ୍ଣ ସ୍ରୋତର ଅନ୍ୟ ନାମ
Answer:
ଇଉରୋପର ଉଷ୍ଣ କମ୍ବଳ

x. ବୃତ୍ତାକାର ଖଣ୍ଡିତ ପ୍ରବାଳ ଘେରିବନ୍ଧ ।
Answer:
ଆଟୋଲ

xi. ଉତ୍ତର ଆମେରିକାର ପ୍ରସିଦ୍ଧ ମାଛଧରା କେନ୍ଦ୍ର ।
Answer:
ନିଉଫାଉଣ୍ଡଲ୍ୟାଣ୍ଡ

xii. ଭୂକମ୍ପ ଜନିତ ସୃଷ୍ଟ ସାମୁଦ୍ରିକ ତରଙ୍ଗ ।
Answer:
ସୁନାମି,

xiii. ଚନ୍ଦ୍ର ଓ ସୂର୍ଯ୍ୟର ମିଳିତ ଆକର୍ଷଣ ଫଳରେ ହେଉଥୁବା ଜୁଆର ।
Answer:
ପ୍ରବଳ ଜୁଆର,

xiv. ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦିଗରେ ସମୁଦ୍ର ଜଳର ନିରନ୍ତର ପ୍ରବାହ ।
Answer:
ସାମୁଦ୍ରିକ ସ୍ରୋତ

xv. ନିୟମିତ ବ୍ୟବଧାନରେ ଦିନକୁ ଦୁଇଥର ଲେଖାଏଁ ସମୁଦ୍ର ଜଳର ଉତ୍‌ଥାନ ଓ ପତନ ।
Answer:
ଜୁଆର-ଇଟ୍ଟା

xvi. ଉଚ୍ଚ ପର୍ବତ ଶିଖରରେ ଓ ମେରୁ ଅଞ୍ଚଳରେ ଜମି ରହିଥିବା ବରଫ ରାଶି ।
Answer:
ହିମଟୋପର

xvii. ପୃଥିବୀର ଗଭୀରତମ ଖାତ ।
Answer:
ମେରିଆନା ଖାତ

xvili. ଅଷ୍ଟ୍ରେଲିଆ ମହାଦେଶର ପୂର୍ବ ଉପକୂଳର ଅନତି ଦୂରରେ ସମୁଦ୍ରରେ ଥ‌ିବା ଏକ ପ୍ରବାଳ ବନ୍ଧ ।
Answer:
ଗ୍ରେଟ୍ ବାରିୟର ରିଫ୍

ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

i. ଉଷ୍ଠ ସ୍ରୋତ ____ ଅଞ୍ଚଳରୁ _____ ଅଞ୍ଚଳକୁ ପ୍ରବାହିତ ହୁଏ ।
Answer:
ବିଷୁବ, ମେରୁ

ii. ପ୍ରବାଳ ଏକ ଶଙ୍ଖ ଜାତୀୟ _____ ଜୀବ ।
Answer:
ସାମୁଦ୍ରିକ

iii. କ୍ୟୁରେସିଓ ସ୍ରୋତ ଏକ _____ ସ୍ରୋତ ଅଟେ ।
Answer:
ଉଷ୍ଣ

iv. ଲାବ୍ରାଡ଼ର ସ୍ରୋତ ଏକ _____ ସ୍ରୋତ ଅଟେ ।
Answer:
ଶୀତଳ

v. ଶୀତଳ ଓ ଉଷ୍ଣ ସ୍ରୋତର ମିଳନ ସ୍ଥଳରେ ____ ଜାତୀୟ ଉଭିଦ ବହୁ ପରିମାଣରେ ଦେଖାଯାଏ ।
Answer:
ପ୍ଳାଙ୍କଟନ୍

vi. ପୂର୍ଣ୍ଣିମା ଓ ଅମାବାସ୍ୟା ତିଥିରେ ସମୁଦ୍ରରେ ____ ଜୁଆର ସୃଷ୍ଟି ହୁଏ ।
Answer:
ଗୁରୁ

vii. ____ ପୃଥ‌ିବୀର ଗଭୀରତମ ଖାତ ଅଟେ ।
Answer:
ମେରିଆନା

viii. ଯେଉଁ ଜଳଭାଗର ତିନିପାର୍ଶ୍ବ ବିସ୍ତୀର୍ଣ୍ଣ ସ୍ଥଳଭାଗ ବେଷ୍ଟିତ, ତାହାକୁ _____ କୁହାଯାଏ ।
Answer:
ଉପସାଗର

ix. ସମୁଦ୍ରର _____ ଅଞ୍ଚଳରୁ ଖଣିଜତୈଳ, ପୋହଳା ଓ ମୁକ୍ତା ସଂଗ୍ରହ କରାଯାଏ ।
Answer:
ମହୀସୋପାନ

x. ବିଷୁବ ଅଞ୍ଚଳରେ ମହାସାଗର ଜଳର ତାପମାତ୍ରା _____ ଡିଗ୍ରୀ ସେଲ୍‌ସିୟସ୍‌ ଅଧିକ ଥାଏ ।
Answer:
୨୫

ଠିକ୍ ଉତ୍ତର ବାଛି ଲେଖ।

Question i.
ପୃଥ‌ିବୀର ସାଗରଗୁଡ଼ିକ ମଧ୍ୟରୁ କେଉଁଟି ସବୁଠାରୁ ବଡ଼ ?
(କ) ଲୋହିତ ସାଗର
(ଖ) ବେଜିଂ ସାଗର
(ଗ) ଦକ୍ଷିଣ ଚୀନ୍ ସାଗର
(ଘ) ଭୂମଧ୍ୟ ସାଗର
Answer:
ଦକ୍ଷିଣ ଚୀନ୍ ସାଗର

Question ii.
ପୃଥ‌ିବୀର ଗଭୀରତମ ସାମୁଦ୍ରିକ ଖାତ କେଉଁ ମହାସାଗରରେ ଅବସ୍ଥିତ ?
(କ) ପ୍ରଶାନ୍ତ
(ଖ) ଆଟ୍‌ଲାଣ୍ଟିକ୍
(ଗ) ଭାରତ
(ଘ) ସୁମେରୁ
Answer:
ପ୍ରଶାନ୍ତ

Question iii.
ପୃଥ‌ିବୀରେ ଉପଲବ୍‌ଧ ମଧୁର ଜଳର ସର୍ବାଧ‌ିକ ଭାଗ କେଉଁ ଠାରେ ରହିଅଛି ?
(କ) ଭୂତଳ ଜଳ
(ଖ) ନଦୀ
(ଗ) ହିମଟୋପର
(ଘ) ବାୟୁମଣ୍ଡଳ
Answer:
ହିମଟୋପର

Question iv.
ଜଳ ଦିବସ କେବେ ପାଳିତ ହୁଏ ?
(କ) ସେପ୍ଟେମ୍ବର ୨୩
(ଖ) ମାର୍ଚ୍ଚ ୨୨
(ଗ) ଅକ୍ଟୋବର ୨୪
(ଘ) ନଭେମ୍ବର ୧୫
Answer:
ମାର୍ଚ୍ଚ ମାସ ୨୨

Question v.
ପୃଥ‌ିବୀରେ ଶତକଡ଼ା କେତେ ଭାଗ ମଧୁର ଜଳ ଯାହା ନଦୀ, ହ୍ରଦ, ତୁଷାର ଓ ବରଫ ଆକାରରେ ରହିଛି ?
(କ) ୨.୬୯
(ଖ) ୨.୬୮
(ଗ) ୨.୬୭
(ଘ) ୨,୬୬
Answer:
୨.୬୯

Question vi.
ସାଗର ଓ ମହାସାଗରର ଜଳଭାଗ ପୃଥ‌ିବୀପୃଷ୍ଠର କ୍ଷେତ୍ରଫଳର ପ୍ରାୟ ଶତକଡ଼ା କେତେ ଭାଗ ଅଧିକାର କରିଛି ?
(କ) ୩
(ଖ) ୨୯
(ଗ) ୭୧
(ଘ) ୯୭
Answer:
୭୧ ଭାଗ

Question vii.
ଉଷ୍ଣସ୍ରୋତ ଓ ଶୀତଳ ସ୍ରୋତର ମିଳନ ସ୍ଥଳରେ କ’ଣ ସୃଷ୍ଟି ହୁଏ ?
(କ) କୁହୁଡ଼ି
(ଗ) ବର୍ଷା
(ଖ) ବାତ୍ଯା
(ଘ) ଜୁଆର
Answer:
କୁହୁଡ଼ି

Question viii.
ଭୂତଳ ଜଳର ଶତକଡ଼ା ପରିମାଣ କେତେ ?
(କ) ୨.୦
(ଖ) ୦.୬୮
(ଗ) ୦.୦୦୯
(ଘ) ୦.୦୦୧୯
Answer:
୦,୬୮

Question ix.
ପୃଥ‌ିବୀର ଜଳଭାଗ କେତେ କୋଟି ବର୍ଗ କିଲୋମିଟର ଅଞ୍ଚଳରେ ପରିବ୍ୟାପ୍ତ ?
(କ) ୨୬
(ଖ) ୩୬
(ଗ) ୪୬
(ଘ) ୬୩
Answer:
୩୬

Question x.
ହାଓ୍ବାଇ ଦ୍ଵୀପପୁଞ୍ଜ କେଉଁ ମହାସାଗରରେ ଅବସ୍ଥିତ ?
(କ) ପ୍ରଶାନ୍ତ
(ଖ) ଆଟଲାଣ୍ଟିକ୍
(ଗ) ଭାରତ
(ଘ) ସୁମେରୁ
Answer:
ପ୍ରଶାନ୍ତ ମହାସାଗର

Question xi.
ଭାରତ ମହାସାଗରରେ କେଉଁ ଦ୍ଵୀପ ଅବସ୍ଥିତ ?
(କ) ଗ୍ରୀଲ୍ୟାଣ୍ଡ
(ଖ) ନ୍ୟୁଜିଲ୍ୟାଣ୍ଡ
(ଗ) ମାଡାଗାସ୍କର
(ଘ) ଆଇସ୍‌ଲ୍ୟାଣ୍ଡ୍
Answer:
ମାଡାଗାସ୍କର

v

Question xii.
କ୍ଷେତ୍ରଫଳ ଦୃଷ୍ଟିରୁ ଆଟଲାଣ୍ଟିକ୍ ମହାସାଗର ପୃଥିବୀରେ କେଉଁ ସ୍ଥାନ ଗ୍ରହଣ କରିଛି ?
(କ) ଦ୍ବିତୀୟ
(ଖ) ତୃତୀୟ
(ଗ) ଚତୁର୍ଥ
(ଘ) ପଞ୍ଚମ
Answer:
ଦ୍ଵିତୀୟ

Question xiii.
ନି ଭସାଇବେରୀୟ ଦ୍ଵୀପ କେଉଁ ମହାସାଗରରେ ଅବସ୍ଥିତ ?
(କ) ସୁମେରୁ
(ଖ) ଆଟଲାଣ୍ଟିକ୍
(ଗ) ଆଟଲାଣ୍ଟିକ୍
(ଘ) ସୁମେରୁ
Answer:
ସୁମେରୁ

Question xiv.
ଲୋହିତ ସାଗର କେଉଁ ମହାସାଗରର ଅନ୍ତର୍ଗତ ?
(କ) ଭାରତ
(ଖ) କୁମେରୁ
(ଗ) ପ୍ରଶାନ୍ତ
(ଘ) ପ୍ରଶାନ୍ତ
Answer:
ଭାରତ

Question xv.
ଜାପାନ ସାଗର କେଉଁ ମହାସାଗରରେ ଅବସ୍ଥିତ ?
(କ) ପ୍ରଶାନ୍ତ
(ଗ) ଭାରତ
(ଖ) ଆଟଲାଣ୍ଟିକ୍
(ଘ) କୁମେରୁ
Answer:
ପ୍ରଶାନ୍ତ

Question xvi.
କାରିବିୟାନ୍ ସାଗର କେଉଁ ମହାସାଗରରେ ଅବସ୍ଥିତ ?
(କ) ପ୍ରଶାନ୍ତ
(ଖ) ଆଟଲାଣ୍ଟିକ୍
(ଗ) ଭାରତ
(ଘ) ସୁମେରୁ
Answer:
ଆଟଲାଣ୍ଟିକ୍

Question xvii.
ଆଟ୍‌ଲାଷ୍ଟିକ୍ ମହାସାଗରରେ କେଉଁ ସାଗର ଅବସ୍ଥିତ ?
(କ) ପୀତ ସାଗର
(ଖ) ଉତ୍ତର ସାଗର
(ଗ) ଭୂମଧ୍ୟ ସାଗର
(ଘ) ପାରସ୍ୟ ଉପସାଗର
Answer:
ଭୂମଧ୍ୟ ସାଗର

Question xviii.
ସମୁଦ୍ରକଳରେ ସୋହିୟମ୍ ସହିତ କେଉଁ ଲବଣର ମାତ୍ରା ଅଧିକ ?
(କ) କ୍ୟାସିୟମ୍
(ଖ) ମ୍ୟାଗ୍ନେସିୟମ୍
(ଗ) ଫସ୍‌ଫରସ୍
(ଘ) ସଲ୍ଫର
Answer:
ମ୍ୟାଗ୍ନେସିୟମ୍

Question xix.
୨୦୦୪ ମସିହା ନଭେମ୍ବର ୨୬ ତାରିଖରେ ସୁନାମିର ସୃଷ୍ଟି କେଉଁଠାରେ ହୋଇଥିଲା ?
(କ) ଜାପାନ
(ଖ) ସୁମାତ୍ରା
(ଘ) ଆଣ୍ଡାମାନ ନିକୋବର
(ଗ) ଜାଭା
Answer:
ସୁମାତ୍ରା

Question xx.
ଅଷ୍ଟ୍ରେଲିଆ ସ୍ରୋତ କେଉଁ ମହାସାଗର ଅନ୍ତର୍ଗତ ଏକ ଶୀତଳ ସ୍ରୋତ ?
(କ) ଭାରତ
(ଖ) ପ୍ରଶାନ୍ତ
(ଗ) ଆଟଲାଣ୍ଟିକ୍
(ଘ) ସୁମେରୁ
Answer:
ଭାରତ

Question xxi.
ପେରୁ ସ୍ରୋତର ଅନ୍ୟନାମ କ’ଣ ?
(କ) କାନାରିସ୍ରୋତ
(ଖ) ହମ୍‌ବୋଲ୍ଟସ୍ରୋତ
(ଗ) ବେଙ୍ଗୁଆଲାସ୍ରୋତ
(ଘ) ଫକ୍‌ଲାଣ୍ଡସ୍ରୋତ
Answer:
ହମ୍ ବୋଲ୍ଟ ଟ ସ୍ରୋତ

Question xxii.
ଉପସାଗରୀୟ ସ୍ରୋତ କେଉଁ ମହାସାଗରରେ ପ୍ରବାହିତ ?
(କ) ପ୍ରଶାନ୍ତ
(ଖ) ଆଟଲାଣ୍ଟିକ୍
(ଗ) ଭାରତ
(ଘ) ସୁମେରୁ
Answer:
ଆଟ୍‌ଲାଣ୍ଟିକ୍

Question xxiii.
କ୍ୟୁରୋସିଓ ସ୍ରୋତକୁ କେଉଁ ସ୍ରୋତ କୁହାଯାଏ ?
(କ) ବାହାମା
(ଗ) ଜାପାନ
(ଖ) ହମ୍‌ବୋଲ୍ଟ
(ଘ) ବ୍ରାଜିଲ
Answer:
ଜାପାନ

Question xxiv.
ଗ୍ରାଣ୍ଡ ବ୍ୟାଙ୍କ କେଉଁ ମହାଦେଶରେ ଅବସ୍ଥିତ ?
(କ) ଏସିଆ
(ଗ) ଉତ୍ତର ଆମେରିକା
(ଖ) ଇଉରୋପ
(ଘ) ଦକ୍ଷିଣ ଆମେରିକା
Answer:
ଇଉରୋପ

ବନ୍ଧନୀ ମଧ୍ଯରୁ ଉପଯୁକ୍ତ ଶବ୍ଦ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

1. ପୃଥ‌ିବୀ କ୍ଷେତ୍ରଫଳର ଶତକଡ଼ା ପ୍ରାୟ _____ ଭାଗ ଜଳଭାଗ । (୭୧, ୭୨, ୭୩, ୭୪)
Answer:
୭୧

2. ପୃଥ‌ିବୀ କ୍ଷେତ୍ରଫଳର ଶତକଡ଼ା ପ୍ରାୟ ____ ଭାଗ ସ୍ଥଳଭାଗ। (୨୬, ୨୭, ୨୮, ୨୯)
Answer:
୨୯

3. ପୃଥ‌ିବୀ ପୃଷ୍ଠରେ ସମୁଦାୟ ଜଳଭାଗର ପ୍ରାୟ ଶତକଡ଼ା _____ ଭାଗ ଜଳ ଲୁଣିଆ। (୯୭.୩, ୯୭.୪, ୯୭.୫, ୯୭.୬)
Answer:
୯୭.୩

4. ପୃଥ‌ିବୀ ପୃଷ୍ଠରେ ସମୁଦାୟ ଜଳଭାଗର ପ୍ରାୟ ଶତକଡ଼ା ____ ଭାଗ ଜଳ ମଧୁର। (୨.୬, ୨.୭, ୨.୮, ୨.୯)
Answer:
୨.୭

5. ପୃଥିବୀର ସର୍ବବୃହତ୍ ମହାସାଗର _____ ମହାସାଗର ଅଟେ | (ପ୍ରଶାନ୍ତ, ଆଟଲାଣ୍ଟିକ୍, ଭାରତ, ଉତ୍ତର)
Answer:
ପ୍ରଶାନ୍ତ

6. ପୃଥ‌ିବୀର ଦ୍ଵିତୀୟ ବୃହତ୍ତମ ମହାସାଗର ମହାସାଗର ____ ଅଟେ । (ପ୍ରଶାନ୍ତ, ଆଟଲାଣ୍ଟିକ, ଭାରତ, ଉତ୍ତର)
Answer:
ଆଟଲାଣ୍ଟିକ୍

7. _____ ପୃଥିବୀର ସବୁଠାରୁ ଛୋଟ ମହାସାଗର ଅଟେ । (ପ୍ରଶାନ୍ତ, ଆଟଲାଣ୍ଟିକ, ଭାରତ, ଉତ୍ତର)
Answer:
ଉତ୍ତର

8. ପୃଥ‌ିବୀର ଗଭୀରତମ ମେରିଆନା ଖାତ _____ ମହାସାଗରରେ ଅବସ୍ଥିତ । (ପ୍ରଶାନ୍ତ, ଆଟଲାଣ୍ଟିକ, ଭାରତ, ଉତ୍ତର)
Answer:
ପ୍ରଶାନ୍ତ

9. _____ ପୃଥିବୀର ତୃତୀୟ ବୃହତ୍ତମ ମହାସାଗର। (ପ୍ରଶାନ୍ତ, ଆଟଲାଣ୍ଟିକ, ଭାରତ, ଉତ୍ତର)
Answer:
ଭାରତ

10. ପୃଥ‌ିବୀର ସାଗର ମଧ୍ଯରୁ ______ ସବୁଠାରୁ ବଡ଼ । (ଜାପାନ ସାଗର, ଦକ୍ଷିଣ ଚୀନ୍ ସାଗର, ଆରବ ସାଗର, ପୀତ ସାଗର)
Answer:
ଦକ୍ଷିଣ ଚୀନ ସାଗର

11. ମହାସାଗରର _____ ଅଞ୍ଚଳରୁ ଖଣିଜତୈଳ, ପୋହଳା ଓ ମୁକ୍ତା ସଂଗ୍ରହ କରାଯାଏ। (ମହୀଜାଲୁ, ମହୀସୋପାନ, ସାଗରତଳ, ସାଗରଖାତ)
Answer:
ମହୀ ସୋପାନ

12. ସମୁଦ୍ର ତଳର ଅଧିକ ଗଡ଼ାଣିଆ ଅଞ୍ଚଳକୁ ______ କୁହାଯାଏ । (ମହୀସୋପାନ, ସାଗରତଳ, ମହୀଢାଲୁ, ସାଗରଖାତ)
Answer:
ମହୀଢାଲୁ

13. ଗୁରୁଜୁଆର _____ ତିଥ୍ୟରେ ହୋଇଥାଏ । (ପୂର୍ଣ୍ଣମୀ, ଅଷ୍ଟମୀ, ନବମୀ, ଦଶମୀ)
Answer:
ପୂର୍ଣ୍ଣମୀ

14. ଲଘୁଜୁଆର ______ ତିଥିରେ ହୋଇଥାଏ । (ପୂର୍ଣ୍ଣମୀ, ଅଷ୍ଟମୀ, ନବମୀ, ଦଶମୀ)
Answer:
ଅଷ୍ଟମୀ

15. ୟୁରୋପ ମହାଦେଶର ________ ଏକ ପ୍ରସିଦ୍ଧ ମାଛଧରା କେନ୍ଦ୍ର । (ଗ୍ରାଣ୍ଡବ୍ୟାଙ୍କ, ନିଉଫାଉଣ୍ଡଲ୍ୟାଣ୍ଡ, ଫିସରଲ୍ୟାଣ୍ଡ, ଫିନ୍‌ଲ୍ୟାଣ୍ଡ)
Answer:
ଗ୍ରାଣ୍ଡବ୍ୟାଙ୍କ

16. ଅଷ୍ଟ୍ରେଲିଆ ମହାଦେଶର _____ ଉପକୂଳରେ ‘ଏକ ବୃହତ୍ ପ୍ରବାଳ ବନ୍ଧର୍ବ ରହିଛି । (ଉତ୍ତର, ଦକ୍ଷିଣ, ପୂର୍ବ, ପଶ୍ଚିମ)
Answer:
ପୂର୍ବ

ସ୍ତମ୍ଭ ମିଳନ କର।

(i) ‘କ’ ସ୍ତମ୍ଭରେ ଥିବା ଶବ୍ଦକୁ ‘ଖ’ ସ୍ତମ୍ଭରେ ଥିବା ସମ୍ପର୍କିତ ଶବ୍ଦ ସହ ମିଳାଇ ଲେଖ ।

Answer:

(ii) ‘କ’ ସ୍ତମ୍ଭରେ ଥିବା ଶବ୍ଦକୁ ‘ଖ’ ସ୍ତମ୍ଭରେ ଥିବା ସମ୍ପର୍କିତ ଶବ୍ଦ ସହ ମିଳାଇ ଲେଖ ।

Answer:

(iii) ‘କ’ ସ୍ତମ୍ଭରେ ଥିବା ଶବ୍ଦକୁ ‘ଖ’ ସ୍ତମ୍ଭରେ ଥିବା ସମ୍ପର୍କିତ ଶବ୍ଦ ସହ ମିଳାଇ ଲେଖ ।

Answer:

ପ୍ରଥମ ଯୋଡ଼ିକୁ ଦେଖୁ ଦ୍ଵିତୀୟ ଯୋଡ଼ି ପୂରଣ କର।

1. ପ୍ରଶାନ୍ତ ମହାସାଗର : ସର୍ବବୃହତ୍ ମହାସାଗର :: ଆଟଲାଣ୍ଟିକ୍ ମହାସାଗର : _____।
Answer:
ଦ୍ଵିତୀୟ ବୃହତ୍ତମ ମହାସାଗର

2. ତିନିପାର୍ଶ୍ଵ ଜଳ : ଉପଦ୍ଵୀପ :: ତିନିପାର୍ଶ୍ଵ ବିସ୍ତୀର୍ଣ୍ଣ ସ୍ଥଳଭାଗ : _____।
Answer:
ଉପସାଗର

3. ଗୁରୁଜୁଆର : ପୂଶ୍ଚିମୀତିଥୁ :: ଲଘୁଜୁଆର : _____।
Answer:
ଅଷ୍ଟମୀତିଥୁ

4. ଇଷ୍ଠସ୍ରୋତ : ବାହାମାସ୍ରୋତ :: ଶୀତଳସ୍ରୋତ : _____।
Answer:
କାନାରିସ୍ରୋତ

5. ଇଉରୋପ ମହାଦେଶ : ଡଗରବ୍ୟାଙ୍କ :: ଉତ୍ତର ଆମେରିକା : _____।
Answer:
ନିଉଫାଉଣ୍ଡଲ୍ୟାଣ୍ଡ

Odisha State Board BSE Odisha 7th Class Hindi Solutions Chapter 4 बस यात्रा का अनुभव Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Hindi Solutions Chapter 4 बस यात्रा का अनुभव

1. निम्नलिखित प्रश्नों के उत्तर दीजिए :

(i) विद्यालय के बच्चे क्या देखने भुवनेश्वर गए?
उत्तर:
विद्यालय के बच्चे राज्य संग्रहालय और ताराघर देखने भुवनेश्वर गए।

(ii) प्रधानशिक्षिका ने बच्चों से क्या कहा ?
उत्तर:
प्रधानशिक्षिका ने बच्चों से कहो, “‘बच्चों ! तुम सब लाइन बनाकर खड़े हो जाआ । फिर एक एक करके बस के अंदर जाकर बैठो । देखो, हल्ला मत करना। गुरुजी और गुरुमाँ तुम्हारे बैठने की व्यवस्था कर देंगे।” गाड़ी चलते समय खिड़की के बाहर हाथ या सिर मत निकालना।’

(iii) बच्चे जब बस में बैठ गए, तब शिक्षक ने क्या कहा ?
उत्तर:
बच्चे जब बस में बैठगए, तब शिक्षक ने उनसे कहा, “तुम नाश्ता कर लो। केले के छिलके, बिस्किट के खाली पैकेट, पत्ते या कागज खिड़की से बाहर मत फेंकना। हम दूसरों को परेशान होने का काम नहीं करेंगे।”

(iv) बस चलते समय क्यों नहीं चिल्लाना चाहिए?
उत्तर:
बस चलते समय नहीं चिल्लाना चाहिए। ऐसा करने से ड्राइवर का ध्यान बँट जाने का डर रहता है ।

(v) बैस में ‘प्राथमिक उपचार पेटिका’ रखना क्यों आवश्यक है ?
उत्तर:
बस में ‘प्राथमिक उपचार पेटिका’ रखना आवश्यक है। क्योंकि दुर्घटना के समय घायल यात्रियों के प्राथमिक उपचार के लिए इसमें कुछ दवाइयाँ रखी जाती हैं।

(vi) ट्रैफिक पोस्ट पर अलग-अलग रंग की बत्तियाँ क्या सूचित करती हैं ?
उत्तर:
ट्रैफिक पोस्ट पर अलग-अलग तीनों रंग की बत्तियाँ होती हैं । पीली बत्ती गाड़ी की गति धीमी करने को, लाल बत्ती गाड़ी रोकने के लिए और हरी बत्ती गाड़ी आगे बढ़ाने को सूचित करती हैं ।

(vii) ट्रैफिक पोस्ट पर गाड़ी रोकते वक्त इंजन को क्यों बंद कर देना चाहिए ?
उत्तर:
ट्रैफिक पोस्ट पर गाड़ी रोकते वक्त इंजन को बंद कर देना चाहिए, क्योंकि इससे इंधन की बचन होती है और धुआँ न होने से प्रदूषण नहीं फैलता ।

(viii) जेब्रा क्रासिंग से लोगों की क्या सुविधा होती है ?
उत्तर:
जेब्रा क्रासिंग के पास गाड़ी रुकते समय पैदल चलते लोग रास्ता पार करते हैं ।

(ix) बच्चों ने संग्रहालय में क्या-क्या देखा ?
उत्तर:
बच्चों ने संग्रहालय में प्राचीन मूर्तियाँ, कलाकृतियाँ ताड़ के पत्ते की पोथियों, पुराने जमाने के सिक्के तरह-तरह के पुराने वस्त्र, आभूषण, अस्त्र-शस्त्र आदि देखे।

(x) युवक की मोटर साइकिल ट्रक से क्यों टकराई ?
उत्तर:
युवक मोटर साइकिल चलाते समय मोबाइल पर बात कर रहा था और अनमना था । इसलिए सामने खड़े ट्रक से उसकी मोटर साइकिल टकरा गई ।

2. निम्नलिखित प्रश्नों के उत्तर एक-एक वाक्य में दीजिए?

(i) ओड़िशा की राजधानी का नाम क्या है ?
उत्तर:
ओड़िशा की राजधानी का नाम भुवनेश्वर है ।

(ii) बच्चे क्या लेकर बस के पास पहुँचे ?
उत्तर:
बच्चे नाश्ता लेकर बस के पास पहुँचे।

(iii) ‘प्राथमिक उपचार पेटिका’ पर कौन-सा चिह्न रहता है ?
उत्तर:
‘प्राथमिक उपचार पेटिका’ पर रेडक्रॉस चिह्न रहता है ।

(iv) ड्राइवर ने कहाँ पर इंजन बंद कर दिया ?
उत्तर:
ड्राइवर ने ट्रैफिक पोस्ट पर इंजन बंद कर दिया ।

(v) ट्रैफिक पोस्ट पर कितने रंगों की बत्तियाँ रहती हैं ?
उत्तर:
ट्रैफिक पोस्ट पर तीन रंगों की बत्तियाँ रहती हैं।

(vi) सड़क पर काली-सफेद धारबाली पट्टी को क्या कहते हैं ?
उत्तर:
सड़क पर काली-सफेद धारबाली पट्टी को जेब्राक्रासिंग कहते हैं ।

(vii) संग्रहालय के पास किसने बच्चों को रास्ता पार कराया ?
उत्तर:
संग्रहालय के पास एक ट्रैफिक पुलिस ने बच्चों को रास्ता पार कराया ।

(viii) सड़क के दोनों तरफ थोड़ी ऊँचाई वाले रास्ते को क्या कहते हैं ?
उत्तर:
सड़क के दोनों तरफ थोड़ी ऊँचाई वाले रास्ते को फूटपाथ कहते हैं ।

(ix) भुवनेश्वर के ताराघर का नाम क्या है ?
उत्तर:
भुवनेश्वर के ताराघर का नाम पठाणि सांमत ताराघर है।

(x) युवक की मोदर साइकिल किससे टकराई ?
उत्तर:
युवक की मोटर साइकिल एक ट्रक से टकराई । भाषा-कार्य :

3. उदाहरण के अनुसार बदलिए :
बच्चा – बच्चे, खिड़की – खिड़कियाँ
उत्तर:

• डिब्बा – डिब्ले
• गाड़ी – गाड़ियाँ
• तारा – तारे
• बत्ती – बत्तियाँ
• नाश्ता – नाश्ते
• नारी – नारियाँ
• केला – केले
• राजधानी – राजधानियाँ

4. उदाहरण के अनुसार बदलिए :
छात्र – छात्रा
उत्तर:
शिक्षक – शिक्षिका
शिष्य – शिष्या
लेखक – लेखिका
पाठक – पाठिका

5. ‘क’ स्तम्भ के साथ ‘ख’ स्तभ्भ का मिलान कीजिए:
‘क’ स्तम्भ — ‘ख’ स्तम्भ
काली — रंग
पीली — बस
धीमी — पट्टी
बड़ी — बत्ती
तीन — गति
उत्तर:
‘क’ स्तम्भ — ‘ख’ स्तम्भ
काली — पट्टी
पीली — बत्ती
धीमी — गति
बड़ी — बस
तीन — रंग

6. कोष्ठक में दिए गए परसर्गों से खाली जगहों को भरिए :
( से, का, को, की, ने )

(i) भुवनेश्वर ओड़िशा ………… राजधानी है ।
उत्तर: की

(ii) गाड़ी की गति ४० कि.मी. ………… अधिक नहीं होनी चाहएि ।
उत्तर: से

(iii) इससे दुर्घटना ………… खतरा नहीं रहता ।
उत्तर: का

(iv) शिक्षक ………… कहा ।
उत्तर: ने

(v) बच्चों ………… भूख लग रही थी।
उत्तर: को

अन्य परीक्षोपयोगी प्रश्नोत्तर

1. निम्नलिखित प्रश्नों के उत्तर दीजिए :

(i) किस विद्यालय के बच्चे भुवनेश्वर गए ?
उत्तर:
बंगीदा उच्च प्राथमिक विद्यालय के बच्चे भुवनेश्वर गए।

(ii) बच्चे शिक्षा-भ्रमण पर कहाँ गए ?
उत्तर:
बच्चे शिक्षा-भ्रमण पर भुवनेश्वर गए।

(iii) बोर्ड़ पर लिखा ‘४०’ क्या संकेत दे रहा था?
उत्तर:
बोर्ड़ पर लिखा ‘४०’ संकेत दे रहा था कि वहाँ गाड़ी की गति प्रति घंटा ४० कि.मी. से अधिक नहीं होनी चाहिए।

(iv) दृष्टिहीन व्यक्ति को किन्होंने रास्ता पार कराया?
उत्तर:
दृष्टिहीन व्यक्ति को कुछ बच्चों ने रास्ता पार कराया।

(v) सड़क पर क्यों भीड़ थी ?
उत्तर:
सड़क पर एक दुर्घटना हो गई थी, इसलिए वहाँ भीड़ थी ।

(vi) एक बुजुर्ग व्यक्ति ने क्या बताया ?
उत्तर:
एक बुजुर्ग व्यक्ति ने बताया, “आजकल के नौजवान किसकी सुनते हैं क्या?”

(vii) घायल युवक के सिर से क्यों खून बह रहा था?
उत्तर:
घायल युवक ने मोटर साइकिल चलाते समय हेलमेट नहीं पहना था । इसलिए सिर पर चोट लगने से खून बह रहा था।

2. सही कथनों के सामने (✓) का और गलत कथनों का सामने (✗) का निशान लगाइए :

(i) कटक ओड़िशा की राजधानी है । (✗)
(ii) बंगीदा पुरी जिले में है । (✗)
(iii) एक छात्रा ने जानना चाहा कि बस में रेडक्रास निशानवाला बक्सा क्यों लटक रहा है । (✓)
(iv) जेब्रा क्रासिंग पर लोग पैदल रास्ता पार करते हैं। (✓)
(v) एक दृष्टिहीन व्यक्ति लाठी का सहारा लेकर रास्ता पार हुआ । (✗)
(vi) ताराघर का नाम है पठाणि सांमत ताराघर । (✓)
(vii) भुवनेश्वर में राज्य संग्रहालय है । (✓)

3. निम्नलिखित प्रश्नों के सही विकल्प उत्तर पर (✓) का निशान लगाइए :

(i) छात्र-छात्राएँ कब शिक्षा-भ्रमण पर निकले ?
(क) रविवार को
(ख) सोमवार को
(ग) शनिवार को
(घ) बुधवार को
उत्तर:
(क) रविवार को

(ii) बच्चों को केले के छिलके का क्या करना था ?
(क) बाहर फेंकना था
(ख) डिब्बे में रखना था
(ग) गाय को दे देना था
(घ) सीट के नीचे रखना था
उत्तर:
(ख) डिब्ले में रखना था

(iii) ड्राइवर ने क्या पहना था ?
(क) कमीज
(ख) टोपी
(ग) जूते
(घ) सीट बेल्ट
उत्तर:
(घ) सीट बेल्ट

(iv) संग्रहालय से निकलते-निकलते कितने बज गए ?
(क) एक
(ख) तीन
(ग) दो
(घ) चार
उत्तर:
(ग) दो

(v) कौन-सी बत्ती देखकर ड्राइवर ने बस रोक दी?
(क) लाल
(ख) हरी
(ग) नीली
(घ) पीली
उत्तर:
(क) लाल

4. शब्दों को उनके अर्थ से मिलाडए :

घायल – प्रांत
खतरा – भ्रमण
छोर – विपदा
सैर – पास
नजदीक – आहत
उत्तर:
घायल – आहत
खतरा – विपदा
छोर – प्रांत
सैर – भ्रमण
नजदीक – पास

पाठ का सारांशः

खोरधा जिले के बंगीदा गाँव में एक उच्च प्राथमिक विद्यालय है। एक बार प्रधान शिक्षिका ने विद्यालय के छात्रछात्राओं को लेकर ओड़िशा की राजधानी भुवनेश्वर शैक्षिक भ्रमण पर जाने की योजना बनाई ।

रविवार को बस आ पहुँची । बच्चे लाइन बनाकर बस की भीतर जाकर बैठे । प्रधान शिक्षिका ने बच्चों को सलाह दी कि बस के भीतर हल्ला न करें और बस चलते समय खिड़की से बाहर हाथ न निकालें। बस में जब विद्यार्थियों ने नाश्ता करना शुरू किया, तब एक शिक्षक ने कहा कि बिस्कुट का खाली पैकेट, केले के छिलके, पत्ते या कागज बाहर न फेंककर अपने-अपने डिब्ये में रख लें, खिड़की से बाहर न फेंकें ।

विद्यार्थियों ने देखा कि बस के ड्राइवर ने छाती पर सीट बेल्ट बाँध रखी है । शिक्षक ने समझा दिया कि दुर्घटना के समय ज्यादा चोट न आने के लिए ड्राइवर बेल्ट बाँधता है । शिक्षक ने यह भी बताया कि बस में एक प्राथमिक उपचार पेटिका रहती है। इसमें रेडक्रॉस का निशान रहता है। दुर्घटना के समय घायल यात्रियों का प्राथमिक उपचार करने के लिए उसमें कुछ जरूरी दवाइयाँ रखी जाती हैं ।

शिक्षक ने कहा कि ड्राइवर से बस तेज चलाने का अनुरोध नहीं करना चाहिए। बस में चिल्लाना भी नहीं चाहिए। इससे ड्राइवर का ध्यान बँट जाता है । आगे सड़क पर एक बोर्ड पर ‘ 40 ‘ संख्या की ओर दिखाकर शिक्षक ने बताया कि यह ड्राइवर को बताने के लिए लिखा गया है कि गाड़ी की एक घंटे में गति चालीस किलोमीटर से अधिक नहीं होनी चाहिए ।

उसी समय पीछे से दूसरी बस का ड्राइवर हर्न बजाने लगा। वह ओवरटेक करके आगे जाना चाहता था । बच्चों की बस के ड्राइवर ने अपनी बस बाई तरफ करके दाहिने हाथ के इशारे से उसे आगे बढ़ जाने का इशारा किया ।

बस खण्डगिरि के पास ट्रैफिक पोस्ट पर रुकी । शिक्षक ने समझाया कि चौराहे पर ट्रैफिक पोस्ट वाहनों का नियंत्रण करने के लिए है । सामने लाल बत्ती जल रही है । यह गाड़ी रोकने का निर्देश है । यहाँ तीन बत्तियाँ जलती हैं । पीली बत्ती गाड़ी की गति धीमी करने के लिए, लाल बत्ती गाड़ी रोक देने के लिए और हरी बत्ती गाड़ी आगे बढ़ाने के लिए संकेत करती हैं। ट्रैफिक पोस्ट पर गाड़ी खड़ी रहते समय इंजन बंद कर देना चाहिए ।

इससे इंधन की बचत होती है और धुएँ का प्रदूषण नहीं होता । शिक्षक ने सामने काली और सफेद धारवाली पट्टियों पर लोगों को रास्ता पार करते हुए देखकर कहा कि इसे जेब्रा क्रॉसिंग कहते हैं। जहाँ जेब्रा क्रासिंग नहीं होती, वहाँ लोग दोनों दरफ की गाड़ियों पर ध्यान देकर रास्ता पार करते हैं ।

बच्चों को रास्ता पार करके खाना खाने के लिए एक भोजनालय में जाना था,। एक ट्रैफिक पुलिस ने कुछ देर के लिए दोनों तरफ से आन-जाने वाली गाड़ियाँ रोक कर बच्चों को रास्ता पार कराया। कुछ बच्चों ने एक दृष्टिहीन व्यक्ति का हाथ पकड़ कर उसे रास्ता पार करा दिया ।

बच्चे पठाणि सामन्त ताराघर के पास पहुँचे तो शिक्षक ने उनसे फूटपाथ पर चलने को कहा। सड़क के दोनों तरफ पैदल चलने के लिए थोड़ी ऊँची रास्ते बनाए गए थे, उन्हें फूटपाथ कहते हैं । बच्चों ने ताराघर में ग्रहनक्षत्रों की गतिविधियाँ देखीं।

लौटते समय बच्चों ने देखा कि सामने एक ट्रक के पास एक मोटर साइकिल पड़ी है । लोगों ने बताया कि मोबाइल पर बात करते हुए एक युवक मोटर साइकिल चला रह्मा था और अनमना हो गया था । उसकी मोटर साइकिल खड़े रहे एक ट्रक से टकरा गई। उसने हेलमेट भी नहीं पहना था । उसके सिर से बहुत खून बह गया है । उसे एंबुलैन्स से अस्पताल भेज दिया गया है । यह सुनकर सब दुखी हुए । शिक्षक ने बच्चों को समझाया कि हमें हमेशा सावधान रहना चाहिए। ऐसा करने से हम बहुत-सी दुर्घटनाओं  से बच सकेंगे ।

ସାରାଂଶ:

ଖୋର୍ଦ୍ଧା ଜିଲ୍ଲାର ବଙ୍ଗିଦା ଗାଁରେ ଗୋଟିଏ ଉଚ୍ଚ ପ୍ରାଥମିକ ବିଦ୍ୟାଳୟ ଅଛି। ଥରେ ପ୍ରଧାନଶିକ୍ଷୟତ୍ରୀ ବିଦ୍ୟାଳୟର ଛାତ୍ର- ଛାତ୍ରୀମାନଙ୍କୁ ନେଇ ଓଡ଼ିଶାର ରାଜଧାନୀ ଭୁବନେଶ୍ଵରକୁ ଶିକ୍ଷା ପରିଭ୍ରମଣରେ ଯିବା ପାଇଁ ଯୋଜନା କଲେ। ରବିବାର ଦିନ ବସ୍ ଆସି ପହଞ୍ଚିଲା। ପିଲାମାନେ ଲାଇନ୍‌ରେ ଯାଇ ବସ୍ ଭିତରେ ବସିଲେ । ପ୍ରଧାନଶିକ୍ଷୟିତ୍ରୀ ପିଲାମାନଙ୍କୁ କହିଲେ ଯେ ବସ୍ ଭିତରେ କେହି ପାଟିତୁଣ୍ଡ କରିବେନି । ବସ୍ ଋଲୁଥିବା ସମୟରେ କେହି ବାହାରକୁ ହାତ ବାହାର କରିବେ ନାହିଁ। ବସ୍‌ରେ ପିଲାମାନେ ଜଳଖୁଆ ଖାଇବା ଆରମ୍ଭ କରିବା ବେଳେ ଶିକ୍ଷକ କହିଲେ, କେହି ବାହାରକୁ ବିସ୍କୁଟର ଖାଲି ପ୍ୟାକେଟ୍, କଦଳୀ ଚୋପା, ପତ୍ର କି କାଗଜ ପକାଇବେ ନାହିଁ। ସେଗୁଡ଼ିକୁ ନିଜ ନିଜ ଡବାରେ ପୂରେଇ ରଖୁଦେବେ।

ପିଲାମାନେ ଦେଖ‌ିଲେ ଯେ ବସ୍‌ର ଡ୍ରାଇଭର ଛାତିରେ ସିଗ୍‌ବେଲ୍ସ ବାନ୍ଧିଛନ୍ତି । ଶିକ୍ଷକ ବୁଝାଇଦେଲେ ଯେ ଦୁର୍ଘଟଣା ସମୟରେ ଅଧ୍ବକ ଆଘାତ ନ ଲାଗିବା ପାଇଁ ଡ୍ରାଇଭର ତାଙ୍କ ଛାତିରେ ସିବେଲ୍ଟ ବାନ୍ଧିଛନ୍ତି। ଶିକ୍ଷକ ବସ୍‌ରେ ଥିବା ପ୍ରାଥମିକ ଉପଚାର ପେଟିକା ବିଷୟରେ ମଧ୍ୟ ପିଲାମାନଙ୍କୁ ବୁଝାଇଦେଲେ । ସେ କହିଲେ ଏଥୁରେ ରେଡ଼କ୍ରସ ଚିହ୍ନ ରହିଛି। ଦୁର୍ଘଟଣା ଘଟିଗଲେ ସେହି ସମୟରେ ଆହତ ଲୋକଙ୍କ ପ୍ରାଥମିକ ଚିକିତ୍ସା ନିମିତ୍ତ ସେଥ‌ିରେ ଜରୁରୀ ଔଷଧପତ୍ର ରଖାଯାଇଥାଏ।

ଶିକ୍ଷକ ପିଲାମାନଙ୍କୁ କହିଲେ ଯେ କେହି ଡ୍ରାଇଭରଙ୍କୁ ଜୋର୍‌ରେ ଗାଡ଼ି ଚଳାଇବାକୁ ଅନୁରୋଧ କରିବା ଠିକ୍ ନୁହେଁ । ବସ୍‌ରେ ଚିତ୍କାର ବି କରିବା ଉଚିତ ନୁହେଁ । ତାହାଦ୍ଵାରା ଡ୍ରାଇଭରଙ୍କ ଏକାଗ୍ରତା ଭଙ୍ଗ ହୋଇଯାଏ। ସଡ଼କ କଡ଼ରେ ‘ଚାଳିଶ’ ଲେଖାଯାଇଥିବା ଗୋଟିଏ ବୋର୍ଡ଼ ଆଡ଼କୁ ହାତ ଦେଖାଇ ଶିକ୍ଷକ କହିଲେ ଡ୍ରାଇଭରଙ୍କୁ ସୂଚାଇ ଦେବାକୁ ଏହା ଲେଖାଯାଇଛି । ଏହା ଦେଖୁ ସେ ଗାଡ଼ିର ଘଣ୍ଟା ପ୍ରତି ଗତି ସ୍ଖଳିଶ କିଲୋମିଟରରୁ ଅଧିକ କରିବେ ନାହିଁ ।

ଏହି ସମୟରେ ପଛରୁ ଆଉ ଗୋଟିଏ ବସ୍‌ର ଡ୍ରାଇଭର ହର୍ଣ୍ଣ ବଜାଇବାକୁ ଲାଗିଲେ । ସେ ଓଭରଟେକ୍ କରି ଆଗକୁ ଯିବାକୁ ଋହୁଁଥିଲେ। ତେଣୁ ପିଲାମାନେ ଯାଉଥୁବା ବସ୍‌ର ଡ୍ରାଇଭର ନିଜ ବସ୍‌କୁ ଟିକିଏ ବାମ ପଟକୁ ନେଇ ଡାହାଣ ହାତରେ ଅନ୍ୟ ବସ୍‌ର ଡ୍ରାଇଭରଙ୍କୁ ଆଗକୁ ଯିବାକୁ ଇସାରା ଦେଲେ। ବସ୍ ଖଣ୍ଡଗିରିର ଗୋଟିଏ ଟ୍ରାଫିକ୍ ପୋଷ୍ଟ ପାଖରେ ଅଟକିଲା। ଶିକ୍ଷକ ବୁଝାଇଦେଲେ ଯେ ଛକ ପାଖରେ ଏହି ଟ୍ରାଫିକ୍ ପୋଷ୍ଟ ଯାନବାହନଗୁଡ଼ିକୁ ନିୟନ୍ତ୍ରଣ କରାଯିବା ପାଇଁ ରହିଛି । ଦେଖ ! ଆଗରେ ଲାଲବତୀ ଜଳୁଛି । ଏହା ଗାଡ଼ି ଅଟକିବା ପାଇଁ ନିର୍ଦ୍ଦେଶ ଦେଉଛି । ଏଠାରେ ତିନୋଟି ରଙ୍ଗର ବତୀ ଜଳେ। ହଳଦିଆବତୀ

ଗାଡ଼ିର ଗତି କମେଇବା ପାଇଁ, ଲାଲ୍‌ବତୀ ଗାଡ଼ି ଅଟକାଇବା ପାଇଁ ଓ ସବୁଜବତୀ ଗାଡ଼ିକୁ ଆଗକୁ ନେବା ପାଇଁ ସଙ୍କେତ ଦିଅନ୍ତି । ଟ୍ରାଫିକ୍ ପୋଷ୍ଟ ପାଖରେ ଗାଡ଼ି ଅଟକିଥିବା ସମୟରେ ଇଞ୍ଜିନ୍ ବନ୍ଦ କରିଦେବା ଉଚିତ । ଏହାଦ୍ଵାରା ଇନ୍ଧନ ସଞ୍ଚୟ ହୁଏ ଓ ଧୂଆଁର ପ୍ରଦୂଷଣରୁ ରକ୍ଷା ମିଳେ।
ଆଗରେ ରାସ୍ତାର କଳା-ଧଳା ପଟିଥିବା ସ୍ଥାନରେ ଲୋକେ ରାସ୍ତା ପାରି ହେଉଥୁବାର ଦେଖୁ ଶିକ୍ଷକ କହିଲେ, ଏହାକୁ ଜେବ୍ରାକୁସିଙ୍ଗ୍ କହନ୍ତି । ଗାଡ଼ି ଅଟକିଥିବା ସମୟରେ ଲୋକେ ଏହି ଜେବ୍ରାକ୍ରାସିଙ୍ଗ୍‌ରେ ରାସ୍ତା ପାର ହୁଅନ୍ତି । ଯେଉଁ ସ୍ଥାନରେ ଜେବ୍ରାକୁସିଙ୍ଗ୍ ନଥାଏ, ସେଠାରେ ଲୋକେ ଦୁଇ ପାଖର ଗାଡ଼ିକୁ ଚାହିଁ ରାସ୍ତା ପାର ହୁଅନ୍ତି।

ଆଗରେ ରାସ୍ତାର କଳା-ଧଳା ପଟିଥିବା ସ୍ଥାନରେ ଲୋକେ ରାସ୍ତା ପାରି ହେଉଥୁବାର ଦେଖୁ ଶିକ୍ଷକ କହିଲେ, ଏହାକୁ ଜେବ୍ରାକୁସିଙ୍ଗ୍ କହନ୍ତି । ଗାଡ଼ି ଅଟକିଥିବା ସମୟରେ ଲୋକେ ଏହି ଜେବ୍ରାକ୍ରାସିଙ୍ଗ୍‌ରେ ରାସ୍ତା ପାର ହୁଅନ୍ତି । ଯେଉଁ ସ୍ଥାନରେ ଜେବ୍ରାକୁସିଙ୍ଗ୍ ନଥାଏ, ସେଠାରେ ଲୋକେ ଦୁଇ ପାଖର ଗାଡ଼ିକୁ ଚାହିଁ ରାସ୍ତା ପାର ହୁଅନ୍ତି। . ଏହି ସମୟରେ ବସ୍ ସଂଗ୍ରହାଳୟ ପାଖରେ ପହଞ୍ଚିଲା । ପିଲାମାନେ ସଂଗ୍ରହାଳୟରେ ପ୍ରାଚୀନ ମୂର୍ତ୍ତି, କଳାକୃତି, ତାଳପତ୍ରର ପୋଥ, ପୁରୁଣା ମୁଦ୍ରା, ପୁରୁଣା ବସ୍ତ୍ର, ଆଭୂଷଣ ଓ ଅସ୍ତ୍ରଶସ୍ତ୍ର ଦେଖୁ ଖୁସି ହେଲେ।

ପିଲାମାନଙ୍କର ରାସ୍ତା ପାର ହୋଇ ଖାଇବା ପାଇଁ ଗୋଟିଏ ଭୋଜନାଳୟକୁ ଯିବାର ଥିଲା। ଜଣେ ଟ୍ରାଫିକ୍ ପୋଲିସ୍ କିଛି ସମୟ ପାଇଁ ଦୁଇ ପାଖରୁ ଯିବାଆସିବା କରୁଥିବା ଗାଡ଼ିକୁ ଅଟକାଇ ପିଲାମାନଙ୍କୁ ରାସ୍ତା ପାର କରାଇଦେଲେ। କିଛି ପିଲା ଜଣେ ଦୃଷ୍ଟିହୀନ ବ୍ୟକ୍ତିଙ୍କ ହାତଧରି ତାଙ୍କୁ ରାସ୍ତା ପାର କରାଇଦେଲେ। ପିଲାମାନେ ପଠାଣି ସାମନ୍ତ ପ୍ଲାନେଟୋରିୟମ୍ ପାଖରେ ପହଞ୍ଚିବା ପରେ ଶିକ୍ଷକ ସେମାନଙ୍କୁ ଫୁଟ୍‌ପାଥ ଉପରେ ଋଲି କରି ଯିବାକୁ କହିଲେ। ସଡ଼କର ଉଭୟ ପାର୍ଶ୍ଵରେ ଲୋକେ ପାଦରେ ଋଲିଗଲି ଯିବା ପାଇଁ ଟିକିଏ ଉଚ୍ଚ ରାସ୍ତା ତିଆରି କରାଯାଇଥାଏ।

ଏହାକୁ ଫୁଟ୍‌ପାଥ କୁହାଯାଏ। ପିଲାମାନେ ପ୍ଲାନେଟୋରିୟମ୍‌ରେ ଗ୍ରହ-ନକ୍ଷତ୍ରଙ୍କ ଗତିବିଧ‌ି ବିଷୟ ଦେଖ‌ିଲେ। ଫେରିବା ସମୟରେ ପିଲାମାନେ ଗୋଟିଏ ଟ୍ରକ୍ ପାଖରେ ମୋଟର ସାଇକେଲଟିଏ ପଡ଼ିଥିବାର ଦେଖ‌ିଲେ। ଲୋକମାନେ କହିଲେ ଯେ ଜଣେ ଯୁବକ ମୋବାଇଲରେ କଥାବାର୍ତ୍ତା ହୋଇ ହୋଇ ମୋଟର ସାଇକେଲ ଚଳାଇ ଯାଉଥିଲେ ।

ସେ ଅନ୍ୟମନସ୍କ ହୋଇପଡ଼ିଥିଲେ । ତାଙ୍କ ମୋଟର ସାଇକେଲ୍ ଠିଆହୋଇଥୁବା ଟ୍ରକ୍ ପଛରେ ଧକ୍କା ହୋଇଗଲା । ସେ ଯୁବକ ହେଲ୍‌ମେଟ୍ ପିନ୍ଧି ନଥଲେ । ତାଙ୍କ ମୁଣ୍ଡରୁ ବହୁତ ରକ୍ତ ବହୁଥିଲା। ତାଙ୍କୁ ଆମ୍ବୁଲାନ୍ସରେ ଡାକ୍ତରଖାନାକୁ ପଠାଇ ଦିଆଗଲା ।ଏକଥା ଶୁଣି ସମସ୍ତେ ଦୁଃଖୀ ହେଲେ। ଶିକ୍ଷକ ପିଲାମାନଙ୍କୁ ବୁଝାଇଦେଲେ ଯେ ଆମେ ସବୁବେଳେ ସାବଧାନ ରହିବା ଉଚିତ। ଏପରି କଲେ ଆମେ ଅନେକ ଦୁର୍ଘଟଣାରୁ ରକ୍ଷା ପାଇପାରିବା।

शब्दार्थ :

Odisha State Board BSE Odisha 7th Class Hindi Solutions Chapter 3 अपना-अपना काम करो Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Hindi Solutions Chapter 3 अपना-अपना काम करो

पाठ्यपुस्तक के प्रश्नोत्तर

1. निम्नलिखित प्रश्नों के उत्तर दीजिए :

(i) आदमी ने क्या सोचा ?
उत्तर:
आदमी ने सोचा कि अभी मौसम अच्छा है, जल्दी से कामनिपटा लूँगा ।

(ii) उसने क्या पहना था ?
उत्तर:
उसने कमर में धोती बाँधी थी। बदन पर कुर्ता पहना था और गले में गमछा लपेट लिया था ।

(iii) सूरज और हवा में क्यों झगड़ा हुआ ?
उत्तर:
सूरज और हवा दोनों अपने को बड़ा बता रहे थे। सूरज का कहना था कि मेरे बिना संसार मर जाएगा। हवा कह रही थी कि मेरे न होने पर संसार साँस नहीं ले पाएगा। दोनों एक दूसरे के दोष भी ढूँढ़ रहे थे। इसलिए दोनों में झगड़ा होनेलगा।

(iv) सूरज ने हवा से क्या कहा ?
उत्तर:
सूरज ने हवा से कहा कि तुम्हारी तो ठाट निराली है, कभी धीर चलती हो तो कभी तेज। कभी तो एकदम चूप हो जाती हो, जरा भी हिलती-डुलती नहीं हो। इस तरह तुम सबको परेशान क्यों करती रहती हो ?

(v) पथिक ने उन्हें क्या उत्तर दिया ?
उत्तर:
पथिक ने उनसे कहा कि तुम अपनी हैसियत को समझो। इस संसार में कोई छोटा या बड़ा नहीं है । हम सिर और पाँव में से किसी को छोटा या बड़ा नहीं कह सकते क्योंकि सिर से हम सोचते हैं, तथा पाँव से चलते हैं । इसलिए आपस में झगड़ा बंद करके अपना-अपना काम करो।

(vi) हमें क्या करना चाहिए ?
उत्तर:
हमें न तो अपने ऊपर घमंड करना चाहिए और न ही दूसरों के दोष़ ढूँढ़ने चाहिए। बस अपना-अपना काम ईमानदारी से करते रहना चाहिए । हमें याद रखना कि इस संसार में वही बड़ा है जो दूसरों को परेशान नहीं करता है ।

2. इन प्रश्नों के उत्तर एक एक वाक्य में दीजिए :

(i) आदमी कहाँ जा रहा था ?
उत्तर:
आदमी पासवाले गाँव में जरूरी काम निपटाने जा रहा था।

(ii) वह किसे देखकर खुश हुआ ?
उत्तर:
वह सूरज के लाल-लाल से गोले को देखकर खुश हुआ ।

(iii) कौन झगड़ा सुन रहा था ?
उत्तर:
सूरज और हवा दोनों का झगड़ा पथिक सुन रहा था।

(iv) गुस्से में हवा की हालत कैसी हो रही थी ?
उत्तर:
गुस्से में हवा सनसना रही थी।

(v) तैश में आकर सूरज कैसा हो गया ?
उत्तर:
तैश में आकर सूरज बहुत गरम हो गया।

(vi) वे पथिक से क्या पूछते हैं ?
उत्तर:
वे पथिक से पूछते हैं कि दोनों में से कौन अच्छा है और कौन बड़ा है ।

(vii) कौन सबसे अच्छा होता है ?
उत्तर:
जो किसी को भी नहीं सताता, वह सबसे अच्छा होता है ।

3. कोष्ठक में से सही शब्द सुनकर भरिए ।
(आपस्म में, दुनिया, सिर, सुहाना-सा, लाल-लालसा, औकात)

(i) ………… सवेरा ।
(ii) सूरज और हवा ………… झगड़ रहे थे ।
(iii) ………… सा सूरज का गोला।
(iv) इतना तपते हो कि ………… तप जाती है ।
(v) पथिक ने कहा, “तुम अपनी-अपनी ………… समझो।”
(vi) चलने के लिए पाँव चाहिए और सोचने को ………… I
उत्तर:
(i) सुहाना-सा
(ii) आपस में
(iii) लाल-लाल-सा
(iv) दुनिया
(v) औकात
(vi) सिर

भाषा-कार्य :
संज्ञा की विशेषता बताने वाले शब्द को विशेषण कहते हैं।
जैसे – लाल सूरज । सूरज संज्ञा है । लाल उसकी विशेषता बताते है ।

4. नीचे कुछ विशेषण और कुछ संज्ञाएँ एक साथ आये हैं। उन्हें अलग-अलग कीजिए :
अच्छी, हवा, काफी, खुशी, मंद, पवन, अपना काम, थोड़ी, दूर, लाल गोला
उत्तर:
विशेषण — संज्ञा
अच्छी — हवा
काफी — खुशी
मंद — पवन
अपना — काम
थोड़ी — दूर
लाल — गोला

5. ‘क’ स्तम्भ के शब्दों को ‘ख’ स्तम्भ के पर्यायवाची शब्दों के साथ मिलान कीजिए :
‘क’ स्तम्भ — ‘ख’ स्तम्भ
तैश — योग्यता
जरूरी — आश्चर्यजनक
औकात — बहुत
निराली — आवश्यक
काफी — गुस्सा
उत्तर:
‘क’ स्तम्भ — ‘ख’ स्तम्भ
तैश — गुस्सा
जरूरी — आवश्यक
औकात — योग्यता
निराली — आश्चर्यजनक
काफी — बहुत

6. निम्नलिखित शब्दों को वाक्यों में प्रयोग कीजिए :
तैश, परेशान, दुनिया, काफी, निराली, औकात, खुश
उत्तर:
तैश – निधि की जली-कटी बातें सुनकर अनुराधा तैश में आ गई।
परेशान – वे लोग अपनी गरीबी से परेशान हैं ।
दुनिया – इस दुनिया में ईमानदार लोगों की कमी नहीं है।
काफी – यात्री के पास काफी सामान था ।
निराली – इन्द्र धनुष की छटा बहुत निराली थी ।
औकात – अपनी औकात में रह्मोगे तो हमेशा खुश रहोगे।
खुश – परीक्षा में प्रथम आने पर अनीता बहुत खुश हो रही थी।

7. निम्नलिखित शब्दों की मात्रागत अशुद्धियों को सुधार कर लिखिए :
सुरज, शांस, परेसान, तूम, खूस
उत्तर:

• सुरज – सूरज शांस – साँस
• परेसान – परेशान तूम – तुम
• खूस – खुश तूम – तुम

अन्य परीक्षोपयोगी प्रश्नोत्तर

1. निम्नलिखित प्रश्नों के उत्तर दीजिए :

(i) आदमी घर सै कब निकला ?
उत्तर:
आदमी सबेरे-सबेरे ही घर से निकला। उस समय मौसम बहुत अच्छा था।

(ii) ‘लेकिन उसे तो चलना ही था न !’ इस कथन का क्या अर्थ है ?
उत्तर:
यह कथन आदमी की लगन को दर्शाता है । वह लाल-लाल सूरज को देखकर खुश हो रहा था, . परंतु उसे अपना काम पूरा करना था। अतः वह चल पड़ा।

(iii) हवा को सूरज में कौन-सा दोष नज़र आया ?
उत्तर:
हवा को सूरज का बहुत तपना अखरता था। सूरज के अधिक तपने के कारण लोग उसके जल्दी डूबने की इच्छा करने लगते हैं ।

(iv) आप कैसे कह सकते हैं सिर और पाँव में से कोई भी बड़ा या छोटा नहीं है ।
उत्तर:
सिर से हम सोचते हैं और पाँव से चलते हैं । हरेक काम का अपना-अपना महत्व है । इसलिए दोनों में से कोई भी छोटा या बड़ा नहीं है ।

2. सही कथनों के सामने (✓) का और गलत कथनों के सामने (✗) का निशान लगाइए :

(i) आदमी जरूरी काम से शहर जा रहा था । (✗)
(ii) वह तेजी से डग भरता हुआ चल रहा था । (✓)
(iii) मंद पवन के चलने से आदमी को खुशी नहीं हो रही थी। (✗)
(iv) सूरज सोच रहा ता कि संसार उसके बिना मर जाएगा। (✓)
(v) सूरज को हवा की ठाट निराली लग रही थी (✓)
(v) आदमी ने सूरज और हवा के झगड़े का निपटारा नहीं किया । (✗)

3. निम्नलिखित प्रश्नों के सही विकल्प उत्तर पर (✓) का निशान लगाइए ：

(i) आदमी घर से किस समय निकला ।
(क) शाम को
(ख) सुबह
(ग) दोपहर को
(घ) रात को
उत्तर:
(ख) सुबह

(ii) आपस में कौन झगड़ रह थे ？
(क) हवा और पवन
(ख) नदी और समुद्र
(ग) सूरंज और हवा
(घ) सूरज और बादल
उत्तर:
(क) सूरज के

(iii) किसके तपने से दुनिया तप जाती है ？
(क) सूरज के
(ख) हवा के
(ग) पहाड़ के
(घ) पानी के
उत्तर:
(क) सूरज के

(iv) सोचने का काम कौन करता है ?
(क) सिर
(ख) आदमी
(ग) जानवर
(घ) वैज्ञानिक
उत्तर:
(क) सिर

(v) सबसे अच्छा कौन होता है ?
(क) किसान
(ख) चित्रकार
(ग) धीरे-धीरे चलने वाला
(घ) किसी को न सताने वाला
उत्तर:
(घ) किसी को न सताने वाला

भाषा-कार्य :

4. दिए गए वाक्यों के रिक्त स्थानों में सही कारकचिह्न भरिए।
ने, का, में, से, कर

(i) वह पढ़ाई ………… होशियार था।
(ii) एक आदमी ………… उसे सड़क ………… पढ़ते देखा ।
(iii) एक गाँव ………… एक किसान रहता था।
(iv) रमेश घर ………… निकल पड़ा।
(v) तानसेन ………… संगीत आज भी अमर है ।
(vi) वहाँ राजा ………… सिपाही आ धमका ।
उत्तर:
(i) में
(ii) ने, पर
(iii) में
(iv) से
(v) का
(vi) का

5. दिए गए शब्दों के दो-दो पर्यायवाची शब्द लिखिए:
दिन, घर, आदमी, पथिक, दुनिया, पाँव
उत्तर:

• दिन – दिवस, घर
• घर – गृह, सदन
• आदमी – मनुष्य, नर
• पथिक- यात्री, बटोही
• दुनिया – संसार, जग
• पाँव – पग, पैर

6. शब्दों को उनके अर्थ से मिलाइए :
जरूरी — मार्ग
फौरन — क्रोध
रास्ता — आवश्यक
खुश — प्रात:
गुस्सा — प्रसन्न
सवेरा — तुरंत
उत्तर:
जरूरी — आवश्यक
फौरन — तुरंत
रास्ता — मार्ग
खुश — प्रसन्न
गुस्सा — क्रोध
सवेरा — प्रात:

पाठ का सारांश:

एक दिन सवेरे एक आदमी पासवाले गाँव में जरूरी काम निपटाने घर से निकला। मौसम अच्छा था वह लंबे-लंबे डग भरते हुए चला। कमर में धोती बाँधी, कुर्ता पहना और गले में गामछा लपेटा ।

सुहावनी हवा चल रही थी। जल्दी ही पूरव दिशा में सूरज निकल आया । आदमी खुश होकर अपनी राह चला जा रहा था । इतने में आदमी को ऐसा लगा कि सूरज और हवा आपस में झगड़ रहे हैं । सूरज ने कहा कि मेरे बिना संसार मर जाता । हवा कह रही थी कि मेरे बिना तो साँस लेना ही कठिन हो जाता। सूरूज ने हवा पर कभी तेज तो कभी धीमा चलकर सब को परेशान करने का आरोप लगाया । हवा ने सूरज पर संसार को तपा देने का दोष लगाया ।

पथिक उनकी बातें सुनते हुए अपनी राह चला जा रहा था। इधर हवा गुस्से में सनसना रही थी और सूरज भी क्रोध में काफी गर्म हो गया था । दोनों ने पथिक से पूछकर इसका फैसला करना तय किया कि दोनों में से कौन बड़ा है ।

पथिक ने दोनों की बातें सुनकर कहा – “संसार में छोटा-बड़ा कोई नहीं है । सबकी अपनी अपनी अहमियत है । कोई यह नहीं कह सकता कि पाँव बड़ा या सिर । इसलिए झगड़ा छोड़कर अपना-अपना काम करो । संसार में वही बड़ा है जो किसी को परेशान नहीं करता है । दोनों ने पथिक का कहना माना। फिर वे खुश होकर अपने-अपने रास्ते पर चल पड़े ।

ସାରାଂଶ:

ଦିନେ ଜଣେ ଲୋକ ପାଖ ଗାଁରେ ଥିବା ଗୋଟିଏ ଜରୁରୀ କାମରେ ଘର ବାହାରିପଡ଼ିଲା। ପାଗ ଭଲ ଥିଲା। ସେ ଲମ୍ବା-ଲମ୍ବା ପାଦ ପକେ ଆଗକୁ ଋଲିଲା। ସେ ଧୋତୀ ପିନ୍ଧିଥିଲା, କୁ । ପିନ୍ଧିଥିଲା, ବେକରେ ଗାମୁଛା ପକାଇଥଲା। ବଢ଼ିଆ ପବନ ବହୁଥିଲା । ଶୀଘ୍ର ପୂର୍ବ ଦିଗରୁ ସୂର୍ଯ୍ୟ ବି ଉଇଁ ଆସିଲା। ଲୋକଟି ମନଖୁସିରେ ବାଟ ଋଲୁଥିଲା। ଏତିକିବେଳେ ଲୋକଟି ଅନୁଭବ କଲା, ସତେ ଯେପରି ସୂର୍ଯ୍ୟ ଓ ପବନ ନିଜ ନିଜ ଭିତରେ କଳି କରୁଛନ୍ତି । ସୂର୍ଯ୍ୟ କହିଲା ଯେ ମୋ ବିନା ସଂସାର ମରିଯାଆନ୍ତା।

ପବନ କହୁଥିଲା ଯେ ମୋ ବିନା ନିଃଶ୍ୱାସ-ପ୍ରଶ୍ଵାସ ନେବା କଷ୍ଟକର ହୋଇପଡ଼ନ୍ତା। ପବନ କେତେବେଳେ ଜୋରରେ ବହେ, ତ କେତେବେଳେ ଧୀର ଗତିରେ ବହି ସମସ୍ତଙ୍କୁ ବ୍ୟସ୍ତ କରିଦେଉଛି ବୋଲି ସୂର୍ଯ୍ୟ ତା’ ଉପରେ ଦୋଷାରୋପ କଲା। ସୂର୍ଯ୍ୟ ସଂସାରକୁ ଉ ପ୍ତ କରିଦେଉଛି ବୋଲି ପବନ ତାକୁ ଦୋଷ ଦେଲା। ବାଟୋଇଟି ସେମାନଙ୍କ କଥା ଶୁଣି ଶୁଣି ବାଟ ଋଲୁଥିଲା।

ଏଷର ପବନ ରାଗରେ ସାଇଁ ସାଇଁ ବହୁଥୁଲା ତ ତେଣେ ସୂର୍ଯ୍ୟ ବି ରାଗରେ ବହୁତ ଗରମ ହୋଇଯାଇଥିଲା। ସେମାନେ ଦୁହେଁ ସ୍ଥିର କଲେ ଯେ ବାଟୋଇକୁ ପଚାରି ଗୋଟିଏ ନିଷ୍ପ କରିନେବେ ଯେ ସେ ଦୁହିଁଙ୍କ ମଧ୍ୟରେ ବଡ଼ କିଏ। ବାଟୋଇଟି ଦୁହିଁଙ୍କ କଥା ଶୁଣି କହିଲା – ‘ସଂସାରରେ କେହି ଛୋଟ-ବଡ଼ ନୁହନ୍ତି, ସମସ୍ତଙ୍କର ନିଜ-ନିଜର ସୀମା ଅଛି। କେହି କହିପାରିବେନି କି ପାଦ ବଡ଼ କି ମୁଣ୍ଡ ବଡ଼ । ତେଣୁ କଳି ତକରାଳ ଛାଡ଼ି ନିଜ ନିଜ କାମ କର। ଯିଏ ଅନ୍ୟକୁ ହଇରାଣ କରେ ନାହିଁ, ସେ ହିଁ ଦୁନିଆରେ ବଡ଼।’’ ଦୁହେଁ ବାଟୋଇଟିର କଥା ମାନିଲେ ଓ ଖୁସି ହୋଇ ନିଜ ନିଜର କାମରେ ବାହାରିପଡ଼ିଲେ।

शब्दार्थ :

Odisha State Board BSE Odisha 7th Class Hindi Solutions Chapter 2 यह मेरा वतन (कविता) Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Hindi Solutions Chapter 2 यह मेरा वतन (कविता)

पाठ्यपुस्तक के प्रश्नोत्तर

प्रश्न 1.
इन प्रश्नों के उत्तर दीजिए :

(i) हमारे देश का परिवेश कैसा है ?
उत्तर:
हमारे देश का परिवेश बहुत सुंदर है । ऊपर खुला आसमान है । यहाँ कोमल पवन बहता है । सुनहरी धूप के चमकने के कारण मौसम सुहावना होता है। रात के समय आसमान में चाँद और तारे चमकते रहते हैं ।

(ii) भारत की संतानों के क्या-क्या गुण है ?
उत्तर:
भारत की संतानें धैर्यवान, वीर और सुंदर हैं । उनके मन में जरा भी अभिमान नहीं है ।

(iii) हम किन-किन चीजों का दान देने चाहें ?
उत्तर:
हम शांति, मैत्री और प्यार का दान देने चाहें ।

(iv) दूसरे मानवों के साथ हमारा बर्ताव कैसा हो ?
उत्तर:
दूसरे मानवों के साथ हमारे व्यवहार में अपनापन होना चाहिए। पूरी दुनिया के लोगों को हमें अपने ही परिवार का एक सदस्य मानना चाहिए।

(v) खतरे में हम क्या करें ?
उत्तर:
यदि हमारे देश के गौरव पर खतरा मँडरा रहा हो तो हमें अपने प्राणों का बलिदान कर देना चाहिए ।

(vi) मातृभूमि के लिए हम क्या करें ?
उत्तर:
मातृभूमि के हित के लिए हमें बार-बार जन्म लेने अपने जीवन की कुर्बानी भी देनी पड़े तो हमें संकोच नहीं करना चाहिए।

प्रश्न 2.
(i) ‘भारत देश – मेरा वतन’ का क्या अर्थ है ?
उत्तर:
‘भारत देश – मेरा वतन’ का अर्थ है – मेरा अपना देश भारत। यह पंक्ति देश के साथ गहरे लगाव का प्रतीक है । कवयित्री को यह कहते हुए गौरव का अनुभव हो रहा है कि भारत उनका अपना देश है ।

(ii) ‘परवाह नहीं हो मान अपमान’ का तात्पर्य समझाइए।
उत्तर:
इस पंक्ति के माध्यम से कवयित्री भारत की संतानों को उनके कर्त्तव्य का स्मरण करा रही हैं । हमें अपना कर्त्तव्य हमेशा याद रखना चाहिए। कर्त्तव्य करते समय चाहे सम्मान मिले या अपमान इसकी जरा भी चिंता नहीं करनी चाहिए।

(iii) ‘निडर तत्पर अचल-चट्टान’ का मतलब क्या है?
उत्तर:
हमें निडर अर्थात् बिना डरे साहसपूर्वक अपना कार्य करते रहना चाहिए । जो व्यक्ति चट्टान की तरह अटल है यानी जिसका निश्चय दृढ़ है, जीवन में सफलता उसे ही मिलती है ।

प्रश्न 3.
शिक्षक प्रत्येक छात्र और छात्रा को मौखिक रूप से अपनी मातृभूमि भारतवर्ष की कुछ विशेषताएँ बताने को प्रेरित करें
उत्तर:
इस कार्य को शिक्षक छात्र-छात्राओं से स्वयं करवाएँ।

प्रश्न 4. भाषाकार्य :
विशेषण – संज्ञा
जैसे – मुक्त — गगन
ऐसे शब्दों को छाँटिए । नीचे लिखिए।
उत्तर:

• मृदुल – पवन
• सुनहरी – धूप
• वीर – जवान
• अचल – चट्टान
• अनमोल – प्राण

प्रश्न 5.
निम्नलिखित वाक्यों को पढ़िए :
यह भारत देश है ।
हमारे मन में अभिमान नहीं है ।
भारत – एक देश का नाम है ।
देश – सभी देशों की जाति या वर्ग का नाम है ।
अभिमान – एक भाव का नाम है ।
नाम को बतानेवाले शब्द को संज्ञा कहते हैं।

प्रश्न 6.
निम्नलिखित शब्दों में से संज्ञा शब्दों को छाँटिए :
हम, हिमालय, गगन, शांति, पत्थर, सामने, नया, लकड़ी, राकेश, उजला ।
उत्तर:
संज्ञा शब्द -हिमालय, गगन, शांति, पत्थर, लकड़ी, राकेश ।

प्रश्न 7.
सही मिलान कीजिए :
मुक्त गगन है — अचल चट्टान
हम धीर वीर — अनमोल प्राण
न्योछावर कर दें — मृदुल पवन
निडर तत्पर — दिव्य संतान
उत्तर:
मुक्त गगन है — मृदुल पवन
हम धीर वीर — दिव्य संतान
न्योछावर कर दें — अनमोल प्राण
निडर तत्पर — अचल चट्टान

अन्य परीक्षोपयोगी प्रश्नोत्तर

1. इन प्रश्नों के उत्तर दीजिए :

(i) हमारे देश का मौसम कैसा है ?
उत्तर:
ॠ्मारे देश का मौसम सुह्लवना है ।

(ii) किनके मन में तनिक भी अभिमान नहीं है ?
उत्तर:
भारत की संतानों के मन में तनिक भी अभिमान नहीं है।

(iii) ‘अचल चट्टान’ किसका प्रतीक है ? कविता के आधार पर समझाइए ।
उत्तर:
अचल चट्टान मानसिक दृढ़ता और बुलंद इरादे का प्रतीक है । कविता में कहा गया है कि भारत के लोग अचल चट्टान की तरह अपने कर्त्तव्य पथ पर अडिग हैं ।

(iv) कविता ‘यह मेरा वतन’ का मूलभाव अपने शब्दों में लिखिए ।
उत्तर:
प्रस्तुत कविता देशभक्ति की भावना पर आधारित है । उसमें भारत के परिवेश, भारत की संतानों के गुण और देशहित में बलिदान होने की उनकी भावना का वर्णन किया गया है । भारत के लोग पूरी दुनिया को अपना कुटुंब मानते है और दुनिया को शांति, मित्रता और प्रेम का दान देते हैं ।

2. कविता की निम्नलिखित पंक्तियों का अर्थ स्पष्ट कीजिए:

(i) हर मानव को अपना मान दुनिया को बना कुटुम्ब समान
उत्तर:
ऊपर लिखी पंक्तियों में कवयित्री ने भारत की संतानों से कहा है कि हरेक आदमी को अपूना मानो । यह भाव ही पूरी दुनिया को एक कुटुंब या परिवार बना देगा। इस प्रकार इन पंक्तियों में विश्ववंधुत्व की भावना पर बल दिया गया है ।

(ii) ‘निडर तत्पर अचल-चट्टान’ का मतलब क्या है?
उत्तर:
हमें निडर अर्थात् बिना डरे साहसपूर्वक अपना कार्य करते रहना चाहिए। जो व्यक्ति चट्टान की तरह अटल है यानी जिसका निश्चय दृढ़ है, जीवन में सफलता उसे ही मिलती है।

3. निम्नलिखित प्रश्नों के सही विकल्प उत्तर पर (✓) का निशान लगाइए :

(i) भारत देश हमारा क्या है ?
(क) वर्तमान
(ख) वतन
(ग) परिवार
(घ) भविष्य
उत्तर:
(ख) वतन

(ii) कविता में भारत की संतानों के किन गुण का उल्लेख नहीं किया गया है ?
(क) धीरता
(ख) वीरता
(ग) गंभीरता
(घ) दिव्यता
उत्तर:
(ग) गंभीरता

(iii) हमें किसकी परवाह नहीं है ?
(क) धन की
(ख) मान-अपमान की
(ग) जीवन की
(घ) शांति की
उत्तर:
(ख) मान-अपमान की

(iv) हम हर मानब को क्या मानें ?
(क) प्रराया
(ख) गरीब
(ग) अमीर
(घ) अपना
उत्तर:
(घ) अपना

(v) देशवासी किसके हित बारंबार जिएँ और मरें ?
(क) मातृभूमि के
(ख) पड़ोसी वेन
(ग) पूरी दुनिया के
(घ) प्रकृति के
उत्तर:
(क) मातृभूमि के

4. दिए गए वाक्यों में संज्ञा शब्दों के नीचे रेखा खींचिए:

(i) भारत मेरा वतन है ।
(ii) हमारे देश की संतानें वीर हैं ।
(iii) पूरी दुनिया एक परिवार के समान है ।
(iv) मातृभूमि की सुरक्षा करना हमारा कर्त्तव्य है ।
उत्तर:
(i) भारत मेरा वतन है ।
(ii) हमारे देश की संतानें वीर हैं ।
(iii) पूरी दुनिया एक परिवार के समान है ।
(iv) मातुभूमि की सुरक्षा करना हमारा कर्त्तव्य है ।

5. बच्चो, संज्ञा या सर्वनाम की विशेषता बनानेवाले शब्दों को विशेषण कहते हैं। जिन शब्दों की विशेषता बताई जाती है, उन्हें विशेष्य कहते हैं । जैसे ‘अचल चट्टान’ में ‘अचल’ विशेषण और ‘चट्टान’ विशेष्य है।
दिए गए वाक्यों में से विशेषण और विशेष्य को छाँटकर लिखिए ।
(i) भारत एक विशाल देश है ।
(ii) हमारे वीर सिपाही युद्ध में डटे रहे ।
(iii) वह बालक ईमानदार है ।
(iv) शाम को मृदुल पवन बह रहा है ।
(v) उस तरफ गहरी खाई है ।
उत्तर:
विशेषण — विशेष्य
विशाल — देश
वीर — सिपाही
ईमानदार — बालक
मृदुल — पवन
गहरी — खाई

6. निम्नलिखित अशुद्ध शब्दों के शुद्ध रूप लिखिए :
बतन, मुकत, मैती, कुटूम्ब, प्रान
उत्तर:
वतन, मुक्त, मैत्री, कुटुम्ब, प्राण

1. मुक्त गगन है, मुदुल पवन
धूप सुनहरी सुहाना मौसम,
चमकता चाँद तारे चमचम
यह भारत देश, यह मेरा वतन !

प्रसंग : प्रस्तुत पंक्तियाँ हमारी पाठ्य पुस्तक ‘मेरी हिन्दी पुस्तक-२’ की कविता ‘यह मेरा वतन’ से ली गई हैं। इन पंक्तियों में कवयित्री स्मरप्रिया मिश्र ने हमारे देश भारत के प्रकृति प्रदत्त स्वरूप का वर्णन किया है ।

व्याख्या : कवयित्री कहती हैं कि हमारे देश का आसमान खुला है तथा यहाँ कोमल व मंद हवा बहती है । सुनहरी धूप होने के कारण मौसम सुहावना रहता है । रात में आसमान में चाँद और तारे चमकते हैं । ऐसा है हमार देश और यही मेरा वतन है ।

ପ୍ରସଙ୍ଗ : ଉକ୍ତ ପଦ୍ୟାଶ ‘ମେରୀ ହିନ୍ଦୀ ପୁସ୍ତକ– ୨ ’ର ‘ୟହ ମେରା‘ ସ୍ଵତନ’ କବିତାରୁ ନିଆଯାଇଛି। ଏଥ‌ିରେ କବୟିତ୍ରୀ ସ୍ମରପ୍ରିୟା ମିଶ୍ର ଆମ ଦେଶ ଭାରତର ପ୍ରାକୃତିକ ରୂପର ବର୍ଣ୍ଣନା କରିଛନ୍ତି ।

ବ୍ୟାଖ୍ୟା : କବୟିତ୍ରୀ କହିଛନ୍ତି ଯେ ଆମ ଦେଶର ଆକାଶ ଉନ୍ମୁକ୍ତ। ଏଠାରେ ଧୀର ପବନ ବହେ । ସୁନେଲି ଖରାରେ ଋତୁ ମନୋମୁଗ୍ଧକର। ରାତିରେ ଚନ୍ଦ୍ର ଓ ତାରା ଝଲସି ଉଠନ୍ତି । ଏହିଭଳି ଦେଶ ଭାରତ ମୋର ଜନ୍ମଭୂମି।

2. हम धीर वीर दिव्य संतान
नहीं मन में तनिक अभिमान,
परवाह नहीं मान अपमान
दें शांति मैत्री प्यार का दान ।

प्रसंग : प्रसुत पंक्तियाँ हमारी पाठ्य पुस्तक ‘मेरी हिन्दी पुस्तक-२’ की कविता ‘यह मेरा वतन’ से ली गई हैं । इन पंक्तियों में भारत के नागरिकों की विशेषताओं का वर्णन किया गया है ।

व्याख्या : भारत के लोग धैर्यवान, वीर और दैवी गुणों से युक्त हैं । यहाँ के निवासियों में थोड़ा भी अभिमान नहीं है । उन्हें मान-अपमान की फिक्र भी नहीं है । हम लोग पूरी दुनिया को शांति, मित्रता और प्यार का दान दे रह हैं ।

ପ୍ରସଙ୍ଗ : ଶଂସିତ ପଦ୍ୟାଶ ଆମ ପାଠ୍ୟ ପୁସ୍ତକ ‘ମେରୀ ହିନ୍ଦୀ ପୁସ୍ତକ’ର ‘ୟହ ମେରା ୱତନ’ କବିତାରୁ ଉଦ୍ଧୃତ ହୋଇଛି। ଏଥବରେ ଭାରତର ନାଗରିକଙ୍କ ବୈଶିଷ୍ଟ୍ୟ ବର୍ଣ୍ଣିତ ହୋଇଛି।

ବ୍ୟାଖ୍ୟା : ଭାରତୀୟ ବ୍ୟକ୍ତି ଧୈର୍ଯ୍ୟବାନ, ବୀର ଓ ଦୈବୀ ଗୁଣସମ୍ପନ୍ନ। ସେମାନଙ୍କର ସାମାନ୍ୟ ଗର୍ବ ମଧ୍ୟ ନାହିଁ । ସେମାନେ ମାନ-ଅପମାନକୁ ଖାତିର କରନ୍ତି ନାହିଁ । ଆମେ ସମଗ୍ର ବିଶ୍ଵକୁ ଶାନ୍ତି, ମୈତ୍ରୀ ଓ ପ୍ରେମର ଦାନ କରି ଆସିଛୁ।

3. हर मानव को अपना मान
दुनिया को बना कुटुम्ब समान,
निडर तत्पर अचल चट्टान
बनाते चलें नये कीर्त्तिमान ।

प्रसंग : प्रस्तुत पंक्तियाँ हमारी पाठ्य पुस्तक ‘मेरी हिन्दी पुस्तक-२’ की कविता ‘यह मेरा वतन’ से ली गई हैं । इन पंक्तियों में भारत के लोगों के मैत्री-भाव और कर्मठता का वर्णन किया गया है ।

व्याख्या : हमारे देश के लोग प्रत्येक मनुष्य को अपना मानते हैं, इसलिए उनके मन में यह भाव है कि पूरी दुनिया के लोग एक ही परिवार के सदस्य हैं । हम लोग साहसी और अपने श्रम से॰त्पर रहने वाले हैं । हमारे अंदर चट्टान की सी दुढ़ता है । हम लोग नए-नए कीर्तिमान बना रह हैं । अर्थात् जीवन के हर क्षेत्र में हम लोग कामयाब हो रहे हैं ।

ପ୍ରସଙ୍ଗ : ଶଂସିତ ପଦ୍ୟାଶ ଆମ ପାଠ୍ୟ ପୁସ୍ତକ ‘ମେରୀ ହିନ୍ଦୀ ପୁସ୍ତକ’ର ‘ୟହ ମେରା ୱତନ’ କବିତାରୁ ଉଦ୍ଧୃତ ହୋଇଛି। ଏଥିରେ ଭାରତୀୟଙ୍କ ମୈତ୍ରୀ ଭାବ ଓ କର୍ମଠତା ସମ୍ବନ୍ଧରେ ବର୍ଣ୍ଣନା କରାଯାଇଛି ।

ବ୍ୟାଖ୍ୟା : ଆମ ଦେଶର ବ୍ୟକ୍ତି ପ୍ରତ୍ୟେକ ମନୁଷ୍ୟକୁ ନିଜର ମନେ କରନ୍ତି । ସେଥପାଇଁ ସେମାନଙ୍କ ମନରେ ସମଗ୍ର ବିଶ୍ଵବାସୀଙ୍କୁ ଗୋଟିଏ ପରିବାରର ସଦସ୍ୟ ରୂପେ ମନେ କରିବାର ଭାବ ରହିଥାଏ। ଆମେ ସାହସୀ, ଶ୍ରମରେ ତତ୍ପର। ଆମ ମନ ଭିତରେ ପଥରଭଳି ଦୃଢ଼ତା ରହିଛି। ଆମେ ନୂଆ ନୂଆ କୀ’ମାନ ପ୍ରତିଷ୍ଠା କରୁଛୁ ଅର୍ଥାତ୍ ଜୀବନର ସବୁ କ୍ଷେତ୍ରରେ ଆମେ ସଫଳତା ଅର୍ଜନ କରୁଛୁ।

4. खतरे में हो’गर अपनी आन
न्योछावर कर दें अनमोल प्राण,
मातृभूमि के हित मेरे यार !
जीएँ हम मरें भी बारम्बार ।

प्रसंग : प्रस्तुत पंक्तियाँ हमारी पाठ्य पुस्तक ‘मेरी हिन्दी पुस्तक-२’ की कविता ‘यह मेरा वतन’ से ली गई हैं। इन पंक्तियों में देश के लोगों के मन में देशहित के लिए वलिदान होने की भावना प्रकट की गई है ।

व्याख्या : यदि किसी समय हमारे देश पर खतरा मँडरा रहा हो, या देश का मान-सम्मान दाँव पर लगा हुआ हो तो भारतवासी अपनी कीमती जानें देश के लिए कुर्बान कर देते हैं । कवयित्री कहती हैं कि अपने देश की भलाई के लिए बारबार जीना और मरना पड़े तो भी हमें स्वीकार है ।

ପ୍ରସଙ୍ଗ : ଶଂସିତ ପଦ୍ୟାଶ ଆମ ପାଠ୍ୟ ପୁସ୍ତକ ‘ମେରୀ ହିନ୍ଦୀ ପୁସ୍ତକ’ର ‘ୟହ ମେରା ୱତନ’ କବିତାରୁ ଉଦ୍ଧୃତ ହୋଇଛି । ଦେଶବାସୀଙ୍କ ମନରେ ଥ‌ିବା ବଳିଦାନ-ଭାବନା ପ୍ରକାଶ କରାଯାଇଛି ।

ବ୍ୟାଖ୍ୟା : ଯଦି କୌଣସି ସମୟରେ ଦେଶ ଉପରେ ବିପଦ ଘୋଟିଆସେ କିମ୍ବା ଦେଶର ସମ୍ମାନ ଉପରେ ଆ ଆସିବାର ଆଶଙ୍କା ଦେଖାଦିଏ, ତେବେ ଭାରତବାସୀ ସେମାନଙ୍କ ଅମୂଲ୍ୟ ଜୀବନକୁ ଦେଶ ପାଇଁ ଉତ୍ସର୍ଗ କରିଦିଅନ୍ତି । କବୟିତ୍ରୀ ଲେଖୁଛନ୍ତି ଯେ ନିଜ ଦେଶମାତୃକାର କଲ୍ୟାଣ ପାଇଁ ବାରମ୍ବାର ଜନ୍ମ ନେବାକୁ ଓ ମୃତ୍ୟୁବରଣ କରିବାକୁ ପଡ଼ିଲେ ମଧ୍ୟ ତାହାକୁ ଆମେ ସହର୍ଷ ସ୍ଵୀକାର କରିଥାଉ।

शब्दार्थ :

Odisha State Board BSE Odisha 7th Class Geography Important Questions Chapter 2 ବାୟୁମଣ୍ଡଳ Important Questions and Answers.

BE Odisha Class 7 Geography Important Questions Chapter 2 ବାୟୁମଣ୍ଡଳ

Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ବାୟୁମଣ୍ଡଳର ସ୍ତରଗୁଡ଼ିକର ନାମ ଲେଖ ଓ ସେଗୁଡ଼ିକ ସମ୍ପର୍କରେ ସଂକ୍ଷେପରେ ଆଲୋଚନା କର ।
Answer:

1. ବାୟୁମଣ୍ଡଳର ତାପମାତ୍ରାକୁ ଭିଭିକରି ବାୟୁମଣ୍ଡଳକୁ ପାଞ୍ଚଗୋଟି ସ୍ତରରେ ବିଭକ୍ତ କରାଯାଇଛି; ଯଥା- ଟ୍ରପୋସ୍ଟି ଅର୍, ଷ୍ଟ୍ରାଟୋସ୍ଟି ଅର୍, ମେସୋସ୍ଟି ଅର୍, ଥର୍ମୋସ୍ଟି ଅର୍ ଏବଂ ଏକ୍‌ସ୍ଟିଅର୍ ।
2. ଟ୍ରପୋସ୍ପିଅର୍ : ଏହା ବାୟୁମଣ୍ଡଳର ସର୍ବନିମ୍ନ ସ୍ତର । ଏହାର ହାରାହାରି ଉଚ୍ଚତା ୧୨ କିଲୋମିଟର । ମେରୁ ଅଞ୍ଚଳରେ ଏହାର ଉଚ୍ଚତା ପ୍ରାୟ ୮ କିଲୋମିଟର ଏବଂ ବିଷୁବ ଅଞ୍ଚ ଳରେ ପ୍ରାୟ ୧୬ କିଲୋମିଟର । ଏହି ସ୍ତରରେ ବୃଷ୍ଟିପାତ, ତୁଷାରପାତ, କୁହୁଡ଼ି, କୁଆପଥର ଆଦି ଜଳବାୟୁ ଓ ପାଣିପାଗ ସମ୍ବନ୍ଧୀୟ ଘଟଣାବଳୀ ଘଟିଥାଏ ।
3. ଷ୍ଟ୍ରାଟୋସ୍ପିଅର୍ : ଟ୍ରପୋସ୍ପିଅର୍ ଉପରକୁ ଅବସ୍ଥିତ ଏହି ସ୍ତରଟି ପ୍ରାୟ ୫୦ କିଲୋମିଟର ଉଚ୍ଚତା ପର୍ଯ୍ୟନ୍ତ ବ୍ୟାପି ରହିଛି । ଏହାର ନିମାଂଶରେ ଓଜୋନ୍‌ ଗ୍ୟାସ୍ ରହିଛି । ଏଠାରେ ଧୂଳିକଣା ଓ ଜଳୀୟବାଷ୍ପ ନ ଥିବାରୁ ଜଳବାୟୁ ସମ୍ବନ୍ଧୀୟ ଘଟଣା ସଂଗଠିତ ହୁଏ ନାହିଁ । ବିମାନ ଚଳାଚଳ ପାଇଁ ଏହି ସ୍ତରଟି ଅନୁକୂଳ ।
4. ମେସୋସ୍ଟିଅର୍ : ମେସୋସ୍ପିଅର୍ ଉପରକୁ ପ୍ରାୟ ୮୦ କି.ମି. ଉଚ୍ଚତା ବ୍ୟାପୀ ଥ‌ିବା ଏହି ସ୍ତରରେ ଉଚ୍ଚତା ବୃଦ୍ଧି ସହ ତାପମାତ୍ରା ହ୍ରାସ ପାଇଥାଏ ।
5. ଥର୍ମୋସ୍ଟିଅର୍ : ମେସୋସ୍ପିଅର୍ ଉପରକୁ ପ୍ରାୟ ୮୦ କି.ମି.ଠାରୁ ବାୟୁମଣ୍ଡଳ ଶେଷ ପର୍ଯ୍ୟନ୍ତ ଏହି ସ୍ତର ପରିବ୍ୟାପ୍ତ । ଏହି ସ୍ତରରେ ଉଚ୍ଚତା ବୃଦ୍ଧି ସହ ତାପମାତ୍ରା ଅଧ‌ିକ ବୃଦ୍ଧି ପାଏ । ଏହାର ନିମାଂଶ ପ୍ରାୟ ୮୦ କି.ମି.ରୁ ୪୦୦ କି.ମି. ଉଚ୍ଚତା ପର୍ଯ୍ୟନ୍ତ ସ୍ତରରେ ଘନୀଭୂତ ଆୟନ କଣିକା ଥିବାରୁ ଏହାକୁ ଆୟୋନୋସ୍ପିଅର୍ କୁହାଯାଏ ।
6. ଏକ୍ସୋସ୍ପିଅର୍ : ହିଲିୟମ୍ ଓ ଉଦ୍‌ଜାନ ଭଳି ହାଲୁକା ଗ୍ୟାସ୍ ଥ‌ିବା ଏହି ପତଳା ସ୍ତରଟି ବାୟୁମଣ୍ଡଳର ବାହ୍ୟ ସ୍ତର ।

Question 2.
ପୃଥ‌ିବୀର ବିଭିନ୍ନ ଚାପ ବଳୟ ଉପରେ ସଂକ୍ଷେପରେ ବର୍ଣ୍ଣନା କର ।
Answer:

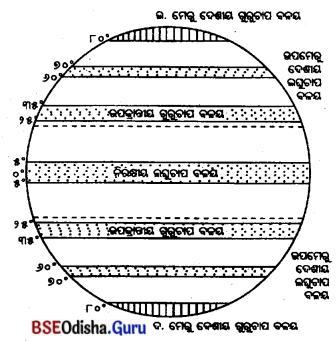
1. ପୃଥ‌ିବୀପୃଷ୍ଠରେ ୩ ଗୋଟି ଲଘୁଚାପ ବଳୟ ଓ ୪ ଗୋଟି ଗୁରୁଚାପ ବଳୟ ସ୍ଥାୟୀଭାବରେ ରହିଛି ।
2. ବିଷୁବମଣ୍ଡଳ ସୂର୍ଯ୍ୟକିରଣରୁ ଅଧ୍ବକ ଉତ୍ତାପ ପାଉଥିବା ହେତୁ ଏଠାରେ ଲଘୁଚାପ ସୃଷ୍ଟି ହୁଏ, ତେଣୁ ଏଠାରେ ନିରକ୍ଷୀୟ ଲଘୁଚାପ ବଳୟ ସୃଷ୍ଟି ହୋଇଛି । ଏଠାରେ ବାୟୁ ସର୍ବଦା ତଳୁ ଉପର ଆଡ଼କୁ ଗତି କରିଥାଏ ।
3. ବିଷୁବ ଅଞ୍ଚଳରୁ ଉତ୍ତପ୍ତ ବାୟୁ ଉପରକୁ ଉଠି ଉଭୟ ମେରୁ ଆଡ଼କୁ ପ୍ରବାହିତ ହୋଇଥାଏ । ଉପର ସ୍ତରରେ ଏହି ବାୟୁ କ୍ରାନ୍ତୀୟ ଅଞ୍ଚଳରେ ପହଞ୍ଚିବାବେଳକୁ ଥଣ୍ଡା ହୋଇ ଉଭୟ ଗୋଲାର୍ଦ୍ଧର ୨୫°ରୁ ୩୫° ସମାକ୍ଷରେଖା ମଧ୍ଯରେ ନିମ୍ନଗାମୀ ହୁଏ । ତେଣୁ ଏଠାରେ ଉପକ୍ରାନ୍ତୀୟ ଗୁରୁଚାପ ବଳୟ ସୃଷ୍ଟି ହୋଇଛି ।
4. ଉଭୟ ଗୋଲାର୍ଦ୍ଧର ୬୦ରୁ ୭୦° ସମାକ୍ଷରେଖା ମଧ୍ଯରେ ସୃଷ୍ଟି ହେଉଥ‌ିବା ଚାପବଳୟକୁ ଉପମେରୁ ଲଘୁଚାପ ବଳୟ କୁହାଯାଏ । ଦୁଇ ମେରୁବୃତ୍ତ ନିକଟରେ ପୃଥ‌ିବୀର ଆବର୍ଜନ ବେଗ ଅଧିକ ଥ‌ିବା ହେତୁ ଏହି ଅଞ୍ଚଳର ବାୟୁ କ୍ରାନ୍ତୀୟ ଅଞ୍ଚଳକୁ ବିକ୍ଷିପ୍ତ ହେଉଥ‌ିବାରୁ ବାୟୁ ପତଳା ହୋଇ ଲଘୁଚାପ ବଳୟ ସୃଷ୍ଟି ହୋଇଛି ।
5. ସେହିପରି ଉଭୟ ମେରୁ ଅଞ୍ଚଳର ବାୟୁ ଶୀତଳ ଓ ଓଜନିଆ ହେତୁ ଏହି ଅଞ୍ଚଳରେ ବାୟୁର ଚାପ ଅଧିକ ହୁଏ । ତେଣୁ ଉଭୟ ମେରୁ ଅଞ୍ଚଳରେ ମେରୁମଣ୍ଡଳୀୟ ଗୁରୁଚାପ ବଳୟ ସୃଷ୍ଟି ହୋଇଛି ।

Question 3.
ପୃଥ‌ିବୀର ଚାପ ବଳୟ ଚିତ୍ର ଆଙ୍କ । ବିଭିନ୍ନ ଚାପ ବଳୟ ଉପରେ ସଂକ୍ଷେପରେ ବର୍ଣ୍ଣନା କର ।
Answer:

Question 4.
ନିୟତ ବାୟୁ ପ୍ରବାହ ଉପରେ ସଂକ୍ଷେପରେ ଲେଖ ।
Answer:

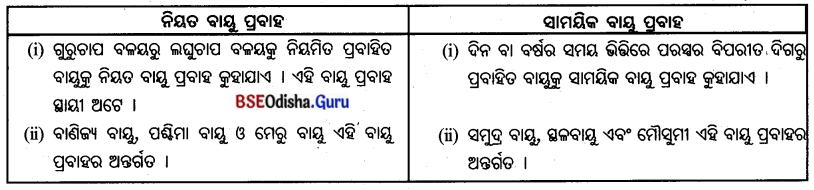
1. ପୃଥ‌ିବୀର ସ୍ଥାୟୀ ଗୁରୁଚାପ ବଳୟରୁ ସ୍ଥାୟୀ ଲଘୁଚାପ ବଳୟକୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦିଗରେ ବହୁଥ‌ିବା ବାୟୁକୁ ନିୟତ ବାୟୁ କୁହାଯାଏ । ଆୟନ ବାୟୁ, ପଶ୍ଚିମା ବାୟୁ ଓ ମେରୁ ବାୟୁ ଏହି ବାୟୁର ଅନ୍ତର୍ଗତ ।
2. ଉପକ୍ରାନ୍ତୀୟ ଗୁରୁଚାପ ବଳୟରୁ ନିରକ୍ଷୀୟ ଲଘୁଚାପ ବଳୟକୁ ପ୍ରବାହିତ ବାୟୁକୁ ଆୟନ ବାୟୁ କୁହାଯାଏ ।
3. ଉତ୍ତର ଗୋଲାର୍ଦ୍ଧରେ ଏହା ଉତ୍ତର-ପୂର୍ବ ଏବଂ ଦକ୍ଷିଣ ଗୋଲାର୍ଦ୍ଧରେ ଦକ୍ଷିଣ-ପୂର୍ବ ଦିଗରୁ ପ୍ରବାହିତ ହେଉଥ‌ିବାରୁ ଏହାର ନାମ ଯଥାକ୍ରମେ ଉତ୍ତର-ପୂର୍ବ ଆୟନ ବାୟୁ ଓ ଦକ୍ଷିଣ- ପୂର୍ବ ଆୟନ ବାୟୁ ଅଟେ ।
4. ଉପକ୍ରାନ୍ତୀୟ ଗୁରୁଚାପ ବଳୟରୁ ଉପମେରୁ ଲଘୁଚାପ ବଳୟକୁ ପ୍ରବାହିତ ହେଉଥ‌ିବା ବାୟୁକୁ ପଶ୍ଚିମାବାୟୁ କୁହାଯାଏ । ଏହି ବାୟୁ ଉତ୍ତର ଗୋଲାର୍ଦ୍ଧରେ ଦକ୍ଷିଣ-ପଶ୍ଚିମ କୋଣରୁ ଏବଂ ଦକ୍ଷିଣ ଗୋଲାର୍ଦ୍ଧରେ ଉତ୍ତର-ପଶ୍ଚିମ କୋଣରୁ ବହେ । ଏହାର ଦିଗ ଓ ବେଗ ପରିବର୍ତ୍ତନଶୀଳ ଥିବାରୁ ଏହାକୁ ପରିବର୍ତ୍ତନଶୀଳ ପଶ୍ଚିମାବାୟୁ କୁହାଯାଏ ।
5. ଉଭୟ ଗୋଲାର୍ଦ୍ଧରେ ମେରୁମଣ୍ଡଳୀୟ ଗୁରୁଚାପ ଅଞ୍ଚଳରୁ ଉପମେରୁ ଲଘୁଚାପ ବଳୟକୁ ପ୍ରବାହିତ ମେରୁବାୟୁ ଉତ୍ତର ଗୋଲାର୍ଦ୍ଧରେ ଉତ୍ତର-ପୂର୍ବ ଦିଗରୁ ଏବଂ ଦକ୍ଷିଣ ଗୋଲାର୍ଦ୍ଧରେ ଦକ୍ଷିଣ-ପୂର୍ବ ଦିଗରୁ ପ୍ରବାହିତ ହୁଏ ।

Question 5.
ବୃଷ୍ଟିପାତ କ’ଣ ? ବିଭିନ୍ନ ପ୍ରକାର ବୃଷ୍ଟିପାତ ସମ୍ବନ୍ଧରେ ଆଲୋଚନା କର ।
Answer:

1. ମେଘରେ ଥିବା ଜଳକଣା ଘନୀଭୂତ ହୋଇ ଜଳ ଆକାରରେ ଭୂପୃଷ୍ଠରେ ପଡ଼ିବାକୁ ବୃଷ୍ଟିପାତ କୁହାଯାଏ ।
2. ବୃଷ୍ଟିପାତ ତିନି ପ୍ରକାରର, ଯଥା- ପରିଚଳନ ବୃଷ୍ଟିପାତ, ଶୈଳୋତ୍‌କ୍ଷେପ ବୃଷ୍ଟିପାତ ଏବଂ ବାତାବର୍ଷ ବୃଷ୍ଟିପାତ ।
3. ପରିଚଳନ ବୃଷ୍ଟିପାତ : ସୂର୍ଯ୍ୟରଶ୍ମି ଦ୍ବାରା ଭୂପୃଷ୍ଠ ଉତ୍ତପ୍ତ ହେଲେ ଭୂପୃଷ୍ଠ ସହ ଲାଗିରହିଥିବା ବାୟୁ ଉତ୍ତପ୍ତ ହୋଇ ଉପରକୁ ଉଠେ ଏବଂ ପରିଚଳନ ବାୟୁପ୍ରବାହ ସୃଷ୍ଟି ହୁଏ । ଏହି ବାୟୁରେ ଜଳୀୟବାଷ୍ପ ଥିଲେ ଏହା ଆକାଶରେ ବହୁ ଉଚ୍ଚରେ ମେଘ ସୃଷ୍ଟିକରି ସଙ୍ଗେ ସଙ୍ଗେ ପ୍ରବଳ ବର୍ଷା କରାଯାଏ । ପରିଚଳନ ବାୟୁସ୍ରୋତ ଫଳରେ ଏହି ବର୍ଷା ହେଉଥ‌ିବାରୁ ଏହାକୁ ପରିଚଳନ ବୃଷ୍ଟିପାତ କୁହାଯାଏ ।
4. ଶୈଳୋତ୍‌କ୍ଷେପ ବୃଷ୍ଟିପାତ : ଜଳୀୟବାଷ୍ପପୂର୍ଣ୍ଣ ବାୟୁ କୌଣସି ଉଚ୍ଚଭୂମି କିମ୍ବା ପର୍ବତରେ ବାଧାପାଇ ଉପରକୁ ଉଠେ । ଉପରକୁ ଉଠିଯିବା ଫଳରେ ତାହା ଶୀତଳ ହୋଇ ପରିପୃକ୍ତ ହୁଏ । ଏହାର କ୍ଷୁଦ୍ର ଜଳକଣାସବୁ ଜଳବିନ୍ଦୁରେ ପରିଣତ ହୋଇ ବୃଷ୍ଟି ଆକାରରେ ପଡ଼େ ।
5. ଏହାକୁ ଶୈଳୋତ୍‌କ୍ଷେପ ବୃଷ୍ଟିପାତ କୁହାଯାଏ । ପର୍ବତର ପ୍ରତିବାତ ପାର୍ଶ୍ଵରେ ପ୍ରବଳ ବୃଷ୍ଟିପାତ ହୁଏ, ମାତ୍ର ଅନୁବାତ ପାର୍ଶ୍ଵରେ କମ୍ ବୃଷ୍ଟିପାତ ହୋଇଥାଏ ।
6. ବାତାବର୍ଷ ଜନିତ ବୃଷ୍ଟିପାତ : କ୍ରାନ୍ତିମଣ୍ଡଳ ଅନ୍ତର୍ଗତ ସମୁଦ୍ର ଉପରେ ବାୟୁଚାପ ହ୍ରାସ ପାଇବା ଫଳରେ ସୃଷ୍ଟି ହୋଇଥିବା ଲଘୁଚାପ କେନ୍ଦ୍ର ଆଡ଼କୁ ବାୟୁ ପ୍ରବାହିତ ହୁଏ । ଏହି ବାୟୁ ଘୂରି ଘୂରି ଉପରକୁ ଉଠିଯାଏ ଓ ଏଥିରେ ଥିବା ଜଳୀୟବାଷ୍ପ ଘନୀଭୂତ ହୋଇ ପ୍ରବଳ ବର୍ଷା କରାଏ ।

Question 6.
ଚିତ୍ର ସହ ପୃଥିବୀପୃଷ୍ଠର ତାପମଣ୍ଡଳଗୁଡ଼ିକ ସମ୍ବନ୍ଧରେ ଆଲୋଚନା କର ।
Answer:
i. ପୃଥ‌ିବୀ ବର୍ଭୁଳାକାର ହୋଇଥିବାରୁ ପୃଥିବୀପୃଷ୍ଠର ସବୁଠାରେ ତାପମାତ୍ରା ସମାନ ନ ଥାଏ । ବିଷୁବ ଅଞ୍ଚଳରେ ସୂର୍ଯ୍ୟଙ୍କର ଲମ୍ବ କିରଣ ପଡ଼େ ଓ ମେରୁ ଅଞ୍ଚଳରେ ତୀର୍ଯ୍ୟକ୍ କିରଣ ପଡ଼େ ।
ii. ତେଣୁ ପୃଥ‌ିବୀପୃଷ୍ଠରେ ୩ ଗୋଟି ତାପମଣ୍ଡଳ ଦେଖାଯାଏ; ଯଥା – ଗ୍ରୀଷ୍ମ ମଣ୍ଡଳ, ନାତିଶୀତୋଷ ମଣ୍ଡଳ ଓ ହିମ ମଣ୍ଡଳ ।

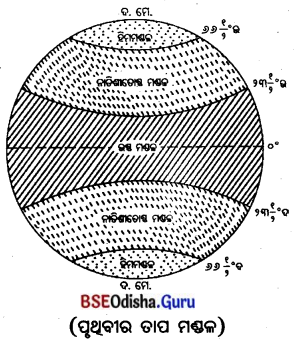
iii. ନିରକ୍ଷ ବୃତ୍ତର ଉଭୟ ପାର୍ଶ୍ଵରେ ଦୁଇ କ୍ରାନ୍ତି ବୃତ୍ତ ମଧ୍ୟବର୍ତ୍ତୀ ଅଞ୍ଚଳ ବର୍ଷସାରା ଲମ୍ବ କିରଣ ପାଉଥିବାରୁ ସେଠାରେ ଅଧିକ ତାପ ଅନୁଭୂତ ହୁଏ । ତେଣୁ ସେହି ଅଞ୍ଚଳକୁ ଗ୍ରୀଷ୍ମମଣ୍ଡଳ କୁହାଯାଏ ।
iv. ଉଭୟ ଗୋଲାର୍ଦ୍ଧରେ କ୍ରାନ୍ତିବୃରଠାରୁ ମେରୁବୃତ୍ତ ପର୍ଯ୍ୟନ୍ତ ଅଞ୍ଚଳରେ ଅଧିକ ଗରମ ବା ଅଧିକ ଥଣ୍ଡା ଅନୁଭୂତ ହୋଇ ନଥାଏ । ତେଣୁ ଏହାକୁ ନାତିଶୀତୋଷ୍ଣ ମଣ୍ଡଳ କୁହାଯାଏ ।
v. ମେରୁବୃତ୍ତରୁ ଉଭୟ ମେରୁ ପର୍ଯ୍ୟନ୍ତ ଅଞ୍ଚଳରେ ସର୍ବନିମ୍ନ ତାପମାତ୍ରା ଅନୁଭୂତ ହୋଇଥାଏ । ତେଣୁ ଏହାକୁ ହିମମଣ୍ଡଳ କୁହାଯାଏ ।

Question 7.
ବାୟୁମଣ୍ଡଳର ଗଠନ ବର୍ଣନା କର ଓ ଏଥିରେ ଥିବା ମୁଖ୍ୟ ଉପାଦାନମାନଙ୍କ ବିଶେଷତ୍ଵ ଲେଖ ।
Answer:

1. ବାୟୁମଣ୍ଡଳ ଅନେକଗୁଡ଼ିଏ ଗ୍ୟାସୀୟ ପଦାର୍ଥ ମିଶ୍ରଣରେ ଗଠିତ ।
2. ଏହାର ଦୁଇଟି ମୁଖ୍ୟ ଉପାଦାନ ମଧ୍ଯରେ ଯବକ୍ଷାରଜାନ ଓ ଅମ୍ଳଜାନ ପ୍ରଧାନ । ଅନ୍ୟାନ୍ୟ ଗ୍ୟାସ୍‌; ଯଥା- ଆର୍‌ଗନ୍ଧ, ଅଙ୍ଗାରକାମ୍ଳ, ହିଲିୟମ୍ ଓ ଉଦ୍‌ଜାନ ସହିତ ଜଳୀୟବାଷ୍ପ ଓ ଧୂଳିକଣା ଅଳ୍ପ ପରିମାଣରେ ବାୟୁମଣ୍ଡଳରେ ରହିଥାଏ ।

ବିଭିନ୍ନ ଗ୍ୟାସ୍‌ର ବିଶେଷତ୍ଵ :

• ଯବକ୍ଷାରଜାନ : ବାୟୁମଣ୍ଡଳରେ ଯବକ୍ଷାର ଜାନର ପରିମାଣ ସର୍ବାଧୁକ ଅର୍ଥାତ୍ ଶତକଡ଼ା ୭୮ ଭାଗ । ମୃରିକା ଓ ଗଛ ମୂଳରେ ଥିବା କେତେକ ବୀଜାଣୁ ଏହାକୁ ପରିବର୍ତ୍ତନ କରି ବୃକ୍ଷଲତାଦିଙ୍କ ଉପଯୋଗୀ କରିଥାନ୍ତି ।
• ଅମ୍ଳଜାନ : ଏହା ବାୟୁମଣ୍ଡଳର ଦ୍ଵିତୀୟ ମୁଖ୍ୟ ଗ୍ୟାସ୍ । ଏହାର ପରିମାଣ ଶତକଡ଼ା ୨୧ ଭାଗ । ଜୀବଜଗତର ଶ୍ଵାସକ୍ରିୟା ତଥା ଶିଳାକ୍ଷୟ, ଭୂତଳ ଖଣିଜ ପଦାର୍ଥ ଗଠନ ଏବଂ ଦହନ ଓ ଜାରଣ ପ୍ରକ୍ରିୟା ନିମନ୍ତେ ଏହାର ଆବଶ୍ୟକତା ରହିଛି ।
• ଅଙ୍ଗାରକାମ୍ଳ : ବାୟୁରେ ଶତକଡ଼ା ୦.୦୩ ଭାଗ ଅଙ୍ଗାରକାମ୍ଳ ଗ୍ୟାସ୍ ରହିଥିଲେ ମଧ୍ୟ ଏହା ଉଭିଦଜଗତର ଖାଦ୍ୟପ୍ରସ୍ତୁତି ତଥା ସୌରରଶ୍ମି ଓ ଭୂପୃଷ୍ଠରୁ ବିକିରିତ ତାପ ଧରିରଖୁବାରେ ସହାୟକ ହୁଏ ।
• ଜଳୀୟବାଷ୍ପ ଓ ଧୂଳିକଣା : ମେଘ ସୃଷ୍ଟି ତଥା ପାଣିପାଗକୁ ପ୍ରଭାବିତ କରିବାରେ ଏମାନଙ୍କର ଭୂମିକା ଗୁରୁତ୍ବପୂର୍ଣ୍ଣ ।

ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ବାୟୁମଣ୍ଡଳକୁ କେତେଗୋଟି ସ୍ତରରେ ବିଭକ୍ତ କରାଯାଇଛି ? ସର୍ବୋଚ୍ଚ ଓ ସର୍ବନିମ୍ନ ସ୍ତରର ନାମ କ’ଣ ?
Answer:

1. ବାୟୁମଣ୍ଡଳକୁ ୫ ଗୋଟି ସ୍ତରରେ ବିଭକ୍ତ କରାଯାଇଛି ।
2. ଟ୍ରପୋସ୍ଟିଅର୍ ବାୟୁମଣ୍ଡଳର ସର୍ବନିମ୍ନ ସ୍ତର ଓ ଏକ୍ସୋସ୍ପିଅର ବାୟୁମଣ୍ଡଳର ସର୍ବୋଚ୍ଚ ସ୍ତର ।

Question 2.
ଟ୍ରପୋସ୍ଟିଅରର ହାରାହାରି ଉଚ୍ଚତା କେତେ ? ମେରୁ ଓ ବିଷୁବ ଅଞ୍ଚଳରେ ଏହି ସ୍ତରର ଉଚ୍ଚତା କେତେ ?
Answer:

1. ଟ୍ରପୋସ୍ପିଅର ହାରାହାରି ଉଚ୍ଚତା ୧୨ କିଲୋମିଟର ।
2. ମେରୁ ଅଞ୍ଚଳରେ ଏହି ସ୍ତରର ଉଚ୍ଚତା ପ୍ରାୟ ୮ କିଲୋମିଟର ଏବଂ ବିଷୁବ ଅଞ୍ଚଳରେ ପ୍ରାୟ ୧୬ କିଲୋମିଟର ।

Question 3.
ବାୟୁମଣ୍ଡଳର କେଉଁ ସ୍ତରଟି ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ଓ କାହିଁକି ?
Answer:

1. ଟ୍ରପୋସ୍ଟି ଅର୍ ବାୟୁମଣ୍ଡଳର ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ସ୍ତର । କାରଣ ଜଳବାୟୁ ଓ ପାଣିପାଗ ସମ୍ବନ୍ଧୀୟ ସମସ୍ତ ଘଟଣାବଳୀ, ଯଥା- ବୃଷ୍ଟିପାତ, ତୁଷାରପାତ, କୁହୁଡ଼ି, କୁଆପଥର ବୃଷ୍ଟି ଆଦି ଏହି ସ୍ତରରେ ଘଟିଥାଏ ।
2. ଜୀବଜଗତ ଶ୍ଵାସକ୍ରିୟା ପାଇଁ ଆବଶ୍ୟକ ଅମ୍ଳଜାନ ଏହି ସ୍ତରରୁ ହିଁ ପାଇଥାନ୍ତି ।

Question 4.
ଷ୍ଟ୍ରାଟୋସ୍ପିଅରର ବିଶେଷତ୍ଵ କ’ଣ ?
Answer:

1. ଷ୍ଟ୍ରାଟୋସ୍କୋ ଅର୍‌ରେ ଧୂଳିକଣା ଓ ଜଳୀୟବାଷ୍ପ ନ ଥାଏ । ତେଣୁ ମେଘ ବା ଜଳବାୟୁ ସମ୍ବନ୍ଧୀୟ ଘଟଣା ଏଠାରେ ସଂଗଠିତ ହୁଏ ନାହିଁ । ବିମାନ ଚଳାଚଳ ପାଇଁ ଏହି ସ୍ତର ଅନୁକୂଳ ।
2. ଏହି ସ୍ତରରେ ଥ‌ିବା ଓଜୋନ୍‌ ଗ୍ୟାସ୍ ସୂର୍ଯ୍ୟଙ୍କଠାରୁ ଆସୁଥିବା କ୍ଷତିକାରକ ରଶ୍ମି ପ୍ରଭାବରୁ ରକ୍ଷା କରିଥାଏ ।

Question 5.
ବାୟୁଚାପ କ’ଣ ? ବାୟୁଚାପ କାହାଦ୍ଵାରା ପ୍ରଭାବିତ ହୋଇଥାଏ ?
Answer:

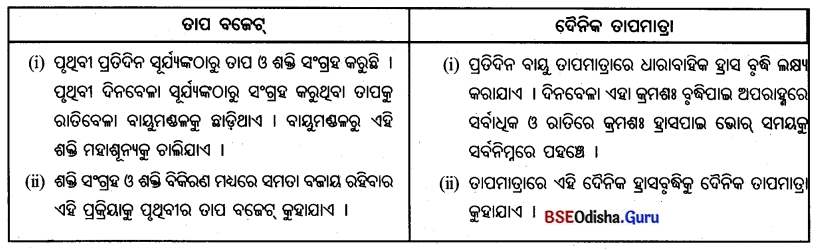
1. କୌଣସି ସ୍ଥାନର ଏକ ବର୍ଗ ସେ.ମି. ପରିମିତ ଅଞ୍ଚଳରେ ବାୟୁମଣ୍ଡଳର ଶେଷସୀମା ପର୍ଯ୍ୟନ୍ତ ବିସ୍ତୃତ ବାୟୁସ୍ତମ୍ଭର ଓଜନକୁ ବାୟୁଚାପ କୁହାଯାଏ । ସମୁଦ୍ର ପତ୍ତନରେ ଏହା ପ୍ରାୟ ୧,୦୫ କିଲୋଗ୍ରାମ୍ ।
2. ବାୟୁଚାପ ତାପମାତ୍ରା ଦ୍ଵାରା ବିଶେଷଭାବେ ପ୍ରଭାବିତ ହୋଇଥାଏ ।

Question 6.
ଉପକ୍ରାନ୍ତୀୟ ଗୁରୁଚାପ ବଳୟ ସୃଷ୍ଟି ହୋଇଛି କିପରି ?
Answer:

1. ନିରକ୍ଷ ଅଞ୍ଚଳର ଊର୍ଦ୍ଧ୍ୱଗାମୀ ବାୟୁ ଉଭୟ ଗୋଲାର୍ଦ୍ଧର ମେରୁ ଆଡ଼କୁ ଗତି କରେ । ଫଳରେ ଏହା ପ୍ରସାରିତ ହୋଇ ଶୀତଳ ଓ ଭାରୀ ହୁଏ ।
2. ଏହି ଭାରୀ ବାୟୁ ଉଭୟ ଗୋଲାର୍ଦ୍ଧରେ ପ୍ରାୟ ୨୫°ରୁ ୩୫° ସମାକ୍ଷରେଖା ମଧ୍ଯରେ ନିମ୍ନଗାମୀ ହୁଏ । ଫଳରେ ଏଠାରେ ଗୁରୁଚାପ ବଳୟ ସୃଷ୍ଟି ହୋଇଛି ।

Question 7.
‘ପରିବର୍ତ୍ତନଶୀଳ ପଶ୍ଚିମା ବାୟୁ’ କ’ଣ ବୁଝାଅ ।
Answer:

1. ଉଭୟ ଗୋଲାର୍ଦ୍ଧରେ ଉପକ୍ରାନ୍ତୀୟ ଗୁରୁଚାପ ବଳୟରୁ ଉପମେରୁଦେଶୀୟ ଲଘୁଚାପ ବଳୟକୁ ପ୍ରବାହିତ ପଶ୍ଚିମାବାୟୁର ବେଗ ଓ ଦିଗ ପରିବର୍ତ୍ତନଶୀଳ ।
2. ଏଣୁ ଏହାକୁ ପରିବର୍ତ୍ତନଶୀଳ ପଶ୍ଚିମାବାୟୁ କୁହାଯାଏ ।

Question 8.
ମୌସୁମୀ ବାୟୁ କ’ଣ ? ଏହା କେଉଁ ବାୟୁ ପ୍ରବାହର ଅନ୍ତର୍ଗତ ? ଭାରତରେ ପ୍ରବାହିତ ମୌସୁମୀ ବାୟୁ” ସମ୍ବନ୍ଧରେ ଲେଖ ।
Answer:

1. ଦକ୍ଷିଣ ଏସିଆରେ ଗ୍ରୀଷ୍ମକାଳରେ ସମୁଦ୍ରଆଡୁ ସ୍ଥଳଭାଗକୁ ଓ ଶୀତକାଳରେ ସ୍ଥଳଭାଗରୁ ସମୁଦ୍ର ଆଡ଼କୁ ବହୁଥୁବା ବାୟୁକୁ ମୌସୁମୀ ବାୟୁ କୁହାଯାଏ ।
2. ମୌସୁମୀ ବାୟୁ ଏକ ଋତୁକାଳୀନ ବାୟୁ । ଏହା ମଧ୍ୟ ଏକ ସାମୟିକ ବାୟୁପ୍ରବାହ ଅଟେ ।
3. ଆମ ଦେଶରେ ଗ୍ରୀଷ୍ମକାଳରେ ଦକ୍ଷିଣ-ପଶ୍ଚିମ ମୌସୁମୀବାୟୁ ସମୁଦ୍ରଆଡ଼ୁ ପ୍ରବାହିତ ହେବା ଫଳରେ ପ୍ରଚୁର ବୃଷ୍ଟି ହୋଇଥାଏ ।
4. ଶୀତକାଳରେ ଦେଶ ମଧ୍ୟଦେଇ ଉତ୍ତର-ପୂର୍ବ ମୌସୁମୀବାୟୁ ସମୁଦ୍ରଆଡ଼କୁ ପ୍ରବାହିତ ହୋଇଥାଏ ।

Question 9.
ଆର୍ଦ୍ରତା କହିଲେ କ’ଣ ବୁଝ ? ବାୟୁର ଆର୍ଦ୍ରତା କେଉଁ ଯନ୍ତ୍ର ଦ୍ଵାରା ମପାଯାଏ ?
Answer:

1. ବାୟୁମଣ୍ଡଳରେ ଜଳୀୟବାଷ୍ପର ଉପସ୍ଥିତି ଓ ପରିମାଣକୁ ବାୟୁର ଆର୍ଦ୍ରତା କୁହାଯାଏ ।
2. ହାଇଡ୍ରୋମିଟର ନାମକ ଯନ୍ତ୍ରଦ୍ୱାରା ବାୟୁର ଆର୍ଦ୍ରତା ମପାଯାଏ ।

Question 10.
ଘନୀଭବନର ଯେକୌଣସି ଅବସ୍ଥାପାଇଁ କେଉଁ ଦୁଇଟି ବିଷୟ ଗୁରୁତ୍ଵପୂର୍ଣ ?
Answer:

1. ପ୍ରଥମତଃ, ବାୟୁ ପରିପୃକ୍ତ ହେବା ଆବଶ୍ୟକ ।
2. ଦ୍ଵିତୀୟତଃ, ଘନଭବନ କାର୍ଯ୍ୟପାଇଁ କୌଣସି ଏକ ଆଶ୍ରୟ ଆବଶ୍ୟକ ।

Question 11.
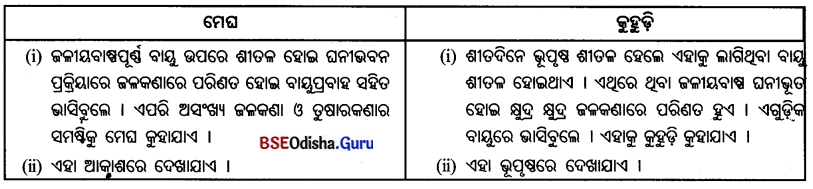
କୁହୁଡ଼ି କିପରି ସୃଷ୍ଟି ହୁଏ ?
Answer:

1. ଶୀତଦିନେ ସୂର୍ଯ୍ୟାସ୍ତ ପରେ ଭୂପୃଷ୍ଠ ଶୀତଳ ହେଲେ ତାହାକୁ ଲାଗିଥିବା ବାୟୁ ଶୀତଳ ହୁଏ । ତେଣୁ ବାୟୁରେ ଥୁବା ଜଳୀୟବାଷ୍ପ ଘନୀଭୂତ ହୋଇ କ୍ଷୁଦ୍ର କ୍ଷୁଦ୍ର ଜଳକଣାରେ ପରିଣତ ହୁଏ ।
2. ଏହି ଜଳକଣାଗୁଡ଼ିକ ବାୟୁରେ ଭାସିବୁଲେ । ଏହାକୁ କୁହୁଡ଼ି କୁହାଯାଏ ।

Question 12.
ବୃଷ୍ଟିପାତ କାହାକୁ କୁହାଯାଏ ?
Answer:

1. ମେଘରେ ଥିବା ଜଳକଣା ଅଧ‌ିକ ଶୀତଳ ହେଲେ ଘନୀଭୂତ ହୋଇ ବଡ଼ ବଡ଼ ଜଳବିନ୍ଦୁରେ ପରିଣତ ହୁଏ । ତେଣୁ ସେଗୁଡ଼ିକ ବାୟୁମଣ୍ଡଳରେ ଭାସି ରହିପାରେ ନାହିଁ ।
2. ତାହା ବର୍ଷାରୂପେ ଭୂପୃଷ୍ଠରେ ପଡ଼େ । ଏହାକୁ ଦୃଷ୍ଟିପାତ କୁହାଯାଏ ।

Question 13.
ବର୍ଷଣ କାହାକୁ କୁହାଯାଏ ? ଏହା କେଉଁ କେଉଁ ରୂପରେ ଦେଖାଯାଏ ?
Answer:

1. ପ୍ରାକୃତିକ ପ୍ରକ୍ରିୟାରେ ଆକାଶରୁ ଜଳ ତରଳ କିମ୍ବା କଠିନ ଅବସ୍ଥାରେ ରୂପୃଷ୍ଠରେ ପଡ଼ିଲେ ତାହାକୁ ବର୍ଷଣ କୁହାଯାଏ ।
2. ଏହି ତିନିଗୋଟି ରୂପରେ ଦେଖାଯାଏ, ଯଥା- ବୃଷ୍ଟିପାତ, ତୁଷାରପାତ ଓ କରକାପାତ (କୁଆପଥର) ।

Question 14.
ପରିଚଳନ ବୃଷ୍ଟିପାତ କାହାକୁ କୁହାଯାଏ ? କେଉଁଠାରେ ପରିଚଳନ ବୃଷ୍ଟିପାତ ହୋଇଥାଏ ଓ କେତେବେଳେ ?
Answer:

1. ପରିଚଳନ ବାୟୁସ୍ରୋତ ଫଳରେ ହେଉଥ‌ିବା ବର୍ଷାକୁ ପରିଚଳନ ବୃଷ୍ଟିପାତ କୁହାଯାଏ ।
2. ନିରକ୍ଷୀୟ ଅଞ୍ଚଳରେ ପ୍ରାୟ ପ୍ରତିଦିନ ଉପରବେଳା ଘଡ଼ଘଡ଼ି ସହ ପରିଚଳନ ବୃଷ୍ଟିପାତ ହୋଇଥାଏ ।

Question 15.
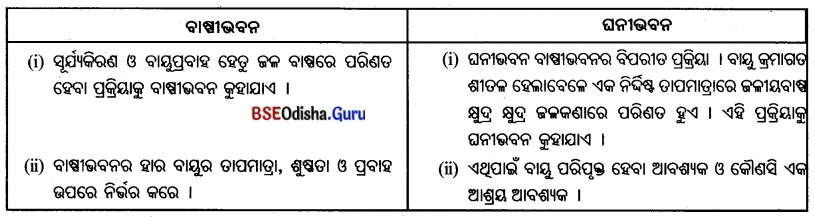
ପରିପୃକ୍ତ ବାୟୁ କ’ଣ ? ଏହା କିପରି ଅପରିପୃକ୍ତ ହୁଏ ?
Answer:

1. ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ତାପମାତ୍ରାରେ କୌଣସି ଅଞ୍ଚଳର ଜଳବାୟୁ ଯେତିକି ଜଳୀୟବାଷ୍ପ ଧାରଣ କରିବା କଥା, ସେତିକି ଜଳୀୟବାଷ୍ପ ସେହି ବାୟୁରେ ରହିଲେ ତାକୁ ପରିପୃକ୍ତ ବାୟୁ କହନ୍ତି ।
2. ତାପମାତ୍ରା ବୃଦ୍ଧି ପାଇଲେ ପରିପୃକ୍ତ ବାୟୁ ଅପରିପୃକ୍ତ ହୁଏ ।

Question 16.
ବାଷ୍ପମୋଚନ ପ୍ରକ୍ରିୟା କାହାକୁ କୁହାଯାଏ ?
Answer:

1. ବୃକ୍ଷଲତାଦିଙ୍କର ଡାଳପତ୍ରରୁ ଜଳ ବାଷ୍ପୀଭୂତ ହୋଇ ବାୟୁମଣ୍ଡଳରେ ମିଶିଥାଏ ।
2. ଏହି ପ୍ରକ୍ରିୟାକୁ ବାଷ୍ପମୋଚନ ପ୍ରକ୍ରିୟା କୁହାଯାଏ ।

Question 17.
ନିରକ୍ଷ ଶାନ୍ତ ବଳୟ କାହାକୁ କୁହାଯାଏ ?
Answer:

1. ନି ରକ୍ଷୀୟ ଲଘୁଚାପ ବଳୟରେ ବାୟୁମଣ୍ଡଳ ଶାନ୍ତ ଓ ଚଳନଶୂନ୍ୟ ।
2. ତେଣୁ ଏହାକୁ ନିରକ୍ଷ ଶାନ୍ତ ବଳୟ କୁହାଯାଏ ।

ସଂକ୍ଷିପ୍ତ ଟିପ୍ପଣୀ ଲେଖ।

Question 1.
ଆୟୋନୋସ୍ଟିଅର
Answer:

1. ଥର୍ମୋସ୍ଟିଅରର ନିମାଂଶକୁ ଆୟନୋସ୍ପିଅର୍ କୁହାଯାଏ, କାରଣ ଏହି ସ୍ତରରେ ଆୟନ କଣିକାଗୁଡ଼ିକ ଘନୀଭୂତ ହୋଇ ରହିଥାନ୍ତି । ଏହା ପ୍ରାୟ ୮୦ କି.ମି.ରୁ ୪୦୦ କି.ମି. ଉଚ୍ଚତା ପର୍ଯ୍ୟନ୍ତ ବିସ୍ତୃତ ।
2. ଏହି ସ୍ତର ଯୋଗୁ ଦୂର ସ୍ଥାନକୁ ବେତାର ତରଙ୍ଗ ପ୍ରସାରଣ ସମ୍ଭବ ହୋଇଥାଏ ।

Question 2.
ବାଣିଜ୍ୟ ବାୟୁ
Answer:

1. ଆୟନ ବାୟୁକୁ ବାଣିଜ୍ୟ ବାୟୁ କୁହାଯାଏ । କାରଣ ପୂର୍ବେ ପାଲଟଣା ବୋଇତରେ ବାଣିଜ୍ୟ କାରବାରରେ ଏହା ସହାୟକ ହେଉଥ‌ିବାରୁ ଏହାର ନାମକରଣ ବାଣିଜ୍ୟ ବାୟୁ ହୋଇଅଛି ।
2. ଏହି ବାୟୁ ଉତ୍ତର ଗୋଲାର୍ଦ୍ଧରେ ଉତ୍ତର-ପୂର୍ବ ଦିଗରୁ ଏବଂ ଦକ୍ଷିଣ ଗୋଲାର୍ଦ୍ଧରେ ଦକ୍ଷିଣ-ପୂର୍ବ ଦିଗରୁ ପ୍ରବାହିତ ହୁଏ ।

Question 3.
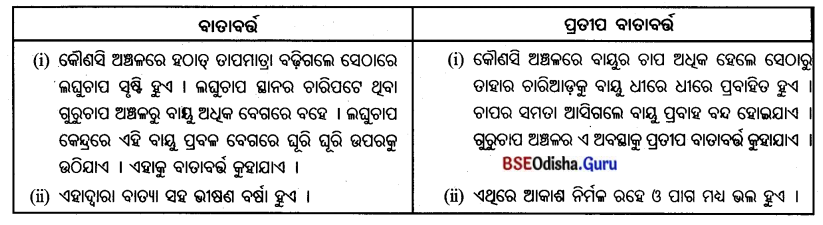
ପ୍ରତୀପ ବାତାବର୍ଷ
Answer:

1. କୌଣସି ସ୍ଥାନରେ ବାୟୁଚାପ ହଠାତ୍ ବୃଦ୍ଧି ପାଇ ଗୁରୁଚାପ କେନ୍ଦ୍ର ସୃଷ୍ଟି ହୁଏ । ଏହି ଗୁରୁଚାପ କେନ୍ଦ୍ରରୁ ବାୟୁ’ଧୀରେ ଧୀରେ ଚାରିପାଖରେ ଥୁବା ଅଳ୍ପ ଚାପ ଅଞ୍ଚଳ ଆଡ଼କୁ ପ୍ରବାହିତ ହୁଏ ।
2. ଉତ୍ତର ଗୋଲାର୍ଦ୍ଧରେ ଏହି ବାୟୁ ଡାହାଣକୁ ବାଙ୍କିଯାଇ ଘଣ୍ଟାକଣ୍ଟାର ଘୂର୍ଣ୍ଣନ ଦିଗରେ (ଦକ୍ଷିଣାବର୍ଷ) ଓ ଦକ୍ଷିଣ ଗୋଲାର୍ଦ୍ଧରେ ‘ବାମକୁ ବାଙ୍କିଯାଇ ଘଣ୍ଟାକଣ୍ଟାର ବିପରୀତ ଦିଗରେ (ବାମାବର୍ଗ) ପ୍ରବାହିତ ହୁଏ ।
3. ପ୍ରତୀପ ବାତାବର୍ତ୍ତ ଯୋଗୁ ପାଗ ଶୁଖୁଲା ରହେ ଓ ଆକାଶ ମେଘମୁକ୍ତ ଥାଏ ।

Question 4.
ସୌରାଭିତାପ
Answer:

• ଭୂପୃଷ୍ଠରେ ସଂଗୃହୀତ ସୌରରଶ୍ମିର ପରିମାଣକୁ ସୌରାଭିତାପ କୁହାଯାଏ ।
• ସୌରାଭିତାପର ପରିମାଣ ବିଷୁବରେଖାଠାରୁ ମେରୁ ଆଡ଼କୁ କ୍ରମଶଃ ହ୍ରାସ ପାଇଥାଏ । ମାତ୍ର ଋତୁଭେଦରେ ଏହି ପରିମାଣରେ ବ୍ୟତିକ୍ରମ ଦେଖାଯାଏ ।

Question 5.
କୁହୁଡ଼ି
Answer:

1. ଶୀତକାଳରେ ବାୟୁର ତାପମାତ୍ରା ଶିଶିରାଙ୍କ ତଳକୁ ଖସିଆସିଲେ ଏଥ‌ିରେ ଥ‌ିବା ଜଳୀୟବାଷ୍ପ ଘନୀଭୂତ ହୁଏ । ବାୟୁରେ ଭାସମାନ ଅବସ୍ଥାରେ ଥ‌ିବା ଧୂଳିକଣାକୁ ଆଶ୍ରୟ କରି ଏଗୁଡ଼ିକ ଭୂପୃଷ୍ଠର ଅଳ୍ପ ଉଚ୍ଚତାରେ ଭାସିବୁଲେ । ଏହାକୁ କୁହୁଡ଼ି କୁହାଯାଏ ।
2. କୁହୁଡ଼ିର ସୃଷ୍ଟିକୁ ଭିଭିକରି ଏହାକୁ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କରାଯାଏ; ଯଥା- ବିକିରଣ କୁହୁଡ଼ି ଓ ଅଭିବହନ କୁହୁଡ଼ି । ଭୂପୃଷ୍ଠର ତାପ ବିକିରଣରୁ ସୃଷ୍ଟି ହେଉଥିବା କୁହୁଡ଼ିକୁ ବିକିରଣ କୁହୁଡ଼ି ଏବଂ ଶୀତଳ ବାୟୁ ଓ ଉଷ୍ଣ ଆର୍ଦ୍ର ବାୟୁର ମିଶ୍ରଣରେ ସୃଷ୍ଟି ହେଉଥ‌ିବା କୁହୁଡ଼ିକୁ ଅଭିବହନ କୁହୁଡ଼ି କୁହାଯାଏ । କୁହୁଡ଼ି ଅତି ପତଳା ହେଲେ ଏହାକୁ ମିଷ୍ଟ୍ କୁହାଯାଏ ।

ଭୌଗୋଳିକ କାରଣ ଦର୍ଶାଅ ।

Question 1.
ଷ୍ଟ୍ରାଟୋସ୍ପିଅର ବିମାନ ଚଳାଚଳ ପାଇଁ ଅନୁକୂଳ ।
Answer:

1. ଷ୍ଟ୍ରାଟୋସ୍ପିଅର୍ ସ୍ତରରେ ଧୂଳିକଣା ଓ ଜଳୀୟବାଷ୍ପ ନ ଥାଏ । ତେଣୁ ମେଘ ବା ଜଳବାୟୁ ସମ୍ବନ୍ଧୀୟ ଘଟଣା ଏଠାରେ ସଂଗଠିତ ହୁଏ ନାହିଁ ।
2. ସେଥ‌ିପାଇଁ ବିମାନ ଚଳାଚଳ ପାଇଁ ଏହା ଏକ ଅନୁକୂଳ ସ୍ତର ।

Question 2.
ଶୀତଋତୁରେ କୁହୁଡ଼ି ସୃଷ୍ଟି ହୁଏ ।
Answer:

1. କୁହୁଡ଼ି ସୃଷ୍ଟି ପାଇଁ ଲମ୍ବା ଶୀତରାତି, ନିର୍ମଳ ଆକାଶ ଓ ଧୀର ବାୟୁପ୍ରବାହ ଆବଶ୍ୟକ । ତେଣୁ ଶୀତରାତିରେ ଦିନଭାଗ ଛୋଟ ଓ ରାତ୍ରିଭାଗ ଅଧିକ ଥାଏ । ଶୀତଋତୁରେ ଆକାଶ ପ୍ରାୟତଃ ନିର୍ମଳ ଥାଏ, ଫଳରେ ପୃଥ‌ିବୀପୃଷ୍ଠ ଶୀଘ୍ର ତାପ ବିକିରଣ କରି ଥଣ୍ଡା ହୁଏ ।
2. ସେତେବେଳେ ଶୀତଳ ଭୂପୃଷ୍ଠକୁ ଲାଗିଥିବା ବାୟୁ ଥଣ୍ଡା ହୁଏ ଓ ଶିଶିରାଙ୍କ ତଳକୁ ତାପମାତ୍ରା ଖସିଲେ ଏଥୁରେ ଥିବା ଜଳୀୟବାଷ୍ପ ଘନୀଭୂତ ହୁଏ । ଏହା ବାୟୁରେ ଥିବା ଭାସମାନ ଧୂଳିକଣାକୁ ଆଶ୍ରୟ କରି କୁହୁଡ଼ି ରୂପରେ ପରିବର୍ତ୍ତିତ ହୁଏ ।

Question 3.
ପଶ୍ଚିମଘାଟ ପର୍ବତମାଳାର ପୂର୍ବପାର୍ଶ୍ବରେ କମ୍ ବୃଷ୍ଟି ହୁଏ ।
Answer:

1. ପଶ୍ଚିମଘାଟ ପର୍ବତମାଳା ଉତ୍ତର-ଦକ୍ଷିଣ ହୋଇ ଭାରତର ପଶ୍ଚିମ ଉପକୂଳରେ ବିସ୍ତୃତ । ସମୁଦ୍ରରୁ ପ୍ରବାହିତ ଜଳୀୟବାଷ୍ପପୂର୍ଣ୍ଣ ଦକ୍ଷିଣ-ପଶ୍ଚିମ ମୌସୁମୀ ବାୟୁ ଏହାର ପଶ୍ଚିମ ପାର୍ଶ୍ଵରେ ବାଧା ପାଇ ବୃଷ୍ଟିପାତ କରାଏ ।
2. ଏହା ଉପରକୁ ଉଠି ଏହି ପର୍ବତମାଳାର ପ୍ରତିବାତ ପାର୍ଶ୍ବ ଅର୍ଥାତ୍ ପୂର୍ବ ପାର୍ଶ୍ବକୁ ନିମ୍ନଗାମୀ ହେବାଫଳରେ ଅଳ୍ପ ବୃଷ୍ଟି କରାଏ । ତେଣୁ ପଶ୍ଚିମଘାଟ ପର୍ବତମାଳାର ପୂର୍ବ ପାର୍ଶ୍ବରେ କମ୍ ବୃଷ୍ଟି ହୁଏ ।

Question 4.
ନିରକ୍ଷ ଲଘୁଚାପ ବଳୟକୁ ନିରକ୍ଷ ଶାନ୍ତ ବଳୟ କୁହାଯାଏ ।
Answer:

1. ନିରକ୍ଷ ଲଘୁଚାପ ବଳୟରେ ବର୍ଷସାରା ସଳଖ ସୂର୍ଯ୍ୟକିରଣ ପଡ଼ୁଥିବାରୁ ତାପମାତ୍ରା ଅଧିକ ରହେ ଓ ବାୟୁଚାପ ହ୍ରାସ ପାଏ ।
2. ତେଣୁ ଏଠାରେ ବାୟୁମଣ୍ଡଳ ଶାନ୍ତ ଓ ଚଳନଶୂନ୍ୟ ଥିବାରୁ ଏହାକୁ ନିରକ୍ଷ ଶାନ୍ତ ବଳୟ କୁହାଯାଏ ।

Question 5.
ପୁରୀ ସହରରେ ବେଶୀ ଗରମ ବା ଥଣ୍ଡା ଅନୁଭୂତ ହୁଏ । ନାହିଁ ।
Answer:

1. ଜଳ ଓ ସ୍ଥଳଭାଗର ବଣ୍ଟନ କୌଣସି ଅଞ୍ଚଳର ଜଳବାୟୁକୁ ପ୍ରଭାବିତ କରିଥାଏ ।
2. ସମୁଦ୍ର ଧୀରେ ଧୀରେ ଉତ୍ତପ୍ତ ଓ ବିଳମ୍ବରେ ଥଣ୍ଡା ହୁଏ । ପୁରୀ ସମୁଦ୍ରକୂଳବର୍ତ୍ତୀ ସହର ହୋଇଥିବାରୁ ଏଠାରେ ସାମୁଦ୍ରିକ ପ୍ରଭାବ ଅନୁଭୂତ ହୁଏ । ତେଣୁ ପୁରୀରେ ଖରାଦିନେ ବେଶୀ ଗରମ ବା ଶୀତଦିନେ ବେଶି ଥଣ୍ଡା ଅନୁଭୂତ ହୁଏ ନାହିଁ ।

Question 6.
ପଶ୍ଚିମାବାୟୁକୁ ଦକ୍ଷିଣ ଗୋଲାର୍ଦ୍ଧରେ ଗର୍ଜନଶୀଳ ଚାଳିଶା କୁହାଯାଏ ।
Answer:

1. ଦକ୍ଷିଣ ଗୋଲାର୍ଦ୍ଧରେ ବିସ୍ତୀର୍ଣ୍ଣ ଜଳରାଶି ଉପରେ ପଶ୍ଚିମାବାୟୁ ପ୍ରବଳ ବେଗରେ ପ୍ରବାହିତ ହୋଇଥାଏ ।
2. ତେଣୁ ଗର୍ଜନଶୀଳ ଏହି ବାୟୁକୁ ଗର୍ଜନଶୀଳ ଚାଳିଶା କୁହାଯାଏ ।

Question 7.
ଜୀବଜଗତ ତିଷ୍ଠି ରହିବା ପାଇଁ ବାୟୁମଣ୍ଡଳର ଭୂମିକା ଅତି ଗୁରୁତ୍ବପୂର୍ଣ ।
Answer:

1. ଜୀବଜଗତ ଶ୍ଵାସକ୍ରିୟାରେ ବାୟୁମଣ୍ଡଳରୁ ଆବଶ୍ୟକ ଅମ୍ଳଜାନ ଗ୍ରହଣ କରିଥାଏ ।
2. ଅସହ୍ୟ ଖରାଶୀତରୁ ବାୟୁମଣ୍ଡଳ ଆମକୁ ରକ୍ଷା କରିଥାଏ । ତେଣୁ ଜୀବଜଗତ ତିଷ୍ଠି ରହିବାପାଇଁ ବାୟୁମଣ୍ଡଳର ଭୂମିକା ଅତି ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ।

Question 8.
ମେରୁ ଅଞ୍ଚଳ ଅତ୍ୟନ୍ତ ଶୀତଳ ।
Answer:

1. ପୃଥ‌ିବୀ ବର୍ତ୍ତୁଳାକାର ହୋଇଥିବାରୁ ବିଷୁବ ଅଞ୍ଚଳ ଲମ୍ବ କିରଣ ପାଏ ଏବଂ ମେରୁ ଅଞ୍ଚଳ ତୀର୍ଯ୍ୟକ୍ କିରଣ ପାଏ ।
2. ବିଷୁବ ଅଞ୍ଚଳରେ ଅଧିକ ତାପ ଅନୁଭୂତ ହୁଏ, ମାତ୍ର ମେରୁ ଆଡ଼କୁ ତାପମାତ୍ରା କ୍ରମଶଃ କମି କମି ଯାଇ ଉଭୟ ମେରୁଠାରେ ସର୍ବନିମ୍ନ ତାପମାତ୍ରା ଅନୁଭୂତ ହୁଏ । ତେଣୁ ମେରୁ ଅଞ୍ଚଳ ଅତ୍ୟନ୍ତ ଶୀତଳ ।

Question 9.
ଆଫ୍ରିକାରେ ସାହାରା ମରୁଭୂମି ସୃଷ୍ଟି ହୋଇଛି ।
Answer:

1. କ୍ରାନ୍ତୀୟ ଅଞ୍ଚଳରେ ପ୍ରବାହିତ ଆୟନବାୟୁ ପ୍ରଭାବରେ ବୃହତ୍ ସ୍ଥଳଭାଗର ପୂର୍ବପାର୍ଶ୍ବରେ ବାଧା ପାଇ ପ୍ରବଳ ବୃଷ୍ଟି କରାଏ ।
2. ପଶ୍ଚିମ ପାର୍ଶ୍ଵରେ ବାୟୁ ଶୁଷ୍କ ହୋଇଯିବାରୁ ସୃଷ୍ଟି କରାଇପାରେ ନାହିଁ । ସାହାରା ଏସିଆର ପଶ୍ଚିମ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ଥିବାରୁ ଏହା ମରୁଭୂମି ହୋଇଛି ।

Question 10.
ଉଷ୍ଣବାୟୁ ଉପରକୁ ଉଠେ, ମାତ୍ର ଶୀତଳ ବାୟୁ ତଳକୁ ଆସେ ।
Answer:

1. ଉଷ୍ଣ ବାୟୁର ଘନତା କମିଯାଏ, ଫଳରେ ଏହା ପ୍ରସାରିତ ଓ ହାଲୁକା ହୋଇ ଉପରକୁ ଉଠେ ।
2. ମାତ୍ର ଶୀତଳ ବାୟୁର ଘନତା ଓ ଓଜନ ବୃଦ୍ଧିପାଏ, ତେଣୁ ଏହା ତଳକୁ ଖସେ ।

ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ

Question 1.
ବାୟୁ ଓ ପବନ
Answer:

Question 2.
ପାଣିପାଗ ଓ ଜଳବାୟୁ
Answer:

Question 3.
ଲଘୁଚାପ ଓ ଗୁରୁଚାପ
Answer:

Question 4.
ଗ୍ରୀଷ୍ମମଣ୍ଡଳ ଓ ହିମମଣ୍ଡଳ
Answer:

Question 5.
ନିୟତ ବାୟୁ ପ୍ରବାହ ଓ ସାମୟିକ ବାୟୁ ପ୍ରବାହ
Answer:

Question 6.
ତାପ ବଜେଟ୍ ଓ ଦୈନିକ ତାପମାତ୍ରା
Answer:

Question 7.
ବାତାବର୍ଷ ଓ ପ୍ରତୀପ ବାତାବର୍ଷ
Answer:

Question 8.
ମେଘ ଓ କୁହୁଡ଼ି
Answer:

Question 9.
ବାଷ୍ପୀଭବନ ଓ ଘନୀଭବନ
Answer:

ଅତିସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ।

i. କେଉଁ ଉପାଦାନକୁ ନେଇ ବାୟୁମଣ୍ଡଳ ଗଠିତ ହୋଇଛି ?
Answer
ଯବକ୍ଷାରଜାନ, ଅମ୍ଳଜାନ, ଆରଗନ୍, ଅଙ୍ଗାରକାମ୍ଳ, ହିଲିୟମ୍ ଓ ଉଦ୍‌ଜାନ ଭଳି ଗ୍ୟାସୀୟ ପଦାର୍ଥର ମିଶ୍ରଣରେ ବାୟୁମଣ୍ଡଳ ଗଠିତ ହୋଇଛି ।

ii. କାହାର ପରିମାଣ ବାୟୁମଣ୍ଡଳରେ ସର୍ବାଧୁକ ରହିଛି ?
Answer:
ଯବକ୍ଷାରଜାନ ବାୟୁମଣ୍ଡଳରେ ସର୍ବାଧ‌ିକ ପରିମାଣରେ ରହିଛି ।

iii. ଶ୍ଵାସକ୍ରିୟା ଛଡ଼ା ଅମ୍ଳଜାନ ଅନ୍ୟ କେଉଁ ପ୍ରକ୍ରିୟାରେ ସହାୟକ ହୋଇଥାଏ ?
Answer:
ଶିଳାକ୍ଷୟ, ଭୂତଳ ଖଣିଜ ପଦାର୍ଥର ଗଠନ ତଥା ଦହନ ଓ ଚ୍ଚାରଣ ପ୍ରକ୍ରିୟାରେ ଅମ୍ଳଜାନ ସହାୟକ ହୋଇଥାଏ।

iv. ଟ୍ରପୋସ୍ଫିୟରର ହାରାହାରି ଉଚ୍ଚତା କେତେ ?
Answer:
ଟ୍ରପୋସ୍ଫିୟରର ହାରାହାରି ଉଚ୍ଚତା ପ୍ରାୟ ୧୨ କି.ମି. ।

v. ଓଜୋନ ଗ୍ୟାସ୍ କେଉଁଠି ରହିଛି ?
Answer:
ଓଜୋନ୍ ଗ୍ୟାସ୍ ଷ୍ଟ୍ରାଟୋସ୍ପିୟର ସ୍ତରର ନିମାଂଶରେ ରହିଛି।

vi. ଓଜୋନ୍ ଗ୍ୟାସ୍ ସ୍ତର ଆମକୁ କିପରି ସାହାଯ୍ୟ କରେ ?
Answer:
ଓଜୋନ୍ ଗ୍ୟାସ୍ ଆମକୁ ସୂର୍ଯ୍ୟଙ୍କଠାରୁ ଆସୁଥିବା କ୍ଷତିକାରକ ରଶ୍ମି ପ୍ରଭାବରୁ ରକ୍ଷା କରିଥାଏ।

vii. ମେସୋସ୍ପିୟର କେତେ ଉଚ୍ଚତା ପର୍ଯ୍ୟନ୍ତ ବ୍ୟାପି ରହିଛି ?
Answer:
ମେସୋସ୍ପିୟର ପ୍ରାୟ ୮୦ କି.ମି. ଉଚ୍ଚତା ପର୍ଯ୍ୟନ୍ତ ରହିଛି ।

viii. କେଉଁ ସ୍ତରଟି ବିମାନ ଚଳାଚଳ ପାଇଁ ଅନୁକୂଳ ଅଟେ ?
Answer:
ଷ୍ଟ୍ରାଟୋସ୍ପିୟର ସ୍ତରଟି ବିମାନ ଚଳାଚଳ ପାଇଁ ଅନୁକୂଳ ଅଟେ ।

ix. ପାଗ କହିଲେ କ’ଣ ?
Answer:
ନିର୍ଦ୍ଦିଷ୍ଟ ସମୟରେ କୌଣସି ସ୍ଥାନର ବାୟୁମଣ୍ଡଳର ସାମୟିକ ଅବସ୍ଥାକୁ ପାଣିପାଗ ବା ସଂକ୍ଷେପରେ ‘ପାଗ’ କୁହାଯାଏ।

x. ଜଳବାୟୁ କାହାକୁ କୁହାଯାଏ ?
Answer:
କୌଣସି ସ୍ଥାନର ପାଣିପାଗର ବହୁବର୍ଷ ଧରି ହାରାହାରି ଅବସ୍ଥାକୁ ଜଳବାୟୁ କୁହାଯାଏ ।

xi. ‘ଦୈନିକ ତାପ ବ୍ୟବଧାନ’ କହିଲେ କ’ଣ ?
Answer:
ଦୈନିକ ସର୍ବୋଚ୍ଚ ଓ ସର୍ବନିମ୍ନ ତାପମାତ୍ରାର ବ୍ୟବଧାନକୁ ‘ଦୈନିକ ତାପ ବ୍ୟବଧାନ’ କୁହାଯାଏ।

xii. କେଉଁଠାରେ ବାୟୁଚାପ ସର୍ବାଧ‌ିକ ?
Answer:
ସମୁଦ୍ର ପତ୍ତନରେ ବାୟୁଚାପ ସର୍ବାଧୁକ ।

xiii. ବାୟୁଚାପ କାହାକୁ କୁହାଯାଏ ?
Answer:
କୌଣସି ସ୍ଥାନର ଏକ ବର୍ଗ ସେ.ମି. ପରିମିତ ଅଞ୍ଚଳରେ ବାୟୁମଣ୍ଡଳର ଶେଷସୀମା ପର୍ଯ୍ୟନ୍ତ ବିସ୍ତୃତ ବାୟୁସ୍ତମ୍ଭର ଓଜନକୁ ବାୟୁଚାପ କୁହାଯାଏ ।

xiv. ବାୟୁଚାପ କାହାଦ୍ଵାରା ପ୍ରଭାବିତ ହୋଇଥାଏ ?
Answer:
ବାୟୁଚାପ ତାପମାତ୍ରାଦ୍ଵାରା ବିଶେଷଭାବେ ପ୍ରଭାବିତ ହୋଇଥାଏ।

xv. କେଉଁ ଯନ୍ତ୍ରଦ୍ୱାରା ବାୟୁଚାପ ନିର୍ଣ୍ଣୟ କରାଯାଏ ?
Answer:
ବ୍ୟାରୋମିଟର ବା ଚାପମାନ ଯନ୍ତ୍ରଦ୍ଵାରା ବାୟୁଚାପ ନିଷ୍କ୍ରିୟ କରାଯାଏ ।

xvi. କାହାଦ୍ଵାରା ବାୟୁର ଦିଗ ମପାଯାଏ ?
Answer:
ଉଇଣ୍ଡଭେନ୍‌ଦ୍ୱାରା ବାୟୁର ଦିଗ ମପାଯାଏ।

xvii. କାହାଦ୍ଵାରା ବାୟୁର ବେଗ ମପାଯାଏ ?
Answer:
ଆନିମୋମିଟରଦ୍ଵାରା ବାୟୁର ବେଗ ମପାଯାଏ।

xvili. ପବନ କହିଲେ କ’ଣ ବୁଝ ?
Answer:
ଭୂପୃଷ୍ଠ ସହ ସମାନ୍ତର ଭାବେ ବହୁଥୁବା ବାୟୁକୁ ପବନ କୁହାଯାଏ ।

xix. ନିୟତ ବାୟୁପ୍ରବାହ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଗୁରୁଚାପ ବଳୟରୁ ଲଘୁଚାପ ବଳୟକୁ ନିୟମିତ ପ୍ରବାହିତ ବାୟୁକୁ ନିୟତ ବାୟୁପ୍ରବାହ କୁହାଯାଏ।

xx. କାହାକୁ ଆୟନ ବାହୁ କୁହାଯାଏ ?
Answer:
ଉପକ୍ରାନ୍ତୀୟ ଗୁରୁଚାପ ବଳୟରୁ ନିରକ୍ଷୀୟ ଲଘୁଚାପ ବଳୟକୁ ପ୍ରବାହିତ ବାୟୁକୁ ଆୟନ ବାହୁ କୁହାଯାଏ।

xxi. କାହାକୁ ପଶ୍ଚିମାବାୟୁ କୁହାଯାଏ ?
Answer:
ଉଭୟ ଗୋଲାର୍ଦ୍ଧରେ ଉପକ୍ରାନ୍ତୀୟ ଗୁରୁଚାପ ବଳୟରୁ ଉପମେରୁ ଦେଶୀୟ ଲଘୁଚାପ ବଳୟକୁ ପ୍ରବାହିତ ବାୟୁକୁ ପଶ୍ଚିମାବାୟୁ କୁହାଯାଏ।

xxii. ସାମୟିକ ବାୟୁପ୍ରବାହ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଦିନ ବା ବର୍ଷର ସମୟ ଭିଭିରେ ପରସ୍ପର ବିପରୀତ ଦିଗରୁ ପ୍ରବାହିତ ବାୟୁକୁ ସାମୟିକ ବାୟୁ ପ୍ରବାହ କୁହାଯାଏ।

xxiii. ସ୍ଥାନୀୟ ବାୟୁପ୍ରବାହ କହିଲେ କ’ଣ ?
Answer:
ଅଞ୍ଚଳ ଭିରିରେ ବର୍ଷର ନିର୍ଦ୍ଦିଷ୍ଟ ସମୟରେ ପ୍ରବାହିତ ବାୟୁକୁ
ସ୍ଥାନୀୟ ବାୟୁପ୍ରବାହ କୁହାଯାଏ।

xxiv. ଚିନୁକ୍ କାହାକୁ କୁହାଯାଏ ?
Answer:
ରକି ପର୍ବତମାଳାର ପୂର୍ବଢାଲୁ ଅଞ୍ଚଳରେ ଶୀତକାଳରେ ପ୍ରବାହିତ ଏକ ଉଷ୍ମ ଓ ଶୁଷ୍କ ବାୟୁକୁ ଚିନୁକ୍ କୁହାଯାଏ ।

xxv. ଆକସ୍ମିକ ବାୟୁପ୍ରବାହ କାହାକୁ କୁହାଯାଏ ?
Answer:
ବେଳେବେଳେ ବାୟୁଚାପରେ ଆକସ୍ମିକ ପରିବର୍ତ୍ତନ ଯୋଗୁଁ ଆକସ୍ମିକ ବାୟୁପ୍ରବାହ ହୋଇଥାଏ।

xxvi. ‘ବାଷ୍ପମୋଚନ ପ୍ରକ୍ରିୟା’ କାହାକୁ କୁହାଯାଏ ?
Answer:
ବୃକ୍ଷଲତାଦିଙ୍କର ଡାଳପତ୍ରରୁ ଜଳ ବାଷ୍ପୀଭୂତ ହୋଇ ବାୟୁମଣ୍ଡଳରେ ମିଶିବାକୁ ‘ ବାଷ୍ପମୋଚନ ପ୍ରକ୍ରିୟା’ କୁହାଯାଏ ।

xxvii. ବାୟୁର ଆର୍ଦ୍ରତା କାହାକୁ କୁହାଯାଏ ?
Answer:
ଜଳୀୟବାଷ୍ପର ଉପସ୍ଥିତି ଓ ପରିମାଣକୁ ‘ବାୟୁର ଆର୍ଦ୍ରତା’ କୁହାଯାଏ ।

xxviii. ପରିପୃକ୍ତ ବାୟୁ କାହାକୁ କୁହାଯାଏ ?
Answer:
ତାପମାତ୍ରା ଅନୁଯାୟୀ ବାୟୁରେ କ୍ଷମତା ପରିମାଣରେ ଜଳୀୟବାଷ୍ପ ଥିଲେ ତାହାକୁ ପରିପୃକ୍ତ ବାୟୁ କୁହାଯାଏ ।

xxix. ଅପରିପୃକ୍ତ ବାୟୁ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଜଳୀୟବାଷ୍ପ ଧାରଣ କ୍ଷମତାଠାରୁ କମ୍ ଜଳୀୟବାଷ୍ପ ଥିଲେ ତାକୁ ଅପରିପୃକ୍ତ ବାୟୁ କୁହାଯାଏ ।

xxx. କେଉଁ ଯନ୍ତ୍ରରେ ବାୟୁର ଆର୍ଦ୍ରତା ମାପ କରାଯାଏ ?
Answer:
ହାଇଗ୍ଲୋମିଟର ଯନ୍ତ୍ରରେ ବାୟୁର ଆର୍ଦ୍ରତା ମାପ କରାଯାଏ।

xxxi. ଶିଶିରାଙ୍କ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଯେଉଁ ତାପମାତ୍ରାରେ ଜଳୀୟବାଷ୍ପ କ୍ଷୁଦ୍ର କ୍ଷୁଦ୍ର ଜଳକଣାରେ ପରିଣତ ହୁଏ, ସେହି ତାପମାତ୍ରାକୁ ‘ଶିଶିରାଙ୍କ’ କୁହାଯାଏ ।

xxxii. ‘ଅଭିବହନ କୁହୁଡ଼ି’ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଶୀତଳ ବାୟୁ ଓ ଉଷ୍ମ ଆର୍ଦ୍ରବାୟୁର ମିଶ୍ରଣରେ ସୃଷ୍ଟ କୁହୁଡ଼ିକୁ ‘ ଅଭିବହନ କୁହୁଡ଼ି’ କୁହାଯାଏ।

xxxiii. ‘ମିଷ୍ଟ’ କ’ଣ ?
Answer:
କୁହୁଡ଼ି ଅତି ପତଳା ହେଲେ ତାହାକୁ ମିଷ୍ଟ କହନ୍ତି ।

xxxiv. ମେଘ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଆକାଶରେ ଭାସମାନ ଅବସ୍ଥାରେ ଥିବା ଜଳକଣା ଓ ତୁଷାରକଣାର ସମାହାରକୁ ମେଘ କୁହାଯାଏ।

xxxv. ସ୍ତରୀଭୂତ ମେଘ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଆକାଶର ବିସ୍ତୀର୍ଣ୍ଣ ଅଞ୍ଚଳରେ ସ୍ତର ସ୍ତର ହୋଇ ଭାସୁଥୁବା ମେଘକୁ ସ୍ତରୀଭୂତ ମେଘ କୁହାଯାଏ ।

xxxvi. ପୁଞ୍ଜିଭୂତ ମେଘ କାହାକୁ କୁହାଯାଏ ?
Answer:
କେତେକ ତୁଳାଗଦା ସଦୃଶ ମେଞ୍ଚା ମେଞ୍ଚା ହୋଇ ବହୁ ଉପରକୁ ଉଠି ରହିଥୁବା ଭଳି ଦେଖାଯାଉଥ‌ିବା ମେଘକୁ ପୁଞ୍ଜିଭୂତ ମେଘ କୁହାଯାଏ ।

xxxvii. କେଉଁ ମେଘରେ ବୃଷ୍ଟିପାତର ସମ୍ଭାବନା ଅଧିକ ରହେ ?
Answer:
ନିମ୍ନ ମେଘରେ ଜଳକଣା ଅଧିକ ଥିବାରୁ ବୃଷ୍ଟିପାତର ସମ୍ଭାବନା ଅଧିକ ରହେ ।

xxxviii. ବର୍ଷଣ କାହାକୁ କୁହାଯାଏ ?
Answer:
ମେଘରେ ଥିବା ଜଳ କିମ୍ବା ତୁଷାରକଣା ଘନୀଭୂତ ହୋଇ ତଳକୁ ଖସିବା ପ୍ରକ୍ରିୟାକୁ ବର୍ଷଣ କୁହାଯାଏ।

xxxix. ବୃଷ୍ଟିପାତ କାହାକୁ କୁହାଯାଏ ?
Answer:
ମେଘରେ ଥିବା ଜଳକଣା ଘନୀଭୂତ ହୋଇ ଜଳ ଆକାରରେ ଭୂପୃଷ୍ଠରେ ପଡ଼ିବାକୁ ବୃଷ୍ଟିପାତ କୁହାଯାଏ ।

xl. ବୃଷ୍ଟିପାତର ପରିମାଣ କେଉଁଥରେ ମପାଯାଏ ?
Answer:
ବୃଷ୍ଟିପାତର ପରିମାଣ ‘ରେନ୍ଗଗଜ’ ବା ବୃଷ୍ଟିମାପକ ଯନ୍ତ୍ରଦ୍ୱାରା ମପାଯାଏ ।

xli. ପରିଚଳନ ବୃଷ୍ଟିପାତ କେଉଁ ଅଞ୍ଚଳରେ ଓ କେଉଁ ସମୟରେ ହୋଇଥାଏ ?
Answer:
ପରି ଚଳନ ବୃଷ୍ଟିପାତ ନିରକ୍ଷୀୟ ଅଞ୍ଚଳରେ ପ୍ରତିଦିନ ଅପରାହ୍ନରେ ଏବଂ କ୍ରାନ୍ତିମଣ୍ଡଳୀୟ ଅଞ୍ଚଳରେ ଅପରାହ୍ନରେ ହୋଇଥାଏ ।

ପ୍ରତ୍ୟେକର ସଂଜ୍ଞା ଗୋଟିଏ ବାକ୍ୟରେ ପ୍ରକାଶ କର।

i. ଟ୍ରପୋସ୍ଟି ଅର
Answer:
ହାରାହାରି ୧୨ କିଲୋମିଟର ଉଚ୍ଚତା ବିଶିଷ୍ଟ ବାୟୁମଣ୍ଡଳର ସର୍ବନିମ୍ନ ସ୍ତର ।

ii. ଷ୍ଟ୍ରାଟୋସ୍ଟି ଅର
Answer:
ଟ୍ରପୋସ୍ପିଅର ଉପରକୁ ପ୍ରାୟ ୫୦ କି.ମି. ଉଚ୍ଚତା ପର୍ଯ୍ୟନ୍ତ ବ୍ୟାପିଥୁବା ବାୟୁ ସ୍ତର ।

iii. ଟ୍ରପୋପଜ୍
Answer:
ଟ୍ରପୋସ୍ପିଅର ଓ ଷ୍ଟ୍ରାଟୋସ୍ପିଅର ମଝିରେ ଥିବା ଏକ ପତଳା ବଳୟ ।

iv. ମେସୋପଜ୍
Answer:
ମେସୋସ୍ପିଅର୍ ଓ ଥର୍ମୋସ୍ପିଅରକୁ ପୃଥକ୍ କରୁଥିବା ଏକ ପତଳା ବଳୟ ।

v. ଥର୍ମୋସ୍ଟି ଅର୍
Answer:
ମେସୋସ୍ପିଅରର ଉପର ସ୍ତରକୁ ଥର୍ମୋସ୍ପିଅର କୁହାଯାଏ ।

vi. ଏକ୍‌ସ୍ଟି ଅର
Answer:
ବାୟୁମଣ୍ଡଳର ବାହ୍ୟ ସ୍ତର ।

vii. ପାଣିପାଗ
Answer:
ନିର୍ଦ୍ଦିଷ୍ଟ ସମୟରେ କୌଣସି ସ୍ଥାନର ବାୟୁମଣ୍ଡଳର ସାମୟିକ ଅବସ୍ଥା ।

viii. ଜଳବାୟୁ
Answer:
କୌଣସି ସ୍ଥାନର ପାଣିପାଗର ବହୁବର୍ଷ ଧରି ହାରାହାରି ଅବସ୍ଥା ।

ix. ସୌରାଭିତାପ
Answer:
ଭୂପୃଷ୍ଠରେ ସଂଗୃହୀତ ସୌରରଶ୍ମିର ପରିମାଣ ।

x. ତାପ ବଜେଟ୍
Answer:
ଶକ୍ତି ସଂଗ୍ରହ ଓ ଶକ୍ତି ବିକିରଣ ମଧ୍ୟରେ ସମତା ରହିବାକୁ ତାପ ବଜେଟ୍ କୁହାଯାଏ ।

xi. ଦୈନିକ ତାପ ବ୍ୟବଧାନ
Answer:
ଦୈନିକ ସର୍ବୋଚ୍ଚ ଓ ସର୍ବନିମ୍ନ ତାପମାତ୍ରା ମଧ୍ୟରେ ବ୍ୟବଧାନ ।

xii. ବାର୍ଷିକ ତାପଚକ୍ର
Answer:
ବର୍ଷକ ମଧ୍ୟରେ ତାପମାତ୍ରାର କ୍ରମଶଃ ହ୍ରାସବୃଦ୍ଧି ।

xiii. ଗ୍ରୀଷ୍ମମଣ୍ଡଳ/ଉଷୁମଣ୍ଡଳ
Answer:
କର୍କଟକ୍ରାନ୍ତି ଓ ମକରକ୍ରାନ୍ତିର ମଧ୍ୟବର୍ତ୍ତୀ ଅଞ୍ଚଳ ।

xiv ହିମମଣ୍ଡଳ
Answer:
ଉଭୟ ଗୋଲାର୍ଦ୍ଧରେ ମେରୁବୃରଠାରୁ ମେରୁ ମଧ୍ୟବର୍ତ୍ତୀ ଅଧ୍ବକ ତୀର୍ଯ୍ୟକ୍ କିରଣ ପଡ଼ୁଥିବା ଅଞ୍ଚଳ ।

x. ନିରକ୍ଷ ଶାନ୍ତ ବଳୟ
Answer:
ବିଷୁବ ବୃତ୍ତର ଉଭୟ ପାର୍ଶ୍ଵରେ ୫° ସମାକ୍ଷରେଖା ମଧ୍ୟବର୍ତ୍ତୀ ଚାପ ବଳୟ ।

xvi. ଉଇଣ୍ଡଭେନ୍‌
Answer:
ବାୟୁର ଦିଗ ମାପକ ଯନ୍ତ୍ର ।

xvii. ଆନିମୋମିଟର
Answer:
ବାୟୁର ବେଗ ମାପକ ଯନ୍ତ୍ର ।

xvili. ନିୟତ ବାୟୁ
Answer:
ଗୁରୁଚାପ ବଳୟରୁ ଲଘୁଚାପ ବଳୟକୁ ପ୍ରବାହିତ ବାୟୁ ।

xix. ଆୟନ ବାୟୁ/ବାଣିଜ୍ୟ ବାୟୁ
Answer:
ଉପକ୍ରାନ୍ତୀୟ ଗୁରୁଚାପ ବଳୟରୁ ନିରକ୍ଷୀୟ ଲଘୁଚାପ ବଳୟକୁ ପ୍ରବାହିତ ବାୟୁ ।

xx. ପଶ୍ଚିମା ବାୟୁ
Answer:
ଉଭୟ ଗୋଲାର୍ଦ୍ଧରେ ଉପକ୍ରାନ୍ତୀୟ ଗୁରୁଚାପ ବଳୟରୁ ଉପମେରୁ ଦେଶୀୟ ଲଘୁଚାପ ବଳୟକୁ ପ୍ରବାହିତ ବାୟୁ ।

xxi. ଗର୍ଜନଶୀଳ ଚାଳିଶା
Answer:
ଦକ୍ଷିଣ ଗୋଲାର୍ଦ୍ଧରେ ବିସ୍ତୀର୍ଣ୍ଣ ଜଳରାଶି ମଧ୍ୟରେ ପ୍ରାୟ ୪୦ରୁ ୪୯° ସମାକ୍ଷରେଖା ମଧ୍ଯରେ ପ୍ରବଳ ବେଗରେ ପ୍ରବାହିତ ପଶ୍ଚିମା ବାୟୁ ।

xxii. ମେରୁ ବାୟୁ
Answer:
ଉଭୟ ଗୋଲାର୍ଦ୍ଧରେ ମେରୁ ଦେଶୀୟ ଗୁରୁଚାପ ବଳୟରୁ ଉପମେରୁ ଦେଶୀୟ ଲଘୁଚାପ ବଳୟକୁ ପ୍ରବାହିତ ବାୟୁ ।

xxiii. ସାମୟିକ ବାୟୁ
Answer:
ଦିନ ବା ବର୍ଷର ସମୟ ଭିତ୍ତିରେ ପରସ୍ପର ବିପରୀତ ଦିଗରୁ ପ୍ରବାହିତ ବାୟୁ ।

xxiv. ସ୍ଥଳ ବାୟୁ
Answer:
ସ୍ଥଳଭାଗରୁ ସମୁଦ୍ର ଆଡ଼କୁ ପ୍ରବାହିତ ବାୟୁ ।

xxv. ସମୁଦ୍ର ବାୟୁ
Answer:
ସମୁଦ୍ରରୁ ସ୍ଥଳଭାଗକୁ ପ୍ରବାହିତ ହେଉଥିବା ବାୟୁ ।

xxvi. ଦକ୍ଷିଣ-ପୂର୍ବ ମୌସୁମୀ ବାୟୁ
Answer:
ଗ୍ରୀଷ୍ମକାଳରେ ଏସିଆ ମହାଦେଶର ଦକ୍ଷିଣରେ ଥ‌ିବା ବିସ୍ତୃତ ଜଳଭାଗରୁ ସ୍ଥଳଭାଗକୁ ଦକ୍ଷିଣ-ପଶ୍ଚିମ ଦିଗରୁ ପ୍ରବାହିତ ମୌସୁମୀ ବାୟୁ ।

xxvi. କାଳବୈଶାଖୀ
Answer:
ଓଡ଼ିଶାର ଉତ୍ତରଭାଗ, ପଶ୍ଚିମବଙ୍ଗ, ଆସାମ, ବାଂଲାଦେଶରେ ଗ୍ରୀଷ୍ମଦିନେ ଅପରାହ୍ନରେ ଉଷ୍ଣ ବାୟୁପ୍ରବାହ ଫଳରେ ଘଡ଼ଘଡ଼ି ସହ ହେଉଥ‌ିବା ବୃଷ୍ଟିପାତ ।

xxvili. କୁ
Answer:
ଗ୍ରୀଷ୍ମଦିନେ ଗାଙ୍ଗେୟ ସମତଳ ଅଞ୍ଚଳ ତଥା ରାଜସ୍ଥାନରେ ପ୍ରବାହିତ ହେଉଥ‌ିବା ଏକ ଅତି ଉଷ୍ଣ ଓ ଶୁଷ୍କ ବାୟୁ ।

xxix. ଚିନୁକ୍
Answer:
ରକି ପର୍ବତମାଳାର ପୂର୍ବ ଢାଲୁ ଅଞ୍ଚଳରେ ଶୀତକାଳରେ ପ୍ରବାହିତ ଏକ ଉଷ୍ଣ ଓ ଶୁଷ୍କ ବାୟୁ ।

xxx. ବାୟୁର ଆର୍ଦ୍ରତା
Answer:
ବାୟୁରେ ଜଳୀୟବାଷ୍ପର ପରିମାଣ ଓ ଉପସ୍ଥିତିକୁ ବାୟୁର ଆର୍ଦ୍ରତା କୁହାଯାଏ ।

xxxi. ଶିଶିରାଙ୍କ
Answer:
ଯେଉଁ ତାପମାତ୍ରାରେ ଜଳୀୟବାଷ୍ପ କ୍ଷୁଦ୍ର କ୍ଷୁଦ୍ର ଜଳକଣାରେ ପରିଣତ ହୁଏ ।

xxxii.ବାଷ୍ପୀଭବନ
Answer:
ଜଳ ଗ୍ୟାସୀୟ ଅବସ୍ଥାରେ ପରିବର୍ତ୍ତିତ ହେବା ପ୍ରକ୍ରିୟା ।

xxxiii. ଘନୀଭବନ
Answer:
ଜଳୀୟବାଷ୍ପ ଗ୍ୟାସୀୟ ଅବସ୍ଥାରୁ ତରଳ ବା କଠିନ ଅବସ୍ଥାକୁ ପରିବର୍ତ୍ତିତ ହେବା ପ୍ରକ୍ରିୟା ।

xxxiv. ଅଭିବହନ କୁହୁଡ଼ି
Answer:
ଶୀତଳ ବାୟୁ ଓ ଉଷ୍ଣ ଆର୍ଦ୍ର ବାୟୁର ମିଶ୍ରଣରେ ସୃଷ୍ଟି ହେଉଥ‌ିବା କୁହୁଡ଼ି ।

xxxv. ମିଷ୍ଟ୍
Answer:
କୁହୁଡ଼ି ଅତି ପତଳା ହେଲେ ତାହାକୁ ମିଷ୍ଟ୍ କୁହାଯାଏ ।

xxxvi. ସ୍ତରୀଭୂତ ମେଘ
Answer:
ଆକାଶରେ ବିସ୍ତୀର୍ଣ୍ଣ ଅଞ୍ଚଳରେ ସ୍ତର ସ୍ତର ହୋଇ ଭାସୁଥ‌ିବା ମେଘ ।

xxxvii.ପୁଞ୍ଜିଭୂତ ମେଘ
Answer:
ତୁଳାଗଦା ସଦୃଶ ମେଞ୍ଚା ମେଞ୍ଚା ହୋଇ ବହୁ ଉପରକୁ ଉଠି ରହି ଦେଖାଯାଉଥ‌ିବା ମେଘ ।

xxxviii.ନିମ୍ନ ମେଘ
Answer:
ଭୂପୃଷ୍ଠରୁ ପ୍ରାୟ ଦୁଇ କିଲୋମିଟର ପର୍ଯ୍ୟନ୍ତ ଉଚ୍ଚତାରେ ଥିବା ମେଘ ।

xxxix. ମଧ୍ୟ ମେଘ
Answer:
ଦୁଇ କିଲୋମିଟରରୁ ୬ କିଲୋମିଟର ଉଚ୍ଚତା ପର୍ଯ୍ୟନ୍ତ ବିସ୍ତୃତ ହୋଇଥିବା ମେଘ ।

xl. ଉଚ୍ଚ ମେଘ
Answer:
୬ କି.ମି.ରୁ ୧୨ କି.ମି. ପର୍ଯ୍ୟନ୍ତ ବ୍ୟାପିଥୁବା ମେଘ ।

xli. ବର୍ଷଣ
Answer:
ମେଘରେ ଥ‌ିବା ଜଳ କିମ୍ବା ତୁଷାରକଣା ଘନୀଭୂତ ହୋଇ ତଳକୁ ଖସିବା ପ୍ରକ୍ରିୟା ।

xlii. ରେନ୍ଗଗଳ
Answer:
ବୃଷ୍ଟିପାତର ପରିମାଣ ମାପ କରାଯାଉଥିବା ଯନ୍ତ୍ର ।

xliii. ହାଇଟ୍ରୋମିଟର
Answer:
ବାୟୁର ଆର୍ଦ୍ରତା ମାପ କରାଯାଉଥିବା ଯନ୍ତ୍ର ।

ପ୍ରତ୍ୟେକ ବାକ୍ୟାଶକୁ ଗୋଟିଏ ଶବ୍ଦରେ ପ୍ରକାଶ କର ।

i. ପୃଥ‌ିବୀକୁ ଘେରି ରହିଥିବା ଗ୍ୟାସୀୟ ବଳୟ ।
Answer:
ବାୟୁମଣ୍ଡଳ

ii. ବାୟୁମଣ୍ଡଳରେ ସର୍ବାଧ‌ିକ ପରିମାଣରେ ରହିଥ‌ିବା ଗ୍ୟାସ୍ ।
Answer:
ଯବକ୍ଷାରଜାନ

iii. ଜୀବଜଗତ ପାଇଁ ସବୁଠାରୁ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ସ୍ତର ।
Answer:
ଟ୍ରପୋସ୍ଫି ୟର

iv. ଭୂପୃଷ୍ଠର ସଂଗୃହୀତ ସୌରରଶ୍ମିର ପରିମାଣ ।
Answer:
ସୌରାଭିତାପ,

v. କୌଣସି ସ୍ଥାନର ଏକ ବର୍ଗ ସେ.ମି. ପରିମିତ ଅଞ୍ଚଳରେ ବାୟୁମଣ୍ଡଳର ଶେଷସୀମା ପର୍ଯ୍ୟନ୍ତ ବିସ୍ତୃତ ବାୟୁସ୍ତରର ଓଜନ ।
Answer:
ବାୟୁଚାପ

vi. ବାୟୁମଣ୍ଡଳର ଶାନ୍ତ ଓ ଚଳନଶୂନ୍ୟ ବଳୟ ।
Answer:
ନିରକ୍ଷୀୟ ଲଘୁଚାପ ବଳୟ

vii. ରକି ପର୍ବତମାଳାର ପୂର୍ବଜାଲୁ ଅଞ୍ଚଳରେ ଶୀତକାଳରେ ପ୍ରବାହିତ ଏକ ଉଷ୍ଣ ଓ ଶୁଷ୍କ ବାୟୁପ୍ରବାହ ।
Answer:
ଚିନୁକ୍

viii. ବାୟୁମଣ୍ଡଳରେ ଜଳୀୟବାଷ୍ପର ଉପସ୍ଥିତି ଓ ପରିମାଣ ।
Answer:
ବାୟୁର ଆର୍ଦ୍ରତା

ix. ଭୂପୃଷ୍ଠର ତାପ ବିକିରଣରୁ ସୃଷ୍ଟ କୁହୁଡ଼ି ।
Answer:
ବିକିରଣ କୁହୁଡ଼ି

x. ଆକାଶରେ ଭାସମାନ ଅବସ୍ଥାରେ ଥିବା ଜଳକଣା ଓ ତୁଷାରକଣାର ସମାହାର ।
Answer:
ମେଘ

xi. ଭୂପୃଷ୍ଠରୁ ଦୁଇ କି.ମି. ପର୍ଯ୍ୟନ୍ତ ଉଚ୍ଚତାରେ ଥିବା ମେଘ
Answer:
ନିମ୍ନମେଘ

xii. ଭୂପୃଷ୍ଠରୁ ୨ ରୁ ୬ କି.ମି. ଉଚ୍ଚତା ମଧ୍ୟରେ ଥିବା ମେଘ ।
Answer:
ମଧ୍ୟମେଘ

xiii. ଦୁଇ କ୍ରାନ୍ତିବୃତ୍ତ ମଧ୍ୟବର୍ତ୍ତୀ ତାପମଣ୍ଡଳ ।
Answer:
ଗ୍ରୀଷ୍ମମଣ୍ଡଳ

xiv ବାୟୁମଣ୍ଡଳର ସର୍ବନିମ୍ନ ସ୍ତର ।
Answer:
ଟ୍ରପୋସ୍ଟିଅର୍

xv ପୃଥ‌ିବୀ ଗ୍ରହଣ କରୁଥିବା ସୂର୍ଯ୍ୟତାପ ।
Answer:
ସୌରାଭିତାପ

xvi. କ୍ରାନ୍ତିବୃତ୍ତ ଓ ମେରୁବୃତ୍ତ ମଧ୍ୟବର୍ତୀ ତାପମଣ୍ଡଳ ।
Answer:
ନାତିଶୀତୋଷ୍ଣ ମଣ୍ଡଳ

xvii. ପ୍ରବାହିତ ବାୟୁ ।
Answer:
ପବନ

xviii.ଖରାଦିନେ ଉତ୍ତର ଭାରତରେ ପ୍ରବାହିତ ଉଷ୍ଣ, ଶୁଷ୍କ ଓ ଧୂଳିପୂର୍ବ ବାୟୁ ।
Answer:
ଲୁ

xix. ଋତୁ ଅନୁଯାୟୀ ପ୍ରବାହିତ ବାୟୁ ।
Answer:
ମୌସୁମୀବାୟୁ

xx. ଦକ୍ଷିଣ ଗୋଲାର୍ଦ୍ଧରେ ବହୁଥ‌ିବା ପଶ୍ଚିମାବାୟୁ ।
Answer:
ଗର୍ଜନଶୀଳ ଚାଳିଶା

xxi. ପ୍ରାକୃତିକ ପ୍ରକ୍ରିୟାରେ ଆକାଶରୁ ଜଳ ତରଳ କିମ୍ବା କଠିନ ଅବସ୍ଥାରେ ଭୂପୃଷ୍ଠରେ ପଡ଼ିବା ।
Answer:
ବର୍ଷଣ

xxii. ଜଳର ବାଷ୍ପୀୟ ଅବସ୍ଥାକୁ ପରିବର୍ତ୍ତନ କରୁଥିବା ପ୍ରକ୍ରିୟା ।
Answer:
ବାଷ୍ପୀଭବନ

xxiii.ଯେଉଁ ତାପମାତ୍ରାରେ ବାୟୁମଣ୍ଡଳରେ ଥିବା ଜଳକଣା ଘନୀଭୂତ ହୁଏ ।
Answer:
ଶିଶିରାଙ୍କ

xxiv. ଜଳୀୟବାଷ୍ପକୁ ଜଳରେ ପରିଣତ କରୁଥିବା ପ୍ରକ୍ରିୟା ।
Answer:
ଘନୀଭବନ

xxv. ଉଷ୍ଣ ଓ ଆର୍ଦ୍ର ବାୟୁ ଉପରକୁ ଉଠି ଝଡ଼ ସହ ହେଉଥ‌ିବା ବୃଷ୍ଟିପାତ ।
Answer:
ବାତାବର୍ଗ ଜନିତ ବୃଷ୍ଟିପାତ

xxvi. ନିରକ୍ଷୀୟ ଅଞ୍ଚଳରେ ହେଉଥୁବା ବୃଷ୍ଟିପାତ ।
Answer:
ପରିଚଳନ ବୃଷ୍ଟିପାତ

xxvi. ବାୟୁର ଜଳୀୟବାଷ୍ପ ପରିମାଣି ମାପୁଥିବା ଯନ୍ତ୍ର ।
Answer:
ହାଇଡ୍ରୋମିଟର

xxvili. ଯେଉଁ ପ୍ରକ୍ରିୟାରେ ବୃକ୍ଷଲତାଦିଙ୍କର ଡାଳପତ୍ରରୁ ଜଳ ବାଷ୍ପୀଭୂତ ହୁଏ ।
Answer:
ବାଷ୍ପୀମୋଚନ ପ୍ରକ୍ରିୟା

xxix. ପର୍ବତର ଯେଉଁ ପାର୍ଶ୍ବରେ ଅଳ୍ପବୃଷ୍ଟି ହୋଇଥାଏ ।
Answer:
ଅନୁବାତ ପାର୍ଶ୍ଵ

xx. ମେଘରୁ ଭୂପୃଷ୍ଠକୁ ଖସୁଥୁବା ଛୋଟବଡ଼ ବରଫଖଣ୍ଡ ।
Answer:
କୁଆପଥର

xxxi.ଶୀତଳ ବାୟୁ ଓ ଉଷ୍ଣ ଆର୍ଦ୍ର ବାୟୁ ମିଶ୍ରଣରେ ସୃଷ୍ଟି ହେଉଥିବା କୁହୁଡ଼ି ।
Answer:
ଅଭିବହନ କୁହୁଡ଼ି

xxxii. ମେକ୍‌ସିକୋ ଉପକୂଳରେ ବାତାବର୍ଭର ନାମ ।
Answer:
ହରିକେନ୍

xxxiii. ଜଳକଣାର ପରିମାଣ ଅପେକ୍ଷାକୃତ ଅଧିକ ଥିବା ମେଘ ।
Answer:
ପୁଞ୍ଜୀଭୂତ ମେଘ

ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

i. ଜୀବଜଗତ ପାଇଁ _______ ସ୍ତର ଅଧିକ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ।
Answer:
ଟ୍ରପୋସ୍ଟି ୟର

ii. ପୃଥ‌ିବୀକୁ _____ ସ୍ତର ଲାଗିରହିଛି ।
Answer:
ଟ୍ରପୋସ୍ଫିୟର

iii. ବାୟୁମଣ୍ଡଳରେ ____ ଗ୍ୟାସ୍ ସର୍ବାଧ‌ିକ ପରିମାଣରେ ରହିଛି ।
Answer:
ଯବକ୍ଷାରଜାନ

iv. ଜୀବଜଗତ ତିଷ୍ଠିବାପାଇଁ _____ ଗ୍ୟାସ୍‌ ଏକାନ୍ତ ଆବଶ୍ୟକ ।
Answer:
ଅମ୍ଳଜାନ

v. ସୂର୍ଯ୍ୟଙ୍କଠାରୁ ଆସୁଥ‌ିବା କ୍ଷତିକାରକ ରଶ୍ମି ପ୍ରଭାବରୁ ______ ସ୍ତର ଆମକୁ ରକ୍ଷା କରିଥାଏ ।
Answer:
ଷ୍ଟ୍ରାଟୋସ୍ଫିୟର

vi. ବିଷୁବ ଅଞ୍ଚଳରେ ଟ୍ରପୋସ୍ପିୟର ଭୂପୃଷ୍ଠରୁ _______ କି.ମି. ଉଚ୍ଚତା ପର୍ଯ୍ୟନ୍ତ ବ୍ୟାପି ରହିଛି ।
Answer:
୧୬

vii. ଚିନୁକ୍ ନାମକ ଉଷ୍ଣ ଓ ଶୁଷ୍କ ବାୟୁ ______ ଅଞ୍ଚଳରେ ପ୍ରବାହିତ ହୋଇଥାଏ ।
Answer:
ରକି ପର୍ବତ

viii. ବାତାବର୍ଷକୁ ଚୀନ୍ ଉପକୂଳରେ ______ କୁହାଯାଏ ।
Answer:
ଟାଇଫୁନ୍

ix. ମୌସୁମୀ ବାୟୁ ______ ବାୟୁପ୍ରବାହର ଅନ୍ତର୍ଗତ ।
Answer:
ସାମୟିକ

x. ଗର୍ଜନଶୀଳ ଚାଳିଶା _____ ଗୋଲାର୍ଦ୍ଧରେ ପ୍ରବାହିତ ହୁଏ ।
Answer:
ଦକ୍ଷିଣ

xi. ବାଣିଜ୍ୟ ବାୟୁ ______ ବାୟୁ ପ୍ରବାହର ଅନ୍ତର୍ଗତ ।
Answer:
ନିୟତ

xii. ବାୟୁର ଦିଗ _____ ଯନ୍ତ୍ର ସାହାଯ୍ୟରେ ମାପ କରାଯାଏ ।
Answer:
ଉଇଣ୍ଡଭେନ୍

xiii. ବାୟୁର ବେଗ ______ ଯନ୍ତ୍ର ସାହାଯ୍ୟରେ ମାପ କରାଯାଏ ।
Answer:
ଆନିମୋମିଟର

xiv ବାୟୁ ଚାପ _____ ଯନ୍ତ୍ର ସାହାଯ୍ୟରେ ମାପ କରାଯାଏ ।
Answer:
ବାରୋମିଟର

xv ଓଡ଼ିଶାରେ ଗ୍ରୀଷ୍ମଋତୁର ଅପରାହ୍ନରେ _____ ବାୟୁ ପ୍ରବାହିତ ହୁଏ ।
Answer:
କାଳବୈଶାଖୀ

xvi. ଶୀତଳ ବାୟୁ ଓ ଉଷ୍ଣ ଆର୍ଦ୍ର ବାୟୁ ମିଳନରେ ______ ସୃଷ୍ଟି ହୁଏ ।
Answer:
ଅଭିବହନ

xvii. ନିରକ୍ଷୀୟ ଅଞ୍ଚଳରେ ପ୍ରତିଦିନ ଅପରାହ୍ନରେ _____ ବୃଷ୍ଟିପାତ ହୋଇଥାଏ ।
Answer:
ପରିଚଳନ

xviii. ପର୍ବତର ଯେଉଁ ପାର୍ଶ୍ଵରେ ଅଧ‌ିକ ବର୍ଷା ହୁଏ ତାହାକୁ ______ ପାର୍ଶ୍ବ କୁହାଯାଏ ।
Answer:
ପ୍ରତିବାତ

xix. ହାଲୁକା ଗ୍ୟାସ୍‌ମାନ_____  ସ୍ତରରେ ମହଜୁଦ ରହିଛି ।
Answer:
ଏକ୍‌ ସୋସ୍ଟି ଅର୍

xx. ସୌରାଭିତାପର ପରିମାଣ ପୃଥୁବୀର ______ ଅଞ୍ଚଳରେ ସର୍ବାଧ୍ବକ ।
Answer:
ବିଷୁବ

xxi. ଗତିଶୀଳ ବାୟୁକୁ _____ କୁହାଯାଏ ।
Answer:
ପବନ

xxii. ବୃକ୍ଷଲତାଦି ____ ପ୍ରକ୍ରିୟାରେ ବାୟୁମଣ୍ଡଳକୁ ବାଷ୍ପ ଛାଡ଼ିଥାନ୍ତି ।
Answer:
ବାଷ୍ପମୋଚନ

ଠିକ୍ ଉତ୍ତର ବାଛି ଲେଖ।

Question i.
ବାୟୁମଣ୍ଡଳରେ କେଉଁ ଗ୍ୟାସ୍‌ର ପରିମାଣ ସବୁଠାରୁ ଅଧିକ ?
(କ) ଅମ୍ଳଜାନ
(ଗ) ଆରଗନ୍
(ଖ) ଅଙ୍ଗାରକାମ୍ଳ
(ଘ) ଯବକ୍ଷାରଜାନ
Answer:
(ଘ) ଯବକ୍ଷାରଜାନ

Question ii.
ସମୁଦ୍ରପତ୍ତନରୁ ଉପରକୁ ଆରୋହଣ କଲେ ପ୍ରତି କେତେ ମିଟରରେ ତାପମାତ୍ରା ୧° ସେଲ୍ସିୟସ୍ ହାରରେ ହ୍ରାସ ପାଏ ?
(କ) ୧୬୦
(ଖ) ୧୬୫
(ଗ) ୧୭୦
(ଘ) ୧୭୫
Answer:
(ଖ) ୧୬୫

Question iii.
୨୩– ଉତ୍ତର ସମାକ୍ଷରେଖାଠାରୁ ୬୬ – ଉତ୍ତର ସମାକ୍ଷରେଖା ମଧ୍ଯରେ କେଉଁ ତାପମଣ୍ଡଳ ଅବସ୍ଥିତ ?
(କ) ଗ୍ରୀଷ୍ମ
(ଖ) ଉତ୍ତର ନାତିଶୀତୋଷ୍ଣ
(ଗ) ଉତ୍ତର ହିମ
(ଘ) ଦକ୍ଷିଣ ନାତିଶୀତୋଷ୍ଣ)
Answer:
(ଖ) ଉତ୍ତର ନାତିଶୀତୋଷ୍ଣ

Question iv.
୬୬- ଦକ୍ଷିଣ ସମାକ୍ଷରେଖାଠାରୁ ୯୦° ଦକ୍ଷିଣ ସମାକ୍ଷରେଖା ପର୍ଯ୍ୟନ୍ତ ଅଞ୍ଚଳ କେଉଁ ତାପ ମଣ୍ଡଳରେ ଅବସ୍ଥିତ ?
(କ) ଦକ୍ଷିଣ ନାତିଶୀତୋଷ୍ଣ
(ଖ) ଉତ୍ତର ହିମ
(ଗ) ଦକ୍ଷିଣ ହିମ
(ଘ) ଉତ୍ତର ନାତିଶୀତୋଷ୍ଣ
Answer:
(ଗ) ଦକ୍ଷିଣ ହିମ

Question v.
ବାୟୁରେ ଅମ୍ଳଜାନ ପ୍ରାୟ ଶତକଡ଼ା କେତେ ଭାଗ ?
(କ) ୧୨
(ଖ) ୨୧
(ଗ) ୭୭
(ଘ) ୯୭
Answer:
(ଖ) ୨୧

Question vi.
ଟ୍ରପୋସ୍ଟିଅର୍ ପୃଥ‌ିବୀପୃଷ୍ଠରୁ ପ୍ରାୟ କେତେ କି.ମି. ପର୍ଯ୍ୟନ୍ତ ବ୍ୟାପି ରହିଛି ?
(କ) ୫-୧୦
(ଖ) ୬–୧୨
(ଗ) ୭-୧୪
(ଘ) ୮-୧୬
Answer:
(ଘ) ୮-୧୬

Question vii.
ମୌସୁମୀ ବାୟୁ କେଉଁ ବାୟୁ ପ୍ରବାହ ଅନ୍ତର୍ଗତ ?
(କ) ନିୟତ
(ଖ) ଆକସ୍ମିକ
(ଗ) ସାମୟିକ
(ଘ) ସ୍ଥାନୀୟ
Answer:
(ଗ) ସାମୟିକ

Question viii.
କୁ କେଉଁ ବାୟୁ ପ୍ରବାହ ଅନ୍ତର୍ଗତି ?
(କ) ଆକସ୍ମିକ
(ଖ) ସ୍ଥାନୀୟ
(ଗ) ସାମୟିକ
(ଘ) ନିୟତ
Answer:
(ଖ) ସ୍ଥାନୀୟ

Question ix.
ଉତ୍ତର ଗୋଲାର୍ଦ୍ଧରେ ପଶ୍ଚିମାବାୟୁ କେଉଁ ଦିଗରୁ ବହେ ?
(କ) ଉତ୍ତର-ପଶ୍ଚିମ
(ଖ) ଦକ୍ଷିଣ-ପଶ୍ଚିମ
(ଗ) ଉତ୍ତର-ପୂର୍ବ
(ଘ) ଦକ୍ଷିଣ-ପୂର୍ବ
Answer:
(ଖ) ଦକ୍ଷିଣ-ପଶ୍ଚିମ

Question x.
ଦକ୍ଷିଣ ଗୋଲାର୍ଦ୍ଧରେ ପଶ୍ଚିମାବାୟୁ କେଉଁ କୋଣରୁ ବହେ ?
(କ) ଉତ୍ତର-ପଶ୍ଚିମ
(ଖ) ଦକ୍ଷିଣ-ପଶ୍ଚିମ
(ଗ) ଉତ୍ତର-ପୂର୍ବ
(ଘ) ଦକ୍ଷିଣ-ପୂର୍ବ
Answer:
(କ) ଉତ୍ତର-ପଶ୍ଚିମ

Question xi.
ଆୟନବାୟୁ ଦକ୍ଷିଣ ଗୋଲାର୍ଦ୍ଧରେ କେଉଁ ଦିଗରୁ ବହେ ?
(କ) ଉତ୍ତର-ପଶ୍ଚିମ
(ଖ) ଦକ୍ଷିଣ-ପଶ୍ଚିମ
(ଗ) ଉତ୍ତର-ପୂର୍ବ
(ଘ) ଦକ୍ଷିଣ-ପୂର୍ବ
Answer:
(ଘ) ଦକ୍ଷିଣ-ପୂର୍ବ

Question xii.
ଉତ୍ତର ଗୋଲାର୍ଦ୍ଧରେ ଆୟନବାୟୁ କେଉଁ ଦିଗରୁ ବହେ ?
(କ) ଉତ୍ତର-ପଶ୍ଚିମ
(ଖ) ଦକ୍ଷିଣ-ପଶ୍ଚିମ
(ଗ) ଉତ୍ତର-ପୂର୍ବ
(ଘ) ଦକ୍ଷିଣ-ପୂର୍ବ
Answer:
(ଗ) ଉତ୍ତର-ପୂର୍ବ

Question xiii.
ମେରୁ ଅଞ୍ଚଳରେ ଟ୍ରପୋସ୍ଟି ଅର୍‌ରେ ଉଚ୍ଚତା ପ୍ରାୟ କେତେ କି.ମି. ?
(କ) ୮
(ଖ) ୧୨
(ଗ) ୧୬
(ଘ) ୨୦
Answer:
(କ) ୮

Question xiv
କେଉଁ ସ୍ତରରେ ଓଜୋନ୍‌ ଗ୍ୟାସ୍ ରହିଛି ?
(କ) ଟ୍ରପୋସ୍ପିଅର୍
(ଖ) ଷ୍ଟ୍ରାଟୋସ୍ପିଅର୍
(ଗ) ଥର୍ମୋସ୍ତ୍ ଅର୍
(ଘ) ମେସୋସ୍ପିଅର୍
Answer:
(ଖ) ଷ୍ଟ୍ରାଟୋସ୍ପିଅର୍

Question xv.
ସମୁଦ୍ର ପତ୍ତନରେ ବାୟୁଚାପ କେତେ ମିଲିବାର ?
(କ)୧୦୦୦
(ଖ)୧୦୧୧
(ଗ)୧୦୧୨
(ଘ)୧୦୧୩
Answer:
(ଘ)୧୦୧୩

Question xvi.
ବାୟୁଚାପ କେଉଁ ଯନ୍ତ୍ରରେ ନିର୍ଣ୍ଣୟ କରାଯାଏ ?
(କ) ଥର୍ମୋମିଟର
(ଖ) ବ୍ୟାରୋମିଟର
(ଗ) ଆନିମୋମିଟର
(ଘ) ସ୍ପିଡୋମିଟର
Answer:
(ଖ) ବ୍ୟାରୋମିଟର

Question xvii.
ଭାରତ ଉପକୂଳରେ କ୍ରାନ୍ତୀୟ ବାତାବର୍ଷକୁ କ’ଣ କୁହାଯାଏ ?
(କ) ଟାଇଫୁନ୍
(ଖ) ସୁନାମୀ
(ଗ) ହରିକେନ୍
(ଘ) ସାଇକ୍ଲୋନ୍
Answer:
(ଘ) ସାଇକ୍ଲୋନ୍

Question xviii.
କେଉଁ ଉପକୂଳରେ ଅଭିବହନ କୁହୁଡ଼ି ଦେଖାଯାଏ ?
(କ) ଭାରତ
(ଗ) ଚୀନ୍
(ଖ) ମେକ୍‌ସିକୋ
(ଘ) ନିଉଫାଉଣ୍ଡଲାଣ୍ଡ
Answer:
(ଘ) ନିଉଫାଉଣ୍ଡଲାଣ୍ଡ

Question xix.
ଆକାଶରେ ଯେପରି ମେଘ ଦେଖାଯାଏ, ଭୂପୃଷ୍ଠରେ ସେହିପରି ଶୀତଦିନେ କ’ଣ ଦେଖାଯାଏ ?
(କ) ଶିଶିର
(ଗ) କୁହୁଡ଼ି
(ଖ) ତୁହିନ
(ଘ) କାକର
Answer:
(ଗ) କୁହୁଡ଼ି

Question xx.
ପର୍ବତରେ ଜଳୀୟବାଷ୍ପପୂର୍ଣ୍ଣ ବାୟୁ ବାଧା ପାଇଲେ କେଉଁଠାରେ ଅଧିକ ବର୍ଷା ହୁଏ ?
(କ) ପ୍ରତିବାତ ପାର୍ଶ୍ବ
(ଖ) ଅନୁବାତ ପାର୍ଶ୍ବ
(ଗ) ବୃଷ୍ଟିଛାୟା ଅଞ୍ଚଳ
(ଘ) ସମୁଦ୍ର
Answer:
(କ) ପ୍ରତିବାତ ପାର୍ଶ୍ବ

Question xxi.
ବାୟୁର ଆର୍ଦ୍ରତା କାହା ଉପରେ ନିର୍ଭର କରେ ?
(କ) ତାପମାତ୍ରା
(ଖ) ବେଗ
(ଗ) ବାଷ୍ପୀଭବନ
(ଘ) ଘନୀଭବନ
Answer:
(କ) ତାପମାତ୍ରା

ବନ୍ଧନୀ ମଧ୍ଯରୁ ଉପଯୁକ୍ତ ଶବ୍ଦ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

1. ବାୟୁମଣ୍ଡଳରେ ଯବକ୍ଷାରଜାନର ପରିମାଣ ଶତକଡ଼ା ____ ଭାଗ । (୭୫, ୭୬, ୭୭, ୭୮)
Answer:
୭୮

2. ବାୟୁମଣ୍ଡଳରେ ଅମ୍ଳଜାନର ପରିମାଣ ଶତକଡ଼ା _____ ଭାଗ। (୨୦, ୨୧, ୨୨, ୨୩)
Answer:
୨୧

3. ବାୟୁମଣ୍ଡଳରେ ଆରଗନ୍ ଗ୍ୟାସ୍‌ର ପରିମାଣ ଶତକଡ଼ା _____ ଭାଗ । (୦.୯୧, ୦,୯୨, ୦,୯୩, ୨,୯୪)
Answer:
୦.୯୪

4. ବାୟୁ ମଣ୍ଡଳରେ ଅଙ୍ଗାରକାମ୍ଳ ଗ୍ୟାସ୍‌ ପରିମାଣ ଶତକଡ଼ା _____ ଭାଗ । (୦.୦୩, ୦.୦୪, ୦,୦୫, ୦,୦୬)
Answer:
୦.୦୩

5. ଜୀବଜଗତ ତିଷ୍ଠିବାପାଇଁ _____ ଗ୍ୟାସ୍ ଏକାନ୍ତ ଆବଶ୍ୟକ । (ଯବକ୍ଷାରଜାନ, ଅମ୍ଳଜାନ, ଅଙ୍ଗାରକାମ୍ଳ, ଆରଗନ୍)
Answer:
ଅମ୍ଳଜାନ

6. ପୃଥ‌ିବୀପୃଷ୍ଠକୁ _____ ସ୍ତର ଲାଗିରହିଛି । (ଟ୍ରପୋସ୍ପିୟର, ମେସୋସ୍ଟି ୟର, ଷ୍ଟ୍ରାଟୋସ୍ଫିୟର, ଆୟୋନୋସ୍ଫିୟର )
Answer:
ଟ୍ରପୋସ୍ଫିୟର

7. ହିଲିୟମ୍ ଓ ଉଦ୍‌ଜାନ ହାଲୁକା ଗ୍ୟାସ୍ _____ ସ୍ତରରେ ଅବସ୍ଥିତ। (ଆୟୋନସ୍କ୍ରି ୟର, ମେସୋସ୍ଫିୟର, ଷ୍ଟ୍ରାଟୋସ୍ପିୟର, ଏକ୍ସୋସ୍ପିୟର)
Answer:
ଏକ୍ରୋସ୍ଫିୟର

8. ବାୟୁ ଚାପକୁ _____ ଏକକରେ ପ୍ରକାଶ କରାଯାଏ। (ମିଲିଲିଟର, ଲିଟର, ମିଲିବାର, ସେଣ୍ଟିମିଟର)
Answer:
ମିଲିବାର

9. ଉଭୟ ଗୋଲାର୍ଦ୍ଧର ୨୫° ରୁ ୩୫° ସମାକ୍ଷରେଖା ମଧ୍ଯରେ _____ ଚାପ ବଳୟ ଦେଖାଯାଏ । ନିରକ୍ଷୀୟ ଲଘୁଚାପ, ଉପକ୍ରାନ୍ତୀୟ ଗୁରୁଚାପ, ଉପମେରୁ- ଦେଶୀୟ ଲଘୁଚାପ, ମେରୁଦେଶୀୟ ଗୁରୁଚାପ)
Answer:
ଉପକ୍ରାନ୍ତୀୟ ଗୁରୁଚାପ

10. ଗୁରୁଚାପ ବଳୟରୁ ଲଘୁଚାପ ବଳୟକୁ ନିୟମିତ ପ୍ରବାହିତ ବାୟୁକୁ _____ ବାୟୁ ପ୍ରବାହ କୁହାଯାଏ । (ନିୟତ ବାୟୁ, ବାୟୁ ସାମୟିକ ବାୟୁ, ଆକସ୍ମିକ ବାୟୁ, ସ୍ଥାନୀୟ)
Answer:
ନିୟତ ବାୟୁ

11. ଗର୍ଜନଶୀଳ ଚାଳିଶା _____ ବାୟୁ ପ୍ରବାହର ଅନ୍ତର୍ଗତ । (ସାମୟିକ, ଆକସ୍ମିକ, ସ୍ଥାନୀୟ, ନିୟତ)
Answer:
ନିୟତ ବାୟୁ

12. ସମୁଦ୍ରବାୟୁ ଓ ସ୍ଥଳବାୟୁ _____ ବାୟୁ ପ୍ରବାହର ଅନ୍ତର୍ଗତ । (ନିୟତ, ସାମୟିକ, ସ୍ଥାନୀୟ, ଆକସ୍ମିକ)
Answer:
ସାମୟିକ

13. କାଳବୈଶାଖୀ _______ ରାଜ୍ୟରେ ପ୍ରବାହିତ ହୋଇଥାଏ। (ପଶ୍ଚିମବଙ୍ଗ, ବିହାର, ରାଜସ୍ଥାନ, ଗୁଜୁରାଟ)
Answer:
ପଶ୍ଚିମବଙ୍ଗ

14. ଲୁ’ _______ ବାୟୁ ପ୍ରବାହର ଅନ୍ତର୍ଗତ। (ନିୟତ, ସାମୟିକ, ସ୍ଥାନୀୟ, ଆକସ୍ମିକ)
Answer:
ସ୍ଥାନୀୟ

15. ଜଳୀୟବାଷ୍ପର ଉପସ୍ଥିତି ଓ ପରିମାପକ ବାୟୁର _____ କୁହାଯାଏ । (ଉଷ୍ଣତା, ବାଷ୍ପୀଭବନ ପ୍ରକ୍ରିୟା, ଆର୍ଦ୍ରତା, ଘନୀଭବନ ପ୍ରକ୍ରିୟା)
Answer:
ଆର୍ଦ୍ରତା

16. ସୌରାଭିତାପର ପରିମାଣ ପୃଥ‌ିବୀର . ଅଞ୍ଚଳରେ ସର୍ବାଧୂକ । (ବିଷୁବରେଖା, କର୍କଟକ୍ରାନ୍ତି, ସୁମେରୁ ବୃତ୍ତ, ଜୁମେରୁ ବୃତ୍ତ)
Answer:
ବିଷୁବରେଖା

ସ୍ତମ୍ଭ ମିଳନ କର

Question 1.

Answer:

Question 2.

Answer:

ପ୍ରଥମ ଯୋଡ଼ିକୁ ଦେଖୁ ଦ୍ଵିତୀୟ ଯୋଡ଼ି ପୂରଣ କର

1. ଯବକ୍ଷାରଜାନ : ୭୮ % :: ଅମ୍ଳଜାନ : _______ ।
Answer:
୨୧ %

2. ଆରଗନ୍‌ : ୦,୯୪% :: ଅଙ୍ଗାରକାମ୍ଳ : _______ ।
Answer:
୦.୦୩ %

3. ଟ୍ରପୋସ୍ଟିୟର : ସର୍ବନିମ୍ନସ୍ତର :: ଏକ୍ସୋସ୍ପିୟର : _______ ।
Answer:
ବାହ୍ୟସ୍ତର

4. ଟ୍ରପୋସ୍ପିୟର : ୧୨ କି.ମି. :: ଷ୍ଟ୍ରାଟୋସ୍ପିୟର : _______ ।
Answer:
୫୦ କି.ମି.

5. ଉଷ୍ଣମଣ୍ଡଳ : ଉଭୟ ଗୋଲାର୍ଦ୍ଧର ୨୩, ସମାକ୍ଷରେଖା :: ନାତିଶୀତୋଷ୍ଣ ମଣ୍ଡଳ : _______ ।
Answer:
ଉଭୟ ଗୋଲାର୍ଦ୍ଧର ୨୩, ସମାକ୍ଷରେଖାଠାରୁ ୬୬, ସମାକ୍ଷରେଖା

6. ନିରକ୍ଷ ଲଘୁଚାପ ବଳୟ : ନିରକ୍ଷ ଶାନ୍ତ ବଳୟ :: ଉପକ୍ରାନ୍ତୀୟ ଗୁରୁଚାପ ବଳୟ : _______ ।
Answer:
ଉପକ୍ରାନ୍ତୀୟ ଶାନ୍ତ ବଳୟ

7. ନିୟତବାୟୁ : ପଶ୍ଚିମା ବାୟୁ :: ସାମୟିକ ବାୟୁ ପ୍ରବାହ : _______ ।
Answer:
ମୌସୁମୀ ବାୟୁ

8. ସ୍ଥାନୀୟ ବାୟୁ : କାଳବୈଶାଖୀ :: ଆକସ୍ମିକ ବାୟୁ : _______ ।
Answer:
ବାତାବର୍ଷ

9. ଅଧିକ ବୃଷ୍ଟିପାତ : ପ୍ରତିବାତ ପାର୍ଶ୍ଵ :: ସ୍ଵଳ୍ପବୃଷ୍ଟି : _______ ।
Answer:
ଅନୁବାତ ପାର୍ଶ୍ବ

10. ଜଳଭାଗ : ୭୧ ଭାଗ :: ସ୍ଥଳଭାଗ : _______ ।
Answer:
୨୯ ଭାଗ

BSE Odisha Class 7 Hindi Solutions Book Pdf Download

• Chapter 1 हम जानते हैं
• Chapter 2 यह मेरा वतन (कविता)
• Chapter 3 अपना-अपना काम करो
• Chapter 4 बस यात्रा का अनुभव
• Chapter 5 आज इतवार है
• Chapter 6 सीखो (कविता)
• Chapter 7 उत्कलमणि
• Chapter 8 होली आई, होली आई (कविता)
• Chapter 9 धागे का बन्धन
• Chapter 10 चूहों की चौकड़ी
• Chapter 11 बना दो मधुर मेरा जीवन (कविता)
• Chapter 12 जंगल रो रहा है
• Chapter 13 वाद-विवाद
• व्याकरण विभाग

BSE Odisha 7th Class Text Book Solutions

Odisha State Board BSE Odisha 7th Class Geography Important Questions Chapter 1.3 ପୃଥ‌ିବୀର ଅଭ୍ୟନ୍ତର Important Questions and Answers.

BE Odisha Class 7 Geography Important Questions Chapter 1.3 ପୃଥ‌ିବୀର ଅଭ୍ୟନ୍ତର

Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ଆମେ ଦେଖୁଥ‌ିବା ସ୍ଥଳ ଓ ଜଳଭାଗର ବଣ୍ଟନ କିପରି ସମ୍ଭବ ହୋଇଛି ବର୍ଣ୍ଣନା କର ।
Answer:

1. ଆମେ ଦେଖୁଥ‌ିବା ସ୍ଥଳ ଓ ଜଳରାଗର ବଣ୍ଟନ ମହାଦେଶୀୟ ସଞ୍ଚଳନର ଫଳ ।
2. ଭୂବିଜ୍ଞାନୀଙ୍କ ମତରେ ନିୟୁତ ନିୟୁତ ବର୍ଷପୂର୍ବେ ସବୁ ମହାଦେଶ ମିଶି ପାଞ୍ଜିଆ ଓ ସବୁ ମହାସାଗର ମିଶି ପାନ୍ଥାଲାସା ନାମରେ ପରିଚିତ ଥିଲା । ପରେ ପାଞ୍ଜିଆର ମଧ୍ୟଭାଗରେ ଟେଣ୍ଟ୍‌ସ୍ ସାଗର ସୃଷ୍ଟି ହେଲା । ଏହାର ଉତ୍ତର ଭାଗକୁ ଆଙ୍ଗାରାଲାଣ୍ଡ ଓ ଦକ୍ଷିଣ ଭାଗକୁ ଗଣ୍ଡୱାନାଲାଣ୍ଡ କୁହାଯାଉଥିଲା ।
3. ଆଙ୍ଗାରାଲାଣ୍ଡରେ ବର୍ତ୍ତମାନର ଉତ୍ତର ଆମେରିକା, ଇଉରୋପ ଓ ଏସିଆ ମହାଦେଶ ଅନ୍ତର୍ଗତ ଥିବାବେଳେ ଗଣ୍ଡାନାଲାଣ୍ଡରେ ଆଫ୍ରିକା, ଦକ୍ଷିଣ ଆମେରିକା, ଆଣ୍ଟାର୍କଟିକା, ଅଷ୍ଟ୍ରେଲିଆ ଓ ଦକ୍ଷିଣ ଭାରତ ମାଳଭୂମି ଅନ୍ତର୍ଗତ ଥିଲା ।
4. ପାଞ୍ଜିଆର ଭୂଭାଗରେ ଫାଟ ସୃଷ୍ଟି ହେବା ଦ୍ଵାରା ଉତ୍ତର ଆମେରିକା ଆଙ୍ଗାରାଲାଣ୍ଡରୁ ଓ ଦକ୍ଷିଣ ଆମେରି କା ଗଣ୍ଡୱାନାଲାଣ୍ଡରୁ ବିଚ୍ଛିନ୍ନ ହେଲା ଓ ଆଟ୍‌ଲାଣ୍ଟିକ ମହାସାଗର ସୃଷ୍ଟି ହେଲା ।
5. ସେହିପରି ଆଫ୍ରିକାରୁ ଆଣ୍ଟାର୍କଟିକା, ଅଷ୍ଟ୍ରେଲିଆ ଓ ଭାରତର ଦକ୍ଷିଣାଶ ବିଚ୍ଛିନ୍ନ ହେବାଦ୍ଵାରା ଭାରତ ମହାସାଗରର ଉଦ୍ଭବ ହେଲା । ଏହିପରି ମହାଦେଶୀୟ ସଞ୍ଚଳନ ଫଳରେ ବର୍ତ୍ତମାନର ଜଳ ଓ ସ୍ଥଳଭାଗର ବଣ୍ଟନ ସମ୍ଭବ ହୋଇପାରିଛି ।

Question 2.
ନଦୀର କାର୍ଯ୍ୟ ଉଲ୍ଲେଖ କର ।
Answer:

1. ନଦୀ ପାର୍ବତ୍ୟ ଶଯ୍ୟାରେ ଗତି କରିବା ସମୟରେ ଏହାର ବେଗ ଅତି ପ୍ରଖର ଥାଏ ଏବଂ ଏହା ତା’ର ଶଯ୍ୟାକୁ ଖୋଳି ପକାଇବା ଫଳରେ ଇଂରାଜୀ ଅକ୍ଷର ‘V” ସଦୃଶ ଉପତ୍ୟକା ସୃଷ୍ଟି ହୋଇଥାଏ ।
2. ବେଳେବେଳେ ନଦୀ ବହୁ ଉଚ୍ଚରୁ କଠିନ ଶିଳା ଉପରକୁ ସିଧାସଳଖ ଲମ୍ଫ ପ୍ରଦାନ କରିଥାଏ । ଏହାକୁ ଜଳପ୍ରପାତ କୁହାଯାଏ ।
3. ସମତଳ ଶଯ୍ୟାରେ ପ୍ରବେଶ କଲାପରେ ନଦୀର ବେଗ କମିଯାଏ । ଏହା ଉପରମୁଣ୍ଡରୁ ବୋହି ଆଣିଥିବା ବାଲି, ଗୋଡ଼ି, ପଥର ଆଦିକୁ ପାହାଡ଼ ତଳେ ହାତ ପଙ୍ଖା ଆକାରରେ ଜମା କରେ । ଏହାକୁ ‘ପଟୁବ୍ୟଜନ’ କୁହାଯାଏ ।
4. ସମତଳ ଶଯ୍ୟାରେ ନଦୀ ସାମାନ୍ୟ ବାଧା ପାଇଲେ ଅଙ୍କାବଙ୍କା ପଥରେ ପ୍ରବାହିତ ହୁଏ । ନଦୀର ଏହି ଅଙ୍କାବଙ୍କା ଗତିପଥକୁ ନଦୀବାଙ୍କ କୁହାଯାଏ ।
5. ବନ୍ୟା ସମୟରେ ନଦୀ ବୁଲାଣି ପଥ ପରିତ୍ୟାଗ କରି ସିଧାସଳଖ ପ୍ରବାହିତ ହେବା ଫଳରେ ନଦୀବାଙ୍କଟି କ୍ଷୁଦ୍ର ଅଗଭୀର ହ୍ରଦ ଆକାରରେ ରହିଯାଏ, ଯାହାକୁ ଅଶୁଖୁରାକୃତି ହ୍ରଦ କୁହାଯାଏ ।
6. ବନ୍ୟା ସମୟରେ ନଦୀର ଜଳ ଏହାର ପାର୍ଶ୍ଵବର୍ତ୍ତୀ ଅଞ୍ଚଳକୁ ପ୍ଲାବିତ କରି ସେଠାରେ ବାଲି, ପଟୁ କମ୍ବାଗତ ଭାବରେ ଜମା କରିବା ଫଳରେ ଯେଉଁ ସମତଳଭୂମି ସୃଷ୍ଟି ହୁଏ, ତାହାକୁ ପ୍ଳାବନ ଭୂମି କୁହାଯାଏ ।
7. ଉପକୂଳ ଅଞ୍ଚଳରେ ନଦୀର ସ୍ରୋତ ଅତି ଧୀର ହେବା ଫଳରେ ଏହା ଅନେକଗୁଡ଼ିଏ ଶାଖା ପ୍ରଶାଖାର ବିଭକ୍ତ ହୋଇଥାଏ । ଏହିଠାରୁ ନଦୀ ମୁହାଣ ପର୍ଯ୍ୟନ୍ତ ଏକ ତ୍ରିକୋଣାକାର ବିସ୍ତୃତ ସମତଳଭୂମି ଗଠିତ ହୁଏ, ଯାହାକୁ ତ୍ରିକୋଣଭୂମି କୁହାଯାଏ ।

Question 3.
ହିମବାହର କାର୍ଯ୍ୟଗୁଡ଼ିକ କ’ଣ ବର୍ଣ୍ଣନା କର ।
Answer:

1. ଅତି ଶୀତଳ ଜଳବାୟୁ ଅଞ୍ଚଳ ତଥା ଉଚ୍ଚ ପର୍ବତ ଶୃଙ୍ଗଗୁଡ଼ିକରେ ତୁଷାରକଣିକାଗୁଡ଼ିକ ବରଫ ଆକାରରେ ଜମା ହୋଇ ବରଫ ଖଣ୍ଡରେ ପରିଣତ ହୋଇ ଧୀରେ ଧୀରେ ଗତି କରିବାକୁ ଲାଗେ । ଏ ପ୍ରକାର ଗତିଶୀଳ ବରଫସ୍ରୋତକୁ ହିମବାହ କୁହାଯାଏ ।
2. ହିମବାହ ନିଜ ଗତିପଥରେ ସମାନ’ ପୃଷ୍ଠତଳ ଓ ତୀଖ ପାର୍ଶ୍ୱବିଶିଷ୍ଟ ଉପତ୍ୟକା ସୃଷ୍ଟିକରେ । ଏହାକୁ ଇଂରାଜୀ ଅକ୍ଷର ‘U” ସଦୃଶ ହୋଇଥିବାରୁ ଏହାକୁ ‘U’ ଉପତ୍ୟକା କୁହାଯାଏ ।
3. ବେଳେବେଳେ ପର୍ବତ ଢାଲୁରେ ହିମବାହଦ୍ବାରା ସୃଷ୍ଟି ହେଉଥିବା ଆରାମଚୌକି ଭଳି ଭୂମିରୂପକୁ ସର୍କ କୁହାଯାଏ ।
4. ହିମବାହ ବୋହି ଆଣୁଥୁବା ଭିନ୍ନ ଭିନ୍ନ ଆକୃତିର ଶିଳାଖଣ୍ଡ ଏହାର ପାର୍ଶ୍ଵ ତଥା ଅଗ୍ରଭାଗରେ ଜମା ହୋଇ ସୃଷ୍ଟ ସ ଭୂମିରୂପକୁ ଗ୍ରାବ କୁହାଯାଏ ।
5. ଏଗୁଡ଼ିକ ହିମବାହର ପାର୍ଶ୍ବରେ ରେଖା ସଦୃଶ ଲମ୍ବି ରହିଥ‌ିବାରୁ ଏଗୁଡ଼ିକୁ ଗ୍ରାବରେଖା କୁହାଯାଏ ।

Question 4.
ଭୂତଳ ଜଳର କାର୍ଯ୍ୟଗୁଡ଼ିକ ଲେଖ ।
Answer:

1. ଚୂନପଥର ଅଞ୍ଚଳରେ ଭୂତଳ ଜଳ ମୁଖ୍ୟ କ୍ଷୟକାରୀ ଶକ୍ତିରୂପେ, କାର୍ଯ୍ୟ କରେ । ଭୂମି ଉପରୁ ନିମ୍ନକୁ ପାଣି ଶୋଷି ହୋଇଯାଇଥିବା ସ୍ଥାନରେ କାହାଳୀ ସଦୃଶ ଗାତ ସୃଷ୍ଟି ହୁଏ । ଏହାକୁ ଡୋଲାଇନ୍ କୁହାଯାଏ ।
2. ଡୋଲାଇନ୍ ଆକାରରେ ବଡ଼ ହେଲେ ତାକୁ ଭରାଲା କୁହାଯାଏ ।
3. ଚୂନପଥର ଅଞ୍ଚଳର ଭୂମିତଳେ ବେଳେବେଳେ ବଡ଼ ବଡ଼ ଗହ୍ଵର ସୃଷ୍ଟି ହୁଏ । ଏହାକୁ ଚୂନପଥର ଗୁମ୍ଫା କୁହାଯାଏ ।
4. ଚୂନପଥର ଅଞ୍ଚଳର ନଦୀ ସୁଡ଼ଙ୍ଗ ପଥ ଦେଇ ଭୂନିମ୍ନରେ ପ୍ରବାହିତ ହେଲେ ରୂପୃଷ୍ଠସ୍ଥ ନଦୀଶଯ୍ୟା ଶୁଷ୍କ ରହେ । ଏହି ଉପତ୍ୟକାକୁ ଅଦୃଶ୍ୟ ଉପତ୍ୟକା କୁହାଯାଏ ।
5. ବଡ଼ ବଡ଼ ଚୂନପଥର ଗୁମ୍ଫାର ଛାତରୁ ଚୂନମିଶ୍ରିତ ଜଳଟୋପା ବିନ୍ଦୁ ବିନ୍ଦୁ ହୋଇ ତଳକୁ ପଡ଼େ ଏବଂ ଚୂନ ଅଂଶ ଭୂମିରେ ଜମା ହୋଇ ହୁଙ୍କା ପରି ଚୂନସ୍ତମ୍ଭ ସୃଷ୍ଟି ହୁଏ । ଏହାକୁ ଷ୍ଟାଲାଗମାଇଟ୍‌ କୁହାଯାଏ ।
6. ଚୂନମିଶ୍ରିତ ଜଳ ଗୁମ୍ଫା ଛାତରୁ ଖସିବା ସମୟର କିଛି ଚୂନ ଅଂଶ ଛାତରେ ଜମିବାକୁ ଲାଗେ । କ୍ରମେ ଏହା ବଡ଼ ହୋଇ ଛାତରୁ ଓହଳ ସଦୃଶ ଝୁଲିରହେ । ଏହାକୁ ଷ୍ଟାଲାକ୍‌ଟାଇଟ୍ କୁହାଯାଏ ।

ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ମହାଦେଶୀୟ ସଞ୍ଚଳନ କ’ଣ ?
Answer:

1. ମହାଦେଶୀୟ ସଞ୍ଚଳନ ଏକ ଅତି ଧୀର ତଥା ନିରବଚ୍ଛିନ୍ନ ପ୍ରକ୍ରିୟା ।
2. ଭୂବିଜ୍ଞାନୀମାନଙ୍କ ମତରେ, ଅଶ୍ମମଣ୍ଡଳ କେତେଗୁଡ଼ିଏ ବିଶାଳ ପ୍ଲେଟ ବା ପଟଳରେ ବିଭକ୍ତ ।
3. ଏଗୁଡ଼ିକ ବର୍ଷକୁ ପ୍ରାୟ ପାଞ୍ଚ ସେଣ୍ଟିମିଟର ବା ତା’ଠାରୁ କମ୍ ବେଗରେ ଗତି କରିଥାନ୍ତି । କାରଣ ଏଗୁଡ଼ିକ ଗତିଶୀଳ ମାତ୍ମା ବା ଅତରଳ ଶିଳା ଉପରେ ଅବସ୍ଥିତ ଥ‌ିବାରୁ ଏହି ପଟଳଗୁଡ଼ିକର ଗତି ସମ୍ଭବ ହୋଇଛି ।
4. ଫଳରେ ଜଳଭାଗ ଓ ସ୍ଥଳଭାଗ ଅନବରତ ସ୍ଥାନ ପରିବର୍ତ୍ତନ କରିବାରେ ଲାଗିଛନ୍ତି ।

Question 2.
ପ୍ଲେଟ୍ ବା ପଟଳ ଗତିର କାରଣ କ’ଣ ?
Answer:

• ଭୂବିଜ୍ଞାନୀଙ୍କ ମତରେ, ଅଶ୍ମମଣ୍ଡଳ କେତେଗୁଡ଼ିଏ ବିଶାଳ ପ୍ଲେଟ୍ ବା ପଟଳରେ ବିଭକ୍ତ ।
• ଏହି ପଟଳଗୁଡ଼ିକର ନିମାଂଶରେ ଥିବା ଅତରଳ ଶିଳା ବା ମାତ୍ମା ଗତିଶୀଳ । ତେଣୁ ଏହି ପ୍ଲେଟ୍ (ପଟଳ)ଗୁଡ଼ିକର ଗତି ସମ୍ଭବ ହୋଇଛି ।

Question 3.
ସ୍ଥାନୀୟ ଭାବେ ଭୂମିକମ୍ପର ପୂର୍ବାନୁମାନ କିପରି କରାଯାଏ ?
Answer:

• ସାଧାରଣଭାବେ ପଶୁପକ୍ଷୀମାନଙ୍କର ବ୍ୟାବହାରିକ ପରିବର୍ତ୍ତନକୁ ଲକ୍ଷ୍ୟ କରି ସ୍ଥାନୀୟଭାବେ ଭୂମିକମ୍ପର ପୂର୍ବାନୁମାନ କରାଯାଇଥାଏ ।
• ଭୂମିକମ୍ପ ହେବା ପୂର୍ବରୁ ପୁଷ୍କରିଣୀରେ ମାଛ ଆନ୍ଦୋଳିତ ହୋଇଥାନ୍ତି, ସାପ ଗାତରୁ ପଦାକୁ ବାହାରି ଆସନ୍ତି ଏବଂ ଗାଈଗୋରୁମାନେ ହଠାତ୍ ବୋବାଳି ଛାଡ଼ିଥାନ୍ତି ।

Question 4.
ସ୍ତବ୍ଲ୍ୟୁତି କାହାକୁ କୁହାଯାଏ ?
Answer:

• କେତେକ ଆଭ୍ୟନ୍ତରୀଣ ଶକ୍ତି ପ୍ରଭାବରେ ଶିଳାସ୍ତର ଉଭୟ ଦିଗରେ ଟାଣି ହୋଇଯାଇ କ୍ରମେ ଫାଟ ସୃଷ୍ଟି ହୁଏ ।
• ଫାଟର ଉଭୟ ପାର୍ଶ୍ଵରେ ଥିବା ଶିଳାସ୍ତରରେ ଚଳନ ହୋଇ ଏହାର କୌଣସି ଅଂଶ ଉପର ବା ତଳକୁ ଚାଲିଯାଏ ।
• ଫଳରେ ବିଭିନ୍ନ ଶିଳାସ୍ତର ମଧ୍ଯରେ ତାଳମେଳ ରହେ ନାହିଁ । ଏହାକୁ ସ୍ତରଚ୍ୟୁତି କୁହାଯାଏ ।

Question 5.
ମାଳଭୂମି କାହାକୁ କୁହାଯାଏ ?
Answer:

• ସମୁଦ୍ର ପତ୍ତନରୁ ପ୍ରାୟ ୪୦୦ ମିଟର ବା ଅଧିକ ଉଚ୍ଚତାରେ ଅବସ୍ଥିତ ସମପ୍ରାୟ ଭୂମିକୁ ମାଳଭୂମି କୁହାଯାଏ ।
• ସମତଳ ଭୂମିରୁ ଏଗୁଡ଼ିକ ତୀଖଭାବେ ଉଠିଥାଆନ୍ତି । ତେଣୁ ମାଳଭୂମିଗୁଡ଼ିକର ପାର୍ଶ୍ୱ ଅଧ‌ିକ ଢାରୁ ବିଶିଷ୍ଟ ।
• ଏକ ବିସ୍ତୀର୍ଣ୍ଣ ଟେବୁଲ ଭଳି ଦେଖାଯାଉ ଥିବାରୁ ମାଳଭୂମିକୁ ଟେବୁଲଲାଣ୍ଡ ମଧ୍ଯ କୁହାଯାଏ ।

Question 6.
ସମାନୀକରଣ ପ୍ରକ୍ରିୟା କ’ଣ ?
Answer:

• ଭୂପୃଷ୍ଠରେ କାର୍ଯ୍ୟ କରୁଥିବା ବାହ୍ୟ ଶକ୍ତିଗୁଡ଼ିକ (ପବନ, ନଦୀ, ହିମବାହ, ଭୂତଳ ଜଳ, ସାମୁଦ୍ରିକ ତରଙ୍ଗ) ଉଚ୍ଚଭୂମିକୁ କ୍ଷୟ କରିବା ସହ କ୍ଷୟଜାତ ପଦାର୍ଥକୁ ନିମ୍ନଭୂମିରେ ଜମା କରିଥାନ୍ତି ।
• ତେଣୁ ଭୂପୃଷ୍ଠ ସମପ୍ରାୟ ଭୂମିରେ ପରିଣତ ହୋଇଥାଏ । ଏହି ପ୍ରକ୍ରିୟାକୁ ସମାନୀକରଣ ପ୍ରକ୍ରିୟା କୁହାଯାଏ ।

Question 7.
ଅଶ୍ଵଖୁରାକୃତି ହ୍ରଦ କିପରି ସୃଷ୍ଟି ହୁଏ ?
Answer:

• ସମତଳ ଶଯ୍ୟାରେ ନଦୀସ୍ରୋତ ଧୀର ହେବାଦ୍ଵାରା ନଦୀବାଙ୍କ ସୃଷ୍ଟି ହୁଏ । ନଦୀ ବାଙ୍କର ଗୋଟିଏ ପାର୍ଶ୍ବରେ ନଦୀଜଳ ଦ୍ଵାରା ବାଡ଼େଇ ହେବାଦ୍ଵାରା କ୍ଷୟ ହୁଏ । ଏହାର ଠିକ୍ ବିପରୀତ ପାର୍ଶ୍ବରେ ବାଲି, ପଟୁ ଆଦି ଜମାହୋଇ ରହେ । ଧୀରେ ଧୀରେ ନଦୀବାଙ୍କର ଉଭୟ ମୁଣ୍ଡ ପରସ୍ପରର ନିକଟବର୍ତ୍ତୀ ହୋଇଥାଏ ।
• ବନ୍ୟା ସମୟରେ ନଦୀ ବୁଲାଣି ପଥ ପରିତ୍ୟାଗ କରି ସିଧାସଳଖ ପ୍ରବାହିତ ହୁଏ । ଫଳରେ ନଦୀବାଙ୍କଟି ଏକ କ୍ଷୁଦ୍ର ଅଗଭୀର ହ୍ରଦ ଆକାରରେ ରହିଯାଏ । ଏହାକୁ ଅଶ୍ଵଖୁରାକୃତି ହ୍ରଦ କୁହାଯାଏ ।

Question 8.
ଗ୍ରାବରେଖା କ’ଣ ?
Answer:

• ହିମବାହ ବୋହି ଆଣୁଥିବା ଭିନ୍ନ ଭିନ୍ନ ଆକୃତିର ଶିଳାଖଣ୍ଡକୁ ଏହାର ପାର୍ଶ୍ଵ ତଥା ଅଗ୍ରଭାଗରେ ଜମା କରିଥାଏ । ଏହାକୁ ସ୍ରାବ କୁହାଯାଏ ।
• ଏହି ଗ୍ରାବ ହିମବାହର ପାର୍ଶ୍ବରେ ରେଖା ସଦୃଶ ଲମ୍ବି ରହିଥ‌ିବାରୁ ଏଗୁଡ଼ିକୁ ଗ୍ରାବରେଖା କୁହାଯାଏ ।

Question 9.
ବାଲୁକାସ୍ତୂପ କିପରି ସୃଷ୍ଟି ହୁଏ ?
Answer:
ମରୁଭୂମିରେ ପବନଦ୍ଵାରା ପରିବାହିତ ହୋଇ ଅପେକ୍ଷାକୃତ ବଡ଼ ବଡ଼ ବାଲୁକାରାଶି ମରୁଭୂମି ଭିତରେ ଛୋଟ ଛୋଟ ପାହାଡ଼ ଆକାରରେ ଜମା ହୁଏ । ଏହାକୁ ବାଲୁକା ସ୍ତୂପ କୁହାଯାଏ ।

Question 10.
ପ୍ଲାବନ ଭୂମି କାହାକୁ କୁହାଯାଏ ?
Answer:

• ବନ୍ୟା ସମୟରେ ନଦୀ ଏହାର ପାର୍ଶ୍ଵବର୍ତ୍ତୀ ଅଞ୍ଚଳକୁ ଜଳପ୍ଲାବିତ କରେ ।
• ଏହି ଅଞ୍ଚଳରେ ବାଲି, ପଟୁ ଆଦି କ୍ରମାଗତ ଭାବେ ଜମାହୋଇ ସମତଳ ଭୂମି ଗଠିତ ହୁଏ । ଏହାକୁ ପ୍ଲାବନଭୂମି କୁହାଯାଏ ।

Question 11.
ଅଦୃଶ୍ୟ ଉପତ୍ୟକା କ’ଣ ?
Answer:

• ଚୂନପଥର ଗୁମ୍ଫା ତଳେ ଜଳ ବହିଯିବା ଯୋଗୁଁ ସୁଡ଼ଙ୍ଗ ପଥ ସୃଷ୍ଟି ହୁଏ ।
• ଚୂନପଥର ଅଞ୍ଚଳରେ ପ୍ରବାହିତ ନଦୀ ସୁଡ଼ଙ୍ଗ ପଥ ଦେଇ ଭୂନିମ୍ନରେ ପ୍ରବାହିତ ହୁଏ । ତେଣୁ ଭୂପୃଷ୍ଠସ୍ଥ ନଦୀଶଯ୍ୟା ଶୁଷ୍କ ରହେ । ଏପ୍ରକାର ଉପତ୍ୟକାକୁ ଅଦୃଶ୍ୟ ଉପତ୍ୟକା କୁହାଯାଏ ।

Question 12.
ଭଙ୍ଗିଳ ପର୍ବତ କିପରି ସୃଷ୍ଟି ହୁଏ, ଦୁଇଟି ଭଙ୍ଗିଳ ପର୍ବତର ଉଦାହରଣ ଦିଅ ।
Answer:

• ଆଭ୍ୟନ୍ତରୀଣ ଶକ୍ତିର ପ୍ରଭାବରେ କୋମଳ ସ୍ତରୀଭୂତ ଶିଳାରେ । ପାର୍ଶ୍ବଚାପ ଯୋଗୁଁ ଭଙ୍ଗିଳ ପର୍ବତ ସୃଷ୍ଟି ହୁଏ ।
• ଉଦାହରଣ : ହିମାଳୟ ପର୍ବତମାଳା, ରକି ପର୍ବତମାଳା ।

Question 13.
ପ୍ରଥମ ଶ୍ରେଣୀ ଓ ଦ୍ଵିତୀୟ ଶ୍ରେଣୀ ଭୂମିରୂପ କ’ଣ ଉଦାହରଣ ସହ ବୁଝାଅ ।
Answer:

• ପୃଥ‌ିବୀପୃଷ୍ଠ ଜଳ ଓ ସ୍ଥଳଭାଗଦ୍ଵାରା ଗଠିତ । ସ୍ଥଳଭାଗକୁ ମହାଦେଶ ଓ ଜଳଭାଗକୁ ମହାସାଗର କୁହାଯାଏ । ଏଗୁଡ଼ିକ ହିଁ ପ୍ରଥମ ଶ୍ରେଣୀ ଭୂମିରୂପ ।
• ମହାଦେଶରେ ପର୍ବତ, ମାଳଭୂମି ଓ ସମତଳ ଭୂମି ଆଦି ଦ୍ୱିତୀୟ ଶ୍ରେଣୀ ଭୂମି ରୂପ । ମହାସାଗରର ଜଳରାଶି ତଳେ ମହୀସୋପାନ, ମହୀଢାଲୁ ଓ ମହାସାଗର ସମତଳ ଆଦି ଦ୍ବିତୀୟ ଶ୍ରେଣୀ ଭୂମିରୂପ ।

Question 14.
ଗ୍ରସ୍ତ ଉପତ୍ୟକା କିପରି ସୃଷ୍ଟି ହୋଇଥାଏ ? ଗ୍ରନ୍ଥ ଉପତ୍ୟକା ଦେଇ ପ୍ରବାହିତ ଭାରତର ଦୁଇଟି ନଦୀର ନାମ ଲେଖ ।
Answer:

• ବେଳେବେଳେ ଦୁଇଟି ଚ୍ଯୁତି ମଧ୍ୟବର୍ତୀ ଅଂଶ ଦବିଯାଇ ଗ୍ରସ୍ତ ଉପତ୍ୟକା ସୃଷ୍ଟି ହୋଇଥାଏ ।
• ଭାରତର ନର୍ମଦା ଓ ତାୟୀ ନଦୀ ଦୁଇଟି ଗ୍ରସ୍ତ ଉପତ୍ୟକା ଦେଇ ପ୍ରବାହିତ ହେଉଛନ୍ତି ।

Question 15.
ସଂରଚନାଜନିତ ସମତଳଭୂମି କ’ଣ ଉଦାହରଣସହ ଲେଖ ।
Answer:

• ଆଭ୍ୟନ୍ତରୀଣ ଶକ୍ତିଗୁଡ଼ିକର ପ୍ରଭାବରେ ସୃଷ୍ଟି ହୋଇଥିବା ସମତଳଭୂମିକୁ ସଂରଚନାଜନିତ ସମତଳ ଭୂମି କୁହାଯାଏ ।
• ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ବୃହତ୍ ସମତଳଭୂମି ଏହାର ଏକ ଉଦାହରଣ ।

Question 16.
ନଦୀବାଙ୍କ କିପରି ସୃଷ୍ଟି ହୁଏ ?
Answer:

• ସମତଳ ଶଯ୍ୟାରେ ନଦୀ ସ୍ରୋତ ଧୀର ହୁଏ ।
• ସାମାନ୍ୟ ବାଧା ପାଇଲେ ଗତି ପରିବର୍ତ୍ତନ କରି ଅଙ୍କାବଙ୍କା ପଥରେ ପ୍ରବାହିତ ହୁଏ । ନଦୀର ଏପରି ଅଙ୍କାବଙ୍କା ଗତିପଥକୁ ନଦୀବାଙ୍କ କୁହାଯାଏ ।

Question 17.
ପଟୁବ୍ୟଜନ କ’ଣ ?
Answer:

• ସମତଳ ଶଯ୍ୟାରେ ଢାଲୁ କମଥ‌ିବାରୁ ନଦୀର ବେଗ ହଠାତ୍ କମିଯାଏ ।
• ଏହା ଉପରମୁଣ୍ଡରୁ ବୋହି ଆଣିଥିବା ବାଲି, ଗୋଡ଼ି, ପଥର ଆଦିକୁ ପାହାଡ଼ ତଳେ ପଙ୍ଖା ଆକାରରେ ଜମା କରିଥାଏ, ଏହାକୁ ପଟୁବ୍ୟଜନ କୁହାଯାଏ ।

Question 18.
ଭୂଚଳନ ପାଇଁ ଦାୟୀ ଆଭ୍ୟନ୍ତରୀଣ ଶକ୍ତିଗୁଡ଼ିକ କ’ଣ ?
Answer:

1. ଭୂଚଳନ ପାଇଁ ଦାୟୀ ଆଭ୍ୟନ୍ତରୀଣ ଶକ୍ତିଗୁଡ଼ିକ ହେଉଛି ତ୍ଵରିତ ଶକ୍ତି ଓ ଧୀର ଶକ୍ତି ।
2. ତ୍ବରିତ୍‌ ଶକ୍ତି ମଧ୍ୟରେ ଭୂମିକମ୍ପ, ଅଗ୍ନି ଉଦ୍‌ଗିରଣ, ଭୂସ୍ଖଳନ ପ୍ରଧାନ ।
3. ସେହିପରି ଧୀର ଶକ୍ତିଗୁଡ଼ିକ ହେଉଛି ପର୍ବତ ଗଠନ ଓ ମହାଦେଶୀୟ ସଞ୍ଚଳନ ।

ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ

Question 1.
ଉର୍ଦୁଭାଙ୍ଗ ଓ ନିମ୍ନଭାଙ୍ଗ
Answer:

Question 2.
ସ୍ତପ ପର୍ବତ ଓ ଗ୍ରସ୍ତ ଉପତ୍ୟକା
Answer:

Question 3.
ମାଳଭୂମି ଓ ସମତଳ ଭୂମି
Answer:

Question 4.
‘U” ଉପତ୍ୟକା ଓ ‘V” ଉପତ୍ୟକା
Answer:

Question 5.
ସମୁଦ୍ର ଗୁମ୍ଫା ଓ ସାମୁଦ୍ରିକ ତୋରଣ
Answer:

Question 6.
ଷ୍ଟାଲାଗମାଇଟ୍‌ ଓ ଷ୍ଟାଲାକ୍‌ଟାଇଟ୍‌
Answer:

Question 7.
ଚୂଷ୍ଣୀଭବନ ଓ କ୍ଷୟୀକରଣ
Answer:

କାରଣ ଦର୍ଶାଅ

Question 1.
ସମତଳଶଯ୍ୟାରେ ନଦୀବାଙ୍କ ସୃଷ୍ଟି ହୁଏ ।
Answer:

• ସମତଳଶଯ୍ୟାରେ ନଦୀସ୍ରୋତ ଧୀର ହୁଏ ।
• ସାମାନ୍ୟ ବାଧାପାଇଲେ ନଦୀ ଗତି ପରିବର୍ତ୍ତନ କରି ଅଙ୍କାବଙ୍କା ପଥରେ ପ୍ରବାହିତ ହେଲେ ନଦୀବାଙ୍କ ସୃଷ୍ଟି ହୁଏ ।

Question 2.
କେତେକ ଶିଳା ଛତୁ ଆକୃତିର ।
Answer:

1. ମରୁଭୂମିରେ ପବନର ବେଗ ଅଧିକ ହୋଇଥାଏ । ପବନ ସହ ବାଲି ଓ ଶିଳାରେଣୁ ମିଶି ଏହାର କ୍ଷୟଶକ୍ତି ବଢ଼ାଇଥାଏ ।
2. ଭୂପୃଷ୍ଠରୁ ଅଳ୍ପ ଉଚ୍ଚତାରେ ପବନ ଅଧିକ କ୍ଷୟ କରିଥାଏ । ଉଚ୍ଚତା ବଢ଼ିବା ସହ ବାଲିର ପରିମାଣ କମ୍ ରହୁଥ‌ିବାରୁ କ୍ଷୟଶକ୍ତି କମିଯାଏ ।
3. ଫଳରେ ମରୁଭୂମିମାନଙ୍କରେ ଛତୁ ଆକୃତିର ଭୂମିରୂପ ସୃଷ୍ଟି ହୋଇଥାଏ ଯାହାର ଆଧାର ଭୂମି ଓ ଉପର ଅଂଶ ପ୍ରଶସ୍ଥ ଓ ମଝି ଅଂଶ ସରୁ ଥାଏ । ।

Question 3.
ସାମୁଦ୍ରିକ ଗୁମ୍ଫା ଷ୍ଟର୍ମରେ ପରିଣତ ହୁଏ ।
Answer:

1. ସମୁଦ୍ର ଭିତରକୁ ଲମ୍ବିଥିବା ପାହାଡ଼ ତରଙ୍ଗ ଦ୍ଵାରା କ୍ଷୟିତ ହୋଇ ଉଭୟ ପାର୍ଶ୍ଵରେ ଗୁମ୍ଫାରେ ପରିଣତ ହୁଏ । ପରେ ଗୁମ୍ଫା ପରସ୍ପର ସହ ମିଶି ସାମୁଦ୍ରିକ ତୋରଣ ସୃଷ୍ଟି କରେ ।
2. ପରେ ଏହାର ଉପର ଅଂଶ କ୍ଷୟ ହୋଇ ଷ୍ଟାକ୍ ଓ ଏହା ଅଧ୍ବକ କ୍ଷୟ ହୋଇ ଷ୍ଟମ୍ପୂରେ ପରିଣତ ହୁଏ, ଯାହା ସମୁଦ୍ର ଭିତରେ ପ୍ରାଚୀରପରି ରହିଥାଏ ।

Question 4.
ଭୂମିକମ୍ପ ଯୋଗୁଁ କୋଠାଘର ଭାଙ୍ଗିଯାଏ ।
Answer:

1. ଆଭ୍ୟନ୍ତରୀଣ ଶକ୍ତି ପ୍ରଭାବରେ ହଠାତ୍ ଭୂଚଳନ ହୋଇ ଭୂମିକମ୍ପ ହୋଇଥାଏ । ଭୂକମ୍ପ କେନ୍ଦ୍ରରୁ ବିପୁଳ ପରିମାଣର ଶକ୍ତି ତରଙ୍ଗ ଆକାରରେ ଚତୁର୍ଦ୍ଦିଗକୁ ଗତି କରେ ।
2. ଭୂପୃଷ୍ଠର ଉପକେନ୍ଦ୍ରଠାରେ ଭୂକମ୍ପଜନିତ କ୍ଷୟକ୍ଷତି ସର୍ବାଧିକ ହୋଇଥାଏ । ୬.୦ ରିଚର ମାନର ଭୂମିକମ୍ପ କ୍ଷେତ୍ରରେ କୋଠାଘର ଭାଙ୍ଗିଯାଏ ।

Question 5.
ସ୍ତରଚ୍ୟୁତି ଯୋଗୁଁ ଗ୍ରସ୍ତ ଉପତ୍ୟକା ସୃଷ୍ଟି ହୁଏ ।
Answer:

1. ଆଭ୍ୟନ୍ତରୀଣ ଶକ୍ତି ପ୍ରଭାବରେ ଶିଳାସ୍ତର ମଧ୍ଯରେ ସ୍ତରଚ୍ୟୁତି ହୋଇଥାଏ ।
2. ବେଳେବେଳେ ଦୁଇଟି ସ୍ତରଚ୍ଯୁତିର ମଧ୍ୟବର୍ତ୍ତୀ ଅଂଶ ଦବିଯାଇ ଗ୍ରସ୍ତ ଉପତ୍ୟକା ସୃଷ୍ଟି ହୋଇଥାଏ ।

Question 6.
ପାମିରକୁ ପୃଥିବୀର ଛାତ କୁହାଯାଏ ।
Answer:

1. ପାମିର ପୃଥ‌ିବୀର ଉଚ୍ଚତମ ମାଳଭୂମି ।
2. ତେଣୁ ଏହାକୁ ‘ପୃଥ‌ିବୀର ଛାତ’ କୁହାଯାଏ ।

ଅତିସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ।

Question i.
କାହାକୁ ଟେଥିବା ଭାଗର କୁହାଯାଇଥିଲା ?
Answer:
କ୍ରମେ ପାଞ୍ଜିଆର ମଧ୍ୟଭାଗରେ ଯେଉଁ ସଂକୀର୍ଣ୍ଣ ତଥା ଅଗଭୀର ସମୁଦ୍ର ସୃଷ୍ଟି ହୋଇଥିଲା ତାହାକୁ ଟେଣ୍ଟ୍‌ସ୍ ସାଗର କୁହାଗଲା ।

Question ii.
କେଉଁ ଅଞ୍ଚଳକୁ ନେଇ ଆଙ୍ଗାରାଲାଣ୍ଡ ଗଠିତ ହୋଇଥିଲା ?
Answer:
ବର୍ତମାନର ଉତ୍ତର ଆମେରିକା, ଇଉରୋପ ଓ ଏସିଆ ମହାଦେଶ ମିଶି ଆଙ୍ଗାରାଲାଣ୍ଡ ଗଠିତ ହୋଇଥିଲା ।

Question iii.
କେଉଁ ଅଞ୍ଚଳକୁ ନେଇ ଗଣ୍ଡାନାଲାଣ୍ଡ ଗଠିତ ହୋଇଥିଲା ?
Answer:
ଆଫ୍ରିକା, ଦକ୍ଷିଣ ଆମେରିକା, ଆଣ୍ଟାର୍କଟିକା, ଅଷ୍ଟ୍ରେଲିଆ ଓ ଦକ୍ଷିଣ ଭାରତ ମାଳଭୂମି ଅଞ୍ଚଳ ମିଳିତଭାବେ ଗଣ୍ଡାନାଲାଣ୍ଡ ଗଠନ କରିଥିଲେ ।

Question iv.
ଭୂମିକମ୍ପ କାହାକୁ କୁହାଯାଏ ?
Answer:
ବେଳେବେଳେ ପୃଥ‌ିବୀପୃଷ୍ଠ କମ୍ପିଉଠେ ବା ଥରିଉଠେ ଏବଂ ଭୂପୃଷ୍ଠର ଏହି କମ୍ପାନକୁ ଭୂମିକମ୍ପ କୁହାଯାଏ।

Question v.
ଭୂକେନ୍ଦ୍ର କାହାକୁ କୁହାଯାଏ ?
Answer:
ଭୂତ୍ବକ୍‌ର ଯେଉଁ ସ୍ଥାନରେ ଭୂମିକମ୍ପ ଉତ୍ପରି ଲାଭ କରେ ତାହାକୁ ଭୂକମ୍ପ କେନ୍ଦ୍ର କୁହାଯାଏ ।

Question vi.
ଭୂମିକମ୍ପ ମାପିବା ପାଇଁ କେଉଁ ଯନ୍ତ୍ର ବ୍ୟବହାର କରାଯାଏ ?
Answer:
ଭୂମିକମ୍ପ ମାପିବା ପାଇଁ ସେସ୍‌ମୋଗ୍ରାଫ୍ ଯନ୍ତ୍ର ବ୍ୟବହାର କରାଯାଏ ।

Question vii.
ଭୂମିକମ୍ପର ତୀବ୍ରତା ମାପିବାପାଇଁ କ’ଣ ବ୍ୟବହାର କରାଯାଇଥାଏ ।
Answer:
ଭୂମିକମ୍ପର ତୀବ୍ରତା ମାପିବାପାଇଁ ରିଚରମାନ ବ୍ୟବହାର କରାଯାଇଥାଏ ।

Question viii.
କାହାକୁ ମାଗ୍ନାକୋଠରି କୁହାଯାଏ ?
Answer:
ଭୂଦ୍ରକର ଯେଉଁ କେତେକ ସ୍ଥାନରେ ମାତ୍ମା ଗଚ୍ଛିତ ହୋଇଥାଏ, ’ତାହାକୁ ମାସ୍ଟାକୋଠରି କୁହାଯାଏ।

Question ix.
ଭୂପୃଷ୍ଠରେ ମାଗ୍ନାକୁ କ’ଣ କୁହାଯାଏ ?
Answer:
ଭୂପୃଷ୍ଠରେ ମାଗ୍ନାକୁ ଲାଭା କୁହାଯାଏ।

Question x.
ଅଗ୍ନି ଉଦ୍‌ଗୀରଣ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଯେଉଁ ପ୍ରକ୍ରିୟାରେ କୂଅଭ୍ୟନ୍ତରରୁ ମାଗ୍ନା ସହ କଠିନ ଓ ଗ୍ୟାସୀୟ ପଦାର୍ଥମାନ ପଦାକୁ ବାହାରିଆସେ, ତାହାକୁ ଅଗ୍ନି ଉଦ୍‌ଗୀରଣ କୁହାଯାଏ ।

Question xi.
ସ୍ତୂପ ପର୍ବତ କିପରି ସୃଷ୍ଟି ହୁଏ ?
Answer:
ବେଳେବେଳେ ଦୁଇଟି ବ୍ୟତିର ମଧ୍ୟବର୍ତୀ ଅଂଶ ଉପରକୁ ଉଠିଯିବା ଫଳରେ ସ୍ତୂପ ପର୍ବତ ସୃଷ୍ଟି ହୁଏ ।

Question xii.
ଗ୍ରସ୍ତ ଉପତ୍ୟକା କିପରି ସୃଷ୍ଟି ହୁଏ ?
Answer:
କେତେକ କ୍ଷେତ୍ରରେ ଦୁଇଟି ବ୍ୟତିର ମଧ୍ୟବର୍ତୀ ଅଂଶ ଦବିଯାଇ ଗ୍ରସ୍ତ ଉପତ୍ୟକା ସୃଷ୍ଟି ହୋଇଥାଏ।

Question xiii.
ମାଳଭୂମି କାହାକୁ କୁହାଯାଏ ?
Answer:
ସମୁଦ୍ର ପତ୍ତନରୁ ପ୍ରାୟ ୪୦୦ ମିଟର ବା ଅଧିକ ଉଚ୍ଚତାରେ ଅବସ୍ଥିତ ସମପ୍ରାୟ ଭୂମିକୁ ମାଳଭୂମି କୁହାଯାଏ।

Question xiv.
ପୃଥ‌ିବୀର ଛାତ କାହାକୁ କୁହାଯାଏ ?
Answer:
ପୃଥ‌ିବୀର ଉଚ୍ଚତମ ମାଳଭୂମି ପାମିରକୁ ‘ପୃଥ‌ିବୀର ଛାତ’ ବୋଲି କୁହାଯାଏ।

Question xv.
ସମତଳଭୂମି କାହାକୁ କୁହାଯାଏ ?
Answer:
ସମୁଦ୍ର ପତ୍ତନର ୩୦୦ ମିଟର ବା କମ୍ ଉଚ୍ଚତାରେ ଥିବା ବିସ୍ତୀର୍ଣ୍ଣ ସମପ୍ରାୟ ଭୂମିକୁ ସମତଳଭୂମି କୁହାଯାଏ।

Question xvi.
ବାହ୍ୟ ଶକ୍ତି କାହାକୁ କହନ୍ତି ?
Answer:
ଭୂପୃଷ୍ଠରେ କାର୍ଯ୍ୟ କରୁଥିବା ଶକ୍ତିକୁ ବାହ୍ୟଶକ୍ତି କହନ୍ତି ।

Question xvii.
ଜଳପ୍ରପାତ କାହାକୁ କୁହାଯାଏ ?
Answer:
ବେଳେବେଳେ ନଦୀ ବହୁ ଉଚ୍ଚରୁ କଠିନ ଶିଳା ଉପରକୁ ସିଧାସଳଖ ଲମ୍ଫ ପ୍ରଦାନ କରିଥାଏ, ତାହାକୁ ଜଳପ୍ରପାତ କୁହାଯାଏ ।

Question xviii.
ପୃଥ‌ିବୀର ଉଚ୍ଚତମ ଜଳପ୍ରପାତର ନାମ କ’ଣ ?
Answer:
ଦକ୍ଷିଣ ଆମେରିକାର ଭେଛୁଆଲା ଦେଶ ଅନ୍ତର୍ଗତ ଆଞ୍ଜେଲ୍ ଜଳପ୍ରପାତଟି ପୃଥ‌ିବୀର ଉଚ୍ଚତମ ଜଳପ୍ରପାତ।

Question xix.
ଷ୍ଟାଜ୍ ବା ସ୍ତମ୍ଭ କାହାକୁ କୁହାଯାଏ ?
Answer:
ସାମୁଦ୍ରିକ ତୋରଣର ଉପର ଅଂଶ ସମ୍ପୂର୍ଣ୍ଣ କ୍ଷୟ ହୋଇଗଲେ ଏକ ପ୍ରାଚୀର ସଦୃଶ ଭୂମିରୂପ ସମୁଦ୍ର ଭିତରେ ରହିଯାଏ, ଯାହାକୁ ଷ୍ଟାକ୍ ବା ସ୍ତମ୍ଭ କୁହାଯାଏ।

ପ୍ରତ୍ୟେକର ସଂଜ୍ଞା ଗୋଟିଏ ବାକ୍ୟରେ ପ୍ରକାଶ କର।

i. ମହାଦେଶ
Answer:
ବିସ୍ତୀର୍ଣ୍ଣ ସ୍ଥଳଭାଗକୁ ମହାଦେଶ କୁହାଯାଏ ।

ii. ପାନ୍ଥାଲାସା
Answer:
ନିୟୁତ ନିୟୁତ ବର୍ଷ ପୂର୍ବେ ସବୁଯାକ ମହାସାଗର ମିଶି ସୃଷ୍ଟି କରିଥିବା ଜଳଭାଗକୁ ପାନ୍ଥାଲାସା କୁହାଯାଉଥିଲା ।

iii. ଟେଥସ
Answer:
ପାଞ୍ଜିଆର ମଧ୍ୟଭାଗରେ ସୃଷ୍ଟି ହୋଇଥିବା ସଂକୀର୍ଣ୍ଣ ତଥା ଅଗଭୀର ସମୁଦ୍ର ।

iv. ଗଣ୍ଡାନାଲାଣ୍ଡ
Answer:
ଟେମ୍ପ୍ଲେସ୍ ସାଗରର ଉତ୍ତରରେ ଥିବା ଭୂଖଣ୍ଡକୁ ଗଣ୍ଡାନାଲାଣ୍ଡ କୁହାଯାଉଥିଲା ।

v. ଆଙ୍ଗାରାଲାଣ୍ଡ
Answer:
ଟେମ୍ପ୍ଲେସ୍ ସାଗରର ଦକ୍ଷିଣରେ ଥ‌ିବା ଭୂଖଣ୍ଡକୁ ଆଙ୍ଗାରାଲାଣ୍ଡ କୁହାଯାଉଥିଲା ।

vi. ଭୂମିଳନ
Answer:
ଭୂପୃଷ୍ଠରେ ହେଉଥିବା କମ୍ପନକୁ ଭୂମିକମ୍ପ କୁହାଯାଏ ।

vii. ଭୂକମ୍ପ କେନ୍ଦ୍ର
Answer:
ଭୂତ୍ବକ୍‌ର ଯେଉଁ ସ୍ଥାନରେ ଭୂମିକମ୍ପ ଉତ୍ପତ୍ତି ଲାଭକରେ, ତାହାକୁ ଭୂକମ୍ପ କେନ୍ଦ୍ର କୁହାଯାଏ ।

viii. ଉପକେନ୍ଦ୍ର
Answer:
ଭୂକମ୍ପ କେନ୍ଦ୍ରର ଠିକ୍ ଉପରକୁ ଭୂପୃଷ୍ଠରେ ଅବସ୍ଥିତ ସ୍ଥାନକୁ ଉପକେନ୍ଦ୍ର କୁହାଯାଏ ।

ix. ସେସ୍‌ମୋଗ୍ରାଫ୍ ଯନ୍ତ୍ର
Answer:
ଭୂମିକମ୍ପ ମାପିବାପାଇଁ ବ୍ୟବହୃତ ହେଉଥିବା ଯନ୍ତ୍ର ।

x. ମାଗ୍ନା
Answer:
କୂଅଭ୍ୟନ୍ତରରେ ଥିବା ଅର୍ବତରଳ ବା ତରଳ ଶିଳା ।

xi. ଲାଭା
Answer:
ଭୂପୃଷ୍ଠରେ ମାଗ୍ନାକୁ ଲାଭା କୁହାଯାଏ ।

xii. ଅଗ୍ନି ଉଦ୍‌ଗିରଣ
Answer:
ଯେଉଁ ପ୍ରକ୍ରିୟାରେ କୂଅଭ୍ୟନ୍ତରରୁ ମାଗ୍ନା ସହ କଠିନ ଓ ଗ୍ୟାସୀୟ ପଦାର୍ଥମାନ ପଦାକୁ ବାହାରିଆସେ ତାହାକୁ ଅଗ୍ନି ଉଦ୍‌ଗିରଣ କୁହାଯାଏ ।

xiii. ଆଗ୍ନେୟ ପର୍ବତ
Answer:
ଭୂପୃଷ୍ଠରେ ଲାଭା ଜମାହୋଇ କ୍ରମେ ଶୀତଳ ଓ କଠିନ ହୋଇ ସୃଷ୍ଟି ହେଉଥିବା ପର୍ବତ ।

xiv. ଭାଙ୍ଗ
Answer:
ଶିଳାସ୍ତର ଉପରେ ଉଭୟ ପାର୍ଶ୍ବରୁ ବା ଏକ ପାର୍ଶ୍ବରେ ଚାପ ପଡ଼ିଲେ ଶିଳାସ୍ତରର ଏକ ଅଂଶ ଉପରକୁ ଅନ୍ୟ ଅଂଶ ନିମ୍ନକୁ ଚାଲିଯାଇଥାଏ, ଏହାକୁ ଭାଙ୍ଗ କୁହାଯାଏ ।

xv. ଉଭାଙ୍ଗ
Answer:
ଭାଙ୍ଗର ଉପରକୁ ଉଠିଥିବା ଅଂଶକୁ ଉର୍ବରାଙ୍ଗ କୁହାଯାଏ ।

xvi. ନିମ୍ନଭାଙ୍ଗ
Answer:
ଭାଙ୍ଗର ନିମ୍ନକୁ ଯାଇଥିବା ଅଂଶକୁ ନିମ୍ନଭାଙ୍ଗ କୁହାଯାଏ ।

xvii. ସ୍ତରଚ୍ଯୁତି
Answer:
ଫାଟର ଉଭୟ ପାର୍ଶ୍ଵରେ ଶିଳାସ୍ତରରେ ଚଳନ ହେବାଦ୍ଵାରା ଶିଳାର ଅଂଶ ଉପର ବା ନିମ୍ନକୁ ଚାଲିଯିବାକୁ ସ୍ତରଚ୍ୟୁତି କୁହାଯାଏ ।

xviii. ସ୍ତୂପ ପର୍ବତ
Answer:
ଦୁଇଟି ନ୍ୟୁତିର ମଧ୍ୟବର୍ତୀ ଅଂଶ ଉପରକୁ ଉଠି ସୃଷ୍ଟି ହେଉଥ‌ିବା ପର୍ବତକୁ ସ୍ତୂପ ପର୍ବତ କୁହାଯାଏ ।

xix. ଗ୍ରସ୍ତ ଉପତ୍ୟକା
Answer:
ଦୁଇଟି ଚ୍ୟୁତିର ମଧ୍ୟବର୍ତୀ ଅଂଶ ଦବିଯାଇ ସୃଷ୍ଟି ହେଉଥ‌ିବା ଉପତ୍ୟକାକୁ ଗ୍ରସ୍ତ ଉପତ୍ୟକା କୁହାଯାଏ ।

xx. ସମାନୀକରଣ
Answer:
ଭୂପୃଷ୍ଠରେ କାର୍ଯ୍ୟ କରୁଥିବା ବାହ୍ୟଶକ୍ତି ପ୍ରଭାବରେ ଉଚ୍ଚଭୂମି କ୍ଷୟ ହୋଇ କ୍ଷୟଜାତ ପଦାର୍ଥ ନିମ୍ନଭୂମିରେ ଜମାହେବା ପ୍ରକ୍ରିୟାକୁ ସମାନୀକରଣ କୁହାଯାଏ ।

xxi. ଚୂର୍ଣ୍ଣୀଭବନ :
Answer:
ବଡ଼ ବଡ଼ ଶିଳାଖଣ୍ଡଗୁଡ଼ିକ ଭାଙ୍ଗି ଚୂର୍ଣ୍ଣବିଚୂର୍ଣ୍ଣ ହେବା ପ୍ରକ୍ରିୟା ।

xxii. କ୍ଷୟୀକରଣ :
Answer:
ଚୂର୍ଣ୍ଣୀଭୂତ ଶିଳା ଏକ ସ୍ଥାନରୁ ଅନ୍ୟ ସ୍ଥାନରେ ଜମା ହେବା “ପ୍ରକ୍ରିୟା ।

xxii. ‘V” ଉପତ୍ୟକା :
Answer:
ପାର୍ବତ୍ୟ ଶଯ୍ୟାରେ ନଦୀର ପ୍ରଖର ବେଗ ଯୋଗୁ ସୃଷ୍ଟି ହୋଇଥିବା ‘V’ ଅକ୍ଷର ସଦୃଶ ଉପତ୍ୟକା ।

xxiv. ଜଳପ୍ରପାତ :
Answer:
ନଦୀ ବହୁ ଉଚ୍ଚରୁ କଠିନ ଶିଳା ଉପରକୁ ସିଧାସଳଖ ଲମ୍ଫ ପ୍ରଦାନ କରିବାକୁ ଜଳପ୍ରପାତ କୁହାଯାଏ ।

xxv. ପଟୁବ୍ୟଜନ :
Answer:
ଉପରମୁଣ୍ଡରୁ ନଦୀଦ୍ୱାରା ଆନୀତ ବାଲି, ଗୋଡ଼ି, ପଥର ଆଦି ପାହାଡ଼ ତଳେ ହାତପଙ୍ଖା ଆକାରରେ ଜମାହୋଇ ସୃଷ୍ଟି ହେଉଥ‌ିବା ଭୂମିରୂପ ।

xxvi. ନଦୀ ବାଙ୍କ :
Answer:
ସମତଳ ଶଯ୍ୟାରେ ନଦୀର ଅଙ୍କାବଙ୍କା ଗତିପଥକୁ ନଦୀ ବାଙ୍କ କୁହାଯାଏ ।

xxvii. ଅଶ୍ଵଖୁରାକୃତି ହ୍ରଦ :
Answer:
ନଦୀ ବାଙ୍କର ଉଭୟ ପାର୍ଶ୍ବ ବା ମୁଣ୍ଡ ପରସ୍ପରର ଅତି ନିକଟବର୍ତ୍ତୀ ହୋଇ ବନ୍ୟା ସମୟରେ ସୃଷ୍ଟି ହେଉଥ‌ିବା ଏକ କ୍ଷୁଦ୍ର ଅଗଭୀର ହ୍ରଦ ।

xxviii. ପ୍ଳାବନଭୂମି :
Answer:
ବନ୍ୟା ସମୟରେ ନଦୀର ପାର୍ଶ୍ଵବର୍ତ୍ତୀ ଅଞ୍ଚଳ ଜଳପ୍ଲାବିତ ହୋଇ ବାଲି, ପଟୁ ଆଦି କ୍ରମାଗତ ଭାବେ ଜମାହୋଇ ଗଠିତ ସମତଳ ଭୂମି ।

xxix. ପ୍ରାକୃତିକ ବନ୍ଧ :
Answer:
ବହୁ ବର୍ଷ ଧରି ନଦୀର ଉଭୟ ପାର୍ଶ୍ଵରେ ଅବକ୍ଷିପ୍ତ ପଦାର୍ଥ ଜମାକରି ସୃଷ୍ଟି ହେଉଥ‌ିବା ବନ୍ଧ ।

xxx. ତ୍ରିକୋଣଭୂମି :
Answer:
ଉପକୂଳ ଅଞ୍ଚଳରେ ନଦୀମୁହାଣ ପର୍ଯ୍ୟନ୍ତ ସୃଷ୍ଟି ହୋଇଥିବା ତ୍ରିକୋଣାକାର ବିସ୍ତୃତ ସମତଳ ଭୂମି ।

xxxi. ହିମବାହ :
Answer:
ଗତିଶୀଳ ବରଫ ସ୍ରୋତକୁ ହିମବାହ କୁହାଯାଏ ।

xxxii. U-ଉପତ୍ୟକା :
Answer:
ହିମବାହ ନିଜ ଗତିପଥରେ ସୃଷ୍ଟି କରୁଥିବା ସମାନ ପୃଷ୍ଠତଳ ଓ ତୀଖ ପାର୍ଶ୍ଵ ବିଶିଷ୍ଟ ଇଂରାଜୀ ‘U’ ଅକ୍ଷର ଆକାର ବିଶିଷ୍ଟ ଉପତ୍ୟକା ।

xxxiii. ସ୍ରାବ :
Answer:
ହିମବାହର ପାର୍ଶ୍ଵ ତଥା ଅଗ୍ରଭାଗରେ ଏହାଦ୍ଵାରା ଆନୀତ ଭିନ୍ନ ଭିନ୍ନ ଆକୃତିର ଶିଳାଖଣ୍ଡ ଦ୍ବାରା ଗଠିତ ସତ ଭୂମିରୂପ ।

xxxiv. ଗ୍ରାବରେଖା :
Answer:
ହିମବାହର ପାର୍ଶ୍ଵରେ ରେଖା ସଦୃଶ ଲମ୍ବିଥିବା ଶ୍ରାବକୁ ଗ୍ରାବରେଖା କୁହାଯାଏ ।

xxxy. ସର୍କ :
Answer:
ପର୍ବତ ଢାଲୁରେ ହିମବାହଦ୍ଵାରା ଆରାମଚୌକି ଭଳି ସୃଷ୍ଟି ହେଉଥ‌ିବା ଭୂମିରୂପ ।

xxxvi. ବାରଖାନ୍ :
Answer:
ଅର୍ଦ୍ଧଚନ୍ଦ୍ର ଆକୃତି ବିଶିଷ୍ଟ ବାଲି ପାହାଡ଼ ।

xxxvii. ଲୋଏସ୍ :
Answer:
ପବନ ଦ୍ଵାରା ପରିବାହିତ ହୋଇ ସୂକ୍ଷ୍ମ ଧୂଳିକଣାଗୁଡ଼ିକ ମରୁଭୂମିଠାରୁ ବହୁ ଦୂରରେ ପବନର ବେଗ କମିବା ପରେ ଜମାହୋଇ ସୃଷ୍ଟି ହେଉଥ‌ିବା ମୃରିକା ।

xxxviii. ସମୁଦ୍ର ଗୁମ୍ଫା :
Answer:
ସାମୁଦ୍ରିକ ତରଙ୍ଗ ଦ୍ଵାରା ସମୁଦ୍ରକୂଳସ୍ଥ ଶିଳା କ୍ଷୟ ହୋଇ ସୃଷ୍ଟି ହୋଇଥିବା ଗୁମ୍ଫା ଆକାର ଗର୍ଭ ।

xxxix. ସାମୁଦ୍ରିକ ଚୋରଣ :
Answer:
ସମୁଦ୍ର ଭିତରକୁ ପଶିଯାଇଥିବା ପାହାଡ଼, ପର୍ବତର ଉଭୟ ପାର୍ଶ୍ଵର ଗୁମ୍ଫା କ୍ରମଶଃ ମିଶିଯାଇ ସୃଷ୍ଟି ହେଉଥ‌ିବା ତୋରଣ ସଦୃଶ ଭୂମିରୂପ ।

xl. ଷ୍ଟର୍ମ :
Answer:
ଷ୍ଟାକ୍ କାଳକ୍ରମେ କ୍ଷୟ ହୋଇ ଛୋଟ ହେଲେ ଏହାକୁ ଷ୍ଟମ୍ପ କୁହାଯାଏ ।

xli. ଡୋଲାଇନ୍ :
Answer:
ଚୂନପଥର ଅଞ୍ଚଳରେ କାହାଳୀ ସଦୃଶ ସୃଷ୍ଟି ହୋଇଥିବା ଗର୍ଭ ।

xlii. ଉଭାଲା :
Answer:
ଡୋଲାଇନ୍ ଆକାର ବଡ଼ ହେଲେ ତାକୁ ଉଭାଲା କୁହାଯାଏ ।

xliii. ଷ୍ଟାଲାର୍‌ମାଇଟ୍ :
Answer:
ଚୂନପଥର ଗୁମ୍ଫାର ଛାତରୁ ଚୂନ ମିଶ୍ରିତ ଜଳଟୋପା ତଳକୁ ପଡ଼ି ଓ ଭୂମିରେ ଜମାହୋଇ ହୁଙ୍କା ପରି ସୃଷ୍ଟି ହେଉଥ‌ିବା ଚୂନସ୍ତମ୍ଭକୁ ଷ୍ଟାଲାଗ୍‌ମାଇଟ୍‌ କୁହାଯାଏ ।

xliv. ଷ୍ଟାଲାକ୍‌ଟାଇଟ୍ :
Answer:
ଚୂନପଥର ଗୁମ୍ଫାର ଛାତରୁ ଓହଳ ସଦୃଶ ଝୁଲି ରହିଥ‌ିବା ଚୂନସ୍ତମ୍ଭକୁ ଷ୍ଟାଲାକ୍‌ଟାଇଟ୍‌ କୁହାଯାଏ ।

ପ୍ରତ୍ୟେକ ବାକ୍ୟାଶକୁ ଗୋଟିଏ ଗୋଟିଏ ଭୌଗୋଳିକ ପଦରେ ପ୍ରକାଶ କର ।

i. ପାଞ୍ଜିଆ ମଧ୍ୟଭାଗରେ ସୃଷ୍ଟି ହୋଇଥିବା ସଂକୀର୍ଣ୍ଣ ତଥା ଅଗଭୀର ସାଗର ।
Answer:
ଟେମ୍ପ୍ଲେସ୍

ii. ପୃଥ‌ିବୀପୃଷ୍ଠରେ ହେଉଥିବା କମ୍ପନ ।
Answer:
ଭୂମିକମ୍ପ

iii. ଭୂମିକମ୍ପ ତୀବ୍ରତା ମାପିବା ଯନ୍ତ୍ର ।
Answer:
ସିସ୍ଟୋଗ୍ରାଫ୍

iv. ଭାରତର ଏକ ସ୍ତୂପ ପର୍ବତ ।
Answer:
ସାତପୁରା

v. ଗ୍ରସ୍ତ ଉପତ୍ୟକା ଦେଇ ପ୍ରବାହିତ ଭାରତର ଏକ ନଦୀ ।
Answer:
ତାଦ୍ରୀ

vi. ଜାପାନର ଏକ ସଞ୍ଚୟଜାତ ପର୍ବତ ।
Answer:
ଫୁଜିୟାମା

vii. ଭାରତର ସଞ୍ଚୟଜନିତ ବୃହତ୍ ସମତଳ ଭୂମି ।
Answer:
ଗାଙ୍ଗେୟ ସମତଳଭୂମି

viii. ଚୂର୍ଣ୍ଣୀଭୂତ ଶିଳା ଏକ ସ୍ଥାନରୁ ଅନ୍ୟ ସ୍ଥାନରେ ଜମା ହେବା ପ୍ରକ୍ରିୟା ।
Answer:
କ୍ଷୟୀକରଣ

ix. ପୃଥିବୀର ଉଚ୍ଚତମ ଜଳପ୍ରପାତ ।
Answer:
ଆଞ୍ଜେଲ

x. ଜାମିଆ ଓ ଜିମ୍ବାୱେ ଦେଶଦ୍ଵୟ ମଧ୍ୟବର୍ତ୍ତୀରେ ଥିବା ଜଳପ୍ରପାତ ।
Answer:
ଭିକ୍ଟୋରି ଆ

xi. ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ଓ କାନାଡ଼ାର ମଧ୍ୟବର୍ତ୍ତୀରେ ଅବସ୍ଥିତ ଜଳପ୍ରପାତ ।
Answer:
ନାଏଗ୍ରା

xii. ଓଡ଼ିଶାର ଏକ ଅଶୁଖୁରାକୃତି ହ୍ରଦ ।
Answer:
ଅଂଶୁପା

xiii. ମରୁଭୂମି ଅଞ୍ଚଳର ମୁଖ୍ୟ କ୍ଷୟକାରୀ ଶକ୍ତି ।
Answer:
ପବନ

xiv. ଅର୍ଦ୍ଧଚନ୍ଦ୍ର ଆକୃତି ବିଶିଷ୍ଟ ବାଲିପାହାଡ଼ ।
Answer:
ବାରଖାନ୍

xv. ଚୂନପଥର ଅଞ୍ଚଳରେ ଦେଖାଯାଉଥ‌ିବା କାହାଳୀ ସଦୃଶ ବଡ଼ ଗର୍ଭ ।
Answer:
ଉଇଲା

xi. ଚୂନପଥର ଗୁମ୍ଫାର ଭୂମିରେ ହୁଙ୍କା ପରି ସୃଷ୍ଟି ହୋଇଥ‌ିବା ଚୂନସ୍ତମ୍ଭ ।
Answer:
ଷ୍ଟାଲାଗ୍‌ମାଇଟ୍‌

xvii. ଚୂନପଥର ଗୁମ୍ଫାର ଛାତରୁ ଓହଳ ସଦୃଶ ଥିବା ଚୂନମିଶ୍ରିତ ଅଂଶ ।
Answer:
ଷ୍ଟାଲାକ୍‌ଟାଇଟ୍

ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

i. ସାମୁଦ୍ରିକ ଗଣ୍ଡ _______ ଶ୍ରେଣୀର ଭୂମିରୂପ ।
Answer:
ତୃତୀୟ

ii. ପାଞ୍ଜିଆର ମଧ୍ୟଭାଗରେ _______ ସାଗର ରହିଥିଲା ।
Answer:
ଟେମ୍ପ୍ଲେସ୍

iii. ଭୂକମ୍ପ କେନ୍ଦ୍ରର ଠିକ୍ ଉପରକୁ ଭୂପୃଷ୍ଠର ଅବସ୍ଥିତ ସ୍ଥାନକୁ ________ କୁହାଯାଏ ।
Answer:
ଉପକେନ୍ଦ୍ର

iv. ଭୂକମ୍ପଜନିତ ସର୍ବାଧ‌ିକ କ୍ଷତି ______ ରେ ହିଁ ହୋଇଥାଏ ।
Answer:
ଉପକେନ୍ଦ୍ର

v. ଭୂକମ୍ପ ମାପିବାପାଇଁ. ________ ଯନ୍ତ୍ର ବ୍ୟବହାର କରାଯାଏ ।
Answer:
ସେସ୍ମୋଗ୍ରାଫ୍

vi. ମାଗ୍ନା ଗଚ୍ଛିତ ସ୍ଥାନକୁ _______ କୁହାଯାଏ ।
Answer:
ମାଗ୍ଲା କୋଠରି

vii. ଭୂପୃଷ୍ଠରେ ମାଗ୍ନାକୁ _______ କୁହାଯାଏ ।
Answer:
ଲାଭା

viii. ଯେଉଁ ପଥଦେଇ ମାଗ୍ନା ପଦାକୁ ଆସେ, ତାହାକୁ _______ ପଥ ବୋଲି କୁହାଯାଏ ।
Answer:
ଗ୍ରୀବାପଥ ବା ନିର୍ଗମ ପଥ

ix. _____ ପୃଥ‌ିବୀର ଉଚ୍ଚତମ ମାଳଭୂମି ।
Answer:
ପାମିର

x. ଭାରତର ଦାକ୍ଷିଣାତ୍ୟ ମାଳଭୂମି _______ ଦ୍ୱାରା ସୃଷ୍ଟି ହୋଇଛି ।
Answer:
ଲାଭା

xi. ମରୁ ଅଞ୍ଚଳ ତଥା ସମୃଦ୍ଧ କୂଳବର୍ତ୍ତୀ ଅଞ୍ଚଳରେ ________ ହଁ ମୁଖ୍ୟ କ୍ଷୟକାରୀ ଶକ୍ତି ।
Answer:
ପବନ

xii. ଅର୍ଦ୍ଧଚନ୍ଦ୍ର ଆକୃତିବିଶିଷ୍ଟ ବାଲି ପାହାଡ଼କୁ ________ କୁହାଯାଏ ।
Answer:
ବାର ଖାନ୍

xiii. ଡୋଲାଇନ୍ ଆକାରରେ ବଡ଼ ହୋଇଥିଲେ ତାକୁ _______ କୁହାଯାଏ ।
Answer:
ଉଇଲା ।

xiv. ଭୂମିରୁ ହୁଙ୍କାପରି ଉଠିଥିବା ଚୂନସ୍ତମ୍ଭକୁ ______ କୁହାଯାଏ ।
Answer:
ଷ୍ଟାଲାମାଇଟ୍‌

xv. ଗତିଶୀଳ ବରଫ ସ୍ରୋତକୁ _______ କୁହାଯାଏ ।
Answer:
ହିମବାହ

xvi. _____ ପୃଥ‌ିବୀର ଉଚ୍ଚତମ ଜଳପ୍ରପାତ ।
Answer:
ଆଞ୍ଜେଲ୍

xvii. ନାଏଗ୍ରା ଜଳପ୍ରପାତ _______ ଦେଶରେ ଅବସ୍ଥିତ ।
Answer:
କାନାଡ଼ା

ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।

Question i.
କେଉଁଟି ଏକ ଦ୍ଵିତୀୟଶ୍ରେଣୀ ଭୂମିରୂପ ?
(କ) ଜଳପ୍ରପାତ
(ଖ) ମହୀସୋପାନ
(ଗ) ମହାସାଗର
Answer:
(ଖ) ମହୀସୋପାନ

Question ii.
କେଉଁଟି ପୃଥବୀର ତ୍ଵରିତ ଚଳନ ଯୋଗୁଁ ହୋଇଥାଏ ?
(କ) ଅଗ୍ନି ଉଦ୍‌ଗିରଣ
(ଖ) ପର୍ବତ ଗଠନ
(ଗ) ମହାଦେଶୀୟ ସଞ୍ଚଳନ
Answer:
(କ) ଅଗ୍ନି ଉଦ୍‌ଗିରଣ

Question iii.
କେଉଁ ନଦୀଟି ଏକ ଗ୍ରସ୍ଥ ଉପତ୍ୟକା ଦେଇ ପ୍ରବାହିତ ହେଉଛି ?
(କ) ମହାନଦୀ
(ଖ) ନର୍ମଦା
(ଗ) କାବେରୀ
Answer:
(ଖ) ନର୍ମଦା

Question iv.
ଉତ୍ତର ଆମେରିକା କେଉଁ ପୁରାତନ ଭୂଖଣ୍ଡର ଅଂଶ ଥୁଲା ?
(କ) ପାନ୍ଥାଲାସା
(ଖ) ଗଣ୍ଡୱାନାଲାଣ୍ଡ
(ଗ) ଆଙ୍ଗାରାଲାଣ୍ଡ
Answer:
(ଗ) ଆଙ୍ଗାରାଲାଣ୍ଡ

Question v.
ଭୂମିକମ୍ପ ଉତ୍ପତ୍ତିସ୍ଥଳକୁ କ’ଣ କୁହାଯାଏ ?
(କ) ଉପକେନ୍ଦ୍ର
(ଖ) ଭୂକମ୍ପ କେନ୍ଦ୍ର
(ଗ) ଗ୍ରସ୍ତ ଉପତ୍ୟକା
Answer:
(ଖ) ଭୂକମ୍ପ କେନ୍ଦ୍ର

Question vi.
ଅଶ୍ଵଖୁରାକୃତି ହ୍ରଦ କେଉଁଠି ଦେଖାଯାଏ ?
(କ) ନଦୀ ଉପତ୍ୟକା
(ଖ) ପାର୍ବତ୍ୟଭୂମି
(ଗ) ମରୁଭୂମି
Answer:
(କ) ନଦୀ ଉପତ୍ୟକା

Question vii.
ଛତୁଶିଳା କାହାଦ୍ଵାରା ସୃଷ୍ଟି ହୁଏ ?
(କ) ନଦୀ
(ଖ) ପବନ
(ଗ) ହିମବାହ
Answer:
(ଖ) ପବନ

Question viii.
କେଉଁଟି ସାମୁଦ୍ରିକ ତରଙ୍ଗ ଦ୍ଵାରା ସୃଷ୍ଟି ହୁଏ ?
(କ) ବେଳାଭୂମି
(ଖ) ପ୍ଲାବନଭୂମି
(ଗ) ତ୍ରିକୋଣଭୂମି
Answer:
(କ) ବେଳାଭୂମି

Question ix.
ପଟୁବ୍ୟଜନ ପାହାଡ଼ର କେଉଁ ଅଂଶରେ ସୃଷ୍ଟି ହୁଏ ?
(କ) ଶୀର୍ଷଦେଶ
(ଖ) ମଧ୍ୟଅଂଶ
(ଗ) ପାଦଦେଶ
Answer:
(ଗ) ପାଦଦେଶ

Question x.
ଚୂନପଥର ଅଞ୍ଚଳର ଭୂପୃଷ୍ଠସ୍ଥ ଶୁଷ୍କ ନଦୀ ଉପତ୍ୟକାକୁ କ’ଣ କୁହାଯାଏ ?
(କ) ଅଦୃଶ୍ୟ ଉପତ୍ୟକା
(ଖ) ‘U’ ଉପତ୍ୟକା
(ଗ) ‘V” ଉପତ୍ୟକା
Answer:
(କ) ଅଦୃଶ୍ୟ ଉପତ୍ୟକା ।

ବନ୍ଧନୀ ମଧ୍ଯରୁ ଉପଯୁକ୍ତ ଶବ୍ଦ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

1. ଭୂକମ୍ପ ମାପିବାପାଇଁ _______ ଯନ୍ତ୍ର ବ୍ୟବହାର କରାଯାଏ। (ଥର୍ମୋମିଟର, ବାରୋମିଟର, ସେସ୍‌ମୋଗ୍ରାଫ, ହାଇଡ୍ରୋମିଟର)
Answer:
ସେସ୍‌ମୋଗ୍ରାଫ୍

2. ଭାରତର ନଦୀ ଗ୍ରସ୍ତ ଉପତ୍ୟକା ମଧ୍ୟଦେଇ ପ୍ରବାହିତ । (ନର୍ମଦା ଓ ତାୟୀ, ମହାନଦୀ ଓ ବ୍ରାହ୍ମଣୀ, କୃଷ୍ଣା ଓ କାବେରୀ, ଗଙ୍ଗା ଓ ଯମୁନା)
Answer:
ନର୍ମଦା ଓ ତାଦ୍ରୀ

3. _______ ଏକ ଭଙ୍ଗିଳ ପର୍ବତଶ୍ରେଣୀ ଅଟେ। (ପୂର୍ବଘାଟ, ପଶ୍ଚିମଘାଟ, ସାତପୁରା, ହିମାଳୟ)
Answer:
ହିମାଳୟ

4. ଭାରତର _______ଏକ ସ୍ତୂପପର୍ବତ ଅଟେ । (ହିମାଳୟ, ସାତପୁରା, ମହାବଳେଶ୍ଵର, ଆରାବଳୀ)
Answer:
ସାତପୁରା

5. ଜାପାନର _______ ଏକ ସଞ୍ଚୟଜାତ ପର୍ବତ ଅଟେ । (ଆଲପ୍‌ସ, ରକି, ଆଣ୍ଡିଜ୍, ଫୁଜିୟାମା)
Answer:
ଫୁଜିୟାମା

6. _______ ମାଳଭୂମିକୁ ପୃଥ‌ିବୀର ଛାତ କୁହାଯାଏ। (ଛୋଟନାଗପୁର, ଡେକାନ, ପାମିର, ବୁନ୍ଦେଇଖଣ୍ଡ)
Answer:
ପାମିର

7. ନଦୀ ତା’ର ଶଯ୍ୟାକୁ ଖୋଳି _______ ସଦୃଶ ଉପତ୍ୟକା ସୃଷ୍ଟି କରେ । (V, U, W, X)
Answer:
V

8. ଓଡ଼ିଶାର _______ ଏକ ଅଶ୍ଵଖୁରାକୃତି ହ୍ରଦ ଅଟେ। (ଚିଲିକା, ପାଟ, ଅଂଶୁପା, କାଞ୍ଜିଆ)
Answer:
ଅଂଶୁପା

9. ପବନ ଦ୍ଵାରା ପରିବାହିତ ବାଲୁକା ସ୍ତୂପକୁ _______ କୁହାଯାଏ । (ଗ୍ରାବରେଖା, ବାରଖାନ, ପ୍ଲାବନଭୂମି, ଛତୁଶିଳା)
Answer:
ବାରଖାନ୍

10. ଚୀନ୍‌ର ପଶ୍ଚିମାଂଶରେ _______ ମୃରିକାଞ୍ଚଳ ରହିଛି । (ଖଦର, ଭାଙ୍ଗର, କଙ୍କର, ଲୋଏସ୍)
Answer:
ଲୋଏସ୍

11. ଉତ୍ତର ଆମେରିକା _______ ପୁରାତନ ଭୂଖଣ୍ଡର ଅଂଶବିଶେଷ । (ପାନ୍ଥାଲାସ, ଗଣ୍ଡନଲାଣ୍ଡ, ଅଙ୍ଗାରଲାଣ୍ଡ, ଟେଣ୍ଟ୍‌ସ୍)
Answer:
ଗଣ୍ଡାନାଲାଣ୍ଡ

12. ଛତୁଶିଳା _______ ଦ୍ଵାରା ଗଠିତ ହୋଇଥାଏ। (ନଦୀ, ସାଗର, ହିମବାହ, ପବନ)
Answer:
ପବନ

13. ଭୂମିକମ୍ପ ଉତ୍ପତ୍ତିସ୍ଥଳକୁ _______ କୁହାଯାଏ । (କେନ୍ଦ୍ର, ଉପକେନ୍ଦ୍ର, ମଧ୍ଯକେନ୍ଦ୍ର, ପାର୍ଶ୍ଵଭାଗ)
Answer:
କେନ୍ଦ୍ର

ସ୍ତମ୍ଭ ଦୁଇଟି ମଧ୍ୟରେ ସମ୍ପର୍କ ସ୍ଥାପନ କର ।

Question i.

Answer:

Question ii.

Answer:

ପ୍ରଥମ ଯୋଡ଼ିକୁ ଦେଖୁ ଦ୍ଵିତୀୟ ଯୋଡ଼ି ପୂରଣ କର

1. ପ୍ରଥମଶ୍ରେଣୀ ଭୂମିରୂପ : ମହାଦେଶ :: ଦ୍ଵିତୀୟ ଶ୍ରେଣୀ ଭୂମିରୂପ : ______।
Answer:
ମହୀସୋପାନ

2. ମହାସାଗର : ପ୍ରଥମଶ୍ରେଣୀ ଭୂମିରୂପ :: ମହୀଢ଼ାଲୁ : ______।
Answer:
ଦ୍ଵିତୀୟ ଶ୍ରେଣୀ ଭୂମିରୂପ

3. ତ୍ଵରିତଶକ୍ତି : ଅଗ୍ନିଉଦ୍‌ଗିରଣ :: ଧୀରଶକ୍ତି : ______।
Answer:
ମହାଦେଶୀୟ ସଞ୍ଚଳନ

4. ବାହ୍ୟଶକ୍ତି : କ୍ଷୟକାରୀ :: ଆଭ୍ୟନ୍ତରୀଣ ଶକ୍ତି : ______।
Answer:
ତ୍ବରିତଶକ୍ତି

5. ମହାଦେଶ : ପାଞ୍ଜିଆ :: ମହାସାଗର : ______।
Answer:
ପାନ୍ଥାଲାସା

6. ଟେଣ୍ଟ୍‌ ସ୍ ଉତ୍ତରରେ : ଆଙ୍ଗାରାଲାଣ୍ଡ :: ଟେଣ୍ଟ୍‌ସ୍ ଦକ୍ଷିଣରେ ______।
Answer:
ଗଣ୍ଡଓ୍ବାନାଲାଣ୍ଡ

7. ଆଙ୍ଗାରାଲାଣ୍ଡ : ଇଉରୋପ : : ଗଣ୍ଡାନାଲାଣ୍ଡ : ______।
Answer:
ଆଫ୍ରିକା

8. ଭାଙ୍ଗର ଊର୍ଦ୍ଧ୍ୱ ଅଂଶ : ଊଭାଙ୍ଗ :: ଭାଙ୍ଗର ନିମ୍ନଅଂଶ : ______।
Answer:
ନିମ୍ନ ଭାଙ୍ଗ

9. ସାତପୁରା : ସ୍ତୂପ ପର୍ବତ : : ଫୁଜିୟାମା ______।
Answer:
ସଞ୍ଚୟଜାତ ପର୍ବତ

10. ନଦୀରୁ ସୃଷ୍ଟି : ‘V” ଉପତ୍ୟକା : ହିମବାହରୁ ସୃଷ୍ଟି : ______।
Answer:
‘U” ଉପତ୍ୟକା

11. ଚୂନସ୍ତମ୍ଭ : ଷ୍ଟାଲାଗମାଇଟ୍‌ : : ଚୂନ ଓହଳ : ______।
Answer:
ଷ୍ଟାଲାକଟାଇଟ୍

Odisha State Board BSE Odisha 7th Class Science Important Questions Chapter 13 କେତୋଟି ପ୍ରାକୃତିକ ଘଟଣା Important Questions and Answers.

BSE Odisha Class 7 Science Important Questions Chapter 13 କେତୋଟି ପ୍ରାକୃତିକ ଘଟଣା

Question 1.
ବିଜୁଳି -ଘଡ଼ଘଡ଼ି ଜନିତ ଝଡ଼ବର୍ଷାର ଏକ ଫ୍ଲୋଚାର୍ଟ ଦିଅ ।
Solution:

Question 2.
ବାୟୁ ପ୍ରବାହ କିପରି ଘଟେ ? କୌଣସି ଆକସ୍ମିକ କାରଣରୁ ହଠାତ୍ ବାୟୁ ଚାପର ହ୍ରାସ କିମ୍ବା ବୃଦ୍ଧି ଘଟିଲେ କ’ଣ ହୁଏ ?
Solution:
(i) ଜଳ ଯେପରି ତା’ର ପତ୍ତନର ସମତା ରକ୍ଷାକରେ ସେହିପରି ବାୟୁ ତା’ର ଚାପର ସମତା ରକ୍ଷା କରିବାକୁ ସବୁବେଳେ ଚେଷ୍ଟା କରେ ।
(ii) କୌଣସି କାରଣରୁ ଏକ ସ୍ଥାନରେ ବାୟୁର ଲଘୁଚାପ ସୃଷ୍ଟିହେଲେ ତାହା ହାଲୁକା ହୋଇ ଉପରକୁ ଉଠିଯାଏ ଏବଂ ତା’ର ସ୍ଥାନ ପୂରଣ କରିବା ପାଇଁ ଗୁରୁଚାପ ଅଞ୍ଚଳରୁ ବାୟୁ ସେହିସ୍ଥାନକୁ ପ୍ରବାହିତ ହୁଏ । ଅର୍ଥାତ୍ ବାୟୁ ଚାପର ତାରତମ୍ୟ ହେଲେ ବାୟୁ ମଧ୍ୟରେ ପ୍ରବାହ ସୃଷ୍ଟି ହୁଏ । ପ୍ରବାହିତ ବାୟୁକୁ ପବନ (wind) କୁହାଯାଏ । ଭୂ-ବାୟୁ, ସାମୁଦ୍ରିକ ବାୟୁ ଏବଂ ମୌସୁମୀ ବାୟୁ ଏହି ବାୟୁ ପ୍ରବାହର ଅନ୍ତର୍ଗତ ।
(iii) କୌଣସି ଆକସ୍ମିକ କାରଣରୁ ହଠାତ୍‌ ବାୟୁଚାପର ହ୍ରାସ କିମ୍ବା ବୃଦ୍ଧି ଘଟିଲେ, ବାତ୍ୟା ବା ବାତାବର୍ଷ (cyclone) ଓ ପ୍ରତୀପ ବାତାବର୍ଷ (Anti-cyclone) ଘଟେ ।
(iv) ଯଦି କୌଣସି ସ୍ଥାନର ବାୟୁର ଚାପ ହଠାତ୍ କମିଯାଏ, ତାହାର ଚତୁର୍ଦ୍ଦିଗରେ ଥ‌ିବା ଗୁରୁଚାପ ବିଶିଷ୍ଟ ବାୟୁ ଲଘୁଚାପ କେନ୍ଦ୍ରକୁ ପ୍ରବଳ ବେଗରେ ପ୍ରବାହିତ ହୁଏ । ଏହାକୁ ବାତ୍ୟା କହନ୍ତି ।
(v) ବାତ୍ୟା ଯେଉଁ କାରଣରୁ ହୁଏ ପ୍ରତୀପ ବାତାବର୍ତ୍ତ ତା’ର ବିପରୀତ କାରଣରୁ ହୋଇଥାଏ । ଏହା ଘଟିବା ସମୟରେ ବାୟୁର ଆର୍ଦ୍ରତା କମିଯାଏ ଏବଂ ଆକାଶ ନିର୍ମଳ ଓ ମେଘମୁକ୍ତ ରହେ ।

ସଂଶିପ୍ତଧାମା ପ୍ରଣୋଉର :

Question 1.
ବାତ୍ୟା ପାଇଁ କେଉଁ କେଉଁ କାରକ ଦାୟୀ ଓ ସେଗୁଡ଼ିକ କେଉଁ ଯନ୍ତ୍ର ଦ୍ୱାରା ଓ କିପରି ଜାଣି ହୁଏ ।
Solution:
ବାତ୍ୟାପାଇଁ ପବନର ବେଗ , ଦିଗ, ତାପମାତ୍ରା ଏବଂ ଆର୍ଦ୍ରତା ଆଦି କାରକ ଦାୟୀ । ପବନର ବେଗ ଏଥ‌ିପାଇଁ ଅଧ୍ଵ ଦାୟୀ ।
ପବନର ବେଗ – ଆନିମୋମିଟର ଯନ୍ତ୍ର ସାହାଯ୍ୟରେ ପବନର ବେଗ ମପାଯାଏ ।
ଦିଗ – ବାୟୁ ପ୍ରାବାହର ଦିଗ ନିର୍ଣ୍ଣୟ କରିବା ପାଇଁ ପବନ ଚକି ବା ପାଗ କୁକୁଡ଼ା ନାମକ ଯନ୍ତ୍ର ବ୍ୟବହାର କରାଯାଇଥାଏ ।
ତାପମାନ ଯନ୍ତ୍ର ବ୍ୟବହାର କରାଯାଏ ।
ପାଣିପାଗ ବେଲୁନ’’ ଆକାଶକୁ ଛଡ଼ାଯାଏ । ଏଥ‌ିରେ ଖଞ୍ଚା ଯାଇଥିବା ବେତାର ପ୍ରେରକଯନ୍ତ୍ରରୁ ଗ୍ରହଣ କେନ୍ଦ୍ରକୁ ବାୟୁମଣ୍ଡଳର ତାପ, ଚାପ, ଆର୍ଦ୍ରତା ଆଦି ସମ୍ବାଦ ମିଳିଥାଏ ।

Question 2.
ମୌସୁମୀ ଶବ୍ଦର ଅର୍ଥ କ’ଣ ? ଖରାଦିନେ ରାଜସ୍ଥାନରେ କେଉଁ ମୌସୁମୀ ବାୟୁ ପ୍ରବାହିତ ହୁଏ ।
Solution:
(i) ଖରାଦିନେ ବିଷୁବରେଖା ନିକଟବର୍ତ୍ତୀ ଅଞ୍ଚଳରେ ମହାସାଗର ଅଞ୍ଚଳରୁ ସ୍ଥଳଭାଗ ଆଡ଼କୁ ବାୟୁ ପ୍ରବାହିତ ହୁଏ । ଏହାକୁ ‘ମୌସୁମୀ ବାୟୁ’’ କୁହାଯାଏ ।
(ii) ଏହି ମୌସୁମୀ ଶବ୍ଦଟି ଆରବିକ୍ ଶବ୍ଦ ‘ମଉସମ୍’ରୁ ଆନୀତ, ଯାହାର ଅର୍ଥ ଋତୁ । ମୌସୁମୀ ବାୟୁ ଜଳ ଧରି ଆସେ ଏବଂ ବର୍ଷା କରାଏ । ଶସ୍ୟ ଉତ୍ପାଦନ ପାଇଁ ଏହା ନିହାତି ଆବଶ୍ୟକ । ଖରାଦିନେ ରାଜସ୍ଥାନରେ ଦକ୍ଷିଣ- ପଶ୍ଚିମ ମୌସୁମୀ ବାୟୁ ପ୍ରବାହରେ ବର୍ଷା ହୁଏ ।

ବସ୍ତୁନିଷ୍ ପ୍ରଣୋଉର :

I. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ______ ବାୟୁକୁ ପବନ କୁହାଯାଏ ।
(ii) ପୃଥ‌ିବୀ ପୃଷ୍ଠରେ ଅସମାନ ______ ହେତୁ ବାୟୁ ପ୍ରବାହ ହୁଏ ।
(iii) ଜଳୀୟବାଷ୍ପ ଧାରଣ କରିଥିବା ବାୟୁ ______ କରାଏ ।
(iv) ବାୟୁ ଗୁରୁଚାପ ଅଞ୍ଚଳରୁ ______ ହେତୁ ବାୟୁ ପ୍ରବାହ ହୁଏ ।
(v) କୌଣସି ଦିନ କୌଣସି ସ୍ଥାନର ପାଣିପାଗ କହିଲେ ସେହି ଦିନ ସେହି ସ୍ଥାନର, ______ ର ଅବସ୍ଥାକୁ ବୁଝାଏ ।
(vi) ବାୟୁର ______ ଥ‌ିବାରୁ ଏହା ଚାପ ପ୍ରଦାନ କରେ ।
(vii) ବାୟୁର ଚାପ ______ ପବନ କୁହାଯାଏ ।
(viii)ସମୁଦ୍ରପତ୍ତନର ବାୟୁମଣ୍ଡଳର ଚାପ ହେଲା ______ ପେ.ମି.ପାରଦର ପ୍ରମ୍ |
(ix) ସମସ୍ତ ଝଡ଼ବର୍ଷା ______ କନିତ ପ୍ରକୃଷ୍ନା |
(x) ______ ମାଧ୍ୟାପରେ ବାତ୍ୟା ସମକରେ ପୂର୍ବ ସୂଚନା ମିଳିପାରୁଛି |
Solution:
(i) ଗତିଶୀଳ,
(ii) ତାପ ସଂଚରଣ,
(iii) ବାୟୁ,
(iv) ଲଘୁ,
(v) ବାୟୁମଣ୍ଡଳ,
(vi) ଓଜନ,
(vii) ବାରୋମିଟର,
(viii) 76,
(ix) ସ୍ଵଳ୍ପ-ଚାପ,
(ix) ରାଡ଼ାର ଓ କୃତ୍ରିମ ଉପଗ୍ରହ

II. ବାମପାର୍ଶ୍ଵର ସମ୍ପର୍କକୁ ଲକ୍ଷ୍ୟକରି ଦକ୍ଷିଣପାର୍ଶ୍ବର ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ବାୟୁର ବେଗ : ଆନିମୋମିଟର :: ବାୟୁର ଚାପ : ______
(ii) କୃତ୍ରିମ ଉପଗ୍ରହ : ଓଡ଼ିଶା ଉପକୂଳର ଫଟୋଚିତ୍ର :: ମାନ ମନ୍ଦିର : ______
(iii) ବାୟୁ ଉତ୍ତପ୍ତ : ଲଘୁଚାପ :: ବାୟୁ ଥଣ୍ଡା : ______
(iv) ବାୟୁମଣ୍ଡଳର ଅବସ୍ଥା : ପାଣିପାଗ ବେଲୁନ୍ :: ବାୟୁପ୍ରବାହର ଦିଗ : ______
Solution:
(i) ବାରୋମିଟର,
(ii) ପାଣିପାଗର ସୂଚନା,
(iii) ଗୁରୁ ଚାପ,
(iv) ପବନ ଚକି

III. ରେଖାଙ୍କିତ ପଦ ନ ବଦଳାଇ ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର ।
(i) ପବନର ବେଗ ବଢ଼ିଲେ ବାୟୁର ଚାପ ବଢ଼େ ।
(ii) ବାୟୁ ଗତିଶୀଳ ହେବାକୁ ଜଳୀୟ ବାଷ୍ପ କୁହାଯାଏ ।
(iii) ଖରାଦିନେ ପବନ ସ୍ଥଳଭାଗରୁ ଜଳଭାଗ ଆଡ଼କୁ ପ୍ରବାହିତ ହୁଏ ।
(iv) ଆନିମୋମିଟର ଯନ୍ତ୍ର ସାହାଯ୍ୟରେ ଆର୍ଦ୍ରତା ମପାଯାଏ ।
(v) ପୃଥ‌ିବୀ ପୃଷ୍ଠରେ ସମାନ ତାପ ସଞ୍ଚରଣ ହେତୁ ବାୟୁ ପ୍ରବାହ ସମ୍ଭବ ହୁଏ ।
Solution:
(i) ପବନର ବେଗ ବଢ଼ିଲେ ବାୟୁର ଚାପ ହ୍ରାସପାଏ ।
(ii) ବାୟୁ ଗତିଶୀଳ ହେବାକୁ ପବନ କୁହାଯାଏ ।
(iii) ଶୀତଦିନେ ପବନ ସ୍ଥଳଭାଗରୁ ଜଳଭାଗ ଆଡ଼କୁ ପ୍ରବାହିତ ହୁଏ ।
(iv) ଆନିମୋମିଟର ଯନ୍ତ୍ର ସାହାଯ୍ୟରେ ପବନର ବେଗ ମପାଯାଏ ।
(v) ପୃଥ‌ିବୀ ପୃଷ୍ଠରେ ସମାନ ତାପ ସଞ୍ଚରଣ ହେତୁ ବାୟୁ ପ୍ରବାହ ସମ୍ଭବ ହୁଏ ।

IV. ‘କ’ ସ୍ତମ୍ଭରେ ଥ‌ିବା ଶବ୍ଦସହ ‘ଖ’ ସ୍ତମ୍ଭରେ ଥ‌ିବା ଶବ୍ଦର ମେଳନ କର ।

V. ନିମ୍ନଲିଖ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଗୋଟିଏ ବା ଦୁଇଟି ଶବ୍ଦରେ ଲେଖ ।
(i) କେଉଁ ଅଞ୍ଚଳର ଲୋକେ ସୂର୍ଯ୍ୟଙ୍କଠାରୁ ସର୍ବାଧିକ ତାପ ପାଇଥାଆନ୍ତି ?
(ii) ପୃଥ‌ିବୀରେ ଦିନରାତି ପୃଥ‌ିବୀର କେଉଁ ଗତି ଯୋଗୁଁ ସମ୍ଭବ ହୁଏ ?
(iii) ବାୟୁ ଉତ୍ତପ୍ତ ହେଲେ ଓ ଥଣ୍ଡା ହେଲେ କ’ଣ ହୁଏ ?
(iv) ବାୟୁ କେଉଁ ଚାପ ଅଞ୍ଚଳରୁ କେଉଁ ଚାପ ଅଞ୍ଚଳକୁ ପ୍ରବାହିତ ହୁଏ ?
(v) ଅଧିକ ବେଗରେ ପବନ ବହିଲେ ବାୟୁର ଚାପରେ କିପରି ପରିବର୍ତ୍ତନ ଘଟେ ?
Solution:
(i) ବିଷୁବରେଖା ନିକଟସ୍ଥ ଅଞ୍ଚଳ
(ii) ଆବରନ
(iii) ପ୍ରସାରିତ, ସଙ୍କୁଚିତ
(iv) ଗୁରୁଚାପ, ଲଘୁଚାପ
(v) ଚାପଦ୍ରାସ ହୁଏ

VI. ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
(କ) ନିମ୍ନୋକ୍ତ କେଉଁ ଯନ୍ତ୍ର ସାହାଯ୍ୟରେ ବାୟୁର ବେଗ ମପାଯାଏ ?
(i) ଥର୍ମୋମିଟର
(ii) ବାରୋମିଟର
(iii) ଓଡ଼ୋମିଟର
(iv) ଆନିମୋମିଟର
Solution:
(iv) ଆନିମୋମିଟର

(ଖ) ପବନ୍ଧର ବେଗ ବଢ଼ିଲେ କାହାର ଚାପ କମେ ?
(i) ଜଳ
(ii) ଚାଯୁ
(iii) ତାପ
(iv) ମଉସମ
Solution:
(ii) ଚାଯୁ

(ଘ) ପବନର ବେଗ ବଢ଼ିଲେ ବାୟୁ ଚାପ କ’ଣ ହୁଏ ?
(i) କାମେ
(ii) ବକେ
(iii) ସ୍ଥିରରଦେ
(iv) ପ୍ରଥମେ ବଢ଼େ ଓ ତା’ପରେ କମେ
Solution:
(i) କାମେ

(ଙ) କେଉଁ ଦିନେ ପବନ ସ୍ଥଳଭାଗରୁ ଜଳଭାଗ ଆଡ଼କୁ ପ୍ରବାହିତ ହୁଏ ?
(i) ଣାତଦିନେ
(ii) ଖରାଦିନେ
(iii) ବଶାଦିନ୍ନେ
(iv) ଶରତ୍ଲାଲରେ
Solution:
(i) ଣାତଦିନେ

(ଚ) ପୃଥ‌ିବୀର କେଉଁ ଗତି ଯୋଗୁଁ ପବନର ଦିଗ ପରିବର୍ତ୍ତନ ହୁଏ ?
(i) ପରିକ୍ରମଣ
(ii) ଆବର୍ତ୍ତନ
(ii) ବଢ଼େ
(iv) ପରିକ୍ରମଣ ଓ ଆବର୍ଜନ
Solution:
(ii) ଆବର୍ତ୍ତନ

(ଛ) କାହା ମାଧ୍ୟମରେ ବାତ୍ୟା ହେତୁ ପବନ ପ୍ରବାହିତ ହୁଏ ?
(i) କମ୍ପ୍ୟୁଟର
(ii) ଟେଲିଭିଜନ
(iii) ବାର୍ଷିକ
(iv) ପରିକ୍ରମଣ ଓ ଆବର୍ଜନ
Solution:
(ii) ଟେଲିଭିଜନ

(ଜ) ପୃଥ‌ିବୀ ପୃଷ୍ଠରେ କାହାର ତାପମାତ୍ରା ତାରତମ୍ୟ ପ୍ରବାହିତ ହୁଏ ?
(i) ଅଶ୍ମମଣ୍ଡଳ
(ii) ଜୀବମଣ୍ଡଳ
(iii) ବର୍ଷାଦିନେ
(iv) କୃତ୍ରିମ ଉପଗ୍ରହ
Solution:

(ଝ) ବାୟୁ ଯେତେବେଳେ ଉତ୍ତପ୍ତ ହୁଏ କ’ଣ ହୁଏ ?
(i) ପ୍ରସାରିତ
(ii) ସଙ୍କୁଚିତ
(iii) ସଞ୍ଚରିତ
(iv) ପ୍ରବାହିତ
Solution:
(iii) ସଞ୍ଚରିତ

(ଞ) ପୃଥ‌ିବୀ ବାୟୁର ଏକ ଘନ ସ୍ତର ଦ୍ବାରା ଆବୃତ ହୋଇଥାଏ, ତାହାକୁ କ’ଣ କୁହାଯାଏ ?
(i) ବାରିମଣ୍ଡଳ
(ii) ବାୟୁମଣ୍ଡଳ
(iii) ଜୈବମଣ୍ଡଳ
(iv) ଓଜୋନ ସ୍ତର
Solution:
(ii) ବାୟୁମଣ୍ଡଳ

VII. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।
(i) ଓଡ଼ିଶାରେ ମହାବାତ୍ୟା କେବେ ହୋଇଥିଲା ?
(ii) ପ୍ରାକୃତିକ ଘଟଣା କ’ଣ ?
(iii) ବାୟୁର ଚାପ ଅଛି ବୋଲି କିପରି ଜାଣୁଛ ?
(iv) ଆମେ ବେଲୁନକୁ ଫୁଙ୍କିଲେ ଫୁଲେ କାହିଁକି ?
(v) ଖରାରେ ଫୁଲିଥିବା ବେଲୁନ ରଖିଲେ ଫାଟି ଯାଏ କାହିଁକି ?
(vi) ପବନ କାହାକୁ କହନ୍ତି ?
(vii) ମେଘ କିପରି ସୃଷ୍ଟି ହୁଏ ?
(viii)କେଉଁ ବାୟୁର ଜଳଧାରଣ କ୍ଷମତା ଅଧିକ ?
(ix) ମୌସୁମୀର ଅର୍ଥ କ’ଣ ?
Solution:
(i) ଓଡ଼ିଶାରେ ମହାବାତ୍ୟା 1999 ମସିହା ଅକ୍ଟୋବର 29 ତାରିଖରେ ହୋଇଥିଲା ।
(ii) ବର୍ଷା, ବାତ୍ୟା ପରି କିଛି ଘଟଣା ପ୍ରକୃତିରେ ଆପେ ଆପେ ହୁଏ, ଏଗୁଡ଼ିକ ପ୍ରାକୃତିକ ଘଟଣା ଅଟେ ।
(iii) ବାୟୁର ଚାପଥିବା ଯୋଗୁଁ ଗଛର ପତ୍ର, ପତାକା, ବ୍ୟାନର ଫଡ଼ ଫଡ଼ ଶବ୍ଦକରି ଉଡ଼େ ।
(iv) ଆମେ ବେଲୁନକୁ ଫୁଙ୍କିବାଦ୍ୱାରା ବେଲୁନ୍ ଭିତରେ ବାୟୁର ଚାପ ବଢ଼ି ବେଲୁନକୁ ଫୁଲାଏ ।
(v) ଖରାରେ ଫୁଲିଥିବା ବେଲୁନ ରଖୁ ଖରାର ତାପ ଯୋଗୁଁ ବେଲୁନ୍ ଭିତର ବାୟୁ ପ୍ରସାରିତ ହୋଇ ବେଲୁନ୍‌ର କାନ୍ଥରେ ଚାପ ଦିଏ, ଫଳରେ ବେଲୁନ ଫାଟି ଯାଏ ।
(vi) ଗତିଶୀଳ ବାୟୁକୁ ପବନ କହନ୍ତି ।
(vii) ଜଳୀୟବାଷ୍ପ ଥଣ୍ଡା ହୋଇ ମେଘ ସୃଷ୍ଟି କରେ ।
(viii) ମହାସାଗରରୁ ଆସୁଥିବା ବାୟୁର ଜଳଧାରଣ କ୍ଷମତା ଅଧ୍ଵ ।
(ix) ମୌସୁମୀର ଅର୍ଥ ଋତୁ ।

Odisha State Board BSE Odisha 7th Class Science Important Questions Chapter 14 ଆଲୋକ Important Questions and Answers.

BSE Odisha Class 7 Science Important Questions Chapter 14 ଆଲୋକ

Question 1.
ଆଲୋକ ସରଳରେଖାରେ ଗତିକରେ, ଚିତ୍ର ସହ ପରୀକ୍ଷା କର ।
Solution:
(i)ଗୋଟିଏ ସିଧା ଓ ଅନ୍ୟ ଗୋଟିଏ ବଙ୍କା ପ୍ଲାଷ୍ଟିକ୍ ନଳୀ ନିଆଯାଉ ।
(ii) ଗୋଟିଏ ଟେବୁଲ ଉପରେ ଜଳୁଥିବା ଏକ ମହମବତୀ ରଖାଯାଉ ।

(iii) ସିଧା ପ୍ଲାଷ୍ଟିକ୍ ନଳୀ ଦେଇ ଟେବୁଲ ଉପରେ ଜଳୁଥିବା ମହମବତୀକୁ ଦେଖ‌ିଲେ ମହମବତୀର ଶିଖାକୁ ଦେଖ୍ହୁଏ ।
(iv) ବଙ୍କା ପ୍ଲାଷ୍ଟିକ୍ ନଳୀ ଦେଇ ଟେବୁଲ ଉପରେ ଜଳୁଥିବା ମହମବତୀକୁ ଦେଖ‌ିଲେ ମହମବତୀର ଶିଖାକୁ ଦେଖୁହୁଏ ନାହିଁ ।
ସିଦ୍ଧାନ୍ତ – ଏହି ପରୀକ୍ଷାଦ୍ବାରା ସିଦ୍ଧାନ୍ତରେ ଉପନୀତ ହେଲୁ ଯେ ଆଲୋକ ସରଳରେଖାରେ ଗତିକରେ ।

Question 2.
ଗୋଟିଏ ବଡ଼ ଦର୍ପଣଠାରୁ 4 ମିଟର ଦୂରରେ ବସ୍ତୁଟିଏ ଅଛି । ଯଦି ଦର୍ପଣଠାରୁ ଆଉ 2 ମିଟର ଦୂରକୁ ଯିବ, ତେବେ ପ୍ରତିଟିମୂ ଦଘଣଠାରୁ କେତେ ଦୁରର ପ୍ଷ୍ମି ହେଲ |
Solution:
(i) ସମତଳ ବପଣରେ ନିସ୍ତୁର ଦୁରତା ପ୍ରତିଟିପୂର ଦୁରତା ମନ୍ତ୍ର ମନାମ |
(ii) ବସ୍ତୁଟି ଦର୍ପଣଠାରୁ (2 ମି. + 4 ମି.) = 6 ମିଟର ଦୂରରେ ରହିବ । ଅର୍ଥାତ୍ ପ୍ରତିବିମ୍ବ ଦର୍ପଣଠାରୁ 6 ମିଟର ଦୂରରେ ସୃଷ୍ଟି ହେବ ।

Question 3.
ଅବତଳ ଦର୍ପଣ କଣ ? ଏଥରେ କି ପ୍ରକାର ପ୍ରତିବିମ୍ବ ଗଠିତ ହୁଏ ?
Solution:
(i) ଯେଉଁ ପ୍ରତିଫଳକର ପ୍ରତିଫଳନ କରୁଥିବା ପୃଷ୍ଠ ଅବତଳ, ତାହାକୁ ଅବତଳ ଦର୍ପଣ କୁହାଯାଏ । ଏହାର ସାମନାପଟ ବକ୍ର ହୋଇ ଭିତରକୁ ପଶିଯାଇଥାଏ ।
(ii) ଅବତଳ ଦର୍ପଣରେ ଗଠିତ ପ୍ରତିବିମ୍ବ ସର୍ବଦା ବାସ୍ତବ ଓ ଓଲଟା ହୋଇଥାଏ । ଏହା କ୍ଷୁଦ୍ର, ବଡ଼ ବା ବସ୍ତୁ ସହ ସମାନ ମଧ୍ୟ ଦ୍ରୋଲପାରେ |

Question 4.
ଆଳାପା ପ୍ତତିତିପୂ କାଣ ?
Solution:
(i) ଯେଉଁ ପ୍ରତିବିମ୍ବ ଦର୍ପଣର ପଛପଟେ ଗଠିତ ହୁଏ ଏବଂ କୌଣସି ପର୍ଦାରେ କେନ୍ଦ୍ରୀଭୂତ କରି ଧରିହୁଏ ନାହିଁ, ତାହାକୁ ଆଭାସୀ ପ୍ରତିବିମ୍ବ କୁହାଯାଏ ।
(ii) କେବଳ ଉତ୍ତଳ ଦର୍ପଣରେ ଆଭାସୀ ପ୍ରତିବିମ୍ବ ଗଠିତ ହୋଇଥାଏ ।

ବସ୍ତୁନିଷ୍ ପ୍ରଣୋଉର :

I. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଅବତଳ ଦର୍ପଣରେ _________ ପ୍ରତିବିମ୍ବ ଗଠିତ ହୁଏ ।
(ii) ସବୁ କ୍ଷେତ୍ରରେ ଉତ୍ତଳ ଦର୍ପଣରେ ବସ୍ତୁ ଅପେକ୍ଷା _________ ପ୍ରତିବିମ୍ବ ଗଠିତ ହୁଏ ।
(iii) ସମତଳ ଦର୍ପଣରେ ବସ୍ତୁର ଉଚ୍ଚତା ପ୍ରତିବିମ୍ବର ଉଚ୍ଚା ସଙ୍ଗେ _________ |
(iv) ପରଦା ଉପରେ ସୃଷ୍ଟି ହେଉଥ‌ିବା ପ୍ରତିବିମ୍ବକୁ _________ ପ୍ରତିବିମ୍ବ କୁହାଯାଏ ।
(v) ଆମେ _________ ଦ୍ଵାରା ଦେଖାରୁ ।
(vi) ଆଲୋକ ରଶ୍ମି _________ ରେଖାରେ ଗତି କରେ ।
(vii) ବସ୍ତୁର ପ୍ରତିବିମ୍ବ _________ ଦର୍ପଣରେ ଓଲଟା ଦେଖାଯାଏ ।
(viii) ସମତଳ ଦର୍ପଣରେ _________ ପ୍ରତିବିମ୍ବ ଗଠିତ ହୁଏ ।
(ix) _________ ଦର୍ପଣରେ ମୁହଁ ଦେଖ‌ିଲେ ମୁହଁ ବଡ଼ ଦେଖାଯାଏ ।
(x) ଅବତଳ ଦର୍ପଣର ଅତି ନିକଟରେ ବସ୍ତୁ ରଖେଲେ ପ୍ରତିବିମ୍ବ ବସ୍ତୁଠାରୁ _________ ହୁଏ ।
(xi) ଅବତଳ ଦର୍ପଣଠାରୁ ଦୂରରେ ବସ୍ତୁ ରଖୁଲେ ତାହାର ପ୍ରତିବିମ୍ବ ବସ୍ତୁଠାରୁ _________ ହୁଏ ।
(xii) _________ ଦର୍ପଣରେ ପ୍ରତିବିମ୍ବର ଆକାର ବସ୍ତୁଠାରୁ ବହୁତ ସାନ ହୋଇଥାଏ ।
Solution:
(i) ବାସ୍ତବ,
(ii) ସାନ,
(iii) ସମାନ,
(iv) ବାସ୍ତବ,
(v) ଆଲୋକ,
(vi) ସରଳ,
(vii) ଅବତଳ,
(viii) ଆଭାସୀ (ଅବାସ୍ତବ),
(ix) ଅବତଳ,
(x) ବଡ଼,
(xi) ସାନ,
(xii) ଉତ୍ତଳ

II. ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ବାମପାର୍ଶ୍ବରେ ଥ‌ିବା ଶବ୍ଦ ଦ୍ଵୟର ସମ୍ପର୍କକୁ ଦେଖ୍ ଦକ୍ଷିଣ ପାର୍ଶ୍ଵର ଶବ୍ଦ ପାର୍ଶ୍ଵରେ ‘?’ ଚିହ୍ନ ମ୍ନରେ ଉପଯୁକ୍ତ ଶବ ଲେଖା |
(i) ସମତଳ ଦର୍ପଣ : ଅବାସ୍ତବ ପ୍ରତିବିମ୍ବ :: ଅବତଳ ଦର୍ପଣ : ?
(ii) ସମତଳ ଦର୍ପଣରେ ବସ୍ତୁର ଦୂରତା : 5 ସେ.ମି. :: ସମତଳ ଦର୍ପଣରେ ପ୍ରତିବିମ୍ବ ଦୂରତା : ?
(iii) କ୍ଷୌର ଦର୍ପଣ : ଅବତଳ :: ମୋଟରଯାନ ଦର୍ପଣ : ?
(iv) ଅବତଳ ଦର୍ପଣ : ବାସ୍ତବ ପ୍ରତିବିମ୍ବ :: ଉତ୍ତଳ ଦର୍ପଣ : ?
(v) କାରର ପ୍ରତିଫଳକ : ଅବତଳ ଦର୍ପଣ :: ସ୍କୁଟର ହ୍ୟାଣ୍ଡଲ୍‌ରେ ଲାଗିଥିବା ଦର୍ପଣ : ?
Solution:
(i) ବାସ୍ତବ ପ୍ରତିବିମ୍ବ,
(ii) 5 ସେ.ମି.,
(iii) ଉତ୍ତଳ,
(iv) ଆଭାସୀ ପ୍ରତିବିମ୍ବ,
(v) ଉତ୍ତଳ ଦର୍ପଣ

III. ନିମ୍ନୋକ୍ତ ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନପାଇଁ ଦିଆଯାଇଥ‌ିବା ଚାରୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।

(i) କେଉଁ ଦର୍ପଣରେ ଆଭାସୀ ପ୍ରତିବିମ୍ବ ବସ୍ତୁଠାରୁ ବଡ଼ ଅଟେ ?
(କ) ସମତଳ
(ଖ) ଉଭଳ
(ଗ) ଅଥବଲ
(ଶ) ଏମାନଙ୍କ ମଧ୍ୟରୁ କେତ୍ର ନୁହେ
Solution:

(ii) ଧରାଶ୍ରୀ ସମତଳ ଦର୍ପଣ ନିକଟରୁ ଦୁଇ ମିଟର ଦୂରତାରେ ରହି ତାହାର ପ୍ରତିବିମ୍ବକୁ ଦେଖୁଥିଲା । ସେ ଦର୍ପଣ ନିକଟରୁ ଏକ ମିଟର ପଛକୁ ଚାଲିଗଲେ ପ୍ରତିବିମ୍ବଠାରୁ ତାର ଦୂରତା କେତେ ହେବ ?

(iii) ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ସର୍ବୋତ୍କୃଷ୍ଟ ପ୍ରତିଫଳକ ?
(କ) ଷ୍ଟେନ୍‌ସ୍ ଷ୍ଟିଲ୍ ଥାଳି
(ଖ) ଖରକାରେ ଲାଗିଥିବା ଜାତ
(ଗ) ଚିକ୍କଣ ମାର୍ବଲ ଚଟାଣ
(ଣ) ସମତଳ ଦପଣ

(iv) କେଉଁ ଦର୍ପଣରେ ବସ୍ତୁର ପ୍ରତିବିମ୍ବ ଛୋଟ ଓ ଦର୍ପଣର ପଛପଟେ ଗଠିତ ହେବାଭଳି ଜଣାପଡ଼େ ?
(କ) ସମତଳ
(ଖ) ର୍ଥବଉଲ
(ଗ) ଭଉଲ
(ଘ) କୌଣସି ଦର୍ପଣରେ ନୁହେଁ

(v) କେଉଁ ଦର୍ପଣରେ ବାସ୍ତବ ପ୍ରତିବିମ୍ବ ଗଠିତ ହୋଇପାରେ ?
(କ) ସମତଳ
(ଖ) ଭଉଲ
(ଗ) ର୍ଥବଉଲ
(ଘ) କୌଣସି ଦର୍ପଣରେ ନୁହେଁ

(vi) ଟର୍ଚ୍ଚ ଲାଇଟ୍‌ରେ କେଉଁ ପ୍ରକାର ଦର୍ପଣ ବ୍ୟବହାର ହୁଏ ?
(କ) ସମତଳ
(ଖ) ର୍ଥବଉଲ
(ଗ) ଉତ୍ତଳ
(ଘ) କୌଣସି ଦର୍ପଣରେ ନୁହେଁ

(vii) କେଉଁ ଦର୍ପଣରେ ଅନେକଗୁଡ଼ିଏ ବସ୍ତୁର ପ୍ରତିବିମ୍ବ ଛୋଟ ଆକାରରେ ଏକ ସମୟରେ ଦେଖାଯାଏ ?
(କ) ସମତଳ
(ଖ) ଉତ୍ତଳ
(ଗ) ଅବତଳ
(ଘ) ଇଉଲ ଅନତଲ

(viii) ରେଳଗାଡ଼ି, ମୋଟର ଯାନ ଆଦିର ହେଡ୍ ଲାଇଟ୍‌ରେ କି ପ୍ରକାର ଦର୍ପଣ ଲଗାଯାଇଥାଏ ?
(କ) ଉତ୍ତଳ
(ଖ) ଅବତଳ
(ଗ) ସମତଳ
(ଘ) କୌଣସିଟି ନୁହେଁ

(ix) ମୋଟର ସାଇକେଲ ଚାଳକ କି ପ୍ରକାର ଦର୍ପଣ ସାହାଯ୍ୟରେ ପଛରୁ ଆସୁଥ‌ିବା ଯାନବାହନକୁ ଦେଖାରେ ?
(କ) ସମତଳ
(ଖ) ଅବତଳ
(ଗ) ଉତ୍ତଳ
(ଘ) କୌଣସି ଦର୍ପଣରେ ନୁହେଁ

(x) କେଉଁ ଦର୍ପଣରେ ଗଠିତ ପ୍ରତିବିମ୍ବକୁ ପରଦାରେ ପକାଇ ହେବ ?
(କ) ଉତ୍ତଳ
(ଖ) ଅବତଳ
(ଗ) ପମଭଲ
(ଘ) କୌଣସି ଦର୍ପଣରେ ନୁହେଁ
Solution:
(i) ଅବତଳ
(ii) ୬ ମି.
(iii) ସମତଳ ଦର୍ପଣ
(iv) ଭଭଲ
(v) ଅବତଳ
(vi) ଅବତଳ
(vii) ଉତ୍ତଳ
(viii) ଥଚତଳ
(ix) ଉତ୍ତଳ
(x) ଅବତଳ

IV. ରେଖାଙ୍କିତ ପଦ ନ ବଦଳାଇ ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର ।
(i) ସମତଳ ଦର୍ପଣରେ ଓଲଟା ପ୍ରତିବିମ୍ବ ଦେଖାଯାଏ ।
(ii) ଗାଡ଼ି ଚାଳକ ପଛର ଦୃଶ୍ୟ ଦେଖିବାକୁ ମଟରଗାଡ଼ିରେ ଅବତଳ ଦର୍ପଣ ଲଗାଯାଇଥାଏ ।
(iii) ଉତ୍ତଳ ଦର୍ପଣରେ ଏକ ସିଧା ଏବଂ ବସ୍ତୁଠାରୁ ବଡ଼ ପ୍ରତିବିମ୍ବ ଗଠିତ ହୁଏ ।
(iv) ସମତଳ ଦର୍ପଣରେ ଏକ ବାସ୍ତବ, ବଡ଼ ଏବଂ ଓଲଟା ପ୍ରତିବିମ୍ବ ଗଠିତ ହୁଏ ।
(v) ଅବତଳ ଦର୍ପଣରେ ଓଲଟା ପ୍ରତିବିମ୍ବ ଦେଖାଯାଏ ।
(vi) ବସ୍ତୁଠାରୁ କମ୍ ଉଚ୍ଚତା ବିଶିଷ୍ଟ ପ୍ରତିବିମ୍ବ ସମତଳ ଦର୍ପଣରେ ଗଠିତ ହୁଏ ।
Solution:
(i) ଅବତଳ ଦର୍ପଣରେ ଓଲଟା ପ୍ରତିବିମ୍ବ ଦେଖାଯାଏ ।
(ii) ଗାଡ଼ି ଚାଳକ ପଛର ଦୃଶ୍ୟ ଦେଖିବାକୁ ମଟରଗାଡ଼ିରେ ଉତ୍ତଳ ଦର୍ପଣ ଲଗାଯାଇଥାଏ ।
(iii) ଅବତଳ ଦର୍ପଣରେ ଏକ ସିଧା ଏବଂ ବସ୍ତୁଠାରୁ ବଡ଼ ପ୍ରତିବିମ୍ବ ଗଠିତ ହୁଏ ।
(iv) ଅବତଳ ଦର୍ପଣରେ ଏକ ସିଧା ବଡ଼ ଏବଂ ଓଲଟା ପ୍ରତିବିମ୍ବ ଗଠିତ ହୁଏ ।
(v) ଅବତଳ ଦର୍ପଣରେ ସମ୍ମୁଖ ବକ୍ର ହୋଇ ଭିତରକୁ ପଶିଯାଇଥାଏ ।
(vi) ବସ୍ତୁଠାରୁ କମ୍ ଉଚ୍ଚତା ବିଶିଷ୍ଟ ପ୍ରତିବିମ୍ବ ଉତ୍ତର ଦର୍ପଣରେ ଗଠିତ ହୁଏ ।

V. ନିମ୍ନଲିଖ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଗୋଟିଏ ବା ଦୁଇଟି ଶବ୍ଦରେ ଲେଖ ।
(i) ଆଲୋକର ପ୍ରଧାନ ପ୍ରାକୃତିକ ଉତ୍ସ କିଏ ?
(ii) ଲୋକ ରଶ୍ମିର ଗତିପଥ କିପରି ?
(iii) ଯେଉଁ ଦର୍ପଣର କେନ୍ଦ୍ରାଞ୍ଚଳ ମୋଟାହୋଇ ଚାରିପଟ କ୍ରମଶଃ ପତଳା ହୋଇଥାଏ, ତାହା କି ପ୍ରକାର ଦର୍ପଣ ?
(iv) ଯେଉଁ ଦର୍ପଣର ସାମ୍ନାପଟ ଚାମଚ ଭଳି ଭିତରକୁ ପଶିଯାଇଥାଏ, ତାହା କି ପ୍ରକାର ଦର୍ପଣ ?
(v) କେଉଁ ପ୍ରକାର ଦର୍ପଣ ମୋଟରଯାନର ପଛରେ ଥ‌ିବା ବସ୍ତୁକୁ ଦେଖିବାପାଇଁ ବ୍ୟବହାର ହୁଏ ? (vi) ମୋଟରଯାନ ଆଦିର ହେଡ୍‌ଲାଇଟ୍ ଭିତରେ କି ପ୍ରକାର ଦର୍ପଣ ଲାଗିଥାଏ ?
(vii) କ୍ଷୌର ହେବା ଦର୍ପଣ କି ପ୍ରକାର ହେବା ଉଚିତ୍ ?
Solution:
(i) ସୂର୍ଯ୍ୟ
(ii) ସରଳରେଖ୍
(iii) ଉତ୍ତଳ ଦର୍ପଣ
(iv) ଅବତଳ ଦର୍ପଣ
(v) ଉତ୍ତଳ ଦର୍ପଣ
(vi) ଅବତଳ ଦର୍ପଣ
(vii) ଅବତଳ ଦର୍ପଣ

VI. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।
(i) ଆଲୋକ କିପରି ଗତି କରେ ?
(ii) ଆଲୋକର ଗତିପଥ କିପରି ବଦଳେ ?
(iii) ଜଳ ଆଲୋକର ଗତିପଥ ବଦଳାଇପାରେ କି ?
(iv) ଆଲୋକ ରଶ୍ମି କାହାକୁ କହନ୍ତି ?
(v) ଆଲୋକ ଗୁଚ୍ଛ କାହାକୁ କହନ୍ତି ?
(vi) ଛାୟା କିପରି ସୃଷ୍ଟି ହୁଏ ।
(vii) ଆମେ ବସ୍ତୁକୁ କିପରି ଦେଖୁ ?
(viii)ରନ୍ଧ୍ର କ୍ୟାମେରାରେ କିପରି ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହୁଏ
Solution:
(i) ଆଲୋକ ସରଳରେଖାରେ ଗତି କରେ ।
(ii) ମସୃଣ ପୃଷ୍ଠରେ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହେଲେ ଆଲୋକର ଗତିପଥ ବଦଳେ ।
(iii) ହଁ, ଜଳ ଆଲୋକର ଗତିପଥ ବଦଳାଇପାରେ ।
(iv) ଆଲୋକ ସ୍ରୋତରୁ ସବୁ ଦିଗକୁ ଗତି କରୁଥ‌ିବା ଆଲୋକ ଧାରାକୁ ଆଲୋକ ରଶ୍ମି କହନ୍ତି ।
(v) ଆଲୋକ ରଶ୍ମୀର ସମାହାରକୁ ଆଲୋକ ଗୁଚ୍ଛ କହନ୍ତି ।
(vi) ଆଲୋକ ସମ୍ମୁଖରେ ଅସ୍ବଚ୍ଛ ବସ୍ତୁ ରହିଲେ ଛାୟା ସୃଷ୍ଟି ହୁଏ ।
(vii) ଆଲୋକ ବସ୍ତୁ ଉପରେ ପଡ଼ି ସେଠାରୁ ପ୍ରତିଫଳିତ ହୋଇ ଆମ ଚକ୍ଷୁରେ ପଡ଼ିଲେ ଆମେ ବସ୍ତୁକୁ ଦେଖିପାରୁ ।
(viii) ଆଲୋକର ଗତିପଥ ସରଳରେଖ୍ ହୋଇଥିବାରୁ ରନ୍ଧ୍ର କ୍ୟାମେରାରେ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହୁଏ ।