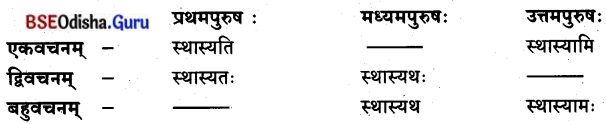Odisha State Board BSE Odisha 8th Class Sanskrit Solutions Chapter 12 ଲକ୍ଷ୍ୟପ୍ରାପ୍ତିଃ Textbook Exercise Questions and Answers.
BSE Odisha Class 8 Sanskrit Solutions Chapter 12 ଲକ୍ଷ୍ୟପ୍ରାପ୍ତିଃ
1. एकपदेन उत्तरं लिखत ।
ଏକପଦେନ ଉତ୍ତରଂ ଲିଖତ । (ଗୋଟିଏ ପଦରେ ଉତ୍ତର ଲେଖ ।)
(क) मण्डूककुले का आयोजिता?
ମଣ୍ଡୁକକୁଳେ କା ଆୟୋଜିତା ?
उत्तर :
ପ୍ରତିଯୋଗିତା
(ख) मण्डूकाः कस्य आरोहणं कृतवन्तः ?
ମଣ୍ଡକା କସ୍ୟ ଆରୋହଣଂ କୃତବନ୍ତଃ ?
उत्तर :
ସ୍ତମ୍ଭସ୍ୟ
(ग) का आरब्धा ? बा चा०था ?
उत्तर :
ପ୍ରତିଯୋଗିତା
(घ) मण्डूकमाता कम् उक्तवती?
ମଣ୍ଡୁକମାତା କମ୍ ଉଦ୍ଭବତୀ ?
उत्तर :
ସ୍ବକନିଷ୍ଠ ପୁତ୍ରମ୍
![]()
(ङ) वयं केषां वचनं शृणुयाम ?
ବରଂ କେବାଂ ବଚନଂ ଶୁଣୁୟାମ ?
उत्तर :
ଗୁରୁଜନାନାଂ
(गुरुजनानां, प्रतियोगिता, स्वकनिष्ठपुत्रम् , प्रतियोगिता, स्तम्भस्य)
(ଗୁରୁଜନାନଂ, ପ୍ରତିଯୋଗିତା, ସ୍ବକନିଷ୍ଠପୁତ୍ରମ, ପ୍ରତିଯୋଗିତା, ସ୍ତମ୍ଭସ୍ୟ)
2. बन्धनी मध्यस्थ यथार्थपदैः शून्यस्थानानि पूरयत ।
(ବନ୍ଧନୀମଧ୍ଯସୁ ଯଥାର୍ଥପଦୌ ଶୂନ୍ୟସ୍ଥାନାନି ପୂରୟତ।)
(ବନ୍ଧନୀମଧ୍ଯରେ ଥିବା ଠିକ୍ ପଦଦ୍ୱାରା ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।)
(क) मण्डूका: ____ आरोहणं कृतवन्त: ।
ମଣ୍ଡୁକା – ସ୍ତମ୍ଭସ୍ଯ
उत्तर :
ଅତ୍ଯୁତଃ
(ख) स्तम्भः _____ आसीत् ।
ସ୍ତମଃ _____ ଆସୀତ୍ବ ।
उत्तर :
ଅତ୍ଯୁଜଃ
(ग) पुत्र ! त्वं स्तम्भस्य _____ कुर्या: ।
ପୁତ୍ର । ବଂ ସ୍ତମ୍ଭସ୍ୟ ____ କୁର୍ଯ୍ୟାଃ
उत्तर :
ଆରୋହଣଂ
(घ) आरोहणसमये कस्यापि वचनं न____।
ଆରୋହଣସମୟେ କନ୍ୟାପି ବଚନଂ ନ ____।
उत्तर :
ଶୁଣୁ
(ङ) अये ! ____ त्वम् ?
ଅୟେ ! ________ ତ୍ୱମ୍ ?
![]()
(अत्युच्चः, आरोहणं, पते :, शृणुया:, स्तम्भस्य)
(ଅଚ୍ୟୁଜଃ, ଆରୋହଣ, ପତଃ, ଶୁଣୁୟା, ସ୍ତମ୍ଭସ୍ୟ)
3. मातृभाषया अनुवादं कुरुत:
(ମାତୃଭାଷୟ ଅନୁବାଦଂ କୁରୁତ ।) (ମାତୃଭାଷାରେ ଅନୁବାଦ କର ।)
(क) सः शिशुः स्तम्भस्य मध्यभागं प्राप्तवान् ।
ସ୍ୱ ଶିଶୁ ସ୍ତମ୍ଭସ୍ୟ ମଧ୍ୟଭାଗ୍ୟ ପ୍ରାପ୍ତବାନ୍ ।
ଅନୁବାଦ – ସେହି ଶିଶୁ ସ୍ତମ୍ଭର ମଧ୍ୟଭାଗରେ ପହଁଞ୍ଚିଲା ।
(ख) तव प्रयास: व्यर्थः।
ତବ ପ୍ରୟାସ ବ୍ୟର୍ଥ ।
ଅନୁବାଦ – ତୁମର ଚେଷ୍ଟା ବୃଥା।
(ग) आरोहणसमये कस्यापि वचनं न शृणुया: ?
ଆରୋହଣସମୟେ କନ୍ୟାପି ବଚନଂ ନ ଶୃଣ୍ମୟୀ ।
ଅନୁବାଦ – ଚଢ଼ିବା ସମୟରେ କାହାରି କଥା ଶୁଣିବା ଅନୁଚିତ ।
(घ) कथं त्वं स्तम्भस्य आरोहणे समर्थ: अभवः ?
କରଂ ପୁଂ ସ୍ତମ୍ଭସ୍ୟ ଆରୋହଣେ ସମର୍ଥ ଅଭବ ?
ଅନୁବାଦ – କିପରି ତୁମେ ଏହି ଖମ୍ବ ଆରୋହଣ କରିବାକୁ ସମର୍ଥ ହେଲ ?
(ङ) वयं गुरुजनानां वचनं शृणुयाम ।
ବୟଂ ଗୁରୁଜନାନାଂ ବଚନଂ ଶୁଶୁୟାମ ।
ଅନୁବାଦ – ଆମ୍ଭେମାନେ ଗୁରୁଜନଙ୍କ ବଚନ ଶୁଣିବା।
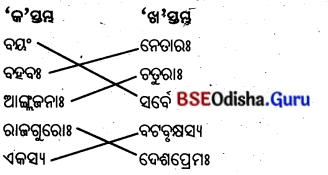
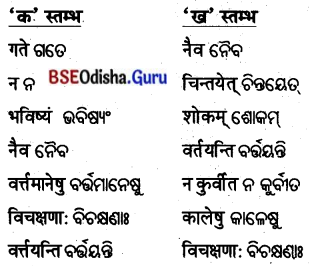
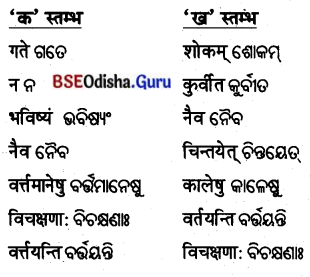
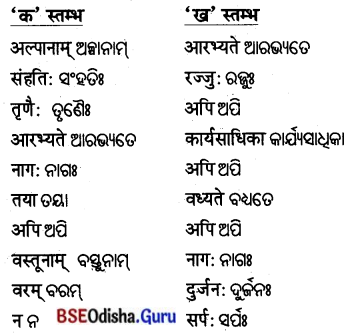
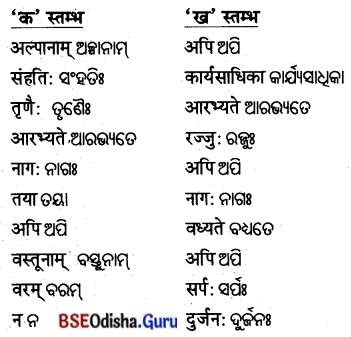
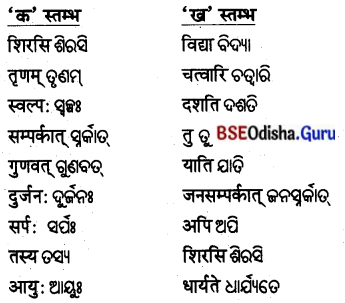
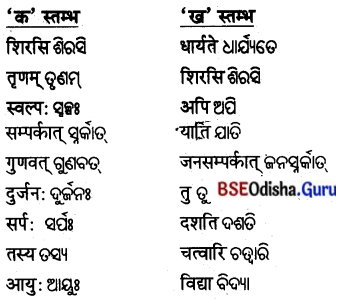
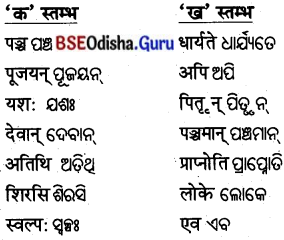
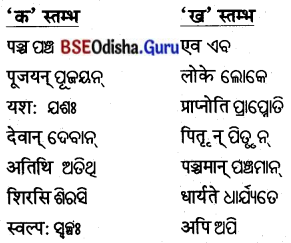
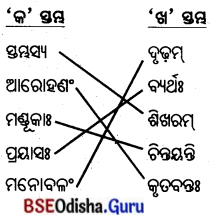
4. विषयानुसारं स्तम्भमेलनं कुरुत ।
ବିଷୟାନୁସାରଂ ସ୍ତମ୍ଭମେଳନଂ କୁରୁତ ।
(ବିଷୟ ଅନୁସାରେ ସ୍ତମ୍ଭ ଯୋଗକର ।)
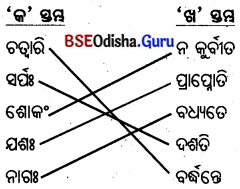
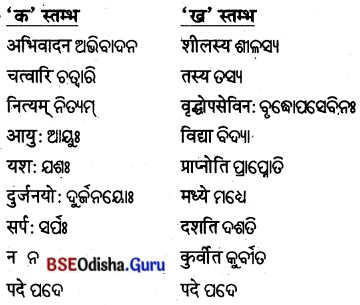
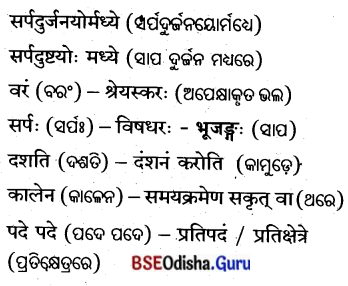
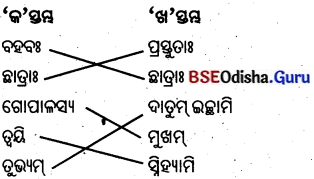
| ‘क’ स्तम्भ: | ‘ख’ स्तम्भ: |
| स्तम्भस्य | दृढम् |
| आरोहणं | व्यर्थः |
| मण्डूका: | शिखरम् |
| प्रयास: | चिन्तियन्ति |
| मनोबलं | कृतवन्त: |
उत्तर :
5. रेखाङ्क्रितपदानां संशोघनं कुरुत।
(ରେଖାଙ୍କିତପଦାନାଂ ସଂଶୋଧନଂ କୁରୁତ।)
ରେଖାଙ୍କିତ ପଦଗୁଡ଼ିକର ସଂଶୋଧନ କର ।
(क) एक: प्रतियोगिता आयोजिता ।
ଏକ ପ୍ରତିଯୋଗିତା ଆୟୋଜିତା ।
उत्तर :
ଏକା ପ୍ରତିଯୋଗିତା ଆୟୋଜିତା ।
(ख) कतिपयाः मण्डूकाः चिन्तयति स्म ।
କତିପୟ ମଣ୍ଡୁକା ଚିନ୍ତୟତି ସ୍ମ ।
उत्तर :
କତିପୟ ମଣ୍ଡୁକା ଚିନ୍ତୟନ୍ତ ସୁ ।
![]()
(ग) विफला: मण्ड़कः नैराश्यं प्राप्तवन्तः ।
ବିଫଳା ମଣ୍ଡକଃ ନୈରାଗ୍ୟ ପ୍ରାପ୍ତବୟଃ ।
उत्तर :
ବିଫଳା ମଣ୍ଡୁକୀ ନୈରାଶ୍ୟ ପ୍ରାପ୍ତବୟଃ ।
(घ) शिशुः अवदन् ।
ଶିଶୁ ଅବଦନ ।
उत्तर :
ଶିଶୁ ଅବଦତ୍ ।
(ङ) मने एकाग्रतां धारयेम ।
ମନେ ଏକାଗ୍ରତା ଧାରୟେମ |
उत्तर :
ମନସି ଏକାଗ୍ରତାଂ ଧାରୟେମ |
6. वाक्यानि रचयत । (ବାକ୍ୟାନି ରଚୟତ।)
ବାକ୍ୟ ରଚନା କର ।
मण्डूकाः, शृणुयाः, दृढम्, उक्तवती, आसीत्
उत्तर :
- मण्डूका: (ମଣ୍ଡୁକା) – ମଶୂନଃ ଶବ୍ଦ କୁର୍ବନ୍ତି ।
- शृणुया: (ଶୁଣୁ) – କନ୍ୟାପି ବଚନଂ ନ ଶୁଣୁ ।
- दृढम् (ଦୃଢ଼ମ୍) – ତସ୍ୟ ମନୋବଳ ଦୃଢ଼ମ୍ ।
- उक्तवती (ଭକ୍ତବତୀ) – ମାତା ପୁତ୍ରୀମ୍ ଉକ୍ତବତୀ।
- आसीत् (ଆସୀତ) – ଡଃ ସାଧୁ ଆସୀତ୍ ।
7. शब्दं रचयत । (ଶବ୍ଦ ରଚୟତ ।) ଶବ୍ଦ ରଚନା କର ।
यथा वा न् प्राप्त प्राप्तवान्
ଯଥା – ବା ନ୍ ପ୍ରାପ୍ତ – ପ୍ରାପ୍ତିବାନ୍
उत्तर :
(क) ता ग नि नि ଡା ଗାଁ ନି ନି = ନିର୍ଗତାନି
(ख) ना ज गु नां रु ନା ଜ ଗୁ ନଂ ରୁ = ଗୁରୁଜନାନାମ
(ग) का: दर्श ଡାଃ ଦ ର୍ଶ = ଦର୍ଶକା
(घ) आ ह ण रो म् ଆ ହ ଣ ରୋମ୍ = ଆରୋହଣମ୍
(ङ) स ता: म्मि लि ସ ତା ମିଳି = ସମ୍ମିଳିତା
8. सन्धिविच्छेदं कुरुत। (ସନ୍ଧିବିଚ୍ଛେଦଂ କୁରୁତ।) ସନ୍ଧିବିଚ୍ଛେଦ କର ।
(क) सर्वादी
उत्तर :
ସର୍ବାଦୌ – ସର୍ବ + ଆଦୌ
(ख) प्राप्नुयात्
उत्तर :
ପ୍ରାପ୍ରୁୟାତ୍ – ପ୍ର + ଆୟୁୟାତ୍
(ग) सम्मिलिता:
उत्तर :
ସମ୍ମିଳିତା – ସମ୍ + ମିଳିତ
![]()
(घ) इत्यादिभि:
उत्तर :
ଇତ୍ୟାଦିଭିଂ – ଇତି + ଆଦିଭି
(ङ) अत्युच्च:
उत्तर :
ଅତ୍ଯୁନଃ – ଅତି + ଉଚ୍ଚ
त्त्व कृते करणीयम्
(ତୁମ ପାଇଁ କାମ)
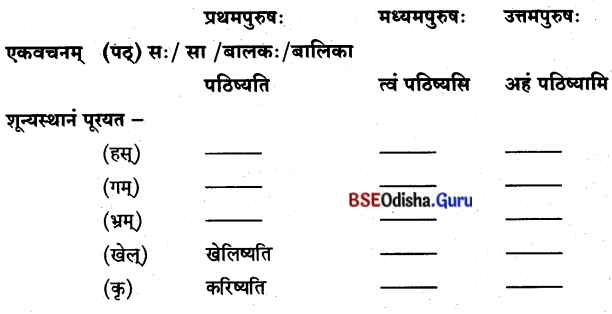
1. उच्चै: पठत लिखत ।
(ଭଜଃ ପଠତ ଲିଖତ । ବଡ଼ ପାଟିରେ ପଢ଼ ଓ ଲେଖ ।)
विधिलिङ-लकार: ବିଧୁଲିଙ୍କ୍ – ଲକାରଃ (ଉଚିତ / ସମ୍ଭାବନା)

ଉଦାହରଣମ୍
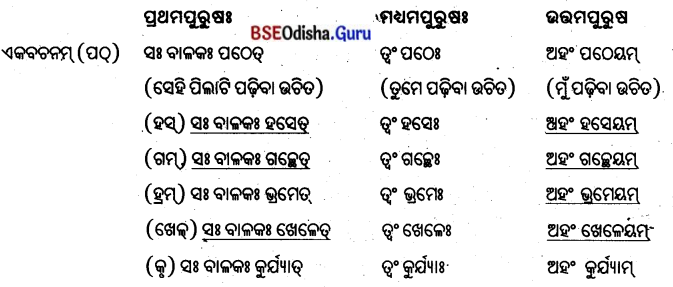
द्विवचनम्

ଦ୍ବିବଚନମ୍

बहुवचनम्

ବହୁ ବଚନମ୍

ପରୀକ୍ଷା ଉପଯୋଗୀ ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତର
Objective
एकपदेन उत्तरं लिखत।
(ଏକପଦେନ ଉତ୍ତରଂ ଲିଖତ।)
प्रश्न 1.
कदाचित् मण्डककले का आयोजिता ?
କଦାଚିତ୍ର ମଣ୍ଡୁକକୁଳେ କା ଆୟୋଜିତା ?
उत्तर :
ପ୍ରତିଯୋଗିତା
प्रश्न 2.
मण्डूका: कुत्र भागं ग्रहीतुम् आगतवन्त: ?
ମଣ୍ଡୁକ କୃତ୍ର ଭାଗ୍ୟ ଗ୍ରହୀତୁମ ଆଗତବନ୍ତଃ ?
उत्तर :
ପ୍ରତିଯୋଗିତାୟାଂ
प्रश्न 3.
प्रतियोगिता द्रष्टुं के तत्र सम्मिलिता ?
ପ୍ରତିଯୋଗିତାଂ ଦ୍ରଷ୍ଟ୍,କେ ତତ୍ର ସମ୍ମିଳିତା ?
उत्तर :
ମଣ୍ଡକା
प्रश्न 4.
मण्डूका: कै: शब्दै: उत्साहं बर्द्धयन्ति स्म ?
ମଣ୍ଡୁକା କୈ ଶରଃ ଉତ୍ସାହଂ ବର୍ଷୟତି ସ୍ବ ?
उत्तर :
ଅରେ । ଅହୋ! ହୋ !
![]()
प्रश्न 5.
कः अत्युच्च: चिक्कण: च आसीत् ?
କଃ ଅଚ୍ୟୁତଃ ଚିକ୍କଶଃ ଚ ଆସୀତ୍ବ ?
उत्तर :
ସ୍ତମ୍ଭ
प्रश्न 6.
य: नूनम् अग्रे गच्छेत् सः कुत्र पतेत् ?
ଯଃ ନୂନମ୍ ଅଗ୍ରେ ଗଛେତ୍ ଡଃ କୁତ୍ର ପତେତ୍ର ?
उत्तर :
ଅଧଃ
प्रश्न 7.
यः सर्वादौ शिखरं प्राप्नुयात् सः किं भवेत् ?
ଯଃ ସର୍ବାଦୌ ଶିଖରଂ ପ୍ରାପ୍ରୁୟାତ୍ ସ କିଂ ଭବତ୍ ?
उत्तर :
ବିଜୟୀ
बन्धनीमध्यात् शून्यस्थानं पूरयत।
(ବନ୍ଧନୀମଧ୍ୟାତ୍ ଶୂନ୍ୟସ୍ଥାନଂ ପୂରୟତ।)
1. विद्यालयेषु छात्रा: ______। (पठेत्, पठेताम्, पठेयुः)
ବିଦ୍ୟାଳୟେଷୁ ଛାତ୍ରା _______। (ପଠେତ୍ର, ପଠେତାମ୍, ପଠେୟୁ)
उत्तर :
ପଠେୟୁ
2. प्रधानमन्त्री दिल्यां _________। (तिष्ठेत्, क्रीड़ेताम्, क्रीड़युः)
ପ୍ରଧାନମନ୍ତ୍ରୀ ଦିଲ୍ୟା _________। (ତିଵେତ, କ୍ରୀଡ଼େତାମ୍, କ୍ରୀଡ଼ୟୁ)
उत्तर :
ତିକ୍ଷେତ୍
3. त्वं रन्थनं _______। (कुर्या:, कुर्यातम् कुर्यात)
ବଂ ରନ୍ଧନଂ _______। (କୁର୍ଯ୍ୟା, କୁର୍ଯ୍ୟାତମ୍, କୁର୍ଯ୍ୟାତ)
उत्तर :
କୁର୍ଯ୍ୟା
4. लोकयाने सम्मर्द _______। (भवेत्, भवेताम्, भवेयुः)
ଲୋକୟାନେ ସମ୍ମ _______। (ଭଵେତ୍, ଭବେତାମ୍, ଭବେୟୁ)
उत्तर :
ଭବେତ୍
5. विफला: मण्डूका: ______ प्राप्तवन्तः। (नैराश्य:, नैराश्यं, नैराश्य:)
ବିଫଳା ମଣ୍ଡୁକା ______ ପ୍ରାପ୍ତବୟଃ । (ନୈରାଶ୍ୟ, ନୈରାଶ୍ୟ, ନୈରାଶ୍ୟ)
उत्तर :
ନୈରାଶ୍ୟ
![]()
6. उत्साहरहितं वचनं श्रुत्वा ______ पतितवन्तः। (अध, अधा, अधः)
ଉତ୍ସାହରହିତଂ ବଚନଂ ଶୁକ୍ଳା _______ ପତିତବହିଃ । (ଅଧ, ଅଧା, ଅଧଃ)
उत्तर :
ଅଧଃ
7. मण्डूका: ______ आगतवन्तः। (अग्रे, अग्र:, अग्र)
ପଶଦ୍ୱାଃ _______ ଆଗତବନ୍ତଃ । (ଅଗ୍ରେ, ଅଗ୍ର, ଅଗ୍ର)
उत्तर :
ଅଗ୍ରେ
8. को वा स्तम्भस्य आरोहणं ______ (कुर्यात्, कुर्याताम्, कुर्युः)
କୋ ବା ସ୍ତମ୍ଭସ୍ୟ ଆରୋହଣଂ _______। (କୁର୍ପାତ, କୁର୍ଯାତାମ, କୁନୁଃ)
उत्तर :
କୁର୍ପାତ
9. ______ सफल: भवे :। (नूनं, नुनं, सर्वदा)
_______ ସଫଳ ଭାବେ । (ନୂନଂ, ନୁନଂ, ସର୍ବଦା)
उत्तर :
ନୂନଂ
10. त्वं ______ आरोहणं कुर्याः। (स्तम्भम्, स्तम्भस्य)
ତଂ _____ ଆରୋହଣଂ କୁର୍ଯ୍ୟା । (ସ୍ତମ୍ଭମ୍, ସ୍ତମ୍ଭସ୍ୟ)
उत्तर :
ସ୍ତମ୍ଭସ୍ଯ
11. विफला: मण्डूका: ______ प्राप्तवन्तः। (नैराश्यम्, नैराश्य:)
ବିଫଳା ମଣ୍ଡକା ______ ପ୍ରାପ୍ତବନ୍ତଃ । (ନୈରାଶ୍ୟମ୍, ନୈରାଶ୍ୟ)
उत्तर :
ନୈରାଶ୍ୟମ୍
12. स: नूनम् _____ पतेत् । (अध:, अर्द्धम्)
ସଃ ନୂନମ୍ _____ ପତେତ୍ । (ଅଧଃ, ଅର୍ଥମ୍)
ଜ –
ଅଧଃ
13. ते पुनरपि _____ कुर्वन्ति । (आरोहणेन, आरोहणम्)
ତେ ପୁନରପି ______ କୁର୍ବନ୍ତି । (ଆରୋହଣେନ, ଆରୋହଣମ୍)
उत्तर :
ଆରୋହଣମ୍
14. भवतः प्रयास: ______ । (व्यर्थ:, व्यर्थम्)
ଭବତଃ ପ୍ରୟାତଃ _____। (ବ୍ୟର୍ଥୀ, ବ୍ୟର୍ଥମ୍)
उत्तर :
ବ୍ୟର୍ଥୀ
![]()
15. स्तम्भः ______ आसीत् । (अत्युच्च:, अत्युच्चम्)
ସ୍ତମଃ ______ ଆସୀତ୍ । (ଅତ୍ଯୁନଃ, ଅତ୍ଯୁଚ୍ଚ)
उत्तर :
ଅତ୍ଯୁନଃ
उत्तरचयनं कुरुत ।
(ଉତ୍ତରଚୟନଂ କୁରୁତ।)
प्रश्न 1.
कदाचित् मण्डूककुले का आयोजिता?
କଦାଚିତ୍ର ମଣ୍ଡୁକକୁଳେ କା ଆୟୋଜିତା ?
(A) କାଚିତ୍ର ପ୍ରତିଯୋଗିତା
(B) ସ୍ପର୍ଧା
(C) ଯାତ୍ରା
(D) ରୂପକମ୍
उत्तर :
କାଚିତ୍ର ପ୍ରତିଯୋଗିତା
प्रश्न 2.
मण्डूकाः कुत्र भागं ग्रहीतुम् आगतवन्तः ?
ମଣ୍ଡୁକା କୁତ୍ର ଭାଗ୍ୟ ଗ୍ରହୀତୁମ୍ ଆଗତବନ୍ତଃ ?
(A) ପ୍ରତିଯୋଗିତାୟାମ୍
(C) ଯାତ୍ରାୟାମ
(B) କାଚିତ୍ର ପ୍ରତିଯୋଗିତା
(D) ରୂପକେ
उत्तर :
ପ୍ରତିଯୋଗିତାୟାମ୍
प्रश्न 3.
प्रतियोगितां द्रष्टं के तत्र सम्मिलिता:?
ପ୍ରତିଯୋଗିତାଂ ଦ୍ରଷ୍ଟୁ କେ ତତ୍ର ସମ୍ମିଳିତା ?
(A) କାକା
(B) ମାର୍କାରା
(C) ବହବ ମଣ୍ଡୁକା
(D) କୁକ୍କୁରା
उत्तर :
ବହବ ମଣ୍ଡୁକା
![]()
प्रश्न 4.
क: अत्युच्च: चिक्कण: च आसीत् ?
କଃ ଅଚ୍ୟୁତଃ ଚିକ୍କଶଃ ଚ ଆସୀତ୍ ?
(A) ବୃକ୍ଷ
(B) ପ୍ରାସାଦଃ
(C) ସାଗରଃ
(D) ସ୍ତୟଃ
उत्तर :
ସ୍ତମଃ
प्रश्न 5.
के नैराश्यं प्राप्तवन्तः ?
କେ ନୈରାଶ୍ୟ ପ୍ରାପ୍ତବନ୍ତଃ ?
(A) ବିଫଳା ମଣ୍ଡୁକା
(B) ଭାଗଗ୍ରହିତାରଃ
(C) କାକା
(D) କୁକୁରା
उत्तर :
ବିଫଳା
प्रश्न 6.
मण्डूकाः कस्य आरोहणं कृतवन्त: ?
ମଣ୍ଡୁକା କସ୍ୟ ଆରୋହଣଂ କୃତବତଃ ?
(A) ଗୃହସ୍ଯ
(B) ସ୍ତମ୍ଭସ୍ୟ
(C) ପ୍ରାସାଦସ୍ୟ
(D) ବୃକ୍ଷସ୍ୟ
उत्तर :
ସ୍ତମ୍ଭସ୍ୟ
प्रश्न 7.
विफला: मण्डूका: किं प्राप्तवन्त: ?
ବିଫଳା ମଣ୍ଡୁକା କିଂ ପ୍ରାପ୍ତବନ୍ତଃ ?
(A) ଦୁଃଖମ୍
(B) ଆନନ୍ଦମ୍
(C) ନୈରାଶ୍ୟମ୍
(D) ସୁଖମ୍
उत्तर :
ନୈରାଶ୍ୟମ୍
![]()
प्रश्न 8.
कस्याः वचनेन पुत्रः स्तम्भस्य आरोहणाय अग्रे अगच्छत् ?
କନ୍ୟା ବଚନେନ ପୁନଃ ସ୍ତମ୍ଭସ୍ୟ ଆରୋହଣାୟ ଅଗ୍ର ଅଗଚ୍ଛତ୍ବ ?
(A) ମାତୁଃ
(C) ଭ୍ରାତଃ
(B) ପିତୁଃ
(D) ମିତବ୍ଯ
उत्तर :
ମାତୁଃ
प्रश्न 9.
अप्ले एव काले स: शिशु : स्तम्भस्य किं प्राप्तवान् ?
ଅର୍ଜ୍ଜୁନ ଏବଂ କାଳେ ଡଃ ଶିଶୁ ସ୍ତମ୍ଭସ୍ୟ କିଂ ପ୍ରାପ୍ତବାନ୍ ?
(A) ଅଧୋଭାଗମ୍
(B) ଉପରିଭାଗମ୍
(C) ତଳଭାଗମ
(D) ମଧ୍ୟଭାଗମ୍
उत्तर :
ମଧ୍ୟଭାଗମ୍
प्रश्न 10.
आरोहणकाले किं भवेयम् ?
ଆରୋହଣକାଳେ କିଂ ଭବେୟମ୍ ?
(A) ଦୂଷ୍ଣୀମ୍
(B) ବଧୂରଃ
(C) ମୂକ
(D) ଅନ୍ଧ
उत्तर :
ବଧୂରଃ
रेखांकित पदानां संशोधनं कुरुत ।
(ରେଖାଙ୍କିତପଦାନାଂ ସଂଶୋଧନଂ କୁରୁତ।)
1. अरे : पतेत् त्वम् ।
ଅରେ ! ପତେତ୍ର ତୁମ୍ ।
उत्तर :
ଥରେ । ପସ୍ତେ ତୁମ୍ ।
2. कस्यापि वचनः न शृणुयात्।
କନ୍ୟାପି ବଚନଃ ନ ଶୁଣୁୟାତ୍ ।
उत्तर :
କନ୍ୟାପି ବଚନଂ ନ ଶୁଣୁଯାତ୍ର
3. स्तम्भः अत्युच्च चिक्कणः च आसन् ।
ସ୍ତମ୍ଭ ଅତ୍ୟୁତଃ ଚିକ୍କଣ ଚ ଆସନ୍।
उत्तर :
ସ୍ତମ୍ଭ ଅତ୍ୟୁତଃ ଚିକ୍କଣ୍ଠ ଆସୀତ୍।
4. मण्डूका: स्तम्भस्य आहरोणं कृतवान् ।
ମଣ୍ଡକା ସ୍ତମ୍ଭସ୍ୟ ଆରୋହଣ କୃତବାନ୍ ।
उत्तर :
ମଣ୍ଡୁକା ସ୍ତମ୍ଭସ୍ୟ ଆରୋହଣଂ କୃତବରଃ ।
![]()
5. भवतः प्रयास: व्यर्थ्य । ଭବତଃ ପ୍ରୟାସ ବ୍ୟର୍ଥ ।
उत्तर :
ଭବତଃ ପ୍ରୟାତଃ ବ୍ୟର୍ଥ ।
6. अहं मने लक्ष्यं निघाय अग्रे आरूढवान् ।
ଅହଂ ମନେ ଲକ୍ଷ୍ୟ ନିଧାୟ ଅଗ୍ରେ ଆରୂଢ଼ବାନ୍ ।
उत्तर :
ଅହଂ ମନସି ଲକ୍ଷ୍ୟ ନିଧାୟ ଅଗ୍ରେ ଆରୂଢ଼ବାନ୍ ।
7. शिशु : मध्यभागं प्राप्तवन्तः ।
ଶିଶୁ ମଧ୍ୟଭାଗ୍ୟ ପ୍ରାପ୍ତବନ୍ତଃ ।
उत्तर :
ଶିଶୁ ମଧ୍ୟଭାଗଂ ପ୍ରାପ୍ତବାନ୍ ।
8. स: विजयी भवे: ।
ଡଃ ବିଜୟୀ ଭବେତ୍ ।
उत्तर :
ଡଃ ବିଜୟୀ ଭବେତ୍ ।
9. मणड़काः अग्रे आगतवान् ।
ମଣ୍ଡୁକା ଅଗ୍ରେ ଆଗତବାନ୍ ।
उत्तर :
ଆଗତବନ୍ତଃ
10. मण्ड़कः तत्र सम्मिलिता:।
ମଣ୍ଡୁକ ତତ୍ର ସମ୍ମିଳିତଃ ।
उत्तर :
ମଣ୍ଡୁକୀ
11. स: नूनं अधः पतेत ।
ଡଃ ନୂନଂ ଅଧଃ ପକ୍ଷେତ ।
उत्तर :
ପତେତ୍ର
12. प्रतियोगिता आरब्ध: ।
ପ୍ରତିଯୋଗିତା ଆରମଃ ।
उत्तर :
ଆରକ୍ତା
13. मातुः वचनेन पुत्र: आगच्छन् ।
ମାତୃ ବଚନେନ ପୁନଃ ଆଗଚ୍ଛନ୍ ।
उत्तर :
ଆଗଛତ୍ର
![]()
14. किमर्थ्यम् एतत् साहस: करोषि।
କିମର୍ଥମ୍ ଏତତ୍ ସାହସ୍ତ କରୋଷି ।
उत्तर :
ସାହସମ୍
सन्धिविच्छेदं कुरुत। (ସନ୍ଧିବିଚ୍ଛେଦଂ କୁରୁତ।)
- सर्वादौ (ସର୍ବାଦୌ) = ସର୍ବ + ଆଦୌ
- अत्युच्च: (ଅତ୍ଯୁଚ୍ଚ) = ଅତି + ଉଚ୍ଚ
- परन्तु (ପରନ୍ତୁ) = ପରମ୍ + ତୁ
- कोऽपि (କୋଽପି) = ଡଃ + ଅପି
सन्धिं कुरुत । (ସନ୍ଧି କୁରୁତ।)
- कस्य + अपि = कस्यापि କସ୍ୟ + ଅପି = କନ୍ୟାପି
- किम् + अर्थम् = किमर्थम् କିମ୍ + ଅର୍ଥମ୍ = କିମର୍ଥମ୍
- पुन: + अपि = पुनरपि छू ପୁନଃ + ଅପି = ପୁନରପି
- पादम् + अपि = पादमपि ପାଦମ୍ + ଅପି = ପାଦମପି
क्रियापदं निर्वाचयत। (କ୍ରିୟାପଦଂ ନିର୍ବାଚୟତ।)
आगतवन्त:, मण्डूका:, कृतवन्त:, प्रतियोगिता, वर्धयन्तिस्म, स्तम्भ:, आसीत्, पतितवन्तः, त्वम्, सफलः।
ଆଗତବନ୍ତଃ, ମଣ୍ଡୁକା, କୃତବନ୍ତଃ, ପ୍ରତିଯୋଗିତା, ବର୍ଧୟରି ସ୍କ, ସ୍ତମଃ, ଆସୀତ, ପତିତବହିଃ, ତ୍ଵମ୍, ସଫଳ ।
उत्तर :
ଆଗତବନ୍ତଃ, କୃତବନ୍ତଃ, ବର୍ଧୟନ୍ତ ସ୍ମ, ଆସୀତ, ପତିତବହିଃ ।
कर्तृपदं चिनुत । (କର୍ତ୍ତୃପଦଂ ଚିନୁତ।)
अभवन्, प्रापुयाम, सर्वे, वयम्, शृणुयाम, त्वम्, पुत्र:, शृणुया:, भवे:, शिशुः।
ଅଭବନ, ପ୍ରାପ୍ୟୟାମ, ସର୍ବେ, ବୟମ୍, ଶୃଣ୍ମୟାମ, ତୁମ୍, ଶୁଣୁୟାଁ, ଭବେ, ଶିଶୁ ।
उत्तर :
ସର୍ବେ, ବୟମ୍, ତ୍ୱମ୍, ପୁତ୍ର, ଶିଶୁ।
शब्दानां मातृभाषया अर्थान् लिखत। (ଶବ୍ଦାନାଂ ମାତଭାଷୟ ଅର୍ଥାନ୍ ଲିଖତ ।)
- द्रष्टुम् (ଦ୍ରଷ୍ଣୁମ୍) – ଦେଖିବାକୁ
- सम्मिलिता (ସମ୍ମିଳିତା) – ଏକାଠିହେଲେ
- कतिपया: (କତିପୟା) – କେତେକ
- यत्नम् (ଯତ୍ନମ୍) – ଚେଷ୍ଟା
- विस्मिता: (ବିସ୍ମିତା) – ଆଶ୍ଚର୍ଯ୍ୟ ହୋଇ
- निरन्तरम् (ନିରନ୍ତରମ୍) – ଅନବରତ
- मनसि (ମନସି) – ମନରେ
![]()
Subjective
ନିଜଭାଷୟ ପ୍ରାୟଶଃ ଦଶତିଃ ବାକ୍ୟ ଉତ୍ତରଂ ଲିଖିତ:
प्रश्न 1.
मण्ड़क: केन प्रकारेण लक्ष्यप्राप्तिं कृतवान् ?
ମଣ୍ଡୁକଃ କେନ ପ୍ରକାରେଣ ଲକ୍ଷ୍ୟପ୍ରାଣ୍ଡିଂ କୃତବାନ୍ ?
उत्तर :
ଥରେ ବେଙ୍ଗକୁଳରେ ଏକ ପ୍ରତିଯୋଗିତା ଆୟୋଜିତ ହେଲା । ସ୍ଥିର ହେଲା ଯେ ସ୍ତମ୍ଭର ଅଗ୍ରଭାଗରେ ପ୍ରଥମେ ପହଁଞ୍ଚିବ ସେ ବିଜୟୀ ହେବ। ପ୍ରତିଯୋଗିତାରେ ଭାଗନେବାକୁ ଇଚ୍ଛୁକ ପ୍ରାର୍ଥୀମାନେ ଆଗକୁ ଆସିଲେ। ପ୍ରତିଯୋଗିତା ଦେଖିବାପାଇଁ ମଧ୍ୟ ଦର୍ଶକ ବେଙ୍ଗମାନଙ୍କ ଭିଡ଼ ଜମିଲା । ପ୍ରତିଯୋଗିତା ଆରମ୍ଭ ହେଲା । ପ୍ରତିଯୋଗୀମାନେ ସ୍ତମ୍ଭ ଚଢ଼ିବାକୁ ଲାଗିଲେ । ଦର୍ଶକ ବେଙ୍ଗ କରତାଳି ଦେଇ ଉତ୍ସାହିତ କଲେ।
କେତେକ ଚିନ୍ତାକଲେ ସ୍ତମ୍ଭ ଅତ୍ୟନ୍ତ ଉଚ୍ଚ ଓ ଚିକ୍କଣ ଅଛି ଯିଏ ଉପରକୁ ଚଢ଼ିବ ସେ ନିଶ୍ଚିତ ତଳେ ପଡ଼ିବ । ତଥାପି କେତେଜଣ ପ୍ରଯତ୍ନ କଲେ କିନ୍ତୁ ଅନ୍ୟମାନଙ୍କ ନିରୁତ୍ସାହିତ ବଚନେ ଶୁଣି ତଳେ ପଡ଼ିବାକୁ ଲାଗିଲେ । ଯାହାର ମନୋବଳ ଦୃଢ଼ ସେ ପୁନଃ ପ୍ରଚେଷ୍ଟା କଲେ । କିନ୍ତୁ କେହି ଜଣେ ହେଲେ ସ୍ତମ୍ଭ ଆରୋହଣ କରିପାରିଲେ ନାହିଁ । ବିଫଳ ବେଙ୍ଗମାନେ ନିରାଶ ହେଲେ ।
ଏହି ସମୟରେ ଏକ କ୍ଷୁଦ୍ରବେଙ୍ଗ ନିଜ ମାଆର ଉତ୍ସାହପୂର୍ଣ ବଚନ ଶୁଣି ସ୍ତମ୍ଭ ଚଢ଼ିବାକୁ ଆରମ୍ଭ କଲା। ଅଳ୍ପ ସମୟରେ ମଧ୍ୟ ସ୍ତମ୍ଭର ମଧ୍ୟଭାଗ ପ୍ରାପ୍ତ କଲା । ଏସବୁ ଦେଖୁ ଅନ୍ୟମାନେ ଛୋଟବେଙ୍ଗକୁ ଏଣୁତେଣୁ କଥା କହି ଭୟଭୀତ କରାଇବାକୁ ଚେଷ୍ଟାକଲେ। କିନ୍ତୁ ସେ କାହାର ବଚନକୁ ଖାତିର ନ କରି ନିରନ୍ତର ଆଗକୁ ଯିବାକୁ ଲାଗିଲା ଏବଂ ସ୍ତମ୍ଭର ଅଗ୍ରଭାଗରେ ପହଁଞ୍ଚିଲା ।
ଏସବୁ ଦେଖୁ ସମସ୍ତେ ଆଶ୍ଚର୍ଯ୍ୟଚକିତ ହୋଇଗଲେ। ସମସ୍ତେ ନାନା ପ୍ରଶ୍ନ କରିବାକୁ ଲାଗିଲେ। ଶିଶୁ ବେଙ୍ଗ ପ୍ରତ୍ୟୁତ୍ତରରେ କହିଲା ଯେ ଯଦି ଆମ୍ଭେମାନେ ଗୁରୁଜନମାନଙ୍କ କଥା ଶୁଣିବା, ମନରେ ଏକାଗ୍ରଭାବ ପୋଷଣ କରିବା ଓ ଆତ୍ମବିଶ୍ଵାସକୁ ଦୃଢ଼ କରିବା ତାହାହେଲେ ସଫଳତାର ସ୍ଵାଦ ନିଶ୍ଚୟ ଖଞ୍ଝାପାରିବା। ଏହି ପରି ଭାବେ ଶିଶୁବେଙ୍ଗଟି ନିଜର ଲକ୍ଷ୍ୟସ୍ଥଳରେ ପହଞ୍ଚି ପାରିଥିଲା ।
मातृभाषयाअनुवादं कुरुत ।
(ମାତୃଭାଷୟା ଅନୁବାଦଂ କୁରୁତ ।)
1. कदाचित् मण्डूककुले काचित् प्रतियोगिता आयोजिता ।
କଦାଚିତ୍ ମଣ୍ଡୁକକୁଳେ କାଚିତ୍ର ପ୍ରତିଯୋଗିତା ଆୟୋଜିତା । ଅନୁବାଦ: କୌଣସି ଏକ ସମୟରେ ବେଙ୍ଗବଂଶରେ ଗୋଟିଏ ପ୍ରତିଯୋଗିତା ଆୟୋଜିତ ହେଲା ।
2. यः स्तम्भस्य शिखरं सर्वादी प्राप्नुयात् सः विजयी भवेत् इति सर्वे मण्डूकाः स्थिरीकृतवन्तः ।
ଯଃ ସ୍ତମସ୍ୟା ଶିଖରଂ ସର୍ବାଦୌ ପ୍ରାପ୍ରୁୟାତ୍ ଡଃ ବିଜୟୀ ଭବେତ୍ ଇତି ସର୍ବେ ମୟୂକା ସ୍ଥିରୀକୃତବରଃ ।
ଅନୁବାଦ: ଯିଏ ଖମ୍ବର ଶିଖରଦେଶରେ ପ୍ରଥମେ ପହଁଞ୍ଚିବ ସେ ବିଜୟୀ ହେବ ବୋଲି ସମସ୍ତ ବେଙ୍ଗ ସ୍ଥିରକଲେ ।
3. प्रतियोगितायां भागं नेतुं बहवो मण्डूकाः अग्रे आगतवन्तः ।
ପ୍ରତିଯୋଗିତାୟାଂ ଭାଗ୍ୟ ନେତୁ ବହବୋ ମଣ୍ଡୁକା ଅଗ୍ରେ ଆଗତବନଃ ।
ଅନୁବାଦ: ପ୍ରତିଯୋଗିତାରେ ଭାଗନେବାକୁ ବହୁତ ବେଙ୍ଗ ଆଗକୁ ଆସିଲେ।
4. प्रतियोगिता द्रष्टुम् अपि असंख्या: मण्डूकाः तत्र सम्मिलिताः ।
ପ୍ରତିଯୋଗିତାଂ ଦ୍ରଷ୍ଟୁମ୍ ଅପି ଅସଂଖ୍ୟା ମକା ତତ୍ର ସମ୍ମିଳିତାଃ ।
ଅନୁବାଦ: ପ୍ରତିଯୋଗିତା ଦେଖିବାକୁ ମଧ୍ୟ ବହୁତ ବେଙ୍ଗ ସେଠାରେ ମିଳିତ ହେଲେ ।
5. प्रतियोगिता आरब्धा ।
ପ୍ରତିଯୋଗିତା ଆରଚ୍ଛା ।
ଅନୁବାଦ: ପ୍ରତିଯୋଗିତା ଆରମ୍ଭ ହେଲା ।
![]()
6. मण्डूका: स्तम्भस्य आरोहणं कृतवन्त: ।
ମଣ୍ଡକା ସ୍ତମ୍ଭସ୍ୟ ଆରୋହଣ କୃତବତଃ ।
ଅନୁବାଦ: ବେଙ୍ଗମାନେ ଖମ୍ବଉପରେ ଚଢ଼ିଲେ।
7. दर्शका: मणडूका: करताड़नेन अरे! अहो ! हो ! इत्यादिभि: शब्दै : प्रतियोगिनाम् उत्माहं बर्घयन्ति स्म।
ଦର୍ଶକା ମଣ୍ଡୁକା କରତାଡ଼ନେନ ଅରେ ! ଅହୋ ! ହୋ ! ଇତ୍ୟାଦିଭି ଶଦ୍ଦି ପ୍ରତିଯୋଗିନାମ୍ ଉତ୍ସାହଂ ବର୍ଧୟନ୍ତ ସୁ ।
ଅନୁବାଦ: ଦର୍ଶକ ବେଙ୍ଗମାନେ କରତାଳିଦେଇ ଆରେ! ଅହୋ! ହୋ ! ଇତ୍ୟାଦି ଶବ୍ଦରେ ପ୍ରତିଯୋଗିମାନଙ୍କ ଉତ୍ସାହ ବଢ଼ାଇଲେ ।
8. स्तम्भ: अत्युच्च: चिक्कण: चआसीत् ।
ସ୍ତମ୍ଭ ଅତ୍ୟତଃ ଚିକ୍କଣ ଚୂ ଆସୀତ୍ ।
ଅନୁବାଦ: ଖମ୍ବ ବହୁତ ଉଚ୍ଚ ଓ ଚିକ୍କଣ ଥିଲା ।
9. कतिपयाः मण्डूकाः चिन्तयन्ति कः वा स्तम्भस्य आरोहणं कुर्यात् ?
କତିପୟା ମକା ଚିନ୍ତୟତି କଃ ବା ସ୍ତମ୍ଭସ୍ୟ ଆରୋହଣଂ କୁର୍ଯ୍ୟାତ୍ ?
ଅନୁବାଦ: କେତେକ ବେଙ୍ଗ ଭାବିଲେ – କିଏ ବା ଖମ୍ବ ଆରୋହଣ କରିପାରିବ ?
10. यः अग्रे गच्छेत् ।
ଯଃ ଅଗ୍ରେ ଗଚ୍ଛେତ୍ ।
ଅନୁବାଦ: ଯିଏ ଆଗରେ ଯିବ ।
11. स: नूनम् अधः पतेत् ।
ଡଃ ନୂନମ୍ ଅଧଃ ପଚେତ୍ ।
ଅନୁବାଦ: ସେ ନିଶ୍ଚୟ ତଳକୁ ପଡ଼ିଯିବାର ସମ୍ଭାବନା ।
12. तथापि कितिपया: मण्डूका: यत्नं कृतवन्तः, परन्तु अन्येषां मण्डूकानाम् उत्साहरहितं वचनं श्रुत्वा अघ: पतितवन्तः ।
ତଥାପି କତିପୟ ମଣ୍ଡୁଳା ଆରୋହଣାୟ ଯବଂ କୃତବତଃ, ପରନ୍ତୁ ଅନ୍ୟଷା ମକାନାମ୍ ଉତ୍ସାହରହିତଂ ବଚନଂ ଶ୍ରୁତ୍ବା ଅଧଃ ପତିତବନ୍ତୀ ।
ଅନୁବାଦ: ତଥାପି କେତେକ ବେଙ୍ଗ ଚଢ଼ିବାକୁ ଚେଷ୍ଟାକଲେ; କିନ୍ତୁ ଅନ୍ୟ ବେଙ୍ଗମାନଙ୍କ ଉତ୍ସାହରହିତ ବାକ୍ୟ ଶୁଣି ତଳକୁ ଖସିପଡ଼ିଲେ।
13. येषां मनोबलं दृढम् अस्ति ते पुनरपि आरोहणं कुर्वन्ति ।
ଯେଷା ମନୋବଳ ଦୃଢ଼ମ୍ ଅସ୍ଥି ତେ ପୁନରପି ଆରୋହଣ କୁଛି ।
ଅନୁବାଦ: ଯେଉଁମାନଙ୍କ ମନୋବଳ ଦୃଢ଼ ଅଛି ସେମାନେ ପୁଣି ମଧ୍ଯ ଚଢ଼ିଲେ ।
14. तथापि कोऽपि मण्डूकः स्तम्भस्य पादमपि न आरूढवान् ।
ତଥାପି କୋଽପି ମଣ୍ଡୁକଃ ସ୍ତମ୍ଭସ୍ୟ ପାଦମପି ନ ଆରୂଢ଼ବାନ୍ ।
ଅନୁବାଦ: ତଥାପି କୌଣସି ବେଙ୍ଗ ଖମ୍ବର ଗୋଟିଏ ପାଦମଧ୍ଯ ଚଢ଼ିପାରିଲେ ନାହିଁ ।
![]()
15. विफला: मण्डूका: नैराश्यं प्राप्तवन्त: ।
ବିଫଳା ମଣ୍ଡୁକା ନୈରାଶ୍ୟ ପ୍ରାପ୍ତବନ୍ତୀ ।
ଅନୁବାଦ: ବିଫଳ ଛେଙ୍ଗମାନେ ନୈରାଶ୍ୟ ଲାଭ କଲେ ।
16. एका मण्डूकमाता स्वलघुपुत्रम् उक्तवती, ‘पुत्र’! त्वं स्तम्भस्य आरोहेणं कुर्याः।
ଏକା ମଣ୍ଡୁକମାତା ସ୍ଵଲଘୁପୁତ୍ରମ୍ ଉଦ୍ଭବତୀ, ‘ପୁତ୍ର’ ! ବଂ ସ୍ତମ୍ଭସ୍ୟ ଆରୋହଣଂ କୁର୍ଯ୍ୟା।
ଅନୁବାଦ: ଗୋଟିଏ ବେଙ୍ଗର ମାଆ ନିଜର ଛୋଟପୁଅକୁ କହିଲା – ‘ ‘ ପୁଅରେ ! ତୁ ଖମ୍ବ ଉପରକୁ ଚଢ଼ିବା ଉଚିତ।
17. वधिरत्वं प्रदर्शये:।
ବଧୂରଣଂ ପ୍ରଦର୍ଶୟଃ ।
ଅନୁବାଦ: କାନ ବନ୍ଦକରିଦେବା ଉଚିତ ।
18. नूनं सफल: भवे: ।
ନୂନଂ ସଫଳ ଭାବେ ।
ଅନୁବାଦ: ନିଶ୍ଚିତ ସଫଳ ହେବୁ।
19. मातु: वचनेन पुत्र: स्तम्भस्य आरोहणाय अग्रे आगच्छत्।
ମାତୁଃ ବଚନେନ ପୁନଃ ସ୍ତମ୍ଭସ୍ୟ ଆରୋହଣାୟ ଅଗ୍ର ଆଗଚ୍ଛତ୍।
ଅନୁବାଦ: ମାଆ କଥାରେ ପୁଅ ଖମ୍ବ ଉପରକୁ ଚଢ଼ିବାକୁ ଆଗକୁ ଆସିଲା।
20. अल्पेन एव कालेन सः शिशुः स्तम्भस्य मध्यभागं प्राप्तवान्।
ଅର୍ଜ୍ଜୁନ ଏବଂ କାଳେନ ଡଃ ଶିଶୁ ସ୍ତମ୍ଭସ୍ୟ ମଧ୍ୟଭାଗ ପ୍ରାପ୍ତବାନ୍ ।
ଅନୁବାଦ: ଅଳ୍ପସମୟ ଭିତରେ ସେହି ପିଲାଟି ଖମ୍ବ ମଝିଭାଗକୁ ଚାଲିଗଲା ।
21. तस्य आरोहाणं दृष्ट्वा अन्ये विस्मिता: अवदन् – ‘अये’! पते : त्वम्।
ତସ୍ୟ ଆରୋହଣଂ ଦୃଷ୍ଟା ଅନ୍ୟ ବିସ୍ତିତା ଅବଦନ – ‘ଅୟେ’ ! ପତଃ ତୁମ୍ ।
ଅନୁବାଦ: ତାହାର ଚଢ଼ା ଦେଖୁ ଅନ୍ୟମାନେ ଆଶ୍ଚର୍ଯ୍ୟ ହୋଇ କହିଲେ – ଆରେ ତୁ ପଡ଼ିଯାଇପାରୁ।
22. भो : ! किमर्थम् एतत् साहसं करोषि ?
ଭୋ ! କିମର୍ଥମ୍ ଏତତ୍ ସାହସଂ କରୋଷି ?
ଅନୁବାଦ: ହେ କାହିଁକି ଏମିତି ସାହସ କରୁଛୁ ?
23. भवतः प्रयास: व्यर्थः।
ଭବତଃ ପ୍ରୟାସ ବ୍ୟର୍ଥ ।
ଅନୁବାଦ: ତୋର ପ୍ରଚେଷ୍ଟା ବୃଥା ହେବ ।
24. तथापि सः शिशुः मण्डूकः निरन्तरम् अग्रे अगच्छत्।
ତଥାପି ଡଃ ଶିଶୁ ମଣ୍ଡୁକଃ ନିରନ୍ତରମ୍ ଅଗ୍ରେ ଅଗଚ୍ଛତ୍।
ଅନୁବାଦ: ତଥାପି ସେହି ବାଳକ ବେଙ୍ଗ ଅନବରତ ଆଗକୁ ଗଲା।
![]()
25. अन्तत : गत्वा सः स्तम्भस्य अग्रभागम् अपि प्राप्तवान् ।
ଅନ୍ତତଃ ଗଡା଼ ଡଃ ସ୍ତମ୍ଭସ୍ୟ ଅଗ୍ରଭାଗମ୍ ଅପି ପ୍ରାପ୍ତବାନ୍ ।
ଅନୁବାଦ: ଶେଷରେ ସେ ସ୍ତମ୍ଭର ଅଗ୍ରଭାଗରେ ପହଁଞ୍ଚିଲା ।
26. एतद् दृष्ट्वा सर्वे विस्मिता: अभवन् ।
ଏତଦ୍ ଦୃଷ୍ଟା ସର୍ବେ ବିସ୍ମିତଃ ପ୍ରତିଯୋଗିତା ଅଭବନ୍ ।
ଅନୁବାଦ: ଏହା ଦେଖୁ ସମସ୍ତେ ଆଶ୍ଚର୍ଯ୍ୟାନ୍ବିତ ହୋଇଗଲେ
संस्कृतभाषया अनुवादं कुरुत।
(ସଂସ୍କୃତଭାଷୟା ଅନୁବାଦଂ କୁରୁତ୍।)
1. ବେଙ୍ଗମାନଙ୍କର ଆରୋହଣ ପ୍ରତିଯୋଗିତା ହେଉଥିଲା।
उत्तर :
ମଶୂକାନାମ୍ ଆରୋହଣପ୍ରତିଯୋଗିତା ଭବତି ସ୍ଵ।
2. ସେଥିରେ ବହୁତ ବେଙ୍ଗମାନେ ଭାଗ ନେଇଥିଲେ ।
उत्तर :
ତତୁଃ ବହବ ମଣ୍ଡୁକା ଭାଗମ ଅନୟନ।
3. ଦର୍ଶକ ବେଙ୍ଗମାନେ ତାଳି ମାରିଥିଲେ।
उत्तर :
ଦର୍ଶକଃ ମଣ୍ଡୁକା କରତାଳମ୍ ଅକୁର୍ବନ୍।
4. ସ୍ତମ୍ଭଟି ଉଚ୍ଚ ଓ ଚିକ୍କଣ ଥିଲା ।
उत्तर :
ସ୍ତତଃ ଅତ୍ୟୁତଃ ଚିକ୍କଶଃ ଚ୍ ଆସୀତ୍ ।
![]()
5. କେହିହେଲେ ସ୍ତମ୍ଭ ଆରୋହଣ କରିପାରିଲେ ନାହିଁ ।
उत्तर :
କୋଽପି ସ୍ତମ୍ଭାରୋହଣଂ ନ ଅକରୋତ୍।
6. ବିଫଳ ବେଙ୍ଗମାନେ ନିରାଶ ହେଲେ।
उत्तर :
ବିଫଳା’ ମଣ୍ଡୁକା ନୈରାଶ୍ୟମ୍ ଅଭବନ।
7. ଆତ୍ମବିଶ୍ବାସ ହିଁ ବିଜୟ ଦିଏ ।
उत्तर :
ଆତ୍ମବିଶ୍ଵାସ୍ତ୍ର ଏବ ବିଜୟଂ ଦଦାତି ।
प्रथम अनुच्छेदः (ପ୍ରଥମ ଅନୁଚ୍ଛେଦଃ)
कदाचित् मण्डूककुले एका प्रतियोगिता आयोजिता।य: स्तम्भस्य शिखरं सर्वादौ प्राप्नुयात् स: विजयी भवेत् इति सर्वे मण्डूकाः स्थिरीकृतवन्तः।
प्रतियोगितायां भागं नेतुं बहवो मण्डूकाः अग्रे आगतवन्तः। प्रतियोगितां द्रष्टुम् अपि असंख्या: मण्डूका: तत्र सम्मिलिताः। प्रतियोगिता आरब्धा। मण्डूकाः स्तम्भस्य आरोहणं कृतवन्तः। दर्शका: मण्डूका: करतताडनेन ‘अरे’! ‘अहो’! ‘हो’! इत्यादिभि: शब्दे: प्रतियोगिनाम् उत्साहं बर्धयन्ति स्म। स्तम्भ: अत्युच्च: चिक्कण: च आसीत्। कतिपया: मण्डूका: चिन्तयन्ति स्म ‘क:वा स्तम्भस्य आरोहणं कुर्यात् ? य: अग्रे गच्छेत् सः नूनम् अधः पतेत्।

କଦାଚିତ୍ ମଣ୍ଡୁକକୁଳେ ଏକା ପ୍ରତିଯୋଗିତା ଆୟୋଜିତା । ଯଃ ସ୍ତମ୍ଭସ୍ୟ ଶିଖରଂ ସର୍ବାଦୌ ପ୍ରାୟୁୟାତ୍ ଡଃ ବିଜୟୀ ଭବେତ୍ ଇତି ସର୍ବେ ମୟୂକା ସ୍ଥିରୀକୃତବତଃ ।
ପ୍ରତିଯୋଗିତାୟାଂ ଭାଗଂ ନେତୁଃ ବହବୋ ମଣ୍ଡୁକା ଅଗ୍ରେ ଆଗତବନ୍ତ ୫ । ପ୍ରତିଯୋଗିତା ଦ୍ରଷ୍ଟୁମ୍ ଅପି ଅସଂଖ୍ୟ ମଣ୍ଡୁକା ତତ୍ର ସମ୍ମିଳିତା । ପ୍ରତିଯୋଗିତାଂ ଆରକ୍ତା । ମଣ୍ଡୁକା ସ୍ତମ୍ଭସ୍ୟ ଆରୋହଣଂ କୃତବନ୍ତ । ଦର୍ଶକଃ ମଣ୍ଡୁକ କରତାଡିନେନ ଅରେ ! ଅହୋ ! ‘ହୋ’ ! ଇତ୍ୟାଦିଭିଂ ଶରଃ ପ୍ରତିଯୋଗିନାମ୍ ଉତ୍ସାହଂ ବର୍ଧୟନ୍ତ ସ୍ମ । ସ୍ତତଃ ଅତୁଃହଃ ଚିକ୍କଶଃ ଚ ଆସୀତ୍ । କତିପୟା ମଣ୍ଡୁକା ଚିନ୍ତୟନ୍ତ କଃ ବା ସ୍ତମ୍ଭସ୍ୟ ଆରୋହଣଂ କୁର୍ଯ୍ୟାତ୍ ? ସ୍ତତଃ ଚିକ୍କଣ ଅସ୍ଥି । ଯଃ ଅଗ୍ରେ ଗଚ୍ଛେତ୍ । ଡଃ ନୂନମ୍ ଅଧଃ ପତେତ୍ ।
ସନ୍ଧିବିଚ୍ଛେଦ
- କଶ୍ଚିତ୍ – କଃ + ଚିତ୍
- ସର୍ବାଦୌ – ସର୍ବ + ଆଦୌ
- ପ୍ରାପ୍ଲ ୟାତ୍ – ପ୍ର + ଆପ୍ ୟାତ୍, ବହବୋ
- ମଣ୍ଡୁକା – ବହନଃ + ମଣ୍ଡୁକା
- ସମ୍ମିଳିତା – ସମ୍ + ମିଳିତା
- ଇତ୍ୟାଦିଭିଂ – ଇତି + ଆଦିଭି
- ଅତ୍ଯୁଟ୍ଟ – ଅତି + ଉଚ୍ଚ।
ଶବ୍ଦାର୍ଥ
- କଦାଚିତ୍ – କୌଣସି ଏକଦିନ
- କଶ୍ଚିତ୍ – କେହିଜଣେ
- ଶିଖରଂ – ଶୀର୍ଷ
- ପ୍ରାପ୍ୟୁ ୟାତ୍ – ପହଁଞ୍ଚିବ
- ଦ୍ରଷ୍ଟୁମ୍ – ଦେଖୁବାକୁ
- ଆରକ୍ତା – ଆରମ୍ଭ ହେଲା
- କରତାଡ଼ନେନ – କରତାଳିରେ
- ଅତ୍ଯୁଚ୍ଚ – ବହୁ ଉଚ୍ଚ
- କତିପୟା – କେତେକ, କଃ
- କୋ ବା – କିଏ ବା
- ଚୂନମ୍ – ନିଶ୍ଚୟ
- ଅଧଃ – ତଳେ।
![]()
ଅନୁବାଦ
କୌଣସି ଏକ ସମୟରେ ବେଙ୍ଗବଂଶରେ ଗୋଟିଏ ପ୍ରତିଯୋଗିତା ଆୟୋଜିତ ହେଲା । ଯିଏ ଖମ୍ବର ଶିଖର ଦେଶରେ ପ୍ରଥମେ ପହଁଞ୍ଚିବ ସେ ବିଜୟୀ ହେବ ବୋଲି ସମସ୍ତ ବେଙ୍ଗ ସ୍ଥିରକଲେ ।
ପ୍ରତିଯୋଗିତାରେ ଭାଗନେବାକୁ ବହୁତ ବେଙ୍ଗ ଆଗକୁ ଆସିଲେ। ପ୍ରତିଯୋଗିତା ଦେଖିବାକୁ ମଧ୍ୟ ବହୁତ ବେଙ୍ଗ ସେଠାରେ ମିଳିତ ହେଲେ । ପ୍ରତିଯୋଗିତା ଆରମ୍ଭ ହେଲା । ବେଙ୍ଗମାନେ ଖମ୍ବ ଉପରେ ଚଢ଼ିଲେ । ଦର୍ଶକ ବେଙ୍ଗମାନେ କରତାଳିଦେଇ ଆରେ ! ଅହୋ ! ହୋ ! ଇତ୍ୟାଦି ଶବ୍ଦରେ ପ୍ରତିଯୋଗୀମାନଙ୍କ ଉତ୍ସାହ ବଢ଼ାଇଲେ। ଖମ୍ବ ବହୁତ ଉଚ୍ଚ ଓ ଚିକ୍କଣ ଥିଲା । କେତେକ ବେଙ୍ଗ ଭାବିଲେ – କିଏ ବା :
ଖମ୍ବ ଆରୋହଣ କରିପାରିବ । ଖମ୍ବ ଚିକ୍କଣ ଅଛି । ଯିଏ ଆଗରେ ଯିବ। ସେ ନିଶ୍ଚୟ ତଳକୁ ପଡ଼ିଯିବାର ସମ୍ଭାବନା ।
द्वितीय अनुच्छेदः (ଦ୍ୱିତୀୟ ଅନୁଚ୍ଛେଦଃ)
तथापि कतिपयाः मण्डूका: आरोहणाय यत्नं कृतवन्तः, परन्तु अन्येषां मण्डूकानाम् उत्साहरहितं वचनं श्रुत्वा अधः पतितवन्तः। येषां मनोबलं दुढम् अस्ति ते पुनरपि आरोहणं कुर्वन्ति । तथापि कोऽपि मण्डूकः स्तम्भस्य पादमपि न आरूढवान् । विफला: मण्डूकाः नैराश्यं प्राप्तवन्तः ।
ତଥାପି କତିପୟା ମଣ୍ଡୁକା ଆରୋହଣାୟ ଯତ୍ନ କୃତିବନ୍ତଃ, ପରନ୍ତୁ ଅନ୍ୟଷା ମଣ୍ଡୁକାନାଂ ଉତ୍ସାହରହିତଂ ବଚନଂ ଶ୍ରୁତ୍ବା ଅଧଃ ପତିତବନ୍ତ ୫ । ଯେଷା ମନୋବଳ ଦୃଢ଼ମ୍ ଅସ୍ଥି ତେ ପୁନରପି ଆରୋହଣଂ କୁର୍ବନ୍ତି । ତଥାପି କୋଽପି ମଣ୍ଡୁକଃ ସ୍ତମ୍ଭସ୍ୟ ପାଦମପି ନ ଆରୂଢ଼ବାନ୍ । ବିଫଳା ମଣ୍ଡୁକା ନୈରାଶ୍ୟ ପ୍ରାପ୍ତିବନ୍ତ ।
ସନ୍ଧି ବିଚ୍ଛେଦ
- ତଥାପି – ତଥା + ଅପି
- ପରନ୍ତୁ – ପରଂ + ତୁ
- ମନୋବଳମ୍ – ମନଃ + ବଳମ୍ବ
- ପୁନରପି – ପୁନଃ + ଅପି
- କୋଽପି – କଃ + ଅପି
- ପାଦମପି – ପାଦମ୍ + ଅପି
- ପ୍ରାପ୍ତବନ୍ତ ୫ – ପ୍ର + ଆପ୍ତବନ୍ତଃ ।
ଶବ୍ଦାର୍ଥ
- କତିପୟା – କେତେକ ବେଙ୍ଗ
- ଯତଂ – ଚେଷ୍ଟା
- ପରନ୍ତୁ – କିନ୍ତୁ
- ଶୁଦ୍ଧା – ଶୁଣି
- ପୁନରପି – ପୁଣି ମଧ୍ୟ
- ଆରୂଢ଼ବାନ୍ – ଆରୋହଣ କଲେ ।
ଅନୁବାଦ
ତଥାପି କେତେକ ବେଙ୍ଗ ଚଢ଼ିବାକୁ ଚେଷ୍ଟାକଲେ, କିନ୍ତୁ ଅନ୍ୟବେଙ୍ଗମାନଙ୍କ ଉତ୍ସାହରହିତ ବାକ୍ୟ ଶୁଣି ତଳକୁ ଖସିପଡ଼ିଲେ । ଯେଉଁମାନଙ୍କ ମନୋବଳ ଦୃଢ଼ ଅଛି ସେମାନେ ପୁଣି ମଧ୍ଯ ଚଢ଼ିଲେ । ତଥାପି କୌଣସି ବେଙ୍ଗ ଖମ୍ବର ପାଦମଧ୍ଯ ଚଢ଼ିପାରିଲେ ନାହିଁ । ବିଫଳ ବେଙ୍ଗମାନେ ନୈରାଶ୍ୟ ଲାଭ କଲେ।
तृतीय अनुच्छेदः (ତୃତୀୟ ଅନୁଚ୍ଛେଦଃ)
एका मण्डूकमाता स्वकनिष्ठपुत्रम् उक्तवती – ‘पुत्र! त्वं स्तम्भस्य आरोहणं कुर्याः। आरोहणसमये कस्यापि वचनं न शृणुयाः। बधिरत्वं प्रदर्शये:। नूनं सफलः भवेः। मातुः वचनेन पुत्रः स्तम्भस्य अरोहरणाय अग्रे आगच्छत्। अल्पेन एव कालेन सः शिशुः स्तम्भस्य मध्यभागं प्राप्तवान्। तस्य आरोहणं दृष्ट्वा अन्ये विस्मिता: अवदन् ‘अये! पतेः त्वम्। भो: ! किमर्थम् एतत् साहसं करोषि? तव प्रयासः व्यर्थ:’ तथापि सः शिशुः मण्डूकः निरन्तरम् अर्गे आगच्छत्। अन्ततः गत्वा सः स्तम्भस्य अग्रभागम् अपि प्राप्तवान्।
ଏକା ମଣ୍ଡୁକମାତ। ସ୍ଵକନିଷ୍ଠପୁତ୍ରମ୍ ଭକ୍ତବତୀ, ‘ପୁତ୍ର’ ! ବଂ ସ୍ତମ୍ଭସ୍ୟ ଆରୋହଣଂ କୁର୍ଯ୍ୟା । ଆରୋହଣସମୟେ କନ୍ୟାପି ବଚନଂ ନ ଶୃଣୁୟା । ବଧୂରତ୍ୱ ପ୍ରଦର୍ଶୟେ । ନୂନଂ ସଫଳ ଭାବେ । ମାତୁଃ ବଚନେନ ପୁନଃ ସ୍ତମ୍ଭସ୍ୟ ଆରୋହଣାୟ ଅଗ୍ର ଆଗଚ୍ଛତ୍ । ଅନ ଏବ କାଳେନ ଡଃ ଶିଶୁ ସ୍ତମ୍ଭସ୍ୟ ମଧ୍ୟଭାଗ୍ୟ ପ୍ରାପ୍ତବାନ୍ । ତଥ୍ୟ ଆରୋହଣଂ ଦୃଷ୍ଟ୍ରା ଅନ୍ୟ ବିସ୍ମିତଃ ଅବଦନ୍ – ‘ଅୟେ ! ପତଃ ତ୍ୱମ୍ । ଭୋ ! କିମର୍ଥମ୍ ଏତତ୍ ସାହସଂ କରୋଷି ? ତବ ପ୍ରୟାସ ବ୍ୟର୍ଥ । ତଥାପି ଡଃ ଶିଶୁ ମଣ୍ଡୁକ ନିରନ୍ତରମ୍ ଅଗ୍ରେ ଅଗଚ୍ଛତ୍ । ଅନ୍ତ ତଃ ଗଡା଼ ଡଃ ସ୍ତମ୍ଭସ୍ୟ ଅଗ୍ରଭାଗମ୍ ଅପି ପ୍ରାପ୍ତବାନ୍ ।
![]()
ସନ୍ଧି ବିଚ୍ଛେଦ
- କନ୍ୟାପି = କସ୍ୟ + ଅପି
- ପ୍ରାପ୍ତବାନ୍ = ପ୍ର + ଆପ୍ତବାନ୍
- କିମର୍ଥମ୍ = କିମ୍ + ଅର୍ଥମ୍ ।
ଶବ୍ଦାର୍ଥ
- ଉକ୍ତବତୀ – କହିଲା
- କସ୍ୟାପି – କାହାରିହେଲେ
- ବଧୂତଂ – କାନବନ୍ଦ
- ନୂନଂ – ନିଶ୍ଚୟ
- ପ୍ରାପ୍ତବାନ୍ – ପହଁଞ୍ଚିଲା
- ପ୍ରୟାସ – ଚେଷ୍ଟା
- ନିରନ୍ତରଂ – ଅନବରତ
- ଅପି – ମଧ୍ୟ
- ଗତ୍ମା – ଯାଇ
ଅନୁବାଦ
ଗୋଟିଏ ବେଙ୍ଗର ମାଆ ନିଜର ଛୋଟପୁଅକୁ କହିଲା – ‘ପୁଅରେ ! ତୁ ଖମ୍ବ ଉପରକୁ ଚଢ଼ିବା ଉଚିତ। ଚଢ଼ିବାବେଳେ କାହାରିକଥା ଶୁଣିବା ଉଚିତ ନୁହେଁ। କାନବନ୍ଦ କରିଦେବା ଉଚିତ। ନିଶ୍ଚିତ ସଫଳ ହେବୁ । ମାଆର କଥାରେ ପୁଅ ଖମ୍ବ ଉପରକୁ ଚଢ଼ିବାକୁ ଆଗକୁ ଆସିଲା। ଅଳ୍ପସମୟ ହିତରେ ସେହି ପିଲାଟି ଖମ୍ବ ମଝିଭାଗକୁ ଚାଲିଗଲା । ତାହାର ଚଢ଼ା ଦେଖୁ ଅନ୍ୟମାନେ ଆଶ୍ଚର୍ଯ୍ୟ ହୋଇ କହିଲେ – ଆରେ ତୁ ପଡ଼ିଯାଇପାରୁ। ହେ ! ତୁ କାହିଁକି ଏମିତି ସାହସ କରୁଛୁ ? ତୋର ପ୍ରଚେଷ୍ଟା ବୃଥା ହେବ। ତଥାପି ସେହି ବାଳକ ବେଙ୍ଗ ଅନବରତ। ଆଗକୁ ଗଲା। ଶେଷରେ ସେ ସ୍ତମ୍ଭର ଅଗ୍ରଭାଗରେ ପହଁଞ୍ଚିଲା।
चतुर्थ अनुच्छेदः (ଚତୁର୍ଥ ଅନୁଚ୍ଛେଦଃ)
एतद् दृष्ट्वा सर्वे विस्मिताः अभवन्। ते अपृच्छन् कथं त्वं स्तम्भस्य आरोहणे समर्थ: अभवः ? सः धीरम् अवदत् यदि वयं गुरुजनानां वचनं शृणुयाम मनसि एकाग्रतां धारयेम आत्मविश्वासं च दृढं कुर्याम तर्हि सफलताम् अवश्यं प्राप्नुयाम।
ଏତଦ୍ ଦୁଷ୍ଟା ସର୍ବେ ବିସ୍ମିତ ଅଭବନ୍ । ତେ ଅପୃଚ୍ଛନ୍ – କର୍ଡିଂ ବଂ ସ୍ତମ୍ଭସ୍ୟ ଆରୋହଣେ ସମର୍ଥୀ ଅଭବ ? ଡଃ ଧୀରମ୍ ଅବଦତ୍ ଯଦି ବୟଂ ଗୁରୁଜନାନାଂ ବଚନଂ ଶୃଣୁୟାମ, ମନସି .ଏକାଗ୍ରତାଂ ଧାରୟେମ ଆତ୍ମବିଶ୍ୱାସଂ ଚ ଦୃଢ କୁର୍ଯାମ ତହିଁ ସଫଳତାମ୍ ଅବଶ୍ୟ ପ୍ରାପ୍ରୁୟାମ ।
ସନ୍ଧି ବିଚ୍ଛେଦ
ପ୍ରାପ୍ରୁୟାମ = ପ୍ର + ଆସୁୟାମ ।
ଶବ୍ଦାର୍ଥ
- ଏତତ୍ – ଏହା,
- ଦୃଷ୍ଟା – ଦେଖୁ,
- ଅପୂଚ୍ଛନ୍ – ପଚାରିଲେ, କଥ୍ୟ କିପରି
- ଶୃଣୁୟାମ – ଶୁଣିବା,
- ମନସି – ମନରେ, ଧାରୟେଉ ଧାରଣ କରିବା,
- ତହିଁ – ତାହାହେଲେ ।
![]()
ଅନୁବାଦ
ଏହା ଦେଖୁ ସମସ୍ତେ ଆଶ୍ଚର୍ଯ୍ୟ ହୋଇଗଲେ। ସେମାନେ ପଚାରିଲେ – ତୁମେ କିପରି ଏହି ସ୍ତମ୍ଭ ଚଢ଼ିବାକୁ ସମର୍ଥ ହୋଇପାରିଲ ? ସେ ଧୀରେ କହିଲା – ଯଦି ଆମେ ଗୁରୁଜନଙ୍କ କଥା ଶୁଣିବା, ମନରେ ଏକାଗ୍ରତା ରଖୁବା ଓ ଆତ୍ମବିଶ୍ଵାସକୁ ଦୃଢ଼ କରିବା, ତେବେ ସଫଳତା ନିଶ୍ଚୟ ପାଇବା।
मण्डूका:, दर्शका:, करताड़नेन, चिक्कण, अथ:, नैराश्यम्, निरस्तरम्, आरोढुम्
ମଣ୍ଡକା, ଦର୍ଶକା, କରତାଡ଼ନେ, ଚିକ୍କଣ, ଅଧଃ, ନୈରାଶ୍ୟମ୍, ନିରନ୍ତର, ଆରୋଜୁମ୍
कर्तृपदानि :
मण्डूका:, दर्शका:, मण्डूकमाता, पुत्र:, शिशु:, अन्ये, सवे, ते
(ମଣ୍ଡୁକା, ଦର୍ଶକା, ମଣ୍ଡୁକମାତା, ପୁନଃ, ଶିଶୁ, ଅନ୍ୟ, ସର୍ବେ, ତେ)
क्रियापदानि :
भवेत्, वर्द्धयन्ति, आसीत्, पतेत्, कुर्वन्ति, आगच्छत, कुर्याम्
(ଭବେତ, ବର୍ଷୟନ୍ତ, ଆସୀତ, ପତେତ, କୁର୍ବନ୍ତ, ଆଗଛତ, କୁର୍ଯାମ୍)
शब्दार्थ:
- शिखरम् – अग्रम्
ଶିଖରମ୍ – ଅଗ୍ରମ୍ ( ଅଗ୍ରଭାଗକୁ) - पादम् – मूलभागम्
ପାଦମ୍ – ମୂଳଭାଗମ୍ (ମୂଳଭାଗ) / ଏକଚତୁର୍ଥାଂଶ - प्रयास: – उद्यम:, परिश्रम:
ପ୍ରୟାସ – ଚେଷ୍ଟା, ପରିଶ୍ରମ - चकिता: – विस्मता:
ଚକିତା – ବିସ୍ମିତଃ – ଆଶ୍ଚର୍ଯ୍ୟାନ୍ବିତ