Odisha State Board BSE Odisha 8th Class Hindi Solutions Chapter 10 ताजमहल की आत्मकहानी (आत्मकथा)Textbook Exercise Questions and Answers.
BSE Odisha Class 8 Hindi Solutions Chapter 10 ताजमहल की आत्मकहानी (आत्मकथा)
1. निम्नलिखित प्रश्नों के उत्तर दीजिए :
(क) ताजमहल क्यों गर्व से फूला नहीं समाता ?
उत्तर:
ताजमहल कहता है कि जिसने मुझे बनवाया है, वह मेरी गोद में सो रहा है । जिसके उद्देश्य से मुझे बनवाया गया था, वह मेरी गोद में सो रही है ।अर्थात् ताजमहल में बादशाह शाहजहाँ और बेगम मुमताज दोनों दफनाए गए। ताजमहल उन दोनों का स्नेह पाकर गर्व से फूला नहीं समाता ।
![]()
(ख) ताजमहल क्या संकेत कर रहा है ?
उत्तर:
ताजमहल में सम्राट शाहजहाँ और सम्राज्ञी मुमताज दोनों की समाधियाँ हैं । यह उनकी प्रेम – समाधि है । प्रेम के कारण मौत केंबाद उन दोनों के बिछुड़े हुए हृदय फिर से जुड़े हुए हैं । भेद-भाव में पड़े मनुष्यों को ताजमहल संकेत कर रहा है कि प्रेम ईशरीय सृष्टि की सबसे बड़ी विभूति है ।
(ग) ताज भौतिक ऐश्वर्य का स्मारक नहीं, अपितु प्रेम का समारक है, कैसे ?
उत्तर:
ताजमहल में बहुमूल्य जवाहरात भरे थे।अत्याचारियों ने उन्हें लूट लिया । उन्होंने भौतिक वैभव तो लूट लिया पर इसके अंदर छिपे दो हृदयों के प्रेम के वैभव को लूटने का साहस वे जुटा नहीं सके ।प्रेम की लौ के सामने उनकी आँखें खुली न रह सकीं। आँखें चौंधिया गई ।
(घ) यमुना के साथ ताजमहल का कैसा संबंध है ?
उत्तर:
ताजमहल यमुना के किनारे खड़ा है । वे दोनों पुराने साथी हैं । यमुना ताजमहल के अतीत-वैभव के स्वर्णिम दिनों की याद कर दु: ख से सूख रही है । वह श्यामा हो गई है । ताजमहल को यमुना से स्वाभाविक रूप से स्नेह है । यमुना हिलोरें लेकर ताजमहल को प्यार करती है, अपनी सुनाती है, उसकी सुनती है ।
![]()
(ङ) वास्तविकता का अद्वितीय उदाहरण ताजमहल है, क्यों?
उत्तर:
ताजमहल वास्तविकता का अद्वितीय उदाहरण है । क्योंकि इसका निर्माण श्वेत संगमरमर से हुआ है 1 इसके निर्माण में करोड़ों रुपये खर्च हुए । हजारों कारींगरों ने इसे बनाने के लिए वर्षों तक परिश्रम किया । इसे देखने देश विदेश से यात्री आते हैं । दुनिया के महान आश्चयों में इसकी गणना की जाती है ।
(च) विदेशी ताजमहल को देखकर क्या करते हैं ?
उत्तर:
ताजमहल की दुनिया के आश्चयों में गणना की जाती है । इसलिए इसे देखने सुदूर विदेशी यात्री आते हैं । वे ताजमहल को देखकर अपना आना सार्थक समझते हैं । वे श्रद्धा से ताज़महल के सामने झुक जाते हैं ।
(छ) लोग ताजमहल को देखकर कैसी कल्पना करते हैं ?
उत्तर:
ताजमहल की नींव में वियोगी सम्राट शाहजहाँ के दो बूँद आँसू गिर पड़े थे । लोग कल्पना करते हैं कि आकाश का हृदय भी उन आँसूओं की स्मृति में द्रवीभूत हो उठता है और दो बूँद आँसुओं से ताजमहल के हुदय को सींचने का प्रतिवर्ष प्रयास करता है।
![]()
(ज) ताजमहल का हुदय क्यों विदीर्ण हो रहा है ?
उत्तर:
मानव-समाज की वर्वरता देखकर ताजमहल क्षुक्ध हो उठता है । भारत की असहाय अवस्था देखकर उसे दु:ख होता है । सम्राट और सम्राजी भी भारत की दुर्दशा देखकर दु:खी हैं । तांजमहल को लगता है कि यदि यही अवस्था रही तो वह दु:ख के बोझ से ढह जाएगा । इसलिए उसका हृदय विदीर्ण हो रहा है ।
2. निम्न प्रश्नों के उत्तर एक या दो वाक्यों में दीजिए ।
(क) ताजमहल की गोद में कौन-कौन सो रहे हैं ?
उत्तर:
ताजमहल की गोद में बादशाह शाहजहाँ और बेगम मुमताज दोनों सो रहे हैं ।
(ख) शताब्दियाँ बीत गई, पर ताजमहल में क्या चीज सुरक्षित है ?
उत्तर:
शताब्दियाँ बीत गई पर ताजमहल में शाहजहाँ और मुमताज के स्नेह का वैभव आज भी सुरक्षित है ।
![]()
(ग) ताज महान् आश्चर्य क्यों बन गया है ?
उत्तर:
ताज में सुरक्षित शाहजहाँ और मुमताज के स्नेह के वैभव को संसार न जाने कब से विस्मय-विमुख्ध होकर देख रह्मा है । इसलिए यह दुनिया का महान आश्चर्य बन गया है ।
(घ) ताज किनका स्मारक है ?
उत्तर:
ताज शाहजहाँ और मुमताज के प्रेम का स्मारक है ।
(ङ) अत्याचारियों ने क्या किया ?
उत्तर:
अत्याचारियों ने ताजमहल के आभूषणों, रत्नों, और जवाहरातों को लूट लिया और ताजमहल के शरीर को नग्न कर दिया|
(च) ताज के अंदर कौन-सा वैभव छिपा पढ़ा है ?
उत्तर:
ताज के अंदर ईश्शरीय सृष्टि का सबसे बड़ा वैभव प्रेम छिपा पड़ा है ।
![]()
(छ) आकाश ताजमहल को क्या करता है ?
उत्तर:
आकाश का हृदय शाहजाहाँ के दो बूँद आँसुओं की स्मृति में द्रवीभूत हो उठता है और वह दो बूँद आँसुओं से ताजमहल के हृदय को सींचने का प्रयास करता है ।
(ज) यमुना क्यों सूख रही है ?
उत्तर:
यमुना ताजमहल के अतीत वैभव के स्वर्णिम दिनों को याद करके दु:ख से सूख रही है ।
(ङ्ञ) ताज क्यों मुस्करा उठता है ?
उत्तर:
अपने संबंध में विदेशों से आए यात्रियों की धारणा को देख ताज मुस्करा उठता है ।
(ज) ताजमहल को किसीसे कोई प्रतिद्वन्दूता क्यों नहीं है ?
उत्तर:
ताजमहल की दुनिया के महान आशयों में गणना की जाती है, इसलिए उसे किसी से कोई प्रतिद्वन्द्रिता नहीं है
(ट) ताजमहल क्या चाहता है ?
उत्तर:
ताजमहल चाहता है कि उससे प्रेम का पाठ लेकर भारतवासी एक सूत्र में बँध जाएँ और अपने देश का कल्याण करें।
3. सही विकल्प चुनकर लिखिए :
(क) कौन गर्व से फूला नहीं समाता ?
(i) शाहजहाँ
(ii) ताजमहल
(iii) मुमताज
(iv) देशवासी
उत्तर:
(ii) ताजमहल
![]()
(ख) ताजमहल क्या है ?
(i) मंदिर
(ii) मस्जिद
(iii) प्रेम-समाधि
(iv) श्रेष्ठमहल
उत्तर:
(iii) प्रेम-समाधि
(ग) में भौतिक एश्वर्य का स्मारक नहीं, प्रेम का स्मारक हूँ, कौन कहता है ?
(i) शाहाजहाँ
(ii) अकबर
(iii) मुमताज
(iv) ताजमहल
उत्तर:
(iv) ताजमहल
(घ) ताजमहल के निर्माण में कितने रुपए व्यय हुए ?
(i) एक लाख
(ii) करोड़ों
(iii) पाँच हुजार
(iv) दस लाख
उत्तर:
(ii) करोड़ों
(ङ) कौन अपनी तुलिका से ताजमहल को अमर करना चाहता है ?
(i) लेखक
(ii) कवि
(iii) नाककार
(iv) चित्रकार
उत्तर:
(iv) चित्रकार
![]()
4. एक-एक शब्द में उत्तर दीजिए :
(क) ‘ताजमहल की आत्म कहानी’ के लेखक कौन हैं?
उत्तर: गुलाबराय
(ख) दुनिया के महान आर्थों में किसकी गणना की जाती है?
उत्तर: ताजमहल
(ग) ताजमहल किसकी प्रेम-समाधि है ?
उत्तर: सम्राट शाहजहाँ और सम्राजी मुमताज
(घ) ताजमहल कहाँ खड़ा है ?
उत्तर: यमुना के किनारे
(ङ) कौन एक सूत्र में बँधकर अपने देश का कल्याण करें?
उत्तर: भारतव्रासी
भाषा ज्ञान
1. कर्ता और क्रिया का संबंध लिंग और वचन दोनों से प्रभावित है । इन उदाहरणों को देखिए :
सम्राट सो रहा है ।
सम्राज़ी सो रही है ।
शताब्दियाँ बीत गई ।
ऐश्र्वर्य के दिन बीत गए।
सही कर्त्ता याक्रिया-पदों द्वारा रिक्त स्थानों को पूरा कीजिए-
उत्तर:
![]()
2. इन पदबंधों को देखिए —
शब्द वाक्यों में प्रयुक्त हो तो पद कहलाते हैं । पदों के समूह को पदबंध कहते हैं ।
(क) अपना अंक – अपने अंक में
मेरी गोद – मेरी गोद में
मेरे आभूषण – मेरे आभूषणों को
मेरा निर्माण – मेरे निर्माण में
आप कुछ ऐसे पदबंध बनाइए :
उत्तर:
- यमुना का किनारा – युमना के किनारे पर
- आगरा का स्नेह – आगरा के स्नेह को
- योगी की समाधि- योगी की समाधि की
- अपनी स्मृतियाँ – अपनी स्मृतियों को
- उनका मनोभाव – उनके मनोभाव को
- उनकी धारणाएँ – उनकी धारणाओं को
- समाज की वर्वरता – समाज की वर्वरता को
- सिनेमा का पट – सिनेमा के पट पर
- अपनी तूलिका – अपनी तूलिका से
- अपनी रचना – अपनी रचना में
(ख) स्नेह का वैभव — मुमजात की प्रेम-समाधि
तल्लींनता का स्मारक — आदमियों के पेट
सम्राट के आँसू — यमुना की लहरें
मेरी माता — मेरे पिताजी
मेरा घर — उनकी कैंची
तुम्हारी साइकिल — तुम्हारा बाग
मेरे बच्चे — गाय के बछड़े
एक थैले के चट्टे-बट्टे
आप कुछ पदबंध लिखिए । उनमें संबंध विभक्ति के प्रयोगों को ध्यान से देखिए ।
- अपना कल्याण — दुःख का बोझ
- मेरी गोद — दुःख का बोझ
- कर्त्तव्य की देवी — भारत की अवस्था
- मेरा साथी — मुमताज की इच्छा
- देश का कल्याण — बनाने का प्रयत्न
- उसकी इच्छा — अपनी रचना
- उसकी कंब्र — प्रेम का पाठ
- संजोने का प्रयास — योगी की समाधि
- मेरा हृदय — यमुना का किनारा
- देवी की बात — आँसुओं की स्मृति
![]()
(ग) सही विभक्ति लगाकर रिक्त स्थानों को भरिए :
(i) शाहजहाँ ने मुझे खड़ा किया ।
(ii) कस्तूरबा को सभी माताजी कहते थे ।
(iii) उनके अप्रमित स्नेह को पाकर में फूला नहीं समाता
(iv) इस असहाय अवस्था से मेरा हृदय क्षुब्ध है ।
(v) श्वेत संगमरमर से मेरा निर्माण हुआ है ।
(vi) मैं गर्व से फूला नहीं समाता ।
(vii) घोबी को कपड़े वे दो ।
(viii) यात्री की आँखों से आँसू टपक पड़े ।
(ix) जाने कब से देख रहा है ।
(x) हजारों का पेट भरा ।
(xi) यमुना के किनारे खड़ा हूँ ।
(xii) मेरी नींव में वियोगी सम्राट के दो बूँद आँसू गिर पड़े थे।
(xiii) मुझे उस पर स्वाभाविक स्नेह है ।
3. इन पदबंधों को देखिए –
‘क’ विभाग के शब्दों के पर्यायवाची शब्द ‘ख’ विभाग में दि, गए हैं। उनका मिलान कीजिए।
(क) विधाता, अंक, वैभव, संदेश, प्रयास, भौतिक; अस्तित्व
(ख) समाचार, गौद, चेष्टा, सांसारिक, ब्रह्मा, संपत्ति, सत्ता
उत्तर:
‘क’ विभाग – ‘ख़’ विभाग
- विधाता – ब्रहमा
- अंक – गोद
- वैभव – संपति
- संदेश – समाचार
- प्रयास , – चेष्टा
- भौतिक – सांसारिक
- अस्तित्व – सत्ता
4. निम्नलिखित शब्दों के स्त्रीलिंग रूप लिखिए ।
विधाता, सम्राट, बावला, बादशाह, योगी
उत्तर:
- विधाता – जद्मदात्री
- सम्राट – सम्राज्ञी
- बावला – बावली
- बादशाह – बेगम
- योगी – योगिन
5. उदाहरणों के अनुसार शब्दों के बहुवचन रूप लिख़िए।
शताब्दी – शताब्दियाँ
आँख – आँखें
उत्तर:
- स्मृति – स्मृतियाँ
- नदी – नदियाँ
- माली – माली
- गाड़ी – गाड़ियाँ
- रानी – रानियाँ
- बूँद – बूँदें
- भूल – भूलें
- चाह – चाहें
- साँस – साँसें
‘काला घोड़ा’। इसमें ‘काला’ घोड़े का रंग या एक विशेषता बताता है। इसे विशेषण कहते हैं। इस पाठ में आए निम्नलिखित शब्द-युग्मों पर ध्यान दीजिए।
अपनी वीरता, राजपुती शान, जख्मी राणा, अनगिनत सैनिक, उसकी फौज, हमारी लड़ाई, कई चोटें, बड़ी फुर्ति, विशाल सेना, चुटकी भर धूल।
![]()
इनमें से प्रथम शब्द विशेषण हैं। ये दूसरे शब्दों की विशेषताएँ बताते हैं। ये हैं: अपनी, राजपुती, जख्मी, अनगिनत, उसकी, हमारी, कई, बड़ी, विशाल, चुटकी भर ।
6. निम्नलिखित संज्ञाओं के विशेषण – रूप लिखिए । सुरक्षा, ईश्वर, तल्लीनता, क्षुब्धता, प्रतिष्ठा, प्रेम, भारत, बर्बरता, विदेश, वास्तविकता, स्वर्ण, योग ।
उत्तर:
- सुरक्षा – सुरक्षित
- ईश्चर – ईश्वरीय
- तल्लीनता – तल्लीन
- क्षुब्धता – क्षुब्ध
- प्रतिष्ठा – प्रतिष्ठित
- प्रेम – प्रेमी
- भारत – भारतीय
- बर्बरता – बर्बर
- विदेश – वैदेशिक
- वास्तविकता – वास्तविक
- स्वर्ण – स्वर्णिम
- योग – यौगिक
7. निम्नलिखित वाक्यों में से विशेषणों को छाँटिए।
(क) हृदय स्मृति में द्रवीभूत हो उठता है ।
उत्तर: द्रवीभूत
(ख) प्रेम ईश्चरीय सृष्टि की विभूति है ।
उत्तर: ईश्चरीय
(ग) दो बूँद आँसू चू पड़े थे ।
उत्तर: दो
(घ) अप्रतिम स्नेह पाकर मैं गर्व से फूला नहीं समाता ।
उत्तर: अप्रतिम
(ङ) मेरा हृदय विदीर्ण होता जा रहा है ।
उत्तर: मेरा
![]()
एक-एक वाक्य में उत्तर वीजिए :
प्रश्न 1.
ताजमहल के विधाता कौन हैं ?
उत्तर:
ताजमहल के विधाता सम्राट शाहजहाँ हैं ।
प्रश्न 2.
ताजमहल किसके लिए खढ़ा किया गया ?
उत्तर:
ताजमहल सम्राजी मुमताज के लिए खड़ा किया गया।
प्रश्न 3.
ताजमहल में आज भी क्या सुरक्षित है ?
उत्तर:
ताजमहल में आज भी सम्राट शाहजहाँ और सम्राजी मुमताज के स्नेह का वैभव सुरक्षित है।
प्रश्न 4.
सप्राट और सम्राजी के स्नेह-वैभव को संसार कैसे देख रहा है ?
उत्तर:
सम्राट और सम्राजी के स्नेह-वैभव को संसार विस्मयविमुग्ध होकर देख रहा है ।
प्रश्न 5.
ताजमहल की गणना किसमें की जाती है ?
उत्तर:
ताजमहल की गणना दुनिया के महान आश्चयों में की जाती है ।
प्रश्न 6.
ताजमहल किनकी प्रेम-समाधि है ?
उत्तर:
ताज़महल सम्राट शाहजहाँ और सम्राजी मुमताज की प्रेम-समाधि है।
प्रश्न 7.
ताजमहल किसका स्मारक है ?
उत्तर:
ताजमहल प्रेम की पवित्रता और तल्लीनता का स्मारक है।
![]()
प्रश्न 8.
आज मनुष्य किस में पड़े हुए हैं ?
उत्तर:
आज मनुष्य भेद-भाव में पड़े हुए हैं ।
प्रश्न 9.
ताजमहल भेद-भाव में पड़े मनुष्यों को क्या संकेत् कर रहा है ?
उत्तर:
ताजमहल भेद-भाव में पड़े मनुष्यों को संकेत कर रहा है कि प्रेम ईश्वरीय सृष्टि की सबसे वड़ी विभूति है ।
प्रश्न 10.
अत्याचारियों ने ताजमहल के प्रति कैसा व्यवहार किया?
उत्तर:
अत्याचारियों ने ताजमहल पर समय-समय पर आक्रमण किया और उसे लूट लिया।
प्रश्न 11.
लोग ताज़महल से क्या ले गए ?
उत्तर:
लोग ताजमहल से उसके आभूषणों, रत्नों और जवाहरातों को ले गए।
प्रश्न 12.
अत्याचारियों को ताजमहल से क्या लूटने का साहस नहीं हुआ है ?
उत्तर:
अत्याचारियों को ताजमहल के अंदर जो वैभव छिपा पड़ा है, जो दो हृदय जुड़े पड़े हैं, उन्हें लूटने का साहस नहीं हुआ।
प्रश्न 13.
प्रेम की लौ के सामने अत्याचारियों की स्थिति क्या हुई?
उत्तर:
प्रेम की लौ के सामने अत्याचारियों के आँखें खुली नहीं रह सकीं।
प्रश्न 14.
ताजमहल किसका समारक नहीं है ?
उत्तर:
ताजमहल भौतिक ऐश्वर्य का स्मारक नहीं है ।
प्रश्न 15.
ताजमहल की नींवं में क्या चू पड़े थे ?
उत्तर:
ताजमहल की नींव में वियोगी सम्राट के दो बूँद आँसू चू पड़े थे।
![]()
प्रश्न 16.
आकाश पर वियोगी सम्राट के आँसूओं का प्रभाव कैसा पड़ता है ?
उत्तर:
सम्राट के आँसूओं की स्मृति में आकाश का हृदय द्रवीभूत हो उठता है ।
प्रश्न 17.
आकाश का हुदय प्रतिवर्ष क्या करता है ?
उत्तर:
आकाश का हृदय प्रतिवर्ष दो बूँद आँसूओं से ताजमहल के हृदय को सींचने का म्रयास करता हैं ।
प्रश्न 18.
आकाश के ह्नय के आँसू कहीं पहुँच जाते हैं ?
उत्तर:
आकाश के ह्यय के आँसू ताजमहल के हुदय तक पहुँच जाते हैं।
प्रश्न 19.
ताजमहल किस पर विश्वास नहीं करता ?
उत्तर:
त्मजमहल कल्पना-जगत के विश्वासों पर विश्वास नहीं करता।
प्रश्न 20.
ताजमहल का कलेवर कैसे निखर उठता है ?
उत्तर:
ताजमहल का कलेवर आकाश के हृदय के आँसूओं से निखर उठता है ।
प्रश्न 21.
ताजमहल किस नदी के किनारे स्थित है ?
उत्तर:
ताजमहल यमुना नदी के किनारे स्थित है ।
प्रश्न 22.
ताजमहल किस शहर में है ?
उत्तर:
ताजमहल आगरा शहर में है।
प्रश्न 23.
ताजमहल किसका स्नेह नहीं भूल सकता है ?
उत्तर:
ताजमहल आगरा का स्नेह नहीं भूल सकता ।
प्रश्न 24.
ताजमहल किसकी समाधि की तरह है ?
उत्तर:
ताजमहल योगी की समाधि की तरह है ।
प्रश्न 25.
ताजमहल योगी की समाधि की तरह क्या करने का प्रयास करता है ?
उत्तर:
ताजमहल योगी की समाधि की तरह यमुना के किनारे अपनी स्मृतियों को संजोग का प्रयास कर रह्म है।
प्रश्न 26.
यमुना क्यों सूख रही है ?
उत्तर:
यमुना ताजमहल के अतीत-वैभव के स्वर्णिम दिनों को याद करके दु: ख से सूख रही है ।
प्रश्न 27.
यमुना का रंग क्य्या हो गया है ?
उत्तर:
यमुना का रंग श्याम हो गया है ।
![]()
प्रश्न 28.
ताजमहल किसे अपना पुरान साथी बता रहा है ?
उत्तर:
ताजमहल यमुना को अपना पुराना साथी बता रहा है ।
प्रश्न 29.
यमुना ताजमहल को कैसे प्यार करती है ?
उत्तर:
यमुना ताजमहल को हिलोरें लेकर प्यार करती है ।
प्रश्न 30.
वास्तविकता का अद्वितीय उदाहरण कौन है ?
उत्तर:
ताजमहल वास्तविकता का अद्वितीय उदाहरण है।
प्रश्न 31.
किस पत्थर से ताजमहल बना है ?
उत्तर:
श्वेत संगमरमर से ताजमहल बना है ।
प्रश्न 32.
ताजमहल को बनवाने में कितने रुपए व्यय हुए ।
उत्तर:
ताजमहल को बनवाने में करोड़ों रुपए व्यय हुए।
प्रश्न 33.
किसकी ताजमहल बनवाए जाने की इच्छा थी ?
उत्तर:
मृत्यु-शय्या पर अंतिम साँस गिनती हुई मुमताज की ताजमहल बनबाए जाने की इच्छा थी ।
प्रश्न 34.
मुमताज की अंतिम इच्छा का परिणाम क्या हुआ ?
उत्तर:
मुमताज की अंतिम इच्छानुसार उसकी बेजोड़ कब्र अस्तित्व में आई ।
प्रश्न 35.
कब्र अपने को क्यो अभागी नहीं मानती?
उत्तर:
कब्र अपने को अभागी नहीं मानती, क्योंकि रात-दिन इसे देखने बहुत-से लोग आते हैं।
प्रश्न 36.
सुदूर विदेशों-से यात्री क्यों अपना आना सार्थक समझते हैं ?
उत्तर:
सुदूर विदेशों-से यात्री ताजमहल को देखकर अपना आना सार्थक समझते हैं।
प्रश्न 37.
ताजमहल के पास आकर यात्री क्या करते हैं ?
उत्तर:
ताजमहल के पास आकर यात्री श्रद्धा से झुक जाते हैं।
प्रश्न 38.
यात्री जब पास आते हैं, तो ताजमहल को कौन-सा अवसर मिलता है ?
उत्तर:
यात्री जब पासआते हैं, तो ताजमहल को उनके मनोभावों को पढ़ने का अवसर मिलजाता है ।
![]()
प्रश्न 39.
ताजमहल क्यों मुस्करा उठता है ?
उत्तर:
ताजमहल अपने संबंध में यात्रियों की धारणाओं को देखकर मुस्करा उठता है ।
प्रश्न 40.
मुग्राल साम्राज्य के कौन-से दिन बीत गए ?
उत्तर:
मुगल साम्राज्य के ऐश्वर्य के दिन बीत गए।
प्रश्न 41.
ताजमहल का पाष्ण-हुदय क्यों क्षुब्ध हो उठा है ?
उत्तर:
मानव-समाज की वर्वरता को देखकर ताजमहल का पाषण हृदय क्षुब्ध हो उठा है ।
प्रश्न 42.
क्या देखकर ताजमहल को आज दु:ख हो रहा है ?
उत्तर:
भारत की असहाय अवस्था को देखकर ताजमहल को आज दु:ख हो रहा है ।
प्रश्न 43.
लोग क्यों ताजमहल के चित्र उतारते हैं ?
उत्तर:
लोग सिनेमा के पट पर ताजमहल की छवि अंकित करने के लिए उसके चित्र उतारते हैं ।
प्रश्न 44.
कौन अपनी तूलिका में वाजमहल को अमर करना चाहता है ?
उत्तर:
चित्रकार अपनी तूलिका में ताजमहल को अमर करना चाहता है ।
प्रश्न 45.
कवि ताजमहल के संबंध में क्या प्रयत्म करता हैं ?
उत्तर:
कवि अपनी रचना में ताजमहल को चिरजीवी बनाने का प्रयत्न करता है ।
प्रश्न 46.
सम्राट और सम्राजी क्यों म्लान हो रहे हैं ?
उत्तर:
सम्राट और सम्राज्ञी अपने भारत की इस दुरवस्था को देखकर म्लान हो रहे हैं।
प्रश्न 47.
ताजमहल क्यों डरता है कि वह आज नहीं तो कल बह जाएगा ?
उत्तर:
ताजमहल डरता है कि अगर भारत की यह दुरवस्था रही तो दु:ख के बोझ से वह आज नहीं तो कल ढह जाएगा।
प्रश्न 48.
ताजमहल क्या चाहता है ?
उत्तर:
ताजमहल चाहता है कि उससे, प्रेम का पाठ लेकर भारतवासी एक सूत्र में बंध जाएँ और अपने देश का कल्याण करें।
प्रश्न 49.
इस युग में ताजमहल का सच्चा साथी कौन है ?
उत्तर:
इस युग में अगा खाँ महल ताजमहल का सच्चा साथी है।
प्रश्न 50.
कस्तूरबा को कहाँ समाधि दी गई है ?
उत्तर:
अगा खाँ महल में कस्तूरबा को समाधि दी गई है।
![]()
प्रश्न 51.
प्रेम की देवी की समाधि कहाँ है ?
उत्तर:
प्रेम की देवी की समाधि ताजमहल में है।
प्रश्न 52.
कर्त्तव्य की देवी की समाधि कहाँ है ?
उत्तर:
कर्त्तव्य की देवी की समाधि अगा खाँ महल में है।
प्रश्न 53.
मानवता अपना कल्याण कैसे करेगी ?
उत्तर:
प्रेम और कर्त्तव्य के संदेश को ले कर मानवता अपना कल्याण करेगी।
एक या दो शब्द में उत्तर दीजिए :
प्रश्न 1.
‘ताजमहल की आत्म-कहानी’ पाठ के लेखक कौन हैं?
उत्तर:
गुलाब राय
प्रश्न 2.
ताजमहल ने किसे अपनी विधाता कहा है ?
उत्तर:
सम्राट शाहजहाँ को
प्रश्न 3.
ताजमहल की गोद में कौन-कौन सो रहे हैं ?
उत्तर:
सम्राट शाहजहाँ और सम्राज्ञी मुमताज महल
प्रश्न 4.
संसार विस्मय-विमुग्ध होकर क्या देख रहा है ?
उत्तर:
स्नेह का वैभव
प्रश्न 5.
दुनिया में ताजमहल की गणना किस रूप में होती है ?
उत्तर:
महान आश्चर्यों में
प्रश्न 6.
कौन अपने को प्रेम-समाधि कहता है ?
उत्तर:
ताजमहल
प्रश्न 7.
ताजमहल किसका समारक है ?
उत्तर:
प्रेम की पवित्रता और तल्लीनता का
![]()
प्रश्न 8.
ईश्वरीय सुष्टि की सबसे बड़ी विभूति कौन है ?
उत्तर:
प्रेम
प्रश्न 9.
नृशंस अत्याचारी क्या लूटने का साहस नहीं कर सके?
उत्तर:
प्रेम का वैभव
प्रश्न 10.
ताजमहल की नींव में किसके आँसू चू-पड़े थे ?
उत्तर:
वियोगी सम्राट के
प्रश्न 11.
किसका हृदय उन आँसुओं की स्मृति में द्रवीभूत हो उठता है ?
उत्तर:
आकाश का
प्रश्न 12.
आकाश आँसुओं से किसका द्वदय सींचता है ?
उत्तर:
ताजमहल का
प्रश्न 13.
आकाश के आँसुओं से क्या निखर उठता है ?
उत्तर:
ताजमहल का शरीर
प्रश्न 14.
ताजमहल किसके किनारे पर है ?
उत्तर:
यमुना के
प्रश्न 15.
ताजमहल क्या नहीं भूल सकता ?
उत्तर:
आगरा का स्नह
प्रश्न 16.
यमुना क्या याद करके दु:खी होती है ?
उत्तर:
ताजमहल के स्वर्णिम दिनों को
![]()
प्रश्न 17.
यमुना क्यों श्यामा हो गई ?
उत्तर:
दु:ख से
प्रश्न 18.
यमुना ताजमहल को कैसे प्यार करती है ?
उत्तर:
हिलोरें लेकर
प्रश्न 19.
ताजमहल किस पत्थर से बना है ?
उत्तर:
संगमरमर
प्रश्न 20.
ताजमहल के निर्माण में कितना समय लगा ?
उत्तर:
एक युग से अधिक
प्रश्न 21.
मुमताज की अंतिम इच्छा क्या थी ?
उत्तर:
उनके लिए बेजोड़ कब्र बनवाना
प्रश्न 22.
ताजमहल का पाषाण हृदय क्या देखकर रो उठता है ?
उत्तर:
मानव-समाज की वर्वरता
प्रश्न 23.
सम्राट भी क्या देखकर म्लान हो रहे हैं ?
उत्तर:
भारत की दुरवस्था
प्रश्न 24.
भारत की दुरवस्था रहने से ताजमहल को क्या डर है?
उत्तर:
ढह जाने का
प्रश्न 25.
भारतवासी ताजमहल से किसका पाठ लें ?
उत्तर:
प्रेम का
प्रश्न 26.
प्रेम का पाठ लेकर भारतवासी किसमें बँध जाएँगे ?
उत्तर:
एक सूत्र में
![]()
प्रश्न 27.
ताजमहल का सच्चा साथी कौन है ?
उत्तर:
आगा खाँ महल
प्रश्न 28.
अगा खाँ महल की गोद में कौन सोई है ?
उत्तर:
कस्तूरबा
प्रश्न 29.
ताजमहल की गोद में कौन है ?
उत्तर:
प्रेम का देवी
प्रश्न 30.
अगा खाँ महल की गोद में कौन है ?
उत्तर:
कर्त्तव्य की देवी
मातृभाषा में अनुवाद कीजिए :
प्रश्न 1.
अपने विधाता को मैं अपने अंक में लिए बैठा हूँ।
उत्तर:
ମୋ ବିଧାତାଙ୍କୁ ମୁଁ ମୋ କୋଳରେ ଧରିବସିଛି।
प्रश्न 2.
जिसने मुझे खड़ा किया वही मेरी गोद में सो रहा है।
उत्तर:
ଯିଏ ମୋତେ ଠିଆକଲେ ସେ ହିଁ ମୋ କୋଳରେ ଶୋଇଛନ୍ତି ।
![]()
प्रश्न 3.
जिसके लिए मैं खड़ा किया गया, वह तो मेरी गोद में सो रही है ।
उत्तर:
ଯାହାପାଇଁ ମୋତେ ଠିଆକରାଗଲା, ସେ ତ ମୋ କୋଳରେ ଶୋଇଛି ।
प्रश्न 4.
उनके इस अप्रतीम स्नेह को पाकर में गर्व से फूला नहीं समाता।
उत्तर:
ସେମାନଙ୍କର ଏହି ଅପ୍ରତୀମ ସ୍ନେହ ପାଇ ମୁଁ ଗର୍ବରେ ବହୁତ ଖୁସି ହୋଇଯାଉଛି।
प्रश्न 5.
शताब्दियाँ बीत गईं,पर उनके स्नेह का वैभव आज भी मुझ में सुरक्षित है ।
उत्तर:
ଅନେକ ଶତାବ୍ଦୀ ବିତିଗଲାଣି; କିନ୍ତୁ ସେମାନଙ୍କର ସ୍ନେହର ବୈଭବ ଆଜି ମଧ୍ୟ ମୋ ଭିତରେ ସୁରକ୍ଷିତ ରହିଛି।
प्रश्न 6.
प्रेम की पवित्रता और तल्लीनता का में स्मारक हैं ।
उत्तर:
ମୁଁ ପ୍ରେମର ପବିତ୍ରତା ଓ ନିମଗ୍ନତାର ସ୍ମାରକ ।
प्रश्न 7.
भेद-भाव में पड़े मनुष्यों को में यह संकेत कर रहा हैं।
उत्तर:
ଭେଦ-ଭାବରେ ପଡ଼ିଯାଇଥିବା ମନୁଷ୍ୟମାନଙ୍କୁ ମୁଁ ଏଇୟା ସୂଚେଇଦେଉଛି।
प्रश्न 8.
प्रेम ईश्वरीय सृष्टि की सबसे बड़ी विभूति है ।
उत्तर:
ପ୍ରେମ ଈଶ୍ବରଙ୍କ ସୃଷ୍ଟିରେ ସବୁଠାରୁ ବଡ଼ ବିଭୂତି ।
प्रश्न 9.
दो बिछड़े हुए हुदय मेरी गोद में जुड़े हुए हैं ।
उत्तर:
ଦୁଇଟି ଅଲଗା ହୋଇଯାଇଥିବା ହୃଦୟ ମୋରି କୋଳରେ ଏକାଠି ହୋଇଛନ୍ତି ।
![]()
प्रश्न 10.
मेरे आभूषणों रत्नों और जवाहरातों को लोग ले गए।
उत्तर:
ମୋ ଅଳଙ୍କାର ଓ ରତ୍ନ ସମୂହକୁ ଲୋକେ ନେଇଗଲେ।
प्रश्न 11.
प्रेम की लौ के सामने उनकी आँखें खुली नहीं रह सकीं।
उत्तर:
ପ୍ରେମର ଅଗ୍ନିଜ୍ୱାଳା ସମ୍ମୁଖରେ ସେମାନେ କୌଣସି କ୍ଷତି କରିବାକୁ ସାହସ କରି ପାରିଲେ ନାହିଁ ।
प्रश्न 12.
मेरी नींव में उस वियोगी सम्राट के दो बूँद आँसू चू पड़े थे।
उत्तर:
ମୋ ମୂଳଦୁଆରେ ସେହି ବିୟୋଗୀ ସମ୍ରାଟଙ୍କର ଦୁଇବୁନ୍ଦା ଲୁହ ଝରିପଡ଼ିଥିଲା ।
प्रश्न 13.
पर मेरे हुदय तक उसके सभी आँसू पहुँच जाते हैं ।
उत्तर: କିନ୍ତୁ ମୋ ହୃଦୟ ପର୍ଯ୍ୟନ୍ତ ତାଙ୍କର ସବୁତକ ଲୁହ ପହଞ୍ଚାଯାଏ ।
प्रश्न 14.
उसके आँसुओं के तो मेरा कलेवर भी निखर उठता है।
उत्तर: ତାଙ୍କ ଲୁହରେ ତ ମୋ ଶରୀର ମଧ୍ୟ ଉଜ୍ଜ୍ବଳ ହୋଇଉଠେ ।
प्रश्न 15.
यमुना के किनारे पर मै खड़ा हैं।
उत्तर: ଯମୁନା କୂଳରେ ମୁଁ ଠିଆହୋଇଛି ।
प्रश्न 16.
योगी की समाधि की तरह में आगरे में यमुना के किनारे अपनी स्मृतियों को संजोने का प्रयास करता हूँ ।
उत्तर:
ଯୋଗୀର ସମାଧ୍ ଭଳି ମୁଁ ଆଗ୍ରାରେ ଯମୁନା କୂଳରେ ମୋ ସ୍ମୃତିଗୁଡ଼ିକୁ ସୁରକ୍ଷିତ ରଖୁବା ପାଇଁ ଚେଷ୍ଟାକରୁଛି ।
प्रश्न 17.
बावली यमुना भी मेरे अतीत वैभव के स्वर्णिम दिनों को याद कर दु:ख से सूख रही है ।
उत्तर:
ପାଗଳୀ ଯମୁନା ମଧ୍ଯ ମୋ ଅତୀତ ବୈଭବରେ ସର୍ଷିମ ଦିନଗୁଡ଼ିକୁ ମନେପକେଇ ଦୁଖରେ ଶୁଖୁଯାଉଛି।
प्रश्न 18.
वह श्यामा हो गई है ।
उत्तर:
ସେ ଶ୍ୟାମଳୀ ହୋଇଯାଇଛି ।
प्रश्न 19.
वह हिल्लोरें लेकर मुझे प्यार करती है ।
उत्तर:
ସେ ତରଙ୍ଗାୟିତ ହୋଇ ମୋତେ ପ୍ରେମ କରୁଛି ।
![]()
प्रश्न20.
वह अपनी सुनाती है,मेरी सुनती है ।
उत्तर:
ସେ ତା’ କଥା ଶୁଣାଉଛି, ମୋ କଥା ଶୁଣୁଛି ।
प्रश्न 21.
श्वेत संगमरमर से मेरा निर्माण हुआ ।
उत्तर:
ଧଳା ଶଙ୍ଖ ମଲମଲ ପଥରରେ ମୁଁ ତିଆରି ହୋଇଛି
प्रश्न 22.
हजारों लोगों का पेट भरा ।
उत्तर:
ହଜାର ହଜାର ଲୋକ ପେଟ ପୋଷିଛନ୍ତି ।
प्रश्न 23.
एक युग में भी मेरा निर्माण-कार्य समाप्त न हो सका।
उत्तर:
ଗୋଟିଏ ଯୁଗ ଭିତରେ ମଧ୍ଯ ମୋର ନିର୍ମାଣକାର୍ଯ୍ୟ ସ୍ମନ୍ନ ହୋଇପାରିଲା ନାହିଁ ।
प्रश्न 24.
मृत्यु-शय्या पर अंतिम साँसें गिनती हुई मुमताज़ की यही तो अंतिम इच्छा थी
उत्तर:
ମୃତ୍ୟୁଶଯ୍ୟାରେ ଶେଷନ୍ନିଶ୍ବାସ ଗଣୁଥିବା ମମତାଜଙ୍କର ଏହା ହିଁ ତ ଅନ୍ତିମ ଇଚ୍ଛା ଥିଲା। .
प्रश्न 25.
उस स्वर्गीय देवी की बात शाहजहाँ कैसे टाल सकता था?
उत्तर:
ସେହି ସର୍ଗୀୟ ଦେବୀଙ୍କ କଥା ଶାହାଜାହାନ କିପରି ବା ଏଡ଼େଇଦେଇ ପାରିଥାଆନ୍ତେ !
प्रश्न 26.
इसीलिए तो उसकी इच्छानुसार उसकी यह बेजोड़ कब्र अस्तित्व में आई।
उत्तर:
ସେଇଥିପାଇଁ ତ ତାଙ୍କ ଇଚ୍ଛାନୁସାରେ ତାଙ୍କର ଏହି ଅଦ୍ବିତୀୟ କବର ଅସ୍ଥିତ୍ଵଲାଭ କଲା ।
प्रश्न 27.
रात-दिन इसे देखने न जाने कितने लोग आते हैं।
उत्तर:
ରାତିଦିନ ଏହାକୁ ଦେଖୁବାକୁ କେଜାଣି କେତେ ଲୋକ ଆସୁଛନ୍ତି ।
प्रश्न 28.
मेरे पास आकर उन्हें श्रद्धा से झुक जाना पड़ता है ।
उत्तर:
ମୋ ପାଖକୁ ଆସି ସେମାନେ ଶ୍ରଦ୍ଧାରେ ମୁଣ୍ଡ ନୁଆଇଁଦିଅନ୍ତି ।
प्रश्न 29.
अपने संबंध में उनकी धारणाओं को देख में मुस्करा उठता हैं ।
उत्तर:
ମୋ ବିଷୟରେ ସେମାନଙ୍କ ଧାରଣା ସବୁ ଦେଖୁ ମୁଁ ହସିପକାଏ।
![]()
प्रश्न 30.
मुगल साम्राज्य के ऐश्वर्य के दिन बीत गए।
उत्तर:
ମୋଗଲ ସାମ୍ରାଜ୍ୟର ଐଶ୍ବର୍ଯ୍ୟର ଦିନ ଚାଲିଯାଇଛି।
प्रश्न 31.
आज मेरा पाषण-हृदय भी क्षूब्य हो उठा है ।
उत्तर:
ଆଜି ମୋର ପାଷାଣ-ହୃଦୟ ମଧ୍ୟ ବ୍ୟର୍ଥାତ ହୋଇଯାଉଛି ।
प्रश्न 32.
लोग मेरे चित्र उतारते हैं ।
उत्तर:
ଲୋକମାନେ ମୋର ଚିତ୍ରସବୁ ଉଠାଉଛନ୍ତି ।
प्रश्न 33.
सम्राट और सम्राज्ञी भी अपने भारत की इस दुरवस्था को देखकर म्लान हो रहे हैं।
उत्तर:
ଯଦି ଏହି ଅବସ୍ଥା ରହିବ; ତେବେ ଦୁଖର ବୋଝରେ ମୁଁ ଆଜି ନୋହିଲେ କାଲି ଭାଙ୍ଗିପଡ଼ିବି ।
प्रश्न 34.
अगर यही अवस्था रही तो दु:ख के बोझ से मैं ढह जाऊँगा आज नही, कल सही।
उत्तर:
ମୁଁ ଚାହୁଁଛି ଯେ ମୋଠାରୁ ପ୍ରେମର ପାଠ ପଢ଼ି ଭାରତବାସୀ ଗୋଟିଏ ସୂତ୍ରରେ ବାନ୍ଧିହୋଇଯାଆନ୍ତୁ ଓ ନିଜ ଦେଶର କଲ୍ୟାଣ କରନ୍ତୁ ।
प्रश्न 35.
मैं चाहता हैं मुझसे प्रेम का पाठ लेकर भारतवासी एक सूत्र में बँध जाएँ और अपने देश का कल्याण करें।
उत्तर:
କସ୍ତୁରବା ତା’ରି କୋଳରେ ରହିଛି।
प्रश्न 36.
कस्तूरवा उसकी गोद में है ।
उत्तर:
କସ୍ତୁରବା ତା’ରି କୋଳରେ ରହିଛି।
प्रश्न 37.
मेरी गोद में प्रेम की देखी है ।
उत्तर:
ମୋ କୋଳରେ ପ୍ରେମର ଦେବୀ ରହିଛନ୍ତି।
![]()
प्रश्न 38.
मुझे विश्वास है, उस प्रेम और कर्तक्य के संदेश को लेकर मानवता अपना कल्याण करेगी ।
उत्तर:
ମୋର ବିଶ୍ୱାସ, ଏହି ପ୍ରେମ ଓ କର୍ତ୍ତବ୍ୟର ବାର୍ତ୍ତା ନେଇ ମାନବତା ନିଜର କଲ୍ୟାଣ କରିବ ।
सही उत्तर चूनिए :
प्रश्न 1.
अपने विधाता को में अपने अंक में लिए बैठा हैं – इस वाक्स में विधाता किसे कहा गया है ?
(A) शाइजहाँ
(B) नुमताज
(C) ताजमहल
(D) ब्रह्मा
उत्तर:
(A) शाइजहाँ
प्रश्न 2.
ताजमहल को किसने खाए किया ?
(A) मुमताज ने
(B) अंक्रेजों ने
(C) और बजेब ने
(D) शाहजहाँ ने
उत्तर:
(C) और बजेब ने
प्रश्न 3.
ताजमहल में किसकी समाधि/कर है ?
(A) सुमताज की
(B) शाहजाईँ की
(C) दोनों की
(D) किसी की नहीं
उत्तर:
(D) किसी की नहीं
प्रश्न 4.
दुनिया के महान् आश्चयों में किसकी गणना होती है?
(A) शीशमल की
(B) अगा खाँ महल की
(C) कुतुबमीनार
(D) ताजमाइल की
उत्तर:
(D) ताजमाइल की
![]()
प्रश्न 5.
ईश्वरीय सृष्टि की सबसे बती विभूति क्या है ?
(A) धर्म
(B) कर्म
(C) वाणी
(D) मेम
उत्तर:
(D) मेम
प्रश्न 6.
तृशंस अत्याचारी किसे लूट नहीं सके ?
(A) रल-वैभव
(B) संगमरमर की नवकाशी
(C) मेम-औरब
(D) ताजमहल की सुंदरता
उत्तर:
(C) मेम-औरब
प्रश्न 7.
ताजमहल किसका समारक है ?
(A) भौतिक ऐश्वर्य का
(B) प्रेमका
(C) रत्लों-जवाहरातें का
(D) मुग्ल कालीन स्थाफरय का
उत्तर:
(B) प्रेमका
प्रश्न 8.
ताजमहल के हाइय तक किसके सभी औसू पहुँच जाते हैं ?
(A) आकाश के हुदय के
(B) बारिश के
(C) वियोगी समाट के
(D) मुमताज के
उत्तर:
(A) आकाश के हुदय के
प्रश्न 9.
ताजमहल किस नदी के पास खड़ा है ?
(A) गंगा
(B) यमुना
(C) ब्रह्मपुत्र
(D) गंडक
उत्तर:
(B) यमुना
प्रश्न 10.
ताजमहल किसका सेह भूल नहीं सकता ?
(A) दिल्ली का
(B) आगरा का
(C) यमुना का
(D) भारत का
उत्तर:
(B) आगरा का
प्रश्न 11.
ताजमहल किसकी तरह अपनी स्मृतियों को संजोता रहता है ?
(A) योगी की समाधि
(B) मुमताज की समाधि
(C) शाहजहाँ की समाधि
(D) महान आश्चर्य
उत्तर:
(A) योगी की समाधि
![]()
प्रश्न 12.
यमुना ताजमहल के स्वर्णिम दिनों की याद करके क्या करती है ?
(A) दुखी होती है
(B) आश्चर्य होती है
(C) दुख से सूखं रही है
(D) रो पड़ती है
उत्तर:
(C) दुख से सूखं रही है
प्रश्न 13.
कौन दुख से श्यामा हो गई है ?
(A) ताजमहल
(B) यमुना
(C) किला
(D) आगरा
उत्तर:
(B) यमुना
प्रश्न 14.
ताजमहल किससे बना है ?
(A) ग्रेनाइट पत्थर से
(B) बलुईपत्थर से
(C) लाल पत्थर से
(D) संगमरमर से
उत्तर:
(D) संगमरमर से
प्रश्न 15.
मुमताज की अंतिम इच्छा क्या थी ?
(A) संगमरमर की कब्र बनाने की
(B) एक बेजोड़ कब्न बनाने की
(C) पति-पत्नी दोनों को एक साथ कब देने की
(D) कब्र में हीरे-जवाहरात जड़ाने की
उत्तर:
(B) एक बेजोड़ कब्न बनाने की
प्रश्न 16.
दर्शक ताजमहल को देखकर क्या करते है ?
(A) शाहजहाँ को याद करते हैं
(B) विस्मित होते हैं
(C) मुमताज को याद करते हैं
(D) श्रद्धा से झुक जाते हैं
उत्तर:
(D) श्रद्धा से झुक जाते हैं
प्रश्न 17.
भारत की असहाय अवस्था देखकर ताजमहल क्या करता है ?
(A) तनावग्रस्त
(B) अकेलापन महसूस करता है
(C) दुखी
(D) रो पड़ता है
उत्तर:
(C) दुखी
प्रश्न 18.
कवि अपनी रचना में किसे चिरंजीवी बनाना चाहंता है?
(A) शाहजहाँ को
(B) यमुना को
(C) प्रेम-वैभव को
(D) ताजमहल को
उत्तर:
(D) ताजमहल को
प्रश्न 19.
भारत की दुरवस्था लगी रही तो ताजमहल की अवस्था क्या होगी ?
(A) सफेदी घट जाएगी
(B) दुखं से रो पड़ेगा
(C) वह श्याम हो जाएगा
(D) दुख से ढह जाएगा
उत्तर:
(D) दुख से ढह जाएगा
प्रश्न 20.
भारतवासी अपने देश का कल्याण कैसे कर, सकते हैं?
(A) हीरे-जवाहराव एकत्रिक करके
(B) एक सूत्र में बैंधकर
(C) ताजमहल को देखकर
(D) सब्या प्रेमी बनकर
उत्तर:
(B) एक सूत्र में बैंधकर
प्रश्न 21.
अगा खाँ महल में किसकी समाधि है ?
(A) कस्तूरबा की
(B) मुमताज की
(C) मब्लत्मा यांधी की
(D) जाकीर हुसेन की
उत्तर:
(A) कस्तूरबा की
![]()
प्रश्न 22.
कर्तव्य की देवी किसकी गोद में सो गई है ?
(A) शीशमल की
(B) ताजमक्ल की
(C) मुमताज की
(D) अगा खाँ महल की
उत्तर:
(D) अगा खाँ महल की
प्रश्न 23.
कर्तव्य की देवी कौन है ?
(A) मुमताज
(B) कस्तुरवा
(C) विजयलक्ष्मी पंडित
(D) सरोजिनी नायह
उत्तर:
(B) कस्तुरवा
प्रश्न 24.
मुमताज को ताजमहल क्या मानता है ?
(A) विभव की देवी
(B) कर्तव्य की देवी
(C) कर्म की देवी
(D) पेम की देवी
उत्तर:
(D) पेम की देवी
प्रश्न 25.
मानवता की रक्षा के लिए किसका संदेश लेना चाहिए?
(A) प्रेम और कर्म का
(B) कर्म और फल का
(C) प्रेम और कर्तव्य का
(D) प्रोपकार और महतुभूति का
उत्तर:
(C) प्रेम और कर्तव्य का
प्रश्न 26.
ताजमहल की आत्म-कहानी के रचयिता कौन हैं ?
(A) गुलाब राय
(B) धनपतराय
(C) सुदर्शन
(D) प्रेमचन्द
उत्तर:
(A) गुलाब राय
प्रश्न 27.
ताजमहल गर्व से फुला नहीं समाता, क्योंकि –
(A) वह संसार में वास्तवता का अद्वितीय उदाहरण है।
(B) उसे शाहजाँ और मुमताज का अमतिम स्नेह मिला।
(C) वह श्वेत संगमरमर से बना है।
(D) ताजमहल आवरा में है।
उत्तर:
(B) उसे शाहजाँ और मुमताज का अमतिम स्नेह मिला।
![]()
प्रश्न 28.
ताजमहल के अंदर जो बैभव छिपा पढ़ा है, उसे लूटने का साहस नृशंस से नृशंस अल्याचारी को भी नहीं हो सका, क्योंकि –
(A) उनको छर लगा कि ऐसा करने से लोग उन्हें मार ज्ञालेंगे।
(B) उनको हर लगा कि कोई अदृश्य शक्ति उनका नुकसान करेगी।
(C) यह वैभव प्रेम वैभव था, प्रेम की लौ के सामने वे टिक न सके।
(D) हर समय पहरेदार रहते थे ।
उत्तर:
(C) यह वैभव प्रेम वैभव था, प्रेम की लौ के सामने वे टिक न सके।
प्रश्न 29.
बावली यमुना दु:ख से सूख रही है, क्योंकि –
(A) वह ताजमहल के अतीत-वैभव के स्वर्णिम दिनों को याद करती है ।
(B) शाहजहाँ कैदी बन गए थे।
(C) उसमें जल-मवाह कम होने लगा है ।
(D) उसको ताजमहल की तरह आदर नहीं मिल सका।
उत्तर:
(A) वह ताजमहल के अतीत-वैभव के स्वर्णिम दिनों को याद करती है ।
प्रश्न 30.
ताजमहल अभागा नहीं है, क्योंकि –
(A) इसके अंदर दो कब्रें हैं ।
(B) इसके सौन्दर्य और प्रेम-वैभव को देखने दिनरात लोग आते रहते हैं।
(C) लोग आते ही इनके सामने झुक जाते हैं।
(D) वह संगमरमर से बना है।
उत्तर:
(B) इसके सौन्दर्य और प्रेम-वैभव को देखने दिनरात लोग आते रहते हैं।
प्रश्न 31.
ताजमहल का पाषण-हुदय आज भुक्य हो उठाहै, क्योंकि-
(A) वह मानव-समाज की बर्बरता को देखती है।
(B) इसके श्वेत संगमरमर में पुराना होने के कारण दरारें आ गई हैं ।
(C) चित्रकार अपनी तूलिका से और कवि अपनी रचना में उसे अमर करना चाहते हैं।
(D) उसे देखने कम लोग आते हैं ।
उत्तर:
(A) वह मानव-समाज की बर्बरता को देखती है।
प्रश्न 32.
सम्राट और सम्राज्ञी म्लान हो रहे हैं, क्योंकि –
(A) वे भारत की दुरवस्था को देखते हैं।
(B) लोगों ने ताजमहल के जवाहरात लूट लिए।
(C) ताजमहल को आनेवाले दर्शक ताजमहल के पास अधिक समय ठहर नहीं सकते।
(D) मुगल साम्राज्य नहीं रह्म।
उत्तर:
(A) वे भारत की दुरवस्था को देखते हैं।
प्रश्न 33.
अगा खाँ महल ताजमहल का सच्चा साथी है, क्योंकि-
(A) यह ताजनहल की तरह पुरानी इमारत है।
(B) इसके अंदर कर्त्तव्य की देवी कस्तूरबा की समाधि है।
(C) अगा खाँ महल और ताजमहल-दोनों के नाम के साथ महल शब्द जुड़ा है ।
(D) अगा खाँ महल कैदखाना है ।
उत्तर:
(B) इसके अंदर कर्त्तव्य की देवी कस्तूरबा की समाधि है।
शून्यस्थानों की पूर्ति कीजिए :
1. अपने ………… को मैं अपने अंक में लिए बैठा हूँ।
उत्तर: विधाता
![]()
2. उनके इस अप्रतीम स्नेह को पाकर मैं गर्व से ………… नहीं समाता।
उत्तर: फूला
3. शताब्दियाँ बीत गई, पर उनके स्नेह का ………… आज भी मूझ में सुरक्षित है।
उत्तर: वैभव
4. दुनिया के महान ………… में मेरी गणना की जाती हैं।
उत्तर: आश्चर्यों
5. सम्राट ………… और सम्राजी मुमताज की मैं प्रेम-समाधि हूँ।
उत्तर: शाहजहाँ
6. प्रेम की पवित्रता और तल्लीनता का मैं ………… हूँ ।
उत्तर: स्मारक
7. प्रेम ईश्वरीय सृष्टि की सबसे बड़ी ………… हैं।
उत्तर:विभूति
8. दो बिछुड़े हुए ………… मेरी गोद में जुड़े हैं।
उत्तर:हृदय
9. मेरे आभूषणों, रत्नों और ………… को लोग ले गए।
उत्तर:जवाहरातों
10. प्रेम की ………… के सामने उनकी आँखें खुली नहीं रह सकीं।
उत्तर: लौ
11. मैं ………… का स्मारक नहीं, प्रेम का स्मारक हूँ ।
उत्तर: भौतिक ऐश्वर्य
12. मेरी ………… में उस वियोगी सम्राट वे दो बूँद आँसू चू पड़े थे।
उत्तर: नींव
![]()
13. मेरे हृदय तक उसके सभी ………… पहुँच जाते हैं ।
उत्तर: आँसू
14. ………… के स्नेह को मैं भूल नहीं सकता ।
उत्तर: आगरे
15. ………… यमुना भी मेरे अतीत वैभव के स्वर्णिम दिनों को याद कर दु:ख से सूंख रही है।
उत्तर: बावली
16. ………… श्यामा हो गई है।
उत्तर: यमुना
17. यमुना ………… लेकर मुझे प्यार करती है।
उत्तर: हिल्लोरें
18. मैं ………… का अद्वितीय उदाहरण हूँ।
उत्तर: वास्तविकता
19. ………… से मेरा (ताजमहल का) निर्माण हुआ।
उत्तर: श्वेत संगमरमर
20. मृत्यु-शय्या पर ………… साँसे गिनती हुई मुमताज की यही तो अंतिम इच्छा थी ।
उत्तर: अंतिम
21. उस स्वर्गीय देवी की बात ………… कैसे टाल सकता था?
उत्तर: शाहजहाँ
![]()
22. उसकी इच्छानुसार उसकी यह बेजोड़ ………… अस्तित्व में आई।
उत्तर: कब्र
23. मेरे पास आकर उन्हें ………… से झुक जाना पड़ता है।
उत्तर: श्रद्धा
24. मुगल साम्राज्य के ………… के दिन बीत गए।
उत्तर: ऐश्वर्य
25. मानव-समाज की ………… को देखकर आज मेरा पाषणहृदय भी क्षुब्ध हो उठा है ।
उत्तर: बर्बरता
26. चित्रकार अपनी तूलिका से मुझे ………… करना चाहता है।
उत्तर: अमर
27. कवि अपनी रचना में मुझे ………… बनाने का प्रयत्न करता है।
उत्तर: चिरजीवी
28. ………… के बोझ से मैं ढह जाऊँगा ।
उत्तर: दुःख
29. मैं चाहता हूँ कि मुझसे प्रेम का पाठ लेकर ………… एक सूत्र में बँध जाएँ।
उत्तर: भारतवासी
30. ………… आज इस युग में मेरा एक सच्चा साथी हुआ है ।
उत्तर: अगाखाँ महल
31. अगा खाँ महल की गोद में ………… की देवी है ।
उत्तर: कर्त्तव्य
![]()
32. मुझे विश्वास है, इस प्रेम और ………… के संदेश को लेकर मानवता अपना कल्याण करेगी।
उत्तर: कर्त्तव्य
उपयुक्त शब्द ले कर खाली जगह भरिए :
1. अपने विधाता को मैं अपने अंक ………… लिए बैठा हूँ। (के, में, पर)
उत्तर: में
2. वही मेरी गोद ………… सो रहा है। (पर, में, को)
उत्तर: में
3. मैं गर्व ………… फूल नहीं समाता। (में, से, केलिए)
उत्तर: से
4. स्नेह का वैभव मुझ ………… सुरक्षित है। (पर, में, केलिए)
उत्तर: में
5. महान आश्चर्यों ………… मेरी गणना की जाती है। (का, में, पर)
उत्तर: में
6. मैं प्रेम ………… पवित्रता का स्मारक हूँ। (का, के, की)
उत्तर: की
7. प्रेम ईश्वरीय सृष्टि ………… सबसे बड़ी विभूति है। (का, के, की)
उत्तर: की
8. जवाहरातों ………… लोग ले गये। (का, को, पर)
उत्तर: को
9. मेरी नींव ………… उस वियोगी सम्राट के दो बूँद आँसू चू पड़े हैं। (में, पर, को)
उत्तर: पर
![]()
10. मेरे हुदय तक उस ………… सभी आँसू पहुँच जाते हैं। (क़ा, के, पर)
उत्तर: के
11. कल्पना जगत के विश्वासों ………… मैं विश्वास नहीं करता। (का, के, पर)
उत्तर: पर
12. यमुना के किनारे ………… मैं खड़ा हूँ। (पर, में, से)
उत्तर: में
13. आगरे के स्नेह ………… मैं भूल नहीं सकता। (को, पर, से)
उत्तर: से
14. मुझे उस ………… प्रेम है। (में, पर, ने)
उत्तर: पर
15. यमुना दुख ………… सूख रही है। (से, को, ने)
उत्तर: से
16. मैं वास्तविकता ………… अद्वितीय उदाहरण हूँ। (का, के, की)
उत्तर: का
17. उस ………… इच्छानुसार कब्र अस्तित्व में आई। (का, के, की)
उत्तर: की
18. विदेशों ………… यात्री आकर मुझे देखकर अपना आना सार्थक समझते हैं। (से, ने, को)
उत्तर: से
19. अपने संबंध ………… उनकी थारणाओं को देख में मुस्करा उठता हूँ। (पर, में, ने)
उत्तर: में
20. मुगल साम्राज्य ………… ऐश्वर्य के दिन बीत गए। (का, के, की)
उत्तर: के
21. मेरी छबि अंकित करने ………… लोग यहाँ आते हैं। (केलिए, को, में)
उत्तर: केलिए
22. दुख के बोझ ………… मैं ढह जाऊँगा। (के, से, में)
उत्तर: से
23. भारतवासी एक सूत्र ………… बँधजाएँ । (में, से, पर)
उत्तर: में
![]()
24. मुझे किसी ………… प्रतिद्वन्द्रिता नहीं है। (में, पर, से)
उत्तर: से
25. मेरी गोद ………… प्रेम की देवी हैं। (में, पर, से)
उत्तर: में
वर्तनी शुद्ध कीजिए :
1. अप्रतीम
2. शताब्दि
3. आस्वर्य
4. साम्राज्ञी
5. विभुति
6. इस्वरीय
7. आभूषण
8. जबाहरात
9. बैभव
10. नृसंस
11. अश्वर्य
12. नीव
13. द्रविभूत
14. बुँद
15. विश्वास
16. जमुना
17. समाधी
18. योगि
19. स्यामा
20. साथि
21. साहजहाँन
22. ममताज
23. यात्रि
24. स्रीधा
25. छबि
26. पासाण
27. चीरजीवी
28. अबस्था
29. तुलिका
30. दुरावस्था
![]()
31. सुत्र
32. प्रतिद्बादिता
33. कस्तुरबा
34. बिश्वास
35. मानबता
36. सामाजी
उत्तर:
1. अप्रतिम
2. शताब्दी
3. आश्चर्य
4. सम्राजी
5. विभूति
6. ईश्वरीय
7. आभूषण
8. जवाहरात
9. वैभव
10. नृशंस
11. ऐश्वर्य
12. नींव
13. द्रवीभूत
14. बूँद
15. विश्वास
16. यमुना
17. समाधि
18. योगी
19. श्यामा
20. साथी
21. शाहजहाँ
22. मुमताज
23. यात्री
24. श्रद्धा
25. छवि
26. पाषाण
27. चिरजीवी
28. अवस्था
![]()
29. तूलिका
30. दुरवस्था
31. सूत्र
32. प्रतिद्वन्द्रिता
33. कस्तूरबा
34. विश्वास
35. मानवता
36. समाज्ञी
वाक्यों को शुद्ध कीजिए :
प्रश्न 1.
जो मुझे खड़ा किया, वही मेरी गोद में सो रहा है।
उत्तर:
जिसने मुझे खड़ा किया, वही मेरी गोद में सो रहा है।
प्रश्न 2.
वह मेरे गोद में सो रही है।
उत्तर:
वह मेरी गोद में सो रही है।
प्रश्न 3.
उनका स्नेह का वैभव आज भी सुरक्षित है।
उत्तर:
उनके स्नेह का वैभव आज भी सुरक्षित है।
प्रश्न 4.
महान् आश्चयों में मेरा गणना किया जाता है।
उत्तर:
महान् आश्वयों में मेरी गणना की जाती है।
प्रश्न 5.
प्रेम ईश्वरीय सृत्टि का सबसे बड़ी विभूति है।
उत्तर:
प्रेंम ईश्वरीय सृष्टि की सबसे बड़ी विभूति है।
प्रश्न 6.
दो बिहुड़ा हुआ हृदय मेरी गोद में जुड़े हुए हैं।
उत्तर:
दो बिछड़े हुए हुदय मेरी गोद में जुड़े हुए हैं ।
![]()
प्रश्न 7.
मैं प्रेम की स्मारक हूँ।
उत्तर:
मैं प्रेम का स्मारक हूँ।
प्रश्न 8.
उसके सभी आँसू पहुँच जाता है।
उत्तर:
उसके सभी आँसू पहुँच जाते हैं।
प्रश्न 9.
उसके आँसू से मेरा कलेवर निखर उठता है।
उत्तर:
उसके आँसुओं से मेरा कलेवर निखर उठता है।
प्रश्न 10.
यमुना का किनारे पर मैं खड़ा है।
उत्तर:
यमुना के किनारे पर मैं खड़ा हूँ।
प्रश्न 11.
यमुना श्यामा हो गया है।
उत्तर:
यमुना श्यामा हो गई हैं।
प्रश्न 12.
वह हिल्लोर लेकर मुझे प्यार करती हैं।
उत्तर:
वह हिल्लोरें लेकर मुझे प्यार करती है ।
प्रश्न 13.
मेरे निर्माण में करोड़ रुपए व्यय हुए।
उत्तर:
मेरे निर्माण में करोड़ रुपए खर्च हुए।
प्रश्न 14.
यह कब्र अभागा नहीं है।
उत्तर:
यह कब्र अभागी नहीं है ।
प्रश्न 15.
मुगल साम्राज्य के ऐश्वर्य का दिन बीत गया।
उत्तर:
मुगल साम्राज्य के ऐश्वर्य का दिन बीत गए।
प्रश्न 16.
भारत का असहाय अवस्था देखकर आज मुझे दु:ख होता है।
उत्तर:
भारत की असह्यय अवस्था देखकर आज मुझे टु:ख हो रहा है।
प्रश्न 17.
वे मेंरा चित्र उतारते हैं ।
उत्तर:
वे मेरे चित्र उतारते हैं।
प्रश्न 18.
चित्रकार अपना तूलिका से मुझे अमर करना चाहता है।
उत्तर:
चित्रकार अपनी तूलिका से मुझे अमर करना चाहते हैं।
![]()
प्रश्न 19.
अगर यही अवस्था रहा तो मैं ढह जाऊँगा।
उत्तर:
अगर यही अवस्था रही, तो मैं ढह जाऊँगा।
प्रश्न 20.
भारतवासी एक सूत्र में बँध जाए।
उत्तर:
भारतवासी एक सूत्र में बँध जाएँ।
प्रश्न 21.
वे अपने देश का कल्याण करो।
उत्तर:
वे अपने देश का कल्याण करें ।
प्रश्न 22.
अगा खाँ महल मेरा सच्ची साथी है।
उत्तर:
अगा खाँ महल मेरा सच्चा साथी है।
प्रश्न 23.
मेरी गोद पर प्रेम की देवी है।
उत्तर:
मेरी गोद में प्रेम की देवी है।
प्रश्न 24.
यह प्रेम और कर्त्तव्य के संदेश को लेकर मानवता अपना कल्याण करेगी।
उत्तर:
इस प्रेम और कर्त्तव्य के संदेश को लेकर मानवता अपना कल्याण करेगी।
लिंग बदलिए
- विधाता – विधात्री
- सम्राट – सम्राजी
- योगी – योगिणी
- यात्री – यात्रिणी
- मानव – मानवी
- देव – देवी
बचन बदलिए
- शताब्दी – शताब्दियाँ
- वैभव – वैभव
- समाधि – समाधियाँ
- विभूति – विभूतियाँ
- आभूषण – आभूषण
- नींव – नींवें
- बूँद – बूँदें
- प्रयास – प्रयास
- किनारा – किनारे
- स्मृति – स्मृतियाँ
- साथी – साथी
- रुपया – रुपए
- शय्या – शय्याएँ
- साँस – साँसें
- कब्र – कब्रें
- धारणा – धारणाएँ
- अवस्था – अवस्थाएँ
- बवि – छवियाँ
- तूलिका – तूलिकाएँ
- रचना – रचनाएँ
- बोझ – बोझ
अव्ययों से रिक्त स्थान भरिए :
1. उनके स्नेह का वैभव ………… मुझमें सुरक्षित है ।
2. प्रेम की पवित्रता ………… तल्लीनता का मैं स्मारक हूँ।
3. मुझे ………… लूटा गया।
4. ………… मेरे ………… जो वैभव छिपा पड़ा है ।
5. उसे छोड़कर मैं ………… जा सकता।
6. शाहजहाँ ………… टाल सकता था ?
7. ………… उसकी इच्छानुसार आज भी यह बेजोड़ कब्र अस्तित्व में आई ।
उत्तर:
1. आज भी
2. और
3. भी
4. पर, अंदर
5. कहीं, नहीं
6. कैसे
7. इसलिए, तो
![]()
३० शब्दों/दो-तीन वाक्यों में उत्तर दीजिए :
प्रश्न 1.
ताजमहल क्यों गर्व से फूला नहीं समाता ?
उत्तर:
ताजमहल सम्राजी मुमताज के लिए सम्राट शाहजहाँ के द्वारा बनवाया गया था । दोंनों कब्र इसी में है । उन दोनों का सम्राट शाहजहाँ और सम्राज्ञी मुमताज का अप्रतिम स्नेह ताजमहल को मिलने से वह गर्व से फूला नहीं समाता ।
प्रश्न 2.
ताजमहल क्या संकेत कर रहा है ?
उत्तर:
ताजमहल सम्राट शाहजहाँ और सम्राजी मुमताज की प्रेम समाधि है । प्रेम की पवित्रता को भूलकर भेदभाव में पड़ गए लोंगों को ताजमहल संकेत कर रहा है कि प्रेम ईश्वरीय सृष्टि की सबसे बड़ी विभूति है ।
प्रश्न 3.
ताज भौतिक ऐश्वर्य का स्मारक नहीं अपितु प्रेम का स्मारक है, कैसे ?
उत्तर:
ताजमहल के अंदर सम्राट शाहजहाँ और सम्राजी मुमताज के प्रेम का वैभव छिपा पड़ा है । उसे कोई भी अत्याचारी लूट न सका । ताजमहल के अंदर आभूषणों, रत्नों और जवाहरातों का भौतिक ऐश्वर्य अत्याचारियों ने लूट लिया पर वह म्रेम का स्मारक था, अब भी है ।
प्रश्न 4.
यमुना के साथ ताजमहल का कैसा सबंध है ?
उत्तर:
ताजमहल यमुना के किनारे खड़ा है । दोनों पुराने साथी हैं । इसलिए बावली यमुना ताजमहल के पुराने वैभव के स्वर्णिम दिनों को याद करके दु: ख से सूख रही है । श्यामा हो गई है । उस पर ताजमहल को स्वाभाविक रूप से स्नेह है । यमुना लहरों से उसे प्यार करती है । अपनी सुनाती है, ताजमहल की सुनती है ।
प्रश्न 5.
वास्तविकता का अद्वितीय उदाहरण ताजमहल है, क्यों ?
उत्तर:
ताजमहल सम्राट शाहजहाँ और सम्राज्ञी मुमताज के वास्तविक प्रेम का अद्वितीय उदाहरण है । मृत्यु-शय्या पर मुमताज की अंतिम इच्छा थी कि उसके लिए एक बेजोड़ कब्र बनाई जाए।सम्राट ने भी करोडों रुपए व्यय करके श्वेत संगमरमर से हजारों कारीगरों की सहायता से ताजमहल बनवाया ।
प्रश्न 6.
विदेशी ताजमहल को देखकर क्या करते हैं ?
उत्तर:
दुनिया? की महान् आश्चयों में ताजमहल की गणना होती है ।इसे देखने विदेशी पर्यटक यहाँ आते हैं । वे इस प्रेम के स्मारक को देखकर अपना आना सार्थक समझते हैं । वे श्रद्धा से इसके सामने सिर झुका देते हैं ।
प्रश्न 7.
लोग ताजमहल को देखकर कैसी कल्पना करते हैं ?
उत्तर:
भिन्न-भिन्न लोग ताजमहल को देखकर भिन्न – भिन्न कल्पनाएँ करते हैं । कुछ लोग सिनेमा के पट पर ताजमहल का चित्र उतारते हैं । चित्रकार अपनी तूलिका से उसे अमर करना चाहते हैं । कवि अपनी रचना में ताजमहल को चिरजीवी बनाने का प्रयास करते हैं ।
![]()
प्रश्न 8.
ताजमहल का हृदय क्यों विदीर्ण हो रहा हैं ?
उत्तर:
मानव समाज की वर्वरता को देखकर ताजमहल का पाषाण हृदय क्षुब्ध हो उठा है । ताजमहल ने भारत के वैभव के दिन देखे हैं । प्रेम भूल गए हैं । सम्राट-सम्राजी भारत की दुरवस्था देखकर म्लान हो रहे हैं । इससे ताजमहल का हृदय विदीर्ण हो रहा है।
प्रश्न 9.
ताज का प्रतिद्वन्द्री नहीं हैं, सच्चा साथी कौन है ?
उत्तर:
ताज का कोई समकक्ष न रहने से उसका किसीसे प्रतिद्वन्द्रिता नहीं है । प्रेम के स्मारक के सभी साथी हैं । ताजमहल का सच्चा साथी आगा खाँ महल है, जहाँ कर्त्तव्य की देवी कस्तूरबा की समाधि है ।
प्रश्न 10.
ताजमहल की इच्छा क्या है ?
उत्तर:
ताजमहल ने मानवसमाज की वर्वरता और भारत की असहाय अवस्था देखी है । यह अवस्था रही तो दु:ख के बोझ से वह ढह जाएगा – ऐसा उसे लगता है । उसकी इच्छा है कि उससे प्रेम का पाठ लेकर भारतवासी एक सूत्र में बँध जाएँ और देश का कल्याण करें ।
प्रश्न 11.
संसार विस्मय विमुग्ध होकर क्या देख रहा है ?
उत्तर:
ताजमहल में सम्राट शाहजहाँ और सम्राजी मुमताज के स्नेह का वैभव सुरक्षित है। इस वैभव को संसार विस्मय विभुग्ध होकर देख रहा है।
प्रश्न 12.
अत्याचारियों ने ताजमहल को क्या हानि पहुँचाई?
उत्तर:
अत्याचारियों ने समय-समय पर ताजमहल पर आक्रमण किया। उन्होंने उसके आभूषणों, रत्नों और जवाहरातों को लूट लिया और उसे नग्न कर दिया।
प्रश्न 13.
वियोगी सम्राट के आँसुओं की स्मृति में आकाश क्या करता है ?
उत्तर:
वियोगी सम्राट के आँसुओं से त्मजमहल के हृदय को सींचने का प्रयास करता है।
प्रश्न 14.
ताजमहल का कलेवर कैसे निखर उठता है ?
उत्तर:
आकाश सम्राट की स्मृति में दो बूँद आँसू बहाता है। ताजमहल के हृदय तक ये आँसू पहुँच जाते हैं। उन आसुओं से ताजमहल का कलेवर निखर उठता है।
प्रश्न 15.
ताजमहल का निर्माण कैसे हुआ?
उत्तर:
ताजमहल का निर्माण श्वेत संगमरमर से हुआ। उसकें निर्माण में करोड़ों रुपए खर्च हुए। हजारों आदमी एक युग से भी अधिक समय में इसका निर्माण पूरा कर सके।
लेखक परिचय:
गुलाब राय का जन्म इटावा में १८८८ ई. में हुआ था। वे एम.ए., एल.एल.बी पास थे । उन्हें आगरा विश्च विद्यालय से सम्मान्रार्थ डी.लिट. की उपाधि मिली थी। संस्कृत का उन्होंने गह्न अध्ययन किया था। उन्होंने काव्यशास्त्रकार, आलोचक, निबंधकार तथा दार्शनिक के रूप में अपनी बहुमुखी प्रतिभा का परिचय दिया था । आधुनिक हिन्दी गद्य को उन्होंने समुद्ध बनाया है । उनकी मृत्यु १ ३ अपैल, १ ९ ६ ३ को हो गई ।
उनकी रचनाएँ – सिद्धांत और अध्ययन, काव्य के रूप, हिन्दी नाट्य विमर्श, मेरी असफलाताएँ, मेरे निबंध, तर्कशास्त्र, मन की बातें आदि ।
![]()
विचारबोध :
सम्रांट शाहजहाँ ने सम्राज़ी मुमताज के अनुरोंध से उनके लिए संगमरमर का मकबरा ताजमहल यमुना के किनारे पर बनवाया था । मुमताज को यहीं दफनाया गया था। बाद में शाहजहाँ को भी वहीं बगल में दफनाया गया। यह ताजमहल प्रेम के प्रतीक के रूप में और बेजोड़ सौंदर्य के लिए विश्च मसिद्ध है । ताजमहल से प्रेमकी और अगा खाँ महल से कर्त्तव्य की प्रेरणा लेने से मानवता का कल्याण होगा।
शब्दार्थ :
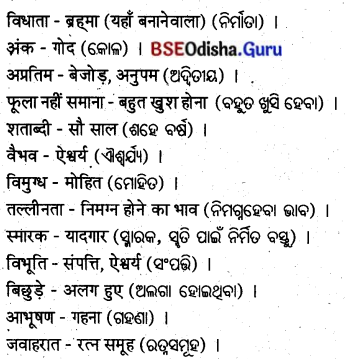
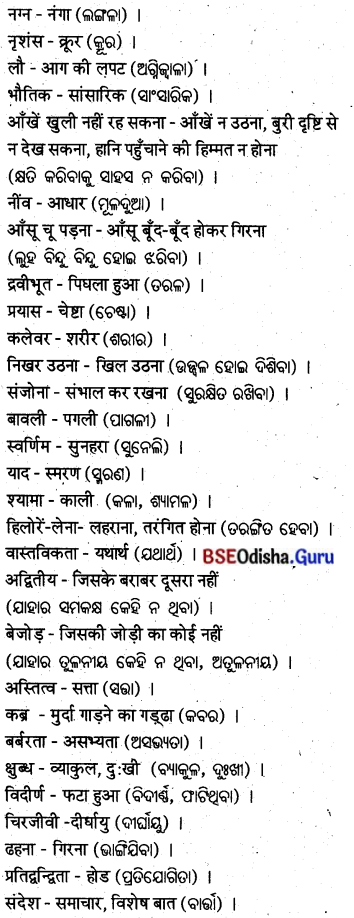
सारांश :
बादशाह शाहजहाँ की बेगम मुमताज की अंतिम इच्छा थी कि उनके लिए शाहजहाँ एक बेजोड़ कब्र बनवाएँ। शाहजहाँ ने अंपने अमर प्रेम की खातिर आगरा में यमुना के किनारे पर श्वेत संगमरमर का मकबरा ताजमहल बनाया । इसमें करोड़ों रुपए खर्च हुए । हजारों कारीगरों के वर्षों के श्रम से यह बना । जवाहरातों से इसे सजाया गया । यह अपनी सुंदरता के लिए दुनिया के सप्ताश्वर्यों में गिना जाता है। ताजमहल में पहले मुमताज को दफनाया गया था। बाद में शाहजहाँ को भी मुमताज की कब्र के बगल में दफनाया गया। ताजमहल शाहजहाँ और मुमताज के प्रेम का स्मारक है ।
![]()
देश – विदेश से लाखों यात्री ताजमहल देखने आते हैं । वे इस अंद्वितीय प्रेम – निशानी को देखकर मुग्ध हो जाते हैं ।जिस समय ताजमहल’बना था, उस समय भारत में वैभव के दिन थे।आज भारत की दुरवस्था देखकर ताजमहल दुःखी हो जाता है ।
उसे आशंका होती है कि भारत की यह दुरवस्था अधिक दिन रही तो वह दु:ख के बोझ से ढह जाएगा । भारतवासी यदि उससे प्रेम का पाठ पढ़ें और एक सूत्र में बँध जाएँ तो भारत का कल्योण होगा । ताजमहल की गोद में मुमताज प्रेम की देवी हैं । अगा खाँ महल की गोद में कस्तूरबा कर्त्तव्य की देवी हैं । यदि भारतवासी इन दोनों से प्रेम और कर्त्तव्य का संदेश लेंगे तो मानवता का कल्याण होगा।
ସାରାଂଶ:
ବାଦଶାହ ଶାହାଜାହାନଙ୍କ ବେଗମ ମମତାଜ ମହଲଙ୍କର ଅନ୍ତିମ ଅଭିଳାଷ ଥୁଲା ଯେ ତାଙ୍କ ପାଇଁ ଶାହାଜାହାନ ଏକ ଅପ୍ରତିମ କବର ଆଗ୍ରାର ଯମୁନା ନଦୀ କୂଳରେ,ଶ୍ଵେତ ଶଙ୍ଖ ମଲମଲ ପଥରରେ ସମାଧୁ ତାଜମହଲ ନିର୍ମାଣ କରାଇଥିଲେ । ଏଥିରେ କୋଟି କୋଟି ଟଙ୍କା ଖର୍ଚ୍ଚ ହେଲା । ହଜାର-ହଜାର କାରିଗର ବର୍ଷ ବର୍ଷ ଧରି ପରିଶ୍ରମ କରି ଏହା ନିର୍ମାଣ କଲେ । ବିଭିନ୍ନ ରନ୍ରେ ଏହା ସଜ୍ଜିତ ହୋଇଥିଲା । ଏହାକୁ ଏହାର ସୌନ୍ଦର୍ଯ୍ୟ ପାଇଁ ପୃଥିବୀର ସପ୍ତାଶ୍ଚର୍ଯ୍ୟ ମଧ୍ୟରେ ଗଣାଯାଏ ।
ପ୍ରଥମେ ମମତାଜଙ୍କୁ ତାଜମହଲରେ କବର ଦିଆଯାଇଥିଲା । ପରେ ଶାହାଜାହାନଙ୍କୁ ମମତାଜଙ୍କ କବର ପାଖରେ କବର ଦିଆଗଲା । ତାଜମହଲ ହେଉଛି ଶାହାଜାହାନ ଓ ମମତାଜଙ୍କ ପ୍ରେମର ସ୍ମାରକୀ । ଦେଶ-ବିଦେଶରୁ ଲକ୍ଷ ଲକ୍ଷ ଲୋକ ତାଜମହଲ ଦେଖିବାକୁ ଆସନ୍ତି । ସେମାନେ ଏହି ଅଦ୍ଵିତୀୟ ପ୍ରେମ- ସ୍ମାରକୀକୁ ଦେଖି ଅଭିଭୂତ ହୋଇଯାଆନ୍ତି ।
ପ୍ରଥମେ ଯେତେବେଳେ ତାଜମହଲ ନିର୍ମାଣ କରାଯାଇଥିଲା, ସେତେବେଳେ ଭାରତରେ ବୈଭବର ଦିନ ଥିଲା । ଆଜି ଭାରତର ଦୁରବସ୍ଥା ଲକ୍ଷ୍ୟ କରି ତାଜମହଲ ବହୁତ ଦୁଃଖୀ ହୋଇଯାଉଛି । ତା’ର ଆଶଙ୍କା ଯେ ଯଦି ଭାରତର ଦୁରବସ୍ଥା ଏହିଭଳି କେତେ ଦିନ ଧରି ରହିବ, ତେବେ ଦୁଃଖର ବୋଝରେ ହୁଏତ ସେ ଭାଙ୍ଗିପଡ଼ିବ । ଭାରତବାସୀ ଯଦି ତା’ଠାରୁ ପ୍ରେମର ପାଠ ଶିଖିବେ, ସମସ୍ତେ ଏକ ସୂତ୍ରରେ ଆବଦ୍ଧ ହେବେ, ତେବେ ଭାରତର କଲ୍ୟାଣ ହୋଇ ପାରିବ ।
![]()
ତାଜମହଲ କୋଳରେ ମମତାଜ ପ୍ରେମର ଦେବୀ ରହିଛନ୍ତି । ଆଗା ଖାଁ ମହଲରେ କସ୍ତୁରବା କର୍ତ୍ତବ୍ୟର ଦେବୀ ରହିଛନ୍ତି । ଯଦି ଭାରତବାସୀ ଏ ଦୁହିଁଙ୍କଠାରୁ ପ୍ରେମ ଓ କର୍ତ୍ତବ୍ୟର ବାଆଁ ଗ୍ରହଣ କରିବେ, ତେବେ ମାନବତାର କଲ୍ୟାଣ ହେବ ।.
आइए, हम कविता बनाएँ
(सिर्फ पढ़ने के लिए)
१. कल करे सो आज कर
आज करे सो अब।
पल में परलय होता है
तब फिर करेगा कब ?
२. वीर तुम बढ़े चलो
धीर तुंम बढ़े चलो
सामने पहाड़ हो
सिंह का दहांड़ हो
रुको नहीं डरो नहीं ।
![]()
३. बड़े देखकर छोटे का,
कभी न करो अपमान
जहाँ काम आये सुई
क्या कर लेगा कमान ।
४. गरजें बादल
बरसें बादल
कड़के बिजली
नदियाँ उछली
भर गई क्यारी
लगती प्यारी
धान की बाली
लाये खुशहाली ।
५. छुक छुक गाड़ी
तेजी से दौड़ी
लचकती पटरी
उचकती गठरी ।
६. दूसरों के दुःख में आँसू बहाओ
दूसरों के सुख में हैसी मिलाओ
तब तुम बनोगे सच्चा इंसान
पाओगे जी भरके सम्मान ।
पहेलियाँ : बूझों बुझाएँ
(सिर्फ पढ़ने के लिए)
धनुष मैं कहलाऊँ
पर तीर न चलाऊँ
घहने सतरंगी कपड़े
दूर गगन में इठलाऊँ
कहो तो मैं कौन हूँ ?
![]()
एक थाल मोती से भरा,
सबके ऊपर औंधा धरा ।
झर झर झरे जल की धारा,
पर एक मोती न नीचे गिरा ।
दोनें बहनें रहतीं साथ,
आपस में न करतीं बात ।
एक दूसरे को तब देखें,
जब हो आइने के साथ ।
कहो ये कौन हैं ?
जल की मैं हूँ रानी,
तैरूँ गहरे पानी ।
पकड़ में कभी न आऊँ
जो मिले सो खा जाऊँ
कहो मैं कौन हूँ ?
नीचे पटको ऊपर जाती,
ऊपर फेंको नीचे आती ।
उछल-कूद है सदा मचाती,
हमको कितने खेल खिलाती ।
बड़े बड़े पेड़ लहकती डालियाँ
भरपूर हरियाली ब्रेटी छोटी पत्तियाँ।
रसीले फल झूमे जैसे झिमियाँ
बिके तो मिले पैसे भर भरथैलियाँ।
कहो ये क्या हैं ?
इन्द्रधनुष, मछली, आसमान, गेंद, प्रतिबिंब, इमली