Odisha State Board BSE Odisha 9th Class History Important Questions Chapter 2 ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧ : କାରଣ ଓ ଫଳାଫଳ Important Questions and Answers.
BSE Odisha Class 9 History Important Questions Chapter 2 ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧ : କାରଣ ଓ ଫଳାଫଳ
Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
୧। ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧର ମୁଖ୍ୟ କାରଣମାନ ଆଲୋଚନା କର।
Answer:
୧୯୧୪ ମସିହାରେ ସଂଘଟିତ ହୋଇଥିବା ପ୍ରଥମ କାରଣମାନ ନିମ୍ନ ପ୍ରକାରର ଥିଲା-
- ଉପନିବେଶ ପ୍ରତିଷ୍ଠା ପାଇଁ ଇଂଲାଣ୍ଡ, ଫ୍ରାନ୍ସ, ଜର୍ମାନୀ, ଇଟାଲୀ ଓ ଜାପାନ ପ୍ରଭୃତି ରାଷ୍ଟ୍ରଗୁଡ଼ିକ ମଧ୍ୟରେ ପ୍ରତିଦ୍ବନ୍ଦିତା ଓ ବାରମ୍ବାର ସଂଘର୍ଷ ପ୍ରଥମ ବିଶ୍ବଯୁଦ୍ଧର ଅନ୍ୟତମ କାରଣ ଥିଲା ।
- କେନ୍ଦ୍ର କରି ଯୁଦ୍ଧଖୋର ମନୋଭାବ ଏବଂ ସାମରିକ ମେଣ୍ଟ ଗଠନ, ଜର୍ମାନୀ, ଇଟାଲୀ ଓ ଅଷ୍ଟ୍ରି ଆ-ହଙ୍ଗେରୀଦ୍ଵାରା ୧୮୮୨ରେ ‘ତ୍ରି ଶକ୍ତି ମେଣ୍ଟ’ ଗଠନ ଏବଂ ଜର୍ମାନୀ ଆତ୍ମପତ୍ୟକୁ ପ୍ରତିହତ କରିବା ପାଇଁ ଇଂଲାଣ୍ଡ, ଫ୍ରାନ୍ସ ଓ ରୁଷକୁ ନେଇ ୧୯୦୭ ମସିହାରେ ‘ତ୍ରିମିତ୍ର ପକ୍ଷ’ ଗଠନ ଏହି ଯୁଦ୍ଧର ବଳିଷ୍ଠ କାରଣ ଥିଲା ।
- କାଇଜର ଦ୍ଵିତୀୟ ଉଇଲିୟମ୍ଙ୍କ ଅସ୍ଥିର ଓ ଅପରିଣାମଦର୍ଶୀ ନୀତି ଓ ଯୁଦ୍ଧର ସମ୍ଭାବନା ଏଡ଼ାଇବାକୁ ଆନ୍ତର୍ଜାତିକ ସଙ୍ଗଠନର ଅଭାବ ପ୍ରଥମ ବିଶ୍ବଯୁଦ୍ଧର ଅନ୍ୟତମ କାରଣ ଥିଲା ।
- ୧୯୧୪ ମସିହା ଜୁନ୍ ୨୮ ତାରିଖରେ ଅଷ୍ଟ୍ରିଆ-ହଙ୍ଗେରୀର ଯୁବରାଜ ଫ୍ରାନ୍ସିସ୍ ଫର୍ଜିନାଣ୍ଡ ଓ ତାଙ୍କର ପତ୍ନୀ ସୋଫିଆଙ୍କୁ ବୋସ୍ ଆର ରାଜଧାନୀ ‘ସାରାଜେଭୋ’ଠାରେ ସର୍ବ ଜାତିର ଜଣେ ଯୁବକଦ୍ଵାରା ଗୁଳିକରି ହତ୍ୟା ଏବଂ ଏହାର ପ୍ରତିକ୍ରିୟାସ୍ଵରୂପ ୧୯୧୪ ମସିହା ଜୁଲାଇ ୨୮ ତାରିଖରେ ଅଷ୍ଟ୍ରିଆ-ହଙ୍ଗେରୀର ସର୍ବିଆ ଆକ୍ରମଣ ବିଶ୍ୱଯୁଦ୍ଧର ଅୟମାରମ୍ଭ କରିଥିଲା ।
୨। ‘ପ୍ୟାରିସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀ’ ବିଷୟରେ ଏକ ଟିପ୍ପଣୀ ଲେଖ ।
Answer:
- ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧ ପରେ ଫ୍ରାନ୍ସର ପ୍ରଧାନମନ୍ତ୍ରୀ କ୍ଲି ମେମ୍ବୁ ଙ୍କ ସଭାପତିତ୍ୱରେ ୧୯୧୯ ମସିହାରେ ପ୍ୟାରିସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀ ଆହୂତ ହୋଇଥିଲା ।
- ଏହି ସମ୍ମିଳନୀରେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ରାଷ୍ଟ୍ରପତି ଉଡ୍ରୋ ଉଇଲ୍ ସନ୍, ଇଂଲଣ୍ଡର ପ୍ରଧାନମନ୍ତ୍ରୀ ଲଏଡ୍ ଜର୍ଜ ଓ ଫ୍ରାନ୍ ସର ପ୍ରଧାନମନ୍ତ୍ରୀ ପ୍ରଧାନମନ୍ତ୍ରୀ କିମେମ୍ବୁ ନୀତି ନିର୍ଦ୍ଧାରଣରେ ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲେ ।
- ଏହି ସମ୍ମିଳନୀରେ ଫ୍ରାନ୍ସର ଭର୍ସାଇଠାରେ ଜର୍ମାନୀ ସହ ‘ଭର୍ସାଇ ଚୁକ୍ତି’ ସ୍ୱାକ୍ଷରିତ ହୋଇଥିଲା । ଏହି ଚୁକ୍ତିର ସର୍ଭଗୁଡ଼ିକ ହୋଇଥିବାରୁ କମୀନୀରେ ପ୍ରତିଶୋଧପରାୟଣତା ସୃଷ୍ଟି ହେଲା ।
- ଏହା ବ୍ୟତୀତ ପ୍ୟାରିସ୍ତାରେ ଅଷ୍ଟ୍ରିଆ ସହ ‘ସେଣ୍ଟଜର୍ମେନ୍ ଚୁକ୍ତି’, ହଙ୍ଗେରୀ ସହ ‘ଟ୍ରାଏନନ୍ ଚୁକ୍ତି’, ବୁଲ୍ଗେରିଆ ସହ ‘ନିଉଲି ଚୁକ୍ତି’, ତୁର୍କୀ ସହ ‘ସେଭର୍ସ’ ଓ ‘ଲସେନ ଚୁକ୍ତି’ ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ।
୩। ବଲ୍କାନ୍ ସମସ୍ୟା ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧର କିପରି ଏକ କାରଣ ଥିଲା ?
Answer:
ନିମ୍ନଲିଖ କାରଣ ଯୋଗୁଁ ବଲ୍କାନ୍ ସମସ୍ୟା ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧର ଏକ କାରଣ ଦୋଥିଲା ।
- ଅଷ୍ଟ୍ରିଆ ଓ ସର୍ବିଆ ମଧ୍ୟରେ ଏବଂ ଅଷ୍ଟ୍ରିଆ ଓ ରୁଷିଆ ମଧ୍ୟରେ କଳହ ବଲକାନ୍ ଅଞ୍ଚଳରେ ଆଞ୍ଚଳିକ ସଙ୍କଟ ସୃଷ୍ଟି କରିଥିଲା ।
- ବଲ୍କାନ୍ ଅଞ୍ଚଳରେ ପ୍ରାଧାନ୍ୟ ବିସ୍ତାର ପାଇଁ ଅଷ୍ଟ୍ରିଆ ଓ ରୁଷିଆ ମଧ୍ୟରେ ପ୍ରତିଦ୍ବନ୍ଦିତା ସମସ୍ୟାକୁ ଅଧ୍ଵକ ଜଟିଳ କରିଥିଲା ।
- ଗୋଟିଏ ପଟେ ଜର୍ମାନୀକୁ ମିତ୍ର ରୂପେ ପାଇ ଅଷ୍ଟ୍ରିଆର ସାହସ ବଢ଼ିଯାଇଥିଲାବେଳେ ଇଂଲାଣ୍ଡ ଓ ଫ୍ରାନ୍ସ ସହିତ ମିତ୍ରତା ଯୋଗୁଁ ରୁଷିଆ ଅଧୁକ ଶକ୍ତିଶାଳୀ ହୋଇଯାଇଥିଲା ।
- ବାସ୍ତବରେ ଅଷ୍ଟ୍ରିଆ, ରୁଷିଆ ଓ ଜର୍ମାନୀର ରାଜନୈତିକ ପ୍ରତିଦ୍ବନ୍ଦିତା ସେହି ଅଞ୍ଚଳରେ ଘୋର ବିପଦ ସୃଷ୍ଟି କରିଥିଲା । ଫଳସ୍ୱରୂପ ୧୯୧୨-୧୩ ମସିହାରେ ସେଠାରେ ଯୁଦ୍ଧ ଲାଗିଗଲା
୪। ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ରାଜନୀତି କ୍ଷେତ୍ରରେ କେହଁ କେହଁ ପରିବର୍ତ୍ତନ ଆଣିଥିଲା ?
Answer:
ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧ ରାଜନୀତି କ୍ଷେତ୍ରରେ ନିମ୍ନଲିଖ ପରିବର୍ତ୍ତନମାନ ଆଣିଥିଲା ।
- ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ଇଉରୋପ ତଥା ଅନ୍ୟାନ୍ୟ ଦେଶଗୁଡ଼ିକରେ ସ୍ୱେଚ୍ଛାଚାରୀ ଓ ରାଜତନ୍ତ୍ର ଶାସନର ଲୋପ ଘଟାଇବା ସଙ୍ଗେ ସଙ୍ଗେ ଜର୍ମାନୀର ହୋଏନ୍ଲେଏଁ, ଅଷ୍ଟ୍ରିଆର ହାସ୍ବର୍ଗ ଏବଂ ରୁଷିଆର ରୋମାନୋଭ୍ ଭଳି ରାଜବଂଶର ପତନ ଘଟାଇଥିଲା ।
- ପୋଲାଣ୍ଡ, ବୁଲ୍ ଗେରି ଆ, ଚେକୋସ୍ଲୋଭାକିଆ ଓ ଫି ନ୍ ଲାଣ୍ଡରେ ଏକଚ୍ଛତ୍ରବାଦୀ ଶାସନର ଅନ୍ତ ଘଟିଲା ଏବଂ ସେଠାରେ ଗଣତାନ୍ତକ ନାତିନିୟମ ଅନୁସୃତ ହୋଇଥିଲା ।
- ପ୍ରଥମେ ଜର୍ମାନୀରେ ସାଧାରଣତନ୍ତ୍ର ପ୍ରତିଷ୍ଠା ହେବା ପରେ ରୁଷିଆ, ଚେକୋସ୍ଲୋଭାକିଆ, ଜର୍ମାନୀ, ଅଷ୍ଟ୍ରିଆ, ପୋଲାଣ୍ଡ, ଲିଥୁଆନିଆ, ଫିନ୍ଲାଣ୍ଡ, ତୁର୍କୀ ଆଦି ଅଞ୍ଚଳରେ ସାଧାରଣତନ୍ତ୍ର ଶାସନ ପ୍ରତିଷ୍ଠା ହୋଇଥିଲା ।
- ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ଜାତୀୟତାବାଦ ଉପରେ ଆଧାରିତ ଚିନ୍ତାଧାରାକୁ ବିଶେଷ ଗୁରୁ ତ୍ବ ଦିଆଯାଇଥ୍ ଏବଂ ସମଗ୍ର ଇଉରୋପରେ କାତାୟତାବାଦର ବିକାଶ ଘଟିଥିଲା ।

୫। ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ବିଜ୍ଞାନ ଓ ସାଂସ୍କୃତିକ କ୍ଷେତ୍ରରେ କି ପରିବର୍ତ୍ତନ ଘଟିଥିଲା ?
Answer:
ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ବିଜ୍ଞାନ ଓ ସାଂସ୍କୃତିକ କ୍ଷେତ୍ରରେ ଘଟିଥିବା ପରିବର୍ତ୍ତନମାନ ନିମ୍ନରେ ଉଲ୍ଲେଖ କରାଗଲା।
- ବିଜ୍ଞାନ କ୍ଷେତ୍ରରେ ଅଧ୍ଵ ଆବିଷ୍କାର ଓ ଉଦ୍ଭ। ବନ କରିବାପାଇଁ ବୈଜ୍ଞାନିକମାନଙ୍କ ମଧ୍ୟରେ ଆଗ୍ରହ ଆସିଥଲା ।
- ବିଜ୍ଞାନର ବିକାଶ ତଥା ଆଧୁନିକ ବୈଜ୍ଞାନିକ ଉପକରଣ ନିର୍ମାଣ କରିବାପାଇଁ ଦେଶଗୁଡ଼ିକ ମଧ୍ୟରେ ଏକ ପ୍ରତିଯୋଗିତାମୂଳକ ମନୋଭାବ ଜାଗ୍ରତ ହେଲା ।
- ସାଂସ୍କୃତିକ କ୍ଷେତ୍ରରେ ପ୍ରଥମ ବିଶ୍ବଯୁଦ୍ଧର ପରିଣାମ ନକାରାତ୍ମକ ଥିଲା । ଏହି ଯୁଦ୍ଧରେ ସାହିତ୍ୟିକ, ଐତିହାସିକ, ଅନେକ ବୈଜ୍ଞାନିକ, କଳାକାର ପ୍ରଭୃତି ଜୀବନ ହରାଇବା ଯୋଗୁଁ ଦେଶର ପ୍ରଗତିରେ ବାଧା ସୃଷ୍ଟି ହେଲା ।
- ସାଂସ୍କୃତିକ ଦୃଷ୍ଟିକୋଣରୁ ବିଶିଷ୍ଟ ସ୍ଥାନ ଅସ୍ଵୀକାର କରିଥିବା ତଥା ଦେଶର ଐତିହ୍ୟ ବହନ କରୁଥିବା ଅନେକ ସୁନ୍ଦର ଅଟ୍ଟାଳିକା ଏବଂ ସାଂସ୍କୃତିକ ବିକାଶରେ ସାହାଯ୍ୟ କରୁଥିବା ବିଦ୍ୟାଳୟ, ପ୍ରେକ୍ଷାଳୟ, ଚିକିତ୍ସାଳୟ, ରେଳପଥ, ସଡ଼କପଥ, ଶିଳ୍ପାନୁଷ୍ଠାନ ଓ ଧର୍ମାନୁଷ୍ଠାନ ବିଶ୍ୱଯୁଦ୍ଧ ଫଳରେ ଧ୍ବଂସ ପାଇଲା ।
୬। ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ବର୍ଷଗତ ତିକ୍ତତା କିପରି ଦୂର କରିପାରିଥିଲା ?
Answer:
ବର୍ଣ୍ଣଗତ ତିକ୍ତତା ଦୂରୀକରଣରେ ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧ ନିମ୍ନଲିଖ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲା ।
- ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପୂର୍ବରୁ ଇଂଲଣ୍ଡର ଲୋକମାନେ କଳା-ଗୋର। ବର୍ଣ୍ଣ ଗତ ବୈଷମ୍ୟ ପାଇଁ ଭାରତ ଓ ଆଫ୍ରି କାର ଲୋକମାନଙ୍କୁ ଘୃଣା କରୁଥିଲେ ।
- ବର୍ଷ ଭିଭିରେ ଜର୍ମାନ୍ ଓ ଫରାସୀମାନେ ନିଜକୁ ଅନ୍ୟ ଦେଶର ଅଧ୍ୟାସୀମାନଙ୍କଠାରୁ ଉତ୍କୃଷ୍ଟ ବୋଲି ମନେ କରୁଥିଲେ ।
- କିନ୍ତୁ ଯୁଦ୍ଧ ପରେ ପରିସ୍ଥିତିରେ ପରିବର୍ତ୍ତନ ହେଲା । ଜାତି, ଧର୍ମ, ବର୍ଣ୍ଣ ନିର୍ବିଶେଷରେ ପ୍ରାୟ ସମସ୍ତ ଜାତି ଓ ବର୍ଷର ଲୋକମାନେ ଯୁଦ୍ଧରେ ସକ୍ରିୟ ଭାଗ ନେଇଥିଲେ ।
- ଭାରତ ଓ ଆଫ୍ରିକାର ସୈନ୍ୟମାନେ ଇଂଲାଣ୍ଡ ସୈନ୍ୟବାହିନୀ ସହିତ ମିଶି ଲଢ଼େଇ କରିବାରୁ ସେମାନେ ଇଂଲାଣ୍ଡର ସହାନୁଭୂତି ପାଇଥିଲେ ଓ ଜାତିଗତ ବିଦ୍ବେଷ ଓ ବର୍ଣ୍ଣଗତ ତିକ୍ତତା ହ୍ରାସ ପାଇଥିଲା ।
୭ । ୧୯୧୪ ଖ୍ରୀ.ଅ.ରେ ହୋଇଥିବା ଯୁଦ୍ଧକୁ ପ୍ରଥମ ବିଶ୍ବଯୁଦ୍ଧ କୁହାଯାଏ କାହିଁକି ?
Answer:
- ୧୯୧୪ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ ଆରମ୍ଭ ହୋଇ ଦୀର୍ଘ ଚାରିବର୍ଷରୁ ଊର୍ଦ୍ଧ୍ବକାଳ ବ୍ୟାପି ରହିଥି ମହାସମର ମନୁଷ୍ୟ ଜାତିର ଇତିହାସରେ ସେ ପର୍ଯ୍ୟନ୍ତ ସଂଘଟିତ ସମସ୍ତ ଯୁଦ୍ଧଠାରୁ ଅଧି ମାରାତ୍ମକ, ଶକ୍ତିଶାଳୀ, ସଙ୍ଗଠିତ ଓ ଭୟାବହ ଥିଲା ।
- ଏଥିରେ ପୃଥିବୀର ଅଧିକାଂଶ ଉନ୍ନତ ଦେଶ ଭାଗ ନେଇଥିଲେ ଏବଂ ଅନେକ ଆଧୁନିକ ଯୁଦ୍ଧାସ୍ତ୍ର ବ୍ୟବହୃତ ହୋଇଥିଲା । ଏଥିରେ ସୈନ୍ୟମାନଙ୍କ ସହିତ ଜନସାଧାରଣ ମଧ୍ଯ ଭାଗ ନେଇଥିଲେ ।
- ଏହି ଯୁଦ୍ଧର ଫଳାଫଳ ସୁଦୂରପ୍ରସାରୀ ଥିଲା ଓ ସମସ୍ତ କ୍ଷେତ୍ରକୁ ପ୍ରଭାବିତ କରିଥିଲା ।
- ଏହି ଯୁଦ୍ଧର ସମାପ୍ତି ହେବାର କୋଡ଼ିଏ ବର୍ଷ ପରେ ଅନ୍ୟ ଏକ ବିଶ୍ବଯୁଦ୍ଧ ସଙ୍ଗଠିତ ହୋଇଥିବାରୁ ଏହାକୁ ‘ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ’ ନାମରେ ନାମିତ କରାଯାଇଛି ।
୮। ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ମହିଳାମାନଙ୍କ ଜୀବନରେ କେଉଁ ପରିବର୍ତ୍ତନ ଆଣିଥିଲା ?
Answer:
ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ମହିଳାମାନଙ୍କ ଜୀବନରେ ନିମ୍ନଲିଖତ ପରିବର୍ତ୍ତନମାନ ଆଣିଥିଲା ।
- ସୈନ୍ୟଙ୍କ ସ୍ଥାନ ପୂରଣ କରିବାପାଇଁ ଦେଶର ସୈନ୍ୟଙ୍କ ସ୍ଥାନ ପୂରଣ କରିବାପାଇଁ ଦେଶର ଜନସାଧାରଣଙ୍କୁ ସୈନ୍ୟବାହିନୀରେ ଉପୁଜି ଥ୍ ଖାଲି ସ୍ଥାନ ଗୁଡ଼ିକ ମହିଳାମାନଙ୍କଦ୍ଵାରା ପୂରଣ ହେଲା ।
- ମହିଳାମାନେ ଦେଶର ଅର୍ଥନୈତିକ ବିକାଶ ପାଇଁ ଅନେକ କାମ କଲେ ଏବଂ ରାଜନୀତିରେ ଅଂଶଗ୍ରହଣ କଲେ ।
- ସେମାନଙ୍କ ମନରେ ଆତ୍ମବିଶ୍ଵାସ ଓ ସାହସ ବୃଦ୍ଧି ପାଇବା ଯୋଗୁଁ ସେମାନେ ପୁରୁଷମାନେ ଉପଭୋଗ କରୁଥିବା ସମସ୍ତ ସୁବିଧା ସୁଯୋଗ ଓ ଅଧିକାର ପାଇବାପାଇଁ ଦାବି କଲେ ।
- ଏହି ଯୁଦ୍ଧ ମହିଳାମାନଙ୍କ ଜୀବନରେ ବୈପ୍ଳବିକ ପରିବର୍ତ୍ତନ ଆଣି ଦେଇଥିଲା ।
କ୍ଷୁଦ୍ର ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
୧ । ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧର ଏପରି ନାମକରଣ ହୋଇଛି କାହିଁକି ?
Answer:
(i) ୧୯୧୪ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ ହୋଇଥିବା ଯୁଦ୍ଧରେ ଅଧିକାଂଶ ଉନ୍ନତ ରାଷ୍ଟ୍ର ଭାଗ ନେଇଥିଲେ ଓ ଅନେକଗୁଡ଼ିଏ ସଂସାତ୍ମକ ଯୁଦ୍ଧାସ୍ତ୍ର ବ୍ୟବହୃତ ହୋଇଥିଲା ।
(ii) ଏହି ଯୁଦ୍ଧରେ ସୈନ୍ୟମାନଙ୍କ ବ୍ୟତୀତ ଯୁଦ୍ଧରତ ଦେଶମାନଙ୍କର କନସାଧାରଣଙ୍କ ମ ପ୍ରକାରାନ୍ତରେ ଭାଗ ନେବାକୁ ପଡ଼ିଥିଲା । ତେଣୁ ଏହି ଯୁଦ୍ଧକୁ ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ କୁହାଯାଏ ।
୨। କେବେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ମିତ୍ର ଶକ୍ତି ସପକ୍ଷରେ ଯୋଗଦେଲା ? ଏହାର ପରିଣତି କ’ଣ ହେଲା ?
Answer:
(i) ୧୯୧୭ ମସିହାରେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ମିତ୍ରଶକ୍ତି ସପକ୍ଷରେ ଯୋଗଦେଲା ।
(ii) ଏହା ଫଳରେ ଯୁଦ୍ଧର ଗତିପଥ ବଦଳିଗଲା । କ୍ରମେ ଜର୍ମାନୀ ଓ କେନ୍ଦ୍ର ଶକ୍ତି ଅନ୍ତର୍ଭୁକ୍ତ ରାଷ୍ଟ୍ରମାନେ ରଣକ୍ଷେତ୍ରରେ ପରାଜୟ ବରଣ କଲେ ।

୩ । କେଉଁ ସ୍ଥାନୀୟ ଘଟଣାକୁ କେନ୍ଦ୍ର କରି ପ୍ରଥମ ବିଶ୍ବଯୁଦ୍ଧର ସୂତ୍ରପାତ ହୋଇଥିଲା ?
Answer:
(i) ୧୯୧୪ ମସିହା ଜୁନ୍ ମାସ ୧୮ ତାରିଖରେ ସର୍ବ ଜାତିର ଜଣେ ଯୁବକ ଅଷ୍ଟ୍ରିଆ- ହଙ୍ଗେରୀର ଯୁବରାଜ ଫ୍ରାନ୍ସିସ୍ ଫର୍ଜିନାଣ୍ଡ ଓ ତାଙ୍କର ପତ୍ନୀ ସୋଫିଆଙ୍କୁ ବୋସ୍ ଆ ରାଜ୍ୟର ରାଜଧାନୀ ସାରାଜେଭୋଠାରେ ଗୁଳି କରି ହତ୍ୟା କଲା ।
(ii) ଏହାର ପ୍ରତିକ୍ରିୟାସ୍ବରୂପ ୧୯୧୪ ମସିହା ଜୁଲାଇ ୨୮ ତାରିଖରେ ଅଷ୍ଟ୍ରିଆ ସର୍ବିଆ ଆକ୍ରମଣ କରିବାରୁ ପ୍ରଥମ ବିଶ୍ଵ ଯୁଦ୍ଧର ସୂତ୍ରପାତ ହୋଇଥିଲା ।
୪। ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ କେବେ ଆରମ୍ଭ ହୋଇଥିଲା ଓ କେବେ ଶେଷ ହେଲା ? ଏହି ଯୁଦ୍ଧରେ କେତେ ଲୋକ ଅଂଶଗ୍ରହଣ କରିଥିଲେ ?
Answer:
(i) ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧ ୧୯୧୪ ମସିହା ଜୁଲାଇ ୨୮ ତାରିଖରୁ ଆରମ୍ଭ ହୋଇ ୧୯୧୮ ମସିହା ନଭେମ୍ବର ୧୧ ତାରିଖରେ ଶେଷ ହେଲା ।
(ii) ଏହି ଯୁଦ୍ଧରେ ଉଭୟ ପକ୍ଷରୁ ପ୍ରାୟ ୬୫୦ ଲ କ୍ଷ ରୁ ଲକ୍ଷରୁ ଅଧିକ ଲୋକ ଅଂଶଗ୍ରହଣ କରିଥିଲେ ।
୫। ଭର୍ସାଇ ଚୁକ୍ତି କେବେ ସ୍ୱାକ୍ଷରିତ ହୋଇଥିଲା ? ଏହି ଚୁକ୍ତିର ସଉଁଗୁଡ଼ିକ କିପରି ଥିଲା ?
Answer:
(i) ଭର୍ସାଇ ଚୁକ୍ତି ୧୯୧୯ ମସିହାରେ ଜର୍ମାନୀ ସହିତ ଭର୍ସାଇଠାରେ ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ।
(ii) ଏହି ଚୁକ୍ତି ର ସର୍ଭଗୁଡ଼ିକ ଏକତରଫା, ନିର୍ଦେଶାତ୍ମକ ଓ ଅପମାନଜନକ ଥିଲା ଯାହାକି ନିର୍ଦେଶାତ୍ମକ ଓ ଅପମାନଜନକ ଥିଲା ଯାହାକି କରିଥିଲା ।
୬। ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧରେ ଲଢ଼ିଥିବା ‘କେନ୍ଦ୍ରଶକ୍ତି’ ଓ ‘ମିତ୍ରଶକ୍ତି’ ଅନ୍ତର୍ଭୁକ୍ତ ରାଷ୍ଟ୍ରଗୁଡ଼ିକର ନାମ ଲେଖ । କିମ୍ବା, ପ୍ରଥମ ବିଶ୍ଵ ଯୁଦ୍ଧରେ କେଉଁ ଦେଶଗୁଡ଼ିକ ‘କେନ୍ଦ୍ରଶକ୍ତି’ ଓ ‘ମିତ୍ରଶକ୍ତି’ ନାମରେ ପରିଚିତ ହୋଇଥିଲେ ?
Answer:
(i) ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧରେ ପୃଥିବୀର ବିଭିନ୍ନ ରାଷ୍ଟ୍ର ଦୁଇଟି ପରସ୍ପର ବିରୋଧୀ ସାମରିକ ମେଣ୍ଟରେ ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇଥିଲେ; ଯଥା – କେନ୍ଦ୍ରଶକ୍ତି ଓ ମିତ୍ରଶକ୍ତି । ଜର୍ମାନୀ, ଅଷ୍ଟ୍ରିଆ, ତୁର୍କୀ ଓ ବୁଲ୍ଗେରିଆ ପ୍ରଭୃତି ଦେଶଗୁଡ଼ିକ ‘କେନ୍ଦ୍ରଶକ୍ତି’ର ଅନ୍ତର୍ଭୁକ୍ତ ଥିଲେ ।
(ii) ଅନ୍ୟ ପକ୍ଷରେ ସର୍ବିଆ, ରୁଷିଆ, ଫ୍ରାନ୍ସ, ଇଂଲାଣ୍ଡ, ବେଲ୍ଜିୟମ୍, ପର୍ତ୍ତୁଗାଲ୍, ଗ୍ରୀସ୍, ରୁ ମାନି ଆ, ଜାପାନ ଓ ଚୀନ୍ ପ୍ରଭୃତି ରାଷ୍ଟ୍ରଗୁଡ଼ିକ ‘ମିତ୍ରଶକ୍ତି’ର ଅନ୍ତର୍ଭୁକ୍ତ ଥିଲେ ।
୭। ତୁର୍କୀର ବୋସ୍ନିଆ ଓ ହର୍ଜିଗୋଭିନା ପ୍ରଦେଶକୁ ନେଇ କେବେ ଓ କିପରି ଅଷ୍ଟ୍ରିଆ ଓ ସର୍ବିଆ ମଧ୍ଯରେ ଶତ୍ରୁତା ବୃଦ୍ଧି ପାଇଲା ?
Answer:
(i) ୧୯୦୮ ମସିହା ଅକ୍ଟୋବର ୨ ତାରିଖରେ ବର୍ଲିନ୍ ମହାସଭାର ସର୍ଭକୁ ଉଲ୍ଲଙ୍ଘନ କରି ଅଷ୍ଟ୍ରିଆ ତୁର୍କୀର ବୋସ୍ନିଆ ଓ ହର୍ଜିଗୋଭିନା ପ୍ରଦେଶଦ୍ ୟକୁ ନି ଜ ସାମ୍ରାଜ୍ୟରେ ମିଶାଇଦେଲା । ଅଷ୍ଟ୍ରିଆର ଏହି ନିଷ୍ପତ୍ତିକୁ ସର୍ବିଆ ବିରୋଧ କଲା ଏବଂ ପ୍ରତିବାଦ ଜଣାଇଲା ।
(ii) ଏହି ଘଟଣାରୁ ଅଷ୍ଟ୍ରିଆ ଓ ସର୍ବିଆ ମଧ୍ୟରେ ଶତ୍ରୁତା ବୃଦ୍ଧି ପାଇଲା ।
୮। ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧର ସାଂସ୍କୃତିକ ଫଳାଫଳ କ’ଣ ଥିଲା ?
Answer:
(i) ସାଂସ୍କୃତିକ କ୍ଷେତ୍ରରେ ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧର ପରିଣାମ ନକାରାତ୍ମକ ଥିଲା । ଏହି ଯୁଦ୍ଧରେ ଅନେକ ସାହିତ୍ୟିକ, ଐତିହାସିକ, ବୈଜ୍ଞାନିକ, କଳାକାର ପ୍ରଭୃତି ଜୀବନ ହରାଇବା ଫଳରେ ଦେଶର ସାଂସ୍କୃତିକ ପ୍ରଗତି ବାଧାପ୍ରାପ୍ତ ହେଲା ।
(ii) ଦେଶର ଐତିହ୍ୟ ବହନ କରୁଥିବା ଅନେକ ସୁନ୍ଦର ଅଟ୍ଟାଳିକା ଏବଂ ସାଂସ୍କୃତିକ ବିକାଶରେ ସାହାଯ୍ୟ କରୁଥିବା ବିଦ୍ୟାଳୟ, ପ୍ରେକ୍ଷାଳୟ, ଚିକିତ୍ସାଳୟ, ରେଳ ପଥ, ସଡ଼କ ପଥ, ଶିଳ୍ପାନୁଷ୍ଠାନ ଓ ଧର୍ମାନୁଷ୍ଠାନ ଆଦି ଧ୍ୱଂସ ପାଇଥିଲା ।
୯। ମହିଳାମାନଙ୍କ ଜୀବନରେ ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ କି କି ରାଜନୈତିକ ଓ ଅର୍ଥନୈତିକ ପରି ବ ର୍ଷ ନ ଆଣିଥିଲା ?
Answer:
(i) ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧ ପରେ ମହିଳାମାନେ ଦେଶର ଅର୍ଥନୈତିକ ବିକାଶ ପାଇଁ କାମ କଲେ ଏବଂ ରାଜନୈତିକ ଆଦୋଳନଗୁଡିକରେ ସକିୟ ଘଟିଲା ଅଂଶଗ୍ରହଣ କଲେ ।
(ii) ସେମାନଙ୍କ ମଧ୍ୟରେ ଆତ୍ମବିଶ୍ଵାସ ଓ ସାହସ ବୃଦ୍ଧି ପାଇଲା । ସେମାନେ ପୁରୁଷମାନଙ୍କ ସହିତ ସମାନ ମର୍ଯ୍ୟାଦା ଓ ସାମାଜିକ ସ୍ଥିତି ଦାବି କଲେ ।
୧୦ । ବର୍ଣ୍ଣଗତ ବୈଷମ୍ୟ ନୀତିକୁ ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ କିପରି ଦୂର କରିପାରିଥିଲା ?
Answer:
(i) ଯୁଦ୍ଧରେ ଜାତି, ଧର୍ମ, ବର୍ଣ୍ଣ ନିର୍ବିଶେଷରେ ପ୍ରାୟ ସମସ୍ତ ଜାତି ଓ ବର୍ଣ୍ଣର ଲୋକମାନେ ଭାଗନେବା ଫଳରେ ସେମାନଙ୍କ ମଧ୍ୟରେ ବର୍ଣ୍ଣଗତ ବୈଷମ୍ୟ ରହିଲା ନାହିଁ ।
(ii) ଭାରତ ଓ ଆଫ୍ରିକାର ସୈନ୍ୟମାନେ ଇଂଲାଣ୍ଡ ସୈନ୍ୟବାହିନୀ ସହିତ ମିଶି ଲଢ଼ିବାରୁ ସେମାନେ ଇଂଲାଣ୍ଡର ସହାନୁଭୂତି ପାଇଲେ ଏବଂ ସେମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ଜାତିଗତ ବିଦ୍ବେଷ ଓ ବର୍ଣ୍ଣଗତ ତିକ୍ତତା ହ୍ରାସ ପାଇଲା ।
୧୧ । ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ଟଙ୍କାର ମୂଲ୍ୟ କାହିଁକି ହ୍ରାସ ପାଇଥିଲା ?
Answer:
(i) ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧ ଲୋକଙ୍କର ଆର୍ଥିକ ଅବସ୍ଥାକୁ ଦୁର୍ବଳ କରି ଦେଇଥିଲା । ଭାରୀ ସଂଖ୍ୟାର କାଗଜ ଟଙ୍କା ପ୍ରଚଳନ କରିବାକୁ ପଡ଼ିଲା ।
(ii) ଏହା ଫଳରେ ମୁଦ୍ରାଷ୍ଟୀତି ଘଟିଲା । ଫଳରେ ଟଙ୍କାର ମୂଲ୍ୟ ହ୍ରାସ ପାଇଲା ଓ ଜିନିଷପତ୍ରର ଦରଦାମ୍ ବୃଦ୍ଧି ପାଇଲା ।

୧୨ । ସରକାର ଲୋକଙ୍କ ଉପରେ କାହିଁକି ଟିକସ ବସାଇଥିଲେ ? ଏହାର ପରିଣାମ କ’ଣ ହେଲା ?
Answer:
(i) ଆର୍ଥିକ ଆବଶ୍ୟକତାକୁ ପୂରଣ କରିବା ଉଦ୍ଦେଶ୍ୟରେ ଅନେକ ଦେଶରେ ସରକାର ବିଭିନ୍ନ ପ୍ରକାର ଟିକସ ବସାଇଲେ ।
(ii) ଆର୍ଥିକ ଦୂରବସ୍ଥାରେ କଷ୍ଟ ପାଉଥ୍ ଉଦ୍ଦେଶ୍ୟରେ ଅନେକ ଦେଶରେ ସରକାର ନଳିତା ବିଡ଼ା ସଦୃଶ ଥିଲା । ଅତିମାତ୍ରାରେ ଟିକସର ବୋଝ ଲୋକମାନଙ୍କ ମଧ୍ୟରେ ଅସନ୍ତୋଷ ବୃଦ୍ଧି କରିଥିଲା ।
୧୩ । କେବେ ଓ କାହିଁକି ପ୍ୟାରିସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀ ଆହୂତ ହୋଇଥିଲା ?
Answer:
ରାଷ୍ଟ୍ରମାନଙ୍କ ମଧ୍ୟରେ ଆନ୍ତର୍ଜାତିକବାଦର ବିକାଶ ଘଟିବା ଫଳରେ ଭବିଷ୍ୟତରେ ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ଭଳି ଯୁଦ୍ଧର ଆଶଙ୍କାକୁ ଦୂର କରି ଶାନ୍ତିପୂର୍ଣ୍ଣ ସହାବସ୍ଥାନ ଅବଲମ୍ବନ କରିବା ଉଦ୍ଦେଶ୍ୟରେ ୧୯୧୯ ମସିହାରେ ପ୍ୟାରିସ୍ ଶାନ୍ତି ସମ୍ମିଳନୀ ଆହୂତ ହୋଇଥିଲା ।
୧୪ । ଭୂମିକା ଗ୍ରହଣ କରିଥିଲେ ? ଏହି ସମ୍ମିଳନୀରେ ସ୍ୱାକ୍ଷରିତ ହୋଇଥିବା ସବୁଠାରୁ ଗୁରୁତ୍ବପୂର୍ଣ୍ଣ ଚୁକ୍ତିର ନାମ କ’ଣ ଥିଲା ?
Answer:
(i) ଫ୍ରାନ୍ସ ପ୍ରଧାନମନ୍ତ୍ରୀ କ୍ଲି ମେନ୍ ଙ୍କ ସଭାପତିତ୍ବରେ ଅନୁଷ୍ଠିତ ପ୍ୟାରିସ୍ ଶାନ୍ତି ସମ୍ମିଳନୀରେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରି କାର ରାଷ୍ଟ୍ରପତି ଉଡ୍ରୋ ଉଇଲ୍ ସନ୍, ଇଂଲାଣ୍ଡର ପ୍ରଧାନମନ୍ତ୍ରୀ ଲଏଡ୍ ଜର୍ଜ ଓ କ୍ଲିମେନ୍ସ୍ ସମସ୍ତ ନିଷ୍ପଭି ନିର୍ଦ୍ଧାରଣରେ ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲେ ।
(ii) ଏହି ସମ୍ମିଳନୀରେ ସ୍ଵାକ୍ଷରିତ ହୋଇଥ ସବୁଠାରୁ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ଚୁକ୍ତିର ନାମ ‘ଭର୍ସାଇ ଚୁକ୍ତି’ ଥିଲା ।
୧୫ । ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ କେଉଁ ଦେଶରେ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲେ ? ସମାପ୍ତି ଘଟି ସାଧାରଣତନ୍ତ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ? ଏହାପରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିବା ସାଧାରଣତନ୍ତ୍ର ରାଷ୍ଟ୍ରଗୁଡ଼ିକର ନାମ କ’ଣ ?
Answer:
(i) ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ଜର୍ମାନ୍ ଦେଶରେ ସାଧାର ଶାସନର ସମାପ୍ତି ଘଟି ସାଧାରଣତନ୍ତ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।
(ii) ଏହାକୁ ଅନୁକରଣ କରି ପ୍ରତିଷ୍ଠିତ ହୋଇଥିବା ସାଧାରଣତନ୍ତ୍ର ରାଷ୍ଟ୍ର ଗୁଡ଼ିକ ହେଲା – ରୁଷିଆ, ଚେକୋସ୍ଲୋଭାକିଆ, ଜର୍ମାନୀ, ଅଷ୍ଟ୍ରିଆ, ପୋଲାଣ୍ଡ, ଲିଥୁଆନିଆ, ଫିନ୍ଲାଣ୍ଡ, ତୁର୍କୀ ପ୍ରଭୃତି ।
୧୬ । ଭର୍ସାଇ ଚୁକ୍ତି କିପରି ଦ୍ଵିତୀୟ ବିଶ୍ବଯୁଦ୍ଧର କାରଣ ହୋଇଥିଲା ?
Answer:
(i) ଭର୍ସାଇ ଚୁକ୍ତିର ସଉଁଗୁଡ଼ିକ ଏକତରଫା,ନି ଶାମ୍ କ ଓ ଅପମାନଜନକ ହୋଇଥ୍ ବାରୁ ଏହା ଜର୍ମାନୀରେ ପ୍ରତିଶୋଧପରାୟଣତା ସୃଷ୍ଟି କଲା ।
(ii) ଏହା ଭବିଷ୍ୟତରେ ଦ୍ଵିତୀୟ ବିଶ୍ଵଯୁଦ୍ଧ ପାଇଁ ଏକ କାରଣ ହୋଇଥିଲା ।
୧୭ । କାହାର ପ୍ରସ୍ତାବ ଅନୁଯାୟୀ ଏକ ଆନ୍ତର୍ଜାତିକ ଅନୁଷ୍ଠାନ ପ୍ରତିଷ୍ଠା ପାଇଁ ନିଷ୍ପତ୍ତି ନିଆଗଲା ଏବଂ ଫଳସ୍ବରୂପ କେଉଁ ଅନୁଷ୍ଠାନ ସୃଷ୍ଟି ହେଲା ?
Answer:
(i)ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ରାଷ୍ଟ୍ରପତି ଉଡ୍ରୋ ଉଇଲ୍ସନ୍ଙ୍କ ପ୍ରସ୍ତାବ ଅନୁଯାୟୀ ରାଷ୍ଟ୍ରମାନଙ୍କ ସମସ୍ୟ।ଗୁଡ଼କୁ ପରସ୍କର ମଧ୍ୟରେ ଆଲୋଚନା ମାଧ୍ୟମରେ ସମାଧାନ କରିବାକୁ ଏବଂ ସ୍ଥାୟୀ ଭାବରେ ଏକ ଆନ୍ତର୍ଜାତିକ ଅନୁଷ୍ଠାନ ପ୍ରତିଷ୍ଠା କରିବାପାଇଁ ପ୍ୟାରିସ୍ ଶାନ୍ତି ସମ୍ମିଳନୀରେ ନିଷ୍ପତ୍ତି ନିଆଯାଇଥିଲା ।
(ii) ଏହି ନିଷ୍ପତ୍ତିର ଫଳସ୍ଵରୂପ ‘ଜାତିସଂଘ’ ସୃଷ୍ଟି ହେଲା ।
୧୮ । ତୁର୍କୀର ସୁଲତାନ୍ କେବେ ଆତ୍ମସମର୍ପଣ କରିଥିଲେ ଏବଂ ଏହାର ପରିଣାମ କ’ଣ ଥିଲା ?
Answer:
(i) ତୁର୍କୀର ସୁଲତାନ୍ ୧୯୨୨ ମସିହା ନଭେମ୍ବର ମାସରେ ଆତ୍ମସମର୍ପଣ କରି ରାଜଗାଦି ପରିତ୍ୟାଗ କରିଥିଲେ ।
(ii) ଏହାଦ୍ଵାରା ରାଜବଂଶ ଶାସନର ସମାପ୍ତି ଘଟିଲା । ଏହାପରେ ୧୯୨୩ ମସିହାରେ ଖଲିଫା ପଦର ଉଚ୍ଛେଦ ଘଟିଥିଲା ।
୧୯ । ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ କେଉଁ କେଉଁ ରାଷ୍ଟ୍ରରେ ଏକଚ୍ଛତ୍ରବାଦୀ ଶାସନର ଅନ୍ତ ଘଟିଥିଲା ଏବଂ କେଉଁ କେଉଁ ରାଷ୍ଟ୍ରରେ ଗଣତାନ୍ତ୍ରିକ ନୀତି ନିୟମ ଅନୁସୃତ ହୋଇଥିଲା ?
Answer:
(i) ପ୍ରଥମ ବିଶ୍ଵ ଯୁଦ୍ଧ ପରେ ପୋଲାଣ୍ଡ, ବୁଲ୍ ଗେରିଆ, ଚେକୋସ୍ଲୋଭାକିଆ ଓ ଫିନ୍ଲାଣ୍ଡରେ ଏକଚ୍ଛତ୍ରବାଦୀ ଶାସନର ଅନ୍ତ ଘଟିଲା ।
(ii) ଇଂଲାଣ୍ଡ, ସ୍ପେନ୍, ଗ୍ରୀସ୍ ଓ ରୁମାନିଆରେ ଇଂଲାଣ୍ଡ, ସ୍ପେନ୍, ଗ୍ରୀସ୍ ଓ ରୁମାନିଆରେ ନଥିଲେ ସୁଦ୍ଧା ସେସବୁ ଦେଶଗୁଡ଼ିକରେ ଗଣତାନ୍ତ୍ରିକ ନୀତି ନିୟମ ଅନୁ ସୂତ ହୋଇଥିଲା ।
୨୦ । କାଇଜର ଦ୍ବିତୀୟ ଉଇଲିୟମ୍ କିଏ ଥିଲେ ? ସେ କେଉଁ ନୀତି ଅବଲମ୍ବନ କରିଥିଲେ ?
Answer:
(i) ଜର୍ମାନୀରେ ହୋଏନ୍ଲେର୍ୟ ବଂଶର ଶେଷ ଶାସକ ଥିଲେ କାଇଜର ଦ୍ବିତୀୟ ଉଇଲିୟମ୍ ।
(ii) ଜର୍ମାନୀରେ ହୋଏନ୍ଲେର୍ୟ ବଂଶର ଶେଷ କରି ଏକ ଅସ୍ଥିର ଓ ଅପରିଣାମଦର୍ଶୀ ନୀତି ଅବଲମ୍ବନ କରିଥିଲେ ।
୨୧ । ନିକଟ ପ୍ରାଚ୍ୟ କହିଲେ କେଉଁ ଅଞ୍ଚଳକୁ ବୁଝାଏ ? ଏହାର ଉତ୍ତର ଓ ଦକ୍ଷିଣରେ କ’ଣ ରହିଛି ?
Answer:
(i) ନିକଟ ପ୍ରାଚ୍ୟ କହିଲେ ବଲ୍କାନ୍ ଅଞ୍ଚଳକୁ ବୁଝାଏ ।
(ii) ଏହାର ଉତ୍ତର ଭାଗଟି ଆଡ୍ରିଆଟିକ୍ ଓ କୃଷ୍ଣସାଗର ମଧ୍ୟବର୍ତ୍ତୀ ଅଞ୍ଚଳ ଏବଂ ଦକ୍ଷିଣ ଭାଗଟି ଆଇଓନିଆନ୍ ଏବଂ ଏଜିଆନ୍ ସାଗର ମଧ୍ୟବର୍ତୀ ଗ୍ରୀସ୍ ଉପଦ୍ଵୀପ ଅଟେ ।
୨୨ । ସର୍ବିଆ କାହାକୁ ଘୁଷୁରୀ ରାଜନୀତି ଭାବେ ଅଭିହିତ କରିଥିଲା ?
Answer:
(i) ବିଦେଶକୁ ଘୁଷୁରୀ ରପ୍ତାନି ସର୍ବିଆର ଏକ ପ୍ରଧାନ ବ୍ୟବସାୟ ଥିଲା ।
(ii) ଆଡ୍ରି ଆଟିକ୍ ସାଗରକୁ ପ୍ରବେଶ ବନ୍ଦ କରିବାଦ୍ଵାରା ସର୍ବିଆର ବ୍ୟବସାୟରେ କ୍ଷତି ହେଲା । ସର୍ବିଆ ଏହାକୁ ଅଷ୍ଟ୍ରିଆର ଘୁଷୁରୀ ରାଜନୀତି ବୋଲି ଅଭିହିତ କଲା ।

୨୩ । ସର୍ବିଆ ଉପରେ ପ୍ରତିଶୋଧ ନେବାପାଇଁ ଅଷ୍ଟ୍ରିଆ କିପରି ସୁଯୋଗ ପାଇଲା ? ଅଷ୍ଟ୍ରିଆକୁ କିଏ ନିଃସର୍ତ୍ତ ସମର୍ଥନ କରିଥିଲା ?
Answer:
(i) ସର୍ବ ଜାତିର ଜଣେ ଯୁବକଦ୍ଵାରା ଅଷ୍ଟିଆ- ହଙ୍ଗେରୀ ରାଜକୁମାରଙ୍କ ହତ୍ୟା ସର୍ବିଆ ଉପରେ ପ୍ରତିଶୋଧ ନେବାପାଇଁ ଅଷ୍ଟ୍ରିଆକୁ ସୁଯୋଗ ଦେଇଥିଲା ।
(ii) ସର୍ବିଆ ବିରୁଦ୍ଧରେ ଅଷ୍ଟ୍ରିଆକୁ ଜର୍ମାନୀ ନିଃସର୍ଭ ସମର୍ଥନ କରିଥିଲା ।
୨୪ । ଅଷ୍ଟ୍ରିଆ ଓ ସର୍ବିଆ ମଧ୍ଯରେ ତିକ୍ତତା ବୃଦ୍ଧି ପାଇବାର ମୁଖ୍ୟ କାରଣ କ’ଣ ଥିଲା ?
Answer:
(i) ବୋସ୍ନିଆ ଓ ହର୍ଜିଗୋଭିନାକୁ ନିଜ ଦେଶରେ ସାମିଲ କରିବା ବିଷୟକୁ ନେଇ ଏବଂ।
(ii) ଆଡ୍ରି ଆଟିକ୍ ସାଗର ମଧ୍ୟକୁ ସର୍ବିଆର ପ୍ରବେଶପଥ ଅବରୋଧ କରିଥିବା ହେତୁ ଅଷ୍ଟ୍ରିଆ ଓ ସର୍ବିଆ ମଧ୍ୟରେ ତିକ୍ତତା ସୃଷ୍ଟି ହୋଇଥିଲା ।
୨୫ । ତୁର୍କୀରେ ଶେଷ ସୁଲତାନ କିଏ ଥିଲେ ? ସେ କେବେ ଆତ୍ମସମର୍ପଣ କରିବାରୁ ତୁର୍କୀରେ ସୁଲତାନୀ ଶାସନର ପରିସମାପ୍ତି ଘଟିଲା ?
Answer:
(i) ତୁର୍କୀରେ ଶେଷ ସୁଲତାନ ଥିଲେ ଷଷ୍ଠ ମହମ୍ମଦ ୱାହିଦଲ୍-ଦିନ୍ ।
(ii) ୧୯୨୨ ମସିହା ନଭେମ୍ବର ମାସରେ ସେ କେବେ ଆତ୍ମସମର୍ପଣ କରିବାରୁ ତୁର୍କୀରେ ସୁଲତାନୀ ଶାସନର ପରିସମାପ୍ତି ଘଟିଲା ।
୨୬ । ଜର୍ମାନୀ କେଉଁଥିପାଇଁ ତୁର୍କୀର ଅନୁମତି ଆବଶ୍ୟକ କରୁଥିଲା ଏବଂ ଏହାକୁ କିଏ ବିରୋଧ କରୁଥିଲା ?
Answer:
(i) ଜର୍ମାନୀ ନିଜର ବାଣିଜ୍ୟ ବ୍ୟବସାୟ ବୃଦ୍ଧି କରିବାପାଇଁ ଓ ବର୍ଲିନ୍-ବାଦ୍ ରେଳପଥ ପ୍ରକଳ୍ପ ନିର୍ମାଣ କରିବାପାଇଁ ତୁର୍କୀର ଅନୁମତି ଆବଶ୍ୟକ କରୁଥିଲା ।
(ii) ଇଂଲାଣ୍ଡ ଏହାକୁ ବିରୋଧ କରୁଥିଲା ।
୨୭ । ଜର୍ମାନୀର ପ୍ରାଚ୍ୟ ନୀତିକୁ ରୁଷିଆ କାହିଁକି ବିରୋଧ କରିଥିଲା ?
Answer:
ଫ୍ରାନ୍ସର ଘନିଷ୍ଠ ବନ୍ଧୁ ହିସାବରେ ରୁଷିଆ ମଧ୍ୟ ଫ୍ରାନ୍ସର ଘନିଷ୍ଠ ବନ୍ଧୁ ହିସାବରେ ରୁଷିଆ ମଧ୍ୟ ଜର୍ମାନୀର ପ୍ରାଚ୍ୟ ନୀତିକୁ ବିରୋଧ କରିଥିଲା ।
୨୮ । ଉଗ୍ର ସାମ୍ରାଜ୍ୟବାଦର ସୃଷ୍ଟି କିପରି ହୋଇଥିଲା ?
(i) ଅର୍ଥନୈତିକ ପ୍ରଭାବ ବିସ୍ତାର ସହ ରାଜନୈତିକ ଆଧୂପତ୍ୟ ବିସ୍ତାର ପାଇଁ ଦେଶ ଦେଶ ମଧ୍ୟରେ ଅହେତୁକ ଔପନିବେଶିକ ପ୍ରତିଦ୍ବନ୍ଦିତା ସୃଷ୍ଟି ହୋଇଥିଲା ।
(ii) ଏହା ପ୍ରତିଦ୍ବନ୍ଦିତାଳକ ଔପନିବେଶିକବାଦରୁ ଉଗ୍ର ସାମ୍ରାଜ୍ୟବାଦ ଜନ୍ମ ନେଲା ।
୨୯ । ଉଗ୍ର ଜାତୀୟତାବାଦରେ ଅନୁପ୍ରାଣିତ ହୋଇ ଜର୍ମାନୀ କ’ଣ କରିଥିଲା ? ବଲ୍କାନ୍ ଅଞ୍ଚଳ ଏହାଦ୍ଵାରା କିପରି ପ୍ରଭାବିତ ହୋଇଥିଲା ?
Answer:
(i) ଉଗ୍ର ଜାତୀୟତାବାଦରେ ଅନୁପ୍ରାଣିତ ହୋଇ ଜର୍ମାନୀର ଜନସାଧାରଣ ଓ ସରକାର ଜର୍ମାନୀକୁ ବିଶ୍ୱର ସର୍ବଶ୍ରେଷ୍ଠ ରାଷ୍ଟ୍ର ବୋଲି ମନେକରିଥିଲେ ।
(ii) ବଲ୍ କାନ୍ ରାଜ୍ୟମାନଙ୍କର ଆଭ୍ୟନ୍ତରୀଣ ରାକନାତି ମଧ୍ୟ ଉଗ୍ର ଜାତୀୟତାବାଦରେ ପ୍ରଭାବିତ ହୋଇଥିଲା ।
୩୦ । ଜର୍ମାନୀ ଏକତ୍ରୀକରଣରେ କିଏ ଓ କେବେ ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲେ ?
Answer:
(i) ବିସ୍ମାର୍କ ୧୮୭୧ ମସିହାରୁ ୧୮୯୦ ମସିହା ପର୍ଯ୍ୟନ୍ତ ଜର୍ମାନୀର ଚାନ୍ ସେଲ୍ର ଥିଲେ ।
(ii) ଜର୍ମାନୀର ଏକତ୍ରୀକରଣରେ ସେ ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲେ ।
୩୧ । ସମଗ୍ର ବିଶ୍ଵରେ ଆଲ୍ପତ୍ୟ ବିସ୍ତାର କରିବାପାଇଁ କିଏ ଓ କେଉଁ ନୀତି ଅବଲମ୍ବନ କରିଥିଲେ ଓ ଏହାର ଫଳାଫଳ କ’ଣ ଥିଲା ?
Answer:
(i) ଜର୍ମାନୀର କାଇଜର ଦ୍ବିତୀୟ ଉଇଲିୟମ୍ ସମଗ୍ର ବିଶ୍ୱ ରେ ଆଧ୍ୟାତ୍ୟ ବିସ୍ତାର କରିବାପାଇଁ ନୀତି ଅବଲମ୍ବନ କରିବା ଯୋଗୁଁ ଇଂଲାଣ୍ଡକୁ ନିଜର ନିରପେକ୍ଷ ନୀତି ତ୍ୟାଗ କରିବାକୁ ପଡ଼ିଲା ।
(ii) ଫଳରେ ୧୯୦୨ ମସିହାରେ ଇଂଲାଣ୍ଡ ବାଧ୍ୟ ହୋଇ ଜାପାନ ସହିତ, ୧୯୦୪ ମସିହାରେ ଫ୍ରାନ୍ସ ସହିତ ଏବଂ ୧୯୦୭ ମସିହାରେ ରୁଷିଆ ସହିତ ଚୁକ୍ତି ସ୍ୱାକ୍ଷର କଲା ।
୩୨ । ଉଡ୍ର ଉଇଲ୍ ସନ୍ କିଏ ? ପ୍ୟାରିସ୍ ଶାନ୍ତି କିଏ ଓ କେଉଁ ନୀତି ଅବଲମ୍ବନ କରିଥିଲେ ଓ ଏହାର କରିଥିଲେ ?
Answer:
(i) ଉଡ୍ରୋ ଉଇଲ୍ସନ୍ ଆମେରିକାର ରାଷ୍ଟ୍ରପତି ଥିଲେ ।
(ii) ପ୍ୟାରିସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀରେ ସେ ଇଂଲାଣ୍ଡର ପ୍ରଧାନ ମନ୍ତ୍ରୀ ଲଏଡ୍ ଜର୍ଜ ଓ ଫ୍ରାନ୍ସ ର ପ୍ରଧାନମନ୍ତ୍ରୀ କ୍ଲିମେନ୍ ଙ୍କ ସହିତ ମିଶି ସମସ୍ତ ନୀତି ନିର୍ଦ୍ଧାରଣରେ ଗୁରୁତ୍ବପୂର୍ଣ୍ଣ ଭୂମିକା ନିର୍ବାହ କରିଥିଲେ ।
୩୩ । ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ଶିକ୍ଷା କ୍ଷେତ୍ରରେ କିଭଳି ପ୍ରଭାବ ପକାଇଥିଲା ?
Answer:
(i) ଯୁଦ୍ଧ କ୍ଷେତ୍ରରେ ଲଢ଼େଇ କରି ବାପାଇଁ ସୈନ୍ୟମାନଙ୍କ ଆବଶ୍ୟକତା ବୃଦ୍ଧି ପାଇବା ବହୁ ସଂଖ୍ୟକ ସୈନ୍ୟବାହିନୀରେ ଯୋଗଦେଲେ । ସମସ୍ତଙ୍କ ପାଇଁ ସାମରିକ ପ୍ରଶିକ୍ଷଣ ବାଧ୍ୟତାମୂଳକ ହେଲା ।
(ii) ବିଦ୍ୟାର୍ଥୀଙ୍କ ସଂଖ୍ୟା ହ୍ରାସ ପାଇବା ଯୋଗୁଁ ଅନେକଗୁଡ଼ିଏ ଶିକ୍ଷାନୁଷ୍ଠାନ ବନ୍ଦ ହୋଇଗଲା । ଫଳରେ ଶିକ୍ଷାର ପ୍ରଗତିରେ ଶି ସ୍ଥୂଳତା ଦେଖାଦେଲା ।
୩୪ । ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧର ଫଳାଫଳ ଶ୍ରମିକ ଶ୍ରେଣୀର ପୁନରୁତ୍ଥାନରେ କିପରି ସାହାଯ୍ୟ କରିଥିଲା ?
Answer:
(i) ଶ୍ରମିକମାନେ ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧ ସମୟରେ ବହୁ ଅସ୍ତ୍ରଶସ୍ତ୍ର ଓ ଯୁଦ୍ଧ ସାମଗ୍ରୀ ଉତ୍ପାଦନରେ ଅଂଶଗ୍ରହଣ କରି ଦେଶର ରାଜନୀତିରେ ଏକ ବିଶିଷ୍ଠ ସ୍ଥାନ ଅଧିକାର କରିପାରିଥିଲେ ।
(ii) ଯୁଦ୍ଧ ଶେଷ ହେବା ପରେ ବ୍ୟବସାୟ ତଥା ଦେଶର ଶାସନରେ ସେମାନଙ୍କ ଭୂମିକା ନିର୍ଦ୍ଧାରଣ କରିବାପାଇଁ ସେମାନେ ଦାବି କଲେ ଏବଂ ଣ୍ତମିକ ସଂଘଗୁଡ଼କି ଆଦୋଳନକୁ ସଫଳ କରିବାପାଇଁ ସମସ୍ତ ଉଦ୍ୟମ କଲେ । ବିଶ୍ବଯୁଦ୍ଧର ଏକ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ପରିଣାମ ଥିଲା ।
୩୫ । ‘ତ୍ରିଶକ୍ତି ମେଣ୍ଟ’ କେବେ ଓ କେଉଁମାନଙ୍କୁ ନେଇ ଗଠିତ ହୋଇଥିଲା ?
Answer:
(i) ୧୮୭୯ ମସିହାରେ ବିସ୍ମାର୍କ ଅଷ୍ଟ୍ରିଆ ସହ ଏକ ରାଜିନାମା ସ୍ବାକ୍ଷର କରିଥିଲେ ।
(ii) ୧୮୮୨ ମସିହାରେ ଇଟାଲୀ ଏଥିରେ ଯୋଗ ଦେବାରୁ ଜର୍ମାନୀ, ଅଷ୍ଟ୍ରିଆ ଓ ଇଟାଲୀ ମଧ୍ୟରେ ‘ତ୍ରିଶକ୍ତି ମେଣ୍ଟ’ ଗଠିତ ହେଲା ।

୩୬ । ‘ତ୍ରିମିତ୍ର ପକ୍ଷ’ କେବେ ଓ କେଉଁମାନଙ୍କୁ ନେଇ ଗଠିତ ହୋଇଥିଲା ?
Answer:
(i) ଇଂଲାଣ୍ଡ ୧୯୦୪ ମସିହାରେ ଫ୍ରାନ୍ସ ସହ ଓ ୧୯୦୭ ମସିହାରେ ରୁଷିଆ ସହ ଚୁକ୍ତି ସ୍ୱାକ୍ଷର କଳା ।
(ii) ଏହି ପରିପ୍ରେକ୍ଷୀରେ ଇଂଲାଣ୍ଡ, ରୁଷିଆ ଓ ଫ୍ରାନ୍ସ ମଧ୍ୟରେ ‘ତ୍ରିମିତ୍ର ପକ୍ଷ’ ଗଠିତ ହୋଇଥିଲା ।
୩୭ । ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧ ପରେ ଜର୍ମାନୀ ସହିତ ସ୍ବାକ୍ଷରିତ ହୋଇଥିବା ସନ୍ଧିର ନାମ କ’ଣ ଥିଲା ? ଏହା କେବେ ସ୍ୱାକ୍ଷରିତ ହୋଇଥିଲା ?
Answer:
(i) ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ଜର୍ମାନୀ ସହିତ ସ୍ୱାକ୍ଷରିତ ହୋଇଥ୍ ସନ୍ଧିର ନାମ ଥିଲା ‘ଭର୍ସାଇ ସନ୍ଧି’ ।
(ii) ଏହି ସନ୍ଧି ୧୯୧୯ ମସିହାରେ ସ୍ଵାକ୍ଷରିତ ହୋଇଥିଲା ।
୩୮ । ‘ତ୍ରିଶକ୍ତି ମେଣ୍ଟ’ର କେଉଁ ସଭ୍ୟ ରାଷ୍ଟ୍ର ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ଆରମ୍ଭରେ ନିରପେକ୍ଷ ରହିଥିଲା ? ‘ତ୍ରିମିତ୍ର ପକ୍ଷ’ର କେଉଁ ସଭ୍ୟ ରାଷ୍ଟ୍ର ୧୯୧୭ ମସିହାରେ ଏହି ଯୁଦ୍ଧରୁ ଅପସରି ଗଲା ?
Answer:
(i) ‘ତ୍ରିଶକ୍ତି ମେଣ୍ଟ’ର ସଭ୍ୟ ରାଷ୍ଟ୍ର ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ଆରମ୍ଭରେ ନିରପେକ୍ଷ ରହିଥିଲା ।
(ii) ‘ତ୍ରିମିତ୍ର ପକ୍ଷ’ର ସଭ୍ୟ ରାଷ୍ଟ୍ର ରୁଷ୍ ୧୯୧୭ ମସିହାରେ ଏହି ଯୁଦ୍ଧରୁ ଅପସରି ଗଲା ।
୩୯ । ପ୍ୟାରିସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀରେ କିଏ ସଭାପତିତ୍ବ କରିଥିଲେ ? ଏଥିରେ କେଉଁମାନେ ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲେ ?
Answer:
(i) ପ୍ୟାରସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀରେ ଫ୍ରାନ୍ ସ ପ୍ରଧାନମନ୍ତ୍ରୀ କିମେନ୍ସ ସଭାପତିତ୍ବ କରିଥିଲେ ।
(ii) ଏଥିରେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ରାଷ୍ଟ୍ରପତି ଉଡ୍ରୋ ଉଇଲ୍ସନ୍, ଇଂଲାଣ୍ଡର ପ୍ରଧାନମନ୍ତ୍ରୀ ଲଏଡ୍ ଜର୍ଜ ଓ କ୍ଲିମେନ୍ସ୍ ସମସ୍ତ ନୀତି କେଉଁମାନେ ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲେ ।
Objective Type Questions With Answers
A ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ ।
୧। ୧୯୧୭ ମସିହାରେ ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧରୁ କେଉଁ ଦେଶ ଓହରିଯାଇଥିଲା ?
Answer:
ପୂର୍ବ ଇଉରୋପରେ ରୁଷିଆ ଜର୍ମାନୀଠାରୁ ପରାଜୟ ସ୍ଵୀକାର କରି ୧୯୧୭ ମସିହାରେ ବିଶ୍ୱଯୁଦ୍ଧରୁ ଓହରିଗଲା
୨। ସର୍ବିଆ କେଉଁ ଗୁପ୍ତ ସଙ୍ଗଠନ ଗଠନ କରିଥିଲା ?
ଅଷ୍ଟ୍ରିଆକୁ ଆତଙ୍କିତ କରିବାପାଇଁ ସର୍ବିଆ ‘ବ୍ଲାକ୍ ହ୍ୟାଣ୍ଡ’ ଗୁପ୍ତ ସଙ୍ଗଠନ ଗଠନ କରିଥିଲା
୩। ଜର୍ମାନୀକୁ ଔପନିବେଶିକ ପ୍ରତିଦ୍ବନ୍ଦିତାରୁ ହଟାଇବାପାଇଁ ଇଂଲାଣ୍ଡ କାହା ସହିତ ହାତ ମିଳାଇଥିଲା ?
Answer:
୧୯୦୭ ମସିହାରେ ଜର୍ମାନୀକୁ ଔପନିବେଶିକ ପ୍ରତିଦ୍ବନ୍ଦିତାରୁ ହଟାଇବାପାଇଁ ଇଂଲାଣ୍ଡ କାହା ଫ୍ତ।ନ୍ସସ ହିତ ହାତ ମିଳାଇଥିଲା ।
୪ । ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପୂର୍ବରୁ ଗଠିତ ମୁଖ୍ୟ ସାମରିକ ମେଣ୍ଟଦ୍ଵୟର ନାମ ଲେଖ ।
Answer:
ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପୂର୍ବରୁ ଗଠିତ ମୁଖ୍ୟ ସାମରିକ ମେଣ୍ଟଦ୍ଵୟର ନାମ ଥିଲା ‘ତ୍ରିଶକ୍ତି ମେଣ୍ଟ’ ଓ ‘ତ୍ରିମିତ୍ର ପକ୍ଷ’ ।
୫। ୧୯୦୮ ମସିହାରେ ତୁର୍କୀର ସାର୍ବଭୌମ ଅଧୀନରେ ଥିବା କେଉଁ ଦୁଇଟି ପ୍ରଦେଶକୁ ଅଷ୍ଟ୍ରିଆ ନିଜ ସାମ୍ରାଜ୍ୟରେ ମିଶାଇଦେଲା ?
Answer:
୧୯୦୮ ମସିହାରେ ତୁର୍କୀର ସାର୍ବଭୌମ ଅଧୀନରେ ଥୁବା ବୋସ୍ନିଆ ଓ ହର୍ଜିଗୋଭିନା ପ୍ରଦେଶଦ୍ଵୟକୁ ଅଷ୍ଟ୍ରିଆ ନିଜ ସାମ୍ରାଜ୍ୟରେ ମିଶାଇଦେଲା ।
୬। ଇଟାଲୀ କେବେ ମିତ୍ରଶକ୍ତି ସପକ୍ଷରେ ଯୁଦ୍ଧରେ ଯୋଗଦେଲା ?
Answer:
ଅଷ୍ଟ୍ରିଆ ଓ ତୁର୍କୀର କିଛି ଅଧ୍ୟାତ ଅଞ୍ଚଳ ଇଟାଲୀକୁ ଦିଆଯିବ ବୋଲି ଇଂଲାଣ୍ଡ ଓ ଫ୍ରାନ୍ସଠାରୁ ପ୍ରତିଶ୍ରୁତି ପାଇବା ପରେ ଇଟାଲୀ ୧୯୧୫ ମସିହା ମେ ମାସରେ ମିତ୍ରଶକ୍ତି ସପକ୍ଷରେ ଯୁଦ୍ଧରେ ଯୋଗଦେଲା ।
୭। ପ୍ୟାରିସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀର ଅବ୍ୟବହିତ ପରେ କେଉଁ କେଉଁ ନୂତନ ରାଷ୍ଟ୍ର ଗଠିତ ହେଲା ?
Answer:
ପ୍ୟାରିସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀର ଅବ୍ୟବହିତ ପରେ ଚେକୋସ୍ଲୋଭାକିଆ, ଯୁଗୋସ୍ଲୋଭିଆ, ହଙ୍ଗେରୀ, ପୋଲାଣ୍ଡ, ଫିନ୍ଲାଣ୍ଡ, ଲିଥୁଆନିଆ, ଇଷ୍ଟୋନିଆ ଓ ଲାଟିଭିଆ ଆଦି ରାଷ୍ଟ୍ର ଗଠିତ ହେଲା ।
୮। ପ୍ରଥମ ବିଶ୍ଵ ଯୁଦ୍ଧରେ କେଉଁ ଦେଶମାନେ ‘ମିତ୍ରଶକ୍ତି’ ସପକ୍ଷରେ ଯୋଗ ଦେଇଥିଲେ ?
Answer:
ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧରେ ସର୍ବିଆ, ରୁଷିଆ, ଫ୍ରାନ୍ସ, ବ୍ରିଟେନ୍, ଇଟାଲୀ, ଗ୍ରୀସ୍, ରୁମାନିଆ, ଜାପାନ, ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ଓ ଚୀନ୍ ପ୍ରଭୃତି ‘ମିତ୍ରଶକ୍ତି’ ସପକ୍ଷରେ ଯୋଗ ଦେଇଥିଲେ।
୯। ପ୍ରଥମ ବିଶ୍ଵ ଯୁଦ୍ଧରେ କେଉଁ ଦେଶମାନେ ‘କେନ୍ଦ୍ରଶକ୍ତି’ର ଅନ୍ତର୍ଭୁକ୍ତ ଥିଲେ ?
Answer:
ପ୍ରଥମ ବିଶ୍ବଯୁଦ୍ଧରେ ଅଷ୍ଟ୍ରିଆ, ଜର୍ମାନୀ, ବୁଲ୍ଗେରିଆ ଓ ତୁର୍କୀ ପ୍ରଭୃତି ଦେଶମାନେ ‘କେନ୍ଦ୍ରଶକ୍ତି’ର ଅନ୍ତର୍ଭୁକ୍ତ ଥିଲେ ।
୧୦ । ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧ ପରେ କେଉଁ କେଉଁ ଦେଶରୁ ରାଜତନ୍ତ୍ର ଲୋପ ପାଇଥିଲା ?
Answer:
ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧ ପରେ ଅଷ୍ଟ୍ରିଆ, ତୁର୍କୀ ଓ ଜର୍ମାନୀ ପ୍ରଭୃତି ଦେଶରୁ ରାଜତନ୍ତ୍ର ଶାସନ ଲୋପ ପାଇଥିଲା ।

୧୧ । ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ କେବେ ଆରମ୍ଭ ହୋଇ କେବେ ଶେଷ ହେଲା ?
Answer:
ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ୧୯୧୪ ମସିହା ଜୁଲାଇ ୨୮ ତାରିଖରୁ ଆରମ୍ଭ ହୋଇ ୧୯୧୮ ମସିହା ନଭେମ୍ବର ୧୧ ତାରିଖରେ ଶେଷ ହେଲା ।
୧୨ । କେଉଁଠାରେ ଅଷ୍ଟ୍ରିଆ-ହଙ୍ଗେରୀ ରାଜକୁମାରଙ୍କୁ ହତ୍ୟା କରାଗଲା ?
Answer:
୧୯୧୪ ମସିହା ଜୁନ୍ ୨୮ ତାରିଖରେ ସର୍ବ ଜାତିର ଜଣେ ଯୁବକ ବୋସ୍ନିଆ ରାଜ୍ୟର ରାଜଧାନୀ ସାରା ଜେଭୋଠାରେ ଅଷ୍ଟ୍ରି ଆ-ହଙ୍ଗେରୀର ରାଜକୁମାରଙ୍କୁ ହତ୍ୟା କଲା ।
୧୩ । ବିସ୍ମାର୍କ କେବେ ଜର୍ମାନୀର ଚାନ୍ସେଲର ଭାବେ କ୍ଷମତାରେ ଥିଲେ ?
Answer:
ଜର୍ମାନୀର ଚାନ୍ସେଲର ଭାବେ ବିସ୍ମାର୍କ ୧୮୭୧ ମସିହାରୁ ୧୮୯୦ ମସିହା ପର୍ଯ୍ୟନ୍ତ କ୍ଷମତାରେ ଥିଲେ ।
୧୪। ଜର୍ମାନୀର ଏକତ୍ରୀକରଣରେ କିଏ ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲେ ?
Answer:
ଜର୍ମାନୀର ଏକତ୍ରୀକରଣରେ ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲେ ।
୧୫ । ସିଦାନ୍ ଯୁଦ୍ଧ କେବେ ହୋଇଥିଲା ?
Answer:
୧୮୭୦ ମସିହାରେ ଫ୍ରାନ୍ସ ଓ ପ୍ରୁସିଆ ମଧ୍ୟରେ ସିଦାନ୍ ଯୁଦ୍ଧ ହୋଇଥିଲା ।
୧୬ । କେଉଁ ରାଷ୍ଟ୍ରର ପରାଜୟ ପରେ ଜର୍ମାନୀ ଏକତ୍ରୀକରଣ ସମ୍ପୂର୍ଣ୍ଣ ହୋଇଥିଲା ?
Answer:
ପରାଜୟ ପରେ ଜର୍ମାନୀ ଏକତ୍ରୀକରଣ ସମ୍ପୂର୍ଣ୍ଣ ହୋଇଥିଲା ।
୧୭ । କେବେ ଅଷ୍ଟ୍ରଆ ରାଜିନାମାରେ ଇଟାଲୀ ଯୋଗଦେଲା ।
Answer:
୧୮୮୨ ମସିହାରେ ଅଷ୍ଟ୍ରିଆ ରାଜିନାମାରେ ଇଟାଲୀ ଯୋଗଦେଲା ।
୧୮। ତ୍ରିଶକ୍ତି ମେଣ୍ଟର ରାଷ୍ଟ୍ରମାନେ ପରସ୍ପର ମଧ୍ୟରେ କି ପ୍ରତିଶ୍ରୁତିବଦ୍ଧ ହେଲେ ?
Answer:
ତ୍ରିଶକ୍ତି ମେଣ୍ଟ ଏକ ପ୍ରତିରକ୍ଷାତ୍ମକ ଚୁକ୍ତି ଥିଲା ଏବଂ ଏହି ମେଣ୍ଟର ରାଷ୍ଟ୍ରମାନେ ପରସ୍ପରର ନିରାପତ୍ତା ଲାଗି କାର୍ଯ୍ୟ କରିବେ ବୋଲି ପ୍ରତିଶ୍ରୁତିବଦ୍ଧ ହେଲେ ।
୧୯ । ବଲ୍କାନ୍ ଅଞ୍ଚଳ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଆଲ୍ବାନିଆ, ବୁଲ୍ଗେରିଆ, ଗ୍ରୀସ୍, ରୁମାନିଆ, ସର୍ବିଆ, ମଣ୍ଟିନିଟ୍ରୋ ଓ ବୋସ୍ନିଆ, ହର୍ଜଗୋଭିନା ଏବଂ ଇଉରୋପୀୟ ତୁର୍କୀକୁ ଧାରଣ କରିଥିବା ଦକ୍ଷିଣ-ପୂର୍ବ ଇଉରୋପର ଉପଦ୍ୱୀପକୁ ବଲ୍ କାନ୍ ଅଞ୍ଚଳ କୁହାଯାଏ ।
୨୦ । କେବେ ଜର୍ମାନୀ ନିଜର ନୌଶକ୍ତିରେ ଇଂଲାଣ୍ଡ ଅପେକ୍ଷା ଅଧ୍ବକ ବୃଦ୍ଧି ଘଟାଇଛି ବୋଲି ଘୋଷଣା କଲା ?
Answer:
୧୮୯୦ ମସିହାରେ ଜର୍ମାନୀ ନିଜର ନୌଶକ୍ତିରେ ଇଂଲାଣ୍ଡ ଅପେକ୍ଷା ଅଧିକ ବୃଦ୍ଧି ଘଟାଇଛି ବୋଲି ଘୋଷଣା କଲା ।
୨୧ । ୧୯୦୭ ମସିହାରେ ଜର୍ମାନୀକୁ ଔପନିବେଶିକ ପ୍ରତିଦ୍ଵନ୍ଦିତାରୁ ହଟାଇବାପାଇଁ କିଏ କିଏ ହାତ ମିଳାଇଥିଲେ ।
Answer:
୧୯୦୭ ମସିହାରେ ଜର୍ମାନୀକୁ ଔପନିବେଶିକ ପ୍ରତିଦ୍ଵନ୍ଦିତାରୁ ହଟାଇବାପାଇଁ ଇଂଲାଣ୍ଡ ଓ ଫ୍ରାନ୍ସ ହାତ ମିଳାଇଥିଲେ ।
୨୨ । ମଧ୍ୟପ୍ରାଚ୍ୟର ଅନ୍ତର୍ଭୁକ୍ତ ଦେଶଗୁଡ଼ିକର ନାମ ଲେଖ ।
Answer:
ଇଜିପ୍ଟ, ପାଲେଷ୍ଟାଇନ୍, ଏସୀୟ ତୁର୍କୀ, ଇରାନ୍, ଆଫଗାନିସ୍ଥାନ, ଇରାକ୍, ସିରିଆ, ଲେବାନନ୍, ଜୋର୍ଡାନ୍, ସାଉଦି ଆରବ ଏବଂ ୟେମେନ୍ ଆଦି ଦେଶଗୁଡ଼ିକ ମଧ୍ୟପ୍ରାଚ୍ୟର ଅନ୍ତର୍ଭୁକ୍ତ ।
୨୩ । ତୁର୍କୀର ସୁଲତାନ କେବେ ଆତ୍ମସମର୍ପଣ କରିଥିଲେ ଏବଂ ଏହା ସହିତ କେଉଁ ରାଜବଂଶରେ ସମାପ୍ତି ଘଟିଲା ?
Answer:
୧୯୨୨ ମସିହା ନଭେମ୍ବର ମାସରେ ତୁର୍କୀର ସୁଲତାନ୍ ଆତ୍ମସମର୍ପଣ କରି ସିଂହାସନ ତ୍ୟାଗ କରିବାଦ୍ୱାରା ତୁର୍କୀର ଉସ୍ମାନୀ ରାଜବଂଶର ସମାପ୍ତି ଘଟିଲା ।
୨୪ । କେନ୍ଦ୍ରଶକ୍ତି ବିରୋଧରେ କେଉଁ ଶକ୍ତିର ଯୁଦ୍ଧୋତ୍ତର ଘୋଷଣା ଲୋକମାନଙ୍କୁ ଗଣତନ୍ତ୍ର ଲାଗି ପ୍ରେରଣ ପ୍ରଦାନ କରିଥିଲା ?
Answer:
କେନ୍ଦ୍ର ଶକ୍ତି ବିରୋଧରେ ମିତ୍ରଶକ୍ତିର ଯୁଦ୍ଧୋତ୍ତର ଘୋଷଣା ଲୋକମାନଙ୍କୁ ଗଣତନ୍ତ୍ର ଲାଗି ପ୍ରେରଣ ପ୍ରଦାନ କରିଥିଲା ।

୨୫ । ପ୍ୟାରସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀ କେବେ ଓ କାହିଁକି ହୋଇଥିଲା ?
Answer:
ଘଟିବା ଫଳରେ ଭବିଷ୍ୟତରେ ଯୁଦ୍ଧର ଆଶଙ୍କାକୁ ଦୂର କରି ଶାନ୍ତିପୂର୍ଣ୍ଣ ସହାବସ୍ଥାନ ଅବଲମ୍ବନ କରିବା ଉଦ୍ଦେଶ୍ୟରେ ୧୯୧୯ ମସିହାରେ ପ୍ୟାରିସ୍ ଶାନ୍ତି ସମ୍ମିଳନୀ ଆହୂତ ହୋଇଥିଲା ।
୨୬ । ପ୍ୟାରିସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀରେ ସ୍ୱାକ୍ଷରିତ ହୋଇଥିବା ଚୁକ୍ତିଗୁଡ଼ିକ ମଧ୍ୟରେ ଗୁରୁତ୍ବପୂର୍ଣ୍ଣ ଚୁକ୍ତିର ନାମ କ’ଣ ଥିଲା ?
Answer:
ପ୍ୟାରିସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀରେ ସ୍ୱାକ୍ଷରିତ ହୋଇଥିବା ଚୁକ୍ତିଗୁଡ଼ିକ ମଧ୍ୟରେ ଗୁରୁତ୍ବପୂର୍ଣ୍ଣ ଚୁକ୍ତିର ନାମ ଭର୍ସାଇ ଚୁକ୍ତି ଥିଲା ।
୨୭ । ଇଂଲାଣ୍ଡ କେବେ ଜାପାନ ସହିତ, କେବେ ଫ୍ରାନ୍ସ ସହିତ ଏବଂ କେବେ ରୁଷିଆ ସହିତ ଚୁକ୍ତି ସ୍ୱାକ୍ଷର କଲା ?
Answer:
ଇଂଲାଣ୍ଡ ୧୯୦୨ ମସିହାରେ ଜାପାନ ସହିତ, ୧୯୦୪ ମସିହାରେ ଫ୍ରାନ୍ସ ସହିତ ଏବଂ ୧୯୦୭ ମସିହାରେ ରୁଷିଆ ସହିତ ଚୁକ୍ତି ସ୍ବାକ୍ଷର କରିଥିଲା ।
୨୮ । ଜର୍ମାନୀ ଦେଶର ଶେଷ ଶାସକ କିଏ ଥିଲେ ?
Answer:
ଜର୍ମାନୀ ଦେଶର ଶେଷ ଶାସକ ଥିଲେ କାଇଜର
୨୯ । କିଏ ତୁର୍କୀର ଶେଷ ଖଲିଫା ଥିଲେ ?
Answer:
ଅବ୍ଦ୍ ଅଲ୍ ମଜିଦ୍ ତୁର୍କୀର ଶେଷ ଖଲିଫା ଥିଲେ ।
୩୦ । ଚେକୋସ୍ଲୋଭାକିଆ କେବେ ଦୁଇଟି ସ୍ଵାଧୀନ ରାଷ୍ଟ୍ରରେ ବିଭାଜିତ ହୋଇଥିଲା ?
Answer:
ଚେକୋସ୍ଲୋଭାକିଆ ୧୯୯୩ ମସିହାରେ ଦୁଇଟି ସ୍ଵାଧୀନ ରାଷ୍ଟ୍ରରେ ବିଭାଜିତ ହୋଇଥିଲା ।
୩୧ । କେବେ ମଣ୍ଟିନିଟ୍ରୋ ସ୍ଵାଧୀନ ରାଷ୍ଟ୍ରରୂପେ ଗଠିତ ହେଲା ?
Answer:
ମଣ୍ଟିନିଟ୍ରୋ ୨୦୦୬ ମସିହା ଜୁନ୍ ୩ ତାରିଖରେ ସ୍ବାଧୀନ ରାଷ୍ଟ୍ର ରୂପେ ଗଠିତ ହେଲା ।
B ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଲେଖ ।
୧। କେଉଁଠାରେ ଉସ୍ମାନୀ ରାଜବଂଶ ଶାସନ କରୁଥିଲା ?
Answer:
ତୁର୍କୀ
୨। ରୁଷିଆରେ ‘ରୋମାନୋଭ୍’ ରାଜବଂଶର ଶେଷ ଶାସକ କିଏ ଥିଲେ ?
Answer:
ଜାର୍ ଦ୍ୱିତୀୟ ନିକୋଲାସ୍
୩। ପ୍ୟାରିସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀରେ କିଏ ସଭାପତିତ୍ବ କରିଥିଲେ ?
Answer:
କ୍ଲିମେନ୍ସ୍
୪। ଫ୍ରାନ୍ସିସ୍ ଯୋସେଫ୍ କେଉଁ ଦେଶର ଶେଷ ଶାସକ ଥିଲେ ?
Answer:
ଅଷ୍ଟ୍ରିଆ
୫। ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ସମୟରେ ଜର୍ମାନୀର କାଇଜର କିଏ ଥିଲେ ?
Answer:
ଦ୍ୱିତୀୟ ଉଇଲିୟମ୍
୬। ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ଶାନ୍ତି ପାଇଁ ପୃଥିବୀରେ କେଉଁ ଅନୁଷ୍ଠାନ ଗଠିତ ହୋଇଥିଲା ?
Answer:
ଜାତିସଂଘ

୭। ‘ଅଗାଦି ବନ୍ଦର’ କେଉଁ ଦେଶରେ ଅବସ୍ଥିତ ?
Answer:
ମରକ୍କୋ
୮। ୨୦୦୬ ଜୁନ୍ ୩ ରେ କେଉଁ ଦେଶ ସ୍ଵାଧୀନ ହୋଇଥିଲା ?
Answer:
ମଣ୍ଟିନିଟ୍ରୋ
୯ । କେଉଁ ଦୁଇ ଦେଶ ମଧ୍ୟରେ ୧୯୦୪ ମସିହାରେ ଏକ ଚୁକ୍ତି ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ?
Answer:
ଇଂଲାଣ୍ଡ ଓ ଫ୍ରାନ୍ସ
୧୦ । ଇଂଲାଣ୍ଡ କେବେ ରୁଷିଆ ସହିତ ଏକ ଚୁକ୍ତି ସ୍ୱାକ୍ଷର କରିଥିଲା ?
Answer:
୧୯୦୭ ମସିହା
୧୧ ।୧୮୯୦ ମସିହା ପରେ କେଉଁ ଦେଶ ନୌଶକ୍ତିରେ ଘୋଷଣା କଲା ?
Answer:
ଜର୍ମାନୀ
୧୨ । ବର୍ଲିନ୍-ବାଗ୍ଦାଦ୍ ରେଳପଥ ପ୍ରକଳ୍ପ ନିର୍ମାଣ କରିବାପାଇଁ କେଉଁ ଦେଶ ଆଗ୍ରହ ପ୍ରକାଶ କରିଥିଲା ?
Answer:
ଜର୍ମାନୀ
୧୩ । ଜର୍ମାନୀର ପ୍ରସାରଣ ଓ ସମରସଜ୍ଜା ତାଙ୍କ ବୈଦେଶିକ ନୀତିର ମୂଳଭିତ୍ତି ବୋଲି କିଏ ଘୋଷଣା କରିଥିଲେ ?
Answer:
ଦ୍ଵିତୀୟ ଉଇଲିୟମ୍
୧୪ । ୧୮୯୯ ଓ ୧୯୦୭ ମସିହାରେ କେଉଁଠାରେ ଅନୁଷ୍ଠିତ ଆଇନ ପ୍ରଣୟନ କରାଯାଇଥିଲା ?
Answer:
ହେଗ୍
୧୫ । ଅଷ୍ଟ୍ରିଆର ଯୁବରାଜ ଫଡ଼ିନାଣ୍ଡ ଓ ତାଙ୍କ ପତ୍ନୀଙ୍କ କେଉଁ ସ୍ଥାନରେ ହତ୍ୟା କରାଯାଇଥିଲା ?
Answer:
ସେରାଜେଭୋ
୧୬ । ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧରେ ପ୍ରାୟ କେତୋଟି ରାଷ୍ଟ୍ର ଯୋଗ ଦେଇଥିଲେ ?
Answer:
୩୬ଟି
୧୭ । ଆମେରିକାର କେଉଁ ରାଷ୍ଟ୍ରପତି ଜାତିସଂଘ ଗଠନ ଦିଗରେ ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲେ ?
Answer:
ଉଡ୍ରୋ ଉଇଲ୍ସସନ୍
୧୮ । ପ୍ୟାରିସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀରେ ଆମେରିକାର ରାଷ୍ଟ୍ରପତି ଉଡ୍ରୋ ଉଇଲସନ୍ କେଉଁ କାର୍ଯ୍ୟକ୍ରମର ଉପସ୍ଥାପନା କରିଥିଲେ ?
Answer:
୧୪ ସୂତ୍ରୀ
୧୯ । ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧପରେ ରାଷ୍ଟ୍ରମାନଙ୍କୁ କାହିଁକି ବହୁ ପରିମାଣରେ କାଗଜ ଟଙ୍କା ପ୍ରଚଳନ କରିବାକୁ ପଡ଼ିଥିଲା ?
Answer:
ଭାରୀ ସଂଖ୍ୟାର ଋଣ ଯୋଗୁଁ
୨୦ । ଜର୍ମାନୀ କେବେ ଯୁଦ୍ଧ ବିରତି ସନ୍ଧିରେ ସ୍ବାକ୍ଷର କଲା ?
Answer:
୧୯୧୮ ନଭେମ୍ବର ୧୧ ।
C ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
୧। ___________ ଜର୍ମାନୀ ଏକତ୍ରୀକରଣର ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲେ ।
Answer:
ବିସ୍ମାର୍କ
୨। ରୁଷିଆ ଓ ତୁର୍କୀ ମଧ୍ୟରେ ____________ ମସିହୋରେ ଯୁକ୍ତ।
ସଂଘଟିତ ହୋଇଥିଲା ।
Answer:
୧୮୭୭
୩ । ____________ ନିବାରଣ ପାଇଁ ହୋଇଥି ଗୁରୁତ୍ବପୂର୍ଣ୍ଣ ଆଇନଗୁଡ଼ିକ ହୋଇଥ ସମ୍ମିଳନୀଗୁଡ଼ିକରେ ପ୍ରଣୟନ କରାଯାଇଥିଲା ।
Answer:
ଯୁଦ୍ଧ

୪ । ____________ମସିହାରେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ପ୍ରଥମ ବିଶ୍ବଯୁଦ୍ଧରେ ଜଡି଼ତ ହୋଇଥିଲା ।
Answer:
୧୯୧୭
୫ । ____________ ମସିହାରେ ପ୍ୟାରିସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀ ଆହୂତ ହୋଇଥିଲା ।
Answer:
୧୯୧୯
୬ | ଫ୍ରାନ୍ସର ଭର୍ସାଇଠାରେ ଜର୍ମାନୀ ସହିତ _______________ ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ।
Answer:
ଭର୍ସାଇ
୭ । _________________ କୁ ଆତଙ୍କିତ କରିବାପାଇଁ ସର୍ବିଆ ‘ବ୍ଲାକ୍ ହ୍ୟାଣ୍ଡ’ ଗୁପ୍ତ ସଙ୍ଗଠନ ସ୍ଥାପନ କରିଥିଲା ।
Answer:
ଅଷ୍ଟ୍ରିଆ
୮। ଇଟାଲୀ ______________ __________________ ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧରେ ଯୋଗଦେଲା ।
Answer:
୧୯୧୫, ମିତ୍ରଶକ୍ତି
୯୮ ପ୍ୟାରିସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀରେ ଫ୍ରାନ୍ସର ପ୍ରଧାନମନ୍ତ୍ରୀ __________________ ସଭାପତିତ୍ୱ କରିଥିଲେ ।
Answer:
କ୍ଲିମେନ୍ସ୍
୧୦। ______________ ର ପରାଜୟ ପରେ ଜର୍ମାନୀ ଏକତ୍ରୀକରଣ ସମ୍ଭବ ହୋଇଥିଲା ।
Answer:
ଫ୍ରାନ୍ସ ।
D ଠିକ୍ ଉକ୍ତି ପାଇଁ (√) ଓ ଭୁଲ ଉକ୍ତି ପାଇଁ (×) ଲେଖ ।
୧। ବିସମାର୍କ ଔପନିବେଶିକ ବିସ୍ତାରଣ ନୀତିର ସପକ୍ଷରେ ଥିଲେ ।
୨। ୧୯୦୪ ମସିହାରେ ଇଂଲାଣ୍ଡ ଓ ଫ୍ରାନ୍ସ ମଧ୍ୟରେ ଏକ ବୁଝାମଣା ପତ୍ର ସ୍ୱାକ୍ଷରିତ ହୋଇଥିଲା ।
୩। ‘ପାନ୍ତର’ ନାମକ ଯୁଦ୍ଧ ଜାହାଜକୁ ଫ୍ରାନ୍ସ ମରକ୍କୋର ଅଗାଦି ବନ୍ଦରକୁ ପଠାଇଥିଲା ।
୪। ‘ଅଗାଦି’ ବନ୍ଦର ଫ୍ରାନ୍ସରେ ଅବସ୍ଥିତ ।
୫୮ ୧୯୧୨-୧୩ ମସିହାରେ ବଲକାନ୍ ଯୁଦ୍ଧ ସଂଗଠିତ
୬। ଫ୍ରାନ୍ସିସ୍ ଫର୍ଡିନାଣ୍ଡଙ୍କୁ ଜର୍ମାନୀରେ ହତ୍ୟା କରାଯାଇଥିଲା ।
୭ । ବିଦେଶକୁ ଘୁଷୁରୀ ରପ୍ତାନି କରିବା ସର୍ବିଆର ଏକ ପ୍ରଧାନ ବ୍ୟବସାୟ ଥିଲା ।
୮। ଅଷ୍ଟ୍ରିଆକୁ ଆତଙ୍କିତ କରିବାପାଇଁ ଫ୍ରାନ୍ସ ‘ବ୍ଲାକ୍ ଲ୍ୟାଣ୍ଡ’’ ଗୁପ୍ତ ସଂଗଠନ ସ୍ଥାପନ କରିଥିଲା ।
୯ । ନିକଟ ପ୍ରାଚ୍ୟ କହିଲେ ବଲ୍କାନ୍ ଅଞ୍ଚଳକୁ ବୁଝାଉଥିଲା ।
୧୦ । ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ୧୯୧୫ ମସିହାରେ ପ୍ରଥମ ବିଶ୍ବଯୁଦ୍ଧରେ ଜଡି଼ତ ହୋଇଥିଲା ।
Answers:
୧। (×)
୨। (√)
୩। (×)
୪। (×)
୫। (√)
୬। (×)
୭ । (√)
୮। (x)
୯୮ (√)
୧୦ । (x)

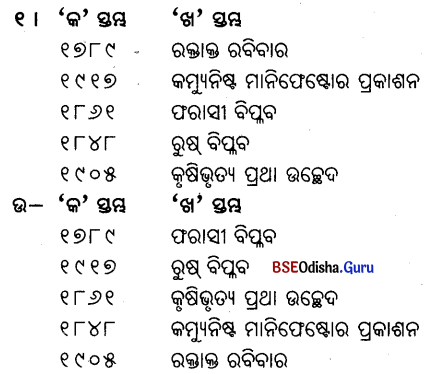
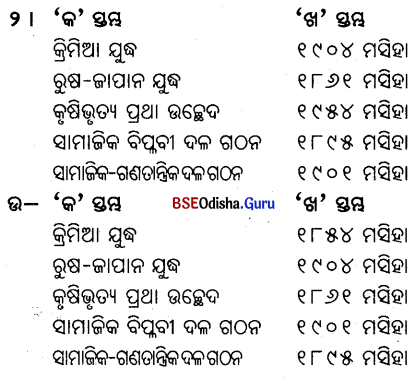
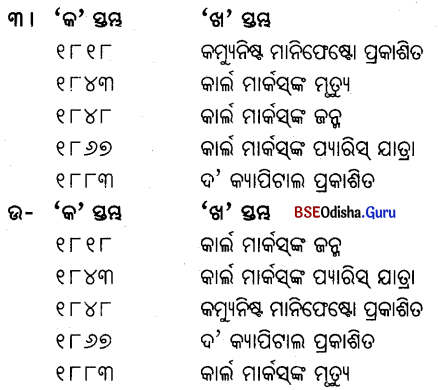
E ‘କ’ ସ୍ତମ୍ଭର ଶବ୍ଦକୁ ‘ଖ’ ସ୍ତମ୍ଭର ଶବ୍ଦ ସହ ମିଳନ କରି ଲେଖ ।




F ରେଖାଙ୍କିତ ପଦକୁ ପରିବର୍ତ୍ତନ କରି ଭ୍ରମ ସଂଶୋଧନ କର ।
୧। ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧର ବାଇଶବର୍ଷ ପରେ ଦ୍ବିତୀୟ ବିଶ୍ଵଯୁଦ୍ଧ ଆରମ୍ଭ ହୋଇଥିଲା ।
Answer:
କୋଡ଼ିଏ ବର୍ଷ
୨। ଫ୍ରାନ୍ସ ଓ ପ୍ରୁସିଆ ମଧ୍ୟରେ ହୋଇଥିବା ସିଦାନ ଯୁଦ୍ଧରେ ପ୍ରୁସିଆ ପରାସ୍ତ ହୋଇଥିଲା ।
Answer:
ଫ୍ରାନ୍ସ
୩। ୧୯୦୫ ମସିହାରେ ଇଂଲାଣ୍ଡ ଓ ଫ୍ରାନ୍ସ ମଧ୍ୟରେ ଏକ ବୁଝାମଣାପତ୍ର ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ।
Answer:
୧୯୦୪
୪। ହିଟଲର ଜର୍ମାନୀ ଏକତ୍ରୀକରଣରେ ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲେ ।
Answer:
ବିସମାର୍କ

୫। ଜାତିସଂଘ କ୍ଲିମେନସୁଙ୍କ ପ୍ରସ୍ତାବରେ ଗଠନ କରାଯାଇଥିଲା ।
Answer:
ଉଡ୍ରୋ ଉଇଲସନ
୬ । ଭୂମଧ୍ୟ ସାଗର ଓ ଭାରତ ମହାସାଗରର ମଧ୍ୟବର୍ତ୍ତୀ ଅଞ୍ଚଳକୁ ନିକଟ ପ୍ରାଚ୍ୟ କୁହାଯାଏ ।
Answer:
ମଧ୍ୟ ପ୍ରାଚ୍ୟ
୭ । ପ୍ରସିଆ ଦେଶର ଏକ ପ୍ରଧାନ ବ୍ୟବସାୟ ଥିଲା ବିଦେଶକୁ ଘୁଷୁରି ରପ୍ତାନି କରିବା ।
Answer:
ସର୍ବିଆ
୮ । ବୋସ୍ନିଆର ରାଜଧାନୀ ଥିଲା ଟାସ୍ମାନିଆ ।
Answer:
ସାରାଜେଭୋ
୯। ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧରେ ୧୯୧୮ ମସିହାରେ ଯୋଗଦେଇଥିଲା ।
Answer:
୧୯୧୭
୧୦ । ସମ୍ରାଟ ଫ୍ରାନ୍ସିସ୍ ଜୋସେଫ୍ ଅଷ୍ଟ୍ରେଲିଆର ଶେଷ ଶାସକ ଥିଲେ ।
Answer:
ଅଷ୍ଟ୍ରିଆ
G ଚାରୋଟି ସମ୍ଭାବ୍ୟ ବିକଳ୍ପ ମଧ୍ୟରୁ ସଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
1. ନିକଟ ପ୍ରାଚ୍ୟ କହିଲେ କେଉଁ ଅଞ୍ଚଳକୁ ବୁଝାଇଥାଏ ?
(A) ବଲ୍କାନ୍ ଅଞ୍ଚଳ
(B) ଆର୍ଡିଆଟିକ୍
(C) ପୂର୍ବ ଇଉରୋପ
(D) ଟାଙ୍ଗାନାଇକା
Answer:
(A) ବଲ୍କାନ୍ ଅଞ୍ଚଳ
2. ଭୂମଧ୍ଯସାଗର ଓ ଭାରତ ମହାସାଗର ମଧ୍ୟବର୍ତ୍ତୀ ଅଞ୍ଚଳକୁ କ’ଣ କୁହାଯାଏ ?
(A) ନିକଟ ପ୍ରାଚ୍ୟ
(B) ଦୂର ପ୍ରାଚ୍ୟ
(C) ମଧ୍ଯ ପ୍ରାଚ୍ୟ
(D) ଆଦ୍ୟ ପ୍ରାଚ୍ୟ
Answer:
(C) ମଧ୍ଯ ପ୍ରାଚ୍ୟ
3. ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ମଧ୍ୟ ପ୍ରାଚ୍ୟର ଅନ୍ତର୍ଭୁକ୍ତ ଦେଶ ନୁହେଁ ?
(A) ଇଜିପ୍ଟ
(B) ପାଲେଷ୍ଟାଇନ୍
(C) ତୁର୍କୀ
(D) ଭାରତ
Answer:
(D) ଭାରତ
4. ‘ଇଣ୍ଡୋନେସିଆ’ କେଉଁ ପ୍ରାଚ୍ୟ ଅନ୍ତର୍ଭୁକ୍ତ ଦେଶ ଅଟେ ?
(A) ଦୂର ପ୍ରାଚ୍ୟ
(B) ନିକଟ ପ୍ରାଚ୍ୟ
(C) ମଧ୍ଯ ପ୍ରାଚ୍ୟ
(D) ଆଦ୍ୟ ପ୍ରାଚ୍ୟ
Answer:
(A) ଦୂର ପ୍ରାଚ୍ୟ
5. ‘ ହୋଏନ୍ ଜୋଲେଣ୍ଡ’ ରାଜବଂଶ କେଉଁ ଦେଶରେ ଶାସନ କରୁଥିଲା ?
(A) ଅଷ୍ଟ୍ରିଆ
(B) ରୁଷ୍
(C) ଜର୍ମାନୀ
(D) ଫ୍ରାନ୍ସ
Answer:
(C) ଜର୍ମାନୀ

6. ଅଷ୍ଟ୍ରିଆରେ କେଉଁ ରାଜବଂଶ ଶାସନ କରୁଥିଲେ ?
(A) ହୋଏନ୍ଲେଣ୍ଡ୍
(B) ହାପସ୍ବର୍ଗ
(C) ରୋମାନୋଭ
(D) ଜାର୍
Answer:
(B) ହାପସ୍ବର୍ଗ
7. ତୁର୍କୀରେ ଖଲିଫା ପଦର ଉଚ୍ଛେଦ କେବେ ହୋଇଥିଲା ?
(A) ୧୯୨୦
(B) ୧୯୨୧
(C) ୧୯୨୨
(D) ୧୯୨୩
Answer:
(D) ୧୯୨୩
8. ଉସ୍ମାନୀ ରାଜବଂଶ କେଉଁଠାରେ ଶାସନ କରୁଥିଲା ?
(A) ଜର୍ମାନୀ
(B) ରୁଷିଆ
(C) ତୁର୍କୀ
(D) ଫ୍ରାନ୍ସ
Answer:
(C) ତୁର୍କୀ
9. ପ୍ୟାରିସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀରେ କିଏ ସଭାପତିତ୍ବ କରିଥିଲେ ?
(A) ଉଡ୍ରୋ ଉଇଲସନ୍
(B) କ୍ଲିମେଣ୍ଟ୍
(C) ଚର୍ଚ୍ଚିଲ
(D) ମ୍ୟାକ୍ସୋନାଲଡ଼
Answer:
(B) କ୍ଲିମେଣ୍ଟ୍
10. ଫ୍ରାନ୍ସିସ୍ ଜୋସେଫ୍ କେଉଁ ଦେଶର ଶେଷ ଶାସକ ଥିଲେ ?
(A) ଜର୍ମାନୀ
(B) ଅଷ୍ଟ୍ରିଆ
(C) ଇଟାଲୀ
(D) ରୁଷ୍
Answer:
(B) ଅଷ୍ଟ୍ରିଆ
11. ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ସମୟରେ ଜର୍ମାନୀର କାଇଜର କିଏ ଥିଲେ ?
(A) ପ୍ରଥମ ଉଇଲିୟମ୍
(B) ଦ୍ଵିତୀୟ ଉଇଲିୟମ୍
(C) ତୃତୀୟ ଉଇଲିୟମ୍
(D) ଚତୁର୍ଥ ଉଇଲିୟମ୍
Answer:
(B) ଦ୍ଵିତୀୟ ଉଇଲିୟମ୍
12. ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ଶାନ୍ତି ପାଇଁ ପୃଥିବୀରେ କେଉଁ ଅନୁଷ୍ଠାନ ଗଠିତ ହୋଇଥିଲା ?
(A) ଜାତିସଂଘ
(B) ମିଳିତ ଜାତିସଂଘ
(C) ସଯୁକ୍ତ ସଂଘ
(D) ମିଳିତ ସଂଘ
Answer:
(A) ଜାତିସଂଘ

13. ‘ଅଗାଦି ବନ୍ଦର’ କେଉଁ ଦେଶରେ ଅବସ୍ଥିତ ?
(A) ଫ୍ରାନ୍ସ
(B) ଇଟାଲୀ
(C) ଜର୍ମାନୀ
(D) ମରକୋ
Answer:
(D) ମରକୋ
14. ୨୦୦୬ ଜୁନ୍ ୩ ରେ କେଉଁ ଦେଶ ସ୍ଵାଧୀନ ହୋଇଥିଲା?
(A) ସର୍ବିଆ
(B) ଅଷ୍ଟ୍ରିଆ
(C) ମଣ୍ଟିନିଟ୍ରୋ
(D) ଯୁଗସ୍ଲୋଭିଆ
Answer:
(C) ମଣ୍ଟିନିଟ୍ରୋ
15. ନିମ୍ନୋକ୍ତ କେଉଁ ରାଷ୍ଟ୍ରଟି ‘ମିତ୍ରଶକ୍ତି’ର ଅନ୍ତର୍ଭୁକ୍ତ ନ ଥିଲା ?
(A) ରୁଷ୍
(B) ରୁମାନିଆ
(C) ଫ୍ରାନ୍ସ
(D) ତୁର୍କୀ
Answer:
(B) ରୁମାନିଆ
16. ନିମ୍ନୋକ୍ତ କେଉଁ ମସିହାରେ ତ୍ରିଶକ୍ତି ମେଣ୍ଟ ଗଠିତ ହୋଇଥିଲା ?
(A) ୧୬୮୨
(B) ୧୭୮୨
(C) ୧୮୮୨
(D) ୧୯୮୨
Answer:
(C) ୧୮୮୨
17. ୧୯୧୭ ମସିହାରେ ପ୍ରଥମ ବିଶ୍ବଯୁଦ୍ଧରୁ କେଉଁ ଦେଶ ପ୍ରଥମେ ଓହରି ଯାଇଥିଲା ?
(A) ଫ୍ରାନ୍ସ
(B) ସ୍ପେନ୍
(C) ସର୍ବିଆ
(D) ରୁଷ୍
Answer:
(D) ରୁଷ୍
18. ‘ମରକ୍’କୁ କେନ୍ଦ୍ର କରି କେଉଁ ଦୁଇ ରାଷ୍ଟ୍ର ମଧ୍ୟରେ କଳହର ସୂତ୍ରପାତ ହୋଇଥିଲା ?
(A) ଫ୍ରାନ୍ସ ଓ ଜର୍ମାନୀ
(B) ଫ୍ରାନ୍ସ ଓ ଇଂଲାଣ୍ଡ
(C) ଇଂଲାଣ୍ଡ ଓ ଜର୍ମାନୀ
(D) ଜର୍ମାନୀ ଓ ରୁଷ୍
Answer:
(A) ଫ୍ରାନ୍ସ ଓ ଜର୍ମାନୀ
19. ନିମ୍ନୋକ୍ତ କେଉଁ ଦେଶ ସାମରିକ ମେଣ୍ଟଭୁକ୍ତ ହୋଇଥିଲେ ମଧ୍ୟ ଯୁଦ୍ଧର ପ୍ରାରମ୍ଭରେ ନିରପେକ୍ଷ ରହିଥୁଲା ?
(A) ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା
(B) ଆଲ୍ବାନିଆ
(C) ଇଟାଲୀ
(D)ସର୍ବିଆ
Answer:
(C) ଇଟାଲୀ
20. ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ନିମ୍ନୋକ୍ତ କେଉଁ ଦେଶରୁ ଏକଚ୍ଛତ୍ରବାଦୀ ଶାସନର ଅନ୍ତ ଘଟିଲା ?
(A) ବ୍ରିଟେନ୍
(B) ପୋଲାଣ୍ଡ
(C) ଇଟାଲୀ
(D) ସେନ୍
Answer:
(B) ପୋଲାଣ୍ଡ

21. ଭର୍ସାଇ ଚୁକ୍ତି ନିମ୍ନୋକ୍ତ କେଉଁ ରାଷ୍ଟ୍ର ପ୍ରତି ଅପମାନଜନକ ଥିଲା ?
(A) ଇଂଲାଣ୍ଡ
(B) ଜର୍ମାନୀ
(C) ସାଉଦି ଆରବ
(D) ଇଟାଲୀ
Answer:
(B) ଜର୍ମାନୀ
22. ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧରେ ପ୍ରାୟ କେତେସଂଖ୍ୟକ ଲୋକ ଅଙ୍ଗପ୍ରତ୍ୟଙ୍ଗ ହରାଇଥିଲେ ?
(A) ୬୦ ଲକ୍ଷ
(B) ୭୦ ଲକ୍ଷ
(C) ୧ କୋଟି
(D) ୨ କୋଟି
Answer:
(B) ୭୦ ଲକ୍ଷ
23. ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା କେବେ ମିତ୍ରଶକ୍ତି ସପକ୍ଷରେ ଯୋଗଦେଲା ?
(A) ୧୯୧୪
(B) ୧୯୧୨
(C) ୧୯୧୫
(D) ୧୯୧୭
Answer:
(D) ୧୯୧୭
24. କେଉଁ ଚୁକ୍ତି ଅନୁସାରେ ଫ୍ରାନ୍ସ ତା’ର ଦୁଇଟି ପ୍ରଦେଶ ଆଲ୍ସେସ୍ ଓ ଲରେନ୍ ଜର୍ମାନୀକୁ ହସ୍ତାନ୍ତର କଲା ?
(A) ଫ୍ରାଙ୍କଫର୍ଟ ସନ୍ଧି
(B) ରାଇନ୍ ସନ୍ଧି
(C) ପାରିସ୍ ଚୁକ୍ତି
(D) ଶାନ୍ତି ଚୁକ୍ତି
Answer:
(A) ଫ୍ରାଙ୍କଫର୍ଟ ସନ୍ଧି
25. ୧୮୮୨ ମସିହାରେ ଜର୍ମାନୀ -ଅଷ୍ଟ୍ରିଆ ରାଜିନାମାରେ କେଉଁ ଦେଶ ଯୋଗ ଦେବା ଫଳରେ ତ୍ରିଶକ୍ତି-ମେଣ୍ଟ ସୃଷ୍ଟି ହୋଇଥିଲା ?
(A) ରୁଷିଆ
(B) ଫ୍ରାନ୍ସ
(C) ଇଟାଲୀ
(D) ଇଂଲଣ୍ଡ
Answer:
(C) ଇଟାଲୀ
26. ରୁଷିଆ ଓ ଫ୍ରାନ୍ସ କେବେ ‘ଦୃଶକ୍ତି ମେଣ୍ଟ’ ନାମକ ଏକ ସାମରିକ ଚୁକ୍ତି ସ୍ୱାକ୍ଷର କରିଥିଲେ ?
(A) ୧୮୯୪ ମସିହା
(B) ୧୯୦୨ ମସିହା
(C) ୧୯୦୪ ମସିହା
(D) ୧୯୦୫ ମସିହା
Answer:
(A) ୧୮୯୪ ମସିହା
27. ଇଂଲଣ୍ଡ କେବେ ରୁଷିଆ ସହିତ ଏକ ଚୁକ୍ତି ସ୍ୱାକ୍ଷର କରିଥିଲା ?
(A) ୧୮୯୪ ମସିହା
(B)୧୯୦୨ ମସିହା
(C) ୧୯୦୪ ମସିହା
(D) ୧୯୦୭ ମସିହା
Answer:
(D) ୧୯୦୭ ମସିହା
28. ୧୮୯୦ ମସିହା ପରେ କେଉଁ ଦେଶ ନୌଶକ୍ତିରେ କଲା ?
(A) ଇଟାଲୀ
(B) ଫ୍ରାନ୍ସ
(C) ଜର୍ମାନୀ
(D) ରୁଷିଆ
Answer:
(C) ଜର୍ମାନୀ
![]()
![]()