CHSE Odisha Class 11 Math Solutions Chapter 12 Conic Sections Ex 12(a)

Odisha State Board CHSE Odisha Class 11 Math Solutions Chapter 12 Conic Sections Ex 12(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 12 Conic Sections Exercise 12(a)

Question 1.
Fill in the blanks by choosing the correct answer from the given alternatives :
(a) The center of the circle x² + y² + 2xy – 6y + 1 = 0 is _____________. [(2, -6), (-2, 6), (-1, 3), (1, -3)]
Solution:
(-1, 3)

(b) The equation 2x² – ky² – 6x + 4y – 1 = 0 represents a circle if k = ____________. [2, -2, 0, 1]
Solution:
-2

(c) The point (-3, 4) lies ______________ the circle x² + y² = 16 [outside, inside, on]
Solution:
Outside

(d) The line y = x + k touches the circle x² + y² = 16 if k = _______________. [±2√2, ±4√2, ±8√2, ±16√2]
Solution:
±4√2

(e) The radius of the circle x² + y² – 2x + 4y + 1 = 0 is _______________. [1, 2, 4, √19]
Solution:
2

Question 2.
State (with reasons), which of the following is true or false :
(a) Every second-degree equation in x and y represents a circle.
Solution:
Every 2nd-degree equation in x and y represents a circle if the coefficients of x and y are equal and the equation does not contain xy term (False)

(b) The circle (x – 1)² + (y – 1)² = 1 passes through origin.
Solution:
(0 – 1)² + (0 – 1)² = 1 + 1 = 2 ≠ 1.
So the circle does not pass through the origin. (False)

(c) The line y = 0 is a tangent to the circle (x + 1)² + (y – 2)²  = 1.
Solution:
The line y = 0 is a tangent to the circle centre at (-1, 2) and the radius is 1. (True)
∴ The distance of the centre from the line y = 0 is 1 which is equal to its radius.

(d) The radical axis of two circles always passes through the centre of one of the circles,
Solution:
As radical axis is the common chord of the circles, which should not pass through the centre of one of the circles. (False)

(e) The circle x² + (y – 3)² = 4 and (x – 4)² + y² = 9 touch each other.
Solution:
The distance between the centres is \(\sqrt{(0-4)^2+(3-0)^2}\) = 5 which is equal to the sum of the radii. (True)

Question 3.
Find the equation of circles determined by the following conditions.
(a) The centre at (1, 4) and passing through (-2, 1).
Solution:

(b) The centre at (-2, 3) and passing through origin.
Solution:
Centre at (-2, 3) and circle passes through origin.
∴ Radius of the circle = \(\sqrt{(-2)^2+3^2}=\sqrt{13}\)
∴ Equation of the circle is (x – h)² + (y – k)² = a²
or, (x + 2)² + (y – 3)² = 13

(c) The centre at (3, 2) and a circle is tangent to x – axis.
Solution:

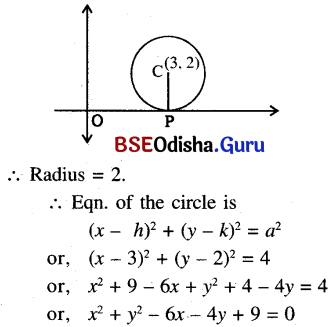
(d) The centre at (-1, 4) and circle is tangent to y – axis.
Solution:

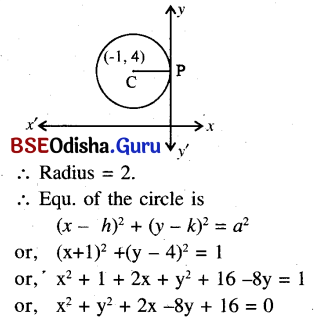
(e) The ends of diameter are (-5, 3) and (7, 5).
Solution:
The endpoints of the diameter of the circle are (-5, 3) and (7, 5).
∴ Equ. of the circle is
(x – h)² + (y – k)² = a²
(x- x₁)(x – x₂) + (y – y₁)(y – y₂) = 0
or, (x + 5)(x – 7) + (y – 3)(y – 5) = 0
or, x² – 7x + 5x – 35 + y² – 5y – 3y + 15 = 0
or, x² + y² – 2x – 8y – 20 = 0

(f) The radius is 5 and circle is tangent to both axes.
Solution:
As the circle is tangent to both axes, we have its centre at (5, 5).
∴ Equation of the circle is
or, (x ± 5)² + (y ± 5)² = 25

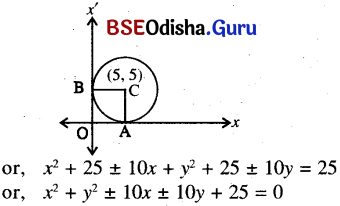
(g) The centre is on the x-axis and the circle passes through the origin and the point (4, 2).
Solution:

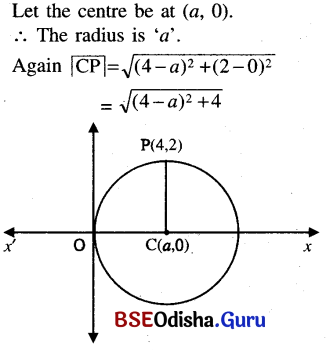
∴ \(\sqrt{(4-a)^2+4}\) = a
or, (4 – a)² + 4 = a²
or, 16 + a² – 8a + 4 = a²
or, 8a = 20 or, a = \(\frac{20}{8}=\frac{5}{2}\)
∴ Equation of the circle is
(x – h)² + (y – k)² = a²
or, (x – \(\frac{5}{2}\))² + (y – 0)² = (\(\frac{5}{2}\))²
or, x² + \(\frac{25}{4}\) – 5x + y² = \(\frac{25}{4}\)
or, x² + y² – 5x = 0

(h) The centre is on the line 8x + 5y = 0 and the circle passes through the points (2, 1) and (3, 5).
Solution:
Let the equation of the circle be x² + 2gx + y² + 2fy + c = 0
∴ Its centre at (- g, -f). As the centre lies on the line 8x + 5y = 0
We have -8g – 5f = 0      …..(1)
Again, as the circle passes through points (2, 1) and (3, 5)
We have
4 + 4g + 1 + 2f + c = 0  …..(2)
and 9 + 6g + 25 + 10f + c = 0   …..(3)
Now from (1), we have g = \(\frac{-5 f}{8}\)
From equation (2), 4g + 2f + c + 5 = 0
or, 4 \(\frac{-5 f}{8}\) + 2f + c + 5 = 0
or, -5f + 4f + 2c + 10 = 0
or, f = 2c + 10    …..(4)
(2) 6g + 10f + c + 34 = 0
or, 6\(\frac{-5 f}{8}\) + 10f + c + 34 = 0
or, -15f + 40f + 4c + 136 = 0
or, 25f = -4c – 136
or, f = \(\frac{-4 c-136}{25}\)
∴ 2c + 10 = \(\frac{-4 c-136}{25}\)
or, 25 (c + 5) = -2c – 68
or, 25c + 2c = -68 – 125
or, 27c = -193 or, c = \(\frac{-193}{27}\)
∴ f = 2C + 10 = 2(\(\frac{-193}{27}\)) + 10
= \(\frac{-386+270}{27}=\frac{-116}{27}\)
∴ g = \(\frac{-5 f}{8}=\frac{-5}{8} \times\left(\frac{-116}{27}\right)=\frac{145}{54}\)
Eqn. of the circle is x² + y² + 2 × \(\frac{145}{54}\) x + 2 \(\frac{-116}{27}\) y + \(\frac{-193}{27}\) = 0
or, 27x² + 27y² + 145x – 232y – 193 = 0

(i) The centre is on the line 2x + y – 3 = 0 and the circle passes through the points (5, 1) and (2, -3).
Solution:
Let the eqn. of the circle be x² + y² + 2gx + 2fy + c = 0
As it passes through (5, 1) and (2, -3),
we have 25 + 1 + 10g + 2f + c = 0 …(1)
and 4 + 9 + 4g – 6f + c = 0    …..(2)
Again as the centre lies on the line 2x + y – 3 = 0,
we have- 2g – f – 3 = 0 or, f= -2g – 3
∴ From equation (1)
10g + 2 (-2g – 3) + c + 26 = 0
or, 10g – 4g – 6 = -c – 26
or, 6g = -c – 20
or, g = \(\frac{-c-20}{6}\)
∴ From equation (2)
4g – 6 (-2g – 3) + c + 13 = 0
or, 4g + 12g + 18 + c + 13 = 0
or, 16g = -c – 31
or, g = \(\frac{-c-31}{16}\)
∴ \(\frac{-c-20}{6}=\frac{-c-31}{16}\)
or, -8c – 160 = -3c – 93
or, 5c = -160 + 93 = -67
or, c = –\(\frac{67}{5}\)
∴ g = \(\frac{-c-20}{6}=\frac{\frac{67}{5}-20}{6}=\frac{67-100}{5 \times 6}\)
= \(\frac{-33}{5 \times 6}=\frac{-11}{10}\)
∴ f = -2g – 3 = (-2)\(\left(\frac{-11}{10}\right)\)
= \(\frac{11-15}{5}=\frac{-4}{5}\)
∴ Eqn. of the circle is x² + y² + 2 (\(\frac{-11}{10}\))x + 2(\(\frac{-4}{5}\))y – \(\frac{67}{5}\) = 0
or, 5x² + 5y² – 11x – 8y – 67 = 0

(j) The circle is tangent to the line x + 2y – 9 = 0 at (5, 2) and also tangent to the line 2x – 3y – 7 = 0 at (2, -1).
Solution:

(k) The circle touches the axis of x at (3, 0) and also touches the line 3y – 4x = 12.
Solution:
Let the centre be at (3, k)
Radius = k

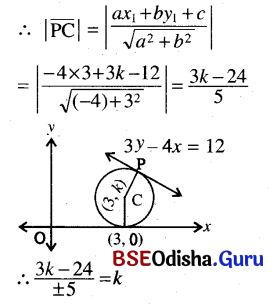
or, 3k – 24 = ±5k or, 2k = -24
or, k = -12
Also k = 3
∴ Equation of the Circle is
(x – 3)² + (y – k)² = k²
or, x² + 9 – 6x + y² + k² – 2ky = k²
or, x² + y2 – 6x – 2 (-12)y = 0
or, x² + y² – 6x + 24y + 9 = 0
and x² + y² – 6x – 6y + 9 = 0

(l) Circle is tangent to x – axis and passes through (1, -2) and (3, -4).
Solution:
Let the centre be at (h, k).
So the radius is k.

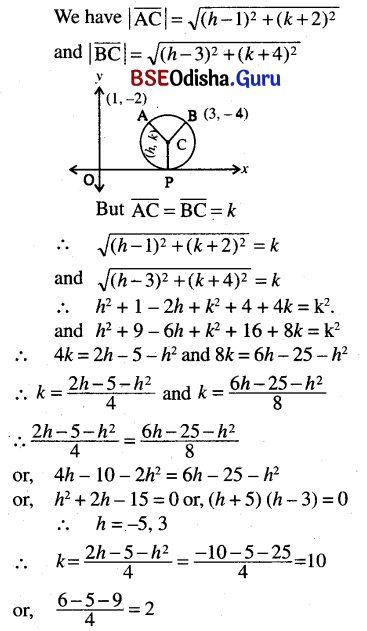
∴ Equation of the circle is (x – h)² + (y – k)² = k²
or, (x + 5)² + (y + 10)² = 100 and (x – 3)² + (y + 2)² = 4

(m) Circle passes through origin and cuts of intercepts a and b from the axes.
Solution:
Let the equation of the circle be x² + y² + 2gx + 2fy + c = 0

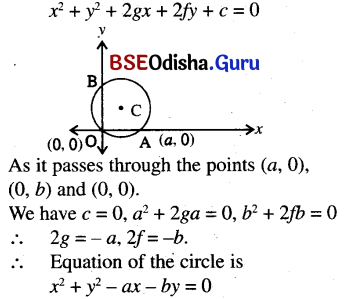
(n) Circle touches the axis of x at a distance of 3 from the origin and intercepts a distance of 6 on the y-axis.
Solution:
Let the centre be at (3, k).
So the radius is k.
∴ Equation of the circle is (x – 3)² + (y – k)² = k²
or, x² + 9 – 6x + y² + k² – 2ky = k²
or, x² + y² – 6x – 2xy + 9 = 0

∴ |y₂ – y₁| = 2\(\sqrt{k^2-9}\) = 6
or, \(\sqrt{k^2-9}\) = 3
or, k² = 18, or, k = ±3√2
∴ Equation of the circle is x² – y² – 6x ± 6y√2 + 9 = 0

Question 4.
Find the centre and radius of the following circles:
(a) x² + y² + 6xy – 4y – 12 = 0
Solution:
x² + y² + 6xy – 4y – 12 = 0
∴ 2g = 6, 2f = – 4, c = -12
∴ 8 = 3, f = -2
Centre of (-g, -f) = (-3, 2) and radius = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{9+4+12}\) = 5

(b) ax² + ay² + 2gx + 2fy + k = 0
Solution:
ax² + ay² + 2gx + 2fy + k = 0
or, x² + y² + \(\frac{2 g}{a}\)x + \(\frac{2 f}{a}\)y + \(\frac{k}{a}\) = 0
∴ Centre of \(\left(\frac{-g}{a}, \frac{-f}{a}\right)\)
and radius = \(\sqrt{\frac{g^2}{a^2}+\frac{f^2}{a^2}-\frac{k}{a}}=\sqrt{\frac{g^2+f^2-a k}{a}}\)

(c) 4x² + 4y² – 4x + 12y – 15 = 0
Solution:
4x² + 4y² – 4x + 12y – 15 = 0
or, x² + y² – 4 + 3y  – \(\frac{15}{4}\) = 0
∴ 2g = -1, 2f = 3, c = \(\frac{15}{4}\)
∴ g = – \(\frac{1}{2}\), f = \(\frac{3}{2}\)
∴ Centre at (-g, -f) = (\(\frac{1}{2}\), \(\frac{-3}{2}\)) and radius \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{\frac{1}{4}+\frac{9}{4}+\frac{15}{4}}=\frac{5}{2}\)

(d) a(x² + y²) – bx – cy = 0
Solution:
a(x² + y²) – bx – cy = 0
or, x² + y² – \(\frac{b x}{a}\) – \(\frac{c y}{a}\) = 0

Question 5.
Obtain the equation of circles passing through the following points and determine the coordinates of the centre and radius of the circle in each case:
(a) the points (3, 4) (4, -3) and (-3, 4).
Solution:
Let the centre be at (h, k)

(b) the points (2, 3), (6, 1) and (4, -6).
Solution:
Let the centre be at (h, k).

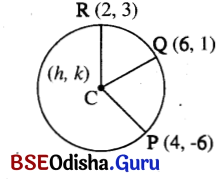
we have \(|\overline{\mathrm{PC}}|=|\overline{\mathrm{QC}}|=|\overline{\mathrm{RC}}|\)
∴ (h – 4)² + (k + 6)² = (h – 6)² + (k – 1)² and (h – 4)² + (k + 6)² = (h – 2)² + (k – 3)²
∴ h² + 16 – 8h + k² + 36 + 12k
= h² + 36 – 12h + k² + 1 – 2k
and h² + 16 – 8h + k² + 36 + 12k
= h² + 4 – 4h + k² + 9 – 6k
or, 14k = -4h – 15 and 18k = 4h – 39
or, k = \(\frac{-4 h-15}{14}\) and k = \(\frac{4 h-39}{18}\)

(c) the points (a, 0), (-a, 0) and (0, b).
Solution:
Let the equation of the circle be x² + y² + 2gx + 2fy + c = 0. As it passes through the points (a, 0), (-a, 0) and (0, b). We have
a² – 2ga + c = 0   …..(1)
a² + 2ga + c = 0   …..(2)

(d) the points (-3, 1), (5, -3) and (-3, 4).
Solution:
Let the equation of the circle be x² + y² + 2gx + 2fy + c = 0
As it passes through the points. we have (-3, 1), (5, -3) and (3, 4).
We have 9 + 1 – 6g + 2f + c = 0    …..(1)
25 + 9 + 10g – 6df + c = 0      …(2)
9 + 16 – 6g + 8f + c = 0     …..(3)

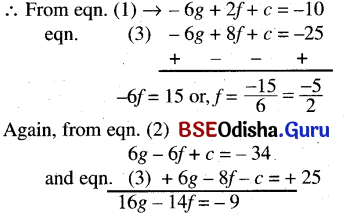
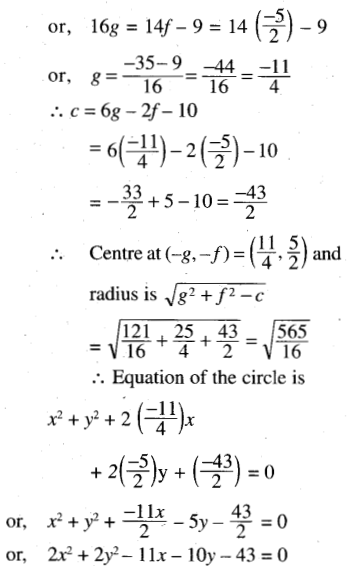
Question 6.
Find the equation of the circles circumscribing the triangles formed by the lines given below :
(a) the lines x = 0, y = x, 2x + 3y = 10
Solution:

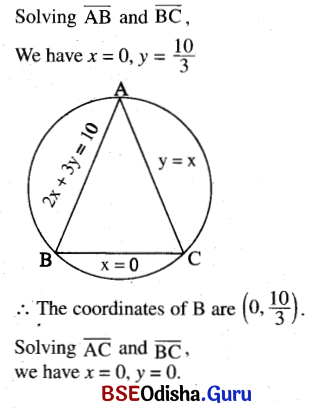
∴ The coordinates. C are (0, 0) of
Lastly, solving \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{AC}}\)
we have y = x, 2x + 3y = 1 0
we have 5x = 10
or, x = 2 and y = 2.
∴ The coordinates of A are (2, 2).
∴ The circle passes through the points (2, 2), (0, \(\frac{10}{3}\)) and (0, 0)
Let the equation of the circle be x² + y² + 2gx + 2fy + c = 0
As it passes through the points A, B, C we have c = 0, 4 + 4 + 4g + 4f = 0,
\(\frac{100}{9}\) + 2. f. \(\frac{10}{3}\) + 0 = 0
∴ f = \(\frac{-100}{9} / \frac{20}{3}=\frac{-5}{3}\)
and g = \(\frac{-4 f-8}{4}=\frac{-4\left(\frac{-5}{3}\right)-8}{4}\)
= \(\frac{20-24}{3 \times 4}=\frac{-1}{3}\)
∴ Equation of the circle is  x² + y² + 2(\(\frac{-1}{3}\))x + 2 \(\frac{-5}{3}\)y + 0 = 0
or, 3(x² +  y²) – 2x – 10y = 0

(b) The lines x = 0, 4x + 5y = 35, 4y = 3x + 25
Solution:



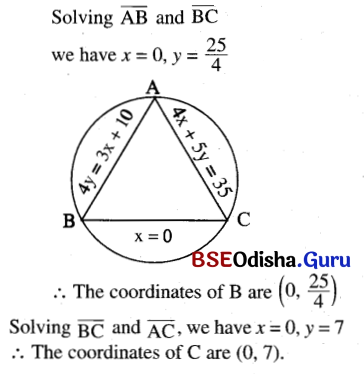
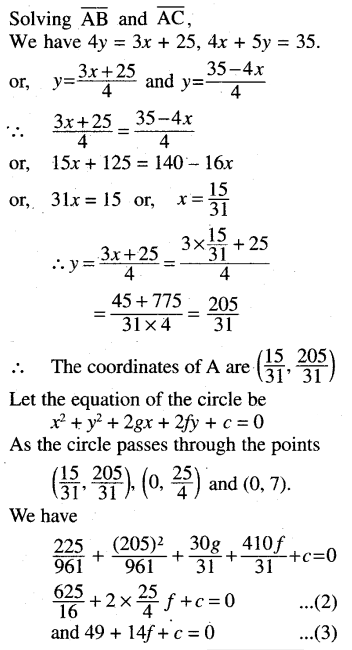
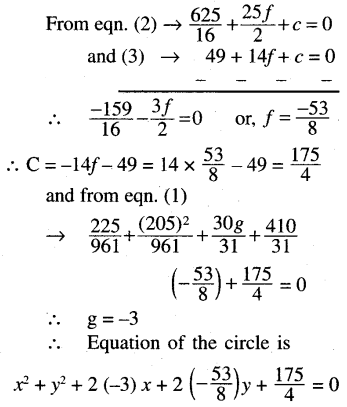
or, 4x² + 4y² – 24x – 53y + 175 = 0

(c) The lines x = 0, y = 0, 3x + 4y – 12 = 0
Solution:
The coordinates of A, B and C are (4, 0), (0, 3) and (0, 0).
Let the equation of the circle be x² + y² + 2gx + 2fy + c = 0

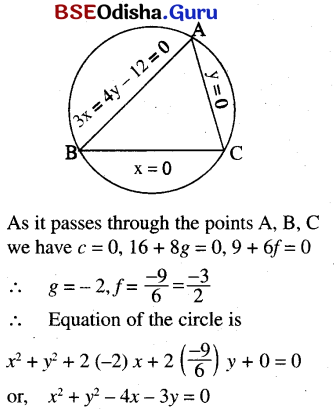
(d) The lines y = x, y =2 and y = 3x + 2
Solution:

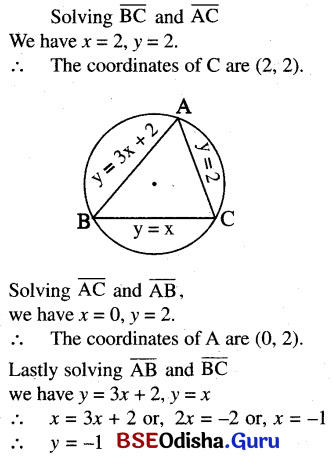
(e) the lines x + y = 6, 2x + y = 4 and x + 2y = 5
Solution:

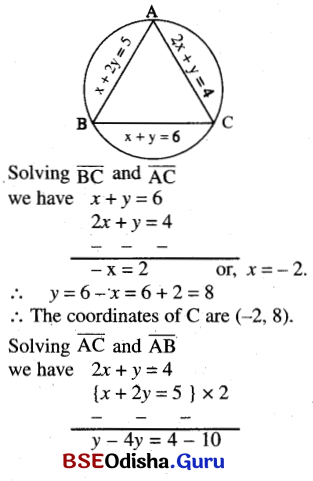
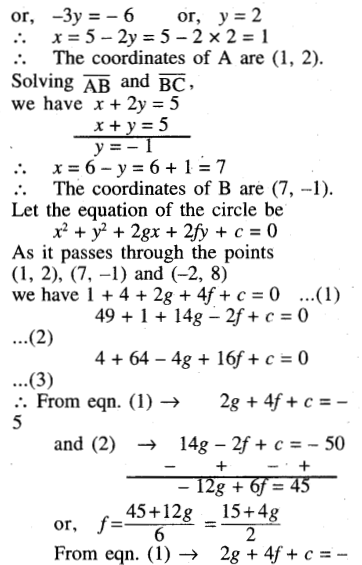
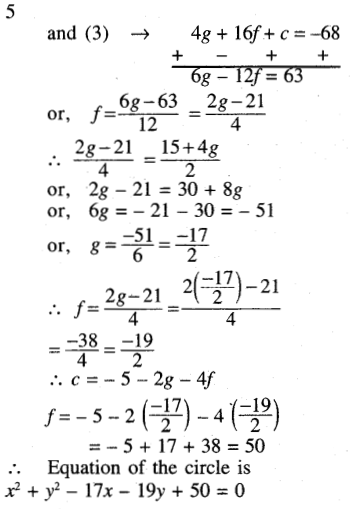
Question 7.
Find the coordinates of the points where the circle x² + y² – 7x – 8y + 12 = 0 meets the coordinates axes and hence find the intercepts on the axes. [Hint: If a circle intersects a line at points A and B, then the length AB is its intercepts on line L]
Solution:
x² + y² – 7x – 8y + 12 = 0
Putting x = 0, we have y² – 8y + 12 = 0 or, (y – 6) (y – 2) = 0, or, y = 6, 2.
∴ The circle meets the Y-axis at (0, 6) and (0, 2) and its Y-intercept is 6 – 2 = 4.
Again putting y = 0,
we have x² – 7x + 12 = 0
or, (x – 4)(x – 3) = 0 or, x = 4, x = 3.
∴ The circle meets the X-axis at (4, 0) and (3, 0) and its x-intercept is 4 – 3 = 1.

Question 8.
Find the equation of the circle passing through the point (1, -2) and having its centre at the point of intersection of lines 2x – y + 3 = 0 and x + 2y – 1 =0
Solution:

Question 9.
Find the equation of the circle whose ends of a diameter are the points of intersections of the lines and x + y – 1 = 0, 4x + 3y + 1 = 0 and 4x +y + 3 = 0, x – 2y +3 = 0.
Solution:
Solving x + y – 1 = 0, 4x + y + 3 = 0

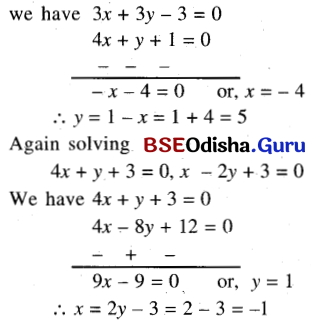
∴ The endpoints of the diameter are (-4, 5) and (-1, 1).
∴ Equation of the circle is
(x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
or, (x + 4) (x + 1) + (y – 5) (y – 1) = 0
or, x² + x + 4x + 4 + y² – y – 5y + 5 = 0
or, x² + y² + 5x – 6y + 9 = 0.

Question 10.
Find the equation of the circle inscribed inside the triangle formed by the line \(\frac{x}{4}+\frac{y}{3}\) = 1 and the coordinate axes.
Solution:
The circle is inscribed in the triangle formed by x = 0, y = 0 and \(\frac{x}{4}+\frac{y}{3}\) = 1
∴ If (h, k) is the centre and r is the radius of the circle then h = k = r.
The perpendicular distance of the centre (h, h) from the line 3x + 4y = 12 is the radius.
⇒ \(\left|\frac{3 h+4 h-12}{5}\right|\) = h
⇒ 7h – 12 = ±5h
⇒ 2h = 12 or 2h = 12
⇒ h = 6 or h = 1
But h can not be 6 thus the circle has equation (x – 1)² + (y – 1)² = 1
⇒ x² + y² – 2x – 2y + 1 =0

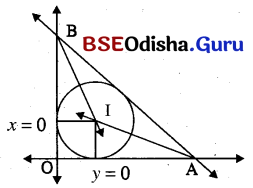
Question 11.
(a) Find the equation of the circle with its centre at (3, 2) and which touches to the line x + 2y – 4 = 0.
Solution:

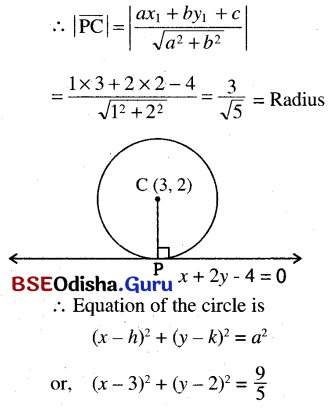
(b) The line 3x + 4y + 30 = 0 is a tangent to the circle whose centre is at (\(-\frac{12}{5},-\frac{16}{5}\)). Find the equation of the circle.
Solution:

(c) Prove that the points (9, 7), and (11, 3) lie on a circle with centre at origin. Find the equation of the circle.
Solution:

(d) Find the equation of the circle which touches the line x = 0, x = a and 3x + 4y + 5a = 0.
Solution:

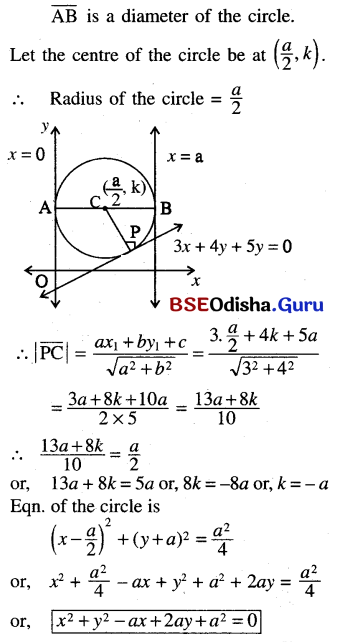
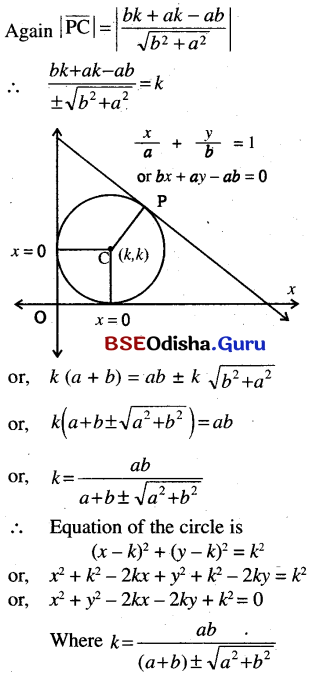
(e) If a circle touches the co-ordinate axes and also touches the straight line \(\frac{x}{a}+\frac{y}{b}\) = 1 and has its centre in the 1st quadrant, And its equation.
Solution:
Let the centre be at (k, k) and the radius is k.

Question 12.
ABCD is a square of side ‘a’ If AB and AD are taken as co-ordinate axes, prove that the equation of the circle circumscribing the square is
x² + y² = a(x + y)
Solution:

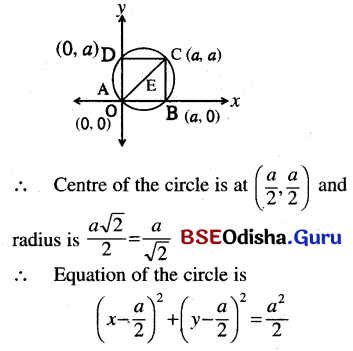
or, x² + \(\frac{a^2}{4}\) – ax + y² + \(\frac{a^2}{4}\) – ay = \(\frac{a^2}{2}\)
or, x² + y² – ax – ay = 0
or, x² + y² = a(x + y)

Question 13.
(a) Find the equation of the tangent and normal to the circle x² + y² = 25 at the point (3, -4).
Solution:
Equation of the tangent to the circle x² + y² = 25 at the point (3, -4) is
xx₁ + yy₁ = a²
3x – 4y = 25
Equation of the normal is x₁y = xy₁
or, 3y = -4x or, 4x + 3y = 0

(b) Find the equation of the tangent and normal, to the circle, x² + y² – 3x + 4y – 31 = 0 at the point (-2, 3).
Solution:
Equation of the tangent of the circle x² + y² – 3x + 4y – 31 = 0 at the point (-2, 3) is
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
or, -2x + 3y – \(\frac{3}{2}\) (x – 2) + 2(y + 3) – 31 = 0
or, – 4x + 6y – 3x + 6 + 4y + 12 – 62 = 0
or, -7x + 10y – 44 = 0
or, 7x – 10y + 44 = 0
Equation of the normal is x(f + y₁) – y(g + x₁) fx₁ + gy₁ = 0
or, x(2 + 3) – y(\(-\frac{3}{2}\) – 2) – 2(-2) – \(\frac{3}{2}\) × 3 = 0
or, 5x + \(\frac{7y}{2}\) + 4 – \(\frac{9}{2}\) = 0
or, 10x + 7y – 1 = 0

(c) Find the equation of the tangents to the circle x² + y² + 4x – 6y – 16 = 0 at the point where it meets the y – axis.
Solution:
Putting x = 0 in the circle equation, we have
y² – 6y – 16 = 0
or, y² – 8y + 2y – 16 = 0
or, y(y – 8) + 2(y – 8) = 0
or, (y – 8)(y + 2) = 0
y = 8 or, -2
The circle meets y – axis at (0, 8) and (0, -2).
Eqn. of the tangents are
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
or, 0 + 8y + 2 (x + 0) – 3(y + 8) – 16 = 0
or, 8y + 2x – 3y – 24 – 16 = 0
or, 2x + 5y = 40 and
x × 0 – 2y + 2 (x + 0) – 3 (y – 2) – 16 = 0
or, -2y + 2x – 3y + 6 – 16 = 0
or, 2x – 5y – 10 = 0

(d) Find the condition under which the tangents at (x₁, y₁) and (x₂, y₂) to the circle x² + y² + 2gx + 2fy + c = 0 are perpendicular.
Solution:
Equation of tangent to the circle
x² + y² + 2gx + 2fy + c = 0 at the point (x₁, y₁) is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
or, (g + x₁)x + y(f + y₁) + gx₁ + fy₁ + c = 0
Again equation of the tangent to the circle at (x₂, y₂) is
x(g + x₂) + y(f + y₂) + gx₂ + fy₂ + c = 0
As the tangent (1) and (2) are perpendicular, we have the product of their slopes is -1.
∴ \(\frac{g+x_1}{f+y_1} \times \frac{g+x_2}{f+y_1}\) = -1
or, (g + x₁)(g + x₂) = -(f + y₁)(f + y₂)
or, (g + x₁)(g + x₂) + (f + y₁)(f + y₂) = 0

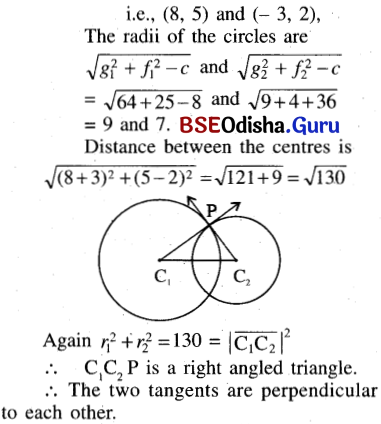
(e) Calculate the radii and distance between the centres of the circles, whose equations are, x² + y² – 16x – 10y + 8 = 0; x² + y² + 6x – 4y – 36 = 0. Hence or otherwise prove that the tangents drawn to the circles at their points of intersection are perpendicular.
Solution:
x² + y² – 16x – 10y + 8 = 0;
x² + y² + 6x – 4y – 36 = 0.
g₁ = -8, f₁ = -5, c₁ = 8,
g₂ = 3, f₂ = -2, c₂ = -36
The centres are (-g₁, -f₁) and (-g₂, -f₂)

Question 14.
(a) Find the equation of the tangents to the circle x² + y² = 9 perpendiculars to the line x – y – 1 = 0
Solution:

(b) Find the equation of the tangent to the circle x² + y² – 2x – 4y = 40, parallel to the line 3x – 4y = 1.
Solution:


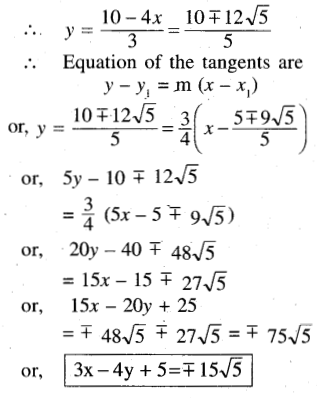
(c) Show that the line x – 7y + 5 = 0 a tangent to the circle x² + y² – 5x + 5y = 0. Find the point of contact. Find also the equation of tangent parallel to the given line.

Solution:
we have the line is x – 7y + 5 = 0
or, y = \(\frac{x+5}{7}\)
Now putting the value of y in the circle, we have x² + y² – 5x + 5y = 0
or, x² + (\(\frac{x+5}{7}\))² – 5x + 5 \(\frac{x+5}{7}\) = 0
or, 49x² + x² + 25 + 10x – 245x + 35x + 175 = 0
or, 50x² – 200x + 200 = 0
or, x² – 4x + 4 = 0
∴ a = 1, b = -4, c = 4
∴ b² – 4ac = (-4)² – 4 × 1 × 4
= 16 – 16 = 0
∴ The line x – 7y + 5 = 0

x – 7y – 45 and x – 7y + 5 = 0

(d) Prove that the line ax + by + c = 0 will be the tangent to the circle x² + y² = r² if r²(a² + b²) = c².
Solution:
We know that a line is a tangent to the circle if the distance of the line from the centre is equal to the radius.
Now the circle is x² + y² = r²
⇒ Centre is at (0, 0) and radius r. The distance of (0, 0) from ax + by + c = 0 is

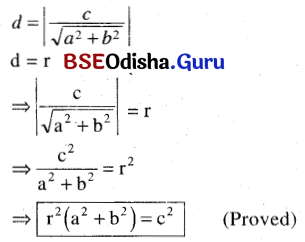
(e) Prove that the line 2x + y = 1 tangent to the circle x² + y² + 6x – 4y + 8 = 0.
Solution:

(f) If the line 4y – 3x = k is a tangent to the circle x² + y² + 10x – 6y + 9 = 0 find ‘k’. Also, find the coordinates of the point of contact.
Solution:
Center of the circle is (-5, 3) and the radius is \(\sqrt{25+9-9}\) = 5
Distance of the centre from the line 4y – 3x – k = 0

Question 15.
(a) Find the length of the tangent, drawn to the circle x² + y² + 10x – 6y + 8 = 0 from the centre of the circle x² + y² + 4x = 0.
Solution:
Center of the circle x² + y² + 4x = 0 is (2, 0)
∴ Length of the tangent drawn from the point (2, 0) to the circle x² + y² + 10x – 6y + 8 = 0
\(\sqrt{\mathrm{x}_1{ }^2+\mathrm{y}_1{ }^2+2 g \mathrm{~g}_1+2 \mathrm{fy}_1+\mathrm{c}}\)
= \(\sqrt{4+0+10 \times 2+0+8}=\sqrt{32}=4 \sqrt{2}\)

(b) Find the length of the tangent drawn from the point (2, -1) to the circle x² + y² + 6x + 10y + 18 = 0
Solution:
Length of the tangent drawn from the point (2, -1) to the circle x² + y² + 6x + 10y + 18 = 0 is
\(\sqrt{\mathrm{x}_1{ }^2+\mathrm{y}_1{ }^2+2 \mathrm{gx}_1+2 \mathrm{fy}_1+\mathrm{c}}\)
= \(\sqrt{4+1+(-6) \times 2+10(-1)+18}\)
= \(\sqrt{5-12-10+18}\) = 1

(c) Find the length of the tangent drawn from the point (4, 7) to the circle x² + y² = 15.
Solution:
Length of the tangent drawn from the point (4, 7) to the circle x² + y² = 15 is \(\sqrt{16+49-15}\) = √50 = 5√2

Question 16.
(a) Prove that the circle given by the equations x² + y² + 2x – 8y + 8 = 0 and x² + y² + 10x – 2y + 22 = 0 touches each other externally. Find also the point of contact
Solution:
x² + y² + 2x – 8y + 8 = 0
g₁ = 1, f₁ = -4, c₁ = 8
Hence centre = c₁(-g₁, -f₁) = c₁(-1, 4)
Radius = r₁ = \(\sqrt{1+16-8}\) = 3
Again x² + y² + 10x – 2y + 22 = 0
g₂ = 5, f₂ = -1, c₂ = 22
Centre c₂(-g₂, -f₂) = c₂(-5, 1)
Radius r₂ = \(\sqrt{25+1-22}\) = 2
Now

(b) Prove that the circle is given by the equations x² + y² = 4 and x² + y² + 6x + 8y – 24 = 0, touch each other and find the equation of the common tangent.
Solution:
x² + y² = 4,
x² + y² + 6x + 8y – 24 = 0
Their centres are (0, 0) and (-3, -4) and radii are 2 and \(\sqrt{9+16+24}\) = 7
∴ Distance between the centres is \(\sqrt{(-3)^2+(-4)^2}\) = 5, which is equal to the difference between the radii.
∴ The circles touch each other internally.
∴ Equation of the common tangent is S₁ – S₂ = 0
or, (x² + y² + 6x + 8y – 24) – (x² + y² – 4) = 0
or, 6x + 8y – 20 = 0
or, 3x + 4y = 10

(c) Prove that the two circle x² + y² + 2by + c² = 0 and x² + y² + 2ax + c² = 0,  will touch each other \(\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{c^2}\).
Solution:
x² + y² + 2by + c² = 0,
x² + y² + 2ax + c² = 0
g₁ = 0, f₁ = b, c₁ = c².
g₂ = a, f₂ = 0, c₂ = c².
The centres of the circle are (0, -b) and (-a, 0) and radii are \(\sqrt{b^2-c^2}\) and \(\sqrt{a^2-c^2}\). As the circles touch each other, we have the distance between the centres is equal to the sum of the radii.

(d) Prove that the circles given by x² + y² + 2ax + 2by + c = 0, and x² + y² + 2bx + 2ay + 2c = 0, touch each other, if (a + b) = 2c.
Solution:
x² + y² + 2ax + 2by + c = 0
x² + y² + 2bx + 2ay + 2c = 0,
The centre of the circle is (-a, -b) and (-b, -a). the radii of the circle are \(\sqrt{a^2+b^2-c}\) and \(\sqrt{b^2+a^2-c}\). As the circles touch each other we have, the distance between the centres is equal to the sum of the radii.

Question 17.
Find the equation of the circle through the point of intersection of circles x² + y² – 6x = 0 and x² + y² + 4y – 1 = 0 and the point (-1, 1).
Solution:
Let the equation of the circle be (x² + y² – 6x) + λ(x² + y² + 4y – 1) = 0
As it passes through the point (-1, 1),
we have (1 + 1 + 6) + λ(1 + 1 + 4 – 1) = 0
or, 8 + 5λ = 0 or, λ = \(\frac{-8}{5}\)
∴ Equation of the circle is (x² + y² – 6x) – \(\frac{8}{5}\) (x² + y² + 4y – 1) = 0
or, 5x² + 5y² – 30x – 8x² – 8y² – 32y + 8 = 0
or, 3x² + 3y² + 30x + 32y – 8 = 0

Question 18.
Find the equation of the circle passing through the intersection of the circles, x² + y² – 2ax = 0 and x² + y² – 2by = 0 and having the centre of the line \(\frac{x}{a}-\frac{y}{b}\) = 2
Solution:

Question 19.
Find the radical axis of the circles x² + y² – 6x – 8y – 3 = 0 and 2x² + 2y² + 4x – 8y = 0
Solution:
x² + y² – 6x – 8y – 3 = 0
2x² + 2y² + 4x – 8y = 0
x² + y² – 6x – 8y – 3 = 0
x² + y² + 2x – 4y = 0
∴ The equation of the radical axis is S₁ – S₂ = 0
or, (x² – y²– 6x – 8y – 3) – (x² + y² + 2x – 4y) = 0
or, -6x – 8y- 3 – 2x + 4y = 0
or, -8x – 4y – 3 = 0
or, 8x + 4y + 3 = 0

Question 20.
Find the radical axes of the circle x² + y² – 6x + 8y – 12 = 0  and x² + y² + 6x – 8y + 12 = 0 Prove that the radical axis is perpendicular to the line joining the centres of the two circles.
Solution:
Equation of the radical axes of the circle x² + y² – 6x + 8y – 12 = 0  and x² + y² + 6x – 8y + 12 = 0
(x² + y² – 6x + 8y – 12) – (x² + y² + 6x – 8y + 12) = 0
or, -12x + 16y – 24 = 0
or, 3x – 4y + 6 = 0
Again, slope of the radical axis is \(\frac{3}{4}\) = m₁ (say)
Centres of the circles are (3, -4) and (-3, 4).
Slope of the line joining the centres is \(\frac{4+4}{-3-3}=\frac{8}{-6}=-\frac{4}{3}\) = m₂ (say)
m₁. m₂ = \(\frac{3}{4}\left(-\frac{4}{3}\right)\) = -1
∴ The radical axis is perpendicular to the line joining centres of the circles. (Proved)

Question 21.
If the centre of one circle lies on or inside another, prove that the circles cannot be orthogonal.
Solution:
The orthogonality condition for two circles.
x² + y² + 2g₁x + 2f₁y + C₁ = 0   …..(1)
and x² + y² + 2g₂x + 2f₂y + C₂ = 0    …..(2)
is 2(g₁g₂ + f₁f₂) – C₁ – C₂ = 0
Let us consider two circles
Case-1. Let the centre of (2) which is C (-g₂, -f₂) lies on the circle (1). Hence it satisfies the equation (i)
i.e., g₂² + f₂² – 2g₁g₂ – 2f₁f₂ + C₂ = 0
⇒ 2g₁g₂ + 2f₁f₂ – C₁ – C₂ = g₂² + f₂² – C₂
Its right-hand side is the square of the radius of 2nd circle which can not be equal
to zero i.e., 2(g₁g₂ + f₁f₂) – C₁ – C₂ ≠ 0
Hence circles are not orthogonal.
Case-2. Let the centre of (2) which is (-g2, -f2) lies inside the circle (1).
Distance between their centres < radius of the first circle.
i,e. \(\sqrt{\left(g_1-g_2\right)^2+\left(f_1-f_2\right)^2}<\sqrt{g_1^2+f_1^2-C_1}\)
⇒ g₁² – 2g₁g₂ + f₁² + f₂² + 2f₁f₂ < g₁² + f₁² – C₁
⇒ 2g₁g₂ – 2f₁f₂ – C₁ – C₂ > g₂² + f₂² – C₂
= square of the radius of 2^nd circle. Hence greater than 0.
⇒ 2(g₁g₂ + f₁f₂) – C₁ – C₂ > 0
So two circles are not orthogonal. By case -1 and case -2 we conclude that if the centres of one circle lie on or inside another, then circles cannot be orthogonal.

Question 22.
If a circle S intersects circles S₁ and S₂ orthogonally. Prove that the centre of S lies on the radical axis of S₁ and S₂. [Hints: Take the line of centres of S₁ and S₂ as x – axis and the radical axis as y – axis. Use conditions for the orthogonal intersection of S, S₁ and S, S₂ simultaneously and prove that S is centred on the y – axis.]
Solution:
Let the equation of the circle S, S₁ and S₂ are
x² + y² + 2gx + 2fy + C = 0      …(1)
x² + y² + 2g₁x + 2f₁y + C = 0      …(2)
and x² + y² + 2g₂x + 2f₂y + C = 0      …(3)
According to the question, the circle S intersects circles S₁ and S₂ orthogonally.
Hence 2 (g₁g + f₁f) – C₁ – C = 0 …(4)
and 2 (g₂g + f₂f) – C₂ – C = 0  ….(5)
Subtracting (4) from (3) we get
2g(g₁ – g₂) + 2f (f₁ – f₂) – C₁ + C₂ = 0 …(6)
Now radical axis of circles S₁ and S₂ is S₁ – S₂ = 0
i, e. 2x (g₁ – g₂) + 2y (f1 – f2)+ C₁ – C₂ = 0 ….(7)
The centre of the circle S is (-g, -f).
If it lies in the radical axis then equation (7) will be satisfied by the centre.
i,.e, 2g (g₁ – g₂) + 2f (f₁ – f₂) – C₁ + C₂ = 0
which is nothing but equation (5). Hence centres of S lie on the radical axis of S₁ and S₂.

Question 23.
R is the radical centre of circles S₁, S₂ and S₃. Prove that if R is on/inside/outside one of the circles then it is similarly situated with respect to the other two.
Solution:
Given R is the radical centre of S₁, S₂ and S₃
The radical centre is the intersection point of three radical axes whose equations are
S₁ – S₂ = 0
S₂ – S₃ = 0    …..(1)
S₃ – S₁ = 0
Let S₁ : x² +y² + 2g₁x + 2f₁y + C₁ =0
S₂ : x² + y² + 2g₂x + 2f₂y + C₂ =0
S₃ : x² + y² + 2g₃x + 2f₃y + C₃ =0
Now equations of radical axes by set of equation (1) are
2x(g₁ – g₂) + 2y(f₁ – f₂) + C₁ – C₂ =0 …(2)
2x(g₂ – g₃) + 2y(f₂ – f₃) + C₂ – C₃ =0 …(3)
and 2x(g₃ – g₁) + 2y(f₃ – f₁) + C₃ – C₁ = 0 …(4)
Let the co-ordinate of R be (x1, y1) the
point R must satisfy (2), (3) and (4).
i.e., 2x₁(g₁ – g₂) + 2y₁(f₁ – f₂) + C₁ – C₂ = 0 …(5)
2x₁(g₂ – g₃) + 2y₁(f₂ – f₃) + C₂ – C₃ =0 …(6)
2x₁(g₃ – g₁) + 2y₁(f₃ – f₁) + C₃ – C₁ =0 …(7)
Subtracting (6) for (5) we get
2x₁(g₁ – g₃) + 2y₁(f₁ – f₃) + C₁ – C₃ =0
⇒ 2g₁x₁ + 2f₁y₁ + C₁ =2g₃x₁ + 2f₃y₁ + C₃
Similarly subtracting (7) from (6) we get
2g₂y₁ + 2f₂y₁ + C₂ = 2g₁x₁ + 2f₁y₁ + C₁
Combining the above two equations we get
2g₂x₁ + 2f₂y₁ + C₂ = 2g₁x₁ + 2f₁y₁ + C₁ = 2g₃x₁ + 2f₃y₁ + C₃
If R x₁ y₁ lies on / inside / outside of S₁ …(8) then x₁² + y₁² + 2g₁x₁ + 2f1y1 + C₂ (= / < / >)0 respectively.
⇒ x₁² + y₁² + 2g₂x₂ + 2f₂y₂ + C₂(=/</>) 0
⇒ x₁² + y₁² + 2g₃x₃ + 2f₃y₃ + C₃(=/</>) 0
respectively by Eqn (8).
This concludes that if R is on /inside/outside. One of the circles then it is similarly situated with respect to the other two.

Question 24.
Determine a circle which cuts orthogonally to each of the circles.
S₁: x² + y² + 4x – 6y + 12 = 0
S₂: x² + y² + 4x + 6y + 12 = 0
S₃: x² + y² – 4x + 6y + 12 = 0
[Hints: The centre of the required circle S must be the radical centre R (why?), which lies outside all the circles. Then show that the radius of S must be the length of the tangent from R to any circle of the system.
Solution:
Let the equation of the required circle is x² + y² + 2gx + 2fy + C = 0    …..(1)
We know if two circles
x² + y² + 2g₁x + 2f₁y + C₂ = 0 and
x² + y² + 2g₂x + 2f₂y + C₂ = 0
are orthogonal then
2(g₁g₂ + f₁f₂) – C₁ – C₂ =0   ….(2)
According to the question circle (1) is orthogonal to the circles
S₁: x² + y² – 4x – 6y + 12 = 0     ….(3)
S₂: x² + y² + 4x + 6y + 12 = 0   ….(4)
S₃: x² + y² – 4x + 6y + 12 = 0     ….(5)
For these circles equation (2) will be
2(-2g – 3f) – C – 12 = 0     ….(6)
2(2g + 3f) – C – 12 = 0     …..(7)
2(-2g + 3f) – C – 12 = 0     …..(8) respectively.
Now subtract eqn. (7) from (6) and (8) from (7) we get
2(- 4g – 6f) = 0
⇒ 2(4g) = 0 ⇒ g = 0 , and f = 0
Using the value of g and f in eq. (6) we get
C = -12
Using g = 0, f= 0 , C = -12 in (1) we get
x² + y² – 12 = 0 is the required equation of the circle.

Question 25.
Prove that no pair of concentric circle can have radical axes.
Solution:
Let the centre of pair of concentric circles is C (h, k) and radii are r₁ and r₂.
So equation of the circles are
S₁: (x – h)² + (y – k)² = r₁²
S₂: (x – h)² + (y – k)² = r₂²
Equation of the radical axis is S₁ – S₂ = 0
⇒ r₁² – r₂² = 0
which is not a straight line as r₁ and r₂ are constants.
Hence it concludes that no pair of concentric circles have a radical axis.