Odisha State Board CHSE Odisha Class 12 Foundation of Education Solutions Chapter 15 ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ Questions and Answers.
CHSE Odisha 12th Class Education Solutions Chapter 15 ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ
ବସ୍ତୁନିଷ୍ଠ ଓ ଅତିସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
A. ପ୍ରତି ପ୍ରଶ୍ନତଳେ ପ୍ରଦତ୍ତ ଚାରିଗୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
1. ପରିସଂଖ୍ୟାନ (Statistics) କେଉଁ ଇଟାଲୀୟ ଶବ୍ଦରୁ ଆସିଛି ?
(i) ଷ୍ଟାଟିଷ୍ଟ (Statista)
(ii) ଷ୍ଟାଟୋ (Stato)
(iii) ଷ୍ଟାଟସ୍ (Status)
(iv) ଷ୍ଟାଟସ୍ କୋ (Status quo)
Answer:
(i) ଷ୍ଟାଟିଷ୍ଟ (Statista)
2. ପରିସଂଖ୍ୟାନ କି ପ୍ରକାର ତଥ୍ୟ ସଂଗ୍ରହ କରେ ?
(i) ସଂଖ୍ୟାତ୍ମକ (Quantitative)
(ii) ବିଷୟାତ୍ମକ (Subjective)
(iii) ଗୁଣାତ୍ମକ (Qualitative)
(iv) ସଂଖ୍ୟାତ୍ମକ ଏବଂ ଗୁଣାତ୍ମକ (Qualitative and quantitative)
Answer:
(i) ସଂଖ୍ୟାତ୍ମକ (Quantitative)
3. 5, 6, 7 ର ମଧ୍ୟମା କେତେ ?
(i) 7
(ii) 6
(iii) 5
(iv) 5.5
Answer:
(ii) 6
![]()
4. 2, 3, 4, 6, 7, 5 ର ମଧ୍ୟମା କେତେ ?
(i) 4
(ii) 5
(iii) 4.5
(iv) 5.5
Answer:
(iii) 4.5
5. ନିମ୍ନ ଶବ୍ଦଗୁଡ଼ିକ ମଧ୍ୟରୁ କେଉଁଟି ପରିସଂଖ୍ୟାନ ସମ୍ବନ୍ଧୀୟ ଶବ୍ଦ ନୁହେଁ ?
(i) ଲବ୍ଧଙ୍କ (Score)
(ii) ପୈାନଃପୁନ୍ୟ (Frequency)
(iii) ସଂଶ୍ଳେଷଣ (Analysis)
(iv) ସଂଭାଗ (Class Interval)
Answer:
(iii) ସଂଶ୍ଳେଷଣ (Analysis)
6. ମାଧ୍ୟ (Mean) ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ର କ’ଣ ?
(i) \(\frac{\Sigma}{\mathrm{N}}\)
(ii) \(\frac{\sum X}{N}\)
(iii) \(\frac{\mathrm{X}}{\mathrm{N}}\)
(iv) \(\frac{\mathrm{NX}}{\Sigma}\)
Answer:
(ii) \(\frac{\sum X}{N}\)
7. ମଧ୍ୟମା (Median) ନିଶ୍ଚୟ କରିବାର ସୂତ୍ର କ’ଣ ?
(i) \(L+\frac{N / 2-F}{f_m} \times \mathrm{i}\)
(ii) \(U-\frac{N / 2-F}{f_m} \times \mathrm{i}\)
(iii) \(L-\frac{N / 2-F}{f_m} \times \mathrm{i}\)
(iv) ଏଗୁଡ଼ିକରୁ କେଉଁଟି ନୁହେଁ
Answer:
(i) \(L+\frac{N / 2-F}{f_m} \times \mathrm{i}\)
8. ଗରିଷ୍ଠକ (Mode) ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ର କ’ଣ ?
(i) 3 ମଧ୍ୟମା – 3 ମାଧ୍ୟ
(ii) 3 ମାଧ୍ୟ – 2 ମାଧ୍ୟମା
(iii) 3 ମଧ୍ୟମା – 2 ମାଧ୍ୟ
(iv) 3 ମଧ୍ୟମା – 4 ମାଧ୍ୟ
Answer:
(iii) 3 ମଧ୍ୟମା – 2 ମାଧ୍ୟ
9. 10, 20, 30, 40, 50, 60, 70 ର ମାଧ୍ୟ (Mean) କେତେ ?
(i) 50
(ii) 40
(iii) 30
(iv) 60
Answer:
(ii) 40
![]()
10. ପରିସଂଖ୍ୟାନର ଜନ୍ମଦାତା କିଏ ?
(i) ଏଚେଲ୍
(ii) କୱେଡ଼େନ୍
(iii) ସାର୍ ରୋନାଲ୍ଡ
(iv) ଟର୍ଟଲ୍
Answer:
(iii) ସାର୍ ରୋନାଲ୍ଡ
11. 40 – 49 ର ଉଚ୍ଚ ବାସ୍ତବ ସୀମା କେତେ ?
(i) 39.5
(ii) 49.5
(iii) 40.5
(iv) 44.5
Answer:
(ii) 49.5
12. ନିମ୍ନରେ କେଉଁଟି କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପ ଅନ୍ତର୍ଭୁକ୍ତ ନୁହେଁ ?
(i) ମାଧ୍ୟ (Mean)
(ii) ମଧ୍ୟମା (Median)
(iii) ଗରିଷ୍ଠକ (Mode)
(iv) ସହବନ୍ଧନ (Co-relation)
Answer:
(iv) ସହବନ୍ଧନ (Co-relation)
13. ମୂଲ୍ୟାୟନ (Evaluation) ବା ପ୍ରୟୋଗ (Application) ରେ ଆମେ ସାଧାରଣତଃ କି ପ୍ରକାର ପ୍ରଶ୍ନ ପଚାରିଥାଉ ?
(i) ବସ୍ତୁନିଷ୍ଠ
(ii) ଦୀର୍ଘ ଉତ୍ତରମୂଳକ
(iii) ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ
(iv) ଏଥରୁ କେଉଁଟି ନୁହେଁ
Answer:
(i) ବସ୍ତୁନିଷ୍ଠ
14. ନିମ୍ନଲିଖ ପ୍ରାପ୍ତାଙ୍କର ଗରିଷ୍ଠକ କେତେ ?
2, 2, 4, 2, 8, 6, 6, 2, 4, 2
(i) 4
(ii) 2
(iii) 8
(iv) 6
Answer:
(ii) 2
15. 100 – 109 ସଂଭାଗର ‘i’ କେତେ ?
(i) 9
(ii) 8
(iii) 10
(iv) 11
Answer:
(iii) 10
16. 10-14 ସଂଭାଗର ମଧ୍ୟବିନ୍ଦୁ (Mid-point) କେତେ ?
(i) 9.5
(ii) 14.5
(iii) 12
(iv) 10
Answer:
(iii) 12
17. 10-14 ସଂଭାଗର ନିମ୍ନ ବାସ୍ତବ ସୀମା କେତେ ?
(i) 9.5
(ii) 14.5
(iii) 5.5
(iv) 4.5
Answer:
(i) 9.5
18. A.M. କ’ଣ ?
(i) କଳ୍ପିତ ମଧ୍ୟବିନ୍ଦୁ
(ii) କଳ୍ପିତ ଗରିଷ୍ଠକ
(iii) କଳ୍ପିତ ମାଧ୍ୟ
(iv) କଳ୍ପିତ ମଧ୍ୟମା
Answer:
(iii) କଳ୍ପିତ ମାଧ୍ୟ
![]()
19. 10 ଜଣ ପିଲା, 15 ଜଣ ପିଲା, 3 ଜଣ ପିଲାଙ୍କର ମାଧ୍ୟ (Mean) କେତେ ?
(i) 9
(ii) 9.33
(iii) 9.4
(iv) ମାଧ୍ୟ ନିର୍ଣ୍ଣୟ କରିହେବ ନାହିଁ
Answer:
(iv) ମାଧ୍ୟ ନିର୍ଣ୍ଣୟ କରିହେବ ନାହିଁ
20. ମଧ୍ୟମା ବାହାର କର ।
5, 6, 3, 2, 1, 4, 10
Answer:
4
B. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
1. ନମୁନା (Sample)ରୁ ଉପନୀତ ପରିସଂଖ୍ୟାନ ସଂଖ୍ୟାକୁ ___________ କୁହାଯାଏ ।
Answer:
ସାଂଖ୍ୟକ (Satistic) ତଥ୍ୟ
2. ନମୁନାକୁ ପରୀକ୍ଷା କରି ପରିସଂଖ୍ୟାନ ସଂଖ୍ୟା ନିର୍ଣ୍ଣୟ କରାଗଲେ ତାହାକୁ ___________ କହନ୍ତି ।
Answer:
ସାଧାରଣ ଚରିତ୍ର (Parameter)
3. ଚଳ ସଂଖ୍ୟା ଦୁଇ ପ୍ରକାର ଗୋଟିଏ ନିରବଚ୍ଛିନ୍ନ (Continuous) ଏବଂ ଅନ୍ୟଟି ___________ ଅଟେ ।
Answer:
ବିଚ୍ଛିନ୍ନ (Discrete)
4. ଯେଉଁ ସଂଖ୍ୟାକୁ ଭାଗ କରିହୁଏ ନାହିଁ, ତାହା ___________ ସଂଖ୍ୟା ।
Answer:
ବିଚ୍ଛିନ୍ନ (Discrete)
5. ଉଚ୍ଚତମ ଲବ୍ଧାଙ୍କ ଏବଂ ନିମ୍ନତମ ଲବ୍ଧାଙ୍କ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟକୁ ___________ କୁହାଯାଏ ।
Answer:
ବ୍ୟବଧାନ ବା ବ୍ୟାପକତା (Range)
6. ଲବ୍ଧାଙ୍କର ସଜ୍ଜୀକରଣ ନିମନ୍ତେ ___________ ନିରୂପଣ କରାଯାଇଥାଏ ।
Answer:
ସଂଭାଗ ବିସ୍ତାର (Size of the class interval)
7. ସମ୍ଭାଗଗୁଡ଼ିକ ସଜାଇ ଲେଖୁରିବା ପରେ ପ୍ରତ୍ୟେକ ସମ୍ଭାଗର ଦକ୍ଷିଣ ପାର୍ଶ୍ଵରେ ଲବ୍ଧାଙ୍କର ___________ ଅଙ୍କନ କରାଯାଇ ପୌନଃପୁନ୍ୟ ଲେଖାଯାଏ ।
Answer:
ଅନୁମେଳକ ଗାର (Tally)
8. କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପର ମାନଗୁଡ଼ିକ ମାଧ୍ଯମାନ (Mean), ମାଧ୍ୟ (Median) ଏବଂ ___________ ଅଟେ ।
Answer:
ଗରିଷ୍ଠକ (Mode)
9. ଅବର୍ଗତ ସଂଖ୍ୟାର ମାଧ୍ୟମାନ ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ରଟି ___________ ଅଟେ ।
Answer:
M = \(\frac{\Sigma X}{N}\)
10. ବର୍ଗତ ସଂଖ୍ୟାର ମାଧମାନ ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ରଟି ___________ ଅଟେ ।
Answer:
M = \(\frac{\Sigma f x}{\mathrm{~N}}\)
11. ଗରିଷ୍ଠକ ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ର ___________ ଅଟେ ।
Answer:
3 ମଧ୍ୟମା – 2 ମାଧ୍ୟମାନ
![]()
C. ରେଖାଙ୍କିତ ପଦକୁ ପରିବର୍ତ୍ତନ କରି ଠିକ୍ କରି ଲେଖ ।
1. ସଙ୍ଗଠିତ ତଥ୍ୟାବଳୀରୁ ମାଧ୍ୟ ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ର AM + \(\frac{\Sigma x^{\prime}}{\mathrm{N}}\) ।
Answer:
ସଙ୍ଗଠିତ ତଥ୍ୟାବଳୀରୁ ମାଧ୍ୟ ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ର AM + \(\frac{\Sigma x^{\prime}}{\mathrm{N}}\) × i ।
2. 20-24 ର ସମ୍ଭାଗ ବିସ୍ତାର 6 ।
Answer:
20-24ର ସମ୍ଭାଗ ବିସ୍ତାର 5 ।
3. ସଙ୍ଗଠିତ ତଥ୍ୟାବଳୀରୁ ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ର L + \(\frac{\frac{\mathrm{N}}{2}-F}{\mathrm{f}_{\mathrm{m}}}\) ।
Answer:
ସଙ୍ଗଠିତ ତଥ୍ୟାବଳୀରୁ ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ର L + \(\frac{\frac{\mathrm{N}}{2}-F}{\mathrm{f}_{\mathrm{m}}}\) × i ।
4. ପରିସଂଖ୍ୟାନର ଜନକ ଭାବରେ ଚାର୍ଲସ୍ ବ୍ୟାବେଜ୍ ପରିଚିତ ।
Answer:
ପରିସଂଖ୍ୟାନର ଜନକ ଭାବରେ ସାର୍ ରୋନାଲ୍ଟ ପରିଚିତ ।
5. ‘ପରିସଂଖ୍ୟାନ’ ହେଉଛି ପ୍ରାକ୍-କଳନା ଓ ସମ୍ଭାବନାର ବିଜ୍ଞାନ । – ଏହା ଟର୍ଗଟ କହିଥିଲେ ।
Answer:
‘ପରିସଂଖ୍ୟାନ’ ହେଉଛି ପ୍ରାକ୍-କଳନା ଓ ସମ୍ଭାବନା ବିଜ୍ଞାନ । – ଏହା ବୋଉଂସନ୍ କହିଥିଲେ ।
6. A.M. ର ଅର୍ଥ କଳ୍ପିତ ମଧ୍ୟ ବିନ୍ଦୁ ।
Answer:
A.M. ର ଅର୍ଥ କଳ୍ପିତ ମାଧ୍ୟ ।
7. ଯେକୌଣସି ବିଷୟ ସମ୍ବନ୍ଧୀୟ ତଥ୍ୟାବଳୀର ଧନୁରୂପୀ ବଣ୍ଟନ ରେଖା ସୃଷ୍ଟି କରିବା ପ୍ରକୃତିକୁ ତଥ୍ୟର ପୌନଃପୁନ୍ୟତା କୁହାଯାଏ ।
Answer:
ଯେକୌଣସି ବିଷୟ ସମ୍ବନ୍ଧୀୟ ତଥ୍ୟାବଳୀର ଧନୁରୂପୀ ବଣ୍ଟନ ରେଖା ସୃଷ୍ଟି କରିବା ପ୍ରକୃତିକୁ ତଥ୍ୟର କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା କୁହାଯାଏ ।
8. 1, 1, 8, 8, 8, 6, 6, 5, 5, 2, 3ର ଗରିଷ୍ଠକ 2 ।
Answer:
1, 1, 8, 8, 8, 6, 6, 5, 5, 2, 3ର ଗରିଷ୍ଠକ 8 ।
9. ପରିସଂଖ୍ୟାନ (Statistics) ଲାଟିନ୍ ଶବ୍ଦ ଷ୍ଟାଟସ୍ କୋ (Status quo) ଆସିଅଛି ।
Answer:
ପରିସଂଖ୍ୟାନ (Statistics) ଲାଟିନ୍ ଶବ୍ଦ ଷ୍ଟାଟସ୍ (Status) ଆସିଅଛି ।
D. ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଗୋଟିଏ ବାକ୍ୟରେ ଲେଖ ।
1. ପରିସଂଖ୍ୟାନ କ’ଣ ?
Answer:
କୌଣସି ବିଷୟରେ ସଂଖ୍ଯାତ୍ମକ ତଥ୍ୟ ସଂଗ୍ରହ, ଉକ୍ତ ତଥ୍ୟର ଯୁକ୍ତିଯୁକ୍ତ ଉପସ୍ଥାପନ, ବିଶ୍ଳେଷଣ ଏବଂ ବ୍ୟାଖ୍ୟାକରଣକୁ ପରିସଂଖ୍ୟାନ କୁହାଯାଏ ।
2. ଲବ୍ଧାଙ୍କ କାହାକୁ କୁହାଯାଏ ? କିମ୍ବା, ଲବ୍ଧାଙ୍କ କ’ଣ ?
Answer:
କୌଣସି ପରୀକ୍ଷାରେ ପରୀକ୍ଷାର୍ଥୀମାନଙ୍କୁ ଯେଉଁ ସାଫଲ୍ୟାଙ୍କଗୁଡ଼ିକ ଦିଆଯାଏ, ତାହାକୁ ଲଜ୍ଜାଙ୍କ କୁହନ୍ତି ।
3. ପୌନଃପୁନଃ କହିଲେ କ’ଣ ବୁଝ ?
Answer:
କୌଣସି ସଂଭାଗ ତାଲିକାରେ ନିର୍ଦ୍ଦିଷ୍ଟ ଲବ୍ଧାଙ୍କଗୁଡ଼ିକ ଯେତେଥର ଥାଏ, ତାହାକୁ ଲବ୍ଧାଙ୍କର ପୌନଃପୁନଃ କୁହାଯାଏ ।
4. ମାଧ୍ୟ ବିଚ୍ୟୁତି କାହାକୁ କହନ୍ତି ?
Answer:
ଲବ୍ଧାଙ୍କମାନଙ୍କରୁ ମାଧ୍ୟମାନର ଅନ୍ତରକୁ ମାଧ୍ଯ ବିଚ୍ୟୁତି କୁହାଯାଏ ।
![]()
5. ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନରେ ମଧ୍ୟମା କ’ଣ ?
Answer:
ମଧ୍ୟମା ହେଉଛି କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତାର ଅନ୍ୟ ଏକ ମାପ ବା ନିର୍ଦ୍ଦେଶକ, ଯାହା ସମଗ୍ର ଲବ୍ଧାଙ୍କ ବିତରଣକୁ ଦୁଇ ସମାନ ଅଂଶରେ ବିଭକ୍ତ କରେ ।
6. ଗୋଟିଏ ପ୍ରାପ୍ତାଙ୍କ ବିତରଣର ମାଧ୍ୟ କହିଲେ କ’ଣ ବୁଝାଏ ?
Answer:
ଗୋଟିଏ ପ୍ରାପ୍ତାଙ୍କ ବିତରଣରେ ଲବ୍ଧଙ୍କଗୁଡ଼ିକର ହାରାହାରି (Average) ପରିମାଣକୁ ମାଧ୍ୟ କୁହାଯାଏ ।
7. ପରିସଂଖ୍ୟାନରେ ବିସ୍ତାର କାହାକୁ କହନ୍ତି ?
Answer:
ପ୍ରତ୍ୟେକ ସଂଭାଗ ଅନ୍ତର୍ଗତ ଲବ୍ଧାଙ୍କ ସଂଖ୍ୟାକୁ ସଂଭାଗ ବିସ୍ତାର କୁହାଯାଏ ।
8. ଗୋଟିଏ ବିସ୍ତୃତିର ମଧ୍ୟଗ କାହାକୁ କହନ୍ତି ?
କିମ୍ବା, ମଧ୍ୟମା ବା ମଧ୍ଯଗ କ’ଣ ?
Answer:
କୌଣସି ଲବ୍ଧଙ୍କ ବିତରଣକୁ ସଜାଇ ଲେଖିଲେ ଯେଉଁ ଲଜ୍ଜାଙ୍କଟି ବିତରଣକୁ ଦୁଇ ସମାନ ଭାଗରେ ବିଭକ୍ତ କରିଥାଏ ତାହା ମଧ୍ୟମା
ଅଟେ ।
9. ପରିସଂଖ୍ୟାନରେ ମାଧ୍ୟ କାହାକୁ କହନ୍ତି ?
କିମ୍ବା, ମାଧ୍ୟର ଗୋଟିଏ ସଂଜ୍ଞା ଦିଅ ।
Answer:
ଅନେକଗୁଡ଼ିଏ କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପ ମଧ୍ୟରେ ହାରାହାରି ପରିମାପକୁ ମାଧ୍ୟ କୁହାଯାଏ ।
କିମ୍ବା, ଲବ୍ଧାଙ୍କଗୁଡ଼ିକର ହାରାହାରି ପରିମାପକୁ ମାଧ୍ୟ କୁହାଯାଏ ।
10. ପରିସଂଖ୍ୟାନ ଆମେ କାହିଁକି ଜାଣିବା ?
Answer:
ବିଭିନ୍ନ ଛାତ୍ର ପରୀକ୍ଷାରେ ରଖିଥିବା ନମ୍ବର ମଧ୍ୟରେ ଏକ ତୁଳନାତ୍ମକ ବିବରଣୀ ପ୍ରଦାନ କରିବାରେ ପରିସଂଖ୍ୟାନ ସାହାଯ୍ୟ କରେ ।
11. ଗୋଟିଏ ସଂଭାଗର ପୌନଃପୁନ୍ୟ କ’ଣ ଜଣାଏ ?
Answer:
ପୌନଃପୁନଃ, ଗୋଟିଏ ସଂଭାଗର କୌଣସି ଏକ ଲବ୍ଧାଙ୍କ ତାଲିକା ମଧ୍ୟରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଲବ୍ଧାଙ୍କକୁ ସୂଚାଏ ।
12. ଗରିଷ୍ଠକର ସଂଜ୍ଞା ଲେଖ ।
Answer:
କୌଣସି ଏକ ବିତରଣରେ ଯେଉଁ ଲବ୍ଧାଙ୍କଟି ସର୍ବାଧ୍ଵ ବାର ରହିଥାଏ, ତାହାକୁ ଗରିଷ୍ଠକ କୁହାଯାଏ ।
13. ଏକ ପ୍ରାପ୍ତାଙ୍କ ବିତରଣରେ ଏକ ପ୍ରାପ୍ତାଙ୍କର ପୌନଃପୁନ୍ୟ ବା ବାରମ୍ବାରତା ଅର୍ଥ କ’ଣ ?
Answer:
ଗୋଟିଏ ସଂଭାଗରେ ଯେତୋଟି ଲବ୍ଧାଙ୍କ ଶ୍ରେଣୀଭୁକ୍ତ ହୋଇ ରହିଥାଏ, ତାହାକୁ ସେହି ସଂଭାଗର ପୌନଃପୁନ୍ଯ ବା ବାରମ୍ବାରତା କୁହାଯାଏ ।
14. ଏକ ପୌନଃପୁନଃ ବିତରଣ ପ୍ରସ୍ତୁତ କରିବାପାଇଁ ପ୍ରଥମ ସୋପାନଟି କ’ଣ ?
Answer:
ଉଚ୍ଚ ଲବ୍ଧାଙ୍କ ଏବଂ ନିମ୍ନ ଲବ୍ଧାଙ୍କ ନିର୍ଣ୍ଣୟ କରି ସଂଭାଗର ବାସ୍ତବ ସୀମା (Size of the class interval) ନିର୍ଣ୍ଣୟ କରିବା ।
15. ନିମ୍ନୋକ୍ତ ଲବ୍ଧାଙ୍କଗୁଡ଼ିକର ଗରିଷ୍ଠକ ନିର୍ଣ୍ଣୟ କର ।
50, 45, 52, 54, 46, 54, 51, 54, 49, 47
Answer:
ପ୍ରଦତ୍ତ ଲବ୍ଧାଙ୍କଗୁଡ଼ିକର ଗରିଷ୍ଠକ 54 ।
16. ସଂଭାଗ 10 – 19 ର ଆକାର କ’ଣ ?
Answer:
ସଂଭାଗ 10 – 19 ର ଆକାର (19 – 10) + 1 = 9 + 1 = 10 ଅଟେ ।
17. ଲବ୍ଧାଙ୍କ 0, 2, 10, 25 ଏବଂ 5 ର ମାଧ୍ୟ (Mean) ନିର୍ଣ୍ଣୟ କର ।
Answer:
ଲବ୍ଧାଙ୍କର ମାଧ୍ୟ (Mean) = \(\frac{\sum x}{N}\) = \(\frac{0+2+10+25+5}{5}\) = \(\frac{42}{5}\) = 8.4
18. ଏକ ପ୍ରାପ୍ତାଙ୍କ ବିତରଣରେ ମଧ୍ୟଗ (Median)କାହାକୁ କହନ୍ତି ?
କିମ୍ବା, ମଧ୍ଯଗ ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ର କ’ଣ ?
Answer:
ମଧ୍ୟଗ ନିର୍ଣ୍ଣୟର ସୂତ୍ର : Mdn = \(L+\frac{N / 2-F}{f_m} \times \mathrm{i}\)
![]()
19. ଏକ ଅଣବର୍ଗୀକୃତ ପ୍ରାପ୍ତାଙ୍କ ବିତରଣରେ ଗରିଷ୍ଠକ (Mode) କ’ଣ ?
Answer:
ଲବ୍ଧାଙ୍କ ଅନୁକ୍ରମରେ ବା ପର୍ଯ୍ୟାୟରେ ଯେଉଁ ଲବ୍ଧାଙ୍କଟି ଅଧିକ ବାର ଦେଖାଯାଏ ସେହି ଲବ୍ଧାଙ୍କଟି ଗରିଷ୍ଠକ (Mode) ଅଟେ ।
20. 3 – 5 ସଂଭାଗରେ ଠିକ୍ ଉଚ୍ଚ ସୀମା (Upper limit) କେତେ ଯଦି ପରବର୍ତ୍ତୀ ସଂଭାଗ 6 – 8 ହୋଇଥାଏ ?
Answer:
3 – 5 ସଂଭାଗର ଠିକ୍ ଉଚ୍ଚ ସୀମା (Upper limit) 5.5 ଅଟେ ।
21. 1.3 – 1.7 ସଂଭାଗରେ ମଧ୍ୟବିନ୍ଦୁ (Mid-point) କେତେ ?
Answer:
1.3 – 1.7 ସଂଭାଗରେ ମଧ୍ୟବିନ୍ଦୁ \(\frac{1.3+1.7}{2}\) = \(\frac{3}{2}\) = 1.5 ଅଟେ ।
22. ସଂଭାଗ (Class interval) କ’ଣ ?
Answer:
ସଂଖ୍ୟାତ୍ମକ ତଥ୍ୟକୁ ନେଇ ଶ୍ରେଣୀବିଭାଗ କଲାବେଳେ ପ୍ରତ୍ୟେକ ଶ୍ରେଣୀବିଭାଗର ଉଚ୍ଚ ଏବଂ ନିମ୍ନ ଲବ୍ଧାଙ୍କ ମଧ୍ୟରେ ଥିବା ଲବ୍ଧାଙ୍କର ସୀମାକୁ ସଂଭାଗ କହନ୍ତି ।
23. ପରିସଂଖ୍ୟାନରେ ବିସ୍ତାର (Size of class interval) କାହାକୁ କହନ୍ତି ?
Answer:
ପ୍ରତ୍ୟେକ ସଂଭାଗ (Class interval) ଅନ୍ତର୍ଗତ ଲବ୍ଧାଙ୍କ ସଂଖ୍ୟାକୁ ବିସ୍ତାର କୁହାଯାଏ ।
24. ‘n’ ସଂଖ୍ୟକ ଏକ ପ୍ରାପ୍ତାଙ୍କ ବିତରଣରେ କେଉଁ ପ୍ରାପ୍ତାଙ୍କଟି ତାହାର ମଧ୍ଯମାକୁ ସୂଚାଏ ?
Answer:
‘n’ ସଂଖ୍ୟକ ଏକ ପ୍ରାପ୍ତାଙ୍କ ବିତରଣରେ (\(\frac{n+1}{2}\)) ତମ ପ୍ରାପ୍ତାଙ୍କଟି ତାହାର ମଧ୍ଯମାକୁ ସୂଚାଏ ।
25. ତଥ୍ୟ (Data) କହିଲେ କ’ଣ ବୁଝ ?
Answer:
ତଥ୍ୟ କହିଲେ ସାଂଖ୍ୟକ ତଥ୍ୟକୁ ବୁଝାଇଥାଏ, ଯଥା – କୌଣସି ପରୀକ୍ଷାରେ ତଥ୍ୟକୁ ସଂଖ୍ୟା ମାଧ୍ୟମରେ ପ୍ରକାଶ କଲେ ତାହା ସାଂଖ୍ୟକ ତଥ୍ୟ ଅଟେ ।
26. ବିଚ୍ଛିନ୍ନ ଚଳସଂଖ୍ୟା (Discrete variable) କ’ଣ ?
Answer:
ବିଚ୍ଛିନ୍ନ ଚଳସଂଖ୍ୟାକୁ ଭଗ୍ନାଂଶ, ଦଶମିକରେ ପ୍ରକାଶ କରାନଯାଇ ପୂର୍ବସଂଖ୍ୟାରେ ପ୍ରକାଶ କରାଯାଇଥାଏ ।
27. ବିଚ୍ଛିନ୍ନ ଚଳସଂଖ୍ୟାର ଗୋଟିଏ ଉଦାହରଣ ଦିଅ ।
Answer:
କୌଣସି ପରିବାରର ଲୋକସଂଖ୍ୟା ଯଥା – 5, 6, 8, 9, 15 ଇତ୍ୟାଦି ।
28. ଅବିଚ୍ଛିନ୍ନ ଚଳସଂଖ୍ୟା (Continuous variable) କ’ଣ ?
Answer:
ଅବିଚ୍ଛିନ୍ନ ଚଳସଂଖ୍ୟା ପୂର୍ଣ୍ଣସଂଖ୍ୟା, ଭଗ୍ନାଂଶ ଏବଂ ଦଶମିକରେ ପ୍ରକାଶ କରାଯାଇଥାଏ ।
29. ଅବିଚ୍ଛିନ୍ନ ଚଳସଂଖ୍ୟା (Continuous variable) ର ଗୋଟିଏ ଉଦାହରଣ ଦିଅ ।
Answer:
ଅବିଚ୍ଛିନ୍ନ ଚଳସଂଖ୍ୟା ସମୟ, ଦୈର୍ଘ୍ୟ, ଓଜନ ଇତ୍ୟାଦିକୁ ପ୍ରକାଶ କରିଥାଏ, ଯାହା 6.3 ସେ.ମି., 5.5 କି.ଗ୍ରା. ଇତ୍ୟାଦି ।
30. ମଧ୍ୟବିନ୍ଦୁ (Mid point) ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ରଟି କ’ଣ ?
Answer:
କୌଣସି ସଂଭାଗ (Class interval) ର ମଧ୍ୟବିନ୍ଦୁ ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ରଟି ହେଲା –
ମଧ୍ୟବିନ୍ଦୁ (Mid point) = Lower limit + \(\frac{\text { Upper limit – Lower limit }}{2}\)
31. Tally କହିଲେ କ’ଣ ବୁଝ ?
Answer:
କୌଣସି ଏକ ସଂଭାଗ (Class interval) ରେ କେତୋଟି ଲବ୍ଧାଙ୍କ ଅଛି ତାହା ଜାଣିବାପାଇଁ Tally ର ବ୍ୟବହାର କରାଯାଏ ।
32. ପୌନଃପୁନଃ ବିତରଣ (Frequency distribution) କହିଲେ କ’ଣ ବୁଝ ?
Answer:
ଲବ୍ଧାଙ୍କଗୁଡ଼ିକୁ ସଂଭାଗ ବିସ୍ତାର ମାଧ୍ୟମରେ ଏକ Table ରେ ପରିପ୍ରକାଶ କରିବାକୁ ପୌନଃପୁନ୍ୟ ବିତରଣ କୁହାଯାଏ, ଯାହା ସଂଭାଗ ଓ ପୌନଃପୁନଃ ପ୍ରକାଶ କରିଥାଏ ।
33. କେ ନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପ (Measures of central tendency) କ’ଣ ?
Answer:
ସମୁଦାୟ ଲବ୍ଧାଙ୍କ ବିତରଣ ତାଲିକାର ହାରାହାରି ମାନ ନିର୍ଣ୍ଣୟ କରିବା ହେଉଛି କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପ ।
34. ଯେକୌଣସି ଗୋଟିଏ କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପ ଲେଖ ।
Answer:
କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପର ଗୋଟିଏ ମାପ (Measure) ହେଉଛି ମାଧ୍ୟ (Mean) ।
35. ମାଧ୍ୟ (Mean) ର ଗୋଟିଏ ବ୍ୟବହାର ଲେଖ ।
Answer:
ଯେତେବେଳେ କୌଣସି ବିତରଣର ହାରାହାରି ମାନ ନିର୍ଣ୍ଣୟ କରିବା ଆବଶ୍ୟକ ହୁଏ, ସେତେବେଳେ ମାଧ୍ୟ (Mean) ବ୍ୟବହାର କରାଯାଏ ।
![]()
36. ମଧ୍ୟମା (Median) ର ଗୋଟିଏ ବ୍ୟବହାର ଲେ ଖ ।
Answer:
ଯେତେବେଳେ ବିତରଣର ନିର୍ଦ୍ଦିଷ୍ଟ ମଧ୍ୟବିନ୍ଦୁ ନିର୍ଣ୍ଣୟ କରିବା ଆବଶ୍ୟକ, ସେତେବେଳେ ମଧ୍ୟମା ବ୍ୟବହାର ହୁଏ ।
37. ଗରିଷ୍ଠକ (Mode) ର ଗୋଟିଏ ବ୍ୟବହାର ଲେଖ ।
Answer:
ଯେତେବେଳେ ବାରମ୍ବାର ଆସୁଥୁବା ଲବ୍ଧାଙ୍କ ଜାଣିବା ଆବଶ୍ୟକ ହୁଏ, ସେତେବେଳେ ଗରିଷ୍ଠକ ବ୍ୟବହାର ହୁଏ ।
38. ଗରିଷ୍ଠକର ଗୋଟିଏ ଅସୁବିଧା ଲେଖ ।
Answer:
ଗରିଷ୍ଠକ ବିତରଣର ସମସ୍ତ ଲବ୍ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବସିତ ନୁହେଁ ।
39. ଶ୍ରେଣୀବଦ୍ଧ ହୋଇ ନଥିବା ଲବ୍ଧାଙ୍କଗୁଡ଼ିକର ମାଧ୍ୟ (Mean) ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ର କ’ଣ ?
Answer:
ମାଧ୍ୟ ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ର ;
Mean = \(\frac{\sum X}{N}\)
∑ = ସମୁଦାୟ
X = ମଧ୍ୟବିନ୍ଦୁ,
N = ସମୁଦାୟ ଲବ୍ଧାଙ୍କର ସଂଖ୍ୟା ।
40. ମାଧ୍ୟ (Mean)ର ଗୋଟିଏ ସୁବିଧା (Advantage) ଲେଖ ।
Answer:
ମାଧ୍ୟ ଏକ ସରଳ ହାରାହାରି ମାନ ଅଟେ, ଯାହାକୁ ବୁଝିବା ଅତ୍ୟନ୍ତ ସହଜ ।
41. ମାଧ୍ୟ (Mean)ର ଗୋଟିଏ ଅସୁବିଧା (Advantage) ଲେଖ ।
Answer:
ମାଧ୍ୟ ନିର୍ଣ୍ଣୟ କରିବାପାଇଁ ଅଧୂକ ପରିଶ୍ରମ ଦରକାର ଏବଂ ସମୟ ବି ଦରକାର ।
42. ମଧ୍ୟମା (Median) ର ଗୋଟିଏ ସୁବିଧା ଲେଖ ।
Answer:
ଯଦି ବିତରଣରେ ଅସମାନ ସଂଭାଗ ଥାଏ, ତେବେ ସେ ସ୍ଥଳରେ ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କରାଯାଇଥାଏ ।
43. ମଧ୍ୟମାର ଗୋଟିଏ ଅସୁବିଧା ଲେଖ ।
Answer:
ମଧ୍ୟମାକୁ ବୀଜଗଣିତ ନିୟମ ପ୍ରୟୋଗଦ୍ଵାରା ନିର୍ଣ୍ଣୟ କରିହେବ ନାହିଁ ।
44. ଗରିଷ୍ଠକର ଏକ ସୁବିଧା ଲେଖ ।
Answer:
ଗରିଷ୍ଠକ ନିର୍ଣ୍ଣୟ ଅତ୍ୟନ୍ତ ସହଜ, କାରଣ ଯେଉଁ ଲବ୍ଧାଙ୍କର ବାରମ୍ବାରତ। ଅଧୂକ ତାହା ଗରିଷ୍ଠକ ।
45. ପରିସଂଖ୍ୟାନର ବ୍ୟୁତ୍ପତ୍ତିଗତ ଅର୍ଥ କ’ଣ ?
Answer:
ପରିସଂଖ୍ୟାନକୁ ଇଂରାଜୀରେ Statistics ବୋଲି କୁହାଯାଏ । Statistics ଶବ୍ଦଟି Latin ଶବ୍ଦ ‘Status’ ରୁ ଆସିଛି ଯାହାର ଅର୍ଥ ରାଜନୈତିକ ସ୍ଥିତି (Political status)
46. ପରିସଂଖ୍ୟାନର ଏକ ସଂଜ୍ଞା ଲେଖ ।
Answer:
କ୍ରକ୍ସଟନ୍ ଏବଂ କୱେଡ଼ନ୍ (Crocston and Cowden) କୁହନ୍ତି, “ସାଂଖ୍ୟକ ତଥ୍ୟ ସଂଗ୍ରହ, ଏହାର ବିଶ୍ଳେଷଣ ଓ ବ୍ୟାଖ୍ୟା ସମ୍ବନ୍ଧୀୟ ବିଜ୍ଞାନ ପରିସଂଖ୍ୟାନ” (Statistics may be defined as collection, presentation, analysis and interpretation of numerical data.) ।
47. ପରିସଂଖ୍ୟାନର ଜନ୍ମଦାତା କିଏ ?
Answer:
ସାର୍ ରୋନାଲ୍ଡ ପରିସଂଖ୍ୟାନର ଜନ୍ମଦାତା ଅଟନ୍ତି ।
48. ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ (Educational Statistics) କ’ଣ ?
Answer:
ଶିକ୍ଷାକ୍ଷେତ୍ରରେ ଛାତ୍ରଛାତ୍ରୀମାନଙ୍କର ମାନସିକ ଶକ୍ତିର ପରିମାପ, ବୁଦ୍ଧିର ପରିମାପ, ବ୍ୟକ୍ତିତ୍ୱର ପରିମାପ ଏବଂ କୃତି (Achievement) ପରିମାପ ପାଇଁ ଯେଉଁ ପରିସଂଖ୍ୟାନ ପଦ୍ଧତିମାନ ବ୍ୟବହାର କରାଯାଏ ତାହା ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ ଅଟେ ।
49. ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନର ଗୋଟିଏ ସଂଜ୍ଞା ଲେଖ ।
Answer:
ଯେଉଁ ପରିସଂଖ୍ୟାନ ମାଧ୍ୟମରେ ଶିକ୍ଷାସଂକ୍ରାନ୍ତୀୟ ତଥ୍ୟଗୁଡ଼ିକର ସଜୀକରଣ, ବିଭାଗୀକରଣ, ବିଶ୍ଳେଷଣ ଏବଂ ସଂଖ୍ୟାତ୍ମକ ପରିପ୍ରକାଶ କରାଯାଇଥାଏ, ତାହା ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ ।
50. ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନର ଗୋଟିଏ ପରି ସର (Scope) ଲେଖ ।
Answer:
କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପ (Measurement of central tendency) ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ ପରିସର ଅନ୍ତର୍ଭୁକ୍ତ ।
51. ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନର ଗୋଟିଏ ଉପଯୋଗିତା ଲେଖ ।
Answer:
ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନର ପ୍ରୟୋଗଦ୍ଵାରା ଶିକ୍ଷକ ଛାତ୍ରଛାତ୍ରୀମାନଙ୍କର ବ୍ୟକ୍ତିଗତ ତାରତମ୍ୟ (Individual difference) ମପାଯାଇ ପାରିଥାଏ, ଯାହାଦ୍ୱାରା ଉଭୟ ଛାତ୍ର ଏବଂ ଶିକ୍ଷକ ନିଜର ପାରଦର୍ଶିତାକୁ ମାପି ପାରିଥା’ନ୍ତି ।
![]()
ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
A. ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦୁଇଟି ବା ତିନୋଟି ବାକ୍ୟରେ ଲେଖ ।
1. ଶିକ୍ଷାରେ ପରିସଂଖ୍ୟାନର ଦୁଇଟି ଗୁରୁତ୍ଵ ଲେଖ ।
Answer:
(i) ପରିସଂଖ୍ୟାନଦ୍ୱାରା ଶିକ୍ଷାର୍ଥୀମାନଙ୍କର କୃତିତ୍ଵକୁ ସଂଖ୍ୟାତ୍ମକ ଭାବରେ ପ୍ରକାଶ କରାଯାଇଥାଏ ।
(ii) ଶିକ୍ଷାନୁଷ୍ଠାନରେ ଉପୁଜୁଥିବା ସମସ୍ୟାବଳୀର ସୂତ୍ର ଖୋଜି ବାହାର କରିବାପାଇଁ ଏହା ପଥ ଦେଖାଏ ।
2. କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପ କ’ଣ ?
Answer:
ସବୁବେଳେ ଆମେ ସମସ୍ତଙ୍କର ହାରାହାରି କୃତିତ୍ଵ ଜାଣିବାକୁ ଚେଷ୍ଟା କରୁ । ଏଗୁଡ଼ିକୁ ମାପିବାପାଇଁ ପରିସଂଖ୍ୟାନରେ ଯେଉଁ ପଦ୍ଧତି ଅବଲମ୍ବନ କରାଯାଏ ତାହା କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପ କୁହାଯାଏ ।
3. କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତାର ମାପଗୁଡ଼ିକ କ’ଣ ?
Answer:
କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତାର ମାପଗୁଡ଼ିକ ହେଲା –
(i) ମାଧ୍ୟ (The Mean)
(ii) ମଧ୍ୟମା (The Median) ଏବଂ
(iii) ଗରିଷ୍ଠକ (The Mode)
4. ଅବର୍ଗତ ଲବ୍ଧଙ୍କଗୁଡ଼ିକର ମାଧ୍ୟ (Mean) ନିର୍ଣ୍ଣୟ କରିବାପାଇଁ କେଉଁ ସୂତ୍ର ଅବଲମ୍ବନ କରାଯାଇଥାଏ ?
Answer:
ମାଧ୍ୟ (Mean) = \(\frac{\sum X}{N}\)
∑ = ସମଷ୍ଟି, X = ଲଜ୍ଜାଙ୍କ, N = ଲଜ୍ଜାଙ୍କର ମୋଟ ସଂଖ୍ୟା ।
5. ମଧ୍ୟମା (Median) ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ର କ’ଣ ?
Answer:
ମଧ୍ୟମା = \(L+\frac{N / 2-F}{f_m} \times \mathrm{i}\)
6. ନିମ୍ନଲିଖୂତ 9 ଜଣ ଛାତ୍ରଙ୍କ ଲବ୍ଧଙ୍କର ମଧ୍ୟମା (Median) ନିର୍ଣ୍ଣୟ କର ।
7, 6, 9, 4, 10, 8, 5, 3, 2
Answer:
ତଥ୍ୟଗୁଡ଼ିକୁ ସଜାଇ ଲେଖିଲେ 2, 3, 4, 5, 6, 7, 8, 9, 10
Median = (\(\frac{N+1}{2}\))th = (\(\frac{9+1}{2}\)) = \(\frac{10}{2}\) = 5
5ମେ ଲବ୍ଧାଙ୍କଟି 6 ଅଟେ ।
∴ Median (ମଧ୍ୟମା) 6 ଅଟେ ।
7. ଗରିଷ୍ଠକର 2ଟି ବ୍ୟବହାର ଲେଖ ।
Answer:
(i) କୌଣସି ବିତରଣର କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପ ତୁରନ୍ତ ଜାଣିବାପାଇଁ ଗରିଷ୍ଠକ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
(ii) କୌଣସି ବର୍ଗୀକୃତ ତଥ୍ୟମାଳାରେ ଯଦି ସ୍ବତନ୍ତ୍ର ବା ଆଦର୍ଶଭୁକ୍ତ ମୂଲ୍ୟର ନିର୍ଦ୍ଦେଶନା ପାଇଁ କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପର ଆବଶ୍ୟକତା ହୁଏ ତେବେ ସେପରି ସ୍ଥଳରେ ଗରିଷ୍ଠକର ବ୍ୟବହାର ହୁଏ ।
(iii) ଏକ ଆଦର୍ଶ ମୂଲ୍ୟ ଜାଣିବା ପାଇଁ ଗରିଷ୍ଠକ ବ୍ୟବହାର କରାଯାଏ । (ଯେକୌଣସି ୨ଟି)
8. ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ (Educational Statistics) କ’ଣ ?
Answer:
(i) ସାଧାରଣ ଅର୍ଥରେ ପରିସଂଖ୍ୟାନ ରାଶିମାଳାକୁ ବୁଝାଇଥାଏ । କୌଣସି ବିଷୟରେ ସଂଖ୍ୟାତ୍ମକ ତଥ୍ୟ ସଂଗ୍ରହ, ଉକ୍ତ ତଥ୍ୟର ଯୁକ୍ତିଯୁକ୍ତ ଉପସ୍ଥାପନ, ବିଶ୍ଳେଷଣ ଏବଂ ବ୍ୟାଖ୍ୟାକରଣ ପରିସଂଖ୍ୟାନ ଅଟେ । ଶିକ୍ଷାକ୍ଷେତ୍ରରେ ଯେଉଁ ପରିସଂଖ୍ୟାନ ଉପରୋକ୍ତ କାର୍ଯ୍ୟ ସମ୍ପାଦନ କରିଥାଏ, ତାକୁ ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ କହନ୍ତି ।
(ii) ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ ପାଠ୍ୟବିଷୟବସ୍ତୁର ଜ୍ଞାନ ପରୀକ୍ଷା ସହିତ ଶିକ୍ଷାର୍ଥୀମାନଙ୍କର ବୁଦ୍ଧି, ମନୋବୃତ୍ତି ପରୀକ୍ଷାର ତଥ୍ୟକୁ ବିଶ୍ଳେଷଣ କରିଥାଏ ।
(iii) ଏହା ପରୀକ୍ଷାଗତ ଫଳାଫଳ ଓ ନମ୍ବରଗୁଡ଼ିକୁ ବିଶ୍ଳେଷଣ କରିଥାଏ ।
(iv) ଶିକ୍ଷା ସମ୍ପର୍କିତ ତଥ୍ୟକୁ ପରିସଂଖ୍ୟାନ ପଦ୍ଧତିରେ ଉପଯୁକ୍ତ ମୂଲ୍ୟାୟନ କରାଯାଇଥାଏ ।
9. ପୌନଃପୁନ୍ୟ (Frequency) କହିଲେ କ’ଣ ବୁଝ ?
Answer:
(i) କୌଣସି ଲକ୍ତାଙ୍କ ତାଲିକାରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଲବ୍ଧଙ୍କ ଯେତେ ଥର ଥାଏ, ତାକୁ ସେହି ଲବ୍ଧାଙ୍କର ପୌନଃପୁନ୍ୟ କୁହାଯାଏ ।
(ii) ପୌନଃପୁନ୍ୟ ସାରଣୀ ତିଆରି କରିବା ସମୟରେ ପୌନଃପୁନଃ ନିର୍ଦ୍ଧାରଣ କରିବାପାଇଁ Tally ଦିଆଯାଏ ।
(iii) ସମସ୍ତ ପୌନଃପୁନ୍ୟର ଯୋଗଫଳ ସମସ୍ତ ଲବ୍ଧାଙ୍କର ସଂଖ୍ୟା ସହ ସମାନ ହୋଇଥାଏ ।
10. ମାଧ୍ୟ (Mean) ର ତିନୋଟି ସୁବିଧା (Advantages) ଲେଖ ।
Answer:
(i) ମାଧ୍ୟକୁ ବୁଝିବା ଏବଂ ହିସାବ କରିବା ସହଜ, କାରଣ ହାରାହାରି ମାନ ନିର୍ଣ୍ଣୟ ସହଜସାଧ୍ୟ ।
(ii) ମାଧ୍ୟ ନିର୍ଣ୍ଣୟ ଯୁକ୍ତିଯୁକ୍ତ ଗାଣିତିକ ସୂତ୍ର ଉପରେ ପର୍ଯ୍ୟବସିତ ।
(iii) ଅନ୍ୟାନ୍ୟ ପରିସଂଖ୍ୟାନ ନିର୍ଣ୍ଣୟ, ଯଥା – S.D./A.D. ଇତ୍ୟାଦି ପାଇଁ ମାଧ୍ୟର ଆବଶ୍ୟକତା ଅଛି ।
11. ମାଧ୍ୟ (Mean) ର ତିନୋଟି ଅସୁବିଧା (Disadvantages) ଲେଖ ।
Answer:
(i) ମାଧ୍ୟ ନିର୍ଣ୍ଣୟ କରିବାକୁ ଅଧିକ ଶ୍ରମ ଏବଂ ସମୟ ଦରକାର ।
(ii) ବିତରଣର ଥିବା ସର୍ବୋଚ୍ଚ ବା ସର୍ବନିମ୍ନ ଲବ୍ଧାଙ୍କଦ୍ଵାରା ମାଧ୍ୟ ପ୍ରଭାବିତ ହୋଇଥାଏ ।
(iii) ମାଧ୍ୟକୁ ସବୁସ୍ଥଳରେ ବ୍ୟବହାର କରାଯାଇନଥାଏ ।
![]()
12. ମଧ୍ୟମା (Mean) ର ତିନୋଟି ଗୁଣ (Advantages) ଲେଖ ।
Answer:
(i) ମଧ୍ୟମା, ସମସ୍ତ ଲବ୍ଧଙ୍କର ମୂଲ୍ୟକୁ ବିଚାରକୁ ନ ନେଇ ନିଜର ସ୍ଥିତି ନିର୍ଣ୍ଣୟ କରିଥାଏ ।
(ii) ମଧ୍ୟମା, ବିତରଣର ସର୍ବନିମ୍ନ ଏବଂ ସର୍ବୋଚ୍ଚ ଲଛାଙ୍କଦ୍ୱାରା ଆଦୌ ପ୍ରଭାବିତ ହୁଏ ନାହିଁ ।
(iii) ମଧ୍ୟମାକୁ ଲେଖଚିତ୍ର (Graph) ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଯାଇ ପାରିଥାଏ ।
13. ମଧ୍ୟମାର ତିନୋଟି ଦୋଷତ୍ରୁଟି ଲେଖ ।
Answer:
(i) ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କରିବା ସମୟରେ ଲବ୍ଧଙ୍କଗୁଡ଼ିକୁ ସଜାଇ କରି ଲେଖୁ ରଖାଯାଏ ।
(ii) ମଧ୍ୟମା, ମାଧ୍ଯ ଭଳି ବିଶେଷ ବିଶ୍ବସ୍ତ ଏବଂ ଉପାଦେୟ ହାରାହାରି ମାନ ନୁହେଁ ।
(iii) ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ ବୀଜଗଣିତ ସୂତ୍ର ପ୍ରୟୋଗ ଉପରେ ନିର୍ଭର କରେନାହିଁ ।
14. ଗରିଷ୍ଠକ (Mode) ର ତିନୋଟି ଭଲ ଗୁଣ ଲେଖ ।
Answer:
(i) ଗରିଷ୍ଠକ ବିତରଣରେ ସର୍ବାଧ୍ଵ ସ୍ଥାନ ପାଇଥ୍ ଲଜ୍ଜାଙ୍କ ।
(ii) ଗରିଷ୍ଠକ ସର୍ବନିମ୍ନ ଏବଂ ସର୍ବୋଚ୍ଚ ଲଜ୍ଜାଙ୍କଦ୍ୱାରା ପ୍ରଭାବିତ ହୋଇ ନ ଥାଏ ।
(iii) ଗରିଷ୍ଠକର ମାନ ଅସମାପ୍ତ ଶ୍ରେଣୀ ସଂଭାଗ ବିଶିଷ୍ଟ ବିତରଣରେ ମଧ୍ୟ ନିର୍ଣ୍ଣୟ କରାଯାଇପାରେ ।
15. ଗରିଷ୍ଠକର ତିନୋଟି ଦୋଷତ୍ରୁଟି ଲେଖ ।
Answer:
(i) ସବୁ ସ୍ଥଳରେ ଗରିଷ୍ଠକର ମାନ ସ୍ଥିର କରାଯାଇପାରେ ନାହିଁ ।
(ii) ଗରିଷ୍ଠକ ବିତରଣର ସମସ୍ତ ଲବ୍ଧଙ୍କର ମାନକୁ ବିଚାର କରି ନ ଥାଏ ।
(iii) ଗରିଷ୍ଠକ ନିର୍ଣ୍ଣୟ ବୀଜଗାଣିତିକ ସୂତ୍ର ପ୍ରୟୋଗ ଉପରେ ନିର୍ଭର କରେନାହିଁ ।
16. ମଧ୍ୟମା(Mean) ର ତିନୋଟି ବ୍ୟବହାର (Uses) ଲେଖ ।
Answer:
(i) କୌଣସି ବିତରଣର ଠିକ୍ ମଧ୍ୟବିନ୍ଦୁ ଜାଣିବାପାଇଁ ମଧ୍ୟମା ବ୍ୟବହାର କରାଯାଇଥାଏ ।
(ii) ନିମ୍ନ ଲଜ୍ଜାଙ୍କ ଏବଂ ଉଚ୍ଚ ଲଜ୍ଜାଙ୍କ ମଧମାକୁ ପ୍ରଭାବିତ କରି ନ ଥାଏ । ତେଣୁ ଆବଶ୍ୟକ ସ୍ଥଳେ ମଧ୍ୟମା ବ୍ୟବହାର କରାଯାଏ ।
(iii) ଯେଉଁ କ୍ଷେତ୍ରରେ ଉଚ୍ଚ ଏବଂ ନିମ୍ନ ଲବ୍ଧଙ୍କ ଅନିର୍ଦ୍ଦିଷ୍ଟ ଥାଏ ସେହି କ୍ଷେତ୍ରରେ ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
17. ମଧ୍ୟଗର ସଂଜ୍ଞା ଲେଖ ।
Answer:
ମଧ୍ୟଗ ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନରେ କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ନିର୍ଣ୍ଣୟ କରିବାର ଏକ ପରିମାପ । ଏହା ଏକ ପ୍ରକାର ହାରାହାରି । କୌଣସି ଲବ୍ଧାଙ୍କ ବିତରଣ ଠିକ୍ ମଧ୍ୟବିନ୍ଦୁ ବା ସ୍ଥାନର ଲବ୍ଧାଙ୍କ (ଯାହାର ଉଭୟ ପାର୍ଶ୍ଵରେ ସମାନ ସଂଖ୍ୟକ ଲବ୍ଧାଙ୍କ ବା 50 ଭାଗ ଲବ୍ଧାଙ୍କ ବିସ୍ତାରିତ ହୋଇ ରହିଥାଏ) କୁ ବୁଝାଏ ।
ଏହା ସମଗ୍ର ବିତରଣକୁ ସମାନ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କରିଥାଏ । ଏହାକୁ ଗ୍ରାଫ୍ରେ ପ୍ରକାଶ କରାଯାଇପାରେ । ଏହା ସମସ୍ତ ଲବ୍ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବସିତ ନୁହେଁ । ଏହା ଏକ ସହଜ ଓ ଶୀଘ୍ର ବାହାରି ପାରୁଥୁବା ହାରାହାରି ଅଟେ ।
18. ନିମ୍ନଲିଖିତ ତିନୋଟି ସଂଭାଗ ବିସ୍ତାରରେ ଲଜ୍ଜାଙ୍କର ବାସ୍ତବ ସୀମା ଏବଂ ମଧ୍ୟବିନ୍ଦୁ ନିର୍ଣ୍ଣୟ କର ।
7 – 9, 12 – 5, 0 – 5
Answer:
| ସଂଭାଗ | ବାସ୍ତବ ସୀମା | ମଧ୍ୟବିନ୍ଦୁ |
| 7 – 9 | 6.5 – 9.5 | 8 |
| 12 – 15 | 11.5 – 15.5 | 13.5 |
| 0 – 5 | -0.5 – 5.5 | 2.5 |
19. ପ୍ରାପ୍ତାଙ୍କ ବିତରଣରେ ମଧ୍ଯଗର ଏକ ଆବଶ୍ୟକତା ଲେଖ ।
Answer:
କୌଣସି ବିତରଣର ଠିକ୍ ମଧ୍ୟବିନ୍ଦୁ ନିର୍ଣ୍ଣୟ କରିବାକୁ ହେଲେ ମଧଗ ନିର୍ଣ୍ଣୟ କରାଯାଇଥାଏ । ଯେତେବେଳେ ସର୍ବୋଚ୍ଚ ଓ ସର୍ବନିମ୍ନ ଉବ୍ଧାଙ୍କ ଅନିର୍ଦ୍ଦିଷ୍ଟ ଥାଏ ସେତେବେଳେ ମଧ୍ୟ ମଧ୍ୟଗ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
20. ଏକ ଲବ୍ଧାଙ୍କ ବିତରଣର ମାଧ୍ୟମାନ ଓ ମଧ୍ୟଗର ମୂଲ୍ୟ ଯଥାକ୍ରମେ 16.5 ଏବଂ 17.0 । ତାହାର ଗରିଷ୍ଠକର ମୂଲ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Answer:
ମାଧ୍ଯମାନର ମୂଲ୍ୟ = 16.5
ମଧ୍ୟଗର ମୂଲ୍ୟ = 17.0
ଗରିଷ୍ଠକର ମୂଲ୍ୟ = {(3 × ମଧ୍ୟଗ) – (2 × ମାଧ୍ଯମାନ)}
= (3 × 17.0 – 2 × 16.5)
= 51.0 – 33.0 = 18.0
B. ନିମ୍ନଲିଖ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ପାଞ୍ଚଟି ବା ଛଅଟି ବାକ୍ୟରେ ଲେଖ ।
1. ମାଧ୍ୟ (Mean) ର ତିନୋଟି ବ୍ୟବହାର ଲେଖ ।
Answer:
ମାଧ୍ୟ (Mean)ର ବ୍ୟବହାର :
(i) କୌଣସି ବିତରଣର କେନ୍ଦ୍ରବିନ୍ଦୁ ଜାଣିବାପାଇଁ ମାଧ୍ୟ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
(ii) କୌଣସି ବିତରଣର ଅଧ୍ଵ ପ୍ରତିନିଧ୍ଵ ମୂଲ୍ୟ ଜାଣିବାପାଇଁ ମାଧ୍ୟ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
(iii) ଯେତେବେଳେ ବିତରଣ ଅତ୍ୟଧ୍ଵ ବିଷମ ବଣ୍ଟନ ହୋଇ ନଥାଏ, ସେତେବେଳେ ମାଧ୍ୟ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
![]()
2. ମାଧ୍ୟମାନ କ’ଣ ?
Answer:
(i) ଅନେକଗୁଡ଼ିଏ କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପ ମଧ୍ୟରୁ ହାରାହାରି ମାପ ପ୍ରଧାନ । ପରିସଂଖ୍ୟାନ ବିଜ୍ଞାନରେ ଏହାକୁ ମାଧ୍ୟମାନ ବା ମାଧ୍ୟ କୁହାଯାଏ ।
(ii) କୌଣସି ଶ୍ରେଣୀବଦ୍ଧ ବା ଅଶ୍ରେଣୀବଦ୍ଧ ଲବ୍ଧାଙ୍କ ବିତରଣରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଲବ୍ଧାଙ୍କର ସ୍ଥିତି ସେହି ତଥ୍ୟାବଳୀର ମାଧ୍ୟ ପରିପ୍ରେକ୍ଷୀରେ ବର୍ଣ୍ଣନା ହୋଇଥାଏ ।
(iii) ତେଣୁ ଗୋଟିଏ ସାଂଖ୍ୟକ ତଥ୍ୟାବଳୀ ଅନ୍ତର୍ଗତ ସମସ୍ତ ଲବ୍ଧାଙ୍କର ହାରାହାରିକୁ ଉକ୍ତ ତଥ୍ୟାବଳୀର ମାଧ୍ଯମାନ ବା ମାଧ୍ୟ କୁହାଯାଏ ।
3. କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପ ନିର୍ଣ୍ଣୟ କରିବାର ମାପଗୁଡ଼ିକ କ’ଣ ? ସେମାନଙ୍କର ସଂଜ୍ଞା ଲେଖ ।
Answer:
ସମୁଦାୟ ବିତରଣ କେନ୍ଦ୍ରସ୍ଥଳୀରେ ଯେଉଁ ଲଜ୍ଜାଙ୍କ ସମୁଦାୟ ଲବ୍ଧାଙ୍କର ହାରାହାରି ମାନ ନିର୍ଣ୍ଣୟ କରିଥାଏ, ତାହାକୁ କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପ କୁହାଯାଏ । ଏହି ହାରାହାରି ମାନ ନିର୍ଦ୍ଧାରଣ ନିମନ୍ତେ 3ଟି ମାପ; ଯଥା – ମାଧ୍ୟ, ମଧ୍ୟମା ଓ ଗରିଷ୍ଠକ ବ୍ୟବହାର କରାଯାଏ ।
ମାଧ୍ୟ – ସମୁଦାୟ ବିତରଣଟିର ସମଷ୍ଟିକୁ ଲବ୍ଧାଙ୍କଗୁଡ଼ିକର ସଂଖ୍ୟାଦ୍ଵାରା ଭାଗ କଲେ ଯେଉଁ ହାରାହାରି ମାନ ବାହାରେ ତାହାକୁ ‘ମାଧ୍ୟ’ କୁହାଯାଏ ।
ମଧ୍ୟମା – ସମଗ୍ର ବିତରଣଟିର ଯେଉଁ ନିର୍ଦ୍ଦିଷ୍ଟ ଲବ୍ଧାଙ୍କଦ୍ୱାରା 2 ସମାନ ଭାଗରେ ବିଭକ୍ତ ହୁଏ ତାହାକୁ ‘ମଧ୍ୟମା’ କୁହାଯାଏ ।
ଗରିଷ୍ଠକ – ସମୁଦାୟ ବିତରଣରେ ଯେଉଁ ଲବ୍ଧାଙ୍କ ସର୍ବାଧ୍ଵ ବାର ରହିଥାଏ ବା ଯାହାର ପୌନଃପୁନଃ ଅନ୍ୟାନ୍ୟ ଲବ୍ଧାଙ୍କର ପୌନଃପୁନ୍ୟ ଅପେକ୍ଷା ଅଧିକ ତାହାକୁ ଗରିଷ୍ଠକ କୁହାଯାଏ ।
4. ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ (Educational Statistics) କ’ଣ ?
Answer:
(i) ସାଧାରଣ ଅର୍ଥରେ ପରିସଂଖ୍ୟାନ କହିଲେ ରାଶିମାଳାକୁ ବୁଝାଇଥାଏ । କୌଣସି ବିଷୟରେ ସଂଖ୍ୟାତ୍ମକ ତଥ୍ୟ ସଂଗ୍ରହ, ଉକ୍ତ ତଥ୍ୟର ଯୁକ୍ତିଯୁକ୍ତ ଉପସ୍ଥାପନ, ବିଶ୍ଳେଷଣ ଏବଂ ବ୍ୟାଖ୍ୟାକରଣ ପରିସଂଖ୍ୟାନ ଅଟେ । ଶିକ୍ଷାକ୍ଷେତ୍ରରେ ଯେଉଁ ପରିସଂଖ୍ୟାନ ଉପରୋକ୍ତ କାର୍ଯ୍ୟ ସମ୍ପାଦନ କରିଥାଏ, ତାହାକୁ ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ କହନ୍ତି ।
(ii) ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ ପାଠ୍ୟ ବିଷୟବସ୍ତୁର ଜ୍ଞାନ ପରୀକ୍ଷା ସହିତ ଶିକ୍ଷାର୍ଥୀମାନଙ୍କର ବୁଦ୍ଧି, ମନୋବୃତ୍ତି ପରୀକ୍ଷାର ତଥ୍ୟକୁ ବିଶ୍ଳେଷଣ କରିଥାଏ ।
(iii) ପରୀକ୍ଷାଗତ ଫଳାଫଳ ଓ ନମ୍ବରଗୁଡ଼ିକ ର ବିଶ୍ଳେଷଣ କରିଥାଏ ।
(iv) ଶିକ୍ଷା ସମ୍ପର୍କିତ ତଥ୍ୟକୁ ପରିସଂଖ୍ୟାନ ପଦ୍ଧତିରେ ଉପଯୁକ୍ତ ମୂଲ୍ୟାୟନ କରାଯାଇଥାଏ ।
5. ପୌନଃପୁନ୍ଯ କହିଲେ କ’ଣ ବୁଝ ?
Answer:
(i) କୌଣସି ଲବ୍ଧଙ୍କ ତାଲିକାରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଲବ୍ଧଙ୍କ ଯେତେବାର ଥାଏ, ତାକୁ ସେହି ଲବ୍ଧାଙ୍କର ପୌନଃପୁନ୍ୟ କୁହାଯାଏ ।
(ii) ପୌନଃପୁନଃ ସାରଣୀ ତିଆରି କରିବା ସମୟରେ ପୌନଃପୁନ୍ୟ ନିର୍ଦ୍ଧାରଣ କରିବାପାଇଁ Tally ଚିହ୍ନ ଦିଆଯାଏ ।
(iii) ସମସ୍ତ ପୌନଃପୁନ୍ୟର ଯୋଗଫଳ ସମସ୍ତ ଲବ୍ଧାଙ୍କର ସଂଖ୍ୟା ସହ ସମାନ ହୋଇଥାଏ ।
6. ମଧ୍ୟମା (Median) ର ତିନୋଟି ବ୍ୟବହାର ଲେଖ ।
Answer:
ମଧ୍ୟମା (Median) ର ବ୍ୟବହାର :
ନିମ୍ନଲିଖ୍ କ୍ଷେତ୍ରରେ ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କରିବା ଆବଶ୍ୟକ ହୋଇଥାଏ ।
(i) କୌଣସି ବିତରଣର ଠିକ୍ ମଧ୍ୟବିନ୍ଦୁ ଜାଣିବାପାଇଁ ।
(ii) ଯେତେବେଳେ ବିତରଣ ଅତି ଉଚ୍ଚକ୍ରମ କିମ୍ବା ଅତି ନିମ୍ନକ୍ରମରେ ସଂଗଠନ କରାଯିବା ଆବଶ୍ୟକ ।
(iii) ଯେତେବେଳେ ବିତରଣର ଉଭୟ ସମ୍ଭାଗ (ନିମ୍ନ ଏବଂ ଉଚ୍ଚ) ସୀମା ଅନର୍ଦ୍ଦିଷ୍ଟ ଥିବେ ।
7. ଗରିଷ୍ଠକର ତିନୋଟି ବ୍ୟବହାର ଲେଖ ।
Answer:
ନିମ୍ନଲିଖତ କ୍ଷେତ୍ରରେ ଗରିଷ୍ଠକ ବ୍ୟବହୃତ ହୋଇଥାଏ ।
(i) ଯେତେବେଳେ କୌଣସି ବିତରଣର କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ତୁରନ୍ତ ଜାଣିବା ଆବଶ୍ୟକ ହୁଏ ।
(ii) ଯେତେବେଳେ କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତାର ବିଶେଷ ମାପକ ବିଷୟରେ ଜାଣିବାକୁ ପଡ଼ିଥାଏ ।
(iii) ଯେତେବେଳେ ଫଳାଫଳରେ ସବୁଠାରୁ ଅଧିକଥର ଆସୁଥିବା ପ୍ରାପ୍ତାଙ୍କ ବିଷୟରେ ଜାଣିବାକୁ ପଡ଼ିଥାଏ ।
8. ନିମ୍ନୋକ୍ତ ଲବ୍ଧଙ୍କଗୁଡ଼ିକର ମଧ୍ୟମା (Median) ନିର୍ଣ୍ଣୟ କର ।
5, 8, 4, 3, 9, 6, 10, 11, 2, 13, 1, 15, 14
Answer:
ସଜାଇ ଲେଖୁ
1, 2, 3, 4, 5, 6, 8, 9, 10, 11, 13, 14, 15
ମଧ୍ୟମା = (\(\frac{N+1}{2}\))th = (\(\frac{13+1}{2}\)) = \(\frac{14}{2}\) = 7th score
7 ମ ଲବ୍ଧାଙ୍କଟି ମଧ୍ୟମା ଯାହା 6 ଅଟେ ।
∴ ମଧ୍ୟମା ୫ ଅଟେ ।
9. ପୌନଃପୁନ୍ୟ ବିସ୍ତୃତି (Frequency distribution) କାହାକୁ କହନ୍ତି ?
Answer:
(i) କୌଣସି ପରୀକ୍ଷାରେ ପ୍ରାପ୍ତ ଲବ୍ଧଙ୍କଗୁଡ଼ିକ ନିର୍ଦ୍ଦିଷ୍ଟ ଭାବରେ ତଥ୍ୟ ଉପସ୍ଥାପନ କରିପାରିନଥାଏ ।
(ii) ଉକ୍ତ ଲବ୍ଧଙ୍କଗୁଡ଼ିକ ପୌନଃପୁନ୍ୟ ବିସ୍ତୃତି ମାଧ୍ୟମରେ ସଜାଇ ରଖାଯାଏ ।
(iii) ଶିକ୍ଷାର୍ଥୀମାନଙ୍କର ବ୍ୟକ୍ତିଗତ ଲଜ୍ଜାଙ୍କଗୁଡ଼ିକୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଗୁଣାବଳୀରେ କ୍ରମାନ୍ୱୟରେ ସଜାଇ ଶ୍ରେଣୀବଦ୍ଧ କରିବାକୁ ପୌନଃପୁନ୍ୟ ବିସ୍ତୃତି କୁହାଯାଏ ।
(iv) ଲଜ୍ଜାଙ୍କର ସଂଖ୍ୟା ଅଧିକ ଅର୍ଥ ଛାତ୍ରଛାତ୍ରୀଙ୍କର ସଂଖ୍ୟା ଅଧ୍ଵ । ତେଣୁ ପୌନଃପୁନ୍ୟ ବିସ୍ତୃତିର ଆବଶ୍ୟକତା ଅଧିକ ହୋଇଦିଏ ।
10. ଶିକ୍ଷାକ୍ଷେତ୍ରରେ ପରିସଂଖ୍ୟାନର ତିନୋଟି ଗୁରୁତ୍ଵ ଲେଖ ।
Answer:
(i) ପରିସଂଖ୍ୟାନର ମୌଳିକ ଜ୍ଞାନ ଶିକ୍ଷାକ୍ଷେତ୍ରରେ ଛାତ୍ରାଛାତ୍ରୀମାନଙ୍କର ଲବ୍ଧଙ୍କଗୁଡ଼ିକ ପୌନଃପୁନ୍ୟ ବିସ୍ତାର ମାଧ୍ୟମରେ ସହଜରେ ପ୍ରକାଶ କରିଥାଏ ।
(ii) ପରିସଂଖ୍ୟାନ ମାଧ୍ୟମରେ କୌଣସି ଏକ ପରୀକ୍ଷାର୍ଥୀ ନିଜର କୃତିକୁ ଅନ୍ୟ ପରୀକ୍ଷାର୍ଥୀମାନଙ୍କ ସହ ତୁଳନା କରିଥାଏ ।
(iii) ଏହା ମାଧ୍ୟମରେ ବିଭିନ୍ନ ବିଷୟ ଏବଂ ବିଭିନ୍ନ ସମୟରେ କରାଯାଉଥିବା ବିଭିନ୍ନ ପରୀକ୍ଷାର ଫଳାଫଳ ମଧ୍ୟରେ ସହ-ସମ୍ବନ୍ଧ (Correlation) ଅନୁଧ୍ୟାନ କରାଯାଇଥାଏ ।
![]()
11. ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନର ଯେକୌଣସି ତିନୋଟି ଉପଯୋଗ ଆଲୋଚନା କର ।
କିମ୍ବା, ପରିସଂଖ୍ୟାନ ଜ୍ଞାନ ଶିକ୍ଷାକୁ କିପରି ସାହାଯ୍ୟ କରେ ଆଲୋଚନା କର ।
Answer:
(i) ପରିଂସଖ୍ୟାନ ମାଧ୍ୟମରେ ପ୍ରତ୍ୟେକ ଶିକ୍ଷାର୍ଥୀ ନିଜର କୃତି (Achievement)କୁ ଅନ୍ୟମାନଙ୍କ କୃତି ସହ ତୁଳନା କରିଥାଏ ।
(ii) ପରୀକ୍ଷାର ଫଳାଫଳ, ଛାତ୍ରଛାତ୍ରୀ, ଶିକ୍ଷକ ଏବଂ ଶିକ୍ଷୟିତ୍ରୀମାନଙ୍କର ସଂଖ୍ୟାକୁ ଗ୍ରାଫ୍ (Graph) ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଯାଇଥାଏ ।
(iii) ମୂଲ୍ୟାୟନର ଫଳାଫଳକୁ ମାଧ୍ୟ (Mean), ମଧ୍ୟମା (Median) ଏବଂ ଗରିଷ୍ଠକ (Mode) ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଯାଇଥାଏ ।
12. ନିମ୍ନୋକ୍ତ ଲବ୍ଧଙ୍କଗୁଡ଼ିକର ମଧ୍ୟମା (Median) ନିର୍ଣ୍ଣୟ କର ।
5, 8, 8, 9, 7, 6, 7
Answer:
| ଲଜ୍ଜାଙ | ପୌନଃପୁନ୍ୟ | କ୍ରମବର୍ଦ୍ଧନ ପୌନଃପୁନ୍ୟ |
| 5 | 1 | 1 |
| 6 | 1 | 2 |
| 7 | 2 | 4 |
| 8 | 2 | 6 |
| 9 | 1 | 7 |
| N = 7 |
\(\frac{N}{2}\) = \(\frac{7}{2}\) = 3.5
ମଧ୍ୟମା = \(L+\frac{N / 2-F}{f_m} \times \mathrm{i}\)
= 6.5 + \(\frac{3.5-2}{2}\) × i
= 6.5 + \(\frac{1.5}{2}\) × 1 = 6.5 + 0.75 = 7.25
∴ ମଧ୍ୟମା (Median) = 7.25
13. ଗରିଷ୍ଠକ (Mode) ର ପ୍ରକାରଭେଦ ଲେଖ ।
Answer:
(i) ଲବ୍ଧଙ୍କ ପର୍ଯ୍ୟାୟରେ ଯେଉଁ ଲଛାଙ୍କଟି ବାରମ୍ବାର ଦେଖାଦିଏ, ସେହି ଲଜ୍ଜାଙ୍କକୁ ଗରିଷ୍ଠକ କହନ୍ତି ।
(ii) ଗରିଷ୍ଠକ ଦୁଇ ପ୍ରକାର; ଯଥା – (i) ସ୍ଥୂଳ ଗରିଷ୍ଠକ ଏବଂ (ii) ପ୍ରକୃତ ବା ବାସ୍ତବ ଗରିଷ୍ଠକ ।
(iii) ସ୍ଥୂଳ ଗରିଷ୍ଠକ – ଯେଉଁ ସଂଭାଗ ବିସ୍ତାରରେ ଯେଉଁ ଲଜ୍ଜାଙ୍କଟି ବାର ମ୍ବାର ଆସିଥାଏ ତାହା ସ୍ଥୂଳ ଗରିଷ୍ଠକ । ଯଦି ପୌନଃପୁନ୍ୟ ସାରଣୀ ହୋଇଥାଏ, ତେବେ ବିତରଣର ଯେଉଁ ସଂଭାଗର ପୌନଃପୁନ୍ୟ ଅଧ୍ବକ ତାହା ଉକ୍ତ ସଂଭାଗର ମଧ୍ୟବିନ୍ଦୁ ।
(iv) ପ୍ରକୃତ ଗରିଷ୍ଠକ – କୌଣସି ପୌନଃପୁନଃ ବିତରଣର ଯେଉଁ ଲଜ୍ଜାଙ୍କ ବିନ୍ଦୁରେ ସର୍ବାପେକ୍ଷା ଅଧିକ ପୌନଃପୁନ୍ୟ ଘନୀଭୂତ ହୋଇଥାଏ, ତାହା ବିତରଣର ବାସ୍ତବ ବା ପ୍ରକୃତ ଗରିଷ୍ଠକ ।
ପ୍ରକୃତ ଗରିଷ୍ଠକ ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ର ;
ଗରିଷ୍ଠକ = 3 ମଧ୍ୟମା – 2 ମାଧ୍ୟ ।
14. ଏକ ପ୍ରାପ୍ତଙ୍କ ବିତରଣର ମଧ୍ଯଗ ଏବଂ ମାଧ୍ୟମାନର ମୂଲ୍ୟ ଯଥାକ୍ରମେ 165 ଏବଂ 158 । ସେହି ପ୍ରାପ୍ତଙ୍କ ବିତରଣର ଗରିଷ୍ଠକ ମୂଲ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Answer:
ମଧ୍ୟମା = 16.5, ମାଧ୍ୟମାନ = 15.8
ଗରିଷ୍ଠକ = 3 ମଧ୍ୟଗ – 2 ମାଧ୍ୟମାନ
= (3 × 16·5) – (2 × 15·8)
= 49.5 – 31.6 = 17.9
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
1. ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ କ’ଣ ? ଶିକ୍ଷକଙ୍କ ପାଇଁ ଏହାର ଆବଶ୍ୟକତା ଆଲୋଚ ନା କର ।
Answer:
ପରିସଂଖ୍ୟାନକୁ ଇଂରାଜୀରେ Statistics କୁହନ୍ତି । Statistics ଶବ୍ଦଟି Latin ଶବ୍ଦ ‘Status’ ଏବଂ ଇଟାଲୀୟ ଶବ୍ଦ ‘Statista’ରୁ ଆସିଅଛି । ଏହି ଶବ୍ଦଦ୍ବୟର ଅର୍ଥ ରାଜନୈତିକ ସ୍ଥିତି । ଅତୀତରେ ରାଜ୍ୟର ରାଜା ନିଜ ରାଜ୍ୟ ସମ୍ପର୍କରେ ଜାଣିବାକୁ ଚାହୁଁଥିବାବେଳେ, ସେ ରାଜ୍ୟର ଜନସଂଖ୍ୟାର ହାର, ମୃତ୍ୟୁହାର, ଆୟବ୍ୟୟ ଇତ୍ୟାଦିକୁ ରାଜ୍ୟର ସ୍ଥିତି ବୋଲି ଧରୁଥିଲେ । ତେଣୁ ଏହା ପରିସଂଖ୍ୟାନ ଅଟେ ।
ପ୍ରଥମେ ଏଚେନ୍ୱାଲ୍ (Achenwall) ନାମକ ଜର୍ମାନ୍ ଗାଣିତିକ 1749 ମସିହାରେ ପରିସଂଖ୍ୟାନ ଶବ୍ଦ ବ୍ୟବହାର କରିଥିଲେ । ପରବର୍ତ୍ତୀ ଅବସ୍ଥାରେ ସାର୍ ରୋନାଲ୍ଡ୍ (1890 -1962)ଙ୍କୁ ପରିସଂଖ୍ୟାନର ଜନ୍ମଦାତା (Father of Statistics) ବୋଲି କୁହାଗଲା । ସମୟକ୍ରମେ କୃଷି, ସ୍ୱାସ୍ଥ୍ୟ, ଆୟବ୍ୟୟ, ଜନସଂଖ୍ୟା ଇତ୍ୟାଦି କ୍ଷେତ୍ରରେ ପରିସଂଖ୍ୟାନର ବ୍ୟବହାର କରାଗଲା । ପ୍ରତ୍ୟେକ ସ୍ଥିତିକୁ ସଂଖ୍ୟା ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଗଲା । ସାଂଖ୍ୟକ ତଥ୍ୟ (Data) କୁ ପରିସଂଖ୍ୟାନ (Statistics) କୁହାଯାଏ । ପରେ ଏହାକୁ ଏକ ବିଜ୍ଞାନ ଭାବେ ଗ୍ରହଣ କରାଗଲା ।
ଶିକ୍ଷାକ୍ଷେତ୍ରରେ ଯେଉଁ ପରିସଂଖ୍ୟାନ ବ୍ୟବହାର କରାଯାଏ ତାହାକୁ ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ (Eductional Statistics) କହନ୍ତି । ପରିସଂଖ୍ୟାନ ଏକ ବିଜ୍ଞାନ ଯାହାକି କୌଣସି ବିଷୟରେ ସଂଖ୍ୟାତ୍ମକ ତଥ୍ୟ (Numerical data) ର ସଂଗ୍ରହ, ଯୁକ୍ତିଯୁକ୍ତ ଉପସ୍ଥାପନ ପାଇଁ ବିଶ୍ଳେଷଣ ଏବଂ ବ୍ୟାଖ୍ୟାକରଣ କରିଥାଏ । ପରିସଂଖ୍ୟାନ ତଥ୍ୟ ଏବଂ ରାଶିମାଳା ସଂକ୍ରାନ୍ତୀୟ ଶାସ୍ତ୍ର ।
ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନର ଗୁରୁତ୍ଵ ବା ଉପାଦେୟତା (Importance of Educational Statistics) :
ପରିସଂଖ୍ୟାନକୁ ଶିକ୍ଷା କ୍ଷେତ୍ରରେ ନିମ୍ନଲିଖିତ କାରଣରୁ ବ୍ୟବହାର କରାଯାଇଥାଏ ।
- ଏହା ଶିକ୍ଷାକ୍ଷେତ୍ରରେ ଛାତ୍ରଛାତ୍ରୀମାନଙ୍କର ମାନସିକ ଶକ୍ତିର ପରିମାପରେ ସାହାଯ୍ୟ କରିଥାଏ । ଶିକ୍ଷାର୍ଥୀର ସ୍ମୃତିଶକ୍ତି, ଆଗ୍ରହ, ସୃଜନଶୀଳ ଶକ୍ତିର ପରିମାପରେ ପରିସଂଖ୍ୟାନର ଭୂମିକା ଗୁରୁତ୍ବପୂର୍ଣ ।
- ଶିକ୍ଷାର୍ଥୀର ବୁଦ୍ଧି ପରିମାପରେ ପରିସଂଖ୍ୟାନ ଅନେକ ତଥ୍ୟକୁ ବିଶ୍ଳେଷଣ କରି ମାନ (Norm) ନିର୍ଦ୍ଧାରଣ କରିଥାଏ । ଉକ୍ତ ମାନ ଅନୁଯାୟୀ ଛାତ୍ରଛାତ୍ରୀମାନଙ୍କୁ ବିଭିନ୍ନ ସ୍ତର; ଯଥା – ଉଚ୍ଚ ବୁଦ୍ଧିସମ୍ପନ୍ନ, ନିମ୍ନ ବୁଦ୍ଧିସମ୍ପନ୍ନ ଇତ୍ୟାଦିରେ ବିଭକ୍ତ କରାଯାଇଥାଏ ।
- ଶିକ୍ଷାକ୍ଷେତ୍ରରେ ପ୍ରତ୍ୟେକ ଛାତ୍ରଛାତ୍ରୀ ଶ୍ରେଣୀ ପରୀକ୍ଷାରେ ନିଜର କୃତି ପରୀକ୍ଷଣରେ ଭାଗ ନେଇଥା’ନ୍ତି । ପରିସଂଖ୍ୟାନ ମାଧ୍ୟମରେ Mean, Median ଏବଂ Mode ନିର୍ଣ୍ଣୟଦ୍ବାରା ଜଣେ ଶିକ୍ଷାର୍ଥୀ ନିଜର ସ୍ଥିତି ସମୁଦାୟ ଛାତ୍ରଛାତ୍ରୀମାନଙ୍କ ସ୍ଥିତି ସହ ତୁଳନା କରି ଜାଣିପାରନ୍ତି ।
- ଶିକ୍ଷାର୍ଥୀମାନଙ୍କର ବ୍ୟକ୍ତିତ୍ଵ (Personality) ପରିମାପରେ ପରିସଂଖ୍ୟାନ ସାହାଯ୍ୟ କରିଥାଏ । ବ୍ୟକ୍ତିର ସମଯୋଜନ କ୍ଷମତା, ଆଗ୍ରହ ଇତ୍ୟାଦି ପରିମାପରେ ପରିସଂଖ୍ୟାନ ସାହାଯ୍ୟ କରିଥାଏ ।
- ଶିକ୍ଷାନୁଷ୍ଠାନର ନଥପତ୍ର, ପରିସଂଖ୍ୟାନ ପଦ୍ଧତିଦ୍ୱାରା ଲିପିବଦ୍ଧ ହୁଏ । ଛାତ୍ରଛାତ୍ରୀମାନଙ୍କର ସଂଖ୍ୟା, ପରୀକ୍ଷାଫଳ, ଶିକ୍ଷକଙ୍କ ସଂଖ୍ୟା, ପରୀକ୍ଷା ହାର, ଆୟବ୍ୟୟ ଇତ୍ୟାଦି Graph ଏବଂ Chart ମାଧ୍ଯମରେ ବିଦ୍ୟାଳୟରେ ପ୍ରଦର୍ଶନ କରାଯାଇଥାଏ । ଏହା ପରିସଂଖ୍ୟାନ ଜ୍ଞାନଦ୍ୱାରା ସମ୍ଭବ ।
- ଛାତ୍ରଛାତ୍ରୀମାନଙ୍କର ଭବିଷ୍ୟତ୍ ଜ୍ଞାନ ପୂର୍ବାନୁମାନ ପାଇଁ ପରିସଂଖ୍ୟାନ ସାହାଯ୍ୟ କରିଥାଏ ।
- ପ୍ରତ୍ୟେକ ମୁହୂର୍ତ୍ତରେ ପରିବର୍ତ୍ତନଶୀଳ ଦୁନିଆରେ ଜ୍ଞାନର ବିଶ୍ଳେଷଣ ଘଟୁଛି । ତେଣୁ ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ Statisticsର ପ୍ରୟୋଗ ଗବେଷଣାକୁ ତ୍ୱରାନ୍ବିତ କରୁଛି ।
ଶିକ୍ଷାକ୍ଷେତ୍ରରେ ପରିସଂଖ୍ୟାନର ପ୍ରୟୋଗ ଏବଂ ଉପାଦେୟତା ଯଥେଷ୍ଟ ଅଛି । ଜଣେ ଆଦର୍ଶ ଶିକ୍ଷକ ପରିସଂଖ୍ୟାନ ଜ୍ଞାନ ବିନା ଶିକ୍ଷାକ୍ଷେତ୍ରରେ ନିଜକୁ ସମଯୋଜିତ କରିପାରିବେ ନାହିଁ ।
![]()
2. ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ କ’ଣ ? ଶିକ୍ଷାରେ ପରିସଂଖ୍ୟାନର ଗୁରୁତ୍ଵ ଆଲୋଚନା କର ।
Answer:
ପରିବର୍ତ୍ତନଶୀଳ ଦୁନିଆରେ ମଣିଷ ଜୀବନର ମୂଲ୍ୟାଙ୍କନ ଭଳି ଏକ ମୌଳିକ ଆବଶ୍ୟକତା ପାଇଁ ପରିସଂଖ୍ୟାନ ବ୍ୟବହୃତ ହୁଏ । ବର୍ତ୍ତମାନର ଏହି ଚାକଚକ୍ୟ ସଭ୍ୟତା କେବଳ ପରିସଂଖ୍ୟାନର ଫଳସ୍ଵରୂପ ଅଟେ । ଏଣୁ ଏହି ଆଧୁନିକ ସଭ୍ୟତାକୁ ପରିସଂଖ୍ୟାନର ସଭ୍ୟତା ବୋଲି କହିଲେ କିଛି ଅତ୍ୟୁକ୍ତି ହେବନାହିଁ । ପରିସଂଖ୍ୟାନ ଗଣିତଶାସ୍ତ୍ରର ଏକ ଅଂଶବିଶେଷ ଯାହାକି ସଂଖ୍ୟା ସମ୍ବନ୍ଧୀୟ ଅନେକ ଆବଶ୍ୟକ ତଥ୍ୟ ଯୋଗାଇଥାଏ ।
ପରିସଂଖ୍ୟାନ ବିନା ଉଚ୍ଚତର ଗବେଷଣା ଅସମ୍ଭବ ହୋଇପଡ଼ିବ । ଜୀବନର ପ୍ରତ୍ୟେକ ଛୋଟ ବଡ଼ ସମସ୍ୟାର ସମାଧାନ ପାଇଁ ପରିସଂଖ୍ୟାନ ବିଶେଷଭାବରେ ବ୍ୟବହୃତ ହୁଏ । ପରୀକ୍ଷା ଫଳ ପ୍ରକାଶ କରିବା, ବିଭିନ୍ନ ଯୋଜନା ପାଇଁ ଅର୍ଥ ବରାଦ କରିବା, ମୁଦ୍ରାଙ୍ଗୀତି ହାର ବାହାର କରିବା, ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ବା ହ୍ରାସର ସୂଚନା ଦେବା, ପାଣିପାଗର ସୂଚନା ଦେବା, ବିଭିନ୍ନ ଗବେଷଣାର ଫଳାଫଳ ଜଣାଇବା, ବୈଜ୍ଞାନିକ ପଦ୍ଧତି ଓ ଗାଣିତିକ ସୂତ୍ରର ତର୍ଜମା କରିବା ସହ ଆଜିର ସଭ୍ୟତାର ମତଦାନ (Voting) କୁ ମୂଲ୍ୟାଙ୍କନ କରିବାରେ ପରିସଂଖ୍ୟାନର ବହୁଳ ବ୍ୟବହାର ପରିଲକ୍ଷିତ ହେଉଛି ।
ଏଣୁ ପରିସଂଖ୍ୟାନକୁ ଛାଡ଼ି ମନୁଷ୍ୟ ତା’ର ସାଧାରଣ ଜୀବନଯାପନ ତୁଲାଇବାକୁ ସକ୍ଷମ ହେବା ଅସମ୍ଭବ । ପରିସଂଖ୍ୟାନର ସଂଜ୍ଞା ଦେବାକୁ ଯାଇ ବୋଡ଼ିଙ୍ଗସନ୍ ମତପୋଷଣ କରିଛନ୍ତି ଯେ – “ପରିସଂଖ୍ୟାନ ହେଉଛି ପ୍ରାକ୍ କଳନା ଓ ସମ୍ଭାବନାର ବିଜ୍ଞାନ’’ (Statistics is the science of estimation and probabilities.) ।
ତେଣୁ ପରିସଂଖ୍ୟାନର ନିମ୍ନୋକ୍ତ ବିଶେଷତ୍ଵମାନ ରହିଛି ।
- ଏହା ଏକ ସଂଖ୍ୟାସୂଚକ ତଥ୍ୟ ।
- ଏହା ଏକ ଗୁଣବାଚକ ତଥ୍ୟ । ସାଧୁତା, ସୌନ୍ଦର୍ଯ୍ୟ ଇତ୍ୟାଦି ଏହା ମାଧ୍ୟମରେ ପ୍ରକାଶିତ ହୁଏ ନାହିଁ ।
- ପରିସଂଖ୍ୟାନ କେବଳ ଗୋଟିଏ ବ୍ୟକ୍ତି ପାଇଁ ଉଦ୍ଦିଷ୍ଟ ନୁହେଁ ।
- ପରିସଂଖ୍ୟାନ ଗୋଟିଏ ଦେଶ, ଅନୁଷ୍ଠାନ, ଜିଲ୍ଲା କିମ୍ବା ଦଳ ବିଷୟରେ ବହୁବାଚକ ସାଂଖ୍ୟକ ତଥ୍ୟ ଯୋଗାଇଥାଏ ।
- ପରିସଂଖ୍ୟାନର ଫଳାଫଳ ଆନୁମାନିକ ହେତୁ ଏଥିରେ କିଛି ଦୋଷତ୍ରୁଟି ରହିଥାଏ ।
ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନର ଗୁରୁତ୍ୱ (Importance of Educational Statistics) :
ପାଠଦାନ ବା ଶିକ୍ଷାଦାନ କେବଳ ଅଧ୍ୟାପନାରେ ସୀମିତ ରହିଥାଏ । ଶିକ୍ଷାଦାନର ଶେଷ ପର୍ଯ୍ୟାୟରେ ଶିକ୍ଷକ ଆବଶ୍ୟକ ପରିମାପକ ସାହାଯ୍ୟରେ ଏହାର ମୂଲ୍ୟାଙ୍କନ କରିଥା’ନ୍ତି । ଶିକ୍ଷାର ପ୍ରକୃତ ଉଦ୍ଦେଶ୍ୟ ଜାଣିବାପାଇଁ ଜଣେ ସଫଳ ଶିକ୍ଷକ ଯେକୌଣସି ବିଷୟରେ ଶିକ୍ଷାଦାନ ପରେ ପରୀକ୍ଷା କରାଇଥା’ନ୍ତି । ଏହାଦ୍ୱାରା ଅଭିଭାବକଙ୍କୁ ଶିକ୍ଷାର୍ଥୀର ବ୍ୟକ୍ତିତ୍ୱ, କୃତିତ୍ୱ ବିଷୟରେ ଅବଗତ କରାଇବା ସହଜ ହେବା ସହିତ ଶିକ୍ଷକ ନିଜର ଶିକ୍ଷାଦାନକୁ ମୂଲ୍ୟାଙ୍କନ କରିଥା’ନ୍ତି ।
ତେଣୁ ପରିସଂଖ୍ୟାନର ଗୁରୁତ୍ଵ ଶିକ୍ଷାକ୍ଷେତ୍ରରେ ବିଶେଷଭାବରେ ଅନୁଭୂତ ହୋଇଥାଏ । ଯେଉଁ ବିଶେଷ କ୍ଷେତ୍ରଗୁଡ଼ିକରେ ପରିସଂଖ୍ୟାନର ଗୁରୁତ୍ଵ ଅନୁଭୂତ ହୁଏ, ସେଗୁଡ଼ିକ ହେଲା –
(i) ଶିକ୍ଷାଦାନରେ ଉପୁଜୁଥିବା ସମସ୍ୟାବଳୀର ସୂତ୍ର ଖୋଜି ବାହାର କରିବାପାଇଁ ଏହା ପଥ ଦେଖାଇଥାଏ ।
(ii) ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ ଛାତ୍ରର ବୁଦ୍ଧି, ଆଗ୍ରହ, ମନୋବୃତ୍ତି, କାର୍ଯ୍ୟଦକ୍ଷତା, ସୃଜନଶୀଳତା, ବିଜ୍ଞତା ଇତ୍ୟାଦିର ମାପରେ ସହାୟକ ହୋଇଥାଏ । ଫଳରେ ଶିକ୍ଷକ ପିଲାଟିକୁ ଠିକ୍ ମାର୍ଗରେ ବୃତ୍ତିଭିତ୍ତିକ ଶିକ୍ଷା ପାଇଁ ପରିଚାଳିତ କରିପାରିଥା’ନ୍ତି ।
(iii) ଏହା କୃତୀ ଛାତ୍ରଛାତ୍ରୀମାନଙ୍କର ସ୍ଥାନୀୟ ମାନ ନିର୍ଣ୍ଣୟ ଓ ବିଭାଗୀକରଣ କରିବାରେ ଶିକ୍ଷକ ଓ ଶିକ୍ଷା ପ୍ରଶାସକଙ୍କୁ ସାହାଯ୍ୟ କରେ ।
(iv) କାର୍ଯ୍ୟାନୁଷ୍ଠାନିକ ଶିକ୍ଷା ଗବେଷଣା ଦିଗରେ ଏହା ଶିକ୍ଷକ, ଗବେଷକ ତଥା ପ୍ରଶାସକଙ୍କୁ ସହାୟତା ଯୋଗାଇଥାଏ ।
(v) ଏହା ସ୍ବଳ୍ପ ସମୟ, ସ୍ଥାନ, ଶ୍ରମ, ସମ୍ବଳ ଓ ଶବ୍ଦାଙ୍କ ପ୍ରୟୋଗରେ ଅନେକଗୁଡ଼ିଏ ବର୍ଣ୍ଣିତ ଜଟିଳ ତଥ୍ୟକୁ ସରଳ ଓ ବୋଧଗମ୍ୟ କରି ପାଠକ ପାଠିକାମାନଙ୍କ ନିକଟରେ ଉପସ୍ଥାପନା କରିବାରେ ସାହାଯ୍ୟ କରିଥାଏ ।
(vi) ଏହା ଗଣିତ ବିଦ୍ୟା ଉପରେ ଏହା ପର୍ଯ୍ୟବସିତ ହୋଇଥିବାରୁ ଏହାକୁ ଅଧ୍ୟୟନ ଓ ଅଭ୍ୟାସ କଲେ ଶିକ୍ଷାର୍ଥୀଙ୍କର ଗଣିତ ବିଦ୍ୟା ଓ କୌଶଳର ଉତ୍ତରୋତ୍ତର ଉନ୍ନତି ହୋଇଥାଏ ।
3. ନିମ୍ନ ପ୍ରଦତ୍ତ ଲବ୍ଧଙ୍କ / ପ୍ରାପ୍ତାଙ୍କ ବିତରଣର ମାଧମାନ (Mean) ନିଶ୍ଚୟ କର । ପାଦକ୍ରମ ଅନୁଯାୟୀ ହିସାବ କରାଯିବା ଆବଶ୍ୟକ ।

Answer:
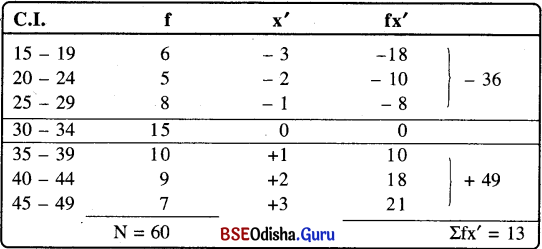
Mean = A.M. + \(\frac{\Sigma \mathrm{fx}^{\prime}}{\mathrm{N}}\) × i
A.M. = କଳ୍ପିତ ମାଧ୍ୟ (ଯେକୌଣସି C.I. ର ମଧ୍ୟବିନ୍ଦୁକୁ Assumed Mean ଭାବରେ ଗ୍ରହଣ କରାଯାଇପାରେ)
x’ = ବ୍ୟତିକ୍ରମ (deviation)
N = ସମୁଦାୟ ଲବ୍ଧାଙ୍କ
i = Size of the Class Interval (ସଂଭାଗର ସୀମା)
Mean = A.M. + \(\frac{\Sigma \mathrm{fx}^{\prime}}{\mathrm{N}}\) × i
= 32 + \(\frac{13}{60}\) × 5
= 32 + \(\frac{13}{12}\)
= 32 + 1.08 = 33.08
4. ନିମ୍ନଲିଖିତ ଲବ୍ଧଙ୍କଗୁଡ଼ିକୁ ନେଇ ଏକ ପୌନଃପୁନ୍ୟ ସାରଣୀ ତିଆରି କର (Tabulate the following scores in a frequency distribution.) ।
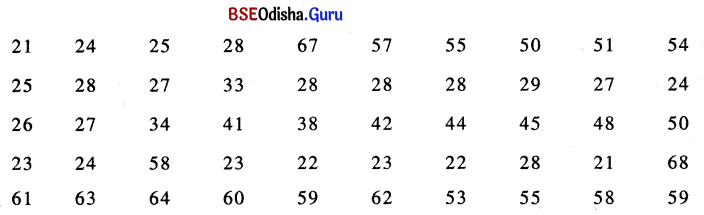
ପୌନଃପୁନ୍ୟ ସାର ଣୀ କରିବାପାଇଁ ନିମ୍ନଲିଖିତ ସୋପାନ ଦେଇ ଗତି କରିବାକୁ ପଡ଼ିବ ।
(i) ଉଚ୍ଚ ଲଜ୍ଜାଙ୍କ ଏବଂ ନିମ୍ନ ଲବ୍ଧଙ୍କ ନିର୍ଣ୍ଣୟ କରି ତାହାର Range ନିର୍ଣ୍ଣୟ କରାଯିବ ।
Range = Highest Score – Lowest Score
= 68 – 21 = 47
(ii) ସଂଭାଗ (Class interval) ନିର୍ଣ୍ଣୟ କରିବାପାଇଁ Range ରେ ସଂଭାଗ ବିସ୍ତାର ଭାଗ କଲେ ସଂଭାଗର
ସଂଖ୍ୟା ଜଣାପଡ଼ିଯିବ ।
ମନେକର ସଂଭାଗ ବିସ୍ତାର ‘5’ ତେବେ
ସଂଭାଗ ବିସ୍ତାର ସଂଖ୍ୟା = 47+ 5 = 9.4 ବା 10 ଟି ।
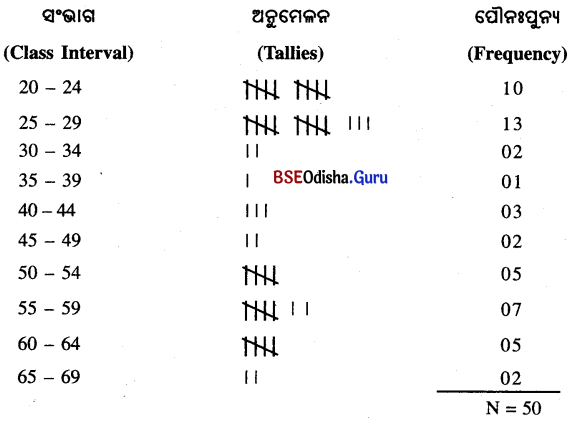
![]()
(iii) ସଂଭାଗ ବିସ୍ତାର ନିର୍ଣ୍ଣୟ ।
ସଂଭାଗ
20 – 24
25 – 29
30 – 34
35 – 39
40 – 44
45 – 49
50 – 54
55 – 59
60 – 64
65 – 69
(iv) Tally ନିଶ୍ଚୟ – ଗୋଟିଏ ସଂଭାଗରେ କେତୋଟି ଲଜ୍ଜାଙ୍କ ଅଛି, ତାକୁ ଜାଣିବାପାଇଁ ଲବ୍ଧଙ୍କଗୁଡ଼ିକୁ ଆଣି ଉକ୍ତ ଲବ୍ଧାଙ୍କରେ ସ୍ଥାନ ଦେବାପାଇଁ Tally ଦିଆଯାଏ ।
(v) ସଂଭାଗର ପୌନଃପୁନଃ ନିର୍ଣ୍ଣୟ – ଗୋଟିଏ ସଂଭାଗର Tallyକୁ ଦେଖ୍ ସଂଭାଗରେ କେତୋଟି ଲବ୍ଧାଙ୍କ ଅଛି, ତାହା ନିର୍ଣ୍ଣୟ କରି ପୌନଃପୁନ୍ୟ / ସଂଖ୍ୟାଟି (f) ରେ ଲେଖାଯାଏ ।
(vi) ‘N’ ନିଶ୍ଚୟ — Frequency ଗୁଡ଼ିକୁ ମିଶାଇଦେଲେ ତାହାର ସମୁଦାୟ ଲବ୍ଧାଙ୍କ ସଂଖ୍ୟା (N) ନିର୍ଣ୍ଣୟ ହୁଏ ।
(vii) ପୌନଃପୁନ୍ୟ ସାରଣୀ ପ୍ରସ୍ତୁତି
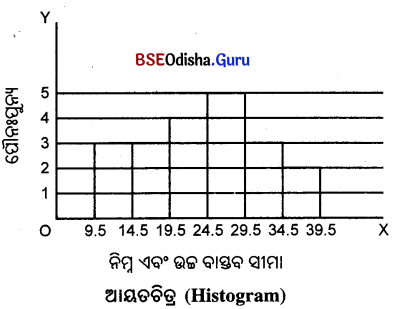
5. ନିମ୍ନ ସାରଣୀରେ ପ୍ରଦତ୍ତ ତଥ୍ୟ ଆଧାରରେ ଏକ ଆୟତଚିତ୍ର ବା ବାର୍ ରେଖାଚିତ୍ର (Histogram) ଅଙ୍କନ କର ।
| ସଂଭାଗ Class Interval |
ପୌନଃପୁନ୍ୟ Frequency |
ନିମ୍ନ ଏବଂ ଉଚ୍ଚ ବାସ୍ତବ ସୀମା Lower limit and Upper limit |
| 35 – 39 | 2 | 34.5 – 39.5 |
| 30 – 34 | 3 | 29.5 – 34.5 |
| 25 – 29 | 5 | 24.5 – 29.5 |
| 20 – 24 | 4 | 19.5 – 24.5 |
| 15 – 19 | 3 | 14.5 – 19.5 |
| 10 – 14 | 3 | 9.5 – 14.5 |
| N = 20 |
Answer:
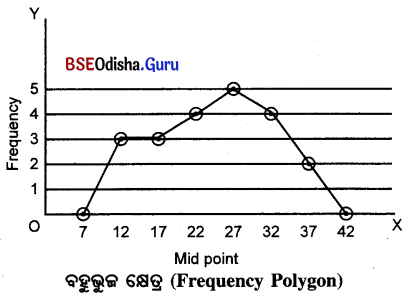
6. ନିମ୍ନ ସାରଣୀରେ ପ୍ରଦତ୍ତ ତଥ୍ୟ ଆଧାରରେ ଏକ ପୌନଃପୁନ୍ୟ ବହୁଭୁଜ କ୍ଷେତ୍ର (Frequency Polygon) ଅଙ୍କନ କର ।
| ସଂଭାଗ Class Interval |
ପୌନଃପୁନ୍ୟ Frequency |
ମଧ୍ୟବିନ୍ଦୁ Mid-point |
| 40 – 44 | 0 | 42 |
| 35 – 39 | 2 | 37 |
| 30 – 34 | 4 | 32 |
| 25 – 29 | 5 | 27 |
| 20 – 24 | 4 | 22 |
| 15 – 19 | 3 | 17 |
| 10 – 14 | 3 | 12 |
| 5 – 9 | 0 | 7 |
Answer:
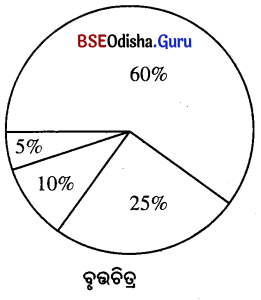
7. ଜଣେ ବ୍ୟକ୍ତିଙ୍କ ମାସିକ ଆୟରୁ ଖର୍ଚ୍ଚର ବିବରଣୀ ନିମ୍ନରେ ପ୍ରଦତ୍ତ ହୋଇଛି । ଏହାକୁ ଆଧାର କରି ଏକ ପାଇ – ଚିତ୍ର (Pie-diagram) ଅଙ୍କନ କର ।
| (1) ଶିକ୍ଷା | 5% |
| (2) ସାମରିକ | 25% |
| (3) ସ୍ବାସ୍ଥ୍ୟ | 10% |
| (4) ଅନ୍ୟାନ୍ୟ | 60% |
| ସମୁଦାୟ | 100% |
Answer:
(i) ଏହାକୁ ବୃତ୍ତଚିତ୍ର ବା ବୃତ୍ତ ଆଲେଖରେ ପ୍ରକାଶ କରିବାକୁ ହେଲେ ପ୍ରତ୍ୟେକ ଶତକଡ଼ାକୁ କୋଣରେ ପ୍ରକାଶ କରିବାକୁ ହେବ ।
(ii) ବୃତ୍ତଟିର କେନ୍ଦ୍ରୀୟ କୋଣ 360° । ଏହାକୁ 100% ମଧ୍ଯରେ ଭାଗ କଲେ 1% ପାଇଁ କେନ୍ଦ୍ରୀୟ କୋଣ ହେଉଛି \(\frac{360}{100}\) = 3.6° ।
(iii) ତେଣୁ
5% = 5 × 3.6° = 18°
10% = 10 × 3.6° = 36°
25% = 25 × 3.6° = 90°
60% = 60 × 3.6 = 216°
(iv) ଉପରୋକ୍ତ ସମସ୍ତ ତଥ୍ୟକୁ ପ୍ରୋଟାକ୍ଟର ମାଧ୍ୟମରେ କୋଣଦ୍ୱାରା ସୂଚାଇଲେ ତାହା ଏକ ବୃତ୍ତଚିତ୍ର ହୋଇଯିବ ।
(v) ପ୍ରତ୍ୟେକ ଅଂଶର ନାମଲେଖୁ ଶତକଡ଼ାର ହାର ଲେଖାଯିବ ।
![]()
8. ନିମ୍ନୋକ୍ତ ବିସ୍ତୃତିର ମାଧ୍ୟ (Mean) ଦୀର୍ଘ ପଦ୍ଧତିରେ ନିର୍ଣ୍ଣୟ କର ।
| Class Interval | Frequency |
| 90 – 94 | 2 |
| 85 – 89 | 4 |
| 80 – 84 | 5 |
| 75 – 79 | 8 |
| 70 – 74 | 10 |
| 65 – 69 | 6 |
| 60 – 64 | 4 |
| 55 – 59 | 4 |
| 50 – 54 | 2 |
| 45 – 49 | 3 |
| N = 48 |
Answer:
| C.I. | f | Mid-point (X) | fX |
| 90 – 94 | 2 | 92 | 184 |
| 85 – 89 | 4 | 87 | 348 |
| 80 – 84 | 5 | 82 | 410 |
| 75 – 79 | 8 | 77 | 616 |
| 70 – 74 | 10 | 72 | 720 |
| 65 – 69 | 6 | 67 | 402 |
| 60 – 64 | 4 | 62 | 248 |
| 55 – 59 | 4 | 57 | 228 |
| 50 – 54 | 2 | 52 | 104 |
| 45 – 49 | 3 | 47 | 141 |
| N = 48 | ∑fx = 3401 |
Mean (ମାଧ୍ୟ) ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ର :
Mean = \(\frac{\mathrm{∑fX}}{\mathrm{N}}\)
ଯାହାର –
∑ = ସମୁଦାୟ (Sum Total)
X = ସଂଭାଗର ମଧ୍ୟବିନ୍ଦୁ (Mid-point of the Class Interval)
f = ପୌନଃପୁନ୍ଯ
Steps:
(1) ପ୍ରଥମେ ସଂଭାଗର ମଧ୍ୟବିନ୍ଦୁ (Mid point) ବାହାର କରାଯାଉ ।
Mid point = Lower limit + \(\frac{\text { Upper limit – Lower limit }}{2}\)
90 – 94 ର Mid point = 89.5 + \(\frac{94.5-89.5}{2}\)
= 89.5 + \(\frac{5}{2}\)
= 89.5 + 2.5
= 92
(2) fX ପାଇବାପାଇଁ ‘f’ ସହ ‘X’ (Mid-point) ଗୁଣନ କରାଯାଉ ।
(3) ସମସ୍ତ ‘fX’ ର ସମଷ୍ଟି ∑fX ଅଟେ ।
(4) Mean ସୂତ୍ର ପ୍ରୟୋଗ କରି Mean ନିର୍ଣ୍ଣୟ କରାଯାଉ ।
Mean = \(\frac{\mathrm{∑fX}}{\mathrm{N}}\)
= \(\frac{3401}{48}\) = 70.85
9. ନିମ୍ନଲିଖିତ ପ୍ରାପ୍ତାଙ୍କ ବିତରଣର ମଧ୍ୟମା (Median) ନିର୍ଣ୍ଣୟ କର ।

Answer:
| (Class Interval) | (Frequency) | Cumulative frequency | Cumulative frequency |
| 10 – 15 | 6 | 43 | 6 |
| 16 – 20 | 5 | 37 | 11 |
| 21 – 25 | 9 | 32 | 20 |
| 26 – 30 | 8 | 23 | 28 |
| 31 – 35 | 7 | 15 | 33 |
| 36 – 40 | 8 | 8 | 43 |
| N = 43 |
Median = L + \(\frac{N / 2-F}{f_m}\) × i, \(\frac{N}{2}\) = \(\frac{43}{2}\) = 21.5
21.5, 26 – 30 Class Intervalରେ ରହୁଛି ।
L = ଯେଉଁ Class Interval ରେ N/2 ରହୁଛି ଉକ୍ତ Class Interval ର ନିମ୍ନ ବାସ୍ତବ ସାମା = 25.5
F = ଯେଉଁ ସଂଭାଗରେ N/2 ଅଛି ଉକ୍ତ ସଂଭାଗ ନିମ୍ନରେ ଥିବା ସମସ୍ତ ସଂଭାଗର ପୌନଃପୁନ୍ୟର ସମଷ୍ଟି = 20
fm = ଯେଉଁ ସଂଭାଗରେ N/2 ଅଛି ତାହାର actual frequency = 8
i = Size of the Class-Interval ବା ସଂଭାଗ ବିସ୍ତାରର ସୀମା = 5

10. ନିମ୍ନଲିଖିତ ପ୍ରାପ୍ତାଙ୍କ ବିତରଣର ମଧ୍ଯଗ ବା ମଧ୍ୟମା (Median) ନିର୍ଣ୍ଣୟ କର ।
| Class Interval (ସଂଭାଗ ବିସ୍ତାର) |
Frequency (ପୌନଃପୁନ୍ୟ) |
| 10 – 14 | 8 |
| 15 – 19 | 7 |
| 20 – 24 | 11 |
| 25 – 29 | 9 |
| 30 – 34 | 5 |
| 35 – 39 | 12 |
| 40 – 44 | 10 |
| N = 62 |
Answer:
| ସଂଭାଗ ବିସ୍ତାର | (ପୌନଃପୁନ୍ୟ) | କ୍ରମବର୍ଦ୍ଧନ ପୌନଃପୁନ୍ୟ |
| 10 – 14 | 8 | 8 |
| 15 – 19 | 7 | 15 |
| 20 – 24 | 11 | 26 |
| 25 – 29 | 9 | 35 |
| 30 – 34 | 5 | 40 |
| 35 – 39 | 12 | 52 |
| 40 – 44 | 10 | 62 |
| N = 62 |
\(\frac{N}{2}\) = \(\frac{62}{2}\) = 31
31, 25 –29 ସଂଭାଗ ବିସ୍ତାର (Class Interval) ରେ ରହୁଛି ।
Median (ମଧ୍ୟଗ ବା ମଧ୍ୟମା) ନିର୍ଣ୍ଣୟ କରିବା ସୂତ୍ର :
Median = L + \(\frac{N / 2-F}{f_m}\) × i
L = ଯେଉଁ ସଂଭାଗରେ N/2 ରହୁଛି ତାହାର ନିମ୍ନ ବାସ୍ତବ ସୀମା = 24.5
F = ଯେଉଁ ସଂଭାଗରେ N/2 ଅଛି ଉକ୍ତ ସଂଭାଗର ନିମ୍ନ ସଂଭାଗଗୁଡ଼ିକର ଲବ୍ଧାଙ୍କର ସମଷ୍ଟି
ବା ଯେଉଁ ସଂଭାଗରେ ଅଛି ଉକ୍ତ ସଂଭାଗ ନିମ୍ନ ସଂଭାଗର C.f. = 26
fm = ଯେଉଁ ସଂଭାଗରେ N/2 ଅଛି ଉକ୍ତ ସଂଭାଗର ପୌନଃପୁନ୍ୟ (Frequency) = 9
i = ସଂଭାଗର ବାସ୍ତବ ସୀମା = 5
![]()
Median = L + \(\frac{N / 2-F}{f_m}\) × i
= 24.5 + \(\frac{31 – 26}{9}\) × 5
= 24.5 + \(\frac{25}{9}\)
= 24.5 + 2.77 = 27.27
Median = 27.27
11. ନିମ୍ନଲିଖିତ ଲବ୍ଧଙ୍କଗୁଡ଼ିକର ମାଧମାନ ନିର୍ଣ୍ଣୟ କର ।
| Class Interval | Frequency |
| 30 – 34 | 2 |
| 35 – 39 | 5 |
| 40 – 44 | 7 |
| 45 – 49 | 9 |
| 50 – 54 | 11 |
| 55 – 59 | 6 |
| N = 40 |
Answer:
| ସମ୍ଭାଗ ବିସ୍ତାର (C.I) |
ମଧ୍ୟବିନ୍ଦୁ (M) |
ପୌନଃପୁନ୍ୟ (f) |
ବିଚ୍ୟୁତି (X’) |
(fX’) |
| 30 – 34 | 32 | 2 | 4 | 8 |
| 35 – 39 | 37 | 5 | 3 | 15 |
| 40 – 44 | 42 | 7 | 2 | 14 |
| 45 – 49 | 47 | 9 | 1 | 9 |
| 50 – 54 | 52 | 11 | 0 | 0 |
| 55 – 59 | 57 | 6 | -1 | -6 |
| N = 40 | fX’ = 40 |
ମାଧ୍ୟ (Mean) = A.M. + \(\frac{\Sigma \mathrm{fX}^{\prime}}{\mathrm{N}}\) × i
ଯେଉଁଠାରେ A.M. = କଳ୍ପିତ ମାଧ୍ୟ
f = ପୌନଃପୁନ୍ୟ, X’ = ବିଚ୍ୟୁତି
f(X’) = ପୌନଃପୁନ୍ୟ × ବିଚ୍ୟୁତି
N = ସମୁଦାୟ ପୌନଃପୁନ୍ୟର ପରିମାଣ
i = ସଂଭାଗ ବିସ୍ତାର
∴ ମାଧ୍ୟ (Mean) = 52 + \(\frac{40}{40}\) × 5 = 57
12. ନିମ୍ନଲିଖିତ ବିସ୍ତୃତିର ମାଧ୍ଯମାନ ନିର୍ଣ୍ଣୟ କର ।
| Scores | Frequency |
| 90 – 94 | 2 |
| 85 – 89 | 2 |
| 80 – 84 | 4 |
| 75 – 79 | 8 |
| 70 – 74 | 6 |
| 65 – 69 | 11 |
| 60 – 64 | 9 |
| N = 42 |
Answer:
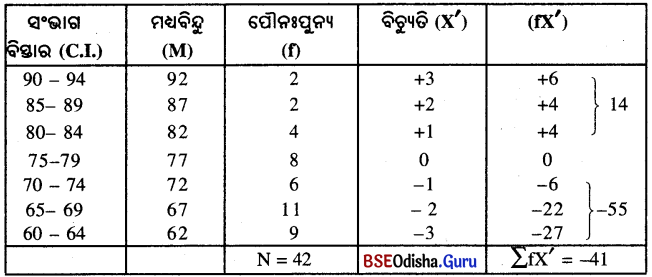
ମାଧ୍ୟ (Mean) = A.M. + \(\frac{\Sigma \mathrm{fX}^{\prime}}{\mathrm{N}}\) × i
ଯେଉଁଠାରେ A.M. = କଳ୍ପିତ ମାଧ୍ୟ
f = ପୌନଃପୁନ୍ୟ,
X’ = ବିଚ୍ୟୁତି
f(X’) = ପୌନଃପୁନ୍ୟ × ବିଚ୍ୟୁତି
N = ସମୁଦାୟ ପୌନଃପୁନ୍ୟର ପରିମାଣ
i = ସଂଭାଗ ବିସ୍ତାର
ମାଧ୍ୟ (Mean) = 77 + \(\frac{-41}{44}\) × 5
= 77 – 4.88 = 72.12
13. ନିମ୍ନଲିଖିତ ବିସ୍ତୃତିର ମଧ୍ୟମା ବା ମଧଗ ନିର୍ଣ୍ଣୟ କର ।
| Class Interval | Frequency |
| 24 – 25 | 2 |
| 23 – 22 | 3 |
| 21 – 20 | 4 |
| 19 – 18 | 6 |
| 17 – 16 | 8 |
| 15 – 14 | 3 |
| 13 – 12 | 2 |
| 11 – 10 | 2 |
| N = 30 |
Answer:
ମଧଗ ନିର୍ଣ୍ଣୟ
| Class Interval | X | f | fX |
| 24 – 25 | 24.5 | 2 | 49 |
| 23 – 22 | 22.5 | 3 | 67.5 |
| 21 – 20 | 20.5 | 4 | 82 |
| 19 – 18 | 18.5 | 6 | 111 |
| 17 – 16 | 16.5 | 8 | 132 |
| 15 – 14 | 14.5 | 3 | 43.5 |
| 13 – 12 | 12.5 | 2 | 25 |
| 11 – 10 | 10.5 | 2 | 21 |
| 30 | 531 |
Long Method ଅନୁସାରେ ମଧ୍ୟଗ = \(\frac{\Sigma fX}{\mathrm{~N}}\) = \(\frac{531}{30}\) = 17.7
![]()
14. ନିମ୍ନଲିଖିତ ପ୍ରାପ୍ତାଙ୍କ ବିତରଣର ମାଧମାନ ନିର୍ଣ୍ଣୟ କର ।
| Class Interval (ସଂଭାଗ ବିସ୍ତାର) |
Frequency (ପୌନଃପୁନ୍ୟ) |
| 60 – 64 | 2 |
| 55 – 59 | 2 |
| 50 – 54 | 4 |
| 45 – 49 | 8 |
| 40 – 44 | 6 |
| 35 – 39 | 11 |
| 30 – 34 | 9 |
| N = 42 |
Answer:
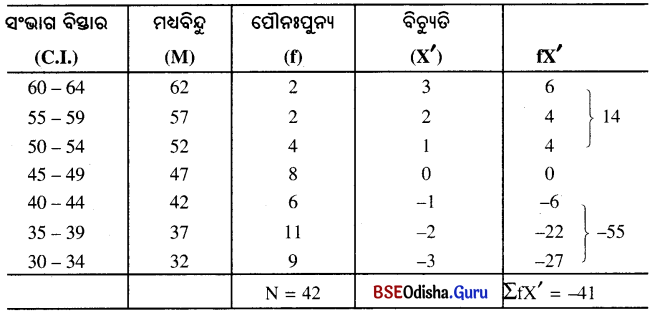
Mean (ମାଧ୍ୟ) = A.M. + \(\frac{\Sigma \mathrm{fX}^{\prime}}{\mathrm{N}}\) × i
= 47 + \(\frac{-41}{42}\) × 5
= 47 + \(\frac{-205}{42}\)
= 47 – 4.88 = 42.12
Mean = 42.12
ଯେଉଁଠାରେ A.M. = କଳ୍ପିତ ମାଧ୍ୟ
N = ସମୁଦାୟ ଲଜ୍ଜାଙ୍କର ସଂଖ୍ୟା
X’ = ବିଚ୍ୟୁତି ।
BSE Odisha Class 12 Education Notes
ବିଷୟଭିତ୍ତିକ ସୂଚନା
ପରିସଂଖ୍ୟାନ (Statistics) – ପରିସଂଖ୍ୟାନ ହେଉଛି ପ୍ରାକ୍ କଳନା ଓ ସମ୍ଭାବନାର ବିଜ୍ଞାନ । ସାଧାରଣତଃ ସଂଖ୍ୟାତ୍ମକ ବା ସଂଖ୍ୟା ବିଷୟକ ତଥ୍ୟ ସଂଗ୍ରହ ପାଇଁ ପରିସଂଖ୍ୟାନର ଗୁରୁତ୍ୱ ରହିଛି । ଶିକ୍ଷାବିଜ୍ଞାନରେ ପରିସଂଖ୍ୟାନ ପଦ୍ଧତିର ଉପାଦେୟତା ଅତ୍ୟନ୍ତ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ । ଏହାଦ୍ଵାରା ପାଠ୍ୟ ବିଷୟବସ୍ତୁର ଜ୍ଞାନ ଆହରଣର ପରୀକ୍ଷା ସହିତ ଶିକ୍ଷାର୍ଥୀମାନଙ୍କର ବୁଦ୍ଧି, ଅଭିରୁଚି, ମନୋବୃତ୍ତି ମଧ୍ୟ ପରୀକ୍ଷା କରାଯାଇଥାଏ । ଏହି ପରୀକ୍ଷାଗତ ଫଳାଫଳ ଓ ନମ୍ବରଗୁଡ଼ିକୁ ବିଶ୍ଳେଷଣ କରିବାପାଇଁ ପରିସଂଖ୍ୟାନର ଆବଶ୍ୟକତା ଅଛି ।
ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ (Educational Statistics) – ଶିକ୍ଷାକ୍ଷେତ୍ରରେ ଯେଉଁ ପରିସଂଖ୍ୟାନର ବ୍ୟବହାର ହୋଇଥାଏ, ତାହାକୁ ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନ କୁହାଯାଏ । ଏହା ମାଧ୍ୟମରେ ଶିକ୍ଷାର୍ଥୀର ବିଭିନ୍ନ ପରୀକ୍ଷଣର ଫଳାଫଳକୁ ବିଶ୍ଳେଷଣ ଏବଂ ତର୍ଜମା କରାଯାଇ ସିଦ୍ଧାନ୍ତ ଗ୍ରହଣ କରାଯାଇଥାଏ ।
ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନର ଗରୁତ୍ଵ (Importance of Educational Statistics) – ଶୈକ୍ଷିକ ପରିସଂଖ୍ୟାନର ନିମ୍ନଲିଖ ଗୁରୁତ୍ଵ ରହିଛି :
- ବିଷୟ ଶିକ୍ଷଣରେ ଶିକ୍ଷାର୍ଥୀର ଅଗ୍ରଗତି ଜାଣିବା ।
- ଜଣେ ଶିକ୍ଷାର୍ଥୀର କୃତିତ୍ବକୁ ଅନ୍ୟ ଜଣେ ଶିକ୍ଷାର୍ଥୀର କୃତିତ୍ବ ସହ ତୁଳନା କରିବା ।
- ଗୋଟିଏ ବିଦ୍ୟାଳୟର ଫଳାଫଳ ସହ ଅନ୍ୟ ବିଦ୍ୟାଳୟର ଫଳାଫଳକୁ ତୁଳନା କରିବା ।
- ଛାତ୍ରଛାତ୍ରୀମାନଙ୍କର ବୁଦ୍ଧି ଅନୁଯାୟୀ ସେମାନଙ୍କୁ ବିଭିନ୍ନ ଶ୍ରେଣୀରେ ବିଭକ୍ତ କରିବା ।
- ଶିକ୍ଷାର୍ଥୀମାନଙ୍କର ହାରାହାରି ଏବଂ ବିଚ୍ୟୁତି (Deviation) ଜାଣିବା ।
- ମୂଲ୍ୟାୟନର ଫଳାଫଳ ଓ ସାରାଂଶ ନିର୍ଣ୍ଣୟ କରିବା ।
- ମୂଲ୍ୟାୟନର ଫଳାଫଳକୁ ବିଶ୍ଳେଷଣ କରି ଶିକ୍ଷାର୍ଥୀଙ୍କୁ ଉପଯୁକ୍ତ ଦିଗ୍ଦର୍ଶନ ଦେବା ।
ପୌନଃପୁନଃ ବିତରଣ (Frequency Distribution) :
ଲବ୍ଧଙ୍କ (Score) – କୌଣସି ପରୀକ୍ଷାରେ ପରୀକ୍ଷାର୍ଥୀ ଯେଉଁ ସାଫଲ୍ୟାଙ୍କ ପାଇଥାଏ, ତାହାକୁ ଲଜ୍ଜାଙ୍କ କୁହାଯାଏ ।
ପୌନଃପୁନ୍ୟ (Frequency) – କୌଣସି ସଂଭାଗ ତାଲିକାରେ କେତୋଟି ନିର୍ଦ୍ଦିଷ୍ଟ ଲବ୍ଧଙ୍କ କେତେଥର ଆସିଥାଏ ତାହାକୁ ଲବ୍ଧଙ୍କଗୁଡ଼ିକର ପୌନଃପୁନ୍ୟ କୁହାଯାଏ ।
ଟାଲି (Tally) – କୌଣସି ଏକ ସଂଭାଗ (Class Interval)ରେ କେତୋଟି ଲବ୍ଧଙ୍କ ଅଛି ତାହା ଜାଣିବାପାଇଁ Tallyର ବ୍ୟବହାର କରାଯାଏ ।
ପୌନଃପୁନଃ ବିତରଣ (Frequency Distribution) – ଲବ୍ଧଙ୍କଗୁଡ଼ିକୁ ସଂଭାଗ ବିସ୍ତାର ମାଧ୍ୟମରେ ପରିପ୍ରକାଶ କରିବାକୁ ପୌନଃପୁନଃ ବିତରଣ କୁହାଯାଏ ।
![]()
ତଥ୍ୟର ରେଖାଚିତ୍ର ବା ଗ୍ରାଫୀୟ ପ୍ରଦର୍ଶନ (Graphical Representation of Data) – ଅନେକ ସମୟରେ ତଥ୍ୟଗୁଡ଼ିକ ସଂଖ୍ୟା ଆକାରରେ ପ୍ରକାଶ କରାଯାଇଥାଏ । ସମସ୍ତ ତଥ୍ୟ ବା ଲବ୍ଧଙ୍କଗୁଡ଼ିକୁ ଅନୁଧ୍ୟାନ କରିବା କଷ୍ଟସାଧ୍ୟ । ତେଣୁ ଯଦି ସେଗୁଡ଼ିକୁ ଗ୍ରାଫ୍ ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଯାଏ ତେବେ ତାହା ବୁଝିବାରେ କୌଣସି ପ୍ରକାର ଅସୁବିଧା ହୋଇନଥାଏ ।
ପୌନପୁନ୍ୟ ବିସ୍ତୃତିରେ ଦିଆଯାଇଥିବା ତଥ୍ୟକୁ ରେଖାଚିତ୍ର ମାଧ୍ୟମରେ ଦର୍ଶାଯାଇପାରିବ । ବିଶେଷକରି ଏଥପାଇଁ ଗ୍ରାଫ୍ ପେପର୍ର ଆବଶ୍ୟକତା ଅଛି ।
ବିଭିନ୍ନ ପ୍ରକାର ଗ୍ରାଫୀୟ ପ୍ରଦର୍ଶନ – ପରିସଂଖ୍ୟାନ ତଥ୍ୟଗୁଡ଼ିକୁ ନିମ୍ନଲିଖ୍ ଗ୍ରାଫୀୟ ଚିତ୍ର ବା ରେଖାଚିତ୍ର ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଯାଇଫାରେ । ସେଗୁଡ଼ିକ ହେଲା –
- ଆୟତଚିତ୍ର ବା ହିଷ୍ଟୋଗ୍ରାମ୍ (Histogram)
- ପୌନପୁନ୍ୟ ବହୁଭୁଜ କ୍ଷେତ୍ର (Frequency Polygon)
- ବୃତ୍ତ ଆରେଖ ବା ପାଇ ଚିତ୍ର (Pie-diagram)
- ସଦୃଶ ପୌନଃପୁନଃ ବକ୍ର (Smoothed Frequency Curve)
- ଅଜାଇଭ୍ ବା କ୍ରମବର୍ଦ୍ଧିଷ୍ଣୁ ପୌନଃପୁନ୍ୟ ବକ୍ର (Ogive or Cumulative Frequency Curve)
ଆୟତଚିତ୍ର (Histogram) – ଆୟତଚିତ୍ରକୁ ବାର୍ ଡାଇଗ୍ରାମ୍ କୁହାଯାଏ । ଏହା କେତେଗୁଡ଼ିଏ ଦଣ୍ଡର ସମାହାର । ପ୍ରତ୍ୟେକ ସଂଭାଗର ପୌନଃପୁନ୍ୟକୁ ଦଣ୍ଡ ଆକାରରେ ପ୍ରକାଶ କରାଯାଇଥାଏ । ଏହି ରେଖଚିତ୍ରର ଦଣ୍ଡଗୁଡ଼ିକ ଯାହା ଆୟତକ୍ଷେତ୍ର ଭଳି ଦେଖାଯାଏ । ତେଣୁ ଏହାକୁ ଆୟତଚିତ୍ର କୁହାଯାଏ ।
ଆୟତଚିତ୍ର ଅଙ୍କନର ନିୟମ :
- ପ୍ରଥମେ ଦୁଇଟି ରେଖା ଯଥା OX (ସମାନ୍ତରାଳ ରେଖା) ଏବଂ OY (ଲମ୍ବାକାର) ରେଖା ଅଙ୍କନ କର ।
- ଦୁଇଟି ରେଖା OX ଏବଂ OY, ୦ ବିନ୍ଦୁରେ ମିଳିତ ହୁଅନ୍ତି ।
- OY ରେଖାଟି OX ରେଖାର 75% ହେବା ଉଚିତ ।
- ପ୍ରତ୍ୟେକ ସଂଭାଗର ନିମ୍ନ ବାସ୍ତବ ସୀମା (Lower limit) ଏବଂ ଉଚ୍ଚ ବାସ୍ତବ ସୀମା (Upper limit) ନିର୍ଣ୍ଣୟ କର ।
- OX ରେଖାଟି ନିମ୍ନ ବାସ୍ତବ ସୀମା ଏବଂ ଉଚ୍ଚ ବାସ୍ତବ ସୀମାକୁ ବୁଝାଇବ ।
- OY ରେଖାଟି ଲମ୍ବାକାର ଅଟେ । ତେଣୁ ତାହା ପୌନଃପୁନ୍ୟକୁ ବୁଝାଇବ ।
- ପ୍ରଥମ ସଂଭାଗର ନିମ୍ନ ବାସ୍ତବ ସୀମା ଏବଂ ଉଚ୍ଚ ବାସ୍ତବ ସୀମାକୁ ତା’ର ପୌନୁପୁନ୍ୟ ସହ ଯୋଗ କର ।
- ଦ୍ଵିତୀୟ ସଂଭାଗର ନିମ୍ନ ବାସ୍ତବ ସୀମା ପ୍ରଥମ ସଂଭାଗର ଉଚ୍ଚ ବାସ୍ତବ ସୀମା ଅଟେ । ତେଣୁ ଦ୍ଵିତୀୟ ସଂଭାଗର ପୌନଃପୁନ୍ଯ ସହ ତାକୁ ସେହିପରି ଯୋଗ କର । ଦେଖୁ ତାହା ଏକ ଆୟତାକାର କ୍ଷେତ୍ରଟି ହେବ । ସେହିପରି କଲେ ଯେଉଁ ଚିତ୍ରଟି ହେବ ତାହା ଆୟତଚିତ୍ର ।
ପୌନଃପୁନ୍ୟ ବହୁଭୁଜ କ୍ଷେତ୍ର (Frequency Polygon) – ପୌନଃପୁନ୍ୟ ସାରଣୀର ଲବ୍ଧଙ୍କକୁ ଆମେ ଗ୍ରାଫ୍ ମାଧ୍ୟମରେ ପ୍ରକାଶ କରିବା ସମୟରେ ଯେଉଁ ଲେଖଚିତ୍ର ଅଙ୍କନ କରାଯାଇଥାଏ, ତାହା ପ୍ରାୟତଃ OX ଅକ୍ଷରେଖାକୁ ଛୁଇଁ ନ ଥାଏ । ଏକ ବହୁଭୁଜ କ୍ଷେତ୍ର ପ୍ରସ୍ତୁତ କରିବାକୁ ହେଲେ ପ୍ରତ୍ୟେକ ରେଖା ସମ୍ମିଳିତ ହେଲେ ବହୁ କୋଣ ସୃଷ୍ଟି ହେବ ଏବଂ ଯେଉଁ କ୍ଷେତ୍ରର ବହୁଭୁଜ ବି ଥିବ । ବହୁ ବାହୁ ପୂବା କ୍ଷେତ୍ରକୁ ବହୁଭୁଜ କ୍ଷେତ୍ର କୁହାଯାଏ ।
ପୌନଃପୁନ୍ୟ ବହୁଭୁଜ କ୍ଷେତ୍ର ଅଙ୍କନର ନିୟମ :
(1) ସର୍ବନିମ୍ନ ଏବଂ ସର୍ବୋଚ୍ଚ ସଂଭାଗର ନିମ୍ନରେ ଏବଂ ଉପରେ ଦୁଇଟି ସଂଭାଗ ସୃଷ୍ଟି କରାଯାଇ ତାହାର ପୌନଃପୁନ୍ୟକୁ ଶୂନ୍ୟ ‘0’ ଦିଆଯାଉ ।
(2) ପ୍ରତ୍ୟେକ ସଂଭାଗର ମଧ୍ୟବିନ୍ଦୁ ନିଶ୍ଚୟ କର ।
(3) ମଧ୍ୟବିନ୍ଦୁ (Mid point) ସମାନ୍ତରାଳ ରେଖା (OX-Axis)ରେ ଦର୍ଶାଯାଉ ।
(4) ପୌନଃପୁନ୍ୟକୁ ଲମ୍ବାକାର ରେଖା (OY-Axis)କୁ ବୁଝାଇବ ।
(5) ଶୂନ୍ୟ ପୌନଃପୁନ୍ୟ ନେବାର କାରଣ ତାହାର ଦୁଇଟି ସଂଭାଗ OX-Axisକୁ ଛାଇଁବ ଯାହା ଏକ ବହୁଭୁଜ କ୍ଷେତ୍ର ଗଠନରେ ସାହାଯ୍ୟ କରିବ ।
(6) ପୌନଃପୁନଃ ସଂଭାଗର ତଳଆଡୁ ସଂଭାଗକୁ ନେଇ ମଧ୍ୟବିନ୍ଦୁ (Mid point)କୁ ବିନ୍ଦୁ ଦେଇ ପୌନଃପୁନ୍ୟର ବିନ୍ଦୁ ସହ ସଂଯୋଗ କର । ଏହିପରି ସମସ୍ତ ମଧ୍ୟବିନ୍ଦୁକୁ ପୌନଃପୁନ୍ଯ ସହ ସଂଯୋଗ କଲେ ଏହା ଏକ ବହୁଭୁଜ କ୍ଷେତ୍ର ହେବ ।
ପାଇ-ଚିତ୍ର ବା ବୃତ୍ତ ଆଲେଖ (Pie-Diagram) – ଯେତେବେଳେ ରାଜ୍ୟ ବା କେନ୍ଦ୍ରର ବଜେଟ ଉପସ୍ଥାପନ କରାଯାଏ ତାହାର ଆୟ ଏବଂ ବ୍ୟୟକୁ ଏକ ମୁଦ୍ରାରେ ଖଣ୍ଡଖଣ୍ଡ କରି ଭାଗ କରାଯାଇଥାଏ, ଯାହା ଏକ ବୃତ୍ତଭଳି ଦେଖାଯାଏ । ବୃତ୍ତକୁ ବିଭିନ୍ନ ବିଭିନ୍ନ କୋଣରେ ଭାଗ କରାଯାଇ ତାକୁ ଶତକଡ଼ାରେ ପ୍ରକାଶ କରାଯାଇଥାଏ । ସେହିପରି ଆମର ବର୍ଷତମାମ ଆୟ ଏବଂ ବ୍ୟୟକୁ ଶତକଡ଼ାରେ ପ୍ରକାଶ କରାଯାଇଥାଏ ।
ବୃତ୍ତ ଚିତ୍ରରେ ପ୍ରକୃତ ସଂଖ୍ୟା ନ ଥାଏ ।
ଏହା ଶତକଡ଼ା ରୂପେ ପ୍ରକାଶ ପାଇଥାଏ ।
କେନ୍ଦ୍ରୀୟ ପ୍ରବୃତ୍ତିର ପଦକ୍ଷେପ (Measures of Central Tendency) :
ଅର୍ଥ (Meaning) ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଆମେ ନିଜର ସାମର୍ଥ୍ୟକୁ ଅନ୍ୟମାନଙ୍କ ସହ ତୁଳନା କରିଥାଉ । ପ୍ରଶ୍ନ ଆସେ, କାହାର କୃତି ସହ ଆମେ ନିଜକୁ ତୁଳନା କରିବା ? ତୁଳନା କରିବାକୁ ହେଲେ ଆମେ ହାରାହାରି (Average) କୃତିତ୍ବ ସହ ତୁଳନା କରିବା ଦରକାର । ଏହାକୁ କେନ୍ଦ୍ରସ୍ଥଳୀ ରୂପେ ଗ୍ରହଣ କରାଯାଇଛି । ତେଣୁ ଏହାର ମାପଗୁଡ଼ିକୁ କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପ କୁହାଯାଏ ।
ଏହି ମାପଗୁଡ଼ିକ ହେଲା-
(1) ମାଧ୍ୟ (Mean)
(2) ମଧ୍ୟମା (Median)
(3) ଗରିଷ୍ଠକ (Mode)
(1) ମାଧ୍ୟ (Mean) – କୌଣସି ବିତରଣର ହାରାହାରି ମାନ ବା ମାପକୁ ମାଧ୍ୟ (Mean) ବା ମାଧ୍ଯମାନ କୁହାଯାଏ ।
ମାଧ୍ୟ (Mean) ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ର :
(i) ଅବର୍ଗତ ସଂଖ୍ୟା ବା ତଥ୍ୟ (Ungrouped data)
ମାଧ୍ୟ = \(\frac{\sum X}{N}\)
![]()
(ii) ବର୍ଗତ ତଥ୍ୟ (Grouped data)
(a) ମାଧ୍ୟ (Long Method) = \(\frac{\sum X}{N}\)
(b) ମାଧ୍ୟ (Short Method) = A.M. + \(\frac{\Sigma \mathrm{Fx}^{\prime}}{\mathrm{N}}\) × i
(2) ମଧ୍ୟମା (Median) – କୌଣସି ବିତରଣର ମଧ୍ୟବିନ୍ଦୁ (ଯେଉଁ ବିନ୍ଦୁ ବିତରଣକୁ ଦୁଇ ସମାନ ଭାଗରେ ବିଭକ୍ତ କରିଥାଏ) ଜାଣିବାପାଇଁ ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କରାଯାଏ । ତେଣୁ ମଧ୍ୟମା ବିତରଣକୁ ଦୁଇ ସମାନ ଭାଗରେ ବିଭକ୍ତ କରିଥାଏ ।
ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ର :
ମଧ୍ୟମା = \(L+\frac{N / 2-F}{f_m} \times \mathrm{i}\) Or, \(U-\frac{N / 2-F}{f_m} \times \mathrm{i}\)
(3) ଗରିଷ୍ଠକ (Mode) – ଗରିଷ୍ଠକ ହେଉଛି କୌଣସି ଏକ ବିତରଣର ସର୍ବାଧିକ ଲବ୍ଧଙ୍କ । ଯେଉଁ ଲଚ୍ଛାଙ୍କଟି ଏକାଧ୍ଵ ବାର ଆସିଥାଏ ତାହା ଗରିଷ୍ଠକ ।
ଗରିଷ୍ଠକ ଦୁଇ ପ୍ରକାର ; ଯଥା –
(a) ସ୍ଥୂଳ ଗରିଷ୍ଠକ – ଅବର୍ଗତ ତଥ୍ୟାବଳୀରେ ଯେଉଁ ଲକ୍ତାଙ୍କ ସର୍ବାଧୁକ ବାର ରହିଥାଏ ବା ଯାହାର ପୌନଃପୁନ୍ୟ ଅନ୍ୟାନ୍ୟ ଇଛାଙ୍କର ପୌନଃପୁନ୍ୟ ଅପେକ୍ଷା ଅଧିକ ତାହାକୁ ବିତରଣର ସ୍ଥୂଳ ଗରିଷ୍ଠକ କୁହାଯାଏ ।
(b) ବାସ୍ତବ ଗରିଷ୍ଠକ – କୌଣସି ପୌନଃପୁନଃ ବିତରଣରେ ଯେଉଁ ଲଜ୍ଜାଙ୍କ ବିନ୍ଦୁରେ ସର୍ବାପେକ୍ଷା ଅଧିକ ପୌନଃପୁନ୍ୟ ଘନୀଭୂତ ହୋଇଥା’ନ୍ତି, ତାହା ବିତରଣର ବାସ୍ତବ ଗରିଷ୍ଠକ ।
ନିମ୍ନଲିଖତ ସୂତ୍ରଦ୍ଵାରା ବାସ୍ତବ ଗରିଷ୍ଠକ ନିର୍ଣ୍ଣୟ କରିହୁଏ ।
Mode = 3 Median – 2 Mean
