BSE Odisha 10th Class Maths Solutions Geometry Chapter 3 ବୃତ୍ତର ସ୍ପର୍ଶକ Ex 3

Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 3 ବୃତ୍ତର ସ୍ପର୍ଶକ Ex 3 Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Geometry Chapter 3 ବୃତ୍ତର ସ୍ପର୍ଶକ Ex 3

Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
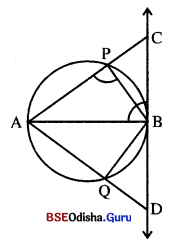
(i) ଏକ ବୃତ୍ତର କେନ୍ଦ୍ର O, ବୃତ୍ତ ବହିଃସ୍ଥ P କୌଣସି ଏକ ବିନ୍ଦୁ ଏବଂ \(\overline{\mathrm{PT}}\) ଉକ୍ତ ବୃତ୍ତର ଏକ ସ୍ପର୍ଶକଖଣ୍ଡ ହେଲେ, m∠OTP = _____ |
(ii) ଏକ ବୃତ୍ତର କେନ୍ଦ୍ର ଠ । ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଏବଂ \(\overline{\mathrm{PX}}\) ଓ \(\overline{\mathrm{PY}}\) ଉକ୍ତ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ଦୁଇଟି ସ୍ପର୍ଶକଖଣ୍ଡ । ∠XPY ଏକ ସୂକ୍ଷ୍ମକୋଣ ହେଲେ, ∠XOY ଏକ
କୋଣ ।
(iii) ଏକ ବୃତ୍ତର କେନ୍ଦ୍ର ଠ, ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଏବଂ \(\overline{\mathrm{PT}}\) ଉକ୍ତ ବୃତ୍ତପ୍ରତି ଏକ ସ୍ପର୍ଶକଖଣ୍ଡ ହେଲେ, m∠TOP + m∠TPO = ____ |
(iv) ଏକ ବୃତ୍ତର କେନ୍ଦ୍ର ଠ, ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଏବଂ \(\overline{\mathrm{PX}}\) ଓ \(\overline{\mathrm{PY}}\) ଉକ୍ତ ବୃତ୍ତ ପ୍ରତି ଦୁଇଟି ସ୍ପର୍ଶକ ଖଣ୍ଡ ହେଲେ,
(a) XOP କୋଣ ଓ ………………… କୋଣ ସମପରିମାଣ ବିଶିଷ୍ଟ;
(b) YPO କୋଣ ଓ ………………… କୋଣ ସମପରିମାଣ ବିଶିଷ୍ଟ ।
(v) ଏକ ବୃତ୍ତର କେନ୍ଦ୍ର ୦ ଏବଂ ବ୍ୟାସାର୍ଦ୍ଧ r ଏକକ । ବୃତ୍ତର ସମତଳରେ P ଏକ ବିନ୍ଦୁ ଏବଂ OP ଓ 1 ମଧ୍ଯରେ – ବୃହତ୍ତର ହେଲେ, P ବିନ୍ଦୁରୁ ବୃତ୍ତ ପ୍ରତି ଏକ ସ୍ପର୍ଶକ ଖଣ୍ଡ ଅଙ୍କନ ସମ୍ଭବ ।
(vi) 5 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତର କେନ୍ଦ୍ରଠାରୁ 13 ସେ.ମି. ଦୂରରେ ଓ ବୃତ୍ତର ସମତଳରେ ଅବସ୍ଥିତ ଏକ ବିନ୍ଦୁ P ହେଲେ, PT ସ୍ପର୍ଶକଖଣ୍ଡର ଦୈର୍ଘ୍ୟ ………………. ସେ.ମି.|
(vii) କେନ୍ଦ୍ର ୦ ଏବଂ 1 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତର ସମତଳରେ ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଠାରୁ ଉକ୍ତ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ଏକ ସ୍ପର୍ଶକ ଖଣ୍ଡର ଦୈର୍ଘ୍ୟ t ସେ.ମି. ହେଲେ OP = ………………. ସେ.ମି.|
(viii) ଦୁଇଟି ବହିଃସ୍ପର୍ଶୀ ବୃତ୍ତର (a) ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ସଂଖ୍ୟା = ………………… ଏକ
(b) ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ସଂଖ୍ୟା = …………………
(ix) ଦୁଇଟି ଅନ୍ତସ୍ପର୍ଶୀ ବୃତ୍ତର (a) ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ସଂଖ୍ୟା = ………………..
(b) ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ ସ୍ପର୍ଶକ ସଂଖ୍ୟା = ……………..
(x) ପରସ୍ପର ବହିଃସ୍ଥ ହୋଇଥ‌ିବା ଦୁଇଟି ଅଣଛେଦୀ ବୃତ୍ତର
(a) ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ସଂଖ୍ୟା = ……………………
(b) ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ ସ୍ପର୍ଶକ ସଂଖ୍ୟା = ………………..
(xi) ପରସ୍ପର ବହିଃସ୍ଥ ହୋଇ ନ ଥ‌ିବା ଦୁଇଟି ଅଣଛେଦୀ ବୃତ୍ତର
(a) ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ସଂଖ୍ୟା = …………….
(b) ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ ସ୍ପର୍ଶକ ସଂଖ୍ୟା = ……………
(xii) △ABC ର AB =AC । △ABC ର ପରିବୃତ୍ତ ଉପରିସ୍ଥ A ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶକ ଉପରେ P ଏକ ବିନ୍ଦୁ, ଯେପରି P ଓ B ବିନ୍ଦୁଦ୍ଵୟ \(\overline{\mathrm{AC}}\) ର ବିପରୀତ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ।
m∠PAC = 70° ଦେଲେ, m∠ABC =
(xiii) ଗୋଟିଏ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ୫ ସେ.ମି. ହେଲେ ଏହାର ଦୁଇଟି ସମାନ୍ତର ସ୍ପର୍ଶକ ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା ………………. ସେ.ମି.|
(xiv) ଦୁଇଟି ବର୍ହିସ୍ପର୍ଶୀ ବୃତ୍ତର କେନ୍ଦ୍ରଦ୍ଵୟ ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା ହେଉଛି ବୃତ୍ତଦ୍ୱୟର ବ୍ୟାସାର୍ଦ୍ଧମାନଙ୍କର ………………. ସଦ୍ ପମାନ |
(xv) ଦୁଇଟି ଅନ୍ତଃସ୍ପର୍ଶୀ ବୃତ୍ତର କେନ୍ଦ୍ରଦ୍ଵୟ ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା ହେଉଛି ବୃତ୍ତଦ୍ଵୟର ବ୍ୟାସାର୍ଦ୍ଧମାନଙ୍କର ……………… ସମାନ |
(xvi) ଏକ ସରଳରେଖା ଉପରିସ୍ଥ ଗୋଟିଏ ବିନ୍ଦୁ P ଠାରେ ସରଳରେଖାଟି ସର୍ବାଧିକ ……………… ହୋଇପାରିବ ।
Solution:
(i) 90°
(ii) ସ୍ଥୂଳକୋଣ
(iii) 90°
(iv) (a) YOP (b) XPO
(v) OP
(vi) 12
(vii) \(\sqrt{\mathrm{r}^2+\mathrm{t}^2}\)
(viii) (a) 2 (b) 1
(ix) (a)1 (b) 0
(x) (a) 2 (b) 0
(xi) (a) 0 (b) 0
(xii) 70°
(xiii) 16 ସେ.ମି.|
(xiv) ସମପୁ
(xv) ଥନ୍ତ୍ରର
(xvi) ଅସଂଖ୍ୟ

Question 2.
ଦତ୍ତ ଥ‌ିବା ଉକ୍ତି ଭୁଲ୍‌ଲେ (ଏହାକୁ ଦତ୍ତ ଉକ୍ତିର ନାସ୍ତିବାଚକ ଉକ୍ତି (Negative Statement) ବ୍ୟବହାର ନ କରି) ସଂଶୋଧନ କର ।
(i) r ଏକକ ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତର L ରେଖା ଏକ ଛେଦକ ହେଲେ, ବୃତ୍ତର କେନ୍ଦ୍ରଠାରୁ L ର ଦୂରତା = r ଏକକ ।
(ii) ଗୋଟିଏ ବୃତ୍ତର କେନ୍ଦ୍ର O ଏବଂ ବୃତ୍ତର ସମତଳରେ ବୃତ୍ତ ବହିଃସ୍ଥ କୌଣସି ଏକ ବିନ୍ଦୁ P | P ବିନ୍ଦୁରୁ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ଏକ ସ୍ପର୍ଶକ ଖଣ୍ଡ \(\overline{\mathrm{PT}}\) ହେଲେ △OPT ରେ ∠POT ଏକ ସମକୋଣ ।
(iii) ଗୋଟିଏ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ r ଏକକ । ବୃତ୍ତର ସମତଳରେ ବୃତ୍ତ ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଠାରୁ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡ \(\overline{\mathrm{PT}}\) ର ଦୈର୍ଘ୍ୟ t ଏକକ ଏବଂ ବୃତ୍ତର କେନ୍ଦ୍ର ୦ ଠାରୁ P ର ଦୂରତା d ଏକକ ହେଲେ, d² + r² = t²|
(iv) ଏକ ବୃତ୍ତର ସମତଳରେ ବୃତ୍ତ ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ Pରୁ ଉକ୍ତ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ \(\overline{\mathrm{PT}}\); P ବିନ୍ଦୁଗାମୀ ଏକ ଛେଦକ, ବୃତ୍ତଟିକୁ A ଓ B ବିନ୍ଦୁରେ ଛେଦ କରେ, ଯେପରି P – A – B । ତେବେ PT² = PA × AB |
(v) ଏକ ବୃତ୍ତର ଅନ୍ତଃସ୍ଥ କୌଣସି ଏକ ବିନ୍ଦୁ Q ଠାରୁ ଉକ୍ତ ବୃତ୍ତ ପ୍ରତି ଦୁଇଟି ସ୍ପର୍ଶକଖଣ୍ଡ ଅଙ୍କନ କରାଯାଇ ପାରିବ ।
(vi) ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବ୍ୟାସାର୍ଦ୍ଧ ଗୋଟିଏ ବୃତ୍ତର ବହିଃସ୍ଥ କେବଳ ଗୋଟିଏ ବିନ୍ଦୁ P ଅଛି, ଯେଉଁଠାରୁ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ହେବ ।
(vii) ଦୁଇଟି ସ୍ପର୍ଶକ ବୃତ୍ତର କେନ୍ଦ୍ରବିନ୍ଦୁ ଦ୍ଵୟ ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା ସହ ଉକ୍ତ ବୃତ୍ତଦ୍ଵୟର ବ୍ୟାସାର୍ଦ୍ଧର ସମଷ୍ଟି ସମାନ ହେଲେ, ବୃତ୍ତ ଦ୍ଵୟ ଅନ୍ତଃସ୍ପର୍ଶୀ ହେବେ ।
(viii) ଦୁଇଟି ଅନ୍ତଃସ୍ପର୍ଶୀ ବୃତ୍ତର କେନ୍ଦ୍ରନ୍ବୟର ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା, ବୃତ୍ତଦ୍ଵୟର ବ୍ୟାସାର୍ଦ୍ଧ ଦ୍ବୟର ପାର୍ଥକ୍ୟ ସହ ସମାନ ।
(ix) ଦୁଇଟି ବୃତ୍ତ ମଧ୍ୟରୁ ଗୋଟିଏ ଅନ୍ୟଟିର ଅନ୍ତର୍ଦେଶରେ ଅବସ୍ଥିତ ହେଲେ, ସେ ଦୁଇଟି ବୃତ୍ତର ଗୋଟିଏ ମାତ୍ର ସାଧାରଣ ସ୍ପର୍ଶକ ରହିବ ।
(x) ଦୁଇଟି ବିନ୍ଦୁରେ ପରସ୍ପରକୁ ଛେଦ କରୁଥିବା ଦୁଇଟି ବୃତ୍ତର କେବଳ ଗୋଟିଏ ତୀର୍ଯ୍ୟକ ସାଧାରଣ ସ୍ପର୍ଶକ ଥାଏ ।
(xi) ଦୁଇଟି ଅନ୍ତଃସ୍ପର୍ଶୀ ସ୍ପର୍ଶକ ବୃତ୍ତର ସ୍ପର୍ଶବିନ୍ଦୁ, ଅନ୍ତଃସ୍ଥ ବୃତ୍ତର ଏକ ବହିଃସ୍ଥ ବିନ୍ଦୁ ନୁହେଁ ।
(xii) ଦୁଇଟି ବହିଃସ୍ପର୍ଶୀ ସ୍ପର୍ଶକ ବୃତ୍ତର ସ୍ପର୍ଶ ବିନ୍ଦୁ, ଉଭୟ ବୃତ୍ତ ମଧ୍ୟରୁ କୌଣସିଟିର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ନୁହେଁ ।
Solution:
(i) <r
(ii) ∠OTP ଟି ∠PTO
(iii) d² = t² + r²
(iv) PT² = PA × PB
(v) ଅନ୍ତର୍ ବଦଲରେ ଦହିମ
(vi) ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଗୋଟିଏ ବୃତ୍ତର ବହିଃସ୍ଥ ଅସଂଖ୍ୟ ବିନ୍ଦୁ P ଅଛି ଯେଉଁଠାରୁ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ ହେବ ।
(vii) ସମଷ୍ଟି ବଦଳରେ ଅନ୍ତର ହେବ ।
(viii) ପାର୍ଥକ୍ୟ ବଦଳରେ ଅନ୍ତର ହେବ ।
(ix) ଗୋଟିଏ ମାତ୍ର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ହେବ ।
(x) ଗୋଟିଏ ତୀର୍ଯ୍ୟକ ବଦଳରେ ଦୁଇଟି ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ହେବ ।
(xi) ଉଭୟର ଏକ ସାଧାରଣ ବିନ୍ଦୁ ।
(xii) ଉଭୟ ବୃତ୍ତର ଏକ ସାଧାରଣ ବିନ୍ଦୁ ।

Question 3.
ଗୋଟିଏ ବୃତ୍ତର କେନ୍ଦ୍ରବିନ୍ଦୁ O ଏବଂ ବ୍ୟାସାର୍ଦ୍ଧ ୫ ସେ.ମି. । ଉକ୍ତ ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଏବଂ PO = 17 ସେ.ମି. ହେଲେ, P ବିନ୍ଦୁରୁ ଉକ୍ତ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡର ଦୈର୍ଘ୍ୟ କେତେ ?
Solution:
ମନେକର S ବୃତ୍ତର କେନ୍ଦ୍ର 80 1
\(\overline{\mathrm{PT}}\) ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ।
ଓ ବ୍ୟାସାର୍ଦ୍ଧ (OT) = 8 ସେ.ମି., P ବହିଃସ୍ଥ ବିନ୍ଦୁ S ।
PO = 17 ସେ.ମି.|

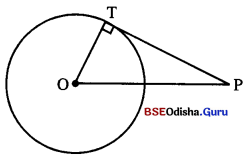
\(\overline{\mathrm{PT}}\) ⊥ \(\overline{\mathrm{OT}}\)
POT ସମକୋଣା ତ୍ରିଭୁଜରେ PT = \(\sqrt{\mathrm{OP}^2-\mathrm{OT}^2}\)
= \(\sqrt{17^2-8^2}\) ସେ.ମି. = \(\sqrt{289-64}\) = \(\sqrt{225}\) = 15 ସେ.ମି.|
∴ P ବିନ୍ଦୁରୁ ଉକ୍ତ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ pତୁର ଦୈର୍ଘ୍ୟ 15 ସେ.ମି. |

Question 4.
ଦୁଇଟି ବହିଃସ୍ପର୍ଶୀ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ 4.5 ସେ.ମି. ଓ 12.5 ସେ.ମି. । ବୃତ୍ତ ଦ୍ଵୟର ଏକ ସାଧାରଣ ସ୍ପର୍ଶକ ବୃତ୍ତ ଦ୍ଵୟକୁ P ଓ Q ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କଲେ, \(\overline{\mathrm{PQ}}\)ର ଦୈର୍ଘ୍ୟ କେତେ ?
Solution:

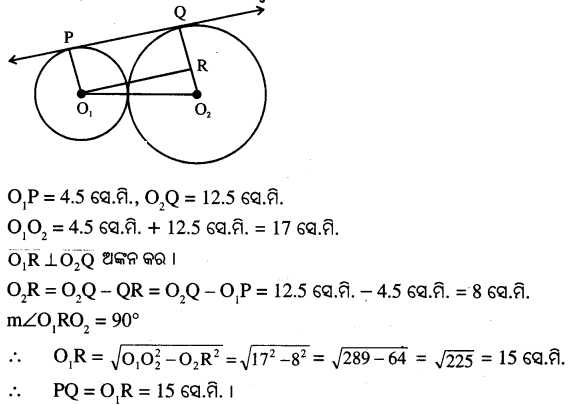
Question 5.
ଦୁଇଟି ଅଣଛେଦୀ ବୃତ୍ତର ଏକ ତୀର୍ଯ୍ୟକ ସାଧାରଣ ସ୍ପର୍ଶକ ବୃତ୍ତ ଦ୍ଵୟକୁ P ଓ ଠୁ ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରନ୍ତି । କେନ୍ଦ୍ରଦ୍ୱୟ ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା 20 ସେ.ମି. ଏବଂ ବ୍ୟାସାର୍ଦ୍ଧ ଦ୍ୱୟ 7 ସେ.ମି. ଓ 5 ସେ.ମି. ହେଲେ, PQ କେତେ ସେ.ମି. ?
Solution:

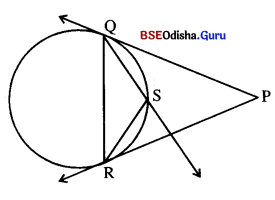
Question 6.
ଚିତ୍ରରେ ବୃତ୍ତର ବହିଃସ୍ଥ ବିନ୍ଦୁ P | P ବିନ୍ଦୁଗାମୀ ଗୋଟିଏ ଛେଦକ ଦର ବୃତ୍ତକୁ A ଓ B ବିନ୍ଦୁରେ ଛେଦ କରେ, ଯେପରିକି P – A – B | P ବିଦୁଗାମୀ ଅନ୍ୟ ଏକ ଛେଦକ ଉକ୍ତ ବୃତ୍ତକୁ C ଓ D ବିନ୍ଦୁରେ ଛେଦ କରେ ଯେପରିକି P – C – D|
Solution:

(i) ସ୍ପର୍ଶକ-ସଂପୃକ୍ତ ଉପପାଦ୍ୟ ପ୍ରୟୋଗ କରି ପ୍ରମାଣ କର ।
PA × PB = PC × PD
(ii) PA = 10 ସେ.ମି., PB = 16 ସେ.ମି. ଓ PD = 20 ସେ.ମି. 6ହଲେ, CD କଣ୍ଡଯ କର |
(iii) PA = 8 ସେ.ମି. ଓ AB =10 ସେ.ମି. ହେଲେ, P ବିନ୍ଦୁଗାମୀ ସ୍ପର୍ଶକଖଣ୍ଡର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ବଭ : ABCD ଦୂଇରେ P ଦହିମ ଏକ ଦିନ୍ଦୁ |
P – C – D ଓ P – A – B ଦୁଇଟି ଛେଦନ |
ତ୍ପ।ମାଣ୍ୟ : (i) PA × PB = PC × PD

ଅକନ : \(\overline{\text { PT }}\) ମ୍ଟଣକଖଣ୍ଡ ଅକନ କର |
ପ୍ତମାଣ: (i) PT² = PA × PB
PT² = PC × PD
∴ PA × PB = PC × PD

(ii) PC = \(\frac{PA \times PB}{PD}\) = \(\frac{10 \times 16}{20}\) ସେ.ମି = 8 ସେ.ମି
∴ CD = PD – PC = 20 ସେ.ମି – 8 ସେ.ମି = 12 ସେ.ମି |

(iii) PT² = PA × PB = PA (PA + AB)
= 8 × (8 + 10) = 8 × 18 ଦଗ ସେ.ମି |

Question 7.
ଚିତ୍ରରେ ଥ‌ିବା ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P | P ବିନ୍ଦୁଗାମୀ ଏକ ଛେଦକ ପୂର୍ବୋକ୍ତ ବୃତ୍ତକୁ A ଓ B ବିନ୍ଦୁରେ ଛେଦ କରେ । ଯେପରି P – A – b | P ବିନ୍ଦୁଗାମୀ ସ୍ପର୍ଶକରଶ୍ମିର ସ୍ପର୍ଶବିନ୍ଦୁ T |

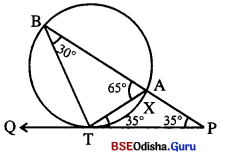
(i) m\(\overparen{\text { AXT }}\) = 60° m\(\overparen{\text { BYT }}\) = 130° ଛେଦକ, m∠ATP, m∠APT, m∠ATB ଓ m∠BTQ ନିଣ୍ଡୟ କର |
(ii) m∠BTQ = 2m∠ATP ହେଲେ ,ପ୍ରମାଣ କର : (a) BT = TP (b) TA = AP
(iii) PA = 8 ସେ.ମି. ଓ PT = 12 ସେ.ମି. ହେଲେ , AB ନିଣ୍ଟୟ କର |
(iv) PT = 2AP ଏବଂ AB = 18 ସେ.ମି. ହେଲେ , PT ନିଣ୍ଟୟ କର |
(v) PT = 2AP ଏବଂ PB = 24 ସେ.ମି. ହେଲେ , PT ନିଣ୍ଟୟ କର |
Solution:
\(\overline{\mathrm{B} T}\) ଓ \(\overline{\mathrm{A} T}\) ଅଙ୍କନ କର ।

(i) m∠ABT = \(\frac { 1 }{ 2 }\)m\(\overparen{\text { AXT }}\) = \(\frac { 1 }{ 2 }\) × 60° = 30°
⇒ m∠ATP = m∠ABT = 30°
m∠BAT = \(\frac { 1 }{ 2 }\)m\(\overparen{\text { BYT }}\) = \(\frac { 1 }{ 2 }\) × 130° = 65°
△ATP ରେ ଦଦ୍ୱିମ m∠BAT = m∠ATP + m∠APT
⇒ m∠APT = m∠BAT – m∠ATP = 65° – 30° = 35°
m∠ATB = 180° – 30° – 65° = 85° (: ATB ଏକ ତ୍ରିଭୁବ)
m∠BTQ = m∠BAT = 65°

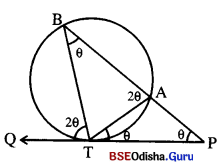
(ii) ମନେକର m∠ATP = θ ⇒ m∠ABT = θ
m∠BTQ = 2m∠ATP = 2θ
m∠BAT = m∠BTQ = 2θ
⇒ m∠APT = 2θ – θ = θ
△BTP ରେ m∠TBP = m∠TPB
⇒ BT = TP
△TAP ରେ m∠ATP = m∠APT ଦ୍ରେତୁ AT = AP

(iii) PT² = PA × PB
⇒ PB = \(\frac{\mathrm{PT}^2}{\mathrm{PA}}\) = \(\frac{12 \times 12}{8}\) = 18 ସେ.ମି
∴ AB = PB – PA = 18 ସେ.ମି – 8 ସେ.ମି = 10 ସେ.ମି |

(iv) PT² = PA × PB = PA × (PA + AB)
⇒ (2AP)² = PA (PA + 18)
⇒ \(\frac{4 \mathrm{AP}^2}{\mathrm{PA}}\) = PA + 18 ⇒ 4AP – AP = 18 ସେ.ମି.
⇒ 3AP = 18 ସେ.ମି. ⇒ PA = \(\frac { 18 }{ 3 }\) ସେ.ମି. = 6 ସେ.ମି.

(v) PT² = PA × PB
⇒ (2AP)² × (PA + AB)
⇒ PB = \(\frac{4 \mathrm{AP}^2}{\mathrm{PA}}\) = 4AP = 24 ସେ.ମି.
∴ PT = 2AP = \(\frac{4 \mathrm{AP}}{2}\) = \(\frac { 24 }{ 2 }\) ସେ.ମି. = 12 ସେ.ମି. |

Question 8.
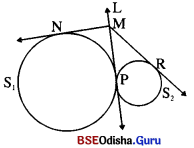
(a) ଦୁଇଟି ବୃତ୍ତ ବହିଃସ୍ପର୍ଶୀ ହେଲେ, ପ୍ରମାଣ କର ଯେ, ଏହାର ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ ସ୍ପର୍ଶକ ଉପରିସ୍ଥ ଯେକୌଣସି ବିନ୍ଦୁରୁ ବୃତ୍ତଦ୍ଵୟ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ଦ୍ବୟ ସର୍ବସମ ।
(b) ଦୁଇଟି ବୃତ୍ତ ଅନ୍ତସ୍ପର୍ଶୀ ହେଲେ, ପ୍ରମାଣ କର ଯେ, ସେମାନଙ୍କର ସାଧାରଣ ସ୍ପର୍ଶକ ଉପରିସ୍ଥ ଯେକୌଣସି ବିନ୍ଦୁରୁ ଉକ୍ତ ବୃତ୍ତ ଦ୍ଵୟ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ଦ୍ଵୟ ସର୍ବସମ ।

Solution:
(a) ଦତ୍ତ : S ଓ S ବୃତ୍ତଦ୍ୱୟ ବହିଃସ୍ପର୍ଶୀ । ସେମାନଙ୍କର ସାଧାରଣ ସ୍ପର୍ଶକ L | L ଉପରିସ୍ଥ M ଏକ ବିନ୍ଦୁ | M ବିନ୍ଦୁରୁ ବୃତ୍ତଦ୍ଵୟ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡଦ୍ଵୟ \(\overline{\mathrm{MN}}\) ଓ \(\overline{\mathrm{MR}}\) |
ପ୍ରାମାଣ୍ୟ : MN = MR
ପ୍ରମାଣ : M ବିନ୍ଦୁରୁ S₁ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ ।
⇒ MN = MP …(i)
ପୁନଶ୍ଚ M ବିନ୍ଦୁରୁ S₂ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ ।
⇒ MR = MP …(ii)
(i) ଓ (ii)ରୁ MN = MR (ପ୍ରମାଣିତ)

(b) ଦତ୍ତ : S₁ ଓ S₂ ବୃତ୍ତଦ୍ୱୟ ଅନ୍ତଃସ୍ପର୍ଶୀ । ସେମାନଙ୍କର ସାଧାରଣ ସ୍ପର୍ଶକ L । L ଉପରିସ୍ଥ M ଏକ ବିନ୍ଦୁ । M ବିନ୍ଦୁରୁ ବୃତ୍ତଦ୍ଵୟ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡଦ୍ଵୟ \(\overline{\mathrm{MN}}\) ଓ \(\overline{\mathrm{MR}}\) |

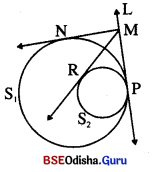
ପ୍ରାମାଣ୍ୟ : MN = MR
ପ୍ରମାଣ : M ବିନ୍ଦୁରୁ ଅନ୍ତବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ ।
⇒ MR = MP
ସେହିପରି M ବିନ୍ଦୁରୁ ବହିଃସ୍ଥ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ
ସ୍ପର୍ଶକଖଣ୍ଡ ଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ ।
⇒ MN = MP
(i) ଓ (ii) ରୁ MN = MR (ପ୍ରମାଣିତ)

Question 9.
ପରସ୍ପରଛେଦୀ ଦୁଇଟି ବୃତ୍ତର ଛେଦବିନ୍ଦୁ A ଓ B । \(\overleftrightarrow{\mathbf{A B}}\) ଉପରିସ୍ଥ P ଏକ ବିନ୍ଦୁ ଯେପରି A – B – P। ପ୍ରମାଣ କର ଯେ, ବୃତ୍ତଦ୍ଵୟ ପ୍ରତି P ବିନ୍ଦୁରୁ ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ଦ୍ଵୟ ସର୍ବସମ ।
ସମାଧାନ :
ଦତ୍ତ : ଦୁଇଟି ବୃତ୍ତ S₁ ଓ S₂, ପରସ୍ପରକୁ A ଓ B ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । \(\overleftrightarrow{\mathbf{A B}}\) ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ P ଠାରୁ ବୃତ୍ତଦ୍ଵୟ ପ୍ରତି \(\overrightarrow{\mathrm{PQ}}\) ଓ \(\overrightarrow{\mathrm{PR}}\) ସ୍ପର୍ଶକ ଅଙ୍କିତ ହୋଇଛି ।
ପ୍ରାମାଣ୍ୟ : PQ = PR
ପ୍ରମାଣ : S₁ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ \(\overrightarrow{\mathrm{PQ}}\) |
S₁ ବୃତ୍ତର ଏକ ଛେଦକ \(\overleftrightarrow{\mathbf{P A B}}\) |
∴ PQ² = PA.PB …(i)

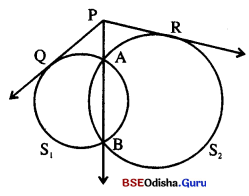
ସେହିପରି S₂ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ \(\overrightarrow{\mathrm{PR}}\) ।
S₂ ବୃତ୍ତର ଏକ ଛେଦକ \(\overleftrightarrow{\mathbf{P A B}}\) |
∴ PR² = PA·PB …(ii)
(i) ଓ (ii) ତି PQ² = PR² ⇒ PQ = PR (ପ୍ରମାଣିତ)

Question 10.
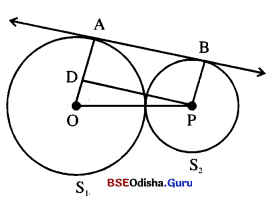
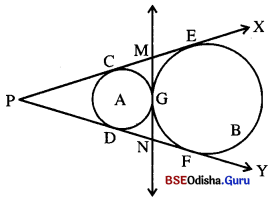
ଚିତ୍ରରେ r₁ ଓ x₂ ଏକକ ବ୍ୟାସାର୍କ ବିଶିଷ୍ଟ ବୃତ୍ତ S₁ ଓ S₂ ର କେନ୍ଦ୍ର ଯଥାକ୍ରମେ A ଓ B । ଚିତ୍ର (a)ରେ ବୃତ୍ତଦ୍ଵୟର ଗୋଟିଏ ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ ସ୍ପର୍ଶକ \(\overline{\mathbf{A B}}\) କୁ M ବିନ୍ଦୁରେ ଛେଦ କରେ । ପ୍ରମାଣ କର ଯେ,
AM : MB = r₁ : r₂ |

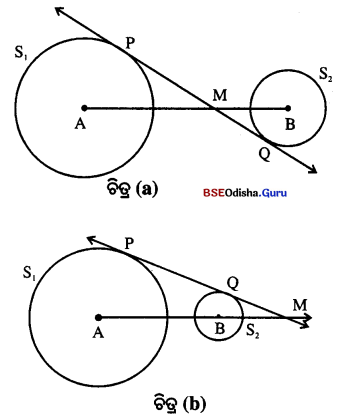
ଚିତ୍ର (b)ରେ ବୃତ୍ତ ଦ୍ଵୟର ଗୋଟିଏ ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ \(\overrightarrow{\mathbf{A B}}\) କୁ M ବିନ୍ଦୁରେ ଛେଦ କରେ, ଯେପରିକି A-B-M | ତ୍ପମାଣ କର ସେ AM : BM = r₁ : r₂ |
ସମାଧାନ :
ଦତ୍ତ : ଦୁଇଟି ଅଣଛେଦୀ ବୃତ୍ତର କେନ୍ଦ୍ର ଯଥାକ୍ରମେ O₁ ଓ O₂ |
\(\overline{\mathrm{PQ}}\) ଏକ ସାଧାରଣ ତୀର୍ଯ୍ୟକ ସ୍ପର୍ଶକ \(\overleftrightarrow{\mathrm{PQ}}\) ଓ O₁O₂ ର ଛେଦବିନ୍ଦୁ R |
ପ୍ରାମାଣ୍ୟ : \(\frac{\mathrm{O}_1 \mathrm{R}}{\mathrm{O}_2 \mathrm{R}}\) = \(\frac{r_1}{r_2}\)
ଅଙ୍କନ : \(\overline{\mathrm{O}_1 \mathrm{P}}\) ଓ \(\overline{\mathrm{O}_1 \mathrm{Q}}\) ଅକନ କର |
ପ୍ରମାଣ : O₁PR ଓ A O₂OR ମଧ୍ୟରେ
m∠O₁PR= m∠0₂QR (ପ୍ତତ୍ୟେକ ସମୟରେ)
m∠O₁RP = m∠O∠0₂RQ (ପ୍ତତ୍ୟେକ ସମୟରେ)
⇒ △O₁PR ~ △O₂QR (କୋ-କୋ ଗାଦଶ୍ୟ)
⇒ \(\frac{\mathrm{O}_1 \mathrm{R}}{\mathrm{O}_2 \mathrm{R}}\) = \(\frac{\mathrm{O}_1 \mathrm{P}}{\mathrm{O}_2 \mathrm{Q}}\) ⇒ \(\frac{r_1}{r_2}\) (ପ୍ରମାଣିତ)

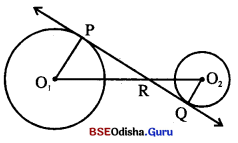
(b) ଦତ୍ତ : S₁ ଓ S₂ ବୃତ୍ତଦ୍ୱୟ ଅଣଛେଦୀ । ସେମାନଙ୍କ କେନ୍ଦ୍ର ଯଥାକ୍ରମେ A ଓ B |
\(\overline{\mathrm{PQ}}\) ସେମାନଙ୍କର ଏକ ସାଧାରଣ ସ୍ପର୍ଶକ ।
\(\overrightarrow{\mathrm{PQ}}\) ଓ \(\overrightarrow{\mathrm{AB}}\) ର ଛେଦ ବିନ୍ଦୁ M, A – B – M |
ପ୍ରାମାଣ୍ୟ : \(\frac { AM }{ BM }\) = \(\frac{r_1}{r_2}\)
ଅଙ୍କନ : \(\overline{\mathrm{AP}}\) ଓ \(\overline{\mathrm{BQ}}\) ଅଙ୍କନ କର ।
ସ୍ତମାଣ: m∠APM = 90°

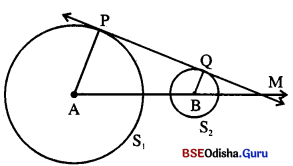
(\(\overline{\mathrm{PM}}\), S₁ ବୃତ୍ତର ସ୍ପର୍ଶକ ହେତୁ)
ସେହିପରି m∠BQM = 90°
⇒ m∠APM = = m∠BQM
m∠PMA = m∠QMB (ପାଧାରଣ କୋଣ)
⇒ △APM ~ △BQM (କୋ-କୋ ଗାଦଶ୍ୟ)
⇒ \(\frac { AM }{ BM }\) = \(\frac{r_1}{r_2}\)

Question 11.
ଗୋଟିଏ ବୃତ୍ତରେ \(\overline{\mathrm{PQ}}\) ଓ \(\overline{\mathrm{PR}}\) ଜ୍ୟା ଦ୍ଵୟ ସର୍ବସମ । ପ୍ରମାଣ କର ଯେ, ବୃତ୍ତ ପ୍ରତି P ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶକ, \(\overline{\mathrm{QR}}\) ସହ ସମାନ୍ତର ।

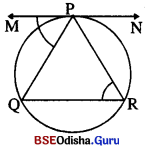
Solution:
ଦତ୍ତ : ବୃତ୍ତର \(\overline{\mathrm{PQ}}\) ଓ \(\overline{\mathrm{PR}}\) ଦୁଇଟି ସର୍ବସମ ଜ୍ୟା ।
P ବିନ୍ଦୁରେ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ \(\overleftrightarrow{M N}\) |
ପ୍ରାମାଣ୍ୟ : \(\overleftrightarrow{M N}\) || \(\overline{\mathrm{QR}}\)
ପ୍ରମାଣ : m∠MPQ = m∠PRQ (ଏକାନ୍ତର ଚାପାନ୍ତର୍ଲିଖ କୋଣ)
PQ = PR ⇒ m∠PQR = m∠PRQ
∴ m∠MPQ = m∠PQR
କିନ୍ତୁ ଏମାନେ ଏକାନ୍ତର ହେତୁ \(\overleftrightarrow{M N}\) || \(\overline{\mathrm{QR}}\) | (ପ୍ରମାଣିତ)

Question 12.
ଦୁଇଟି ଏକକେନ୍ଦ୍ରିକ ବୃତ୍ତ ମଧ୍ୟରୁ ଗୋଟିକର ଏକ ଜ୍ୟା \(\overline{\mathrm{AB}}\) ଅନ୍ୟ ବୃତ୍ତକୁ P ବିନ୍ଦୁରେ ସ୍ପର୍ଶକଲେ, ପ୍ରମାଣ କର ଯେ P ବିନ୍ଦୁରେ \(\overline{\mathrm{AB}}\) ସମଦ୍ଵିଖଣ୍ଡିତ ହୁଏ ।
Solution:

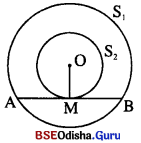
ଦତ୍ତ : S₁ ଓ S₂ ଦୁଇଟି ଏକକେନ୍ଦ୍ରିକ ବୃତ୍ତ । S₁ ବୃତ୍ତର ଜ୍ୟା \(\overline{\mathrm{AB}}\),
ଯାହା S₂ ବୃତ୍ତପ୍ରତି M ବିନ୍ଦୁରେ ସ୍ପର୍ଶକ ଅଟେ ।
ପ୍ରାମାଣ୍ୟ : \(\overline{\mathrm{AB}}\) ଜ୍ୟା M ବିନ୍ଦୁରେ ସମଦ୍ବିଖଣ୍ଡିତ ହେବ । ଅର୍ଥାତ୍ AM = MB |
ଅଙ୍କନ : \(\overline{\mathrm{OM}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : S₂ ବୃତ୍ତର ‘M’ ସ୍ପର୍ଶବିନ୍ଦୁ । \(\overline{\mathrm{OM}}\) ସ୍ପର୍ଶବିନ୍ଦୁଗାମୀ ବ୍ୟାସାର୍ଦ୍ଧ । ⇒ \(\overline{\mathrm{OM}}\) ⊥ \(\overline{\mathrm{AB}}\)
ପୁନଶ୍ଚ S₂ ବୃତ୍ତର \(\overline{\mathrm{AB}}\) ଜ୍ୟା ପ୍ରତି \(\overline{\mathrm{OM}}\) ଲମ୍ବ ହେତୁ M, \(\overline{\mathrm{AB}}\) ର ମଧ୍ୟବିନ୍ଦୁ ।
ଅର୍ଥାତ୍ \(\overline{\mathrm{AB}}\) କ୍ୟାଟି M ବିନ୍ଦୁରେ ସମଦ୍ଵିଖଣ୍ଡିତ ହେବ । (ପ୍ରମାଣିତ)

Question 13.
ପ୍ରମାଣ କର ଯେ, ବୃତ୍ତର ଦୁଇ ସମାନ୍ତର ସ୍ପର୍ଶକର ସ୍ପର୍ଶବିନ୍ଦୁ ଦ୍ଵୟର ସଂଯୋଜକ ରେଖାଖଣ୍ଡ ଉକ୍ତ ବୃତ୍ତର ଏକ ବ୍ୟାସ ।
Solution:
ଦତ୍ତ : S ବୃତ୍ତର ଠ କେନ୍ଦ୍ର ।
\(\overline{\mathrm{AB}}\) || \(\overline{\mathrm{CD}}\) ଏବଂ \(\overline{\mathrm{AB}}\) ଓ \(\overline{\mathrm{CD}}\) ବୃତ୍ତ Sର ଦୁଇଟି ସ୍ପର୍ଶକ ।
ସେମାନଙ୍କ ସ୍ପର୍ଶବିନ୍ଦୁ ଯଥାକ୍ରମେ E ଓ F |
ପ୍ରାମାଣ୍ୟ : E-O-F ଏକ ରେଖ୍ୟ ଅର୍ଥାତ୍‌ \(\overline{\mathrm{EF}}\) ବୃତ୍ତର ବ୍ୟାସ ।
ଅଙ୍କନ : \(\overline{\mathrm{EO}}\) ଓ \(\overline{\mathrm{OF}}\) ଅଙ୍କନ କର । O ବିନ୍ଦୁରେ \(\overline{\mathrm{AB}}\) ଓ \(\overline{\mathrm{CD}}\) ସହ ସମାନ୍ତର କରି \(\overleftrightarrow{\mathrm{MON}}\) ଅଙ୍କନ କର ।

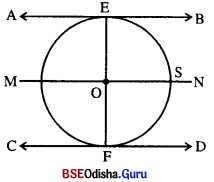
ତ୍ପମାଣ : m∠OEA = 90° ଓ \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) || \(\stackrel{\leftrightarrow}{\mathrm{MN}}\)
⇒ m∠EOM = 90°
ସେଦ୍ୱିପରି m∠FOM = 90°
∴ m∠EOM + m∠FOM = 90° + 90° = 180°
⇒ E-O-F ଏକରେଖ୍ୟ ଅର୍ଥାତ୍ \(\overline{\mathrm{EF}}\) ବୃତ୍ତର ବ୍ୟାସ ।

Question 14.
△ABC ସମ୍ପୃକ୍ତ \(\overline{\mathrm{BC}}\) ବାହୁ, \(\overrightarrow{\mathbf{A B}}\) ରଶ୍ମି ଓ \(\overrightarrow{\mathbf{A C}}\) ରଶ୍ମିକୁ POR ବୃତ୍ତ ଯଥାକ୍ରମେ P, Q ଓ R ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରେ | ତ୍ପମାଣ କର ଯେ, AQ = \(\frac { 1 }{ 2 }\) (AB + BC + AC)|
Solution:
ଦତ୍ତ : △ABC ର ବହିଃସ୍ଥ ଏକ ବୃତ୍ତ POR, \(\overline{\mathrm{BC}}\) ବାହୁକୁ P ବିନ୍ଦୁରେ ସ୍ପର୍ଶକରେ ଏବଂ \(\overrightarrow{\mathrm{AB}}\) ଓ \(\overrightarrow{\mathrm{AC}}\) ରଶ୍ମି ଦ୍ଵୟକୁ ଯଥାକ୍ରମେ Q ଓ R ବିନ୍ଦୁରେ ସ୍ପର୍ଶକରେ ।
ପ୍ରାମାଣ୍ୟ : AQ = \(\frac { 1 }{ 2 }\) (AB + BC + CA)
ପ୍ରମାଣ : ବହିଃସ୍ଥ ବିନ୍ଦୁ A ରୁ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ ।
∴ AQ = AR

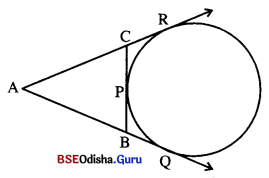
ପୁନଶ୍ଚ BQ = BP ଏବଂ CP = CR
2AQ = AQ + AQ = AQ + AR = AB + BQ + AC + CR
= AB + BP + AC + CP = AB + (BP + CP) + AC = AB + BC + AC
∴ AQ = \(\frac { 1 }{ 2 }\) (AB + BC + AC) (ପ୍ରମାଣିତ)

Question 15.
ଏକ ସାମାନ୍ତରିକ ଚିତ୍ରର ସମସ୍ତ ବାହୁକୁ ଗୋଟିଏ ବୃତ୍ତ ସ୍ପର୍ଶ କଲେ, ପ୍ରମାଣ କର ଯେ ସାମାନ୍ତରିକ ଚିତ୍ରଟି ଏକ ରମ୍ବସ୍ ।
Solution:
ଦତ୍ତ :
ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । ଏହାର \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\), \(\overline{\mathrm{CD}}\) ଓ \(\overline{\mathrm{DA}}\) ଯଥାକ୍ରମେ ଏକ ବୃତ୍ତକୁ P, Q, R, S ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରେ ।
ପ୍ରାମାଣ୍ୟ : ABCD ଏକ ରମ୍ବସ୍ ।
ପ୍ରମାଣ : ବହିଃସ୍ଥ ବିନ୍ଦୁ A ରୁ AP = AS
ସେହିପରି BP = BQ, DR = DS ଓ CR = CQ
∴ AP + BP + DR + CR = AS + BQ + DS + CQ = AS + DS + BQ + CQ

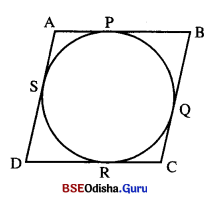
⇒ AB + CD = AD + BC
⇒ AB + AB = AD + AD (‘.’ AB = CD ଓ AD = BC)
⇒ 2AB = 2AD
⇒ AB = AD
ଅର୍ଥାତ୍ ABCD ଏକ ରମ୍ବସ୍ । (ପ୍ରମାଣିତ)

Question 16.
ଗୋଟିଏ ବୃତ୍ତର କେନ୍ଦ୍ର O ଏବଂ ଏହି ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P | P ଠାରୁ ପୂର୍ବୋକ୍ତ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡ ଦ୍ଵୟ ହେଉଛନ୍ତି \(\overline{\mathrm{PA}}\) ଓ \(\overline{\mathrm{PB}}\) | \(\overline{\mathrm{OP}}\) ର ଦୈର୍ଘ୍ୟ ବୃତ୍ତଟିର ବ୍ୟାସ ସହ ସମାନ ହେଲେ, ପ୍ରମାଣ କର ଯେ, △ABP ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ।
Solution:

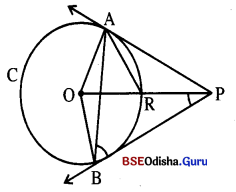
ଦତ୍ତ : ABC ବୃତ୍ତର କେନ୍ଦ୍ର ଠ ଓ P ଏକ ବହିଃସ୍ଥ ବିନ୍ଦୁ । \(\overline{\mathrm{PA}}\) ଓ \(\overline{\mathrm{PB}}\) ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ।
OP = ବୃତ୍ତର ବ୍ୟାସ ।
ପ୍ରାମାଣ୍ୟ : △ABP ଏକ ସମବାହୁ ଅର୍ଥାତ୍ AP = BP = AB |
ଅଙ୍କନ : \(\overline{\mathrm{OA}}\), \(\overline{\mathrm{OB}}\) ଓ \(\overline{\mathrm{AR}}\) ଅଙ୍କନ କର ।
∴ OP = 2r = 2OR ⇒ R, \(\overline{\mathrm{OP}}\) ର ମଧ୍ୟବିନ୍ଦୁ ।
∴ △OAP ସମକୋଣୀ (∵ m∠OAP = 90°)
ସମକୋଣରୁ କର୍ଣ୍ଣର ମଧ୍ୟବିନ୍ଦୁ Rକୁ ସଂଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡ \(\overline{\mathrm{AR}}\), \(\overline{\mathrm{OP}}\) ର ଅର୍ଦ୍ଧେକ ଦୈର୍ଘ୍ୟ ବିଶିଘୁ |
∴ AR = OA = OR
∴ AROA = OR
m∠AOR = 60°
ସେହିପରି m∠BOR = 60°
∴ m∠AOB 120° ⇒ m∠APB = 60°
ବର୍ତ୍ତମାନ △APBରେ PA = PB ଏବଂ m∠APB = 60°
∴ △APB ସମବାହୁ ।

Question 17.
ଗୋଟିଏ ବୃତ୍ତର କେନ୍ଦ୍ର O ଏବଂ P ବୃତ୍ତର ବହିଃସ୍ଥ ଏକବିନ୍ଦୁ । \(\overrightarrow{\mathbf{P T}}\) ସ୍ପର୍ଶକରଶ୍ମିର ସ୍ପର୍ଶବିନ୍ଦୁ T, \(\overline{\mathrm{OP}}\)ର ମଧ୍ୟବିନ୍ଦୁ Q ହେଲେ ପ୍ରମାଣ କର ଯେ, QT = QP |
Solution:

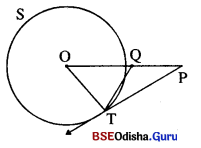
ଦତ୍ତ : S ବୃତ୍ତର ‘O’ କେନ୍ଦ୍ର । P ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ ।
\(\overline{\mathrm{OP}}\) ର ମଧ୍ୟବିନ୍ଦୁ Q । \(\overrightarrow{\mathbf{P T}}\) ବୃତ୍ତପ୍ରତି P ବିନ୍ଦୁରୁ ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ।
ପ୍ରାମାଣ୍ୟ : QT = OP
ଅଙ୍କନ : \(\overline{\mathrm{OT}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : m∠OTP = 90° (ସ୍ପର୍ଶକ, ସ୍ପର୍ଶବିଦୁଗାମୀ ବ୍ୟାସାର୍ଦ୍ଧ ପ୍ରତି ଲମ୍ବ)
∴ △OTP ସମକୋଣୀ । ଉକ୍ତ ତ୍ରିଭୁଜର କର୍ଣ୍ଣର ମଧ୍ୟବିନ୍ଦୁ Q |
∴ ସମକୋଣା ତ୍ରିଭୁକର ସମକୋଣରୁ କଣ୍ଡର ମଧ୍ୟ ବିନ୍ଦୁକୁ ଯୋଗ କରୁଥିବା ସରକରେଖା କଣ୍ଡର ବୈଶ୍ୟର ଅର୍ଦ୍ଧେକ ।
∴ QT = \(\frac { 1 }{ 2 }\) OP = QP (ପ୍ରମାଣିତ)

Question 18.
ଗୋଟିଏ ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଏବଂ ସ୍ପର୍ଶକ ରଶ୍ମି \(\overrightarrow{\mathbf{P T}}\) ର ସ୍ପର୍ଶବିନ୍ଦୁ T | P ବିନ୍ଦୁଗାମୀ ଏକ ରେଖା ଉକ୍ତ ବୃତ୍ତକୁ A ଓ B ବିନ୍ଦୁରେ ଛେଦ କରେ, ଯେପରିକି P-A-B | \(\overline{\mathrm{AB}}\) ଉପରେ A ଓ Bର ମଧ୍ୟବର୍ତ୍ତୀ C ଏକ ବିନ୍ଦୁ ।
ପ୍ରମାଣ କର :
(a) \(\overrightarrow{\mathbf{T C}}\), ∠ATB , ସମଦ୍ବିଖଣ୍ଡିତ ତ୍ରିଭୁଜର PC = PT
(b) PC = PT ହେଲେ \(\overrightarrow{\mathbf{T C}}\) ଦ୍ଵାରା ∠ATB ସମଦ୍ବିଖଣ୍ଡିତ ହୁଏ ।
Solution:
(a)
ଦତ୍ତ : ଏକ ବୃତ୍ତର ବହିଃସ୍ଥ ବିନ୍ଦୁ P । PT ଏକ ସ୍ପର୍ଶକଖଣ୍ଡ ଏବଂ P – A – B ଏକ ଛେଦକରେଖା ।
\(\overrightarrow{\mathbf{T C}}\), ∠ATBର ସମଦ୍ବିଖଣ୍ଡକ ।
ପ୍ରାମାଣ୍ୟ : PC = PT
ପ୍ରମାଣ : m∠PTA = m∠ABT (ଏକାନ୍ତର ବୃତ୍ତଖଣ୍ଡସ୍ଥ )

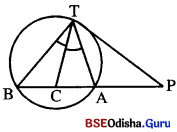
m∠ATC = m∠BTC (ଦଇ)
⇒ m∠PTA + m∠ATC = m∠ABT + m∠BTC
⇒ m∠ABT + m∠BTC = m∠CBT + m∠BTC = m∠TCA
(△BTCର ବହିଃସ୍ଥ କୋଣ)
ପୁନଶ୍ଚ m∠PTA + m∠ATC = m∠PTC
∴ m∠PTC = m∠TCA ⇒ m∠PTC = m∠TCP ⇒ PT = PC

(b) ଦତ୍ତ : ଏକ ବୃତ୍ତର P ବହିଃସ୍ଥ ବିନ୍ଦୁ । \(\overline{\mathrm{PT}}\) ଏକ ସ୍ପର୍ଶକଖଣ୍ଡ ଏବଂ P-A–B ଏକ ଛେଦକ ।
\(\overline{\mathrm{AB}}\) ର ମଧ୍ୟସ୍ଥ C ଏକ ବିନ୍ଦୁ ଓ PT = PC |
ପ୍ରାମାଣ୍ୟ : \(\overrightarrow{\mathbf{T C}}\), ∠ATBର ସମଦ୍ଵିଖଣ୍ଡକ ।
ପ୍ରମାଣ : △PTCରେ PT = PC (ଦତ୍ତ)

⇒ m∠PTC= m∠PCT
⇒ m∠PTA + m∠ATC = m∠CBT + m∠BTC
(∵ △TBC ରେ ଦହିମ କୋଣ ∠PCT)
m∠PTA = m∠CBT (ଏକାନ୍ତ୍ରର ଦ୍ବରଖଣ୍ଡମ)
⇒ m∠ATC = m∠BTC ⇒ \(\overrightarrow{\mathbf{T C}}\), ∠ATBର ସମଦ୍ଵିଖଣ୍ଡକ (ପ୍ରମାଣିତ)

Question 19.
△ABCର ବାହୁ AB ଓ AC ଉପରେ ଯଥାକ୍ରମେ X ଓ Y ବିନ୍ଦୁ ଅବସ୍ଥିତ, ଯେପରିକି △ABCର ଅନ୍ତଃବୃତ୍ତକୁ \(\overline{\mathbf{XY}}\) ସ୍ପର୍ଶ କରିବ । ପ୍ରମାଣ କର ଯେ AX + XY+YA = AB + AC – BC |

Solution:
ଦତ୍ତ : △ABC ର ଅନ୍ତଃ ବୃ ତ୍ତ ବାହୁ ମାନ ଙ୍କୁ AB, BC, AC କୁ ଯଥାକ୍ରମେ P, Q, R ବିନ୍ଦୁ ରେ B ସ୍ପର୍ଶକରେ । △ABC ର AB ଓ AC ବାହୁ ଉପରେ X ଓ Y ଏପରି ଦୁଇରି ବିନ୍ଦୁ ଯେ XY, AABC Q ଅନ୍ତଃବୃତ୍ତକୁ M ବିନ୍ଦୁରେ ସ୍ପର୍ଶକରେ ।
ହ୍ମାଣ୍ୟ: AX + XY + YA = AB + AC – BC
ପ୍ରମାଣ: AB+ AC – BC

= AP + BP + AR + RC − (BQ + QC)
= (AX + XP) + BP + (AY + YR) + RC – BQ – QC
[ଦତ୍ତ XM = XP, YM = YR, BP = BQ 19° RC = QC]
= AX + XM + BQ + AY + MY + QC − BQ – QC
= AX + AY + (XM + MY) = AX + AY + XY
∴ AX + AY + XY = AB + AC – BC

Question 20.
ବହିଃସ୍ପର୍ଶୀ ଦୁଇଟି ବୃତ୍ତ S₁ ଓ S₂ ପରସ୍ପରକୁ P ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରନ୍ତି ।
ବୃତ୍ତଦ୍ଵୟର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ S₁ ଓ S₂ ବୃତ୍ତ ଦ୍ଵୟକୁ ଯଥାକ୍ରମେ A ଓ B ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରନ୍ତି । P ବିନ୍ଦୁ ଦେଇ ଅଙ୍କିତ ସାଧାରଣ ସ୍ପର୍ଶକ \(\stackrel{\leftrightarrow}{\mathbf{A B}}\) କୁ C ବିନ୍ଦୁରେ ଛେଦ କଲେ, ପ୍ରମାଣ କର :
(a) AC = BC ଏର୍ତ (b) m∠APB = 90° |

Solution:
ଦତ୍ତ : ଦୁଇଟି ବୃତ୍ତ ପରସ୍ପରକୁ P ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରନ୍ତି । ସାଧାରଣ ସ୍ପର୍ଶକ \(\stackrel{\leftrightarrow}{\mathbf{A B}}\), ବୃତ୍ତଦ୍ଵୟକୁ A ଓ B ବିନ୍ଦୁରେ ସ୍ପର୍ଶକରେ । P ବିନ୍ଦୁଗାମୀ ସ୍ପର୍ଶକ \(\stackrel{\leftrightarrow}{\mathbf{A B}}\) କୁ ‘C’ ବିନ୍ଦୁରେ ଛେଦ କରୁଛି ।
ପ୍ରାମଣ୍ୟ: (i) AC = CB (ii) m∠APB = 90°
ପ୍ରମାଣ : C ବହିଃସ୍ଥ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡ ଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ । ଅର୍ଥାତ୍ CA = CP |
ସେହିପରି ଅନ୍ୟ ବୃତ୍ତରେ CP = CB ∴CA = CB .. (i) (ପ୍ରମାଣିତ)
∵ CA = CP → m∠CAP = m∠CPA
∵ CP = CB → m∠CBP = m∠CPB
∴ m∠CAP + m∠CBP = m∠CPA + m∠CPB
⇒ m∠CAP +m∠CBP = m∠APB
⇒ m∠CAP+m∠CBP + m∠APB = 2m∠APB
⇒ 180° = 2m∠APB ⇒ m∠APB = 90° …(ii) (ପ୍ରମାଣିତ)

Question 21.
S₁ ଓ S₂ ବୃତ୍ତଦ୍ଵୟ ପରସ୍ପରକୁ A ଓ B ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । S₁ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ P ଦେଇ ଅଙ୍କିତ \(\overrightarrow{\mathbf{P A}}\) ଓ \(\overrightarrow{\mathbf{P B}}\) S, ବୃତ୍ତକୁ ଯଥାକ୍ରମେ C ଓ D ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । ପ୍ରମାଣ କର ଯେ P ବିନ୍ଦୁରେ S₁ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ, \(\overline{\mathbf{CD}}\) ସହ ସମାନ୍ତର ।
Solution:

ଦତ୍ତ : S₁ ଓ S₂ ବୃତ୍ତ ଦ୍ବୟ ପରସ୍ପରକୁ A ଓ B ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । P, S₁ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ । \(\overrightarrow{\mathbf{P A}}\) ଓ \(\overrightarrow{\mathbf{P B}}\), S₂ କୁ ଯଥାକ୍ରମେ C ଓ D ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।
ପ୍ରାମାଣ୍ୟ : \(\overleftrightarrow{\mathrm{XY}}\) || \(\overline{\mathbf{CD}}\)
ଅଙ୍କନ : \(\overline{\mathbf{AB}}\) ଅଙ୍କନ କର ।

ପ୍ରମାଣ : m∠XPA = m∠ABP (ଏକାନ୍ତର ବୃତ୍ତଖଣ୍ଡସ୍ଥ କୋଣ)
ପୁନଶ୍ଚ ABDC ଏକ ବୃତ୍ତାନ୍ତର୍ଲିଖତ ଚତୁର୍ଭୁଜ ।
∠ABP ଚତୁର୍ଭୁଜଟିର ବହିଃସ୍ଥ କୋଣ ।
ଏଠାରେ m∠ABP = m∠ACD
∴ m∠XPA = m∠ACD କିନ୍ତୁ ଏମାନେ ଏକାନ୍ତର ।
∴ \(\overleftrightarrow{\mathrm{XY}}\) || \(\overline{\mathbf{CD}}\) (ପ୍ରମାଣିତ)

Question 22.
ଦୁଇଟି ପରସ୍ପର ଅଣଛେଦୀ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ r₁ ଓ r₂ ଏକକ ଏବଂ r₁ > r₂ ବୃତ୍ତଦ୍ଵୟର କେନ୍ଦ୍ରଦ୍ଵୟ ମଧ୍ୟରେ ଦୂରତା d ଏକକ ହେଲେ ଏବଂ
(a) ଉଭୟ ବୃତ୍ତର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକର ସ୍ପର୍ଶବିନ୍ଦୁ A ଓ B ହେଲେ, ପ୍ରମାଣ କର ଯେ
AB² = d²(r₁ – r₂) ଏବଂ
(b) ଉଭୟ ବୃତ୍ତର ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ ସ୍ପର୍ଶକର ସ୍ପର୍ଶବିନ୍ଦୁ C ଓ D ହେଲେ, ପ୍ରମାଣ କର ଯେ CD² = d²(r₁ + r₂)²
Solution:
(a) ଦତ୍ତ : O ଓ P ଯଥାକ୍ରମେ S₁ ଓ S₂ ଦୁଇଟି ବୃତ୍ତର କେନ୍ଦ୍ରବିନ୍ଦୁ ଓ OP = d |
S₁ ଓ S₂ ବୃତ୍ତର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକର ସ୍ପର୍ଶବିନ୍ଦୁ
ଯଥାକ୍ରମେ A ଓ B|

OA = r, PB = r₂ , r₁ > r₂
ପ୍ରାମାଣ୍ୟ : AB² = d² – (r₁ – r₂)²
ଅଙ୍କନ : \(\overline{\mathbf{OA}}\) ଏବଂ \(\overline{\mathbf{PB}}\) ଅଙ୍କନ କର । \(\overline{\mathbf{PD}}\) ⊥ \(\overline{\mathbf{OA}}\) ଅଙ୍କନ କର ।
\(\overline{\mathbf{PD}}\) || \(\overleftrightarrow{\mathrm{AB}}\) ଅଙ୍କନ କର ।

ପ୍ରମାଣ : ADPB ଏକ ଆୟତକ୍ଷେତ୍ରର ପ୍ରତ୍ୟେକ କୋଣ ସମକୋଣ
∴ AD = PB = r₂
⇒ OD = OA – AD = r₁ – r₂ ଓ AB = PD
△ODPରେ m∠ODP = 90°
⇒ OP² = OD² + PD² (ପିଥାଗୋରାସ୍ ଉପପାଦ୍ୟ)
⇒ PD² = OP² – OD² ⇒ AB = d² – (r₁ – r₂)²

(b) ଦତ୍ତ: O ଓ P ଯଥାକ୍ରମେ S₁ ଓ S₂ ବୃତ୍ତର କେନ୍ଦ୍ରବିନ୍ଦୁ ଏବଂ OP = d |
S₁ ଓ S₂ ବୃତ୍ତର ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ ସ୍ପର୍ଶକ ଯଥାକ୍ରମେ S₁ ଓ S₂ ବୃତ୍ତକୁ C ଓ D ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରେ ।
OC= r₁, PD = r₂ ଓ r₁ > r₂ |
ପ୍ରାମାଣ୍ୟ : CD² = d² – (r₁ + r₂)²
ଅଙ୍କନ : \(\overline{\mathbf{OC}}\), \(\overline{\mathbf{PD}}\) ଅଙ୍କନ କର ।
\(\overline{\mathbf{PE}}\) || \(\overline{\mathbf{CD}}\) ଅକନ କର ଯେବେକି \(\overline{\mathbf{PE}}\)
\(\overrightarrow{\mathrm{OF}}\) କୁ E ବିନ୍ଦୁରେ ଛେଦ କରିବ ।

ପ୍ରମାଣ : CEPD ଏକ ଆୟତଚିତ୍ର (ପ୍ରତ୍ୟେକ କୋଣ ସମକୋଣ)
CE = PD = r₂
∴ OE = OC+CE = r₁ + r₂
OP = d (ଦତ୍ତ) ଓ PE = CD
m∠OCD = 90°, ∠CDP = 90°, m∠CEP = 90°
△OEPରେ OP² = OE² + PE² (ପିଥାଗୋରାସ୍ ଉପପାଦ୍ୟ)
∴PE² = OP² – OE²
⇒ CD² = OP² – OE² = d² – (r₁ + r₂)² (ପ୍ରମାଣିତ)

Question 23.
ଗୋଟିଏ ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଏବଂ P ବିନ୍ଦୁଗାମୀ ସ୍ପର୍ଶକ ରଶ୍ମିଦ୍ଵୟର ସ୍ପର୍ଶବିନ୍ଦୁ ଯଥାକ୍ରମେ Q ଏବଂ R | \(\overline{\mathbf{QR}}\) ଜ୍ୟାଦ୍ଵାରା ଛେଦିତ କ୍ଷୁଦ୍ରଚାପର ମଧ୍ୟବିନ୍ଦୁ S ହେଲେ, ପ୍ରମାଣ କର ଯେ, \(\overrightarrow{\mathrm{QS}}\) ଦ୍ଵାରା ∠PQR ସମଦ୍ବିଖଣ୍ଡିତ ହୁଏ |
Solution:
ଦତ୍ତ : ଗୋଟିଏ ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଏବଂ P ବିନ୍ଦୁଗାମୀ ସ୍ପର୍ଶକ ରଶ୍ମିଦ୍ବୟର ସ୍ପର୍ଶବିନ୍ଦୁ ଯଥାକ୍ରମେ Q ଏବଂ R । \(\overline{\mathbf{QR}}\) ଜ୍ୟାଦ୍ଵାରା ଛେଦିତ କ୍ଷୁଦ୍ରଚାପର ମଧ୍ୟବିନ୍ଦୁ S ।
ପ୍ରାମାଣ୍ୟ : \(\overline{\mathbf{QS}}\), ∠PORର ସମଦ୍ବିଖଣ୍ଡକ ।
ଅଙ୍କନ : \(\overline{\mathbf{SR}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : \(\overparen{\mathrm{QSR}}\) ଚାପର ମଧ୍ୟବିନ୍ଦୁ S |

⇒ \(\overline{\mathbf{QS}}\) ≅ \(\overline{\mathbf{SR}}\) ⇒ m∠SRQ = m∠SQR
\(\overline{\mathbf{PQ}}\) ଏକ ସ୍ପର୍ଶକ ଏବଂ \(\overline{\mathbf{QS}}\) ସ୍ପର୍ଶକ ବିନ୍ଦୁଗାମୀ ଜ୍ୟା ।
⇒ m∠POS = m∠SRQ (ଏକାନ୍ତର ବୃତ୍ତଖଣ୍ଡସ୍ଥ )
∴ m∠PQS = m∠SQR
ଅର୍ଥାତ୍ \(\overrightarrow{\mathrm{SQ}}\), ∠PORର ସମଦ୍ବିଖଣ୍ଡକ ।

Question 24.
ଚିତ୍ରରେ ଥିବା ବୃତ୍ତର AT ଏକ ବ୍ୟାସ । ବୃତ୍ତ ଉପରିସ୍ଥ ଅନ୍ୟ ଏକ ବିନ୍ଦୁ B । \(\overrightarrow{\mathrm{AB}}\) ଏବଂ I ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶକ ପରସ୍ପରକୁ P ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । B ବିନ୍ଦୁରେ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ \(\overleftrightarrow{ T P}\) କୁ ( ବିନ୍ଦୁରେ ଛେଦ କଲେ, ପ୍ରମାଣ କର ଯେ Q ବିନ୍ଦୁ ହେଉଛି PT ର ମଧ୍ୟବିନ୍ଦୁ ।

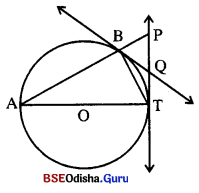
Solution:
ଦତ୍ତ : \(\overline{\mathbf{AT}}\) ବୃତ୍ତର ଏକ ବ୍ୟାସ । ABT ବୃତ୍ତ ଉପରିସ୍ଥ B ଏକ ବିନ୍ଦୁ |
\(\overrightarrow{\mathrm{AB}}\) ଓ T ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶ \(\overleftrightarrow{ T P}\) ର ଛେଦବିନ୍ଦୁ Q |
ପ୍ରାମାଣ୍ୟ : Q, \(\overline{\mathbf{TP}}\)ର ମଧ୍ୟବିନ୍ଦୁ ।
ଅଙ୍କନ : \(\overline{\mathbf{BT}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : ବହିଃସ୍ଥ ( ବିନ୍ଦୁରୁ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ଦ୍ଵୟ \(\overline{\mathbf{QB}}\) ଓ \(\overline{\mathbf{QT}}\) |
⇒ QB = QT
⇒ m∠QBT = m∠QTB
m∠ABT = 90° (∵ \(\overline{\mathbf{AT}}\) ବୃତ୍ତ ଏକ ବ୍ୟାସ)
m∠PBT = 90°
⇒ m∠PBQ + m∠QBT = 90°
ପୁନମ୍ନ m∠BTQ + m∠BPQ = 90°

⇒ m∠PBQ + m∠QBT = m∠BTQ + m∠BPQ
(: m∠QBT = m∠QTB)
⇒ m∠PBQ = m∠BPQ ⇒ BQ = QP
ପୁନମ୍ନ BQ = QT ⇒ QP = QT (ପ୍ରମାଣିତ)

Question 25.
ଗୋଟିଏ ବୃତ୍ତରେ \(\overline{\mathbf{AB}}\) ଏକ ବ୍ୟାସ । B ବିନ୍ଦୁରେ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଉପରେ C ଏପରି ଏକ ବିନ୍ଦୁ ଯେପରି \(\overline{\mathbf{CA}}\), ବୃତ୍ତକୁ D ବିନ୍ଦୁରେ ଛେଦ କରେ । ପ୍ରମାଣ କର ଯେ AB² = AC × AD |

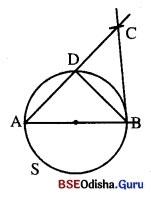
Solution:
ଦତ୍ତ : \(\overline{\mathbf{AB}}\), S ବୃତ୍ତର ଏକ ବ୍ୟାସ ।
\(\overrightarrow{\mathrm{BC}}\) ବୃତ୍ତପ୍ରତି B ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶକ C – D – A ଏକ ଛେଦକ ।
ପ୍ରାମାଣ୍ୟ : AB² = AC × AD
ଅଙ୍କନ : \(\overline{\mathbf{BD}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : BC ସ୍ପର୍ଶକ ⇒ ∠ABC = ସମକୋଣ
△ACBରେ AB² + BC² = AC² ⇒ AB² = AC² – BC²
ପୁନଶ୍ଚ CB² = CD · CA
⇒ AB² = AC² – BC² = AC² – CD · CA
= AC (AC – CD) = AC × AD (ପ୍ରମାଣିତ)

Question 26.
ଗୋଟିଏ ବୃତ୍ତରେ \(\overline{\mathbf{AB}}\) ଏକ ବ୍ୟାସ । B ବିନ୍ଦୁରେ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଉପରେ C ଓ D ଦୁଇଟି ବିନ୍ଦୁ ଯେପରି C-B-D | ଯଦି CA ଓ \(\overline{\mathbf{DA}}\) ଯଥାକ୍ରମେ ବୃତ୍ତକୁ P ଓ Q ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି, ପ୍ରମାଣ କର ଯେ AC × AP = AD × AQ |
Solution:
ଦତ୍ତ : \(\overline{\mathbf{AB}}\) ଏକ ବୃତ୍ତର ବ୍ୟାସ । B ବିନ୍ଦୁରେ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ \(\stackrel{\leftrightarrow}{C D}\) । AC ଓ \(\overline{\mathbf{AD}}\) ବୃତ୍ତକୁ P ଓ Q ବିନ୍ଦୁରେ ଛେଦକରନ୍ତି ।
ପ୍ରାମାଣ୍ୟ : AC × AP = AD × AQ
ଅଙ୍କନ : \(\overline{\mathbf{BP}}\) ଓ \(\overline{\mathbf{BQ}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : △APB ଓ △ABC ମଧ୍ୟରେ
m∠APB m∠ABC (ପ୍ରତ୍ୟେକ ସମକୋଣ)
m∠PAB = m∠BAC (ସାଧାରଣ କୋଣ)

⇒ △APB ~ △ABC (କୋ.କୋ, ସାଦୃଶ୍ୟ)
⇒ \(\frac { AP }{ AB }\) = \(\frac { AB }{ AC }\) ⇒ AB² = AP × AC …(i)
ସେହିପରି △ABQ ~ △ABD
AB² = AD × AQ …(ii)
∴ (i) ଓ (ii)ରୁ AP × AC = AD × AQ (ପ୍ରମାଣିତ)

Question 27.
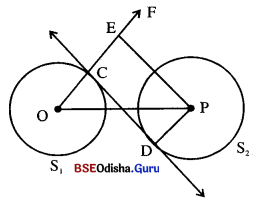
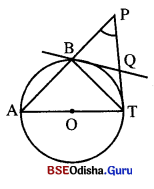
ଚିତ୍ରରେ S₁ ଓ S₂ ବୃତ୍ତ ଦୁଇଟି ବହିଃସ୍ପର୍ଶୀ ଏବଂ G ସେମାନଙ୍କର ସ୍ପର୍ଶବିନ୍ଦୁ । ବୃତ୍ତଦ୍ଵୟର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ରଶ୍ମି \(\overrightarrow{\mathrm{PX}}\) ଓ \(\overrightarrow{\mathrm{PY}}\) ଦ୍ଵୟର ସାଧାରଣ ମୂଳ ବିନ୍ଦୁ P | S₁ ଓ S, ବୃତ୍ତକୁ \(\overrightarrow{\mathrm{PX}}\) ଯଥାକ୍ରମେ C ଓ ଯ ବିନ୍ଦୁରେ ଏବଂ \(\overrightarrow{\mathrm{PY}}\) ଯଥାକ୍ରମେ D ଓ F ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରନ୍ତି ।
(a) ପ୍ରମାଣ କର :
(i) P, A, G, B ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ଓ
(ii) CE = DF

(b) ଉଭୟ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସାଧାରଣ ସ୍ପର୍ଶକ \(\overrightarrow{\mathrm{PX}}\) ଓ \(\overrightarrow{\mathrm{PY}}\) କୁ ଯଥାକ୍ରମେ M ଓ N ବିନ୍ଦୁରେ ଛେଦକଲେ, ପ୍ରମାଣ କର :
(i) PM = PN, (ii) MG = NG ।
Solution:
ଦତ୍ତ : S₁ ଓ S₂ ଦୁଇଟି ବହିଃସ୍ପର୍ଶୀ ବୃତ୍ତ ପରସ୍ପରକୁ G ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରନ୍ତି । ବୃତ୍ତଦ୍ୱୟର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ରଶ୍ମି \(\overrightarrow{\mathrm{PX}}\) ଓ \(\overrightarrow{\mathrm{PY}}\), S₁ ଓ S₂ ବୃତ୍ତକୁ ଯଥାକ୍ରମେ C ଓ E ଏବଂ D ଓ F ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରନ୍ତି । ଓ ବିନ୍ଦୁରେ ଅଙ୍କିତ ସାଧାରଣ ସ୍ପର୍ଶକ PX ଓ PY କୁ ଯଥାକ୍ରମେ M ଓ N ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । ବୃତ୍ତଦ୍ୱୟର କେନ୍ଦ୍ର ଯଥାକ୍ରମେ A ଓ B |

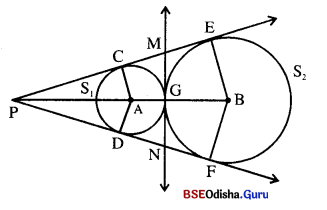
ପ୍ରାମାଣ୍ୟ : (a) (i) P, A, G ଓ B ସରଳରେଖାରେ ଅବସ୍ଥିତ । (ii) CE = DF
(b) (i) PM = PN, (ii) MG = NG
ଅଙ୍କନ : \(\overline{\mathbf{AC}}\) ଓ \(\overline{\mathbf{AD}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : PE = PD (ବହିଃସ୍ଥ P ବିନ୍ଦୁରୁ S₂ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡ)
ପୁନଶ୍ଚ PC = PD (ବହିଃସ୍ଥ P ବିନ୍ଦୁରୁ S₁ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡ)
∴ PE – PC = PF – PD ⇒ CE = DF (ପ୍ରମାଣିତ)
CM = MG ଏବଂ ME = MG ⇒ CM = ME
ସେହିପରି DN = NG ଏବଂ NG = NF
DN = NF, CE = DF (ପୂର୍ବରୁ ପ୍ରମାଣିତ)
⇒ 2 CM = 2 DN ⇒ CM = DN ….(i)
PC = PD = PC + CM = PD + DN → PM = PN
(i)ରୁ CM= DN →:MG = NG
(∵ MC = MG, DN = NG)
PM = PN (ପୂର୍ବରୁ ପ୍ରମାଣିତ)
⇒ m∠PMG = m∠PNG ⇒ m∠CMG = m∠DNG
ଦଇମାନ CAGM ଚତୁରିକରେ m∠ACM + m∠AGM = 180°
∴ m∠CMG + m∠CAG = 180° … (ii)
ସେହିପରି m∠DNG + m∠DAG = 180° …(iii)
m∠CMG + m∠CAG = m∠DNG + m∠DAG
m∠CAG = m∠DAG (∵ m∠CMG = m∠DNG)
m∠PAC = m∠PAD ….(iv)
(iv)ରୁ 2m∠CAG + 2m∠PAC = 360° ⇒ m∠CAG + m∠PAC = 180°
⇒ P, A, G ଏକରେଖ କିନ୍ତୁ A, G, B ଏକ ରେଞ୍ଜ
∴ P, A, G, B ଏକସରଳରେଖାରେ ଅବସ୍ଥିତ । (ପ୍ରମାଣିତ)

Question 28.
ପରସ୍ପର ଅନ୍ତଃସ୍ପର୍ଶୀ ଦୁଇଟି ବୃତ୍ତର ସ୍ପର୍ଶବିନ୍ଦୁ P । ଏକ ସରଳରେଖା ଗୋଟିଏ ବୃତ୍ତକୁ A ଓ B ବିନ୍ଦୁରେ ଓ ଅନ୍ୟ ବୃତ୍ତକୁ C ଓ Ð ବିନ୍ଦୁରେ ଛେଦ କରେ । ପ୍ରମାଣ କର ଯେ ∠APC ଓ ∠BPD ସର୍ବସମ । [A-C-D ଓ A-D-C ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ପ୍ରମାଣ ଯୋଗ୍ୟ ।
Solution:

ଦତ୍ତ : ପରସ୍ପର ଅନ୍ତଃସ୍ପର୍ଶୀ ଦୁଇଟି ବୃତ୍ତର ସ୍ପର୍ଶବିନ୍ଦୁ P । ଏକ ସରଳରେଖା ବୃତ୍ତଦ୍ଵୟକୁ ଯଥାକ୍ରମେ A, B ଓ C, D ବିନ୍ଦୁରେ ଛେଦକରନ୍ତି ।
ପ୍ରାମାଣ୍ୟ : ∠APC ≅ ∠BPD
ଅଙ୍କନ : P ବିନ୍ଦୁରେ ବୃତ୍ତପ୍ରତି ସାଧାରଣ ସ୍ପର୍ଶକ X – P – Y ଅଙ୍କନ କର ।
ମନେକର \(\overline{\mathrm{PC}}\)ର ଏକ ପାର୍ଶ୍ବରେ A ଓ X ଅବସ୍ଥାନ କରୁ ।
\(\overline{\mathrm{PA}}\), \(\overline{\mathrm{PD}}\), \(\overline{\mathrm{PC}}\) ଓ \(\overline{\mathrm{PB}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : ମନେକର A – C – D – B|
m∠DPY = m∠DCP (ଏକାନ୍ତର ବୃତ୍ତଖଣ୍ଡସ୍ଥ)
ସେହିପରି m∠BPY = m∠DAP
∴ m∠DPY – m∠BPY = m∠DCP – m∠DAP
⇒ m∠DPB = m(∠CAP + m∠APC) – m∠DAP
(∵ ବହିଃସ୍ଥ m∠DCP = m∠CAP + m∠APC)
= m∠CAP + m∠APC – m∠CAP = m∠APC
ସେହିପରି A – D – C – B ହେଲେ ପ୍ରମାଣ ଅନୁରୂପ ।

Question 29.
△ABC ର ଅନ୍ତଃବୃତ୍ତ, \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\) ଓ \(\overline{\mathrm{CA}}\) କୁ ଯଥାକ୍ରମେ P, Q ଓ R ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରେ । ଚିତ୍ରରେ BQ = 8 ସେ.ମି., CQ = 6 ସେ.ମି. ଏବଂ △ABCର ପରିସୀମା 36 ସେ.ମି. ହେଲେ, AB ଓ AC ନିର୍ଣ୍ଣୟ କର ।

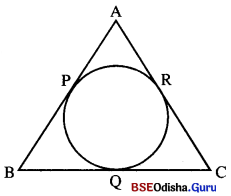
Solution:
ଦତ୍ତ : △ABCର ଅନ୍ତଃବୃତ୍ତ \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\) ଓ \(\overline{\mathrm{CA}}\) କୁ ଯଥାକ୍ରମେ P, Q ଓ R ବିନ୍ଦୁରେ ଛେଦକରେ ।
BQ = 8 ସେ.ମି., CQ = 6 ସେ.ମି.
△ABCର ପରିସୀମା = 36 ସେ.ମି.
ନିର୍ଦେୟ : BQ = 8 ସେ.ମି. ⇒ BP = 8 ସେ.ମି.
CQ = 6 ସେ.ମି. ⇒ CR = 6 ସେ.ମି.
ମନେକର AP = AR = x ସେ.ମି.
△ABCର ପରିସୀମା = 36 ସେ.ମି.
⇒ AP + PB + BQ + QC +CR + RA = 36
⇒ (x + 8 + 8 + 6 + 6 + x) = 36 ⇒ 2x + 28 = 36
⇒ 2x = 36 – 28 = 8 ⇒ x = \(\frac { 8 }{ 2 }\) = 4
∴ AB = AP + BP = 4 ସେ.ମି. + 8 ସେ.ମି. = 12 ସେ.ମି.
AC = AR + CR = 4 ସେ.ମି. + 6 ସେ.ମି. = 10 ସେ.ମି. |

Question 30.
ଗୋଟିଏ ବୃତ୍ତର କେନ୍ଦ୍ର O ଏବଂ ପରିଲିଖ୍ ଚତୁର୍ଭୁଜ ABCD ହେଲେ, ପ୍ରମାଣ କର ଯେ ∠AOB ଓ ∠COD ପରସ୍ପର ପରିପୂରକ । ∠B0C ଏବଂ ∠AOD ମଧ୍ୟରେ ଥ‌ିବା ସମ୍ପର୍କ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ଦତ୍ତ : ABCD ଚତୁର୍ଭୁଜ S ବୃତ୍ତର ପରିଲିଖ । ବୃତ୍ତର କେନ୍ଦ୍ର O |
gla: (i) m∠AOB + m∠COD = 180°
(ii) ∠BOC ଏବଂ ∠COD ମଧ୍ୟରେ ସଂପର୍କ ।
ପ୍ରମାଣ : m∠ABO = m∠CBO ⇒ m∠ABO = \(\frac { 1 }{ 2 }\) m∠B
m∠BAO = m∠DA0 ⇒ m∠BAO = \(\frac { 1 }{ 2 }\) m∠A
m∠OCD = m∠OCB ⇒ m∠OCD = \(\frac { 1 }{ 2 }\) m∠C
m∠ODC = m∠ODA ⇒ m∠ODC = \(\frac { 1 }{ 2 }\) m∠D

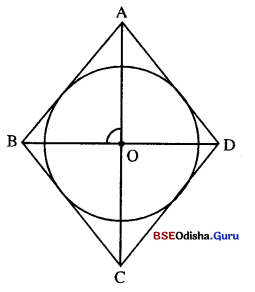
∴ m∠ABO + m∠BAO + m∠OCD + m∠ODC
= \(\frac { 1 }{ 2 }\) (m∠A + m∠B + m∠C + m∠D) = \(\frac { 1 }{ 2 }\) × 360° = 180°
ପୁନଶ୍ଚ m∠ABO + m∠BAO + m∠OCD + m∠ODC + m∠AOB + ∠COD = 180° + 180° = 360° …(ii)
∴ (i) ଓ (ii) ରୁ m∠AOB + m∠COD = 180° (ପ୍ରମାଣିତ)
ସେହିପରି m∠AOD + m∠BOC = 180° ଦେବ |

Question 31.
ଗୋଟିଏ ବୃତ୍ତର ଏକ ଜ୍ଯା \(\overline{\mathrm{AB}}\), ଏହି ବୃତ୍ତ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ P ଠାରେ ଅଙ୍କିତ ସ୍ପର୍ଶକ ସହ ସମାନ୍ତର ହେଲେ, ପ୍ରମାଣ କର ଯେ P ବିନ୍ଦୁଠାରେ \(\overparen{\mathbf{A P B}}\) ସମଦ୍ବିଖଣ୍ଡିତ ହୁଏ ।
ସମାଧାନ :
ଦତ୍ତ : ABP ବୃତ୍ତର AB ଏକ ଜ୍ୟା । P ଠାରେ \(\overline{\mathrm{AB}}\) ସହ ସମାନ୍ତର ଭାବେ ଅଙ୍କିତ ସ୍ପର୍ଶକ \(\overleftrightarrow{\mathrm{XY}}\), \(\overline{\mathrm{PB}}\)ର ଏକ ପାର୍ଶ୍ଵରେ X ଓ A ଅବସ୍ଥିତ ।
ପ୍ରାମାଣ୍ୟ : \(\widehat{\mathrm{AP}}\) ≅ \(\widehat{\mathrm{BP}}\)

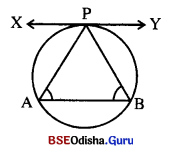
ଅଙ୍କନ : \(\overline{\mathrm{PA}}\) ଓ \(\overline{\mathrm{PB}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : m∠XPA = m∠PBA (ଏକାନ୍ତର ବୃତ୍ତଖଣ୍ଡସ୍ଥ)
m∠XPA = m∠PAB (ଏକାନ୍ତର କରେ)
⇒ m∠PBA = m∠PAB
⇒ \(\widehat{\mathrm{PA}}\) ≅ \(\widehat{\mathrm{PB}}\)

Question 32.
ଚିତ୍ରରେ ଥ‌ିବା ବୃତ୍ତର କେନ୍ଦ୍ର 0, L₁ ଓ L₂ ଦୁଇଟି ସ୍ପର୍ଶକ ଏବଂ L₁ || L₂ | ବୃତ୍ତର K ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶକ \(\stackrel{\leftrightarrow}{\mathbf{P Q}}\), L₁ ଓ L₂ କୁ ଯଥାକ୍ରମେ M ଓ N ବିନ୍ଦୁରେ ଛେଦ କରେ । ପ୍ରମାଣ କର ଯେ ∠MON ଏକ ସମକୋଣ ।

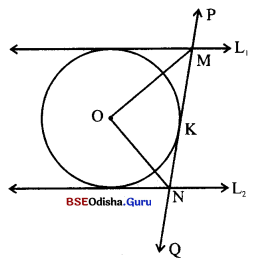
Solution:
ଦତ୍ତ : S ବୃତ୍ତର କେନ୍ଦ୍ର O,
L₁ ଓ L₂ ବୃତ୍ତପ୍ରତି ଦୁଇଟି ସ୍ପର୍ଶକ ଏବଂ L₁ || L₂| ବୃତ୍ତର K ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶକ PO
L₁ ଓ L₂ କୁ ଯଥାକ୍ରମେ M ଓ N ବିନ୍ଦୁରେ ଛେଦକରେ ।
ପ୍ଵାମଣ୍ୟ: m∠MON = 90°
ଅଙ୍କନ : \(\overline{\mathrm{CO}}\), \(\overline{\mathrm{DO}}\), \(\overline{\mathrm{OK}}\), \(\overline{\mathrm{MO}}\) ଓ \(\overline{\mathrm{NO}}\) ଅଙ୍କନ କର ।
L₁ ଓ L₂, S ବୃତ୍ତକୁ ଯଥାକ୍ରମେ C ଓ D ବିନ୍ଦୁରେ ସ୍ପର୍ଶକରୁ ।
ପ୍ରମାଣ : △OCM ଓ △OKMରେ
MC = MK. \(\overline{\mathrm{MO}}\) ସାଧାରଣ ବାହୁ ।
ଓ m∠OCM= m∠OKM (ସାଧାରଣ)
∴ △OCM = △OKM = m∠CMO = m∠OMK

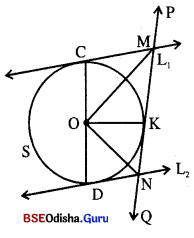
ସେହିପରି ପ୍ରମାଣ କରାଯାଇପାରେ ଯେ △OKN ≅ △ODN ⇒ m∠ONK = m∠OND L₁ || L₂, \(\stackrel{\leftrightarrow}{\mathrm{PQ}}\) ଛେଦକ ।
ତେଣୁ m∠CMK + m∠DNK= 180° ⇒ \(\frac { 1 }{ 2 }\) m∠CMK + \(\frac { 1 }{ 2 }\) m∠DNK = 90°
⇒ m∠KMO + m∠KNO = 90° …(i)
କିନ୍ତୁ m∠KMO + m∠KNO + m∠MON = 180°
90° + m∠MON = 180° [(i) ରୁ]
m∠MON = 180° – 90° = 90° (ପ୍ରମାଣିତ)