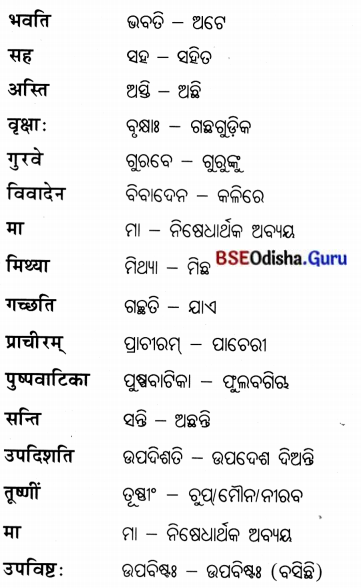
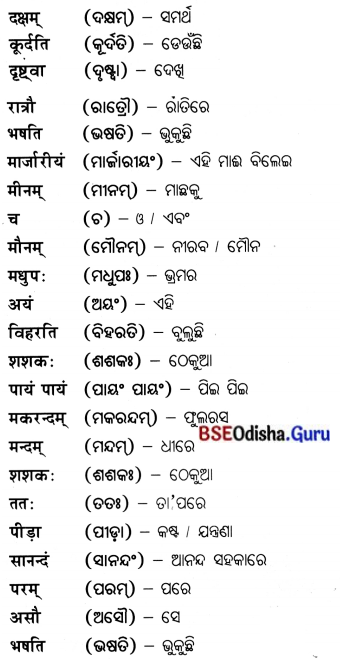
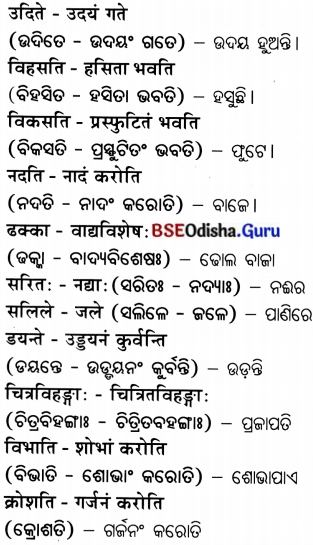
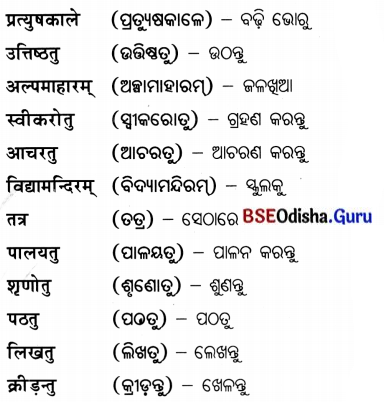
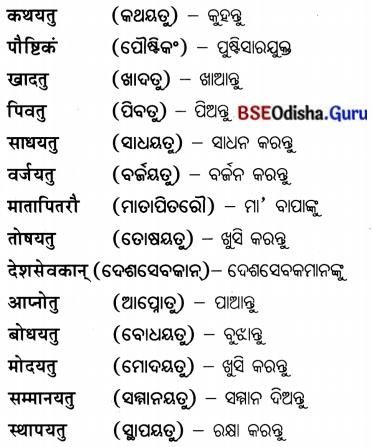
Odisha State Board CHSE Odisha Class 12 Economics Solutions Chapter 8 Market Questions and Answers.
CHSE Odisha 12th Class Economics Chapter 8 Question Answer Market
Group – A
Short type Questions with Answers
I. Answer within Two/Three sentence.
Question 1.
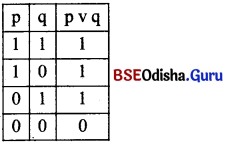
In perfect competition, price is uniform.
Answer:
In perfect competition, goods are hemogeneous & transacted among the large number of buyers & sellers. Neither the buyers nor the sellers have any influence over this. So, the price remains uniform.
Question 2.
Normal price is an imaginary price.
Answer:
Normal price is a long-run price determined by the interaction of supply of & demand for a goods. Since long-period is an imaginary concept, the normal price is conceived as an imaginary price.
Question 3.
Market price is real price.
Answer:
Market price is the price that prevails in the market & at this price goods are bought & sold. So market price is real price.
Question 4.
Normal profit is the part of the cost of production.
Answer:
Normal profit is determined in the long-run in which AR & MR becomes equal to AC at its minimum point. So it is part of the average cost of production.

Question 5.
Super-normal profit is generally earned in the short-run.
Answer:
In the short run, the entry of new firm is restricted. The existing firms lam super normal profit because of favirable cost condition & price structure. So it is a short-run phenomenon.
Question 6.
The supply in the market period is inelastic.
Answer:
The market period is a very short-period during which additional supply is impossible. So the supply in market period is quite inelastic.
Question 7.
Monopoly indicates absence of any type of competition.
Answer:
In monopoly, there is single seller/producer selling/producing a goods having no close substitutes. So, it indicates absence of competition.
Question 8.
Price discrimination is possible only under monopoly.
Answer:
Under monopoly, there is single seller selling a product having no close substitutes. So it is viable under this to change different prices at different places for the same product.
Question 9.
Mopoly price is higher than price under perfect competition.
Answer:
Unlike the perfect competition monopolist sell a product having no close substitute & it has sole control over the price & market. So to get more profit, monopolist can charge higher price.
Question 10.
Monopolistic competition is the blending of perfect compeition & monopoly.
Answer:
In monopolistic competition, there observed a mixture of competitive elements like large number of buyers & sellers, free entry & exit along with some monopoly element like product differentiation etc. So, it is the blending of perfect competition & monopoly.
Question 11.
Each seller under monopolistic competition is a monopolist.
Answer:
In monopplistic competition, each seller sells a product having no perfect substitute but having close substitute. So each seller is a monopolist of his own product facing a competition from its rivals producing close substitutes.
Question 12.
In perfect competition price of goods is uniform.
Answer:
Under perfect competition, the Homogeneous goods are bought & sold by the large number of buyers & sellers. Neither the buyers nor the sellers have any control over the price.
Question 13.
Demand curve under perfect cometition is perfectly elastic.
Answer:
Under perfect competition, the goods are homogeneous & price is uniform. So the demand curve is perfectly elastic.
Question 14.
Both the demand for & supply of product determine the price under competition.
Answer:
As per Prof. Marshal both the demand side as well as supply side of a goods are equally influential in determining the price under perfect competition.
Question 15.
Monopoly price is higher than the competitive price.
Answer:
Under monopoly, there is single seller selling a goods having no close substitutes & hence it has sole control over the price. But under perfect competition neither the buyers nor the sellers have any control over the price because of homogeneous goods & uniform price.
Question 16.
Under monopoly, there is no distinction between firm & industry.
Answer:
Under monopoly, there is only one firm & it also constitutes the whole industry. So there is no distinction between firm and industry.
Question 17.
Monopolistic competition is the mixture of both monopoly & perfect competition.
Answer:
The monopolistic competition bears some features of perfect competition & monopoly. Every seller firm under this market structure is a monopolist facing competition.
Question 18.
Normal price is a long-run price.
Answer:
Normal price is determined by the interaction of supply & demand in the long-run.
II. Answer within Five/Six sentence :
(A) WRITE SHORT NOTES ON :
Question 1.
Market:
Answer:
In Economics, the market is not related to a place rather it is associated with goods. Market consists of a group of buyers & sellers sufficiently close contact with each other that exchange takes place among them. Hence, market is formed with buyers & sellers. These buyers & sellers are sufficiently attached with each other for the exchange of goods. Broadly market is of two types i.e. perfectly competitive market & imperfect market. Further, imperfect market may be in form of monopoly, monopolistic competition, Oligopoly etc.
Question 2.
Perfect Competition:
Answer:
Perfect competition is said to prevails when there are large number of buyers & sellers exchanging a homogeneous goods at a uniform price without any restriction. A large number of buyers & sellers, homogeneous goods, free entry and free exit, uniform price, perfect mobility etc. are the prominent features of perfect competition. Under perfect competition, the demand curve is perfectly elastic. Neither the buyers nor the seller can influence the price of the product. Price stands as a given datum & all the sellers are the “price-takers”. Perfect competition is an ideal market structure but it is rarely found in real world.
Question 3.
Homogeneous Goods:
Answer:
Homogeneous goods are those goods which are indentical in all respect. All the goods are similar with regard to quality, quantity, size, packing etc. All are similar in nature. All these goods are perfect substitute for each other & hence all these can be used alternatively. The price of such goods is likely to be uniform & any change in price of it will lead to infinite change in quantity demanded.
Question 4.
Equilibrium:
Answer:
Equilibrium is a state of rest or balance. It is free from all sorts of fluctuation. In this situation, there will be no tendency on the part of the buyers or sellers to change the quantity of goods purchased or sold. All the economic variables are found to be stable and indicate no symptom of change. This situation is possible only when the economic agents derive the best. The economic forces are in balance & shows no tendency for change.
Question 5.
Equilibrium Price:
Answer:
Equilibrium price refers to that price at which quantity demanded of a goods equates to its quantity supplied. It is determined by the interaction of forces of demand & supply. When these two forces are balance with each other, the equilibrium price results. In this situation, both the buyers & sellers maximise their satisafaction. The buyers maximise their utility whereas sellers maximise thir profit. Any change in either demand or supply takes place , this equilibrium price is changed.
Question 6.
Market Price :
Answer:
Market price refers to that price which actually prevails in the market at a particular point of time. It is the real price at which the commodities are but & sold in the market at a particular span of time. This market price is determined by the equilibrium of forces of demand & supply. During this period supply is fixed. So the demand for the product plays the vital role in determining the price. Any change in price in this period happens due to the fluctuations of demand for the product. Thus, market price is constructed as the equilibrium price determined in a very short period in which supply of the commodity is fixed.

Question 7.
Normal Price:
Answer:
Normal price denotes that price which is expected to prevail to in the long-run. Hence it is called long-run price. This price is determined by the forces of demand & supply. Supply of the product can be fully adjusted to any change in its demand. Normal price is an imaginary price based on expectation. As such normal prices are not found in real world. According to Marshall, “Normal price is the price which tends to prevails in a market when full time is given to the forces of demand & supply to .adjust themselves.” It is the long-run equilibrium price of a commodity with supply adjusted to demand.
Question 8.
Monopoly:
Answer:
Monopoly is a market structure in which there exists a single seller selling a product having no close substitutes. Literary speaking ‘mono’ means one & ‘poly’ means seller. Thus, in monopoly there is only one seller who controls the entire market. This partnership or a joint stock company. Besides, the product in monopoly market does n’t have any close substitute. This product is a unique product.
Question 9.
Oligopoly:
Answer:
Oligopoly denotes an inperfect market in which a few sellers/producers selling/producing either homogeneous goods or differentiated goods. In this market there is a few sellers or producers. The product is either homogeneous or differentiated. The competition is restricted to the few sellers selling very close or perfect substitute. The oligopoly is of two types. In case the sellers deals with homogeneous product, it is called “pure oligopoly” & in case of differentiated product, it is called “differentiated oligopoly.”
Question 10.
Differentiated Product:
Answer:
The products which are slightly different from each other are called differentiated products. These products are close substitutes for each other but not perfect substitutes. In these products, there observed the least differences in respect of their quality, quantity, size, colour or packing. This type of product becomes the feature of monopolistic competition. This product differentiation makes this monopolistic competition as a seperate market structure.
Question 11.
Selling Cost:
Answer:
Selling cost is a special cost incurred by the producer in imperfect market to promote the sale of.its product. This cost takes the form of advertisement cost. It is incurred to inform the consumer about the various aspect of the product. It is spent to attract the new customer towards a particular product. This cost is usally spent in monopoly, monopolistic competition & oligopoly.
Question 12.
What is equilibrium price ?
Answer:
The price of a commodity is determined somewhere between the maximum limit (demand price) and the minimum limit (supply price). Naturally the customers will like to strike the deal as low as possible compared to the demand price and the sellers will try their best to get as high a price as possible compared to the supply price. The point at which the quantity demanded and the quantity offered balance each other shall be the deciding point. That price is, therefore, known as the ‘equilibrium price’.
Question 13.
Define equilibrium.
Answer:
Equilibrium refers to a point of rest or stage of no change. It is a state of balance between various economic forces. In other words it means no movement away from the present position. In economics the term is used in the context of a consumer, a producer, a firm or an industry etc. A consumer is said to be in equilibrium when he feels no urge to change his combination of things as long as circumstances are not changed. Similarly a firm is said to be in equilibrium when it has no tendency either to expand or to contract its output. It is a position when the firm earns maximum profits or minimum losses. The same is true of an industry. An industry consisting of a group of firms is said to be in equilibrium only when no firm has the tendency to enter Into it or leave out of it. An industry is considered to be in equilibrium when all firms are earning normal profits.
Question 14.
Define market price.
Answer:
Market price is the price of a product which prevails at any given time as a result of temporary equilibrium between demand and supply. It is a fluctuating price. It is influenced more by demand which is especially true in case of perishable goods. It may sometimes be below the cost of production.
Question 15.
Distinguish between short period and long period.
Answer:
Short period refers to a situation where the time involved is not too short as in market period nor too long as in long period. During short period supply cannot fully adjust to change in demand, because the fixed factors like plant and machinery cannot be changed at short notice. Hence, plant size remains unaltered. Production can be increased or decreased to some extent by changing the variable factors only. Demand forces play an important role in determining price in the short period. Firms may reap supernormal profits in the short period.
Under long period, however, supply can fully adjust to demand conditions as all factors are variable during this period. Sufficient time is available to change the plant size by changing the factor inputs. New firms may enter the industry or old firms may quit depending upon the demand conditions. Thus adjustment between supply and demand becomes possible. In the long period the cost of production plays a dominant role in determining price. Firms earn only normal profits in the ! long period.
(B) DISTINGUISH BETWEEN
Question 16.
Homogeneous Product & Differentiated Product.
Answer:
The product which is similar in all respect is called homogeneous product, but the product which is slightly different from other product of similar nature is called differentiated product. The quality, quantity, size, packing etc are identical in case of homogeneous product whereas there found slight differences in quality, quanity, size, packing etc in case of differentiated product.
The homogeneous product are perfect substitutes for each other whereas the ditferentiated product are close substitutes for each other.
The price of homogeneous goods is uniform but there is difference in price in case of differentiated product. The homogeneous goods are found in perfectly competitive market but the differentiated goods are found in monopolistic competition.
Question 17.
Monopoly & Monopolistic Competition :
Answer:
Monopoly is an extreme form of imperfect market in which there exist single seller; but in monopolistic competition there are many sellers.
In monopoly, the product does not have close substitute whereas in monopolistic competition the product has close substitutes.
A producer under monopoly faces no competition but a producer under monopolistic competition faces stif competition.
Entry of new is restricted under monopoly but there is free entry in case of monopolistic competition.. ‘
Price discrimination is possible under monopoly but it is not possible under monopolistic competition.
Question 18.
Market Price & Normal Price.
Answer:
Market price prevails in the market at a particular point of time whereas normal price is expected to prevails in the long-run.
Market price is the real price what the consumer actually pays but normal price is an expected imaginary price.
Market price prevails during very short-period but normal price is prevails during long-run Market price is highly fluctuating but normal price is some how-stable.
All the goods have market price but only the reproducible goods have the normal price.
Question 19.
Perfect Competition & Pure Competition:
Answer:
Perfect competition possesses the features like large number of buyers & seller, homogeneous goods, free entry & exit, perfect knowledge about the market, free mobility of the factors, no transportation cost etc. But pure competition covers only first three features of perfect competition.
Perfect competition is a broader concept whereas pure competition is a narrow concept. Pure competition is a part of the perfect competition.
Question 20.
Perfect Competition & Imperfect Competition.
Answer:
Under perfect competition, there exists a large number of sellers whereas under imperfect competition, the number of sellers may be limited.
There prevails uniform price in perfect competition but different prices are charged under imperfect competition.
The buyers are well-informed about the market but the buyers lack perfect knowledge in imperfect competition.
There is no selling cost in perfect competition but it is very much present in imperfect competition.
Group – B
Long Type Questions With Answers
Question 1.
What do you mean by perfect competition ? Discuss its important features & find out the difference between perfect competition & pure competition.
Answer:
Broadly, market is classified into perfect competition and imperfect market. Perfect competition is an extreme form of market which is not seen in reality. Perfect competition is said to prevail in the market in which a large number of buyers & sellers with an easy access to enter into & exit from the market make the exchange of a homogeneous goods at a uniform .price. In other words, a perfectly competitive market is that market in which a large number of buyers & sellers exchange a homogeneous goods at a uniform price. All these features exposed in the definition indicate that neither a buyer nor a seller can influence this market structure in any manner. It is considered to be an ideal market.
Features : The salient features of perfect competition are mentioned below :
(a) Large number of buyers & sellers : In perfect competition, there observed innumerable of buyers and sellers. One seller or buyer is treated to be one amongst many. So a buyer can not influence the demand for the goods because of such limitation. Similarly, an individual seller can not also influence the supply of the goods in the market. Both the buyers & sellers are compelled to accept the prevailing price in the market. They are the price takers.
(b) Free entry & free exit: In perfect competition, there is no restriction on the part of the buyers or sellers with respect to their entry into & exit from the market. They are quite free & independent to enter into the market at their own will or they may exit from the market when- evej desire. It is because of the large size of the buyers & sellers who may earn normal or abnormal profit. In case of normal profit, the sellers may not be encouraged to enter into or exit from the market – But in case of abnormal profit, the out-side sellers are encouraged to enter into the market. On the other hand, the buyers are also extremely free to go or to come to the market.
(c) Homogeneous Goods : The goods which are exchanged in the perfectly competitive market are homogeneous. The goods which are identical in quality, quantity, size, packing etc are called homogeneous goods. This goods are identical in all respect. In such a case the buyers do not reveal their preference for any particular goods. In another angle, the buyers will never pay different price for the same goods or the sellers can not charge different price for the same good.
(d) Perfect knowledge about the market: The buyers in such market are completely aware of the market structure & condition. The buyers gather information about the type of goods & price of the goods. Similarly, the sellers are also quite aware of the market condition. Under this situation, bargaining about the price becomes a futile exercise on the part of the buyers or sellers.
(e) Perfect mobility of factors : The factors in this market are perfectly mobile. Mobility refers to easy & free movement from one place to another. As such, the factors can freely move from one place to another if there occurs imbalance between demand & supply. This feature leads to create a uniform price all over the market.
(f) No Transport Cost: As the product & price are uniform in perfect competition, there will be absense of transport cost. With the addition or inclusion of transport cost, the price of the product shall never be uniform rather it will vary from place to place. All these features indicate the prevalence of uniform price in perfect competition. So uniform price of the product is a derived feature in perfectly competitive market. All the buyers & sellers are forced to exchange the goods at this unifom price.
Difference between Perfect competition & pure competition:
E.H. Chamberlin, a noted American economists made the distinction between perfect competition & pure competition. According to him, perfect competition is a broader concept & pine competition is a narrower concept & it is a part of the perfect competition.
Pure competition possesses the features like a large number of buyers & sellers, free entry & exit, homogeneous goods along with uniform price. But perfect competition possesses all the features as mentioned above. Hence, pure competition is a part of the compehensive perfect competition. Though perfect competition is an ideal market, it is never found in the real world. It is an imaginary concept which has only theoretical validity.

Question 2.
How is the “Equilibrium Price” determined in the perfectly competitive market ?
Answer:
Perfectly Competitive Market or perfect competition is an ideal market in which a large number of buyers & sellers participate in exchange a homogenous goods at a uniform price without any restriction. The features of perfect competition reveal a uniform price which can not be challenged either by the buyers or the sellers. The price is uniform & it is same for all. So it is very much essential to determine the policy or process of price determination under perfect competition. .
The principle of price – determination under perfect competition was a controversial & debatable issue for the economists before the arrival of Alfred Marshall. Before Marshall, there was a dispute among the economists regarding this. One group of economists argued that the price under perfect competition can alone be determined by the demand-side & other group emphasised on the supply- side as the sole determinant. But Marshall outrightly rejected these two notions & enunciated that neither the demand side nor the supply side of the product can alone determine the price. Rather both the sides are equally Important for the price-determination under perfect competition. In case of absence of any one of the sides, the price can not be determined.
According to Marshall’s view, the price under perfect competition can be determined through the simultaneous interaction of the demand-side as well as the supply-side of the product. The equilibrium price can be determined at that level when the demand for goods is equal to supply of goods. Thus, equilibrium price is that price where the quantity demanded of a good is equal to the quantity supplied of it. As such, for the equilibrium price under perfect competition, the demand must coincide with the supply of goods.
Keeping the Marshallian concept in view, it is required to analyse both the demand -side as well as supply-side of the determination of price under perfect competition.
Demand Side :The demand for any product is the function of price. It is guided by the “Law of Demand”. According to this law, in an unchanged situation, more is demanded at lower prices & less is demanded at higher price. As such, there exists inverse relationship between price of a goods and quantity demanded. The demand-curve, thus, has a negative slope.
Supply – Side : The supply of a product is also a function of price. But unlike to demand- side, there exists direct functional relationship between price of a goods & its quantity supplied. As stated in law of supply,, more is supplied at higher price & less is supplied at lower price. Hence, the supply curve has a positive slope & it slopes upward from left to right.
Interaction : The determination of equilibrium price can be made by the interaction of demand side as well as supply-side. This interaction is mentioned below with the help of numerical analysis & graphcial analysis.
Numerical Analysis
| Price (in Rs.) |
Quantity Demanded (in units.) |
Quantity Supplied (in units) |
| 10 |
90 |
50 |
| 20 |
80 |
60 |
| 30 |
70 |
70 |
| 40 |
60 |
80 |
| 50 |
50 |
90 |
The above schedule is a numerical explanation of the interaction between supply-side & demand side for the product. In the schedule, the range of the price varies from Rs 10 to Rs 50 where as the range of the demand & supply varies from 50 units to 90 units. The demand-side in the schedule exhibits that when the price of the product rises from Rs 10 to Rs. 50, the quantity demanded of it decreases from 90 units to 50 units. It just describes the inverse relationship between the price of the product & its quantity demanded. On the other hand, with the rise in the price from Rs. 10 to Rs.50 the quantity-supplied of the product increases from 50 units to 90 units. It is just the direct relationship between price & quantity supplied of a product.
Further, it is also revealed that both the demand for & supply of the product, interacting with each other becomes equal when price is Rs.30. At this price, demand for the product & supply of the product are found to be 70 units each. So, the Price Rs.30 is accepted as “equilibrium price” as per Marshall’s assertions. The same analysis can be made with the help of a graphical illustration which is as follows :
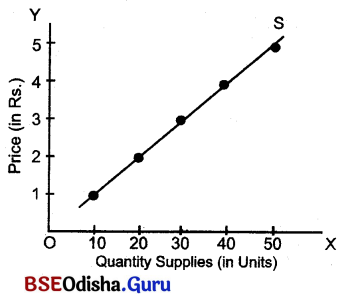
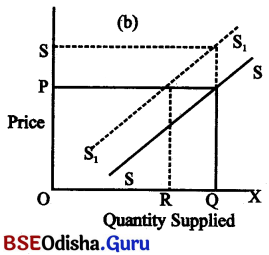
Graphical analysis:
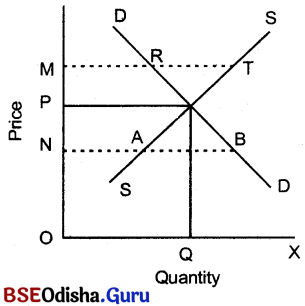
The above diagram measures quantity demanded & supplied of the product on OX-axis & price of the product on OY-axis.
The figure illustrates the downward slope (negative slope) of the demand curve (DD) & upward slope (positively slope) of the supply curve (SS). Both the demand curve & supply curve meet at point E resulting equilibrium price, OP. This point of intersection (E) results from the interaction of both the demand-side & supply-side. So in Marshallian framework, P is the equilibrium price & OQ is the equilibrium quantity that represents both the demand for & supply of the product. Justification of Equilibrium Point (E) :
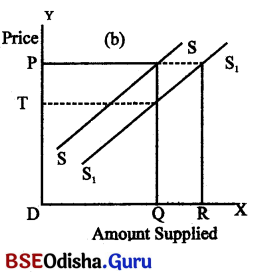
Equilibrium denotes a state of rest or balance. At point E, the demand for the product equals to supply of the product & it is believed that this situation is free from fluctuation. To establish this, the price deviation may be made.
If equilibrium price (OP) becomes higher i.e. OM, the quantity supplied exceeds the quanity demanded to the extent of RT. This excess amount remains unsold unless the price gets reduced. So the sellers will be forced to reduce the price. This price reduction will continue till OP is restored. On the other hand, if the price falls to ON, there shall be excess demand to the extent of AB: So the buyers will compete with each other for the goods. As such, the sellers will be encouraged to raise the price & ultimately ‘OP’ price will be restored.
Thus, it is affirmed the ‘OP’ price is the equilibrium price. Neither OM nor ON loses its validity to be the equilibrium price. Hence, the price ‘OP’ is justified as equilibrium price.
Question 3.
What is normal price ? How can it be determined ?
Answer:
Normal price is an ideal price which is determined in the long-run through the interaction of demand for & supply of the product. It is other wise called long-run price. Normal price is determined at that level where the equilibrium between demand for & supply of a product is confirmed. In other words, it is determined at that level where demand for product is equal to supply of product.
It is a fact that long-period is a period during which all the factors are found to be variable & hence there is every possibility of full adjustment of supply to any change in demand for product. In the long-run, supply can be increased to any extent to match with the increase in demand.
With all the features of long-run, the normal price prevails. According to Marshall, “Normal value of a commodity is that which economic forces would tend to bring about in the long-run. Thus, normal price is viewed as that price to which one may expect actual prices to tend. It is not same thing as average price till price is constant.”
Like the price-determination in general, the normal price is also determined by the forces of demand and supply. The real force behind the demand is the marginal utility of the commodity whereas on the supply-side, it is the cost of production. In the long-run, as the supply can be fully adjusted to increase in demand, the supply-side plays the vital role in the long-run while determining the price. In the long-run, there is also no distinction between fixed cost & variable cost. All the costs are variable & undergo change with the change in the level of output. Besides, all these costs incurred are covered up & hence price in the long-run (Normal Price) is equal to average cost in the long-run. There is no question of earning abnormal profit nor incurring abnormal loss because of free entry & exit of firms. So, the price is equal to long-run average cost resulting in normal profit.
The process of price determinination in the long-run is illustrated with the help of diagram which is presented below :
Graphical Analysis:
In the figure, demand for & supply of the product is reflected on OX-axis & price on OY-axis.
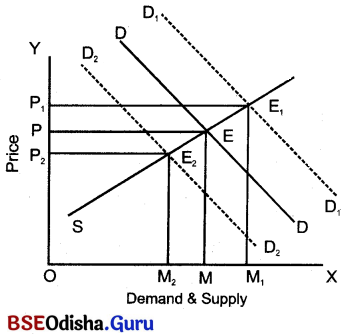
The DD & SS are the demand curve & supply curve respectively. Demand curve (DD) & supply curve (SS) take traditional shape. DD has negative slope & SS has the positive slope.
The demand curve (DD) intersects supply curve (SS) at point E resulting in price OP & quantity (OM). Suppose demand curve (DD) curve shifts upward to D1D1. This new demand curve (D1D1) cuts the supply curve at point E1 & new price will be OP1 & quantity OM1, This price (OP1) is greater than the previous price (OP). On the contrary, if demand decreases, the demand curve is D2D2. This demand curve (D2D2) cuts the supply curve at point E2 resulting price (OP2). This new (OP2) price is less than the previous price (OP).
The above analysis reflects that any change in demand is matched by adequate change in supply. Hence OP1 & OP2 are the normal price determined under the full adjustment of demand-side with supply side. All these prices are equilibrium price determined by equating demand & supply of the product. An increase in demand leads to higher price & decrease in demand leads to lower price. Hence supply is adjusted fully with demand. All these expressed above are the situations that happen in the long-run. So all these prices are stable price determined by the long-run equilibrium of demand & supply of the product.
Question 4.
Explain the market price & Normal Price. What are the differences between Market Price & Normal Price.
Answer:
On the basis of time elements of Marshall, time period can be classified into market period, short period & long-period. Thus, the price determined in the market period, short-period or long-period can be called as market price, short-run price & long-run price (Normal price). respectively. Market price & Normal price are the two level of price of a goods prevailing at two different time periods i.e. market period & long period.
Market price refers to that price which actually prevails in the market at a particular point of time. It is the real price at which the commodities are bought & sold in the market at a particular span of time. This market price is determined by the equilibrium of forces of demand & supply. During this period supply is fixed. So the demand for the product plays the vital role in determining the price.
Any change in price in this period happens due to the fluctuations of demand for the product. Thus market price is construed as the equilibrium price determined in a very short period in which supply of the commodity is fixed.
Normal price denotes that price which is expected to prevail to in the long-run. Hence it is called long-run price. This price is determined by the forces of demand & supply. Supply of the product can be fully adjusted to any change in its demand. Normal price is an imaginary price based on expectation. As such normal prices are not found in real world. According to Marshall, “Normal price is the price which tends to prevails in a market when full time is given to the forces of demand & supply to adjust themselves.” It is the long-run equilibrium price of a commodity with supply adjusted to demand. The noteworthy differences between market price & normal price are described below:
DIFFERENCE BETWEEN MARKET PRICE&NORMAL PRICE:
(a) Time element: Market price refers to that price which prevails in the market period (very short period). But the normal price is that price which is expected to prevail in the long-run. (long period)
Thus, market price prevails during a point time where as normal price prevails over a period of time.
(b) Real price & Imaginary Price : Market price is said to be the real price that rules in the market. The commodities are bought & sold in the market at this price. It is uniqe & uniform price what the purchase actually pays.
On the other hand, Normal price is an imaginary price expected to prevail in the market in the long run. It is a probable price based on an imaginary impression of long-run equilibrium of demand & supply. Its prevalene in the market is questionble.
Thus, market price is real price whereas the normal price is an imaginary price based on guess mark.
(c) Stability : Market price is not a stable price. It is highly fluctuating on account of frequent changes in demand. This fluctuation takes place due to temporary changes in the market.
But normal price is a stable price. Because the temporary events hapens in market period that naturalise each other in the long-run. The price comes to be settled at a particular level. So market price is found to be fluctuating but normal price is observed to be stable.
(d) Relative influence of demand & supply : Market period is a very short period during which supply of the commodity is fixed. So, in case of market price, demand plays the dominant role in determining it. Any fluctuation in market price is due to the change in the factors of demand as supply remains as a neutral component.
In case of normal price, it is determined by the long-run equilibrium of demand & supply. As all the factors are variable,, supply of the commodity can be fully-adjusted to change in demand to any extent. Supply of the commodity is quite flexible. In this case, supply-side plays the significant role.
(e) Relationship with cost of production : Market price is the price prevailed in the market period during which supply is fixed. As such market price does not have any relevance to the cost of production. In the determination of market price, demand-side is dominant which is guided by consumers, behaviour. Henqe market price is no way related to the cost of production.
On the other hand, supply-side plays the dominant role in determining the normal price. Supply is greatly influenced by the cost of production. So price in the long-run is somehow related to the cost of production. It must be equal to average cost of production. If it is more than the average cost, there shall be abnormal profit which attracts new producers. This new entry brings back the price to normal. Similarly, if the price is less than the average cost, there shall be abnormal loss for which existing producers will leave. This exit will bring back the normal price. Thus, market price is not related to cost of production,but normal price is related to it.
(f) Relevance to kinds of Goods : Market price is the price which prevails in the market. So all the commodities whether producible or non-reproduciable have market price. But only the reproducible goods have normal price. Hence rare paintings, old coins, ancient arts do not have normal price but those goods have market price.
(g) Emergence of Profit Loss : Market price is not associated with the cost of production. So the producer may earn super normal profit by charging higher price or may incur loss. But normal price always assures normal profit which is a part of the cost of production.
The above analysis affirms that market price is real price & the consumers are to rely on it. In real world, the market price is emphasised as the goods are bought & sold with this price. But normal price is an imaginary price which is expected in the 16ng-run. Long-run is a long period which is not categorically marked. So normal price is exclusively a theoretical concept which is not valid in the real world.

Question 5.
What is monopoly ? Explain the features of monopoly.
Answer:
Monopoly is a market structure in which there exists a single seller selling a product having no close substitutes. Literary speaking ‘mono’ means one & ‘poly’ means seller. Thus, in monopoly there is only one seller who controls the entire market. This may be a partnership or a joint stock company. Besides, the product in monopoly market does n’t have any close substitute. This product is a unique product.
FEATURES :
(a) Single seller & Innumerable buyers : Under monopoly, there is only seller who deals with a large number of buyers. This single seller dominates all over the market. This single seller may be in form of an individual or partnership or joint stock company. A large number of buyers in such market are to depend on this single seller.
(b) No close substitutes : The product exchanged in this market is unique. It does not have any close substitute. So no good can be substitute for this good. Non-availability of any close substitute makes the seller supreme & he may charge any price keeping the demand for the product in view. So under monopoly, higher price is very often charged.
(c) Free entry is restricted : In the monopoly, the entry of new sellers firm is completely ruled out. There is no scope for other sellers to reign over the market. This single seller is considered as the sole supplier or dealer of the product. There is no rival of it.
(d) Price discrimination: Under monopoly, there observed price discrimination. The monopolist can discriminate the price. Price-discrimination occurs when seller charges different prices from different buyers for the same good. As under monopoly, there is only one seller, he has ample scope to discriminate the price by keeping the demand for goods in view.
(e) Selling Cost: The monopoly incurs selling cost towards the advertisement. By spending this amount, the monopolist makes the consumers aware of the product & also informs the consumers about the quality & nature of product.
(f) Independent decision : Being a sole seller the monopolist takes his own decision regarding his business. It fixes the price of his product independently. He is the ‘price-maker’ very often it changes higher price & imposes a burden on the consumer.
(g) Demand Curve : Under monopoly, demand curve or avarage revenue curve slopes downward from left to right. It indicates that whenever a monopolist wants to sell more, he is to reduce the price & incase of higher price, he is to reduce the sale. Thus, the average revenue curve as well as marginal revenue curve slopes downward from left to right.
(h) Profit & Loss : It is not always true that monopolist earns super normal profit. Though a monopolist very often earns super normal profit by manipulating the supply of goods, yet it sometimes incurs loss because of insufficient demand for the product. If the demand for the product becomes inadequate, the monopolist incurs loss. So profit & loss also arise under monopoly.
Question 6.
Make a comparative analysis of perfect competition with monopoly.
Answer:
On the basis of the relative strength of competitive aspects in the market, market may be view as perfectly competitive market & imperfect market. Perfectly competitive market (perfect competition) market is constituted with a large number of buyers & sellers making the exchange of a homogeneous goods at a uniform price without any restriction to their entry & exit. In this market, no buyer nor seller has control over the market in influencing it. On the contrary, monopoly is a market structure comprising of a single sellerselling a product having no close substitute. Hence, this single seller has sole authority & control over the entire market & the price charged is not also uniform.
The critical analysis of both the extreme forms of market dictates certain similarities and disimilarities. The important concepts in this regard are describe below :
SIMILARTIES : Both the perfect competition & monopoly have certain common characters.
(a) Common goal: Both monopolist & perfectly competitive firm have a common goal. The seller or producer in both the market structures pursues to maximise its profit. So profit maximisation becomes the common goal or objective in perfect competition & monopoly.
(b) Perfect Knowledge : Under monopoly & perfect competition, the buyers & seller gather perfect information about the market, product & price. All the buyers & the seller (in monopoly single seller) are completely aware of the market condition & accordingly they behave for the maximisation of profit.
DISSIMILARITIES : Along with these similarities, there are number of dissimilarities between these market structures.
(i) Goods : The first & foremost difference between these two market is about the goods exchanged. In perfect competition, the goods are identical in all respect i.e. same in quality, quantity, size, packing etc. & hence the goods re homogeneous. In other words, under perfect competition the goods are perfect substitute for each other. On the other hand, under monopoly, the goods does not have any close substitute. The goods exchanged is unique & no other good can be substitute for it.
(ii) Number of buyers & sellers : Though the number of buyers in both the markets are innumerable, yet there is spectacular difference over the number of sellers. In perfect competition there is a large number of sellers selling a product. There is a large number of sellers in perfect competitive market. No individual seller has its own influence in the market. But, in monopoly, there is only one seller which can form the entire market. He has the sole authority or control over the market. He himself deals with the product & it is treated to be the single supplier. This single seller may be an individual, partnership or joint stock company.
(iii) Entry : In perfect competition, there exists free entry & exit in respect of the firms or selles. The buyers & sellers are free to enter into the market & they also leave the market at their own will.
On the other hand, this free entry & exit are quite banned under monopoly. As a single seller forms the market, the entry & exit are not possible. Thus entry & exit are restricted under monopoly.
(iv) Price : In perfect competition, price is uniform because of its inhertied features. Neither the buyers nor the sellers can influence the price. Price stands as a constant entity which is universally accepted.
But under monopoly, the price is not uniform. The monopolist can change prices to different buyers at different times. Besides it monopolist desires to sell more, he may reduce the price or if wants sell less, he may change higher price. As such the price is quite a variable concept.
(v) EquiHbrium Price & Output: In perfect competition, the equilibrium price is less than that of under monopoly. On the other hand, the equilibrium output in perfect competition is found to be higher than that of monopoly.
(vi) Price Discrimination : As the price is uniform in perfect competition, there is no scope for price-discrimination. A uniform price is changed & is same for all the buyers. But monopolist practise price-discrimination. He can charge different prices to different buyers for selling the same quantity of a commodity. This is not possible in perfect competition.
(vii) Demand Curve : The demand curve for an individual seller in perfect competition is found to be a horizontal straight line. It shows that the demand is perfectly elastic. But under monopoly, the demand curve slopes downward from left to right indicating that more is sold at lower price & vice-versa.
From the above analysis, its observed that the perfect competition & monopoly are two extreme forms of market. They possess certain distinct different features. Though these market structure seem to be theoretically valid, there are rarely structure seem to be theoretically valid, there are rarely found in real world.
Question 7.
What is Monopolistic Competition ? State its features.
Answer:
The concept of monopolistic competition is a joint contribution of E.H. Chamberlin & Joan Robinson. Both the economists treat this special market structure as a blending of perfect competition & monopoly. They term it as “Imperfect competition.”
Monopolistic competition is a market structure in which there are many sellers of a particular product but the product of each seller is in some way differentied in the minds of the consumers from the product of every other seller.
Simply speaking, monopolistic competition is a mixture of perfect competition & monopoly in which a large number of buyers & sellers exchange a differentiated product. Here the goods are not perfect substitute as in perfect competition rather close substitutes. Unlike monopoly, the goods is not unique rather close substitutes for each other. The monopolistic competition embraces some features of perfect competition & some features of monopoly. Thus, it is a combination of both these extreme forms of market & expressed in a unified manner.
In a single statement, it can be expressed that monopolistic competition is said to exist when a large number of sellers sell a slightly differentiated product to large number of buyers & enjoy a freedom of entry & exit. It is a competition amongst number of sellers selling close but not perfect substitutes.
FEATURES:
(i) A Large number of buyers & sellers : In monopolistic competition, there found sufficiently large number of buyers & sellers. There is no feeling of mutual inter-dependence among them. Thus, all the participants are quite independent &• activity take part in exchange of goods.
(ii) Product differentiation : Another unique feature of monopolistic competition is the product differentiation. The products are not homogenous nor unique as in perfect competition or in monopoly. The product is slightly differentiated so that these seem to be similar but they are close substitutes instead of perfect substitutes. The degree of differentiation describes the presence of competitive elements & monopoly elements. Thus, in this market, each is a monopolist & each is a competitor.
(iii) Free entry & free exit: Like perfect competition there found freedom of entry & exit in respect new firms/sellers. The entry & exit are permissible. The seller interested in selling the similar product may enter into the market freely & may leave it freely.
(iv) Selling cost: Selling cost is the cost incurred by the producer /seller to promote the product. As the products are close substitutes, there needs to provide certain eye catching information by the way of advertisement. It can attract the new consumer towards a particular brand. It is quite a non-product cost incurred in monopolistic competition.
(v) Price-Policy : The theory of monopolistic competition has its own price-policy. This policy is certainty different from that of perfect competition & monopoly. Neither the perfect competition nor the monopoly can provide an adequate explanation for price determination under monopolistic competition. It is because these are two mutually exclusive alternatives.
(vi) Imperfect Knowledge : Unlike perfect competition, the buyers are not completely aware of the nature & quality of the product. Hence, in monopolistic competition, the producer is able to create an imaginary superiority about the product in the minds of the consumer. For this the producer spends a lot in form of advertisement cost.
(vii) Non-Price Competition: In monopolistic competition, the non-price competition is quite visible. This non-price competition is also inevitable for each producer in order to promote their sale. This competition is visible in the form of warranty free, services, discount, free exchange etc.
All are the features of monopolistic competition. It quite revels that monopolistic competition is quite a new market structure which contains certain distinct features. Though it embraces the features of perfect competition & monopoly, yet it can be rightly told that monopolistic competition opens a new chapter in the theory of market.

Question 8.
What is monopolistic competition ? Compare it with the perfect competition.
Answer:
Monopolistic competition is a market structure in which there are many sellers of a particular product but the product of each seller is in some way differentied in the minds of the consumers from the product of every other seller. Simply speaking, monopolistic competition is a mixture of perfect competition & monopoly in which a large number of buyers & sellers exchange a differentiated product. Here the goods are not perfect substitute as in perfect competition rather close substitutes. Unlike monopply, the goods is not unique rather close substitutes for each other. The monopolistic competition embraces some features of perfect competition & some features of monopoly. Thus, it is a combination of both these extreme forms of market & expressed in a unified manner.
COMPARISION :
Monopolistic competition contains certain features of perfect competition like a large number of buyers & sellers “free entry & exit” etc. Besides these, there observed several points of difference between price & output decision & other aspects under perfect competition & monopolistic competition.
(i) Kinds of Goods : In perfect competition, the goods are homogeneous. They are identical in all respects so that all the goods act as perfect substitutes for each other. The quality, quantity, size & packing are similar in all respect.
But under monopolistic competition, there found “product differentiation”. The products are not perfect substitutes for each other rather there are close substitute. The products under monopolistic competition are slightly different from each other so that these goods can not be taken as identical or homogeneous goods.
(ii) Price : Under perfect competition, price of the goods remains uniform. All goods are exchanged at that uniform price. Neither the seller nor the buyer can influence this price. All the sellers or buyers are the “price-takers” but not the “price-jmaker”.
On the other hand, under monopolistic competition, price does not remain uniform because of interdependence of firms/sellers. The sellers /firms independently determines the price keeping the supply demand for its product in view. While determining price-policy, the seller/firm carefully analyses the rivals reaction. As the products are close substitutes, each seller / firm is a competitor as well as a monopolistic for his own product
(iii) Non-Production cost: Under perfect competition, the goods are homogenous & hence these are similar in all respect. Besides, the consumers are well informed about the market & product. Hence, there is no need of incurring non-production cost to promote the sale.
On the contrary, under monopolistic competition, the products are the close substitutes & the consumers are not well informed. Hence, the producer is compelled to incure non-production cost on warranty, free service etc. Thus, the non-production cost is visible in this market which is not in perfect competition.
(iv) Selling Cost: The selling costs are the costs which are incurred by the producer to provide information about the product to the consumer. This cost is spent on advertisement & hence it is also called advertise cost.
Under perfect competition, no such cost is incurred as the products are homogeneous & the consumers are folly aware of the market structure. But under monopolistic competition, the products are slightly differentiated. Each producer has its own competitors and every producer is also a monopolist of his own product. As such, the producer is to spend on advertisement.
(v) Relation with cost of production & revenue : Under perfect competition, price concide with average revenue, marginal revenue as well as average cost in the long run. But under monopolistic competition, price is equal to average revenue but it is greater than the marginal revenue.
(vi) Demand Curve : Under perfect competition, an individual firm faces with a perfectly elastic demand, curve which is a horizontal straight line. In this case, price of the product is equal to average revenue as well as marginal revenue. On the contrary, a firm under monopolistic competition faces a downward sloping demand curve. In this case price is equal to average revenue but greater than marginal revenue.
(vii) Excess capacity : Under perfect competition, the firm produces socially optimum output in the long-run. Hence, no excess capacity is realised because firm produces at the minimum point of long-run average cost.
But it does not happen under monopolistic competition. In this market, a firm produces the output at the falling portion of the average cost curve. Hence, socially optimum output is not produced & there found some inefficiency & excess capacity. All these indicate wasteful utilisation of productive resources. The facts presented above indicate that the monopolistic competition combines some elements of perfect competition & some of monopoly. So there observed the differences between these two market.
Question 9.
Illustrate the features of Oligopoly.
Answer:
Oligopoly denotes an inperfect market in which a few sellers/producers selling/producing either homogeneous goods or differentiated goods. In this market there is a few sellers or producers. The product is either homogeneous or differentiated. The competition is restricted to the few sellers selling very close or perfect substitute. The oligopoly is of two types. In case the sellers deals with homogeneous product, it is called “pure oligopoly” & in case of differentiated product, it is called “differentiated oligopoly.”
FEATURES:
(i) Interdependence : The sellors/firms under oligopoly are interdependent. Any decision taken by an individual seller/producer, with respect to price or product creates certain reaction among the rival firms. Any move taken by any seller has immediate counter move by the rivals. Hence, while assessing the market demand for its own product, the seller/firm concerned is to consider the reactions of its rivals. So no individual firm/seller can take independent decision of its own regarding the price & output.
(ii) Uncertainty : Uncertainty is another peculiar features under oligopoly. It arises because of the wide varieties of reaction patterns of the firm/seller. Any action taken by any firm /seller is well retaliated by the rivals which causes uncertainty. So, while taking decision, the firm/seller has to recognise the possible counter reaction of the rivals. Thus, the uncertainty under oligopoly creates difficulty in taking independent decision.
(iii) Selling Cost: The selling cost stands as an aggressive & defensive marketing device to achieve a greater share in the market. It appears due to the interdependence of the firms and uncertainty as well.
(iv) Group Behaviour : As the firms/sellers are interdependent & there exists uncertainty among them, the group behaviour acts as a proper solution. For maximising profitm the firms/ sellers act as a group by adopting a unanimously accepted norms. The group behaviour may reduce the degree of uncertainty that exists among the existing firms/sellers.
(v) Indeterminate Demand curve: The demand curve facing by an oligopoly is indeterminate. The demand curve usually reveals the price & product combination. In case of other market structures, the demand curve has got a definite shape. But in oligopoly, the demand curve is indeterminate because of inter dependence of firms that cause uncertainty. The concerned firm is not certain about the quantity he can sell at the price determined by him. It is because the firm concerned is not fully sure of the retaliatory move of its rivals. Such unpredictable response of the rivals to any action of the individual firm makes the demand curve indeterminate.
(vi) Price-rigidity & non-price competition : Price – rigidity is another feature in oligopoly. Any price, if accepted can not be easily changed & it continues to prevails over a long period. Thus, the price, under oligopoly is trend to be sticky & rigid, In spite of changes in cost-demand structure, the price is, not changed. Maintaining the quoted price, firms pursue to improve their competitive in the market through various types of non-price elements like rebate, free delivery, warranty etc. Thus non-price competition is believed to be a suitable business device. ‘
(viii) Non-Profit motive : Proft maximisation is not only objective of the oligopolist. Besides the entrepreneurs have many other motives like sales maximisation, security, risk minimisation etc. This is the special feature in oligopoly.
From the above features, it is believed that oligopoly is a real market structure that operates in real world. For a particular product, there is a few seller/producer competing with each other for having a greater share in the market. From this point of view, it is felt that oligopoly is a suitable market structure having practical validity.
Question 10.
What is market price ? How is it determined under condition of perfect competition ?
Answer:
Market price is the price of a commodity which prevails at any given time.’ This price is determined by momentary equilibrium between demand and supply at a time. Time in the market period is very small and the prices have a tendency to change very quickly during this period. Sometimes the prices change everyday and even every hour, The price of a good can be different in the morning and different in the evening. Market price is determined by the forces of demand and supply. But in the market period the price is influenced more by the demand. The main force behind demand side is the marginal utility of the commodity whereas from the side of supply the real force is the cost of production of the commodity. In the market period supply is almost fixed and cannot be increased. That is why when demand increases, price rises and when demand falls price also falls. We shall consider the price of the following two types of goods.
- Perishable goods.
- Durable or non-perishable goods.
Perishable goods – Perishable goods are those goods which do not last for a long time. These goods cannot be stored or kept. These goods go waste if stored. The perishable goods like fish, milk etc. have to be sold in the market whatever may be the price of these goods. Therefore, the supply curve of a perishable commodity in the market period is perfectly inelastic and is a vertical straight line. The pricing of a perishable commodity under market period can be shown with the diagram below.
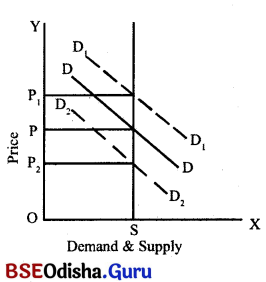
On OX-axis we measure demand and supply and on OY-axis we represent the price. SS is the supply curve which is parallel to OY-axis. This supply curve shows that supply is absolutely fixed and it cannot be changed. DD demand curve has a negative slope showing thereby that demand will extend when prices fall. Demand and supply are in equilibrium at price OP. Therefore, OP is the equilibrium market price. Now if the demand curve moves forward from DD to D1D1, the market price shall go up from OP to OP1 the supply of the commodity remaining fixed at OS.
Now if the demand curve moves downward from DD to D2D2 the market price falls from OP to OP2 the supply again remaining constant at OS. Hence we find that changes in the demand produces sharp changes in price in the market period, supply being costant dining that period.
Non-perishable goods – There are some goods which can be kept for a long period such as wheat, tea etc. In case of these commodities the firm fixes a reserve price and below this price the firm is not prepared to sell anything. If demand falls and as a result of it price falls below the reserve price the sellers instead of selling at this low price will keep their prdduce in the godowns. The supply in this period can be increased only out of the fixed stock which are already in hand. The reserve price is determined by several factors which are discussed below :
1. Future expectation – The reserve price of a commodity depends upon the expectations of the sellers regarding the future prices of the commodity. The reserve price will be higher if the producer expects the prices to go up in future and vice versa.
2. Need for cash – If the need of the sellers for pash is great, they will fix a low reserve price as they shall be interested to sell the commodity. But if they do not need cash early, they fix a higher reserve price.
3. Durability of the goods – The durability of thq goods also has its influence upon the reserve price because durable goods can be stored without fear of loss and anticipation of better price.
4. Future cost of production – Production cost to be incurred in the future on the commodity also has its effect on the reserve price. The producers will fix a higher reserve price, if they think that production cost in future shall be high.
5. Cost of storage – The reserve price also depends upon the cost of storage. The length of period for which the stock is to be stored is therefore, very important. The longer the period and the higher the cost of storing, the lower will be the reserve price and vice versa.
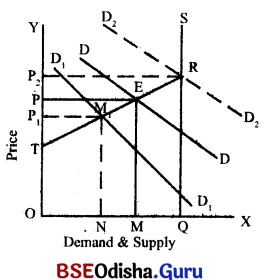
The diagram in the previous page shows the determination of market price of a durable commodity:
In the diagram TRS is the market period supply curve. OQ is the total stock of the goods. In the beginning the demand curve for the goods in the market is shown by the demand curve DD. The demand curve and the supply curve intersect each other at point E and price OP is determined. At this price the quantity purchased and sold is OM. Out of total stock OQ only OM is sold in the market and the remaining i. e., MQ is withheld by the sellers. If demand falls to D1D1 the equilibrium between demand and supply is established at point M and price shall be OP1. In this case the quantity sold is ON and NQ is kept in store. Now if demand increases to D2D2 the new equilibrium is established at point R and now the market price will rise to OP2 As is Clear from the above diagram, all the stock OQ shall be sold at OP2 price.
Group – C
Objective type Questions with Answers
I. Multiple Choice Questions with Answers :
Question 1.
In economics, which factor is not the essentials of the market ?
(i) Goods
(ii) Buyers & sellers
(iii) competition
(iv) cost of production
Answer:
(iv) cost of production
Question 2.
Large number of buyers & sellers are present in
(i) perfect competative market
(ii) monopolistic competition
(iii) obligopoly
(iv) Both (i) and (ii)
Answer:
(ii) monopolistic competition
Question 3.
Generally homogeneous goods are bought & sold in the
(i) monopolistic competiton
(ii) perfect competiton
(iii) obligopoly
(iv) monopoly
Answer:
(iv) monopoly
Question 4.
Which is.not one of the features of perfect competition ?
(i) uniform price
(ii) perfect mobility of factors
(iii) normal profit
(iv) identical cost
Answer:
(iv) identical cost
Question 5.
Absence of transportation cost is present
(i) monopoly
(ii) obligopoly
(iii) monopolistic competiton
(iv) perfect competiton
Answer:
(iv) perfect competiton
Question 6.
Under perfect competition AR is always
(i) equal to MR
(ii) greater than MR
(iii) less than marginal revenue
(iv) none of the above
Answer:
(i) equal to MR
Question 7.
Firm & industry lose their difference in
(i) perfect competition
(ii) monopoly
(iii) obligopoly
(iv) monopolistic competiton
Answer:
(ii) monopoly
Question 8.
In monopoly, the seller generally sells
(i) homogeneous goods
(ii) differentiated goods
(iii) goods having no close substitutes
(iv) goods having no perfect substitutes
Answer:
(iii) goods having no close substitutes
Question 9.
The elasticity of demand for the goods is zero in
(i) perfect competition
(ii) monopoly
(iii) obligopoly
(iv) monopolistic competiton
Answer:
(ii) monopoly
Question 10.
The entry of the new firm is restricted under
(i) perfect competition
(ii) monopolistic competition
(iii) monopoly
(iv) obligopoly
Answer:
(iii) monopoly
Question 11.
Absence of all sorts competition is found in
(i) perfect competition
(ii) monopoly
(iii) obligopoly
(iv) monopolistic competiton
Answer:
(ii) monopoly
Question 12.
One individual seller/ firm cannot influence the price of the product in
(i) monopoly
(ii) perfect competition
(iii) obligopoly
(iv) none of the above
Answer:
(ii) perfect competition
Question 13.
Under monopoly, AR is always
(i) greater than MR
(ii) Less than MR
(iii) equal to MR
(iv) none of the above
Answer:
(i) greater than MR
Question 14.
For the same goods, different prices can be changed in
(i) monopolistic competition
(ii) perfect competition
(iii) monopoly
(iv) obligopoly
Answer:
(iii) monopoly

Question 15.
Product differentiation is a feature of
(i) monopoly
(ii) perfect competition
(iii) monopolistic competition
(iv) obligopoly
Answer:
(iii) monopolistic competition
Question 16.
Non-price Competition is generally formed in
(i) perfect competition
(ii) monopolistic competition
(iii) monopoly
(iv) obligopoly
Answer:
(ii) monopolistic competition
Question 17.
Under perfect competition, price is determined by
(i) seller
(ii) buyer
(iii) firm
(iv) industry
Answer:
(iv) industry
Question 18.
Name the market were identical goods are sold at uniform price
(i) perfect competition
(ii) monopoly
(iii) obligopoly
(iv) monopolistic competiton
Answer:
(i) perfect competition
Question 19.
Charging different prices for the same goods happens in
(i) perfect competition
(ii) monopoly
(iii) monopolistic competition
(iv) obligopoly
Answer:
(ii) monopoly
Question 20.
The price at which the buyers purchase goods in the market is known as
(i) Real price
(ii) Normal price
(iii) Market price
(iv) All of the above
Answer:
(iii) Market price
Question 21.
Equilibrium price is influenced by
(i) demand for product
(ii) supply of product
(iii) lost of production
(iv) Both (i) and (ii)
Answer:
(iv) Both (i) and (ii)
Question 22.
If the demand for & supply of product changing in equal proportion, the equilibrium price
(i) increases
(ii) decreases
(iii) remains unaffected
(iv) all of the above
Answer:
(iii) remains unaffected
Question 23.
In determining equilibrium price, demand for a product is
(i) greater than supply
(ii) less than supply
(iii) equal to supply
(iv) both (i) and (ii)
Answer:
(iii) equal to supply
Question 24.
The price at which demand is equal to supply of a product is known as
(i) Normal price
(ii) market price
(iii) equlibrium price
(iv) all of the above
Answer:
(iii) equlibrium price
Question 25.
Other things remaining constant, if the demand for a product increases, the price
(i) rises
(ii) falls
(iii) remains uncharged
(iv) Both (i) and (ii)
Answer:
(i) rises
Question 26.
Long run price is otherwise knwon as
(i) Normal price
(ii) market price
(iii) short cut price
(iv) Both (i) and (ii)
Answer:
(i) Normal price
Question 27.
Most important condition of a perfect market is :
(i) A single producer or seller of a product.
(ii) No close substitutes for the product.
(iii) Homogenous product.
(iv) All of the above.
Answer:
(iii) Homogenous product.
Question 28.
Condition of a monopoly market:
(i) Uniformprice
(ii) Homogeneous product
(iii) Strong barriers to the entry into the industry
(iv) All of the above.
Answer:
(iii) Strong barriers to the entry into the industry
Question 29.
What is market price ?
(i) Price expected to prevail
(ii) Price actually prevailing in the market.
(iii) Both (i) and (iv)
(iv) None of he above
Answer:
(ii) Price actually prevailing in the market.
Question 30.
Under perfect competition :
(i) P>MR
(ii) P<MR
(iii) P = MR
(iv) None of the above
Answer:
(iii) P = MR
Question 31.
Under perfect competition price is determined by:
(i) Firm
(ii) industry
(iii) Seller
(iv) Buyer
Answer:
(ii) Industry
Question 32.
Normal price is a:
(i) Short-term price
(ii) Long-run price
(iii) All of the above
(iv) None of the above.
Answer:
(ii) Long-run price
Question 33.
Normal price is:
(i) A real price
(ii) An imaginary price
(iii) An unstabe price
(iv) None of the above.
Answer:
(ii) An imaginary price
Question 34.
Under monopoly the goods have:
(i) Close substitutes
(ii) Do not have close substitutes
(iii) All of the above
(iv) None of these
Answer:
(ii) Do not have close substitutes
Question 35.
Market in Economics refers to:
(i) Market for a commodity
(ii) A place
(iii) All of the above
(iv) None of the above
Answer:
(i) Market for a commodity
Question 36.
Under perfect competition goods are:
(i) Differentiated
(ii) Homogenous
(iii) Imperfect substitutes
(iv) None of the above
Answer:
(ii) Homogenous
II. Fill in the blanks:
Question 1.
In economics Market refers to _____
Answer:
a goods.
Question 2.
There is a large number of sellers and buyers in a _____ market.
Answer:
perfectly competitive
Question 3.
Under _____, there is free entry and free exit of the firms.
Answer:
perfect competition
Question 4.
Under _____, goods are homogeneous.
Answer:
perfect competition
Question 5.
Under _____, the goods are perfect substitutes for each other.
Answer:
perfect competition
Question 6.
Under perfect competition, price is represented through _____ Price = AR.
Answer:
Average Revenue
Question 7.
Under perfect competition, AR = _____
Answer:
MR.
Question 8.
Factors are perfectly mobile under _____
Answer:
perfect competition.
Question 9.
Price under perfect competition remains _____
Answer:
uniform.
Question 10.
Under _____ buyers have very weak bargaining power.
Answer:
perfect competition
Question 11.
Under perfect competition, the demand curve is a horizontal _____ line.
Answer:
straight
Question 12.
Under _____ the goods do not have any close substitutes.
Answer:
monopoly

Question 13.
The demand curve, under monopoly slopes _____ from left to right.
Answer:
downward
Question 14.
In monopoly there is a single _____ but many buyers.
Answer:
seller
Question 15.
Under monopoly the _____ is a price maker.
Answer:
monopolist
Question 16.
Under _____ competition the product is differentiated.
Answer:
monopolistic
Question 17.
Under monopolistic competition, the product is _____
Answer:
differentiated.
Question 18.
Entry and exit of firms are restricted under _____
Answer:
monopoly
Question 19.
Firm under _____ competition promotes its product through the selling cost.
Answer:
monopolistic
Question 20.
Under _____ there is only few sellers of the commodity.
Answer:
oligopoly
Question 21.
The price which is equal to MR is _____
Answer:
normal price.
Question 22.
_____ competition is a mixture of perfect competition and monopoly.
Answer:
Monopolistic
Question 23.
Demand curve under _____ competition is perfectly elastic.
Answer:
perfect
Question 24.
Normal price is influenced more by _____ under monopoly.
Answer:
supply
Question 25.
Only the _____ goods have normal price.
Answer:
reproducible
Question 26.
_____ price is determined by demand and supply of the goods.
Amwer:
Equilibrium
Question 27.
Firms under perfect competition earn _____ profit in the long-run.
Answer:
normal
Question 28.
Competitive output is _____ than monopoly output.
Answer:
higher
Question 29.
_____ price is a long-run price.
Answer:
Normal
Question 30.
_____ price is the price prevailing during very short period.
Answer:
Market
Question 31.
_____ price is an imaginary price
Answer:
Normal
III. Correct the Sentences :
Question 1.
Market, in economics, is associated with the name of a place.
Answer:
Incorrect.
Correct: Market in economics is associated with the name of a product
Question 2.
Market implies only perfectly competitive market.
Answer:
Incorrect.
Correct : Market implies both perfect & imperfect market.
Question 3.
The absence of competition is called perfect competition.
Answer:
Incorrect.
Correct: The absence of competition is called monopoly.
Question 4.
There are many buyers & few seller in perfect competition.
Answer:
Incorrect.
Correct: There are many buyers & many seller in perfect competition.
Question 5.
Buyers are influential in perfect competition.
Answer:
Incorrect.
Correct: Neither the buyers nor the sellers are influential in perfect competition.
Question 6.
There is free entry & free exit in perfect competition.
Answer:
Correct
Question 7.
In perfect competition, the goods are close substitutes for each other.
Answer:
Incorrect.
Correct: In perfect competition, the goods are perfect substitute for each other.
Question 8.
The buyers are ignorant of market condition in perfect competition.
Answer:
Incorrect.
Correct: The buyers have perfect knowledge about market conditions in perfect competition.
Question 9.
The factors ate immobile in perfect competition.
Answer:
Incorrect.
Correct: The factors are perfectly mobile in perfect competition.
Question 10.
There is no transportation cost in perfect competition.
Answer:
Correct
Question 11.
In perfect competition, the goods are homogeneous but price are different.
Answer:
Incorrect.
Correct: In perfect competition, the goods are homogeneous & price is uniform.

Question 12.
Under perfect competition, Average Revenue exceeds marginal Revenue.
Answer:
Incorrect.
Correct: Under perfect competition, average revenue equates marginal revenue.
Question 13.
Under perfect competition, demand for good is perfectly elastic.
Answer:
Correct
Question 14.
Perfect competition is a real market condition.
Answer:
Incorrect.
Correct: Perfect competition is a theoretical market condition.
Question 15.
Under perfect competition, price exceeds marginal revenue.
Answer:
Incorrect.
Correct: Under perfect competition, price is equal to marginal revenue.
Question 16.
Under Perfect competition, the buyers have strong bargaining power.
Answer:
Incorrect.
Correct: Under perfect competition, the buyers have very weak bargaining power.
Question 17.
In perfect competition, demand curve is a horizontal straight line.
Answer:
Correct
Question 18.
Equilibrium means a state of balance.
Answer:
Correct.
Question 19.
Equilibrium price is the price determined when demand for product exceeds supply of product.
Answer:
Incorrect.
Correct: Equilibrium price is the price determined when demand for the product is equal to supply of product.
Question 20.
In the determination of equilibrium price, both the demand & supply are dominant.
Answer:
Incorrect.
Correct: In the determination of equilibrium price, both the demand & supply are important.
Question 21.
Market price is stable but normal price is fluctuating.
Answer:
Incorrect.
Correct: Market price is fluctuating but normal price is stable.
Question 22.
All the goods have normal price but only the reproducible goods have market price.
Answer:
Incorrect.
Correct: All the goods have market price but only the reproducible goods have normal price.
Question 23.
Rare goods have normal price.
Answer:
Incorrect.
Correct: Rare goods have market price.
Question 24.
Normal price is real but market price is imaginary.
Answer:
Incorrect.
Correct: Market price is real but market price is imaginary.
Question 25.
All the goods have normal price.
Answer:
Incorrect.
Correct: All the goods have market price.
Question 26.
Market price is related with the cost of production.
Answer:
Correct.
Question 27.
Market price is Long – run price.
Answer:
Incorrect.
Correct: Normal price is long-run price.
Question 28.
Market period is a very short-period.
Answer:
Correct
Question 29.
In market period, supply of goods is fixed.
Answer:
Correct
Question 30.
In the determination of market price supply is dominant but in case of normal price demant is dominant.
Answer:
Incorrect.
Correct: In the determination of market price demand is dominant, but in case of normal price, supply is dominant.
Question 31.
There is single seller in monopoly.
Answer:
Correct
Question 32.
Under monopoly, the goods have close substitutes but under perfect competition the goods have perfect substitutes.
Answer:
Incorrect.
Correct: Under monopoly, the goods have no loss substitutes but under perfect competition. the goods have perfect substitutes.
Question 33.
In monopoly, entry is restricted.
Answer:
Correct
Question 34.
In monopoly, the seller adpot independent prices.
Answer:
Correct
Question 35.
Under monopoly. AR = MR.
Answer:
Incorrect.
Correct: Under monopoly. AR >MR.
Question 36.
Under monopoly, price equates MR.
Answer:
Incorrect.
Correct: Under monopoly, price equates AR
Question 37.
Under monopoly, price is uniform.
Answer:
Incorrect.
Correct : Under monopoly, price is different.
Question 38.
Price discrimination is possible under monopoly.
Answer:
Correct.
Question 39.
Under monopoly, AR curve is a vertical straight line.
Answer:
Incorrect.
Correct: Under monopoly, AR curve is a downward sloping curve.
Question 40.
In price discrimination, the monopolists sells different goods at same price.
Answer:
Incorrect.
Correct: In price discrimination, the monopolist sells same goods at different prices.
Question 41.
Monopolistic competition is a blending of perfect competition & monopoly.
Answer:
Correct
Question 42.
Monopolist charges high price to sell more & low price to sell less.
Answer:
Incorrect.
Correct: Monopolist charges low price to sell more & high price to sell less.
Question 43.
In monopolistic competition, there is only one seller.
Answer:
Incorrect.
Correct: In monopolistic competition, there are large number of sellers.
Question 44.
The products under monopolistic competition are the perfect substitutes for each other.
Answer:
Incorrect.
Correct: The products under monopolistic competition are close substitutes for each other.
Question 45.
Under monopolistic competition each firm is a monopolist.
Answer:
Correct

Question 46.
Under monopolistic competition, the price is less than that of perfect competition.
Answer:
Incorrect.
Correct: Under monopolistic competition, the price is higher than that of perfect competition.
Question 47.
In perfect competition, we find product differentiation.
Answer:
Incorrect.
Correct: In monopolistic competition, we find product differentiation.
Question 48.
Under oligopoly, there are many sellers.
Answer:
Incorrect.
Correct: Under oligopoly, there are few sellers.
Question 49.
Under oligopoly, demand curve slopes downward.
Answer:
Incorrect.
Correct: Under oligopoly, demand curve is indeterminate.
Question 50.
Under oligopoly, price is very flexible.
Answer:
Incorrect.
Correct: Under oligopoly, price is very rigid.
Question 51.
Group behaviour is found under monopoly.
Answer:
Incorrect.
Correct: Group behaviour is found under oligopoly.
Question 52.
Under oligopoly, each firm produces a small share of the market.
Answer:
Correct.
Question 53.
Under oligopoly, firms are independent.
Answer:
Incorrect.
Correct: Under oligopoly, firms are interdependent.
Question 54.
Under monopoly, the seller is a price maker.
Answer:
Incorrect.
Correct; Under monopoly, the seller is a price maker.
Question 55.
Selling cost is present both in monopoly & monopolistic competition.
Answer:
Correct.
Question 56.
In case of pure oligopoly, products are differentiated.
Answer:
Incorrect.
Correct: In case of pure oligopoly, products are homogeneous.
Question 57.
Under monopolistic competition, there is price-variation.
Answer:
Correct.
Question 58.
Uncertainty in the market is found in monopoly.
Answer:
Incorrect.
Correct: Uncertainty in the market is found in oligopoly.
Question 59.
Under duopoly, there are few sellers in the market.
Answer:
Incorrect.
Correct: Under duopoly, there are only two sellers in the market.
Question 60.
Duopoly is another form of monopoly
Answer:
Incorrect.
Correct: Duopoly is another form of oligopoly.
Question 61.
Oligopoly is a form of imperfect market.
Answer:
Correct.
IV. Answer the following questions in one word/One sentence :
Question 1.
What is a market ?
Answer:
Market consists of buyers & sellers sufficiently close contact with themeselves for the exchange of a particular goods.
Question 2.
What do you mean by perfect competition ?
Answer:
Perfect competition is said to prevail when a large number of buyers & sellers exchange a homogeneous goods at a uniform price without any restriction.
Question 3.
Write two features of perfect competition ?
Answer:
(i) Presence of a large number of buyers & sellers
(ii) Homogeneous goods.
Question 4.
What is homogeneous goods ?
Answer:
Homogeneous goods are those goods which are identical in all respects.
Question 5.
In which market there is uniform price ?
Answer:
In perfect competition there is uniform price.
Question 6.
What is.the shape of the demand curve for an individual firm under perfect competition ?
Answer:
Under perfect competition, the demand curve of an individual is a horizontal straight line (perfectly elastic demand curve).
Question 7.
Can a seller influence the price under perfect competition ?
Answer:
No, a seller cannot influence the price under prefect competition.
Question 8.
When does a market attain equilibrium ?
Answer:
Market is in equilibrium when there is no excess demand or excess supply.
Question 9.
What is meaning of equilibrium ?
Answer:
Equilibrium means a state of rest or balance.
Question 10.
What do mean by equilirium price ?
Answer:
Equilibrium price is that price at which quantity demanded is equal to quantity supplied.

Question 11.
What is pure competition ?
Answer:
Pure competition is perfect competition in narrow form which is characterised by the presence of a large number of buyers & sellers, homogeneous goods & free entry & exit.
Question 12.
How is the price determined under perfect competition ?
Answer:
Under perfect competition, price is determined by the interaction of forces of demand & forces of supply.
Question 13.
What sort of relationship exists between AR & MR under perfect competition ?
Answer:
AR & MR are equal under perfect competition
Question 14.
Who has propounded “price determination theory’ under perfect competition ?
Answer:
Alfred Marshall.
Question 15.
Which market deals with homogeneous goods ?
Answer:
Perfectly competitive market deals with homogeneous goods.
Question 16.
What is market price ?
Answer:
Market price is the real price which actually prevails in the market in a very short span of time.
Question 17.
What is Normal Price ?
Answer:
Normal price is an expected price which prevails in the long-run.
Question 18.
Write a distinction between Market price & normal Price ?
Answer:
Market price is real price but normal price is an expected price.
Question 19.
Which goods have only normal price ?
Answer:
Only the reproducible goods have normal price.
Question 20.
In which market, there is no transportation cost ?
Answer:
In perfectly competitive market, there is no transportation cost.
Question 21.
What is literacy meaning of ‘Monopoly’ ?
Answer:
Literacy meaning of ‘monopoly’ means one seller because ‘mono’ means one ‘poly’ means seller.
Question 22.
What are the various forms of imperfect market ?
Answer:
Imperfect market has three forms like monopoly, monopolistic competition & oligopoly.
Question 23.
What is the extreme form of imperfect market ?
Answer:
Monopoly is the extreme form of imperfect market.
Question 24.
What is monopoly ?
Answer:
Monopoly is a market structure in which single sellers sells a product having no close substitutes.
Question 25.
How many sellers are present in monopoly ?
Answer:
There is only one seller present in monopoly.
Question 26.
What a monopolist does to sell more of his product ?
Answer:
Monopolist reduces price to sell more of his product.
Question 27.
What is the shape of the demand curve under monopoly ?
Answer:
Monopolist has a downward sloping demand curve.
Question 28.
In which market price – discrimination is possible ?
Answer:
Price discrimination is possible under monopoly.
Question 29.
What is price discrimination ?
Answer:
Price discrimination is policy of charging different prices to different buyers for the same good.
Question 30.
What is relationship between AR & MR under monopoly ?
Answer:
AR is greater than MR under monopoly.
Question 31.
What is meant by dumping ?
Answer:
Dumping is the act of selling the same commodity at higher prices in the home market & at the lower price in the foreign market.
Question 32.
What is monopolistic competition ?
Answer:
Monopolistic competition is one form of imperfect competition which embraces some features of both the perfect competition & monopoly.
Question 33.
What is a differentiated product ?
Answer:
Diflfereentiated product is that product which is slightly different from other product of similar nature.
Question 34.
Which market product differentiation is visible ?
Answer:
In monopolistic competition product differentiation is visible.
Question 35.
What feature of monopoly is present in monopolistic competition ?
Answer:
The feature like product differentiation is present in monopolistic competition.
Question 36.
What common feature perfect competition is also present in monopolistic competition ?
Answer:
Presence of a large number of buyers & sellers is a common feature of perfect competition present in monopolistic competition.
Question 37.
What is selling cost ?
Answer:
Selling cost is the cost specially incurred to promote the sale of a product.
Question 38.
In which market selling cost is incurred ?
Answer:
In imperfect market selling cost is incurred.
Question 39.
What is the other name of selling cost ?
Answer:
Advertisement cost is the other name of selling cost.
Question 40.
What is oligopoly ?
Answer:
Oligopoly is an imperfect market in which a few sellers sell either homogeneous product or differentiated product.
Question 41.
What is pure oligopoly ?
Answer:
If a homogeneous product is produced or sold by a few producer/sellers, it is called pure oligopoly.
Question 42.
In which market, interdependent of firms are more visible.
Answer:
In oligopoly, interdependence of firms are more visible.
Question 43.
In which market, Group behaviour is found ?
Answer:
In oligopoly, group behaviour is found.
Question 44.
In which market demand curve is indeterminate ?
Answer:
In oligopoly, demand curve is indeterminate.
Question 45.
In which market, price is found stickly & rigid ?
Answer:
In oligopoly, price is found stickly & rigid.
![]()
![]()

![]()
![]()
![]()
![]()
![]()

![]()