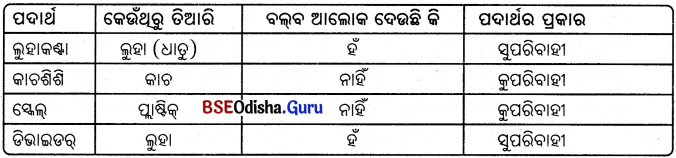
Odisha State Board CHSE Odisha Class 11 Odia Solutions Chapter 1 ଶର୍ଶୁପଦର Textbook Exercise Questions and Answers.
CHSE Odisha Class 11 Odia Chapter 1 ଶର୍ଶୁପଦର Question Answer
ପାଠ୍ୟପୁସୃଜମ ପ୍ତଖାବଲାଭ ଇଉର :
Question 1.
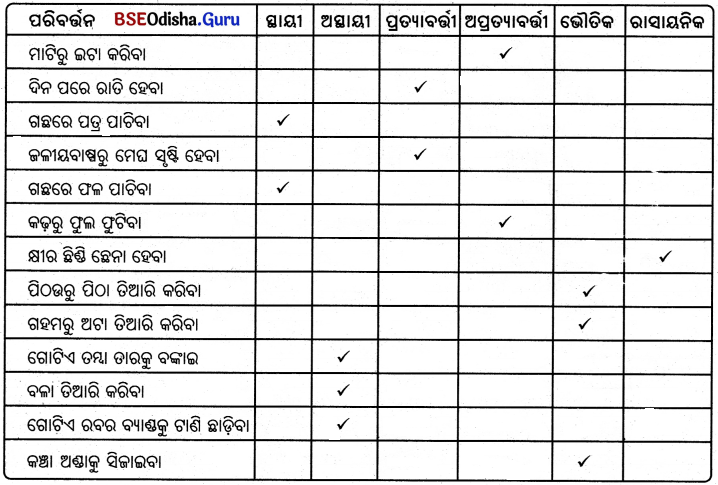
ପ୍ରଶ୍ନର ମୂଲ୍ୟ ୧ ନମ୍ବର ଚାରିଗୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
(କ) କୋରାପୁଟରୁ ଲକ୍ଷ୍ମୀପୁର ଯିବା ରାସ୍ତାରେ କେଉଁ ଘାଟି ପଡ଼େ ? (ସାଲୁର୍, ପାଲୁର୍, ଲକ୍ଷ୍ମୀପୁର, ଧର୍ମଦୁଆର)
Solution:
ଧର୍ମଦୁଆର ।
(ଖ) ସୁକୃଜାନିର ଭାରିଯା କିଭଳି ମରିଥିଲା ? (ରୋଗରେ, ବାଘ ନେଇଯିବାରୁ, ପାଣିରେ ବୁଡ଼ିଯିବାରୁ, ନିଆଁ ଲାଗିଯିବାରୁ)
Solution:
ବାଘ ନେଇଯିବାରୁ ।
(ଉ) ତେଲ ହେବାପାଇଁ ସୁକୃଜାନିର ବଖରା କଣରେ କେଉଁ ମଞ୍ଜି ଥାଏ ? (ବାରି ବାଇଗବା, ଆମ୍ବଟାକୁଆ, ମାଣ୍ଡିଆ, ଅଳସି)
Solution:
ଗାରି ଗାଲଗଣା।
(ଘ) ସୁକୃଜାନିର ସାନପୁଅ କିଏ ? (ମାଣ୍ଡିଆ ଜାନି, ଟିକ୍ରାଜାନି, ଲାକ୍ରାଜାନି, ଗୁଡ଼ାଜାନି)
Solution:
ଟିକ୍ରାଜାନି ।
(ଙ) ବିଲି କେଉଁ ଫଳର ସାବୁନ୍ ଫେଣରେ ମୁଣ୍ଡ ରଗଡ଼ୁଥିଲା ? (ବାଇଗଣ, ଚିଲି, କାନ୍ଦୁଲି, ଅଠା)
Solution:
ଚିଲି ।
(ଚ) ସିଟି ମାରିମାରି ବୁଲାଣି ବାଟରେ ଧୀରେ ଧୀରେ ଜଙ୍ଗଲ ଜମାନ୍ କେଉଁଆଡ଼େ ଗଲା ? (ଗାଆଁ, ଜଙ୍ଗଲ, ଝରଣା, ସହର)
Solution:
ଗାଆଁ ।
(ଞ) ସୁକୃଜାନି କେଉଁ ଗାଆଁର ଲୋକ ? (ଲକ୍ଷ୍ମୀପୁର, ଶର୍ଶୁପଦର, ଅମ୍ବାଝୋଲା, କଦମ ଝୋଲା)
Solution:
ଶର୍ଶୁପଦର
(ଟ) ଧର୍ମଦୁଆର ଘାଟିଠାରୁ କେଉଁ ଦିଗକୁ ‘ଶଶୁପଦର’ ଗାଁ ପଡ଼େ ? (ପୂର୍ବ, ପଶ୍ଚିମ, ଉତ୍ତର, ଦକ୍ଷିଣ)
Solution:
ଉତ୍ତର ।
![]()
(୦) ‘ଧର୍ମଦୁଆର ଘାଟିଠାରୁ କେତେ ଦୂରରେ ଶଶୁପଦର ଗାଁ ? (କୋଶେ, ଦୁଇକୋଶ, ତିନିକୋଶ, ଚାରିକୋଶ)
Solution:
କୋଶେ ।
(ଡ) ଶଶୁପଦର ଗାଁ’ରେ କେତେ ଜାତିର ଲୋକ ବାସ କରନ୍ତି ? (ଦୁଇ, ତିନି, ଚାରି, ପାଞ୍ଚ)
Solution:
ତିନି ।
(ଢ) ‘ଜୋଣା’ ଶବ୍ଦର ଅର୍ଥ କ’ଣ ? (ଲଙ୍କାମରିଚ, ମକ୍କା, ଧୂଆଁପତ୍ର, କାନ୍ଦୁଲ)
Solution:
ମକ୍କା ।
(ଣ) ସମ୍ବାରି କେଉଁଠିକୁ ଶାଗ ତୋଳିବାକୁ ଯାଇଥିଲା ? (ବୁଦାଗହଳକୁ, ଭାଲୁଗାଡ଼କୁ, ବିଲକୁ, ପୋଖରୀ ହୁଡ଼ାକୁ)
Solution:
ଭାଲୁଗାଡ଼କୁ ।
(ତ) କେତେ ବର୍ଷ ତଳେ ସମ୍ବାରି ଶାଗ ତୋଳିବାକୁ ଯାଇ ଆଉ ଫେରିନାହିଁ ? (ଦୁଇବର୍ଷ, ତିନିବର୍ଷ, ଚାରିବର୍ଷ, ପାଞ୍ଚବର୍ଷ)
Solution:
ତିନିବର୍ଷ ।
(ଥ) ଜିଲି ଓ ବିଲି ଚିକ୍କଣ ଖୋଷାରେ କେଉଁ ରଙ୍ଗର ଫୁଲ ଖୋସିଥା’ନ୍ତି ? (ଲାଲ୍, ହଳଦିଆ, ଗୋଲାପି, ଧଳା)
Solution:
ଲାଲ୍ ।
(ଦ) କେଉଁଥରେ ମାଣ୍ଡିଆ ଯାଉ ପୂରାଇ ବିଲକୁ ନିଆଯାଏ ? (କୁମ୍ପିରେ, ଲାଉ ତୁମ୍ବାରେ, ହାଣ୍ଡିରେ, ତଲାରିରେ)
Solution:
ଲାଉ ତୁମ୍ବାରେ ।
(ଧ) ସବୁରି କର୍ରା ଗୋଟିଏ ଭୂତ ବା ଡୁମା, ଏହା କାହାର ବିଶ୍ଵାସ ? (ସୁକୃଜାନି, ନାଇକ, ଜମାନ୍, ଗାରଦ)
Solution:
ସୁକୃଜୀନି ।
(ନ) କିଏ ଆଣିଦିଏ ଝଡ଼ ତୋଫାନ, ଦୁଃଖ ଦୁର୍ଦ୍ଦଶା ବୋଲି ସୁକୃଜାନି ଭାବିଛି ? (ଡଙ୍ଗର, ଜଙ୍ଗଲ, ଡୁମା, ବୁଢ଼ାରଜା)
Solution:
ଡୁମା ।
(ପ) ଢୁ ଢୁ ବରଷାରେ ସୁକୃଜାନି’ ଓ ‘ଆଉ କିଏ ମିଶି ସାନ ପାହାଡ଼କୁ ଚାଷଭୂଇଁ କରିଥିଲେ ? (ମାଣ୍ଡିଆ, ଟିକ୍ରା, ଲୋଗୋଁ, ବାଗଲା)
Solution:
ଲୋବୋ ।
(ଫ) ସୁକୃଜାନିର ଆବୁଆବୁଆ ବଳୁଆ ଦେହର ଗୋଡ଼ପେଣ୍ଡା କିପରି ? (ବର୍ଷାତି, କାଉଡ଼ି, ପଥର, ଗଛ)
Solution:
ପଥର ।
(ବ) ମାଣ୍ଡିଆଜାନି ଠିକ୍ କାହାପରି ? (ଟିକ୍ରାଜାନି, ସୁକୃଜାନି, ଝିଲି, ବିଲି)
Solution:
ସୁକୃଜାନି ।
(ଭ) ମଲା ମା’କୁ କିଏ ମନେ ପକେଇଦିଏ ? (ମାଣ୍ଡିଆଜାନି, ଟିକ୍ରାଜାନି, ସୁକୃଜାନି, ଝିଲି ଓ ବିଲି)
Solution:
ଟିକ୍ରାଜାନି ।
(ମ) ଜିଲି ସାମ୍ନାକୁ ମୁହଁ କରି ତା’ର ପିନ୍ଧା ________ ଖଣ୍ଡିକ ଚଟାଣ ଉପରେ କାଚୁଥିଲା ? (ଲୁଗା, ଶାଢ଼ୀ, ପାଞ୍ଚୁଆ, କୌପୁନୀ)
Solution:
ପାଞ୍ଚୁଆ ।
(ଯ) ବଣଗାରଡ଼ କେଉଁ ଚଢ଼େଇ ଖୋଜିବାର ବାହାନାରେ ଏକଡ଼ ସେକଡ଼ ହେଉଥିଲା ? (ମୟୂର, କୁକୁଡ଼ା, ହରଡ଼ ଚଢ଼େଇ, ଗେଣ୍ଡାଳିଆ)
Solution:
ହରଡ଼ ଚଢ଼େଇ ।
(ର) ନାଇକ ଖଜଣା ଅସୁଲ କରି ରାଜାଘର ________ କୁ ଦିଏ । (ଚପରାଶି, ଗାରଡ଼, ରିବିଣି, ଜମାନ୍)
Solution:
ରିବିଣି ।
(ଳ) ଜଙ୍ଗଲ ଜମାର ଦଖଲରେ ________ କୋଶ ନିଘଞ୍ଚ ଜଙ୍ଗଲ । (ଦଶ ପନ୍ଦର କୋଶ, ଦୁଇକୋଶ, କୋଡ଼ିଏ କୋଶ, ଅଠର କୋଶ)
Solution:
ଦଶ ପନ୍ଦର କୋଶ ।
(ବି) ରେଙ୍ଗୁ ପରଜାର ପୁଅର ନାମ କ’ଣ ? (କାଜୋଡ଼ି, ବାଗଲା, ଭାଟ )
Solution:
ବାଗଲା ।
![]()
Question 2.
ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ । ପ୍ରଶ୍ନର ମୂଲ୍ୟ ୧ ନମ୍ବର ।
(କ) ଲକ୍ଷ୍ମୀପୁରରୁ ଦେଢ଼ କୋଶ ଦୂରରେ କେଉଁ ଘାଟି ପଡ଼େ ?
Solution:
ଲକ୍ଷ୍ମୀପୁରରୁ ଦେଢ଼ କୋଶ ଦୂରରେ ଧର୍ମଦୁଆର ଘାଟିପଡ଼େ ।
(ଖ) ‘ଧର୍ମଦୁଆର’ ଘାଟିର ଏ ପାଖରୁ କେତେ ଓ ସେ ପାଖରୁ କେତେ ପାହାଡ଼ ଠିଆ ହୋଇଛନ୍ତି ?
Solution:
ଧର୍ମଦୁଆର ଘାଟିରୁ ଏପାଖରୁ ଚାଳିଶ ଓ ସେପାଖରୁ ପଚାଶ ପାହାଡ଼ ଠିଆ ହୋଇଛନ୍ତି । (ଗ) ‘ଧର୍ମ ଦୁଆର’ ଘାଟିର ଉତ୍ତରକୁ କେଉଁ ଗାଁ ?
(ଘ) ‘ଧର୍ମ ଦୁଆର’ ଘାଟିର କେତେ ଦୂରରେ ‘ଶଶୁପଦର’ ଗାଁ ପଡ଼େ ?
Solution:
ଧର୍ମ ଦୁଆର ଘାଟିର କୋଶେ ଦୂରରେ ପଡ଼େ ‘ଶଶୁପଦର’ ଗାଁ ପଡ଼େ ।
(ଙ) ଶର୍ଶୁପଦର ଗାଁରେ କେଉଁସବୁ ଜାତିର ଲୋକ ବାସ କରନ୍ତି ?
Solution:
ଶଶୁପଦର ଗାଁରେ ଡମ୍ବ, ଗାଦ୍ବା ଓ ପରଜା ଜାତିର ଲୋକେ ବାସ କରନ୍ତି ।
(ଚ) ‘ଟଣିଅଁ’ ଶବ୍ଦର ଅର୍ଥ କ’ଣ ?
Solution:
‘ଟଣିଅଁ’ ଏକ ପ୍ରକାର ଝାଟି, ଯେଉଁଥରେ ଆଦିବାସୀମାନେ କ୍ଷେତର ବାଡ଼ ଦେଇଥା’ନ୍ତି ।
(ଛ) କେତେ ଘର ଲୋକ ଶଶୁପଦର ଗ୍ରାମରେ ବାସ କରନ୍ତି ?
Solution:
କୋଡ଼ିଏ ଦୁଇ ବା ବାଇଶ ଘର ଲୋକ ଶଶୁପଦର ଗ୍ରାମରେ ବାସ କରନ୍ତି ।
(ଜ) ସୁକୃଜାନିର ସ୍ତ୍ରୀର ନାମ କ’ଣ ?
Solution:
ସୁକୃଜାନିର ସ୍ତ୍ରୀର ନାମ ସମ୍ବାରି ।
(ଝ) ସମ୍ବାରି ସକାଳୁ ସକାଳୁ କେଉଁଠିକୁ ଶାଗ ତୋଳିବାକୁ ଯାଇଥିଲା ?
Solution:
ସମ୍ବାରି ସକାଳୁ ସକାଳୁ ‘ଭାଲୁଗାଡ଼’ ଝୋଲାକୁ ଶାଗ ତୋଳିବାକୁ ଯାଇଥିଲା ।
(୦) ସୁକୃଜାନି କ’ଣ ପିକା କରି ଟାଣେ ?
Solution:
ସୁକୃଜାନି ଧୂଆଁପତ୍ର ବଳାକୁ ପିକାକରି ଟାଣେ ?
(ଡି) ‘ତଲରା’ ଓ ‘ତଲରି’ ଶବ୍ଦର ଅର୍ଥ କ’ଣ ?
Solution:
‘ତଲରା’ ଅର୍ଥ ପିଠିପଖିଆ ଓ ‘ତଲରି’ ଅର୍ଥ ମୁଣ୍ଡର ଛତା ।
(ଢ) ସୁକୃଜାନିକୁ କ’ଣ ଭଲଲାଗେ ?
Solution:
ସୁକୃଜାନିକୁ ଅଳିଆ ଦଳିଆ ଘରକରଣା, ଛାତତଳେ ନାକ କାନ ରୁନ୍ଧା ମଠୁଆ ମଠୁଆ ଧୂଆଁ ଭଲଲାଗେ ।
(ଣ) ସୁକୃଜାନି କ’ଣ ବିଶ୍ଵାସ କରେ ?
Solution:
ଯେ ସବୁରି କର୍ତ୍ତା ଗୋଟାଏ ଲେଖାଁ ଭୂତ ବା ‘ଡୁମା’ ବୋଲି ସୁକୃଜାନି ବିଶ୍ଵାସ କରେ ।
(ତ) ଶଶ୍ରୁପଦରର ପାହାଡ଼ୀ ନଈରେ କିପରି ଡେଇଁ ଡେଇଁକା ପାଣି ଚାଲେ ?
Solution:
ଶଶୁପଦରର ପାହାଡ଼ୀ ନଈରେ କବ କବ କରି ଡେଇଁ ଡେଇଁକା ପାଣି ଚାଲେ ।
(ଥ) ପାହାଡ଼ ତଳର କେଉଁ ଜମିରେ ଧାନ ହୁଏ ?
Solution:
ପାହାଡ଼ ତଳର ସନ୍ତସନ୍ତିଆ ଜମିରେ ଧାନ ହୁଏ ।
(ଦ) ସୁକୃଜାନି ଓ ଆଉ କିଏ ମିଶି ସାନ ପାହାଡ଼କୁ ଚାଷଭୂଇଁ କରିଥିଲେ ?
Solution:
ସୁକୃଜାନି ଓ ଲୋବୋ କନ୍ଧ ମିଶି ସାନ ପାହାଡ଼କୁ ଚାଷଭୂଇଁ କରିଥିଲେ ।
(ଧ) ମଣିଷ ମରିଗଲେ କେଉଁଠାରେ ତା’ ନାଁରେ ଖଣ୍ଡେ ଗୋଜିଆ ପଥର ପୋତା ହୁଏ ବୋଲି ସୁକୃଜାନି ଭାବିଛି ?
Solution:
ମଣିଷ ମରିଗଲେ ଗାଁ-ମଝି ଗୁରୁଡ଼ି ଆମ୍ବଗଛ ତଳେ ତା’ ନାଁରେ ଖଣ୍ଡେ ଗୋଜିଆ ପଥର ପୋତା ହୁଏ ବୋଲି ସୁକୃଜାନି ଭାବିଛି ।
(ନ) ସୁକୃଜାନି କାହା ଉପରେ ଭରସା ରଖେ ?
Solution:
ସୁକୃଜାନି ବାହାର ବଳ ଉପରେ ଭରସା ରଖେ ।
(ପ) ସୁକୃଜାନି ପାହାଡ଼ ଲଣ୍ଡା କଲାବେଳେ ଏକାବେଳେକେ କେତେ ଘଣ୍ଟା କୁରାଢ଼ି ଓହ୍ଲାଏ ନାହିଁ ?
Solution:
ସୁକୃଜାନି ପାହାଡ଼ ଲଣ୍ଡା କଲାବେଳେ ଏକାବେଳେକେ ପାଞ୍ଚ ଘଣ୍ଟା, ଛଅ ଘଣ୍ଟା କୁରାଢ଼ି ଓହ୍ଲାଏ ନାହିଁ ।
(ଫ) ସୁକୁଜାନି ହାକିମମାନଙ୍କ ବୋଝକୁ ନେଇ କେଉଁଠାରେ ପହଞ୍ଚାଏ ?
Solution:
ସୁକୃଜାନି ହାକିମମାନଙ୍କ ବୋଝକୁ ନେଇ ମାଙ୍କଡ଼ଝୋଲା କି କାକିରିଗୁମ୍ମା ବଙ୍ଗଳାର ପହଞ୍ଚାଏ ।
(ବି) ସୁକୃଜାନି କୋଶେ ବାଟ ହାକିମମାନଙ୍କ ବୋଝ ନେଇଗଲେ କେତେ ପଇସା ମିଳେ ?
Solution:
ସୁକୃଜାନି କୋଶେ ବାଟ ହାକିମମାନଙ୍କ ବୋଝ ନେଇଗଲେ ପଇସାଏ ମିଳେ ।
(ମ) ପରଜା ସ୍ତ୍ରୀଲୋକଙ୍କ ତୁଠ କେଉଁଠାରେ ?
Solution:
ପରଜା ସ୍ତ୍ରୀଲୋକଙ୍କ ତୁଠ ନାଳର ବାଙ୍କରେ ।
(ଯ) ଟିକ୍ରା ଜାନିକୁ ଦେଖିଲେ କିଏ ମନେ ପଡ଼ିଯାଏ ?
Solution:
ଟିକ୍ରା ଜାନିକୁ ଦେଖୁଲେ ତା’ର ମଲା ମାଆ ମନେ ପଡ଼ିଯାଏ ।
(ର) ଜିଲି ଓ ବିଲି ଦି’ ଭଉଣୀ କେଉଁଠାରେ ଗାଧୋଉଥିଲେ ?
Solution:
ଜିଲି ଓ ବିଲି ଦି’ ଭଉଣୀ ପାହାଡ଼ତଳେ ଝୋଲାରେ ଗାଧୋଉଥିଲେ ।
(ଳ) ଜମାନ୍ ହସି ହସି କେଉଁଠାରେ ଛପିଗଲା ?
Solution:
ଜମାନ୍ ହସି ହସି ବୁଦା ଉଢୁଆଳରେ ଛପିଗଲା ।
(ବି) ଜଙ୍ଗଲ ଜମାନ୍ର ଛାଉଣି କେଉଁଠାରେ ପଡ଼େ ?
Solution:
ଜଙ୍ଗଲ ଜମାନ୍ର ଛାଉଣି ଗାଁ ନାଇକ ଘର ପିଣ୍ଡାରେ ପଡ଼େ ।
(ଶ) ନାଇକ ଖଜଣା ଅସୁଲ କରି କାହାକୁ ଦିଏ ?
Solution:
ନାଇକ ଖଜଣା ଅସୁଲ କରି ରାଜାଘର ରିବିଣି ଅମିନକୁ ଦିଏ ।
(ଷ) କିଏ ରଇତମାନଙ୍କଠାରୁ ଉଚ୍ଚରେ ?
Solution:
ଗାଁରେ ନାଇକ ରଇତମାନଙ୍କଠାରୁ ଉଚ୍ଚରେ ।
(ସ) ଶଶୁପଦର ଗାଁ’ର ଚାରିଆଡ଼େ କ’ଣ ହୁଲର ହୋଇଗଲା ?
Solution:
ଶଶୁପଦର ଗାଁ’ର ଚାରିଆଡ଼େ ‘ଗାରଡ଼, ଗାରଡ଼, ଜମାନ୍ ଜମାନ୍’ ହୁଲର ହୋଇଗଲା ।
![]()
(ହ) ବଣରେ ଗୋରୁ ଚରାଇବା ପାଇଁ ଜଙ୍ଗଲ ଜମାକୁ କ’ଣ ଦେବାକୁ ପଡ଼େ ?
Solution:
ବଣରେ ଗୋରୁ ଚରାଇବା ପାଇଁ ଜଙ୍ଗଲ ଜମାନ୍କୁ ‘ପାନୁ’ (ଟିକସ) ଦେବାକୁ ପଡ଼େ ।
(କ୍ଷ) କ’ଣ କଲେ ଜମାକୁ ଜୋରିମାନା ଦେବାକୁ ପଡ଼ିବ ?
Solution:
‘ପୋଡୁଚାଷ’ କଲେ ଜମାକୁ ଜୋରିମାନା ଦେବାକୁ ପଡ଼ିବ ।
(ୟ) ସୁକୃଜାନିର କ’ଣ ଦରକାର ?
Solution:
ସୁକୃଜାନିର କମି ଦରକାର |
(ଲ) ‘ପରଜା’ ସମାଜର ରୀତି କ’ଣ ?
Solution:
ପୁଅମାନେ ବିଭାହେଲେ ନିଆରା ଘରେ ରହିବେ, ଏହା ‘ପରଜା’ ସମାଜର ରୀତି ।
(°) କେତେ ଟଙ୍କା ଦେଇ ସୁକୃଜାନି ଜଙ୍ଗଲ ଜମାନକୁ ଜମି ପାଇଁ ନିବେଦନ କଲା ?
Solution:
ଯୋଡ଼ିଏ ଟଙ୍କା ଦେଇ ସୁକୃଜାନି ଜଙ୍ଗଲ ଜମାନ୍କୁ ଜମି ପାଇଁ ନିବେଦନ କଲା ।
(8) ଗାଁ’ ତୁଠରେ ଜିଲି କ’ଣ କରୁଥିଲା ?
Solution:
ଗାଁ’ ତୁଠରେ ଜିଲି ‘ଗୁର୍ଦି’ ଶାଗ ଧୋଉଥିଲା ।
(ଥଁ) କାଜୋଡ଼ି କାହାର ଝିଅ ?
Solution:
କାଜୋଡ଼ି ପୁରିଜାନିର ଝିଅ ।
(i) ମାଣ୍ଡିଆଜାନି ପାଇଁ କାହାକୁ ମନୋନୀତ କରାଯାଇଥିଲା ?
Solution:
ମାଣ୍ଡିଆଜାନି ପାଇଁ କାକୋଡ଼ିକ୍ତି ମନୋନୀତ କରାଯାଇଥିଲା |
(ii) ଦିନା କାତେ ହେଲା ଶଶୁପଦର ଗାଁ’ରେ କେଉଁ ଗପ ଚହଟିଛି ?
Solution:
ଦିନା କାତେ ହେଲା ଶଶୁପଦର ଗାଁ’ରେ ବାଗ୍ ଆଉ ଜିଲି ପରସ୍ପରକୁ ଭଲ ପାଉଛନ୍ତି ବୋଲି ଗପ
Question 3.
ଦୁଇଟି ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ । ପ୍ରଶ୍ନର ମୂଲ୍ୟ ପାଇଁ ୨ ନମ୍ବର । ଲେଖା ଓ ଲେଖକଙ୍କ ସୂଚନା ୧ ନମ୍ବର ଏବଂ ଉତ୍ତର ପାଇଁ ୧ ନମ୍ବର ରହିବ ।
(କ) କେଉଁଠାରେ ‘ଧର୍ମଦୁଆର’ ଘାଟି ପଡ଼େ ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । କେଉଁଠାରେ ଯିବା ରାସ୍ତାରେ, ଲକ୍ଷ୍ମୀପୁର ମୋଟେ ଦେଢ଼କୋଶ ଥାଇ ‘ଧର୍ମଦୁଆର’ ଘାଟିପଡ଼େ ।
(ଖ) ‘ଶଶୁପଦର’ରେ ଥିବା ସାହିମାନଙ୍କ ନାମ କ’ଣ ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ‘ଶଶୁପଦର’ରେ ଥିବା ସାହିମାନଙ୍କ ନାମ – ‘ଡମ୍ବ’ ସାହି, ‘ଗାଦ୍ବା’ ସାହି ଓ ‘ପରଜା’ ସାହି ।
(ଗ) ସୁକୃଜାନିର ସଂସାର କହିଲେ କିଏ ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ସୁଜାନିର ସଂସାର କହିଲେ, ସୁକୃଜାନି ନିଜେ, ବଡ଼ ପୁଅ ମାଣ୍ଡିଆଜାନି, ସାନପୁଅ ଟିକ୍ରାଜାନି, ଆଉ ଝିଅ ଯୋଡ଼ିକ, ଜିଲି ଆଉ ବିଲି ।
(ଘ) ସମ୍ବାରି କିପରି ମୃତ୍ୟୁବରଣ କଲା ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ସମ୍ବାରି ସକାଳୁ ସକାଳୁ ମାରି ଦେଇଥିଲା ।
(ଙ) ସୁକୃଜାନି ତା’ ଟିକି ସଂସାରକୁ ଘେନି କିପରି ଚଳୁଥୁଲା ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ଘେନି ଖୁସିବାସିରେ ଚଳୁଥିଲା ।
(ଚ) ସମକାନି କୋଳେଦେଲେ । ପ୍ରାୟମଯ୍ନ ତୃପ୍ତି ଯାଏ |
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ଧୂଆଁପତ୍ରରେ ବଳାଯାଇଥିବା ପିଙ୍କା ଖଣ୍ଡିଏ ଟାଣିଲାବେଳେ ମନ ଭିତରେ ଆଶ୍ରୟମୟ ତୃପ୍ତି ପାଏ ।
(ଛ) କିଲି ଓ ବିଲି ହାଣ୍ଡିରେ କ’ଣ ଅଜାଡ଼ି ଚୂଲିରେ ବସାନ୍ତି ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ଜିଲି ଓ ବିଲି ହାଣ୍ଡିରେ ମାଣ୍ଡିଆଚୂନା କି ଶାଗ କି ଫେସା ହୋଇଥିବା ଆମ୍ବଟାକୁଆର କୋଇଲି ଅଜାଡ଼ି ଦେଇ ଚୂଲିରେ ବସାନ୍ତି ।
(ଜ) ମାଣ୍ଡିଆ ଓ ଟିକ୍ରା କେତେବେଳେ ପିଣ୍ଡାରେ ହାଲିଆ ଘାଲିଆ ହୋଇ ବସିପଡ଼ନ୍ତି ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ମାଣ୍ଡିଆ ଓ ଟିକ୍ରା ସଞ୍ଜବୁଡ଼ିଲେ, ପାହାଡ଼ ଖୋଳି ଖୋଳି ଘରକୁ ଫେରି ପିଣ୍ଡାରେ ହାଲିଆ ଘାଲିଆ ହୋଇ ବସିପଡ଼ନ୍ତି ।
(ଝ) ମାଣ୍ଡିଆଜାନି କାହାପରି ଦେଖିବାକୁ ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ମାଣ୍ଡିଆଜାନି ଠିକ୍ ବାପା ସୁକୃଜାନି ପରି ଦେଖୁବାକୁ ।
(ଞ) ଟିକ୍ରା ଓ ତା’ ମା’ ମଧ୍ୟରେ ଥିବା କେଉଁ ସମାନତା ସୁକୃଜାନିର ମନେ ପଡ଼ିଯାଏ ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ମଧ୍ୟରେ ଥିବା ଡବ ଡବ ଆଖୁ, ତର ତର କଥାର ସମାନତା ସୁକୃଜାନିର ମନେ ପଡ଼ିଯାଏ ।
(ଟ) ସୁକୃଜାନି କେତେବେଳେ ସଞ୍ଜର ଶାନ୍ତି ଓ ଖୋଲା ପାହାଡ଼ର ଶାନ୍ତି ପିଇଯାଏ ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । କାନରୁ ଦରପୋଡ଼ା ପିଙ୍କା ଖଣ୍ଡିଏ ଟାଣିନେଇ ନିଆଁ ଲଗାଏ ଓ ଧୂଆଁ ପିଉ ପିଉ ସଞ୍ଜର ଶାନ୍ତି ଓ ଖୋଲା ପାହାଡ଼ର ଶାନ୍ତି ପିଇଯାଏ ।
(୦) ବିଲି କେତେବେଳେ ଦୁଇ ହାତରେ ପାଣି ଚବର ଡବର କରୁଥିଲା ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ବିଲି ଖଟା ‘ଚିଲି’ ଫଳର ସାବୁନ ଫେଣରେ ମୁଣ୍ଡ ରଗଡ଼ି ଧୋଉଥିବାବେଳେ, ମୁଣ୍ଡକୁ ପାଣିରେ ମାଡ଼ିଦେଇ ଦୁଇ ହାତରେ ପାଣି ଚବର ଚବର କରୁଥୁଲା ।
(ଡ) ଜିଲି ଓ ବିଲି ଗାଧୋଉ ଥିଲାବେଳେ କିଏ ସିଧା ଆଖୁ ଚାଲିଗଲେ ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ଜିଲି ଓ ବିଲି ଗାଧୋଉ ଥିଲାବେଳେ, ବାହୁଙ୍ଗିରେ ଭାର କାନ୍ଧେଇ, କପାଳର ଝାଳ ପୋଛି ପୋଛି ଦୁଇଟି ପରଜା ସିଧା ଆଖରେ ଚାଲିଗଲେ ।
![]()
(ଢ) ଝୋଲା କୂଳେ କୂଳେ ଆଉ ଜଣେ ଲୋକ କ’ଣ କରୁଥିଲା ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ଝୋଲା କୂଳେ କୂଳେ ପକେଇ ଏକର ସେକର ହେଉଥିଲା ।
(ଣ) ଜଙ୍ଗଲ ଜମାନ୍ ଏକ ଜାଗାକେ କାହାକୁ କିପରି ଚାହିଁ ରହିଥିଲା ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ଏକାଜାଗାକେ, ଦି’ଭଉଣୀ ଜିଲି ଓ ଚିଲି ଗାଧୋଇ ଚାଲିଯିବାର ଦୃଶ୍ୟକୁ, ନାକ ଫୁଲେଇ ଆଖୁ ନିଆଁ ଜାଳି ଉଠପଡ଼ ଛାତିରେ ଚାହିଁ ରହିଥିଲା ।
(ତ) ‘ତୁମ ପାଦୁକା ଶୀତଳ ଥାଉ’ କିଏ କାହାକୁ କହିଛି ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ‘ତୁମ ପାଦୁକା ଶୀତଳ ଥାଉ’ ଗାଁ ନାଇକ ଜଙ୍ଗଲ ଜମାକୁ ଏହା କହିଛି ।
(ଥ) କିଏ ଗାରଡ଼ ଜମାନ୍ କଥା ଚାରିଆଡ଼େ ଚହଳ ପକାଇ ବୁଲିଲା ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । କର୍ମକର୍ତ୍ତା ଡମ୍ବ ‘ବାରିକ’ ଗାରଡ଼ ଜମାନ୍ କଥା ଚାରିଆଡ଼େ ଚହଳ ପକାଇ ବୁଲିଲା ।
(ଦ) ଗାରଡ଼ ଜମାନ୍ କଥା ଚହଳ ପଡ଼ିବାପରେ କ’ଣ ହେଲା ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ଗାରଡ଼ ଜମାନ୍ କଥା ଚହଳ ପଡ଼ିଯିବା ପରେ, ଚାଉଳ, ଡାଲି, ଗାଁ ଫସଲ, ପନିପରିବା, କୁକୁଡ଼ା ଆଦି ଆଣି ଗାଁ ଲୋକ ରୁଣ୍ଡ ହେଲେ ।
(ଧ) ସୁକୃଜାନି କେଉଁ ଆଡ଼କୁ ଚାହିଁ ଦୀର୍ଘଶ୍ଵାସ ଯାଏ ଓ କାହିଁକି ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ଆଡ଼କୁ ଚାହିଁ ଦୀର୍ଘଶ୍ଵାସ ଯାଏ, କାରଣ ଅନ୍ୟମାନଙ୍କ ପରି ଜଙ୍ଗଲ ଜମାକୁ କହି ସେ କିପରି ଜମି ହାତେଇବ ।
(ନ) ସୁକୃଜାନିର ବଡ଼ ବଡ଼ କାଠ କାହିଁକି ଦରକାର ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ସୁକୃଜାନି ପୁଅମାନଙ୍କ ବିଭାଘର କରିଲା ପରେ ନିଆରା ଘର କରିବ, ସେଥିପାଇଁ ତା’ର ବଡ଼ ବଡ଼ କାଠ ଦରକାର ।
(ପ) ସୁକୃଜାନି କାହା ପାଖରେ କେତେବେଳେ ଓ କ’ଣ ଧରି ଉପାଧ୍ଵ ପଡ଼ିଲା ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ପାଖରେ ଦିନ ଦି’ପହରେ ଯୋଡ଼ିଏ କୁକୁଡ଼ା, ତିନୋଟି ପଣସ ଧରି ଉପାଧ୍ଵ ପଡ଼ିଲା ।
(ଫ) ସୁକୃଜାନି ପରଜାର ବିନୟ ଭଙ୍ଗୀରେ କ’ଣ କହିଲା ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ଭଙ୍ଗୀରେ କହିଲା, ‘ମହାପ୍ରଭୁ’ ତୁ ଦୟା ନକରେ ଆମେ ମରିଯିବୁ ନାହିଁକି ।’’
(ବ) ଆଜି ଗାଁ’ର ଗପ କ’ଣ ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ରେଙ୍ଗୁ ପରଜାର ପୁଅ ବାଗ୍ଲା ଆଉ ଜିଲି ପରସ୍ପରକୁ ଭଲ ପାଉଛନ୍ତି, ବିଭା ହେବେ, ସେହି ବିଷୟ ଆଜି ଗାଁର ଗପ ହୋଇଛି । ବାଗଲା କିଏ ?
(ମ) କାଜୋଡ଼ି ମୁହଁ ଝାଡ଼ି ଝାଡ଼ି କ’ଣ କହିଲା ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । କାଜୋଡ଼ି ମୁହଁ ଝାଡ଼ି ଝାଡ଼ି କହିଲା, ‘‘ଆମି ନିଚୁ ନିଚୁ (ଆମର ଦରକାର ନାହିଁ), ଆମର ‘ଭାଟ’ (ଭିଣୋଇ) କଥା କହ, ଶୁଣିବାକୁ
Question 4.
ପ୍ରାୟ ତିରିଶଗୋଟି ଶବ୍ଦରେ ଉତ୍ତର ଦିଅ । ପ୍ରଶ୍ନର ମୂଲ୍ୟ ୩ ନମ୍ବର । ଲେଖା ଓ ଲେଖକଙ୍କ ସୂଚନା ପାଇଁ ୧ ନମ୍ବର ଓ ଉତ୍ତର ପାଇଁ ୨ ନମ୍ବର ରହିବ।
(କ) ଲକ୍ଷ୍ମୀପୁରର ଅବସ୍ଥିତି ଉପସ୍ଥାପନ କର ।
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । କୋରାପୁଟରୁ ଲକ୍ଷ୍ମୀପୁର ଯିବାକୁ ହୁଏ । ଏହି ଯିବା ବାଟରେ ଲକ୍ଷ୍ମୀପୁର ଆଉ ଦେଢ଼ କୋଶ ବାଟ ଥାଇ ‘ଧର୍ମଦୁଆର’ ଘାଟି ପଡ଼େ । ସେହି ଘାଟିରେ ଏପାଖୁ ଚାଳିଶ, ସେପାଖୁ ପଚାଶ ପାହାଡ଼ ଠେଲାଠେଲି ଧକ୍କା ଧକ୍କି ହୋଇ ମୁହାମୁହିଁ ଠିଆ ହେଲାଭଳି ରହିଥା’ନ୍ତି । ସେହି ଘାଟିର ଦୂରରେ ଥାଏ ଛୋଟ ଛୋଟ ଆଦିବାସୀ ଗାଁ ।
(ଖ) ସୁକୃଜାନିର ସଂସାର ବିଷୟରେ ସଂକ୍ଷିପ୍ତରେ ଲେଖ ।
Solution:
ସୁକୃଜାନି ପରଜା ସମ୍ପ୍ରଦାୟର । ପରଜା ସାହିରେ ତା’ର ଟିକି ସଂସାରଟିକୁ ନେଇ ଖୁସିବାସିରେ ଚଳୁଥଲା । ଖାଇବା ପାଇଁ ମାଣ୍ଡିଆ ପେଜ ସଞ୍ଜ ସକାଳେ ଊଣା ପଡ଼େନାହିଁ କିମ୍ବା ଅଣ୍ଟାରେ ଡୋରକୁ ଚାରିଆଙ୍ଗୁଳି କୌପୁନୀ ଖଣ୍ଡିକର ଅଭାବ ନାହିଁ । ଭଲ ମନ୍ଦେ ଚଳିଯାଏ । ସଂସାର ବୋଇଲେ ସ୍ତ୍ରୀ ଗଲାପରେ ଦୁଇ ପୁଅ ମାଣ୍ଡିଆ ଓ ଟିକ୍ରା ଏବଂ ଦୁଇ ଝିଅ ଜିଲି ଓ ବିଲି । ଏହି ପିଲାମାନଙ୍କ ସୁଖ ସ୍ଵପ୍ନକୁ ନେଇ ସୁକୃଜାନିର ସଂସାର ।
(ଗ) ସୁକୃଜାନିର କାହା ଭିତରେ ନିଜକୁ ଖୋଜିପାଏ ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ଯାଇ ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ସୁକୃଜାନି ତା’ର ନୁଆଣିଆଁ କୁଡ଼ିଆର ଅଣଓସାର ପିଣ୍ଢାରେ ସଞ୍ଜ ପହରେ ଧୂଆଁପତ୍ର ପିକା ଟାଣୁ ଟାଣୁ ସଂସାର କଥା ଭାବି ଅନେକ ସୁଖ ସ୍ଵପ୍ନ ଦେଖେ । – ତା’ର ଚାରୋଟି ଛୁଆ ଧାଙ୍ଗଡ଼ା ଓ ଧାଙ୍ଗଡ଼ୀ, ନୁଆଁଣିଆ କୁଡ଼ିଆ, ଚାରି ପାଖରେ ପାହାଡ଼ ଜଙ୍ଗଲ ଓ ମଥା ଉପରେ ଆକାଶ, ଏତେ ବଡ଼ ବିସ୍ତୃତି ଭିତରେ ସେ ନିଜକୁ ଖୋଜିପାଏ ।
(ଘ) ସୁକୃଜାନିର ଘରକରଣା ସମ୍ପର୍କରେ ବର୍ଣ୍ଣନା କର ।
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି, ସୁକୃଜାନିର ସଂସାର ସମ୍ପର୍କରେ ପରିଚୟ ଦେବାକୁଯାଇ ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ସୁଗ୍ଧଜାନିର ବଖୁରିଆ ଘରଟିର ଅନ୍ଧାରୁଆ ଦେଖାଯାଉଥାଏ । ସେଥିରେ ଠାଆକୁ ଠାଆ ଜମା ହୋଇ ରହିଥାଏ ଆମ୍ବ ଟାକୁଆ, ତେଲ ପାଇଁ ବାରି ବାଇଗବା ମଞ୍ଜି, ଆଠ ଦଶମାଣ ମାଣ୍ଡିଆ ଓ ଥୁଆ ହୋଇଥାଏ ତିନି ଚାରୋଟି ହାଣ୍ଡି । ଚାଳରୁ ଓହଳିଥାଏ କେତୋଟି କୌପୁନୀ ଓ ଲୁଗା । ଆହୁରି ଥାଏ ତିନି ଚାରିପୁଞ୍ଜା ଲାଉତୁମ୍ବା, ପତରସିଆଁ ‘ତଲ୍’ ଓ ‘ତଲାରି’ । ଏତିକି ଘରକରଣା ଘରେ ଅଳିଆ ଦଳିଆ ହୋଇ ରହିଥାଏ ।
(ଙ) ‘ଡୁମା’ ବିଷୟରେ ସୁକୃଜାନିର ବିଶ୍ଵାସ କ’ଣ ?
Solution:
ବିଶ୍ଵାସକୁ ସୂଚିତ କରାଇଛନ୍ତି। ସୁକୃଜାନି ପ୍ରକୃତିର ଅପରୂପ ରୂପଶୋଭା ଓ ତା’ର ପରିବର୍ତ୍ତନକୁ ବିଶ୍ଵାସ କରେ, ଏସବୁ ହେଉଛି ଗୋଟିଏ ଗୋଟିଏ ଭୂତ ବା ‘ଡୁମା’ର କାମ । ସେହି ଡୁମା ପାଇଁ ସୃଷ୍ଟି ହୋଇଛି ଆକାଶ, ଜଙ୍ଗଲ, ସଞ୍ଜ ଆଉ ରାତି । କେଉଁ ଡୁମା ସୌଭାଗ୍ୟ ଦେଲାବେଳେ, ଆଉ କେଉଁ ଡୁମା ଆଣିଦିଏ ଝଡ଼ ତୋଫାନ ଓ ଦୁଃଖଦୁର୍ଦ୍ଦଶା ।
![]()
(ଚ) ସାନ ପାହାଡ଼କୁ ଦେଖ୍ କେଉଁ ଦୃଶ୍ୟ ସୁଗ୍ଧଜାନିର ଆଖ୍ ଆଗରେ ନାଚି ଯାଉଛି ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି, ସୁକୃଜାନିର ସଂସାର ସମ୍ପର୍କରେ ପରିଚୟ ଦେବାକୁଯାଇ ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି ।ଏହା ସୂଚିତ କରିଛନ୍ତି । ସାନ ପାହାଡ଼କୁ ଦେଖ୍ ସୁକୃଜାନିର ଆଖ୍ରେ ଅତୀତଟା ନାଚିଯାଏ । ସେ ଦେଖେ, ସେ ଆଉ ଲୋବୋ କନ୍ଧ ମିଶି ଢୁ ଢୁ ବରଷାରେ କୁରାଢ଼ିରେ ହାଣି ପାହାଡ଼କୁ ଚନ୍ଦା କରିଛନ୍ତି । ସେଦିନର ସେହି ପାହାଡ଼ ବର୍ତ୍ତମାନ ହୋଇଛି ଚାଷଭୂଇଁ ।
(ଜ) ‘ବୟସ ପଚାଶକୁ ଧକ୍କା ଖାଇଲା’ କାହା ପ୍ରସଙ୍ଗରେ ଓ କ’ଣ କୁହାଯାଇଛି ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି, ସୁକୃଜାନିର ଅତୀତ ସମ୍ପର୍କରେ ସୂଚନା ଦେବାକୁ ଯାଇ ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ସୁଜାନି ଅତୀତରେ କେବଳ ବଳକୁ ଚିହ୍ନିଥିଲା । ସେଥିପାଇଁ ସେ ଚାଷ କରିବାପାଇଁ ପାହାଡ଼ ଲଣ୍ଡା କରୁଥିଲା, ଯାହାକି ପାଞ୍ଚ ଛଅ ଘଣ୍ଟା କୁରାଢ଼ି ନଥୋଇ କାମ କରୁଥିଲା । ହାକିମମାନଙ୍କ ଦି’ମହଣ ବୋଝ ପାହାଡ଼ ଡେଇଁ ନେଇ ଯାଉଥିଲା । ଆବୁଆବୁଆ ବଳୁଆ ଦେହରେ ଗୋଡ଼ ପେଣ୍ଡା ପଥର ଓ ଚମଡ଼ା ଥିଲା ବର୍ଷାତି । କେବେ ବେମାର ପଡୁନଥିଲା । ମାତ୍ର ଏବେ ସେ ବଳ ନାହିଁ, ବୟସ ପଚାଶକୁ ଧକ୍କା ଖାଇଲା ।
(ଝ) ପାହାଡ଼ ତଳ ଝୋଲାର ଚିତ୍ର ଉପସ୍ଥାପନ କର ।
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି, ପାହାଡ଼ୀ ଇଲାକାର ପ୍ରାକୃତିକ ଶୋଭା ବର୍ଣ୍ଣନା ଅବକାଶରେ ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ପାହାଡ଼ ତଳ ଝୋଲା, ଉଞ୍ଚ ଚାଞ୍ଚରା ଉପରେ ଧଳାପାଣି ଡେଇଁ ଡେଇଁ ଦୁଲ୍ ଦୁଲ୍ କଚାଡ଼ି ହେଉଛି ଓ ଗଡ଼ିଗଡ଼ିକା ତଳକୁ ଆସୁଛି । ବଣଦେଶରେ ଏଗୁଡ଼ିକ ଯେପରି ଡୁଡୁମା ପରି । ମୁଣ୍ଡ ଉପରେ ବରଗଛ ଛାଇ ଓ ଢାଲୁ ଅତଡ଼ାରେ ସାବୁଜା ମାଣ୍ଡିଆ କ୍ଷେତ । ସରୁ ନାଲିରାସ୍ତା କଡ଼ରେ କଡ଼ରେ ଚାଲିଯାଉଛି ।
(ଟ) ଜଙ୍ଗଲ ଜମାନ୍ ଉପରେ ଦୃଷ୍ଟି ପଡ଼ିବା ପରେ ଦୁଇ ଭଉଣୀ କ’ଣ କଲେ ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି, ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ଜିଲି ଓ ବିଲି ଝୋଲାରେ, ଖୋଲା ଦେହରେ ଗାଧୋଉଥିବା ବେଳେ, ସେମାନଙ୍କୁ ଜଙ୍ଗଲ ଜମାନ୍ ଲୁଚି ଲୁଚି ଦେଖୁବା ସେମାନେ ଜାଣିଲେ । ଜିଲିର ଦୃଷ୍ଟିପଡ଼ିବା ପରେ ଦି’ଭଉଣୀ କିଲିକାଲିଆ ହୋଇ ଉଠିପଡ଼ିଲେ ଓ କାଚୁଥିବା ଲୁଗାକୁ ଜିଲି ବେଢ଼ାଇ ହେଲା ପରେ, ବିଲି ଭଉଣୀ ପଛରେ ଲୁଚିଯାଇ ତା’ର ନାଲି ଲୁଗା ଖଣ୍ଡକ ନେଇଆସିଲା । ହସରେ ହସରେ ସେମାନେ ତରତରରେ ଗାଧୁଆ ଶେଷକରି, ଓଦାଲୁଗାରେ ମାଠିଆ କାଖେଇ ଘରକୁ ଫେରିଲେ ।
(୦) ନାଇକର ଚରିତ୍ର ଚିତ୍ରଣ କର ।
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି, ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ଆଦିବାସୀ ସମ୍ପ୍ରଦାୟର ଲୋକମାନଙ୍କ ମଧ୍ୟରେ ଗାଁ ନାଇକର ଟିକିଏ ଗୁରୁତ୍ଵ ରହିଥାଏ । ନାଇକ ପିଣ୍ଢାରେ ଜଙ୍ଗଲ ଜମାନ୍ର ଛାଉଣି ପଡ଼େ । ସେ ଖଜଣା ଅସୁଲ କରି, ରାଜାଘର ରିବିଣି ଅମିନକୁ ଦିଏ ଏବଂ ଗାଁର ଖବର ଅନ୍ତର ସରକାରକୁ ଜଣାଏ । ଜଙ୍ଗଲ ଜମାନ୍ ଆସିଲେ ସେ କୈପୁନୀ ଉପରେ ପୁରୁଣା କୋଟ୍ ଖଣ୍ଡି ପିନ୍ଧି, ମୁଣ୍ଡରେ ପଗଡ଼ି ଭିଡ଼ି, ଜମାକୁ ଅଣ୍ଟାଭାଙ୍ଗି ଜୁହାର ହୁଏ । ଜମାନ୍ ଆସିବା କଥା ଜଗୁଆଳ ମାଧ୍ୟମରେ ପ୍ରଚାରକରି, ଜମାନ୍ କିପରି ଜିନିଷପତ୍ର ସହିତ ଗାଁରୁ ଫେରିବ ସେ ବ୍ୟବସ୍ଥା କରେ ।
(ଡ) ଜଙ୍ଗଲ ଜମାକୁ କ’ଣ ପାଇଁ କେତେ ଟିକସ ବା ଜୋରିମାନା ଦେବାକୁ ପଡ଼େ ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି, ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ଗୋରୁ ଚରାଇବା ପାଇଁ ହଳପିଛା ଲଙ୍ଗଳ ‘ପାନୁ’ ଦେବାକୁ ପଡ଼େ । ଜଙ୍ଗଲରେ ପୋଡୁଚାଷ କଲେ ଅଧିକ ଜୋରିମାନା ପଡ଼େ । କିଏ ବୋଆଇନ ଭାବେ ରିଜାର୍ଡ଼ଡ଼ ଜଙ୍ଗଲରୁ ମହୁ ଆଣିଛି, ଘର କରିବାକୁ ଶାଳ, ପିଆଶାଳ ଗଛ କାଟିଛି, ସବୁକଥାରେ ଜୋରିମାନ ଦେବାକୁ ହୋଇଥାଏ ।
(ଢ) ସୁକ୍ଳଜାନି କାହିଁକି ଉପାଧୂଆ ପଡ଼ିଥିଲା ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି, ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ସୁଜାନି ନିଜର ବଢ଼ନ୍ତା ପରିବାର ପାଇଁ ଜମି ଓ ଘର କରିବାପାଇଁ ବଡ଼ କାଠ ଦରକାର କରୁଥିଲା । କାରଣ ପୁଅ ବିଭା ହେଲେ ନିଆରା ଘର କରିବାର ଆବଶ୍ୟକତା ଥିଲା । ତେଣୁ ସୁକୃଜାନି ଦିନ ଦି’ପହରେ ଯୋଡ଼ିଏ କୁକୁଡ଼ା, ତିନୋଟି ପଣସ ଧରି ଜଙ୍ଗଲ ଜମାନ୍ ପାଖେ ଯାଇ ଉପାଧୂଆ ପଡ଼ିଥିଲା ।
(ଣ) ଜଙ୍ଗଲ ଜମାନର ହାବଭାବକୁ ପରଜା ଝିଅମାନେ କିପରି ସମାଲୋଚନା କରୁଥିଲେ ?
Solution:
‘ଶଶୁପଦର’ରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି, ଏହା ଉଲ୍ଲେଖ କରିଛନ୍ତି । ଜଙ୍ଗଲ ଜମାନର ହାବଭାବକୁ ପରଜା ଝିଅମାନେ ବିଭିନ୍ନ କଥାକହି ସମାଲୋଚନା କରୁଥିଲେ । କେହି କହୁଥିଲା, ‘ମୋତେ ଅନୋଉଁଥୁଲା’, ଆଉ କେହି କହୁଥିଲା, ‘ମୋର ପଛ ପଛ ଧାଉଁଥିଲା ।’ ‘ଛୋଟ-ସରୁ ଡାଙ୍ଗପରି ମଣିଷଟେ, ସେଇଟା ତହିଁରେ ପୁଣି କେଡ଼େ ହମହମ’, ‘ଯୋଉ ପାଟି, ମୁଁ ତ ଡରିଗଲି’, ‘ଦେଖତ ଆମର କାଳି କୁକୁଡ଼ାଟା ଡିମ୍ବ ଦେଇଥୁଲା, ବାପା ତାକୁ ଦେଇଦେଲା’, ଏହିପରି ଅନେକ କଥା କହି ସେମାନେ ହସୁଥିଲେ ।
Question 5.
ନମ୍ବର ସମ୍ବଳିତ । ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୧୫୦ ଶବ୍ଦରେ ଦେବାକୁ ହେବ ।
(କ) ପରଜା ସମାଜ ଜୀବନର ବାସ୍ତବ ଚିତ୍ର ‘ଶଶୁପଦର’ ପାଠ୍ୟଶରେ କିପରି ପ୍ରତିଫଳିତ ଆଲୋଚନା କର ।
Solution:
ସମାଜ ଜୀବନର ଚଳଣି, ରୁଚିବୋଧ ଓ ସେଠାରେ ରହିଥିବା ପରିବେଶକୁ ଏପରି ଖଞ୍ଜି ଦେଇଛନ୍ତି, ଯାହା ଫଳରେ ତାଙ୍କର ସାରସ୍ବତ ସାଧନା ହୋଇଛି କାଳଜୟୀ ଓ ଅନତିକ୍ରମଣୀୟ ! ବିଶେଷ କରି ଆଦିବାସୀ ଜନଜୀବନକୁ ନେଇ ସେ ଯେଉଁ କେତୋଟି ଉପନ୍ୟାସ ରଚନା କରିଛନ୍ତି, ସେଥୁରୁ ତାଙ୍କର ଉନ୍ନତ ଅନୁସନ୍ଧିତ୍ସୁ ଦୃଷ୍ଟିଭଙ୍ଗୀକୁ ଆକଳନ କରାଯାଇପାରେ ।
ଧର୍ମଦୁଆର ଘାଟିରୁ ଉତ୍ତରକୁ କୋଶେ ଦୂରରେ ରହିଥାଏ ଛୋଟ ଗାଁଟିଏ ଶଶୁପଦର । ଏଠାରେ ଗୋଟିଏ ଜାତିର ଲୋକେ ବାସ କରନ୍ତି ନାହିଁ । ଗାଁରେ ତିନୋଟି ଜାତିର ଲୋକ ବାସ କରନ୍ତି । ସେଗୁଡ଼ିକ ହେଉଛି ଡମ୍ବ ସାହି, ଗାଦ୍ବା ସାହି ଓ ପରଜା ସାହି । ଗାଁରେ ଧାଡ଼ି ଧାଡ଼ି ଘର ଓ ଘରପାଖକୁ ଟଣିଅଁ ବାଡ଼ରେ ନିବୁଜ ହୋଇ ରହିଥାଏ, ବିଭିନ୍ନ ପ୍ରକାର ଫସଲ । ଏ ଛୋଟ ଗାଁରେ ପରଜା ସମ୍ପ୍ରଦାୟର ପରିବାର ମଧ୍ୟରେ ଗୋଟିଏ ହେଉଛି ସୁକୃଜାନିର ପରିବାର ।
ସୁକୃଜାନି ପରିବାରର ଚଳଣି, ଛୋଟ କୁଡ଼ିଆଘରେ ଗଦା ହୋଇଥିବା ଜିନିଷକୁ ନେଇ, ସେହି ସମାଜର ଯଥାର୍ଥ ଚିତ୍ର ଉପସ୍ଥାପନ କରେ । ସଞ୍ଜ ହେଲେ ସୁକୃଜାନି ତା’ କୁଡ଼ିଆର ଅଣଓସାରିଆ ପିଣ୍ଡାରେ ବସି ପିଙ୍କା ଟାଣେ । ଝିଅ ଜିଲି କିମ୍ବା ବିଲି ଗୋଟିଏ ହାଣ୍ଡିରେ ମାଣ୍ଡିଆଚୂନା କି ଶାଗ କି ଫେସା ହୋଇଥିବା ଆମ୍ବ ଟାକୁଆର କୋଇଲି ଅଜାଡ଼ି ଦେଇ, ଚୂଲିରେ ବସାଇଦେଇ ଗୋଡ଼ ଲମ୍ବାଇ ବସି ଚୁଲି ଜାଳନ୍ତି । ଫାଳିକିଆ ଖୋସାରେ ସେମାନେ ଗୋଟିଏ ନାଲିଫୁଲ ଖୋସି ଦେଉଥିଲେ । ଏହି ଗୋଟିଏ ପରିବାର ଚଳଣି ଓ ଚିତ୍ର ସମଗ୍ର ପରଜା ଜୀବନକୁ ପ୍ରତୀକିତ କରେ ।
ସୁକୃଜାନିର ସ୍ତ୍ରୀ ସମ୍ବାରି ଗଲାଦିନୁ ସେ ଦୁଇ ପୁଅ ଓ ଦୁଇ ଝିଅଙ୍କୁ ନେଇ ଅନେକ ସ୍ବପ୍ନ ଦେଖେ । ତା’. ଶେଷ ଜୀବନ କଥା ଭାବେ । ସେ ମରିଗଲା ପରେ, ତା’ନାଁରେ ଗାଁ ଗୁରୁଡ଼ି ଆମ୍ବଗଛତଳେ ଗୋଜିଆ ପଥର ପୋତାହେବ ଏବଂ ସେ ଡୁମା ପରଜାମାନେ କିପରି ଝୋଲାରେ ଲଙ୍ଗଳା ହୋଇ ସ୍ନାନ କରନ୍ତି, କେହି ସଭ୍ୟମଣିଷ ଦେଖିଲେ ସେମାନେ କିପରି ପ୍ରତିକ୍ରିୟା ପ୍ରକାଶ କରନ୍ତି; ଜଙ୍ଗଲ ଜମାନ୍ ସରଳ ଆଦିବାସୀ ଲୋକଙ୍କୁ କିପରି ବିଭିନ୍ନ ଭାବରେ ଶୋଷଣ କରନ୍ତି, ଜଙ୍ଗଲ ଅତି ମନୋଜ୍ଞ ଭାବରେ ପ୍ରକାଶ କରିଛନ୍ତି । ଉପରୋକ୍ତ ଦୃଷ୍ଟିକୋଣରୁ ବିଚାରକଲେ ‘ଶଶୁପଦର’ର ସାମାଜିକ ମୂଲ୍ୟବୋଧ ଅନନ୍ୟ ।
(ଖ) ‘ଶଶୁପଦର’ ‘ସରକା’ ଉମଲଘର ମମତସ ପଦଣ – ଏହାର ସତ୍ୟତା ବିଚାର କର ।
Solution:
ସାହିତ୍ୟ ସୃଷ୍ଟିରେ ବା ଯେକୌଣସି ସାରସ୍ଵତ ସାଧନା ପୁସ୍ତକରେ ମୁଖବନ୍ଧର ମୂଲ୍ୟକୁ ଅସ୍ଵୀକାର କରାଯାଇ ପାରେନା । ମୁଖବନ୍ଧ ହିଁ ସମଗ୍ର ପୁସ୍ତକର ଇତିବୃତ୍ତ । ମନ୍ଦିରକୁ ପ୍ରବେଶ କରିବା ପୂର୍ବରୁ ମୁଖଶାଳାକୁ ଦେଖୁଲେ, ଯେପରି ମନ୍ଦିରର ବିଶେଷତା, ଭାସ୍କର୍ଯ୍ୟକୁ ଅନୁମାନ କରିହୁଏ, ଠିକ୍ ସେହିପରି ମୁଖବନ୍ଧରୁ ହିଁ ପୁସ୍ତକର କଥାବସ୍ତୁ, ବର୍ଣ୍ଣନା ଚାତୁରୀ, ଚରିତ୍ରଚିତ୍ରଣ, ସାମାଜିକ ମୂଲ୍ୟବୋଧ ଆଦିକୁ ବିଚାର କରାଯାଇଥାଏ । ଅନ୍ୟ ଅର୍ଥରେ ଦେଖିଲେ ଅନେକ ସମୟରେ ବିନ୍ଦୁରେ ସିନ୍ଧୁ ଦର୍ଶନ କଲାଭଳି ମୁଖବନ୍ଧରେ ହିଁ, ସାରା ସାଧନାର ମୂଲ୍ୟାୟନ କରାଯାଇପାରେ । ଆଲୋଚ୍ୟ ଉପନ୍ୟାସ ପର୍ଯ୍ୟାୟ ।
ଏଥିରେ ଶଶୁପଦର ଗାଁର ଜୀବନଚିତ୍ର ଓ ସମଗ୍ର ଉପନ୍ୟାସର ମୁଖ୍ୟଚରିତ୍ର, ସରକାରୀ ମଣିଷ ବା ସଭ୍ୟମଣିଷଙ୍କର ଆଦିବାସୀଙ୍କ ଶୋଷଣକୁ ଯେଭଳି ଚିତ୍ରଣ କରାଯାଇଛି, ସେଥୁରୁ ସମଗ୍ର ଉପନ୍ୟାସର କଥାବସ୍ତୁକୁ ବିଚାର କରିହୁଏ । ସୁତରାଂ ‘ଶଶୁପଦର’ ‘ପରଜା’ ଉପନ୍ୟାସର ହିଁ ମୁଖବନ୍ଧ ସଦୃଶ । ଧର୍ମୀୟ ଭାବନା ସୃଷ୍ଟି ହୁଏ । ଉପନ୍ୟାସର ଅନ୍ୟତମ ମୂଳଚରିତ୍ର ସୁକୃଜାନି ପ୍ରକୃତି ପରିବର୍ତ୍ତନକୁ ଦେଖ୍ ଅନୁମାନ କରେ, ସବୁଗୁଡ଼ିକ ହେଉଛି ଗୋଟିଏ ଲେଖାଁ ଭୂତ ବା ‘ଡୁମା’ । ଏହି ଡୁମାପାଇଁ ସବୁକିଛି ହେଉଛି । ସୁକୃଜାନିର ପାରିବାରିକ ଜୀବନଚିତ୍ର, ଘରକରଣା, ହସଖୁସିର ସଂସାର, ପିଲାମାନଙ୍କୁ ନେଇ ସୁଖସ୍ବପ୍ନ ଦେଖିବା ଯେ ଉପନ୍ୟାସର ମୁଖ୍ୟ କଥାବସ୍ତୁ, ଏହା ଅନୁମାନ କରିହୁଏ ।
ସହରୀ ମଣିଷ ବିଭିନ୍ନ ଭାବରେ ଶୋଷଣ କରନ୍ତି ଆଦିବାସୀମାନଙ୍କୁ । ସରକାରୀ ମଣିଷ ଭାବରେ, ସଭ୍ୟମଣିଷ ରୂପରେ ଏହି ଅଧାଲଙ୍ଗୁଳି ଲୋକଙ୍କୁ କେତେ କ’ଣ କହି କଷ୍ଟ ଉପାର୍ଜିତ ଦରବକୁ ଠକିନିଅନ୍ତି । ଏଥିରେ ସହାୟ ହୋଇଥା’ନ୍ତି, ସେମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ଗାଁ ନାଇକ । ସେମାନେ ଯେ କେବଳ ଧନଦରବ, ଫସଲ ଉପରେ ଆଖୁ ରଖନ୍ତି ନାହିଁ, ବରଂ ସେମାନଙ୍କ ବଢ଼ିଲା ଝିଅ, ଯାହାକି ଆଦିବାସୀ ମଣିଷର ମର୍ଯ୍ୟାଦା, ତାହାକୁ ମଧ୍ୟ ସମୟ ସୁଯୋଗ ଦେଖ୍ ହରଣ କରନ୍ତି । ଜଙ୍ଗଲ ଜମାନ୍ ପର୍ଯ୍ୟାୟରେ ଔପନ୍ୟାସିକ ଏହା ସୂଚାଇ ଅଛନ୍ତି । ଉପନ୍ୟାସର କଥାବସ୍ତୁରେ ଏହାହିଁ ବିଶେଷ ପ୍ରସଙ୍ଗ ବୋଲି ବିଚାର କରାଯାଏ ।
ଆଦିବାସୀମାନଙ୍କ ମଧ୍ୟରେ ଔପନ୍ୟାସିକ ସୁଜାନି ଭଳି ଚରିତ୍ରର ବର୍ଣନା କରିଥିଲେ ହେଁ, ମାଣ୍ଡିଆଜାନି, ଟିକ୍ରାଜାନି, ବାଗଲ୍, ଜିଲି, ବିଲି, କାଜୋଡ଼ିମାନଙ୍କ ଚରିତ୍ର ମାଧ୍ୟମରେ ଧାଇଁ ଓ ଧାଙ୍ଗୁଡ଼ୀମାନଙ୍କ ମନରେ ଗୋପନକଥାକୁ ସୂଚାଇ ଅଛନ୍ତି । ମାଣ୍ଡିଆଜାନି କାଜୋଡ଼ିକୁ ବିବାହ କରିବାକୁ ଥିଲାବେଳେ, ଜିଲି ବାଗ୍ଲାର ମନୋନୀତ । ଏମାନଙ୍କର ପ୍ରେମକାହାଣୀ କେଉଁ ପର୍ଯ୍ୟାୟରେ ପହଞ୍ଚିବ ତାହାକୁ ବିଚାର କରାଯାଇପାରେ । ଏହିପରି ବିଭିନ୍ନ ଦୃଷ୍ଟିକୋଣରୁ ବିଚାରକରି ଦେଖିଲେ, ‘ଶଶୁପଦର’ ହିଁ ‘ପରଜା’ ଉପନ୍ୟାସର ମୁଖବନ୍ଧ ବୋଲି ଆକଳନ କରାଯାଇପାରେ |
(ଗ) ସୁଜାନିର ଚରିତ୍ର ଚିତ୍ରଣ କର।
Solution:
ଚରିତ୍ର ଚିତ୍ରଣ ସାହିତ୍ୟରେ ଏକ ସ୍ବତନ୍ତ୍ର କଳା । ଚରିତ୍ରମାନେ ସାହିତ୍ୟ ସ୍ରଷ୍ଟାର ମାନସ ସନ୍ତାନ । ସ୍ରଷ୍ଟା ଯାହା କହିବାକୁ ଚାହେଁ, ଯାହା ସନ୍ଦେଶ ଦେବାକୁ ଚାହେଁ, ସେ ସିଧାସିଧ୍ ନିଜେ ନକହି ଚରିତ୍ର ମାଧ୍ୟମରେ ହିଁ କହିଥାଏ । ଚରିତ୍ରମାନେ ‘ପରଜା’ ଉପନ୍ୟାସର ପ୍ରଥମ ପର୍ଯ୍ୟାୟରେ ‘ଶଶୁପଦର’ରେ ଆଦିବାସୀ ମଣିଷ ସୁକୃଜାନିର ଚରିତ୍ରକୁ ସୁନ୍ଦର ଭାବରେ ଚିତ୍ରଣ କରିଛନ୍ତି । ସୁକୃଜାନି ଚରିତ୍ରକୁ ଅଧ୍ୟୟନ କଲେ, ପରଜା ମଣିଷର ଚିନ୍ତାଚେତନା, ସମ୍ଭାବନାମୟ ଦୃଷ୍ଟିଭଙ୍ଗୀକୁ ଆକଳନ କରିହୁଏ । ସୁକୃଜାନି ଆଦିବାସୀ ମଣିଷ ହିସାବରେ ଦେହ ମେହନତ କରି ସଂସାର ଗଢ଼ିଛି । ବୟସ ପଡ଼ିଆସିଲାବେଳକୁ ଯୁଆନ ପୁଅଙ୍କଠାରେ ନିଜର ଅତୀତକୁ ଖୋଜି ବସିଛି ।
ସବୁଥରେ ସେ ଖୁସି । ତା’ର ଛୋଟ ସଂସାରରେ ସବୁବେଳେ ପିନ୍ଧିବାକୁ ଅଣ୍ଟାର ଡୋରକୁ ଚାରି ଆଙ୍ଗୁଳିଆ କୌପୁନୀ ଖଣ୍ଡିକରେ କେବେ ଊଣା ହୋଇନାହିଁ । ସେ ଖୁସି ଭିତରେ ସେ ତିନିବର୍ଷ ଭିତରେ ଭାରିଯା ସମ୍ମାରିକୁ ହରାଇଛି । ସଂସାରରେ ରହିଛନ୍ତି, ସୁକୃଜାନି ନିଜେ, ବଡ଼ପୁଅ ମାଣ୍ଡିଆ, ସାନପୁଅ ଟିକ୍ରା ଓ ଝିଅ ଦୁଇଜଣ ଜିଲି ଓ ବିଲି । ସଞ୍ଜବେଳେ ସୁକୃଜାନି ତା’ର ଛୋଟ କୁଡ଼ିଆଘରର ଅଣଓସାରିଆ ପିଣ୍ଡାରେ ବସି ପିଙ୍କା ଟାଣେ । ପିଙ୍କା ଟାଣୁ ଟାଣୁ ସେ ଭବିଷ୍ୟତକୁ ନେଇ ସୁଖର ସ୍ଵପ୍ନକୁ କେତେ କ’ଣ ଆଶାର ଗାଲିଚା ବୁଣେ । ତା’ର ଗୋଟିଏ ବୋଲି ବଖରା ଘର । ସେଥିରେ କେତେ କ’ଣ ଘରକରଣା ଚିଜ ପୁଳା ପୁଳା ରହିଥାଏ । ଅନ୍ଧାର ଘରୁ ନାକ କାନ ରୁନ୍ଧା ମଠୁଆ ମଠୁଆ ଧୂଆଁ ତା’କୁ ଭଲଲାଗେ ।
କାରଣ ସବୁକୁ ସେ ନିଜର ବୋଲି ଭାବିଥାଏ । ସୁକୃଜାନି ପ୍ରକୃତିର ପରିବର୍ତ୍ତନ, ସଞ୍ଜ ସକାଳ, ଆକାଶ ଜଙ୍ଗଲର ସ୍ରଷ୍ଟାକୁ ଭୂତ ବା ଡୁମା ବିଚାରରେ ‘ଯାଦୁକର ‘ଡୁମା’ ଏସବୁ ଗଢ଼ିଛି– ଆକଶ ଆଉ ଜଙ୍ଗଲ, ସଞ୍ଜ ଆଉ ରାତି । କେଉଁ ଡୁମା ଆଉ ଆନନ୍ଦ । କିଏ ଆଣିଦିଏ ଝଡ଼ ତୋଫାନ, ଦୁଃଖଦୁର୍ଦ୍ଦଶା ।
ସୁକୃଜାନି ଆଗରେ ଥିବା ସାନ ପାହାଡ଼କୁ ଦେଖ୍, ତା’ର ଅତୀତକୁ ମନେପକାଏ । ସେ ଆଉ ଲୋବୋ କନ୍ଧ ମିଶି ପୁଣି ଭବିଷ୍ୟତକୁ ଦେଖ, କେଉଁସେ ଉପକାରୀ ଡୁମା ପାଇଁ କେତେ ଘର ବଂଶଧର ରହିବେ । ସେ ମରିଗଲା ପରେ, ତା’ପାଇଁ ଗାଁ ମଝି ଗୁରୁଡ଼ି ଆମ୍ବଗଛ ତଳେ, ତା ନାଁରେ ଗୋଜିଆ ପଥର ପୋତାହେବ ଏବଂ ସେଥିରେ ସେ ଗୋଟିଏ ଆତ୍ମା ବା ଡୁମା ହୋଇ ଭବିଷ୍ୟତର ପୁଅନାତିର ସୁଖ ସୌଭାଗ୍ୟ ଦେଖୁବ ।
ନିଜ ପରିବାରର ଭବିଷ୍ୟତ ଓ ସୁଖସୁବିଧା ପାଇଁ ସେ ଜଙ୍ଗଲ ଜମାନ୍ ପାଖରେ ଉପାଧୂଆ ପଡ଼ିଛି । କୁକୁଡ଼ା ଓ ପଣସ ଦେଲାପରେ ପୁଣି ଅଣ୍ଟାରୁ ଦୁଇଟଙ୍କା କାଢ଼ିଦେଇଛି । ପୁଅ ବିବାହ ପାଇଁ ନୂଆଘର କରିବ, ଚାଷଜମି କରିବାପାଇଁ ସ୍ୱୀକୃତି ନେଇଛି । ଜଙ୍ଗଲ ଜମାନ୍ ‘ହଉ’ କହିଦେଲା ପରେ, ସୁକୃଜାନିର ଆନନ୍ଦ ରଖିବାକୁ ଜାଗା ନଥାଏ ।
![]()
(ଶ) ପଣ୍ୟ ମଣିଶ ଓ କନକାତି ମଣିକର କାବନହମି ‘ଶଶୁପଦର’ ପାଠ୍ୟାଶାରେ କିପରି ପ୍ରାଥମ ଭାବରେ ଉପସ୍ଥାପିତ ହୋଲଛି – ଆଲୋଚନା କର ।
Solution:
ଔପନ୍ୟାସିକ ସୁନ୍ଦର ଭାବରେ ଉପସ୍ଥାପିତ ହୋଇଛି ଆଲୋଚନା କର । ରଚନା କରିଛନ୍ତି । ସେହିସବୁ ଜନଜାତିର ଜୀବନଚର୍ଯ୍ୟା ବର୍ଣ୍ଣନା, ତାଙ୍କ ସାରସ୍ଵତ ଲେଖନୀକୁ ଦେଇଛି ସ୍ବତନ୍ତ୍ର ମର୍ଯ୍ୟାଦା । ସଭ୍ୟମଣିଷଠାରୁ ଦୂରରେ ରହି, ସରଳ ଜୀବନ ଯାପନ କରି ସେମାନେ ହସି ଖେଳି ଆନନ୍ଦରେ ରହିବାକୁ ଚାହାଁନ୍ତି । ମାତ୍ର ଅନେକ ସମୟରେ ସଭ୍ୟମଣିଷ, ନିଜର ସ୍ଵାର୍ଥପାଇଁ ବୁଦ୍ଧିବଳରେ ସେହି ଜନଜାତିର ଲୋକମାନଙ୍କୁ ଶୋଷଣ କରିଥାଏ ।
ଆଦିବାସୀ ମଣିଷ ବନ୍ୟ ପ୍ରକୃତି କୋଳରେ ଜନ୍ମ ନେଇଛି, ବଢ଼ିଛି, ଖେଳିଛି ଓ ସେଥିରେ ସେ ଅନେକ ସୁଖସ୍ଵପ୍ନକୁ ହାତେଇ ନେବାକୁ ଇଚ୍ଛା କରିଛି । ମାଣ୍ଡିଆ ପେଜ ଟୋପିକ ପିଇବେ ଓ ଚାରିଆଙ୍ଗୁଳିଆ କୌପୁନୀ ପିନ୍ଧିବେ, ସେତିକି ସେ ଆଶାକରେ । ପୁଣି ପୁଅ ବିବାହ କଲେ, ପୁଅ ପାଇଁ ଅଲଗା ଘର ତୋଳିବାର ଇଚ୍ଛା ପ୍ରକାଶ କରେ । ପୁଅ ଓ ପୁଅର ପୁଅ, ପୁଣି ଆହୁରି ପୁଅକୁ ନେଇ ସେ ମନ ଆନନ୍ଦ କରେ । ସେତିକିରେ ସେ ଖୁସିଥାଏ । ସେହିପରି ଜଙ୍ଗଲ ଦେଶର ଧାଙ୍ଗୁଡ଼ା ବା ଯୁବକମାନେ ଦିନସାରା ଖଟି ଖଟି ଘରକୁ ଫେରନ୍ତି । ଘରେ ପେଜ ମୁନ୍ଦିକ ପିଇଦେଇ ମନ ଖୁସି କରିବାକୁ ଚାଲିଯାଆନ୍ତି । ଝିଅମାନେ ଘରକାମ ସାଙ୍ଗକୁ ଶାଗ ତୋଳିବା, ପେଜ ରାନ୍ଧିବା କାମ କରନ୍ତି ।
ମୁଣ୍ଡରେ ବଙ୍କା ଖୋସାକରି, ସେଥୁରେ ନାଲିଫୁଲ ଖୋସି, ରଙ୍ଗରଙ୍ଗିଆ ଲୁଗାପିନ୍ଧି ସାଙ୍ଗମାନଙ୍କୁ ସହିତ ଥଟ୍ଟାମଜାରେ ବେଳନିଅନ୍ତି । ସେମାନଙ୍କର ଦେହ ଅଭିମାନ ନଥାଏ । ଏପରିକି ପୁଅମାନେ ଚାରିଆଙ୍ଗୁଳିଆ କୈପୁନୀ ପିନ୍ଧିଲାବେଳେ, ଝିଅମାନେ ଲଙ୍ଗଳାହୋଇ ଗାଧାନ୍ତି । ଝିଅମାନଙ୍କ ଗାଧୁଆ ତୁଠକୁ ଜନଜାତିର ପୁରୁଷଲୋକ ଯାଆନ୍ତି ନାହିଁ କିମ୍ବା ଅନାନ୍ତି ନାହିଁ ।
ସଭ୍ୟମଣିଷ ସରକାରୀ ମଣିଷ ଭାବରେ ଜନଜାତିର ଲୋକମାନଙ୍କ ପାଖରେ ପହଞ୍ଚାଯାଏ । ସରଳ ଆଦିବାସୀ ମଣିଷ ସଭ୍ୟ ମଣିଷକୁ ଖାତିରି କରେ, ମର୍ଯ୍ୟାଦା ଦିଏ, ଏପରିଙ୍କ ମହାପ୍ରଭୁ ବୋଲି ସମ୍ବୋଧନ କରେ । ସେହି ସୁଯୋଗରେ ସଭ୍ୟମଣିଷ ବିଭିନ୍ନ ଟିକସ ନାମରେ, ଜନଜାତିର ମଣିଷଙ୍କ ଫସଲ, ଫଳମୂଳ, କୁକୁଡ଼ା ଓ ଟଙ୍କା ଆଦି ଠକିନିଏ । ବିନା ପାରିଶ୍ରମିକରେ ବୋଝ ବୋହିବାକୁ ଜନଜାତିର ଲୋକଙ୍କୁ ବାଧ୍ୟକରେ । ଦିମହଣ ବୋଝକୁ ଭାରକରି ପାହାଡ଼ ଜଙ୍ଗଲ ରାସ୍ତାରେ କୋଶେ ଗଲେ ପଇସାଏ ଦିଏ । କେବଳ ପରିଶ୍ରମ ଓ ଧନ ଉପରେ ସଭ୍ୟମଣିଷ ଆଖୁ ରଖୁଥାଏ । ଦରକାର ପଡ଼ିଲେ ସୁଯୋଗ ଦେଖ୍, ସେମାନଙ୍କ ଝିଅମାନଙ୍କ ଉପରେ ପାପ ଆଖୁ ପକାଏ ।
ଜଙ୍ଗଲ ଜମାନ୍ ଜିଲି ବିଲିର ଲଙ୍ଗଳା ଦେହକୁ ଲୁଚି ଲୁଚି, ବାଆଁରେଇ ଦେଖୁଛି । ସେମାନଙ୍କ ସହିତ ଥଟ୍ଟା ମଜା ହୋଇଛି । ଜଙ୍ଗଲ ଜମାନ୍ ଚାଲିଗଲାପରେ ଗାଁ ଝିଅମାନେ ପରିହାସ କରି ପଛରେ କେତେକଥା କହିଛନ୍ତି । ସେମାନେ କହିଛନ୍ତି – ‘ମୋତେ ଅନୋଉଁଥୁଲା’’, ‘ମୋର ପଛ ପଛ ଧାଉଁଥୁଲା’’, ‘‘ଛେ ସରୁ ଡ଼ାଙ୍ଗ ପରି ମଣିଷଟେ ସେଇଟା ତହିଁରେ ପୁଣି ହମହମ୍ ।’’ ସବୁ କଥା ହସରେ ହସରେ ସେମାନେ କହିଛନ୍ତି ।
(ଙ) ‘ଶଶୁପଦର’ ଅନୁସରଣରେ ଗୋପୀନାଥଙ୍କ ବର୍ଣ୍ଣନା ବୈଚିତ୍ର ଓ ଭାଷା ଉପସ୍ଥାପନାର ସ୍ବତନ୍ତ୍ରତା ବିଚାର କର ।
Solution:
ଓଡ଼ିଆ ଉପନ୍ୟାସ ସାହିତ୍ୟରେ ଯେଉଁ କେତେଜଣ କାଳଜୟୀ ଔପନ୍ୟାସିକ ସେମାନଙ୍କ ସୃଷ୍ଟି ପାଇଁ ଏକାଧ୍ଵକବାର ପୁରସ୍କୃତ ହୋଇଛନ୍ତି, ସେମାନଙ୍କ ମଧ୍ୟରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଅନ୍ୟତମ । ସେ ବିଭିନ୍ନ କଥାବସ୍ତୁକୁ ନେଇ, ଏପରିକି ଜନଜାତିର ବାସ୍ତବ ଜୀବନଚର୍ଯ୍ୟାକୁ ନେଇ ଉପନ୍ୟାସ ରଚନା କରିଥିଲେ ବି, ସବୁଥିଲେ ତାଙ୍କର ଉପସ୍ଥାପନ କୌଶଳ ଥିଲା ନିଆରା । ସେ ଯାହା କହନ୍ତି ଏମିତି ଟିକିନିଖ୍ କରି କହନ୍ତି, ଯାହାକି ପାଠକ ନିକଟରେ ଅବିକଳ ଚିତ୍ରପଟ ଭଳି ଉଦ୍ଭାସିତ ହୋଇଉଠେ । ପୁନଶ୍ଚ ସେ ମନ ପୂରିଗଲା ଭଳି, ଆତ୍ମା ବୁଝିଗଲା ଭଳି ରୂପକଳ୍ପ ଓ ଚିତ୍ରକଳ୍ପରେ ‘ଶଶୁପଦର’ର ଅବସ୍ଥିତିକୁ ବର୍ଣ୍ଣନା କରି ଲେଖକ କହିଛନ୍ତି, କୋରାପୁଟରୁ ଲକ୍ଷ୍ମୀପୁର ଯିବା ରାସ୍ତାରେ, ଲକ୍ଷ୍ମୀପୁର ମୋଟେ ଦେଢ଼କୋଶ ଥାଇ ଧର୍ମଦୁଆର ଘାଟି ପଡ଼େ ।
ସେହି ଧର୍ମଦୁଆର ଘାଟିରୁ ଉତ୍ତରକୁ କୋଶେ ଗଲେ ପଡ଼େ ଶଶୁପଦର ! ଘାଟିର ବର୍ଣ୍ଣନା କରି ସେ ଲେଖୁଛନ୍ତି – ‘ଏ ପାଖୁ ଚାଳିଶ ସେପାଖୁ ପଚାଶ ପାହାଡ଼ ଠେଲାଠେଲି ଧକ୍କା ଧକ୍କି ହୋଇ ମୁହାଁମୁହିଁ ଠିଆ ହୋଇଛନ୍ତି ।’’ ସୁକୃଜାନି ସଞ୍ଜବେଳେ ତା’ର ଅଣଓସାରିଆ ପିଣ୍ଡାରେ ବସି ପିଙ୍କା ଟାଣେ । ସେହି ପିଙ୍କା ଟଣାରୁ, ‘ମନଭିତରେ କିପରି ଗୋଟିଏ ଆଶ୍ରୟମୟ ତୃପ୍ତି ସେ ପାଏ । X X ଚାରିପାଖରେ ପାହାଡ଼ ଜଙ୍ଗଲ ଆଉ ମଥା ଉପରେ ଏତେବଡ଼ ଆକାଶ, ଏତେବଡ଼ ବିସ୍ତୃତି – ଏହା ଭିତରେ ବି ନିଜକୁ ସେ ଖୋଜିଲେ ପାଏ, ନିଜେ ରହିଛି ବୋଲି ବୁଝେ ।
ସୁଜାନିର ଘର ଓ ଘରକରଣାର ବର୍ଣ୍ଣନା ପୂରା ଫଟୋଗ୍ରାଫିକ୍, ଯାହାକି ଆଦିବାସୀ ଘରର ଚଳଣି ଓ ଦୃଶ୍ୟକୁ ପାଠକଙ୍କ ନିକଟରେ ପହଞ୍ଚାଇଦିଏ । ସେହିପରି ସଞ୍ଜବୁଡ଼ିବାର ଦୃଶ୍ୟକୁ ବର୍ଣ୍ଣନାକରି ଔପନ୍ୟାସିକ ଲେଖୁଛନ୍ତି – ‘ସଞ୍ଜବୁଡ଼େ – ଢେଉ ଢେଉକା ପୂର୍ବଘାଟର ପାହାଡ଼ ଉପରେ ଛିରିକି ପଡ଼େ କେତେ ରଙ୍ଗ, ମଥାରେ ଅବିର, ପଖାରେ ହଳଦୀଗୁଣ୍ଡା, ତଳର ଗହୀର ଜଙ୍ଗଲରେ ସମୁଦ୍ରର ନେଳି-କଳା ନେଳି କଳା ।’’ ସୁକୃଜାନିର ଅତୀତକୁ ବର୍ଣ୍ଣନା କରିଛନ୍ତି ଔପନ୍ୟାସିକ । ଶେଷ ପର୍ଯ୍ୟାୟରେ ଲେଖୁଛନ୍ତି – ‘ଆବୁଆବୁଆ ବଳୁଆ ଦେହର ଗୋଡ଼-ପେଣ୍ଡା ତା’ର ପଥର, ଚମଡ଼ାଟି ତା’ର ବର୍ଷାତି ।’’
‘‘ଉଞ୍ଚ ଚାଞ୍ଚରା (ଚଟାଣ) ଉପରେ ଧଳା ପାଣି ଡେଇଁ ଡେଇଁ ଦୁଲ୍ ଦୁଲ୍ ହୋଇ କଚାଡ଼ି ହେଉଛି, ଗଡ଼ି ଗଡ଼ିକା ଆସୁଛି ଶୂଳକୁ, ବଣଦେଶରେ ଏହିପରି ଅସଂଖ୍ୟ ଡୁ-ଡୁ-ମା । ମୁଣ୍ଡ ଉପରେ ବରଗଛ ଛାଇ, ଢାଲୁ ଅତଡ଼ାର ସାବୁଜା ମାଣ୍ଡିଆ କ୍ଷେତ କେନା କେନା ହୋଇ ପାଣି ଉପରକୁ ଓହଳି ପଡ଼ିଛି । ସରୁ ନାଲି ନାଲି ବାଟଚଲା ତୁଠରାସ୍ତା, ସାପେଇ ସାପେଇ ଅତଡ଼ାଏ ଅତଡ଼ାଏ ।’’ ସୁଜାନି ଜଙ୍ଗଲ ଜମାନ୍ଠାରୁ ‘ହଉ’ ଶବ୍ଦଟି ଶୁଣିଲା ପରେ, ତା’ର ଖୁସିକୁ ବର୍ଣ୍ଣନା କରି ଲେଖାଯାଇଛି – “‘ସୁକୃଜାନିର ଆନନ୍ଦ ରଖ୍କୁ ଜାଗାନଥାଏ ।’’
ଉପରୋକ୍ତ ଆଲୋଚନାରୁ ଗୋପୀନାଥଙ୍କ ବର୍ଣ୍ଣନା ବୈଚିତ୍ରର ଭାବ ସ୍ପଷ୍ଟ ହୋଇଥାଏ ।
(ଚ) ଜଙ୍ଗଲ ଜମାର ଚରିତ୍ର ଚିତ୍ରଣ କର ।
Solution:
ରୀତିକୁ ବର୍ଣନା କରିଥିଲେ ବି, ଜଙ୍ଗଲ ଜମାନ୍ ପହଞ୍ଚିଛି ଶଶୁପଦର ଗାଁରେ । ସେ ସଭ୍ୟ ଜଗତର ଲୋକ ହିସାବରେ ଜଙ୍ଘିଆ ପିନ୍ଧିଥିଲା । ଦେହରେ ତା’ର ଥିଲା ଅଧାକାମିଜ୍ । ଅଧାଲଙ୍ଗୁଳି ଦେଶରେ ସେ ସ୍ବତନ୍ତ୍ର ପୋଷାକ ପିନ୍ଧିଥିଲା ବୋଲି ବାରିହୋଇ ପଡ଼ୁଥିଲା । ସେ ଜଙ୍ଗଲ ‘ଅଧିକାରୀ’ – ହାକିମ । ସେ ବଣର ଗାରଡ଼ ବା ଜଙ୍ଗଲ ଜମାନ୍ । ତା’ର କାମ ହେଉଛି ବଣକୁ ଜଗିବା, କିଏ କରିବା । ଜଙ୍ଗଲ ଜମାନ୍ର ସେ ଅଞ୍ଚଳକୁ ଗସ୍ତ ପଡ଼ିଥିଲା ।
ମାତ୍ରେ, ଗାଁ ନାଇକ ପିଣ୍ଡାରେ ଛାଉଣି ପଡୁଥିଲା । ନାଇକର ହାତବାରିଶି ଗାଁର ଜଗୁଆଳ ବାଡ଼ି ହଲେଇ ହଲେଇ ଚହଳ ପକେଇ କହୁଥୁଲା ଜମାନ୍ ଆସିଛି ବୋଲି । ଜମାନ୍ ପାଇଁ ଗାଁରୁ ସିଧା ଆସେ ଚାଉଳ, ଡାଲି, ପନିପରିବା ଓ ଗାଁ ଫସଲ । କାରଣ ଆଦିବାସୀଙ୍କ ଦୃଷ୍ଟିରେ ଜଙ୍ଗଲ ଜମାନ କମ୍ ମହାପୁ ନୁହଁନ୍ତି । ସେ ବିଭିନ୍ନ ଭାବରେ ଟିକସ ନିଏ । ବଣରେ ଗୋରୁ ଚରାଇଲେ ଟିକସ ନିଏ । ଏହାଛଡ଼ା ପୋଡୁଚାଷ ପାଇଁ ଜୋରିମାନା ଆଦାୟ କରେ । କେହି ଯଦି ବେଆଇନ ଭାବେ ବଣରୁ ମହୁ ଆଣିଛି, କାଠ କାଟିଛି, ସବୁକଥାକୁ ନେଇ ସେ ପଇସା ଆଦାୟ କରେ । ଦରମା ମାସକୁ ଆଠଟଙ୍କା ହେଲେ ବି, ତା’ର ଦଖଲରେ ଦଶ ପନ୍ଦର କୋଶ ନିଘଞ୍ଚ ଜଙ୍ଗଲ । ଜମାନ୍ କୁକୁଡ଼ା ନିଏ, ଡିମ୍ବ ନିଏ ।
ଔପନ୍ୟାସିକଙ୍କ ଭାଷାରେ – ‘ଅନେକ ଉପାଧୂଆ ପଡ଼ିଲେ, ଜଙ୍ଗଲ ଜମାନ୍ ଭୋଗ ପାଇ ପାଇ ବର ବୃଷ୍ଟିକଲା ।’’ ସୁକୃଜାନି ଜମି ପାଇଁ ଓ କାଠ ପାଇଁ, ପଣସ ଓ ଦୁଇଟଙ୍କା ଦେଇଥିଲା । ବିନୟଭାବରେ ସମସ୍ତେ ମହାପ୍ରଭୁ ଡାକିଲେ, ସେଥ୍ପାଇଁ ସେ ଲୋକଙ୍କୁ ଶୋଷଣ କଲା । ଜଙ୍ଗଲ ଜମାନ୍ କେବଳ ଯେ ଆଦିବାସୀଙ୍କର ଧନ ଶୋଷଣ କରୁଥିଲା, ତା’ନୁହେଁ ସମୟ ସୁବିଧା ଦେଖ୍, ଝିଅମାନଙ୍କ ଉପରେ ପାପ ନଜର ପକାଉଥିଲା । ଜଙ୍ଗଲ ଜମାନ୍ ଲୁଚି ଲୁଚି, ହରଡ଼ ଚଢ଼େଇ ଖୋଜିବା ବାହାନାରେ ଜିଲି ବିଲିଙ୍କର ଲଙ୍ଗଳା ଦେହକୁ ଦେଖୁଥିଲା । ଜଙ୍ଗଲ ଜମାନ୍ ଯିବା ସମୟରେ ଜିଲି ସହିତ ଥଟ୍ଟା କଥା କହୁଥିଲା । ତେଣୁ ଜମାନ୍ ଯିବାପରେ ଗାଧୁଆ ତୁଠରେ ଝିଅମାନେ କଥାବାର୍ତ୍ତା ହେଉଥିଲେ – ‘ମୋତେ ଅନୋଉଁଥୁଲା’’, ‘ମୋର ପଛ ପଛ ଧାଉଁଥୁଲା’’, ‘‘ଯେଉଁ ପାଟି, ମୁଁ ତ ଡରିଗଲି’’, ‘ଦେଖତ ଆମର କାଳି କୁକୁଡ଼ାଟା ନିମ୍ବ ଦେଉଥିଲା ବାପା ତାକୁ ଦେଇଦେଲା’’ । ଏହି ଜଙ୍ଗଲ ଜମାନ୍ ଚରିତ୍ର ମାଧ୍ୟମରେ ଔପନ୍ୟାସିକ, ସଭ୍ୟ ମଣିଷର ଅସଭ୍ୟ ବିଚାରବୋଧକୁ ପ୍ରକାରାନ୍ତରେ ବଖାଣି କପିଚିନ୍ତ |
(କ) ଲେଖକ ପରିତିନି :
ସ୍ଵାଧୀନତା ପରବର୍ତୀ ଓଡ଼ିଆ ସାହିତ୍ୟରେ ଯେଉଁ କେତେଜଣ ବିଶିଷ୍ଟ ସାରସ୍ଵତ ସାଧକଙ୍କ କୃତିରେ ଆଧୁନିକ ଓଡ଼ିଆ ଗଦ୍ୟ ସାହିତ୍ୟର ଏକ ସ୍ଵତନ୍ତ୍ର ବିଭାଗ ଉପନ୍ୟାସ ସାହିତ୍ୟର ସମୃଦ୍ଧି ଘଟିଛି, ସେମାନଙ୍କ ମଧ୍ୟରେ ଔପନ୍ୟାସିକ ଗୋପୀନାଥ ମହାନ୍ତି ଜଣେ ପ୍ରବୀଣ ସ୍ରଷ୍ଟା ଭାବରେ ସ୍ଵତନ୍ତ୍ର ସମ୍ମାନର ଅଧିକାରୀ ହୋଇପାରିଛନ୍ତି । ଆଧୁନିକ ଓଡ଼ିଆ ଗଦ୍ୟ ସାହିତ୍ୟ ଅନ୍ତର୍ଭୁକ୍ତ ପ୍ରବନ୍ଧ, ରମ୍ୟରଚନା, ସମାଲୋଚନା, ଗଳ୍ପ ଓ ବିଶେଷତଃ ଶିଳ୍ପୀ । ତଦୀୟ ଶିଳ୍ପୀମାନସ ଗଦ୍ୟ ସାହିତ୍ୟର ବିଭିନ୍ନ ବିଭାଗରେ ପାରଦର୍ଶିତା ହାସଲ କରିଥିଲେ ମଧ୍ୟ ଉପନ୍ୟାସ କ୍ଷେତ୍ରରେ ଅଧ୍ବକ ସିଦ୍ଧି ଅର୍ଜନ କରିପାରିଛି । ଜୀବନରେ ସାରସ୍ଵତ ସାଧନା କରିବା ଦିଗରେ ସେ ବହୁସମୟ ବ୍ୟୟ କରିଛନ୍ତି, ଓଡ଼ିଆ
ଉପନଯାପନ୍ତ ଯଥାର୍ଥ ସମ୍ଦ୍ଧ କରିଛିନ୍ତି |
ଗୋପୀନାଥ ମହାନ୍ତି ୧୯୧୪ ମସିହା ଏପ୍ରିଲ ମାସ କୋଡ଼ିଏ ତାରିଖରେ କଟକ ଜିଲ୍ଲାର ନାଗବାଲି ଗ୍ରାମରେ ସମ୍ଭ୍ରାନ୍ତ କରଣ ପରିବାରରେ ଜନ୍ମଗ୍ରହଣ କରିଥିଲେ । କୃତୀ ଓ ମେଧାବୀ ଛାତ୍ରଭାବରେ ସେ ବାଲ୍ୟକାଳରୁ ଶିକ୍ଷା ଲାଭ କରି ନିଜର ମେଧା ପ୍ରଦର୍ଶନ କରିପାରିଥିଲେ । ୧୯୩୬ ମସିହାରେ ଶ୍ରୀଯୁକ୍ତ ମହାନ୍ତି ଇଂରାଜୀ ସାହିତ୍ୟରେ ପ୍ରଥମ ଶ୍ରେଣୀରେ ଏମ୍. ଏ. ପାଶ୍ କରିଥିଲେ । ଏହାପରେ ତାଙ୍କ କର୍ମଜୀବନ ଆରମ୍ଭ ହୋଇଥିଲା ଓ ସେ ଓଡ଼ିଶାର ଶାସନ ବିଭାଗରେ ଜଣେ ନିଷ୍ଠାପର କର୍ମଚାରୀ ଭାବରେ ଯୋଗଦେଇ ନିଜର ପ୍ରଶାସନିକ ଦକ୍ଷତାର ପରିଚୟ ଦେଇପାରିଥିଲେ ।
ଓଡ଼ିଆ ଉପନ୍ୟାସ ଜଗତରେ ଶିଳ୍ପୀ ଗୋପୀନାଥ ଜଣେ ଅପ୍ରତିଦ୍ବନ୍ଦୀ ସ୍ରଷ୍ଟା । ତାଙ୍କର ଅଜସ୍ରସ୍ରାବୀ ଲେଖନୀରୁ ବହୁ ସମାଜର ବିଭିନ୍ନ ସ୍ଥାନର ଓ ବିଭିନ୍ନ ସ୍ତରର ମଣିଷର ଜୀବନଚିତ୍ର ଦେଖିବାକୁ ମିଳିଥାଏ । ସାମାଜିକ ମଣିଷର ସଂଘର୍ଷମୟ ଜୀବନଧାରା ଓ ଅନ୍ତଃସଂଘର୍ଷକୁ ସେ ଅତି କଳାତ୍ମକ ଭାବରେ ତାଙ୍କର ଉପନ୍ୟାସଗୁଡ଼ିକରେ ଚିତ୍ରଣ କରିପାରିଛନ୍ତି । ମଣିଷର ଚରିତ୍ରକୁ ସେ ମନସ୍ତାତ୍ତ୍ଵିକ ଦୃଷ୍ଟିକୋଣରୁ ବିଚାର କରିଛନ୍ତି ଏବଂ ତା’ର ଅବଚେତନ ଚିତ୍ତର ସଂଗୁପ୍ତ ରହସ୍ୟକୁ ମଧ୍ୟ ବହୁ ଭାବରେ ଉଦ୍ଘାଟନ କରିବାରେ କ୍ଷମ ହୋଇପାରିଛନ୍ତି ।
ଗୋପୀନାଥଙ୍କ ଶିଳ୍ପଦୃଷ୍ଟି ଅତି ପ୍ରବୀଣ । ଏଥିରେ ରହିଛି ସ୍ରଷ୍ଟା ହୃଦୟର ଆତ୍ମୀୟତା, ଶିଳ୍ପୀର କଳାଚେତନା ଏବଂ ବ୍ୟକ୍ତିମାନସର ଆଦର୍ଶବୋଧ । ପାରିବେଶିକ ବର୍ଣ୍ଣନାର ଚମକପ୍ରଦ ବାସ୍ତବତା ତାଙ୍କ ଉପନ୍ୟାସ ବର୍ଣ୍ଣିତ ଚରିତ୍ରକୁ ଯଥେଷ୍ଟ ସରସ, ସୁନ୍ଦର ଓ ସୁଖପାଠ୍ୟ କରିଥାଏ। ତାଙ୍କ ରଚିତ ଦାଦିବୁଢ଼ା, ପରଜା, ଅମୃତର ସନ୍ତାନ, ଶିବୁଭାଇ ଓ ଅପହଞ୍ଚ ହେଉଛି ତାଙ୍କର କ୍ରାନ୍ତିକାରୀ ଉପନ୍ୟାସ । ୧୯୫୬ ମସିହାରେ ଏହି ଉପନ୍ୟାସ ପାଇଁ ଗୋପୀନାଥ ମହାନ୍ତି କେନ୍ଦ୍ର ସାହିତ୍ୟ ଏକାଡ଼େମୀଦ୍ୱାରା ପୁରସ୍କୃତ ହୋଇଥିଲେ । ଏହା ବ୍ୟତୀତ ଗୋପୀନାଥଙ୍କ ଔପନ୍ୟାସିକ ଶିଳ୍ପୀମାନସ ରାହୁର ଛାୟା, ଦାନାପାଣି, ମାଟିମଟାଳ, ପ୍ରେମର ନିୟତି, ଲୟ ବିଲୟ, ପୋଡ଼ାକପାଳ, ସପନମାଟି, ମନ ଗହୀରର ଚାଷ, ଦୁଇପତ୍ର, ଶରତବାବୁଙ୍କ ଗଳି ଇତ୍ୟାଦି ବହୁ ସାର୍ଥକ ଉପନ୍ୟାସ ରଚନା କରିଛନ୍ତି । ନିଜର ସୃଜନୀ ପ୍ରତିଭାର ଚୂଡ଼ାନ୍ତ ସ୍ବାକ୍ଷରକୁ ସେ କେତେକ ଉପନ୍ୟାସରେ ପ୍ରକାଶ କରିଛନ୍ତି । ଗୋପୀନାଥ ସ୍ୱୀୟ ସୃଷ୍ଟିକର୍ମ ପାଇଁ ହେଉଛନ୍ତି ସର୍ବପ୍ରଥମ ଓଡ଼ିଆ ଲେଖକ ଯିଏ ୧୯୭୪ ମସିହାର ‘ମାଟି ମଟାଳ’ ଉପନ୍ୟାସ ପାଇଁ ଜ୍ଞାନପୀଠ ପୁରସ୍କାର ଲାଭ କରିଛନ୍ତି ।
ଅନ୍ତର୍ନିହିତ ଅନୁପ୍ରେରଣା ନେଇ ସେ ଲେଖିବା କାର୍ଯ୍ୟରେ ପ୍ରବୃତ୍ତ ହୋଇଛନ୍ତି । ନିଜର ଲେଖା ସମ୍ପର୍କରେ ‘ମୁଁ କାହିଁକି ଲେଖେ’’ ପ୍ରସଙ୍ଗରେ ସେ ‘ଡଗର’ ପତ୍ରିକାରେ ଲେଖିଥିଲେ – ‘ତେବେ ମୁଁ ଲେଖେ କାହିଁକି ?’’ ତା’ର ସହଜ ଉତ୍ତର- ‘କାରଣ ଲେଖା ମାଡ଼େ । ଏ ମୋ ମନର ସହଜ ସ୍ଵାଭାବିକ ପ୍ରତିକ୍ରିୟା । ଏ ପ୍ରତିକ୍ରିୟାକୁ ଆଲୋଚି ଦେଖିଲେ ପ୍ରଥମେ ଲାଗେ ମୁଁ ଲେଖେ, କାରଣ ମୁଁ ଭଲପାଏ । ମାଠିଆର ପାଣି ପଶିଲା ପରି ଗଦ୍ଗଦ୍ ହୋଇଉଠେ ମୋର ଭଲପାଇବା, ଉଛୁଳି ପଡ଼ି ହୁଏ ମୋର ଲେଖା ।’ କୃତିତ୍ଵ ଓଡ଼ିଆ ସାହିତ୍ୟର ଇତିହାସରେ ନିଶ୍ଚୟ ସମ୍ମାନନୀୟ ଏହା ବିନାଦ୍ଵିଧାରେ ସ୍ଵୀକାର କରିବାକୁ ହୋଇଥାଏ ।
(ଖ) ପ୍ରବନ୍ଧର ସାରକଥା :
କୋରାପୁଟରୁ ଲକ୍ଷ୍ମୀପୁର ଯିବା ବାଟରେ,ଲକ୍ଷ୍ମୀପୁର ଆଉ ମୋଟ ଦେଢ଼କୋଶ ବାଟ ଥାଇ ପଡ଼େ ‘ଧର୍ମଦୁଆର ଘାଟି’ । ଘାଟିଟି ବଡ଼ ଭୟଙ୍କର । ସେଠାରେ ଅନେକଗୁଡ଼ିଏ ପାହାଡ଼ ଲାଗି ଲାଗି ରହିଥାନ୍ତି । ସେହି ଧର୍ମଦୁଆର ଘାଟିରୁ ଉତ୍ତର ଦିଗକୁ କୋଶେ ଦୂରରେ ପଡ଼େ ଗୋଟିଏ ଆଦିବାସୀ ଛୋଟ ଗାଁ । ସେହି ଗାଁର ନାମ ‘ଶଶୁପଦର’ । ସେହି ଗାଁଟି ଗୋଟିଏ ପାହାଡ଼ର ମଝାମଝି ରହିଥାଏ, ଯାହାକୁ ଔପନ୍ୟାସିକ ଲେଖୁଛନ୍ତି, ‘ଢାଲୁରେ ଠିକ୍ ଅଣ୍ଟା ପାଖେ ।’’
ସେହି ଛୋଟ ଗାଁଟିରେ ତିନି ଜାତିର ଲୋକ ବାସ କରନ୍ତି । ସେହି ତିନି ଜାତିର ଲୋକେ ମେଞ୍ଚ୍ ମେଞ୍ଚ୍ ହୋଇ କୁଡ଼ିଆ ଘରେ ରହିଥାନ୍ତି । ତିନୋଟି ଜାତି ହେଉଛି ‘ଡମ୍ବ’ ସାହି, ‘ଗଦ୍ବା’ ସାହି ଓ ‘ପରଜା’ ସାହି । ସବୁ ଘରଗୁଡ଼ିକ ଥାଏ ଧାଡ଼ି ଧାଡ଼ି ହୋଇ । ଗାଁ ପାଖରେ ଥାଏ ‘ଟଣିଅଁ’ ଝାଟିରେ ଜାଲି ବାଡ଼ ଭିତରେ ସବୁଜ ଫସଲ । ସେହି ଫସଲଗୁଡ଼ିକ ହେଉଛି ‘ଜୋଣା’ (ମକ୍କା) କ୍ଷେତ, ଲଙ୍କାମରିଚ କ୍ଷେତ, ଧୂଆଁପତ୍ର କ୍ଷେତ, ମାଣ୍ଡିଆ, ଅଳସି, ଜଡ଼ା, କାନ୍ଦୁଲ (ବଡ଼ ହରଡ଼) କ୍ଷେତ । ଗାଆଁରେ ରହିଥାଏ ମୋଟ ବାଇଶଟି ଘର । ସେହି ଗାଁରେ ରହିଥାଏ ପରଜା ସଂପ୍ରଦାୟର ଆଦିବାସୀ ସୁଜାନି । ସୁଜାନିର ଥାଏ ଖୁସିବାସିର ଛୋଟ ସଂସାରଟିଏ । ଆଦିବାସୀ ସଂପ୍ରଦାୟର ଚଳଣି ଭିତରେ, ସୁକ୍ଜାନି ପରିବାରର ଖାଇବା ପିନ୍ଧିବାରେ କିଛି ଅସୁବିଧା ନଥାଏ ଅର୍ଥାତ୍ ‘ମାଣ୍ଡିଆ ପେଜ (ଯାଉ) ମନ୍ଦିକ ସତ୍ତ୍ୱେ ସକାଳେ କେବେ ଊଣା ହୋଇନାହିଁ, ଅଣ୍ଟାର ଡୋରକୁ ଚାରି ଆଙ୍ଗୁଳିଆ କୌପୁନୀ ଖଣ୍ଡିଏ ଲେଖାଁ କେବେ ଅଭାବ ହୋଇନାହିଁ । ଭଲେ ମନ୍ଦେ ଚଳୁଛି ।’’
ତିନିବର୍ଷ ତଳେ ସୁକୃର ଭାରିଯା ସମ୍ବାରି ‘ଭାଲୁଗା’ ଝୋଲାକୁ ସକାଳୁ ସକାଳୁ ଯାଇଥିଲା ଶାଗ ତୋଳିବା ପାଇଁ । ସେହି ଯାଇଛି ଯେ ଯାଇଛି । ସେ ଆଉ ଘରକୁ ଫେରିନାହିଁ । ‘କୋରାପୁଟିଆ ବୁଟା’ର ବୁଦା ଗହଳରୁ ମଣିଷଖିଆ ବାଘ ବାହାରି ଆସି ତାକୁ ଘୋଷାରି ନେଇଯାଇଛି । ଫଳରେ ସୁକୃର ସଂସାରରୁ ସମ୍ବାରି ବାଦ୍ ପଡ଼ିଯାଇଛି । ସଂସାର ବୋଇଲେ ରହିଛନ୍ତି ଦୁଇପୁଅ ଓ ଦୁଇଝିଅ । ଦୁଇପୁଅଙ୍କ ଭିତରେ ବଡ଼ପୁଅ ମାଣ୍ଡିଆଜାନି ଓ ସାନପୁଅ ଟିକ୍ରାଜାନି । ଆଉ ଦୁଇଝିଅ ହେଉଛନ୍ତି ଜିଲି ଓ ବିଲି ।
ସଞ୍ଜ ବୁଡ଼ିଲେ ସୁକୃଜାନି ତା’ର ନୁଆଣିଆଁ କୁଡ଼ିଆଘର ଅଣଓସାରିଆ ପିଣ୍ଡାରେ ବସି ଧୂଆଁ ଖାଏ । ପାଖ ଚୁଲିରେ ଜିଲି କିମ୍ବା ବିଲି କେହିଜଣେ ଗୋଟିଏ ହାଣ୍ଡିରେ ମାଣ୍ଡିଆ ଚୁନା, କି ଶାଗ, କି ଫେସା ହୋଇଥିବା ଆମ୍ବଟାକୁଆର କୋଇଲି ଅଜାଡ଼ି ଦେଇ, ଚୂଲି ଜାଳୁଥାନ୍ତି ଗୋଡ଼ ଲୟେଇଦେଇ । ସେମାନଙ୍କ ମୁଣ୍ଡରେ ଥାଏ ଫାଳିକିଆ ଖୋଷା । ସେଥିରେ ଗୋଟିଏ ଯୋଡ଼ିଏ ନାଲିଫୁଲ ଖୋସା ଯାଇଥାଏ । ସେହି ସମୟକୁ କାମରୁ ଫେରି ଆସିଥାନ୍ତି ଦୁଇଭାଇ ମାଣ୍ଡିଆ ଓ ଟିକ୍ରା । ସେମାନେ ଦିନଯାକ ପାହାଡ଼ ଖୋଳି ଖୋଳି, କାନ୍ଧରେ ଟାଙ୍ଗିଆ ଓ ହାତରେ କୋଡ଼ିଧରି ଘରେ ପହଞ୍ଚିଯାଆନ୍ତି ।
ଥକାମରା ହୋଇ ପିଣ୍ଡା ଉପରେ ବସି ପଡ଼ନ୍ତି । ପିଣ୍ଡାରେ ବସି ସୁଗ୍ଧଜାନି ଧୂଆଁପତ୍ର ଖଣ୍ଡେ ବଳି ବଳିକା ପିଙ୍କାଖଣ୍ଡେ ଟାଣିଲାବେଳେ ଅସୁମାରି ସ୍ଵପ୍ନ ଦେଖେ । ସୁଖ ସଂସାର ପାଇଁ କେତେ କ’ଣ ଆଶାକରେ । ଔପନ୍ୟାସିକ ଏହାକୁ ସୁନ୍ଦର ଭାବରେ ବର୍ଣ୍ଣନା କରିଛନ୍ତି ‘‘ସୁକୃଜାନି ଧୂଆଁପତ୍ର ଖଣ୍ଡେ ବଳି ବଳିକା ପିଙ୍କା ଖଣ୍ଡିଏ କରି ଟାଣେ ଆଉ ମନ ଭିତରେ କିପରି ଗୋଟିଏ ଆଶ୍ରୟମୟ ତୃପ୍ତି ସେ ପାଏ । ତା’ର ଏ ଛୁଆ ଚାରୋଟି ଧାଙ୍ଗୁଡ଼ା (ଯୁବା), ଧାଙ୍ଗୁଡ଼ୀ (ଯୁବତୀ), ତା’ରି ଏ ଘର, ନୁଆଁଣିଆ କୁଡ଼ିଆଟି । ଚାରିପାଖରେ ପାହାଡ଼ ଜଙ୍ଗଲ ଆଉ ମଥା ଉପରେ ଏତେ ବଡ଼ ଆକାଶ, ଏତେ ବଡ଼ ବିସ୍ତୃତି – ଏହା ଭିତରେ ବି ନିଜକୁ ସେ ଖୋଜିଲେ ପାଏ । ନିଜେ ରହିଛି ବୋଲି ସେ ବୁଝେ ।’’
ସୁକୃର ଘର ବୋଇଲେ ବଖୁରିକିଆ ଛୋଟଘର । ଭିତରଟି ଅନ୍ଧାରୁଆ । ସେଥୁରେ ପୁଳା ପୁଳା ହୋଇ ରହିଥାଏ, ଆମ୍ବ ଟାକୁଆ । ତେଲ ହେବାପାଇଁ ବାରି ବାଇଗବା ମଞ୍ଜି, ପତର-ସିଆଁ କୁଞ୍ଚିରେ ପଶି, ନୋହିଲେ ତଳେ ଅଜଡ଼ା ହୋଇ ଆଠ ଦଶମାଣ ମାଣ୍ଡିଆ, ତିନି ଚାରୋଟି ହାଣ୍ଡି । ଏତିକି ଘରକରଣା ସାଙ୍ଗକୁ, ଏଠି ସେଠି ଅଲରା ବଲରା ହୋଇ ଚାଳରୁ ଓହଳିଛି କୌପୁନୀ, ଲୁଗା ଓ ତିନି ଚାରି ପୁଞ୍ଜା ଲାଉତୁମ୍ବା । ଏହି ଲାଉତୁମ୍ବାଗୁଡ଼ିକରେ ମାଣ୍ଡିଆ ଯାଉ ପୂରାଇ ବିଲକୁ ବାଟକୁ ନିଆଯାଏ ।’ସେଥିରେ ମଧ୍ୟ ଆହୁରି ଥାଏ ପତର ସିଆଁ ‘ତଲ୍’ ବା ପିଠିପଖିଆ ‘ତଲାରି’ ବା ମୁଣ୍ଡର ଛତା । ଏତିକି ଘରକରଣା ସବୁ ଅସଜଡ଼ା ହୋଇ ରହିଥିଲେ ବି, ସୁକ୍କୁ ତାହା ଭଲ ଲାଗେ । ଏହାକୁ ବର୍ଣ୍ଣନା କରି ଔପନ୍ୟାସିକ ଲେଖିଛନ୍ତି – ‘ଏତିକି ଘେନି ତା’ର ଘରକରଣା, ସବୁ ଅଳିଆ ଦଳିଆ, କିନ୍ତୁ ଏଇ ଅଳିଆ ଦଳିଆ ତା’କୁ ଭଲଲାଗେ, ଛାତତଳେ ନାକକାନରୁନ୍ଧା ମଠୁଆ ମଠୁଆ ଧୂଆଁ ତା’କୁ ଭଲ ଲାଗେ, ସବୁ ତା’ର, ତେଣୁ ।’’
ସଞ୍ଜ ବୁଡ଼ିଲେ, ସୂର୍ଯ୍ୟ ଅସ୍ତ ହେବାକୁ ଗଲେ, ପାହାଡ଼ର ଉପରିଭାଗ ଲାଲ୍ ହଳଦିଆ କିରଣରେ ଶୋଭାପାଏ । ତଳର ଜଙ୍ଗଲ ନେଳିନେଳି, କଳା-କଳା ଦେଖାଯାଏ । ଏହି ଦୃଶ୍ୟକୁ ଦେଖି, ସୁକୃଜାନି ଭାବେ ସବୁରି କର୍ଭା ଗୋଟାଏ ଲେଖାଁ ଭୂତ ବା ‘ଡୁମା’ । ମନ ତୃପ୍ତିରେ ସେ ଭାବେ କେଉଁ ଯାଦୁକର ଡୁମା ଏସବୁ ଗଢ଼ିଛି । ଆକାଶ, ଜଙ୍ଗଲ, ସଞ୍ଜ ଆଉ ରାତି ତାହାରି ସୃଷ୍ଟି । ସେହି ଭିତରୁ କେଉଁ ଡୁମା ଆଣି ଦେଇଥାଏ, ସୌଭାଗ୍ୟ ଆଉ ଆନନ୍ଦ । ଆଉ କିଏ ଦେଇଥାଏ ଝଡ଼ ତୋଫାନ, ଦୁଃଖ ଦୁର୍ଦ୍ଦଶା ସବୁକିଛି ।
ପାହାଡ଼ର ମଥାନରୁ ତଳ ପର୍ଯ୍ୟନ୍ତ ଖାଲି ପାହାଚ ପାହାଚ ଚାଷଜମି । ପାହାଡ଼ ତଳେ ଚାଲିଯାଇଛି ଗୋଟିଏ ଭୀମଙ୍କ ଲଙ୍ଗଳସିଅ ବା ଝୋଲା । ସେଗୁଡ଼ିକ ହେଉଛି ପାହାଡ଼ୀ ନଈ । ସେହି ପାହାଡ଼ୀ ନଈରେ କଳ କଳ କରି, ଡେଇଁ ଡେଇଁକା ପାଣି ତଳକୁ ଗଡ଼ି ଯାଉଥାଏ । ସେହି ପାଖାପାଖି ଢିପତଳ, ସନ୍ତସନ୍ତିଆ ଧାନଜମି । ତେଣିକି ତେଣିକି ଚାରିପାଖ ଗୋଲେଇ ହୋଇ ଢାଙ୍କି ରହିଥାଏ ସାନ ବଡ଼ କେତେ ପାହାଡ଼ ଓ ଅଗ୍ନିଗ୍ନି ବନସ୍ତ । ସୁକ୍ଳଜାନି ଏହିସବୁ ଦୃଶ୍ୟ ଦେଖିଲାବେଳେ, ତା’ଆଖିରେ ଅତୀତ ଦେଖାଯାଏ । ସାନ ପାହାଡ଼ଟିଏ । ସେହି ପାହାଡ଼କୁ ସେ ଆଉ ଲୋବୋ କନ୍ଧ ମିଶି କୁ ଢୁ ବରଷାରେ କୁରାଢ଼ିରେ ହାଣି ଚନ୍ଦା କରିଛନ୍ତି । ବର୍ତ୍ତମାନ ସେ ହୋଇଛି ଚାଷଭୁଇଁ । ପୁଣି ସେ ଭବିଷ୍ୟତ ଦେଖେ । କେଉଁ ଉପକାରୀ ଡୁମାର ହାତ ଲାଗି ସବୁ ଘର ତୋଳା ହୋଇଛି । ମାଣ୍ଡିଆ, ଟିକ୍ରା ବାହା ହୋଇଛନ୍ତି ।
ସେମାନଙ୍କର ସଂସାର ବଢ଼ିଛି । ପୁଅର ପୁଅ-ପୁଅର ପୁଅ ହୋଇଛନ୍ତି । ଦି କୋଡ଼ି ତିନି କୋଡ଼ି ଗୋରୁଗାଈ, ଘର ଆଗରେ ବଡ଼ ଗୁହାଳ ଓ ଗୋବର ଖାତ ମାଡ଼ିଯାଇଛି । ଆଉ ଚାରିକଡ଼ରେ ଯେତେସବୁ ସାନବଡ଼ ପାହାଡ଼ ସେଗୁଡ଼ିକର ଜଙ୍ଗଲ ସଫାହୋଇ ଚାଷଜମି ହୋଇଛି । କ୍ଷେତ ଆଉ କ୍ଷେତ, ଯାହାକୁ କି ନାତିର ନାତି ଓ ତା’ ନାତି ଭୋଗକରି ଚାଲିଛନ୍ତି । ସେହି ଭାବନା ଭିତରେ ସୁଗ୍ଧଜାନି ବୁଢ଼ା ହୋଇଯାଇଛି । ସେ ମରିଗଲା ପରେ ଗାଁ ମଝି ଗୁରୁଡ଼ି ଆମ୍ବଗଛ ତଳେ ତା’ପାଇଁ ଖଣ୍ଡେ ଗୋଜିଆ ପଥର ପୋତା ହୋଇଛି । ସେହି ଗୋଜିଆ ପଥର ଭିତରେ ସୁଗ୍ଧଜାନିର ଆତ୍ମା ଗୋଟିଏ ଡୁମା ହୋଇ, ଭବିଷ୍ୟତର ପୁଅ ନାତିଙ୍କର ସୁଖ ସୌଭାଗ୍ୟକୁ ମିଟି ମିଟି କରି ଅନେଇ ରହିଛି । ଏହି ଭାବନା ଭିତରେ ରାତି ଘୋଟିଯାଏ ।
![]()
ସୁକୃଜାନି କେବଳ ବାହୁର ବଳ ଉପରେ ଭରସା ରଖେ । ସେପାଖ ପାହାଡ଼କୁ ଲଣ୍ଡା କଲାବେଳେ ସେ ଏକା ଥରକେ ପାଞ୍ଚଘଣ୍ଟା, ଛଅଘଣ୍ଟା ଧରି କୁରାଢ଼ି ଚଳାଇ ପାରୁଥିଲା । ଅଧିକାରୀ (ହାକିମ) ପାଇଁ ଦି ମହଣ ବୋଝକୁ ବାହୁଙ୍ଗୀ କରି ଏକୁଟିଆ, କେତେଥର ମାଙ୍କଡ଼ ଝୋଲା କି କାକିରିଗୁମ୍ମା ବଙ୍ଗଳାରେ ପହଞ୍ଚାଇ ଦେଇ ଆସୁଥିଲା । ସେ ସମୟରେ ତା’ଦେହରେ ବଳ ଥିଲା । ‘ଆବୁ ଆବୁଆ ବଢୁଆ ଦେହରେ ଗୋଡ଼ ପେଣ୍ଡା ତା’ର ପଥର, ଚମଡ଼ାଟି ତା’ର ବର୍ଷାତି ।’ କେବେ ବେମାର ପଡ଼େ ନାହିଁ କିମ୍ବା ଅଳସ ସେ କରେ ନାହିଁ ।
ସୁକୃଜାନି ପରି ହୋଇଛି ମାଣ୍ଡିଆ ଜାନି । ଟୋକାବେଳେ ସୁକୁ ଯାହା ଥିଲା ଠିକ୍ ସେଇଆ ଦେଖାଯାଉଛି ମାଣ୍ଡିଆ । ବୃଷାଳ ଦେହ, ମୁହଁ ପିଲା ମୁହଁ ପରି ସରଳ । ସେ କେତେବେଳେ ଭୋକଶୋଷ ମାନେ ନାହିଁ । ସବୁବେଳେ ତା’ର ଖାଲି ହସ ଆଉ ହସ । ମାତ୍ର ଟିକ୍ରା ହୋଇଛି ତା’ ମା’ପରି । ଟିକ୍ରାକୁ ଦେଖିଲେ ତା’ର ମା’କଥା ମନେପଡ଼େ ।
ସ୍ତ୍ରୀ ସମ୍ବାରି ପରି ଟିକ୍ରାର ଡବ ଡବ ଆଖି ଓ ତରତର କଥା । ସଞ୍ଜବେଳେ ନିଆଁ ପାଖେ ବସି ବଉଁଶ କୁଟୁମ୍ବଙ୍କର ଭଲ ପଙ୍ଗତଟିଏ ବସେ । ତଳ ଝୋଲାରୁ ପାଣି ମାଠିଆ ଆଣି ଜଲି ବିଲି ଆସନ୍ତି । ସବୁବେଳେ ସେମାନଙ୍କର ହସ ଖେଳ ଥଟ୍ଟା ନକଲ । ଏହି ଦୃଶ୍ୟକୁ ଦେଖି ସୁକୃଜାନି ଆନନ୍ଦିତ ହୁଏ । ଔପନ୍ୟାସିକଙ୍କ ଭାଷାରେ – ‘ସୁକୃଜାନି କାନରୁ ଦରପୋଡ଼ା ପିଙ୍କା ଖଣ୍ଡିଏ ଟାଣିନେଇ ନିଆଁ ଲଗାଏ, ଧୂଆଁ ପିଉ ପିଉ ପିଇଯାଏ ସଞ୍ଜ ଶାନ୍ତି, ଖୋଲା ପାହାଡ଼ର ଶାନ୍ତି – ସବୁ ।”’ ଦିନେ ଗାଧୁଆବେଳେ ଜିଲି ଆଉ ବିଲି ପାହାଡ଼ ତଳ ଝୋଲାରେ ଗାଧୋଉଛନ୍ତି । ସେହି ପର୍ଯ୍ୟାୟରେ ଔପନ୍ୟାସିକ ଝୋଲାର ପ୍ରାକୃତିକ ଦୃଶ୍ୟକୁ ଦେଖାଇଛନ୍ତି । ଦିଲି ଓ ବିଲିର ବୟସ ୧୭ ଓ ୧୬ । ପରଜା ସଂପ୍ରଦାୟର ଗାଧୋଇବା ଅଭ୍ୟାସ ନେଇ ଦୁହେଁଯାକ ଲଙ୍ଗଳା । ସେହି ପାଖଦେଇ ଢିପ ଉପରେ ଭାରବୋହି ପରଜା ଦୁଇଜଣ ଚାଲିଗଲେ । ସେମାନଙ୍କର ବାଟ ସିଧା ଓ ଆଖି ସିଧା । ମାତ୍ର ଆଉ ଜଣେ ଖୋଲା କୂଳେ କୂଳେ ହରଡ଼ ଚଢ଼େଇ ଖୋଜିବା ବାହାନାରେ, କାନ୍ଧରେ ବନ୍ଧୁକ ପକାଇ ଏପାଖ ସେପାଖ ହେଉଥିଲା ।
ସ୍ଵେ ଥିଲା ସଭ୍ୟ ଜଗତର ମଣିଷ । ସେ ଥିଲା ଅଧିକାରୀ କହାକିମ । ଚଢ଼େଇ ଖୋଜିବା ବାହାନାରେ ସେ ଜିଲି ଓ ବିଲିକୁ ଦେଖୁଥିଲା । ହଠାତ୍ ଜିଲିର ସେ ଆଡ଼େ ଆଖି ପଡ଼ିଗଲା । ସେମାନେ କିଲିକାଲିଆ ହୋଇ କୌଣସି ପ୍ରକାରେ ନିଜର ଲୁଗା ପିନ୍ଧି ପକାଇଲେ । ଜମାନ୍ ହସି ହସିକା ବୁଦା ଉହାଡ଼ରେ ଲୁଚିଗଲା । ତରତରରେ ସେମାନେ ଗାଧୁଆ ସାରି, ଦି ଭଉଣୀ ମାଠିଆ କାଖେଇ ଘରକୁ ଫେରିଲେ । ଜଙ୍ଗଲ ଜମାନ୍ ସେମାନଙ୍କର ଫେରିବା ବାଟକୁ ସେଇମିତି ଚାହିଁ ରହିଥିଲା । ଜିଲ୍ ବିଲି ଚାଲିଗଲା ପରେ ଜମାନ୍ ସିଟି ମାରି ମାରି ବୁଲାଣି ବାଟରେ ଗାଁ ଆଡ଼କୁ ଗଲା । ଆସନ୍ତି ରାଜାଘର ରେଭେନ୍ୟୁ ଦେବାପାଇଁ ।
ଗାଁ ନାଇକ ସମସ୍ତଙ୍କ ସବୁକଥା ଜଣାଏ । ଗାଁର ଖବର ଅନ୍ତର ସରକାରକୁ ଜଣାଏ । ତେଣୁ ସାଧାରଣ ରଇତମାନଙ୍କ ପାଖରେ ତା’ର ଖାତିରି ବେଶି । ଯେଉଁଦିନ ସରକାରୀ ଲୋକ ଆସନ୍ତି ସେଦିନ ନାଇକ କୌପୁନୀ ଉପରେ ପୁରୁଣା କୋଟ୍ ଖଣ୍ଡିକ ପିନ୍ଧି ପିଙ୍କା ଟାଣି, ସେମାନଙ୍କୁ ଅପେକ୍ଷା କରି ରହିଥାଏ । ସରକାରୀ ଲୋକ ଦେଖିଲେ ଅଣ୍ଟା ପର୍ଯ୍ୟନ୍ତ ବଙ୍କା ହୋଇ, ଦୁଇ ହାତରେ ଅଧିକାରୀର ପାଦ ଛୁଏଁ। ଗୋଟାପଣେ ନିଜର ଦେଖେଇ ହୋଇ ଗଦ୍ ଗଦ୍ ସ୍ୱରରେ କୁହେ, ‘ଜୁହାର ଗାରଡ଼ ମହାପୁ, ତୁମର ପାଦୁକା ଶୀତଳ ଥାଉ ।’’
ସେଦିନ ଚାରିଆଡ଼େ ଚହଳ ପଡ଼ିଗଲା ‘ଗାରଡ଼, ଗାରଡ଼, ଡ଼, ଜମାନ୍ ଜମାନ୍’ । ନାଇକର ହାତବାରିଶି, ଗାଁ ଜଗୁଆଳ ଏବଂ କର୍ମକର୍ତ୍ତା ଡମ୍ବ ‘ବାରିକ’ ବାଡ଼ି ହଲେଇ ହଲେଇ ସବୁଆଡ଼େ ଜଣେଇଦେଲା । ବାରିକ କଥାନୁସାରେ ‘ସମସ୍ତେ ଆସି ନାଇକ ଦାଣ୍ଡରେ ରୁଣ୍ଡ ହେଲେ । ସାଙ୍ଗରେ ଆଣିଥିଲେ, ଚାଉଳ, ଡାଲି, ପନିପରିବା ଓ ଗାଁର ଫସଲ । କାରଣ ଜଙ୍ଗଲ
କରିବାପାଇଁ ବାଘୁଆ ଅରମା ମାରିଛି ତା’ପାଇଁ ଟିକସ, କିଏ ବେଆଇନ ଭାବେ ପୋଡୁଚାଷ କରିଛି, ବଣୁଆ ମହୁ ଆଣିଛି ଚାଲେ । ଜମାନ୍ ହିସାବରେ ସେ ମାସକୁ ଦରମା ପାଏ ଆଠଟଙ୍କା, ମାତ୍ର ସେହି ଦଶ ପନ୍ଦର କୋଶ ନିଘଞ୍ଚ ଜଙ୍ଗଲ, ଯାହା ପଡ଼ିଲେ, ଜଙ୍ଗଲ ଜମାନ୍ ଭୋଗ ପାଇ ପାଇ ବର ବୃଷ୍ଟି କଲା । ସୁକ୍ଜାନିର ଜମି ଦରକାର। ତା’ର ବଢ଼ନ୍ତା ପରିବାର । ଜମି ସଫାକରି ଚାଷ କଲେଣି । ସୁଜାନି ପୁଆ
ବିଭାକଲେ, ତା’ର ଅଲଗା ଘର ଦରକାର। ଏ ହେଉଛି ପରଜା ଜାତିର ବିନୟ ଭଙ୍ଗୀରେ କହିଲା, ‘‘ମହାପ୍ରଭୁ ତୁ ଦୟା ନକଲେ ଆମେ ଏତିକିରେ କାହିଁରେ କେତେ ଖୁସି ହୋଇ ସୁଜାନି ଘରକୁ ଫେରିଲା ।
ଖିଆପିଆ ସାରି ପୁଟୁଳା, ବୁଜୁଳା, ବାନ୍ଧି ଜଙ୍ଗଲ ଜମାନ୍ ଛାଉଣି ଉଠେଇଲା ଚାଲିଲା ଆଉ ଗୋଟିଏ ଗାଁକୁ । ଜିନିଷ ବୋହିବାପାଇଁ ବିଲରୁ ଦୁଇଜଣ ଭେଣ୍ଡିଆକୁ ବାରିକ ଘୋଷାରି ଆଣିଲା । ବୋଝ ଉଠିଲା । କାନ୍ଧରେ ବନ୍ଧୁକ ପକାଇ ଥଟ୍ଟାରେ ଉତ୍ତର ଦେଲା ସରଳ ଭାବରେ ।
ଝୋଲା ତୁଠରେ ପରଜା ଟୋକୀମାନେ ଜମିଗଲେ । ଛଳ ଛଳ ସ୍ବଭାବରେ କେତେ କ’ଣ କୁହାବେଲା ହେଲେ । ବଡ଼ମାନେ ସିନା ଜଙ୍ଗଲ ହାଣିବା, ଚାଷ କରିବା କଥାକୁ ଆଲୋଚନା କରୁଥିଲେ ହେଲେ ଟୋକୀମାନେ ଜଙ୍ଗଲ ଜମାନ୍ର ହାବଭାବକୁ ସମାଲୋଚନା କରୁଥିଲେ । କେହି କହିଲା ‘‘ମତେ ଅନେଉଁଥୁଲା’’ ‘ମୋର ପଛ ପଛ ଧାଇଁଥୁଲା’’, ‘ଛେ- ସରୁ ଡାଙ୍ଗ ପରି ମଣିଷଟେ ସେଇଟା ତହିଁରେ ପୁଣି କେଡ଼େ ହମ ହମ’’, ‘ଯୋଉ ପାଟି, ମୁଁ ତ ଡରିଗଲି’’, ‘ଦେଖତ ଆମ କାଳି କୁକୁଡ଼ାଟା ଡିମ୍ବ ଦେଉଥ୍ଲା ବାପା ତାକୁ ଦେଇଦେଲା’’ । ଏହିପରି କେତେ କଥାବାର୍ତ୍ତା ହେଉଥିଲେ ପରଜା ଝିଅମାନେ, ସବୁ କିନ୍ତୁ ହସଖୁସିରେ ।
(ଗ) କଠିନ ଶବ୍ଦ ଓ ଏହାର ଅର୍ଥ :
ଠେଲାଠେଲି ଧକ୍କା ଧକ୍କି ହୋଇ – ଲାଗି ଲାଗି ରହିଥିବା ପାହାଡ଼କୁ ଏପରି ବର୍ଣ୍ଣନା କରାଯାଇଛି । ସତେ ଯେପରି ପାହାଡ଼ଗୁଡ଼ିକ ଠେଲାଠେଲି ଧକ୍କା ଧକ୍କି ହୋଇ ରହିଛି ।