Odisha State Board CHSE Odisha Class 12 Odia Solutions Chapter 12 ରୂପନାରାୟଣ ସାହା Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Odia Chapter 12 ରୂପନାରାୟଣ ସାହା Question Answer
ପାଠ୍ୟପୁସ୍ତକସ୍ଥ ପ୍ରଶ୍ନବଳୀର ଉତ୍ତର
(କ) ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନ । ଚାରିଗୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ । ପ୍ରଶ୍ନର ମୂଲ୍ୟ ୧ ନମ୍ବର ।
Question ୧ ।
‘ରୂପନାରାୟଣ ସାହା’ ଗଳ୍ପଟି କେଉଁ ସମୟର କଥା କହିଛି ?
ଗୁଡ଼ଫ୍ରାଇଡ଼େ ଛୁଟି, କ୍ରିଷ୍ଟମାସ ଛୁଟି, ନିଉଇୟର ଛୁଟି, ଏକ୍ସମାସ ଛୁଟି ।
Answer:
କ୍ରିଷ୍ଟମାସ ଛୁଟି
Question ୨ ।
ଭାରତ ଭୂମିର ଅସଂଖ୍ୟ ପୁଣ୍ୟ କାଙ୍ଗାଳ ଜନତାର ଚିର ଇପ୍ସିତ ସ୍ଥାନ ବୋଲି କାହାକୁ କୁହାଯାଇଛି ?
ତିରୁପତି, ବୃନ୍ଦାବନ, ମଥୁରା, ବନାରସ୍ ।
Answer:
ବନାରସ୍
Question ୩ ।
ବନାରସରେ କେଉଁ ମନ୍ଦିର ଅବସ୍ଥିତ ?
ସୋମନାଥ, କେଦାରନାଥ, କାଶୀବିଶ୍ଵନାଥ, ବଦ୍ରିନାଥ ।
Answer:
କାଶୀବିଶ୍ଵନାଥ
Question ୪।
ହତଶ୍ରୀ ସଭ୍ୟତାର ଡଷ୍ଟବିନ୍ ବୋଲି କାହାକୁ କୁହାଯାଇଛି ?
ଡାଳୁଣ୍ଡି, ରାମ୍ନଗର, ସଦରବଜାର, ଗୋଧୂଳିଆ ।
Answer:
ଡାଳୁଣ୍ଡି
Question ୫।
ଗୋଧୂଳି ଓ ଗଙ୍ଗାଜୀ-ଉଭୟଙ୍କୁ କ’ଣ ବୋଲି କୁହାଯାଇଛି ?
ମାନମୟୀ, ପ୍ରେମମୟୀ, ରହସ୍ୟମୟୀ, ଭାବମୟୀ ।
Answer:
ରହସ୍ୟମୟୀ
Question ୬।
ଗଙ୍ଗାର କେଉଁ ରଙ୍ଗର ପାଣି ଲାଲେ-ଲାଲ୍ ଲାଗୁଥିଲା ?
ପେସ୍ତା, ଗହମ, ବାଜରା, ବାଦାମ ।
Answer:
ଗହମ
Question ୭ ।
ନୌକାର ପାଲ କେତେ ଫଣା ବାସୁକୀ ପରି ନଇଁଯାଇ ଉପରକୁ ଉଠିଯାଏ ବୋଲି କୁହାଯାଇଛି ?
ସପ୍ତଫଣା, ଶତଫଣା, ସହସ୍ର ଫଣା, ସହସ୍ରାତ୍ମକ ଫଣା ।
Answer:
ସହସ୍ର ଫଣା
Question ୮ ।
ଅଶୋକଙ୍କ ବାପା ବନାରସରେ କି ଚାକିରି କରିଥିଲେ ?
ପୋଲିସ ଅଫିସର, ମିଲିଟାରୀ ମେଜର, ପ୍ରଫେସର, ମିଲିଟାରୀ ଡାକ୍ତର ।
Answer:
ମିଲିଟାରୀ ଡାକ୍ତର
Question ୯ ।
କାହାରି ଅଦୃଶ୍ୟ ଇଙ୍ଗିତରେ ନୌକା ଘାଟରେ ଲାଗିଥିଲା ?
ମାଝିର, କର୍ପୋରେସନର, ପୋଲିସ ଷ୍ଟେସନର, ମାଜିଷ୍ଟ୍ରେଟଙ୍କର ।
Answer:
କର୍ପୋରେସନର
Question ୧୦ ।
କିଏ ଇଂରାଜୀ ଭାଷାରେ ବିରକ୍ତି ପ୍ରକଟ କରି କହିଥିଲେ – ‘ଇଡ଼ିୟଟ୍’ ?
ବାପା, ବଡ଼ଭାଇ, ଦାଦା, ମାଆ।
Answer:
Question ୧୧ ।
ରାମ୍ଗର ଦେଖୁରି ଗଙ୍ଗାପାର ହେଉଥିବାବେଳେ ଅଶୋକଙ୍କ ବୟସ କେତେ ଥିଲା ?
ବାର, ଏଗାର, ଦଶ, ଆଠ ।
Answer:
ଦଶ

Question ୧୨ ।
ଅଶୋକର ପିଠି ଉପରେ ମାଷ୍ଟରଜୀଙ୍କ ବଡ଼ପାପୁଲି କିପରି କମ୍ପି ଉଠିଥିଲା ?
ଦେବଦାରୁପତ୍ର ପରି, ବରପତ୍ର ପରି, କଦଳୀପତ୍ର ପରି, ଅଶ୍ଵତ୍ପତ୍ରପରି ।
Answer:
ଅଶ୍ଵତ୍ପତ୍ରପରି
Question ୧୩ ।
ମାଷ୍ଟରଜୀ କେତେ ଟଙ୍କା ଦରମାରେ ଅଶୋକଙ୍କର ଟ୍ୟୁସନମାଷ୍ଟର ଥିଲେ ?
Answer:
ପାଞ୍ଚଟଙ୍କା
Question ୧୪।
ମାଷ୍ଟରଜୀଙ୍କ ପ୍ରତିଟି ତନ୍ତ୍ରୀ, ପ୍ରତିଟି ରେଣୁକୁ ଉଜ୍ଜୀବିତ କରି କିଏ ନିଜକୁ ପ୍ରକାଶ କରୁଥିଲା ?
ବିବେକ, ବିଚାର, ଜ୍ଞାନ, ସତ୍ୟ ।
Answer:
ସତ୍ୟ
Question ୧୫ ।
ମାଷ୍ଟରଜୀଙ୍କ ନାସିକା କେଉଁପରି ଥିଲା ବୋଲି କୁହାଯାଇଛି ?
ପିକଚଞ୍ଚୁ ପରି, ଚିଲଚଞ୍ଚୁ ପରି, କାକଚଞ୍ଚୁ ପରି, ଶୁକଚଞ୍ଚୁ ପରି ।
Answer:
ଶୁକଚଞ୍ଚୁ ପରି
Question ୧୬ ।
ଅଶୋକଙ୍କର ଡାକନାମ କ’ଣ ଥିଲା ?
ମନୁ, ମୁନ୍ନା, ଚିନ୍ନା, କାହ୍ନା ।
Answer:
ମୁନ୍ନା
Question ୧୭ ।
କାହାର ନାମ ମନ୍ତୁ ଦିଆ ଯାଇଥିଲା ?
କୁକୁର ଛୁଆର, ବଣିଆଛୁଆର, ପାତିମାଙ୍କଡ଼ ଛୁଆର, ପୋଷା ବିଲେଇ ଛୁଆର ।
Answer:
ପାତିମାଙ୍କଡ଼ ଛୁଆର
Question ୧୮ ।
ମାତାଜୀଙ୍କ ହାତ ତିଆରି କେଉଁ ଖାଦ୍ୟ ଥରେ ଯେ ଖାଇଛି ସେ ଜୀବନସାରା ଭୁଲି ପାରିବନି ବୋଲି କୁହାଯାଇଛି ?
ପକୁଡ଼ି, ଉପମା, ସନ୍ଦେଶ, ହାଲୁଆ।
Answer:
ହାଲୁଆ
Question ୧୯ ।
ଉତ୍ତର ଭାରତ ବ୍ୟାପୀ ପ୍ରାଥମିକ ଶିକ୍ଷକ ଧର୍ମଘଟରେ ମାଷ୍ଟରଜୀ କ’ଣ ଥିଲେ ?
ବିଦ୍ରୋହୀ, ସମର୍ଥକ, ପୁରୋଧା, ପଳାତକ ।
Answer:
ପୁରୋଧା
Question ୨୦ ।
ଧର୍ମଘଟ ବେଳେ ମାଷ୍ଟରଜୀଙ୍କ ଦରମା କେତେ ଥିଲା ?
ପନ୍ଦର ଟଙ୍କା, ତେର ଟଙ୍କା, ଏଗାର ଟଙ୍କା, ଦଶଟଙ୍କା ।
Answer:
ତେର ଟଙ୍କା
Question ୨୧ ।
ମାଷ୍ଟରଜୀଙ୍କୁ କେଉଁ ରୋଗ ହୋଇଥିଲା ବୋଲି ଡାକ୍ତର କହିଥିଲେ ?
ପ୍ଲୁରେସି, ଡିସେଣ୍ଡି, ଡାଏବେଟିକ୍, ନିମୋନିଆ ।
Answer:
ପ୍ଲୁରେସି
Question ୨୨ ।
ମାଷ୍ଟରଜୀଙ୍କ ପୁଅର ନାମ କ’ଣ ଥିଲା ?
ରାମଗୋପାଳ, ରାମଦୁଲାଳ, ରାମସରନ୍, ରାମମନୋହର ।
Answer:
ରାମସରନ୍
Question ୨୩ ।
ମାଷ୍ଟରଜୀଙ୍କ ସ୍ତ୍ରୀ ନାମ କ’ଣ ଥିଲା ?
ରୂପା, ସୁନା, ହୀରା, ପଦ୍ମା ।
Answer:
Question ୨୪ ।
ମାଷ୍ଟରଜୀ ତାଙ୍କ କାହାଣୀରେ କେଉଁ ସିଂହ କଥା କହୁଥିଲେ
ଚେକୋସ୍ଲୋଭିଆର, ଆଲୋକ୍ଜାଣ୍ଡ୍ରିଆର, ଆସିଲିସ୍ର, କାଲିଫର୍ନିଆର ।
Answer:
ଆଲୋକ୍ଜାଣ୍ଡ୍ରିଆର
Question ୨୫ ।
କାହାର ଭୀରୁ ସଙ୍କୁଚିତ ବିବେକ ନେଇ ଅଶୋକ ରାସ୍ତାରେ ଚାଲିଥିଲେ ?
ହତ୍ୟାକାରୀର, ପ୍ରଶାସକର, ବିଶ୍ବାସଘାତକର, ଅବିବେକୀର ।
Answer:
ହତ୍ୟାକାରୀର
Question ୨୬ ।
ଏ ଜାତିକୁ କ’ଣ ନୂଆକରି ଦେବାକୁ ମାଷ୍ଟରଜୀ କହୁଥିବା ପରି ଅଶୋକର ମନେହୋଇଛି ?
ପ୍ରାଥମିକ ଶିକ୍ଷା, ଉପଯୁକ୍ତ ଶିକ୍ଷା, ନୈତିକ ଶିକ୍ଷା, ମାଧ୍ୟମିକ ଶିକ୍ଷା ।
Answer:
ପ୍ରାଥମିକ ଶିକ୍ଷା
Question ୨୭ ।
ଏ ଜାତି ଧୀରେ ଧୀରେ କାହା କୁଣ୍ଡଳିର ଶୀତ-ଶଯ୍ୟାରୁ ଚଞ୍ଚଳ ହୋଇ ଉଠିବ ବୋଲି କୁହାଯାଇଛି ?
ଗୋଖର, ଅଜଗର, ଅହିରାଜ,
Answer:
ଅହିରାଜ
(ଖ) ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନ । ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ । ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ମୂଲ୍ୟ ୧ ନମ୍ବର ।
Question ୧ ।
ବନାରସ ରାସ୍ତାରେ ଲୋକଙ୍କ ଧାଡ଼ି କେଉଁପରି ଲାଗୁଥିଲା ବୋଲି କୁହାଯାଇଛି ?
Answer:
ବନାରସ ରାସ୍ତାରେ ଲୋକଙ୍କ ଧାଡ଼ି ଜମାଟ ବାନ୍ଧି ଯାଇଥିବା ବରଫ ପରି ଲାଗୁଥିଲା ବୋଲି କୁହାଯାଇଛି ।
Question ୨ ।
ରୂପ-ପିୟାସୀ ନାଗରିକଙ୍କ ତୀର୍ଥ କିଏ ?
Answer:
ରୂପ-ପିୟାସୀ ନାଗରିକଙ୍କ ତୀର୍ଥ ଡା୍ଲ୍ମଣ୍ଡି ।
Question ୩ ।
ଗଙ୍ଗାର ଲାଲେ-ଲାଲ୍ ପାଣି ମୁକ୍ତକେଶୀ ଦ୍ରୌପଦୀଙ୍କ କେଉଁ ଦୃଶ୍ୟ ପରି ମନେହେଉଛି ?
Answer:
ଗଙ୍ଗାର ଲାଲେ-ଲାଲ୍ ପାଣି ମୁକ୍ତକେଶୀ ଦ୍ରୌପଦୀଙ୍କ ବେଣୀବନ୍ଧନ ଦୃଶ୍ୟ ପରି ମନେହୋଇଛି ।
Question ୪ ।
ବହୁ ଯାତ୍ରୀବାହୀ ନୌକା କେଉଁପରି ଗଙ୍ଗାର ଏ କୂଳରୁ ସେ କୂଳକୁ ଯାତାୟାତ କରୁଥିବାର କୁହାଯାଇଛି ?
Answer:
ବହୁ ଯାତ୍ରୀବାହୀ ନୌକା ଉଜ୍ଜ୍ବଳ ଚକ୍ରବାଳର ପଟ୍ଟଭୂମିରେ ସିହୁଟ ଛବିପରି ଗଙ୍ଗାର ଏ କୂଳରୁ ସେ କୂଳରୁ ଯାତାୟାତ କରୁଥିବାର କୁହାଯାଇଛି ।
Question ୫।
ହରିଶ୍ଚନ୍ଦ୍ରଘାଟ ପରେ ନୌକା କେଉଁ ଘାଟରେ ପହଞ୍ଚିବ ବୋଲି କୁହାଯାଇଛି ?
Answer:
ହରିଶ୍ଚନ୍ଦ୍ରଘାଟ ପରେ ନୌକା ଦଶ।ଶ୍ଵାମେଧ ଘାଟରେ ପହଞ୍ଚିବ ବୋଲି କୁହାଯାଇଛି ।
Question ୬ ।
ମାଝିର ଭାଷା କେଉଁସବୁ ଭାଷାର ମିଶାମିଶି ଭାଷା ଥିଲା ?
Answer:
ମାଝିର ଭାଷା ହିନ୍ଦି, ମୈଥୁଳୀ ଆଉ ଭୋଜପୁରୀ ଭାଷାର ମିଶାମିଶି ଭାଷା ଥିଲା ।
Question ୭।
ହର୍ ଆଡ୍ମିକୋ କେତେ ଟ୍ୟାକ୍ସ ଲଗାଯାଏଗା ବୋଲି ‘ମାଝି’ କହିଛି ?
Answer:
ହର୍ ଆଡ୍ମିକୋ ଏକ୍ ଏକ୍ ରୂପିୟା ଟ୍ୟାକ୍ସ ଲଗାଯାଏଗା ବୋଲି ମାଝି କହିଛି ।

Question ୮।
ସୁବିଧାବାଦୀ ସାନ ଭଉଣୀ ଖନେଇ ଖନେଇ କ’ଣ କହିଥିଲା ?
Answer:
ସୁବିଧାବାଦୀ ସାନ ଭଉଣୀ ଖନେଇ ଖନେଇ, ‘ଭାଇର ଆଉ ପ୍ୟାଣ୍ଟ କିଣାହେବନି’’ ବୋଲି କହିଥିଲା ।
Question ୯ ।
ଜେଜେମା’ଙ୍କର କେଉଁ ଆଦେଶ ପିଲାଦିନେ ଅଶୋକ ଅମାନ୍ୟ କରିଥିଲା ?
Answer:
ଜେଜେମା’ଙ୍କର ଅଫିମ ପାଇଁ ବଜାରକୁ ଯିବା ଆଦେଶ ପିଲାଦିନେ ଅଶୋକ ଅମାନ୍ୟ କରିଥିଲା
Question ୧୦ ।
ଆର୍ଦ୍ର, ବାଷ୍ପକୁଳ କଣ୍ଠରେ କ’ଣ ମିଶି ମାଷ୍ଟରଜୀଙ୍କ କଣ୍ଠସ୍ଵର ଅଦ୍ଭୁତ ଶୁଣାଯାଉଥିଲା ?
Answer:
ଆର୍ଦ୍ର, ବାଷ୍ପକୁଳ କଣ୍ଠରେ କ୍ରୋଧର ଉତ୍ତେଜନା ମିଶି ମାଷ୍ଟରଜୀଙ୍କ କଣ୍ଠସ୍ଵର ଅଦ୍ଭୁତ ଶୁଣାଯାଉଥିଲା ।
Question ୧୧ ।
ଗତାୟୁ ଗୋଧୂଳିର ସେଇ ଲଗ୍ନରେ ଅଶୋକ ପ୍ରଥମଥରପାଇଁ କ’ଣ ଅନୁଭବ କରିଥିଲେ ?
Answer:
ଗତାୟୁ ଗୋଧୂଳିର ସେଇ ଲଗ୍ନରେ ଅଶୋକ ପ୍ରଥମଥରପାଇଁ ତାହାର ସମସ୍ତ ଇନ୍ଦ୍ରିୟ ଆଚ୍ଛନ୍ନକରି ମାଷ୍ଟରଜୀଙ୍କ ସମଗ୍ର ସତ୍ତା ଯେପରି ଅନୁଭବ କରିଥିଲେ ।
Question ୧୨ ।
ତୁହାଇ ତୁହାଇ କେଉଁକଥା ଅଶୋକଙ୍କ ମନ ଭିତରେ ଉତୁରି ପଡୁଥିଲା ?
Answer:
ତୁହାଇ ତୁହାଇ ଶୈଶବର ସ୍ମୃତି ଅଶୋକଙ୍କ ମନ ଭିତରେ ଉତୁରି ପଡ଼ୁଥିଲା ।
Question ୧୩ ।
ମାଷ୍ଟରଜୀଙ୍କ ଦୁଇଟି ଶିଷ୍ୟଙ୍କ ନାମ କ’ଣ ଥିଲା ?
Answer:
ମାଷ୍ଟରଜୀଙ୍କ ଦୁଇଟି ଶିଷ୍ୟଙ୍କ ନାମ ମୁନ୍ନା ଓ ମନୁ ଥିଲା ।
Question ୧୪ ।
ମାଷ୍ଟରଜୀ କେତେବେଳେ ଡରି ଅସ୍ଥିର ହୋଇଥା’ନ୍ତି ?
Answer:
ମାଷ୍ଟରଜୀଙ୍କୁ ମନୁ ଦାନ୍ତ ଦେଖେଇଲେ ସେ ଡରି ଅସ୍ଥିର ହୋଇଥା’ନ୍ତି ।
Question ୧୫ ।
କେଉଁ ପୋଷାକରେ ମାଷ୍ଟରଜୀ ତାଙ୍କୁ ଚିହ୍ନି ପାରିବେନି ବୋଲି ଅଶୋକ ଆଶଙ୍କା କରିଥିଲେ ?
Answer:
ସୁଟ୍ ଆଉ ଟାଇର ପୋଷାକରେ ମାଷ୍ଟରଜୀ ତାଙ୍କୁ ଚିହ୍ନି ପାରିବେନି ବୋଲି ଅଶୋକ ଆଶଙ୍କା କରିଥିଲେ ।
Question ୧୬ ।
ମାଷ୍ଟରଜୀଙ୍କୁ ଚକରି ଚିହ୍ନିନେବା ପରେ ଅଶୋକ ପ୍ରଥମେ କ’ଣ କରିବେ ବୋଲି କହିଛନ୍ତି ?
Answer:
ମାଷ୍ଟରଜୀଙ୍କୁ ଚକରି ଚିହ୍ନିନେବା ପରେ ଅଶୋକ ପ୍ରଥମେ ତାଙ୍କର ପାଦଧୂଳି ନେବେ ବୋଲି କହିଛନ୍ତି ।
Question ୧୭ ।
ପୋଷ୍ଟ ଅଫିସର ସାମ୍ନାରେ ଦୁଇଟି ରାସ୍ତା ଦୁଇଆଡ଼କୁ କିପରି ବାଙ୍କିଯାଇଛି ବୋଲି କୁହାଯାଇଛି ?
Answer:
ପୋଷ୍ଟ ଅଫିସର ସାମ୍ନାରେ ଦୁଇଟି ରାସ୍ତା ଦୁଇଆଡ଼କୁ ଯୂପକାଷ୍ଠ ପରି ବାଙ୍କିଯାଇଛି ବୋଲି କୁହାଯାଇଛି ।
Question ୧୮ ।
ପିଣ୍ଡା ଉପରେ ଗପ ଜମେଇଥିବା କେଇଜଣଙ୍କୁ ଅଶୋକ କ’ଣ ପଚାରିଥିଲେ ?
Answer:
ପିଣ୍ଡା ଉପରେ ଗପ ଜମେଇଥିବା କେଇଜଣଙ୍କୁ ଅଶୋକ ‘ରୂପନାରାୟଣଜୀ କେଉଁଠି ରହନ୍ତି ବୋଲି ପଚାରିଥିଲେ ।
Question ୧୯ ।
‘‘ରୂପନାରାୟଣକି ସୋନେକା ଦୁକାନ୍’’ କେଉଁଠି ଥିଲା ବୋଲି କୁହାଯାଇଛି ?
Answer:
‘ରୂପନାରାୟଣକି ସୋନେକା ଦୁକାନ୍’’ ‘ଗୋଧୂଳିଆରେ’ ଥିଲା ବୋଲି କୁହାଯାଇଛି ।
Question ୨୦ ।
କେଉଁ ଆଖୁର ଏକ୍ସରେ ଦେଇ ରିକ୍ସାବାଲା ଅଶୋକଙ୍କ ଅଭ୍ୟନ୍ତରକୁ ଦେଖିବାକୁ ଚେଷ୍ଟା କରୁଥିଲା ?
Answer:
ପରଳ ଲଗା ପେଜୁଆ ପେଜୁଆ ଆଖର ଏକ୍ସରେ ଦେଇ ରିକ୍ସାବାଲା ଅଶୋକଙ୍କ ଅଭ୍ୟନ୍ତରକୁ ଦେଖିବାକୁ ଚେଷ୍ଟା କରୁଥିଲା ।
Question ୨୧ ।
ମନୁଷ୍ୟ କଥାକହିବା ଅପେକ୍ଷା କେଉଁଥିରେ ଯଥେଷ୍ଟ ବେଶି ପ୍ରକାଶ କରିପାରେ ?
Answer:
ମନୁଷ୍ୟ କଥାକହିବା ଅପେକ୍ଷା ନୀରବରେ ଯଥେଷ୍ଟ ବେଶି ପ୍ରକାଶ କରିପାରେ ।
Question ୨୨ ।
କେଉଁଥ୍ରେ ତାଙ୍କର ଗୋଟାଏ ବଡ଼ ସମାଧାନ ହୋଇଯାଇଛି ବୋଲି ମାଷ୍ଟରଜୀ ଅଶୋକଙ୍କୁ କହିଥିଲେ ?
Answer:
ଜେଲ୍ରେ ଥିଲାବେଳେ ସ୍ତ୍ରୀ ମରିଯିବା ଘଟଣା ସେ ତାଙ୍କର ଗୋଟାଏ ବଡ଼ ସମାଧାନ ହୋଇଯାଇଛି ବୋଲି ମାଷ୍ଟରଜୀ ଅଶୋକଙ୍କୁ କହିଥିଲେ ।
Question ୨୩ ।
ଝାଙ୍କ କାଶରେ ମାଷ୍ଟରଜୀଙ୍କର କ’ଣ ଦୋହଲି ଯାଇଥିଲା ?
Answer:
ଝାଙ୍କ କାଶରେ ମାଷ୍ଟରଜୀଙ୍କର ଜୀର୍ଣ୍ଣ କଙ୍କାଳଗୁଡ଼ାକ ଦୋହଲି ଯାଇଥିଲା ।
Question ୨୪ ।
ବଡ଼ ପିଲାଦିନୁ ‘ରାମସରନ୍’ ଉପରେ କ’ଣ ପଡ଼ିଗଲା ବୋଲି କୁହାଯାଇଛି ?
Answer:
ବଡ଼ ପିଲାଦିନୁ ‘ରାମସରନ୍’ ଉପରେ ଅନେକ ଦାୟିତ୍ଵ ପଡ଼ିଗଲା ବୋଲି କୁହାଯାଇଛି ।
Question ୨୫ ।
କାହାର ଆକାଶ ଉପରେ ଅନ୍ଧାର ଜମି ଆସିଛି ବୋଲି କୁହାଯାଇଛି ?
Answer:
ସଦର ବଜାରର ଆକାଶ ଉପରେ ଅନ୍ଧାର ଜମି ଆସିଛି ବୋଲି କୁହାଯାଇଛି ।
Question ୨୬ ।
କେଉଁଥରେ ମାଷ୍ଟରଜୀଙ୍କର ଅସାଧାରଣ ଦକ୍ଷତା ଥିଲା ?
Answer:
କାହାଣୀ କହିବାରେ ମାଷ୍ଟରଜୀଙ୍କର ଅସାଧାରଣ ଦକ୍ଷତା ଥିଲା ।
Question ୨୭ ।
କାହାଣୀର ପ୍ରତ୍ୟେକଟି ଚରିତ୍ରକୁ ମାଷ୍ଟରଜୀ କ’ଣ କରି ପାରୁଥିଲେ ?
Answer:
କାହାଣୀର ପ୍ରତ୍ୟେକଟି ଚରିତ୍ରକୁ ମାଷ୍ଟରଜୀ ଆଖ୍ ଆଗରେ ଜୀବନ୍ତକରି ତୋଳି ଧରି ପାରୁଥିଲେ ।
Question ୨୮ ।
ଏଇ ବିଶ୍ଵର ବିରାଟ ବହି ଉପରେ କାହାଙ୍କ ହୃତ୍ପଦ୍ମର ସ୍ପନ୍ଦନ ଅଶୋକ ଶୁଣିପାରିଛନ୍ତି ?
Answer:
ଏହି ବିଶ୍ଵର ବିରାଟ ବହି ଉପରେ ବହୁ ବିଚିତ୍ର ମନୁଷ୍ୟ ନାୟକ ନାୟିକାର ହୃତ୍ପଦ୍ମର ସ୍ପନ୍ଦନ ଅଶୋକ ଶୁଣିପାରିଛନ୍ତି ।
Question ୨୯ ।
କର୍ପୋରେସନ କର୍ମଚାରୀ କ’ଣ କରୁଥିବାର କୁହାଯାଇଛି ?
Answer:
କର୍ପୋରେସନ କର୍ମଚାରୀ ଲାଇଟ୍ ପୋଷ୍ଟ ଦେହରେ ଶିଡ଼ି ଆଉଜେଇ ଉପରକୁ ଉଠି ଆଲୁଅ ଜାଳିବା କଥା କୁହାଯାଇଛି ।
Question ୩୦ ।
ପଳା ପଳା କରି କିରାସିନି ମାପି ଦେଉଥିବା ବୃଦ୍ଧାଟିର ବୟସ କେତେ ଥିଲା ?
Answer:
ପଳା ପଳା କରି କିରାସିନି ମାପି ଦେଉଥିବା ବୃଦ୍ଧାଟିର ବୟସ ୭୦ ଉପରେ ଥିଲା ।
Question ୩୧ ।
‘‘କୈସାଲ ହୁଅ ଦିମାକ ବିଗଡ଼ ଗୈ’’ – କାହାକୁ ଲକ୍ଷ୍ୟ କରି ଏହା କୁହାଯାଇଛି ?
Answer:
‘‘କୈ ସାଲ ହୁଆ ଦିମାକ ବିଗଡ଼ ଗୈ’’ – ବୃଦ୍ଧା ମାତାଜୀଙ୍କୁ ଲକ୍ଷ୍ୟକରି ଏହା କୁହାଯାଇଛି ।
Question ୩୨ ।
କ୍ୟାଣ୍ଟନ୍ମେଣ୍ଟ ରୋଡ଼ର କେଉଁ ରାସ୍ତାରେ ଅଶୋକ ଧୀରେ ଧୀରେ ପାଦ ଗଣି ଗଣି ଚାଲୁଥିଲେ ?
Answer:
କ୍ୟାଣ୍ଟନ୍ମେଣ୍ଟ ରୋଡ଼ର ମସୃଣ ମ୍ୟାକାଡ଼।ମାଇକଡ଼ ର।ପ୍ରାରେ ଅଶୋକ ଧୀରେ ଧୀରେ ପାଦ ଗଣି ଗଣି ଚାଲୁଥିଲେ ଚାଲୁଥିଲେ ।
(ଗ) ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନ । ଦୁଇଟି ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ । ପ୍ରଶ୍ନର ମୂଲ୍ୟ ୨ ନମ୍ବର । ଲେଖା ଓ ଲେଖକଙ୍କ ସୂଚନା ପାଇଁ ୧ ନମ୍ବର ଓ ଠିକ୍ ଉତ୍ତର ପାଇଁ ୧ ନମ୍ବର ।
ଗଳ୍ପ – ରୂପନାରାୟଣ ସାହା, ଗାଳ୍ପିକ – ଅଳମୋହନ ପଟ୍ଟନାୟକ
Question ୧ ।
କାଶୀ ବିଶ୍ଵନାଥ ମନ୍ଦିରର ରାସ୍ତା ସମ୍ପର୍କରେ କ’ଣ ବର୍ଣ୍ଣନା କରାଯାଇଛି ?
Answer:
କାଶୀ ବିଶ୍ଵନାଥ ମନ୍ଦିରର ରାସ୍ତା ନାତି ପ୍ରଶସ୍ତ ଏବଂ ସେହି ରାସ୍ତାରୁ ମନ୍ଦିରର ଅଳ୍ପ ଆଗରୁ ଜନ୍ମନେଇଛି ଆଉ ଏକ ସଂକାର୍ଣ୍ଣ ଉପପଥା
Question ୨ ।
ଡାଲମଣ୍ଡିର ସନ୍ଧ୍ୟା ସମ୍ପର୍କରେ କ’ଣ କୁହାଯାଇଛି ?
Answer:
ଏଥିରେ ଡାଲ୍ମଣ୍ଡିର ସନ୍ଧ୍ୟା ସମ୍ପର୍କରେ କୁହାଯାଇଛି, ‘ଏଠାରେ ସନ୍ଧ୍ୟା ଆସେ ଆତୁରା ନାୟିକାର ନିମନ୍ତ୍ରଣ- ଭୀରୁ ଆସ୍ର ଇଙ୍ଗିତରେ’ ।
Question ୩ ।
କେଉଁ ଆନେଇ ଅଶୋକ ଆଉଥରେ ଗଙ୍ଗା-ଗୋଧୂଳିର କରୁଣ ଏକାଙ୍କିକା ଦେଖୁଥିଲେ ?
Answer:
କୈଶୋରର କୌତୂହଳୀ ଆଞ୍ଜେଇ ଅଶୋକ ଆଉଥରେ ଗଙ୍ଗା-ଗୋଧୂଳିର କରୁଣ ଏକାଙ୍କିକା ଦେଖୁଥିଲେ ।
Question ୪ ।
ଉଜ୍ଜଳ ଚକ୍ରବାଳର ପଟ୍ଟଭୂମିରେ ଯାତ୍ରୀବାହୀ ନୌକାଗୁଡ଼ିକ ସମ୍ପର୍କରେ କ’ଣ କୁହାଯାଇଛି ?
Answer:
ଉଜ୍ଜ୍ଵଳ ଚକ୍ରବାଳର ପଟ୍ଟଭୂମିରେ ସିହୁଟ ଛବିପରି ବହୁ ଯାତ୍ରୀବାହୀ ନୌକା ଏ କୂଳରୁ ସେ କୂଳକୁ ଯାତାୟାତ କରୁଥିବ ବୋଲି କୁହାଯାଇଛି ।
Question ୫ ।
ଅଶୋକଙ୍କ ପୁରାତନ ଅନୁଭୂତିର ରୋମନ୍ଥନ କିପରି ଅନୁଭୂତ ହୋଇଥିଲା ?
Answer:
ଅଶୋକଙ୍କ ପୁରାତନ ଅନୁଭୂତିର ରୋମନ୍ଥନ, ସମୁଦ୍ର ମନ୍ଥନରେ ବହୁ ପୁରାତନ ସ୍ମୃତିର ବୁଦ୍ବୁଦ ପରି ଭାସି ଉପରକୁ ଉଠିଲା ପରି ଅନୁଭୂତ ହୋଇଥିଲା ।
Question ୬ ।
ପବନର ପ୍ରତିକୂଳରେ ମାଝି କ’ଣ କରୁଥିଲା ?
Answer:
ପବନର ପ୍ରତିକୂଳରେ ମାଝି ଜୋର୍ରେ ଆହୁଲା ଟାଣୁଥିଲା ।

Question ୭ ।
କର୍ପୋରେସନର ଅଦୃଶ୍ୟ ଇଙ୍ଗିତରେ କ’ଣ ହୋଇଥିଲା ?
Answer:
କର୍ପୋରେସନର ଅଦୃଶ୍ୟ ଇଙ୍ଗିତରେ ବାଧ୍ୟ ଶିଶୁପରି ନୌକା ଲାଗିଲା ଘାଟରେ, ସେ ନିଶୁଆ ଲୋକ ପାଖରେ ।
Question ୮ ।
ରାମନଗରର ଜଲିଟ୍ରିପ୍ଟୋଟାକୁ କିପରି କିଣିବାକୁ ହେଲା ବୋଲି କୁହାଯାଇଛି ?
Answer:
ରାମନଗରର ଜଲିଟ୍ରିପ୍ଟୋଟାକୁ ଯୁଦ୍ଧ ସମୟରେ କଳାବଜାର ପଇସାରେ କିଣିବାକୁ ହେଲା ବୋଲି କୁହାଯାଇଛି ।
Question ୯ ।
ବାପା କ’ଣ ଆରମ୍ଭ କରିଦେଲେ ବୋଲି କୁହାଯାଇଛି ?
Answer:
ଟ୍ୟାକ୍ସ ଦେବାଟା ବାପାଙ୍କୁ ବାଧିବାରୁ ସେ ଆରମ୍ଭ କରିଦେଲେ, ‘ସବୁ ବଡ଼ ବଡ଼ ଲୋକଙ୍କ ସାଙ୍ଗରେ ତୁ ବି ଜଣେ ବଡ଼ ମଣିଷ ହୋଇଗଲୁଣି ନାଇଁ ।’
Question ୧୦ ।
ସାନଭଉଣୀର କରୁଣ ମିନତି ସମ୍ପର୍କରେ କ’ଣ କୁହାଯାଇଛି ?
Answer:
ଶିକାରୁ ଆଚାର ଚୋରି କରିବାକୁ ସାନଭଉଣୀର ବହୁ କରୁଣ ମିନତିକୁ ବାରମ୍ବାର ଉପେକ୍ଷା କରି ଅଶୋକ ନିଜର ସୁବିଧା ଦେଖୁ ତାଙ୍କର ଦୀର୍ଘ ହାତକୁ ବ୍ୟବହାର କରିଛନ୍ତି ।
Question ୧୧ ।
ଅଶୋକଙ୍କ ସମ୍ପର୍କରେ ଜେଜେମା’ଙ୍କ ଟିପ୍ପଣୀ କ’ଣ ଥିଲା ?
Answer:
ଅଶୋକଙ୍କ ପାଇଁ ଟ୍ୟାକ୍ ଦେବାକୁ ପଡ଼ିବାରୁ ଜେଜେମା’ ଟିପ୍ପଣୀ ଦେଇ କହିଥିଲେ – ‘‘କ’ଣ ଆଜି ? ସବୁଦିନ ପରା ସେଇଟା ଡ଼ବଡ଼ବିଟାଏ ।’’
Question ୧୨ ।
‘‘ଆପଣମାନେ ୟେ କ’ଣ କଲେ’’ କହି ମାଷ୍ଟରଜୀ କ’ଣ କହିଛନ୍ତି ?
Answer:
ସାରା ପରିବାର ଅଶୋକକୁ ଆକ୍ଷେପ କଲାବେଳେ, ‘ଆପଣମାନେ ୟେ କ’ଣ କଲେ’ କହି ମାଷ୍ଟରଜୀ କହିଛନ୍ତି, ଅଶୋକ କିଛି ଭୁଲ କରିନାହିଁ, ସେ କେବଳ ସତକଥା କହିଛି ।
Question ୧୩ ।
ଅକାଳ-ପ୍ରୌଢ଼, ଚିନ୍ତାଜୀର୍ଣ୍ଣ, ଦରିଦ୍ର ଶିକ୍ଷକଟି କେଉଁ ପଦକୁ ଉତ୍ତୀର୍ଣ୍ଣ ହୋଇଯାଇଥିଲେ ବୋଲି କୁହାଯାଇଛି ?
Answer:
ଅକାଳ-ପ୍ରୌଢ଼, ଚିନ୍ତାଜୀର୍ଣ, ଦରିଦ୍ର ଶିକ୍ଷକଟି ସମଗ୍ର ପରିବାରର ମୁରବୀ ପଦକୁ ଉତ୍ତୀର୍ଣ୍ଣ ହୋଇଯାଇଥିଲେ ବୋଲି କୁହାଯାଇଛି ।
Question ୧୪ ।
ମୁନ୍ନା ଓ ମନୁ ଭିତରେ କ’ଣ ପାର୍ଥକ୍ୟ ଥିଲା ?
Answer:
ମୁନ୍ନା ହେଉଛି ଅଶୋକଙ୍କ ଡାକ ନାମ ଏବଂ ମନ୍ତ୍ର ହେଉଛି ତାଙ୍କର ପୋଷା ପାତିମାଙ୍କଡ଼ର ଛୁଆର ନାଁ ।
Question ୧୫ ।
ମନୁ ଦାନ୍ତ ଦେଖେଇ ଖେଲି ହେଲେ ମାଷ୍ଟରଜୀ କ’ଣ କୁହନ୍ତି ?
Answer:
ମନ୍ତୁ ଦାନ୍ତ ଦେଖେଇ ଖେଙ୍କି ହେଲେ ମାଷ୍ଟରଜୀ ଡରିଯାଇ ଦି ହାତ ପଛକୁ ଘୁଞ୍ଚିଯାଇ କହନ୍ତି, ‘ସମ୍ଲକ ମୁନ୍ନା ସମ୍ଲ୍କେ – ଚେନ୍ ପକଡ଼ତା ରହ୍ମା, ଅଗର ଛୁଟ୍ ଯାଏତୋ ।’’
Question ୧୬ ।
ମାଷ୍ଟରଜୀ କପଟ ଭର୍ତ୍ସନା କରି ମନୁକୁ କ’ଣ କହିଥା’ନ୍ତି ?
Answer:
ମାଷ୍ଟରଜୀ କପଟ ଭର୍ସନା କରି ମନୁକୁ କହନ୍ତି, ‘କର୍ତା ଯାଓ ହାଁ । ହାଁ ଯେ ତୁମ୍ହାରା ଖୁସି କର୍ତା ଯାଓ, ମେରା କ୍ତ ଆଜାନେସେ ଆଛେତେରା ସମ୍ବଝାହୁଙ୍ଗା ।’’
Question ୧୭ ।
ପଢ଼ିସାରିଲା ବେଳକୁ ମାତାଜୀ କ’ଣ କରିଥା’ନ୍ତି ?
Answer:
ପଢ଼ିସାରଲା ବେଳକୁ ମାତାଜୀ ପ୍ରାୟ ହାତରେ ପିଜୁଳି, ଆମ୍ବ ନ ହେଲେ ହାଲୁଆ ଧରି ଆସି ପହଞ୍ଚିଯିବେ ।
Question ୧୮ ।
ପିଣ୍ଡା ଉପରେ ବସିଥିବା ଲୋକଙ୍କୁ ଅଶୋକ କ’ଣ ପଚାରିଥିଲେ ?
Answer:
ପିଣ୍ଡା ଉପରେ ବସିଥିବା ଲୋକଙ୍କୁ ଅଶୋକ ପଚାରିଥିଲେ, କହିପାରିବେ ରୂପୁନାରାୟଣଜୀ କେଉଁଠି ରହନ୍ତି ?’’
Question ୧୯ ।
ପିଣ୍ଡା ଉପରର ଲୋକଙ୍କ ମଧ୍ୟରୁ ଜଣେ ଅଶୋକଙ୍କ ପ୍ରଶ୍ନର କି ଉତ୍ତର ଦେଇଥିଲା ?
Answer:
ପିଣ୍ଡା ଉପରର ଲୋକଙ୍କ ମଧ୍ୟରୁ ଜଣେ ଅଶୋକଙ୍କ ପ୍ରଶ୍ନର ଉତ୍ତର ଦେଇ କହିଥିଲା, ‘ଗଲତ୍ କିଏ ହୋଇଂ ଆପ୍ ବାବୁଜୀ, ଏକ ରୂପନାରାୟଣ କି ସୋନେକେ ଦୁକାନ୍ ହୋଗା ମେରେ ଖିଆଲ ପର୍ ଗୋଧୂଳିଆ ପର ।’’
Question ୨୦ ।
ଅଶୋକ ଆଉଥରେ ବୁଝାଇ ପିଣ୍ଡା ଉପରର ଲୋକମାନଙ୍କୁ କ’ଣ କହିଥିଲେ ?
Answer:
ଅଶୋକ ଆଉଥରେ ବୁଝାଇ ପିଣ୍ଡା ଉପରର ଲୋକମାନଙ୍କୁ କହିଥିଲେ, ‘ମୁଁ ଅଳଙ୍କାର ପାଇଁ ଆସିନି, ଛୋଟ ଛୋଟ ପିଲାଙ୍କୁ ପଢ଼ାନ୍ତି – ଏଇଠି କୋଉଠି ଥାଆନ୍ତି ମାଷ୍ଟରଜୀ……. ରୂପନାରାୟଣ……… ।”
Question ୨୧ ।
ରିକ୍ସାବାଲାଟା ତା’ର କୋଟରଗତ ପେଜୁଆ ପେଜୁଆ ଆଖରେ କ’ଣ ଦେଖିବାକୁ ଚେଷ୍ଟା କରୁଥିଲା ?
Answer:
ରିକ୍ସାବାଲାଟା ତା’ର କୋଟରଗତ ପେଜୁଆ ପେଜୁଆ ଆଖର ଲେନ୍ସରେ ଅଶୋକର ଅଭ୍ୟନ୍ତରଟା ଦେଖିବାକୁ ଚେଷ୍ଟା କରୁଥିଲା ।
Question ୨୨ ।
ମାଷ୍ଟରଜୀଙ୍କ ପାଦଧୂଳି ନେବାକୁ ଅଶୋକ ହାତ ବଢ଼ାଇଲା ପରେ ମାଷ୍ଟରଜୀ କ’ଣ କହିଥିଲେ ?
Answer:
ମାଷ୍ଟରଜୀଙ୍କ ପାଦଧୂଳି ନେବାକୁ ଅଶୋକ ହାତ ବଢ଼ାଇଲା ପରେ ମାଷ୍ଟରଜୀ କେଇହାତ ପଛକୁ ଘୁଞ୍ଚାଇ ଅଶୋକର ଦୁଇ ବାହା ଧରି ଉପରକୁ ତୋଳିନେଇ କହିଲେ – ‘‘ଦୀର୍ଘଜୀବୀ ହୁଅ ତୁ ଅଶୋକ – ମନେଥିଲା ଏଇ ବୁଢ଼ା ରୂପନାରାୟଣର କଥା ?’’
Question ୨୩ ।
ମାଷ୍ଟରଜୀଙ୍କ ସେଇ ପୁରୁଣା ପିଣ୍ଡାରେ ଅଶୋକ କାହିଁକି ମୂକ ହୋଇ ବସିଥିଲେ ?
Answer:
ମାଷ୍ଟରଜୀଙ୍କ ସେଇ ପୁରୁଣା ପିଣ୍ଡାରେ ଅଶୋକ ଠିକ୍ କ’ଣ ପଚାରିବା ଉଚିତ୍ ସେଇକଥା ଭାବି ଭାବି ମୂକ ହୋଇ ବସିଥିଲେ ।
Question ୨୪ ।
କେଉଁ କଥାରେ ମାଷ୍ଟରଜୀଙ୍କର ଗୋଟାଏ ବଡ଼ ସମାଧାନ ହୋଇଯାଇଥିଲା ବୋଲି ସେ କହିଛନ୍ତି ?
Answer:
ବର୍ଷକ ପରେ ଜେଲ୍ରୁ ଫେରି ତାଙ୍କର ସ୍ତ୍ରୀ ମରିଯାଇଥିବା କଥା ଦେଖ୍ ମାଷ୍ଟରଜୀଙ୍କର ଗୋଟାଏ ବଡ଼ ସମାଧାନ ହୋଇଯାଇଥିଲା ବୋଲି ସେ କହିଛନ୍ତି ।
Question ୨୫ ।
କିଏ ସାମ୍ନାର ରିକ୍ସାକୁ ଦେଖ୍ ଅଟକି ଯାଇଥିଲେ ?
Answer:
ଗୋଟିଏ ସୁଦୃଶ୍ୟ ଦମ୍ପରି ସାମ୍ନାର ରିକ୍କୁ ଦେଖ୍ ଅଟକି ଯାଇଥିଲେ ।
Question ୨୬ ।
କାହାଣୀ-ଦକ୍ଷ ମାଷ୍ଟଜୀଙ୍କ ଆତ୍ମକାହାଣୀର ସ୍ଵରୂପ କିପରି ଥିଲା ?
Answer:
କାହାଣୀ ଦକ୍ଷ ମାଷ୍ଟରଜୀଙ୍କ ଆତ୍ମକାହାଣୀ ଥିଲା ପରୀ ରାଜ୍ୟର କଳ୍ପନାକୁ ପରାସ୍ତ କଲାଭଳି ଏବଂ ଇତିହାସଠାରୁ ଆହୁରି ସତ୍ୟ ।
Question ୨୭ ।
ମାତାଜୀଙ୍କ ପାଦଧୂଳି ନେଇ ଅଶୋକ ସେଥୁରୁ କେଉଁ ଗନ୍ଧ ଆଘ୍ରାଣ କରିପାରୁଥିଲେ ?
Answer:
ମାତାଜୀଙ୍କର ପାଦଧୂଳି ନେଇ ଅଶୋକ ସେଥୁରୁ ହାଲୁଆର ଗନ୍ଧ ଆଘ୍ରାଣ କରିପାରୁଥିଲେ ।
Question ୨୮ ।
ମାତାଜୀଙ୍କ ଅବସ୍ଥା ଶେଷବେଳକୁ କ’ଣ ହୋଇଥିଲା ?
Answer:
କେତେ ବର୍ଷ ହେଲା ମାତାଜୀଙ୍କ ମୁଣ୍ଡ ବିଗିଡ଼ି ଯାଇ ସେ ପାଗଳୀ ହୋଇଯାଇଥିଲେ ।
Question ୨୯ ।
ମାତାଜୀଙ୍କର କେଉଁ କଥାରେ ମାଷ୍ଟରଜୀ ସଙ୍କୁଚିତ ହୋଇଯାଇଥିଲେ ?
Answer:
ମାତାଜୀଙ୍କର ‘‘କ୍ୟା ତୁମ୍ହରା ଦିମାକ୍ ତୋ’ ବିଗଡ଼ ନେହିଁ ଗିୟା ରୂପନାରାୟଣ ବଢାକୋ ଦାଣ୍ଡତା ହେ ତୁମ୍ ? ’’ କଥାରେ ମାଷ୍ଟରଜୀ ସଙ୍କୁଚିତ ହୋଇଯାଇଥିଲେ ।
Question ୩୦।
ମାଷ୍ଟରଜୀ ଅଶୋକଙ୍କ ହାତରେ ଖଣ୍ଡେ କାଗଜ ବଢ଼େଇ ଦେଇ ତାଙ୍କୁ କ’ଣ କହିଥିଲେ ?
Answer:
ମାଷ୍ଟରଜୀ ଅଶୋକଙ୍କ ହାତରେ ଖଣ୍ଡେ କାଗଜ ବଢ଼େଇଦେଇ ତାଙ୍କୁ କହିଲେ – ‘‘ୟେ ରହା ହମାରା କାଁହା କା ପଢା – କଭି କଭି ୟାଦ୍ ଆଯାଏ ତୋ ଚିଙ୍ଗୁଠି ଲିଖୁ ହାଁ….. ।’’
Question ୩୧ ।
ମାଷ୍ଟରଜୀଙ୍କ କଥା ଅଶୋକଙ୍କର କେଉଁଠି ତୁହାଇ ତୁହାଇ ମନେପଡ଼ୁଥିଲା ?
Answer:
ମାଷ୍ଟରଜୀଙ୍କ କଥା ଅଶୋକଙ୍କର କ୍ୟାଣ୍ଟନମେଣ୍ଟ ରୋଡ଼ର ମସୃଣ ମ୍ୟାକାଡ଼ାମାଇଜ୍ ରାସ୍ତା ଉପରେ ଧୀରେ ଧୀରେ ଚାଲୁଥିଲାବେଳେ ତୁହାଇ ତୁହାଇ ମନେପଡ଼ୁଥିଲା ।
Question ୩୨ ।
କେଉଁ କଥା ଇଚ୍ଛାକରି ବି ବିଶ୍ଵାସ କରିବାକୁ ଚାହାଁନ୍ତି ନାହିଁ ବୋଲି ଅଶୋକ କହିଛନ୍ତି ?
Answer:
‘ସତରେ କ’ଣ ସେଇ ଜରାଜୀର୍ଣ୍ଣ, ଦରିଦ୍ର, ରିକ୍ସାବାଲାଟା ବିଦ୍ୟାଦାତା ରୂପ୍ନାରାୟଣ !’ କଥାଟି ଇଚ୍ଛାକରି ବି ବିଶ୍ଵାସ କରିବାକୁ ଚାହାଁନ୍ତି ନାହିଁ ବୋଲି ଅଶୋକ କହିଛନ୍ତି ।
Question ୩୩ ।
କ’ଣ କରି ଏ ଜାତି ମାଷ୍ଟରଜୀଙ୍କ ଚାଟଶାଳୀକୁ ଫେରିଆସିବ ବୋଲି କୁହାଯାଇଛି ?
Answer:
ଏ ଜାତି ଧୀରେ ଧୀରେ ଅହିରାଜ କୁଣ୍ଡଳିର ଶୀତ-ଶଯ୍ୟାରୁ ଚଞ୍ଚଳ ହୋଇ ଉଠିବ – ଆଉ ତା’ର ଜନକର ପାଦତଳେ ଜାନୁପାତି କ୍ଷମା ମାଗି, ପୁଣିଥରେ ବାଧ୍ୟ ଶିଶୁପରି ସିଲଟ ଧରି ଚାଟଶାଳୀକୁ ଫେରିଆସିବ ବୋଲି କୁହାଯାଇଛି ।
Question ୩୪ ।
ବାଧ ଶିଶୁ ପରି ମାଷ୍ଟରଜୀଙ୍କ ଚାଟାଶାଳୀକୁ ଏ ଜାତି ଫେରିଆସିଲେ ସେଦିନ ମାଷ୍ଟରଜୀ କ’ଣ କରିବେ ?
Answer:
ବାଧ୍ୟ ଶିଶୁ ପରି ମାଷ୍ଟରଜୀଙ୍କ ଚାଟଶାଳୀକୁ ଏ ଜାତି ଫେରି ଆସିଲେ ସେଦିନ ମାଷ୍ଟରଜୀ କହିବେ, ‘ମୁଁ ତୁମକୁ କ୍ଷମା କରିଛି – ଯାଅ – ତମମାନଙ୍କର ବିଦ୍ୟା ଏଥର ସମାପ୍ତ ।’
Question ୩୫ ।
ମଇଳା କାଗଜ ଗୁଳାଟିକୁ ଖୋଲି ଅଶୋକ ସେଥିରେ କ’ଣ ଲେଖାଥିବାର ଦେଖୁଥିଲେ ?
Answer:
ମଇଳା କାଗଜ ଗୁଳାଟିକୁ ଖୋଲି ଅଶୋକ ସେଥ୍, ‘ରୂପନାରାୟଣ ସାହା, ସଦର ବଜାର, କ୍ୟାଣ୍ଟନମେଣ୍ଟ ରୋଡ଼, ବନାରସ୍’ ଲେଖାଥିବାର ଦେଖୁଥିଲେ । ରୋଡ଼, ବନାରସ୍’ ଲେଖାଥିବାର ଦେଖିଥିଲେ ।
(ଘ) ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନ । ୩୦ଟି ଶବ୍ଦରେ ଉତ୍ତର ଲେଖ । ପ୍ରଶ୍ନର ମୂଲ୍ୟ ୩ ନମ୍ବର । ଲେଖା ଓ ଲେଖକଙ୍କ ସୂଚନା ପାଇଁ ୧ ନମ୍ବର ଓ ଉତ୍ତର ପାଇଁ ୨ ନମ୍ବର ରହିବ ।
ଗଳ୍ପ – ରୂପନାରାୟଣ ସାହା, ଗାଳ୍ପିକ – ଅଖଳମୋହନ ପଟ୍ଟନାୟକ
Question ୧ ।
ବନାରସର ରାସ୍ତା ସମ୍ପର୍କରେ କ’ଣ ବର୍ଣ୍ଣନା କରାଯାଇଛି ?
Answer:
କ୍ରିଷ୍ଟମାସ ଛୁଟିରେ ବନାରସ ରାସ୍ତାରେ ଲୋକଙ୍କର ଅସମ୍ଭବ ଭିଡ଼ ରହିଥିଲା । ରାସ୍ତାରେ ସିଆର ସିଆର ହୋଇ ଲୋକର ଧାଡ଼ି ଯେମିତି ଜମାଟ ବାନ୍ଧିଯାଇଛି ବରଫ ପରି । ଜମାଟବନ୍ଧା ବରଫର ସ୍ତୂପ ସୂର୍ଯ୍ୟକିରଣରେ ପ୍ରସରିଗଲା ପରି ସେହି ଜମା ହୋଇଥିବା ଲୋକମାନେ ପୁନଶ୍ଚ ସବୁଆଡ଼କୁ ପ୍ରସାରିତ ହୋଇ ଯାଉଥିଲେ ।
Question ୨।
ଡାଲମଣ୍ଡିକୁ ଏକ ହତଶ୍ରୀ ସଭ୍ୟତାର ଡଷ୍ଟବିନ୍ ବୋଲି କାହିଁକି କୁହାଯାଇଛି ?
Answer:
ଡାଲମଣ୍ଡିକୁ ଏକ ହତଶ୍ରୀ ସଭ୍ୟତାର ଡଷ୍ଟବିନ୍ ବୋଲି ଲେଖକ କହିଛନ୍ତି, କାରଣ ଏଠାରେ ରହିଥା’ନ୍ତି ସହସ୍ରାଧିକ ବାରାଙ୍ଗନା । ଲକ୍ଷ ଲକ୍ଷ ରୂପପିୟାସୀ ନାଗରିକ ଡାଲ୍ମଣ୍ଡିରେ ନିଜର ରୂପତୃଷ୍ଣା ମେଣ୍ଟାଇଥା’ନ୍ତି । ଏଠାରେ ସନ୍ଧ୍ୟା ଆସେ ବାରାଙ୍ଗନାମାନଙ୍କ ଆସ୍ର ନିମନ୍ତ୍ରଣରେ ଏବଂ ରାତ୍ରି ଆସେ ରତିକ୍ଳାନ୍ତ କାମୁକୀ ନାରୀର ସ୍ବେଦସିକ୍ତ ଆଖୁର ପତାରେ ପତାରେ ।
Question ୩ ।
ବନାରସରେ କାହିଁକି ସନ୍ଧ୍ୟା ହୁଏନା ବୋଲି କୁହାଯାଇଛି ?
Answer:
ସାଧାରଣତଃ ସନ୍ଧ୍ୟା ହେଲେ ଲୋକମାନେ ଗୃହାଭିମୁଖୀ ହୋଇଥା’ନ୍ତି; ମାତ୍ର ବନାରସରେ ସନ୍ଧ୍ୟାରେ ଅନେକ ଲୋକ ଆନନ୍ଦର ସନ୍ଧାନ କରିବାକୁ ବାହାରେ ବୁଲାବୁଲି କରୁଥା’ନ୍ତି । ସୁତରାଂ ଅସମ୍ଭବ ଲୋକଙ୍କ କୋଳାହଳ ସାଙ୍ଗକୁ ବିଦ୍ୟୁତ୍ ଆଲୋକର ଛଟାକୁ ଦେଖ୍ ବନାରସରେ ସନ୍ଧ୍ୟା ହୁଏନା ବୋଲି ଲେଖକ କହିଛନ୍ତି ।
Question ୪।
ଗଙ୍ଗାର କେଉଁ ଦୃଶ୍ୟ ମୁକ୍ତକେଶୀ ଦ୍ରୌପଦୀର ବେଣୀବନ୍ଧନ ପରି ମନେହୋଇଛି ?
Answer:
ଅସ୍ତଗାମୀ ସୂର୍ଯ୍ୟଙ୍କର ଲାଲ୍କିରଣ, ଗଙ୍ଗାର ଜଳ ଉପରେ ପଡ଼ି ଲାଲେ-ଲାଲ୍ ଦେଖାଦେଇଛି । ସେହି ଦୃଶ୍ୟକୁ ଦେଖ୍ ଗାଳ୍ପିକ କହିଛନ୍ତି, ମୁକ୍ତକେଶୀ ଦ୍ରୌପଦୀର ଯେପରି – ବେଣୀବନ୍ଧନ ହୋଇଛି । ଦ୍ରୌପଦୀ ଦୀର୍ଘଦିନ ଧରି କେଶକୁ ମୁକୁଳା ରଖୁଥିଲା ଏବଂ ଶପଥ କରିଥିଲା, ଦୁଃଶାସନର ରକ୍ତରେ ବେଣୀବନ୍ଧନ କରିବ । ଗଙ୍ଗାର ଜଳ ଲାଲ୍ବର୍ଣ୍ଣ ଦେଖାଯାଉଥିବାରୁ କଥାକାର ତା’ ସହିତ ମହାଭାରତର ପ୍ରସଙ୍ଗକୁ ତୁଳନା କରିଛନ୍ତି ।
Question ୫ ।
ବେଣୀବନ୍ଧନର ଲଗ୍ନ ଅତିକ୍ରମ କରିବାର ଦୃଶ୍ୟକୁ କିପରି ବର୍ଣ୍ଣନା କରାଯାଇଛି ?
Answer:
ବେଣୀବନ୍ଧନର ଲଗ୍ନ ଅତିକ୍ରମ କରିବାପରେ, ସନ୍ଧ୍ୟାର ଦିଗହରା ପବନରେ ଗଙ୍ଗାର କୃଷ୍ଣନୀଳ ପାଣି ଅସଂଖ୍ୟ ଢେଉରେ ଭାଙ୍ଗି ପଡୁଥିଲା । ପ୍ରତିଟି ଢେଉର ନୀଳ ଗାତ୍ରରେ ଅଳ୍ପକିଛି ଧୂସର ଅନ୍ଧାର ରହିଥିଲା। ତାହାକୁ ଦେଖିଲେ ଜଣା ଯାଉଥିଲା, ସତେଯେପରି ଗଙ୍ଗାମାତା ତନ୍ଦ୍ରାତୁରା ଶେଷ ସିନ୍ଧ୍ୟାକୁ କୋଳେଇ ନଚେଇ ନଚେଇ ଶୁଆଇ ପକାଉଛି, ରାତ୍ରିର ଗଭୀର ନିଦ୍ରାରେ ।
Question ୬ ।
ଗଙ୍ଗାବକ୍ଷରେ ବିଦ୍ୟୁତ ଆଲୋକର ପ୍ରତିବିମ୍ବ କିପରି ମନେହୋଇଛି ?
Answer:
ଗଙ୍ଗା ବକ୍ଷରେ ବିଦ୍ୟୁତ୍ ଆଲୋକର ପ୍ରତିବିମ୍ବ ପଡ଼ି ଅପୂର୍ବ ଶ୍ରୀଧାରଣ କରିଛି । ତାହାକୁ ଦେଖ୍ କଥାକାର କାବ୍ୟକ ଭାବ ପ୍ରକାଶ କରି କହିଛନ୍ତି, କେଶରୀ ମଧ୍ୟମା ଗଙ୍ଗାର କଟି ଆବୃତ କରିଛି ସୁବର୍ଣ୍ଣ ମେଖଳା । ଆଉ ଗଙ୍ଗାର ଦେହେ ଦେହେ ଗଭୀର ନୀଳରଙ୍ଗର ବୁଟିଦାର ବନାରସୀ ଶାଢ଼ୀ – ଛତ୍ରେ ଛତ୍ରେ ରୂପେଲୀ ଜରିର ତାରା ଫୁଟିଛି ।
Question ୭ ।
‘‘ନୌକା ଉଠିବ ଦଶାଶ୍ବମେଧ ଘାଟରେ’’ – ନୌକାର ଗତିପଥ ସମ୍ପର୍କରେ ଏଠାରେ କ’ଣ କୁହାଯାଇଛି ?
Answer:
ହରିଶ୍ଚନ୍ଦ୍ର ଘାଟର ଚିତା ନିକଟରେ, ଆଉ ଡାକେବାଟ ଦୂରରେ ପଡ଼ିବ ଦଶାଶ୍ବମେଧ ଘାଟ, ଯେଉଁଠାରେ କି ନୌକା ଉଠିବ । ପବନର ପ୍ରତିକୂଳରେ ମାଝି ଆହୁଲା ଟାଣୁଥିଲା ଜୋର୍ରେ । ମାତ୍ର ନୌକାର ଗତି କମିଗଲା । ମାଝିର ହାତ ହୁଗୁଳା ହୋଇ ଆସିଲା। ଫଳରେ ନୌକାରେ ଥିବା ପରିବାରଟିର ମୃଦୁଗୁଞ୍ଜନ ମଧ୍ଯ ନିରବ ହୋଇ ଆସିଥିଲା ।

Question ୮।
‘ରାମନଗର କା ନାମ୍ ମତ ଲିଜିୟେ ବାବୁଜୀ’ – ମାଝିଜଣକ ଏକଥା କାହିଁକି କହିଛି ?
Answer:
ଦଶାଶ୍ବମେଧ ଘାଟରେ ନୌକା ଉଠିବା ପୂର୍ବରୁ, ମାଝିଟି ଚାପାକଣ୍ଠରେ, ତା’ ଭାଷାରେ ଯାହା କହୁଥୁଲା, ତାହା ଅଳ୍ପ ବୁଝି ହେଉଥିଲା । କୂଳରେ ବସିଥ୍ ଗୋଟାଏ ନିଶୁଆ ଲୋକକୁ ଦେଖାଇ ଦେଇ କହିଲା, ‘ରାମ୍ନଗର କା ନାମ ମତ୍ ଲିଜିୟେ ବାବୁଜୀ’ । କାରଣ ଏହି ନାମ କହିଲେ ପ୍ରତ୍ୟେକଙ୍କ ପିଛା ଗୋଟିଏ ଗୋଟିଏ ଟଙ୍କା ଟ୍ୟାକ୍ସ ଦେବାକୁ ପଡ଼ିବ । ଏହା ହେଉଛି କର୍ପୋରେସନ୍ର ।
Question ୯ ।
‘‘ସର୍ବନାଶ ! କାହାରି ମୁହଁରେ ଭାଷା ନାହିଁ?’’ – ଏହାର ପ୍ରସଙ୍ଗଟି କ’ଣ ?
Answer:
ମାଝିଟି ସେମାନଙ୍କୁ ସତର୍କ କରିଦେଇଥିଲା, ରାମନଗର ନାମ ନ କହିବାକୁ । ମାତ୍ର ନିଶୁଆ ଲୋକଟି ଚିତ୍କାର କରି କେଉଁଆଡ଼େ ଯାଇଥିଲା ବୋଲି ପଚାରିବାରୁ ଅଶୋକ ବଡ଼ ପାଟିରେ କହିଥିଲା – ‘ରାମନଗର ଗୟେଥେ ହାମଲୋଗ’ । ସର୍ବନାଶ ହୋଇଯାଇଥିଲା, କାହାରି ମୁହଁରେ ଭାଷା ନଥିଲା । କାରଣ ଏହାଦ୍ଵାରା ସେମାନଙ୍କୁ ଟ୍ୟାକ୍ସ ଦେବାକୁ ପଡ଼ିବ ।
Question ୧୦।
କେଉଁ ମୁହୂର୍ତ୍ତକୁ ତା’ର ବିପନ୍ନ ମୁହୂର୍ତ୍ତ ବୋଲି ଅଶୋକ କହିଛି ?
Answer:
ବାରଣ ସତ୍ତ୍ଵେ ‘ଆମେ ରାମନଗର ଯାଇଥିଲୁ’ ବୋଲି ଅଶୋକ କହିବାରୁ, ତାଙ୍କ ବାପାଙ୍କୁ ଟ୍ୟାକ୍ସ ଦେବାକୁ ପଡ଼ିଥିଲା । ଅଶୋକର ଭୁଲ ପାଇଁ ସାରା ପରିବାର ତାକୁ ପଦେ ପଦେ କହିଥିଲେ । ଆଉ ଯେଉଁମାନେ କିଛି କହି ନଥିଲେ, ସେମାନେ ମଧ୍ୟ ପରିବାରର କଥାକୁ ସମର୍ଥନ କରିଥିଲେ । ଏହା ଦଶବର୍ଷର ଶିଶୁ ଅଶୋକର ସହିବାର ସୀମା ଅତିକ୍ରମ କରିଯାଇଛି । ଆସ୍ରେ ଲୁହ ଟଳମଳ ହେଉଛି । ସେହି ମୁହୂର୍ତ୍ତକୁ ତା’ର ବିପନ୍ନ ମୁହୂର୍ତ୍ତ ବୋଲି ଅଶୋକ କହିଛି ।
Question ୧୧ ।
ମାଷ୍ଟରଜୀ କିପରି ଅଶୋକର ମଦତ୍ କରିଥିଲେ ?
Answer:
ଅଶୋକକୁ ସାରା ପରିବାର ପଦେ ପଦେ କହିବାରୁ, ସେ ଅସହ୍ୟ ହୋଇପଡ଼ିଛି । ଆଗ୍ରେ ତା’ର ଲୁହ ଟଳମଳ ହୋଇଛି । ଏହି ବିପନ୍ନ ମୁହୂର୍ତ୍ତରେ ମାଷ୍ଟରଜୀ ଅଶୋକକୁ ମଦତ୍ କରିଛନ୍ତି । ତା’ ଆଡ଼କୁ ଅନାଇ ଧୀରେ ଧୀରେ ମୁଣ୍ଡ ହଲାଇ ବ୍ୟସ୍ତ ନ ହେବାକୁ କହିଛନ୍ତି । ଅଶୋକ ତାଙ୍କ କୋଳରେ ମୁଣ୍ଡରଖ୍ କାନ୍ଦିବାରୁ ସେ ପିଠି ଥାପୁଡ଼ାଇ ନ କାନ୍ଦିବାକୁ କହିଛନ୍ତି ।
Question ୧୨ ।
‘‘ତା’ ବୁଝିବାର କ୍ଷମତା ଆପଣମାନଙ୍କର ନାହିଁ ’’ – ଏହା ଜେଉଁ ପ୍ରସଙ୍ଗରେ କୁହ। ଯାଇଛି ?
Answer:
ଅଶୋକକୁ ପରିବାରର ସବୁ ସଦସ୍ୟ ଆକ୍ଷେପ କରିବାରୁ, ସେ ଅସହାୟ ହୋଇପଡ଼ିଛି । ସେହି ସମୟରେ ଗୁରୁଜନ, କିନ୍ତୁ ଆପଣମାନେ ତା’ର ଯେ କି କ୍ଷତି କରୁଛନ୍ତି, ତା’ ବୁଝିବାର କ୍ଷମତା ଆପଣମାନଙ୍କର ନାହିଁ ।’
Question ୧୩ ।
ମାଷ୍ଟରଜୀଙ୍କ ସମଗ୍ର ସଭାରେ ଅଶୋକ ପ୍ରଥମଥର ପାଇଁ କ’ଣ ଅନୁଭବ କରିଥିଲା ?
Answer:
ମାଷ୍ଟରଜୀ ଥିଲେ ପାଞ୍ଚଟଙ୍କା ବେତନର ଜଣେ ସାଧାରଣ ଟ୍ୟୁସନ୍ ମାଷ୍ଟର । ସେ ଥିଲେ ଭୀରୁ, ପରାନ୍ନଭୋଜୀ ଓ ନିରୀହ । ମାତ୍ର ଅଶୋକକୁ ସାହାଯ୍ୟ କରିବାକୁ ଯାଇ, ମାଷ୍ଟରଜୀ ସାରା ପରିବାରକୁ ସମାଲୋଚନା କରିଥିଲେ । ରହିଛି, ସମଗ୍ର ସତ୍ତାରେ ଅଶୋକ ପ୍ରଥମଥରପାଇଁ ଅନୁଭବ କରିଥିଲେ ।
Question ୧୪ ।
ମାଷ୍ଟରଜୀଙ୍କ ଶାରୀରିକ ଗଠନ କିପରି ଥିଲା ?
Answer:
ମାଷ୍ଟରଜୀ ଥିଲେ ଉଜ୍ଜ୍ଵଳ ଗୌରବର୍ଷର । ଈଷତ୍ ଦୀର୍ଘ ମୁହଁ ଉପରେ ଉନ୍ନତ ଶୁକଚଞ୍ଚୁ ପରି ନାସିକା । ବଡ଼ ବଡ଼ ଦୁଇଟି କାନ ଉପରେ ବିପର୍ଯ୍ୟସ୍ତ ବାଳ ଲମ୍ବି ଆସିଥିଲା କେରା କେରା ହୋଇ । ସାମାନ୍ୟ ଭିତରକୁ ପଶି ପଶି ଯାଇଥିଲା, ଦୁଇଟି ବୁଦ୍ଧିଦୀପ୍ତ ଆଖି ।
Question ୧୫ ।
ମାଷ୍ଟରଜୀଙ୍କୁ ଥରେ ଯାଇ ଦେଖୁ ଆସିବାକୁ ଅଶୋକ କାହିଁକି ମନ ବଳାଇଥିଲେ ?
Answer:
ଅଶୋକ ବନାରସରେ ଥିଲାବେଳେ, ସେ ତାଙ୍କର ଅତୀତର ସ୍ମୃତିକୁ ସ୍ମରଣ କରିଥିଲେ । ସେହି ଅବସରରେ ତାଙ୍କର ମନେପଡ଼ିଥିଲା ପିଲାଦିନର ଟ୍ୟୁସନ ମାଷ୍ଟର, ମାଷ୍ଟରଜୀଙ୍କ କଥା । ଜୀବନରେ ଶିକ୍ଷା ଓ ପଦବୀରେ ପ୍ରତିଷ୍ଠିତ ହେଲାପରେ, ଶିକ୍ଷାର ମୂଳଦୁଆ ପକାଇଥିବା ମାଷ୍ଟରଜୀଙ୍କ କଥା ସେ ମନେପକାଇ, ଯିବାପାଇଁ ମନ ବଳାଇଥିଲେ ।
Question ୧୬ ।
କେଉଁ ଘଟଣାରେ ମାଷ୍ଟରଜୀ ଡରି ଅସ୍ଥିର ହୋଇଯାଇଥିଲେ ।
Answer:
ଅଶୋକ ଓରଫ ମୁନ୍ନା, ତା’ର ପୋଷା ପାତିମାଙ୍କଡ଼ ମନୁକୁ ଧରି ମାଷ୍ଟରଜୀଙ୍କ ପାଖକୁ ପାଠ ପଢ଼ିବାକୁ ଯାଉଥିଲା । ଦୁହେଁ ପାଠ ପଢ଼ି ବସୁଥିଲେ । ଅଶୋକ ଦାନ୍ତ ଦେଖାଇଲେ, ମାଷ୍ଟରଜୀ ତା’କୁ ଡରାନ୍ତି । ମାତ୍ର ପାତିମାଙ୍କଡ଼ ମନ୍ତୁ ଦାନ୍ତ ଦେଖାଇଲେ ମାଷ୍ଟରଜୀ ଡରି ଅସ୍ଥିର ହୋଇଯାଉଥିଲେ ।
Question ୧୭ ।
କେଉଁ ଅବସ୍ଥାକୁ ମାଷ୍ଟରଜୀଙ୍କ ବିପନ୍ନ ମୁହୂର୍ତ୍ତ ବୋଲି କୁହାଯାଇଛି ?
Answer:
ମୁନ୍ନା ଓ ମନୁ ପାଠ ପଢ଼ିଲାବେଳେ ମାଷ୍ଟରଜୀଙ୍କ ପାଖରେ ଦୁଷ୍ଟାମି କରନ୍ତି । ମୁନ୍ନା ଲଣ୍ଡନର ଠିପି ଖୋଲି ପାଣି ପୂରାଇଲା ବେଳେ, ମାଷ୍ଟରଜୀ ସେପରି ନକରିବାକୁ କହିଛନ୍ତି ଓ ସେହି ସମୟରେ ମନୁ ମାଷ୍ଟରଜୀଙ୍କ ପାନବଟାରୁ ପାନ କାଢ଼ି ପାଟିରେ ପୂରାଇବାର ସୂଚନା ଦେଇଥାଏ । ଏହି ବିପନ୍ନ ମୁହୂର୍ଭରେ ମାଷ୍ଟରଜୀ କିଛି କରିନପାରି କପଟ ଭର୍ସନାକରି, ‘କରତା ଯାଓ ହଁ’ ବୋଲି କହିଥା’ନ୍ତି ।
Question ୧୮ ।
‘‘ଓ ଦୁଇ ଦୁଇଟା ମାଙ୍କଡ଼ଙ୍କୁ ମଣିଷ କାହାଁତକ କରେ ମୁଁ?’- ଏହା କେଉଁ ପ୍ରସଙ୍ଗରେ କୁହାଯାଇଛି ?
Answer:
ମୁନ୍ନା ଓ ମନ୍ତୁ ଦୁଇଜଣ ପାଠ ପଢ଼ିବାକୁ ଯାଇ ଅନେକ ସମୟରେ ମାଷ୍ଟରଜୀଙ୍କୁ ହଇରାଣ କରନ୍ତି । ମନୁ ପାନଖାଉଥିଲା ବେଳେ ମୁନ୍ନା ଲଣ୍ଡନରେ ପାଣି ପୂରାଏ ଏବଂ ପାଣି ଛାଟି ଲଣ୍ଡନ କାଚ ଫଟାଇଦିଏ । ମାଷ୍ଟରଜୀ କପଟ ଭର୍ସନା କରିକହନ୍ତି, ‘ମୁନ୍ନା ମନ୍ତୁ ଭାଇ ଭାଇ- ଓ ଦୁଇ ଦୁଇଟା ମାଙ୍କଡ଼ଙ୍କୁ ମଣିଷ କାହାଁତକ୍ କରେ ମୁଁ ?”
Question ୧୯।
ରିକ୍ସା ଆସି କେଉଁଠି ପହଞ୍ଚି ଯାଇଥିଲା ଓ ଅଶୋକ ସେଠାରେ କ’ଣ ଖୋଜୁଥିଲେ ?
Answer:
ରିକ୍ସା ଆସି ପହଞ୍ଚି ଯାଇଥିଲା କ୍ୟାଣ୍ଟନ୍ମେଣ୍ଟ ଛକ ଉପରେ ଓ ଅଶୋକ ସେଠାରେ ମାଷ୍ଟରଜୀଙ୍କ ଘରକୁ ଯିବାପାଇଁ ଛୋଟ ପୋଷ୍ଟଅଫିସ୍ ସାମ୍ନାରେ ଗଳି ଖୋଜୁଥିଲେ । କାରଣ ଦୀର୍ଘ ବ୍ୟବଧାନ ପରେ ମାଷ୍ଟରଜୀଙ୍କର ଦରିଦ୍ର କୁଟୀରଟି ତାଙ୍କର ଠିକ୍ରୂପେ ମନେ ନଥିଲା ।
Question ୨୦ ।
ନାଲି କିରାସିନିର ଲଣ୍ଠନ ଆଲୁଅରେ ମାଷ୍ଟରଜୀ କ’ଣ କରୁଥିବେ ବୋଲି ଅଶୋକ କଳ୍ପନା କରିଛନ୍ତି ?
Answer:
ନାଲି କିରାସିନିର ଲଣ୍ଠନ ଆଲୁଅରେ ମାଷ୍ଟରଜୀ ତାଙ୍କର ପିଣ୍ଡା ଉପରେ ବସି ରହିଥିବେ, ଆଉ ତାଙ୍କୁ ଘେରି ବସିଥ୍ ଅନେକ ପଠନରତ ଶିଶୁ ।
Question ୨୧ ।
ସ୍ନେହ ଦୁର୍ବଳ ଶିକ୍ଷକର ଦୁଇଆଖୁ କାହିଁକି ଆନନ୍ଦର ଅଶ୍ରୁରେ ଭାସିଯିବବୋଲି କୁହାଯାଇଛି ?
Answer:
ଅଶୋକ ନିଜର ପିଲାଦିନର ଶିକ୍ଷକଙ୍କୁ ଦେଖାକରିବାକୁ ଯିବା ଅବକାଶରେ ମନେ ମନେ ଭାବିଛନ୍ତି, ସେ ଶିକ୍ଷକଙ୍କୁ ଦେଖିଲେ ପାଦଧୂଳି ନେବେ ଓ ଶିକ୍ଷକ ତାଙ୍କୁ କୁଣ୍ଢେଇ ପକେଇବେ ଗଦ୍ଗଦ୍ ହୋଇ । ସ୍ନେହ-ଦୁର୍ବଳ ଶିକ୍ଷକଙ୍କର ଦୁଇଆଖୁ ତାଙ୍କ ଆଦରର ଛାତ୍ରକୁ ଦେଖ୍ ଆନନ୍ଦର ଅଶ୍ରୁରେ ଭାସିଯିବ ବୋଲି କୁହାଯାଇଛି ।
Question ୨୨ ।
ପ୍ରତ୍ୟେକ ଶିକ୍ଷକ କେଉଁଦିନକୁ ଅପେକ୍ଷା କରି ରହିଥାଏ ?
Answer:
ଜାତିର ଶ୍ରେଷ୍ଠ ସନ୍ତାନ କେଉଁ ଦିନ ଆସି ତା’ର ବାଲ୍ୟଗୁରୁର ପାଦତଳେ ମଥାନତ କରି ତା’ର କୃତଜ୍ଞତା ଜଣାଇବ ସେଇ ଚିର-ଈପ୍ସିତ ଦିନକୁ ଅତିଷ୍ଠ ହୋଇ ଅପେକ୍ଷା କରି ରହିଥାଏ ପ୍ରତ୍ୟେକ ଶିକ୍ଷକ । ଏତିକିତ ତା’ର ଗର୍ବ ! ଚିର ନିର୍ଯାତିତ ଶିକ୍ଷକ ଗୋଷ୍ଠୀର ଏତିକି ଚରମ କ୍ଷତିପୂରଣ ।
Question ୨୩ ।
ଅଶୋକଙ୍କୁ ଚିହ୍ନିବା ଅବସରରେ ରିକ୍ସାବାଲାର ଆଖ୍ ଓ ଓଠର ଅବସ୍ଥା କିପରି ଥିଲା ?
Answer:
ଅଶୋକଙ୍କୁ ଚିହ୍ନିବା ଅବସରରେ ରିକ୍ସାବାଲାର ଆସ୍ରେ ତା’ର ସୁଦୂରର ଦୃଷ୍ଟି-ଆଖ୍ କଣର ଚମଡ଼ାଗୁଡ଼ାକ କୁଞ୍ଚ୍ କୁଞ୍ଚ୍ ହେଇଯାଇ ଅସଂଖ୍ୟ ରେଖା ସୃଷ୍ଟି କରିଥିଲା। ସେ ଯେପରି କ’ଣ କହିବ କହିବ ହଉଥିଲା ଓ ସେହି ଉତ୍ତେଜନାରେ ତା’ର କଳା କଳା ଓଠ କମ୍ପି ଉଠୁଥିଲା ବାରମ୍ବାର ।
Question ୨୪ ।
‘‘ସେଇ ବିସ୍ମୟ ବର୍ଣ୍ଣନାର ଅତୀତ’’ ଏଠାରେ କେଉଁ ବିସ୍ମୟ କଥା କୁହାଯାଇଛି ?
Answer:
ମାଷ୍ଟରଜୀ ଅନାଇ ଅନାଇ ଅଶୋକକୁ ଚିହ୍ନିଲା ପରେ, ଅଶୋକ ଦେଖୁଲା ତାହାର ଈପ୍ସିତ ଶିକ୍ଷକଙ୍କୁ । ସେ ଦେଖିଲା, ସେହି ବିପର୍ଯ୍ୟସ୍ତ, ଜରାକ୍ଳାନ୍ତ, ଦୀନ ରିକ୍ସାବାଲାର ମଳିନ ପ୍ରତିକୃତି ଭିତରୁ ଧୀରେ ଧୀରେ ଉଇଁ ଆସୁଥିଲା ତାଙ୍କର ମାଷ୍ଟରଜୀଙ୍କର ସେଦିନର ଚେହେରା । ସେହି ଚେହେରା ‘ସେଇ ବିସ୍ମୟ ବର୍ଣ୍ଣନାର ଅତୀତ କଥା’ ବୋଲି କୁହାଯାଇଛି ।
Question ୨୫ ।
ମାଷ୍ଟରଜୀ ଆଉ କିଛି ନକହି ପାରିବାର ଦୃଶ୍ୟଟି କିପରି ଥିଲା ?
Answer:
ମାଷ୍ଟରଜୀ ଅଶୋକକୁ ଦେଖୁଲା ପରେ ଭାବବିଭୋର ହୋଇଯାଇଛନ୍ତି । ସେ କିଛି କହିପାରି ନ ଥିଲେ; ବରଂ ଆନନ୍ଦର ଅଶ୍ରୁ ତାଙ୍କର କଣ୍ଠରୁଦ୍ଧ କରି ଦେଇଥିଲା । ଅଶୋକ ଅନୁଭବ କରିଥିଲେ ମନୁଷ୍ୟ କଥା କହିବା ଅପେକ୍ଷା ନୀରବରେ ତା’ଠାରୁ ପ୍ରକାଶ କରିପାରେ ଯଥେଷ୍ଟ ବେଶି ।
Question ୨୬ ।
ମାଷ୍ଟରଜୀ ସେ ମୁହୂର୍ତ୍ତରେ ପୃଥିବୀର ସବୁଠାରୁ ସୁଖୀ ମନୁଷ୍ୟ ବୋଲି ସେ କାହିଁକି ଯେ କହି କହିଥା’ନ୍ତା ?
Answer:
ବହୁଦିନ ପରେ ମାଷ୍ଟରଜୀ ଅଶୋକକୁ ଦେଖିଲାପରେ ଆନନ୍ଦିତ ହୋଇଥିଲେ । ତାଙ୍କ କ୍ଷୁଦ୍ର ଘରେ ସେ ବୁଲାଇ ଆଣିଥିଲେ । ସେହି ଅବସରରେ କଥା କଥାକେ ପ୍ରଶଂସା, ଗର୍ବ ଆଉ ଆନନ୍ଦରେ ଅସ୍ଥିର ହୋଇଯାଉଥିଲେ । ସେହି ମୁହୂର୍ତ୍ତରେ ମାଷ୍ଟରଜୀ ପୃଥିବୀର ସବୁଠାରୁ ସୁଖୀ ମନୁଷୀ ବୋଲି ଲେଖକ ପ୍ରକାଶ କରିଛନ୍ତି ।
Question ୨୭ ।
ମାଷ୍ଟରଜୀ କାହିଁକି ଜେଲ୍ ଯାଇଥିଲେ ?
Answer:
ସମଗ୍ର ଉତ୍ତର ଭାରତ ବ୍ୟାପୀ ହୋଇଥିବା ନିମ୍ନ ପ୍ରାଥମିକ ଶିକ୍ଷକ ଧର୍ମଘଟର ପୁରୋଧା ଥିଲେ ମାଷ୍ଟରଜୀ । ମାସିକ ୧୩ ଟଙ୍କା ଦରମାରେ ସେମାନେ ଚଳି ନ ପାରିବାରୁ ଧର୍ମଘଟ କରିଥିଲେ । ମାତ୍ର ତାଙ୍କୁ ରାଷ୍ଟ୍ର ବିରୁଦ୍ଧରେ ଷଡ଼ଯନ୍ତ୍ର କରିବା ଅଭିଯୋଗରେ ଜେଲ୍ ଯିବାକୁ ହୋଇଥିଲା ।
Question ୨୮ ।
ଜେଲ୍ରୁ ଫେରିବା ପରେ ମାଷ୍ଟରଜୀ କ’ଣ କରିଥିଲେ ?
Answer:
ଜେଲ୍ରୁ ଫେରିଲା ପରେ ସେ ଦେଖିଲେ ତାଙ୍କ ସ୍ତ୍ରୀ ମରିଯାଇଛି । ସେଥିପାଇଁ ସେ ସ୍ତ୍ରୀର ଅଳ୍ପ କିଛି ଅଳଙ୍କାର ବିକି ଏବଂ ସେଥିରେ କରଜ ଟଙ୍କା ମିଶେଇ ଖଣ୍ଡେ ରିକ୍ କରିଦେଇ ପରିବାର ଚଳାଇବାର ବ୍ୟବସ୍ଥା କରିଥିଲେ ।
Question ୨୯ ।
ମାଷ୍ଟରଜୀଙ୍କ ଝାଙ୍କ-କାଶ ସମ୍ପର୍କରେ କ’ଣ କୁହାଯାଇଛି ?
Answer:
ମାଷ୍ଟରଜୀ ଅଶୋକଙ୍କ ସହିତ କଥା ହେଉଥିଲା ବେଳେ ତାଙ୍କର ଝାଙ୍କ କାଶ ଉଠିଥିଲା । ସେହି କାଶରେ ତାଙ୍କର ଜୀର୍ଣ୍ଣ କଙ୍କାଳଗୁଡ଼ିକ ଯେପରି ଦୋହଲି ଯାଇଥିଲା । କେତେ ସମୟ ପରେ କହିଲେ, ଦେହ ଭଲ ରହୁନାହିଁ । ଡାକ୍ତର ଦେଖେଇବାକୁ ଯାଇଥିଲେ ଏବଂ ଡାକ୍ତର ତାଙ୍କୁ ପ୍ରେସି ହୋଇଛି ବୋଲି କହିଲେ ଏବଂ ଚିକିତ୍ସା ପାଇଁ ଅନେକ ପଇସା ଲାଗିବ ବୋଲି ମଧ୍ୟ କହିଥିଲେ ।
Question ୩୦ ।
‘ରାମସରନ୍’ ସମ୍ପର୍କରେ କ’ଣ କୁହାଯାଇଛି ?
Answer:
ରାମସରନ୍ ମାଷ୍ଟରଜୀଙ୍କ ବାର ଚଉଦ ବର୍ଷର ପୁଅ । ବାପାଙ୍କୁ ରିଵାଟଣା କାମରେ ସାହାଯ୍ୟ କରେ ସେ । ଅଶୋକ ସହିତ ମାଷ୍ଟରଜୀ କଥାବାର୍ତ୍ତା ହେଉଥିଲାବେଳେ, ଏକ ସୁଦୃଶ୍ୟ ଦମ୍ପତ୍ତିଙ୍କୁ ରିକ୍ସାରେ ନେବାପାଇଁ ରାମସରନ୍ କହିଛନ୍ତି, ପିଲାଟିବେଳୁ ତା’ଉପରେ ଅନେକ ଦାୟିତ୍ଵ ପଡ଼ିଛି ।
Question ୩୧ ।
ମାଷ୍ଟରଜୀଙ୍କ କାହାଣୀରେ କେଉଁ ଚରିତ୍ରସବୁ ଜୀବନ୍ତ ହୋଇ ଉଠୁଥିଲେ ?
Answer:
କାହାଣୀ କହିବାରେ ମାଷ୍ଟରଜୀଙ୍କର ଅସାଧାରଣ ଦକ୍ଷତା ଥିଲା। ତାଙ୍କ କାହାଣୀର ସ୍ଵର୍ଗର ପରୀ, ଆଣ୍ଡ୍ରୋସିଲିସର୍ ସିଂହ, ସୁନୀତି ସନ୍ତାନ ଧ୍ରୁବ, ରାଜପୁତ୍ ବୀର ପ୍ରତାପ ସିଂହ, ପୃଥୀରାଜ, ଶିଖୁମନାଇ, ଜୟଦ୍ରଥ ଭଳି ପ୍ରତ୍ୟେକଟି ଚରିତ୍ର ଜୀବନ୍ତ ହୋଇ ଉଠୁଥିଲେ ।
Question ୩୨ ।
ମାଷ୍ଟରଜୀଙ୍କ ଆତ୍ମକାହାଣୀ ଶୁଣିବା ପରେ ଅଶୋକଙ୍କୁ ହଠାତ୍ କ’ଣ ମନେ ହୋଇଥିଲା ?
Answer:
ମାଷ୍ଟରଜୀଙ୍କ ଆତ୍ମକାହାଣୀ ଶୁଣିବାପରେ ଅଶୋକଙ୍କୁ ହଠାତ୍ ମନେହୋଇଥିଲା, ତାଙ୍କର ଏବେବି ଯେପରି ପାଠପଢ଼ା ଅସମାପ୍ତ ହୋଇ ରହିଯାଇଛି ଆଉ ସେ ସେଦିନର କୁତୂହଳୀ ଶିଶୁପରି ଆଜିବି ମାଷ୍ଟରଜୀଙ୍କ ପାଖରେ ବସି ବସି ବହି ପଢୁଛନ୍ତି । ଏହି ବିଶ୍ଵର ବିରାଟ ‘ବହି ଉପରେ ବହୁ ବିଚିତ୍ର ମନୁଷ୍ୟ ନାୟକ ନାୟିକାର ହୃତ୍ସ୍ପନ୍ଦନ ଶୁଣାଯାଉଛି ।
Question ୩୩ ।
ମାଷ୍ଟରଜୀଙ୍କ କେଉଁ କଥାର ଉତ୍ତର ଦେବାର କିଛି ନଥିଲା ବୋଲି ଅଶୋକ କହିଛନ୍ତି ?
Answer:
ସନ୍ଧ୍ୟା ହେବାରୁ ଅଶୋକ ମାଷ୍ଟରଜୀଙ୍କଠାରୁ ବିଦାୟ ନେବାକୁ ଚାହିଁଛି । ମାଷ୍ଟରଜୀ ନିଜେ ସ୍ଵୀକାର କରିଛନ୍ତି, ଅଶୋକକୁ ଏତେଦିନ ପରେ ଦେଖ୍ ଖୁସିଲାଗିଲେ ବି, ଏ ଭଙ୍ଗାଘରେ ସେ ଗୋଟିଏ ରାତି ପାଇଁ ଅତିଥ୍ ନକରି ପାରିବା ତାଙ୍କ ପାଇଁ ଦୁର୍ଭାଗ୍ୟ ମାଷ୍ଟରଜୀଙ୍କ ଏଭଳି କଥା ଶୁଣି ଅଶୋକଙ୍କର କିଛି ଉତ୍ତର ଦେବାର ନ ଥିଲା ବୋଲି ସେ କହିଛନ୍ତି ।
Question ୩୪ ।
ସତୁରିରୁ ଅଧ୍ବ ବୟସ ହୋଇଥିବା ମାତାଜୀ କ’ଣ କରୁଥିବାର ଅଶୋକ ଦେଖୁଥିଲା ?
Answer:
ସତୁରିରୁ ଅଧ୍ବ ବୟସ ହୋଇଥିବା ମାତାଜୀ, ଯାହାର କି ଦେଖୁବାର ଓ ଶୁଣିବାର ଶକ୍ତି କ୍ରମଶଃ ଲୋପପାଇ ଆସୁଥୁଲା, ଛୋଟ ଛୋଟ ଦୁଇଟି କିରାସିନି ଟିଣଧରି, କିରାସିନି ବିକ୍ରି କରୁଥିଲା । ଜଣ ଜଣ କରି ରିକ୍ସାବାଲା ଆସୁଥିଲେ ଓ କିରାସିନି ନେଉଥିଲେ । ମାତାଜୀ ଦୀପ ଆଲୁଅରେ ଖୁବ୍ ନିରୀକ୍ଷଣ କରି ପଇସାକୁ ଦେଖୁରିବା ପରେ ଥରିଲା ହାତରେ ପଳା ପଳା କରି କିରାସିନି ମାପି ଦେଉଥିଲେ ।
Question ୩୫ ।
‘‘ୟେ କ୍ୟା ହୋଗୟା ହେ ମାତାଜୀ କେ ?’’ – ଏ କଥା ଅଟୋକ ମ।ଷ୍ଠରକୀଙ୍କୁ କେତେବେଳେ ପଚାରିଛନ୍ତି ।
Answer:
ପିଲାଦିନରୁ ମାତାଜୀଙ୍କ ପାଖରୁ ହାଲୁଆ ଖାଇଥିବା କଥା ଅଶୋକ ଭୁଲି ନଥିଲେ । ସେ ମାତାଜୀଙ୍କ ପାଦଛୁଇଁ ପାଦଧୂଳି ନେଲେ ଏବଂ ନିଜର ପରିଚୟ ଦେଲେ ମଧ୍ୟ, ମାତାଜୀ ଚିହ୍ନିପାରିଲେ ନାହିଁ କିମ୍ବା ଚିହ୍ନିବାକୁ ଚେଷ୍ଟା ମଧ୍ୟ କଲେନାହିଁ । ଏଭଳି ପରିସ୍ଥିତି ଦେଖୁ, ‘ୟେ କ୍ୟା ହୋଗୟା ହେ ମାତାଜୀ କେ ?’’ ବୋଲି ଅଶୋକ ମାଷ୍ଟରଜୀଙ୍କୁ ପଚାରିଛନ୍ତି ।
Question ୩୬ ।
ମାତାଜୀ ସେଦିନ ତୃପ୍ତ କଣ୍ଠରେ ପଦାକୁ ବାହାରି ଆସି କ’ଣ କହୁଥିଲେ ବୋଲି ଅଶୋକ ମନେ ପକାଇଛନ୍ତି ।
Answer:
ଅଶୋକଙ୍କର ମନେପଡ଼ିଛି, ଯଦି କେବେ ମାଷ୍ଟରଜୀ ନାଲି ଆଖ୍ ଦେଖେଇ ଟିକିଏ କିଛି କହିଲେ ସେ ସିଲଟ ଫିଙ୍ଗିଦେଇ ଦୌଡ଼ିଯାଉଥିଲେ ମାତାଜୀଙ୍କ କୋଳକୁ । ମାତାଜୀ ମଧ୍ୟ ଦୃପ୍ତ ପଦକ୍ଷେପରେ ପଦାକୁ ବାହାରି ଆସି କହୁଥିଲେ ମାଷ୍ଟରଜୀଙ୍କୁ, ‘କ୍ୟା ତୁମ୍ହରା ଦିମାକ୍ ତୋ’ ବିଗଡ୍ ନେହିଁ ଗୟା ରୂପନାରାୟଣ – ବଚ୍ଚାକୋ ଦାଣ୍ଡତା ହେ ତୁମୁ ?”
Question ୩୭ ।
‘ଜଣେ ହତ୍ୟାକାରୀର ଭୀରୁ ସଙ୍କୁଚିତ ବିବେକ ନେଇ ଚାଲିଛି ମୁଁ”? ଏହା କେଉଁ ପ୍ରସଙ୍ଗରେ କୁହାଯାଇଛି ?
Answer:
ମାଷ୍ଟରଜୀଙ୍କ ପାଖରେ ଅଶୋକ କଥାବାର୍ତ୍ତା ହେଲେ ବି, ସେ ଭାରତ ସରକାରଙ୍କ ଶିକ୍ଷା ବିଭାଗର ପଦସ୍ଥ କର୍ମଚାରୀ ଏବଂ ତାଙ୍କ ନିର୍ଦ୍ଦେଶରେ ଲକ୍ଷ ଲକ୍ଷ ଶିକ୍ଷକଙ୍କ ଭାଗ୍ୟ ନିୟନ୍ତ୍ରିତ ହେଉଛି ବୋଲି ସେ ପରିଚୟ ଦେଇନଥିଲେ । କାରଣ ମାଷ୍ଟରଜୀ ଏହା ଜାଣିଥିଲେ, ସେ ହୁଏତ ଘୃଣା କରିଥା’ନ୍ତେ । ତେଣୁ ଅଶୋକ ମନେ ମନେ ‘ଜଣେ ହତ୍ୟାକାରୀର ଭୀରୁ ସଂକୁଚିତ ବିବେକ ନେଇ ଚାଲିଛି ମୁଁ” ବୋଲି ବିଚାର କରିଛନ୍ତି ।
Question ୩୮ ।
ଅଶୋକଙ୍କ କାନ ପାଖରେ କିଏ ଜଣେ କ’ଣ ଫିସ୍ ଫିସ୍ କରି କହୁଛି ବୋଲି ତାଙ୍କର ମନେହୋଇଛି ?
Answer:
ଅଶୋକ ମାଷ୍ଟରଜୀଙ୍କ ପାଖରୁ ଆସିଲାବେଳେ ନିଜକୁ ଦୋଷୀ ମନେକରିଛନ୍ତି । ସେହି ସମୟରେ ସେ ଅନୁଭବ କରିଛନ୍ତି, ତାଙ୍କ କାନ ପାଖରେ କିଏ ଜଣେ ଫିସ୍ ଫିସ୍ କରି କହୁଛି, ‘ଏ ଦୋଷ ତୋ’ର ଏକା ନୁହଁରେ ଅଶୋକ – ଏ ମୂର୍ଖତା ଏଇ ସମଗ୍ର ଅନ୍ଧଜାତିର ।’
Question ୩୯ ।
ଚୂନନାରାୟଣ ଏ ଜାତି ପାଇଁ କ’ଣ କରିବା ଉଚିତ ବୋଲି ଅଶୋକଙ୍କୁ କହିଛନ୍ତି ?
Answer:
ରୂପନାରାୟଣ ପରି ଅନେକ ଶିକ୍ଷକ ନିରନ୍ନ ଭାବରେ ଏ ଜାତିକୁ ପାଠ ପଢ଼ାଇଲେ, ସେମାନେ କିଛି ନାହିଁ । ତେଣୁ ଏ ଜାତିର ଶୈଶବ ଏବେ ବି ବାକୀ – ଆଉ ଥରେ ନୂଆକରି ଏମାନଙ୍କୁ ପ୍ରାଥମିକ ଶିକ୍ଷାଦେବା ଉଚିତ ବୋଲି ସେ ଅଶୋକଙ୍କୁ କହିଛନ୍ତି ।
Question ୪୦ ।
ଏ ଜାତିକୁ ଜାଗ୍ରତ କରିବାକୁ ହେବ ବୋଲି ଅଶୋକ ମାଷ୍ଟରଜୀଙ୍କୁ କାହିଁକି କହିଛନ୍ତି ?
Answer:
ଅଶୋକ ମନେ ମନେ କହିଛନ୍ତି, ଏ ଜାତି ଆଜି କ୍ଷମତା ମଦପିଇ ବେହୋସ ହୋଇଛି ମାଷ୍ଟରଜୀ । ଏମାନେ କୌଣସି ସମୟରେ ଆପଣଙ୍କର କରୁଣ ନିବେଦନ ଶୁଣି ନାହାଁନ୍ତି । ଆଜି ଆଉ ନୁହେଁ, ଏ ଜାତିକୁ ଜାଗ୍ରତ କରିବାକୁ ହେବ ।
Question ୪୧ ।
ମାଷ୍ଟରଜୀ କ’ଣ କଲେ ଏ ଅଚେତନ ଜାତିର ମସ୍ତିଷ୍କରେ ଚେତନା ସଞ୍ଚାରିତ ହେବ ବୋଲି ଅଶୋକ କହିଛନ୍ତି ?
Answer:
ଅଶୋକ ମାଷ୍ଟରଜୀଙ୍କୁ କହିଛନ୍ତି, ‘‘ଆଜି ସେଇ ଲମ୍ବା ଚାବୁକ୍ଟା ଧରି ପିଟନ୍ତୁ ଏ ଜାତିକୁ – ଖୁବ୍ ଜୋର୍ରେ ପିଟନ୍ତୁ – ବିଟ୍ ଦେମ୍ ରାଇଟ୍ ଆଣ୍ଡ ଲେଫଟ୍-ବ୍ଲାକ୍ ଆଣ୍ଡ ବୁ । ଦେଖିବେ- ଏ ଅଚେତନ ଜାତିର ମସ୍ତିଷ୍କରେ ଧୀରେ ଦୀରେ ଚେତନା ସଞ୍ଚାରିତ ହେବ ।’’
(ଙ) ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନ । ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୧୫୦ ଶବ୍ଦରେ ଦେବାକୁ ହେବ । ପ୍ରଶ୍ନର ମୂଲ୍ୟ ୫ ନମ୍ବର ।
Question ୧।
ପଠିତ ଗଳ୍ପରେ ବନାରସ୍ର ବର୍ଣ୍ଣନା କିପରି ରହିଛି – ଉଲ୍ଲେଖ କର ।
Answer:
ଆଧୁନିକ ଓଡ଼ିଆ ଗଳ୍ପ ସାହିତ୍ୟରେ ଯେଉଁ କେତେଜଣ ଗାଳ୍ପିକ, ଗଳ୍ପକୁ ସମ୍ଭ୍ରାନ୍ତ ଶ୍ରେଣୀୟ ଭାଷାରେ ସଜ୍ଜିତ କରିଛନ୍ତି, ସେମାନଙ୍କ ମଧ୍ୟରେ କଥାକାର ଅସ୍ଥୂଳମୋହନ ପଟ୍ଟନାୟକ ଅନ୍ୟତମ । ଗାଳ୍ପିକ ପରିବେଶ ଓ ପ୍ରାକୃତିକ ଲକ୍ଷ୍ୟ କରିଛନ୍ତି ଏବଂ ତାହାକୁ ଗଳ୍ପର ପ୍ରଥମ ପର୍ଯ୍ୟାୟରେ ପରିପ୍ରକାଶ କରିଛନ୍ତି । ସେଭଳି ବନାରସର ବର୍ଣ୍ଣନା ପାଠକଲେ ପାଠକ ମନରେ କାବିକ ରସତୃଷ୍ଣା ପ୍ରଶମିତ ହୋଇଯାଏ ।
ଗଳ୍ପନାୟକ ଅଶୋକ କ୍ରିଷ୍ଟମାସ୍ ଛୁଟିରେ ବୁଲି ଯାଇଥିଲେ ବନାରସ । ବନାରସ ତାଙ୍କର ପରିଚିତ ସ୍ଥାନ । ସେ ବନାରସରେ ନିଜର ଶୈଶବ ଓ କୈଶୋର ସମୟ ଅତିବାହିତ କରିଥିଲେ । ମାତ୍ର ବନାରସକୁ ଅଭିଜ୍ଞ ଦୃଷ୍ଟିରେ ସେ ଲକ୍ଷ୍ୟ କରିଛନ୍ତି ।
ବନାରସ୍ ଲୋକମାନଙ୍କର ଅସମ୍ଭବ ଭିଡ଼ । କାରଣ ଏହି ସ୍ଥାନକୁ ଭାରତର ବିଭିନ୍ନ ସ୍ଥାନର ଲୋକ କାଶୀ ବିଶ୍ଵନାଥ ଦର୍ଶନ କରିବାକୁ ଆସିଥା’ନ୍ତି । ସେମାନଙ୍କ ମନରେ ରହିଥାଏ ପୁଣ୍ୟ ଅର୍ଜନ କରିବାର ମାନସିକତା । ସେଠାରେ ଲୋକ ଧାଡ଼ି ଧାଡ଼ି ହୋଇ ବିଭିନ୍ନ ବାଟରେ ଆସି ମନ୍ଦିର ପାଖରେ ଏକାଠି ହୋଇଥା’ନ୍ତି ଏବଂ ପୁଣି ସେମାନେ ସେଇ ରାସ୍ତାବାଟେ ଦେଇ ଫେରିଯାଇଥା’ନ୍ତି । କଥାକାରଙ୍କ ଭାଷାରେ – ‘‘ବନାରସ – ଭାରତଭୂମିର ଅସଂଖ୍ୟ ପୁଣ୍ୟ କାଙ୍ଗାଳ ଜନତାର ଚିର ଈପ୍ସିତ ବନାରସ । ରାସ୍ତାରେ ସିଆର ସିଆର ହୋଇ ଲୋକର ଧାଡ଼ି ଯେମିତି ଜମାଟ ବାନ୍ଧିଯାଇଛି ବରଫ ପରି । XX X । ଜମାଟବନ୍ଧା ବରଫର ସ୍ତୂପ ଯେମିତି ସୂର୍ଯ୍ୟର ପ୍ରଥମ କିରଣରେ ଧୀରେ ଧୀରେ ଗ୍ଲେସିଅର ପରି ପ୍ରସରି ଯାଇଛି, ତା’ର ପ୍ରବାହରେ ସଂକୀର୍ୟ ରାଜପଥର ପ୍ରତିଟି ବର୍ଗଇଞ୍ଚକୁ ଆଲିଙ୍ଗନ କରି ।’’
ଟାକ୍ସିକ ପର୍ବ ନାୟକଙ୍କ ଦୃଷ୍ଟିରେ ବନାରସ ସହର ହୋଇ ରହିନାହିଁ; ବରଂ ସେ ହୋଇଛି ବହୁବର୍ଣ୍ଣରେ ବିଭୂଷିତ ଓ ବହୁବିଚିତ୍ର ପରିବେଶରେ ଚିତ୍ରିତ ସ୍ଥାନଟିଏ । ସୂର୍ଯ୍ୟ ହୋଇଥା’ନ୍ତି ଅସ୍ତାଚଳାଭିମୁଖୀ । ତାଙ୍କର ନରମ ଲାଲ୍ରଣ କାଶୀ ବିଶ୍ଵନାଥଙ୍କ ମନ୍ଦିରର ସ୍ଵର୍ଣ୍ଣଚୂଡ଼ାରେ ପଡ଼ି ଚକ୍ ଚକ୍ କରୁଛି । ମନ୍ଦିରର ରାସ୍ତା ନାତି ପ୍ରଶସ୍ତ ଏବଂ ସେହି ରାସ୍ତାର ଅଳ୍ପ ଆଗକୁ ଜନ୍ମ ନେଇଛି ସଂକୀର୍ଣ୍ଣ ପଥଟିଏ । ସେହି ପଥଟି ପଡ଼ିଛି ଡାଲ୍ ମଣ୍ଡି ଆଡ଼କୁ । ଡାଲ୍ ମଣ୍ଡି ହେଉଛି ପାଇଁ ଓ ମନଖୁସି ପାଇଁ ।
ସେଠାରେ ନାୟିକାର କଟାକ୍ଷ ନାୟକକୁ ବିମୋହିତ କରେ । ଗାଳ୍ପିକ କେବଳ ସେହି ପରିବେଶ ନୁହେଁ, ସେଠାକାର ପରିସ୍ଥିତିକୁ ବର୍ଣ୍ଣନା କରି ଲେଖୁଛନ୍ତି – ‘ଲକ୍ଷ ରୂପ-ପିୟାସୀ ନାଗରିକ ପଦରଜ ସିକ୍ତ ତୀର୍ଥ ଡାଲମଣ୍ଡି । ନାୟିକାର ଆସ୍ର ବଚ୍ଛାରେ ସେଠି ସନ୍ଧ୍ୟା ତ୍ରସ୍ତା-ମଦନ ଅର୍ଜନାର କୋଳାହଳରେ ରାତ୍ରି ନିର୍ବାସିତା । କିନ୍ତୁ ସେଠି ବି ସନ୍ଧ୍ୟା ଆସେ ଆତୁରା ନାୟିକାର ନିମନ୍ତ୍ରଣ-ଭୀରୁ ଆସ୍ର ଇଙ୍ଗିତରେ – ରାତ୍ରି ଆସେ ରତିକ୍ଳାନ୍ତକାମୁକୀ ନାରୀର ସ୍ବେଦସିକ୍ତ ଆଖର ପତାରେ ପତାରେ ।’’ ଯାହାକୁ କି ଗାଳ୍ପିକ ମଧ୍ୟ ହତଶ୍ରୀ ସଭ୍ୟତାର ଡଷ୍ଟବିନ୍ ଭାବରେ ତୁଳନା କରିଛନ୍ତି।
ବନାରସକୁ ଲୋକମାନେ ଆନନ୍ଦ ସନ୍ଧାନ ଉଦ୍ଦେଶ୍ୟରେ ଆସୁଛନ୍ତି । ଯାହାଫଳରେ ସେଠାକାର ରାସ୍ତା ଅନେକ ଲୋକଙ୍କୁ ନେଇ ଉଛୁଳି ପଡ଼ୁଛି । ଅସମ୍ଭବ ଭିଡ଼ ଦେଖାଦେଇଛି । ଯାହା ଫଳରେ କେତେବେଳେ ଦିନ ସରି ସନ୍ଧ୍ୟା ଆସିଯାଉଛି, ତାହା ଜାଣିହେଉ ନାହିଁ । କାରଣ ବିଦ୍ୟୁତ୍ ଆଲୋକରେ, ଲୋକଙ୍କର ଭିଡ଼ ଦେଖିଲେ, ସନ୍ଧ୍ୟାର ନୀରବତା ସେଠାରେ ଆକଳନ କରିବା ଅସମ୍ଭବ ।
ବାସ୍ତବରେ କଥାକାର ବନାରସର ଯେଭଳି ବର୍ଣ୍ଣନା କରିଛନ୍ତି, ତାହା ଅତ୍ୟନ୍ତ ମନୋଜ୍ଞ ହୋଇଛି ।
Question ୨।
କଥାକାରଙ୍କ ବର୍ଣ୍ଣନାଚାତୁରୀ କିପରି ସନ୍ଧ୍ୟା ଓ ରାତ୍ରିକାଳୀନ ଗଙ୍ଗାର ଦୃଶ୍ୟକୁ ଚିତ୍ରାୟିତ କରିଛି – ଦର୍ଶାଅ ।
Answer:
ସାରସ୍ଵତ ସାଧକଙ୍କ ଦୃଷ୍ଟି ଅସାଧାରଣ । ସାଧାରଣ ଦର୍ଶକ ଯାହା ଦେଖୁ ମଧ୍ୟ ଦେଖିପାରେ ନାହିଁ, କିମ୍ବା ସେହି ଦୃଶ୍ୟ ତାଙ୍କ ମନରେ ସେମିତି କିଛି ଗଭୀର ପ୍ରତିକ୍ରିୟା ସୃଷ୍ଟି କରିପାରେ ନାହିଁ, ସେହି ଦୃଶ୍ୟରୁ ସାରସ୍ଵତ ସାଧକ ନିଆରା ବିଚାରଧାରା ଖୋଜିବସେ । କ୍ରିଷ୍ଟମାସ୍ ଛୁଟିରେ ଗଳ୍ପନାୟକ ଅଶୋକ ଯାଇଛନ୍ତି, ତାଙ୍କର ବହୁ ପରିଚିତ ଓ ତାଙ୍କ ପାଇଁ ବହୁପୁରୁଣା ସହର ବନାରସକୁ । କୌଣସି ଏକ ଲାଇଟ୍ପୋଷ୍ଟକୁ ଆଉଜି ସେ ଅନ୍ୟମନସ୍କ ଭାବରେ ଦେଖୁଛନ୍ତି ବନାରସକୁ ଓ ଗଙ୍ଗାନଦୀର ବିଚିତ୍ର ଦୃଶ୍ୟକୁ । ସେହି ଦୃଶ୍ୟକୁ ଅତ୍ୟନ୍ତ ମନୋଜ୍ଞ ଭାବରେ ସେ ପ୍ରକାଶ କରିଛନ୍ତି । ବର୍ଣ୍ଣନାକରି, ଗଛଟିକୁ ସୁଖପାଠ୍ୟ କରାଇଛନ୍ତି ଏବଂ ପାଠକ. ମନରେ ଏକ ଅପୂର୍ବ ଦୃଶ୍ୟକୁ ଅବତାରଣା କରାଇଛନ୍ତି ।
ଗଙ୍ଗାର ଅପରୂପ ଦୃଶ୍ୟ ଗାଳ୍ପିକଙ୍କୁ ବିମୋହିତ କରିଛି । ଅସ୍ତଗାମୀ ସୂର୍ଯ୍ୟକିରଣ ଗଙ୍ଗାନଦୀର ବକ୍ଷରେ ପଡ଼ି, ସତେ ଯେପରି ସୁନାର କିରଣ ଝଲମଲ ହେଲାପରି ମନେହୋଇଛି । ଗଙ୍ଗାର ଗହମ ରଙ୍ଗର ପାଣି ଲାଲେ-ଲାଲ ହୋଇଯାଇଛି । ତାହାକୁ ଦେଖ୍ କଥାକାର, ମହାଭାରତର ଏକ ପ୍ରସଙ୍ଗ ଯେପରି ଚିତ୍ରକଳ୍ପ ଭାବରେ ଗ୍ରହଣ କଲାଭଳି ମନେହୋଇଛି । ସେ ଲେଖୁଛନ୍ତି – ‘ଆଜି କ’ଣ ମୁକ୍ତକେଶୀ ଦ୍ରୌପଦୀର ବେଣୀବନ୍ଧନ ? ବେଣୀ ବନ୍ଧନର ଲଗ୍ନ ଏଇ ଅତିକ୍ରମ କରିଗଲା ।’’ ଅର୍ଥାତ୍ ସୂର୍ଯ୍ୟ କ୍ରମଶଃ ଅସ୍ତ ହୋଇଗଲେ ଏବଂ ସନ୍ଧ୍ୟାର ପ୍ରାକ୍ପର୍ଯ୍ୟାୟ ଆରମ୍ଭ ହୋଇଗଲା । ପରିପ୍ରକାଶିତ ହେଉଥିଲା କିଛି ଧୂସର ଅନ୍ଧାର । ସନ୍ଧ୍ୟାର ଆଗମନକୁ ଦେଖ୍ ଲେଖକ କହିଛନ୍ତି – ‘ଗଙ୍ଗାମାତା ଯେମିତି ତନ୍ଦ୍ରାତୁରା ଶିଶୁ ସନ୍ଧ୍ୟାକୁ କୋଳରେ ନଚେଇ ନଚେଇ ଶୁଆଇ ପକାଉଛି ରାତ୍ରିର ଗଭୀର ନିଦ୍ରାରେ ।’’ ନିଦ୍ରାରେ ।’’
ସନ୍ଧ୍ୟା କ୍ରମଶଃ ଉତ୍ତୀର୍ଣ୍ଣ ହୋଇ ରାତ୍ରିରେ ଉପନୀତ ହୋଇଛି । କୂଳରେ ଦେଖାଦେଇଛି ବିଦ୍ୟୁତ୍ ଆଲୋକ । ବିଦ୍ୟୁତ୍ ଆଲୋକର ପ୍ରତିବିମ୍ବରେ ପ୍ରତିବିମ୍ବିତ ହୋଇଛି ଗଙ୍ଗାନଦୀର ଜଳ । ସତେଯେପରି ସେହି ଦୃଶ୍ୟ ଦେଖିଲେ ଜଣାଯାଉଛି ‘‘କେଶରୀ ମଧ୍ୟମା ଗଙ୍ଗାର କଟି ଆବୃତ କରିଛି ସୁବର୍ଷ ମେଖଳା । ଆଉ ଗଙ୍ଗାର ଦେହେ ଦେହେ ଗଭୀର ନୀଳରଙ୍ଗର ବୁଟିଦାର ବନାରସୀ ଶାଢ଼ୀ – ଛତ୍ରେ ଛତ୍ରେ ରୂପେଲୀ ଜରିର ତାରା ଫୁଟିଛି ।’’
କଥାକାର ଗଙ୍ଗାର ସନ୍ଧ୍ୟା ଓ ରାତ୍ରିକାଳୀନ ଦୃଶ୍ୟର ବର୍ଣ୍ଣନା ଦେଇ, ଗଳ୍ପଟିକୁ ମନୋଜ୍ଞ କରିପାରିଛନ୍ତି ।
Question ୩ ।
ରୂପନାରାୟଣ ସାହା ଗଳ୍ପ ଅବଲମ୍ବନରେ ଗଙ୍ଗାରେ ଅଶୋକର ନୌକାଯାତ୍ରା ସମ୍ପା କିତ ଶୌଶବକ।ଳୀନ ସ୍ମୃତି ସମ୍ପର୍କରେ ଉଲ୍ଲେଖ କର ।
Answer:
ଆଧୁନିକ ଓଡ଼ିଆ କଥାସାହିତ୍ୟରେ ଯେଉଁ କେତେଜଣ ଯଶସ୍ୱୀ ଗଳ୍ପସ୍ରଷ୍ଟା, ସେମାନଙ୍କ ସୃଷ୍ଟି ପାଇଁ ପାଠକୀୟ ଶ୍ରଦ୍ଧା ଲାଭ କରିଛନ୍ତି, ସେମାନଙ୍କ ମଧ୍ୟରେ ଅଞ୍ଛଳମୋହନ ପଟ୍ଟନାୟକ ଅନ୍ୟତମ । ସେ ତାଙ୍କର ‘ରୂପନାରାୟଣ ସାହା’’ ଗଳ୍ପରେ ଗଳ୍ପନାୟକ ଅଶୋକଙ୍କର ସ୍ମୃତିଚାରଣ ମାଧ୍ୟମରେ ଗଙ୍ଗାରେ ନୌକାଯାତ୍ରା ସମ୍ପର୍କିତ ଶୈଶବକାଳୀନ ସ୍ମୃତିକୁ ସୁନ୍ଦର ଭାବରେ ବର୍ଣ୍ଣନା କରିଛନ୍ତି ।
ଅଶୋକଙ୍କର ତାହା ଥିଲା ଶୈଶବ ଦିନର ସ୍ମୃତି । ବାପା ତାଙ୍କର ଥିଲେ ଜଣେ ମିଲିଟାରୀ ଡାକ୍ତର । କୌଣସି ଏକ ସନ୍ଧ୍ୟାରେ ସେମାନେ ବୁଲିଯାଇଥିଲେ ରାମନଗର ଦେଖିବାପାଇଁ । କ୍ଷୁଦ୍ର ପରିବାରଟିକୁ କୋଳରେ ଧରି ନୌକା ଫେରୁଥାଏ, ଗଙ୍ଗା ଆରପାରିର ରାମନଗର ଦେଖୁରି । ନୌକାଟି ହରିଶ୍ଚନ୍ଦ୍ର ଘାଟ ଓ ଦଶ୍ଵାଶ୍ଵମେଧ ଘାଟ ଦେଇ ଆଗକୁ ଆଗକୁ ଯାଉଥାଏ । ପବନର ପ୍ରତିକୂଳରେ ନୌକା ଚାଲୁଥିବାରୁ ମାଝି ଜୋର୍ରେ ଆହୁଲା ମାରୁଥାଏ । କ୍ରମଶଃ କିଛି ବାଟ ଗଲାପରେ ମାଝିର ହାତ ହୁଗୁଳା ହୋଇଗଲା । ନୌକାର ଗତି କମି ଆସିବାରୁ ପରିବାର ମଧ୍ୟରେ ଚାଲିଥିବା ଆଳାପ ଜନିତ ମୁଦୁଗୁଞ୍ଜନ ମଧ୍ଯ ନୀରବ ହୋଇଯାଇଥିଲା । ଚାପା କଣ୍ଠରେ ମାଝିଟି, ହିନ୍ଦି, ମୈଥୁଳୀ ଆଉ ଭୋଜପୁରୀ ମିଶାମିଶି ଅଦ୍ଭୁତ ଭାଷାରେ କହିଲା, କୂଳରେ ବସିଥିବା ନିଶୁଆ ଲୋକଟି ହେଉଛି କର୍ପୋରେସନର । ସେ କିଛି ପଚାରିଲେ କିଛି କହିବ ନାହିଁ । ରାମନଗର ନାମ ମୋଟେ କହିବ ନାହିଁ । ଯଦି କହିବ, ତା’ହେଲେ ସମସ୍ତଙ୍କ ପାଇଁ ଗୋଟିଏ ଗୋଟିଏ ଟଙ୍କା ଟ୍ୟାକ୍ସ ଦେବାକୁ ପଡ଼ିବ ।
ନୌକାଟି ସେଇ ବାଟଦେଇ ଗଲାବେଳେ, ଲୋକଟି ହାତଟେକି ଚିତ୍କାର କଲା, ‘ରୋକିଏ ରୋକିଏ, ଜୀଇଇ କହାଁ ଗଇଥ୍ ନାଓ ।’’ ଅଶୋକ ସେତେବେଳକୁ ହିନ୍ଦି ଶିଖ୍ ନେଇଥିଲେ । ତେଣୁ ସେହି ଲୋକର କଥାର ଉତ୍ତର ଦେଇ କହିଲେ, ‘ରାମନଗର୍ ଗୟେଥେ ହାମ୍ ଲୋଗ୍’। ଅଶୋକର କଥା ଶୁଣି ସମସ୍ତଙ୍କ ମୁହଁ ଶୁଖୁଲା । କର୍ପୋରେସନର ଅଦୃଶ୍ୟ ଇଙ୍ଗିତରେ ନୌକା ଘାଟରେ ଲାଗିଲା । ଅଶୋକଙ୍କ ବାପାଙ୍କୁ ଗଣି ଗଣି କରି ପ୍ରତ୍ୟେକଙ୍କ ପାଇଁ ଟଙ୍କାଏ ଲେଖାଁ ଟ୍ୟାକ୍ସ ଦେବାକୁ ପଡ଼ିଲା । ନୌକା ଟ୍ୟାକ୍ସ ଦେଇ କୂଳରୁ ମୁକୁଳିଗଲା ପରେ, ଅଶୋକ ସାରା ପରିବାରର ରୋଷର ଶିକାର ହୋଇଥିଲେ । ସମସ୍ତେ ପଦେ ପଦେ କହିଥିଲେ । ବାପା, ବୋଉ, ଦାଦା, ବଡ଼ଭାଇ ଏପରିକି ସାନ ଭଉଣୀ ଓ ଜେଜେମା’ ମଧ୍ୟ ବିରକ୍ତି ପ୍ରକାଶ କରି କହିଥିଲେ । ସମସ୍ତଙ୍କଠାରୁ ପଦେ ପଦେ କଥା ଶୁଣି, ତାଙ୍କର ସହିବାର ସୀମା ଅତିକ୍ରମ କରିଯାଇଥିଲା ।

ଆଖ୍ୟାରେ ଲୁହ ଟଳମଳ ହୋଇଥିଲା । ଅଶୋକର ଏପରି ଅବସ୍ଥାରେ ସାହାଯ୍ୟକାରୀ ଭାବରେ ମାଷ୍ଟରଜୀ, ତାଙ୍କ ଆଡ଼କୁ ଅନାଇଥିଲେ ଓ ମୁଣ୍ଡ ହଲେଇ କହିଥିଲେ – ‘ପରିଶାନ୍ ନ ହୋ ଅଶୋକ ୟେ’ ତୋ’।’ ଆଶ୍ଵାସନାଭରା କଥା ପଦକରେ ଅଶୋକ ମାଷ୍ଟରଜୀଙ୍କ କୋଳରେ ମୁଣ୍ଡରଖ୍ କଇଁ କଇଁ କାନ୍ଦିଥିଲେ । ସେହି ସମୟରେ ମାଷ୍ଟରଜୀ ତାଙ୍କର ବଡ଼ ପାପୁଲିରେ ଥାପୁଡ଼େଇ ଦେଇ, ନ କାନ୍ଦିବାପାଇଁ କହିଥିଲେ । ସେ କେବଳ ସାହସ ଦେଇ ନଥିଲେ ବରଂ ସାରା ପରିବାରର ଏପରି ମନ୍ତବ୍ୟକୁ ସେ ଆକ୍ଷେପ କରିଥିଲେ । ଗାଳ୍ପିକ ମାଷ୍ଟରଜୀଙ୍କ ସମ୍ପର୍କରେ ଅଶୋକ ମାଧ୍ୟମରେ ପ୍ରକାଶ କରି ଲେଖୁଛନ୍ତି – ‘ପାଞ୍ଚଟଙ୍କା ଦରମାର ସେଇ ଅକାଳ ପ୍ରୌଢ଼, ଚିନ୍ତାଜୀର୍ଣ୍ଣ, ଦରିଦ୍ର ଶିକ୍ଷକ ହଠାତ୍ ଯେପରି ମୁହୂର୍ତ୍ତକ ଭିତରେ ଉତ୍ତୀର୍ଣ୍ଣ ହୋଇଗଲା ସମଗ୍ର ପରିବାରର ମୁରବୀପଦକୁ ।’’ ମାଷ୍ଟରଜୀଙ୍କର ସମଗ୍ର ସତ୍ତାକୁ ଅଶୋକ ଅନୁଭବ କରିଥିଲେ ପ୍ରଥମଥର ପାଇଁ । କାରଣ ‘ସତ୍ୟର ପ୍ରଚଣ୍ଡ ଅସ୍ଥିତ୍ଵ’ ଯେପରି ତାଙ୍କର ଦୁର୍ବଳ ବ୍ୟକ୍ତିତ୍ଵର ପ୍ରତିଟି ତନ୍ତ୍ରୀ, ପ୍ରତିଟି ରେଣୁକୁ ଉଜ୍ଜୀବିତ କରିଥିବା ସେ ଜାଣିପାରିଥିଲେ । ଶେଷରେ ବାପା ଅଶୋକଙ୍କୁ କୋଳକୁ ନେଇଥିଲେ ।
ବାସ୍ତବରେ, ଅଶୋକଙ୍କ ଶୈଶବକାଳୀନ ସ୍ମୃ ତିର ବର୍ଣ୍ଣନା ଓ ସେହି ଅବସରରେ ମାଷ୍ଟରଜୀଙ୍କ ବ୍ୟକ୍ତିତ୍ଵ ଆକଳନ ସୁନ୍ଦର ହୋଇପାରିଛି ।
Question ୪ ।
ଅଶୋକଙ୍କର ନୌକାଯାତ୍ରା ସମୟରେ ଉପୁଜିଥିବା ବିପନ୍ନ ମୁହୂର୍ଭରେ ମାଷ୍ଟରଜୀଙ୍କ ଭୂମିକା ନିର୍ୟୟ କର ।
Answer:
ଆଧୁନିକ ଓଡ଼ିଆ କଥାସାହିତ୍ୟରେ ଯେଉଁ କେତେଜଣ ଯଶସ୍ବୀ ଗଳ୍ପସ୍ରଷ୍ଟା, ସେମାନଙ୍କ ସୃଷ୍ଟି ପାଇଁ ପାଠକୀୟ ଶ୍ରଦ୍ଧା ଲାଭ କରିଛନ୍ତି, ସେମାନଙ୍କ ମଧ୍ୟରେ ଅସ୍ଥୂଳମୋହନ ପଟ୍ଟନାୟକ ଅନ୍ୟତମ । ସେ ତାଙ୍କର ‘‘ରୂପନାରାୟଣ ସାହା’’ ଗଳ୍ପରେ ଗଳ୍ପନାୟକ ଅଶୋକଙ୍କର ସୁନ୍ଦର ଭାବରେ ବର୍ଣ୍ଣନା କରିଛନ୍ତି ।
ଅଶୋକଙ୍କର ତାହା ଥିଲା ଶୈଶବ ଦିନର ସ୍ମୃତି । ବାପା ତାଙ୍କର ଥିଲେ ଜଣେ ମିଲିଟାରୀ ଡାକ୍ତର । କୌଣସି ଫେରୁଥାଏ, ଗଙ୍ଗା ଆରପାରିର ରାମନଗର ଦେଖୁରି । ନୌକାଟି ହରିଶ୍ଚନ୍ଦ୍ର ଘାଟ ଓ ଦର୍ଶାଶ୍ବମେଧ ଘାଟଦେଇ ଆଗକୁ ଆଗକୁ ଯାଉଥାଏ । ପବନର ପ୍ରତିକୂଳରେ ନୌକା ଚାଲୁଥିବାରୁ ମାଝି ଜୋର୍ରେ ଆହୁଲା ମାରୁଥାଏ । କ୍ରମଶଃ କିଛି ବାଟ ଗଲାପରେ ମାଝିର ହାତ ହୁଗୁଳା ହୋଇଗଲା । ନୌକାର ଗତି କମି ଆସିବାରୁ ପରିବାର ମଧ୍ୟରେ ଚାଲିଥିବା ଆଳାପ ଜନିତ ମୃଦୁଗୁଞ୍ଜନ ମଧ୍ଯ ନୀରବ ହୋଇଯାଇଥିଲା । ଚାପା କଣ୍ଠରେ ମାଝିଟି, ହିନ୍ଦି, ମୈଥୁଳୀ ଆଉ ଭୋଜପୁରୀ ମିଶାମିଶି ଅଦ୍ଭୁତ ଭାଷାରେ କହିଲା, କୂଳରେ ବସିଥିବା ନିଶୁଆ ଲୋକଟି ହେଉଛି କର୍ପୋରେସନର । ସେ କିଛି ପଚାରିଲେ କିଛି କହିବ ନାହିଁ । ରାମନଗର ନାମ ମୋଟେ କହିବ ନାହିଁ । ଯଦି କହିବ, ତା’ହେଲେ ସମସ୍ତଙ୍କ ପାଇଁ ଗୋଟିଏ ଗୋଟିଏ ଟଙ୍କା ଟ୍ୟାକ୍ସ ଦେବାକୁ ପଡ଼ିବ ।
ନୌକାଟି ସେଇ ବାଟଦେଇ ଗଲାବେଳେ, ଲୋକଟି ହାତଟେକି ଚିତ୍କାର କଲା, ‘ରୋକିଏ ରୋକିଏ, ଜୀଇଇ କହାଁ ଗଇଥ ନାଓ ।’’ ଅଶୋକ ସେତେବେଳକୁ ହିନ୍ଦି ଶିଖ୍ ନେଇଥିଲେ । ତେଣୁ ସେହି ଲୋକର କଥାର ଉତ୍ତର ଦେଇ କହିଲେ, ‘ରାମନଗର ଗୟେଥେ ହାମ୍ ଲୋଗ୍’। ଅଶୋକର କଥା ଶୁଣି ସମସ୍ତଙ୍କ ମୁହଁ ଶୁଖୁଲା । କର୍ପୋରେସନର ଅଦୃଶ୍ୟ ଇଙ୍ଗିତରେ ନୌକା ଘାଟରେ ଲାଗିଲା । ଅଶୋକଙ୍କ ବାପାଙ୍କୁ ଗଣି ଗଣି କରି ପ୍ରତ୍ୟେକଙ୍କ ପାଇଁ ଟଙ୍କାଏ ଲେଖାଁ ଟ୍ୟାକ୍ସ ଦେବାକୁ ପଡ଼ିଲା । ନୌକା ଟ୍ୟାକ୍ସ ଦେଇ କୂଳରୁ ମୁକୁଳିଗଲା ପରେ, ଅଶୋକ ସାରା ପରିବାରର ରୋଷର ଶିକାର ହୋଇଥିଲା । ସମସ୍ତେ ପଦେ ପଦେ କହିଥିଲେ । ବାପା, ବୋଉ, ଦାଦା, ବଡ଼ଭାଇ ଏପରିକି ସାନ ଭଉଣୀ ଓ ଜେଜେମା’ ମଧ୍ୟ ବିରକ୍ତି ପ୍ରକାଶ କରି କହିଥିଲେ । ସମସ୍ତଙ୍କଠାରୁ ପଦେ ପଦେ କଥା ଶୁଣି, ତାଙ୍କର ସହିବାର ସୀମା ଅତିକ୍ରମ କରିଯାଇଥିଲା । ଆଖରେ ଲୁହ ଟଳମଳ ହୋଇଥିଲା । ଅଶୋକର ଏପରି ଅବସ୍ଥାରେ ସାହାଯ୍ୟକାରୀ ଭାବରେ ମାଷ୍ଟରଜୀ, ତାଙ୍କ ଆଡ଼କୁ ଅନାଇଥିଲେ ଓ ମୁଣ୍ଡ ହଲେଇ କହିଥିଲେ – ‘ପରିଶାନ୍ ନ ହୋ ଅଶୋକ ୟେ’ ତୋ’।’’ ଆଶ୍ଵାସନାଭରା କଥା ପଦକରେ ଅଶୋକ ମାଷ୍ଟରଜୀଙ୍କ କୋଳରେ ମୁଣ୍ଡରଖ୍ କଇଁ କଇଁ ମାଷ୍ଟରଜୀ ତାଙ୍କର ବଡ଼ ପାପୁଲିରେ ଥାପୁଡ଼େଇ ଦେଇ, ନ କାନ୍ଦିବାପାଇଁ କହିଥିଲେ । ସେ କେବଳ ସାହସ ଦେଇ
ନଥିଲେ ବରଂ ସାରା ପରିବାର ଏପରି ମନ୍ତବ୍ୟକୁ ସେ ଆକ୍ଷେପ କରିଥିଲେ । ଗାଳ୍ପିକ ମାଷ୍ଟରଜୀଙ୍କ ସମ୍ପର୍କରେ ଅଶୋକ ମାଧ୍ୟମରେ ପ୍ରକାଶ କରି ଲେଖୁଛନ୍ତି – ‘ପାଞ୍ଚଟଙ୍କା ଦରମାର ସେଇ ଅକାଳ ପ୍ରୌଢ଼, ଚିନ୍ତାଜୀର୍ଣ, ଦରିଦ୍ର ଶିକ୍ଷକ ହଠାତ୍ ଯେପରି ମୁହୂର୍ଭକ ଭିତରେ ଉତ୍ତୀର୍ଣ୍ଣ ହୋଇଗଲା ସମଗ୍ର ପରିବାରର ମୁରବୀପଦକୁ ।’’ ମାଷ୍ଟରଜୀଙ୍କର ସମଗ୍ର ସଭାକୁ ଅଶୋକ ଅନୁଭବ କରିଥିଲେ ପ୍ରଥମଥର ପାଇଁ । କାରଣ ‘ସତ୍ୟର ପ୍ରଚଣ୍ଡ ଅସ୍ତିତ୍ଵ’ ଯେପରି ତାଙ୍କର ଦୁର୍ବଳ ବ୍ୟକ୍ତିତ୍ଵର ପ୍ରତିଟି ତନ୍ତ୍ରୀ, ପ୍ରତିଟି ରେଣୁକୁ ଉଜ୍ଜୀବିତ କରିଥିବା ସେ ଜାଣିପାରିଥିଲେ । ଶେଷରେ ବାପା ଅଶୋକଙ୍କୁ କୋଳକୁ ନେଇଥିଲେ ।
ବାସ୍ତବରେ, ଅଶୋକଙ୍କ ଶୈଶବକାଳୀନ ସ୍ମୃତିର ବର୍ଣ୍ଣନା ଓ ସେହି ଅବସରରେ ମାଷ୍ଟରଜୀଙ୍କ ବ୍ୟକ୍ତିତ୍ଵ ଆକଳନ ସୁନ୍ଦର ହୋଇପାରିଛି ।
Question ୫।
ଅଶୋକର ଶୈଶବକାଳୀନ ସ୍ମୃତି ତାଙ୍କ’ମନ ଭିତରେ ମାଷ୍ଟରଜୀଙ୍କ ସମ୍ବନ୍ଧରେ ଯେଉଁ ସବୁକଥା ମନେ ପକାଇଥିଲା, ତାହାର ଏକ ଚିତ୍ର ଦିଅ ।
Answer:
ଆଧୁନିକ ଓଡ଼ିଆ କଥାସାହିତ୍ୟରେ ଯେଉଁ କେତେଜଣ ଯଶସ୍ୱୀ ଗଳ୍ପସ୍ରଷ୍ଟା, ସେମାନଙ୍କ ସୃଷ୍ଟି ପାଇଁ ପାଠକୀୟ ଶ୍ରଦ୍ଧା ଲାଭ କରିଛନ୍ତି, ସେମାନଙ୍କ ମଧ୍ୟରେ, ଅଞ୍ଛଳମୋହନ ପଟ୍ଟନାୟକ ଅନ୍ୟତମ । ସେ ତାଙ୍କର ‘ରୂପନାରାୟଣ ସାହା’’ ଗଳ୍ପରେ ଗଳ୍ପନାୟକ ଅଶୋକଙ୍କର ସ୍ମୃତିର।ରଶ୍ର ମାଧ୍ୟମରେ ଗାଙ୍ଗ।ରେ ନୌକାଯାତ୍ରା ସମ୍ପର୍କିତ ଶୈଶବକାଳୀନ ସ୍ମୃତିକୁ ସୁନ୍ଦର ଭାବରେ ବର୍ଣ୍ଣନା କରିଛନ୍ତି ।
ଅଶୋକଙ୍କର ତାହା ଥିଲା ଶୈଶବ ଦିନର ସ୍ମୃତି । ବାପା ତାଙ୍କର ଥିଲେ ଜଣେ ମିଲିଟାରୀ ଡାକ୍ତର । କୌଣସି ଏକ ସନ୍ଧ୍ୟାରେ ସେମାନେ ବୁଲିଯାଇଥିଲେ ରାମନଗର ଦେଖିବାପାଇଁ । କ୍ଷୁଦ୍ର ପରିବାରଟିକୁ କୋଳରେ ଧରି ନୌକା ଫେରୁଥାଏ, ଗଙ୍ଗା ଆରପାରିର ରାମନଗର ଦେଖୁରି । ନୌକାଟି ହରିଶ୍ଚନ୍ଦ୍ର ଘାଟ ଓ ଦର୍ଶାଶ୍ବମେଧ ଘାଟ ଦେଇ ଆଗକୁ ଆଗକୁ ଯାଉଥାଏ । ପବନର ପ୍ରତିକୂଳରେ ନୌକା ଚାଲୁଥିବାରୁ ମାଝି ଜୋର୍ରେ ଆହୁଲା ମାରୁଥାଏ । କ୍ରମଶଃ କିଛି ବାଟ ଗଲାପରେ ମାଝିର ହାତ ହୁଗୁଳା ହୋଇଗଲା । ନୌକାର ଗତି କମି ଆସିବାରୁ ପରିବାର ମଧ୍ୟରେ ଚାଲିଥିବା ଆଳାପ ଜନିତ ମୁଦୁଗୁଞ୍ଜନ ମଧ୍ଯ ନୀରବ ହୋଇଯାଇଥିଲା । ଚାପା କଣ୍ଠରେ ମାଝିଟି, ହିନ୍ଦି, ମୈଥୁଳୀ ଆଉ ଭୋଜପୁରୀ ମିଶାମିଶି ଅଦ୍ଭୁତ ଭାଷାରେ କହିଲା, କୂଳରେ ବସିଥିବା ନିଶୁଆ ଲୋକଟି ହେଉଛି କର୍ପୋରେସନର । ସେ କିଛି ପଚାରିଲେ କିଛି କହିବ ନାହିଁ । ରାମନଗର ନାମ ମୋଟେ କହିବ ନାହିଁ । ଯଦି କହିବ, ତା’ହେଲେ ସମସ୍ତଙ୍କ ପାଇଁ ଗୋଟିଏ ଗୋଟିଏ ଟଙ୍କା ଟ୍ୟାକ୍ସ ଦେବାକୁ ପଡ଼ିବ ।
ନୌକାଟି ସେଇ ବାଟଦେଇ ଗଲାବେଳେ, ଲୋକଟି ହାତଟେକି ଚିତ୍କାର କଲା, ‘ରୋକିଏ ରୋକିଏ, ଜୀଇଇ କହାଁ ଗଇଥ୍ ନାଓ ।’’ ଅଶୋକ ସେତେବେଳକୁ ହିନ୍ଦି ଶିଖ୍ ନେଇଥିଲେ । ତେଣୁ ସେହି ଲୋକର କଥାର ଉତ୍ତର ଦେଇ କହିଲେ, ‘ରାମନଗର ଗୟେଥେ ହାମ୍ ଲୋଗ୍ ’। ଅଶୋକର କଥା ଶୁଣି ସମସ୍ତଙ୍କ ମୁହଁ ଶୁଖୁଲା । କର୍ପୋରେସନର ଅଦୃଶ୍ୟ ଇଙ୍ଗିତରେ ନୌକା ଘାଟରେ ଲାଗିଲା । ଅଶୋକଙ୍କ ବାପାଙ୍କୁ ଗଣି ଗଣି କରି ପ୍ରତ୍ୟେକଙ୍କ ପାଇଁ ଟଙ୍କାଏ ଲେଖାଁ ଟ୍ୟାକ୍ସ ଦେବାକୁ ପଡ଼ିଲା । ନୌକା ଟ୍ୟାକ୍ସ ଦେଇ କୂଳରୁ ମୁକୁଳିଗଲା ପରେ, ଅଶୋକ ସାରା ପରିବାରର ରୋଷର ଶିକାର ହୋଇଥିଲା । ସମସ୍ତେ ପଦେ ପଦେ କହିଥିଲେ । ବାପା, ବୋଉ, ଦାଦା, ବଡ଼ଭାଇ ଏପରିକି ସାନ ଭଉଣୀ ଓ ଜେଜେମା’ ମଧ୍ୟ ବିରକ୍ତି ପ୍ରକାଶ କରି କହିଥିଲେ । ସମସ୍ତଙ୍କଠାରୁ ପଦେ ପଦେ କଥା ଶୁଣି, ତାଙ୍କର ସହିବାର ସୀମା ଅତିକ୍ରମ କରିଯାଇଥିଲା । ଆସ୍ରେ ଲୁହ ଟଳମଳ ହୋଇଥିଲା ।
ଅଶୋକର ଏପରି ଅବସ୍ଥାରେ ସାହାଯ୍ୟକାରୀ ଭାବରେ ମାଷ୍ଟରଜୀ, ତାଙ୍କ ଆଡ଼କୁ ଅନାଇଥିଲେ ଓ ମୁଣ୍ଡ ହଲେଇ କହୁଥିଲେ – ‘‘ପରିଶାନ୍ ନ ହୋ ଅଶୋକ ୟେ’ ତୋ’।’’ ଆଶ୍ଵାସନାଭରା କଥା ପଦକରେ ଅଶୋକ ମାଷ୍ଟରଜୀଙ୍କ କୋଳରେ ମୁଣ୍ଡରଖ୍ କଇଁ କଇଁ କାନ୍ଦିଥିଲେ । ସେହି ସମୟରେ ମାଷ୍ଟରଜୀ ତାଙ୍କର ବଡ଼ ପାପୁଲିରେ ଥାପୁଡ଼େଇ ଦେଇ, ନ କାନ୍ଦିବାପାଇଁ କହିଥିଲେ । ସେ କେବଳ ସାହସ ଦେଇ ନଥିଲେ ବରଂ ସାରା ପରିବାର ଏପରି ମନ୍ତବ୍ୟକୁ ସେ ଆକ୍ଷେପ କରିଥିଲେ । ଗାଳ୍ପିକ ମାଷ୍ଟରଜୀଙ୍କ ସମ୍ପର୍କରେ ଅଶୋକ ମାଧ୍ୟମରେ ପ୍ରକାଶ କରି ଲେଖୁଛନ୍ତି – ‘ପାଞ୍ଚଟଙ୍କା ଦରମାର ସେଇ ଅକାଳ ପ୍ରୌଢ଼, ଚିନ୍ତାଜୀର୍ଣ୍ଣ, ଦରିଦ୍ର ଶିକ୍ଷକ ହଠାତ୍ ଯେପରି ମୁହୂର୍ତ୍ତକ ଭିତରେ ଉତ୍ତୀର୍ଣ୍ଣ ହୋଇଗଲା ସମଗ୍ର ପରିବାରର ମୁରବୀପଦକୁ ।’’ ମାଷ୍ଟରଜୀଙ୍କର ସମଗ୍ର ସଭାକୁ ଅଶୋକ ଅନୁଭବ କରିଥିଲେ ପ୍ରଥମଥର ପାଇଁ । କାରଣ ‘ସତ୍ୟର ପ୍ରଚଣ୍ଡ ଅସ୍ତିତ୍ଵ ଯେପରି ତାଙ୍କର ଦୁର୍ବଳ ବ୍ୟକ୍ତିତ୍ଵର ପ୍ରତିଟି ତନ୍ତ୍ରୀ, ପ୍ରତିଟି ରେଣୁକୁ ଉଜ୍ଜୀବିତ କରିଥିବା ସେ ଜାଣିପାରିଥିଲେ । ଶେଷରେ ବାପା ଅଶୋକଙ୍କୁ କୋଳକୁ ନେଇଥିଲେ ।
ବାସ୍ତବରେ, ଅଶୋକଙ୍କ ଶୈଶବକାଳୀନ ସ୍ମୃତିର ବର୍ଣ୍ଣନା ଓ ସେହି ଅବସରରେ ମାଷ୍ଟରଜୀଙ୍କ ବ୍ୟକ୍ତିତ୍ଵ ଆକଳନ ସୁନ୍ଦର ହୋଇପାରିଛି ।
Question ୬ ।
ମାଷ୍ଟରଜୀଙ୍କ ସହ ଅଶୋକଙ୍କ ସାକ୍ଷାତର ଏକ ବିବରଣୀ ଦିଅ ।
Answer:
ଅ।ଧୁନିକ ଓଡ଼ିଆ କଥାସାହିତତ୍ୟର ଅନ୍ୟତମ ପୁରେ।ଧା କଥାକାର ଅଖିଳମୋହନ ପଟ୍ଟନାୟକ । ଗଳ୍ପନାୟକ ଅଶୋକଙ୍କ ସହିତ ଜଣେ ହୃଦୟପ୍ରବଣ, ଛାତ୍ରବତ୍ସଳ, କର୍ତ୍ତବ୍ୟନିଷ୍ଠ ଟ୍ୟୁସନ ମାଷ୍ଟରଙ୍କ ଉତ୍ତୀର୍ଣ୍ଣ ଜୀବନର ଅସହାୟତା ଓ ତାଙ୍କ ସହିତ ସାକ୍ଷାତକାଳୀନ ପରିବେଶ ସୁନ୍ଦର ଭାବରେ ସେ ଉପସ୍ଥାପନ କରି ପାଠକୀୟ ଶ୍ରଦ୍ଧାଲାଭ କରିପାରିଛନ୍ତି । ଗଳ୍ପର ଶିରୋନାମ ‘ରୂପନାରାୟଣ ସାହା’ ସେହି ମାଷ୍ଟରଜୀଙ୍କର ପ୍ରକୃତ ପରିଚୟ ଓ ଗଳ୍ପର ମୁଖ୍ୟ ଚରିତ୍ର ।
କ୍ରିଷ୍ଟମାସ ଛୁଟିରେ ଅଶୋକ ପହଞ୍ଚିଛନ୍ତି ବନାରସରେ । ବନାରସ ତାଙ୍କର ବହୁପରିଚିତ ସହର, ଯେଉଁଠାରେ କି ତାଙ୍କର ଶୈଶବକାଳୀନ ସ୍ମୃତି ଜଡ଼ିତ ହୋଇରହିଛି । ସେ ବନାରସର କାଶୀ ବିଶ୍ଵନାଥ ଓ ଗଙ୍ଗାନଦୀକୁ ଦେଖୁ ଦେଖୁ ମନରେ ଉଙ୍କିମାରିଛି ତାଙ୍କର ଶୈଶବ ଜୀବନର ଶିକ୍ଷକ ମାଷ୍ଟରଜୀଙ୍କ କଥା । ତେଣୁ ତାଙ୍କ ପାଠର ମୂଳଦୁଆ ପକାଇଥିବା ଏବଂ ସେହି ମୂଳଦୁଆ ଉପରେ ଶିକ୍ଷାର ବହୁସୋପାନର ଅଧିକାରୀ ହୋଇଥିବା ଅଶୋକ, ମାଷ୍ଟରଜୀଙ୍କ ଘରକୁ ଯାଇ ବୁଲି ଆସିବାକୁ ଚାହିଁଛନ୍ତି ।
ଅଶୋକ ରିକ୍ସାଯୋଗେ ଯାଇଛନ୍ତି କ୍ୟାଣ୍ଟନମେଣ୍ଟରୋଡ଼୍ । ସେହି ଯବା ଅବସରରେ ରିକ୍ସାରେ ବସି ତାଙ୍କର ତୁହାଇ ତୁହାଇ ମନେପଡ଼ିଛି ମାଷ୍ଟରଜୀଙ୍କ ସ୍ନେହପ୍ରବଣ ଭାବ । ସେ ଓ ତାଙ୍କର ପୋଷା ପାତିମାଙ୍କଡ଼ ବିଷୟରେ ଅନେକ କଥା ମନେ ପକାଇଛନ୍ତି । ମାଷ୍ଟରଜୀଙ୍କୁ ଦେଖାହେଲେ କିପରି ଭାବ ସୃଷ୍ଟିହେବ ବୋଲି, ବିଚାର କରିଛନ୍ତି । ରିକ୍ସାବାଲାର କଥାରେ ତାଙ୍କର ଭାବନା ବଦଳିଯାଇଛି । ସେ ମନେ ପକେଇ ପକେଇ ମାଷ୍ଟରଜୀଙ୍କ ଘର ପା ସେଠାରେ ବସି ଗପ ଜମେଇଥିବା ଲୋକଙ୍କୁ ମାଷ୍ଟରଜୀଙ୍କ ନାମ କହି ଠିକଣା ବୁଝିଛନ୍ତି । ରିକ୍ସାବାଲାଟି ଅଶୋକଙ୍କ ପାଖରେ ପହଞ୍ଚି ତାଙ୍କୁ ଅପଲକ ନୟନରେ ଚାହିଁ ରହିଛି । କ’ଣ କହିବ କହିବ ହେଲେ ବି କିଛି କହିପାରି ନାହିଁ । ଶେଷରେ କହିଛି -‘ତୁମ ଅଶୋକ ହୋ ନାଁ – ଇତନେ ବଡ଼ା ହୋ ଗୈ ତୁମ ?’’
ଏହି ପର୍ଯ୍ୟାୟରେ ଗୁରୁଶିଷ୍ୟର ବା ଅଶୋକ ଓ ମାଷ୍ଟରଜୀଙ୍କର ହୋଇଛି ସାକ୍ଷାତ । ଅ ଦେଖୁଛନ୍ତି ଠିକ୍ ସେଇ ଦିହ, ସେହି ମୁହଁ, ସେହି ମଳିନ ପ୍ରତିକୃତି ଭିତରୁ ଧୀରେ ଧୀରେ ଉଇଁ ଆସିଲା ମାଷ୍ଟରଜୀଙ୍କର ଚେହେରା । ଅଶୋକ ସଙ୍ଗେ ସଙ୍ଗେ ନଇଁପଡ଼ି ପାଦଧୂଳି ନୋବକୁ ହାତ ବଢ଼ାଇଲାବେଳେ ମାଷ୍ଟରଜୀ କେଇ ହାତ ପଛକୁ ଘୁଞ୍ଚିଯାଇ, ଦୁଇ ବାହା ଧରି ସ୍ନେହରେ ତୋଳି ନେଇଥିଲେ । ଦୀର୍ଘଜୀବୀ ହେବାକୁ ଆଶୀର୍ବାଦ କରିଥିଲେ । ଅଶୋକଙ୍କର ମନେପଡ଼ିଲା ଏହି ରୂପନାରାୟଣଙ୍କ ଅତୀତ କଥା । ଆଉ ସେ କିଛି କହି ପାରିନଥିଲେ । ଦୁହେଁ କେବଳ ଦୁହିଁଙ୍କୁ ଚାହିଁଥିଲେ । ଅଶୋକ ସେଦିନ ମନେକରିଥିଲେ, ମନୁଷ୍ୟ କଥା କହିବା ଅପେକ୍ଷା ନୀରବରେ ତା’ଠାରୁ ଯଥେଷ୍ଟ ଅଧିକ ପ୍ରକାଶ କରିପାରେ ।
ମାଷ୍ଟରଜୀ ଆନନ୍ଦରେ ତାଙ୍କର ସେହି ଦରିଦ୍ର କୁଟୀରକୁ ବୁଲାଇ ଆଣିଲେ । କଥାକଥାକେ ଅଶୋକର ପ୍ରଶଂସା, ଗର୍ବ ଓ ଆନନ୍ଦରେ ସେ ଯେପରି ଅସ୍ଥିର ହୋଇପଡ଼ୁଥିଲେ । ଦୁହେଁ ତାଙ୍କର ପୁରୁଣା ପିଣ୍ଡାରେ ବସି ଗପ ହେଲେ । ତାଙ୍କ ବିପର୍ଯ୍ୟୟର ଅବସ୍ଥା ଗୋଟି ଗୋଟି କରି ବଖାଣି ବସିଲେ । ସରକାରୀକଳର ଅବିଚାର ଭାବ ପାଇଁ ସେ ଆଜି ରିକ୍ସାବାଲା ଓ ରୋଗୀ ମଣିଷଯିଏ ପାଲଟି ଯାଇଛନ୍ତି ବୋଲି ବହୁ କରୁଣାଭରା ପ୍ରସଙ୍ଗ କହିଲେ ।
ଗଳ୍ପଟିରେ, ଅଶୋକଙ୍କ ସହିତ ମାଷ୍ଟରଜୀଙ୍କର ସାକ୍ଷାତ ଅତ୍ୟନ୍ତ ଜୀବନ୍ତ ଓ ହୃଦୟସ୍ପର୍ଶୀ ହୋଇପାରିଛି ।
Question ୭ ।
ପଠିତ ଗଳ୍ପରୁ ମାଷ୍ଟରଜୀଙ୍କ ଜୀବନର କ୍ଷୁଦ୍ର ଇତିହାସ ସମ୍ପର୍କରେ ସୂଚନା ଦିଅ ।
Answer:
ଓଡ଼ିଆ କ୍ଷୁଦ୍ରଗଳ୍ପର ଅନନ୍ୟ ପ୍ରତିଭା ଗାଳ୍ପିକ ଅଖ୍ଳମୋହନ ପଟ୍ଟନାୟକ । ଆଲୋଚ୍ୟ ଗଳ୍ପ ‘ରୂପନାରାୟଣ ସାହା’ ତାଙ୍କର ପ୍ରଥମ ଗଳ୍ପ ସଙ୍କଳନ ‘ଝଡ଼ର ଈଗଲ ଓ ଧରଣୀର କୃଷ୍ଣସାର’ରୁ ଗୃହୀତ । ଏଥିରେ ଆମର ତ୍ରୁଟିପୂର୍ଣ୍ଣ ଶିକ୍ଷାବ୍ୟବସ୍ଥା ଓ ଶିକ୍ଷକମାନଙ୍କର ଦୟନୀୟ ଜୀବନକୁ ଯଥାର୍ଥ ଭାବରେ ପରିପ୍ରକାଶ କରାଯାଇଛି ।
ଅଶୋକ କ୍ରିଷ୍ଟମାସ୍ ଛୁଟିରେ ବନାରସ ବୁଲି ଯାଇଥା’ନ୍ତି, ଯେଉଁଠାରେ କି ଶୈଶବର ଅନେକ ସ୍ମୃତିପୂର୍ଣ୍ଣ ମୁହୂର୍ତ୍ତ ମୁହୂର୍ତ୍ତ ତାଙ୍କର କଟିଯାଇଛି । ବନାରସର ରାଜପଥ, କାଶୀବିଶ୍ଵନାଥ ମନ୍ଦିର, ଡାଲ୍ମଣ୍ଡିର ହତଶ୍ରୀ ସଭ୍ୟତା, ଗଙ୍ଗାନଦୀର ସନ୍ଧ୍ୟା ଓ ରାତ୍ରିର ନିତ୍ୟ ନୂତନତା ତାଙ୍କ ପରିପକ୍ବ ଜୀବନର ଚିନ୍ତାଧାରାକୁ ବିମୋହିତ କରିଛି । ଏହି ଅବସରରେ ଦେଖାକରିବାର ଅନୁଚିନ୍ତା ତାଙ୍କୁ ସଂକ୍ରମିତ କରିଛି ଏବଂ ସେ ଯିବାପାଇଁ ଇଚ୍ଛା କରିଛନ୍ତି ।
ଅଶୋକ ରିକ୍ସାରେ ବସି ଯାଇଛନ୍ତି ମାଷ୍ଟରଜୀଙ୍କ ଘରକୁ । ପୁରୁଣା ବାଟକୁ ମନେପକେଇ ପହଞ୍ଚି ଯାଇଛନ୍ତି ମାଷ୍ଟରଜୀଙ୍କ ଘର ପାଖରେ । ଶେଷରେ ସେ ଜାଣିପାରିଛନ୍ତି, ତାଙ୍କୁ ରିକ୍ସାରେ ଆଣିଥିବା ରିକ୍ସାବାଲାଟି ହେଉଛି, ତାଙ୍କର ଅଭିଳଷିତ ମାଷ୍ଟରଜୀ । ଉଭୟଙ୍କର ସାକ୍ଷାତ ହୋଇଛି । ଭାବବିମୁଗ୍ଧ ହୋଇ କେହି କାହାକୁ କିଛି କହିପାରି ନାହାଁନ୍ତି । ଅଶୋକଙ୍କ ସମ୍ମାନ ଦେବାରେ, ଗୁରୁଭକ୍ତିରେ ସେ ବିମୋହିତ ହୋଇଛନ୍ତି । ନିଜ ଜୀବନର କରୁଣ ଇତିହାସକୁ, ପ୍ରିୟ ଛାତ୍ର ଅଶୋକ ପାଖରେ ଉପସ୍ଥାପନ କରିଛନ୍ତି । ପିଲାଦିନେ ତାଙ୍କୁ କାହାଣୀ କହିବାରେ ଅସାଧାରଣ ଦକ୍ଷତା ରଖ୍ ମାଷ୍ଟରଜୀ ନିଜ କାହାଣୀର କରୁଣାନ୍ତକ ପରିସ୍ଥିତିକୁ ଗୋଟି ଗୋଟି କରି ଖୋଲି କହିଛନ୍ତି ।
କିଛିଦିନ ତଳେ ସାର! ଉତ୍ତର ଭାରତ ବ୍ୟାପୀ ଯେଉଁ ନିମ୍ନ ପ୍ରାଥମିକ ଶିକ୍ଷକ ଧର୍ମଘଟ ହୋଇଥିଲା, ତାହାର ମୁଖ୍ୟ ପୁରୋଧା ଥିଲେ ମାଷ୍ଟରଜୀ । କରୁଣସ୍ଵରରେ ସେ କହିଲେ – ‘‘ଆମର ଧର୍ମଘଟ କରି ସରକାର ଗଠନ କରିବାର ଇଚ୍ଛା ନଥିଲା ବରଂ ୧୩ ଟଙ୍କା ଦରମାରେ ଆମେ ଚଳି ପାରୁନଥିଲୁ ।’ ମାତ୍ର ସରକାର ଷଡ଼ଯନ୍ତ୍ର କରି, ରାଷ୍ଟ୍ରଦ୍ରୋହୀ ଭାବରେ ତାଙ୍କୁ ଜେଲ୍ ପଠାଇ ଦେଇଥିଲେ । ବର୍ଷକ ପରେ ଫେରି ସେ ଦେଖିଲେ ସ୍ତ୍ରୀ ମରିଯାଇଛି । ସ୍ତ୍ରୀ ମରିଯିବା କଥାଟାକୁ ‘ଗୋଟାଏ ବଡ଼ ସମାଧାନ ହୋଇଯାଇଛି’’ ବୋଲି ସେ କହିଛନ୍ତି । କେତେ ଦୁଃଖରେ ଜଣେ ସଂସାରୀ ମଣିଷ ଏହା କହିପାରେ, ତାହା ଅନୁମାନ କରିହେବ । ପରିବାରର ବୋଝ ସମ୍ଭାଳିବାକୁ ଯାଇ, ସ୍ତ୍ରୀର ଗହଣା ଓ କିଛି କରଜ ଟଙ୍କା ମିଶାଇ ରିକ୍ସା ଖଣ୍ଡେ କରିଛନ୍ତି । ମାଷ୍ଟରଜୀରୁ ସେ ପାଲଟି ଯାଇଛନ୍ତି ରିକ୍ସାବାଲା । କଥା କହୁ କହୁ ସେ ଆଖୁରୁ ଲୁହ ପୋଛିଲେ । ଝାଙ୍କ କାଶ ଉଠିବାରୁ ସେ ସମ୍ପର୍କରେ କହିଲେ – ‘ଡାକ୍ତର ଦେଖେଇବାକୁ ଯାଇଥିଲି । କ’ଣ ଦେଖୁ କହିଲେ – ‘ପ୍ଲା ରେସି ହୋଇଛି । ଚିକିତ୍ସା କରିବାକୁ ଅନେକ ପଇସା ଲାଗିବ ।’ ଅଶୋକ ରୋଗକଥା ଶୁଣି ଚମକି ପଡ଼ିଲେ ବି, ମାଷ୍ଟରଜୀ କହିଲେ, ‘କେତେ ରୋଗ ବାହାରିଲାଣି, ଟିକିଏ କାଶ ପାଇଁ ଏତେ ଟଙ୍କା ଖର୍ଚ୍ଚ କରିବି କୁଆଡ଼ୁ ।’ ବାରଚଉଦ ବର୍ଷର ପୁଅ ତାଙ୍କର ରିକ୍ସା ଚଳାଇ ବାପାଙ୍କୁ ସାହାଯ୍ୟ କରୁଛି । ଆଡ଼ପାଗଳୀ ମା’ ତାଙ୍କର କିରୋସିନି ବିକ୍ରିକରି ବଞ୍ଚିବାର ସମ୍ବଳ ଯୋଗାଡ଼ କରୁଛି ।
ବ।ସ୍ତ୍ରବରେ ମାଷ୍ଟରକୀଙ୍କ କଚୁଣ ଇତିହାସ ମର୍ମସ୍ପର୍ଶୀ
Question ୮ ।
ମାତାଜୀଙ୍କ ସହ ଅଶୋକଙ୍କର ଶେଷ ସାକ୍ଷାତ କିପରି ଥିଲା, ଉଲ୍ଲେଖ କର।
Answer:
ଗାଳ୍ପିକ ଅଶୂଳମୋହନ ପଟ୍ଟନାୟକ, ‘ରୂପନାରାୟଣ ସାହା’ ଗଳ୍ପରେ ଏହି ପ୍ରସଙ୍ଗ ଉଲ୍ଲେଖ କରିଛନ୍ତି । ଦାରିଦ୍ର୍ୟ ମଣିଷକୁ କେଉଁଠାରୁ ନେଇ କେଉଁଠାରେ ପହଞ୍ଚାଇ ଦିଏ ତାହାର ପ୍ରତ୍ୟକ୍ଷ ଉଦାହରଣ ହେଉଛନ୍ତି, ମାତାଜୀ । ଫଳ ଟିକେ କିମ୍ବା ହାଲୁଆ ଟିକେ ଦେଇ ନିଜର କରିନେବାର ଚରିତ୍ର ହେଉଛନ୍ତି ମାତାଜୀ । ମାତ୍ର ଜୀବନର ଶେଷ ପର୍ଯ୍ୟାୟରେ ସେ ମାନସିକ ଭାରସାମ୍ୟ ହରାଇ ନିଜର ଚିନ୍ତା ଚେତନା ଭିତରେ ବୁଡ଼ି ରହିବାକୁ ଚାହିଁଛନ୍ତି, ହେଲେ ପରିବାରର ବୋଝ ହୋଇ ରହିବାକୁ ଚାହିଁନଥିବା ମଣିଷ ମାତାଜୀ ।
ମାଷ୍ଟରଜୀ ନିଜ ଜୀବନର ଅଶ୍ରୁଳ ଇତିହାସକୁ ବଖାଣି ବସିଲାପରେ, ଆଗରେ ବସିଥିବା ବୃଦ୍ଧାକୁ ହାତ ବଢ଼େଇ ଦେଖେଇ ଦେଇଛନ୍ତି । ପିଠି ଆଉ ଆଣ୍ଠୁ ତାଙ୍କର ଲାଗିଯାଇଛି । ମୁଣ୍ଡରେ କେଇ କେରା ବାଳ ଝୋଟପରି ଫର୍ ଫର୍ ଉଡ଼ୁଛି । ସାମ୍ନାରେ ଥୁଆହୋଇଛି କିରୋସିନି ଟିଣ । ଦେଖିବା ଓ ଶୁଣିବାର ଶକ୍ତି ତାଙ୍କର କ୍ରମଶଃ କମି କମି ଆସିଛି । ସତୁରୀ ବର୍ଷରେ ପହଞ୍ଚିବା ବୃଦ୍ଧାଜଣକ ପଇସାକୁ ଦୀପ ଆଲୁଅରେ ଦେଖୁ ଥରିଲା ହାତରେ ପଳା ପଳା କିରାସିନି ମାପି ଦେଉଛନ୍ତି ।
ଅଶୋକ ତାଙ୍କ ବହୁପରିଚିତ ମାତାଜୀଙ୍କ ପାଖକୁ ଯାଇଛନ୍ତି ଏବଂ ଦିନେ ହାଲୁଆ ଖୁଆଉଥିଲେ, ଯାହାକି ଆଉ କେବେ ସେ ଖାଇନାହାଁନ୍ତି । ସାମାନ୍ୟ ବଡ଼ପାଟିରେ ଅଶୋକ ନିଜର ପରିଚୟ ଦେଲେ, ହେଲେ ମାତାଜୀ ଚିହ୍ନିପାରିଲେ ନାହିଁ କିମ୍ବା ଚିହ୍ନିବାକୁ ଚେଷ୍ଟାକଲେ ନାହିଁ । କାରଣ ତାଙ୍କୁ ଚିହ୍ନି ତାଙ୍କର ଟିକିଏ ବି ଲାଭ ହେବନାହିଁ । ବରଂ କିରାସିନି ମାପୁ ମାପୁ ବିଡ଼ି ବିଡ଼ି ହୋଇ ଅସ୍ପଷ୍ଟ ସ୍ବରରେ କହିଲେ ‘ଜୀତେ ରହୋ ବେଟା-ଜୀତେ ରହେ ।’’ ମାତାଜୀଙ୍କ ସମ୍ପର୍କରେ ମାଷ୍ଟରଜୀଙ୍କୁ ପଚାରିବାରୁ ସେ କହିଥିଲେ, କେତେ ବର୍ଷ ହେଲା ମୁଣ୍ଡ ଖରାପ ହୋଇଯାଇଛି । ମାତ୍ର ଏହି ମାଷ୍ଟରଜୀ ପିଲାଙ୍କୁ ନାଲିଆଖ୍ ଦେଖେଇ ଟିକିଏ କିଛି କହିଲେ, ସେ ସିଲଟ ଫିଙ୍ଗିଦେଇ ମାତାଜୀଙ୍କ କୋଳକୁ ଦୌଡ଼ି ଯାଉଥିଲା । ମାତାଜୀ ତା’ପରେ ପରେ ପଦାକୁ ବାହାରି ଆସି କହନ୍ତି – ‘କ୍ୟା ତୁମ୍ହରା ଦିମାକ୍ ତୋ’ ବିଗଡ଼ ନେହିଁ ଗିୟା ରୂପନାରାୟଣ – ବଢାକୋ ଦାଣ୍ଡତା ହେ ତୁମ ।’ ମାତ୍ର ସେହି ମାତାଜୀ ଆଜି ଲୋଳିତ ଚର୍ମ ଶିଥୁଳା ବୃଦ୍ଧା ।
ରୂପନାରାୟଣଙ୍କ ବିଟିଡ଼ି ଯାଇଥିବା କଥାକାର ସୁନ୍ଦର ଭାବରେ ବର୍ଣ କାର୍ରିଛନ୍ତି।
Question ୯।
ମାଷ୍ଟରଜୀଙ୍କଠାରୁ ବିଦାୟ ନେବାପରେ ଅଶୋକଙ୍କ ମନରେ ଯେଉଁସବୁ ପ୍ରତିକ୍ରିୟା ଦେଖାଦେଇଛି, ସେଗୁଡ଼ିକର ବିଶ୍ଳେଷଣ କର ।
Answer:
ଜୀବନର ସଂଘର୍ଷମୟ ବାସ୍ତବତା ଓ ମନନଶୀଳତାର ଅପୂର୍ବ ରୂପକାର କଥାଶିଳ୍ପୀ ଆଖିଳଳେମେ।ହୁନି ପଟ୍ଟନାୟକ । ସେ ତାଙ୍କର ‘ରୂପନାରାୟଣ ସାହା’ ଗଳ୍ପରେ ଆମ ଦେଶରେ ପ୍ରଚଳିତ ଶିକ୍ଷା ବ୍ୟବସ୍ଥା ଏବଂ ଶିକ୍ଷକମାନଙ୍କର ଅଧ୍ୟାୟକୁ ଶୁଣିସାରିଲା ପରେ ଗଳ୍ପପୁରୁଷ ଅଶୋକଙ୍କ ମାନସପଟରେ ଯେଉଁ ଭାବ ଦେଖାଦେଇଛି କଥାକାର ତାହାକୁ ଯୁକ୍ତିଯୁକ୍ତ ଭାବେ ଉପସ୍ଥାପନ କରିଛନ୍ତି ।
ଅଶୋକ ଯାଇଛନ୍ତି ଛୁଟି କଟାଇବାପାଇଁ ବନାରସ । ବନାରସରେ ତାଙ୍କର ଶୈଶବ ଜୀବନ ଅତିବାହିତ ହୋଇଥିଲା । ବନାରସର ସେ ବିଭିନ୍ନ ଦୃଶ୍ୟକୁ ମନଭରି ଉପଭୋଗ କରିଛନ୍ତି । ଶେଷରେ ତାଙ୍କର ମନେପଡ଼ିଯାଇଛି, ତାଙ୍କୁ ଦଶ ବାର ବର୍ଷ ହୋଇଥିବା ବେଳର ନୌକାଯାତ୍ରା କଥା ଓ ମାଷ୍ଟରଜୀଙ୍କର ସହ।ନୁଭୂତିଶୀଳ ବ୍ୟବହାର ପ୍ରସଙ୍ଗ। ଯେତେବେଳେ ଅଶୋକଙ୍କ ସାରା ପରିବାର ଟ୍ୟାକ୍ସ ଦେବା କଥାକୁ ନେଇ ପଦେ ପଦେ କହିଥିଲେ, ସେହି ବିପନ୍ନ ମୁହୂର୍ତ୍ତରେ ମାଷ୍ଟରଜୀଙ୍କର ଉତ୍ତମ ବ୍ୟବହାରର କଥା । ପରେ ସେ କେବଳ ଭାବିଚାଲିଛନ୍ତି, ମାଷ୍ଟରଜୀଙ୍କ କଥା । ମାଷ୍ଟରଜୀଙ୍କ ପାଖରେ ପହଞ୍ଚିବାକୁ ରିକ୍ସାର ସାହାଯ୍ୟ ନେଇଛନ୍ତି । ଯେଉଁ ରିକ୍ସାବାଲାଟି ତାଙ୍କୁ ନେଇଛି, ସେହି ରିକ୍ସାବାଲାଟି ଯେ ତାଙ୍କର ଈପ୍ସିତ ମାଷ୍ଟରଜୀ ସେ ପହଞ୍ଚିଲା ପରେ ଜାଣିପାରିଛନ୍ତି ।
ପ୍ରଣାମ କରି ବିଦାୟ ନେଇ ଅଶୋକ ଫେରିଛି ହୋଟେଲ୍କୁ । କ୍ୟାଣ୍ଟନମେଣ୍ଟ ରୋଡ଼ର ମସୃଣ ମ୍ୟାକାଡ଼ାମାଇଜ୍ ଗୁରୁ ଶିଷ୍ୟଙ୍କର ହୋଇଛି ଅପୂର୍ବ ମିଳନ । ଗୁରୁଙ୍କୁ ଶିଷ୍ୟ ସଭକ୍ତି ସମ୍ଭାଷଣ ଜଣାଇଲା ପରେ, ଗୁରୁ ନିଜ ଜୀବନର କରୁଣ ଅଧ୍ୟାୟକୁ ଖୋଲି ଦେଇଛନ୍ତି । ପତ୍ନୀଙ୍କର ବିୟୋଗ, ତାଙ୍କ ଶରୀର ଅସୁସ୍ଥତା, ରିକ୍ସାବାଲାର ଜୀବନ, ବାର ଲୁହପୋଛି ଅଶୋକଙ୍କୁ ନିଜର ଠିକଣା କାଗଜକୁ ଧରାଇ ଦେଇ ବିଦାୟ ଦେଇଛନ୍ତି ।
ପ୍ରଣାମ କରି ବିଦାୟ ନେଇ ଅଶୋକ ଫେରିଛି ହୋଟେଲ୍କୁ । କ୍ୟାଣ୍ଟନମେଣ୍ଟ ରୋଡ଼ର ମସୃଣ ମ୍ୟାକାଡ଼ାମାଇଜ୍ ରାସ୍ତାରେ ଚାଲୁ ଚାଲୁ ଅଶୋକ ଭାବିଛନ୍ତି ମାଷ୍ଟରଜୀଙ୍କ କଥା । ସେ ନିଜକୁ ନିଜେ ବିଶ୍ବାସ କରିପାରି ନାହାଁନ୍ତି, ସତରେ କ’ଣ ସେଇ ଜରାଜୀର୍ଣ୍ଣ, ଦରିଦ୍ର ରିକ୍ସାବାଲାଟା ହେଉଛି ତାଙ୍କ ଶୈଶବ ଜୀବନର ବିଦ୍ୟାଦାତା ରୂପନାରାୟଣ । ସେ ଫିସ୍ଫିସ୍ ହୋଇ କହିଛି – ‘ଏ ଦୋଷ ତୋ’ର ଏକା ନୁହେଁରେ ଅଶୋକ – ଏ ମୂର୍ଖତା ଏଇ ସମଗ୍ର ଅନ୍ଧଜାତିର ।’’ କାରଣ ସେମାନେ ପ୍ରାଣପାତ କରି ଏ ଜାତିକୁ ଶିକ୍ଷାଦେଲେ, କିନ୍ତୁ କେହି କିଛି ଶିଖୁନାହାଁନ୍ତି । ଏ ଜାତିର ଶୈଶବ ଏବେ ମଧ୍ୟ ବାକିଥିଲା ଭଳି ମନେହୋଇଛି । ଆଉଥରେ ସମସ୍ତଙ୍କୁ ନୂଆକରି ପ୍ରାଥମିକ ଶିକ୍ଷା ଦେବାକୁ ହେବବୋଲି ମାଷ୍ଟରଜୀ ଯେପରି କହିଚାଲିଛନ୍ତି ।
ତେଣୁ ଅଶୋକ ଭାବିଛନ୍ତି – ‘କିନ୍ତୁ ରୂପନାରାୟଣ, ତମେ ନାଁ ଏ ଜାତିର ଜନକ ? ତମେଇତ ମଣିଷ କରିବ ଏ ଜାତିକୁ ? ଶିଥୁଳତା କାହିଁକି ଆଜି ? ତମର ସେଇ ଲମ୍ବା ବେତଟା ଅନେକ ଛୋଟ ମାଷ୍ଟରଜୀ । ସେଟାକୁ ଫିଙ୍ଗିଦେଇ ତା’ ବଦଳରେ ଗୋଟାଏ ଖୁବ୍ ଲମ୍ବା ଚାବୁକ୍ ଧର ।’’ ମାତ୍ର ମାଷ୍ଟରଜୀ କେବେ କାହାକୁ ଶାସନ କରି ନାହାଁନ୍ତି କିମ୍ବା ସେଭଳି ମାନସିକତା ତାଙ୍କର ନାହିଁ । ତଥାପି ସ୍ନେହପ୍ରବଣ ଓ ବିଚାରକ ଭାବରେ ଅଶୋକ କହିଛନ୍ତି – ‘ନାଁ ଆପଣ ବୁଝି ପାରିବେ ନାହିଁ ମାଷ୍ଟରଜୀ – ଏ ମଦ୍ୟପ ଜାତି ଯେ ଆଜି କ୍ଷମତାର ମଦପିଇ ବେହୋସ୍ ହୋଇପଡ଼ିଛି । ଏମାନେ କ’ଣ ଟିକିଏ ଶୁଣିଛନ୍ତି । ଆପଣମାନଙ୍କର ଏତେଦିନର କରୁଣ ନିବେଦନ । ଆଜି ଆଉ ନୁହେଁ – ଏ ଜାତିକୁ ଜାଗ୍ରତ କରିବାକୁ ପଡ଼ିବ ।’’ପରବର୍ତୀ ସମୟରେ ଅଶୋକ ମନର କ୍ଷୋଭକୁ ପ୍ରତିକ୍ରିୟାଶୀଳ ଭାବରେ ପ୍ରକାଶ କରିଛନ୍ତି।
ବାସ୍ତବରେ ଅଶୋକଙ୍କ ପ୍ରତିକ୍ରିୟା ଯୁକ୍ତିଯୁକ୍ତ ମନେ ହୋଇଥାଏ ।
Question ୧୦ ।
ପଠିତ ଗଳ୍ପକୁ ଆଧାର କରି ମାଷ୍ଟରଜୀଙ୍କ ଚରିତ୍ର ଚିତ୍ରଣ କର ।
Answer:
ଚରିତ୍ରମାନେ ହେଉଛନ୍ତି ସାରସ୍ଵତ ସାଧକର ମାନସ ସନ୍ତାନ । ବିଶେଷକରି କଥାକାରମାନେ ଯାହା କହିବାକୁ ଚାହିଁଥା’ନ୍ତି କିମ୍ବା ସମାଜକୁ ଯାହା ସନ୍ଦେଶ ଦେବାକୁ ଇଚ୍ଛା କରିଥା’ନ୍ତି, ସେମାନେ ସେହି ଚରିତ୍ର ମାଧ୍ୟମରେ ହିଁ ଉପସ୍ଥାପିତ କରିଛନ୍ତି । ଗାଳ୍ପିକଙ୍କ ମନର ଭାଷା ହିଁ ଚରିତ୍ରଦେଇ ପ୍ରକାଶ ପାଇଥାଏ । ଆଲୋଚ୍ୟ ଗଳ୍ପ ‘ରୂପନାରାୟଣ ଶିକ୍ଷା ବ୍ୟବସ୍ଥା ଓ ଶିକ୍ଷକମାନଙ୍କର ଦୟନୀୟ ପରିଣତିକୁ ଦେଖାଇବାକୁ ଚାହିଁଛନ୍ତି । ଶିକ୍ଷକମାନେ ମଣିଷ ତିଆରି କରନ୍ତି, କିମ୍ବା ତାଙ୍କୁ କେହି ମୂଲ୍ୟାୟନ କରନ୍ତି ନାହିଁ । ଆଲୋଚ୍ୟ ଗଳ୍ପରେ ମାଷ୍ଟରଜୀଙ୍କ ଚରିତ୍ର ମାଧ୍ୟମରେ ଏହା ଆକଳନ କର।ଯାଚ୍ଚପାରୋ
ଅଶୋକ କ୍ରିଷ୍ଟମାସ୍ ଛୁଟି କଟାଇବାକୁ ଯାଇ ବନାରସର ମନ୍ଦିର ବୁଲି ଯାଇଛନ୍ତି । ବନାରସ ରାଜପଥ, କାଶୀ ବିଶ୍ଵନାଥ ମନ୍ଦିର, ଡାମଣ୍ଡି ଓ ଗଙ୍ଗାର ସନ୍ଧ୍ୟା ଓ ରାତ୍ରିକାଳୀନ ଦୃଶ୍ୟକୁ ସେ ମନଭରି ଉପଭୋଗ କରିଛନ୍ତି । ସେହି ଅବସରରେ ସେ ମନେ ପକାଇଛନ୍ତି, ତାଙ୍କ ଶୈଶବର ଶିକ୍ଷାଦାତା ମାଷ୍ଟରଜୀଙ୍କ କଥା। କଥାକାର ଏହି ପ୍ରସଙ୍ଗରେ ମାଷ୍ଟରଜୀଙ୍କ ଅସାଧାରଣ ବ୍ୟକ୍ତିତ୍ଵ ସମ୍ପର୍କରେ ପରିଚୟ ଦେଇଛନ୍ତି । ଥରେ ଅଶୋକଙ୍କ ପରିବାର ନୌକାଯୋଗେ ବୁଲିଯାଇଥିଲେ ରାମନଗର । ରାମନଗରରୁ ଫେରିବା ବାଟରେ କର୍ପୋରେସନର ଲୋକଙ୍କୁ ସତକଥା କହି, ସାରା ପରିବାରର ରୋଷର ଶିକାର ହୋଇଥିଲା । ଅଶୋକ ପହଞ୍ଚିଯାଇଥିଲା ବିପନ୍ନ ମୁହୂର୍ତ୍ତରେ । ସେହି ସମୟରେ ମାଷ୍ଟରଜୀ ବୁଝିଥିଲେ ଶିଶୁର ମାନସିକତାକୁ । ତେଣୁ ସେ କୋଳେଇ ନେଇଥିଲେ ଏବଂ ପରିବାରର ଆକ୍ଷେପକୁ ସମାଲୋଚନା କରିଥିଲେ । ଅଶୋକ ସତକଥା କହି କିଛି ଭୁଲ୍ କରିନାହିଁ ବୋଲି ସାବ୍ୟସ୍ତ କରିଥିଲେ । ଆର୍ଦ୍ର, ବାଷ୍ପକୁଳ କଣ୍ଠରେ କ୍ରୋଧର ଉତ୍ତେଜନା ମିଶି ସେ ସମସ୍ତଙ୍କୁ ଶୁଣାଇଦେଲେ – ‘ମାନୁଛି ଆପଣମାନେ ଅଶୋକର ଗୁରୁଜନ କିନ୍ତୁ ଆପଣମାନେ ତା’ର ଯେ କି କ୍ଷତି କରୁଛନ୍ତି, ତା’ ବୁଝିବାର କ୍ଷମତା ଆପଣମାନଙ୍କର ନାହିଁ ।’’ ମାଷ୍ଟରଜୀ ପାଞ୍ଚ ଟଙ୍କାର ଟ୍ୟୁସନ୍ ମାଷ୍ଟର ହେଲେବି ସେ ସେତେବେଳକୁ ଉତ୍ତୀର୍ଣ୍ଣ ହୋଇଯାଇଥିଲେ ସମଗ୍ର ପରିବାରର ମୁରବୀ ସ୍ତରକୁ । ମାଷ୍ଟରଜୀଙ୍କ କଥାର ଗୁରୁତ୍ଵ ଅଶୋକର ବାପା ବୁଝିଥିଲେ ଏବଂ ତାକୁ କୋଳେଇ ନେଇଥିଲେ ।
ମାଷ୍ଟରଜୀ ଥିଲେ ଜଣେ ସଚ୍ଚାଶିକ୍ଷକ । ଶିକ୍ଷକ ହିସାବରେ ବିଭିନ୍ନ ଶିକ୍ଷାମୂଳକ ଗଳ୍ପ କହି, ଅଶୋକଭଳି ପିଲାମାନଙ୍କୁ ପ୍ରଭାବିତ କରିଥିଲେ । ଏପରିକି ଅଶୋକ ଓ ତାଙ୍କର ପୋଷା ମାଙ୍କଡ଼କୁ ନେଇ ସେ ସାଧାରଣ ବିରକ୍ତି ପ୍ରକାଶ କରୁଥିଲେ ବି, ନିଜର ସ୍ଥିତି ହରାଇ ନଥିଲେ । ସନ୍ଧ୍ୟାବେଳେ ଲଣ୍ଡନ ଜାଳି ସେ ପିଲାମାନଙ୍କୁ ପାଠ ପଢ଼ାଇ ନିଜର ଗୁଜୁରାଣ ମେଣ୍ଟାଇବାକୁ ଚେଷ୍ଟା କରିଥିଲେ । ତାଙ୍କର ମାତାଙ୍କ ପ୍ରତି ମାଷ୍ଟରଜୀଙ୍କର ଥିଲା ଅଧ୍ଵ ସମ୍ମାନବୋଧ । କୌଣସି ପିଲାଙ୍କୁ ଆକଟ କଲାବେଳେ ଯଦି ମାତାଜୀ ସେଥୁରେ ହସ୍ତକ୍ଷେପ କରୁଥିଲେ, ତା’ହେଲେ ସେ ଚୁପ୍ ରହିଯାଉଥିଲେ ।
ମାଷ୍ଟରଜୀ ଧନରେ ଦରିଦ୍ର ଥିଲେ ବି ମନରେ ଥିଲେ ଦାୟିକ ଓ ଉଦାର । ଶିକ୍ଷକ ଧର୍ମଘଟରେ ଯୋଗଦେଇ, ନିଜର ଅଧିକାର ସାବ୍ୟସ୍ତ କରି ଜେଲ୍ ଯାଇଛନ୍ତି । ଜେଲ୍ରୁ ଫେରି ସେ ଭାଙ୍ଗି ପଡ଼ିନାହାଁନ୍ତି, ବରଂ ପରିବାର ପ୍ରତିପୋଷଣ ପାଇଁ ସ୍ତ୍ରୀର ଗହଣା ଓ କିଛି କରଜ କରି ରିଟିଏ କରିଛନ୍ତି । ରିକ୍ଟାଣି ପରିବାର ପ୍ରତିପୋଷଣ କରିଛନ୍ତି । ମାତ୍ର ଶିକ୍ଷକର ମନ ଓ ହୃଦୟ ନେଇ ସେ ଯେତେବେଳେ ଅଶୋକକୁ ଚିହ୍ନି ପାରିଛନ୍ତି, ସେତେବେଳେ ଆନନ୍ଦରେ ବିଭୋର ହୋଇଛନ୍ତି । କଥାକାରଙ୍କ ଭାଷାରେ -‘ତାଙ୍କ କ୍ଷୁଦ୍ର ପରିଚିତ ମହଲ ଭିତରେ ସେ ମତେ ଘୂରେଇ ଫେରେଇ ବୁଲାଇ ଆଣିଥିବେ ତିନିଥର । କଥା କଥାକେ ପ୍ରଶଂସା, ଗର୍ବ ଆଉ ଆନନ୍ଦରେ ସେ ଅସ୍ଥିର । ସେ ମୁହୂର୍ତ୍ତରେ ତାଙ୍କୁ ଯେ କେହି ଦେଖୁଥିଲେ କହିଥାଆନ୍ତେ ସେ ପୃଥିବୀର ସବୁଠାରୁ ସୁଖୀ ମନୁଷ୍ୟ ?’’ ନିଜର ଦାରିଦ୍ର୍ୟ ଓ ଅସୁସ୍ଥତା ସତ୍ତ୍ଵେବି ମାଷ୍ଟରଜୀ ପ୍ରିୟ ଶିଷ୍ୟ ଅଶୋକ ଆଗରେ ବଖାଣି ବସିଛନ୍ତି, ନିଜର ଦୟନୀୟ ପରିସ୍ଥିତିକୁ ।
ବିଭିନ୍ନ ଦୃଷ୍ଟିକୋଣରୁ ବିଚାରକରି ଦେଖିଲେ, ଗାଳ୍ପିକ ମାଷ୍ଟରଜୀଙ୍କୁ ଏକ ଆଦର୍ଶ ମଣିଷ ଭାବରେ ଚିତ୍ରଣ କରିଛନ୍ତି ।
(କ) ଗାଳ୍ପିକ ପରିଚିତି :
ଅଝିଳମେ।ହନ ପଟ୍ଟନାୟକ ଓଡ଼ିଆ ଗଳ୍ପ ସାହିତ୍ୟରେ ଜଣେ ସୁପ୍ତ ତିଷ୍ଠିତ ଗାଳ୍ପକା ସୁପ୍ରତିଷ୍ଠିତ ଗାଳ୍ପିକ । ତାଙ୍କର ଆବିର୍ଭାବ ହୁଏ ତା ୧୮.୧୨.୧୯୨୭ ମସିହାରେ ଓ ତିରୋଧାନ ହୁଏ ତା ୨୯.୧୧.୧୯୮୨ରେ । ସେ ଥିଲେ ଲେଖକ ସାମ୍ମୁଖ୍ୟର ପ୍ରତିଷ୍ଠାତା, ସଭାପତି ଓ କୃତବିଦ୍ୟ ସାହିତ୍ୟିକ । ଭୁବନେଶ୍ୱରରୁ ପ୍ରକାଶିତ ପ୍ରଖ୍ୟାତ ‘ସମାବେଶ’ ପତ୍ରିକାର ସେ ଥିଲେ ସମ୍ପାଦକ । ସମାବେଶ ପତ୍ରିକାର ମୃତ୍ୟୁ ପୂର୍ବରୁ ତାଙ୍କର ଶେଷ ସମ୍ପାଦନୀୟ ଲେଖା ହେଉଛି, ‘ଶେଷପୃଷ୍ଠା’, ‘ଅପୁର ସଂସାର’ ଇତ୍ୟାଦି । ତାଙ୍କର ପ୍ରତ୍ୟେକ ଗଳ୍ପରେ ସାହିତ୍ୟିକ ଆଲେଖ୍ୟ, ନୂତନ ଦୃଷ୍ଟିଭଙ୍ଗୀ, ସ୍ଵାଭାବିକ ପ୍ରକାଶଶୈଳୀ, ପାଠକମାନଙ୍କୁ ଆକୃଷ୍ଟ କରିଥାଏ ।
ଆଧୁନିକ ଓଡ଼ିଆ ସାହିତ୍ୟରେ ସାଧନା ଓ ସିଦ୍ଧି ଉଭୟକୁ ଏକାସାଥରେ ଆପଣାର କରି କଥାକାର ପଟ୍ଟନାୟକ ସ୍ୱନାମଧନ୍ୟ ହୋଇପାରିଛନ୍ତି । ଉଚ୍ଚକୋଟୀର କଳ୍ପନାବିଳାସ ସହ ଉପଯୁକ୍ତ ମିଥର ସଂଯୋଜନା ଅଖିଳମୋହନଙ୍କ ଗଳ୍ପର ଏକ ପ୍ରଧାନ ବିଶେଷତ୍ଵ । ପ୍ରାୟ ତାଙ୍କର ପ୍ରତ୍ୟେକ ଗଳ୍ପ କାହାଣୀ ଧର୍ମୀ । ବ୍ୟକ୍ତିଗତ ଜୀବନରେ ନୈରାଶ୍ୟ, ବ୍ୟର୍ଥତା ଓ ଯନ୍ତ୍ରଣାସିକ୍ତ ଅନୁଭୂତିକୁ ସମ୍ବଳକରି ଲେଖକ ତାଙ୍କର ସାହିତ୍ୟର ସୌଧ ରଚନା କରିଥିଲେ । ‘‘There is a no rose without thorn.’’ ଯୁକ୍ତିରେ ପ୍ରାୟ ପ୍ରତ୍ୟେକ ସ୍ରଷ୍ଟା ନିଜର ଯନ୍ତ୍ରଣାସିକ୍ତ ଜୀବନର ଅନ୍ତର୍ଦାହ ମଧ୍ୟରୁ ହିଁ ସାରସ୍ଵତ ସୁମନର ମାଳା ଗୁନ୍ଥି ଦେଇଥା’ନ୍ତି । ଗାଳ୍ପିକ ପଟ୍ଟନାୟକ ଏ ସମ୍ପର୍କରେ ନିଜର ସ୍ଵୀକାରୋକ୍ତି ପ୍ରଦାନ କରି କହିଛନ୍ତି – ‘ମୁଁ ଗଭୀର ଭାବେ ବିଶ୍ଵାସ କରେ ଯେ ଜଣେ ଲୋକ ହତାଶ, ବ୍ୟର୍ଥ ନହେଲେ ବଡ଼ ଲେଖକ ହୋଇପାରେ ନାହିଁ ।’’ ଅଖିଳମୋହନଙ୍କ ବ୍ୟକ୍ତିଗତ ଜୀବନର ନୈରାଶ୍ୟବୋଧ ହିଁ ତାଙ୍କର ଗଳ୍ପ ରଚନାର ପ୍ରଧାନ ରହସ୍ୟ ।
ଜୀବନରେ କଥାକାର ହିସାବରେ ତାଙ୍କର ସୃଷ୍ଟି ସୀମିତ, ମାତ୍ର ସିଦ୍ଧି ସୁଦୂରପ୍ରସାରୀ । ବର୍ଣ୍ଣନାର ଅନର୍ଗଳତା, ସାବଲୀଳ ‘ଝଡ଼ର ଈଗଲ ଓ ଧରଣୀର କୃଷ୍ଣସାର’, ‘ନଦୀର ନାମ ଗଣତନ୍ତ୍ର’ ଏବଂ ‘ଓ ଅନ୍ଧଗଳି’ । ଏହି ସୀମିତ ସଙ୍କଳନ ମାଧ୍ୟମରେ ସେ ଜଣେ ଅତି ପ୍ରତିଭାଶାଳୀ କଥାକାର ଭାବରେ ପରିଚିତ ହୋଇଛନ୍ତି ।
(ଖ) ଗଳ୍ପର ପୃଷ୍ଠଭୂମି :
ଗଳ୍ପଟିକୁ କଥାକାର ପ୍ରଥମ ପୁରୁଷ ଭାବରେ ପ୍ରକାଶ କରିଛନ୍ତି, ଅର୍ଥାତ୍ ଗଳ୍ପନାୟକ ଅଶୋକ ଦେଖିଛନ୍ତି ବନାରସ ସହରକୁ । ପ୍ରାକ୍ ସନ୍ଧ୍ୟା ସମୟରେ ବନାରସର ବିଭିନ୍ନ ଦୃଶ୍ୟକୁ ଦେଖି ସେ ଯେତିକି ଭାବପ୍ରବଣ ହୋଇଛନ୍ତି, ସେତିକି ନିଜର ଅତୀତ ଦିନକୁ ସ୍ମରଣ କରିଛନ୍ତି । ଅତୀତକୁ ମନେପକାଇ ସେ ନିଜର ଗୃହଶିକ୍ଷକ ରୂପନାରାୟଣ ସାହାଙ୍କ ଜୀବନର ବିତର୍କିତ ଅପରାହ୍ନକୁ ଜଣେ ସମ୍ବେଦନଶୀଳ ମଣିଷ ଭାବରେ ବଖାଣି ବସିଛନ୍ତି । ସେଭଳି ବର୍ଣ୍ଣନାରୁ କଥାକାରଙ୍କ ଦରଦୀ ମନୋଭାବରୁ ଆକଳନ କରିହୁଏ ।
(ଗ) ଗଳ୍ପର ସାରକଥା :
କ୍ରିଷ୍ଟମାସ ଛୁଟିରେ ଅଶୋକ ଗୋଟିଏ ଲାଇଟ୍ ପୋଷ୍ଟକୁ ଆଉଜି ଦେଖିଛନ୍ତି ବନାରସ ସହରର ରାସ୍ତାକୁ । ରାସ୍ତା ଥୁଲା ଅସମ୍ଭବ ଭାବରେ ଭିଡ଼ । ଲୋକମାନେ କ୍ରମଶଃ ଚାରିଆଡ଼କୁ ଖେଳାଇ ହୋଇଯାଉଥିଲେ । ଲାଇଟ୍ ପୋଷ୍ଟ ପାଖରୁ ଦେଖାଯାଉଥିଲା କାଶୀ ବିଶ୍ଵନାଥଙ୍କ ସ୍ଵର୍ଣ୍ଣଚୂଡ଼ା । ଆସନ୍ନ ସନ୍ଧ୍ୟାର ମଳିନ ଆଲୋକରେ ତାହା ଚକ୍ ଚକ୍ କରୁଥିଲା । ମନ୍ଦିର ରାସ୍ତାପାଖରୁ ଆଉ ଏକ ଉପରାସ୍ତା ବାହାରି ଯାଇଥିଲା । ଯେଉଁ ରାସ୍ତା କି ପଡ଼ିଥିଲା ଡାଳମଣ୍ଡି ଆଡ଼କୁ । ସେହି ‘ଡାଳମଣ୍ଡି’ ଏକ ବାରାଙ୍ଗନା ବସ୍ତି, ଏକ ଉପରାସ୍ତା ବାହାରି ଯାଇଥିଲା । ଯେଉଁ ରାସ୍ତା କି ପଡ଼ିଥିଲା ଡାଳମଣ୍ଡି ଯାହାକୁ କି କଥାକାର ଅତି ମନୋଜ୍ଞ ଭାବରେ ବର୍ଣ୍ଣନା କରିଛନ୍ତି ।
ସେତେବେଳେ ସମୟ ଛ’ଅଟା ବାଜିବାକୁ ଆଉ ଦଶମିନିଟ୍ ବାକିଥାଏ । ସନ୍ଧ୍ୟା ଆସିଥିଲେ ବି ସବୁଆଡ଼େ ବିଜୁଳି ଆଲୁଅ ଖେଳାଇ ହୋଇ, ସନ୍ଧ୍ୟାର କାଳିମାକୁ ଦୂରେଇ ଦେଇଥାଏ । ଏହି ପ୍ରସଙ୍ଗରେ କଥାକାର ଗଙ୍ଗାନଦୀର ଜଳ ଓ କୂଳର ବର୍ଣ୍ଣନା ଦେଇଛନ୍ତି । କଥାକାରଙ୍କ ଲେଖନୀରେ ସେହି ପ୍ରାକୃତିକ ଦୃଶ୍ୟ ନିର୍ଜୀବ ନହୋଇ, ହୋଇଛି ସଜୀବ ।

ଏହି ପ୍ରସଙ୍ଗରେ ଅର୍ଥାତ୍ ଗଙ୍ଗାନଦୀକୁ ଦେଖି ଗଳ୍ପନାୟକ ଅତୀତର ଏକ ବିଶେଷ ଘଟଣାକୁ ମନେପକାଇଛନ୍ତି । ଗଳ୍ପନାୟକ ଅଶୋକ ଯୌବନର ଅସ୍ତଲଗ୍ନରେ ପହଞ୍ଚିଥିଲେ ବି କୈଶୋରର ସେହି ଘଟଣାକୁ ବିସ୍ମୃତ ହୋଇନାହାଁନ୍ତି । କଥାକାରଙ୍କ ଭାଷାରେ – ‘ଲାଇଟ୍ ପୋଷ୍ଟକୁ ତଥାପି ଆଉଜି ରହି ପୁରାତନ ଅନୁଭୂତିକୁ ରୋମନ୍ଥନ କରୁଥୁଲି । ଅନୁଭୂତିର ସମୁଦ୍ର ମନ୍ଥନରେ ବହୁପୁରାତନ ସ୍ମୃତିର ବୁଦ୍ ବୁଦ୍ ଭାସି ଉଠିଛି ଉପରକୁ।’’
ଅଶୋକଙ୍କ ବାପା, ଥିଲେ ବନାରସର ମିଲିଟାରୀ ଡାକ୍ତର । ତେଣୁ ଅଶୋକଙ୍କ ଶୈଶବ ସମୟ ବିତିଯାଇଥିଲା ସେହି ବନାରସରେ । ଫଳରେ ସେ ବନାରସର ଅନେକ ରାସ୍ତା ସହିତ ଥିଲେ ବହୁପରିଚିତ । ଥରେ ତାଙ୍କର କ୍ଷୁଦ୍ର ପରିବାରଟିକୁ ନେଇ ନୌକାଟି ଫେରୁଥାଏ, ଗଙ୍ଗା ଆରପାରି ରାମନଗରରୁ । ନୌକାଟି ହରିଶ୍ଚନ୍ଦ୍ର ଘାଟରୁ ଦର୍ଶ୍ୱଶ୍ଵମେଧ ଘାଟକୁ ଯାଉଥାଏ । ନୌକା ଯିବା ସମୟରେ, କାତ ମାରୁଥିବା ମାଝିର ବାରଣ ସତ୍ତ୍ବେ ଛୋଟପିଲା ହିସାବରେ କର୍ପୋରେସନର ଲୋକକୁ ରାମନଗର ଯାଇଥିବା କଥା ଅଶୋକ କହିଥିଲେ । ଫଳରେ ପ୍ରତ୍ୟେକଙ୍କ ପାଇଁ ଟଙ୍କାଟିଏ ହିସାବରେ ବାପାଙ୍କୁ ଦଶଟଙ୍କା ଅଯଥାରେ ବାପାଙ୍କୁ ଟ୍ୟାକ୍ସ ଦେବାକୁ ପଡ଼ିବାରୁ, ବାପାଙ୍କ ସମେତ ପରିବାରର ସମସ୍ତ ସଦସ୍ୟ ହୋଇଥିଲେ । ବାପା, ଦାଦା, ମା’ ଓ ଭାଇ ଭଉଣୀଙ୍କ ରୋଷର ଭାବ ଜାଣିପାରି ଅଶୋକ ଅସହାୟ ହୋଇପଡ଼ିଥିଲେ । ତାଙ୍କ ଆଖିରେ ଲୋତକ ପୂରି ଯାଇଥିଲା ।
ସେହି ସମୟରେ ତାଙ୍କର ଘରୋଇ ଶିକ୍ଷକ ଯାହାକୁ ସେ ମାଷ୍ଟରଜୀ ଡାକୁଥିଲେ, ତାଙ୍କଠାରୁ ସାମାନ୍ୟ ଆଶ୍ୱାସନାର ସୂଚନା ପାଇଲାପରେ, ସେ କାନ୍ଦି ପକାଇଥିଲେ । ମାଷ୍ଟରଜୀଙ୍କ କୋଳରେ ମୁଣ୍ଡରଖି କାନ୍ଦିଥିଲା ବେଳେ, ତାଙ୍କ ପିଠିରେ ଆଶ୍ଵାସନାର ଥାପୁଡ଼ାକୁ ସେ ଅନୁଭବ କରିଥିଲେ । ମାଷ୍ଟରଜୀ ତାଙ୍କ ପାଇଁ ପରିବାରର ସମସ୍ତଙ୍କୁ ମୃଦୁ ଗାଳି ଦେଇଥିଲେ । କାରଣ ତାଙ୍କ ବିଚାରରେ ଅଶୋକ ସତ କହି କିଛି ଭୁଲ୍ କରିନାହିଁ । ଅଶୋକର ଅବସ୍ଥା ବୁଝିଲା ପରେ, ତାଙ୍କ ବାପା ନୀରବରେ ତାଙ୍କୁ କୋଳକୁ ନେଇଥିଲେ । ମାଷ୍ଟରଜୀଙ୍କୁ ମନେପକାଇବା ଘଟଣାକୁ ଲେଖକ ଲେଖିଛନ୍ତି – ‘ମାଷ୍ଟରଜୀ – ତାଙ୍କ ମୁହଁ ବି ସ୍ପଷ୍ଟ ମନେପଡ଼ୁଛି ମୋର । ଉତ୍କଳ ଗୌରବର୍ଷ-ଈଷତ୍ ଦୀର୍ଘ ମୁହଁ ଉପରେ ଉନ୍ନତ ଶୁକ ଚଞ୍ଚୁ ନାସିକା – ବଡ଼ ବଡ଼ ଦୁଇଟା କାନ ଉପରେ ବିପର୍ଯ୍ୟସ୍ତ ବାଳ ଲମ୍ବି ଆସିଛି କେରା କେରା ହୋଇ । ସାମାନ୍ୟ ଭିତରକୁ ପଶି ପଶି ଯାଉଛି, ଦୁଇଟି ବୁଦ୍ଧି ଦୀପ୍ତ ଆଖି । ମାଷ୍ଟରଜୀ ଏଇ ମୋର ମାଷ୍ଟ୍ରଜୀ ।’’
ମାଷ୍ଟ୍ରଜୀଙ୍କୁ ମନେ ପକାଉ ପକାଉ ଅଶୋକ ଚାହିଁଛନ୍ତି, ତାଙ୍କୁ ଥରେ ଦେଖି ଆସିବା ପାଇଁ । କାରଣ ମାଷ୍ଟ୍ରଜୀଙ୍କର ଘର ଥିଲା ସେହି ବନାରସରେ । ମାଷ୍ଟ୍ରଜୀ ତାଙ୍କୁ ଦେଖିଲେ ନିଶ୍ଚୟ ଖୁସି ହେବେ ବୋଲି ସେ ଜାଣିଥିଲେ । କାରଣ ମାଷ୍ଟ୍ରଜୀ ତାଙ୍କ ପାଠ ଜୀବନରେ ଯେଉଁ ମୂଳଦୁଆ ପକାଇଥିଲେ, ତାହା ଉପରେ ସେ ଅନେକ ଘର କଲେଣି ବୋଲି ଜାଣିଥିଲେ ।
ସଙ୍ଗେ ସଙ୍ଗେ ରିକ୍ସାକୁ ଡାକି ସେ ମାଷ୍ଟରଜୀଙ୍କ ଘରକୁ ଯିବାକୁ ବାହାରି ପଡ଼ିଲେ । କ୍ୟାଣ୍ଟନମେଣ୍ଟ ରୋଡ଼ରେ ରିକ୍ସା ଚାଲୁଥିଲାବେଳେ, ଅଶୋକଙ୍କ ମନରେ ଶୈଶବର ସ୍ମୃତି ଜାଗି ଉଠିଥିଲା । ପିଲାଦିନେ ତାଙ୍କ ଡାକ ନାମ ଥିଲା ମନ୍ନା ଏବଂ ତା’ର ପୋଷା ପାତିମାଙ୍କଡ଼ ଛୁଆର ନାମ ଥିଲା ମନ୍ତୁ । ମନ୍ନା ଓ ମହୁ ପାଠ ପଢ଼ି ଯାଉଥିଲେ । କାରଣ ମଜ୍ଜାକୁ ଛାଡ଼ି ପାତିମାଙ୍କଡ଼ ଛୁଆ ମନ୍ତୁ ରହିପାରୁ ନଥିଲା । ମଜ୍ଜାକୁ ଅନୁକରଣ କରି ମନ୍ତୁ ସିଲଟ ଧରି ବସୁଥିଲା । ବେଳେବେଳେ ମନ୍ତ୍ରୀ ଓ ମନ୍ତୁ ଦୁହେଁ ମାଷ୍ଟରଜୀଙ୍କୁ ହଇରାଣ କରୁଥିଲେ । ଦୁଷ୍ଟାମି କରି ମଜା କରୁଥିଲେ । ହେଲେ ସେହି ପାଠପଢ଼ା ସରିଲା ବେଳକୁ ମାଷ୍ଟରଜୀଙ୍କ ମାତାଜୀ ପିଜୁଳି, ଆମ୍ବ କିମ୍ବା ହାଲୁଆ ଖୁଆଉଥିଲେ । ମାତାଜୀଙ୍କ ପାଇଁ ମଜ୍ଜା କେବେବି ମାଷ୍ଟରଜୀଙ୍କଠାରୁ ମାଡ଼ ଖାଇନଥିଲେ ।
ଏମିତି ଭାବନା ଭିତରେ ରିକ୍ସା ଯେ ଆସି ପହଞ୍ଚି ଯାଇଥିଲା କ୍ୟାଣ୍ଟନମେଣ୍ଟ ଛକ ଉପରେ । ଆଉ ଅଳ୍ପବାଟ ଗଲାପରେ ପଡ଼ିବ ସଦର ବଜାର, ଯେଉଁଠିକି ଛୋଟ ପୋଷ୍ଟଅଫିସର ଆଗଗଳିରେ ମାଷ୍ଟରଜୀଙ୍କ ଘର । ମାଷ୍ଟରଜୀଙ୍କ ଘରକୁ ଯାଉଥିବାରୁ ଅଶୋକଙ୍କ ମନରେ ଭାବନାର ଡୋରି ଆଗକୁ ଆଗକୁ ଲମ୍ବିଯାଇଛି । ସେ ସ୍ଵାଭାବିକ ଭାବେ ଚିନ୍ତା କରିଛନ୍ତି – ‘‘କେମିତି ଦେଖାହବ ମାଷ୍ଟରଜୀଙ୍କ ସହିତ ? ଏଇ ସୁଟ୍ ଆଉ ଟାଇର ପୋଷାକରେ ସେ କ’ଣ ଚିହ୍ନି ପାରିବେ ମତେ ? ନା, ମୁଁ ତାଙ୍କ ଆଖିରେ ଆଜି ପର୍ଯ୍ୟନ୍ତ ମଧ୍ୟ ଥିବି ସେଇ ପୁରାତନ ଚପଳ ଶିଶୁ । ଏଇତ ସନ୍ଧ୍ୟା ହେଲା ନାଲି କିରାସିନିର ସେଇ ମୁମୂର୍ଷୁ ଲଣ୍ଡନ ଆଲୁଅରେ ସେ ତାଙ୍କର ପିଣ୍ଡା ଉପରେ ବସି ରହିଥିବେ, ଆଉ ତାଙ୍କୁ ଘେରି ବସିଥିବେ ଅନେକ ପଠନରତ ଶିଶୁ । ମୁଁ ଚରି ଚିହ୍ନିନେବି ତାଙ୍କୁ ଆଉ ଯାଇ ତାଙ୍କର ପଦଧୂଳି ନେବି । ମଥାପାତି କୃତଜ୍ଞତା ସ୍ବୀକାର କରିବି । ପରିଚୟ ପାଇ ସେ ନିଶ୍ଚୟ ମତେ କୁଣ୍ଢେଇ ପକଇବେ ଗଦ୍ ଗଦ୍ ହୋଇ ।
ସ୍ନେହ ଦୁର୍ବଳ ଏଇ ଶିକ୍ଷକର ଦୁଇ ଆଖି ଭାସିଯିବ ଆନନ୍ଦର ଅଶ୍ରୁରେ ।’’ ଇତ୍ୟାଦି… । ଏହି ଭାବନା ସମୟରେ ରିକ୍ସାବାଲା ପଚାରିଲା ଯିବାର ଠିକଣା । କାରଣ ରିକ୍ସା ସେତେବେଳକୁ ପହଞ୍ଚି ସାରିଥିଲା ସଦର ବଜାର ପୋଷ୍ଟ ଅଫିସ୍ ପାଖରେ । ନିକଟରେ ପିଣ୍ଡା ଉପରେ କେତେଜଣ ଗପ କରୁଥିବା ଲୋକଙ୍କୁ, ଅଶୋକ ପଚାରିଥିଲେ, ମାଷ୍ଟରଜୀଙ୍କ ଠିକଣା । ରୂପନାରାୟଣ ସାହା ନାମରେ ଏକ ଗହଣା ଦୋକାନୀର ଠିକଣା ସେମାନେ ଦେଇଥିଲେ । କାରଣ ଯେ କି ଛୋଟ ଛୋଟ ପିଲାଙ୍କୁ ପଢ଼ାନ୍ତି । ଏଇଠି କୋଉଠି ସେ ଥାଆନ୍ତି । ସେ ହେଉଛନ୍ତି ମାଷ୍ଟରଜୀ । ଅଶୋକଙ୍କ କଥା ଶୁଣି ସମସ୍ତେ ଏକାସାଙ୍ଗରେ ମୁହଁ ଟେକି ରିକ୍ସାବାଲା ମୁହଁକୁ ଚାହିଁଲେ । ରିକ୍ସାବାଲାଟି ଆଶ୍ଚର୍ଯ୍ୟ ହୋଇ ଅଶୋକଙ୍କୁ ଚାହିଁ ରହିଲା । ଶେଷରେ ତା’ର କୋଟରଗତ ପରଳଲଗା ଆଖିରେ, ସେ ଯେପରି ଅଶୋକର ଭିତରଟିକୁ ଦେଖିନେଲା । ଆଖିରେ ସେ ଦେଖୁଥିଲା ସୁଦୂର ଅତୀତକୁ । କିଛି ସମୟପରେ କହିଥୁଲା, ତୁମେ ବୋଧହୁଏ ଅଶୋକ ।
ଅଶୋକ ମଧ୍ୟ ରିକ୍ସାବାଲା ଯେ କି ତା’ର ମାଷ୍ଟରଜୀ ତାଙ୍କୁ ଦେଖି ବିଦ୍ୟୁତ୍ର ଶିହରଣ ଅନୁଭବ କଲା । ତାଙ୍କର ଗୋଟି ଗୋଟି ସବୁ ମନେପଡ଼ିଗଲା ମାଷ୍ଟରଜୀଙ୍କୁ ଦେଖି ।
ଅଶୋକ ନଇଁପଡ଼ି ତାଙ୍କର ପାଦଧୂଳି ନେବାକୁ ହାତ ବଢ଼ାଇବାରୁ, ସେ ପଛକୁ ଘୁଞ୍ଚିଯାଇ, ତାକୁ ତୋଳି ଧରିଥିଲେ ଗୁରୁସୁଲଭ ଭଙ୍ଗୀରେ ଦୀର୍ଘଜୀବୀ ହେବାକୁ ଆଶୀର୍ବାଦ କରିଥିଲେ । ଦୁହେଁ ଦୁହିଁଙ୍କୁ କିଛି ସମୟ ଚାହିଁ ରହିଲେ । ମାଷ୍ଟରଜୀଙ୍କ ନୀରବତାରୁ ଅଶୋକ ଅନୁମାନ କଲେ, ‘କହିବା ଅପେକ୍ଷା ନୀରବରେ ତା’ଠାରୁ ପ୍ରକାଶ କରିପାରେ ଯଥେଷ୍ଟ ବେଶି !’’ ପରେ ପରେ ମାଷ୍ଟରଜୀ ଯଥେଷ୍ଟ ଆନନ୍ଦିତ ହୋଇଥିଲେ । ସେହି ଆନନ୍ଦ ଦେଖିଲେ ଜଣାଯାଉଥିଲା, ସତେଯେପରି ‘ପୃଥିବୀର ସବୁଠାରୁ ସୁଖୀ ମନୁଷ୍ୟ’ ।
ଦୁହେଁ ବସିଲେ ଅତୀତର ସେହି ପୁରୁଣା ପିଣ୍ଡାରେ । ଅଶୋକ କିଛି କହିବେ କହିବେ ହେଉଥିଲେ ବି କିଛି କହିପାରୁ ନଥିଲେ । ମାତ୍ର ମାଷ୍ଟରଜୀ ନିଜେ ଛାଏଁ ଆରମ୍ଭ କରିଦେଇଥିଲେ ନିଜ ଜୀବନର ଦୁଃଖଦ ଅଧ୍ୟାୟକୁ । ସେ ସ୍ଵଚ୍ଛ ବେତନଭୋଗୀ କର୍ମଚାରୀ ଭାବରେ ଶିକ୍ଷକ ଧର୍ମଘଟରେ ସାମିଲ୍ ହୋଇଥିଲେ । ତାଙ୍କର ଧର୍ମଘଟ ପାଇଁ, ସେ ହୋଇଯାଇଥିଲେ ରାଷ୍ଟ୍ର ବିରୁଦ୍ଧରେ ଷଡ଼ଯନ୍ତ୍ରକାରୀ । ତେଣୁ ତାଙ୍କୁ ବର୍ଷକପାଇଁ ଜେଲକୁ ପଠାଇ ଦିଆଯାଇଥିଲା । ଜେଲରୁ ଫେରି ଦେଖିଥିଲେ ତାଙ୍କର ସ୍ତ୍ରୀ ମରିଯାଇଥିଲେ । ସ୍ତ୍ରୀର ସବୁ ଗହଣାକୁ ବିକିବା ପରେ ଆଉ କିଛି ହାତଉଧାର କରି କିଣିଥିଲେ ରିକ୍ସଟିଏ । କାରଣ ଅନ୍ୟପିଲାଙ୍କୁ ପଢ଼ାଇ ପରିବାର ଚଳାଇବା ଅସମ୍ଭବ ହେବାରୁ ସେ ଏପରି କରିବାକୁ ବାଧ୍ୟ ହୋଇଥିଲେ । ନିଜ କଥା କହିଲାବେଳେ ତାଙ୍କ ଆଖିରୁ ଲୁହ ଝରୁଥୁଲା । ହଠାତ୍ ତାଙ୍କର କାଶ ଉଠିବାରୁ, କାଶି କାଶି ସେ ଥକିପଡ଼ିଲା ପରି ଲାଗିଲେ । ଏହା ଭିତରେ ସେ ଅସୁସ୍ଥ ହୋଇ ଯାଇଛନ୍ତି । ଡାକ୍ତରଖାନାକୁ ଯାଇ ଡାକ୍ତର ଦେଖାଇଛନ୍ତି । ମାତ୍ର ଘୁରେସି ହୋଇଥବାର ଚିକିତ୍ସା ପାଇଁ ଅନେକ ପଇସା ଲାଗିବ ଜାଣିବାପରେ, ସେ ଆଉ କିଛି କରିନାହାଁନ୍ତି ।
ମାଷ୍ଟରଜୀଙ୍କ ରିକ୍ସା ପାଖରେ ସୁଦୃଶ୍ୟ ଦମ୍ପତି ପହଞ୍ଚିବାରୁ, ସେ ନିଜର ବାର ଚଉଦ ବର୍ଷର ପିଲାକୁ ରିକ୍ସାନେଇ ଯିବାକୁ ବରାଦ କଲେ । ପୁଅ ପାଇଁ ଶୋଚନା ମଧ୍ୟ କଲେ । କାରଣ ଖୁବ୍ କମ୍ ବୟସରୁ ପୁଅକୁ ମଧ୍ୟ ରିକ୍ସା ଚଳାଇବାକୁ ହେଉଛି । ଏଥିପାଇଁ ଅବଶୋଷରେ ସେ ଦୀର୍ଘଶ୍ଵାସ ଛାଡୁଥିଲେ ।
ମାଷ୍ଟରଜୀ କଥା କହିସାରି ଆଖିରୁ ଲୁହ ପୋଛିଲେ । ବୋଧହୁଏ ତାଙ୍କ ଜୀବନର କ୍ଷୁଦ୍ର ଇତିହାସ ସରିଆସିଥିଲା । ଯେଉଁ ମାଷ୍ଟରଜୀ ଅତୀତରେ ପିଲାଙ୍କୁ କଥା କହିଲାବେଳେ, ଚରିତ୍ରଗୁଡ଼ିକୁ ସୁନ୍ଦରଭାବେ ବର୍ଣ୍ଣନା କରୁଥିଲେ, ସେ ଆଜି ଚରିତ୍ରଟିଏ ପାଲଟି ଯାଇଥିଲେ । ଅଶୋକ ମଧ୍ୟ ସେହି ଚରିତ୍ରର ହୃତ୍ପଦ୍ମର ସ୍ପନ୍ଦନ ଶୁଣିପାରୁଥିଲା ଭଳି ମନେକରିଥିଲେ ।
ସନ୍ଧ୍ୟା ଆସି ଯାଇଥବାରୁ, ମାଷ୍ଟରଜୀ ତାଙ୍କୁ ରାତିଟିଏ ପାଇଁ ତାଙ୍କ ଭଙ୍ଗାଘରେ ରଖି ନପାରିବାରୁ ନିଜକୁ ନିଜେ ଦୋଷୀ ମନେକରିଥିଲେ । ନିଜର ଦୁର୍ଭାଗ୍ୟ ବୋଲି ବିଚାର କରିଥିଲେ ।
ଅଶୋକ ବିଦାୟ ନେଲା ପୂର୍ବରୁ ଦେଖିଥିଲେ ମାଷ୍ଟରଜୀଙ୍କ ମାତାଜୀଙ୍କୁ । ମାତାଜୀ, ଯେ କି ଅତୀତରେ ଅନେକ ମଧୁର ସମ୍ପର୍କ ରଖିଯାଇଥିଲେ ଅଶୋକଙ୍କ ସହିତ । ସେହି ମାତାଜୀ ସାମୟିକ ଭାବରେ ମାନସିକ ଭାରସାମ୍ୟ ହରାଇ ବସୁଥିଲେ । ରିକ୍ସାବାଲାଙ୍କୁ ପଳାଏ ପଳାଏ କିରୋସିନି ବିକ୍ରିକରି ବଞ୍ଚିବାର ସାମର୍ଥ୍ୟ ସଂଗ୍ରହ କରୁଥିଲେ । ଅଶୋକ ଯାଇ, ମାତାଜୀଙ୍କ ପାଦଛୁଇଁ ପ୍ରଣାମ କଲେବି, ସେ ସେପରିକିଛି ଆଗ୍ରହ ପ୍ରକାଶ କରିନଥିଲେ କିମ୍ବା ଚିହ୍ନିବାକୁ ଚାହିଁ ନଥୁଲେ । ବରଂ ଅଭ୍ୟସ୍ତ ଭାବରେ କେବଳ ଆଶୀର୍ବାଦ ଦେଇଥିଲେ ।
ଅଶୋକ ଦେଖିଥିଲେ ରୂପନାରାୟଣ ସାହାଙ୍କ ବିଲ୍କୁଲ୍ ବିଗିଡ଼ି ଯାଇଥିବା ସଂସାରକୁ । ସେ ମାଷ୍ଟରଜୀଙ୍କୁ ପ୍ରଣାମକରି ହୋଟେଲ୍କୁ ଫେରିଥିଲେ । ଫେରିବାବେଳେ ମାଷ୍ଟରଜୀ ତାଙ୍କର ଠିକଣା ଥିବା କାଗଜଟି ଗୁଞ୍ଜି ଦେଇଥିଲେ । କହିଥିଲେ, ଇଚ୍ଛାକଲେ । ଚିଠି ଲେଖିବ ।
କ୍ୟାଣ୍ଟନ୍ମେଣ୍ଟ ରାସ୍ତାରେ ଧୀରେ ଧୀରେ ପାଦ ଗଣି ଗଣି ଅଶୋକ ଫେରୁଥିଲେ । ସେହି ଫେରିବାବେଳେ ମାଷ୍ଟରଜୀଙ୍କ କଥା ତୁହାଇ ତୁହାଇ ମନେପକାଉଥିଲେ । ରୂପନାରାୟଣଙ୍କ ଜୀବନର ନାଟକକୁ ସେ ଯାହା ଦେଖି ଆସିଥିଲେ, ତାହାକୁ ବିଶ୍ବାସ କରିପାରୁ ନ ଥିଲେ । ଇଚ୍ଛାକରି ମଧ୍ୟ ବିଶ୍ୱାସ କରୁନଥିଲେ । କାରଣ ସେ ଥିଲେ ସେତେବେଳର ଭାରତ ସରକାରଙ୍କର ଶିକ୍ଷାବିଭାଗ ନିର୍ଦ୍ଦେଶକ । ସେ ଥିଲେ ରୂପନାରାୟଣଙ୍କ ପରି ଲକ୍ଷ ଲକ୍ଷ ଶିକ୍ଷକଙ୍କର ଭାଗ୍ୟନିୟନ୍ତ୍ରଣକାରୀ । ନିଜ ପାଖରେ ନିଜେ ସେ ଦୋଷୀ ଦୋଷୀ ମନେ କରୁଥିଲେ । ତେଣୁ ତାଙ୍କ କାନ ପାଖରେ ଭାସି ଉଠୁଥୁଲା, ମାଷ୍ଟରଜୀଙ୍କ କଣ୍ଠସ୍ବର । ସେ କହୁଥିଲେ – ‘ଏ ଦୋଷ ତୋ’ର ଏକା ନୁହଁରେ ଅଶୋକ – ଏ ମୂର୍ଖତା ଏଇ ସମଗ୍ର ଅନ୍ଧ ଜାତିର ।’ ଅଶୋକଙ୍କ ଭାବନାରେ, ଏ ଅନ୍ଧଜାତିକୁ ଉପଯୁକ୍ତ ମଣିଷ କରିବାପାଇଁ ରୂପନାରାୟଣଙ୍କୁ ଆହୁରି ବଡ଼ ବେତ ଧରି ଶାସନ କରିବାକୁ ପଡ଼ିବ । ମାତ୍ର ରୂପନାରାୟଣ ଗୋଷ୍ଠୀର
ହୋଇ ଯାଇଥିଲେ । ବିବେକର ଦ୍ବାହିନେଇ ସେ ଭାବିଥିଲେ – ‘ଏ ମଦ୍ୟପ ଜାତି ଯେ ଆଜି କ୍ଷମତାର ମଦ ପିଇ ବେହୋସ ହୋଇପଡ଼ିଛି । ଏମାନେ କ’ଣ ଟିକିଏ ଶୁଣିଛନ୍ତି ଆପଣମାନଙ୍କର ଏତେଦିନର କରୁଣ ନିବେଦନ ! ଆଜି ଆଉ ନୁହେଁ – ଏ ଜାତିକୁ ଜାଗ୍ରତ କରିବାକୁ ହେବ ।’’
ଏହିଭଳି ଅନେକ କଥା ଚିନ୍ତା କରୁଥିଲାବେଳେ, ସେ ଯେ କେତେବେଳେ ରାସ୍ତାକଡ଼ର କଫି ବରାଦ କରିଦେଇ ଭାବନା ରାଜ୍ୟରେ ବୁଡ଼ି ଯାଇଛନ୍ତି, ସେ କଥା ଜାଣିପାରି ନଥିଲେ । ଅନ୍ୟମନସ୍କ ଭାବରେ ହାତରେ ଥିବା ଠିକଣା କାଗଜଟିକୁ ପାପୁଲିରେ ସେ ବଳି ଚାଲିଥିଲେ ।
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

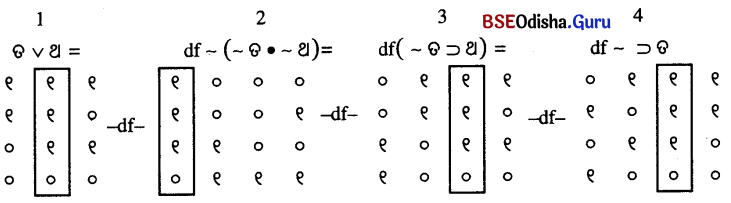
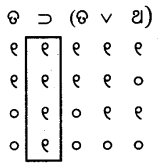 ପୁନରୁକ୍ମିକ
ପୁନରୁକ୍ମିକ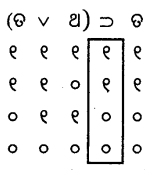 ଆପାତିକ
ଆପାତିକ ଆପାତିକ
ଆପାତିକ ପୁନରୁକ୍ମିକ
ପୁନରୁକ୍ମିକ ପୁନରୁକ୍ମିକ
ପୁନରୁକ୍ମିକ ପୁନରୁକ୍ମିକ
ପୁନରୁକ୍ମିକ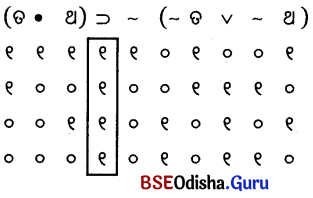 ପୁନରୁକ୍ମିକ
ପୁନରୁକ୍ମିକ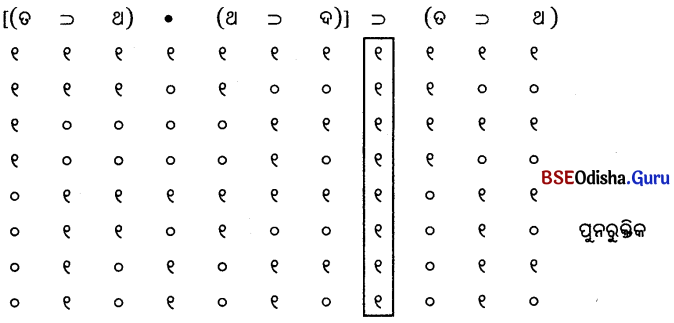
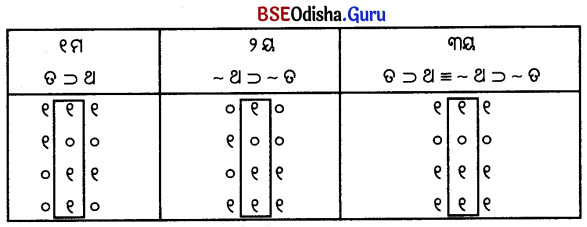
 ୧ମର ମୂଲ୍ୟ ୨ୟ ସହିତ ସମାନ
୧ମର ମୂଲ୍ୟ ୨ୟ ସହିତ ସମାନ ୧ମର ମୂଲ୍ୟ ୨ୟ ସହିତ ସମାନ
୧ମର ମୂଲ୍ୟ ୨ୟ ସହିତ ସମାନ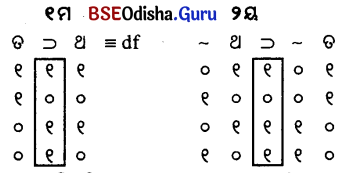 ୧ମ ଓ ୨ୟର ମୂଲ୍ୟ ସମାନ
୧ମ ଓ ୨ୟର ମୂଲ୍ୟ ସମାନ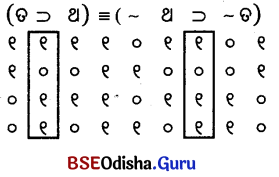 ପୁନରୁକ୍ମିକ
ପୁନରୁକ୍ମିକ ବିରୁଦ୍ଧ
ବିରୁଦ୍ଧ ଆପାତିକ
ଆପାତିକ