Odisha State Board CHSE Odisha Class 12 Math Notes Chapter 9 Integration will enable students to study smartly.
CHSE Odisha 12th Class Math Notes Chapter 9 Integration
Indefinite integral:
If \(\frac{d}{d x}\)F(x) = f(x) then the indefinite integral of f(x) w.r.t x is
∫f(x)dx = F(x) + C
which represents the entire class of anti-derivatives.
(a) Algebra of integrals:
(i) ∫[f(x) ± g(x)] dx = ∫f(x) dx ± ∫g(x) dx
(ii) ∫af(x) dx = α ∫f(x) dx
(iii) ∫f(x) g(x) dx = f(x) ∫g(x) dx – ∫\(\left[(\frac{d}{d x} f(x)\right) \cdot \int g(x) d x]\) dx (Integration by parts)
(b) Some standard indefinite integrations:
(1) ∫xn dx = \(\frac{x^{n+1}}{n+1}\) + C, n ≠ (-1)
(2) ∫\(\frac{d x}{x}\) = loge|x| + C.
(3) ∫sin x dx = -cos x + C
(4) ∫cos x dx = sin x + C
(5) ∫tan x dx = -log |cos x| + C or log |(sec x)| + C
(6) ∫cot x dx = log |(sin x)| + C or -log |(cosec x)| + C
(7) ∫sec x dx = log |sec x + tan x| + C
(8) ∫cosec x dx = log |cosec x – cot x| + C
(9) ∫sec2 x dx = tan x +C
(10) ∫cosec2 x dx = -cot x + C
(11) ∫sec x tan x dx = sec x + C
(12) ∫cosec x cot x dx = -cosec x + C
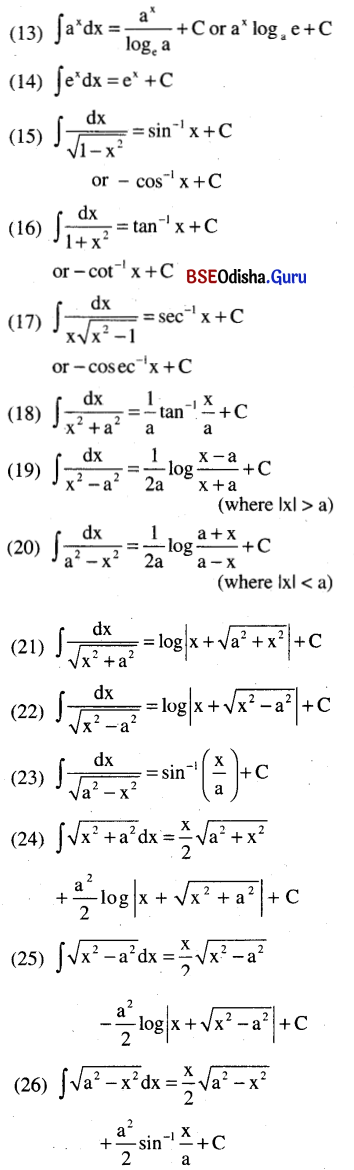
[Note: To integrate by parts choose 1st function according to I LATE]
Where I → Inverse trigonometric functions.
L → Logarithmic function
A → Algebraic function
T → Trigonometric function
E → Exponential function
(c) Techniques of integration:




Definite integration:

