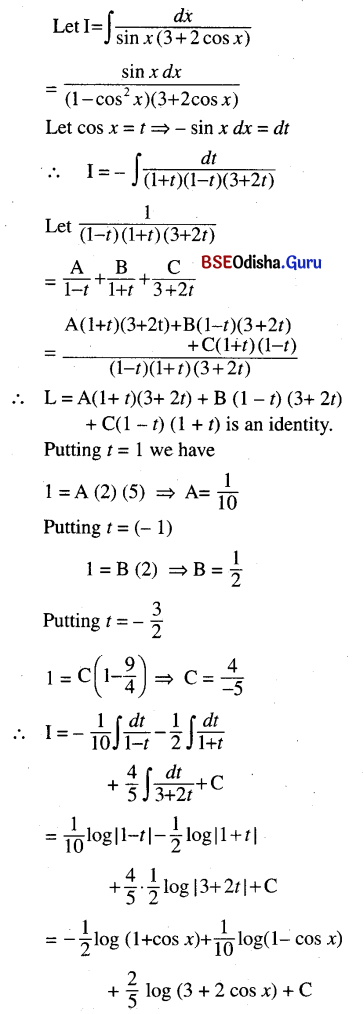Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 9 Integration Ex 9(f) Textbook Exercise questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Exercise 9(f)
Evaluate the following Integrals.
Question 1.
(i) ∫\(\frac{4 x-9}{x^2-5 x+6}\) dx
Solution:

(ii) ∫\(\frac{3 x}{(x-4)(x+2)}\) dx
Solution:

(iii) ∫\(\frac{5 x-12}{(2 x-3)(x-6)}\) dx
Solution:

![]()
(iv) ∫\(\frac{20 x+3}{6 x^2-x-2}\) dx
Solution:
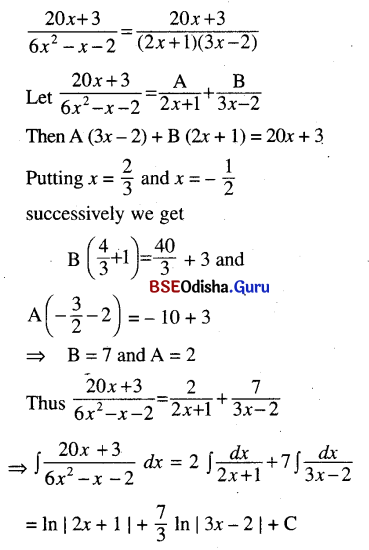
(v) ∫\(\frac{2 x^2}{(x-1)(x-2)(x-3)}\) dx
Solution:

(vi) ∫\(\frac{12 x^4-2 x^3-4 x^2+x-3}{6 x^2-x-2}\) dx
Solution:

Question 2.
(i) ∫\(\frac{2 x+9}{(x+3)^2}\) dx
Solution:

(ii) ∫\(\frac{5 x^2+4 x+4}{(x+2)(x+2)^2}\) dx
Solution:

![]()
(iii) ∫\(\frac{x^2+7 x+4}{x^3+x^2-x-1}\) dx
Solution:

(iv) ∫\(\frac{x^4+3 x^3+x^2-1}{x^3+x^2-x-1}\) dx
Solution:

Question 3.
(i) ∫\(\frac{4 x^2-x+3}{\left(x^2+1\right)(x-1)}\) dx
Solution:

(ii) ∫\(\frac{5 x}{\left(x^2-2 x+2\right)(x+1)}\) dx
Solution:

(iii) ∫\(\frac{3}{x^3-1}\) dx
Solution:

![]()
(iv) ∫\(\frac{x^5+x^4+x^3+x^2+4 x+1}{x^3+1}\) dx
Solution:

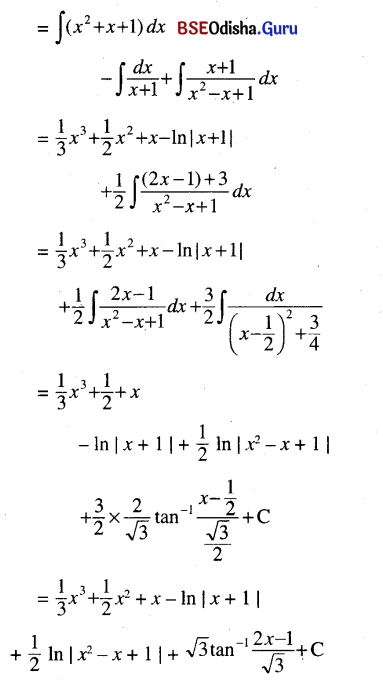
Question 4.
(i) ∫\(\frac{d x}{x^2-5}\)
Solution:

(ii) ∫\(\frac{d x}{2 x^2+8 x+7}\)
Solution:

(iii) ∫\(\frac{x+3}{2 x^2+8 x+7}\) dx
Solution:

(iv) ∫\(\frac{4 x^2+20 x+25}{2 x^2+8 x+7}\) dx
Solution:

![]()
(v) ∫\(\frac{e^x}{e^{2 x}+3 e^x+1}\) dx
Solution:

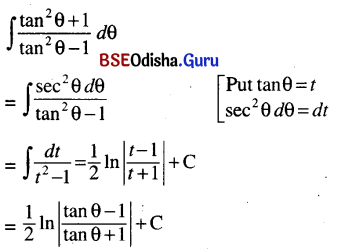
(vi) ∫\(\frac{\tan ^2 \theta+1}{\tan ^2 \theta-1}\) dθ
Solution:
Question 5.
(i) ∫\(\frac{d x}{3-x^2}\)
Solution:

(ii) ∫\(\frac{d x}{7-x^2+6 x}\)
Solution:

(iii) ∫\(\frac{x-5}{7-x^2+6 x}\) dx
Solution:

(iv) ∫\(\frac{\cos \theta}{3-\sin ^2 \theta}\) dθ
Solution:

(v) ∫\(\frac{x^2 d x}{\left(x^2+3\right)\left(x^2+2\right)}\)
Solution:

![]()
(vi) ∫\(\frac{x^3 d x}{x^4+3 x^2+2}\) (Put x2 = t)
Solution:

(vii) ∫\(\frac{d x}{\sin x(3+2 \cos x)}\) (Put cos x = z)
Solution: