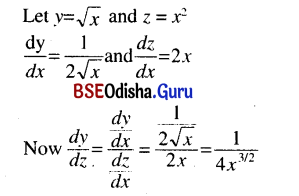Bhagya

Odisha State Board BSE Odisha 10th Class Physical Science Solutions Chapter 1 ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ଓ ରାସାୟନିକ ସମୀକରଣ Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Physical Science Solutions Chapter 1 ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ଓ ରାସାୟନିକ ସମୀକରଣ

Question 1.
ନିମ୍ନରେ ଦର୍ଶାଯାଇଥ‌ିବା ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ସମ୍ବନ୍ଧରେ କେଉଁ ଉକ୍ତିଗୁଡ଼ିକ ଠିକ୍ ନୁହେଁ ?
2PbO (s) + C(s) → 2Pb(s) + CO₂ (g)
(a) ଲେଡ୍ (Pb) ବିଜାରିତ ହେଉଛି ।
(b) କାର୍ବନ୍ ଡାଇଅକ୍‌ସାଇଡ୍ (CO₂) ଜାରିତ ହେଉଛି
(c) କାର୍ବନ୍ (C) ଜାରିତ ହେଉଛି
(d) ଲେଡ୍ ଅକ୍‌ସାଇଡ୍ (PbO) ବିଚ୍ଚାରିତ ହେଉଛି
(i) (a) ଓ (b)
(ii) (a) ଓ (c)
(iii) (a), (b) ଓ (c)
(iv) ସମସ୍ତ ରକ୍ତ୍ରି
Answer:
(i) (a) ଓ (b)

Question 2.
Fe₂O₃ + 2Al → Al₂O₃ + 2Fe
ଉପରେ ଦିଆଯାଇଥ‌ିବା ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାଟି ଏକ
(a) ସଂଶ୍ଳେଷଣ ପ୍ରତିକ୍ରିୟା
(b) ଦ୍ଵୈତ ବିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟା
(c) ବିଘଟନ ପ୍ରତିକ୍ରିୟ
(d) ବିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟା
Answer:
(d) ବିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟା

Question 3.
ଲଘୁ ହାଇଡ୍ରୋକ୍ଲୋରିକ୍ ଏସିଡ୍‌କୁ ଲୁହାଗୁଣ୍ଡରେ ମିଶାଇଲେ କ’ଣ ଘଟେ ? ଠିକ୍ ଉତ୍ତରରେ ଟିକ୍ (✓ ) ଚିହ୍ନ ଦିଅ
(a) ହାଇଡ୍ରୋଜେନ୍ ଗ୍ୟାସ୍ ଓ ଆଇରନ୍ କ୍ଲୋରାଇଡ୍ ଉତ୍ପନ୍ନ ହୁଏ ।
(b) ହାଇଡ୍ରୋଜେନ୍ ଗ୍ୟାସ୍ ଓ ଆଇରନ୍ କ୍ଲୋରାଇଡ୍ ଉତ୍ପନ୍ନ ହୁଏ ।
(c) କ୍ଲୋରିନ୍ ଗ୍ୟାସ୍ ଓ ଆଇରନ୍ ହାଇଡ୍ରିକସାଇଡ୍ ଉତ୍ପନ୍ନ ହୁଏ ।
(d) ଲୌହ ଲବଣ ଓ ଜଳ ଉତ୍ପନ୍ନ ହୁଏ ।
Answer:
(a) ହାଇଡ୍ରୋଜେନ୍ ଗ୍ୟାସ୍ ଓ ଆଇରନ୍ କ୍ଲୋରାଇଡ୍ ଉତ୍ପନ୍ନ ହୁଏ ।

Question 4.
ଏକ ସମତୁଲ ରାସାୟନିକ ସମୀକରଣ କ’ଣ ? ରାସାୟନିକ ସମୀକରଣଗୁଡ଼ିକ କାହିଁକି ସମତୁଲ ହେବା ଉଚିତ ?
Answer:
ସମତୁଲ ରାସାୟନିକ ସମୀକରଣ
(i) ଯେଉଁ ରାସାୟନିକ ସମୀକରଣରେ ବାମପାର୍ଶ୍ଵରେ ଥିବା ପ୍ରତ୍ୟେକ ମୌଳିକର ପରମାଣୁ ସଂଖ୍ୟା, ଦକ୍ଷିଣ ପାର୍ଶ୍ଵରେ ଥ‌ିବା ପ୍ରତ୍ୟେକ ମୌଳିକର ପରମାଣୁ ସଂଖ୍ୟା ସହ ସମାନ ହୋଇଥାଏ, ତାହାକୁ ସମତୁଲ ରାସାୟନିକ
(ii)ଡାଲଟନ୍‌ଙ୍କ ପରମାଣୁ ତତ୍ତ୍ବ ଅନୁସାରେ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ସମୟରେ ପରମାଣୁଗୁଡ଼ିକର ସୃଷ୍ଟି ହୁଏ ନାହିଁ କିମ୍ବା ବିନାଶ ଘଟେ ନାହିଁ । ଏକ ଅସମତୁଲ ସମୀକରଣରେ ଉଭୟ ପାର୍ଶ୍ଵର ପରମାଣୁଗୁଡ଼ିକର ମୋଟ ବସ୍ତୁତ୍ଵ
(iii) ବସ୍ତୁତ୍ୱ ସଂରକ୍ଷଣ ନିୟମ ଅନୁସାରେ କୌଣସି ଏକ ରାସାୟନିକ ସମୀକରଣ ଉତ୍ପାଦରେ ଥ‌ିବା ମୌଳିକଗୁଡ଼ିକର ମୋଟ ବସ୍ତୁତ୍ଵ ପ୍ରତିକାରକରେ ଥ‌ିବା ମୌଳିକଗୁଡ଼ିକର ମୋଟ ବସ୍ତୁତ୍ବ ସହିତ ନିଶ୍ଚୟ ସମାନ ରହିବ । ମୌଳିକର ମୋଟ ବସ୍ତୁତ୍ଵ ଏହାର ପରମାଣୁ ସଂଖ୍ୟା ଉପରେ ନିର୍ଭର କରୁଥିବାରୁ ରାସାୟନିକ ସମୀକରଣକୁ ସମତୁଲ କରିବାକୁ ପଡ଼ିଥାଏ ।

Question 5.
ନିମ୍ନଲିଖ ଉକ୍ତିଗୁଡ଼ିକୁ ରାସାୟନିକ ସମୀକରଣରେ ଲେଖୁ ସେଗୁଡ଼ିକ ସମତୁଲ କର ।
(a) ହାଇଡ୍ରୋଜେନ୍ ଗ୍ୟାସ୍ ନାଇଟ୍ରୋଜେନ୍ ସହିତ ମିଳିତ ହେଲେ ଏମୋନିଆ ହୁଏ ।
ଉ : H₂ + N₂ – NH₂ : ସୂଚକ ସମୀକରଣ
3H₂(g) + N₂(g) → 2NH₃ (g) : ସମତୁଲ ସମୀକରଣ

(b) ହାଇଡ୍ରୋଜେନ୍ ସଲ୍‌ଫାଇଡ୍ ଗ୍ୟାସ୍ ବାୟୁରେ ଜଳିଲେ ଜଳ ଓ ସଲ୍‌ଫର୍ ଡାଇଅକ୍‌ସାଇଡ୍ ହୁଏ ।
ଉ : H₂S + O₂ → SO₂ + H₂O : ଅସମତୁଲ ସମୀକରଣ
2H₂S (g) + 3O₂(g) ) → 2SO₂ (g) + 2H₂O : ସମତୁଲ ସମୀକରଣ

(C) ବେରିୟମ୍ କ୍ଲୋରାଇଡ୍ ଓ ଏଲୁମିନିୟମ୍ ସଲ୍‌ଫେଟ୍ ଦ୍ରବଣର ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ହେଲେ ବେରିୟମ୍ ସଲ୍‌ଫେଟ୍‌ର ଅବକ୍ଷେପ ଏବଂ ଏଲୁମିନିୟମ୍ କ୍ଲୋରାଇଡ୍ ଦ୍ରବଣ ମିଳେ ।
ଉ : BaCl₂ + Al₂ (SO₄)₃ → BaSO₄ + AICI₃ : ଅସମତୁଲ ସମୀକରଣ
3BaCl₂ (aq) + Al₂ (SO₄)₃ → 3BaSO₄ (s) + 2AICI₃ (aq) : ସମତୁଲ ସମୀକରଣ

(d) ପୋଟାସିୟମ୍ ଜଳ ସହିତ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା କରି ପୋଟାସିୟମ୍ ହାଇଡ୍ରକ୍‌ସାଇଡ୍ ଓ ହାଇଡ୍ରୋଜେନ୍ ଗ୍ୟାସ୍ ଉତ୍ପନ୍ନ କରେ ।
ଉ : K + H₂O → KOH + H₂ : ଅସମତୁଲ ସମୀକରଣ
2K(s) + 2H₂O (l) → 2KOH (l) + H₂ (g) : ସମତୁଲ ସମୀକରଣ

Question 6.
ନିମ୍ନଲିଖ ରାସାୟନିକ ସମୀକରଣଗୁଡ଼ିକୁ ସମତୁଲ କର ।
(a) HNO₃ + Ca(OH)₂ → Ca(NO₃)₂ + H₂O
ଉ : 2HNO₃ + Ca(OH)₂ → Ca (NO₃)₂ + H₂O

(b) NaOH + H₂SO₄ → Na₂SO₄ + H₂O
ଉ : 2NaOH + H₂SO₄ → Na₂SO₄ + 2H₂O

(c) NaCl + AgNO₂ → AgCl + NaNO₃
ଉ : NaCl + AgNO₂ → AgCl + NaNO₃

(d) BaCl₂ + H₂SO₄ → BaSO₄ + HCI
ଉ : BaCl₂ + H₂SO₄ → BaSO₄ + 2HCI

Question 7.
ନିମ୍ନଲିଖ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାଗୁଡ଼ିକ ପାଇଁ ସମତୁଲ ରାସାୟନିକ ସମୀକରଣ ଲେଖ ।
(a) କ୍ୟାଲସିୟମ୍ ହାଇଟ୍ରକ୍‌ସାଇଡ୍ + କାର୍ବନ୍ ଡାଇଅକ୍‌ସାଇଡ୍ → କ୍ୟାଲ୍‌ସିୟମ୍ କାର୍ବୋନେଟ୍ + ଜଳ
ଊ : Ca (OH)₂ + CO₂ → CaCO₃ + H₂O

(b) ଜିଙ୍କ୍ + ସିଲଭର୍‌ ନାଇଟ୍ରେଟ୍ – → ଜିଙ୍କ୍ ନାଇଟ୍ରେଟ୍ + ସିଲ୍‌ଭର୍
ଊ : Zn + 2AgNO₃ → Zn(NO₃)₂ + 2Ag

(C) ଏଲୁମିନିୟମ୍ + କପର୍ କ୍ଲୋରାଇଡ୍ → ଏଲୁମିନିୟମ୍ କ୍ଲୋରାଇଡ୍ + କପର
ଊ : 2Al + 3CuCl₂ → 2AlCl₃ + 3Cu

(d) ବେରିୟମ୍ କ୍ଲୋରାଇଡ୍ + ପୋଟାସିୟମ୍ ସଲଫେଟ୍ → ବେରିୟମ ସଲ୍‌ଫେଟ୍ + ପୋଟାସିୟମ୍ କ୍ଲୋରାଇଡ୍
ଉ : BaCl₂ + K₂SO₄ → BaSO₄ + 2KCI

Question 8.

କେଉଁ ପ୍ରକାରର ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ସୂଚାଅ ।
(a) ଆଇରନ୍‌ ସଲ୍‌ଫାଇଡ୍‌ (କଠିନ) + ସଲ୍‌ଫ୍ୟୁରିକ୍ ଏସିଡ୍ (ଜଳୀୟ) → ଆଇରନ୍ ସଲ୍‌ଫେଟ୍ (ଜଳୀୟ) + ହାଇଡ୍ରୋଜେନ୍ ସଲ୍‌ଫାଇଡ୍ (ଗ୍ୟାସ୍)
ଉ : FeS (s) + H₂SO₄ (ag) → FeSO₄ (aq) + H₂S (g) (ଦ୍ୱୈତ ବିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟା)

(b) ଜିଙ୍କ୍ କାର୍ବୋନେଟ୍ (କଠିନ) → ଜିଙ୍କ୍ ଅକସାଇଡ୍ (କଠିନ) + କାର୍ବନ୍ ଡାଇଅକ୍‌ସାଇଡ୍ (ଗ୍ୟାସ୍)
ଉ : ZnCO₃ (s) → ZnO(s) + CO₂ (g) (ଦ୍ୱୈତ ବିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟା)

(c) ହାଇଡ୍ରୋଜେନ୍ (ଗ୍ୟାସ୍) + କ୍ଲୋରିନ୍ (ଗ୍ୟାସ୍) → ହାଇଡ୍ରୋଜେନ କ୍ଲୋରାଇଡ୍ (ଗ୍ୟାସ୍)
ଉ : H₂(g) + Cl₂ (g) → 2HCl (g) (ସଂଶ୍ଳେଷଣ ପ୍ରତିକ୍ରିୟା)

(d) ମ୍ୟାଗ୍‌ନେସିୟମ (କଠିନ) + ହାଇଡ୍ରୋକ୍ଲୋରିକ୍ ଏସିଡ୍ (ଜଳୀୟ) → ମ୍ୟାଗ୍ନେସିୟମ୍ କ୍ଲୋରାଇଡ୍ (ଜଳୀୟ) + ହାଇଡ୍ରୋଜେନ୍ (ଗ୍ୟାସ୍)
ଉ : Mg (s) + 2HCl (aq) → MgCl₂ (aq) + H₂(g) (ବିଘଟନ ପ୍ରତିକ୍ରିୟା)

Question 9.
ତାପଉତ୍ପାଦୀ ଓ ତାପଶୋଷୀ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା କହିଲେ କ’ଣ ବୁଝ ? ଉଦାହରଣ ଦିଅ ।
Answer:
ତାପଉତ୍ପାଦୀ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା : ଯେଉଁ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାରେ ଉତ୍ପାଦ ଉତ୍ପନ୍ନ ହେବା ସଙ୍ଗେ
ସଙ୍ଗେ ତାପ ନିର୍ଗତ ହୋଇଥାଏ, ତାହାକୁ ତାପ ଉତ୍ପାଦୀ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା କୁହାଯାଏ ।
ଉଦାହରଣ:
(i) କ୍ୟାଲସିୟମ୍ ଅକ୍‌ସାଇଡ୍‌ର ଜଳ ସହିତ ତୀବ୍ର ପ୍ରତିକ୍ରିୟା ଘଟି ପ୍ରଚୁର ପରିମାଣର ତାପ ନିର୍ଗତ ହେବା ସଙ୍ଗେ
CaO(s) + H₂O(l) → Ca(OH)₂ (aq)
(କଲିଚୂନ)                     (ଶମିତ ଚୂନ)

(ii) ପ୍ରାକୃତିକ ଗ୍ୟାସ୍‌ର ଦହନ ଫଳରେ ଅଙ୍ଗାରକାମ୍ଳ ଓ ଜଳୀୟବାଷ୍ପ ସୃଷ୍ଟି ହେବା ସହିତ ପ୍ରଚୁର ତାପଶକ୍ତି ନିର୍ଗତ ହୋଇଥାଏ ।
CH₄(g) + 2O₂(g) → CO₂(g) + 2H₂O (g)

(iii) ଶ୍ଵାସକ୍ରିୟା ବା ଶ୍ୱସନ ପ୍ରକ୍ରିୟା ମଧ୍ୟ ଏକ ତାପ ଉତ୍ପାଦୀ ପ୍ରତିକ୍ରିୟା ଅଟେ । ପରିପାକ ପ୍ରକ୍ରିୟାରେ ଖାଦ୍ୟ ସରଳତର ପଦାର୍ଥରେ ପରିଣତ ହୁଏ । ଭାତ, ରୁଟି, ଆଳୁ ଇତ୍ୟାଦି ଶ୍ଵେତସାର ଜାତୀୟ ଖାଦ୍ୟରୁ ରୁ କୋଜ୍ (C₆H₁₂O₆) ସୃଷ୍ଟି ହୁଏ । ଗ୍ଲ କୋଜ୍ ଆମ ଶରୀରର ଜୀବକୋଷ ମଧ୍ୟରେ ଥ‌ିବା ଅକ୍‌ସିଜେନ ସହିତ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା କରେ ଏବଂ ଶରୀରକୁ ଶକ୍ତି ଯୋଗାଇଥାଏ ।
C₆H₁₂O₆ (aq) + 6O₂(aq) → 6CO₂(aq) + 6H₂O(l) + energy

ତାପଶୋଷୀ ପ୍ରତିକ୍ରିୟା: ଯେଉଁ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାରେ ତାପଶକ୍ତି ଶୋଷିତ ହୋଇଥାଏ, ତାହାକୁ ତାପଶୋଷୀ ବା ତାପଗ୍ରାହୀ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା କୁହାଯାଏ ।
ଉଦାହରଣ:
ବେରିୟମ୍ ହାଇଡ୍ରୋକ୍‌ସାଇଡ୍ ସହିତ ଏମୋନିୟମ୍ କ୍ଲୋରାଇଡ୍ ମିଶିଲେ, ତାପଶକ୍ତି ଶୋଷିତ ହୋଇଥାଏ ଏବଂ ଅନ୍ୟାନ୍ୟ ଯୌଗିକମାନ ସୃଷ୍ଟି ହୁଏ ।
Ba (OH)₂ + 2 NH₄Cl → 2NH₄OH + BaCl₂

Question 10.
ଶ୍ଵାସକ୍ରିୟାକୁ କାହିଁକି ଏକ ତାପଉତ୍ପାଦୀ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ଭାବରେ ଧରାଯାଇଥାଏ ? ବୁଝାଅ ।
Answer:
(i) ଶ୍ଵାସକ୍ରିୟା ମାଧ୍ୟମରେ ଆମ ଶରୀରର ଜୀବକୋଷଗୁଡ଼ିକ ମଧ୍ୟରେ ସଞ୍ଚିତ ଥିବା ଅକ୍‌ସିଜେନ୍ (0₂) ସହିତ ରକ୍ତରେ ଥ‌ିବା ଗ୍ଲୁକୋଜର ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ଘଟି ଅଙ୍ଗାରକାମ୍ଳ ଓ ତାପଶକ୍ତି ଉତ୍ପନ୍ନ ହୋଇଥାଏ ।

(ii) ଏହା ଆମ ଶରୀରକୁ କାର୍ଯ୍ୟକାରୀ ଶକ୍ତି ଯୋଗାଇଥାଏ । ତେଣୁ ଶ୍ଵାସକ୍ରିୟାକୁ ଏକ ତାପ ଉତ୍ପାଦୀ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ଭାବରେ ଧରାଯାଇଥାଏ ।
C₆H₁₂O₆(aq) + 6O₂ (aq) → 6CO₂(aq) + 6H₂O (l) + energy

Question 11.
ବିଘଟନ ପ୍ରତିକ୍ରିୟାକୁ କାହିଁକି ସଂଶ୍ଳେଷଣ ପ୍ରତିକ୍ରିୟାର ବିପରୀତ ବୋଲି କୁହାଯାଏ ? ଏହି ଦୁଇଟି ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ପାଇଁ ରାସାୟନିକ ସମୀକରଣ ଲେଖ ।
Answer:
(i) ସଂଶ୍ଳେଷଣ ପ୍ରତିକ୍ରିୟାରେ ଦୁଇ ବା ଅଧ୍ଵ ମୌଳିକ କିମ୍ବା ଯୌଗିକ ସଂଯୁକ୍ତ ହୋଇ ଏକ ନୂତନ ଯୌଗିକ ଉତ୍ପନ୍ନ ହୁଏ ।
(ii) କିନ୍ତୁ ବିଘଟନ ପ୍ରତିକ୍ରିୟାରେ ଗୋଟିଏ ଯୌଗିକ ବିଘଟିତ ହୋଇ ଏକାଧ୍ଵ ସରଳତର ମୌଳିକ କିମ୍ବା ଯୌଗିକ ସୃଷ୍ଟି କରନ୍ତି । ତେଣୁ ବିଘଟନ ପ୍ରତିକ୍ରିୟାକୁ ସଂଶ୍ଳେଷଣ ପ୍ରତିକ୍ରିୟାର ବିପରୀତ ବୋଲି କୁହାଯାଇଥାଏ । ସଂଶ୍ଳେଷଣ ପ୍ରତିକ୍ରିୟା: ସଂଶ୍ଳେଷଣ ପ୍ରତିକ୍ରିୟା : 2H₂(g) + O₂(g) → 2H₂O (l)
ବିଘଟନ ପ୍ରତିକ୍ରିୟା : CaCO₃ (s) → CaO(s) + CO₂(g)

Question 12.
ତାପ, ଆଲୋକ କିମ୍ବା ବିଦ୍ୟୁତ୍ ଶକ୍ତି ପ୍ରୟୋଗ ଦ୍ବାରା ସମ୍ପାଦିତ ହେଉଥ‌ିବା ପ୍ରତ୍ୟେକ ବିଘଟନ ପ୍ରତିକ୍ରିୟା ପାଇଁ ରାସାୟନିକ ସମୀକରଣ ଲେଖ ।
Answer:
(i) ତାପ ପ୍ରୟୋଗ ଦ୍ଵାରା ଘଟୁଥ‌ିବା ବିଘଟନ ପ୍ରତିକ୍ରିୟା:
କ୍ୟାଲସିୟମ୍ କାର୍ବୋନେଟ୍‌କୁ ଉତ୍ତପ୍ତ କଲେ ଏହା ବିଘଟିତ ହୋଇ କ୍ୟାଲ୍‌ସିୟମ୍ ଅକ୍‌ସାଇଡ଼ ଓ କାର୍ବନ
ଡାଇଅକ୍‌ସାଇଡ଼ର ଉତ୍ପନ୍ନ କରେ ।

(ii) ସିଲଭର୍ କ୍ଲୋରାଇଡ଼ ସୂର୍ଯ୍ୟାଲୋକ ଉପସ୍ଥିତିରେ ବିଘଟିତ ହୋଇ ସିଲଭର୍ ଓ କ୍ଲୋରିନ୍‌ ଗ୍ୟାସ୍‌ ଉତ୍ପନ୍ନ କରେ ।

(iii) ବିଦ୍ୟୁତ୍ ଶକ୍ତି ପ୍ରୟୋଗଦ୍ଵାରା ଘଟୁଥ‌ିବା ବିଘଟନ ପ୍ରତିକ୍ରିୟା:
ବିଦ୍ୟୁତ୍ ଶକ୍ତି ପ୍ରୟୋଗଦ୍ଵାରା ଜଳ ବିଘଟିତ ହୋଇ ଉଦ୍‌ଜାନ ଗ୍ୟାସ୍ ଓ ଅମ୍ଳଜାନ ଗ୍ୟାସ୍ ଉତ୍ପନ୍ନ କରେ ।

Question 13.
ବିସ୍ଥାପନ ଓ ଦ୍ଵୈତ ବିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟା ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ କ’ଣ ? ଏହି ଦୁଇ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ପାଇଁ
Answer:
ବିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟାରେ ଗୋଟିଏ ମୌଳିକ କୌଣସି ଏକ ଯୌଗିକର ମୌଳିକକୁ ଅପସାରଣ କରେ ।
Zn(s) + CuSO₄ (aq) → ZnSO₄ (aq) + Cu(s)
Fe(s) + Cu SO₄ (aq) → FeSO₄(aq) + Fe (s)
ଦ୍ୱୈତ ବିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟାରେ ପ୍ରତିକାରକ ଦୁଇଟି ମଧ୍ଯରେ ଆୟନ ବିନିମୟ ଘଟିଥାଏ ।
AgNO₃(aq) + NaCl (aq) → AgCl (s)↓ + NaNO₃(aq)
BaCl₂(aq) + Na₂SO₄(aq) → BaSO₄(s) ↓ + 2NaCl (aq)

Question 14.
ସିଲ୍‌ଭର୍ ଶୋଧନରେ, କପର୍ ଧାତୁ ଦ୍ବାରା ସିଲ୍‌ଭର୍‌ ନାଇଟ୍ରେଟ୍ ଦ୍ରବଣରୁ ସିଲ୍କଭରକୁ ଅପସାରଣ କରି ସିଲ୍‌ଭର୍ ନିଷ୍କାସନ କରାଯାଏ । ଏହା ସହିତ ସମ୍ପୃକ୍ତ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାଟିକୁ ଲେଖ ।
Answer:
କପର ଓ ସିଲ୍‌ଭର୍‌ ନାଇଟ୍ରେଟ୍ ଦ୍ରବଣ ମଧ୍ୟରେ ପ୍ରତିକ୍ରିୟା ଘଟିଲେ କପର ନାଇଟ୍ରେଟ୍ ଓ ଧାତବ ସିଲ୍‌ଭର୍‌ ସୃଷ୍ଟିହୁଏ ।
Cu(s) + 2AgNO₃(aq) → Cu(NO₃)₂(aq) + 2Ag (s) ↓
କପର + ସିଲଭର ନାଇଟ୍ରେଟ୍ → କପର ନାଇଟ୍ରେଟ୍ + ସିଲଭର

Question 15.
ଅବକ୍ଷେପଣ ପ୍ରତିକ୍ରିୟା କହିଲେ କଣ ବୁଝ ? ଉଦାହରଣ ଦେଇ ବୁଝାଅ ।
Answer:
ଅବକ୍ଷେପଣ ପ୍ରତିକ୍ରିୟା :
ଅଧିକାଂଶ ଦ୍ଵୈତ ବିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟାରେ ଜଳୀୟ ଦ୍ରବଣରେ ଦୁଇଟି ଆୟନିୟ ଯୌଗିକ ମଧ୍ୟରେ ପ୍ରତିକ୍ରିୟା ଘଟି ଏକ ଅଦ୍ରବଣୀୟ ଉତ୍ପାଦନ ସୃଷ୍ଟି କରିଥାଏ । ଏହାକୁ ଅବକ୍ଷେପ କୁହାଯାଏ ।
ଯେଉଁ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାରେ ଏକ ଅଦ୍ରବଣୀୟ ଉତ୍ପାଦ ବା ଅବକ୍ଷେପ ସୃଷ୍ଟି ହୁଏ, ତାହାକୁ ଅବକ୍ଷେପଣ ପ୍ରତିକ୍ରିୟା (Precipitation reaction) କୁହାଯାଏ ।
ଉଦାହରଣ:
ସୋଡ଼ିୟମ୍‌ ସଲଫେଟ୍ ସହିତ ବେରିୟମ୍ କ୍ଲୋରାଇଡ୍ ଦ୍ରବଣ ମିଶିଲେ ଏକ ଧଳା ଅଦ୍ରବଣୀୟ ପଦାର୍ଥ ସୃଷ୍ଟି ହୋଇଥାଏ । ଏହି ପଦାର୍ଥଟି ହେଉଛି ବେରିୟମ ସଲ୍‌ଫେଟ୍ । ଉତ୍ପନ୍ନ ହୋଇଥିବା ଏହି ଅଦ୍ରବଣୀୟ ପଦାର୍ଥକୁ ଅବକ୍ଷେପ କହନ୍ତି ।

Question 16.
ଅକ୍‌ସିଜେନ୍ ଗ୍ରହଣ ଓ ଅକ୍‌ସିଜେନ୍‌ ପରିହାର ଦୃଷ୍ଟିରୁ ନିମ୍ନଲିଖତ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ଦୁଇଟିକୁ ବୁଝାଅ । ପ୍ରତ୍ୟେକ ପାଇଁ ଦୁଇଟି ଲେଖାଏଁ ଉଦାହରଣ ଦିଅ । (a) ଜାରଣ, (b) ବିଜାରଣ
Answer:
ଜାରଣ (Oxidation) : ଯେଉଁ ପ୍ରତିକ୍ରିୟାରେ ପ୍ରତିକାରକ ଅକ୍‌ସିଜେନ୍ ଗ୍ରହଣ କରେ କିମ୍ବା ହାଇଡ୍ରୋଜେନ୍ ହରାଏ ତାହାକୁ ଜାରଣ କୁହାଯାଏ ।
କପର ସହିତ ଅକ୍‌ସିଜେନର ରାସାୟନିକ ସଂଯୋଗ ଘଟି କପର ଅକ୍‌ସାଇଡ୍ ଉତ୍ପନ୍ନ ହୋଇଥାଏ ।
ଉଦାହରଣ:
(i) କପର ସହିତ ଅକ୍‌ସିଜେନର ରାସାୟନିକ ସଂଯୋଗ ଘଟି କପର ଅକ୍‌ସାଇଡ୍ ଉତ୍ପନ୍ନ ହୋଇଥାଏ ।

ଏଠାରେ କପର ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାରେ ଅକ୍ସିଜେନ୍ ଗ୍ରହଣ କରିଥାଏ ।

(ii) ମ୍ୟାଗ୍ନେସିୟମ୍ ପାତ ବାୟୁରେ ଉଜ୍ଜ୍ଵଳ ଭାବରେ ଜଳି ଏକ ଧଳା ପଦାର୍ଥ, ମ୍ୟାଗ୍ନେସିୟମ୍ ଅକ୍‌ସାଇଡ୍ ସୃଷ୍ଟି କରେ ।

(b) ବିଜାରଣ (Reduction): ଯେଉଁ ପ୍ରତିକ୍ରିୟାରେ ପ୍ରତିକାରକ ଅକ୍‌ସିଜେନ୍ ହରାଏ କିମ୍ବା ହାଇଡ୍ରୋଜେନ୍ ଗ୍ରହଣ କରେ ତାହାକୁ ବିଜାରଣ କୁହାଯାଏ ।
ଉଦାହରଣ:
(i) ହାଇଡ୍ରୋଜେନ୍ ଗ୍ୟାସ୍‌କୁ ଉତ୍ତପ୍ତ କପର ଅକ୍‌ସାଇଡ୍ ଉପରେ ପ୍ରବାହିତ କଲେ, କପର ଅକସାଇଡ୍ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ସମୟରେ ବିଜାରିତ ହୋଇ ଅକ୍‌ସିଜେନ ହରାଇଥାଏ ।

(ii) ଜିଙ୍କ୍ ଅକ୍‌ସାଇଡ୍‌ର କାର୍ବନ ସହିତ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ବେଳେ ଜିଙ୍ଗ୍ ଅକ୍‌ସାଇଡ୍ , ଅକ୍‌ସିଜେନ୍ ହରାଇଥାଏ ।
ZnO + C → Zn + CO

Question 17.
ଏକ ଉଜ୍ଜଳ ବାଦାମୀ ବର୍ଷର ମୌଳିକ ‘X’କୁ ଗରମ କଲେ କଳା ହୋଇଯାଏ । ମୌଳିକ ‘X’ ଏବଂ ସୃଷ୍ଟି ହୋଇଥ‌ିବା କଳା ଯୌଗିକର ନାମ ଲେଖ ।
Answer:
ଏକ ଉଜ୍ଜ୍ବଳ ବାଦାମୀ ବର୍ଷର ମୌଳିକ ‘X’କୁ ଗରମ କଲେ କଳା ହୋଇଯାଏ । ମୌଳିକ ‘X’ ର ନାମ କପର ଏବଂ ସୃଷ୍ଟି ହୋଇଥିବା କଳା ଯୌଗିକର ନାମ କପର (II) ଅକ୍‌ସାଇଡ୍ ।
2Cu + O₂ → 2CuO

Question 18.
ଲୌହ ନିର୍ମିତ ପଦାର୍ଥଗୁଡ଼ିକ ଉପରେ ଆମେ କାହିଁକି ରଙ୍ଗ ଲଗାଇଥାଉ ?
Answer:
(i) ଲୌହ ନିର୍ମିତ ପଦାର୍ଥ ଯଦି କିଛି ଦିନ ପାଇଁ ବାହାରେ ପଡ଼ିରହେ ତେବେ ତା’ଉପରେ ଏକ ଲୋହିତ-ବାଦାମୀ
ରଙ୍ଗର ପ୍ରଲେପ ମାଡ଼ିଯାଏ । ଏହି ପ୍ରାକୃତିକ ପ୍ରକ୍ରିୟାକୁ ‘ଲୁହାରେ କଳଙ୍କି ଲାଗିବା’’ କୁହାଯାଏ ।

(ii) ଲୁହା ବାୟୁମଣ୍ଡଳର ଜଳୀୟବାଷ୍ପ ସହ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା କରି ଲୌହ ଅକ୍‌ସାଇଡ୍ ସୃଷ୍ଟି କରେ । ଏହି ଧାତବ ଅକ୍‌ସାଇଡ୍ ଲୁହା ଉପରେ ଏକ ଲୋହିତ ବାଦାମୀ ରଙ୍ଗର ପ୍ରଲେପ ସୃଷ୍ଟି କରିଥାଏ । ଏହା ଫଳରେ ଲୌହ ନିର୍ମିତ ପଦାର୍ଥର ଧୀରେ ଧୀରେ କ୍ଷୟ ଘଟିଥାଏ ଏବଂ ଲୁହା ତା’ର ଦୀପ୍ତି ହରାଇଥାଏ ।

(iii) ତେଣୁ ଲୌହ ନିର୍ମିତ ପଦାର୍ଥଟି ବାୟୁମଣ୍ଡଳରେ ଜଳୀୟବାଷ୍ପ ସଂସ୍ପର୍ଶରେ ନ ଆସିବା ପାଇଁ ତା’ଉପରେ ରଙ୍ଗର ପ୍ରଲେପ ଦିଆଯାଇଥାଏ ।
ତୈଳ ଓ ଚର୍ବିଯୁକ୍ତ ଖାଦ୍ୟସାମଗ୍ରୀ ଥ‌ିବା ଡବା ମଧ୍ୟରେ ନାଇଟ୍ରୋଜେନ୍ ଗ୍ୟାସ୍ କାହିଁକି ପ୍ରବେଶ କରାଯାଇଥାଏ ?

Question 19.
ତୈଳ ଓ ଚର୍ବିଯୁକ୍ତ ଖାଦ୍ୟ ସାମଗ୍ରୀ ଡବା ମଧ୍ୟରେ ଥିବା ବାୟୁ ସଂସ୍ପର୍ଶରେ ଆସି ଜାରିତ ହୋଇଥାଏ ଏବଂ ସେଥୁରୁ ରହଣିଆ ଗନ୍ଧ ବାହାରିଥାଏ ।
Answer:
(i) ତୈଳ ଓ ଚର୍ବିଯୁକ୍ତ ଖାଦ୍ୟ ସାମଗ୍ରୀ ଡବା ମଧ୍ୟରେ ଥ‌ିବା ବାୟୁ ସଂସ୍ପର୍ଶରେ ଆସି ଜାରିତ ହୋଇଥାଏ ଏବ ସେଥୁରୁ ରହଣିଆ ଗନ୍ଧ ବାହାରିଥାଏ । ତେଣୁ ଜାରଣକୁ ପ୍ରତିହତ କରିବା ପାଇଁ ଖାଦ୍ୟ ସାମଗ୍ରୀ ଥ‌ିବା ଡବ ମଧ୍ୟରେ ବାୟୁ ବଦଳରେ ନାଇଟ୍ରୋଜେନ ଗ୍ୟାସ୍ ବ୍ୟବହାର କରାଯାଇଥାଏ । ଏହାଫଳରେ ଖାଦ୍ୟ ସାମଗ୍ରୀ ବହୁତ ଦିନ ପର୍ଯ୍ୟନ୍ତ ସଂରକ୍ଷିତ ହୋଇ ରହିଥାଏ ।
(ii) ଏହାଫଳରେ ଖାଦ୍ୟ ସାମଗ୍ରୀ ବହୁତ ଦିନ ପର୍ଯ୍ୟନ୍ତ ସଂରକ୍ଷିତ ହୋଇ ରହିଥାଏ ।

Question 20.
ପ୍ରତ୍ୟେକ ପାଇଁ ଉଦାହରଣ ଦେଇ ନିମ୍ନଲିଖତ ପ୍ରତିକ୍ରିୟାକୁ ବୁଝାଅ ।
ସଂକ୍ଷାରଣ (Corrosion):
(i) ଏକ ଲୌହ ନିର୍ମିତ ଦ୍ରବ୍ୟ ନୂତନ ଅବସ୍ଥାରେ ଉଜ୍ଜ୍ଵଳ ଓ ମସୃଣ ହୋଇଥାଏ । କିନ୍ତୁ ଏହା କିଛି ଦିନ ବାହାରେ ପଡ଼ିରହିଲେ, ଏହା ଉପରେ ଏକ ଲୋହିତ-ବାଦାମୀ ରଙ୍ଗର ପ୍ରଲେପ ମାଡ଼ିଯାଏ । ଏହି ପ୍ରାକୃତିକ ‘‘ ପ୍ରକ୍ରିୟାକୁ ‘‘ଲୁହାରେ କଳଙ୍କି ଲାଗିବା’’ କୁହାଯାଏ ।

(ii) ଯେତେବେଳେ ଏକ ଧାତୁ ତାକୁ ଘେରି ରହିଥ‌ିବା ଉପାଦାନ ଗୁଡ଼ିକ (ଯଥା – ଜଳୀୟବାଷ୍ପ, ଅମ୍ଳ ଇତ୍ୟାଦି) ସହିତ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା କରେ, ସେତେବେଳେ ଧାତୁଟିର ଧୀରେ ଧୀରେ କ୍ଷୟ ଘଟିଥାଏ । ଧାତୁର ଏହି କ୍ଷୟ ହେବା ପ୍ରକ୍ରିୟାକୁ ସଂକ୍ଷାରଣ ବା କ୍ରମକ୍ଷୟ କୁହାଯାଏ ।

(iii) ସିଲ୍‌ ଭର ଉପରେ ପଡୁଥିବା କଳା ଆସ୍ତରଣ ଓ କପର ଉପରେ ପଡୁଥିବା ସବୁଜ ଆସ୍ତରଣ ହେଉଛି ସଂକ୍ଷାରଣର ଉଦାହରଣ ।

(iv) ସଂକ୍ଷାରଣ ହେତୁ ମଟରଗାଡ଼ି, ପୋଲ, ଲୁହାବାଡ଼, ଜାହାଜ ଏବଂ ଧାତୁ ନିର୍ମିତ ସମସ୍ତ ବସ୍ତୁ ବିଶେଷକରି ଲୌହ ନିର୍ମିତ ବସ୍ତୁଗୁଡ଼ିକର କ୍ଷୟ ଘଟିଥାଏ !

(b) ରହୁଣିଆ ଅବସ୍ଥା (Rancidity):
(i) ବହୁତ ଦିନ ଧରି ରହିଯାଇଥ‌ିବା ଚର୍ବି ଏବଂ ତେଲ ବାୟୁ ସଂସ୍ପର୍ଶରେ ଆସି ଜାରିତ ହୋଇଥାଏ । ଏହାଫଳରେ ତା’ର ଗନ୍ଧ ଓ ସ୍ବାଦ ବଦଳିଯାଇଥାଏ । ତହିଁରୁ ରହଣିଆ ଗନ୍ଧ ବାହାରୁଛି ବୋଲି କୁହାଯାଏ । ଏହାକୁ ପଦାର୍ଥର ସଢ଼ା ଅବସ୍ଥା କୁହାଯାଏ ।

(ii) ଯେଉଁ ପଦାର୍ଥ ଜାରଣକୁ ନିରୋଧ କରେ ତାକୁ ପ୍ରତିଜାରକ (Antioxidant) କହନ୍ତି । ଖାଦ୍ୟ ସାମଗ୍ରୀରେ ସାଧାରଣତଃ ପ୍ରତିଜାରକକୁ ମିଶାଇ ସେଗୁଡ଼ିକୁ ବହୁଦିନ ପର୍ଯ୍ୟନ୍ତ ସଂରକ୍ଷଣ କରାଯାଇଥାଏ ।

(iii) ବାୟୁରୋଧୀ ପାତ୍ରରେ ଖାଦ୍ୟପଦାର୍ଥ ରଖେଲେ ଜାରଣ ପ୍ରକ୍ରିୟା ମନ୍ଥର ହୁଏ । ଏହାଫଳରେ ସେଗୁଡ଼ିକର ସଂରକ୍ଷଣ ସହଜ ହୋଇଥାଏ । ଜାରଣକୁ ପ୍ରତିହତ କରିବାପାଇଁ ନାଇଟ୍ରୋଜେନ୍ ଗ୍ୟାସ୍‌କୁ ମଧ୍ୟ ଖାଦ୍ୟ ମଧ୍ୟରେ ପୁରାଯାଇଥାଏ ।

ପ୍ରଣ୍ଠ| ଚ୍ ଳ 1 ଓଙତ୍ତର:

Question 1.
ମ୍ୟାଗ୍‌ନେସିୟମ୍ ପାତକୁ ବାୟୁରେ ଜଳାଇବା ପୂର୍ବରୁ କାହିଁକି ସଫାକରିବା ଉଚିତ ?
Answer:
ମ୍ୟାଗ୍ନେସିୟମ୍ ଏକ କ୍ରିୟାଶୀଳ ଧାତୁ ହୋଇଥିବାରୁ ଏହା ଅମ୍ଳଜାନ ସହ ପ୍ରତିକ୍ରିୟା କରି ମ୍ୟାଗ୍ନେସିୟମ୍ ପାତ ବାୟୁରେ ଜଳିନଥାଏ । ତେଣୁ ମ୍ୟାଗ୍ନେସିୟମ ପାତକୁ ବାୟୁରେ ଜଳାଇବା ପୂର୍ବରୁ ସଫା କରାଯାଇଥାଏ ।

Question 2.
ନିମ୍ନଲିଖତ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାଗୁଡ଼ିକ ପାଇଁ ସମତୁଲ ସମୀକରଣ ଲେଖ ।
(i) ହାଇଡ୍ରୋଜେନ୍ + କ୍ଲୋରିନ୍ → ହାଇଡ୍ରୋକର୍ କ୍ଲୋରାଇଡ୍‌
ଉ : H₂ + Cl₂ → 2HCI

(ii) ବେରିୟମ୍ କ୍ଲୋରାଇଡ୍ + ଏଲୁମିନିୟମ୍ ସଲ୍‌ଫେଟ୍ → ବେରିୟମ୍ ସଲ୍‌ଫେଟ୍ + ଏଲୁମିନିୟମ୍ କ୍ଲୋରାଇଡ
ଉ : 3BaCl₂ + Al₂ (SO₄)₃ → 3 BaSO₄ + 2AlCl₃

(iii) ସୋଡ଼ିୟମ୍‌ + ଜଳ → ସୋଡ଼ିୟମ୍‌ ହାଇଡ୍ରକ୍‌ସାଇଡ୍ + ହାଇଡ୍ରୋଜେନ୍
ଉ : 2Na + 2H₂O → 2NaOH + H₂

Question 3.
ନିମ୍ନଲିଖ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାଗୁଡ଼ିକ ପାଇଁ ଅବସ୍ଥା ପ୍ରତୀକ ସହିତ ସମତୁଲ ରାସାୟନିକ ସମୀକରଣ ଲେଖ ।
(i) ବେରିୟମ୍ କ୍ଲୋରାଇଡ୍ ଓ ସୋଡ଼ିୟମ୍‌ ସଲ୍‌ଫେଟ୍ରର ଜଳୀୟ ଦ୍ରବଣ ଦୁଇଟି ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା କରି ଅଦ୍ରବଣୀୟ ବେରିୟମ୍ ସଲ୍‌ଫେଟ୍ ଓ ସୋଡ଼ିୟମ୍ କ୍ଲୋରାଇଡ୍ ଦ୍ରବଣ ପ୍ରଦାନ କରନ୍ତି ।
ଉ : BaCl₂ (aq) + Na₂SO₄ (aq) → BaSO₄(s) + 2NaCl (aq)

(ii) ସୋଡ଼ିୟମ୍‌ ହାଇଡ୍ରକ୍‌ସାଇଡ଼ର ଜଳୀୟ ଦ୍ରବଣ ହାଇଡ୍ରୋକ୍ଲୋରିକ୍ ଏସିଡ୍‌ର ଜଳୀୟ ଦ୍ରବଣ ସହିତ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା କରି ସୋଡ଼ିୟମ୍ କ୍ଲୋରାଇଡ୍ ଦ୍ରବଣ ଓ ଜଳ ଉତ୍ପନ୍ନ କରନ୍ତି ।
ଉ :
NaOH(aq) + HCl (aq) → NaCl (aq) + H₂O (l)

Question 4.
ପଦାର୍ଥ ‘X’ ର ଏକ ଦ୍ରବଣ କାନ୍ଥକୁ ଧଉଳାଇବା ପାଇଁ ବ୍ୟବହାର କରାଯାଇଛି ।
(କ) ପଦାର୍ଥ ‘X’ ର ନାମ କ’ଣ ଏବଂ ତା’ର ସଂକେତ ଲେଖ ।
ଉ : ପଦାର୍ଥ ‘X’ ର ନାମ କ୍ୟାଲ୍‌ସିୟମ୍ ହାଇଡ୍ରକ୍‌ସାଇଡ୍ ଏବଂ ଏହାର ସଂକେତ ହେଉଛି Ca(OH)₂ ।

(ଖ) CO₂, ସହିତ ପଦାର୍ଥ ‘X’ର ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାଟି ଲେଖ ।

Question 5.
“ତୁମ ପାଇଁ କାମ 1.7 ରେ ଗୋଟିଏ ପରୀକ୍ଷାନଳୀରେ ସଂଗୃହୀତ ଗ୍ୟାସ୍‌ ପରିମାଣ ଅନ୍ୟ ପରୀକ୍ଷା ନଳୀରେ ସଂଗୃହୀତ ଗ୍ୟାସ୍‌ର ପରିମାଣର ଦୁଇଗୁଣ କାହିଁକି ? ଏହି ଦୁଇଟି ଗ୍ୟାସ୍‌ର ନାମ ଲେଖ ।
Answer:
ଅମ୍ଳୀକୃତ ଜଳରେ ବିଦ୍ୟୁତ୍ ଶକ୍ତି ପ୍ରବାହିତ ହେଲେ ଜଳ ଅଣୁ ବିଘଟିତ ହୋଇ H₂, ଏବଂ O₂, ଗ୍ୟାସ୍ ଉତ୍ପନ୍ନ କରେ । ଏହି ଦୁଇ ଗ୍ୟାସ୍‌ର ଅନୁପାତ ଯଥାକ୍ରମେ 2 : 1 । ତେଣୁ ଗୋଟିଏ ପରୀକ୍ଷାନଳୀରେ ସଂଗୃହୀତ ଗ୍ୟାସ୍‌ ପରିମାଣ ଅନ୍ୟ ପରୀକ୍ଷାନଳୀରେ ସଂଗୃହୀତ ଗ୍ୟାସ୍‌ ପରିମାଣର 2 ଗୁଣ ।

Question 6.
ଗୋଟିଏ ଲୁହାକଣ୍ଟାକୁ କପର୍ ସଲ୍‌ଫେଟ୍ ଦ୍ରବଣରେ ବୁଡ଼ାଇଲେ, ଦ୍ରବଣର ରଙ୍ଗରେ ପରିବର୍ତ୍ତନ ଘଟେ କାହିଁକି ?
Answer:
ଲୁହାକଣ୍ଟାର କପର ସଲ୍‌ଫେଟ୍ ଦ୍ରବଣ ସହିତ ବିସ୍ଥାପନ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ଘଟି ଆଇରନ ସଲଫେଟ୍ ଦ୍ରବଣ ଓ କପର ସୃଷ୍ଟି ହୁଏ । ଏହି ବିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟାରେ ଅଧିକ କ୍ରିୟାଶୀଳ ମୌଳିକ ଲୁହା କମ୍ କ୍ରିୟାଶୀଳ ମୌଳିକ କପରକୁ ନୀଳରଙ୍ଗର ତୀବ୍ରତାରେ ହ୍ରାସ ଘଟେ । ଲାଲ୍ କପର ଧାତୁ ଲୁହାକଣ୍ଟା ଉପରେ ଜମାହୁଏ । ଫେରସ୍ ଆୟନ (Fe²⁺) ସୃଷ୍ଟି ହେବା ଯୋଗୁଁ ନୀଳରୁ ଇଷତ୍ ସବୁଜ ରଙ୍ଗକୁ ପରିବର୍ତ୍ତିତ ହୁଏ ।

Question 7.
ତୁମପାଇଁ କାମ: 1.10 ର ଉଦାହରଣ ଭିନ୍ନ ଅନ୍ୟ ଏକ ଦ୍ୱୈତ ବିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟା ପାଇଁ ଉଦାହରଣ ଦିଅ ।
Answer:
ଦ୍ୱୈତ ବିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟାର ଅନ୍ୟ ଏକ ଉଦାହରଣ ହେଲା
NaCl (aq) + AgNO₃ (aq) → NaNO₃(aq) + AgCl (s) ↓

Question 8.
ନିମ୍ନଲିଖ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାଗୁଡ଼ିକରେ କେଉଁଗୁଡ଼ିକ ଜାରିତ ହୋଇଛି ଏବଂ ହୋଇଛି ତାହା ସୂଚାଅ ।
Answer:
(i) 4Na(s) + O₂(g) → 2Na₂O(s)
(ii) CuO(s) + H₂(g) → Cu(s) + H₂O (l)

ମିଳିମିଶି କରିତ୍।

ତୁମ ନିଜର ସୂଚକ ପ୍ରସ୍ତୁତ କର :

• ଚାରୋଟି ବିକର୍ ନିଅ ଏବଂ ସେଗୁଡ଼ିକୁ A, B, C ଓ D ଭାବରେ ନାମାଙ୍କିତ କର ।
• 25 ମିଲି ଲି. ଲେଖାଏଁ ଜଳ A, B ଓ C ବିକର୍‌ରେ ଏବଂ କପର୍ ସଲ୍‌ଫେଟ୍ ଦ୍ରବଣ D ବିକର୍‌ରେ ରଖ ।
• ଦୁଇ ଚାମଚ ଲେଖାଏଁ ପୋଟାସିୟମ୍ ସଲ୍‌ଫେଟ୍, ଏମୋନିୟମ୍ ନାଇଟ୍ରେଟ୍, ନିର୍ଜଳ କପର୍ ସଲ୍‌ଫେଟ୍ ଏବଂ ସରୁ ଲୁହାଗୁଣ୍ଡ ଯଥାକ୍ରମେ A, B, C ଓ Ð
• ବିକର୍‌ରେ ମିଶାଅ ଏବଂ ପ୍ରତ୍ୟେକ ମିଶ୍ରଣକୁ ଘାଣ୍ଟି ଦିଅ । ସର୍ବଶେଷରେ ପ୍ରତ୍ୟେକ ମିଶ୍ରଣର ତାପମାତ୍ରା ମାପ ଏବଂ ଲେଖୁ ରଖ ।
• କେଉଁ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାଗୁଡ଼ିକ ତାପଉତ୍ପାଦୀ ଏବଂ କେଉଁଗୁଡ଼ିକ ତାପଶୋଷୀ ନିର୍ଣ୍ଣୟ କର ।
• ଉ – ଛାତ୍ରଛାତ୍ରୀମାନେ ଶିକ୍ଷକଙ୍କ ସହାୟତାରେ ପ୍ରସ୍ତୁତ କରିବେ ।

କାର୍ଯ୍ୟାବଳୀ (ACTIVITY):

କର୍ଯ୍ୟାବଳୀ-1 (Activity-1)
2 ସେ.ମି. ଲମ୍ବ ଏକ ମ୍ୟାଗ୍ନେସିୟମ୍‌ର ପତଳା ପାତକୁ

ଏହାର ଏକ ପାର୍ଶ୍ଵକୁ ଚିମୁଟାରେ ଧରି ଅନ୍ୟ ପାର୍ଶ୍ଵକୁ ବର୍ଣ୍ଣର (Burner) କିମ୍ବା ସ୍ପିରିଟ୍ ଲ୍ୟାମ୍ପ୍ରେ ଜଳାଇ ପାଉଁଶକୁ ଏକ ୱାବ୍‌ଗ୍ଲାସ୍‌ରେ ସଂଗ୍ରହ କରାଯାଉ । ଆଖୁର ସୁରକ୍ଷା ପାଇଁ ଚଷମା ପିନ୍ଧି ଆଖ୍ୟାଠାରୁ ଯଥାସମ୍ଭବ ଦୂରରେ ରଖ୍ ମ୍ୟାଗ୍ନେସିୟମ୍ ପାତକୁ ଜଳାଯାଉ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ : ମ୍ୟାଗ୍ନେସିୟମ୍ ପାତଟି ଅତି ଉଜ୍ଜ୍ବଳ ଧଳାଶିଖା ପ୍ରଦାନ କରି ଜଳିଉଠିବ । ଏହାଫଳରେ କିଛି ଧଳା
ଚୂର୍ଣ୍ଣ ସୃଷ୍ଟି ହେବ । ଏହି ଧଳା ଚୂର୍ଣ୍ଣ ହେଉଛି ମ୍ୟାଗ୍ନେସିୟମ ଅକ୍‌ସାଇଡ୍ ।

ସିଦ୍ଧାନ୍ତ : ମ୍ୟାଗ୍ନେସିୟମ ଓ ବାୟୁରେ ଥ‌ିବା ଅକ୍‌ସିଜେନ ମଧ୍ୟରେ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ଘଟି ମ୍ୟାଗ୍ନେସିୟମ୍ ଅକ୍‌ସାଇଡ୍
ସୃଷ୍ଟି ହୋଇଛି । ଏହା ଏକ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ।
ମ୍ୟାଗ୍ନେସିୟମ + ଅକ୍ସିଜେନ → ମ୍ୟାଗ୍ନେସିୟମ ଅକ୍‌ସାଇଡ
2Mg + 0₂ → 2MgO

କର୍ଯ୍ୟାବଳୀ-2 (Activity-2)
ଏକ ପରୀକ୍ଷାନଳୀରେ କିଛି ଲେଡ୍‌ନାଇଟ୍ରେଟ୍‌ର ଜଳୀୟଦ୍ରବଣ ନିଆଯାଉ ।
ସେଥ୍ରେ ପୋଟାସିୟମ୍ ଆୟୋଡାଇଡ୍‌ର ଜଳୀୟଦ୍ରବଣ ମିଶାଯାଉ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ : ଲେଡ୍ ନାଇଟ୍ରେଟ୍ (Pb (NO₃)₂) ର ଜଳୀୟଦ୍ରବଣ ପୋଟାସିୟମ୍ ଆୟୋଡାଇଡ୍ (KI) ର ଜଳୀୟ ଦ୍ରବଣ ସହ ମିଶିଲେ ଏଥରେ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ଘଟି ଏକ ଯୌଗିକ ସୃଷ୍ଟି ହେବ ।

ସିଦ୍ଧାନ୍ତ : : ଉତ୍ପନ୍ନ ଯୌଗିକର ନାମ ପୋଟାସିୟମ ନାଇଟ୍ରେଟ୍ (KNO₃) ଓ ଲେଡ୍ ଆୟୋଡାଇଡ୍ (PbI₂)
ଲେଡ୍ ନାଇଟ୍ରେଟ୍ + ପୋଟାସିୟମ୍ ଆୟୋଡାଇଡ୍ → ପୋଟାସିୟମ୍ ନାଇଟ୍ରେଟ୍ + ଲେଡ୍ ଆୟୋଡାଇଡ୍
Pb(NO₃)₂ + KI → 2KNO₃ + Pb₂,

କର୍ଯ୍ୟାବଳୀ-3 (Activity-3)
ଏକ କୋନିକାଲ୍ ଫ୍ଲାସ୍‌ କିମ୍ବା ଏକ ପରୀକ୍ଷା
ନଳୀରେ କିଛି ଜିନା ନିଆଯାଉ ।
ସେଥ‌ିରେ କିଛି ଲଘୁ ହାଇଡ୍ରୋକ୍ଲୋରିକ୍ ଏସିଡ୍
କିମ୍ବା ସଫ୍ୟୁରିକ୍ ଏସିଡ୍ ମିଶାଯାଉ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ : ଏକ କୋନିକାଲ ଫ୍ଲାସ୍‌ କିମ୍ବା
ପରୀକ୍ଷାନଳୀରେ କିଛି ଜିନା ସହିତ ଲଘୁ ଗନ୍ଧକାମ୍ଳ ବା ଲଘୁ ଲବଣାମ୍ଳ ମିଶାଇଲେ ସଙ୍ଗେ ସଙ୍ଗେ ପରୀକ୍ଷା ନଳୀଟି ତାତି ଯିବ ଏବଂ ହାଇଡ୍ରୋଜେନ୍ ଗ୍ୟାସ୍ ନିର୍ଗତ ହେବ ।

ସିଦ୍ଧାନ୍ତ : ଜିଙ୍କ୍ ଦାନା ସହିତ ଲଘୁ ଗନ୍ଧକାମ୍ଳ ବା ଲଘୁ ଲବଣାସ୍କର ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ଘଟି ଜିଙ୍କ୍ ସଲଫେଟ୍ (ZnSO₄) ହାଇଡ୍ରୋଜେନ୍ ଗ୍ୟାସ୍ ସୃଷ୍ଟି ହୋଇଥାଏ |
ଜିଙ୍କ୍ + ଲଘୁ ସଫ୍ୟୁରିକ ଏସିଡ୍ → ଜିଙ୍କ୍ ସଲଫେଟ୍ + ହାଇଡ୍ରୋଜେନ୍ (↑)
Zn + H₂SO₄ → ZnSO₄ + H₂↑

କାର୍ଯ୍ୟାବଳୀ -4 (Activity-4)
ଅକ୍ ପରମ।ଣର କଥାକସିସ୍ମ ଅକ୍ସାଇଡ୍
କିମ୍ବା କଲିଚୂନ (Quick lime) ଏକ ବିକର୍‌ରେ ନିଆଯାଉ ।
ଏଥ‌ିରେ ଧୀରେ ଧୀରେ ଜଳ ମିଶାଯାଉ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :
କ୍ୟାଲସିୟମ୍ ଅକସାଇଡ୍ ବା କଲିଚୂନର ଜଳ ସହିତ ପ୍ରତିକ୍ରିୟା ଘଟି ପ୍ରଚୁର ପରିମାଣର ତାପ ନିର୍ଗତ ହେବା ସଙ୍ଗେ ସଙ୍ଗେ ଶର୍ମିତ ଚୂନ (Slaked lime) ଉତ୍ପନ୍ନ ହୁଏ ।

ବିକରଟିକୁ ଛୁଇଁଲେ ଜଣାଯିବ ଯେ, ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାରେ ପ୍ରଚୁର ପରିମାଣର ତାପ ସୃଷ୍ଟି ହେଉଛି ।

ସିଦ୍ଧାନ୍ତ :
ଉପରୋକ୍ତ ପ୍ରତିକ୍ରିୟାରେ କ୍ୟାଲ୍‌ସିୟମ୍‌ ଅକ୍‌ସାଇଡ୍ (CaO) ଓ ଜଳ (H₂O) ସଂଯୁକ୍ତ ହୋଇ ଏକମାତ୍ର ଉତ୍ପାଦ କ୍ୟାଲସିୟମ୍ ହାଇଡ୍ରିକ୍‌ସାଇଡ୍ (Ca(OH)₂)ଉତ୍ପନ୍ନ ହୋଇଛି । ଏହା ଏକ ସଂଶ୍ଳେଷଣ ପ୍ରତିକ୍ରିୟା । ସଂଶ୍ଳେଷଣ ପ୍ରତିକ୍ରିୟାକୁ ନିମ୍ନମତେ ପ୍ରକାଶ କରାଯାଏ ।

ସଂଶ୍ଳେଷଣ ପ୍ରତିକ୍ରିୟାରେ ପ୍ରତିକାରକଗୁଡ଼ିକର ପରମାଣୁଗୁଡ଼ିକ ମଧ୍ୟରେ ଥ‌ିବା ରାସାୟନିକ ବନ୍ଧଗୁଡ଼ିକ ଭାଙ୍ଗିଯାଏ ଏବଂ ନୂତନ ରାସାୟନିକ ବନ୍ଧ ଗଠିତ ହୁଏ । ସଂଶ୍ଳେଷଣ ପ୍ରତିକ୍ରିୟାର ଭିନ୍ନ ଉଦାହରଣଗୁଡ଼ିକୁ ଲକ୍ଷ୍ୟକର : ସଂଶ୍ଳେଷଣ ପ୍ରତିକ୍ରିୟାର ଅନ୍ୟ କେତେକ ଉଦାହରଣ ନିମ୍ନରେ ଦିଆଯାଇଛି :

(i) କୋଇଲାର ଦହନରୁ ଅଙ୍ଗାରକାମ୍ଳ ଗ୍ୟାସ୍ ସୃଷ୍ଟି ହୋଇଥାଏ ।
C(s) + 0₂(g) → CO₂(g)

(ii) ହାଇଡ୍ରୋଜେନ୍ ଓ ଅକ୍ସିଜେନ୍ ସଂଯୋଗରୁ ଜଳ ସୃଷ୍ଟି ହୋଇଥାଏ ।

କାର୍ଯ୍ୟାବଳୀ -5 (Activity-5)
ଏକ ଶୁଷ୍କ ସ୍ଫୁଟନ ନଳୀ (Boiling tube) ରେ ପ୍ରାୟ 2 ଗ୍ରାମ୍ ଫେରସ୍ ସଲ୍‌ଫେଟ୍ ସ୍ଫଟିକ (Crystal) ନିଆଯାଉ ।
ସ୍ଫଟିକ ନଳୀକୁ ବର୍ଣ୍ଣର୍ ବା ସ୍ପିରିଟ୍ ଲ୍ୟାମ୍ପ୍ରେ ଗରମ କରାଯାଉ ।
ଫେରସ୍ ସଲ୍‌ଫେଟ୍ ସ୍ଫଟିକର ରଙ୍ଗକୁ ଲକ୍ଷ୍ୟ

ପର୍ଯ୍ୟବେକ୍ଷଣ: ଫେରସ୍ ସଲ୍‌ଫେଟ୍ ସ୍ଫଟିକ
(FeSO₄, 7H₂O) ଉତ୍ତପ୍ତ ହେଲେ ଏହା
ରଙ୍ଗକୁ ବଦଳିଯାଇଥାଏ ।

ସିଦ୍ଧାନ୍ତ:
ଫେରସ୍ ସଲ୍‌ଫେଟ୍ ସ୍ଫଟିକ ବିଘଟିତ ହୋଇ ଫେରିକ୍ ଅକ୍‌ସାଇଡ୍ (Fe₂O₃), ସଲଫର ଡାଇଅକ୍‌ସାଇଡ (SO₂) ଏବଂ ସଲଫର ଟ୍ରାଇଅକ୍‌ସାଇଡ (SO₃)ରେ ପରିଣତ ହୁଏ ।

କାର୍ଯ୍ୟାବଳୀ -6 (Activity-6)
ଏକ ସ୍ଫୁଟନ ନଳୀରେ ପ୍ରାୟ 2 ଗ୍ରାମ୍ ଲେଡ୍‌ନାଇଟ୍ରେଟ୍ ଚୂର୍ଣ୍ଣ ନିଆଯାଉ ।
ସ୍ଫୁଟନ ନଳୀଟିକୁ ଏକ ଚିମୁଟା (Tongs)ରେ ଧରି ଗରମ କରାଯାଉ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ:
ନଳୀର ଗରମ ଫଳରେ ବାଦାମୀ ରଙ୍ଗର ଧୂମ ଉତ୍‌ସର୍ଜନ (cmission) ହେବ । ଏହି ଧୂମ ହେଉଛି ନାଇଟ୍ରୋଜେନ୍ ଡାଇଅକ୍‌ସାଜି (NO₂) |

ସିଦ୍ଧାନ୍ତ:
ଲେଡ୍ ନାଇଟ୍ରେଟ୍ ଚୂର୍ଣ ବିଘଟିତ ହୋଇ ଲେଡ୍ ଅକ୍‌ସାଇଡ୍, ନାଇଟ୍ରୋଜୋନ୍ ଡାଇଅକ୍‌ସାଇଡ୍ ଓ ଅକ୍ସିଜେନ୍ ଗ୍ୟାସ୍‌ରେ ପରିଣତ ହୋଇଥାଏ ।

ଅନ୍ୟ କେତେକ ରତ୍ନାତୂତଣ:
(i) ସିଲ୍‌ଭର କ୍ଲୋରାଇଡ୍ ସୂର୍ଯ୍ୟାଲୋକରେ ବିଘଟନ ହୋଇ ସିଲ୍‌ଭର ଓ କ୍ଲୋରିନ୍ ଗ୍ୟାସ୍ ଉତ୍ପନ୍ନ ହୋଇଥାଏ ।

(ii) ସିଲ୍‌ଭର ବ୍ରୋମାଇଡ୍ ସୂର୍ଯ୍ୟାଲୋକ ଉପସ୍ଥିତିରେ ବିଘଟନ ହୋଇ ସିଲ୍‌ଭର୍ ଓ ବ୍ରୋମିନ୍ ଗ୍ୟାସ୍ ଉତ୍ପନ୍ନ ହୋଇଥାଏ ।

କାର୍ଯ୍ୟାବଳୀ -7 (Activity-7)
(i) ଗୋଟିଏ ପ୍ଲାଷ୍ଟିକ୍ ମର୍ ନେଇ ଏହାର ତଳପଟରେ ଦୁଇଟି କଣା କରାଯାଉ । କଣାଥ‌ିବା ଦୁଇଟି ରବର ଠିପି ଏଥରେ ଲଗାଯାଉ । ଚିତ୍ରରେ ଦର୍ଶାଯାଇଥ‌ିବା ଭଳି କାର୍ବନ ଇଲେକ୍‌ଟ୍ରୋଡ୍ ଦୁଇଟିକୁ ଏହି ରବର

(ii) ଏହି ଇଲେକ୍‌ଟ୍ରୋଡ୍ ଦୁଇଟିକୁ ଗୋଟିଏ 6 ଭୋଲ୍ଟ ବ୍ୟାଟେରୀ ସହିତ ସଂଯୋଗ କରାଯାଉ ।

(iii) ମଲ୍ଟିଟିରେ ଜଳ ଭର୍ତ୍ତି କରାଯାଉ ଯେପରିକି ବୁନ୍ଦା ଲଘୁ ସଲ୍‌ଫ୍ୟୁରିକ୍ ଏସିଡ଼୍ ଜଳରେ ମିଶାଯାଉ ।

(iv) ଜଳପୂର୍ଣ୍ଣ ଦୁଇଟି ପରୀକ୍ଷାନଳୀ ନେଇ ସେଗୁଡ଼ିକୁ କାର୍ବନ ଇଲେକ୍‌ଟ୍ରୋଡ଼ ଦୁଇଟି ଉପରେ ଓଲଟା ରଖାଯାଉ ।

(v) ସୁଇଚ୍ ଟିପି ଉପକରଣ ମଧ୍ୟକୁ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ କରାଯାଉ । .

ପର୍ଯ୍ୟବେକ୍ଷଣ :
(i) କିଛି ସମୟ ପରେ ଲକ୍ଷ୍ୟକଲେ ଦେଖାଯିବ ଯେ, ଉଭୟ ଇଲେକ୍‌ଟ୍ରୋଡ଼ଠାରେ ପାଣି ଫୋଟକା ସୃଷ୍ଟି ହେଉଛି ।

(ii) ପରୀକ୍ଷାନଳୀ ଦୁଇଟି ଗ୍ୟାସ୍ ପୂର୍ଣ ହୋଇଗଲା ପରେ ସତର୍କତାର ସହ ସେହି ଦୁଇଟିକୁ କାଢ଼ି ନିଆଯାଉ ।

(iii) ଏକ ଜଳନ୍ତା ମହମବତୀକୁ ପରୀକ୍ଷାନଳୀର ମୁହଁ ପାଖକୁ ଆଣି ଦେଖାଇଲେ ଗୋଟିଏ ପରୀକ୍ଷାନଳୀରେ ଥ‌ିବା ଗ୍ୟାସ୍ ପପ୍ ଶବ୍ଦ କରି ଜଳିବ ଏବଂ ଅନ୍ୟଟିରେ କାଠିଟି ଅତି ଉଜ୍ଜଳ ଭାବରେ ଜଳିବ । ଯେଉଁ ଗ୍ୟାସ୍ଟ୍ରି ପପ୍ ଶବ୍ଦ କରି ଜଳିଯିବ ତାହା ଉଦ୍‌ଜାନ ଏବଂ ଉଜ୍ଜ୍ଵଳ ଭାବେ ଜଳୁଥିବା ଗ୍ୟାସ୍‌ ଅମ୍ଳଜାନ ।

ସିଦ୍ଧାନ୍ତ :
ଜଳରୁ ବିଦ୍ୟୁତ୍ ବିଶ୍ଳେଷଣ କଲେ ସେଥୁରୁ ଉଦ୍‌ଜାନ ଓ ଅମ୍ଳଜାନ ଗ୍ୟାସ୍ ନିର୍ଗତ ହୁଏ, ଯେତିକି ଅମ୍ଳଜାନ ଗ୍ୟାସ୍ ନିର୍ଗତ ହୁଏ, ତାହାର ଆୟତନର ଦୁଇଗୁଣ ଉଦ୍‌ଜାନ ଗ୍ୟାସ୍ ନିର୍ଗତ ହୁଏ । ବିଘଟନ ପ୍ରତିକ୍ରିୟା ମାଧ୍ୟମରେ ଜଳରେ ବୈଦ୍ୟୁତିକ ବିଶ୍ଳେଷଣ୍ଢ ସମ୍ଭବ ।

ଉଦାହରଣ:
(i) ତରଳ ଆଲୁମିନା ମଧ୍ୟ ଦେଇ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ପ୍ରବାହିତ କଲେ ତାହା ବିଘଟିତ ହୋଇ ଆଲୁମିନିୟମ୍ ଓ ଅମ୍ଳଜାନ ମିଳିଥାଏ । ଏହା ଆଲୁମିନିୟମ୍ ଉତ୍ପାଦନର ଔଦ୍ୟୋଗିକ ପଦ୍ଧତି ଅଟେ ।

(ii) ତରଳ ଆଲୁମିନା ମଧ୍ୟ ଦେଇ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ପ୍ରବାହିତ କଲେ ତାହା ବିଘଟିତ ହୋଇ ଆଲୁମିନିୟମ୍ ଓ ଅମ୍ଳଜାନ ମିଳିଥାଏ । ଏହା ଆଲୁମିନିୟମ୍ ଉତ୍ପାଦନର ଔଦ୍ୟୋଗିକ ପଦ୍ଧତି ଅଟେ ।
କ୍ଲୋରିନ୍ ମିଳିଥାଏ । ଏହା ମଧ୍ୟ ଏକ ଔଦ୍ୟୋଗିକ ପଦ୍ଧତି ଅଟେ ।

(iii) ଅମ୍ଳୀକୃତ ଜଳ ମଧ୍ୟରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ କଲେ ଜଳ ଉଦ୍‌ଜାନ ଓ ଅମ୍ଳଜାନକୁ ବିଘଟିତ ହୋଇଥାଏ ।

କାର୍ଯ୍ୟାବଳୀ -8 (Activity-8)

(i) ଏକ ଚିନାମାଟି ଥାଳିଆରେ ପ୍ରାୟ 2 ଗ୍ରାମ୍ ସିଲଭର୍ କ୍ଲୋରାଇଡ୍ ନିଆଯାଉ ।

(ii) ଏହି ଚିନାମାଟି ଥାଳିଆକୁ କିଛି ସମୟ ପାଇଁ ସୂର୍ଯ୍ୟାଲୋକରେ ରଖାଯାଉ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :
(i) କିଛି ସମୟ ପରେ ଦେଖାଯିବ ଯେ, ସିଲ୍‌ଭର୍ କ୍ଲୋରାଇଡ଼ ସୂର୍ଯ୍ୟାଲୋକ ଉପସ୍ଥିତିରେ ଧଳାରଙ୍ଗରୁ ଧୂସର ରଙ୍ଗରେ ପରିଣତ ହୋଇଛି ।

(ii) ସୂର୍ଯ୍ୟାଲୋକରେ ସିଲ୍‌ଭର କ୍ଲୋରାଇଡ୍‌ର ବିଘଟନ ଘଟି ସିଲ୍‌ଭର୍‌ ଓ କ୍ଲୋରିନ୍‌ ଉତ୍ପନ୍ନ ହେଉଥ‌ିବା ଯୋଗୁଁ ଏପରି ହୋଇଛି ।

ସିଦ୍ଧାନ୍ତ :
ବିଘଟନ ପ୍ରତିକ୍ରିୟାଗୁଡ଼ିକ ପ୍ରତିକାରକଗୁଡ଼ିକର ବିଘଟନ ପାଇଁ ତାପ, ଆଲୋକ କିମ୍ବା ବିଦ୍ୟୁତ୍ ଶକ୍ତି ଆବଶ୍ୟକ କରିଥା’ନ୍ତି ।

ଉଦାହରଣ:
(i) ଆଲୋକ ଉପସ୍ଥିତିରେ ହାଇଡ୍ରୋଜେନ୍ ପେରକ୍‌ସାଇଡ଼ ବିଘଟିତ ହୋଇ ହାଇଡ୍ରୋଜେନ୍ ଓ ଅମ୍ଳଜାନ ଗ୍ୟାସ୍ ଉତ୍ପନ୍ନ ହୋଇଥାଏ ।

(ii) ଆଲୋକ ଉପସ୍ଥିତିରେ ନାଇଟ୍ରିକ୍ ଅମ୍ଳ ବିଘଟିତ ହୋଇ ଜଳ, ନାଇଟ୍ରୋଜେନ୍ ଡାଇଅକ୍‌ସାଇଡ୍ ଓ ଅମ୍ଳଜାନ ଗ୍ୟାସ୍ ମିଳିଥାଏ ।

କାର୍ଯ୍ୟାବଳୀ -9 (Activity-9)
(i) ତିନୋଟି ଲୁହା କଣ୍ଟା ନେଇ ସେଗୁଡ଼ିକୁ ବାଲିକାଗଜରେ ଘସି ସଫା କରାଯାଉ ।

(ii) A ଓ B ଚିହ୍ନିତ କରି ଦୁଇଟି ପରୀକ୍ଷାନଳୀ ନିଆଯାଉ । ପ୍ରତ୍ୟେକ ପରୀକ୍ଷାନଳୀରେ ପ୍ରାୟ 10 ମିଲିଲିଟର କପର ସଲ୍‌ଫେଟ୍ ଦ୍ରବଣ ନିଆଯାଉ ।

(iii) ଖଣ୍ଡିଏ ସୂତାରେ କଣ୍ଟା ଦୁଇଟିକୁ ବାନ୍ଧି ସାବଧାନତା ସହ ପରୀକ୍ଷାନଳୀରେ ଥ‌ିବା କପର୍ ସଲ୍‌ଫେଟ୍ ଦ୍ରବଣରେ ପ୍ରାୟ 20 ମିନିଟ୍ ପାଇଁ ବୁଡ଼ାଇ ରଖାଯାଉ । ତୁଳନା କରିବା ନିମନ୍ତେ ଗୋଟିଏ ଲୁହାକଣ୍ଟା ଅଲ ଗା ରଖାଯାଉ ।

(iv) 20 ମିନିଟ୍ ପରେ ଲୁହାକଣ୍ଟା ଦୁଇଟିକୁ କପର୍ ସଲ୍‌ଫେଟ୍ ଦ୍ରବଣରୁ ବାହାର କରି ଆଣି ପରୀକ୍ଷାନଳୀ A ଓ Bରେ ଥିବା କପର ସଲ୍‌ଫେଟ୍ ଦ୍ରବଣର ନୀଳରଙ୍ଗର ତୀବ୍ରତା ସହିତ ତୁଳନା କରାଯାଉ ।

(v) କପର୍ ସଲ୍‌ଫେଟ୍ ଦ୍ରବଣରେ ବୁଡ଼ାଯାଇଥିବା ଲୁହାକଣ୍ଟା ଦୁଇଟିର ରଙ୍ଗକୁ ଅଲଗା ରଖାଯାଇଥିବା ଲୁହାକଣ୍ଟାର ରଙ୍ଗ ସହିତ ମଧ୍ୟ ତୁଳନା କରାଯାଉ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :
ଲୁହାକଣ୍ଟା ଟିକିଏ ବାଦାମି ରଙ୍ଗ ଧାରଣ କରିଛି ଏବଂ କପର୍ ସଲ୍‌ଫେଟ୍ ଦ୍ରବଣର ନୀଳରଙ୍ଗର ତୀବ୍ରତର ହ୍ରାସ ଘଟିଛି । କାରଣ ଲୌହ କପର୍ ସଲ୍‌ଫେଟ୍ ଦ୍ରବଣରୁ କପର୍‌କୁ ବିସ୍ଥାପିତ କରିଛି । ଏଠାରେ ଲୌହ କପଠାରୁ ଅଧିକ କ୍ରିୟାଶୀଳ ଧାତୁ ।

ସିଦ୍ଧାନ୍ତ :
ଏହି ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାରେ ଆଇରନ୍ (Fe) ଅନ୍ୟ ମୌଳିକ କପର୍ (Cu)କୁ କପର୍ ସଲ୍‌ଫେଟ୍ ଦ୍ରବଣରୁ ଅପସାରଣ ବା ବିସ୍ଥାପନ କରିଛି । ଏହି ପ୍ରତିକ୍ରିୟାକୁ ବିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟା କୁହାଯାଏ ।

କାର୍ଯ୍ୟାବଳୀ -10 (Activity-10)
ଏକ ପରୀକ୍ଷାନଳୀରେ ପ୍ରାୟ 3 ମିଲି ଲି. ସୋଡ଼ିୟମ୍‌ ସଲ୍‌ଫେଟ୍ ଦ୍ରବଣ ନିଆଯାଉ ।
ଅନ୍ୟ ଏକ ପରୀକ୍ଷା ନଳୀରେ ପ୍ରାୟ 3 .ମିଲି ଲି. ବେରିୟମ୍ କ୍ଲୋରାଇଡ୍ ଦ୍ରବଣ ନିଆଯାଉ ।
ଦୁଇଟି ଦ୍ରବଣକୁ ମିଶାଇ ଦିଆଯାଉ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :
ବେରିୟମ୍ କ୍ଲୋରାଇଡ଼ ଦ୍ରବଣ ସହିତ ମିଶାଇଲେ, ଉକ୍ତ ମିଶ୍ରଣ ଫଳରେ ଏକ ଧଳା ପଦାର୍ଥ ସୃଷ୍ଟି ହୋଇଥାଏ । ଯାହା ଜଳରେ ଦ୍ରବଣୀୟ ନୁହେଁ । ଉତ୍ପନ୍ନ ଅଦ୍ରବଣୀୟ ପଦାର୍ଥକୁ ଅବକ୍ଷେପ କହନ୍ତି । ହେଉଥ‌ିବା ଏହି

ଯେଉଁ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାରେ ଅବକ୍ଷେପ ସୃଷ୍ଟି ହୁଏ, ତାକୁ ଅବକ୍ଷେପଣ ପ୍ରତିକ୍ରିୟା (Precipitation reaction) କହନ୍ତି । ସୋଡ଼ିୟମ୍‌ ସଲଫେଟ୍ ଓ ବେରିୟମ୍ କ୍ଲୋରାଇଡ୍ ମଧ୍ୟରେ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ଘଟି ବେରିୟମ ସଲଫେଟ୍ (ଅଦ୍ରବଣୀୟ ଧଳା ଅବକ୍ଷେପ) ଓ ସୋଡ଼ିୟମ୍ କ୍ଲୋରାଇଡ୍ (ଜଳରେ ଦ୍ରବଣୀୟ) ସୃଷ୍ଟି ହୋଇଥାଏ । ଏ କ୍ଷେତ୍ରରେ SO₄^2- ଓ Ba²⁺ ମଧ୍ୟରେ ପ୍ରତିକ୍ରିୟା ହେତୁ ଅଦ୍ରବଣୀୟ ଧଳା ଅବକ୍ଷେପ BaSO₄, ଉତ୍ପନ୍ନ ହୁଏ ଏବଂ ଅନ୍ୟ ଉତ୍ପାଦଟି Na⁺ ଓ CI^– ର ପ୍ରତିକ୍ରିୟା ହେତୁ ସୋଡ଼ିୟମ କ୍ଲୋରାଇଡ ଉତ୍ପନ୍ନ ହୋଇଥାଏ, ଯାହା ଦ୍ରବଣ ମଧ୍ୟରେ ରହିଯାଏ ।

ସିଦ୍ଧାନ୍ତ :
SO₄^2- ଓ Ba²⁺ ମଧ୍ୟରେ ପ୍ରତିକ୍ରିୟା ଯୋଗୁଁ ଧଳା ଅବକ୍ଷେପ BaSO₄, ଉତ୍ପନ୍ନ ହୋଇଛି । ଅନ୍ୟ ଉତ୍ପାଦ ସୋଡ଼ିୟମ୍‌ କ୍ଲୋରାଇଡ଼ ଜଳରେ ଦ୍ରବଣୀୟ । ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାରେ ପ୍ରତିକାରକ ଦୁଇଟି ମଧ୍ୟରେ ଆୟନ ବିନିମୟ ଘଟିଥାଏ । ତେଣୁ ଏହା ଏକ ଦୈତ୍ୟ ବିସ୍ଥାପିତ ପ୍ରତିକ୍ରିୟା ଅଟେ ।

ଉଦାହରଣ:
ଲେଡ୍ ନାଇଟ୍ରେଟ୍ ଦ୍ରବଣ ସହିତ ପୋଟାସିୟମ୍ ଆୟୋଡ଼ାଇଡ୍ ଦ୍ରବଣ ମିଶାଇଲେ ଲେଡ୍ ଆୟୋଡ଼ାଇଡ୍ ଓ ପୋଟାସିୟମ୍ ନାଇଟ୍ରେଟ୍ ଦ୍ରବଣ ଉତ୍ପନ୍ନ ହେବ ।
Pb (NO₃)₂ + KI → PbI₂, + KNO₃ ଏହା ଏକ ଦ୍ଵୈତ ବିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟା ଅଟେ ।

କାର୍ଯ୍ୟାବଳୀ -11 (Activity-11)
(i) ଏକ ଚିନାମାଟି ଥାଳିଆରେ ପ୍ରାୟ l ଗ୍ରାମ୍ କପର ଗୁଣ୍ଡ ନେଇ ଗରମ କରାଯାଉ ।
(ii) କପର୍ ଗୁଣ୍ଡର ଚାରିପଟେ କପର୍ (II) ଅକ୍‌ସାଇଡ୍‌ର ଏକ କଳା ଆସ୍ତରଣ ସୃଷ୍ଟି ହେବ ।
(iii) ଏହି କଳା ଆସ୍ତରଣ ହେଉଛି କପର୍ ଅକ୍ ସାଇଡ଼ । ଅକ୍‌ସିଜେନ୍‌ର କପର୍ ସହିତ ସଂଯୋଗ ଘଟି କପର୍ ଅକ୍‌ସାଇଡ୍ ଉତ୍ପନ୍ନ ହୋଇଛି ।


(iv) ଯଦି ହାଇଡ୍ରୋଜେନ୍ ଗ୍ୟାସ୍‌କୁ ଏହି ଉତ୍ତପ୍ତ ପଦାର୍ଥ (CuO) ଉପରେ ପ୍ରବାହିତ କରାଯାଏ, ତେବେ ବିପରୀତ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ଘଟି କଳା ଆସ୍ତରଣଟି ବାଦାମୀ ରଙ୍ଗରେ ପରିଣତ ହୁଏ ଓ କପର୍ ମିଳିଥାଏ ।

ସିଦ୍ଧାନ୍ତ :
(i)ଯଦି ଏକ ପଦାର୍ଥ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ସମୟରେ ଅକ୍‌ସିଜେନ୍ ଲାଭ କରେ, ତେବେ ପଦାର୍ଥଟି ଜାରିତ (Oxidised) ହେଲା ବୋଲି କୁହାଯିବ । କିନ୍ତୁ ଯଦି ପଦାର୍ଥଟି ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ସମୟରେ ଅକ୍‌ସିଜେନ୍ ହରାଇଥାଏ, ତେବେ ତାହା ବିଜାରିତ (Reduced) ହେଲା ବୋଲି କୁହାଯିବ ।

(ii) ଏହି ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା ସମୟରେ କପର୍ (II) ଅକ୍‌ସାଇଡ୍ ଅକ୍‌ସିଜେନ୍ ହରାଉଛି ଏବଂ ବିଜାରିତ ହେଉଛି । ହାଇଡ୍ରୋଜେନ୍ ଅକ୍‌ସିଜେନ୍ ଲାଭ କରୁଛି ଏବଂ ଜାରିତ ହେଉଛି । ଏହା ଜାରଣ-ବିଜାରଣ ପ୍ରତିକ୍ରିୟାର ଅନ୍ତର୍ଗତ ।

Odisha State Board CHSE Odisha Class 12 Invitation to English 4 Solutions Grammar Interrogatives Textbook Activity Questions and Answers.

CHSE Odisha 12th Class English Grammar Interrogatives

We usually make questions by changing the word order :

(a) Look at these sentences.

A	B
This is the road to your house.	Is this the road to your house?
He has a car	Has he a car?
There is a canteen in the office	Is there a canteen in the office?

The sentences in ‘A’ are statements and those in ‘B’ are questions. The verb in each sentence in ‘B’ here comes first and the subject is put after it. In other words, there is an inversion of subject and verb. They are all interrogative sentences.
(b) Look at these sentences.

A Statements	B Yes/No Questions
My friend works on a firm	Has he a car?
You sold your car	Is there a canteen in the office?
They go to the cinema every evening.	Do they go to the cinema every evening?

For questions in ‘B’ the auxiliary do or a form of it is provided in questions and it is put before the subject.
(c) 1. (i) Did you see my sister anywhere here?
(ii) Did you see my sister somewhere here?
2. (i) Is anyone absent?
(ii) Is someone absent?

Notice the difference between (1) sentences and (2) sentences. In the latter the speaker tends to believe that the answer is ‘yes’ but not so in the former.

(d) Study those information questions, made with phrases formed by the question word how joined to an adjective or adverb.

A Statements	B Yes/No Questions
There are five colleges in the district	How many colleges are there in the district?
This pen costs twenty rupees.	How much does this pen cost?
The postman comes here two times a day.	How often does the post man come here?

(e) Negative questions (Isn’t it…. ? / didn’t you…. ?) We use negative questions specially to show surprise :
Didn’t you hear the bell? I rang it five times.

Activity -1
Divide the following sentences into two broad categories and state why you have done so.
1. Where’s my pen?
2. Isn’t that my pen?
3. Why haven’t you done your homework?
4. How are you?
5. Would you like something to eat?
6. What’s the time by your watch?
7. Are you listening?
8. You have been to Delhi before, haven’t you?

1. Where	is my pen?
2. Is	not that my pen?
3. Why	(haven’t you done your homework?
4. How	are you?
5. Would	you like something to eat?
6. What	(is) the time by your watch?
7. Are	you listening?
8. You have been to haven’t you? (Yes-No Qn) Delhi before

Activity- 2
Write yes/no questions or wh-questions, using the following expressions :
1 . you / go / to Puri / last year?
2. where / be / Seema / today?
3. you / write / class notes?
4. what / be / the STD code / for Bhubaneswar?
5. where / Samar / live / at the moment?
Answers :
1. Did you go to Puri last year? (Yes – No Qn.)
2. Where is Seema today? (Wh-Qn.)
3. Do you write class notes? (Yes – No Qn.)
4. What is the STD code for Bhubaneswar? (Wh – Qn.)
5. Where does Samar live at the moment? (Wh – Qn.)

Activity -3
Change these statements into wh-questions, using the in the brackets :
1 . Seema put that letter on my desk. (Who)
2. Jatin left his bag on the bus. (Where)
3. That is my friend’s bag. (Whose)
4. He means this one. (Which)
5. All the trains were late yesterday because of heavy rain. (Why)
6. They walked two kilometres before they found the shop. (How far)
7. 54,763 eggs were used in the world’s biggest omelette. (How many)

Answers:
1 . Who put that letter on your desk?
2. Where did Jatin leave his bag?
3. Whose bag is that?
4. Which one does he mean?
5. Why were all the trains late yesterday?
6. How far did they walk before they found the shop?
7. How many eggs were used in the world’s biggest omelette?

Activity- 4
Ask questions to get the following answers.
1. I’m fine, thank you.
2. About 40 kilos.
3. Yesterday evening.
4. The giraffe.
5. Yes, just before my eyes.
Answers :
1. How are you?
2. How much does it weigh?
3. When did you come?
4. Which animal has the longest neck?
5. Did the accident happen before your eyes?

Activity – 5
Work in small groups. One member goes out, and in his / her absence other members choose an object in the classroom. When (s)he comes back, (s)he has to guess the article by asking yes/no questions to the other members, asking them serially, for example :
O: Is it the blackboard?
S1: No, it isn’t.
O: Is it the teacher’s table?
S2: No, it isn’t…

1 . O: Is that the chair?
S1: No, that isn’t
O: Is it the duster in my hand?
S2: No, it isn’t.

2. O: Is it the map of India?
S1: No, it isn’t.
O: Is it a globe?
S2: No, it isn’t

3. O: Is it the blackboard?
S1: Yes, it is.
O: Is it the teacher’s table?
S2: Yes, it is.

4. O: Is that the chair?
S1: Yes, that is.
O: Is it the map of India?
S2: Yes, it is

Activity – 6
One student stands in front of the class. He thinks of a person or a place. Other students ask him yes/no or wh-questions in order to guess the person or the place. The students ask in turn and twenty questions are allowed. If a student guesses correctly, he replaces the first student.

Example :
S, = have you thought of a person.
X = Person.
S2 = Is the person dead?
X = Yes.
S3 = Was the person a man?
X = Yes.
S4 = When did he die?
X = In Twentieth Century. (Here X can refuse to answer, because (s) he may give away
the secret.)
S5 = Was he a filmstar?
X = No.
S6 = Was he famous?
X = Yes.
S7 = In which field was he famous?
X = Politics.
Sg = Was he a freedom fighter?
X = Yes.
S9 = Was he a minister?
X = No.
S10 = Is it Mahatma Gandhi?
X = Yes. [And now S,0 becomes X]

Activity- 7
Look at the questions in the left column and the list of functions in the right column. Decide on a function for each question :

1. What time is it?	a. asking to distinguish
2. Is that poisonous or nonpoisonous?	b. expressing lack of belief.
3. You’re back rather early, aren’t you?	c. offering assistance
4. What do you mean by early?	d. asking for assistance
5. Must you sing at this time of the night?	e. asking for information
6. Shall I do that for you?	f. expressing irritation
7. Would you mind holding this for a moment	g. asking for an opinion
8. Why are you late?	h. expressing mild surprise.
9. What did he look like?	i. asking for an explanation.
10. What do you think of the new bowler?	j. asking for a description

Answers :
1. = e
2. = j
3. = b
4. = h
5. = f
6. = c
7. = d
8. = g
9. = i
10. = a

Activity- 8
In the light of your findings from the previous activity, what is the distinction between the terms question and interrogative?
Questions are used to elicit information or to clear a doubt or problem requiring solution. Interrogative has the force of a question (used formally)

Activity – 9
How many questions can you frame to get the following sentence or a part of it as the answer?
When Amar Nath and his partners took over the place, it was in ruins and was inhabited by bats and mice.
1. What was the place like when Amar Nath and his partners took over it?
2. What was the place inhabited with when Amar Nath and his partners took over it?
3. Who took over the place which was in ruins and was inhabited by bats and mice?
4. Whose partners took over the place?

Multiple-Choice Questions (MCQs)
Transfer the following sentences into interrogative ones

Question 1.
He goes there.
(A) Did he go there?
(B) Does he go there?
(C) Do he go there?
(D) Does he goes there?
Answer:
(B) Does he go there?

Question 2.
My mother cooked well.
(A) Do my mother cook well?
(B) Did my mother cooked well?
(C) Did my mother cook well?
(D) Did my mother cooks well?
Answer:
(C) Did my mother cook well?

Question 3.
You have not seen the Taj Mahal.
(A) Have you not seen the Taj Mahal?
(B) Have you not saw the Taj Mahal?
(C) Have you not see the Taj Mahal?
(D) none of these
Answer:
(A) Have you not seen the Taj Mahal?

Question 4.
My friends go to the cinema.
(A) Does my friends go to the cinema?
(B) Do my friends goes to the cinema?
(C) Do my friends go to the cinema?
(D) Does my friends goes to the cinema?
Answer:
(C) Do my friends go to the cinema?

Question 5.
I like mangoes.
(A) Am I liking mangoes?
(B) Do I liked mangoes?
(C) Does I like mangoes?
(D) Do I like mangoes?
Answer:
(D) Do I like mangoes?

Question 6.
How long you will stay here.
(A) How long will you stay here?
(B) How long you shall stay here?
(C) How long would you stay here?
(D) none of these
Answer:
(A) How long will you stay here?

Question 7.
When you last visited him.
(A) When had you last visited him?
(B) When did you last visit him?
(C) When you had last visited him?
(D) When had you last visit him?
Answer:
(B) When did you last visit him?

Question 8.
This bunch of grapes tastes sour.
(A) Do this bunch of grapes taste sour?
(B) Do this bunch of grapes tastes sour?
(C) Does this bunch of grapes taste sour?
(D) Does this bunch of grapes tastes sour?
Answer:
(C) Does this bunch of grapes taste sour?

Question 9.
I saw you go there.
(A) Do I saw you go there?
(B) Did I saw you go there?
(C) Had I seen you go there?
(D) Did I see you to go there?
Answer:
(D) Did I see you to go there?

Question 10.
We are good friends.
(A) Were we good friends?
(B) Have you been good friends?
(C) Are we good friend?
(D) none of there
Answer:
(C) Are we good friend?

Question 11.
We shall never forget those happy days.
(A) Shall we never forget those happy days?
(B) Should we never forget those happy days?
(C) Shall we ever forget these days?
(D) Can we ever forget those happy days?
Answer:
(C) Shall we ever forget these days?

Question 12.
I have somebody with me.
(A) Have I somebody with me?
(B) Have I anybody with me?
(C) Have I nobody with me?
(D) none of these
Answer:
(B) Have I anybody with me?

Question 13.
I have never been to London.
(A) Have I never been to London?
(B) Have I hardly been to London?
(C) Have I ever been to London?
(D) none of these
Answer:
(C) Have I ever been to London?

Question 14.
A leopard can never change its spot.
(A) Can a leopard change its spot?
(B) Can a leopard never change its spot?
(C) Can a leopard sometimes change its sport?
(D) Can a leopard ever change its spot?
Answer:
(D) Can a leopard ever change its spot?

Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 9 Integration Ex 9(b) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Exercise 9(b)

Integrate the following:
(In some cases suggestions have been given for substitution.)
(i) ∫sin 3x dx
Solution:

(ii) ∫cos ax dx
Solution:

(iii) ∫cos (2 – 7x) dx
Solution:

(iv) ∫sin \(\frac{x}{2}\) dx
Solution:

(v) ∫sec² 4x dx
Solution:

(vi) ∫cosec² \(\frac{x}{3}\) dx
Solution:

(vii) ∫sec (x + 2) tan (x + 2) dx
Solution:
∫sec (x + 2) tan (x + 2) dx
[Put x + 2 = θ
Then dx = dθ]
= ∫sec θ . tan θ dθ
= sec θ + C = sec (x + 2) + C

(viii) ∫cosec (x + \(\frac{\pi}{4}\)) cot (x + \(\frac{\pi}{4}\)) dx (x + \(\frac{\pi}{4}\) = z)
Solution:

(ix) ∫x² cos x³ dx (x³ = z)
Solution:

(x) ∫e^x . sec e^x tan e^x dx (e^x = z)
Solution:
∫e^x . sec e^x . tan e^x dx
[Put e^x = z
Then e^x dx = dz]
= ∫ sec z . tan z dz
= sec z + C = sec e^x + C

(xi) ∫\(\frac{\sec ^2 \sqrt{x}}{\sqrt{x}}\) dx
Solution:

Question 2.
(i) ∫sin x cos x dx (sin x = v)
Solution:
∫sin x cos x dx
[Put sin x = v
Then cos x dx = dv]
= ∫v dv = \(\frac{1}{2}\)v² + C
= \(\frac{1}{2}\)sin² x + C

(ii) ∫tan³ x sec² x dx (tan x = t)
Solution:
∫tan³ x sec² x dx
[Put tan x = t
Then sec² x dx = dt]
= ∫t³ dt = \(\frac{1}{4}\)t⁴ + C
= \(\frac{1}{4}\)tan⁴ x + C

(iii) ∫\(\frac{{cosec}^2 x}{1+\cot x}\) dx
Solution:
∫\(\frac{{cosec}^2 x}{1+\cot x}\) dx
[Put 1 + cot x = t
Then -cosec² x dx = dt
or, cosec² x dx = – dt]
= ∫\(\) = -∫\(\) = -ln |t| + C
= -ln |1 + cot x| + C

(iv) ∫\(\frac{\sin x}{\cos ^3 x}\) dx
Solution:

(v) ∫\(\frac{\cos x}{\sin ^5 x}\) dx
Solution:

(vi) ∫\(\frac{{cosec}^2 x(\ln x)}{x}\) dx (In x = z)
Solution:
∫\(\frac{{cosec}^2 x(\ln x)}{x}\) dx
[Put ln x = z
Then \(\frac{d x}{x}\) = dz]
= ∫cosec² z dz
= -cot z + C = -cot (ln x) + C

(vii) ∫\(\sqrt{1-\sin x}\) cos x dx
Solution:

Question 3.
(i) ∫x\(\sqrt{x^2+3}\) dx (x² + 3 = v)
Solution:

(ii) ∫\(\frac{7 d x}{2-3 x}\) dx
Solution:

(iii) ∫\(\frac{x}{\sqrt{x^2-a^2}}\) dx
Solution:

(iv) ∫\(\frac{x^2+1}{\left(x^3+3 x+7\right)^3}\) dx
Solution:

(v) ∫(x⁴ – 3x² + 1)⁴ (2x³ – 3x) dx
Solution:

Question 4.
(i) ∫e^3x dx
Solution:
∫e^3x dx
[Put 3x = t
Then 3 dx = dt
or, dx = \(\frac{1}{3}\)dt]
= ∫e^t . \(\frac{1}{3}\)dt = \(\frac{1}{3}\)e^t + C
= \(\frac{1}{3}\)e^3x + C

(ii) ∫e^2x+7 dx
Solution:
∫e^2x+7 dx
[Put 2x + 7 = t
Then 2 dx = dt
or, dx = \(\frac{1}{2}\)dt]
= ∫e^t . \(\frac{1}{2}\)dt = \(\frac{1}{2}\)e^t + C
= \(\frac{1}{2}\)e^2x+7 + C

(iii) ∫e^x/3 dx
Solution:
[Put \(\frac{x}{3}\) = t
Then dx = 3 dt
= ∫e^t . 3dt = 3e^t + C = 3e^x/3 + C

(iv) ∫\(e^{x^3}\) x² dx
Solution:

(v) ∫a^2x dx
Solution:

(vi) ∫2\(a^{x^2}\) x dx
Solution:

(vii) ∫e^2tanx sec² x dx
Solution:

(viii) ∫\(\frac{e^x}{\left(e^x-2\right)^2}\) dx
Solution:

(ix) ∫\(e^{\cos ^2 x}\) sin 2x dx
Solution:
∫\(e^{\cos ^2 x}\) sin 2x dx
[Put cos2 x = t
Then 2cos x (-sin x)dx – dt
or, -sin 2x dx = dt
or, sin 2x dx = -dt]
= ∫e^t (-dt) = e^t + C = –\(e^{\cos ^2 x}\) + C

Question 5.
(i)∫\(\frac{\sin ^{-1} x}{\sqrt{1-x^2}}\) dx
Solution:

(ii)∫\(\frac{d x}{\sqrt{1-(x-1)^2}}\)
Solution:

(iii)∫\(\frac{\left(\sec ^{-1} x\right)^2 d x}{x \sqrt{x^2-1}}\)
Solution:

(iv)∫\(\frac{d x}{x\left[1+(\ln x)^2\right]}\)
Solution:

(v)∫\(\frac{d x}{x^2+2 x+2}\) (Integrate \(\frac{d x}{(x+1)^2+1}\))
Solution:

Question 6.
(i) ∫tan 3x dx
Solution:

(ii) ∫cos \(\frac{x}{3}\) dx
Solution:

(iii) ∫sec (2x + 1) dx
Solution:
∫sec (2x + 1) dx
[Put 2x + 1 = t
Then 2 dx = dt
or, dx = \(\frac{1}{2}\)dt]
= ∫sec t . \(\frac{1}{2}\)dt = \(\frac{1}{2}\) ∫sec t dt
= \(\frac{1}{2}\) ln |sec t + tan t| + C
= \(\frac{1}{2}\) ln |sec (2x + 1) + tan (2x + 1)| + C

(iv) ∫cosec 7x dx
Solution:
∫cosec 7x dx
[Put 7x = t
Then 7 dx = dt
or, dx = \(\frac{1}{7}\)dt]
= ∫cosec t . \(\frac{1}{7}\)dt
= \(\frac{1}{7}\) ln |cosec t + cot t| + C
= \(\frac{1}{7}\) ln |cosec 7x + cot x| + C

(v) ∫2x cot (x² + 3) dx    (x² + 3 = z)
Solution:
∫2x cot (x² + 3) dx
[Put x² + 3 = z
Then 2x dx = dz]
= ∫cot dz
= In |sin z| + C
= In |sin (x² + 3)| + C

(vi) ∫e^x tan e^x dx
Solution:
∫e^x tan e^x dx
[Put e^x = t
Then e^x dx = dt]
= ∫tan t dt
= In |sec t| + C
= In |sec e^x| + C

(vii) ∫(sec 2x – 3)² dx
Solution:
∫(sec 2x – 3)² dx
∫sec² 2x dx – 6∫sec 2x dx + 9∫dx
= \(\frac{1}{2}\) tan 2x – 3 ln |sec 2x + tan 2x| + 9x + C

Question 7.
(i) ∫\(\frac{e^x+e^{-x}}{e^x-e^{-x}}\) dx
Solution:
∫\(\frac{e^x+e^{-x}}{e^x-e^{-x}}\) dx
[Put (e^x – e^-x) = t
Then (e^x + e^-x)dx = dt]
= ∫\(\frac{d t}{t}\) = ln |t| + C = ln |(e^x – e^-x| + C

(ii) ∫3^x e^2x dx
Solution:

(iii) ∫\(\frac{(x+1) \ln \left(x^2+2 x+2\right)}{x^2+2 x+2}\) dx
Solution:

Question 8.
(i) ∫\(\frac{\sin x}{\sin (x+\alpha)}\) dx
Solution:

= ∫(cos α – sin α . cot t) dt
= cos α ∫dt – sin α ∫cot dt
= cos α . t – sin α . ln |sin t| + C
= (x + α) cos α – sin α  ln |sin (x + α)| + C
= x cos α – sin α ln |sin (x + α)| + C

(ii) ∫\(\frac{\sin x}{\cos (x-\alpha)}\) dx
Solution:

(iii) ∫\(\frac{\tan x+\tan \alpha}{\tan x-\tan \alpha}\) dx
Solution:

 

Odisha State Board BSE Odisha 10th Class Hindi Solutions Poem 4 चाँद का झंगोला Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Hindi Solutions Poem 4 चाँद का झंगोला

प्रश्न और अभ्यास (ପ୍ରଶ୍ନ ଔର୍ ଅଭ୍ୟାସ)

निम्नलिखित प्रश्नों के उत्तर दो-तीन वाक्यों में दीजिए:
(ନିମ୍ନଲିଖୂ ପ୍ରଶ୍ନ କେ ଉତ୍ତର୍ ଦୋ-ତୀନ ୱାର୍କୋ ମେଁ ଦୀଜିଏ : )
(ନିମ୍ନଲିଖୂତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦୁଇ-ତିନୋଟି ବାକ୍ୟରେ ଦିଅ : )

(क) एक दिन चाँद क्या हठ करने लगा?
(ଏକ ଦିନ୍ ଚୌଦ୍ କ୍ୟା ହଠ୍ କର୍‌ନେ ଲଗା ?)
उत्तर:
एक दिन चाँद अपनी माँ से हठ करने लगा कि माँ, मुझे ऊन का एक मोटा झिंगोला सिलवा दो। ठंड के कारण मुझे अपनी यात्रा पूरी करने में असुविधा होती है। मैं जाड़े से बचना चाहता हूँ।

(ख) बिना झिंगोले से चाँद को क्या कष्ट होता है?
(ବିନା ଝିଗୋଲେ ସେ ଚୌଦ୍ କୋ କ୍ୟା କଷ୍ଟ୍ ହୋତା ହୈ ?)
उत्तर:
बिना झिंगोले से चाँद को रात में सरदी से काँपना पड़ता है। ठिठुर ठिठुर कर उसे अपनी यात्रा पूरी करनी पड़ती है।

(ग) माँ जाड़े से नहीं, पर किससे डरती है?
(ମାଁ ଜାଡ଼େ ସେ ନର୍ଜୀ, ପର୍ କିସ୍‌ ଡର୍‌ତୀ ହୈ ?)
उत्तर:
माँ जाड़े से नहीं, लेकिन जादू-टोने से डरती है कारण बेटे की सुन्दरता पर मोहित होकर उसे कोई जादू-टोना न कर दे। इसलिए वह भगवान से अपने बेटे के कुशल क्षम चाहती है।

(घ) माँ चाँद के लिए झिंगोला क्यों नहीं बना पाती?
(ମାଁ ଚୌଦ୍ କେ ଲିଏ ଝିଗୋଲା କ୍ୟା ନହିଁ ବନା ପାତୀ ?)
उत्तर:
माँ चाँद के लिए झिंगोल नहीं बना पाती। क्योंकि वह चाँद को कभी भी एक ही नाप में देख नहीं पाती। क़भी चाँद एक ऊँगली चौड़ा हो जाता है तो कभी एक फूट मोटा। किसी दिन बड़ा हो जाता है तो किसी दिन छोटा।

2. अर्थ स्पष्ट कीजिए: (ଅର୍ଥି ଲକ୍ଷ କର)
(क) हठ कर बैठा चाँद एक दिन माता से वह बोला, सिलवा दो माँ, मुझे ऊन का मोटा एक झिंगोला।
(ହଠ୍ କର୍ ବୈଠା ଚୌଦ୍ ଏକ୍ ଦିନ୍ ମାତା ସେ ୱହ ବୋଲା, ସିଲୱା ଦୋ ମାଁ, ମୁଝେ ଊନ୍ କା ମୋଟା ଏକ୍ ଝିଗୋଲା)।
उत्तर:
हठ कर बैठा ………………………. एक झिंगोला॥
एक दिन चाँद अपनी माँ से ऊन का एक मोटा झिंगोला सिलवा देने की जिद करता है।

(ख) बच्चे की सुन बात कहा, माता ने, “अरे सलोने!
कुशल करे भगवान, लगे मत, तुझको जादू-टोने।
ବଢେ କୀ ସୁନ୍ ବାତ୍ କହା, ମାତା ନେ, ‘ଅରେ ସଲୋନେ!
କୁଶଳ କରେ ଭଗବାନ୍, ଲଗେ ମତ, ତୁଝେ ଜାଦୁ-ଟୋନେ।
उत्तर:
बच्चे की सुन ……………… तुझपर जादू-टोना
बच्चे की हठ भरी बातें सुनकर माँ कहती है कि मेरे प्यारे बेटे! भगवान करें तुझे किसी की नजर न लगे। कोई तुझपर जादू-टोना न कर पाए।

(ग) कभी एक उँगल भर चौड़ा, कभी एक फुट मोटा,
बड़ा किसी दिन हो जाता है, और किसी दिन छोटा।
କଭୀ ଏକ୍ ଉଁଗଲ୍ ଭର୍ ଚୌଡ଼ା, କଭୀ ଏକ୍ ଫୁଟ୍ ମୋଟା,
ବଡ଼ା କିସୀ ଦିନ୍ ହୋ ଜାତା ହୈ, ଔର୍ କିସୀ ଦିନ୍ ଛୋଟା।
उत्तर:
कभी एक उँगल किसी ……………. दिन छोटा।
माँ चाँद से कहती है कि कभी तुम एक उँगली चौड़ा हो जाते हो तो एक फुट मोटा हो जाते हो। किसी दिन बड़ा हो जाते हो तो किसी दिन छोटा हो जाते हो।

(घ) अब तू ही यह बता, नाप तेरी किस रोज लिवाए,
सीदें एक झिंगोला जो, हर रोज बदन में आए ?”
ଅବ୍ ତୁ ହୀ ଯହ ବତା, ନାପ ତେରୀ କିସ୍ ରୋଜ୍ ଲିୱାଏ,
ସୀ ହେଁ ଏକ୍ ଝିଗୋଲା ଜୋ, ହର୍ ରୋଜ୍ ବଦନ୍ ମେଁ ଆଏ ?”
उत्तर:
बचे की सुन ………………… तुझको जादू-टोने
माँ चाँद से कहती है कि तू ही मुझे बता दे मैं तुम्हारे लिए किस नाप से एक झिंगोला सिलवा दूँ ताकि हर रोज तुम उसे पहन सको।

3. निम्नलिखित प्रश्नों के उत्तर एक-एक वाक्य में दीजिए:
(ନିମ୍ନଲିଖତ୍ ପ୍ରକ୍ଷ୍ନୌ କେ ଉତ୍ତର ଏକ୍-ଏକ୍ ୱାକ୍ୟ ମେଁ ଦୀଜିଏ : )
(ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଗୋଟିଏ-ଗୋଟିଏ ବାକ୍ୟରେ ଦିଅ : )

(क) एक दिन चाँद ने माँ से क्या कहा?
(ଏକ୍ ଦିନ୍ ର୍ତାଦ୍ ନେ ମାଁ ସେ କ୍ୟା କହା ?)
उत्तर:
एक दनि चाँद ने माँ से कहा कि उसके लिए ऊन का एक मोटा सा झिंगोला सिला दे।

(ख) रात भर किस तरह की हवा चलती है।
(ରାଡ୍ ଭର୍ କିସ୍ ତରହ କୀ ହ ଚଲ୍‌ ହୈ ।)
उत्तर:
रात भर सन-सन हवा चलती है।

(ग) जोड़े में वह किस तरह मरता है?
(ଜୋଡ଼େ ମେଁ ୱହ କିସ୍ ତରହ ମର୍‌ତା ହୈ ?)
उत्तर:
जाड़े में वह सरदी से मरता है।

(घ) चाँद किस तरह यात्रा पूरी करता है?
(ଚୌଦ୍ କିସ୍ ତରହ ୟାତ୍ରା ପୂରୀ କର୍‌ତା ହୈ ?)
उत्तर:
चाँद ठिठुर-ठिठुरकर यात्रा पूरी करता है।

(ङ) यदि झिंगोला न मिले तो फिर चाँद क्या लेना चाहता है?
(ୟଦି ଝୋଗୋଲା ନ ମିଲେ ତୋ ଫିର୍ ଚୌଦ୍ କ୍ୟା ଲେନା ଚାହତା ହୈ ?)
उत्तर:
यदि झिंगोला न मिले तो फिर चाँद भाड़े में एक कुरता लेना चाहता है।

(च) चाँद कभी कभी माँ को कितना चौड़ा दिखाई देता है?
(ଚୌଦ୍ କଭୀ କଭୀ ମାଁ କୋ କିନା ଚୌଡ଼ା ଦିଖାଈ ଦେତା ହୈ ?)
उत्तर:
चाँद कभी कभी माँ को एक उँगल चौड़ा दिखाई देता है।

(छ) चाँद कितना मोटा दिखाई देता है?
(ର୍ବାଦ୍ କିନା ମୋଟା ଦିଖାଈ ଦେତା ହୈ ?)
उत्तर:
चाँद एक फूट मोटा दिखाई देता है।

(ज) ऐसा कौन सा दिन होता है जब चाँद बिलकुल नहीं दिखाई देता?
(ଐସା କୌନ୍ ସା ଦିନ୍ ହୋତା ହୈ ଜବ୍ ର୍ବାଦ୍ ବିଲକୁଲ୍ ନହୀ ଦିଖାଈ ଦେତା ?)
उत्तर:
अमावास्या की तिथि में चाँद बिलकुल नहीं दिखाई देता।

(झ) चाँद का झिंगोले के लिए नाप लेना क्यों संभव नहीं है?
(ଚୌଦ୍ କା ଲିଂଗୋଲେ କେ ଲିଏ ନାପ୍ ଲେନା କ୍ୟା ସଂଭ ନହିଁ ହୈ ?)
उत्तर:
चाँद कभी भी एक ही आकार में नहीं होता है। इसलिए चाँद के झिंगोले के लिए नाप लेना संभव नहीं।

भाषा-ज्ञान (ଭାଷା-ଜ୍ଞାନ)

1. निम्नलिखित शब्दों के विपरीत/ विलोम शब्द लिखिए।
(ନିମ୍ନଲିଖ୍ ଶକେଁ କେ ବିପରୀତ/ବିଲୋମ୍ ଶବ୍ଦ ଲିଖିଏ ।)
(ନିମ୍ନଲିଖତ ଶବ୍ଦଗୁଡ଼ିକର ବିପରୀତ ବିଲୋମ ଶବ୍ଦ ଲେଖ ।)
कुशल, जाड़ा, ठीक, मोटा, घटता
उत्तर:
कुशल- अकुशल, जाड़ा- गरमी, ठीक-भूल, मोटा-पतला, घटता-बढ़ता

2. निम्नलिखित शब्दों के वचन बदलिए:
(ନିମ୍ନଲିଖ୍ ଶକେଁ କେ ବଚ୍ଚନ ବଦଲିଏ)
(ନିମ୍ନଲିଖତ ଶବ୍ଦଗୁଡ଼ିକର ବଚନ ପରିବର୍ତ୍ତନ କର : )
हवा, वह, माता, बच्चा, भाड़ा, बड़ा, बात, दिन, ह।
उत्तर:
हवा – हवाएँ
माता – माताएँ
वह – वे
बच्चा – बच्चे
भाड़ा – भाड़े
बड़ा – बड़े
बात – बातें
दिन – दिन
यह – ये

Very Short & Objective Type Questions With Answers

A. निम्नलिखित प्रश्नों के उत्तर एक वाक्य में दीजिए।

1. ‘चाँद का झिंगोला’ कविता के कवि कौन है?
उत्तर:
चाँद का झिंगोला’ कविता के कवि रामधारी सिंह ‘दिनकर’ है।

2. माँ किस बात से डरती है?
उत्तर:
माँ इस बात से डरती है कि चाँद कभी भी एक नाप में नहीं दिखाई देता है।

3. किसी दिन चाँद ऐसा विचित्र सा क्या करता है?
उत्तर:
किसी दिन चाँद किसी को भी आँखों से दिखाई ही नहीं पड़ता है।

B. निम्नलिखित प्रश्नों के उत्तर एक शब्द/एक पद में दीजिए।

1. चाँद कभी-कभी कितना मोटा हो जाता है?
उत्तर:
एक फुट

2. चाँद माँ से क्या माँगता है?
उत्तर:
ऊन का झिंगोला

3. चाँद अपने लिए झिंगोला कब चाहता है?
उत्तर:
जाडे के मौसम में

4. चाँद किससे बचने के लिए माँ से झिंगोला सिलवा देने के लिए कहता है?
उत्तर:
जोड़े से

5. चाँद कभी-कभी कितना चौड़ा हो जाता है?
उत्तर:
एक उँगली भर

6. कौन एक नाप में कभी नहीं रहता है?
उत्तर:
चांद

7. ‘चाँद का झिंगोला’ कविता के कवि कौन है?
उत्तर:
रामधारी सिंह ‘दिनकर’

8. चाँद किस तरह यात्रा पूरी करता है?
उत्तर:
ठिठुर-ठिठुर कर

9. एक दिन चाँद ने माँ से क्या कहा?
उत्तर:
झिंगोला सिलवाने के लिए

10. चाँद अपने लिए कैसा झिंगोला चाहता है?
उत्तर:
ऊन का

C. रिक्त स्थानों की पूर्ति कीजिए।

1. ………………….. के दिन चाँद बिलकुल नहीं दिखाई देता।
उत्तर:
अमावया

2. चाँद ………………….. भाड़े पर लाने को माँ से कहता है।
उत्तर:
कुरता

3. घटते घटते चाँद एकदिन ऐसा हो जाता है कि वह ……………………।
उत्तर:
दिखाई नहीं देता

4. चाँद …………………… सफर करता है।
उत्तर:
आसमान का

5. …………………….. रोज घटता-बढ़ता है।
उत्तर:
चाँद

6. रात भर ………………… तरह की हवा चल रही थी।
उत्तर:
सन – सन

7. ‘अरे सलोने ?’ – इस शब्द …………………… प्रयोग हुआ है।
उत्तर:
चाँद के लिए

8. जाड़े में चांद …………………. से मरता है।
उत्तर:
सरदी

9. ‘सफर’ का अर्थ है…………………।
उत्तर:
यात्रा

10. चाँद आसमान का सफर ………………………… मौसम में कर रहा था।
उत्तर:
जाड़े

D. ठिक् या भूल लिखिए।

1. जोड़े में चाँद सरदी से मरता है?
उत्तर:
ठिक्

2. चाँद को नजर लग जाने का डर माँ को है।
उत्तर:
भूल

3. सलोने शब्द का अर्थ असुन्दर है।
उत्तर:
भूल

4. चाँद अपनी माता से ऊन का एक झिंगोला माँग रहा था।
उत्तर:
ठिक्

5. चाँद के लिए माँ झिंगला इसलिए बना नहीं पा रही थी, क्योंकि – वह हमेशा एक नाप का नहीं रहता।
उत्तर:
ठिक्

6. चाँद झिंगोले के बदले में एक पतलून माँगा।
उत्तर:
भूल

7. चाँद आसमान का सफर जाढ़े मौसम में कर रहा था।
उत्तर:
ठिक्

8. चाँद दूध-सा गोरा दिखाई देता है।
उत्तर:
ठिक्

9. चाँद गर्मी से परेशान होकर यात्रा पूरी करता है।
उत्तर:
भूल

Multiple Choice Questions (mcqs) with Answers

सही उत्तर चुनिए : (MCQs)

1. चाँद कभी – कभी कितना मोटा हो जाता है?
(A) एक हाथ
(B) एक गज
(C) एक अंगुल
(D) एक फुट
उत्तर:
(D) एक फुट

2. चाँद माँ से क्या माँगता है?
(A) रुई का झिंगोला
(B) एक फुट का झिंगोला
(C) ऊन का झिंगोला
(D) उंगली भर चौडा झिंगोला
उत्तर:
(C) ऊन का झिंगोला

3. चाँद अपने लिए झिंगोला कब चाहता है?
(A) जाडे के मौसम में चाँद किससे बचने के लिए माँ से हिंगोला सिलवा देने के लिए कहता है?
(B) गर्मी के दिनों में
(C) बरसात में
(D) ऊन मिलने के समय में
उत्तर:
(A) जाडे के मौसम में चाँद किससे बचने के लिए माँ से हिंगोला सिलवा देने के लिए कहता है?

4. चाँद किससे बचने के लिए माँ से हिंगोला सिलवा देने के लिए कहता है?
(A) हवा से
(B) जोड़े से
(C) आसमान से
(D) भगवान से
उत्तर:
(B) जोड़े से

5. चाँद कभी-कभी कितना चौड़ा हो जाता है?
(A) एक फुट भर
(B) एक उँगली भर
(C) एक हाथ भर
(D) एक इंच भर
उत्तर:
(B) एक उँगली भर

6. जोड़े में चाँद किस तरह मरता है?
(A) गरम
(B) शरर्मी
(C) सरदी
(D) जखमी
उत्तर:
(C) सरदी

7. चाँद कितना मोटा दिखाई देता है?
(A) एक फूट
(B) दो फूट
(C) तिन फूट
(D) चार फूट
उत्तर:
(A) एक फूट

8. माँ किस बात से डरती है?
(A) कड़वी वात से
(B) एक नाप में नहीं दिखाई देने से
(C) अमावास्या में गायब होने से
(D) एक नाम में रहने से
(B) एक नाप में नहीं दिखाई देने से

9. चाँद किस तरह यात्रा पूरी करता है?
(A) ठिठुर-ठिठुर
(B) हौले-हौले
(C) जल्दी-जल्दी
(D) सावधानी से
उत्तर:
(A) ठिठुर-ठिठुर

10. कौन – सा दिन चाँद बिलकुल नहीं दिखाई देता?
(A) पूर्णिमा
(B) संक्रान्ति
(C) अमावास्या
(D) इनमें से कोई नहीं
उत्तर:
(C) अमावास्या

11. चाँद कभी-कभी माँ को कितना चौड़ा दिखाई देता है?
(A) चार अंगुली
(B) दो अंगुली
(C) तीन अंगुली
(D) एक अंगुली
उत्तर:
(D) एक अंगुली

12. सलोने शब्द का अर्थ पहचानिए
(A) कुच्छित
(B) सुन्दर
(C) असुन्दर
(D) आसमा
उत्तर:
(B) सुन्दर

13. ऐसी कौन-सी तिथि है, जिस तिथि में चाँद गायब हो जाता, वह तिथि है
(A) पूर्णिमा
(B) एकदशी
(C) अमावास
(D) इनमें से कोई नहीं
उत्तर:
(A) पूर्णिमा

14. चाँद क्या भाड़े पर लाने को माँ से कहता है?
(A) झिंगोला
(B) कोट
(C) ऊनी चादर
(D) कुरता
उत्तर:
(D) कुरता

15. चाँद को क्या लग जाने का डर माँ को है?
(A) जादू-टोने
(B) ठंड़
(C) लू
(D) नजर
उत्तर:
(A) जादू-टोने

16. चाँद अपने लिए झिंगोला चाहता है जो
(A) सूती का हो
(B) ऊन का हो
(C) पशम का हो
(D) चमड़े का हो
उत्तर:
(B) ऊन का हो

17. चाँद झिंगोला चाहता है क्योंकि मौसम था
(A) बारिश का
(B) गर्मी का
(C) जाड़े का
(D) वसन्त का
उत्तर:
(C) जाड़े का

18. घटते घटते चाँद एकदिन ऐसा हो जाता है कि वह
(A) पतला हो जाता है
(B) दुःखी हो जाता है
(C) दिखाई नहीं देता
(D) ठिठूरता रहता है
उत्तर:
(C) दिखाई नहीं देता

यह कविता
बच्चे दिन-व-दिन बढ़ते हैं। इसलिए उनकी पोशाक बड़ी साइज की बना ली जाती है। लेकिन चाँद घटता घटता अमावस के दिन दिखाई नहीं देता। वह चाहता है कि उसके लिए एक झिंगोला या कुर्ती सिलवा दिया जाय। माँ पूछती है, बेटा, किस नाप का बनाया जाय? जिसे तू रोज-रोज पहन सके? इसमें एक मज़ाक और व्यंग्य है। सदा अस्थिर के लिए कुछ नहीं किया जा सकता।
ଓଡ଼ିଆ ଅନୁବାଦ:
ପିଲାମାନେ ଦିନକୁ ଦିନ ବଢ଼ିଚାଲନ୍ତି। ତେଣୁକରି ତାଙ୍କ ପୋଷାକ ବଡ଼ ସାଇଜର ତିଆରି କରା ହୋଇଥାଏ। କିନ୍ତୁ ଜହ୍ନ କମି କମି ଅମାବାସ୍ୟା ଦିନ ଦେଖାଯାଏ ନାହିଁ। ତା’ର ଇଚ୍ଛା ତା’ପାଇଁ ମଧ୍ୟ ଗୋଟିଏ ଜାମା ସିଲାଇ କରାଯାଉ। ମା’ ପଚାରିଛନ୍ତି ପୁଅ, କେଉଁ ସାଇଜର ଜାମା ତିଆରି କରାହେବ? ଯାହାକୁ ତୁ ପ୍ରତିଦିନ ପିନ୍ଧି ପାରିବୁ। ଏହି କବିତାରେ କିଛି ଥଟ୍ଟା ଓ ପରିହାସ ମଧ୍ୟ ଅଛି। ସବୁବେଳେ ଅସ୍ଥିର ପାଇଁ କିଛି କରାଯାଇ ପାରିବ ନାହିଁ।

(i) हठ कर बैठा चाँद एक दिन, माता से वह बोला,
“सिलबा दो माँ, मुझे ऊन का मोटा एक झिंगोला।
सन-सन चलती हवा रात भर, जाड़े से मरता हूँ,
ठिठुर-ठिठुर कर किसी तरह, यात्रा पूरी करता हूँ।
आसमान का सफर और यह, मौसम है जाड़े का”
न हो अगर तो लादो कुरता ही कोई भाड़े का।
” बच्चे की सुन बात कहा माता ने, “अरे सलोने।

ହଠ୍ କର ବୈଠା ର୍ବାଦ ଏକ ଦିନ୍, ମାତା ସେ ୱହ ବୋଲା,
‘‘ସିଲବା ଦୋ ଗାଁ, ମୁଝେ ଊନ୍ କା, ମୋଟା ଏକ୍ ଝିଲା।
ସନ୍-ସନ୍ ଚଲ୍‌ ହଓ୍ବା ରାଡ୍ ଭର୍, ଜାଡ଼େ ସେ ମର୍‌ତା
ଠିଠୁର୍-ଠିଠୁର୍ କର୍ କିସୀ ତରହ, ଯାତ୍ରା ପୂରୀ କର୍‌ତା ହୁଁ।
ଆସମାନ୍ କା ସଫର୍ ଔର୍ ୟହ, ମୌସମ୍ ହୈ ଜାଡ଼େ କା’’
ନ ହୋ ଅଗର୍ ତୋ ଲା ଦୋ କୁର୍‌ତା ହୀ କୋଈ ଭାଡ଼େ କା।’
ବଢେ କୀ ସୁନ ବାତ କହା ମାତା ନେ, ‘ଅରେ ସଲୋନେ।

हिन्दी व्याख्या:
इन पक्तियों में कवि ने वर्णना किया है कि एक दिन चाँद अपनी माँ से हठ करता है कि ऊन का एक मोटा सा झिंगोला सिला दो। क्योंकि जब रात में सन-सन करके जोरो हवा चलती है, तो मैं जाड़े से काँपता रहता हूँ। सरदी से ठिठुरता हुआ किसी प्रकार मैं अपनी यात्रा को पूरी करता हूँ। एक तो आसमान में सफर करना पड़ता है उस पर यह जाड़े का मौसम है। अगर तुम मेरे लिए एक झिंगोलों नहीं ला सकती तो किराए पर मेरे लिए एक कुरता ही लाकर दे दो ताकि किसी तरह मैं जाड़े से अपनी रक्षा सँ।
ଓଡ଼ିଆ ଅନୁବାଦ :
କବି କହୁଛନ୍ତି ଦିନେ ଜହ୍ନ ତା’ ମା’ ପାଖରେ ଜିଦ୍ କରୁଅଛି କି ତା’ ପାଇଁ ପଶମ (ଉଲ୍)ର ଗୋଟିଏ ମୋଟା ପୋଷାକ ତିଆରି କରିବା ପାଇଁ। ଶୀତଦିନ ରାତିରେ ଯେତେବେଳେ ଥଣ୍ଡା ପବନ ଜୋର୍‌ରେ ବହିବାକୁ ଲାଗୁଛି ମୁଁ ଶୀତରେ ଥରିବାକୁ ଲାଗୁଛି । ଶୀତରେ ଥରି ଥରି ମୁଁ କୌଣସି ପ୍ରକାର ମୋ’ ଯାତ୍ରା ଶେଷ କରୁଛି। ଆକାଶରେ ଯାତ୍ରା କରିବାକୁ ପଡ଼ୁଛି ପୁଣି ଶୀତ ରାତିରେ। ତେଣୁ ତୁ ମୋ ପାଇଁ ଗୋଟିଏ ପୋଷାକ ତିଆରି କରିଦେ। ଯଦି ତିଆରି ନ କରିପାରୁଛୁ ତାହାହେଲେ ଭଡ଼ାରେ ହେଉ ପଛକେ ମୋ’ ପାଇଁ ଗୋଟିଏ ପୋଷାକ ଆଣି ଦେ ମୁଁ ଯେପରି ଶୀତରୁ ରକ୍ଷା ପାଇ ପାରିବି।

(ii) कुशल करे भगवान, लगें मत, तुझको जादु-टोने।
जाड़े कि तो बात ठीक है, पर मैं तो डरती हूँ।
एक नाप में कभी नहीं, तुझको देखा करती हूँ।
कभी एक ऊँगली भर चौड़ा, कभी एक फुट मोटा,
बड़ा किसी दिन हो जाता है किसी दिन छोटा।

କୁଶଲ୍ କରେ ଭଗୱାନ୍, ଲଗେ ମତ୍, ତୁଝେ ଜାଦୁ-ଟୋନେ
ଜାଡ଼େ କି ତୋ ବାତ୍ ଠିକ୍ ହୈ, ପର ମେଁ ତୋ ଡତୀ ହୁଁ,
ଏକ୍ସ୍ ନାପ୍ ମେଁ କଭୀ ନହୀଁ, ତୁ ଦେଖା କର୍‌ତୀ ହୁଁ।
କଭୀ ଏକ ଉଁଗଲୀ ଭର୍ ଚୌଡ଼ା, କଭୀ ଏକ ଫୁଟ୍ ମୋଟା,
ବଡ଼ା କିସୀ ଦିନ୍ ହୋ ଜାତା ହୈ, ଔର କିସୀ ଦିନ୍ ଛୋଟା।

हिन्दी व्याख्या:
बच्चे की बात सुन कर माता कहती है कि बेटे। भगवान करे तुझको किसी की नजर न लगे, कोई तुझपर जादू-टोना न कर पाए। जाड़े की तो बात ठीक है लेकिन मुझे एक ही बात खटकती है। क्योंकि मैं तुझे एक नाप (साइज) में कभी भी नहीं देख पाती हूँ। कभी तुम एक उँगली चौड़ा हो जाते हो तो कभी एक फुट मोटा हो जाते हो। किसी दिन बड़े हो जाते हो तो किसी दिन छोटे।
ଓଡ଼ିଆ ଅନୁବାଦ:
ପିଲାଟିର କଥା ଶୁଣି ମାଆ କହୁଛି ଅରେ ପୁଅ ! ଭଗବାନ୍ କରନ୍ତୁ ଯେପରି କାହାରି ଦୃଷ୍ଟି ତୋ’ ଉପରେ ନ ପଡୁ। ତୋତେ ଯେପରି କେହି ଗୁଣି ଗାରେଡ଼ି ନ କରନ୍ତୁ। ଶୀତ ଦିନ କଥା ତ ଠିକ୍। କିନ୍ତୁ ମୋର ଗୋଟିଏ ଚିନ୍ତା। ମୁଁ ତୋତେ କେବେହେଲେ ଗୋଟିଏ ଆକାର (ସାଇଜ୍)ରେ ଦେଖୁନାହିଁ। କେତେବେଳେ ତୁ ଆଙ୍ଗୁଳିଏ ଚଉଡ଼ା ହେଇଯାଉଛୁ ତ କେତେବେଳେ ଫୁଟେ ମୋଟା ହୋଇଯାଉଛୁ। କେଉଁ ଦିନ ବଡ଼ ହୋଇଯାଉଛୁ ତ କେଉଁ ଦିନ

(iii) घटा-बढ़ता रोज, किसी दिन, ऐसा भी करता है,
नहीं किसीकी आँखो का, तु दिखलाई पड़ता है।
अब तू ही यह बता, नाप तेरी किस रोज लिवाएँ,
सी दें एक झिंगोला जो, हर रोज बदन में आए?”

ଘଟତା-ବଢ଼ତା ରୋଜ୍, କିସୀ ଦିନ୍, ଐସା ଭୀ କରତା ହୈ,
ନଦୀ କିସୀକୀ ଆର୍ଡୋ କା, ତୁ ଦିଖଲାଈ ପଡ଼ତା ହୈ ।
ଅବ୍ ତୂ ହୀ ୟହ ବତା, ନାପ୍ ତେରୀ କିସ୍ ରୋଜ ଲିଓ୍ବାଏଁ,
ସୀ ହେଁ ଏକ ଲିଂଗୋଲା ଜୋ, ହର୍ ରୋଜ୍ ବଦନ୍ ମେଁ ଆଏ ??’

हिन्दी व्याख्या:
तुम्हारा रोज का घटना बढ़ना और किसी दिन ओझल हो पाना ये बातें मेरी समझ में कुछ नहीं आता। अब तू ही मुझे बता दे कि मैं तुम्हारा कौन सा नाप लेकर तेरे लिए एक झिंगोला सिला दूँ ताकि हर रोज तू उसे पहन सेक।
ଓଡ଼ିଆ ଅନୁବାଦ:
ତୋର ପ୍ରତିଦିନ ବଢ଼ିବା କମିବା ଓ କେଉଁ ଦିନ ଅଦୃଶ୍ୟ ହୋଇଯିବା କଥା ମୁଁ କିଛି ବୁଝିପାରୁ ନାହିଁ। ତୁ ମୋତେ କହ, ମୁଁ ତୋ’ ପାଇଁ କେଉଁ ସାଇଜର ଜାମା ତିଆରି କରିବି ଯାହାକୁ ତୁ ପ୍ରତିଦିନ ପିନ୍ଧି ପାରିବୁ।

शबनार: (ଶରାର୍ଥି)

झिंगोला – छोटे बच्चे का कमीज या कुरता (ଛୋଟପିଲାଙ୍କ ଜାମା)।
हठ – जिद (ଜିଦ୍)।
ऊन – भेड़ बकरी के रोएँ (ପଶମ)।
नाप – माप ପଶମ)।
आसमान – आकाश (ମାପ)।
मौसम – ऋतु (ଋତୁ)।
सलोने – सुंदर (ସୁନ୍ଦର)।
घटना – कम होना (କମିବା)।
बदन – शरीर (ଶରୀର)।
उँगल – उँगली (ଆଙ୍ଗୁଳିଏ)।
सिलवा दो – बना दो जाड़ा (ଶୀତ)।
ठिठुर-ठिठुर कर – काँप कर (ଥରିଥରି)।
सफर – यात्रा (ଯାତ୍ରା)।
भाड़ा – किराया (ଭଡ଼ା)।
जादू-टोना – (ଗୁଣିଗାରେଡ଼ି)।
रोज – प्रतिदिन (ପ୍ରତିଦିନ)।
कुशल – मंगल (ମଙ୍ଗଳ)।
लिवाएँ – लेना (ନେବା)।

कवि परिचय

रामधारी सिंह ‘दिनकर’ जी का जन्म 30 सितम्बर, सन् 1908 को सिमरिया घाट, मुंगेर ( बिहार ) हुआ। छात्रावस्था में ही ‘दिनकर’ का ओजस्वी कवि-रूप सामने आ गया। ‘दिनकर’ राष्ट्रीय भावधारा के प्रमुख कवि रहे। उन्हें शौर्य और वीरता का कवि माना जाता है।

‘दिनकर’ जी की बहुमुखी प्रतिभा का विस्तार गद्य और पद्य दोनों में हुआ है। उनके काव्य ग्रंथों प्रमुख हैं- रेणुका, हँकार, रसवंती, कुरुक्षेत्र, रश्मिरथी, उर्वशी, हारे को हरिनाम, बापू, दिल्ली इत्यादि। गद्य ग्रंथों में प्रमुख हैं- देश – विदेश, मेरी यात्राएँ, अर्द्ध-नारीश्वर, मिट्टी की ओर, रेती के फूल, संस्कृति के चार अध्याय इत्याद। ‘दिनकर’ जी राज्य सभा के सम्मानित सदस्य रहे। भारत सरकार ने उनको ‘पद्मभूषण’ की उपाधि से अलंकृत किया। उन्हें ‘उर्वशी’ महाकाव्य के लिए ज्ञानपीठ पुरस्कार दिया गया।

Odisha State Board BSE Odisha 10th Class Hindi Solutions Poem 3 एक तिनकाTextbook Exercise Questions and Answers.

BSE Odisha Class 10 Hindi Solutions Poem 3 एक तिनका

प्रश्न और अभ्यास (ପ୍ରଶ୍ନ ଔର୍ ଅଭ୍ୟାସ)

1. निम्नलिखित प्रश्नों के उत्तर दो/तीन वाक्यों में दीजिए:
(ନିମ୍ନଲିଖୂ ପ୍ରଶ୍ନୋ କେ ଉତ୍ତର୍ ଦୋ-ତୀନ ୱାର୍କୋ ମେଁ ଦୀଜିଏ : )
(ନିମ୍ନଲିଖ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦୁଇ/ତିନି ବାକ୍ୟରେ ଦିଅ : )

(क) एक दिन कवि को क्या हो गया?
(ଏକ ଦିନ୍ କଵି କୋ କ୍ୟା ହୋ ଗୟା ?)
उ:
एक दिन कवि अपने घमण्ड में भरकर एकदम ऐंठे हुए से तनकर छत के मुंडेरे पर खड़े थे। ऐसे में कहीं दूर से एक छोटा-सा तिनका आकर उनकी आँख में गिर गया।

(ख) आँख में तिनका पड़ने पर घमंड़ी की क्या दशा हुई?
(ଆଁଖ୍ ମେଁ ତିନ୍‌କା ପଡ଼େନେ ପର୍ ଘମଣ୍ଡୀ କୀ କ୍ୟା ଦଶା ହୁଈ ?)
उ:
आँख में तिनका पड़ने पर कवि झुंझलाकर परेशान हो उठे। आँख जल रही थी और सूजन के कारण लाल भी हो गई थी। फलस्वरूप आँख जोर से दुखने लगी थी।

(ग) आँख में तिनका पड़ने पर लोग क्या करने लगे?
(ଆଁଖ୍ ମେଁ ତିନ୍‌କା ପଡ଼ନେ ପର୍ ଲୋଗ୍ କ୍ୟା କର୍‌ନେ ଲଗେ ?)
उ:
आँख में तिनका पड़ने पर लोग कपड़े की मूँठ देकर कवि की आँख को सेकने लगे कि शायद थोड़ा आराम मिल जाए पर नहीं। दर्द किसी तरह कम होने का नाम नहीं ले रहा था।

(घ) किसी तरह आँख से तिनका निकल गया तो कवि को क्या अनुभव हुआ?
(କିସୀ ତରହ ଆଁଖ୍ ସେ ତିନ୍‌ ନିକଲ୍ ଗୟା ତୋ କଵି କୋ କ୍ୟା ଅନୁଭବ ହୁଆ ?)
उ:
किसी तरह आँख से तिनका निकल गया तो कवि को अनुभव हुआ कि जैसे उनका विवेक उन्हों ताना मार रहा था। और साथ ही साथ कह रहा था – इतना अकड़ किसलिए। एक छोटा सा तिनका तुम्हारे अहंकार को तोड़ने में काफी है।

(ङ) एक तिनका कविता का मूल भाव क्या है?
(कछेका छा की। नृम बठ्ठ Q4 6@ ?)
उ:
‘एक तिनका’ कविता का मूल भाव है- कभी भी अपने को बड़ा मत समझो। ज्यादा घमण्ड करना ठीक नहीं हैं। एक छोटा-सा तिनका किसीका भी घमण्ड तोड़ सकता है। छोटी-छोटी चीजें भी हमारे जीवन को एकदम बदल सकती है।

2. अर्थ स्पष्ट कीजिए: थर्थ ଅର୍ଥ ସ୍ପଷ୍ଟ କୀଜିଏ : (ଅର୍ଥ ସ୍ପଷ୍ଟ କର : )
(क) घमंडों में भरा ऐंठा हुआ,
एक दिन जब था मुंडेरे पर खड़ा।
ଘର୍ମଣ୍ଡୋ ମେଁ ଭରା ଏଁଠା ହୁଆ,
ଏକ୍ ଦିନ୍ ଜବ୍ ଥା ମୁଣ୍ଡରେ ପର୍ ଖଡ଼ା।
उ:
घमंडो में …………………… पर खड़ा।
इस पंक्ति में कवि कह रहे हैं कि एक दिन वे घमण्ड से भरे एकदम ऐंठे हुए से तनकर छत के मुँडेरे पर खड़े थे।

(ख) मैं झिझक उठा, हुआ बेचैन – सा।
लाल होकर आँख भी दुखने लगी।
ମେଁ ଝିଝକ୍ ଉଠା, ହୁଆ ବେସୈନ୍-ସା।
ଲାଲ୍ ହୋକର୍ ଆଁଖ୍ ଭୀ ଦୁଗ୍‌ ଲଗୀ।
उ:
मैं झिझक …………………. दुखने लगी।
कवि कहते हैं कि अचानक कहीं दूर से एक तिनका उड़ता हुआ आया और उनकी आँख में आ गिरा। इससे कवि झुंझलाकर परेशान हो उहे। उनकी अँख जल रही थी और लाल होकर दुखने भी लगी।

(ग) ऐंठता तू किस लिए इतना रहा,
एक तिनका है बहुत तेरे लिए।
ଐଠତା ତୂ କିସ୍ ଲିଏ ଇତ୍‌ନା ରହା,
ଏକ୍ ତିନ୍‌ ହୈ ବହୁତ୍ ତେରେ ଲିଏ।
उ:
ऐंठता तू ………………….तेरे लिए।
इस अप्रत्याशित घटना से कबि ने जब छुटकारा पाया तो उनका विवेक जैसे उन्हे ताना मारता था। उन्होंने अनुभव किया जैसे उनका विवेक उनसे कह रहा था – इतना अकड़ क्यों दिखाता है। एक छोटा- सा तिनका तुम्हारे अहंकार को तोड़ने के लिए काफी है।

3. निम्नलिखित प्रश्नों के उत्तर एक-एक वाक्यों में दीजिए:
(ନିମ୍ନଲିଖୂ ପ୍ରଶ୍ନୋ କେ ଉତ୍ତର୍‌ ଏକ୍-ଏକ୍ ୱାଜ୍ୟୋ ମେଁ ଦୀଜିଏ : )
(ନିମ୍ନଲିଖ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଗୋଟିଏ-ଗୋଟିଏ ବାକ୍ୟରେ ଦିଅ : )

(क) ‘एक तिनका’ कविता के कवि का नाम क्या है?
(ଏକ ତିନ୍‌ କମ୍ପିତା କେ କବି କା ନାମ୍ କ୍ୟା ହୈ ?)
‘एक तिनका’ कविता के कवि का मान अयोध्यासिंह उपाध्याय ‘हरिऔध’ है।

(ख) एक दिन कवि कहाँ खड़े थे?
(ଏକ୍ ଦିନ୍ କମ୍ପି କହାଁ ଖଡ଼େ ଥେ ?)
उ:
एक दिन कवि घमण्ड से भरे एकदम ऐंठे हुए से तनकर छत के मुँडेरे पर खड़े थे।

(ग) अचानक क्या हुआ?
(ଅଚାନକ୍ କ୍ୟା ହୁଆ ?)
उ:
अचानक कहीं दूर से एक तिनका उड़ता हुआ आया और कवि की आखों में गिरा।

(घ) कौन दबें पाँव भागी?
(କୌନ୍ ଦର୍ବେ ପାଁୱ ଭାଗୀ ?)
उ:
घमण्ड दबे पाँव भागी।

(ङ) घमंडी के घमण्ड को दूर करने के लिए क्या बहुत है?
(ଘମଣ୍ଡୀ କେ ଘମଣ୍ଟ୍ କୋ ଦୂର୍ କର୍‌ନେ କେ ଲିଏ କ୍ୟା ବହୁତ୍ ହୈ ?)
उ:
घमण्डी के घमण्ड को दूर करने के लिए एक तिनका बहुत है।

भाषा-ज्ञान (ଭାଷା-ଜ୍ଞାନ)

1. नीचे दी गई कविता की पंक्तियों को सामान्य वाक्य में बदलिए:
(ନୀଚେ ଦୀ ଗଈ କମ୍ପିତା କୀ ପଂକ୍ତିର୍ଲୋ କୋ ସାମାନ୍ୟ ୱାକ୍ୟ ମେଁ ବଦଲିଏ।)
(ନିମ୍ନରେ ପ୍ରଦତ୍ତ କବିତାର ପଦଗୁଡ଼ିକୁ ସାମାନ୍ୟ ବାକ୍ୟରେ ପରିବର୍ତ୍ତନ କର।)

जैसे- एक तिनका आँख में मेरी पड़ा – मेरी आँख में एक तिनका पड़ा।
मूँठ देने लोग कपड़े की लगे – लोग कपड़े की मूँठ देने लगे।

(क) एक दिन जब था मुँडेरे पर खड़ा ………………..
(ख) लाल होकर आँख भी दुखने लगी …………………
(ग) ऐंठ बेचारी दबे पाँवों भागी …………………..
(घ) जब किसी ढब से निकल तिनका गया …………………
(ङ) एक तिनका है बहुत तेरे लिए …………………
उत्तर:
(क) एक दिन जब था मुँडेरे पर खड़ा – एक दिन जब मुँडेरे पर खड़ा था।
(ख) लाल होकर आँख भी दुखने लगी – आँख भी लाल होकर दुखने लगी।
(ग) ऐंठ बेचारी दबे पाँवों भागी – बेचारी ऐंठ दबे पावों भागी।
(घ) जब किसी ढब से निकल तिनका गया – जब तिनका किसी ढब से निकल गया।
(ङ) एक तिनका है बहुत तेरे लिए –  तेरे लिए एक तिनका बहुत है।

2. निम्नलिखित शब्दों के बिलोम/विपरीत शब्द लिखिए:
(ନିମ୍ନଲିଖ୍ ଶବ୍ଦା କେ ବିଲୋମ୍/ବିପରୀତ୍ ଶବ୍ଦ ଲିଖିଏ : )
(ନିମ୍ନଲିଖ୍ ଶବ୍ଦଗୁଡ଼ିକର ବିଲୋମ/ବିପରୀତ ଶବ୍ଦ ଲେଖ।)
झिझक, बेचैन, दुःख, दुःखद, बहुत
उत्तर:
झिझक – बेझिझक
दुःखद – सुखद
बेचैन – चैन
दुःख – सुख
बहुत – कम

3. ‘किसे ढब से निकलना’ का अर्थ है किसी ढंग से निकलना। ‘ढब से’ जैसे कई वाक्यांशों से आप परिचित होंगे, जैसे- ‘धम से’ वाक्यांश है, लेकिन ध्वनियों में समानता होने के बाद भी ‘ढब से’ और ‘धम से’ वाक्यांशों के प्रयोग में अंतर है। नीचे कुछ ध्वनिद्वारा क्रिया को सूचित करनेवाले वाक्यांश और कुछ अधूरे वाक्य दिये गये हैं। उचित वाक्यांश चुनकर वाक्यों के खाली स्थान भरिए-
( छपाक से, टपटप, सर्र से, फुरे से)
(ଛପାକ୍ ସେ, ଟପ୍‌ଟପ୍, ସର୍ଗ ସେ, ଫୁରେ ସେ)

(क) मेढक पानी में ……………… कूद गया।
(ख) नल बंद होने पर भी पानी की कुछ बूँदें …………….. चू गईं।
(ग) शोर होते ही चिड़िया ………………….. उड़ी।
(घ) मोटर साइकिल ………………… गई।
उत्तर:
(क) छपाक से
(ख) टपटप
(ग) फुर्र से
(घ) सर्र से

4. पाठ के आधार पर सही परसर्गों से शून्य स्थानों को भरिए:
(ପାଠ୍ କେ ଆଧାର ପର୍ ସହୀ ପରସଗୋଁ ସେ ଶୂନ୍ୟ ସ୍ଥାନୌ କୋ ଭରିଏ :
(ପାଠକୁ ଆଧାର କରି ଉପଯୁକ୍ତ ପରସର୍ଗଦ୍ଵାରା ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।)

(क) घमंडों ………………. भरा ऐंठा हुआ।
उत्तर:
में

(ख) एक दिनका आँख ………………. मेरी पड़ा
उत्तर:
में

(ग) आ अचानक दूर ………………. उड़ता हुआ।
उत्तर:
से

(घ) जब किसी ढब ……………….. निकल तिनका गया।
उत्तर:
से

(ङ) तब ‘समझ’ ……………….. यों मुझे ताने दिए।
उत्तर:
ने

Very Short & Objective type Questions with Answers

A. निम्नलिखित प्रश्नों के उत्तर एक वाक्य में दीजिए।

प्रश्न 1.
आँख में तिनका पड़ने पर कवि की मानसिक दशा क्या थी?
उत्तर:
आँख में तिनका पड़ने पर कवि का घमण्ड चूर हो गया और कवि बेचैन हो गए।

प्रश्न 2.
कवि को क्या समझ में आया?
उत्तर:
कवि को यह समझ में आया कि मनुष्य के घमण्ड को चूर करने के लिए एक तिनका ही काफी है।

प्रश्न 3.
कवि जब मुंडेर पर खड़ा था तब क्या हुआ?
उत्तर:
कवि जब मुंडेरे पर खड़ा था, तब अचानक दूर से उड़ता हुआ एक तिनका आकर उसकी आँख में गिर पड़ा।

प्रश्न 4.
कवि को कब आराम मिला?
उत्तर:
जब किसी उपाय से आँख से तिनका निकल गया, तब कवि को आराम मिला।

प्रश्न 5.
‘एक तिनका’ कविता का मूल भाव क्या है?
उत्तर:
‘एक तिनका’ कविता का मूल भाव है कि किसी को घमंड नहीं करना चाहिए, अंत में घमंडी को दुख ही मिलता है।

B. निम्नलिखित प्रश्नों के उत्तर एक शब्द/एक पद में दीजिए।

प्रश्न 1.
जब तिनका आँख में पड़ा, तब कवि कहाँ खड़े थे?
उत्तर:
मुंड़ेरे पर

प्रश्न 2.
क्या विचार करके मृत्यु से नहीं डरना चाहिए?
उत्तर:
मर्त्य विचार कर

प्रश्न 3.
आँख से तिनका निकल जाने के बाद कवि को किसने ताने दिए?
उत्तर:
समझ ने

प्रश्न 4.
कवि की आँख में क्या आ पड़ा?
उत्तर:
एक तिनका

प्रश्न 5.
तिनका का अर्थ क्या है?
उत्तर:
सूखी घास

प्रश्न 6.
‘एक तिनका’ कविता के कवि कौन है?
उत्तर:
अयोध्यासिंह उपाध्याय हरी औध

प्रश्न 7.
अचानक क्या हुआ?
उत्तर:
तिनका आखों में गिरा

प्रश्न 8.
आँख क्या होकर दुःखने लगी?
उत्तर:
लाल

प्रश्न 9.
ताना’ शब्द का सही अर्थ क्या है?
उत्तर:
उपहास

प्रश्न 10.
कवि मुंडेर पर क्य करते थे?
उत्तर:
खड़े थे

C. रिक्त स्थानों की पूर्ति कीजिए।

प्रश्न 1.
………………… दवे पाँव भागी।
उत्तर:
घमण्डी

प्रश्न 2.
‘एक तिनका’ कविता का मूल भाब ………………… है।
उत्तर:
अहंकार दूर करने की

प्रश्न 3.
कवि की ………………… दुखने लगी थी।
उत्तर:
आँख

प्रश्न 4.
कवि ……………. पर खड़े थे।
उत्तर:
मुंडेरे

प्रश्न 5.
ऐंठ वेचारी ………………. भागी।
उत्तर:
दवे पाँवो

प्रश्न 6.
कवि को आँख में अचानक एक …………………. गिरा।
उत्तर:
तिनका

प्रश्न 7.
मुँठ का अर्थ है …………………।
उत्तर:
कपड़े का गुब्बारा

प्रश्न 8.
कवि के मन में ………………… भाव भरा था।
उत्तर:
गर्व

प्रश्न 9.
कवि को ………………… ने ताने दिए।
उत्तर:
समझा

प्रश्न 10.
………………. कवि मुँड़रे पर खड़े थे।
उत्तर:
एक दिन

D. ठिक् या भूल लिखिए।

प्रश्न 1.
मूँठ का अर्थ रुई का प्रलेप है।
उत्तर:
भूल

प्रश्न 2.
एक तिनका अहंकार तोड़ने को काफी है।
उत्तर:
ठिक्

प्रश्न 3.
‘एक तिनका’ कविता जिन्होंने लिखी है, वे प्रसादजी हैं।
उत्तर:
भूल

प्रश्न 4.
आँख में तिनका गिरने से आँख का रंग लाल हो गया।
उत्तर:
ठिक्

प्रश्न 5.
कवि के अहंकार को तोड़ ने के लिए एक तिनका काफी है।
उत्तर:
ठिक्

प्रश्न 6.
अकड़ के साथ कवि सड़क पर खड़े थे।
उत्तर:
भूल

प्रश्न 7.
ऐंठ दवे पाँव भागी।
उत्तर:
ठिक्

प्रश्न 8.
‘ताना’ का अर्थ हे नाचना और गाना।
उत्तर:
भूल

प्रश्न 9.
कवि की मन में प्रेम भाव था।
उत्तर:
भूल

प्रश्न 10.
ऐंठ को वेचारी कहा गया है।
उत्तर:
ठिक्

Multiple Choice Questions (mcqs) with Answers

सही उत्तर चुनिए : (MCQS)

1. जब तिनका आँख में पड़ा, तब कवि कहाँ खड़े थे?
(A) मुंड़ेरे पर
(B) बहुत दूरी पर
(C) तिनके के ऊपर
(D) कपड़े के ऊपर
उत्तर:
(A) मुंड़ेरे पर

2. क्या विचार करके मृत्यु से नहीं डरना चाहिए, क्योंकि तुम
(A) अमर्त्य हो
(B) सत्य हो
(C) असत्य हो
(D) मर्त्य हो
उत्तर:
(D) मर्त्य हो

3. कवि को किसने ताने दिए?
(A) अपनों ने
(B) समझ ने
(C) मन ने
(D) पत्नी ने
उत्तर:
(B) समझ ने

4. आँख से तिनका निकल जाने के बाद कवि को किसने ताने दिए?
(A) ऐंठ ने
(B) समझ ने
(C) पिताजी ने
(D) मित्रों ने
उत्तर:
(B) समझ ने

5. कवि की आँख में क्या आ पड़ा?
(A) एक कीड़ा
(B) एक कंकड़
(C) एक तिनका
(D) एक झंझट
उत्तर:
(C) एक तिनका

6. कौन दवे पाँव भागी?
(A) सुख
(B) दुःख
(C) शांति
(D) घमण्डी
उत्तर:
(D) घमण्डी

7. तिनका का अर्थ क्या है?
(A) सूखी पत्र
(B) सूखी घास
(C) कीचड़
(D) काई
उत्तर:
(B) सूखी घास

8. ‘एक तिनका’ कविता के कवि कौन है?
(A) जयशंकरप्रसाद
(B) हरीवंशराय वच्चन
(C) सुदर्शन
(D) अयोध्यासिंह उपाध्याय हरी औध
उत्तर:
(D) अयोध्यासिंह उपाध्याय हरी औध

9. अचानक क्या हुआ?
(A) तिनका आखों में गिरा
(B) तिनका सर पर गिरा
(C) तिनका नाक में गिरा
(D) तिनका पाद पर गिरा
उत्तर:
(A) तिनका आखों में गिरा

10. एक दिन कबि कहाँ खड़े थे?
(A) मुँडेरे
(B) बरामदे
(C) दीवार
(D) मैदान
उत्तर:
(A) मुँडेरे

11. ‘एक तिनका’ कविता का मूल भाब क्या है?
(A) दुःख दूर करने की
(B) अहंकार दूर करने की
(C) सुख दूर करने की
(D) कलंक दूर करने की
उत्तर:
(B) अहंकार दूर करने की

12. मूँठ का अर्थ चुनिए
(A) रुई का प्रलेप
(B) सूखी घास
(C) मुछ
(D) कपड़े का गुव्बारा
उत्तर:
(D) कपड़े का गुव्बारा

13. कौन सा अंग दुखने लगा था?
(A) आँख
(B) नाक
(C) पैर
(D) कान
उत्तर:
(A) आँख

14. ‘ ताना’ शब्द का सही अर्थ छाँटिए
(A) सजा
(B) उपहास
(C) नाचना
(D) गाना
उत्तर:
(B) उपहास

15. एक तिनका क्या तोड़ने को काफी है?
(A) अहंकार
(B) शांति
(C) वैर
(D) सुख
उत्तर:
(A) अहंकार

16. ‘एक तिनका’ कविता जिन्होंने लिखी है, वे हैं
(A) हरिऔधजी
(B) प्रसादजी
(C) प्रेमचंदजी
(D) गुप्तजी
उत्तर:
(A) हरिऔधजी

17. कवि किस जगह पर खड़े थे?
(A). छत पर
(B) टेबिल पर
(C) मुंडेरे पर
(D) जमीन पर
उत्तर:
(C) मुंडेरे पर

18. कवि के साथ अचानक कैसी दुर्घटना घटी?
(A) सर पर पत्थर गिरा
(B) आँख में तिनका गिरा
(C) आँख में धूल गिरी
(D) इनमें से कोई नहीं
उत्तर:
(B) आँख में तिनका गिरा

19. आँख में तिनका गिरने से आँख का रंग हो गया
(A) काला
(B) सफेद
(C) गीला उत्तर
(D) लाल
उत्तर:
(D) लाल

यह कविता :
यह एक छोटी सी कविता है पर है बड़े काम की। छोटी छोटी चीजें ही हमारे जीवन को एकदम बदल देती हैं। मनुष्य को अपने पर बड़ा गर्व होता है। कवि कहते हैं वे एक दिन घमण्ड में भरकर एकदम ऐंठे हुए से तन कर छत के मुँडेरे पर खड़े थे। ऐसे में कहीं दूर से एक छोटा-सा तिनका आकर उनकी आँखों में गिरा। कवि झुंझलाकर परेशान हो उठे। आँख जल रही थी और लाल होकर दुखने भी लगी।

लेखक की ऐसी हालत देखकर लोग कपड़े की मुँठ देकर उनकी आँख को सेंकने लगे कि शायद थोड़ा आराम मिल जाए पर नहीं। दर्द किसी तरह कम नहीं हुआ। ऐसे में कवि की ऐंठ (घमण्ड ) मानों चुपचाप भाग गई थी। वे तो किसी भी तरह उस पीड़ा से छुटकारा पाना चाहते थे। जब किसी तरह आँख से तिनका निकला तो मानो उनका विवेक उन्हें ताना मार रहा था। तू इतना अकड़ क्यों दिखाता है। एक छोटा-सा तिनका ही तेरे अहंकार को तोड़ने में काफी है।

ଏହି କବତ।:
ଦେଇଥାଏ। ମନୁଷ୍ୟର ନିଜ ଉପରେ ବଡ଼ ଗର୍ବ ଆସେ। କବି କହୁଛନ୍ତି ଯେ ସେ ଦିନେ ଅହଂଭାବ ନେଇ ଆତ୍ମବଡ଼ିମା ସହ ଛାତ ଉପରେ ଛିଡ଼ା ହୋଇଥିଲେ। ଏହି ସମୟରେ କେଉଁ ଦୂରରୁ ଗୋଟିଏ ଛୋଟିଆ ଶୁଖୁଲା ଘାସ ଖଣ୍ଡ ଉଡ଼ି ଆସି ତାଙ୍କ ଆଖୁରେ ପଡ଼ିଲା। କବି ବିରକ୍ତ ହେଲେ ଓ କଷ୍ଟ ମଧ୍ୟ ଅନୁଭବ କଲେ। ତାଙ୍କ ଆଖି ପୋଡ଼ିବାକୁ ଲାଗିଲା ଏବଂ ଲାଲ ପଡ଼ିଗଲା। ଲେଖକଙ୍କର ଏପରି ଅବସ୍ଥା ଦେଖୁ ପାଖରେ ଥ‌ିବା ଲୋକମାନେ କପଡ଼ା ପୁଡ଼ା କରି ତାଙ୍କ ଆଖରେ ସେକ ଦେବାକୁ ଲାଗିଲେ କାଳେ ଟିକେ ଆରାମ ମିଳିବ; କିନ୍ତୁ ଆରାମ ମିଳିଲା ନାହିଁ।

ବିନ୍ଧା ଛିଟିକା କୌଣସି ପ୍ରକାର କମିଲା ନାହିଁ। ଏପରି ଅବସ୍ଥାରେ କବିଙ୍କର ଆତ୍ମବଡ଼ିମା ଯେପରି ଚୁପ୍‌ଚାପ୍ କୁଆଡ଼େ ପଳାଇ ଯାଇଥିଲା। ସେ କୌଣସି ପ୍ରକାର ସେହି ପୀଡ଼ାରୁ ଆରାମ ପାଇବାକୁ ଚାହୁଁଥିଲେ। କୌଣସି-ପ୍ରକାର ତାଙ୍କ ଆଖୁ ସେହି ଛୋଟିଆ ଘାସ ଖଣ୍ଡିକ ବାହାରିଗଲା। କିନ୍ତୁ ସେହି ଛୋଟିଆ ଘାସ ଖଣ୍ଡିକ ଯେମିତି ତାଙ୍କୁ ବିଦ୍ରୁପ କରୁଥିଲା। ଗୋଟିଏ ଛୋଟିଆ ଘାସ ଖଣ୍ଡ ତାଙ୍କ ଅହଂକାରକୁ ଯେପରି ଭାଙ୍ଗିବାପାଇଁ ଯଥେଷ୍ଟ, ସେ ଏହା ଅନୁଭବ କରୁଥିଲେ।

मैं घमंडों में भरा ऐंठा हुआ,
एक दिन जब था मुंडेरे पर खड़ा।
आ अचानक दूर से उड़ता हुआ,
एक तिनका आँख में मेरी पड़ा।
ମେଁ ଘର୍ମଣ୍ଡୋ ମେଁ ଭରା ଏଁଠା ହୁଆ,
ଏକ୍ ଦିନ୍ ଜବ୍ ଥା ମୁଁଡେରେ ପର୍ ଖଡ଼ା।
ଆ ଅଚାନକ୍ ଦୂର୍ ସେ ଉଡ଼ତା ହୁଆ,
ଏକ ତିନ୍‌ ଆଁଖ ମେଁ ମେରୀ ପଢ଼ା।

हिन्दी व्याख्या:
कवि कहते हैं कि एक दिन वे घमण्ड से भरे ऐंठे हुए तनकर छत के मुंडेरे पर खड़े थे। उसी समय कहीं दूर से अचानक एक तिनका उड़ता हुआ आया और उनकी आँख में आकर पड़ा।
ଓଡ଼ିଆ ଅନୁବାଦ:
ଏଠାରେ କବି କହୁଛନ୍ତି ଯେ ଦିନେ ଅହଂଭାବ ନେଇ ଆତ୍ମବଡ଼ିମା ସହ ନିଜ ଛାତ ଉପରେ ଛିଡ଼ା ହୋଇଥିଲେ। ଠିକ୍ ଏହି ସମୟରେ କେଉଁ ଦୂରରୁ ଗୋଟିଏ ଛୋଟିଆ ଶୁଖୁଲା ଘାସ ଖଣ୍ଡ ଉଡ଼ି ଆସି ତାଙ୍କ ଆଖ ରେ ପଡ଼ିଲ

मैं झिझक उठा, हुआ बेचैन-सा,
लाल होकर आँख भी दुखने लगी।
मूँठ देने लोग कपड़े की लगे,
ऐंठ बेचारी दबे पाँवों भागी॥
ମେଁ ଝିଝକ୍ ଉଠା, ହୁଆ ବେସୈନ୍-ସା,
ଲାଲ୍ ହୋକର୍ ଆଁଖ୍ ଭି ଦୁଗ୍‌ନେ ଲଗୀ।
ମୁଁଠ ଦିନେ ଲୋଗ୍ କପ୍‌ଡ଼େ କୀ ଲଗେ,
ଐଠ୍ ବେଚାରୀ ଦବେ ପାଁର୍ଡୋ ଭାଗୀ।

हिन्दी व्याख्या:
कवि झुंझलाकर परेशान हो उठे। तिनके के पड़ने से उनकी आँख जल रही थी. और दुःखने भी लगी थी। सूजन के मारे उनकी आँखें लाल हो गई थीं। कवि की ऐसी हालत देखकर लोग कपड़े की मूँठ देकर उनकी आँख को सेंकने लगे कि शायद थोड़ा आराम मिल जाए। पर आराम नहीं मिला। दर्द किसी तरह कम होने का नाम नहीं ले रहा था। एसे में कवि का घमंड़ मानों चुपचाप भाग गया था। वे तो किसी भी प्रकार उस पीड़ा से छुटकारा पाना चाहते थे।
ଓଡ଼ିଆ ଅନୁବାଦ:
କବି ବିରକ୍ତ ହୋଇ ଉଠିଲେ ଓ କଷ୍ଟ ମଧ୍ୟ ଅନୁଭବ କଲେ। ଆଖୁ ପୋଡ଼ିବାକୁ ଲାଗିଲା ଓ ଧୀରେ ଧୀରେ ଲାଲ ପଡ଼ିଗଲା। ଏହି ଅବସ୍ଥା ଦେଖୁ ପାଖରେ ଥିବା ଲୋକମାନେ କପଡ଼ା ପୁଡ଼ା କରି ତାଙ୍କ ଆସ୍‌ରେ ସେକ ଦେଲେ କିନ୍ତୁ ଆରାମ ମିଳିଲା ନାହିଁ। କୌଣସି ପ୍ରକାର ଯନ୍ତ୍ରଣା (ବିନ୍ଧା ଛିଟିକା) କମିଲା ନାହିଁ। ଏପରି ସ୍ଥିତିରେ କବିଙ୍କର ଆତ୍ମବଡ଼ିମା ଚୁପ୍‌ଚାପ୍ କୁଆଡ଼େ ପଳାଇ ଯାଇଥିଲା। କିନ୍ତୁ କବି କୌଣସି ପ୍ରକାର ସେହି ପିଡ଼ାରୁ ଆରାମ ପାଇବାକୁ ଚାହୁଁଥିଲେ।

(iii) जब किसी ढब से निकल तिनका गया,
तब ‘समझ’ ने यों मुझे ताने दिए।
ऐंठता तू किसलिए इतना रहा,
एक तिनका है बहुत तेरे लिए।
ଜବ୍ କିସୀ ଢବ୍ ସେ ନିକଲ୍ ତିନ୍‌ ଗୟା,
ତବ୍ ‘ସମ’ ନେ ୟୈ ମୁଝେ ତାନେ ଦିଏ।
ଐଠତା ତୁ କିସ୍‌ଲିଏ ଇତ୍‌ ରହା,
ଏକ ତିନ୍‌ ହୈ ବହୁତ୍ ତେରେ ଲିଏ।

हिन्दी व्याख्या:
कवि कहते हैं कि जब किसी तरह आँख से तिनका निकला तो मानो उनका विवेक उन्हे ताना मार रहा था। जैसे कह रहा था इतना अकड़ किसलिए दिखा रहे थे। एक छोटा सा तिनका तुम्हारा सारे अहंकार को तोड़ने में काफी है।

ଓଡ଼ିଆ ଅନୁବାଦ:
କୌଣସି ପ୍ରକାର କବିଙ୍କ ଚକ୍ଷୁରୁ ସେହି ଛୋଟିଆ ଘାସଖଣ୍ଡକ ବାହାରି ଗଲା କିନ୍ତୁ ସେହି ଛୋଟିଆ ଘାସଖଣ୍ଡକ ଯେମିତି ତାଙ୍କୁ ବିଦ୍ରୁପ କରୁଥିଲା। ସେ ଅନୁଭବ କରିଥିଲେ, ଛୋଟିଆ ଘାସଖଣ୍ଡକ ତାଙ୍କ ଅହଂକାରକୁ ଭାଙ୍ଗିବା ପାଇଁ ଯଥେଷ୍ଟ।

तिनका – सूखी घास (ଶୁଖୁଲା ଘାସ)।
घमंड – गर्व, अहंकार (ଅହଂକାର, ଗର୍ବ)।
ऐंठा हुआ- अकड़ कर (ଜିଦ୍ କରି)।
मुंडेरे – दीवाल का सबसे ऊपर भाग जो छत के ऊपर रहता है। ଉପରିଭାଗ)।
अचानक – सहसा (ହଠାତ୍)।
झिझकना – हिचकिचाना (ଚିଡ଼ି ଉଠିବା)।
बेचैन – व्याकुल (ବ୍ୟାକୁଳ)।
दुखने – पीड़ा (କଷ୍ଟ)।
मूँठ – कपड़े का गुब्बारा जो आँख को सेंकता है। (ଚୁପ୍ଚାପ୍ )।
दबे पाँव – चुपचाप (ଢଙ୍ଗ)।
ढब – तरीका (ଉପହାସ )।
ताना – उपहास (କପଡ଼ା ପୁଡ଼ା ଆଖୁକୁ ସେକିବା ପାଇଁ)।

कवि परिचय

अयोध्यासिंह उपाध्याय ‘हरिऔध’ का जन्म उत्तर प्रदेश के अजमगढ़ जिले के निजामाबाद कस्वे में सन् 1865 में हुआ था। स्कूली शिक्षा समाप्त करके वे सरकारी नौकरी में लग गए। हिन्दी, संस्कृत और फारसी में उन्होंने अच्छा ज्ञान प्राप्त किया था। वे हिन्दू विश्वविद्यालय, वारणसी में अध्यापक भी रहे। है। हरिऔधजी खड़ीबोली हिन्दी के प्रथम कवियों में हैं। उनकी भाषा सरल, मुहावरेदार और भावगर्भक हरिऔध की प्रमुख रचनाएँ हैं- प्रिय प्रवास, वैदेही वनवास, कर्मवीर, रसकलश, चोखे चौपदे, चुभते चौपदे, आदि।

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Ex 8(d) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Exercise 8(d)

Question 1.
Find the extreme points of the following functions. Specify if the extremum is a maximum or minimum.
Find the extreme values.
(i) y = x² + 2x + 3
Solution:

(ii) y = 5x² – 2x⁵
Solution:

∴ The function attains minimum at x = 0.
and maximum at x = 1 .
The minimum value = 0
The maximum value = 5 – 2 = 3

(iii) y = \(\frac{3 x}{x^2+1}\)
Solution:

(iv) y = x²\(\sqrt{1-x^2}\)
Solution:

(v) y = 2x³ – 15x² – 36x + 18
Solution:

The function attains maximum at x = -1 and minimum at x = 6.
Maximum value
= -2 – 15 + 36 + 18 = 37
Minimum value
= 2 × 216 – 15 × 36 – 36 × 6 + 13
= 432 – 540 – 216 + 18
= 450 – 756
= -306

(vi) y = 60/(x⁴ – x² + 25)
Solution:

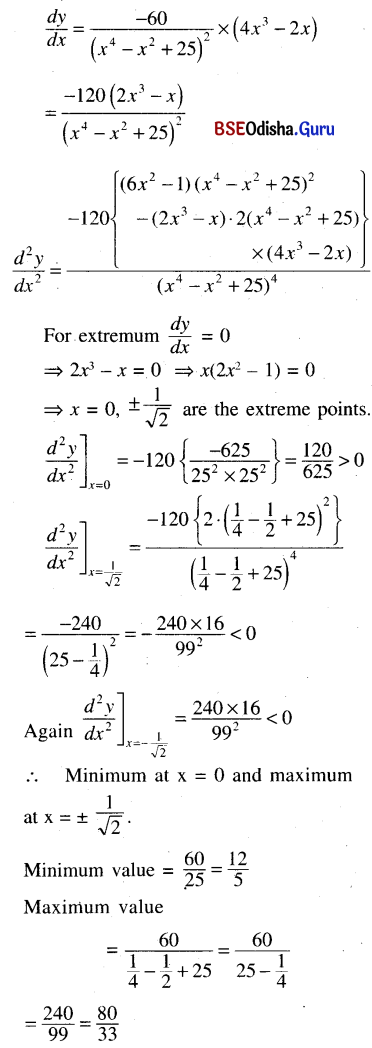
(vii) y = (x – 1)³
Solution:

So the point x = 1 is neither a point of maximum nor a point of minimum. It is an inflexion point.

(viii) y = (x – 2)³ (x + 3)⁴
Solution:

(ix) y = x + \(\frac{1}{x}\)
Solution:

∴ Maximum at x = -1
and minimum at x = 1
Maximum value = -1 – 1 = -2
Minimum value = 2.

(x) y = 4 cos 2x – 3 sin 2x, x ∈ (-\(\frac{\pi}{2}\), \(\frac{\pi}{2}\))
Solution:

(xi) y = sin x cos x, x ∈ (\(\frac{\pi}{8}\), \(\frac{\pi}{2}\))
Solution:

But there is no minimum in the domain.

(xii) y = cos x (1 + sin x), x ∈ [0, 2π]
Solution:

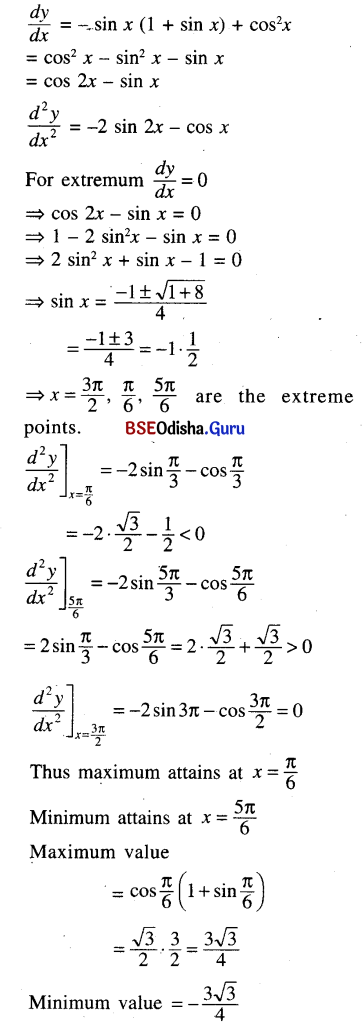
(xiii) y = sin^p x cos^q x; p, q > 0, x ∈ [0, \(\frac{\pi}{2}\))
Solution:

(xiv) y = x e^-x ; x ∈ (-2, 2)
Solution:

Question 2.
Show that the following functions do not possess maximum or minimum.
(i) x³
Solution:
y = x³

Thus the function does not possess a maximum or a minimum. (Proved)

(ii) x⁵
Solution:
Processed as in (i)

(iii) 3x³ – 12x² + 16x – 15
Solution:
Let y = 3x³ – 12x2 + 16x – 5

So the function does not possess a maximum or a minimum. (Proved)

(iv) 4 – 3x + 3x² – x³
Solution:
Processed as in (iii).

(v) ln |x|, x ≠ 0
Solution:
y = ln |x|, x ≠ 0

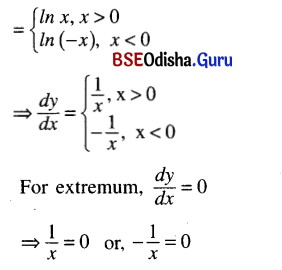
Which have no solution. Hence the function has neither a maximum nor a minimum.
(Proved)

Question 3.
Use the function f(x) = \(x^{\frac{1}{x}}\), x > 0 to show that e^x > π^c.
Solution:
f(x) = \(x^{\frac{1}{x}}\), x > 0

Question 4.
Prove the inequality x² \(e^{-x^2}\) ≤ e^-1, x ∈ R.
Solution:

Question 5.
If f(x) = a ln x + bx² + x has extreme values at x = -1 and x = 2 then find a and b.
Solution:
f(x) = a ln x + bx² + x
f'(x) = \(\frac{a}{x}\) + 2b x + 1
Given that f(x) attains extreme values at x = -1 and x = 2
Then f(-1) = 0 and f(2) = 0
⇒ -a – 2b + 1 = 0 … (1)
\(\frac{a}{2}\) + 4b + 1 = 0 … (2)
From (1) we get a = -2b + 1
Putting it in (2)
we get \(\frac{1-2 b}{2}\) + 4b + 1 = 0
⇒ 1 – 2b + 8b + 2 = 0
⇒ 3 + 6b = 0
⇒ b = \(-\frac{3}{6}\) = \(-\frac{1}{2}\)
Again a = 1 – 2b = 1 + 1 = 2
∴ a = 2, b = \(-\frac{1}{2}\)

Question 6.
Show that \(\frac{x}{1+x \tan x}\), x ∈ (0, \(\frac{\pi}{2}\)) is maximum when x = cos x.
Solution:

Thus the function attains maximum when x = cos x. (Proved)

Question 7.
Determine the absolute maximum and absolute minimum of the following function on [-1, 1]
f(x) = \(\left\{\begin{array}{l}
(x+1)^2, x \leq 0 \\
(x-1)^2, x>0
\end{array}\right.\)
Solution:
f(x) = \(\left\{\begin{array}{l}
(x+1)^2, x \leq 0 \\
(x-1)^2, x>0
\end{array}\right.\)
f(x) = \(\left\{\begin{array}{l}
2(x+1), x \leq 0 \\
2(x-1), x>0
\end{array}\right.\)
For extremum f'(x) = 0
⇒ x + 1 = 0 if x < 0
or, x – 1 = 0 if x > 0
⇒ x = -1 or x = 1
Now f(-1) = 0, f(1) = 0
Again f is not differentiable at x = 0 and f(0) = 1
The function attains absolute minimum at x = ±1. Absolute minimum value = 0.
The function attains absolute maximum at x = 0. Absolute Maximum value = 1.

Question 8.
Find extreme values of
f(x) = \(\left\{\begin{array}{l}
\frac{x}{1-x^2},-1<x<0 \\
x^3-x, 0 \leq x<2
\end{array}\right.\) on (-1, 2)
Solution:
Given that

Question 9.
Find two numbers x and y whose sum is 15 such that xy² is maximum.
Solution:
Let z = xy²
Given that x + y = 15
Then y = 15 – x
Thus z = x (15 – x)²
\(\frac{d z}{d x}\) = (15 – x)² + x² (15 – x) . (-1)
= (15 – x) (15 – x – 2x)
= (15 – x) (15 – 3x)
= 3(15 – x) (5 – x)
\(\frac{d^2 z}{d x^2}\) = -3(5 – x) – 3(15 – x)
= -3 (20 – 2x)
= -6 (10 – x)
For extreme points
\(\frac{d z}{d x}\) = 0
⇒ 3(15 – x) (5 – x) = 0
⇒ x = 15 or 5.
\(\left.\frac{d^2 z}{d x^2}\right]_{x=15}\) = 30 > 0
\(\left.\frac{d^2 z}{d x^2}\right]_{x=5}\) = 30 < 0
∴ z = xy² is maximum when x = 5.
In this case y = 10
∴The two numbers are 5, 10.

Question 10.
If the sum of two positive numbers in constant then show that their product is maximum when they are equal.
Solution:
Let x and y be two positive numbers such that x + y = c (constant)
Then y = c – x
Let p = xy = x(c – x) = cx – x²

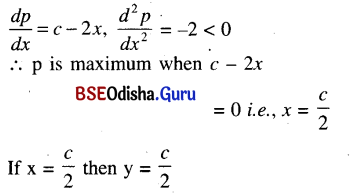
∴ The two numbers are equal. (Proved)

Question 11.
Determine a rectangle of area 25 sq. units which has minimum perimeter.
Solution:
Let x and y be the length and breadth of a rectangle of area 25 sq. units.

∴ The perimeter is minimum when the rectangle is a square of side 5 units.

Question 12.
Find the altitude of a right circular cylinder of maximum volume inscribed in a sphere of radius r.
Solution:
Let ABCD be a right circular cylinder inscribed in a sphere with centre at O and radius ‘r’. Let x be the altitude of the cylinder.

Question 13.
Show that the radius of the right circular cylinder of greatest curved surface that can be inscribed in a given cone is half the radius of the base of the cone.

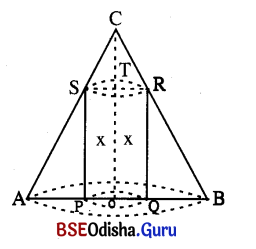
Solution:
Let ABC be a cone, Let r be the radius of the base and h be the height of the cone. Let PQRS be a cylinder inscribed in the cone whose height is x.
In the diagram OT = x.
Then CT = h – x
Now Δ CTR and Δ RQB are similar.

∴ Radius of the right circular cylinder of greatest curved surface is half the base of the cone. (Proved)

Question 14.
Show that the semi vertical angle of a cone of given slant height is tan^-1√2 when its volume is maximum.
Solution:

Question 15.
A cylindrical open water tank with a circular base is to be made out of 30 sq. metres of metal sheet. Find the dimensions so that it can hold maximum water. (Neglect thickness of sheet)
Solution:

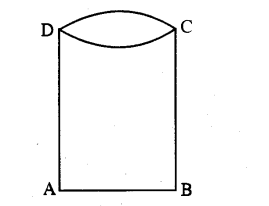
Let ABCD be an open cylindrical tank with circular base.
Let r be the radius of the base and x be the height of the tank.
Given that the tank is made out of 30 square metres of metal sheet.
The surface area of the tank
= 27πrx + πr² [∵ The tank is open.
So 2πrx + πr² = 30
⇒ 2πrx = 30 – πr²

Question 16.
A cylindrical vessel of capacity 500 cubic metres open at the top is to be constructed. Find the dimensions of the vessel if the material used is minimum given that the thickness of the material used is 2 cm.
Solution:

Question 17.
Find the coordinates of the point on the curve x²y – x + y = 0 where the slope of the tangent is maximum.
Solution:
Let (x, y) be the point on the curve
x²y – x + y = 0.

The slope is maximum when x = 0. when x = 0, y = 0
The point is (0, 0) at which the slope of the tangent is maximum.

Question 18.
Find the points on the curve y = x² + 1 which are nearest to the point (0, 2).
Solution:
Let A = (0, 2)
Let P (x, y) be any point on the curve
y = x² + 1. …(1)

Question 19.
Show that the minimum distance of a point on the curve \(\frac{a^2}{x^2}\) + \(\frac{b^2}{y^2}\) = 1
from the origin is a + b.
Solution:
Let P(x, y) be any point on the curve

Question 20.
Show that the vertical angle of a right circular cone of minimum curved surface that circumscribes a given sphere is 2 sin^-1(√2 – 1).
Solution:

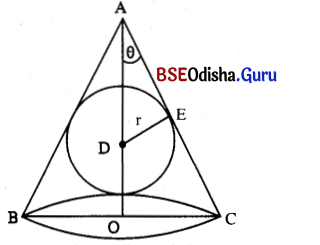
Let r is the radius of the given sphere, R is the radius of the base, H is the height and l is the C lant height of the cone ABC. Let θ is the semi vertical angle.

Question 21.
Show that the semi-vertical angle of a right circular cone of minimum volume that circumscribes a given sphere is sin^-1(\(\frac{1}{3}\)).
Solution:

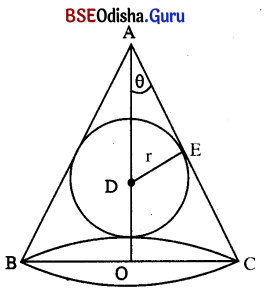
Let ABC be a right circular cone which circumscribes a sphere of radius ‘r’.
Let θ be the semi-vertical angle of the cone.
Let D be the centre of the sphere. By symmetry D must lie on AO, where O is the centre of the base.
In the diagram DO = r.
Again in the Δ ADE

Question 22.
Show that the shortest distance of the point (0, 8a) from the curve ax² = y³ is 2a√11.
Solution:
Given curve is 2x² = y³ … (1)
Let any point on it is P(x, y)
Distance of P from A (0, 8a)

Question 23.
Show that the triangle of greatest area that can be inscribed in a circle is equilateral.
Hints: It BC is any chord then for the Δ ABC to have maximum area, the point A must be on the perpendicular bisector of BC so as to have the largest height AD. Let mDBAD = a. Let BO = OA = r. Then area of Δ ABC = \(\frac{1}{2}\)|BC| |AD| = \(\frac{1}{2}\) . 2r sin 2α (r + r + cos 2α) = r² sin 2a . (1 + cos 2a). Then maximise Δ to obtain 2a = \(\frac{\pi}{3}\)
Solution:

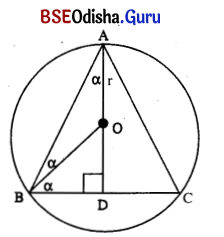
Let ABC be a triangle inscribed in a circle with centre at O and radius ‘r’.
The triangle ABC has maximum area if the point A is on the perpendicular bisector of BC.
Let ∠BAD = α, Let BO = AO = r,
Then ∠BOD = 2α.
In Δ OBD, sin 2α = \(\frac{\mathrm{BD}}{\mathrm{OB}}\)
⇒ BD = OB sin 2α = r sin 2α
Again OD = r cos 2α.
Thus AD = r + r cos 2α
Let Z be the area of the triangle ABC.

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 7 Continuity and Differentiability Ex 7(g) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Exercise 7(g)

Find \(\frac{d y}{d x}\)
Question 1.
xy² + x²y + 1 = 0
Solution:
xy² + x²y + 1 = 0

Question 2.
\(x^{\frac{1}{2}} y^{-\frac{1}{2}}\) + \(x^{\frac{3}{2}} y^{-\frac{3}{2}}\) = 0
Solution:

Question 3.
x² + 3y² = 5
Solution:
x² + 3y² = 5
⇒ \(\frac{d}{d x}\)(x²) + 3 \(\frac{d}{d x}\)(y²) = 0
⇒ 2x + 6y\(\frac{d y}{d x}\) = 0
⇒ \(\frac{d}{d x}\) = –\(\frac{x}{3 y}\)

Question 4.
y² cot x = x² cot y.
Solution:
y² cot x = x² cot y

Question 5.
y = tan xy
Solution:
y = tan xy

Question 6.
x = y In (xy).
Solution:
x = y In (xy).

Question 7.
e^xy + y sin x = 1
Solution:
e^xy + y sin x = 1

Question 8.
In \(\sqrt{x^2+y^2}\) = tan^-1 \(\frac{y}{x}\)
Solution:

Question 9.
y^x = x^{sin y}
Solution:
y^x = x^{sin y}

Question 10.
If sin (x + y) = y cos (x + y) then prove that \(\frac{d y}{d x}\) = –\(\frac{1+y^2}{y^2}\).
Solution:

Question 11.
If \(\sqrt{1-x^4}\) + \(\sqrt{1-y^4}\) = k(x² – y²) then show that \(\frac{d y}{d x}\) = \(\frac{x \sqrt{1-y^4}}{y \sqrt{1-x^4}}\).
Solution:

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Ex 8(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Exercise 8(a)

Question 1.
Find the velocity and acceleration at the end of 2 seconds of the particle moving according to the following rules.
(i) s = 2t² + 3t + 1
Solution:
s = 2t² + 3t + 1

∴ Velocity is 11 units/sec and acceleration is 4 units/sec².

(ii) s = √t +1
Solution:
s = √t +1

(iii) s = \(\frac{3}{2 t+1}\)
Solution:

(iv) s = t³ – 6t² + 15t + 12
Solution:
s = t³ – 6t² + 15t + 12

∴ Velocity is 3 units/sec and acceleration is 0.

Question 2.
The sides of an equilateral triangle are increasing at the rate of √3 cm/sec. Find the rate at which the area of the triangle is increasing when the side is 4 cm long.
Solution:
Let x be the lenght of each side of an equilateral triangle.

∴ Area of the triangle is increasing at the rate of 6 cm²/sec

Question 3.
Find the rate at which the volume of a spherical balloon will increase when its radius is 2 metres if the rate of increase of its radius is 0.3 m/min.
Solution:
Let r be the radius of a spherical balloon.

∴ The volume increase at the rate of 4.8π m³/min.

Question 4.
The surface area of a cube is decreasing at the rate of 15 sq. cm/sec. Find the rate at which its edge is decreasing when the length of the edge is 5 cm.
Solution:
Let s be the surface area of a cube.
Let x be the length of each side of the cube.

∴ The edge is decreasing at the rate of 0.25 cm/sec

Odisha State Board BSE Odisha 6th Class English Solutions Follow-Up Lesson 6 Mahagiri – The Kind Elephant Textbook Exercise Questions and Answers.

BSE Odisha Class 6 English Solutions Follow-Up Lesson 6 Mahagiri – The Kind Elephant

BSE Odisha 6th Class English Follow-Up Lesson 6 Mahagiri – The Kind Elephant Text Book Questions and Answers

Session – 1

I. Pre-Reading

□ Teacher will plan the activity.
( ଶିକ୍ଷକ କାର୍ଯ୍ୟାବଳୀ ଯୋଜନା କରିବେ ।)

II. While-Reading

Text

SGP-l
Read paragraph – 1 silently and answer the questions that follow.
(ଅନୁଚ୍ଛେଦ – ୧ କୁ ନୀରବରେ ପଢ଼ ଏବଂ ପରବର୍ତ୍ତୀ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।)

1. Mahagiri was a big elephant. He was trained at a special school. He was bought by a merchant. The merchant made a lot of money by putting Mahagiri to work. The elephant was often sent to the forest to carry heavy logs of wood. Sometimes, he carried people from one place to another. Once, he even carried a bridegroom to the bride’s house ! At times he was sent to a famous temple in a village nearby to lead the festival procession.

ଓଡ଼ିଆ ଅନୁବାଦ :
୧. ମହାଗିରି ଗୋଟିଏ ବଡ଼ ହାତୀ ଥିଲା । ସେ ଏକ ସ୍ବତନ୍ତ୍ର ବିଦ୍ୟାଳୟରେ ତାଲିମ ପାଇଥିଲା । ତାକୁ ଜଣେ ବଣିକ (ବ୍ୟବସାୟୀ) କିଣି ନେଇଥିଲେ । ବଣିକ ଜଣକ ମହାଗିରିକୁ କାମରେ ଲଗାଇ ପ୍ରଚୁର ଟଙ୍କା ରୋଜଗାର କଲେ । ହାତୀଟିକୁ ଅଧିକାଂଶ ସମୟରେ ଓଜନିଆ କାଠ ଗଡ଼ଗୁଡ଼ିକୁ ବୋହିବାକୁ ଜଙ୍ଗଲକୁ ପଠାଯାଉଥିଲା । ବେଳେବେଳେ ସେ ଲୋକମାନଙ୍କୁ ଗୋଟିଏ ସ୍ଥାନରୁ ଅନ୍ୟସ୍ଥାନକୁ ବୋହି ନେଉଥିଲା । ଏପରିକି ଥରେ ସେ ଜଣେ ବରପାତ୍ର (ଜ୍ୱାଇଁ)କୁ କନ୍ୟା (ବୋହୂ) ଘରକୁ ବହନ କରି ନେଇଥିଲା ! ବହୁ ସମୟରେ ତାକୁ ନିକଟସ୍ଥ ଗ୍ରାମରେ ଥିବା ଏକ ପ୍ରସିଦ୍ଧ ମନ୍ଦିରକୁ ଉତ୍ସବ ଶୋଭଯାତ୍ରାକୁ ଆଗେଇ ନେବାପାଇଁ ପଠାଯାଉଥିଲା ।

Comprehension Questions

Question 1.
What is this paragraph about?
(ଏହି ଅନୁଚ୍ଛେଦଟି କାହା ବିଷୟରେ ?)
Answer:
This paragraph is about an elephant named Mahagiri and his work for his owner the merchant.

Question 2.
Where was Mahagiri trained?
(ମହାଗିରି କେଉଁଠାରେ ତାଲିମ ପାଇଥିଲା ?)
Answer:
Mahagiri was trained at a special school.

Question 3.
Who bought it?
(କିଏ ଏହାକୁ କିଣିଥିଲା ?)
Answer:
A merchant bought it.

Question 4.
How did the merchant make a lot of money?
(କିପରି ବଣିକଟି ପ୍ରଚୁର ଟଙ୍କା ରୋଜଗାର କଲା ?)
Answer:
The merchant made a lot of money by putting Mahagiri to work.

Question 5.
Mahagiri did four kinds of work. They are :
(i) ———- (ii) ———–
(iii) ———- (iv) ———-
Answer:
(i) He was often sent to the forest to carry heavy logs of wood.
(ii) Sometimes he carried people from one place to another.
(iii) Once, he even carried a bridegroom to the bride’s house.
(iv) At times, he was sent to a famous temple in a village nearby to lead the festival procession.

SGP-2
Read paragraphs – 2 silently and answer the questions that follow.
(ଅନୁଚ୍ଛେଦ – ୨ କୁ ନୀରବରେ ପଢ଼ ଏବଂ ପରବର୍ତ୍ତୀ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।)

2. Once the people of the village wanted to celebrate their temple festival. The festival could not start till the temple flag was put up. The temple had the flag, but no flagpole. So the villagers went to the forest and made a fine flagpole out of a tall tree. The flagpole was too heavy for the villagers to carry. And so Mahagiri brought it to the temple. The villagers also wanted the elephant’s help to fix the flagpole in the ground. They had already dug a hole in front of the temple.

ଓଡ଼ିଆ ଅନୁବାଦ :
୨. ଥରେ ଗାଁର ଲୋକମାନେ ସେମାନଙ୍କର ମନ୍ଦିର ଉତ୍ସବଟିକୁ ପାଳନ କରିବାକୁ ଚାହିଁଲେ । ମନ୍ଦିର ପତାକା ବନ୍ଧା ନ ହେଲା ପର୍ଯ୍ୟନ୍ତ ଉତ୍ସବ ଆରମ୍ଭ ହୋଇପାରୁ ନ ଥିଲା । ମନ୍ଦିରର ପତାକା ଥିଲା, କିନ୍ତୁ ପତାକା ଖୁଣ୍ଟ ନଥିଲା । ତେଣୁ ଗାଁ ଲୋକମାନେ ଜଙ୍ଗଲକୁ ଗଲେ ଏବଂ ଗୋଟିଏ ଡେଙ୍ଗା ଗଛରୁ ଗୋଟିଏ ସୁନ୍ଦର ପତାକା ଖୁଣ୍ଟ ତିଆରି କଲେ । ପତାକା ଖୁଣ୍ଟଟି ଗ୍ରାମବାସୀମାନଙ୍କ ପାଇଁ ବୋହିନେବାକୁ ବହୁତ ଓଜନିଆ ଥିଲା । ତେଣୁ ମହାଗିରି ଏହାକୁ ମନ୍ଦିରକୁ ଆଣିଲା । ଗ୍ରାମବାସୀମାନେ ମଧ୍ୟ ପତାକା ଖୁଣ୍ଟଟିକୁ ଭୂମିରେ ପୋତିବାକୁ ହାତୀଟିର ସାହାଯ୍ୟ ଚାହିଁଲେ । ସେମାନେ ମନ୍ଦିର ସମ୍ମୁଖରେ ଗୋଟିଏ ଗାତ ଖୋଳି ସାରିଥିଲେ ।

Comprehension Questions

Question 1.
What are these paragraphs about?
(ଏହି ଅନୁଚ୍ଛେଦ କେଉଁ ବିଷୟରେ ଲେଖାଯାଇଛି ?)
Answer:
This paragraph is about the celebration of the temple festival and making flagpole and bringing it to the temple.

Question 2.
What did the villagers want to do?
(ଗ୍ରାମବାସୀମାନେ କ’ଣ କରିବାକୁ ଚାହିଁଲେ ?)
Answer:
The villagers wanted to celebrate their temple festival.

Question 3.
What did they have but what did not have?
(ସେମାନଙ୍କର କ’ଣ ଥିଲା କିନ୍ତୁ ସେମାନଙ୍କର କ’ଣ ନଥିଲା ?)
Answer:
They had the flag for the temple, but they did not have the flagpole.

Question 4.
Who carried the flagpole?
(ପତାକା ଖୁଣ୍ଟକୁ କିଏ ବୋହି ଆଣିଥିଲା ?)
Answer:
Mahagiri carried the flagpole.

Question 5.
What did they want Mahagiri to do next?
(ତା’ପରେ ମହାଗିରି କ’ଣ ସେମାନେ ଚାହିଁଲେ କରିବାକୁ ?)
Answer:
Next, the villagers also wanted Mahagiri’s help to fix the flagpole in the ground in front of the temple.

Session – 2

SGP-3
Read paragraphs 3-4 silently and answer the questions that follow
(ଅନୁଚ୍ଛେଦ ୩ – ୪ କୁ ନୀରବରେ ପଢ଼ି ପରବର୍ତ୍ତୀ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।)

3. Now, Mahagiri carried the flagpole up to the hole. But suddenly he stopped and turned back. The mahout, who was sitting on him, ordered him to put the flagpole in the hole, but Mahagiri would not move. The mahout shouted and screamed at him but still he did not move. The villagers were angry and they shouted at the mahout. Mahagiri could not stand the noise any longer. He threw away the flagpole. And the mahout was also thrown off. The people became so frightened that they ran away for their lives.
4. Mahagiri was now alone. He moved to the hole and went down on his forelegs. He put his long trunk into the hole and gently picked up a kitten ! The little cat had been hiding in the hole. The people had been watching all this. They now knew why the elephant had not obeyed the mahout’s orders. He did not like to kill the kitten. Mahagiri then placed the flagpole into the hole and held it straight with his trunk. Everyone at the temple gave sweets and fruits to the elephant. From that day Mahagiri became the villagers’ favourite elephant and the children’s best friend.

ଓଡ଼ିଆ ଅନୁବାଦ :
୩. ବର୍ତ୍ତମାନ ମହାଗିରି ପତାକା ଖୁଣ୍ଟକୁ ଗାତ ନିକଟକୁ ବୋହିନେଲା । କିନ୍ତୁ ହଠାତ୍‌ ସେ ଅଟକିଗଲା ଓ ପଛକୁ ଫେରିଆସିଲା । ତା’ଉପରେ ବସିଥିବା ମାହୁନ୍ତ ଜଣକ ତାକୁ ଆଦେଶ ଦେଲା ଖୁଣ୍ଟକୁ ଗାତରେ ପକାଇବାକୁ, କିନ୍ତୁ ମହାଗିରି ଆଦୌ ଘୁଞ୍ଚିଲା ନାହିଁ । ମାହୁନ୍ତ ତା’ଆଡ଼କୁ ଅନାଇ ବଡ଼ପାଟିରେ ଚିତ୍କାର କଲା । କିନ୍ତୁ ତଥାପି ସେ ଆଦୌ ଘୁଞ୍ଚିଲା ନାହିଁ । ଗ୍ରାମବାସୀମାନେ ବହୁତ ରାଗିଗଲେ ଏବଂ ମାହୁନ୍ତ ଆଡ଼କୁ ଅନାଇ ବଡ଼ପାଟିରେ ଚିତ୍କାର କଲେ । ମହାଗିରି ଅଧ‌ିକ ସମୟପାଇଁ କୋଳାହଳକୁ ସହ୍ୟ କରିପାରିଲା ନାହିଁ । ସେ ପତାକା ଖୁଣ୍ଟକୁ ଫୋପାଡ଼ି ଦେଲା ଏବଂ ମାହୁନ୍ତକୁ ମଧ୍ଯ ଫୋପାଡ଼ି ଦେଲା ।
୪. ମହାଗିରି ବର୍ତ୍ତମାନ ଏକୁଟିଆ ରହିଲା । ସେ ଗାତ ନିକଟକୁ ଗଲା ଏବଂ ତା’ ଆଗଗୋଡ଼ରେ ତଳକୁ ଗଲା । ସେ ତା’ର ଲମ୍ବା ଶୁଣ୍ଢଟିକୁ ଗାତ ଭିତରକୁ ପୂରାଇଲା ଏବଂ ଅତି କୋମଳ ଭାବରେ ଗୋଟିଏ ବିଲେଇ ଛୁଆକୁ ଗାତ ଭିତରୁ ବାହାରକୁ ଉଠାଇ ଆଣିଲା । ଛୋଟ ବିରାଡ଼ି ଛୁଆଟି ଗାତ ଭିତରେ ଲୁଚି ରହିଥିଲା । ଗାଁର ଲୋକମାନେ ଏସବୁ ଲକ୍ଷ୍ୟ କରୁଥିଲେ । ବର୍ତ୍ତମାନ ସେମାନେ ଜାଣିପାରିଲେ କାହିଁକି ହାତୀଟି ମାହୁନ୍ତର ଆଦେଶକୁ ମାନି ନଥିଲା । ସେ ଚାହୁଁ ନଥୁଲା ବିରାଡ଼ି ଛୁଆଟିକୁ ମାରିଦେବାକୁ । ତା’ପରେ ମହାଗିରି ପତାକା ଖୁଣ୍ଟକୁ ଗାତ ଭିତରକୁ ପୂରାଇ ଦେଲା ଏବଂ ତା’ର ଶୁଣ୍ଢ ସାହାଯ୍ୟରେ ଏହାକୁ ସିଧାକରି ଧରିଲା । ମନ୍ଦିର ନିକଟରେ ଥ‌ିବା ପ୍ରତ୍ୟେକ ଲୋକ ହାତୀକୁ ମିଠା ଓ ଫଳସବୁ ଅର୍ପଣ କଲେ । ସେଦିନଠାରୁ ମହାଗିରି ଗ୍ରାମବାସୀମାନଙ୍କର ପ୍ରିୟ ହାତୀ ଏବଂ ପିଲାମାନଙ୍କର ସବୁଠାରୁ ଉତ୍ତମ ବନ୍ଧ ହୋଇଗଲା ।

Comprehension Questions

Question 1.
Did Mahagiri fix the pole?
(ମହାଗିରି ଖୁଣ୍ଟଟିକୁ ପୋତିଥିଲା କି ?)
Answer:
Yes, Mahagiri fixed the pole himself at last.

Question 2.
Why were the villagers angry?
(କାହିଁକି ଗ୍ରାମବାସୀମାନେ ରାଗିଗଲେ ?)
Answer:
The villagers were angry because Mahagiri would not move at though (3) the mahout shouted and screamed at him.

Question 3.
What did they do?
(ସେମାନେ କ’ଣ କଲେ ?)
Answer:
They shouted at the mahout.

Question 4.
What did Mahagiri bring out?
(ମହାଗିରି କ’ଣ ବାହାରକୁ ଆଣିଲା ?)
Answer:
Mahagiri gently picked up a kitten out of the hole.

Question 5.
What did the villagers realize?
( ଗ୍ରାମବାସୀମାନେ କ’ଣ ହୃଦୟଙ୍ଗମ କଲେ ?)
Answer:
The villagers realized why the elephant had not obeyed the mahouts orders.

Question 6.
What did they give to Mahagiri?
(ସେମାନେ ମହାଗିରିକୁ କ’ଣ ଦେଲେ ?)
Answer:
They gave Mahagiri sweets and fruits.

Session – 3

III. Post-Reading

1. Writing:
(a) Write answers to the following questions.
(ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।)

Question (i)
Who is Mahagiri?
(ମହାଗିରି କିଏ ? )
Answer:
Mahagiri is a big elephant.

Question (ii)
Who carried the flagpole for the villagers?
(ଗ୍ରାମବାସୀଙ୍କ ପାଇଁ ପତାକା ଖୁଣ୍ଟ କିଏ ବୋହି ଆଣିଲା ?)
Answer:
Mahagiri carried the flagpole to the temple for the villagers.

Question (iii)
Why did Mahagiri not fix the pole first time?
(କାହିଁକି ମହାଗିରି ପ୍ରଥମ ଥର ଖୁଣ୍ଟଟି ପୋତିଲା ନାହିଁ ?)
_________________________ Because there was a _____________________________.
Answer:
Mahagiri did not fix the pole first time. Because the little cat (kitten) had been hiding in the hole. So he picked up the kitten gently first. (Or) Mahagiri did not fix the pole first time because there was a kitten hidden in the hole. He did not like to kill it.

Question (iv)
How did Mahagiri pick up the kitten?
(କିପରି ମହାଗିରି ବିଲେଇ ଛୁଆକୁ ବାହାର କଲା ?)
_____________________________ He Went ________________________.
Answer:
Mahagiri moved to the hole. He went down on his forelegs. He put his . long trunk into the hole and gently picked up the kitten.

(b) One villager narrates the incident to a man from another village. Read and fill in the gaps. (Question with Answer)
(ଜଣେ ଗ୍ରାମବାସୀ ଘଟଣାଟିକୁ ଅନ୍ୟ ଗୋଟିଏ ଗାଁର ଜଣେ ଲୋକ ଆଗରେ ବର୍ଣ୍ଣନା କରୁଛନ୍ତି । ପଢ଼ ଏବଂ ଶୂନ୍ୟସ୍ଥାନଗୁଡ଼ିକୁ ପୂରଣ କର ।)

Answer:

To celebrate our festival, we wanted to fix the flagpole. We wanted Mahagiri to do this. But he did not do that first time. The mahout forced him to do. But he would not move. The villagers were angry. They shouted at the mahout. Mahagiri was angry. He threw off the flagpole. He also threw off the mahout. They all ran away out of fear. Do you know what Mahagiri did next ? He pulled out a kitten from the hole. What a kind elephant !

Word Note

(The words / phrases have been defined mostly on contextual meanings.)
(ଶବ୍ଦ । ଖଣ୍ଡବାକ୍ୟଗୁଡ଼ିକ ଅଧିକାଂଶତଃ ପ୍ରସଙ୍ଗଗତ ଅର୍ଥ ଉପରେ ନିର୍ଭର କରି ବ୍ୟାଖ୍ୟା କରାଯାଇଛି)
state – ରାଜ୍ୟ
mountain range – ପର୍ବତମାଳା
valleys – ଉପତ୍ୟକା
rivers – ନଦୀଗୁଡ଼ିକ
flow – ପ୍ରବାହ
feet – ପାଦ
plain land – ସମଭୂମି
all around – ଚାରିଆଡ଼େ
thick forest – ଘନ ଜଙ୍ଗଲ
across – ଆରପାରିରେ
special – ସ୍ୱତନ୍ତ୍ର
Guess – | କଳ୍ପନା କରିବା
trainers – ପ୍ରଶିକ୍ଷକ
Timetable – ସମୟ ନିର୍ଘଣ୍ଟ ବା
according to – ଅନୁଯାୟୀ
naughty – ଦୁଷ୍ଟ
baby elephants – ହାତୀ ଛୁଆମାନେ
Learn – ଶିଖନ୍ତୁ |
Example – ଉଦାହରଣ |
out of – ବାହାରକ
salute – ବା ସଲାମ ମାରିବା
Perform – ସମ୍ପାଦନ କରିବା
ring – ବାଜାଲବା
bell – ଘଣ୍ଟି
Offer – ଅର୍ପଣ କରିବା
flowers – ଫୁଲ
God – ଈଶ୍ଵର ବା ଠାକୁର
instructions – ନିର୍ଦ୍ଦେଶାବଳୀ
mainly – ମୁଖ୍ୟତଃ
through – ମଧ୍ୟଦେଇ
praises – ପ୍ରଶଂସା କରିବା
Punishment – ଦଣ୍ଡ ବା ମାଡ଼
food – ଖାଦ୍ୟ
fond of – ପ୍ରିୟ
banana – କଦଳୀ
Sugarcane – ଆଖୁ
Raise – ଟେକି ଧରିବା |
a piece of – ଖଣ୍ଡେ
over – ଉପରକୁ
many a time – ଅନେକ ଥର
in this way – ଏହି ମାର
without giving – ଦାନ ନକରି
act – କାର୍ଯ୍ୟ କରିବା
trained – ତାଲିମପ୍ରାପ୍ତ
demand – ଚାହିଦା |
great – ବହୁତ
shows – ଖୋଲ
Ride – ଚଢ଼ିବା
music – ସଙ୍ଗୀତ
need – ଦରକାର କରିବା
popular – ଜନପ୍ରିୟ
all the more – ପୁନଶ୍ଚ ବା ଅଧୂକନ୍ତୁ
bridegroom – ବରପାତ୍ର
Celebrate – ଉତ୍ସବ ପାଳନ କରିବା
Flagpole – ପତାକା ଦଣ୍ଡ ବା
frightened – ଭୟଭୀତ
instructions – ନିର୍ଦ୍ଦେଶାବଳୀ
mahout – ମହୂତ
Obey – ଆଦେଶ ମାନିବା
shouted and screamed – ବଡ଼ ପାଟି କରୁଥିଲେ ବା ଚିଲେଉଥିଲେ ।

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 7 Continuity and Differentiability Ex 7(m) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Exercise 7(m)

Question 1.
Verify Rolle’s theorem for the function
f(x) = x (x – 2)², 0 ≤ x ≤ 2.
Solution:
f(x) = x (x – 2)², 0 ≤ x ≤ 2
Here a = 0, b = 2
f(x) is a polynomial function hence it is continuous and also differentiable.
∴ f is continuous on [0. 2]
f is differentiable on (0, 2)
f(0) = 0 = f(2)
Thus conditions of Rolle’s theorem are satisfied.
f'(x) = (x – 2)² + 2x (x – 2)
= (x – 2) (x – 2 + 2x)
= (x – 2) (3x – 2)
f'(x)= 0 ⇒ x = 2, x = \(\frac{2}{3}\)
But x = 2 ∉ (0, 2). Thus c = \(\frac{2}{3}\) such that f'(c) = 0
Thus Rolle’s theorem is verified.

Question 2.
Examine if Rolle’s theorem is applicable to the following functions:
(i) f(x) = |x| on [-1, 1]
Solution:
f(x) = |x| on [-1, 1]
As f(x) = |x| is not differentiable at x = 0 ∈ (-1, 1)
We have Rolle’s theorem is not applicable.

(ii) f(x) = [x] on [-1, 1]
Solution:
f(x) = [x] on [-1, 1]
f(x) = [x] is not continuous at 0 ∈ [-1, 1]
Rolle’s theorem is not applicable.

(iii) f(x) = sin x on [0, π]
Solution:
f(x) = sin x on [0, π]
f is a trigonometric function hence continuous and differentiable on its domain.
∴ f is continuous on [0, π]
f is differentiable on (0, π]
f(0) = f(π)
Thus Rolle’s theorem is applicable for f(x) = sin x on [0, π]

(iv) f(x) = cot x on [0, π]
Solution:
f(x) = cot x on [0, π]
Clearly cot (0) and cot (π] are not defined hence Rolle’s theorem is not applicable.

Question 3.
Verify Lagrange’s Mean-Value theorem for
F(x) = x³ – 2x² – x + 3 on [1, 2]
Solution:
f(x) = x³ – 2x² – x + 3 on [1, 2]
f is a polynomial function hence continuous as well as differentiable.
∴ f is continuous on [1, 2]
f is differentiable on (1, 2)
Thus Largange’s mean value theorem is applicable.
Now f(1) = 1 – 2 – 1 + 3 = 1
f(2) = 8 – 8 – 2 + 3 = 1
∴ f(x) = 2x² – 4x – 1

Thus Lagrange’s mean value theorem is verified.

Question 4.
Test if Lagrange’s mean value theorem holds for the functions given in question no. 2.
Solution:
(i) f(x) = |x| is not differentiable at x = 0 ∈ (-1, 1)
Thus Lagrange’s mean value theorem, does not hold.

(ii) f(x) = [x] is discontinuous at 0 ∈ [-1, 1]
Thus Lagrange’s mean value theorem is not applicable.

(iii) f(x) = sin x is a trigonometric function, which is continuous as well as differentiable in its domain.
∴ f is continuous on [0, π]
f is differentiable on (0, π)
Thus conditions of Lagrange’s mean value theorem are satisfied.
Hence mean value theorem is applicable.

(iv) f(x) = cot x
Which is undefined x = 0 and x = π
Thus Lagrange’s mean value theorem is not applicable.

Question 5.
(Not for examination) Verify Cauchy’s mean value theorem for the functions x² and x³
in [1, 2].
Solution:
Let f(x) = x², and g(x) = x³ on [1, 2]
Both f and g are polynomial functions, hence continuous and differentiable.
∴ f and g are continuous on [1, 2]
f and g are differentiable on (1, 2)
g'(x) = 3x² ≠ 0 ∀ x ∈ (1, 2)
Thus conditions of Cauchy’s mean value theorem are satisfied.
Now f(1) = 1, f(2) = 4, g(1) = 1, g(2) = 8
f'(x) = 2, and g'(x) = 3x²

Odisha State Board BSE Odisha 10th Class Hindi Solutions Poem 2 मनुष्यता Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Hindi Solutions Poem 2 मनुष्यता

प्रश्न और अभ्यास (ପ୍ରଶ୍ନ ଔର୍ ଅଭ୍ୟାସ)

1. निम्नलिखित प्रश्नों के उत्तर दो-तीन वाक्यों में दीजिए:
(ନିମ୍ନଲିଖୂ ପ୍ରଶ୍ନୋ କେ ଉତ୍ତର ଦୋ-ତୀନ୍ ୱାଜ୍ୟୋ ମେଁ ଦୀଜିଏ : )
(ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦୁଇ-ତିନୋଟି ବାକ୍ୟରେ ଦିଅ : )

(क) कवि ने कैसी मृत्यु को सुमृत्यु कहा है?
(କବିନେ କୈସୀ ମୃତ୍ୟୁ କୋ ସୁମୃତ୍ୟୁ କହା ହୈ ?)
उत्तर:
जो मरने के बाद भी अमर हो जाएँ, ऐसी मृत्यु को कवि ने सुमृत्यु कहा है। जीवन में जो सत्कर्म छुप छुप है? करता है उसे ही सुमृत्यु मिलता है क्योंकि उसके अच्छे कर्म के कारण उसे सब याद करते हैं। इसलिए जो व्यक्ति दूसरों के काम आता है, वह कभी नहीं मरता

(ख) यहाँ कोई अनाथ नहीं है ऐसा कवि ने क्यों कहा है ?
(ୟହାଁ କୋଈ ଅନାଥ୍ ନହୀ ହୈ ଐସା କବିନେ କ୍ୟା କହା ହୈ ?)
उत्तर:
यहाँ कोई अनाथ नहीं है क्योंकि ईश्वर जो तीनों लोकों के नाथ हैं, वे सदैव सबके साथ होते हैं। वे गरीबों पर दया करनेवाले परम दयालु हैं। वे दीनबंधु हैं। सबकी मदद करने के लिए हमेशा तत्पर रहते हैं।

(ग) ‘मनुष्य मात्र बंधु है’ से आप क्या समझते हैं? स्पष्ट कीजिए।
(‘ମନୁଷ୍ୟ ମାତ୍ର ବନ୍ଧୁ ହୈ’ ସେ ଆପ୍ କ୍ୟା ସମସ୍ତେ ହେଁ ? ସ୍ପଷ୍ଟ କୀଜିଏ। )
उत्तर:
मनुष्य के लिए प्रत्येक मनुष्य बंधु है, परम मित्र है। इसे हमें समझना होगा। यही हमारा विवेक है। एक ही भगवान हम सबके पिता हैं।

2. निम्नलिखित पंक्तियों के भाव दो-तीन वाक्यों में स्पष्ट कीजिए:
(ନିମ୍ନଲିଖତ୍ ପଂକ୍ତିକ୍ଷ୍ନୌ କେ ଭାବ ଦୋ-ତୀନ ୱାର୍କୋ ମେଁ ସ୍ପଷ୍ଟ କୀଜିଏ 🙂
(ନିମ୍ନଲିଖ ପଂକ୍ତିଗୁଡ଼ିକର ଅର୍ଥ ଦୁଇ ତିନୋଟି ବାକ୍ୟରେ ସ୍ପଷ୍ଟ କର ।)

(क) ‘मनुष्य मात्र बंधु है’ यही बड़ा विवेक है,
पुराण पुरुष स्वयंभू पिता प्रसिद्ध एक है॥
‘ମନୁଷ୍ୟ ମାତ୍ର ବନ୍ଧୁ ହୈ ୟହୀ ବଡ଼ ୱିକ ହୈ,
ପୁରାଣ ପୁରୁଷ୍ ସ୍ଵୟଂଭୂ-ପିତା ପ୍ରସିଦ୍ଧ ଏକ୍ ହୈ ॥
उत्तर:
‘मनुष्य मात्र प्रसिद्ध एक है॥
इसमें कवि कहते हैं कि प्रत्येक मनुष्य बंधु है, परममित्र है। इसे हमें समझना चाहिए। यही हमारा विवेक है। एक ही भगवान हम सबके पिता हैं। वे पुराण प्रसिद्ध पुरूष हैं। वे ईश्वर हैं।

(ख) रहो न भूल के कभी मदांध तुच्छ वित्त में।
सनाथ जान आपको करो न गर्व चित्त में॥
ରହୋ ନ ଭୂଲ୍ କେ କଭୀ ସନାଥ୍ ଜାନ ଆପ୍‌ ମଦାନ୍ଧ ତୁଚ୍ଛ ବିତ୍ତ ମେଁ।
(ସନାଥ୍ ଜାନ ଆପ୍‌ କରୋ ନ ଗର୍ବ ଚିଭ୍ ମେଁ ॥)
उत्तर:
रहो न भूल ……………….. गर्व चित्त में॥
कवि कहते हैं कि संपत्ति के लोभ में पड़कर हमें गर्व से इठलाना नहीं चाहिए। अपने मित्र और परिवार आदि लोगों को देखकर भी अपने को बलवान नहीं मानना चाहिए क्योंकि इस संसार में कोई भी अनाथ. या गरीब नहीं होता। अंह भाव मनुष्य की मनुष्यता को नष्ट कर देता है।

3. निम्नलिखित प्रश्नों के उत्तर एक शब्द/एक वाक्य में दीजिए:
(ନିମ୍ନଲିଖୂ ପ୍ରଶ୍ନୋ କେ ଉତ୍ତର୍ ଏକ୍ ଶବ୍ଦ ଏକ୍ ୱାକ୍ୟ ମେଁ ଦୀଜିଏ : )
(ନିମ୍ନଲିଖ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଗୋଟିଏ ଶବ୍ଦ ଗୋଟିଏ ବାକ୍ୟରେ ଦିଅ : )

(क) कवि किससे न डरने की बात कर रहे हैं?
(କଞ୍ଜି କିସ୍‌ ନ ଡର୍‌ନେ କୀ ବାତ୍ କର୍ ରହେ ହୈ ?)
उत्तर:
कवि मृत्यु से न डरने की बात कर रहे हैं।

(ख) कवि कैसी मृत्यु को प्राप्त करने का परामर्श दे रहे हैं?
(କ କୈସୀ ମୃତ୍ୟୁ କୋ ପ୍ରାପ୍ତ କର୍‌ନେ କା ପରାମର୍ଶ ଦେ ରହେ ହୈ ?)
उत्तर:
कवि सुमृत्यु को प्राप्त करने का परामर्श दे रहे हैं।

(ग) कवि मनुष्य की किस पशु प्रवृत्ति की बात कर रहे हैं?
(କ ମନୁଷ୍ୟ କୀ କିସ୍ ପଶୁପ୍ରବୃତ୍ତି କୀ ବାତ୍ କର୍ ରହେ ହୈ ?)
उत्तर:
कवि मनुष्य की, परन्तु जिस प्रकार अपने आप चरते रहते हैं, पशु प्रवृत्ति की बात कर रहे हैं।

(घ) मनुष्य क्या पाकर मदांध हो जाता है?
(ମନୁଷ୍ୟ କ୍ୟା ପାକର୍ ମଦାଦ୍ ହୋ ଜାତା ହୈ ?)
उत्तर:
मनुष्य संपत्ति पाकर मदांध हो जाता है।

(ङ) सनाथ होने का घमण्ड क्यों नहीं करना चाहिए?
(ସନାଥ୍ ହୋନେ କା ଘମଣ୍ଡ୍ କୈ ନହୀ କର୍‌ନା ଚାହିଏ ?)
उत्तर:
सनाथ होने का घमण्ड नहीं करना चाहिए क्योंकि तीनों लोकों के नाथ सदैव सबके साथ रहते हैं।

(च) भाग्यहीन कौन है?
(ଭାଗ୍ୟହୀନ୍ କୌନ୍ ହୈ ?)
उत्तर:
अधीर होकर अंहकारी बन जानेवाला व्यक्ति भाग्यहीन है।

(छ) संसार में मनुष्य का बंधु कौन है?
(ସଂସାର୍ ମେଁ ମନୁଷ୍ୟ କା ବନ୍ଧୁ କୌନ୍ ହୈ ?)
उत्तर:
संसार में मनुष्य का बंधु दीनबंधु यानि ईश्वर है।

(ज) पुराण पुरुष हमारे क्या हैं?
(ପୁରାଣୁ ପୁରୁଷ୍ ହମାରେ କ୍ୟା ହେଁ ?)
उत्तर:
पुराण पुरुष हम सबके पिता हैं।

(झ) वेद किसका प्रमाण देते हैं?
(ବେଦ୍ କିସ୍‌ ପ୍ରମାଣ୍ ଦେତେ ହୈ ?)
उत्तर:
वेद अंतरैक्य अर्थात् अंतर की एकता का प्रमाण देते हैं।

(ञ) कौन बंधु की व्यथा हरण कर सकता है?
(କୌନ୍ ବନ୍ଧୁ କୀ ବ୍ୟଥା ହରଣ କର୍ ସକ୍ତା ହୈ ?)
उत्तर:
बंधु ही बंधु की व्यथा हरण कर सकता है।

भाषा-ज्ञान (ଭାଷା-ଜ୍ଞାନ)

1. उपयुक्त विभक्ति-चिह्नों से शून्य स्थान भरिए:
(ଉପଯୁକ୍ତ ବିଭକ୍ତି ଚିହ୍ନ ପ୍ରୟୋଗ କରି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର : )
(से, में, के, का, को, के, लिए)
(क) फलानुसार कर्म ………………… अवश्य वाह्य भेद हैं।
उत्तर:
के

(ख) वेद अंतरैक्य ……………….. प्रमाण हैं।
उत्तर:
में

(ग) वही मनुष्य है जो मनुष्य ……………….. मरे।
उत्तर:
के लिए

2. निम्नलिखित शब्दों के लिंग बताइए:
(ନିମ୍ନଲିଖତ୍ ଶବ୍ଦା କେ ଲିଙ୍ଗ୍ ବତାଇଏ : )
(ନିମ୍ନଲିଖ୍ ଶବ୍ଦଗୁଡ଼ିକର ଲିଙ୍ଗ ନିରୂପଣ କର : )
प्रवृत्ति, अंतरिक्ष, मृत्यु, विचार, व्यथा, अनर्थ
उत्तर:
प्रवृत्ति – स्रीरिंग
मृत्यु – स्रीलिंग
व्यथा – स्रीलिंग
अंतरिक्ष – पुंलिंग
विचार – पुंलिंग
अनर्थ – पुंलिंग

3. निम्नलिखित शब्दों के प्रयोग से एक-एक वाक्य बनाइए:
(ନିମ୍ନଲିଖ୍ ଶବ୍ଦା କେ ପ୍ରୟୋଗ ସେ ଏକ୍-ଏକ୍ ୱାକ୍ୟ ବନାଇଏ : )
(ନିମ୍ନଲିଖତ ଶବ୍ଦଗୁଡ଼ିକୁ ପ୍ରୟୋଗ କରି ଗୋଟିଏ-ଗୋଟିଏ ବାକ୍ୟ ଗଠନ କର ।)
विवेक, प्रवृत्ति, मर्त्य, बंधु, व्यथा
उत्तर:
विवेक – हमें विवेक से काम लेना है।
प्रवृत्ति – मनुष्य की प्रवृत्ति पशु प्रवृत्ति जैसी नहीं होनी चाहिए।
मर्त्य – मर्त्य में जो भी ज़न्म लेता है, उसको एक न एक दिन अवश्य मरना पड़ता है।
बंधु – ईश्वर गरीबों के बंधु हैं।
व्यथा – मेरे पैर में चोट के कारण व्यथा हो रही है।

Very Short & Objective Type Questions with Answers

A. निम्नलिखित प्रश्नों के उत्तर एक वाक्य में दीजिए।

प्रश्न 1.
‘मनुष्यता’ कविता के रचयिता कौन हैं?
उत्तर:
‘मनुष्यता’ कविता के रचयिता श्री मौथिलीशरण गुप्त हैं।

प्रश्न 2.
कवि गुप्तजी के अनुसार कौन सा कार्य वहुत बड़ा अनर्थ है?
उत्तर:
कबि गुप्तजी के अनुसार एक भाई यदि दूसरे भाई के दुःख को दूर न करे तो यह बड़ा अनर्थ है।

प्रश्न 3.
दयालु दीनबन्धु के विशाल हाथ होने का क्या अर्थ है?
उत्तर:
विशाल हाथ होने का अर्थ है कि ईश्वर अपनी सभी सन्तानों को दुःख में सहायता पहुँचा ही देते हैं।

B. निम्नलिखित प्रश्नों के उत्तर एक शब्द/एक पद में दीजिए।

प्रश्न 1.
कवि के अनुसार कौन साथ होने से कोई अनाथ नहीं हो सकता?
उत्तर:
त्रिलोकनाथ

प्रश्न 2.
मैथिलीशरण गुप्त के अनुसार, अतीव भाग्यहीन कौन है?
उत्तर:
अधीर भाव जो करे

प्रश्न 3.
यहाँ कोई अनाथ क्यों नहीं है?
उत्तर:
क्योंकि सबके साथ त्रिलोकनाथ हैं

प्रश्न 4.
कवि के विचार से मर्त्य में किससे नहीं डरना चाहिए?
उत्तर:
मृत्यु से

प्रश्न 5.
पशु प्रवृत्ति किसे कहते हैं?
उत्तर:
जो आप ही आप चरे

प्रश्न 6.
दयालु दीनबंधु के हाथ कैसा हैं?
उत्तर:
विशाल

प्रश्न 7.
महान मनुष्य किसे कहा जा सकता है?
उत्तर:
जो मनुष्य के लिए मरे

प्रश्न 8.
परमेश्वर किसके पिता है?
उत्तर:
हम सब के

प्रश्न 9.
‘मैथिलीशरण गुप्त’ किस कविता के रचयिता हैं?
उत्तर:
मनुष्यता

प्रश्न 10.
किसका प्रमाण देते है?
उत्तर:
अन्तर की एकता

C. रिक्त स्थानों की पूर्ति कीजिए।

प्रश्न 1.
मनुष्य ……………… पाकर मदांध हो जाता है।
उत्तर:
संपति

प्रश्न 2.
अपने को …………….. जानकर चित्त में गर्व नहीं करना चाहिए।
उत्तर:
सनाथ

प्रश्न 3.
कवि ……………… को प्राप्त होने को कहते हैं।
उत्तर:
सुमृत्यु

प्रश्न 4.
‘आप आप ही चरे’ ………………. प्रवृत्ति है।
उत्तर:
पशु

प्रश्न 5.
‘मनुष्यता’ कविता में मनुष्य को ……………. बनने को कहा गया है।
उत्तर:
महान

प्रश्न 6.
……………….. भाग्यहीन है।
उत्तर:
अहंकारी

प्रश्न 7.
…………… होकर अहंकारी बन जाने वाला व्यक्ति को भाग्यहीन कहा जाता है।
उत्तर:
अधीर

प्रश्न 8.
दुनिया में कोई ………………….. नहीं है?
उत्तर:
अनाथ

प्रश्न 9.
……………… वन्धु की व्यथा हरण कर सकता है।
उत्तर:
वंधु ही

प्रश्न 10.
……………… स्वयंभू है।
उत्तर:
परमात्मा

D. ठिक् या भूल लिखिए।

प्रश्न 1.
भाग्यहीन उसे कहा गया है जो अधीर हो।
उत्तर:
ठिक्

प्रश्न 2.
इस संसार में मनुष्य का बंधु देवता है।
उत्तर:
भूल

प्रश्न 3.
सनाथ होने के बाद भी शर्म नहीं करना चाहिए।
उत्तर:
भूल

प्रश्न 4.
वेद अन्तर की एकता प्रमाण देते हैं।
उत्तर:
ठिक्

प्रश्न 5.
पुराण पुरुष हमारे भाई हैं।
उत्तर:
भूल

प्रश्न 6.
प्रमाणभूत का अर्थ साक्षी है।
उत्तर:
ठिक्

प्रश्न 7.
जो मनुष्य के लिए मरता है, वह महान है।
उत्तर:
ठिक्

प्रश्न 8.
इनसान संपत्ति पाकर विनयी बन जाता है।
उत्तर:
भूल

प्रश्न 9.
अहंकारी व्यक्ति को भाग्यवान कहा गया है।
उत्तर:
भूल

प्रश्न 10.
कवि मृत्यु से न डरने की बात कर रहे हैं।
उत्तर:
ठिक्

Multiple Choice Questions (mcqs) with Answers

सही उत्तर चुनिए : (MCQs)

1. कवि के अनुसार कौन साथ होने से कोई अनाथ नहीं हो सकता?
(A) सच्चा मित्र
(B) विश्वनाथ
(C) अपनी माँ
(D) त्रिलोकनाथ
उत्तर:
(D) त्रिलोकनाथ

2. ‘मनुष्यता’ कविता के कवि हैं
(A) मैथिलीशरण गुप्त
(B) कबीर
(C) रहीम
(D) हरिवंश राय
उत्तर:
(A) मैथिलीशरण गुप्त

3. कवि के विचार से मर्त्य में किससे नहीं डरना चाहिए
(A) तूफान से
(B) तलवार से
(C) मृत्यु से
(D) अहंकार से
उत्तर:
(C) मृत्यु से

4. पशु प्रवृत्ति किसे कहते हैं?
(A) जो दूसरों के लिए मरे
(B) जो आप ही आप चरे
(C) जो साधना करे
(D) इनमें से कोई नहीं
उत्तर:
(B) जो आप ही आप चरे

5. मनुष्य क्या पाकर मदांध हो जाता है?
(A) वित्त
(B) किताबें
(C) यश
(D) चीजें
उत्तर:
(A) वित्त

6. अपने को क्या जानकर चित्त में गर्व नहीं करना चाहिए?
(A) अनाथ
(B) सनाथ
(C) दोनाथ
(D) भोलेनाथ
उत्तर:
(B) सनाथ

7. ‘अतीव भाग्यहीन हैं अधीर भाव जो करे’ – इस पंक्ति में भाग्यहीन है
(A) जो धीर है
(B) जो अधीर है
(C) जो अस्थिर है
(D) जो स्थिर है
उत्तर:
(B) जो अधीर है

8. पुराण पुरुष हमारे क्या हैं?
(A) चाचा
(B) परचाचा
(C) पिता
(D) मामा
उत्तर:
(C) पिता

9. ‘परन्तु अंतरैक्य है’ इसका प्रमाण देता है
(A) ग्रंथ
(B) कचहरी
(C) साक्षी
(D) वेद
उत्तर:
(D) वेद

10. इस संसार में मनुष्य का बंधु है
(A) भगवान
(B) देवता
(C) मनुष्य
(D) मुनि
उत्तर:
(C) मनुष्य

11. दयालु दीनबंधु के हाथ हैं:
(A) छोटे
(B) मोटे
(C) विशाल
(D) वड़े
उत्तर:
(C) विशाल

12. भाग्यहीन उसे कहा गया है जो
(A) धीर हो
(B) अधीर हो
(C) स्थिर हो
(D) व्याकुल हो
उत्तर:
(B) अधीर हो

13. ‘आप आप ही चरे’ कैसी प्रवृत्ति है?
(A) पशु
(B) मनुष्य
(C) राक्षस
(D) देवता
उत्तर:
(A) पशु

14. कवि गुप्त जी के अनुसार किससे डरना नहीं चाहिए?
(A) मृत्यु से
(B) शेर से
(C) शिक्षक से.
(D) रात से
उत्तर:
(A) मृत्यु से

15. वेद किसका प्रमाण देते हैं ?
(A) अन्तर की एकता
(B) वाहर की एकता
(C) बन्धु की एकता
(D) ग्रन्थ की एकता
उत्तर:
(A) अन्तर की एकता

यह कविता (ଏହି କବିତା)

इस कविता में मनुष्य को महान बनने की प्रेरणा दी गई है। कवि कहते हैं कि जिसने इस धरा पर जन्म लिया है, एक न एक दिन अवश्य मरेगा। इसलिए हमें कभी मृत्यु से नहीं डरना चाहिए। हम ऐसे मरे कि ने के बाद भी अमर हो जाएँ। यदि हम जीवन भर सत्कर्म नहीं करेंगे तो हमें अच्छी मृत्यु नहीं मिलेगी अर्थात् मरने के बाद कोई याद नहीं रखेगा। जो व्यक्ति दूसरों के काम आता है वह कभी मरता नहीं है। क्योंकि वह कभी भी अपने लिए नहीं जीता है। पशु जिस प्रकार अपने आप चरते रहते हैं उसी तरह की प्रवृत्ति मनुष्य में भी कई बार दिखाई देती है जो ठीक नहीं है।

मनुष्य को तो मनुष्य की मदद करने में प्राण दे देना चाहिए। संपत्ति के लोभ में पड़कर हमें गर्व से नहीं इठलाना चाहिए। कुछ अपने मित्र और परिवार आदि लोगों को देखकर भी अपने को बलवान नहीं मानना चाहिए क्योंकि इस संसार में कोई भी अनाथ या गरीब नहीं होता। यहाँ कोई भी अनाथ नहीं हो सकता क्योंकि ईश्वर जो तीनों लोकों के नाथ हैं, वे सदा सबके साथ रहते हैं। क्योंकि ईश्वर दीनबंधु हैं। गरीबों पर दया करने वाले भी हैं परम दयालु हैं। विशाल हाथ वाले हैं अर्थात् वे सबकी मदद करने के लिए सदा तत्पर रहते हैं।

जो अधीर होकर अहंकारी बन जाते हैं वे तो सच में भाग्यहीन हैं। मनुष्य तो वही है जो मनुष्य की सेवा करे और उसके लिए मरे। मनुष्य के लिए प्रत्येक मनुष्य बंधु है, परम मित्र है। इसे हमें समझना होगा। यही हमारा विवेक है। एक ही भगवान हम सब के पिता हैं। वे पुरातन प्रसिद्ध पुरुष हैं। वे ईश्वर हैं। यह तो सत्य है कि हमें अपने कर्मों के अनुरूप फल भोगना होता है। इसलिए बाहरी तौर पर हम भले ही अलग अलग दिखाई देते हैं पर अंदर से एक हैं। हममें अन्तर की एकता है। वेद ऐसा ही कहते हैं। समाज में अनर्थ तब होता है जब मनुष्य दूसरे को अपना बंधु नहीं मानता। मनुष्य को ही मनुष्य की पीड़ा को दूर करना होगा । इसलिए सही माईने में मनुष्य वह है जो मनुष्य के लिए मरता है।

ଏହି କବିତା:
ଏହି କବିତା ରେ ମଣିଷକୁ ମହାନ୍ ହେବାପାଇଁ ପ୍ରେରଣା ଦିଆଯାଇଅଛି। କବି କହୁଛନ୍ତି ଯିଏ ଏହି ପୃଥ‌ିବୀ ପୃଷ୍ଠରେ ଜନ୍ମ ନେଇଛନ୍ତି, ଦିନେ ନା ଦିନେ ତା’ର ମୃତ୍ୟୁ ସୁନିଶ୍ଚିତ। ଏଣୁ ଆମେ କେବେହେଲେ ମୃତ୍ୟୁକୁ ଭୟ କରିବା ନାହିଁ। ଆମେ ଏପରି ଭାବେ ମରିବା ଯେପରି ମୃତ୍ୟୁ ପରେ ମଧ୍ୟ ଅମର ହୋଇ ରହିବା। ଯଦି ଆମେ ସତ୍‌କର୍ମ ନ କରିବା ତାହାହେଲେ ଆମକୁ ଭଲ ମରଣ ମିଳିବ ନାହିଁ ଅର୍ଥାତ୍‌ ମଲାପରେ କେହି ଆମକୁ ମନେରଖିବେ ନାହିଁ। ଯେଉଁ ବ୍ୟକ୍ତି ଅନ୍ୟର କାମରେ ଆସେ ସେ କେବେ ମରେ ନାହିଁ, ଯେହେତୁ ସେ କେବେହେଲେ ନିଜ ପାଇଁ ବଞ୍ଚେ ନାହିଁ। ପଶୁ ଯେପରି ଆପଣା
ସାହାଯ୍ୟ କରିବାପାଇଁ ଜୀବନ ଉତ୍ସର୍ଗ କରିବା ଦରକାର।

ବଳବାନ୍ ବୋଲି ଭାବିବା ଠିକ୍ ନୁହେଁ, ଯେହେତୁ ଏହି ସଂସାରରେ କେହି ଅନାଥ ବା ଗରିବ ନୁହଁନ୍ତି। ଏଠାରେ କେହି ଅନାଥ ହୋଇପାରେନା ଯେହେତୁ ଈଶ୍ଵର ତ୍ରିଲୋକର ସ୍ବାମୀ, ସେ ସବୁବେଳେ ସମସ୍ତଙ୍କ ସାଙ୍ଗରେ ରୁହନ୍ତି। ଈଶ୍ଵର ଦୀନବନ୍ଧୁ ଅଟନ୍ତି। ଗରିବମାନଙ୍କୁ ଦୟା କରୁଥିବା ଲୋକ ମଧ୍ୟ ପରମ ଦୟାଳୁ । ସେ ସବୁବେଳେ ସମସ୍ତଙ୍କୁ ସାହାଯ୍ୟ କରିବାକୁ ମଣିଷର ସେବା କରିଥାଏ ଏବଂ ମଣିଷ ପାଇଁ ମରିଥାଏ । ମଣିଷ ପାଇଁ ପ୍ରତ୍ୟେକ ମଣିଷ ବନ୍ଧୁ ଓ ପରମ ମିତ୍ର ଅଟେ । ଏହା ଆମକୁ ବୁଝିବାକୁ ହେବ। ଏହା ଆମର ବିବେକ।

ସେ ଜଣକ ହିଁ ଆମର ପିତା। ସେ ପ୍ରସିଦ୍ଧ ପୁରୁଷ ଅଟନ୍ତି। ସେ ହିଁ ଈଶ୍ଵର। ଏହା ସତ୍ୟ ଯେ ଆମକୁ ଆମର କର୍ମ ଅନୁସାରେ ହିଁ ଫଳ ମିଳିଥାଏ। ବାହାରକୁ ଆମେ ସଭିଏଁ ଅଲଗା ଅଲଗା ଦେଖାଯାଉଥିଲେ ମଧ୍ୟ ଭିତରେ ଆମେ ସଭିଏଁ ଏକ। ସମାଜରେ ଅନର୍ଥ ସେତେବେଳେ ଉପୁଜେ ଯେତେବେଳେ ମଣିଷ ଅନ୍ୟକୁ ନିଜର ବନ୍ଧୁ ବୋଲି ଭାବେ ନାହିଁ, ମଣିଷକୁ ହିଁ ମଣିଷର ଦୁଃଖ ଦୂର କରିବାକୁ ହେବ। ଏଣୁ ପ୍ରକୃତ ଅର୍ଥରେ ମଣିଷ ସେହି ଯିଏ ମଣିଷ ପାଇଁ ମରେ।

विचार लो कि मर्त्य हो न मृत्यु से डरो कभी,
मरो परंतु यों करो कि याद जो करें सभी।
हुई न यों सुमृत्यु तो वृथा मरे, वृथा जिए,
मरा नहीं वही कि जो जिया न आपके लिए।
वही पशु प्रवृत्ति है कि आप आप ही चरे,
वही मनुष्य है कि जो मनुष्य के लिए मरे।।

हिन्दी व्याख्या:
कवि कहते हैं कि जिसने इस धरा पर जन्म लिया है, वह एक न एक दिन अवश्य मरेगा। इसलिए मृत्यु से कभी डरना नहीं चाहिए, हमारी मृत्यु ऐसी हो कि मरने के बाद भी हम अमर होकर रहें। इसके लिए हमें जीवन में सुकर्म करना होगा, वरना मरने के बाद कोई भी हमें याद नहीं रखेगा। जो व्यक्ति दूसरों के काम आता है, वह कभी भी नहीं मरता। क्योंकि कभी भी अपने लिए जीता ही नहीं। पशु जिस प्रकार अपने आप चरते रहते हैं, उसीप्रकार की प्रवृत्ति मनुष्य में भी कई बार दिखाई देती है जो ठीक नहीं है। मनुष्य को हमेशा मनुष्य की मदद करने में प्राण दे देना चाहिए।

କବିଙ୍କ ମତ ଅନୁସାରେ ଜନ୍ମ ମୃତ୍ୟୁ ଚିରନ୍ତନ ସତ୍ୟ। ଏହି ଧରାଧାମରେ ଯିଏ ଜନ୍ମ ନେଇଛି, ତେଣୁ ଆମେ ମୃତ୍ୟୁକୁ ଭୟ କରିବା ଉଚିତ ନୁହେଁ। ଜୀବନସାରା ଏପରି କାମ ରହିବ। ଅର୍ଥାତ୍ ସତ୍ କର୍ମ କରି ଅମର ରହିବା। ଯଦି କୁକର୍ମ କରିବା ତେବେ ପରେ ଆମକୁ କେହି ମନେ ରଖୁବେ ନାହିଁ। ପଶୁ ଯେପରି ଆପଣା ଛାଏଁ ଭିତରେ ମଧ୍ୟ ଅନେକ ଥର ଦେଖାଯାଏ ଯାହା ଠିକ୍ ନୁହେଁ। ମଣିଷକୁ ମଣିଷ ସାହାଯ୍ୟ ଦିନେ ନା ଦିନେ ତା’ର ମୃତ୍ୟୁ ସୁନିଶ୍ଚିତ। କରିବା ତାହା ମୃତ୍ୟୁ ପରେ ଅମର ହୋଇ ଆମକୁ ଭଲ ମରଣ ହେବ ନାହିଁ। ମୃତ୍ୟୁ ମରିଥା’ନ୍ତି ସେହିପରି ପ୍ରବୃତ୍ତି ମନୁଷ୍ୟ

(ii) रहो न भूल के कभी मदांध तुच्छ वित्त सें,
सनाथ जान आपको करो न गर्व चित्त में।
अनाथ कौन है यहाँ ? त्रिलोकनाथ साथ हैं,
दयालु दीनबंधु के बड़े विशाल हाथ हैं।
अतीव भाग्यहीन हैं अधीर भाव जो करे,
वही मनुष्य है कि जो मनुष्य के लिए मरे॥

हिन्दी व्याख्या:
कवि कहते हैं कि संपत्ति के लोभ में पड़कर हमें गर्व से इठलाना नहीं चाहिए। मित्र और परिवार आदि लोगों को देखकर कभी भी अपने को बलवान नहीं मानना चाहिए क्योंकि इस संसार कोई भी अनाथ या गरीब नहीं होता। ईश्वर जो तीनों लोकों के नाथ हैं, वे सदैव हमारे साथ रहते हैं। वे दीनबंधु हैं। गरीबों पर दया करनेवाले परम दयालु हैं। वे विशाल हाथ वाले हैं और सबकी मदद करने के लिए सदैव तत्पर रहते हैं। जो अधीर होकर अहंकारी बन जाते हैं वे तो वास्तव में भाग्यहीन हैं। मनुष्य वही है जो मनुष्य की सेवा करे और उसके लिए मरे।

ଓଡ଼ିଆ ଅନୁବାଦ:
ଧନ ଲୋଭରେ ପଡ଼ି ଆମେ ଗର୍ବ କରିବା ଠିକ୍ ନୁହେଁ। ନିଜ ପରିବାରବର୍ଗ ଓ ମିତ୍ରକୁ ଦେଖୁ କରି ନିଜକୁ ବଳବାନ ବୋଲି ଭାବିବା ଅନୁଚିତ। କାରଣ ଏହି ସଂସାରରେ କେହି ଗରିବ ବା ଅନାଥ ନୁହଁନ୍ତି। ଏହି ବ୍ୟକ୍ତି ପରମ ଦୟାଳୁ। ଯେ ଅଧର ହୋଇ ଅହଂକାରୀ ହୋଇଯାଏ ସେ ବାସ୍ତବରେ ଭାଗ୍ୟହୀନ ଅଟନ୍ତି। ମଣିଷ ସେହି ଅଟନ୍ତି ଯେ ମଣିଷର ସେବା କରିଥାଏ ଏବଂ ମଣିଷ ପାଇଁ ଜୀବନ ହାରିଥାଏ।

(iii) ‘मनुष्य मात्र बंधु है, यही बड़ा विवेक है,
पुराण पुरुष स्वयं पिता प्रसिद्ध एक है।
फलानुसार कर्म के अवश्य बाह्य भेद हैं।
परंतु अंतरैक्य में प्रमाणभूत वेद हैं।
अनर्थ है कि बंधु ही न बंधु की व्यथा हरे;
वही मनुष्य है कि जो मनुष्य के लिए मरे।।

हिन्दी व्याख्या:
इसमें कवि कहते हैं कि मनुष्य के लिए प्रत्येक मनुष्य बंधु है, परम मित्र है। इसे हमें समझाना चाहिए। यही हमारा विवेक है। एक ही भगवान हम सबके पिता हैं। वे स्वयं पुराण प्रसिद्ध पुरुष हैं। इस संसार में हमें अपने कर्मों के अनुसार फल मिलता है। इसलिए बाहरी तौर पर हम भले ही अलग-अलग दिखाई देते हैं पर अंदर से एक हैं। हम में अन्तर की एकता है। वेद में ऐसा कहा गया है। समाज में अनर्थ उस समय होता है जब मनुष्य दूसरे को अपना बंधु नहीं मानता है। मनुष्य को ही मनुष्य की पीड़ा को दूर करना होगा। सही अर्थ में मनुष्य वही होता है जो मनुष्य के लिए मरता है।

ଓଡ଼ିଆ ଅନୁବାଦ:
କବିଙ୍କ ମତରେ ମଣିଷ ପାଇଁ ପ୍ରତ୍ୟେକ ମଣିଷ ବନ୍ଧୁ ଓ ପରମ ମିତ୍ର ଅଟେ। ଏହା ଆମକୁ ବୁଝିବାକୁ ହେବ, ଏହାହିଁ ବିବେକ। ଏହା ମଧ୍ୟ ସତ୍ୟ ଯେ ଆମକୁ ଆମର କର୍ମ ଅନୁଯାୟୀ ଫଳ ମିଳିଥାଏ। ଆମେ ସଭିଏଁ ବାହାରକୁ ଅଲଗା-ଅଲଗା ଦେଖାଯାଉଥିଲେ ମଧ୍ୟ ଭିତରେ ସମସ୍ତେ ଏକ ଅଛନ୍ତି। ଯେତେବେଳେ ମଣିଷ ଅନ୍ୟକୁ ନିଜର ବୋଲି ଭାବେ ନାହିଁ, ସେହି ସମୟରେ ସମାଜରେ ଅନେକ ଅନର୍ଥ ସୃଷ୍ଟି ହୁଏ। ମଣିଷକୁ ହିଁ ମଣିଷର ଦୁଃଖ ଲାଘବ କରିବାକୁ ହେବ। ପ୍ରକୃତ ଅର୍ଥରେ ମଣିଷ ସେହି ଯିଏ ମଣିଷ ପାଇଁ ଜୀବନ ଦେଇଥାଏ।

शबनार: (ଶରାର୍ଥି)

मर्त्य धरा/पृथ्वी (ପୃଥବୀ)।

परंतु – किन्तु (ପରନ୍ତୁ )।

मदांध – गर्व से अंध (ଗର୍ବରେ ଅନ୍ଧ)।

आप – खुद (ନିଜେ)।

चित्त – मन (ମନ )।

दीनबंधु – ईश्वर (ଦୀନଙ୍କ ବନ୍ଧୁ )।

अतीव – अत्यन्त (ଅଧ୍ଵ )।

प्रमाणभूत- साक्षी (ସାକ୍ଷୀ)।

बाहूय – बाहारी (ବାହାର )।

पशु प्रवृत्ति – पशु जैसा स्वभाव (ପଶୁ ପରି ସ୍ବଭାବ)।

याद – स्मरण (ମନେପକାଇବା)।

प्रवृत्ति – प्रकृति (ପ୍ରକୃତି )।

वित्त – संपत्ति (ସମ୍ପତ୍ତି)।

सनाथ – परिजन का होत (ସପରିବାର )।

अंतरैक्य – आत्मा की एकता (ଆତ୍ମାର ଏକତା)।

स्वयं – खुद (ନିଜେ )।

व्यथा – कष्ट (କଷ୍ଟ)।

कवि परिचय

मैथिली शरण गुप्त का जन्म चिरगाँव झाँसी में सन् 1886 में हुआ था। उनकी पढ़ाई घर पर ही हुई। उन्होंने हिन्दी के अलावा संस्कृत, बंगला, मराठी और अँग्रेजी में भी अच्छा ज्ञान प्राप्त किया। बचपन से ही वे कविता लिखने लगे थे। अपने जीवन काल में ही वे राष्ट्रकवि के नाम से प्रसिद्ध हुए। गुप्तजी का परिवार रामभक्त था। उन्होंने भारतीय जीवन के आदर्श, इतिहास और संस्कृति को अपने काव्य का आदर्श बनाया। स्नेह, प्रेम, दया, उदारता आदि मानवीय भावों को भी साहित्य के माध्यम से उजागर किया।